Multiple Ion Binding Equilibria, Reaction Kinetics, and Thermodynamics in Dynamic Models of Biochemical Pathways

Abstract

The operation of biochemical systems in vivo and in vitro is strongly influenced by complex interactions between biochemical reactants and ions such as H⁺, Mg²⁺, K⁺, and Ca²⁺. These are important second messengers in metabolic and signaling pathways that directly influence the kinetics and thermodynamics of biochemical systems. Herein we describe the biophysical theory and computational methods to account for multiple ion binding to biochemical reactants and demonstrate the crucial effects of ion binding on biochemical reaction kinetics and thermodynamics. In simulations of realistic systems, the concentrations of these ions change with time due to dynamic buffering and competitive binding. In turn, the effective thermodynamic properties vary as functions of cation concentrations and important environmental variables such as temperature and overall ionic strength. Physically realistic simulations of biochemical systems require incorporating all of these phenomena into a coherent mathematical description. Several applications to physiological systems are demonstrated based on this coherent simulation framework.

1. Introduction

1.1. The physicochemical basis of biology

It is essential that modern research in biology and biomedical science, which is increasingly focused on gaining quantitative understanding of the behavior of biochemical systems, be grounded in the physical chemical principles that govern the organization and behavior of matter. In particular, it is crucial to recognize that living systems, which continuously transport and transform material and transduce free energy among chemical, electrical, and mechanical forms, operate in nonequilibrium thermodynamic states. Thus effective characterization of the operation of living systems, through quantitative analysis and computational simulation, must account for the chemical thermodynamics of such systems. From this perspective, a useful characterization of a biological network includes an investigation and appreciation of its thermodynamic properties. Similarly, a realistic simulation of a biological system must be constrained to operate in a thermodynamically feasible manner.

1.2. Basic principles of chemical thermodynamics

The basic laws of thermodynamics are familiar to most readers. The two laws most relevant to systems biology may be stated as follow. (1) Energy is neither created nor destroyed; a net change in energy of a system must be due to a net transport of energy in or out. (2) In systems away from equilibrium, entropy is produced and never consumed; entropy may decrease only if the rate of export exceeds the rate of import.

By the second law, isolated systems move naturally in the direction of increasing entropy, always heading toward a thermodynamic equilibrium where the entropy is maximized. Yet biological systems are not isolated and, in the context of biology, equilibrium can be equated with death. Thus increasing entropy does not provide a gauge to predict or constrain the operation of biological systems that exchange material and energy with their environment. For such systems the concept of free energy provides a useful metric for describing thermodynamic status.

Various forms of free energy are defined for various sorts of systems. The most useful form of free energy for biological systems is Gibbs free energy, which is defined

$$G=E+PV-TS,$$ (2.1)

where E, P, V, T, and S, are the internal energy, pressure, volume, temperature, and entropy of the system. Gibbs free energy is a useful metric for biological systems because it can be shown that systems without import or export of chemical substances, held at constant pressure and temperature, spontaneously move down the gradient in G (Beard and Qian, 2008b).

For a chemical reaction in dilute solution the change in Gibbs free energy per number of times the reaction turns over is given by the well-known formula (Alberty, 2003; Beard and Qian, 2008b)

$${\mathrm{\Delta }}_{r}G={\mathrm{\Delta }}_r{G}^o+RT\sum _{i=1}^{N_s}{\upsilon }_{i}ln(C_i/C_o),$$ (2.2)

where Δ_rG^o is the equilibrium free energy for the reaction, which does not depend on the concentrations of the chemical components, R is the gas constant, T is the absolute temperature, υ_i is the stoichiometric number of species i for the reaction, C_i is the concentration of species I, and C_o is the reference concentration, taken to be 1 M. The summation in Eq. (2.2) is over all species in the system; N_s is the number of species.

The equilibrium free energy for a reaction may be computed based on the values of free energy of formation, ${\mathrm{\Delta }}_f{G}_i^o$, for the species involved in a reaction:

$${\mathrm{\Delta }}_r{G}^o=\sum _{i=1}^{N_s}{\mathrm{\Delta }}_f{G}_i^o.$$ (2.3)

The value of ${\mathrm{\Delta }}_f{G}_i^o$ for a given species depends on the environmental conditions, most notably temperature, pressure, and the ionic solution strength, as discussed later. Chemical equilibrium is achieved when the driving force for the reaction Δ_rG goes to zero. Equilibrium yields

$$\begin{array}{l}-\frac{{\mathrm{\Delta }}_r{G}^o}{R\text{T}}=\sum _{i=1}^{N_s}{\upsilon }_{i}ln(C_i/C_o)=ln\prod _{i=1}^{N_s}{(C_i/C_o)}^{{\upsilon }_i}\\ exp\left(-\frac{{\mathrm{\Delta }}_r{G}^o}{R\text{T}}\right)=K_{eq}=\prod _{i=1}^{N_s}{(C_i/C_o)}^{{\upsilon }_i},\end{array}$$ (2.4)

where K_eq is the equilibrium constant for the reaction.

1.3. Simulating biochemical systems

In living systems operating away from equilibrium, each chemical process (including reactions and transport processes) obeys the following relationship between flux and free energy:

$$J^{+}/J^{-}=e^{-\mathrm{\Delta }G/R\text{T}},$$ (2.5)

where J = J⁺ − J⁻ is the net flux for the process and J⁺ and J⁻ are the forward and reverse fluxes. For example, for an enzyme-catalyzed reaction, J⁺ and J⁻ are the forward and reverse rates of turnover for the enzyme’s catalytic cycle.

Equation (2.5) reveals that nonzero net flux occurs only when the free energy change for a given process is nonzero. Also, it is apparent that the quantity

$$-\mathrm{\Delta }G·J=\mathit{RT}ln(J^{+}/J^{-})·(J^{+}-J^{-})$$ (2.6)

is always positive. In fact, −ΔG·J is the process’s rate of free energy dissipation. Thus it follows that systems maintained away from equilibrium dissipate free energy. Dissipation of free energy is a hallmark of nonequilibrium systems and thus a hallmark of life.

At the center of our biochemical systems modeling approach is an explicit accounting of the fact that biochemical reactants (e.g., ATP) exist in solution as a number of rapidly interconverting species (e.g., ATP⁴⁻, HATP³⁻, MgATP²⁻, and KATP³⁻)(Beard and Qian, 2008a, c). Accounting for all of these species for systems composed of many (tens to hundreds) of reactants is theoretically straightforward, but practically messy. Notably, Wu and colleagues (2007b) have detailed how a model of nontrivial complexity is constructed. However, before going into computational details, the following list is a number of benefits of accounting for this level of chemical detail in biochemical systems simulation.

1. Nonambiguous meaning. By tracking the species-level distribution of biochemical reactants, model variables have a nonambiguous physical meaning. Because species participate in enzyme-catalyzed reactions, a species-level model allows us to represent chemical reactions with greater physical realism than is possible when the species distributions of reactants are not calculated. By expressing enzyme mechanisms in terms of species, changes in apparent kinetic properties brought on by changes in pH and ion concentration are handled explicitly. More details on this point are provided in Section 2.5 and in Beard et al. (2008).

2. Nonambiguous integration. In biosystems modeling it is common to track certain species but not others. For example, some models of cellular energetics account for Mg²⁺-bound and -unbound ATP (Korzeniewski, 2001; Vendelin et al., 2000, 2004). However, in these cases the unbound state is a mixture of many states. Other modeling applications may be based on treating all reactants, including ATP, as the total sum of species (Zhou et al., 2005). As a result, there is often not one unique way to integrate models that simulate different components of a larger system. By imposing a formalism where model variables have nonambiguous meaning this problem of nonuniqueness is resolved.

3. Resulting models are thermodynamically feasible. By computing species distribution of reactants, we can track how changes in pH and cationic concentrations affect overall thermodynamic driving forces and ensure that these changes are handled by our models. Thus simulation at this level of detail ensures thermodynamically validity, an important requirement for model reliability.

4. Model uncertainty is reduced. One might imagine that imposing the level of detail outlined previously may introduce unnecessary complexity and increase the number of unknown parameters into biochemical systems models. However, the opposite is true when ionic dissociation constants and basic thermodynamic data are available for the reactions and reactants in a given model. The thermodynamic and dissociation data constrain the enzyme mechanisms and reduce the number of adjustable parameters necessary to describe their behavior.

   In addition to these practical advantages related to model building and identification, the major advantage is scientific.

5. Model reliability is improved. We have greater confidence in the behavior predicted by physically grounded models than in models that invoke phenomenological descriptions of components or in models that do not account for chemical species distribution and/or biochemical thermodynamics. This is particularly important when using models to predict behavior outside of the operational regime of the data set(s) used for parameterization and validation.

2. Biochemical Conventions and Calculations

Equation (2.2) is the formula for Gibbs free energy for a chemical reaction. However, biochemical reactions are not typically expressed as mass-and charge-balanced chemical reactions Alberty (2003).

2.1. Thermodynamics of biochemical reactions

Metabolites in intracellular milieu exist as protonated, metal ion bound and free unbound forms described by ionic equilibria in solution with multiple cations. Each metabolite concentration is therefore described as a sum of its individual constituent species concentrations computed by ionic equilibria principles. A biochemical reaction involves sums of species on both the reactant and the product sides, which results in each reaction having effective proton and metal ion stoichiometries due to binding changes across the biochemical reaction. The proton generation stoichiometry of a biochemical reaction is the total difference of average proton binding between the reactants and the products, plus the proton generation stoichiometry of the reaction defined in terms of its most unbound species in the pH range of interest, also known as the reference reaction. The apparent equilibrium constant of a biochemical reaction defined in terms of sums of species for each metabolite therefore depends on proton and metal binding of the reactants and products.

Alberty developed these concepts in terms of transformed variables by using Legendre transforms to gain a global view of biochemical systems by treating pH and free magnesium ion concentrations as independent variables. Fundamental principles underlying this work are reviewed in Alberty (2004). More detailed treatment of this subject matter and basic biochemical data and calculations are given in Alberty (2003). Vinnakota et al. (2006) extended the application of concepts developed by Alberty to a system with finite buffer capacity and variable pH. The pH variation itself is computed from proton binding changes in each of the biochemical reactions. Using mass balance constraint for protons and Mg²⁺ ions, we applied these concepts to compute a pH time course while accounting for pH, Mg²⁺, and K⁺ effects on kinetics and thermodynamics of the reactions. The methodology in Vinnakota et al. (2006) was extended and improved by Wu et al. (2007b) and Beard and Qian (2008a) to account for more metal ions and was applied to coupled electrophysiological and metabolic systems.

During the past decade, tables of fundamental biochemical data have been generated by Alberty (2003), which enabled the computation of standard free energies of many biochemical reactions in terms of their reference species and therefore their apparent equilibrium constants at specified pH and metal ion concentrations. The methods presented here demonstrate that the thermodynamic analysis and the biochemical network representation are unified through proton and other metal ion mass balance constraints.

2.2. Enzyme kinetics and the Haldane constraint

Thermodynamic analyses predict equilibria for pathways at specified pH, temperature, ionic strength, ion concentrations, and cofactor concentrations. However, this gives only part of the picture, because the kinetics govern the dynamics of approach of biochemical systems to these equilibria in a closed system and in an open system the combined effect of kinetics constrained by thermodynamics govern the fluxes and the metabolite transients. Likewise, kinetic models with inappropriate thermodynamic constraints will not yield a realistic prediction of fluxes and concentrations, as the apparent equilibrium constant can change by orders of magnitude per unit pH depending on the proton stoichiometry of the biochemical reaction. These two approaches can be combined by incorporating the apparent equilibrium constant computed by biochemical thermodynamic principles into the Haldane relationship, which relates the forward and reverse maximal velocities of the enzyme kinetic flux. This unified approach combining both kinetics and thermodynamics is applied in Vinnakota et al. (2006), Wu et al. (2007b, 2008), and Beard and Qian (2008a). Alberty (2006) has demonstrated that the overall apparent equilibrium constant of a biochemical reaction is independent of the internal enzyme kinetic mechanisms for simple enzyme kinetic mechanisms.

While the study of the catalytic kinetics of enzymes represents one of the most established and well-documented fields in biochemical research, the impact of the biochemical state (pH, ionic strength, temperature, and certain cation concentrations) is typically not formally accounted for in kinetic studies (Alberty, 1993, 2006). In vitro experiments using purified proteins and controlled substrate concentrations to characterize enzyme kinetics are conducted under conditions that do not necessarily match the physiological environment, but are determined based on a number of factors, including the requirements of the assays used to measure the kinetics. Therefore, it is difficult to compare results obtained from different studies and to use available kinetic data to predict in vivo function without ambiguity.

Outlining these and other issues in somewhat greater detail, the following specific challenges associated with interpreting in vitro kinetic data must be overcome to make optimal use of them.

1. While a great deal of high-quality data may be available for a particular enzyme, much of these data were obtained in the 1960s and 1970s when tools for proper analysis of data were not available. As a result, the reported kinetic parameter values [typically obtained from double reciprocal plots of inverse flux versus inverse substrate (Lineweaver and Burk, 1934)] may not optimally match reported data.

2. Data on biochemical kinetics are typically obtained under nonphysiological pH and ionic conditions. Therefore the reported kinetic constants must be corrected to apply to simulations of physiological systems.

3. A third problem related to the second is that kinetic constants are associated with apparent mechanisms that operate on biochemical reactants, which are sums of biochemical species (Alberty, 1993). The result is that the reported mechanisms and associated parameter values are dependent on the biochemical state and not easily translated to apply to different biochemical states or to simulations in which the biochemical state changes.

4. The reported kinetic mechanisms and parameters are often not constrained to match thermodynamic data for a given reaction. Since the basic thermodynamics of a given reaction is typically characterized with greater precision than the kinetics of an enzyme catalyzing the reaction, putative kinetic mechanisms should be constrained to match the biochemical reaction thermodynamics.

A study on citrate synthase addressed and corrected these problems by posing reaction mechanisms in terms of species and ensuring that mechanisms properly account for thermodynamics. This basic approach was first introduced by Frieden and Alberty (1955), yet has received little attention. By reanalyzing legacy data from a variety of sources of kinetic data on citrate synthase, for example, we are able to show that data used to support the consensus model of the mechanism for this enzyme (random bi-bi mechanism) are all consistent with the compulsory-order ternary-complex mechanism and not consistent with the random bi-bi model (Beard et al., 2008).

2.3. Multiple cation equilibria in solutions: Apparent equilibrium constant, buffering of cations, and computing time courses of cations as a consequence of biochemical reaction networks

Most metabolites in physiological milieu are anionic and bind to H⁺, Mg²⁺, K⁺, and Ca²⁺ ions in rapid equilibrium. To compute the distribution of a metabolite into ion bound and unbound species, we choose as a reference form the species with no dissociable protons or metal ions in the pH range of 5–9 for physiological models. Based on this definition, the following steps and calculations are needed to account for H⁺ and metal cation binding to metabolites, buffer capacity and pH change, and the effects of these parameters on reaction equilibria.

1. Based on binding equilibria, the total concentration of a biochemical reactant is defined in terms of its reference species concentration and the free concentrations of ions and their binding affinities.

2. On the basis of the definition of reference and biochemical reactions, the reference and apparent equilibrium constants of each biochemical reaction are computed. The apparent equilibrium constant is a function of the reference equilibrium constant and the binding polynomials of the reactants and the products. The apparent equilibrium constant constrains the enzyme kinetic flux through the Haldane relationship.

3. The flux through each biochemical reaction is derived on the basis of a detailed catalytic scheme. The reference reaction is balanced with respect to mass and charge and has a reference proton stoichiometry.

4. The coupled differential equations for ion and biochemical reactant concentrations are integrated to simulate the system dynamics.

2.3.1. Calculation of proton binding fraction for each metabolite using multiple cation equilibria

A biochemical reactant in physiological milieu exists in different ion bound species in rapid equilibrium. These ions include H⁺, Mg²⁺, K⁺, and other cations. Multiple cation equilibria principles are used to describe the distribution of each biochemical reactant in various ion bound species. For example, the reactant phosphocreatine (PCr) will exist in the following forms:

$$[{\text{PCr}}_{\mathit{total}}]=[{\text{HPCr}}^{2-}]+[{\text{H}}_2{\text{PCr}}^{-}]+[\text{MgHPCr}]+[{\text{KHPCr}}^{-}].$$ (2.7)

Each ion bound species is in turn computed in terms of an equilibrium relationship between the most unbound form of the reactant and the metal ion that it binds to. Detailed examples are provided in Sections 2.4 and 2.5. Table 2.1 defines the conventions and nomenclature used in our biochemical models.

Table 2.1.

Terminology

Symbol	Definition	Unit
I	Ionic strength	M
Ka,l	Dissociation constant for the lth protonation reaction	M
pKal	−log10 (Ka,l/c0)	Dimensionless
KM,m	Dissociation constant for metabolite binding to metal M	M
pKaM,m	−log10 (KM,m/c0)	Dimensionless
c0	Reference concentration for all species (1 M)	M
Pi	Binding polynomial for ith metabolite	Dimensionless
${\overline{N}}_H^i$	Average proton binding of ith metabolite at specified T, P, pH, pMg, and I	Dimensionless, noninteger
nk	Proton generation stoichiometry of the kth reference reaction	Dimensionless
${\mathrm{\Delta }}_r{N}_H^k$	Proton generation stoichiometry of the kth biochemical reaction at specified T, P, pH, pMg, and I	Dimensionless, noninteger
NH(j)	Number of H atoms in species j	Dimensionless, integer
zj	Charge on species j	Dimensionless, integer
${\mathrm{\Delta }}_f{G}_j^0(I=0)$	Gibbs energy of formation at zero ionic strength of species j	kJ/mol
$v_j^k$	Stoichiometric coefficient of species j in the kth reference reaction
$K_{\mathit{ref}}^k$	Equilibrium constant of kth reference reaction	Dimensionless
${\mathrm{\Delta }}_r{G}_k^0$	Standard free energy of kth reference reaction	kJ/mol
$K_{\mathit{app}}^k$	Apparent equilibrium constant of kth biochemical reaction	Dimensionless
${\mathrm{\Delta }}_r{G^{\prime }}_k^0$	Standard free energy of kth biochemical reaction	kJ/mol
ΔrGk	Free energy span of kth biochemical reaction	kJ/mol
${\mathrm{\Delta }}_r{H}_j^0$	Standard Enthalpy of jth proton dissociation reaction at a given ionic strength	kJ/mol
$J_r^k$	Flux through reaction kth biochemical reaction	M/min
[Li]	Concentration of biochemical reactant i	M

In general, let [L] represent the concentration of unbound anionic form of biochemical reactant L and [L_total] be its total concentration in all forms. The total concentration is expressed as

$$[{\text{L}}_{\mathit{total}}]=[\text{L}]+\sum _{p=1}^{N_p}[{\text{LH}}_p]+\sum _{m=1}^{N_m}[{\text{LM}}^m],$$ (2.8)

where [LH_p] is L bound to p [H⁺] ions and N_p is the highest number of protons that can bind to L; [LM^m] is L bound to the mth metal ion. The second term on the right refers to the sum of the proton bound forms, and the third term refers to the sum of the metal bound forms. Any number of cations can be included in this scheme if their dissociation constants are known for a given reactant. For simplicity, we assume that at most only one metal ion of each type binds to L. Note that the net charge on each of the species is not stated here for simplicity of notation, but this quantity is equal to the sum of the charge of the reference species and the total charge of the metal ions bound for each species. The concentration [LH_p] is given by the equilibrium relation:

$$[{\text{LH}}_p]=\frac{[\text{L}]{[{\text{H}}^{+}]}^p}{{\displaystyle \prod _{l=1}^p}{K}_{a,l}},p\ge 1,$$ (2.9)

where K_a,l is the dissociation constant for the reaction, [LH_l] ⇌ [LH_{l − 1}] + [H⁺] and $K_{a,l}={\left(\frac{[{\text{H}}^{+}][{\text{LH}}_{l-1}]}{[{\text{LH}}_l]}\right)}_{eq}$ at a given temperature and ionic strength.

For example, for phosphocreatine, $[{\text{H}}_2{\text{PCr}}^{-}]=\frac{[{\text{HPCr}}^{2-}][{\text{H}}^{+}]}{K_{a,1}}$.

The dissociation constants [usually expressed as pKa = −log₁₀(K_a)] are obtained from sources such as the NIST Database 46. Typically, these pK values must be recalculated for specific temperature and ionic strength to be simulated. The following equation can be applied for the temperature correction (Alberty, 2003):

$${\mathit{pKa}}_{T2}=pK{a}_{T1}+\left(\frac{1}{T_2}-\frac{1}{T_1}\right)·\frac{\mathrm{\Delta }{H}^0}{2.303·R},$$ (2.10)

where T₁ is the temperature at which the pK was reported in the database, T₂ is the temperature at which pKa_T2 is calculated, and R =8.314 JK⁻¹ mol⁻¹ is the universal gas constant.

The enthalpy of dissociation reactions is a function of ionic strength. The following empirical equation (Alberty, 2003) gives ionic strength dependence of enthalpy at 298.15 K:

$$\mathrm{\Delta }{H}^0=\mathrm{\Delta }{H}^0(I=0)+\frac{1.4775I^{1/2}\sum {\nu }_i{z}_i^2}{1+1.6I^{1/2}}.$$ (2.11)

The effects of ionic strength on pK can be approximated using the following empirical equation (Alberty, 2003):

$$\mathit{pKa}(I)=\mathit{pKa}(I_1)+\frac{1.17582}{2.303}\left(\frac{I_1^{1/2}}{1+1.6I_1^{1/2}}-\frac{I^{1/2}}{1+1.6I^{1/2}}\right)\sum {\nu }_i{z}_i^2.$$ (2.12)

The numerical constants in Eqs. (2.11) and (2.12) are derived from Alberty’s fits to experimental data from Clarke and Glew (1980) as described in Alberty (2003). In summary, the pK at a given temperature and ionic strength is corrected for the desired ionic strength using Eq. (2.12). A temperature-corrected value is then obtained from Eq. (2.10) in which the dissociation enthalpy is first corrected for ionic strength using Eq. (2.11).

The concentration of each of the mth metal bound species [LM^m] is given by

$$[{\text{LM}}^m]=\frac{[\text{L}][{\text{M}}^m]}{K_{M,m}},$$ (2.13)

where K_M,m is the dissociation constant for metal ion [M^m] binding to [L]. We assume in Eq. (2.13) that each species binds at most one metal ion per molecule.

The concentration of bound protons due to each bound form [LH_p] with p dissociable protons is given by p[LH_p]. The sum total of bound proton concentration is given by ${\sum }_{p=1}^{N_p}p[{\text{LH}}_p]$ for the biochemical reactant L.

For example, for phosphocreatine, $[\text{MgHPCr}]=\frac{[{\text{HPCr}}^{2-}][{\text{Mg}}^{2+}]}{K_{Mg}}$.

The average proton binding for biochemical reactant L is the ratio of bound proton concentration to total concentration of L, which is given by

$$\begin{array}{l}{\overline{N}}_H^L=\frac{{\displaystyle \sum _{p=1}^{N_p}}p[{\text{LH}}_p]}{[{\text{L}}_{\mathit{total}}]}=\frac{{\displaystyle \sum _{p=1}^{N_p}}p[{\text{LH}}_p]}{[\text{L}]+{\displaystyle \sum _{p=1}^{N_p}}[{\text{LH}}_p]+{\displaystyle \sum _{m=1}^{N_m}}[{\text{LM}}^m]}\\ =\frac{{\displaystyle \sum _{p=1}^{N_p}}\frac{p[\text{L}]{[H]}^p}{{\displaystyle \prod _{l=1}^p}{K}_{a,l}}}{[\text{L}]+{\displaystyle \sum _{p=1}^{N_p}}\frac{[\text{L}]{[{\text{H}}^{+}]}^p}{{\displaystyle \prod _{l=1}^p}{K}_{a,l}}+{\displaystyle \sum _{m=1}^{N_m}}\frac{[\text{L}][{\text{M}}^m]}{K_{M,m}}}=\frac{{\displaystyle \sum _{p=1}^{N_p}}\frac{p{[{\text{H}}^{+}]}^p}{{\displaystyle \prod _{l=1}^p}{K}_{a,l}}}{P_{\text{L}}}\end{array}$$ (2.14)

where P_L is defined as the binding polynomial of L.

$$P_L=1+\sum _{p=1}^{N_p}\frac{{[{\text{H}}^{+}]}^p}{{\displaystyle \prod _{l=1}^p}{K}_{a,l}}+\sum _{m=1}^{N_m}\frac{[{\text{M}}^m]}{K_{M,m}}$$ (2.15)

For example, the binding polynomial for phosphocreatine would be written as

$$P_L=1+\frac{[{\text{HPCr}}^{2-}][{\text{H}}^{+}]}{K_{a,1}}+\frac{[{\text{HPCr}}^{2-}][{\text{Mg}}^{2+}]}{K_{Mg}}+\frac{[{\text{HPCr}}^{2-}][{\text{K}}^{+}]}{K_K}.$$ (2.16)

A similar expression can be written for average metal ion binding, where the numerator contains metal ion binding equilibria instead of just proton binding equilibria. The number p in Eqs. (2.8) and (2.14) denotes the number of dissociable protons bound in each proton bound form of the metabolite L. Note that the product of [L] and P_L gives [L_total] and that each term the binding polynomial represents the ratio of the unbound, proton bound, and metal ion bound forms of L to the unbound form of L.

2.3.2. Reference and biochemical reactions and the flux through an enzyme catalyzed reaction

We define the reference species of the biochemical reactant as the most deprotonated species in the pH range 5.5–8.5, which are used to calculate the average proton binding ${\overline{N}}_H^L$ for each biochemical reactant L. As an example the creatine kinase reaction is shown here in terms of its reference species to illustrate this point:

$${\text{HPCr}}^{2-}+{\text{ADP}}^{3-}+{\text{H}}^{+}\rightleftarrows {\text{HCr}}^0+{\text{ATP}}^{4-}.$$ (2.17)

The biochemical reaction associated with this reference reaction is defined in terms of sums of species constituting each of the reactants and products:

$${\text{PCr}}_{\text{total}}+{\text{ADP}}_{\text{total}}\rightleftarrows {\text{Cr}}_{\text{total}}+{\text{ATP}}_{\text{total}}.$$ (2.18)

The average proton generation stoichiometry, Δ_rN_H of the biochemical reaction, is the difference between the average proton binding of the reactants and the products plus the proton generation stoichiometry, n, of the reference reaction:

$${\mathrm{\Delta }}_r{N}_H=\sum _{\text{reactants}}{\overline{N}}_H^{\text{reactant}}-\sum _{\text{products}}{\overline{N}}_H^{\text{product}}+n.$$ (2.19)

Defined in this way, n is an integer but Δ_rN_H is not because the first two terms on the right-hand side of Eq. (2.19), which are sums of average proton binding of the reactants and the products computed from Eq. (2.14), are nonintegers. Note that the first two terms on the right-hand side of Eq. (2.19) go to zero at highly alkaline pH values. For a system of reactions we define ${\mathrm{\Delta }}_r{N}_H^k$ and n_k as the proton generation stoichiometries of the biochemical and reference reactions, respectively, for the kth reaction.

The proton generation flux through a reaction is given by the product of the proton stoichiometry for that reaction and the flux through the reaction. For a set of reactions in a system, the total proton generation flux is given by a summation of the individual proton fluxes for all biochemical reactions:

$$\text{Proton}\text{flux}=\sum _{k=1}^{N_r}{\mathrm{\Delta }}_r{N}_H^k{J}_k,$$ (2.20)

where J_k is the flux through the kth biochemical reaction.

2.3.3. Apparent equilibrium constant and the Haldane constraint

Changes in the apparent equilibrium constant due to pH and other cations will impact the reverse V_max as defined in the model by the Haldane relationship. The standard free energy of the kth reference reaction is the difference between the free energies of formation of the products and the reactants in that reaction:

$${\mathrm{\Delta }}_r{G}_k^0=\sum _j{\nu }_j^k{\mathrm{\Delta }}_f{G}_j^0.$$ (2.21)

The free energy of formation of each reference species is a function of ionic strength:

$${\mathrm{\Delta }}_f{G}_j^0={\mathrm{\Delta }}_f{G}_j^0(I=0)-\frac{2.91482z_j^2{I}^{1/2}}{1+1.6I^{1/2}}.$$ (2.22)

Since the reference reaction is balanced with respect to protons, the free energy of the reference reaction, ${\mathrm{\Delta }}_r{G}_k^0$, is independent of pH and therefore a constant at a given ionic strength and temperature.

The equilibrium constant of the reference reaction is given by

$$K_{\mathit{ref}}^k=e^{-{\mathrm{\Delta }}_r{G}_k^0/RT}.$$ (2.23)

The apparent equilibrium constant of a biochemical reaction is defined in terms of the metabolite concentrations at equilibrium [indicated by the subscript “eq” in Eq. (24)], which are sums of their constituent species:

$$K_{\mathit{app}}^k=\frac{\prod {[L_{\mathit{total}}^{\text{product}}/c_0]}_{eq}^{{\nu }_{\text{product}}^k}}{\prod {[L_{\mathit{total}}^{\text{reactant}}/c_0]}_{eq}^{{\nu }_{\text{reactant}}^k}}=K_{\mathit{ref}}^k{[{\text{H}}^{+}]}^{-n_k}\frac{\prod P_{\mathit{products}}}{\prod P_{\mathit{reactants}}},$$ (2.24)

where n_k is the proton stoichiometry of the reference reaction and P is the binding polynomial for a biochemical reactant as defined in Eq. (2.15).

The standard free energy for a biochemical reaction is given by

$${\mathrm{\Delta }}_r{G^{\prime }}_k^0=-\mathit{RT}ln(K_{\mathit{app}}^k).$$ (2.25)

2.3.4. Ion mass balance and the differential equations for ion concentrations

The differential equation for a particular ion concentration is derived from a statement of mass conservation for that ion. For metal ions, the total concentration (bound plus free) concentration is

$$[{\text{M}}_{j,\mathit{total}}^{z_j+}]=[{\text{M}}_j^{z_j+}]+[{\text{M}}_{j,\mathit{bound}}^{z_j+}],$$ (2.26)

where [ ${\text{M}}_j^{z_j+}$] is the jth free metal ion concentration and [ ${\text{M}}_{j,\mathit{total}}^{z_j+}$] is the metabolite bound dissociable metal ion concentration.

The conservation equation for protons includes an additional term for covalently bound protons in reference species:

$$[{\text{H}}_{\mathit{total}}^{+}]=[{\text{H}}^{+}]+[{\text{H}}_{\mathit{bound}}^{+}]+[{\text{H}}_{\mathit{reference}}^{+}],$$ (2.27)

where [ ${\text{H}}_{\mathit{reference}}^{+}$] denotes the protons in reference species.

In a closed system, the total proton pool is constant ( $\frac{d[{\text{H}}_{\mathit{total}}^{+}]}{dt}=0$). Differentiating Eq. (2.27) for proton conservation with respect to time, we get

$$0=\frac{d[{\text{H}}^{+}]}{dt}+\frac{d[{\text{H}}_{\mathit{bound}}^{+}]}{dt}+\frac{d[{\text{H}}_{\mathit{reference}}^{+}]}{dt}.$$ (2.28)

The second term in Eq. (2.28) can be expanded by using the chain rule:

$$\frac{d[{\text{H}}_{\mathit{bound}}^{+}]}{dt}=\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{H}}^{+}]}\frac{d[{\text{H}}^{+}]}{dt}+\sum _j\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{M}}_j^{z_j+}]}\frac{d[{\text{M}}_j^{z_j+}]}{dt}+\sum _i\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}.$$ (2.29)

The third term is obtained from summation of the product of proton stoichiometry of each of the reference reactions with the flux through the reaction (generation of free protons from the reference pool diminishes the reference pool):

$$\frac{d[{\text{H}}_{\mathit{reference}}^{+}]}{dt}=-\sum _{k=1}^{N_r}{n}_k{J}_k.$$ (2.30)

Using Eqs. (2.29) and (2.30) in Eq. (2.28) and transposing terms, we obtain the following equation for d[H⁺]/dt:

$$\frac{d[{\text{H}}^{+}]}{dt}=\frac{-{\displaystyle \sum _j}\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{M}}_j^{z_j+}]}\frac{d[{\text{M}}_j^{z_j+}]}{dt}-{\displaystyle \sum _i}\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+{\displaystyle \sum _{k=1}^{N_r}}{n}_k{J}_k}{1+\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{H}}^{+}]}}.$$ (2.31)

When hydrogen ion is transported into and out of the system, this equation becomes

$$\frac{d[{\text{H}}^{+}]}{dt}=\frac{-{\displaystyle \sum _j}\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{M}}_j^{z_j+}]}\frac{d[{\text{M}}_j^{z_j+}]}{dt}-{\displaystyle \sum _i}\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+{\displaystyle \sum _{k=1}^{N_r}}{n}_k{J}_k+J_t^{\text{H}}}{1+\frac{\partial [{\text{H}}_{\mathit{bound}}^{+}]}{\partial [{\text{H}}^{+}]}},$$ (2.32)

where $J_t^{\text{H}}$ is the flux of [H⁺] transport into the system.

Similarly, the rate of change of each metal ion [ ${\text{M}}_j^{z_j+}$] is written as

$$\frac{d[{\text{M}}_j^{z_j+}]}{dt}=\frac{-\frac{\partial [{\text{M}}_{j,\mathit{bound}}^{z_j+}]}{\partial [{\text{H}}^{+}]}\frac{d[{\text{H}}^{+}]}{dt}-{\displaystyle \sum _l}\frac{\partial [{\text{M}}_{j,\mathit{bound}}^{z_j+}]}{\partial [{\text{M}}_l^{z_l+}]}\frac{d[{\text{M}}_l^{z_l+}]}{dt}-{\displaystyle \sum _i}\frac{\partial [{\text{M}}_{j,\mathit{bound}}^{z_j+}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+J_t^{{\text{M}}_j}}{1+\frac{\partial [{\text{M}}_{j,\mathit{bound}}^{z_j+}]}{\partial [{\text{M}}_j^{z_j+}]}}.$$ (2.33)

For a total of N_j metal ions, Eq. (2.33) plus either Eq. (2.31) or Eq. (2.32) results in N_j + 1 coupled differential equations for the ion concentrations. Solving for the time derivatives, we can obtain N_j + 1 differential equations for the ion concentration time derivatives that may be numerically integrated simultaneously with the N_L differential equations for the biochemical reactants [L_{total, i}].

The set of differential equations for biochemical reactant L_i is given by

$$\frac{d[{\text{L}}_{\mathit{total},i}]}{dt}=\sum _k{\nu }_k^i{J}_k,$$ (2.34)

where ${\nu }_k^i$ is the stoichiometry of the ith metabolite in the kth reaction and J_k is the flux through the kth reaction.

As an example, we apply these general equations to treat muscle cell cytoplasm. The cation species in cardiac and skeletal muscle cell cytoplasm that significantly influence the kinetics and apparent equilibrium constants of biochemical reactions are H⁺, Mg²⁺, and K⁺. The Ca²⁺ ion is also an important second messenger for cellular processes whose concentration changes by at least two orders of magnitude during rest and mechanical contraction (Guyton and Hall, 2006). However, the contribution of Ca²⁺ to the binding polynomial of most metabolites is much smaller when compared to that of H⁺, Mg²⁺, and K⁺. For each reactant in the cytoplasm, the binding polynomial is

$$P_i([{\text{H}}^{+}],[\text{M}{g}^{2+}],[{\text{K}}^{+}])=1+[{\text{H}}^{+}]/K_i^{\text{H}}+[{\text{Mg}}^{2+}]/K_i^{Mg}+[{\text{K}}^{+}]/K_i^K,$$ (2.35)

where $K_i^H,K_i^{Mg}$, and $K_i^K$ are the binding constants for H⁺, Mg²⁺, and K⁺. Here we consider only one binding reaction per ion per reactant. Following Eqs. (2.32) and (2.33), we can write the differential equations for the H⁺, Mg²⁺, and K⁺ concentrations:

$$\frac{d[{\text{H}}^{+}]}{dt}=\frac{-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}\frac{d[{\text{Mg}}^{2+}]}{dt}-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}\frac{d[{\text{K}}^{+}]}{dt}-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+{\displaystyle \sum _{k=1}^{N_f}}{n}_k{J}_k+J_t^{\text{H}}}{1+\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}}$$ (2.36)

$$\frac{d[{\text{Mg}}^{2+}]}{dt}=\frac{-\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\frac{d[{\text{H}}^{+}]}{dt}-\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}\frac{d[{\text{K}}^{+}]}{dt}-\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+J_t^{Mg}}{1+\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}}$$ (2.37)

$$\frac{d[{\text{K}}^{+}]}{dt}=\frac{-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\frac{d[{\text{H}}^{+}]}{dt}-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}\frac{d[{\text{Mg}}^{2+}]}{dt}-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+J_t^K}{1+\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}}.$$ (2.38)

These equations can be solved as a system of linear equations for the derivatives of [H⁺], [Mg²⁺], and [K⁺]. We now define the expressions for partial derivatives and buffering terms based on the binding polynomial defined in Eq. (2.35):

$$\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{H}}^{+}]/K_i^{\text{H}}}{K_i^{Mg}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.39)

$$\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{H}}^{+}]/K_i^{\text{H}}}{K_i^K{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.40)

$$\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}=\sum _{i=1}^{N_r}\frac{[{\text{L}}_i](1+[{\text{Mg}}^{2+}]/K_i^{Mg}+[{\text{K}}^{+}]/K_i^K)}{K_i^{\text{H}}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.41)

$$\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{Mg}}^{2+}]/K_i^{Mg}}{K_i^{\text{H}}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.42)

$$\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{Mg}}^{2+}]/K_i^{Mg}}{K_i^K{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.43)

$$\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}=\sum _{i=1}^{N_r}\frac{[{\text{L}}_i](1+[{\text{H}}^{+}]/K_i^{\text{H}}+[{\text{K}}^{+}]/K_i^K)}{K_i^{Mg}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.44)

$$\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{K}}^{+}]/K_i^K}{K_i^{\text{H}}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.45)

$$\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}=-\sum _{i=1}^{N_r}\frac{[{\text{L}}_i][{\text{K}}^{+}]/K_i^K}{K_i^{Mg}{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2},$$ (2.46)

$$\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}=\sum _{i=1}^{N_r}\frac{[{\text{L}}_i](1+[{\text{H}}^{+}]/K_i^{\text{H}}+[{\text{Mg}}^{2+}]/K_i^{Mg})}{K_i^K{\left(P_i([{\text{H}}^{+}],[{\text{Mg}}^{2+}],[{\text{K}}^{+}])\right)}^2}.$$ (2.47)

The flux terms for H⁺, Mg²⁺, and K⁺ are

$${\mathrm{\Phi }}^{\text{H}}=-\sum _{i=1}^{N_r}\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+\sum _{k=1}^{N_f}{n}_k{J}_k+J_t^{\text{H}},$$ (2.48)

$${\mathrm{\Phi }}^{Mg}=-\sum _{i=1}^{N_r}\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+J_t^{Mg},$$ (2.49)

$${\mathrm{\Phi }}^K=-\sum _{i=1}^{N_r}\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{L}}_i]}\frac{d[{\text{L}}_i]}{dt}+J_t^K,$$ (2.50)

where N_r is the number of reactants, N_f is the number of reactions, n_k is the stoichiometric coefficient of the kth reaction, J_k is the flux of the kth reaction, and $J_t^H(J_t^{Mg},J_t^K)$ is the transport flux of [H⁺]([Mg²⁺], [K⁺]) into the system.

The buffering terms are

$${\alpha }_{\text{H}}=1+\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]},$$ (2.51)

$${\alpha }_{Mg}=1+\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]},$$ (2.52)

$${\alpha }_K=1+\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]},$$ (2.53)

The time derivatives of [H⁺], [Mg²⁺], and [K⁺] obtained from solving Eqs. (2.36), (2.37), and (2.38) are given in terms of the buffering terms and the flux terms defined in the preceding equations:

$$\begin{array}{l}\frac{d[{\text{H}}^{+}]}{dt}=[\left(\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}-{\alpha }_{Mg}{\alpha }_K\right){\mathrm{\Phi }}^{\text{H}}\\ +\left({\alpha }_K\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}·\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}\right){\mathrm{\Phi }}^{Mg}\\ +\left({\alpha }_{Mg}\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}\right){\mathrm{\Phi }}^K]/D,\end{array}$$ (2.54)

$$\begin{array}{l}\frac{d[{\text{Mg}}^{2+}]}{dt}=[\left({\alpha }_K\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}\right){\mathrm{\Phi }}^{\text{H}}\\ +\left(\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}·\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}-{\alpha }_{\text{H}}{\alpha }_K\right){\mathrm{\Phi }}^{Mg}\\ +\left({\alpha }_{\text{H}}\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}-\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\right){\mathrm{\Phi }}^K]/D,\end{array}$$ (2.55)

$$\begin{array}{l}\frac{d[{\text{K}}^{+}]}{dt}=[\left({\alpha }_{Mg}\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\right){\mathrm{\Phi }}^{\text{H}}\\ +\left({\alpha }_{\text{H}}\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}-\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}·\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}\right){\mathrm{\Phi }}^{Mg}\\ +\left(\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}·\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}-{\alpha }_{\text{H}}{\alpha }_{Mg}\right){\mathrm{\Phi }}^K]/D,\end{array}$$ (2.56)

where

$$\begin{array}{l}D={\alpha }_{\text{H}}\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}+{\alpha }_K\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\\ +{\alpha }_{Mg}\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}·\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}-{\alpha }_{Mg}{\alpha }_K{\alpha }_{\text{H}}\\ -\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}·\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}\\ -\frac{\partial [{\text{H}}_{\mathit{bound}}]}{\partial [{\text{Mg}}^{2+}]}·\frac{\partial [{\text{Mg}}_{\mathit{bound}}]}{\partial [{\text{K}}^{+}]}·\frac{\partial [{\text{K}}_{\mathit{bound}}]}{\partial [{\text{H}}^{+}]}.\end{array}$$ (2.57)

2.4. Multiple cation equilibria in solutions: Proton, magnesium, and potassium ion binding in the creatine kinase reaction

The creatine kinase reaction catalyzes the phosphorylation of ADP by PCr to produce ATP and creatine (Cr). At given pH and free Mg²⁺ and K⁺ concentrations, ATP, ADP, PCr, and Cr are distributed as a mixture of different ion bound forms. In a solution with given total amounts of ions and metabolites, the free ion concentrations are determined by the simultaneous binding equilibria of the metabolites with the cations. Experimentally, total concentrations of metabolites and ions are measured in solution and the free ion concentrations are calculated from ion mass balance equations derived from multiple cation equilibria. Lawson and Veech (1979) determined experimentally the effect of Mg²⁺ and pH on the creatine kinase equilibrium constant at 38 °C by starting with known quantities of either ATP and Cr or PCr and ADP and adding the creatine kinase enzyme to let the reaction proceed to equilibrium. The free magnesium ion concentration was calculated by subtracting total bound magnesium from total magnesium ion concentration. Ionic strength was maintained at 0.25 M in these solutions by the addition of almost 250 mM of KCl. From the observed equilibrium constants and theoretical calculations, they calculated the creatine kinase apparent equilibrium constant at pH 7, 1 mM Mg²⁺, and 0.25 M ionic strength to be 166. This is the number that is often used as the in vivo creatine kinase equilibrium constant. However, they did not take potassium binding into account, which was later shown to be comparable to magnesium binding to ATP at physiological concentrations of the potassium ion by Kushmerick (1997). The consequence of not accounting for potassium binding is the underestimation of free magnesium concentration. The ionic strength of I = 0.25 M used in these experiments is also very high when compared to values computed from the ionic composition of myoplasm. Godt and Maughan (1988) estimated I = 0.18 M for frog myoplasm. Teague and Dobson (1992) studied the effect of temperature on creatine kinase equilibrium experiment under similar conditions as in the Lawson and Veech (1979) study, but varied the temperature. From binding polynomials of metabolites, the reference equilibrium constant was computed at different temperatures. The slope of the plot of log of apparent equilibrium constant versus 1/T was used to estimate the reaction enthalpy from the van’t Hoff relationship. Subsequent computations of the creatine kinase equilibrium as a function of temperature, Mg²⁺, and ionic strength (Golding et al., 1995; Teague et al., 1996) were based on Teague and Dobson (1992) data. Vinnakota (2006) reinterpreted data of Teague and Dobson (1992) with potassium binding in addition to magnesium and proton binding and obtained the values of equilibrium constant and the enthalpy change of the reference reaction.

The reference reaction for the creatine kinase reaction is written in terms of its most deprotonated species in the physiological pH range:

$${\text{HPCr}}^{2-}+{\text{ADP}}^{3-}+{\text{H}}^{+}\rightleftarrows {\text{HCr}}^0+{\text{ATP}}^{4-}.$$ (2.58)

The biochemical reaction is written in terms of sums of species as they exist in solution governed by their individual equilibria with protons, magnesium, and potassium ions:

$$\text{PCr}+\text{ADP}\rightleftarrows \text{ATP}+\text{Cr}.$$ (2.59)

Table 2.2 lists the binding reactions, pK values, and dissociation enthalpies for each metabolite in the experimental system of Teague and Dobson (1992).

Table 2.2.

Binding reactions and equilibrium constants

Metabolite	Binding reaction	pK (T = 298.15K, I = 0.1)	ΔH (I = 0) kJ/mol
ATP	HATP3− ⇋ ATP4− + H+	6.48	−5
	MgATP2− ⇋ ATP4− + Mg2+	4.19	−18
	MgHATP2− ⇋ HATP3− + Mg2+	2.32	—
	Mg2ATP ⇋ MgATP2− + Mg2+	1.7	—
	KATP3− ⇋ ATP4− + K+	1.17	−1
ADP	HADP2− ⇋ ADP3− + H+	6.38	−3
	MgADP− ⇋ ADP3− + Mg2+	3.25	−15
	Mg2ADP+ ⇋ MgADP− + Mg2+	1	—
	KADP2− ⇋ ADP3− + K+	1	—
PCr	H2PCr− ⇋ HPCr2− + H+	4.5	2.66
	MgHPCr ⇋ HPCr2− + Mg2+	1.6	8.19
	KHPCr− ⇋ HPCr2− + K+	0.31	—
Cr	H2Cr+ ⇋ HCr + H+	2.3	—
Pi	H2Pi− ⇋ HPi2− + H+	6.75	3
	MgHPi ⇋ HPi2− + Mg2+	1.65	−12
	MgH2Pi+ ⇋ H2Pi− + Mg2+	1.19	—
	KHPi− ⇋ HPi2− + K+	0.5	—

The concentrations of free magnesium and potassium ions are calculated by solving ion mass conservation relation equations at a given pH:

$$\begin{array}{l}[{\text{Mg}}_{\mathit{total}}^{2+}]=[{\text{Mg}}^{2+}]+[{\text{MgATP}}^{2-}]+2[{\text{Mg}}_2\text{ATP}]+[{\text{MgHATP}}^{-}]\\ +[{\text{MgADP}}^{-}]+[{\text{Mg}}_2{\text{ADP}}^{+}]+[\text{MgHPCr}]+[\text{MgHPi}]\\ +[{\text{MgH}}_2{\text{Pi}}^{+}]\end{array}$$ (2.60)

$$[{\text{K}}_{\mathit{total}}^{+}]=[{\text{K}}^{+}]+[{\text{KATP}}^{3-}]+[{\text{KADP}}^{2-}]+[{\text{KHPCr}}^{-}]+[{\text{KHPi}}^{-}].$$ (2.61)

At each temperature, Teague and Dobson’s (1992) data give the final equilibrium composition in terms of total Mg²⁺ and K⁺ concentrations, total ATP, ATP, PCr and Cr concentrations, and the final pH. We treat the measured final pH as the negative logarithm of [H⁺] activity (−log₁₀(γ[H⁺])) and compute the [H⁺] concentration and pH as −log₁₀([H⁺]) using an approximate activity coefficient γ calculated from the extended Debye-Huckel equation (Alberty, 2003). Phosphate was added to the medium as one of the buffers. Therefore, phosphate binding to ions is accounted in the overall ion mass balance.

The apparent equilibrium constant of the creatine kinase reaction is given by

$$\begin{array}{l}{K}_{\mathit{app}}^{CK}=\frac{{[\text{ATP}]}_{eq}·{[\text{Cr}]}_{eq}}{{[\text{PCr}]}_{eq}·{[\text{ADP}]}_{eq}}\\ =\frac{({[{\text{ATP}}^{4-}]}_{eq}+{[{\text{HATP}}^{3-}]}_{eq}+{[{\text{MgATP}}^{2-}]}_{eq}+{[{\text{MgHATP}}^{-}]}_{eq}+{[{\text{Mg}}_2\text{ATP}]}_{eq}+{[{\text{KATP}}^{3-}]}_{eq})({[\text{HCr}]}_{eq}+{[{\text{H}}_2{\text{Cr}}^{+}]}_{eq})}{({[{\text{ADP}}^{3-}]}_{eq}+{[{\text{HADP}}^{2-}]}_{eq}+{[{\text{MgADP}}^{-}]}_{eq}+{[{\text{Mg}}_2{\text{ADP}}^{+}]}_{eq}+{[{\text{KADP}}^{2-}]}_{eq})({[{\text{HPCr}}^{2-}]}_{eq}+{[{\text{H}}_2{\text{PCr}}^{-}]}_{eq}+{[\text{MgHPCr}]}_{eq}+{[{\text{KHPCr}}^{-}]}_{eq})}\end{array}$$ (2.62)

Each species of a metabolite can be expressed in terms of the most unbound species through ionic equilibrium relationships defined by binding reactions in Table 2.2. For example, ATP⁴⁻ is given by

$${[{\text{ATP}}^{4-}]}_{eq}=\frac{{[\text{ATP}]}_{eq}}{1+\frac{[{\text{H}}^{+}]}{K_{\mathit{HATP}}}+\frac{[{\text{Mg}}^{2+}]}{K_{\mathit{MgATP}}}+\frac{[{\text{H}}^{+}][{\text{Mg}}^{2+}]}{K_{\mathit{HATP}}{K}_{Mg\mathit{HATP}}}+\frac{{[{\text{Mg}}^{2+}]}^2}{K_{\mathit{MgATP}}{K}_{Mg2\mathit{ATP}}}+\frac{[{\text{K}}^{+}]}{K_{K\mathit{ATP}}}}.$$ (2.63)

The denominator of the RHS of Eq. (2.63) is known as the binding polynomial (P_ATP) for ATP:

$$\begin{array}{l}{P}_{\mathit{ATP}}=1+\frac{[{\text{H}}^{+}]}{K_{\mathit{HATP}}}+\frac{[{\text{Mg}}^{2+}]}{K_{\mathit{MgATP}}}+\frac{[{\text{H}}^{+}][{\text{Mg}}^{2+}]}{K_{\mathit{HATP}}{K}_{Mg\mathit{HATP}}}\\ +\frac{{[{\text{Mg}}^{2+}]}^2}{K_{\mathit{MgATP}}{K}_{Mg2\mathit{ATP}}}+\frac{[{\text{K}}^{+}]}{K_{K\mathit{ATP}}}.\end{array}$$ (2.64)

Therefore, [ATP]_eq = [ATP⁴⁻]_eq P_ATP. Similarly, other metabolite concentrations can be expressed in terms of their most unbound forms and binding polynomials. From Eqs. (2.62), (2.63), and (2.64), the apparent equilibrium constant of creatine kinase reaction can be expressed as

$$K_{\mathit{app}}^{CK}=\frac{{[{\text{ATP}}^{4-}]}_{eq}{[\text{HCr}]}_{eq}}{{[{\text{HPCr}}^{2-}]}_{eq}{[{\text{ADP}}^{3-}]}_{eq}[{\text{H}}^{+}]}[{\text{H}}^{+}]\frac{P_{\mathit{ATP}}{P}_{Cr}}{P_{\mathit{PCr}}{P}_{\mathit{ADP}}}=K_{\mathit{ref}}^{CK}[{\text{H}}^{+}]\frac{P_{\mathit{ATP}}{P}_{Cr}}{P_{\mathit{PCr}}{P}_{\mathit{ADP}}}.$$ (2.65)

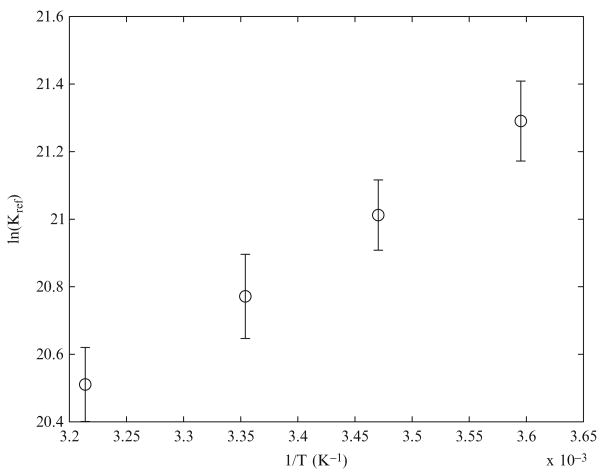
Binding equilibria were corrected to experimental ionic strength and temperature using the methods described in Section 2.3.1. These constants are also corrected to experimental temperatures using the van’t Hoff relationship. We analyzed the equilibrium compositions of solutions in Teague and Dobson’s study to compute the reference equilibrium constant of creatine kinase plotted as a function of 1/T in Fig. 2.1. From our analysis, we estimate the equilibrium constant of the reference reaction, $K_{\mathit{ref}}^{CK}$, to be 9.82e8 at 298.15 K and 0.25 M ionic strength, whereas the value of this constant was estimated to be 3.77e8 by Teague and Dobson (1992). From the slope of the plot in Fig. 2.1, we estimate the enthalpy of the reference reaction to be −17.02 ± 3.32 kJ/mol as opposed to the estimate of −16.73 kJ/mol by Teague and Dobson (1992).

Figure 2.1.

lnK_ref of creatine kinase reaction vs 1/T. −R times the slope of this plot gives the enthalpy of the reference reaction.

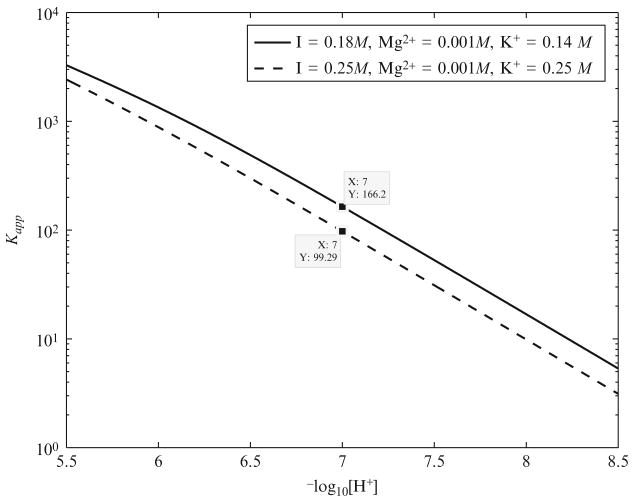
After estimating the $K_{\mathit{ref}}^{CK}$, we then compute the apparent equilibrium constant of the creatine kinase reaction as a function of pH at physiological conditions found in muscle, that is, 310.15 K, 0.18 M ionic strength, 1 mM free magnesium (Konishi, 1998), and 140 mM free potassium (Kushmerick, 1997)(Fig. 2.2). At pH 7 the apparent equilibrium constant under physiological conditions is 166.2. This is very close to the previous estimates of 166 by Lawson and Veech (1979) and Teague and Dobson (1992) at −log₁₀(γ[H⁺]) = 7 under unphysiological experimental conditions at a high potassium concentration and a high ionic strength. Errors in the analyses by Lawson and Veech (1979) and Teague and Dobson (1992)(ignoring potassium binding and underestimating free magnesium ion concentration and the effect of high ionic strength) tended to cancel out, resulting in an estimate of $K_{\mathit{app}}^{CK}$ at −log₁₀(γ[H⁺]) = 7 similar to ours at pH 7. Under the experimental conditions of the previous studies (Lawson and Veech, 1979; Teague and Dobson, 1992), that is, 0.25 M ionic strength and 250 mM K⁺ concentration, we compute the apparent equilibrium constant at pH 7 to be 99.3, which is very low compared to the physiological value.

Figure 2.2.

Apparent equilibrium constant of creatine kinase reaction as a function of pH at 310 K, 1 mM free magnesium, and two different ionic strength and potassium concentrations: I = 0.18 M, K⁺ = 140 mM; I = 0.25 M, K⁺ = 250 mM.

2.5. Example of detailed kinetics of a biochemical reaction: Citrate synthase

Here we present details of modeling a single-reaction system—citrate synthase—applying the principles detailed in the preceding sections. The biochemical reaction is

$$\text{oxaloacetate}+\text{acetyl}-\text{CoA}\rightleftarrows \text{coenzyme}\text{A}+\text{citrate}.$$ (2.66)

If we denote the flux of this reaction as a function of reactant concentrations by the variable J, then the concentration kinetics of the reactants is governed by the differential equation:

$$\begin{array}{c}d[\text{oxaloacetate}]/dt=-J\\ d[\text{acetyl}-\text{CoA}]/dt=-J\\ d[\text{coenzyme}\text{A}]/dt=+J\\ d[\text{citrate}]/dt=+J.\end{array}$$ (2.67)

What remains is to impose an appropriate mathematical expression for J that effectively models the kinetics of the reaction in Eq. (2.66). Such expressions are the domain of enzyme kinetics, in which mechanisms are proposed and data are fit to obtain estimates of associated parameters. In searching the literature, we are likely to discover that the existing kinetic models for the enzyme are parameterized from in vitro experiments conducted at nonphysiological pH, ionic strength, and [Mg²⁺]. Furthermore, the given mechanism will either violate the Haldane constraint or, if it does not, obey the constraint with a value of the apparent equilibrium constant that matches the nonphysiological conditions of the in vitro assay. Accounting and correcting for these facts require treating the detailed biochemical thermodynamics of the reaction system.

To do this we, define reactions in terms of the reference stoichiometry, which in contrast to the biochemical reaction of Eq. (2.66) conserves mass (in terms of elements) and charge:

$${\text{OAA}}^{2-}+{\text{ACCOA}}^0+{\text{H}}_2\text{O}\rightleftharpoons {\text{COAS}}^{-}+{\text{CIT}}^{3-}+2{\text{H}}^{+}.$$ (2.68)

Reference species associated with reactants in Eq. (2.66) are listed in Table 2.3. A thermodynamically balanced model for the kinetics of this reaction relies on a calculation of the thermodynamic properties of the reaction. Using data in Table 2.3, the thermodynamic properties are computed:

$$\begin{array}{l}{\mathrm{\Delta }}_r{G}^o={\mathrm{\Delta }}_f{G}_{\mathit{COASH}}^o+{\mathrm{\Delta }}_f{G}_{\mathit{CIT}}^o-{\mathrm{\Delta }}_f{G}_{\mathit{OAA}}^o-{\mathrm{\Delta }}_f{G}_{\mathit{ACCOA}}^o-{\mathrm{\Delta }}_f{G}_{H_{2}O}^o\\ =+42.03\text{kJ}/\text{mol},\end{array}$$ (2.69)

$$K_{\mathit{app}}^{CS}=e^{-{\mathrm{\Delta }}_r{G^{\prime }}^o/RT}=\frac{P_{\mathit{COA}}·P_{\mathit{CIT}}}{P_{\mathit{OAA}}·P_{\mathit{ACCOA}}·{({10}^{-\text{pH}})}^2}{e}^{-{\mathrm{\Delta }}_r{G}^o/RT},$$ (2.70)

where $K_{\mathit{app}}^{CS}$ is the apparent equilibrium constant for the reaction of Eq. (2.66). In other words, in chemical equilibrium $([\text{CoA}][\text{citrate}])/([\text{oxaloacetate}][\text{acetyl}-\text{CoA}])=K_{\mathit{app}}^{CS}$, where these concentrations correspond to sums over all species associated with each reactant. The binding polynomials in Eq. (2.71) depend on pH and binding ion concentration through the following relationships:

$$\begin{array}{l}{P}_{\mathit{OAA}}=1+[{\text{Mg}}^{2+}]/K_{Mg,\mathit{OAA}},\\ P_{\mathit{CIT}}=1+{10}^{-\text{pH}}/K_{\text{H},\mathit{CIT}}+[{\text{Mg}}^{2+}]/K_{Mg,\mathit{CIT}}+[{\text{K}}^{+}]/K_{K,\mathit{CIT}}\\ P_{\mathit{ACCOA}}=1,P_{\mathit{COASH}}=1+{10}^{-\text{pH}}/K_{\text{H},\mathit{COASH}}\end{array}$$ (2.71)

Table 2.3.

Reactants, reference species, Gibbs free energy of formation, and binding constants for Eqs. (2.66) and (2.76) (298.15 K, 1 M reactants, I = 0.17 M, P = 1 atm)

Reactant	Reference species	ΔfGo (kJ/mol)	Ion bound species	pKa
Water	H2O	−235.74	—	—
Oxaloacete	OAA2−	−794.41	MgOAA0	0.8629b
Acetyl-co- enzyme A	ACCOA0	−178.19	—	—
Citrate	CIT3−	−1165.59	HCIT2−	5.63
			MgCIT−	3.37b
			KCIT2−	0.339b
Coenzyme A	COAS−	−0.72	COASH0	8.13
Adenosine triphosphate (ATP)	ATP4−	−2771.00	HATP3−	6.59
			MgATP2−	3.82
			KATP3−	1.01
Adenosine diphosphate (ADP)	ADP3−	−1903.96	HADP2−	6.42
			MgADP−	2.79
			KADP2−	0.882
Inorganic phosphate (Pi)	HPO42−	−1098.27	H2PO4−	6.71
			MgHPO40	1.69
			KHPO4−	−0.0074

^aAll values from Alberty (2003) unless otherwise noted.

^bNIST Database 46: Critical Stability Constants.

Setting pH = 7, [K⁺] = 150 mM, and [Mg²⁺] = 1 mM, we obtain the apparent thermodynamic properties:

$$\begin{array}{l}{\mathrm{\Delta }}_r{G^{\prime }}^o=-47.41\text{kJ}·{\text{mol}}^{-1}\\ K_{\mathit{app}}^{CS}=2.02\times {10}^8.\end{array}$$ (2.72)

The relationships between the reference species concentrations and the reactant concentrations are

$$\begin{array}{l}[{\text{OAA}}^{2-}]=[\text{OAA}]/P_{\mathit{OAA}}\\ [{\text{ACCOA}}^0]=[\text{ACCOA}]/P_{\mathit{ACCOA}}\\ [{\text{CIT}}^{3-}]=[\text{CIT}]/P_{\mathit{CIT}}\\ [{\text{COAS}}^{-}]=[\text{COASH}]/P_{\mathit{COASH}}.\end{array}$$ (2.73)

The computed species concentrations and thermodynamic values are used in the kinetic model of this enzyme.

The enzyme kinetic flux, which is based on a compulsory-order ternary-complex mechanism,

$$\begin{array}{c}\text{E}+{\text{OAA}}^{2-}\underset{k_{21}}{\overset{k_{12}}{\rightleftharpoons }}\text{E}·{\text{OAA}}^{2-}\\ \text{E}·{\text{OAA}}^{2-}+{\text{ACCOA}}^0\underset{k_{32}}{\overset{k_{23}}{\rightleftharpoons }}\text{E}·{\text{OAA}}^{2-}·{\text{ACCOA}}^0.\\ \text{E}·{\text{OAA}}^{2-}·{\text{ACCOA}}^0+{\text{H}}_2\text{O}\underset{k_{43}}{\overset{k_{34}}{\rightleftharpoons }}\text{E}·{\text{CIT}}^{3-}+{\text{COAS}}^{-}+2{\text{H}}^{+}\\ \text{E}·{\text{CIT}}^{3-}\underset{k_{14}}{\overset{k_{41}}{\rightleftharpoons }}\text{E}+{\text{CIT}}^{3-}\end{array}$$ (2.74)

where E denotes the enzyme and is tested and parameterized against experimental data in Beard et al. (2008). In addition to treating the enzyme kinetic mechanism explicitly in terms of biochemical species, the Beard et al. (2008) model also accounts for pH dependence of enzyme activity by treating the enzyme as a monobasic acid with the unbound form of the enzyme as the active form. The following expression for V_max as a function of [H⁺] concentration accounts for the pH dependence of enzyme activity:

$$V_{\mathit{max}}=\frac{V_{\mathit{max}}^{\mathit{opt}}}{1+\frac{[{\text{H}}^{+}]}{K_{iH}}},$$ (2.75)

where $V_{\mathit{max}}^{\mathit{opt}}$ is the maximum enzyme velocity attained when all of the enzyme is unbound and K_iH is the proton dissociation constant.

3. Application to Physiological Systems

3.1. pH dynamics and glycogenolysis in cell free reconstituted systems and in skeletal muscle

Intracellular pH is an important physiological variable that is regulated within a narrow range. The preceding sections showed that pH significantly affects enzyme activities and apparent equilibrium constants of biochemical reactions. These in turn may influence the energetic state of muscle and the metabolic fluxes. Computational models of biochemical pathways with the capability to predict the metabolic proton load and the consequent changes in muscle pH are useful tools for investigating pH regulation during physiological situations such as exercise and pathological conditions such as ischemia/reperfusion. The models of glycogenolysis developed by Vinnakota (2006) and Vinnakota et al. (2006) compute the metabolic proton load due to glycogenolysis in isolated cell free reconstituted systems and in intact mouse skeletal muscle during anoxia/reperfusion. Vinnakota et al. (2006) considered H⁺, Mg²⁺, and K⁺ ion binding to the metabolites in the pathways modeled. However, the K⁺ concentration was kept constant because of its low relative change during the transients modeled.

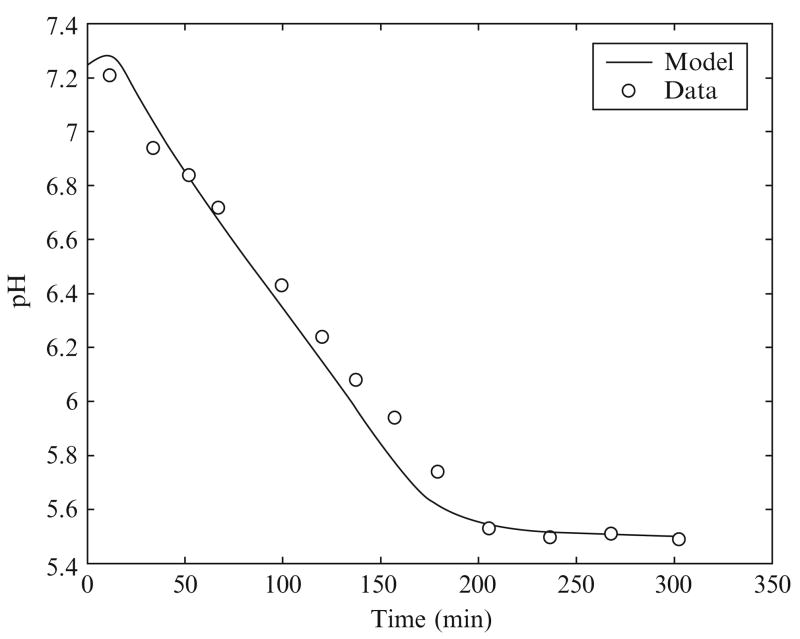
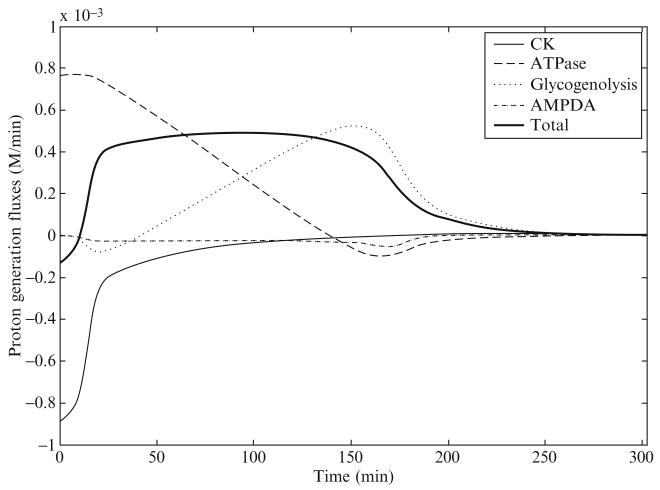
Scopes (1974) simulated postmortem glycogenolysis in a reconstituted system with rabbit and porcine enzymes from the glycogenolysis pathway, breaking down glycogen into lactate. ATPase and AMPdeaminase were added to this system with an initial concentration of PCr at 24 mM and an initial pH of 7.25. Figures 2.3 and 2.4 show pH time course data and model simulation and the computed proton generation fluxes due to biochemical reactions from the study of Vinnakota et al. (2006). The pH time course shows a slight initial rise in pH and thereafter a nearly linear decline until a final pH is reached near 5.5 at 190 min that continues until 300 min. The proton fluxes due to CK, ATPase, glycogenolysis, and AMP deaminase are plotted along with the sum total of all fluxes in Fig. 2.4. These fluxes identify the role of each biochemical reaction in shaping the pH transient. The creatine kinase flux initially consumes protons, which explains the initial rise in pH. The sum of proton fluxes due to the ATPase reaction and the glycogenolysis pathway has a flat time course, which explains the nearly linear decline of pH from 20 to 190 min. However, the important features that emerge from these computations are that (1) the ATPase proton flux is acidifying in the physiological pH range 7.2—6.8 and (2) the contribution of proton fluxes from the glycogenolysis pathway is relatively small during this pH range. The sharp decline in glycogenolysis at the end is due to a reduction in glycogen and a degradation of the adenine nucleotide pool. In summary, near-normal resting pH ATP hydrolysis is the source of metabolic acid load during anaerobic glycogenolysis. However, it is important to note that proton stoichiometries of biochemical reactions are variable with pH, which means that ATP hydrolysis is not always acidifying and that the combined proton stoichiometry of all biochemical reactions in the pathway breaking down glycogen into lactate is not always slightly alkalinizing at all pH values. These results are important for computing metabolic acid load during ischemia and anoxia in cardiac and skeletal muscle, where oxidative ATP generation is impaired, and the creatine kinase and the ATP generation from glycogenolysis work toward maintaining energy balance. Calculations following the principles outlined here provide mechanistic and accurate answers to continued discussions in the physiological literature on the source of protons in muscle glycogenolysis and glycolysis.

Figure 2.3.

pH transient during simulated postmortem glycogenolysis and model-derived proton fluxes. Reproduced from Vinnakota et al. (2006) with permission.

Figure 2.4.

Proton generation fluxes during simulated postmortem glycogenolysis in a cell free reconstituted system. Reproduced from Vinnakota et al. (2006) with permission.

3.2. Cardiac energetics

The heart in healthy mammals is a highly oxidative organ in which normal function is tightly coupled with energetic state, which is maintained by a continuous supply of substrates to fuel energy metabolism (Katz, 2006). When under stresses or disease, such as ischemia or chronic heart failure, impaired cardiac function is associated with the altered energetic state of the heart (Ingwall and Weiss, 2004; Stanley et al., 2005; Zhang et al., 1993, 2001).

3.2.1. The gibbs free energy of ATP hydrolysis in the heart

The Gibbs free energy of ATP hydrolysis reaction, Δ_rG_ATPase, represents an effective marker of the cardiac energetic state. Based on the chemical reference reaction of the ATP hydrolysis,

$${\text{ATP}}^{4-}+{\text{H}}_2\text{O}={\text{ADP}}^{3-}+{\text{PI}}^{2-}+{\text{H}}^{+},$$ (2.76)

the standard Gibbs free energy of ATP hydrolysis, ${\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^o$, can be calculated from Eq. (2.3) as

$${\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^o={\mathrm{\Delta }}_f{G}_{\mathit{ADP}}^o+{\mathrm{\Delta }}_f{G}_{PI}^o+{\mathrm{\Delta }}_f{G}_{\text{H}}^o-{\mathrm{\Delta }}_f{G}_{\mathit{ATP}}^o-{\mathrm{\Delta }}_f{G}_{\text{H}2\text{O}}^o,$$ (2.77)

with the corresponding equilibrium constant

$$K_{\mathit{ref}}^{\mathit{ATPase}}=exp\left(-\frac{{\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^o}{RT}\right)={\left(\frac{{[{\text{ADP}}^{3-}]}_{\text{c}}[{\text{PI}}^{2-}][{\text{H}}^{+}]}{{[\text{ATP}]}^{4-}}\right)}_{eq}.$$ (2.78)

For the biochemical reaction of ATP hydrolysis,

$$\text{ATP}=\text{ADP}+\text{PI},$$ (2.79)

the transformed equilibrium constant and standard Gibbs free energy can be calculated as

$${\text{K}}_{\mathit{app}}^{\mathit{ATPase}}={\left(\frac{[\text{ADP}][\text{PI}]}{[\text{ATP}]}\right)}_{eq}=\frac{K_{\mathit{ref}}^{\mathit{ATPase}}}{[{\text{H}}^{+}]}\frac{P_{\mathit{ADP}}{P}_{PI}}{P_{\mathit{ATP}}},$$ (2.80)

and

$${\mathrm{\Delta }}_r{G}_{\text{ATPase}}^{\prime \text{o}}=-\text{RT}ln{K}_{\mathit{app}}^{\mathit{ATPase}},$$ (2.81)

where P_ATP, P_ADP, and P_PI are the binding polynomials as functions of ionic concentrations (e.g., [H⁺], [Mg²⁺], and [K⁺]) and Δ_rG_ATPase is obtained from the definition stated in Eq. (2.2),

$${\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}={\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^{\prime o}+\mathit{RT}ln\left(\frac{[\text{ADP}][\text{PI}]}{[\text{ATP}]}\right).$$ (2.82)

3.2.2. Calculations of ${\mathrm{\Delta }}_{\text{r}}{G}_{\mathit{ATPase}}^{\prime o}$ and ΔG_ATPase in the heart in vivo

Cardiomyocytes contain multiple subcellular organelles (Katz, 2006), including myofibrils, mitochondria, sarcoplasmic reticulum, and nuclei, among which myofibrils and mitochondria occupy the largest fractions of intracellular volume (Vinnakota and Bassingthwaighte, 2004 ). Most metabolites and ions require specific protein carriers to traverse the inner mitochondrial membrane (LaNoue and Schoolwerth, 1979; Nelson and Cox, 2005), which constitutes a compartment. To account for this compartmentation, we divide the cellular volume of cardiomyocytes into cytoplasm and mitochondria, where the local concentrations of metabolites drive local biochemical reactions. The free energies for a biochemical reaction are generally different in different intracellular compartments (Gibbs, 1978). Since most of the most energy-consuming processes coupled to ATP hydrolysis, such as mechanical contraction due to myosin ATPase, calcium handling, and maintenance of ion gradients across the sarcolemma, are located in the cytoplasm, the cytoplasmic Δ_rG_ATPase provides the driving force for normal cardiac function (Gibbs, 1985).

Under the physiological conditions with assumed temperature T = 310.15 K, ionic strength I = 0.17 M, pH_c = 7.1, [Mg²⁺]_c = 1 mM, and [K⁺]_c = 130 mM, we are able to compute $\mathrm{\Delta }{G^{\prime }}_{\text{eq},\text{ATPase}}^{\text{o}}=-34.7\text{kJ}{\text{mol}}^{-1}$ in the cytoplasm of the cardiomyocytes based on thermodynamic data listed in Table 2.2. Here the subscript “c” denotes cytoplasm. A more detailed process for estimating $\mathrm{\Delta }{G^{\prime }}_{\text{eq},\text{ATPase}}^{\text{o}}$ is given later.

3.2.3. Example 1: Calculating cytoplasmic ${\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^{\prime o}$ in the heart under in vivo physiological conditions

Step 1: Based on basic thermodynamic data and computational algorithm presented elsewhere (Alberty, 2003; Beard and Qian, 2007; Golding et al., 1995; Teague et al., 1996), $K_{\mathit{ref}}^{\mathit{ATPase}}$ under the physiological conditions (T = 310.15 K and I = 0.17 M ) is calculated to be 1.16 − 10⁻¹.

Step 2: Using the binding constants presented in Table 2.2, we can calculate the binding polynomials under the environmental conditions and cytoplasmic ion concentrations to be P_ADP = 2.82, P_PI = 1.58, and P_ATP = 9.28, respectively.

Step 3: From Eq. (2.80),

$$K_{\mathit{app}}^{\mathit{ATPase}}={\left(\frac{[\text{ADP}][\text{PI}]}{[\text{ATP}]}\right)}_{eq}=\frac{K_{\mathit{ref}}^{\mathit{ATPase}}}{{[{\text{H}}^{+}]}_c}\frac{P_{\mathit{ADP}}{P}_{PI}}{P_{\mathit{ATP}}}=7.03\times {10}^5.$$ (2.83)

Step 4: From Eq. (2.81),

$${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ATPase}}^o=-\mathit{RT}ln{K}_{\mathit{app}}^{\mathit{ATPase}}=-34.72\text{kJ}{\text{mol}}^{-1}.$$ (2.84)

3.2.4. Example 2: Calculating Δ_r G_ATPase at basal work rate in the heart in vivo

The values of basal [ATP]_c, [ADP]_c, and [PI]_c are 9.67 × 10⁻³, 4.20 × 10⁻⁵, and 2.90 × 10⁻⁴ M, respectively, as reported previously (Wu et al., 2008). Thus,

$$\begin{array}{l}{\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}={\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ATPase}}^{\prime o}+\mathit{RT}ln\left(\frac{[\text{ADP}][\text{PI}]}{[\text{ATP}]}\right)\\ =-34.7+2.58\times (-13.6)=-69.8\text{kJ}{\text{mol}}^{-1}.\end{array}$$ (2.85)

[Note that in Wu et al.2008 this value was reported as −70.0 kJ mol ⁻₁ because ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ATPase}}^o$ was computed based on slightly different dissociation constants.] A previous computational analysis (Wu et al., 2008) showed that Δ_rG_ATPase changes from −70 kJ mol⁻¹ at the basal work rate to −64 kJ mol⁻¹ at the maximal work rate in the normal dog heart in vivo, which means that the threefold of work increase results in an increase of around 2.5 RT in Δ_rG_ATPase. The values of Δ_rG_ATPase over the threefold increase of workload are calculated by assuming pH_c, [Mg²⁺]_c, and [K⁺]_c fixed at the basal values.

3.2.5. Effects of changes in ion concentrations on Δ_r G′^o of biochemical reactions in the mitochondrial matrix

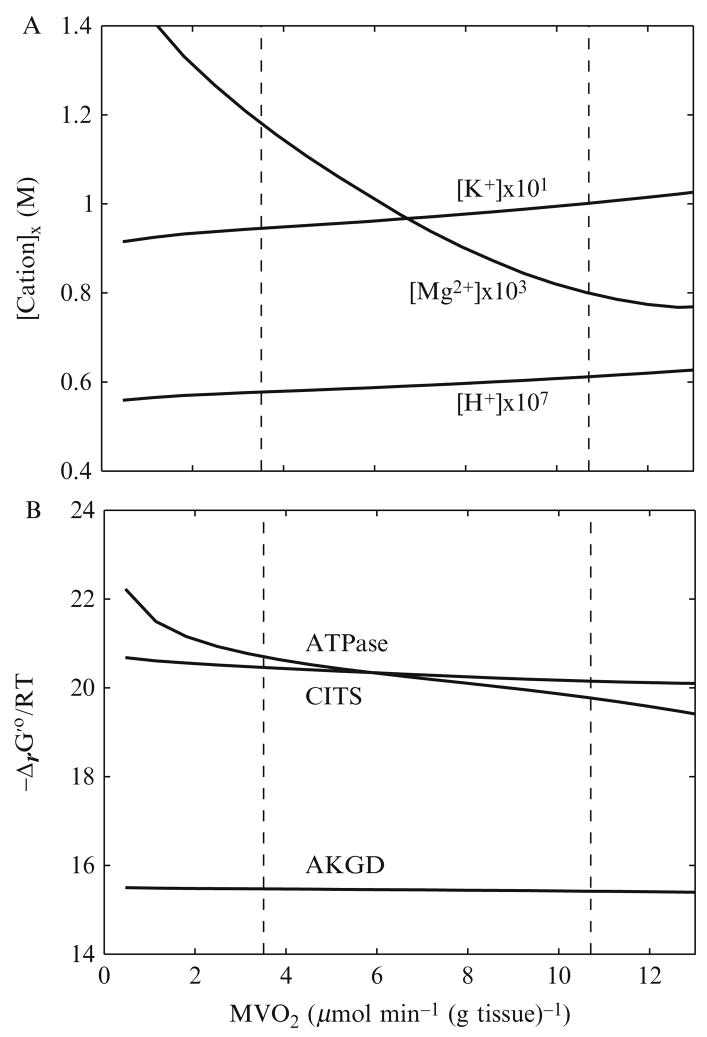
The preceding sections showed that the standard free energy of a biochemical reaction is a function of the binding polynomials of the biochemical reactants and is therefore dependent on free ion concentrations. In the mitochondrial matrix, the temporal changes in free ion concentrations are determined by ion transport fluxes across the mitochondrial inner membrane and the ion fluxes are due to biochemical reactions. The differential equations for the time derivatives of ion concentrations derived based on the principles and methods described in the preceding sections are presented in detail elsewhere (Beard and Qian, 2007; Vinnakota, 2006). Figure 2.5 shows the changes in ion concentrations in the mitochondrial matrix (A) and the resulting changes in standard free energies of selected biochemical reactions (B). In Fig. 2.5A, steady-state values of [H⁺]_matrix, [Mg²⁺]_matrix, and [K⁺]_matrix are plotted against an increased in vivo cardiac work rate, that is, oxygen consumption rate (MVO₂). As MVO₂ increases from its baseline workload value [3.5 μmol min⁻¹ (g tissue)⁻¹] to its maximal workload value [10.7 μmol min⁻¹ (g tissue)⁻¹], [H⁺]_matrix increases from 5.77 × 10⁻⁷ to 6.12 × 10⁻⁸ M, [Mg²⁺]_matrix decreases from 1.18 to 0.80 × 10⁻³ M, and [K⁺]_matrix increases from 9.45 × 10⁻² to 1.00 × 10⁻¹ M, respectively. Since the K⁺/H⁺ antiporter on the inner mitochondrial membrane is operated near equilibrium in the computational model (Wu et al., 2007b), the increase of [K⁺]_matrix is almost linearly proportional to that of [H⁺]_matrix. Figure 2.5B shows that changes in [H⁺]_matrix, [Mg²⁺]_matrix, and [K⁺]_matrix impact the values of Δ_r G′^o of mitochondrial ATP hydrolysis (ATPase), α-ketoglutarate dehydrogenase (AKGD), and citrate synthase (CITS) differently over the range of the in vivo work rate. When the workload is elevated from the baseline value to the maximal value, $-{\mathrm{\Delta }}_r{G}_{\mathit{ATPase}}^{\prime o}/RT$ decreases from 20.70 to 19.77, $-{\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{AKGD}}^o/RT$ decreases from 15.47 to 15.42, and ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{CITS}}^{\text{o}}/RT$ decreases from 20.46 to 20.15. ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ATPase}}^{\text{o}}$ changes the most by around 1 RT unit (i.e., 2.58 kJ mol⁻¹), which means that the apparent equilibrium constant of the mitochondrial ATP hydrolysis varies around threefold. For a biochemical reaction operating near equilibrium, the ratio of forward and reverse reaction fluxes is closely coupled to changes in the apparent equilibrium constants via the mass action law (Beard and Qian, 2007). Equation (81) shows that a small change in ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ATPase}}^{\text{o}}$ results in a large change in $K_{\mathit{app}}^{\mathit{ATPase}}$ due to exponentiation. For example, the reaction catalyzed by aconitase in the citric acid cycle, which converts citrate into isocitrate, is maintained near equilibrium under physiological conditions (Wu et al., 2007b) with ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ACON}}^o=9.42\text{kJ}{\text{mol}}^{-1}$ at the baseline work rate and ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ACON}}^o=8.99\text{kJ}{\text{mol}}^{-1}$ at the maximal work rate. The decrease of ${\mathrm{\Delta }}_r{G^{\prime }}_{\mathit{ACON}}^o$ by 0.43 kJ mol⁻¹ leads to the increase of corresponding $K_{\mathit{app}}^{\mathit{ACON}}$ by about 18 %.

Figure 2.5.

Model-predicted steady-state cation concentrations in the mitochondrial matrix and corresponding $\mathrm{\Delta }{G^{\prime }}_{\text{eq}}^{\text{o}}$ of ATP hydrolysis, AKGD, and CITS at various work rates in the heart in vivo. (A) Changes in [H⁺]_x, [Mg²⁺]_x, and [K⁺]_x, where subscript “x” denotes the mitochondrial matrix. (B) Changes in $\mathrm{\Delta }{G^{\prime }}_{\mathit{ATPase}}^0$ of ATP hydrolysis (ATPase), AKGD, and CITS.

3.3. Physiological significance of multiple ion binding equilibria, reaction kinetics, and thermodynamics in cardiac energetics

The advantages of accounting for multiple ion binding equilibria, reaction kinetics, and thermodynamics are demonstrated in recent cardiac energetics studies by Wu et al. (2007b, 2008). As shown in Wu et al. (2007b), the enzyme mechanisms are presented in terms of chemical species, Δ_r G′^o of the biochemical reactions are computed by explicitly accounting for effects of ion concentrations, and the corresponding apparent equilibrium constants are used to establish the Haldane constraints for modeling the enzyme kinetics. Accurate estimation of the free energy of ATP hydrolysis is important for determining the energetic state of the heart under various conditions.

The application of the methodologies explained in this chapter in a detailed computational model of cardiac energetics (Wu et al., 2008) has resulted in the first estimates of free energy of ATP hydrolysis in the heart in vivo at rest and during increased workloads that account for intracellular compartmentation. The capability of the heart to maintain its “energy homeostasis” in a wide range of cardiac workloads has been a puzzle since the mid-1980s (Balaban et al., 1986). The ³¹P magnetic resonance spectroscopy (³¹P-MRS) technique has been applied widely and successfully as a noninvasive technique in studying in vivo cardiac energetics, albeit with difficulties in detecting subcellular concentrations of chemical species and low concentrations of phosphate metabolites, such as ADP and resting Pi. Because of these limitations, the ³¹P-MRS experimental observations may not provide quantitative measurement on concentration changes of certain metabolites (e.g., cytosolic [Pi]) and may lead to an inaccurate estimation of energy states in the heart in vivo. Thus, it is necessary to use a computational tool to unambiguously determine the concentrations and energetic states based on the experimental observations. Also, modeling reveals details of the underlying mechanisms that are not amenable to direct experimental observation and quantification.

The model of Wu et al. (2008) predicts significant changes in cytosolic [Pi] from the basal work rate to the maximal work rate and leads to two novel conclusions that will be contentious and inspire more thinking and experimenting. The first conclusion is that oxidative phosphorylation is controlled by Pi feedback in the heart in vivo; the second conclusion is that decreased ATP hydrolysis potential—caused by increased cytoplasmic Pi and ADP concentrations—limits ATP utilization rates at a high workload and during ischemia. These two hypotheses are supported by agreement between the model predictions and experimental observations on independent experimental data on transient changes and steady states in ischemic heart in vivo (Wu et al., 2008).

4. Discussion

4.1. Integrating thermodynamic information in biochemical model building

We have described the methods for accounting for detailed thermodynamics in kinetic simulations of biochemical systems. These methods are crucial for a number of applications, including identifying and parameterizing catalytic mechanisms for enzymes based on in vitro data and translating from in vitro experiments to predicting in vivo function of enzymes. In addition, in analyzing ex vivo data (such as from purified mitochondria) or simulating extreme in vivo states (such as ischemia/hypoxia), even normally irreversible reactions approach or go to equilibrium. Thus it is always important to accurately account for thermodynamics.

Studies of specific enzymes and transporters (Beard et al., 2008; Dash and Beard, 2008; Qi et al., 2008) have shown that raw data in the literature are very useful because they are consistent and may be explained with consensus mechanistic models. However, the kinetic parameters originally reported based on those raw data are not always consistent. By reanalyzing raw data from several kinetic studies for enzymes and transporters, we have been able to show that data introduced to support competing hypotheses (different mechanisms) are actually consistent with one consensus mechanism for each enzyme or transporter, and obtain associated kinetic parameter estimates. In general, it is necessary to reanalyze reported data and determine a mechanism (or mechanisms) and associated parameter estimates that account for biochemical state and the kinetic data for each enzyme and transporter.

4.2. Databases of biochemical information

Simulation of large-scale systems will require the development of databases of kinetic and thermochemical data from which models can be assembled. Recently developed models of glycolysis (Vinnakota, 2006; Vinnakota et al., 2006) and mitochondrial energetics (Wu et al., 2007a, b, 2008) have been built in part based on thermodynamic data complied by Alberty (2003). Analysis and simulation of larger scale systems will require extending Alberty’s thermodynamic database for species and reactions not currently included and developing and parameterizing mechanistic models for large numbers of enzymes and metabolite transporters.

In addition to data on thermodynamic constants, databases of kinetic mechanisms and parameters are needed. For many enzymes, detailed mechanistic models have been previously developed based on kinetic measurements made using purified enzymes in vitro. However, in nearly all cases much work remains to adapt and extend these mechanistic models to account for the biochemical state (pH, ionic strength, etc.) so that each enzyme model may be incorporated into an integrated system model in a rigorous way. Therefore, it will be necessary to collect kinetic mechanisms and associated parameters.

A number of databases on enzyme kinetics currently exist, with BRENDA (www.brenda.uni-koeln.de) being perhaps the most widely recognized. BRENDA is a clearinghouse of a vast amount of information on enzymes, including estimates of functional parameters (i.e., apparent kinetic constants) and pointers to the primary literature. A recent effort called System for the Analysis of Biochemical Pathways (SABIO-RK, sabio. villa-bosch.de) aims to collect kinetic models and data from the literature. While these tools are useful, much more focused and specialized tools are needed as well. Along these lines we have begun construction of a Biological Components Databank (www.biocoda.org) to provide an online clearinghouse of mechanistic models of functional biological components to use as building blocks to construct computational models of biological systems. Here, rather than compiling the reported estimates of kinetic constants obtained from the original sources, we are reanalyzing reported data and determining mechanisms and associated parameter estimates for a number of enzymes and transporters. As pilot studies, we have gone through this process for several components.

Our goal is to build a data bank where each entry meets detailed validation and mechanistic standards. However, it is important to realize that it is unavoidable that each entry will pose a unique challenge, requiring a critical assessment of the literature and an expert analysis of data. Therefore, building this data bank will be a huge effort, requiring widespread collaboration within the community. Information on how to contribute to the data bank can be found on the Web site.