Multi-View AAM Fitting and Construction

Abstract

Active Appearance Models (AAMs) are generative, parametric models that have been successfully used in the past to model deformable objects such as human faces. The original AAMs formulation was 2D, but they have recently been extended to include a 3D shape model. A variety of single-view algorithms exist for fitting and constructing 3D AAMs but one area that has not been studied is multi-view algorithms. In this paper we present multi-view algorithms for both fitting and constructing 3D AAMs.

Fitting an AAM to an image consists of minimizing the error between the input image and the closest model instance; i.e. solving a nonlinear optimization problem. In the first part of the paper we describe an algorithm for fitting a single AAM to multiple images, captured simultaneously by cameras with arbitrary locations, rotations, and response functions. This algorithm uses the scaled orthographic imaging model used by previous authors, and in the process of fitting computes, or calibrates, the scaled orthographic camera matrices. In the second part of the paper we describe an extension of this algorithm to calibrate weak perspective (or full perspective) camera models for each of the cameras. In essence, we use the human face as a (non-rigid) calibration grid. We demonstrate that the performance of this algorithm is roughly comparable to a standard algorithm using a calibration grid. In the third part of the paper, we show how camera calibration improves the performance of AAM fitting.

A variety of non-rigid structure-from-motion algorithms, both single-view and multi-view, have been proposed that can be used to construct the corresponding 3D non-rigid shape models of a 2D AAM. In the final part of the paper, we show that constructing a 3D face model using non-rigid structure-from-motion suffers from the Bas-Relief ambiguity and may result in a “scaled” (stretched/compressed) model. We outline a robust non-rigid motion-stereo algorithm for calibrated multi-view 3D AAM construction and show how using calibrated multi-view motion-stereo can eliminate the Bas-Relief ambiguity and yield face models with higher 3D fidelity.

1 Introduction

Active Appearance Models (AAMs) (Cootes et al. 1998, 2001; Cootes and Kittipanyangam 2002; Edwards 1999), and the related concepts of Active Blobs (Sclaroff and Isidoro 1998, 2003) and Morphable Models (Blanz and Vetter 1999; Jones and Poggio 1998; Vetter and Poggio 1997), are generative models of a certain visual phenomenon. AAMs are examples of statistical models that are used to characterize the shape and the appearance of the underlying object by a set of model parameters. Though AAMs are useful for other phenomena (Gross et al. 2006; Hu et al. 2004), they are commonly used to model faces. In a typical application, once an AAM has been constructed, the first step is to fit it to an input image, i.e. model parameters are found to maximize the match between the model instance and the input image. The model parameters can then be passed to a classifier. Many different classification tasks are possible.

Although AAMs were originally formulated as 2D, there are other deformable 3D models (3D Morphable Models (Blanz and Vetter 1999)) and AAMs have also been extended to 3D (2D+3D AAMs (Xiao et al. 2004a)). A number of algorithms have been proposed to build deformable 3D face models and to fit them efficiently (Xiao et al. 2004a; Romdhani and Vetter 2003; Ahlberg 2001; Sung and Kim 2004; Wen and Huang 2003; Pighin et al. 1999; Dornaika and Ahlberg 2004). Deformable 3D face models have a wide variety of applications. Not only can they be used for tasks like pose estimation, which just require the estimation of the 3D rigid motion, but also for tasks such as expression recognition and lipreading, which require, explicitly or implicitly, estimation of the 3D non-rigid motion.

Most of the previous algorithms for AAM fitting and construction have been single-view. One area that has not been studied much in the past (an exception is Cootes et al. 2000) is the development of simultaneous multi-view algorithms. Multi-view algorithms can potentially perform better than single-view as they can take into account more visual information. In this paper we present multi-view algorithms to both fit and build 3D AAMs.

In the first part of the paper we study multi-view fitting of AAMs. Fitting an AAM to an image consists of minimizing the error between the input image and the closest model instance; i.e. solving a nonlinear optimization problem. Face models are usually fit to a single image of a face. In many application scenarios, however, it is possible to set up two or more cameras and acquire simultaneous multiple views of the face. If we integrate the information from multiple views, we can possibly obtain better application performance. For example, Gross et al. (2004) demonstrated improved face recognition performance by combining multiple images of the same face captured from multiple widely spaced viewpoints. In Sect. 3, we describe how a single AAM can be fit to multiple images, captured by cameras with arbitrary locations, rotations, and response functions.

The main technical challenge is relating the AAM shape parameters in one view with the corresponding parameters in the other views. This relationship is complex for a 2D shape model but is straightforward for a 3D shape model. We use 2D+3D AAMs (Xiao et al. 2004a) in this paper. A 2D+3D AAM contains both a 2D shape model and a 3D shape model. Besides the requirement of having a 3D shape model, the main advantage of using a 2D+3D AAM is that 2D+3D AAMs can be fit very efficiently in real-time (Xiao et al. 2004a). Corresponding multi-view fitting algorithms could also be derived for other 3D face models such as 3D Morphable Models (Blanz and Vetter 1999). We could easily have used a 3D Morphable Model instead to conduct the research in this paper, but the fitting algorithms would have been slower.

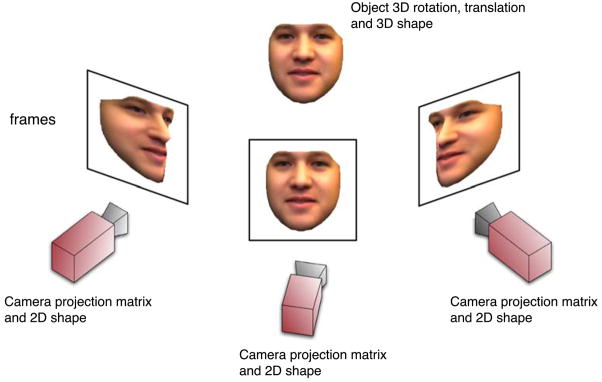
To generalize the 2D+3D fitting algorithm to multiple images, we use a separate set of 2D shape parameters for each image, but just a single, global set of 3D shape parameters as represented in Fig. 1. We impose the constraints that for each view separately, the 2D shape model for that view must approximately equal the projection of the single 3D shape model. Imposing these constraints indirectly couples the 2D shape parameters for each view in a physically consistent manner. Our algorithm can use any number of cameras, positioned arbitrarily. The cameras can be moved and replaced with different cameras without any retraining. The computational cost of the multi-view 2D+3D algorithm is only approximately N times more than the single-view algorithm where N is the number of cameras. In Sect. 3 we present a qualitative evaluation of our multi-view 2D+3D fitting algorithm. We defer the quantitative evaluation to Sect. 5 where we also compare it with a calibrated multi-view algorithm.

Fig. 1.

A representation of the experimental setup for multi-view 2D+3D AAM fitting. For each view we have a separate set of 2D shape parameters and camera projection matrices, but just a single, global set of 3D shape parameters and the associated global 3D rotation and translation. Our fitting algorithm imposes the constraints that for each view separately, the 2D shape model for that view must approximately equal the projection of the single 3D shape model

In the second part of the paper we study how our multi-view fitting algorithm can be used for camera calibration. The multi-view fitting algorithm of Sect. 3 uses the scaled orthographic imaging model used by previous authors, and in the process of fitting computes, or calibrates, the scaled orthographic camera matrices. In Sect. 4 we describe an extension of this algorithm to calibrate weak perspective (or full perspective) camera models for each of the cameras. In essence, both of these algorithms use the human face as a (non-rigid) calibration grid. Such an algorithm may be useful in a surveillance setting where we wish to install the cameras on the fly, but avoid walking around the scene with a calibration grid.

The perspective algorithm requires at least two sets of multi-view images of the face at two different locations. More images can be used to improve the accuracy if they are available. We evaluate our algorithm by comparing it with an algorithm that uses a calibration grid and show the performance to be roughly comparable.

In the third part of the paper we show how camera calibration can improve the performance of multi-view face model fitting. We present an extension of the multi-view AAM fitting algorithm of Sect. 3 that takes advantage of calibrated cameras. We use the calibration algorithm of Sect. 4 to explicitly provide calibration information to the multi-view fitting algorithm. We demonstrate that this algorithm results in far better fitting performance than either the single-view fitting (Sect. 2) or the uncalibrated¹ multi-view fitting (Sect. 3) algorithms. We consider two performance measures: (1) the robustness of fitting—the likelihood of convergence for a given magnitude perturbation from the ground-truth, and (2) speed of fitting—the average number of iterations required to converge from a given magnitude perturbation from the ground-truth.

In the final part of the paper we study calibrated multi-view construction of AAMs. A variety of non-rigid structure-from-motion algorithms have be proposed, both nonlinear (Brand 2001; Torresani et al. 2001) and linear (Bregler et al. 2000; Xiao et al. 2004b; Xiao and Kanade 2005) that can be used for deformable 3D model construction from both a single view (Brand 2001; Bregler et al. 2000; Xiao et al. 2004b; Xiao and Kanade 2005) and multiple views (Torresani et al. 2001).

In most cases, it is only practical to apply face model construction algorithms to data with relatively little pose variation. Tracking facial feature points becomes more difficult the more pose variation there is. Unfortunately, single-view and multi-view algorithms such as non-rigid structure-from-motion have a tendency to scale (stretch or compress) the face in the depth-direction when applied to data with only medium amounts of pose variation. The problem is not the algorithms themselves, but the Bas-Relief ambiguity between the camera translation/rotation and the depth (Zhang and Faugeras 1992a; Szeliski and Kang 1997; Soatto and Brockett 1998; Hartley and Zisserman 2000). The Bas-Relief ambiguity is normally formulated in the case of rigid structure-from-motion, but applies equally in the non-rigid case. As empirically validated in Sect. 6, the result is a compressed/stretched face model, which gives erroneous estimates of the 3D rigid and non-rigid motion.

One way to eliminate the ambiguity is to use a calibrated stereo rig instead of a single camera. The known, fixed translation between the cameras then sets the scale and breaks the ambiguity. The straightforward approach is to use stereo to build a static 3D model at each time instant and then build the deformable model by modeling how the 3D shape changes across time. Two algorithms that takes this approach are (Cootes et al. 1996; Gokturk et al. 2001), one in the uncalibrated case (Cootes et al. 1996), the other in the calibrated case (Gokturk et al. 2001). An alternative approach is to extend the non-rigid structure-from-motion paradigm of (Bregler et al. 2000; Brand 2001; Torresani et al. 2001; Xiao et al. 2004b) and pose the face model construction problem as a single large optimization over the unknown shape model modes, in essence a large bundle adjustment. In Sect. 6 of this paper we derive a calibrated multi-view non-rigid motion-stereo algorithm (Waxman and Duncan 1986; Zhang and Faugeras 1992b) to do exactly this. Our multi-view algorithm explicitly incorporates the knowledge of the calibrated relative orientation of the cameras in the stereo rig. In Sect. 6.5 we present qualitative results to validate these claims. We also use the multi-view calibration algorithm described in Sect. 4 to quantitatively compare the fidelity of 3D models.

2 Background

In this section we review 2D Active Appearance Models (AAMs) (Cootes et al. 2001) and 2D+3D Active Appearance Models (Xiao et al. 2004a). We also revisit the efficient inverse compositional fitting algorithms (Baker and Matthews 2004; Xiao et al. 2004a).

2.1 2D Active Appearance Models

The 2D shape s of a 2D Active Appearance Model is a 2D triangulated mesh. In particular, s is a column vector containing the vertex locations of the mesh. AAMs allow linear shape variation. This means that the 2D shape s can be expressed as a base shape s₀ plus a linear combination of m shape vectors s_i:

$$\mathbf{s}={\mathbf{s}}_0+\sum _{i=1}^m{p}_i{\mathbf{s}}_i$$ (1)

where the coefficients p_i are the shape parameters. AAMs are normally computed from training data consisting of a set of images with the shape mesh (hand) marked on them (Cootes et al. 2001). The Procrustes alignment algorithm and Principal Component Analysis (PCA) are then applied to compute the base shape s₀ and the shape variation s_i (Cootes et al. 2001).

The appearance of an AAM is defined within the base mesh s₀. Let s₀ also denote the set of pixels u = (u, v)^T that lie inside the base mesh s₀, a convenient notational short-cut. The appearance of the AAM is then an image A(u) defined over the pixels u ∈ s₀. AAMs allow linear appearance variation. This means that the appearance A(u) can be expressed as a base appearance A₀(u) plus a linear combination of l appearance images A_i (u):

$$A(\mathbf{u})=A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i{A}_i(\mathbf{u})$$ (2)

where the coefficients λ_i are the appearance parameters. The base (mean) appearance A₀ and appearance images A_i are usually computed by applying Principal Component Analysis to the shape normalized training images (Cootes et al. 2001).

Although (1) and (2) describe the AAM shape and appearance variation, they do not describe how to generate a model instance. The AAM model instance with shape parameters p and appearance parameters λ_i is created by warping the appearance A from the base mesh s₀ to the model shape mesh s. In particular, the pair of meshes s₀ and s define a piecewise affine warp from s₀ to s denoted² W(u; p) (Matthews and Baker 2004).

2.2 Fitting a 2D AAM to a Single Image

The goal of fitting a 2D AAM to a single input image I (Matthews and Baker 2004) is to minimize:

$$\begin{array}{l}\sum _{\mathbf{u}\in {\mathbf{s}}_0}{\left[A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i{A}_i(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))\right]}^2\\ ={\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i{A}_i(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))\Vert }^2\end{array}$$ (3)

with respect to the 2D shape p and appearance λ_i parameters. In Matthews and Baker (2004) it was shown that the inverse compositional algorithm (Baker and Matthews 2004) can be used to optimize the expression in (3). The algorithm uses the “project out” algorithm (Hager and Belhumeur 1998; Matthews and Baker 2004) to break the optimization into two steps. The first step consists of optimizing:

$$\left|\right|A_0(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))|{|}_{\text{span}{(A_i)}^{\perp }}^2$$ (4)

with respect to the shape parameters p where the subscript span(A_i)^⊥ means project the vector into the subspace orthogonal to the subspace spanned by A_i, i = 1, …, l. The second step consists of solving for the appearance parameters:

$${\lambda }_i=-\sum _{\mathbf{u}\in {\mathbf{s}}_0}{A}_i(\mathbf{u})[A_0(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))]$$ (5)

where the appearance vectors A_i are orthonormal. Optimizing (4) itself can be performed by iterating the following two steps. Step 1 consists of computing:

$$\mathrm{\Delta }\mathbf{p}=-H_{2\text{D}}^{-1}\mathrm{\Delta }{\mathbf{p}}_{\text{SD}}$$

where

$$\mathrm{\Delta }{\mathbf{p}}_{\text{SD}}=\sum _{\mathbf{u}\in {\mathbf{s}}_0}{[\mathbf{S}{\mathbf{D}}_{2\text{D}}(\mathbf{u})]}^{\text{T}}[A_0(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))]$$

where the following two terms can be pre-computed (and combined) to achieve high efficiency:

$$\begin{array}{l}\mathbf{S}{\mathbf{D}}_{2\text{D}}(\mathbf{u})={\left[\nabla A_0\frac{\partial \mathbf{W}}{\partial \mathbf{p}}\right]}_{\text{span}{(A_i)}^{\perp }},\\ H_{2\text{D}}=\sum _{\mathbf{u}\in {\mathbf{s}}_0}{[\mathbf{S}{\mathbf{D}}_{2\text{D}}(\mathbf{u})]}^{\text{T}}\mathbf{S}{\mathbf{D}}_{2\text{D}}(\mathbf{u})\end{array}$$

where

$$\nabla A_0=\left[\frac{\partial A_0}{\partial x}\frac{\partial A_0}{\partial y}\right].$$

Step 2 consists of updating the warp by composing with the inverse incremental warp:

$$\mathbf{W}(\mathbf{u};\mathbf{p})\leftarrow \mathbf{W}(\mathbf{u};\mathbf{p})\circ \mathbf{W}{(\mathbf{u};\mathrm{\Delta }\mathbf{p})}^{-1}.$$ (6)

The resulting 2D AAM fitting algorithm runs at over 200 frames per second. See Matthews and Baker (2004) for more details.

2.3 2D+3D Active Appearance Models

Most deformable 3D face models, including 3D Morphable Models (Blanz and Vetter 1999) and the models in (Bregler et al. 2000; Brand 2001; Torresani et al. 2001; Xiao et al. 2004b), use a 3D linear shape variation model, essentially equivalent to a 3D generalization of the model in Sect. 2.1. The 3D shape s̄ is a 3D triangulated mesh which can be expressed as a base shape s̄₀ plus a linear combination of m̄ shape vectors s̄_j:

$$\overline{\mathbf{s}}={\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j$$ (7)

where the coefficients p̄_i are the shape parameters.

A 2D+3D AAM (Xiao et al. 2004a) consists of the 2D shape variation s_i of a 2D AAM governed by (1), the appearance variation A_i (u) of a 2D AAM governed by (2), and the 3D shape variation s̄_j of a 3D AAM governed by (7). The 2D shape variation s_i and the appearance variation A_i (u) of the 2D+3D AAM are constructed exactly as for a 2D AAM. The construction of the 3D shape variation s̄_j is the subject of Sect. 6 of this paper.

To generate a 2D+3D model instance, an image formation model is needed to convert the 3D shape s̄ into a 2D mesh, onto which the appearance is warped. In Xiao et al. (2004a) the following scaled orthographic imaging model was used:

$$\mathbf{u}={\mathbf{P}}_{so}\mathbf{x}=\sigma \left(\begin{array}{lll}{i}_x\hfill & i_y\hfill & i_z\hfill \\ j_x\hfill & j_y\hfill & j_z\hfill \end{array}\right)\mathbf{x}+\left(\begin{array}{l}{o}_x\hfill \\ o_y\hfill \end{array}\right)$$ (8)

where x = (x, y, z) is a 3D vertex location, (o_x, o_y) is an offset to the origin, σ is the scale and the projection axes i = (i_x, i_y, i_z) and j = (j_x, j_y, j_z) are unit length and orthogonal: i · i = j · j = 1; i · j = 0. The model instance is then computed by projecting every 3D shape vertex onto a 2D vertex using (8). The 2D appearance A(u) is finally warped onto the 2D mesh (taking into account visibility) to generate the final model instance.

2.4 Fitting a 2D+3D AAM to a Single Image

The goal of fitting a 2D+3D AAM to an image I (Xiao et al. 2004a) is to minimize:

$$\begin{array}{l}{\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i{A}_i(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))\Vert }^2\\ +K{\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i{\mathbf{s}}_i-{\mathbf{P}}_{so}\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j\right)\Vert }^2\end{array}$$ (9)

with respect to p, λ_i, P_so, and p̄ where K is a large constant weight. Equation (9) should be interpreted as follows. The first term in (9) is the 2D AAM fitting criterion. The second term enforces the (heavily weighted, soft) constraints that the 2D shape s equals the projection of the 3D shape s̄ with projection matrix P_so. In Xiao et al. (2004a) it was shown that the 2D AAM fitting algorithm (Matthews and Baker 2004) can be extended to a 2D+3D AAM. The resulting algorithm still runs in real-time (Matthews et al. 2007).

As with the 2D AAM algorithm, the “project out” algorithm (Matthews and Baker 2004) is used to break the optimization into two steps, the first optimizing:

$$\left|\right|A_0(\mathbf{u})-I(\mathbf{W}(\mathbf{u};\mathbf{p}))|{|}_{\text{span}{(A_i)}^{\perp }}^2+K\sum _i{F}_i^2(\mathbf{p};{\mathbf{P}}_{so};\overline{\mathbf{p}})$$ (10)

with respect to p, P_so, and p̄, where F_i (p; P_so; p̄) is the error inside the L2 norm in the second term in (9) for each of the mesh x and y vertices. The second step solves for the appearance parameters using (5). The 2D+3D algorithm has more unknowns to solve for than the 2D algorithm. As a notational convenience, concatenate all the unknown parameters into one vector q = (p; P_so; p̄). Optimizing (10) is then performed by iterating the following two steps. Step 1 consists of computing³:

$$\begin{array}{l}\mathrm{\Delta }\mathbf{q}=-H_{3\text{D}}^{-1}\mathrm{\Delta }{\mathbf{q}}_{\text{SD}}\\ =-H_{3\text{D}}^{-1}\left[\left(\begin{array}{c}\mathrm{\Delta }{\mathbf{p}}_{\text{SD}}\\ 0\end{array}\right)+K\sum _i{\left(\frac{\partial F_i}{\partial \mathbf{q}}\right)}^{\mathbf{T}}{F}_i(\mathbf{q})\right]\end{array}$$ (11)

where:

$$H_{3\text{D}}=\left(\begin{array}{cc}{H}_{2\text{D}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)+K\sum _i{\left(\frac{\partial F_i}{\partial \mathbf{q}}\right)}^{\mathbf{T}}\frac{\partial F_i}{\partial \mathbf{q}}.$$ (12)

Step 2 consists of first extracting the parameters p, P_so, and p̄ from q, and then updating the warp using (6), and the other parameters P_so and p̄ additively (Matthews et al. 2007).

3 Fitting a Single 2D+3D AAM to Multiple Images

In the previous section we reviewed some of the efficient algorithms to fit an AAM to a single image. If we have multiple, simultaneous, views of the face, the performance of AAM fitting can be improved if we use all views. We now describe an algorithm to fit a single 2D+3D AAM simultaneously to multiple images.

Suppose that we have N images Iⁿ: n = 1, …, N of a face that we wish to fit the 2D+3D AAM to. In this section we assume that the images are captured simultaneously by synchronized, but uncalibrated cameras (see Sect. 5 for a calibrated algorithm.) The naive algorithm is to fit the 2D+3D AAM independently to each of the images. This algorithm can be improved upon by using the fact that, since the images Iⁿ are captured simultaneously, the 3D shape of the face is the same in all views. We therefore pose fitting a single 2D+3D AAM to multiple images as minimizing:

$$\begin{array}{l}\sum _{n=1}^N({\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i^n{A}_i(\mathbf{u})-I^n(\mathbf{W}(\mathbf{u};{\mathbf{p}}^n))\Vert }^2\\ +K{\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i^n{\mathbf{s}}_i-{\mathbf{P}}_{so}^n\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j\right)\Vert }^2)\end{array}$$ (13)

simultaneously with respect to the N sets of 2D shape parameters pⁿ, the N sets of appearance parameters ${\lambda }_i^n$ (the appearance may be different in different images due to different camera response functions, etc.), the N sets of camera matrices ${\mathbf{P}}_{so}^n$, and the one, global set of 3D shape parameters p̄. Note that the 2D shape parameters in each image are not independent, but are coupled in a physically consistent⁴ manner through the single set of 3D shape parameters p̄. Optimizing (13) therefore cannot be decomposed into N independent optimizations. The appearance parameters ${\lambda }_i^n$ can, however, be dealt with using the “project out” algorithm (Hager and Belhumeur 1998; Matthews and Baker 2004), in the usual way; i.e. we first optimize:

$$\begin{array}{l}\sum _{n=1}^N(\left|\right|A_0(\mathbf{u})-I^n(\mathbf{W}(\mathbf{u};{\mathbf{p}}^n))|{|}_{\text{span}{(A_i)}^{\perp }}^2\\ +K{\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i^n{\mathbf{s}}_i-{\mathbf{P}}_{so}^n\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j\right)\Vert }^2)\end{array}$$ (14)

with respect to pⁿ, ${\mathbf{P}}_{so}^n$, and p̄, and then solve for the appearance parameters:

$${\lambda }_i^n=-\sum _{\mathbf{u}\in {\mathbf{s}}_0}{A}_i(\mathbf{u})[A_0(\mathbf{u})-I^n(\mathbf{W}(\mathbf{u};{\mathbf{p}}^n))].$$

Organize the unknowns in (14) into a single vector $\mathbf{r}=({\mathbf{p}}^1;{\mathbf{p}}_{so}^1;\dots ;{\mathbf{p}}^N;{\mathbf{P}}_{so}^N;\overline{\mathbf{p}})$. Also, split the single-view 2D+3D AAM terms into parts from (11) and (12) that correspond to the 2D image parameters (pⁿ and ${\mathbf{P}}_{so}^n$) and the 3D shape parameters (p̄):

$$\begin{array}{l}\mathrm{\Delta }{\mathbf{q}}_{\text{SD}}^n=\left(\begin{array}{c}\mathrm{\Delta }{\mathbf{q}}_{\text{SD},2\text{D}}^n\\ \mathrm{\Delta }{\mathbf{q}}_{\text{SD},\overline{\mathbf{p}}}^n\end{array}\right),\\ H_{3\text{D}}^n=\left(\begin{array}{cc}{H}_{3\text{D},2\text{D},2\text{D}}^n& H_{3\text{D},2\text{D},\overline{\mathbf{p}}}^n\\ H_{3\text{D},\overline{\mathbf{p}},2\text{D}}^n& H_{3\text{D},\overline{\mathbf{p}},\overline{\mathbf{p}}}^n\end{array}\right).\end{array}$$

Optimizing (14) can then be performed by iterating the following two steps. Step 1 consists of computing:

$$\mathrm{\Delta }\mathbf{r}=-H_{\text{MV}}^{-1}\mathrm{\Delta }{\mathbf{r}}_{\text{SD}}=-H_{\text{MV}}^{-1}\left(\begin{array}{c}\mathrm{\Delta }{\mathbf{q}}_{\text{SD},2\text{D}}^1\\ ⋮\\ \mathrm{\Delta }{\mathbf{q}}_{\text{SD},2\text{D}}^N\\ {\sum }_{n=1}^N\mathrm{\Delta }{\mathbf{q}}_{\text{SD},\overline{\mathbf{p}}}^n\end{array}\right)$$ (15)

where:

$$H_{\text{MV}}=\left(\begin{array}{ccccc}{H}_{3\text{D},2\text{D},2\text{D}}^1& \mathbf{0}& \dots & \mathbf{0}& H_{3\text{D},2\text{D},\overline{\mathbf{p}}}^1\\ \mathbf{0}& H_{3\text{D},2\text{D},2\text{D}}^2& \dots & \mathbf{0}& H_{3\text{D},2\text{D},\overline{\mathbf{p}}}^2\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ \mathbf{0}& \dots & \mathbf{0}& H_{3\text{D},2\text{D},2\text{D}}^N& H_{3\text{D},2\text{D},\overline{\mathbf{p}}}^N\\ H_{3\text{D},\overline{\mathbf{p}},2\text{D}}^1& H_{3\text{D},\overline{\mathbf{p}},2\text{D}}^2& \dots & H_{3\text{D},\overline{\mathbf{p}},2\text{D}}^N& {\sum }_{n=1}^N{H}_{3\text{D},\overline{\mathbf{p}},\overline{\mathbf{p}}}^n\end{array}\right).$$

Step 2 consists of extracting the parameters pⁿ, ${\mathbf{P}}_{so}^n$, and p̄ from r, and updating the warp parameters pⁿ using (6), and the other parameters ${\mathbf{P}}_{so}^n$ and p̄ additively.

The N image algorithm is very similar to N copies of the single image algorithm. Almost all of the computation is just replicated N times, one copy for each image. The only extra computation is adding the N terms in the components of Δr_SD and H_MV that correspond to the single set of global 3D shape parameters p̄, inverting the matrix H_MV, and the matrix multiply in (15). Overall, the N image algorithm is therefore approximately N times slower than the single image 2D+3D fitting algorithm. (It is more than N times slower due to the large matrix inversion and matrix multiplication step, but in practice only slightly so.)

3.1 Experimental Results

An example of using our algorithm to fit a single 2D+3D AAM to three simultaneously captured images⁵ of a face is shown in Fig. 2. In the results in this paper, the translation and scale of the 2D face model in each view is initialized by hand and the 2D shape set to be the mean shape. However, 2D+3D AAMs can easily be initialized with a face detector (Matthews et al. 2007). See the movie iterations.mpg for the fitting video sequence. The initialization is displayed in the top row of the figure, the result after 5 iterations in the middle row, and the final converged result in the bottom row. In each case, all three input images are overlaid with the 2D shape pⁿ plotted in dark dots. We also display the recovered pose angles (roll, pitch and yaw) extracted from the three scaled orthographic camera matrices ${\mathbf{P}}_{so}^n$ in the top left of each image. Each camera computes a different relative head pose, illustrating that the estimate of ${\mathbf{P}}_{so}^n$ is view dependent. The single 3D shape p̄ for all views at the current iteration is displayed in the top-right of the center image. The view-dependent camera projection of this 3D shape is also plotted as a white mesh overlaid on the face.

Fig. 2.

An example of using our uncalibrated multi-view fitting algorithm to fit a single 2D+3D AAM to three simultaneous images of a face. Each image is overlaid with the corresponding 2D shape for that image in dark dots. The head pose (extracted from the camera matrix ${\mathbf{P}}_{so}^N$) is displayed in the top left of each image as roll, pitch and yaw. The single 3D shape p̄ for the current ‘3-frame’ is displayed in the top right of the center image. This 3D shape is also overlaid in each image, using the corresponding ${\mathbf{P}}_{so}^N$, as a white mesh. See the movie iterations.mpg for a video of the whole fitting sequence

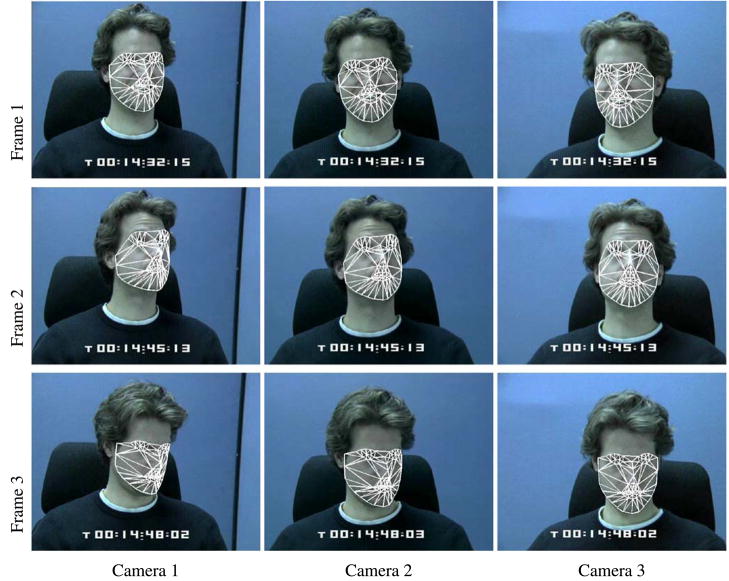
Applying the multi-view fitting algorithm sequentially allows us to track the face simultaneously in N video sequences. Some example frames of the algorithm being using to track a face in a trinocular sequence is shown in Fig. 3. We also include the movie tracking.mpg for the complete tracking sequence. The tracking remains accurate and stable both over time and between views. In Sect. 5 we present a quantitative evaluation of this multi-view algorithm.

Fig. 3.

An example of our multi-view fitting algorithm being used to track a face in a trinocular sequence. As the face is tracked we compute a single 3D shape and three estimates of the head pose using three independent camera matrices. See the movie tracking.mpg for the complete sequence

4 Camera Calibration

4.1 Image Formation Model

The multi-view fitting algorithm in Sect. 3 uses the scaled orthographic image formation model in (8). A more powerful model when working with multiple cameras (because it models the coupling between the scales across the cameras through the focal lengths and average depths) is the weak perspective model:

$$\mathbf{u}={\mathbf{P}}_{\text{wp}}(\mathbf{x})=\frac{f}{o_z+\overline{z}}\left(\begin{array}{ccc}{i}_x& i_y& i_z\\ j_x& j_y& j_z\end{array}\right)\mathbf{x}+\left(\begin{array}{c}{o}_u\\ o_v\end{array}\right).$$ (16)

In (16), o_z is the depth of the origin of the world coordinate system and z̄ is the average depth of the scene points measured relative to the world coordinate origin. The “z” (depth) direction is k = i × j where × is the vector cross product, i = (i_x, i_y, i_z), and j = (j_x, j_y, j_z). The average depth relative to the world origin z equals the average value of k · x computed over all points x in the scene.

The weak perspective model is an approximation to the full perspective model:

$$\begin{array}{l}\mathbf{u}={\mathbf{P}}_{\text{persp}}(\mathbf{x})\\ =\left(\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}{i}_x& i_y& i_z& o_u\\ j_x& j_y& j_z& o_v\\ k_x& k_y& k_z& o_z\end{array}\right)\left(\begin{array}{c}\mathbf{x}\\ 1\end{array}\right)\end{array}$$ (17)

where the depth of the scene k · x is assumed to be roughly constant z̄. The calibration parameters of the two perspective models in (16) and (17) are interchangeable. When evaluating the calibration results in Sect. 4.6 below we use the full perspective model. In the calibrated fitting algorithms in Sect. 5 we use the weak perspective model because it is reasonable to assume that the depth of the face is roughly constant, a common assumption in many face modeling papers (Romdhani and Vetter 2003; Xiao et al. 2004a).

4.2 Camera Calibration Goal

Suppose we have N cameras n = 1, …, N. The goal of our camera calibration algorithm is to compute the 2 × 3 camera projection matrix (i, j), the focal length f, the projection of the world coordinate system origin into the image (o_u, o_v), and the depth of the world coordinate system origin (o_z) for each camera. If we superscript the camera parameters with n we need to compute ${\mathbf{P}}_{\text{wp}}^n={\mathbf{i}}^n,{\mathbf{j}}^n,f^n,o_u^n,o_v^n$, and $o_z^n$. There are 7 unknowns in ${\mathbf{P}}_{\text{wp}}^n$ (rather than 10) because there are only 3 degrees of freedom in choosing the 2 × 3 camera projection matrix (i, j) such that it is orthonormal.

4.3 Calibration Using Two Time Instants

For ease of understanding, we first describe an algorithm that uses two sets of multi-view images captured at two time instants. Deriving this algorithm also allows us to show that two sets of images are needed and derive the requirements on the motion of the face between the two time instants. In Sect. 4.4 we describe an algorithm that use an arbitrary number of multi-view image sets and in Sect. 4.5 another algorithm that poses calibration as a single large optimization.

The uncalibrated multi-view fitting algorithm of Sect. 3 uses the scaled orthographic camera matrices ${\mathbf{P}}_{\text{so}}^n$ in (8) and optimizes over the N scale parameters σⁿ. Using (16) instead of (8) and optimizing over the focal lengths fⁿ and origin depths $o_z^n$ is ambiguous. Multiple values of fⁿ and $o_z^n$ yield the same value of ${\sigma }^n=\frac{f^n}{o_z^n+{\overline{z}}^n}$. However, the values of fⁿ and $o_z^n$ can be computed by applying (a slightly modified version of) the uncalibrated multi-view fitting algorithm a second time with the face at a different location. With the first set of images we compute iⁿ, jⁿ, $o_u^n,o_v^n$. Suppose that ${\sigma }^n={\sigma }_1^n$ is the scale at this location. Without loss of generality we also assume that the face model is at the world coordinate origin at this first time instant. Finally, without loss of generality we assume that the mean value of x computed across the face model (both mean shape s₀ and all shape vectors s_i) is zero. It follows that z̄ is zero and so:

$$\frac{f^n}{o_z^n}={\sigma }_1^n.$$ (18)

Suppose that at the second time instant the face has undergone a global 3D rotation R⁶ and 3D translation T. Both the rotation R and translation T have three degrees of freedom. We then perform a modified multi-view fit, minimizing:

$$\begin{array}{l}\sum _{n=1}^N({\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i^n{A}_i(\mathbf{u})-I^n(\mathbf{W}(\mathbf{u};{\mathbf{p}}^n))\Vert }^2\\ +K{\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i^n{\mathbf{s}}_i-{\mathbf{P}}_{\text{so}}^n\left(\mathbf{R}\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j\right)+\mathbf{T}\right)\Vert }^2)\end{array}$$ (19)

with respect to the N sets of 2D shape parameters pⁿ, the N sets of appearance parameters ${\lambda }_i^n$, the one global set of 3D shape parameters p̄, the 3D rotation R, the 3D translation T, and the N scale values ${\sigma }^n={\sigma }_2^n$. In this optimization all of the camera parameters (iⁿ, jⁿ, $o_u^n$, and $o_v^n$) except the scale (σ) in the scaled orthographic model ${\mathbf{P}}_{\text{so}}^n$ are held fixed to the values computed in the first time instant. Since the object underwent a global translation T then z̄ⁿ = kⁿ · T where kⁿ = iⁿ × jⁿ is the z-axis of camera n. It follows that:

$$\frac{f^n}{o_z^n+{\mathbf{k}}^n·\mathbf{T}}={\sigma }_2^n.$$ (20)

Equations (18) and (20) are two sets of linear simultaneous equations in the 2∗N unknowns (fⁿ and $o_z^n$). Assuming that kⁿ · T ≠ 0 (the global translation T is not perpendicular to any of the camera z-axes), these two equations can be solved for fⁿ and $o_z^n$ to complete the camera calibration. Note also that to uniquely compute all three components of T using the optimization in (19) at least one pair of the cameras must be verged (the axes (iⁿ, jⁿ) of the camera matrices ${\mathbf{P}}_{\text{so}}^n$ must not all span the same 2D subspace).

4.4 Multiple Time Instant Algorithm

Rarely are two sets of multi-view images sufficient to obtain an accurate calibration. The approach just described can easily be generalized to T time instants. The first time instant is treated as above and used to compute iⁿ, jⁿ, $o_u^n,o_v^n$ and to impose the constraint on fⁿ and $o_z^n$ in (18). Equation (19) is then applied to the remaining T − 1 frames to obtain additional constraints:

$$\frac{f^n}{o_z^n+{\mathbf{k}}^n·{\mathbf{T}}_t}={\sigma }_t^n\text{for}t=2,3,\dots ,T$$ (21)

where T_t is the translation estimated in the t^th time instant and ${\sigma }_t^n$ is the scale of the face in the n^th camera at the t^th time instant. Equations (18) and (21) are then re-arranged to obtain an over-constrained linear system which can then be solved to obtain fⁿ and $o_z^n$.

4.5 Calibration as a Single Optimization

The algorithms in Sects. 4.3 and 4.4 have the disadvantage of being two stage algorithms. First they solve for iⁿ, jⁿ, $o_u^n$, and $o_v^n$, and then for fⁿ and $o_z^n$. It is better to pose calibration as the single large non-linear optimization of:

$$\begin{array}{l}\sum _{n=1}^N\sum _{t=1}^T({\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i^{n,t}{A}_i(\mathbf{u})-I^{n,t}(\mathbf{W}(\mathbf{u};{\mathbf{p}}^{n,t}))\Vert }^2\\ +K\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i^{n,t}{\mathbf{s}}_i\\ {-{\mathbf{P}}_{\text{wp}}^n\left({\mathbf{R}}^t\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j^t{\overline{\mathbf{s}}}_j\right)+{\mathbf{T}}^t\right)\Vert }^2)\end{array}$$ (22)

summed over all cameras n and time instants t with respect to the 2D shape parameters p^n,t, the appearance parameters ${\lambda }_i^{n,t}$, the 3D shape parameters p̄^t, the rotations R^t, the translations T^t, and the calibration parameters iⁿ, jⁿ, fⁿ, $o_u^n,o_v^n$, and $o_z^n$. In (22), I^n,t represents the image captured by the n^th camera in the t^th time instant and the average depth z̄ = kⁿ · T^t in ${\mathbf{P}}_{\text{wp}}^n$ given by (16). Finally, we define the world coordinate system by enforcing R¹ = I and T¹ = 0.

The expression in (22) can be optimized by iterating two steps: (1) The calibration parameters are optimized given the 2D shape and (rotated translated) 3D shape; i.e. the second term in (22) is minimized given fixed 2D shape, 3D shape, R^t, and T^t. This optimization decomposes into a separate 7 dimensional optimization for each camera. (2) A calibrated multi-view fit (see Sect. 5) is performed on each frame in the sequence; i.e. the entire expression in (22) is minimized, but keeping the calibration parameters in ${\mathbf{P}}_{\text{wp}}^n$ fixed and just optimizing over the 2D shape, 3D shape, R^t, and T^t. The entire large optimization can be initialized using the multiple time instant algorithm in Sect. 4.4.

4.6 Empirical Evaluation of Calibration

We tested our calibration algorithms on a trinocular stereo rig. Two example images of the 1300 input images from each of the three cameras are shown in Fig. 4. The complete input sequence is included in the movie calib_input.mov. We wish to compare our calibration algorithm with an algorithm that uses a calibration grid. In Sects. 4.6.1 and 4.6.2 we present results for the epipolar geometry. We compute a fundamental matrix from the camera parameters iⁿ, jⁿ, fⁿ, $o_u^n,o_v^n$, and $o_z^n$ estimated by our algorithm and use the 8-point algorithm (Hartley 1995) to estimate the fundamental matrix from the calibration grid data. In Sect. 6.5.3 we present results for the camera focal length and relative orientation of the cameras, while also comparing the 3D model building algorithms.

Fig. 4.

Example inputs to our calibration algorithms: A set of simultaneously captured image sets of a face at a variety of different positions and expressions. See calib_input.mov for the complete input

4.6.1 Qualitative Comparison of Epipolar Geometry

In Fig. 5 we show a set of epipolar lines computed by the algorithms. In Fig. 5(a) we show an input image captured by camera 1, with a few feature points marked on it. In Fig. 5(b) we show the corresponding points in the other image and the epipolar lines. The solid dark colored epipolar lines are computed using the 8-point algorithm on the calibration grid data. The dashed black epipolar lines are computed using the two stage multiple time instant algorithm of Sect. 4.4. The solid light colored epipolar lines are computed using the single large optimization algorithm of Sect. 4.5. Figures 5(d) and (c) are similar for feature points marked in camera 3. While all three sets of epipolar lines are very similar, the epipolar lines for the single large optimization algorithm are overall closer to those for the 8-point algorithm than those of the two stage algorithm.

Fig. 5.

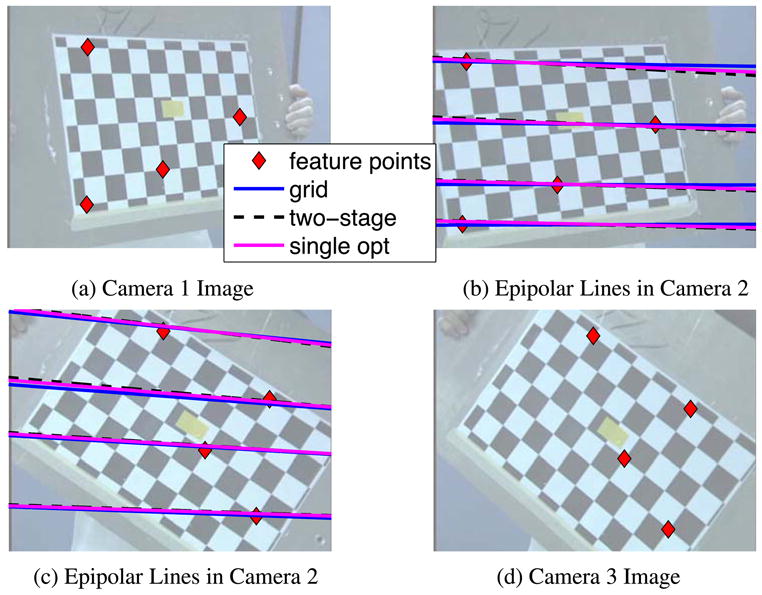
Qualitative comparison between our AAM-based calibration algorithms and the 8-point algorithm (Hartley 1995). a An input image captured by the first camera with several feature points marked on it. b The corresponding points and epipolar lines of the other image. The solid dark colored epipolar lines are computed using the 8-point algorithm, the dashed black epipolar lines using the two stage multiple time instant algorithm, and the solid light colored epipolar lines are computed using the optimization algorithm. d Shows the input image of the third camera, and c the corresponding points and epipolar lines for the second camera

4.6.2 Quantitative Comparison of Epipolar Geometry

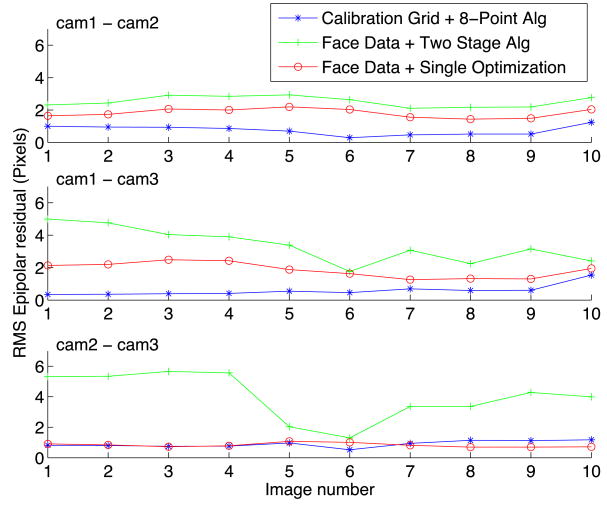
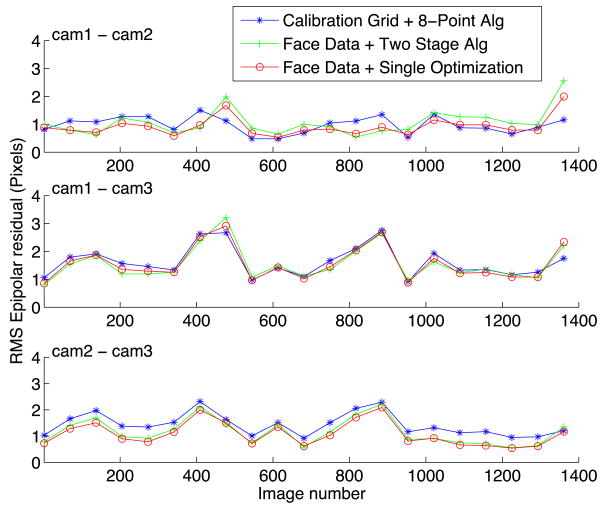
In Figs. 6 and 7 we present the results of a quantitative comparison of the fundamental matrices by extracting a set of ground-truth feature point correspondences and computing the RMS distance between each feature point and the corresponding epipolar line predicted by the fundamental matrix. In Fig. 6 we present results on 10 images of a calibration grid, similar (but not identical) to that used by the calibration grid algorithm. The ground-truth correspondences are extracted using a corner detector. In Fig. 7 we present results on 1400 images of a face at different scales. The ground-truth correspondences are extracted by fitting a single-view AAM independently to each image (i.e. no use of the multi-view geometry is used).

Fig. 6.

Quantitative comparison between our AAM-based calibration algorithms and the 8-point algorithm (Hartley 1995) using a calibration grid. The evaluation is performed on 10 images of a calibration grid (data similar to, but not used by the 8-point algorithm). The ground-truth is extracted using a corner detector. We plot the RMS distance error between epipolar lines and the corresponding feature points for each of the 10 images

Fig. 7.

Quantitative comparison between our AAM-based calibration algorithms and the 8-point algorithm (Hartley 1995) using a calibration grid. The evaluation is performed on 1400 images of a face. The ground-truth is extracted using a single-view AAM fitting algorithm. We plot the RMS distance error between epipolar lines and the corresponding feature points for each of the 1400 images

Although the optimization algorithm of Sect. 4.5 performs significantly better than the two stage algorithm in Sect. 4.4, both AAM-based algorithms perform slightly worse than the 8-point algorithm on the calibration grid data in Fig. 6. The main reason is probably that the ground-truth calibration grid data covers a similar volume to the data used by the 8-point algorithm, but a much larger volume than the face data used by the AAM-based algorithms. When compared on the face data in Fig. 7 (which covers a similar volume to that used by the AAM-based algorithm), the 8-point algorithm and the optimization algorithm of Sect. 4.5 perform comparably well.

5 Calibrated Multi-View Fitting

Once we have calibrated the cameras and computed iⁿ, jⁿ, fⁿ, $o_u^n,o_v^n$, and $o_z^n$ we can then use a weak perspective calibrated multi-view fitting algorithm to fit a given AAM to multiple images. We optimize:

$$\begin{array}{l}\sum _{n=1}^N({\Vert A_0(\mathbf{u})+\sum _{i=1}^l{\lambda }_i^n{A}_i(\mathbf{u})-I^n(\mathbf{W}(\mathbf{u};{\mathbf{p}}^n))\Vert }^2\\ +K\Vert {\mathbf{s}}_0+\sum _{i=1}^m{p}_i^n{\mathbf{s}}_i\\ {-{\mathbf{P}}_{\text{wp}}^n\left(\mathbf{R}\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j{\overline{\mathbf{s}}}_j\right)+\mathbf{T}\right)\Vert }^2)\end{array}$$

with respect to the N sets of 2D shape parameters pⁿ, the N sets of appearance parameters ${\lambda }_i^n$, the one global set of 3D shape parameters p̄, the global rotation R, and the global translation T. In this optimization, ${\mathbf{P}}_{\text{wp}}^n$ is defined by (16) where z̄ = kⁿ · T. It is also possible to formulate a similar scaled orthographic calibrated algorithm in which ${\mathbf{P}}_{\text{wp}}^n$ is replaced with ${\mathbf{P}}_{\text{so}}^n$ defined in (8) and the optimization is also performed over the additional N scales σ_n. Note that in these calibrated fitting algorithms, the calibration parameters iⁿ, jⁿ, fⁿ, $o_u^n,o_v^n$, and $o_z^n$ are constant and not optimized. As shown below, this leads to a lower dimensional optimization and more robust fitting.

5.1 Empirical Evaluation

5.1.1 Qualitative Results

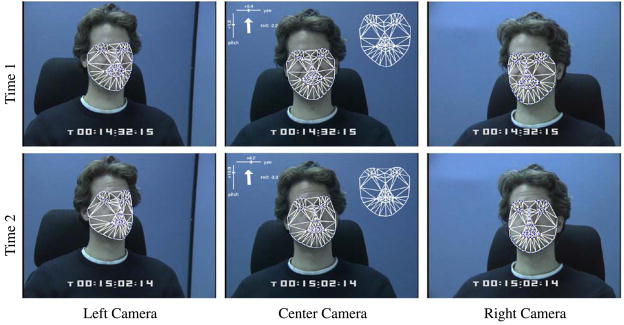
An example of using our calibrated multi-view fitting algorithm to track by fitting a single 2D+3D AAM to three concurrently captured images of a face is shown in Fig. 8. The complete fitting sequence is included in the movie calib_fitting.mpg. The top row of the figure shows the tracking result for one frame. The bottom row shows the tracking result for a frame later in the sequence. In each case, all three input images are overlaid with the 2D shape pⁿ plotted in dark dots. The view-dependent camera projection of this 3D shape is also plotted as a white mesh overlaid on the face. The single 3D shape p̄ at the current frame is displayed in the top-right of the center image. We also display the recovered roll, pitch, and yaw of the face (extracted from the global rotation matrix R) in the top left of the center image. The three cameras combine to compute a single head pose, unlike Fig. 3 where the pose is view dependent.

Fig. 8.

An example of using our calibrated multi-view fitting algorithm to fit a single 2D+3D AAM to three simultaneously captured images of a face. Each image is overlaid with the corresponding 2D shape for that image in dark dots. The single 3D shape p̄ for the current triple of images is displayed in the top right of the center image. This 3D shape is also projected into each image using the corresponding Pⁿ, and displayed as a white mesh. The single head pose (extracted from the rotation matrix R) is displayed in the top left of the center image as roll, pitch, and yaw. This should be compared with the algorithm in Sect. 3 in which there is a separate head pose for each camera. See the movie calib_fitting.mpg for the complete fitting sequence

5.1.2 Quantitative Results

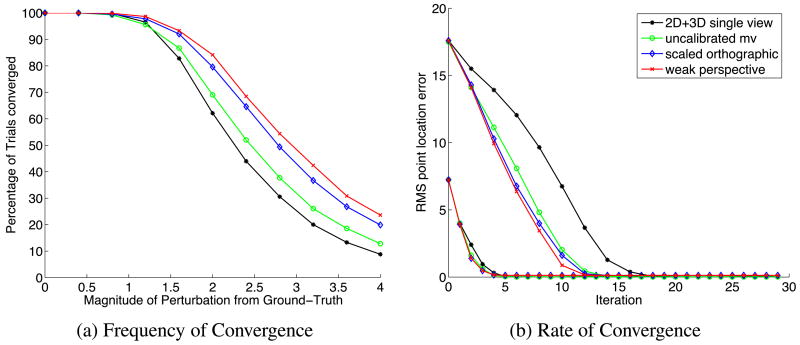
In Fig. 9 we show quantitative results to demonstrate the increased robustness and convergence rate of our calibrated multi-view fitting algorithms. In experiments similar to those in Matthews and Baker (2004), we generated a large number of test cases by randomly perturbing from a ground-truth obtained by tracking the face in the multi-view video sequences. The global 3D shape parameters p̄, global rotation matrix R, and global translation T were all perturbed and projected into each of the three views. This ensures the initial perturbation is a valid starting point for all algorithms. We then run each algorithm from the same perturbed starting point and determine whether they converged or not by computing the RMS error between the mesh location of the fit and the ground-truth mesh coordinates. The algorithm is considered to have converged if the total spatial error is less than 2.0 pixels. We repeat the experiment 20 times for each set of 3 images and average over all 300 image triples in the test sequences. This procedure is repeated for different values of perturbation energy. The magnitude of the perturbation is chosen to vary on average from 0 to 4 times the 3D shape standard deviation. The global rotation R, and global translation T are perturbed by a scalar multiples α and β of this value. The values of α and β were chosen so that the rotation and translation components introduce the same amount of perturbation energy as the shape component (Matthews and Baker 2004).

Fig. 9.

a The likelihood (frequency) of convergence plot against the magnitude of a random perturbation to the ground-truth fitting results computed by tracking through a trinocular sequence. The results show that the calibrated multi-view algorithms are more robust than the uncalibrated multi-view algorithm discussed in Sect. 3, which itself is more robust than the 2D+3D single-view algorithm (Xiao et al. 2004a). b The rate of convergence is estimated by plotting the average error after each iteration against the iteration number. The results show that the calibrated multi-view algorithms converge faster than the uncalibrated algorithm, which converges faster than the single-view 2D+3D algorithm

In Fig. 9(a) we plot a graph of the likelihood (frequency) of convergence against the magnitude of the random perturbation for the 2D+3D single-view fitting algorithm (Xiao et al. 2004a) applied independently to each camera, the uncalibrated multi-view fitting algorithm described in Sect. 3 and the two calibrated multi-view fitting algorithms: scaled orthographic and weak perspective. The results clearly show that the calibrated multi-view algorithms are more robust than the uncalibrated multi-view algorithm, which is more robust than the 2D+3D single-view algorithm. Overall, the weak perspective calibrated multi-view fitting algorithm performs the best. The main source of the increased robustness of the calibrated multi-view fitting algorithms is imposing the constraint that the head pose is consistent across all N cameras. We also compute how fast the algorithms converge by computing the average RMS mesh location error after each iteration. Only trials that actually converge are used in this computation. The results for two different magnitudes of perturbation (0.8 and 2.0) to the ground-truth are included in Fig. 9(b). The results indicate that the calibrated multi-view algorithms converge faster than the uncalibrated algorithm, which converges faster than the single-view 2D+3D algorithm.

We include the movie fit_compare.mpg to demonstrate a few examples of the perturbation experiments. The movie illustrates how the calibrated multi-view algorithms impose a consistent head pose (c.f. uncalibrated algorithm) and a single 3D face shape (c.f. 2D+3D algorithm). As a result, the calibrated algorithms sometimes converges when the other algorithms diverge. The speed of convergence is also visibly faster.

In Table 1 we include timing results for our Matlab implementations of the four fitting algorithms compared in this section. The results were obtained on a dual 2.5 GHz Power Mac G5 machine and were averaged over 600 image triples with VGA (640 × 480) resolution. Each algorithm was allowed to iterate until convergence over each image triple. Note that the results for the single-view algorithm⁷ is just the cost of processing one image from the image triple. The multi-view algorithms are all therefore approximately 3 times slower than the single-view algorithm, as should be expected. Also note that since the weak perspective algorithm is more constrained it converges more quickly than the uncalibrated and scaled orthographic multi-view algorithms. The single-view algorithm requires slightly fewer iterations than all of the multi-view algorithms because it does not have to impose consistency on the 2D shapes in the different views.

Table 1.

This table shows the timing results for our Matlab implementations of the four fitting algorithms evaluated in Sect. 5.1.2 in milliseconds. The results were obtained on a dual 2.5 GHz Power Mac G5 machine and were averaged over 600 image triples with VGA (640 × 480) resolution. Each algorithm was allowed to iterate until convergence over each image triple. Note that the results for the single-view algorithm is just the cost of processing one image from the image triple

Algorithm	Time per frame	Iterations per frame	Time per iteration
2D+3D single-view	33.808	2.5209	13.401
uncalibrated multi-view	152.33	3.2915	46.247
scaled orthographic	152.94	3.2178	47.534
weak perspective	125.94	2.6131	48.158

6 Multi-View 3D Model Construction

In the previous section we have shown that the performance of AAM fitting can be improved by using multiple views and calibration information. Similarly, a 3D AAM can be constructed more reliably using multiple calibrated cameras. In this section, we outline a calibrated multi-view motion-stereo algorithm for 3D AAM construction and compare its performance with other existing single-view and multi-view non-rigid structure-from-motion algorithms.

6.1 Non-Rigid Structure-from-Motion

One way to build a deformable 3D face model is to use 3D range data. In Blanz and Vetter (1999), the 3D mesh vertices s̄ are first located in a set of “training” 3D range scans. Principal Component Analysis is then used to extract the base (or mean) shape s̄₀ and the m̄ dominant shape modes s̄_j. More recently, however, the task of building deformable face models from a video captured by a single camera using non-rigid structure-from-motion has received a great deal of attention (Bregler et al. 2000; Brand 2001).

Suppose that we have a sequence of images I^t of a face captured across time t = 1, …, T. Either the face, the camera, or both may be moving. Assume we can track K 2D feature points in the 2D images I^t. Denote the tracking results:

$${\mathbf{u}}^t=\left(\begin{array}{cccc}{u}_1^t& u_2^t& \dots & u_K^t\\ v_1^t& v_2^t& \dots & v_K^t\end{array}\right).$$

Also denote the camera matrix of the camera at time t by P^t. Non-rigid structure-from-motion can then be posed as minimizing:

$$\sum _{t=1}^T{\Vert {\mathbf{P}}^t\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j^t{\overline{\mathbf{s}}}_j\right)-{\mathbf{u}}^t\Vert }^2$$ (23)

with respect to the base shape s̄₀, the shape modes s̄_j, the shape parameters ${\overline{p}}_j^t$ and the camera matrices P^t. If P^t is a perspective camera model, the above optimization is non-linear, but can be solved using an appropriate nonlinear optimization algorithm (Xiao and Kanade 2005). If P^t is a linear camera model, such as the scaled orthographic model (P = P_so), the above optimization can be solved using a linear algorithm (Bregler et al. 2000; Brand 2001; Xiao et al. 2004b).

6.2 Multi-View Structure-from-Motion

The single-view non-rigid structure-from-motion (NR-SFM) paradigm can be extended to include information from multiple views/cameras to yield a multi-view non-rigid structure-from-motion algorithm (Torresani et al. 2001) (MV-SFM).

Suppose we have a set of N > 1 cameras that simultaneously capture videos I^n,t for n = 1, …, N across time t = 1, …, T. Denote the unknown camera matrices by Pⁿ for n = 1, …, N and the global 3D rotation and translation of the face across time by R^t and T^t. Assume that we can track K feature points across time in the videos I^n,t. Denote the tracking results as:

$${\mathbf{u}}^{n,t}=\left(\begin{array}{cccc}{u}_1^{n,t}& u_2^{n,t}& \dots & u_K^{n,t}\\ v_1^{n,t}& v_2^{n,t}& \dots & v_K^{n,t}\end{array}\right).$$ (24)

The problem then becomes one of minimizing:

$$\sum _{n=1}^N\sum _{t=1}^T{\Vert {\mathbf{P}}^n\left({\mathbf{R}}^t\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j^t{\overline{\mathbf{s}}}_j\right)+{\mathbf{T}}^t\right)-{\mathbf{u}}^{n,t}\Vert }^2$$ (25)

with respect to the base shape s̄₀, the shape modes s̄_j, the shape parameters p̄^t_j, the camera matrices Pⁿ, the global 3D rotation R^t and translation T^t of the face across time.

6.3 Stereo

Both the single-view and multi-view structure-from-motion algorithms suffer from the Bas Relief ambiguity (Zhang and Faugeras 1992a; Szeliski and Kang 1997; Soatto and Brockett 1998; Hartley and Zisserman 2000). The Bas Relief ambiguity is an ambiguity between the motion (translation or small rotation) of the cameras and the depths of the points in the scene. In both the single-view and multi-view cases, the camera matrices must be solved for as well as the structure of the scene. So, the ambiguity can manifest itself in the form of scaled depths and motion between the cameras. If we have multiple calibrated cameras, however, it is possible to derive better algorithms that do not suffer from the Bas-Relief ambiguity. As we now describe, the simplest approach is to use stereo to fulfill the same role as a range-scanner.

Suppose now that we have a calibrated stereo rig with N > 1 cameras in it. Denote the known (calibrated) camera matrices Pⁿ for n = 1, …, N. Suppose that the n^th camera captures the images I^n,t across time t = 1, …, T as the face (and possibly the stereo rig) move. Assume that we can track K feature points across time in the videos I^n,t, and also compute correspondence between the cameras. Denote the tracked feature points as:

$${\mathbf{u}}^{n,t}=\left(\begin{array}{cccc}{u}_1^{n,t}& u_2^{n,t}& \dots & u_K^{n,t}\\ v_1^{n,t}& v_2^{n,t}& \dots & v_K^{n,t}\end{array}\right).$$ (26)

A stereo algorithm (similar to those in (Cootes et al. 1996; Gokturk et al. 2001)) to compute the deformable model is then as follows:

1. Perform stereo at each time t by minimizing:

   $$\sum _{n=1}^N\left|\right|{\mathbf{P}}^n({\overline{\mathbf{s}}}^t)-{\mathbf{u}}^{n,t}|{|}^2$$

   with respect to the 3D static shape s̄^t.

2. Align the 3D static shapes s̄^t with a transformation consisting of a 3D rigidity transformation (6 degrees of freedom) and a single scale (1 degree of freedom); i.e. perform a 3D “Procrustes” alignment.

3. Compute s̄₀, s̄_j using Principal Component Analysis.

6.4 Motion-Stereo

The above stereo algorithm can be improved upon by posing the problem as a single large optimization, a generalization of the non-rigid structure-from-motion formulation in (23). The input to the motion-stereo algorithm is the same as the stereo algorithm, namely the camera matrices Pⁿ and the tracked feature points u^n,t. Denote the global 3D rotation and translation of the face across time by R^t and T^t. In the stereo algorithm above, R^t and T^t are computed by the 3D similarity Procrustes algorithm. The model construction problem can then be posed as minimizing:

$$\sum _{n=1}^N\sum _{t=1}^T{\Vert {\mathbf{P}}^n\left({\mathbf{R}}^t\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j^t{\overline{\mathbf{s}}}_j\right)+{\mathbf{T}}^t\right)-{\mathbf{u}}^{n,t}\Vert }^2$$ (27)

with respect to the base shape s̄₀, the shape modes s̄_j, the shape parameters p̄^t_j, the global rotations R^t, and the global translations T^t. The construction goal in (27) can be minimized using the following motion-stereo algorithm:

1. Initialize using the stereo algorithm in Sect. 6.3

   1. 3D similarity Procrustes → R^t, T^t.

   2. Principal Components Analysis → s̄₀, s̄_j, p̄^t_j.

2. Iterate the following two steps until convergence:

   1. Fix s̄₀, s̄_j, solve for R^t, T^t, p̄^t_j.

   2. Fix p̄^t_j, R^t, T^t, solve for s̄₀, s̄_j.

3. Project out any scale, rotation, or translation components left in the 3D shape modes s̄_j.

In Step 2a, the optimization can be broken down into separate optimizations for each time t; i.e. for each t minimize:

$$\sum _{n=1}^N{\Vert {\mathbf{P}}^n\left({\mathbf{R}}^t\left({\overline{\mathbf{s}}}_0+\sum _{j=1}^{\overline{m}}{\overline{p}}_j^t{\overline{\mathbf{s}}}_j\right)+{\mathbf{T}}^t\right)-{\mathbf{u}}^{n,t}\Vert }^2$$

with respect to R^t, T^t, p̄^t_j. In Step 2b, we break the optimization down in m̄ + 1 sub-steps. We first solve for the mean shape s̄₀ and then for each shape mode s̄_j in turn.

6.5 Experimental Evaluation

6.5.1 Input

The input to our four face model construction algorithms consists of a set of 2D tracked facial feature points u^n,t (see (26)) in 312 images captured by n = 1, 2, 3 synchronized cameras at t = 1, …, 104 time instants. We tracked 68 feature points independently in each video sequence using a 2D Active Appearance Model (AAM) (Cootes et al. 2001; Matthews and Baker 2004). Example results for 9 images (3 cameras × 3 time instants) are shown in Fig. 10. We also include the movie 2d_track.mpg showing the complete tracked input sequence. Note that the head pose variation is substantial, but not too extreme. None of the videos contain any full profiles. The input sequences were carefully chosen to maximize the head pose variation, while not causing the 2D AAM to fail. In our experience, the head pose variation shown in Fig. 10 is the most that a single 2D AAM can cope with. While more sophisticated tracking algorithms, which can cope with occlusions, severe foreshortening, and non-Lambertian reflectance have been proposed, the pose variation in Fig. 10 is about the most that can be tracked using the basic algorithm.

Fig. 10.

Three example frames from each of three synchronized stereo cameras. In total, we tracked the head independently through 104 frames in each camera using a 68 point 2D AAM (Cootes et al. 2001; Matthews and Baker 2004). The pose variation in the three sequences is the most that a single 2D AAM can cope with before it fails. See the movie 2d_track.mpg for the complete tracked input sequence

6.5.2 Qualitative Multi-View Model Construction Comparison

The results of applying each of the four algorithms: (1) non-rigid structure-from-motion (NR-SFM) (Xiao et al. 2004b), (2) multi-view non-rigid structure-from-motion (MV-SFM) (Torresani et al. 2001), (3) stereo, and (4) motion-stereo are summarized in Fig. 11. Note that the input to the NR-SFM is generated by stacking together the image sequences from each of the three cameras. All four algorithms therefore use exactly the same set of input image data.

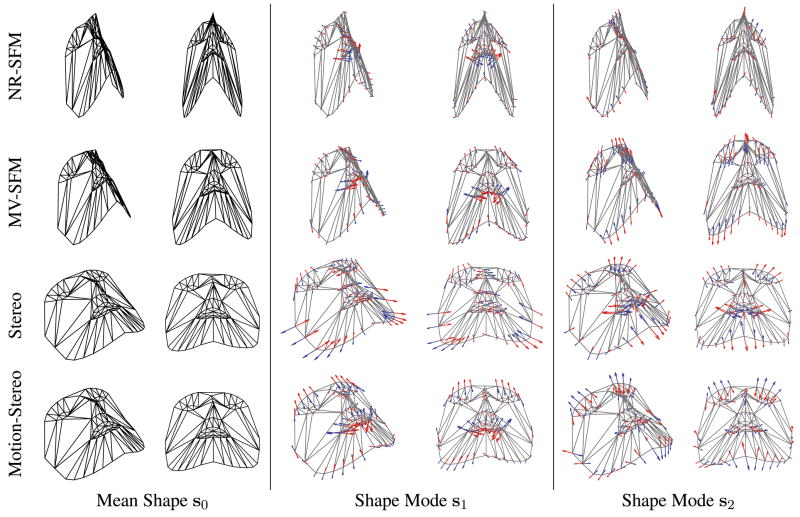
Fig. 11.

This figure shows the mean shape and first two shape modes of the single-view and multi-view non-rigid structure-from-motion models, the stereo model and the motion-stereo model. The main thing to note is that the non-rigid structure-from-motion models are “stretched” in the depth direction

For each model, we display the mean shape (s̄₀) and the first two shape modes (s̄₁, s̄₂) from two viewpoints to help the reader visualize the 3D structure. The main thing to note in Fig. 11 is how “stretched” the NR-SFM and the MV-SFM models are. The depth (z) values of all of the points in the mean shape appear to have been scaled by a constant multiplier. The underlying cause of this stretching is the Bas-Relief ambiguity which occurs when applying (non-rigid) structure-from-motion to data with little pose variation (Zhang and Faugeras 1992a; Szeliski and Kang 1997; Soatto and Brockett 1998; Hartley and Zisserman 2000). The problem manifests itself for both linear (NR-SFM) (Bregler et al. 2000; Brand 2001; Xiao et al. 2004b) and nonlinear (MV-SFM) (Torresani et al. 2001) algorithms. The MV-SFM model is slightly better than the NR-SFM model but the ambiguity persists as the problem is in the data. (Because the problem is an ambiguity, it is possible that by chance the scale may be chosen more accurately. The chance of accurate estimation of scale increases the more pose variation there is, and the less noise there is (Zhang and Faugeras 1992a; Szeliski and Kang 1997; Soatto and Brockett 1998; Hartley and Zisserman 2000).) The motion-stereo and stereo models do not suffer from this problem. In the next section we present a quantitative comparison using the calibration algorithm derived in Sect. 4.

6.5.3 Quantitative Comparison using Camera Calibration

In this section we quantitatively compare the performance of the four 3D face model construction algorithms in terms of how well the resulting models can be used to perform camera calibration using the algorithm in Sect. 4.5. One possible way of obtaining quantitative results might be to capture range data as ground-truth. This approach, however, requires (1) calibrating and (2) aligning the range data to the image data. Static range data also cannot be used to evaluate the deformable 3D shape modes. Ideally, we would like a way of evaluating the 3D fidelity of the face models using video data of a moving face.

The algorithm in Sect. 4.5 is used to calibrate weak perspective camera matrices for a set of stereo cameras using a 3D face model. By comparing the results of this algorithm with ground-truth calibration data, we can indirectly measure the 3D fidelity of the face models. The relative orientation component of the calibration primarily measures the pose estimation accuracy of the algorithms, without any absolute head pose ground-truth. Estimating the focal lengths and the epipolar geometry requires more than the relative orientation. Accurate focal lengths and epipolar geometry requires the accurate non-rigid 3D tracking of the face in an extended sequence.

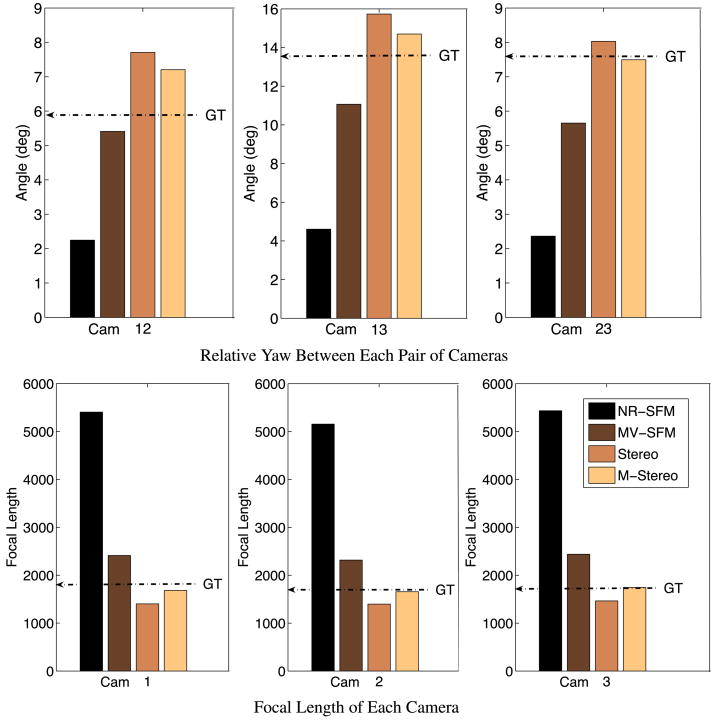
We implemented the multi-view single optimization calibration algorithm in Sect. 4.5 and compared the results with a calibration performed using a calibration standard grid and the Matlab Camera Calibration Toolbox (Bouguet 2005). In Fig. 12 we present results for the yaw rotation (about the vertical axis) between each pair of the three cameras and for each of the three focal lengths. The yaw between each pair of the three cameras was computed from the relative rotation matrices of the three cameras. We include results for each of the four models, and compare them to the ground-truth. The results in Fig. 12 clearly show the motion-stereo algorithm to perform the best. The results for the NR-SFM model are a long way off. The yaw⁸ is underestimated by a large factor, and the focal length overestimated by a similar factor. Based on the results in Fig. 11, this is to be expected. The face model is too deep, so a medium amount of parallax is generated by a too small yaw angle. Similarly, a scaling of the model is interpreted as a too large motion in the depth direction and so too large a focal length. The MV-SFM model also suffers from the same problem due to the scaled nature of the model albeit generating better results than the NR-SFM model. Overall, the motion-stereo⁹ algorithm clearly out performs both these algorithms and gives estimates of yaw and focal lengths that are comparable to ground-truth calibration data (computed using the Matlab camera calibration toolbox (Bouguet 2005)). To further emphasize this observation, we compute the percentage deviation of the yaw and focal length estimates of each 3D model from the ground-truth data. Although the bar graphs in Fig. 12 may look similar, the motion-stereo results for the focal length are several times better than the stereo or MV-SFM results by the relative error measure in Table 2.

Fig. 12.

A quantitative evaluation of the 3D fidelity of the models, obtained by using the models to calibrate the cameras using the algorithm in Sect. 4.5. The results show the motion-stereo algorithm to perform the best. The single-view non-rigid structure-from-motion model results in estimates of the yaw and focal length that are both off by a large factor. The two error factors are roughly the same. Using multi-view non-rigid structure-from-motion does help in reducing the errors to a significant degree, but the results are still not as good as the motion-stereo model. GT refers to the ground truth values computed using the Matlab camera calibration toolbox (Bouguet 2005)

Table 2.

This table summarizes the results presented in Fig. 12. For each 3D model we compute the percentage deviation of the relative “yaw” between each pair of cameras and focal length of each camera from the ground-truth data (computed using the Matlab camera calibration toolbox (Bouguet 2005)). The motion-stereo model results in estimates of yaw and focal length that are both comparable to the ground-truth values whereas the estimates from the non-rigid structure-from-motion (NR-SFM) model are both off by a large factor. The multi-view non-rigid structure-from-motion (MV-SFM) model performs better than the NR-SFM model but overall the motion-stereo model performs the best

	Relative yaw			Focal length
	Cam 12	Cam 13	Cam 23	Cam 1	Cam 2	Cam 3
NR-SFM	62.1%	66.2%	68.9%	193.5%	201.7%	214.8%
MV-SFM	8.6%	18.8%	25.7%	30.9%	35.5%	41.2%
Stereo	30.2%	15.4%	5.5%	23.9%	18.2%	15.1%
Motion-Stereo	21.7%	7.8%	1.5%	8.7%	3.0%	1.1%

7 Conclusion

7.1 Summary

In this paper we have studied multi-view AAM model fitting and construction. In Sect. 3 we have described an algorithm to fit a single 2D+3D AAM to N images captured simultaneously by N uncalibrated cameras. In the process, our algorithm computes: 2D shape parameters for each image, a single set of global 3D shape parameters, the scaled orthographic camera matrix for each view, and appearance parameters for each image (which may be different due to different camera response functions). Our algorithm enforces the constraints that all of these quantities are physically consistent in the 3D scene. The algorithm operates approximately N times slower than the real-time single image 2D+3D AAM fitting algorithm (Matthews et al. 2007; Xiao et al. 2004a). We have shown our multi-view 2D+3D AAM algorithm to be both slightly more robust and converge more quickly than the single-view 2D+3D AAM algorithm, which is itself more robust than the single-view 2D AAM algorithm (Matthews and Baker 2004).

In Sect. 4 we have shown how the multi-view face model fitting algorithm can be extended to calibrate a weak perspective (or full perspective) camera model. In essence, we use the human face as a (non-rigid) calibration grid.

We demonstrated that the resulting calibration is of comparable accuracy to that obtained using a calibration grid. We have also shown in Sect. 5, how the calibration algorithms described in this paper can be used to improve the performance of multi-view face model fitting. The calibrated multi-view algorithms perform better than the uncalibrated multi-view algorithm, which performs better than the 2D+3D single-view algorithm in terms of frequency of convergence and rate of convergence towards ground-truth when perturbed from the ground-truth data.

In Sect. 6 we proposed a calibrated multi-view 3D model construction algorithm that is superior to existing single-view and multi-view algorithms. We have shown that constructing a 3D face model using a single-view or multi-view non-rigid structure-from-motion algorithm suffers from the Bas-Relief ambiguity that may result in a “scaled” (stretched/compressed) model when applied to data containing pose variation typical of that which can be obtained using a standard face tracker such as a 2D Active Appearance Model (Cootes et al. 2001; Matthews and Baker 2004). We have shown how using calibrated multi-view motion-stereo can eliminate this ambiguity and yield face models with higher 3D fidelity. In Sect. 6.5.3 we quantitatively compared the fidelity of the 3D models described in Sect. 6 using the calibration algorithm in Sect. 4.5 and showed that calibrated multi-view motion-stereo algorithm performs the best for calibration of camera relative orientations and focal lengths.

7.2 Discussion

In this paper we have shown how multi-view data can be used to improve both the fitting and construction of face models. Multiple images always provide more information, but it is not always obvious how best to take advantage of it. One of the interesting results of this paper is that camera calibration considerably improves the performance of multi-view model fitting and construction. In fact the results in Figs. 9 and 12 show that the benefit of using calibrated multi-view over uncalibrated multi-view is in most cases perhaps even bigger than the benefit of using uncalibrated multi-view over single-view. As model construction is typically performed offline it is not a problem to use calibrated cameras. However, in the case of model fitting, assuming calibration is not so easy. The cameras may be moved, they may be pan-tilt, or it may not be possible to enter the scene. So automatic calibration is important in many applications and dramatically improves fitting performance.

7.3 Future Work

In terms of multi-view 3D model construction, one limitation of our motion-stereo algorithm is that it only computes the shape model for 68 points on the face. One area for future work would be to extend our algorithm to compute dense 3D shape models. One possibility is to use dense stereo to compute the 3D model, assuming calibrated cameras, followed by optical flow methods (Brand 2001; Jones and Poggio 1998) or automatic construction methods (Baker et al. 2004) to find the relationship between views.

In terms of multi-view fitting, one area of future work is batch fitting over time to a video sequence. The main difference between a video sequence and a set of simultaneously captured multi-view images is that the face cannot be assumed to have the same 3D shape in all images. However, it is possible that the multi-view algorithms can be extended to temporal sequences by imposing the constraint that the 3D shape does not change very fast; i.e. impose soft constraints on the 3D shape over time instead of the hard constraint that it is exactly the same in each of the views.