Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2009 Sep 22;81(20):8577–8584. doi: 10.1021/ac901563j

Inkjet Metrology: High-Accuracy Mass Measurements of Microdroplets Produced by a Drop-on-Demand Dispenser

R Michael Verkouteren 1,*, Jennifer R Verkouteren 1
PMCID: PMC2762308  PMID: 19824716

Abstract

We describe gravimetric methods for measuring the mass of droplets generated by a drop-on-demand (DOD) microdispenser. Droplets are deposited, either continuously at a known frequency or as a burst of known number, into a cylinder positioned on a submicrogram balance. Mass measurements are acquired precisely by computer, and results are corrected for evaporation. Capabilities are demonstrated using isobutyl alcohol droplets. For ejection rates greater than 100 Hz, the repeatability of droplet mass measurements was 0.2%, while the combined relative standard uncertainty (uc) was 0.9%. When bursts of droplets were dispensed, the limit of quantitation was 72 μg (1490 droplets) with uc = 1.0%. Individual droplet size in a burst was evaluated by high-speed videography. Diameters were consistent from the tenth droplet onward, and the mass of an individual droplet was best estimated by the average droplet mass with a combined uncertainty of about 1%. Diameters of the first several droplets were anomalous, but their contribution was accounted for when dispensing bursts. Above the limits of quantitation, the gravimetric methods provided statistically equivalent results and permit detailed study of operational factors that influence droplet mass during dispensing, including the development of reliable microassays and standard materials using DOD technologies.

Quality assurance procedures for nanoliter and picoliter dispense technologies are critically important across many advanced and emerging applications. Microfabrications of ceramics,1,2 electronics,3−5 advanced polymers,(6) photovoltaic arrays,7,8 and solder-based materials(9) require quantitative deposition and exact positioning of micrometer-sized “building blocks” to ensure reproducible feature size in partially and fully dense materials. Small volume dispense technologies are also used for precise and accurate delivery of fluid volumes in miniaturized analytical assays,10−18 microfluidic chips,(19) microelectromechanical system devices,(20) olfactometers,(21) vapor generators,(22) and trace reference materials.(23) In large part, the limitations and uncertainties inherent in these applications are due to practical difficulties associated with determination and control of the size of the dispensed aliquots. These practical difficulties include subtle changes in operational and environmental variables, and physicochemical changes around the dispense orifice that can influence mass delivery.

A rich and varied literature exists on the physics of liquid jets and droplet formation.24−30 Volumes in the zeptoliter (10−21 L) range have been reported,(31) although femtoliter (10−15 L) and picoliter (10−12 L) dispensing are more common. Calibrated microscopic optical imaging and fluorescent techniques have been widely utilized to measure ejected droplet dimensions, and these approaches can offer fairly high precision when automated boundary and threshold recognition procedures are employed. However, because these procedures are somewhat arbitrary, and effects such as fluid oscillations, droplet flattening during flight, and refraction may introduce bias as well, uncertainties in boundary delineations and diameter measurements can translate to volume and mass uncertainties easily exceeding 10%.

Individual droplet masses in the nanogram (10−9 g) range have been measured precisely on cantilevers, quartz crystal microbalances, and nanomechanical resonators.32−35 Absolute uncertainties, however, may be high because sensor responses are significantly influenced by surface morphology, fluid rheology, and contact variables. As a result, these systems require careful calibration specific to the application.36−40 If calibrated correctly, these systems are useful for characterizations of small numbers of droplets but not for applications that utilize drop-on-demand (DOD) dispensing of multiple droplets.(41) The first several droplets that emerge from an orifice may vary in character (mass, velocity, trajectory) from later droplets because of acoustic and fluid resonances and orifice conditioning effects such as wetting.42,43 Applications that utilize droplets from DOD bursts or continuous ejection (e.g., printing “on-the-fly”) require calibration that realistically reflects the dispense method.

Curiously, no gravimetric methods were found in the open literature that employ a traditional microbalance for characterizing microdroplet mass. Such gravimetric measurements would be unaffected by the geometrical factors (and presence of satellites) that confound optical approaches and would enable strong traceability to primary standards in the Systeme Internationale (SI).(44) Here, we report the development of three such methods for reliable determination of microdroplet mass with relative combined standard uncertainties near 1%, a level not previously reported for DOD dispensing. These methods were demonstrated using isobutyl alcohol droplets ejected from a commercial piezoelectric DOD microdispenser. We correct for evaporation, consider air−vapor buoyancy, and other systematic effects, and compare gravimetric data with optical determinations. High-speed videography of droplet sequences is used to evaluate variation in individual droplet sizes during ejection and delivery of droplet bursts.

Experimental Section

Droplet Dispense and Characterization System

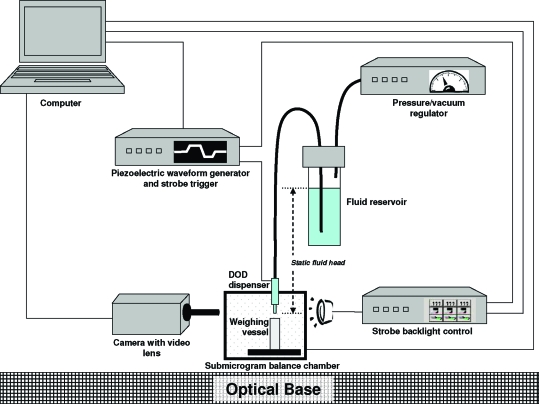
All work was performed within the NIST Advanced Measurement Laboratory complex, in which room temperature and relative humidity are specified to within 0.25 °C and 5%, respectively. A commercial piezoelectric DOD system (JetLab4, MicroFab Technologies, Plano, TX) was used with some modifications (Figure 1). (Certain commercial equipment, instruments, or materials are identified in this document. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products identified are necessarily the best available for the purpose.) A submicrogram balance (Mettler-Toledo Model UMT2, 0.1 μg resolution, with serial interface to a computer) was positioned under the DOD dispensing device (MicroFab model MJ-ABP-01−50-DLC, 50 μm orifice), the holder for which was designed to allow vertical adjustment by the Z-stage into the balance chamber to a position about 2 mm from the mouth of a lightweight weighing vessel {Elemental Microanalysis Ltd., 12 mm (height) × 6 mm (diameter) smooth-tin cylinder}. Two antistatic strips (241Am, NRD Model 2U500, Grand Island, NY) were hung within 2 cm of the dispensing device and balance pan. Fluid {isobutyl alcohol (IBA), Fisher Scientific, ACS grade} for the dispensing device was introduced through microbore polytetrafluoroethylene tubing (1.1 mm ID, 1.7 mm OD) from a fluid reservoir positioned above the dispensing device. Because this positioning generated an excessively positive static fluid head, the headspace pressure in this reservoir was reduced below atmospheric pressure through a pneumatic pressure/vacuum regulator (Fairchild, Model 16) and monitored by a differential capacitance manometer (MKS Baratron, Model 698A, 1000 mbar full-scale with 0.001 mbar resolution). The JetLab4 has an integrated piezoelectric waveform generator that also outputs a 3.5 V trigger signal. We added an oscilloscope (Tektronics, Model TDS 2024B) with passive voltage probes (10 MΩ,13.3 pF inputs) to monitor the driving waveform and used the 3.5 V signal to trigger a light-emitting diode backlight array (Advanced Illumination, model BL1520-WHI) powered by a strobe controller (Advanced Illumination, model S4000). Digital images were captured by either a charged-coupled-device (CCD) camera (5 Mpixels, 1.7 cm sensor size) with video lens (Edmund Optics Infinistix, 3× magnification, 18 mm working distance, 1.4 μm per pixel resolution) using a strobed LED backlight array, or a high-speed camera (Photron Ultima APX-RS) with adjustable magnification (4× to 64×, 35 mm working distance) using constant backlight illumination. The images from either camera were transmitted to a computer by firewire bus and processed through image analysis software (Media Cybernetics, ImagePro Plus v. 5.1).

Figure 1.

Figure 1

Open in a new tab

Droplet generation and characterization system.

Selection of Operational Dispense Conditions

Operational factors that affect droplet size in DOD printing include the orifice diameter and its surface condition, the rheological properties of the dispensed fluid, the driving waveform and ejection frequency, the total fluidic head, and environmental factors such as ambient temperature and mechanical vibration background. For this study we attempted to hold all operational variables constant; detailed descriptions and measurements of operational effects are reserved for later studies. Here, a fixed driving waveform was used to dispense a single fluid from a DOD device at only a few ejection frequencies. As practically possible, we controlled the surface condition of the orifice, the total fluidic head, and environmental conditions, yet together these still represented inherent sources of variation that randomly influenced droplet size. Day-to-day droplet mass variations of about 1% were observed and will be described in the uncertainty evaluation. The cleanliness of the dispense orifice was greatly facilitated by using a pure fluid. We have found that the use of solutions requires frequent ultrasonic treatments to prevent material buildup around the dispense orifice, buildup that otherwise would lead to significant changes in droplet size over time.

Droplet Diameter Analysis

Both camera systems were calibrated against a pitch standard from Geller Microanalytical Laboratory (Topsfield, MA) and were used to determine average droplet diameters at a location 1000 μm below the orifice. At this location, asphericities in actual droplet shape, due to induced oscillations from absorption of the liquid thread, were sufficiently quenched and assumed to be negligible. Grey level of the background was adjusted manually to match a fixed standard, and an automated thresholding process was used to find the perimeter of the droplet. For the CCD camera, these images were captured by strobed illumination (duration 2 μs) accompanied by an elongation artifact of the droplet in the direction of travel (for a droplet traveling 2 m/s, this elongation amounted to 4 μm, or about 8% of the diameter). Therefore, we chose the minimum diameter (measured normal to the direction of travel and therefore lacking a velocity component) to estimate the average droplet diameters. The minimum diameter was converted to volume by assuming sphericity and then to mass through multiplication with density of IBA at room temperature.

Droplet images captured by high-speed videography were used to intercompare selected individual droplet diameters from the first droplet to beyond the 8000th droplet. Video images of droplets ejected from the orifice were taken at 30 000 frames/s, with a shutter speed of 11 μs and 128 × 256 pixel resolution. Background pixels were subtracted from each image, and smoothed droplet perimeters were determined through an arbitrary but consistent contrast threshold procedure. Diameters were determined for individual droplets within the following dispense intervals: 1 to 100 droplets, 500 to 530 droplets, 1000 to 1030 droplets, 2000 to 2030 droplets, 5000 to 5030 droplets, and 8800 to 8830 droplets.

Gravimetry

Droplet mass was measured by jetting into a weighing vessel centered on the pan of the submicrogram balance. Time-stamped balance readings were collected at 11-s intervals by a computer that controlled the mass acquisition through the program BalanceLink, v.4.0.2 (Mettler-Toledo). [Mass acquisition intervals of 11-s were used to avoid periodic variations observed in measured mass differences arising from phase effects with the serial communication update rate of the balance (specified by the manufacturer as about one update per second). This effect would be less of an issue with microbalances that have speedier communication update rates, but the user should still be aware of this effect and, if necessary, take appropriate measures to synchronize the mass acquisition interval with the update rate.] Control over the evaporation of the jetted fluid was accomplished by (1) placing several open vessels of fluid inside the balance chamber to help saturate the air with fluid vapors, (2) minimizing air drafts in and around the balance by use of a secondary enclosure, and (3) having at least 30 mg of fluid in the weighing vessel so that the steady-state evaporation from the vessel would be unchanged by the droplet ejection. Vibrations affecting performance of the microbalance were minimized by disabling the movement stages of the JetLab4. We developed three methods: burst gravimetry, continuous droplet gravimetry, and pulsed burst gravimetry. Each was used to determine either average droplet mass or the cumulative mass of individual bursts of droplets. Table 1 distinguishes these methods on the basis of droplet delivery and application.

Table 1. Summary of Gravimetric Methods.

gravimetric method delivered aliquot application example
burst droplet bursts totaling over 1000 droplets biochemical delivery systems
continuous droplets ejected continuously at a fixed frequency continuous trace vapor generation
pulsed burst continuous bursts containing less than 1000 droplets per burst; droplets ejected at fixed frequency; 1-s wait between bursts reference material deposited in 10-droplet arrays
Open in a new tab

Burst Gravimetry

After measurement of a stable fluid evaporation rate for at least five 11-s intervals, a known number of droplets is ejected into the weighing vessel at a chosen ejection frequency, and mass measurements are collected for at least five more intervals. Results are calculated through eq 1,

graphic file with name ac-2009-01563j_m001.jpg

where m is the average mass of a single droplet in the burst, N is the total number of droplets deposited, and M1 and M2 are extrapolated balance readings of the evaporation trend, before and after ejection, respectively, at time τ. We define time τ as the point halfway between the last stable differential evaporation reading before ejection (ta) and the first stable differential evaporation reading after ejection (tb) (see Figure 2). We apply the FORECAST linear regression function in Microsoft Excel to obtain the predictions of M1 and M2. Because this method requires the least amount of dispensing and fluid waste, it is highly applicable to characterizing droplets from limited or precious solutions. This method also allows the use of multiple bursts rather than a single burst of droplets. In certain applications, large numbers of droplets may be deposited in arrays of multiple bursts, so the mass per burst may be the desired quantity. In these cases, eq 1 may still be applied, where the value of m is the mass per burst and N is the number of bursts dispensed. Note that this method depends on the total droplet or burst count rather than on ejection frequency.

Figure 2.

Figure 2

Open in a new tab

Typical time-stamped microbalance data in burst gravimetry. Mass data were collected in 11-s intervals, and a single burst of 999 droplets was dispensed immediately after time ta. Dispensed mass was determined by subtraction of M1 from M2, which are the extrapolated estimates of the steady-state evaporation trends before and after the ejection, respectively, at time τ. Here, average mass per droplet was 48.07 ng.

Continuous Droplet Gravimetry

After verification of a stable evaporation rate for at least five 11-s intervals, droplets are ejected continuously into the weighing vessel for another five intervals. When ejection is stopped, the evaporation measurements are repeated for an additional five intervals. Results are obtained through eq 2, where m is the average mass of a single

graphic file with name ac-2009-01563j_m002.jpg

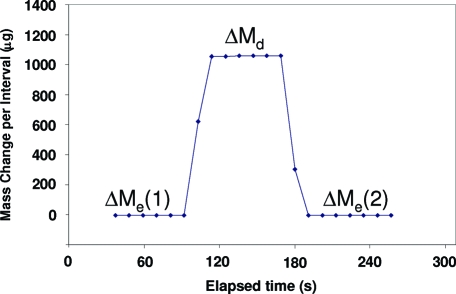
droplet, ΔMd and ΔMe are the average changes in mass measured during the droplet dispense intervals and evaporation intervals, respectively, ti is the acquisition interval, and f is the ejection rate. Figure 3 shows typical data. This method is apt for calibrating systems that use uninterrupted streams of droplets, such as continuous inkjet printer systems and vapor generators or where individual droplets are deflected from droplet streams to a target by electrostatic lenses.

Figure 3.

Figure 3

Open in a new tab

Typical time-stamped data for continuous ejection gravimetry using a droplet ejection frequency of 2004 Hz. The plot shows processed data from the microbalance (collected in 11-s intervals) before, during, and after droplet delivery, where ΔMe(1) and ΔMe(2) are the average mass changes per interval due to fluid evaporation from the vessel before and after continuous ejection, and ΔMd is the average mass change per interval observed during droplet delivery.

Pulsed Burst Gravimetry

Where small to moderate (10 to 1000) numbers of droplets are deposited together as a burst, the mass per burst may be the desired quantity. For these cases, the method is applied to continuously pulsed bursts of droplets. The dispense system is programmed to eject a fixed number of droplets at each trigger signal, and trigger signals separated by 1-s delays are transmitted for at least 1 min. For this particular method, eq 2 is applied because this method is similar to the continuous droplet approach, except that now the value of m is the mass per burst. The value of f is the reciprocal of the pulse time, which is the sum of the wait time and the burst duration. Note that the continuous droplet and pulsed burst methods depend on droplet or burst ejection frequency and not on the total number of droplets or bursts deposited. Also note that continuous droplet ejection at 1 Hz is essentially the same as pulsed burst ejection for single droplet “bursts”.

Results and Discussion

We report performance metrics for the gravimetric methods described, as applied to IBA. These include the short-term repeatabilities and long-term combined standard uncertainties of the measurements, the latter which consider analytical imprecision and potential biases arising from unavoidable variations in operating conditions. Also, we report the limits of quantitation (LOQ); that is, the minimum droplet (or burst) ejection rate or dispensed mass that will grant reliable determination of average droplet (or burst) mass. The appropriateness of applying average droplet mass to the mass of individual droplets will be discussed, followed by an evaluation of uncertainty.

Gravimetric Performance and Limits of Quantitation

The variance in the fluid evaporation rate from the weighing vessel places a lower limit of quantitation on the continuous droplet method. The evaporation rate observed for IBA from the weighing vessel was 490 ng/s with a standard deviation of 2.7 ng/s. This was determined by monitoring the evaporation for 125 eleven-second intervals and averaging every five measurements to obtain 25 independent values. The LOQ for the continuous droplet method, defined as 5 times the standard deviation of the measured IBA evaporation rate, corresponded to 14 ng/s and was equivalent to the mass of individual droplets delivered at about 0.3 Hz. Replicated (n = 12) measurements of average droplet mass dispensed at 1 Hz gave 53.2 ng with an RSD = 5%. This was repeated at 4 Hz, which again gave 53.2 ng but with an improved RSD of 0.9%. At an ejection frequency of 2004 Hz, repeatability improved to 0.2% while average droplet mass decreased to 48.4 ng. These observations suggest that “first droplets” emerge at ejection frequencies up to at least 4 Hz, a dispense rate allowing sufficient time for return to quiescence between droplets; then, at higher frequencies, subsequent droplets in the continuous stream change in size due to wetting changes at the orifice and the establishment of fluidic resonances. This observation is supported later in the discussion on droplet scalability and the “first droplets” incongruity. To determine LOQ values for other jetable fluids in our system, we separately monitored the evaporation of n-propanol, 2-propanol, 2-ethylhexanol, ethyl lactate, and water, which span pertinent thermodynamic and kinetic properties, including viscosity, enthalpy of vaporation, vapor density, surface tension, and relative evaporation rate.(45) All these fluids had LOQs similar to IBA. 2-Propanol had the highest rate of evaporation and variation in our system: about 2500 ng/s ± 6.6 ng/s, yet this amount still represented an LOQ below a droplet dispense rate of 1 Hz.

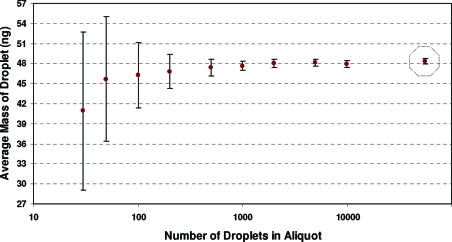
The LOQ of the burst method was restricted by the limitations of the microbalance rather than by the variance in the evaporation measurements. The microbalance manufacturer reported two specifications for the minimum weight quantifiable: “USP” (0.45 mg + 7.5G × 10−5) and “U = 1%” (0.03 mg + 5G × 10−6), where G is the gross (tare + sample) weight. Under these specifications, the two minimum weights for our system were 476 μg (USP) and 32 μg (U = 1%), which corresponded to aliquots of about 9500 droplets and 640 droplets, respectively. These quantitation levels were tested empirically by replicated measurements of average droplet mass taken across dispensed aliquots of 30 to 10 000 droplets ejected at 2004 Hz. Figure 4 shows the average droplet mass determined at each level along with dispersion intervals (±2 standard deviations; n = 12). The average droplet mass determined by the continuous droplet method is also displayed. The uncertainties in the burst method data increased significantly when attempting to measure less than a few thousand drops, and mean values also decreased. We chose to define the burst method LOQ as the minimum amount of analyte that resulted in an average droplet size within 1% of the continuous droplet method value. This was 72 μg (1490 droplets), a value between the two LOQ values specified by the microbalance manufacturer. For a larger number of droplets, measurement repeatability approached the limit defined by the variations in the evaporation measurements, which was 0.21% as propagated through eq 1. We obtained a repeatability of 0.31% (uc = 1.1%) for replicated burst mass determinations using 5000 droplets. Using a two-sided t test, the continuous droplet value was compared with the burst levels above the LOQ, which allowed us to conclude that, at the 95% confidence level, the two methods gave equivalent results.

Figure 4.

Figure 4

Open in a new tab

Microbalance performance in burst gravimetry. The 30, 50, 100, 200, and 500 droplet aliquots were dispensed in single bursts. For larger aliquots, multiple bursts of 500 droplets were used. All analyses were repeated 12 times; averages and 2σ error bars are shown. The average droplet mass determined by continuous gravimetry is shown within the octagon.

Other Comparisons

Results from dimensional analysis and from the continuous droplet and burst methods, all obtained by measurements replicated across different days with operational variables nominally identical, were compared to test for systematic differences in the determination of droplet mass (Table 2). As before, two-sided t tests allow us to conclude that, at 95% confidence, the droplet mass values obtained by continuous droplet and burst methods were equivalent statistically. In contrast, systematic differences were quite evident when comparing dimensional analysis results to the gravimetric results. Estimates of droplet mass determined through diameter measurements were greater by about 16%. This corresponds to a positive bias in measured droplet diameter of about 5%, about half which could be due to the limited resolution of our optical system and the remainder by uncertainties in droplet boundary distinctions that are influenced by refraction and background contrast levels. Optical systems exist that are superior to the optical system described here, and they are an important tool for imaging droplet formation and monitoring stability, but to compete with the precision and accuracy of a gravimetric determination of droplet mass or volume, the standard uncertainty and combined uncertainty for an optical diameter measurement of a 50 μm spherical droplet would need to approach 0.04 and 0.17 μm, respectively.

Table 2. Comparison of Average Droplet Mass Calculated by Three Methods.
method calculated droplet mass (ng) and reproducibility (RSD)
continuous droplet gravimetry (2004 Hz) 48.70 (0.9%) N = 12
burst gravimetry (5000 drops @ 2004 Hz) 48.75 (1.1%) N = 12
dimensional analysis (CCD camera system) 56.41 (7.8%) N = 10
Open in a new tab

Scalability and the “First Droplets” Incongruity

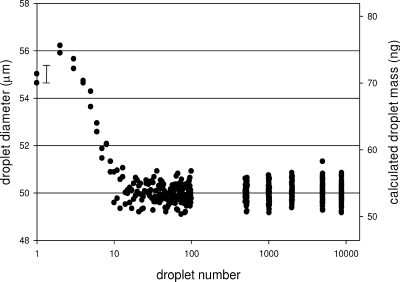
The gravimetric methods described here provide an average mass per droplet dispensed. Prior studies30,33 have suggested that variations in individual droplet size from DOD dispensers, at least after the first several droplets are ejected, are insignificant to most applications and usually within the uncertainty of the optical measurements. If so, it was expected that integrated mass measurements of large numbers of droplets were applicable to the mass of a single droplet. This assumption was addressed by measuring and intercomparing individual droplet diameters emerging from our DOD dispenser. Using high-speed videography, droplet diameters were measured within a 8850-drop burst ejected at 2004 Hz (Figure 5). This experiment was repeated at several fluidic head pressures, which substantially influenced the droplet diameter profiles.(46) The profile in Figure 5 represents an extreme case where fluidic head pressure was set at a value about 15 mbar below atmospheric pressure. Measurements indicate that the first nine or ten ejected droplets were substantially different in diameter (hence mass) from subsequent droplets. In this sequence, the first droplet appeared different in character. It emerged with the highest velocity (data not shown) while the second droplet had the largest diameter. The third through tenth droplets decreased in diameter until reaching a steady state. Variation of the mean in droplet diameter was estimated by the average in relative standard errors (RSEs) in the 30-droplet sequences starting at the 70th, 500th, 1000th, 2000th, 5000th, and 8800th droplets. In this case, average RSE = 0.13%. As droplet mass is proportional to the cube of the diameter, the measurement imprecision in estimating individual droplet mass by this dimensional method translates to 0.38%. While optical bias is present (here, about +10% when converted to mass), the method is adequately precise for the purpose of projecting droplet calibration to all droplets dispensed after the tenth droplet. The problem, of course, is that unless the first several droplets are somehow deflected away during delivery, they are included in the dispense process and would bias the mass delivered at a proportion dependent upon their dilution by subsequent droplets in the dispensed aliquot. In this particular instance, we determined that the average mass of the first ten droplets was about 25% larger than subsequent droplets. This would result in biases of about 7% when delivering 30 droplets, 2% for 100 droplets, and 1% for 200 droplets. If an application requires highly accurate deposition of tens of droplets, the effect may be accounted for, albeit tediously, by analysis with a high-speed camera. Alternatively, determining the average mass per burst, as outlined in the pulsed burst method, accounts directly for mass differences in the droplets dispensed. We set the fluidic head pressure to a value about 2 mbar lower than normal to induce a “first droplets” incongruity and programmed the dispense device to deliver 200 ten-drop bursts, each burst followed by a time delay of 1 s with the experiment repeated five times. The gravimetric measurement data were evaluated two ways: (1) through eq 1 where N = 200 bursts, which gave 486 ng (RSD = 2.3%) per burst, and (2) through eq 2 where f = 0.858 Hz, which gave 479 ng (RSD = 1.9%) per burst. These results indicate that 48 ng was the average droplet mass for the first ten droplets dispensed. Under the same fluid head pressure and ejection frequency, we then dispensed droplets continuously and obtained an average mass of 44.7 ng (RSD = 0.6%) per droplet through eq 2 where f = 2004 Hz. These measurements established that the first ten drops were significantly different from subsequent droplets because of a “first droplets” incongruity similar to that seen in Figure 5. The incongruity has been explained as an approach to steady-state acoustic resonances within the dispense device, as well as the establishment of fluid resonances at the meniscus and wetting of the orifice.42,47 Fortunately, the incongruity may be minimized by careful tuning and control of fluidic head pressure.(46)

Figure 5.

Figure 5

Open in a new tab

Nearly ten thousand droplets were individually imaged by a high-speed video camera, and diameters of 250 selected droplets were determined by image analysis. Diameters (and derived masses) are plotted for the following sequences: droplets 1 to 100, droplets 500 to 529, droplets 1000 to 1029, droplets 2000 to 2029, droplets 5000 to 5030, and droplets 8800 to 8829. Imprecision of any single measurement is represented by the 2σ error bar placed near the data for the first droplet. Variation in the mean diameter of droplet numbers 10 through 8829 is approximated by the thickness of a horizontal grid line.

Uncertainty Evaluation

The uncertainty in the values of droplet (or burst) mass m, derived from gravimetric measurements, is expressed as either a standard combined uncertainty (uc) or a relative combined uncertainty (uc/m) and is determined according to the ISO and NIST Guides.(48) Values of uc are intended to represent, at the level of one standard deviation, the combined effects of gravimetric imprecision, microbalance calibration uncertainty, and irreproducibility in dispense conditions leading to variations in droplet size. Gravimetric imprecision was determined empirically for each method as previously outlined and ranged from 0.2% to 5% depending on method and aliquot amount. Microbalance uncertainty for differential mass measurements, after testing with standard weights, was 0.05%. Slight but unavoidable variations in fluidic head pressure and orifice condition contributed about 0.5% random variation in droplet mass. We considered other possible systematic effects arising from buoyancy effects, droplet momentum transfer, droplet evaporation, baseline evaporation changes, and fluidic head control. It was discovered that some of these factors could be significant under certain circumstances, but their effects could also be minimized. The gravimetric procedures as described were developed in consideration of these factors, and while some factors add random uncertainty none significantly bias the gravimetric results under the conditions specified. The following paragraphs describe our efforts in this regard.

Buoyancy Correction

Forces produced on the single-pan microbalance are proportional to the masses and volumes of the dispensed microdroplets. On such microbalances, buoyancy corrections (CB) arising from the volume factor are normally applied through eq 3, where

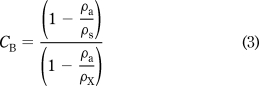graphic file with name ac-2009-01563j_m003.jpg

ρa, ρx, and ρs are the densities of air, the weighed material, and the standard material used for calibration, respectively.(49) Taking the density of air as 1.2 kg m−3, the density of IBA as 802 kg m−3, and the density of the standard material (303 stainless steel) as 8027 kg m−3, the correction multiplier was an insignificant 1.00135. In our case, droplets were weighed in a vapor-saturated atmosphere, so the air density value was uncertain. We determined the correction from the vapor density effect empirically. Two stable weights were selected that would not significantly absorb IBA vapors: an empty tin vessel (40 mg; density = 7300 kg m−3), and an industrial grade diamond (100 mg; density = 3500 kg m−3). These objects were chosen to represent closely the extremes of mass and average density (hence buoyancy) of a tin vessel being filled with IBA during the gravimetric procedure. The issue was not whether the zero of the balance would change between air and vapor conditions (which it would) but rather whether a discrepancy existed in the differences between the two extreme weights when measured in air (the calibrated condition) versus when measured in vapor (the operating condition). Each object was weighed in air and in the vapor-saturated environment, and the buoyancy correction was calculated through eq 4, where CV was the correction to be applied to the observed mass difference (i.e., all differential measurements as taken in this study), and M1 and M2 were the observed weights of the tin and diamond weights in air (a) or air saturated with the fluid vapor (v), respectively. For the system utilized here, CV = 1.0005, so again the correction proved to be insignificant.

graphic file with name ac-2009-01563j_m004.jpg

Droplet Momentum

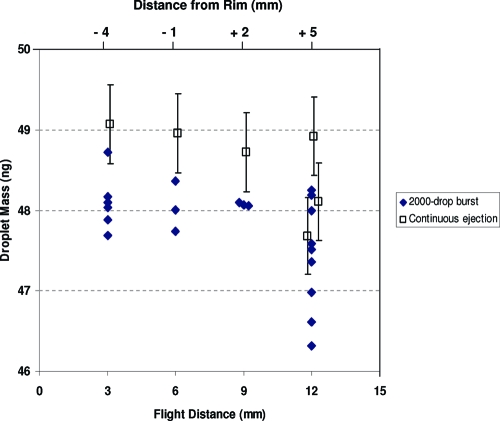
Because droplets possess velocity as well as mass, inertial force imparted by linear momentum may add to the gravitational force imparted by static droplet mass when measured by the continuous droplet method, potentially inflating the measured mass of the average droplet. Typically, a 50 ng droplet emerges from the dispense device with a velocity between 2 and 3 m/s, and after about 10 mm decelerates by air resistance to less than 0.5 m/s before impacting and coalescing with the liquid at the bottom of the weighing vessel. At 0.5 m/s, droplet momentum is 25 pN-s, and if all this momentum were transferred as an axial force during a coalescence process lasting the droplet ejection period (500 μs), a significant force of 50 nN would add to the force imparted by gravity alone: 490 nN, equal to m × g where g is the gravitational acceleration (9.81 m/s2). However, the potential mechanisms for axial and tangential partitioning of droplet momentum in the interfacial fluid layer are complex,50−53 so we measured the effect empirically. With 5 mm of fluid in the weighing vessel, droplets were ejected from the dispense device at heights of 3 mm, 6 mm, and 9 mm from the fluid. This was accomplished using the Z-stage to maintain the static head and reservoir headspace pressure, ensuring that emerging droplet mass was consistent. At the various heights, momentum transfer during droplet coalescence was expected to be systematic. Figure 6 shows the average droplet masses determined by both the continuous droplet and burst gravimetric methods at various heights (i.e., flight distance) from the surface of the fluid inside the weighing vessel. As expected, average droplet masses determined by the burst method exhibited no height influence, although scatter appeared greater at the extremes. For the continuous droplet method, there was suggestion of about a 5% increase in apparent droplet mass as the amount of transferred momentum was increased by lowering flight distance from 9 mm to 3 mm. To avoid the effect, a height of 9 mm ± 2 mm (about 2 mm above the rim of the weighing vessel) was normally maintained in our experiments. While longer distances would ensure minimal momentum transfer, a taller weighing vessel would be needed to avoid the effects seen at the 12 mm flight distance in Figure 6. There, variability in average droplet mass increases dramatically for both gravimetric methods. That variability we attribute mainly to evaporative effects (described in next section). Note that the mass values for the continuous droplet method are about 1% larger than the mass values determined by the burst method. This was the expected bias due to microbalance hysteresis in the burst method when using droplet numbers near the LOQ.

Figure 6.

Figure 6

Open in a new tab

Effect of droplet flight distance (and distance of nozzle from weighing vessel rim) on droplet mass determination. Droplets were ejected into a weighing vessel 12 mm high and filled with 5 mm of fluid. Droplet mass was determined by continuous gravimetry (open squares with 1% RSD) and burst gravimetry using 2000 droplets (filled diamonds with 1% RSD, hidden for clarity).

Droplet Evaporation

Even with open pans of IBA inside the weighing chamber, the vapor concentration inside the balance chamber was variable and less than the thermodynamic saturation limit. This suggested that partial evaporation of the droplets during their travel from the dispenser orifice into the weighing vessel may influence the mass measurements. This factor would be unimportant if the total droplet mass delivered to the target surface was the essential quantity. However, if the delivered concentration of an analyte dissolved in a droplet is the parameter of interest, then the extent of droplet evaporation during flight must be controlled. The effect of droplet evaporation was studied during the same experiment that considered the droplet momentum factor (see Figure 6). Droplets were delivered at different distances away from the rim of the weighing vessel, which changed the flight time and resultant evaporation. When the dispense device was inserted into the weighing vessel (negative values of distance to rim, Figure 6), where vapor concentrations were highest, no change in droplet mass was observed using the burst method (whereas the marginally significant increase in continuous droplet method results was attributed to momentum effects). Even at 2 mm above the rim, no effect was observed. However, when ejecting droplets at a position 5 mm above the rim, there was an increase in droplet mass variability and droplet mass loss up to 4%. Optimally, droplet ejection at 2 mm above the rim avoids evaporation effects and allows for imaging of the droplet formation process.

Conclusions

We have developed and compared methods for determination of droplet mass dispensed from a DOD dispenser that are applicable to a wide range of fluids, including semivolatile solvents. The gravimetric methods require either a continuous ejection rate of at least 14 ng/s or a burst aliquot of at least 72 μg. Above these limitations, all gravimetric methods provided consistent results. Total relative uncertainties in average droplet mass were about 1% while repeatabilities were usually less than 0.5%, which are significantly superior to optical methods. Using high-speed videography, individual diameters were measured in droplet bursts, which indicated that the first several droplets emerging from a dispense device may differ significantly in size from subsequent droplets. This effect is accounted for by pulsed burst gravimetry. Sources of uncertainty (i.e., the corrections for buoyancy, droplet momentum transfer, and evaporative losses during droplet flight) were determined to be insignificant under the operating conditions described. We anticipate use of these gravimetric methods will permit detailed study of operational and environmental factors that influence droplet mass during dispensing, facilitate calibration of high-sensitivity sensors such as quartz crystal microbalances, and enable the use of DOD dispense devices for the reliable production of trace standard materials.

Acknowledgments

We gratefully acknowledge the Science & Technology Directorate of the U.S. Department of Homeland Security and the NIST Office of Law Enforcement Standards for sponsoring this work.

References

  1. Seerdon K. A. M.; Reis N.; Evans J. R. G.; Grant P. S.; Halloran J. W.; Derby B. J. Am. Ceram. Soc 2001, 84, 2514–2520. [Google Scholar]
  2. Reis N.; Ainsley C.; Derby B. J. Appl. Phys. 2005, 97, 094903. [Google Scholar]
  3. MacFarlane D. L.; Narayan V.; Tatum J. A.; Cox W. R.; Chen T.; Hayes D. J. IEEE Photon. Technol. Lett. 1994, 6, 1112–1114. [Google Scholar]
  4. Tsai M. H.; Hwang W. S.; Chou H. H.; Hsieh P. H. Nanotechnology 2008, 19, 335304. [DOI] [PubMed] [Google Scholar]
  5. Gamerith S.; Klug A.; Scheiber H.; Scherf U.; Moderegger E.; List E. J. W. Adv. Funct. Mater. 2007, 17, 3111–3118. [Google Scholar]
  6. Shore H. J.; Harrison G. M. Phys. Fluids 2005, 17, 033104. [Google Scholar]
  7. Hebner T. R.; Wu C. C.; Marcy D.; Lu M. H.; Sturm J. C. Appl. Phys. Lett. 1998, 72, 519–521. [Google Scholar]
  8. Hoth C. N.; Schilinsky P.; Choulis S. A.; Brabec C. J. Nano Lett. 2008, 8, 2806–2813. [DOI] [PubMed] [Google Scholar]
  9. Lee T.-M.; Kang T. G.; Yang J.-S.; Jo J.; Kim K.-Y.; Choi B.-O.; Kim D.-S. IEEE Trans. Electron. Packag. Manuf. 2008, 31, 202–210. [Google Scholar]
  10. Niles W. D.; Coassin P. J. Assay Drug Dev. Technol. 2005, 3, 189–202. [DOI] [PubMed] [Google Scholar]
  11. Bruns A.; Hoffelner H.; Overmann J. FEMS Microbiol. Ecol. 2003, 45, 161–171. [DOI] [PubMed] [Google Scholar]
  12. Litborn E.; Stjernström M.; Roeraade J. Anal. Chem. 1998, 70, 4847–4852. [Google Scholar]
  13. Clark R. A.; Hietpas P. B.; Ewing A. G. Anal. Chem. 1997, 69, 259–263. [DOI] [PubMed] [Google Scholar]
  14. McGuire S.; Fisher C.; Holl M.; Meldrum D. Rev. Sci. Instrum. 2008, 79, 086111. [DOI] [PubMed] [Google Scholar]
  15. Quintero C.; Rosenstein C.; Hughes B.; Middleton R.; Kariv I. J. Biomol. Screen. 2007, 12, 891–899. [DOI] [PubMed] [Google Scholar]
  16. Englmann M.; Fekete A.; Gebefügi I.; Schmitt-Kopplin P. Anal. Bioanal. Chem. 2007, 388, 1109–1116. [DOI] [PubMed] [Google Scholar]
  17. Fittschen U. E. A.; Hauschild S.; Amberger M. A.; Lammel G.; Streli C.; Förster S.; Wobrauschek P.; Jokubonis C.; Pepponi G.; Falkenberg G.; Broekaert J. A. C. Spectrochim. Acta B 2006, 61, 1098–1104. [Google Scholar]
  18. Fittschen U. E. A.; Bings N. H.; Hauschild S.; Förster S.; Kiera A. F.; Karavani E.; Frömsdorf A.; Thiele J. Anal. Chem. 2008, 80, 1967–77. [DOI] [PubMed] [Google Scholar]
  19. Xu J.; Attinger D. J. Micromech. Microeng. 2008, 18, 065020. [Google Scholar]
  20. Bedair S. S.; Fedder G. K.. Sensors, Oct. 2007 IEEE Conference, 2007, pp 1164−1167
  21. Wallace D. B.; Taylor D.; Antohe B. V.; Achiriloaie I.; Comparini N.; Stewart R. M.; Sanghera M. K. Meas. Sci. Technol. 2006, 17, 3102–3109. [Google Scholar]
  22. Verkouteren R. M.; Gillen G.; Taylor D. W. Rev. Sci. Instrum. 2006, 77, 085104. [Google Scholar]
  23. Verkouteren M.; Gillen G.; Verkouteren J.; Fletcher R.; Windsor E.; Smith W. ITEA J. Test Eval. 2007, 28, 16–18. [Google Scholar]
  24. Fromm J. E. IBM J. Res. Dev. 1984, 28, 322–333. [Google Scholar]
  25. Eggers J.; Villermaux E. Rep. Prog. Phys. 2008, 71, 036601. [Google Scholar]
  26. Eggers J. Rev. Modern Phys. 1997, 69, 865–929. [Google Scholar]
  27. Shield T. W.; Bogy D. B.; Talke F. E. IBM J. Res. Dev. 1987, 31, 96–110. [Google Scholar]
  28. Lee E. R.Microdrop generation; CRC Press LLC: Boca Raton, 2003. [Google Scholar]
  29. Yang A.-S.; Tsai W.-M. J. Fluids Eng.-Trans. ASME 2006, 128, 1144–1152. [Google Scholar]
  30. Dong H.; Carr W. W.; Morris J. F. Phys. Fluids 2006, 18, 072102. [Google Scholar]
  31. Fang A.; Dujardin E.; Ondarçuhu T. Nano Lett. 2006, 6, 2368–2374. [DOI] [PubMed] [Google Scholar]
  32. Bonaccurso E.; Butt H.-J. J. Phys. Chem. B 2005, 109, 253–263. [DOI] [PubMed] [Google Scholar]
  33. Deravi L. F.; Gerdon A. E.; Cliffel D. E.; Wright D. W. Appl. Phys. Lett. 2007, 91, 113114. [Google Scholar]
  34. Zhuang H.; Lu P.; Lim S. P.; Lee H. P. Langmuir 2008, 24, 8373–8378. [DOI] [PubMed] [Google Scholar]
  35. Arcamone J.; Dujardin E.; Rius G.; Prez-Murano F.; Ondaruhu T. J. Phys. Chem. B 2007, 111, 13020–13027. [DOI] [PubMed] [Google Scholar]
  36. Burnham N. A.; Chen X.; Hodges C. S.; Matei G. A.; Thoreson E. J.; Roberts C. J.; Davies M. C.; Tendler S. J. B. Nanotechnology 2003, 14, 1–6. [Google Scholar]
  37. Zhuang H.; Lu P.; Lim S. P.; Lee H. P. Langmuir 2007, 23, 7392–7397. [DOI] [PubMed] [Google Scholar]
  38. Shin W.; Nishibori M.; Itoh T.; Izu N.; Matsubara I. J. Ceram. Soc. Jpn. 2008, 116, 459–461. [Google Scholar]
  39. Zhuang H.; Lu P.; Lim S. P.; Lee H. P. Anal. Chem. 2008, 80, 7347–7353. [DOI] [PubMed] [Google Scholar]
  40. Cole D. G. Meas. Sci. Technol. 2008, 19, 125101. [Google Scholar]
  41. Microfab Technologies Inc., Plano, TX, Technical Notes No. 99−01. Background on ink-jet technology (1999) http://www.microfab.com/equipment/technotes/technote99-01.pdf.
  42. Kang H. R. J. Imaging Sci 1991, 35, 195–201. [Google Scholar]
  43. Dong H.; Carr W. W.; Morris J. F. Rev. Sci. Instrum. 2006, 77, 085101. [Google Scholar]
  44. ISO/IEC Guide 99:2007. International vocabulary of metrology -- Basic and general concepts and associated terms (VIM). International Organization for Standardization/International Electrotechnical Commission, Geneva, Switzerland.
  45. Rocklin A. L. J. Coatings Technol. 1976, 48, 45–57. [Google Scholar]
  46. Verkouteren R. M.; Verkouteren J. R.. Unpublished work, National Institute of Standards and Technology, Gaithersburg, MD, 2009.
  47. Bogy D. B.; Talke F. E. IBM J. Res. Develop 1984, 28, 314–321. [Google Scholar]
  48. Taylor B. N., , Kuyatt C. E., . ISO/IEC Guide 98−3:2008 Uncertainty of measurement -- Part 3: Guide to the expression of uncertainty in measurement. International Organization for Standardization/International Electrotechnical Commission, Geneva, Switzerland. See also.; Guidelines for Evaluating and Expressing Uncertainty of NIST Measurement Results. NIST Technical Note 1297, U.S. Government Printing Office: Washington, DC,1994; available athttp://physics.nist.gov/Pubs/.
  49. Schoonover R. M.; Jones F. E. Anal. Chem. 1981, 53, 900–902. [Google Scholar]
  50. Liu X.; Gabour L. A.; Lienhard J. H. V. J. Heat Transfer 1993, 115, 99–105. [Google Scholar]
  51. Bach G. A.; Koch D. L.; Gopinath A. J. Fluid Mech. 2004, 518, 157–185. [Google Scholar]
  52. Balasubramaniam R.; Subramanian R. S. Ann. N.Y. Acad. Sci. 2004, 1027, 303–310. [DOI] [PubMed] [Google Scholar]
  53. Li Z.; Wu J. Ind. Eng. Chem. Res. 2008, 47, 4988–4995. [Google Scholar]

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES