Exhaustive Search for Over-represented DNA Sequence Motifs with CisFinder

Abstract

We present CisFinder software, which generates a comprehensive list of motifs enriched in a set of DNA sequences and describes them with position frequency matrices (PFMs). A new algorithm was designed to estimate PFMs directly from counts of n-mer words with and without gaps; then PFMs are extended over gaps and flanking regions and clustered to generate non-redundant sets of motifs. The algorithm successfully identified binding motifs for 12 transcription factors (TFs) in embryonic stem cells based on published chromatin immunoprecipitation sequencing data. Furthermore, CisFinder successfully identified alternative binding motifs of TFs (e.g. POU5F1, ESRRB, and CTCF) and motifs for known and unknown co-factors of genes associated with the pluripotent state of ES cells. CisFinder also showed robust performance in the identification of motifs that were only slightly enriched in a set of DNA sequences.

1. Introduction

Transcription factor (TF) binding motifs in eukaryotes have been identified by examining binding sequences of purified TFs (e.g. SELEX¹ and Protein Binding Microarrays²) and by carrying out chromatin immunoprecipitation coupled with massively parallel sequencing (ChIP-seq^3–5) and microarray (ChIP-chip).⁶ The ChIP methods can account for biological context of TF binding^7–10 because many TFs require co-factors for sequence-specific binding to DNA, which are not present in in vitro assays. On the other hand, TF binding sites identified in the ChIP methods will include not only direct binding sites but also binding sites indirectly associated with the TF through the protein–protein interaction of other TFs that binds directly to DNA. Furthermore, ChIP-seq data often include several million sequence tags and >10 000 binding locations.^4,9,11 These features of high-throughput genome-wide ChIP technology make the bioinformatic task of identifying TF binding motifs a great challenge.

Various software tools have been developed to identify over-represented DNA sequence motifs (reviewed in Das and Dai,¹² Sandve et al.,¹³ and Tompa et al.¹⁴). For example, traditional probabilistic methods include expectation maximization (MEME¹⁵), Gibbs sampling,^7,16 genetic algorithms (GAME¹⁷), integrated Bayesian models,¹⁸ neural networks, support vector machines, Bayesian additive regression trees,¹⁹ and approximate maximum a posteriory (MAP) scoring functions.²⁰ These methods work well when data sets are small, and thus, only a small fraction of top-scored binding sites is usually processed with these algorithms.¹⁰ Weeder, which is based on counting matching patterns with a certain maximum number of mismatches, has been reported to outperform many other software tools.¹⁴ However, most existing algorithms are limited to searching only for a single motif at a time. To find additional motifs, the software has to be run again after removing the first motif from the sequence.¹⁵ With this approach, results may be different depending on the order in which motifs are processed. For example, a composite motif that supports binding of two TFs (TF₁ and TF₂) may be lost if a more abundant motif (TF₁) is processed first and then removed from the sequence. Machine-learning algorithms, such as Gibbs sampler and neural networks, tend to fall into local maxima⁷ and often fail to differentiate between similar motifs.

In this paper, we present a new algorithm for de novo identification of over-represented DNA motifs, which is implemented as the online software tool CisFinder (http://lgsun.grc.nia.nih.gov/CisFinder). It is a complementary method to existing probabilistic algorithms and has advantages in the exploratory analysis of large input files typical for ChIP-chip or ChIP-seq data sets. CisFinder can effectively process large sequences (up to 50 Mb), extract a comprehensive list of over-represented motifs in a single run, and analyze data with poor enrichment of DNA-binding motifs. Because of high processing speed (<1 min for complete data analyses), the software can be used in an interactive manner to test many different parameter sets. The software has been tested using available ChIP-seq data on TFs expressed in ES cells.⁹

2. Materials and methods

2.1. Estimating position frequency matrices from n-mer word counts

The proposed algorithm is based on estimating position frequency matrices (PFMs) directly from n-mer word counts in the test set and control set of sequences. To explain the algorithm, we first describe a numerical example and then present the formal justification of the method. Consider a specific n-mer word W (e.g. W = ‘ATGCAAAT’), which has T(W) = 200 matches (instances) in the set of test sequences and C(W) = 50 matches in the set of control sequences. For simplicity, we count only a total number of instances as if all sequences in a set are concatenated. (However, the CisFinder has an option to count only one match of each word per sequence.) In this example, the total length of both test and control sequences is 3 Mb. For a word W, we define a nucleotide substitution matrix [W_pi], which contains words that are derived from W by placing a nucleotide i in a position p (Fig. 1A). The frequency of each word from the nucleotide substitution matrix counted in the same target sequence makes the frequency substitution matrix (Fig. 1B). For convenience, we will use brief notations T_pi = T(W_pi) and C_pi = C(W_pi) for the frequency of word W_pi instances in the test and control sequence sets (elements of frequency substitution matrices). Then, the proposed method to estimate PFMs is

e1

where φ_pi is the estimate of PFM element, and T_pi and C_pi are the counts of word W_pi, in the test and control sequences, respectively. Because word counts are random variables, they may appear smaller in the test sequences than in the control sequences by chance, resulting in a negative PFM element. To avoid this, negative differences are replaced with zero and then normalized as shown in Fig. 1C–E. Thus, the estimate of PFM element (φ_pi) can now be presented as follows:

e2

Figure 1.

CisFinder algorithm for de novo identification of DNA motifs. (A) Example of a nucleotide substitution matrix for word ATGCAAAT; (B) frequency substitution matrices for the test and control sequences; (C) subtraction of matrices; (D) negative values are replaced by zero; (E) normalized PFM; (F) position and width of gaps in the words; (G) extending the PFM over the gaps and flanking sequences; (H) clustering and combining of PFMs to generate a sequence logo.

If test and control sequence sets have different total lengths, then the number of word counts in the control sequences is adjusted by the total sequence length.

This method is justified by the following model. Let us assume that a TF binds to a set of locations in the genome where corresponding DNA sequences can be aligned together. Using this alignment, we can estimate the frequency, f_pi, of each nucleotide i in each position of aligned sequences, p, which is the element of the PFM. We further assume that binding strength of the TF is additive with no interaction between positions. This simplification is justified by the fact that all existing databases use PFMs to describe TF motifs, and this strategy works reasonably well. Consider a word W with a sequence of nucleotides that corresponds to the maximum values of the PFM at each position. This word is then used to generate frequency substitution matrices [T_pi] and [C_pi] for the test and control sets of sequences, respectively. Each instance of word W_pi in the test or control sequences can either correspond to a true binding site of the TF (we call it functional) or not (non-functional). Factors determining the functionality of different instances of the same DNA word are largely unknown and may include sequence context and chromatin status. Because the probability of TF binding is proportional to PFM elements at each position (based on the assumption of additive contribution of each position to TF binding), the number of functional instances, FT(W_pi), of word W_pi in the test sequences is proportional to f_pi:

e3

The total number of instance of word W_pi in test sequences equals the sum of functional, FT(W_pi), and non-functional, NT(W_pi), instances:

e4

Similarly, the total number of instance of word W_pi in control sequences equals the sum of functional, FC(W_pi), and non-functional, NC(W_pi), instances. Although the functional instances are enriched in the test sequences compared with control sequences, some functional instances may be present in the control sequences, because of possible false negatives in ChIP data. Because we can assume that non-functional instances of the word are not affected by the ChIP procedure, their counts are equal in the test and control sets of sequences: NT(W_pi) = NC(W_pi). Then, the numerator in Equation (e1) is

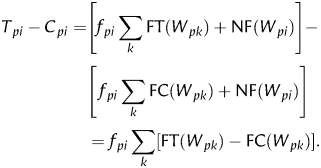e5

Because functional instances of word W are over-represented in the test set of sequences compared with control, the final sum in Equation (e5) is always positive and the difference (T_pi − C_pi) is proportional to f_pi. Thus, Equation (e1) gives a true estimate of f_pi in the PFM. This reasoning holds true, if the word W is shorter than the full binding motif or includes a gap. However, the word should be long enough to capture the informative portion of the motif so that it remains strongly over-represented in the set of test sequences compared with control.

Because the PFM is estimated as a difference between word counts in the test and control sets of sequences [Equations (e1) and (e2)], the variance of PFM elements is equal to the sum of variances of word counts in the test and control sequences. The variance of word counts is very close to the mean, which is expected from the Poisson distribution. This was also checked using pseudo-random sequences generated with the third order Markov process. For example, if word counts are 120 in the test set of sequences and 40 in the control set (i.e. 3-fold over-representation), then the relative error (accuracy) is equal to sqrt(120 + 40)/(120–40) = 0.158.

2.2. Implementation of the method for PFM estimation

A successful ChIP-seq experiment generates a set of genome locations that are enriched in TF binding sites. For a test sequence set, we usually extract 200 bp sequence segments centered at a peak of projected TF binding sites. For a control sequence set, we usually extract 500 bp sequence segments starting from nucleotide positions 400 bp away from both ends of 200 bp test sequence segments. (However, the CisFinder allows users to choose different sequence lengths.) The CisFinder identifies binding motifs of TFs using direct counts of all possible 8-mer words with and without gaps in both test and control sequence sets (Fig. 1F). This word length was selected experimentally based on the observation that longer words have too few matches in target sequences, whereas shorter words may fail to capture the most informative portion of the motif and show lower rates of over-representation. (Note: the command-line version of CisFinder allows the use of 6- and 10-mer words.) Word counts are stored in the array of integers. Although there are many different ways to insert gaps in the 8-mer words, we consider only 8 specific patterns of gap insertions (Fig. 1F). We found that this limited set of gap insertion effectively helps to capture composite motifs with multiple functional elements. For example, search for a word ‘ATGCAAAT’ with a 2 bp gap in the middle is equivalent to the search for word ‘ATGCNNAAAT’. PFM is then estimated for each word based on >1.5-fold (default threshold) enrichment in the test sequences compared with the control sequences using Equation (e2). The adjustable fold enrichment criterion is optional (it can be set to 1), which provides additional flexibility in the use of the program.

Over-representation of word counts in the test sequences compared with the control sequences is then evaluated using a z-score which is estimated based on the hypergeometric probability distribution. Let us first consider the case where only one instance of each word is counted per each sequence of equal (or approximately equal) length. The proportion of sequences, q, with a given word in the set of test sequences is compared with the proportion of sequences, p, with the same word in the combined set of test and control sequences (if the null-hypothesis is true, then test and control sets of sequences can be combined) with z-score: where n is the number of test sequences, and N is the number of combined test and control sequences. If multiple instances of each word are counted per each sequence, then the method is modified as follows. The set of test sequences with the total length T is split into T/m segments of length m, where m is the actual length of the word including gaps. Each instance of the word is then associated with the segment where it starts. Because overlapping instances of the same word are counted as one instance, there is not more than one instance associated with the same segment. Similarly, the set of control sequences with the total length C is split into C/m segments of length m. We use the same equation for the z-score (see above) where q is the proportion of test segments with the word, p is the proportion of test and control segments with the word, n = T/m, and N = (T + C)/m. Although occurrences of word instances in adjacent segments may be weakly correlated, the hypergeometric distribution gives a reasonable approximation of the z-score.

To fill the gaps and extend the length of PFMs, the test and control sequences are searched again for the exact match to each word with z > 1.643 (to satisfy the condition of P < 0.05 for one-tail z-test). Each match of the word in the test (or control) sequence is then examined for nucleotides in the gaps and flanking sequences (2 bp at each side) that are not included in the word. In this way, we can count nucleotide frequencies in gaps and flanking regions and estimate the PFM for these positions using Equation (e2) (Fig. 1G). The program is also designed to trim flanking sequences if they are not informative (if the ratio of maximum frequency to minimum frequency is <3). To increase the information content of PFMs, we use the contrasting procedure: the median of minimum PFM values at each position is subtracted from all PFM values; negative values are then replaced by zero; and the PFM is re-normalized.

The frequency distribution of nucleotides in the flanking regions and in gaps of a certain word may differ substantially between the test and control sets of sequences. In such a case, this difference can be used to increase the statistical power for identification of significant motifs. To incorporate this factor into the statistical evaluation of motif significance, we compared frequency distributions of nucleotides (counted for each nucleotide and each flanking/gap position) in the test and control sequences using the G-test.²¹ Assuming that this test is independent from the z-test for over-representation of word counts (see above), we combined P-values from these tests using Fisher's method.²² Finally, we used the false discovery rate (FDR) to account for simultaneous testing of multiple hypotheses.²³ We designed the program to generate at least 100 top-scored motifs and additional motifs, if they satisfy the criterion of FDR < 0.05.

PFMs are then clustered based on similarity and/or co-occurrence (Fig. 1H). Various methods have been proposed to measure the similarity of PFMs, including Bayesian models.²⁴ Here, we use a simpler method and measure similarity by Pearson correlation between elements of the corresponding position weight matrices (PWMs) for all overlapping positions, where PWM is derived from PFM by log-transformation: x_ij = log(p_ij/q_j), x_ij is the weight of nucleotide j in position i, p_ij the probability to find nucleotide j in position i, and q_j the background frequency of nucleotide j. For simplicity, here equal background frequencies (q_j = 0.25) are assumed and zero probabilities are avoided by adding pseudo-count = 1 to nucleotide counts in the PFM. Offset and orientation of motifs are selected based on the maximum correlation, restricted to the minimum overlap of 6 bp and maximum overhang of 2 bp. Because correlation is estimated for a minimum of six overlapping positions, there are at least 24 points (six positions × four nucleotides) for estimating correlation. Thus, even low correlation is significant (e.g. r = 0.5; d.f. = 22; P < 0.05). Therefore, the default correlation threshold set in CisFinder (r = 0.7) is always significant (however, users can also adjust the correlation threshold to increase or decrease the size of clusters). As a measure of motif similarity, we use a correlation between PWM elements rather than a previously proposed correlation between PFM elements,²⁵ because the log-transformation increases the contribution of low values to the correlation and represents the binding strength of TFs better. For example, the difference between probabilities 0.99 and 0.7 corresponds to the 1.41-fold change in binding strength, whereas the same difference between probabilities 0.01 and 0.3 corresponds to the 30-fold change in binding strength. After log-transformation (log₁₀), the difference in the second pair of probabilities (1.477) is greater than that in the first pair (0.151).

We use single-linkage clustering, and then each cluster is checked for homogeneity. If the cluster is not homogeneous, it is separated into subclusters using the second round of clustering. Subclustering is done iteratively starting from a pair of seed motifs, adding sequentially most similar motifs, and re-estimating the combined PFM for the subcluster. Each pair of motifs is characterized by the score =r m₁ m₂, where r is the correlation between PWMs, and m₁ and m₂ are the numbers of linked members for motifs 1 and 2, respectively. Then the pair with the highest score is selected as a seed for the subcluster. This procedure is different from the single-linkage clustering because motifs are added to the subcluster based on the similarity to the combined PFM of all motifs that are already included into the subcluster, whereas the single-linkage clustering is based on the similarity between individual (non-combined) motifs. Motifs are added until no motif within the cluster can be added to the subcluster using the given threshold of similarity. If all elements in the cluster appear to be in the same subcluster, then the cluster is considered homogeneous. Otherwise, the elements of the subcluster are removed from the cluster, and the same algorithm is applied to the remaining elements.

The advantage of clustering PFMs compared with clustering words (as in RSAT²⁶) is that PFMs contain more information than words alone. Words differ qualitatively (the nucleotide either matches or mismatches), whereas PFMs differ quantitatively (i.e. the probability of each nucleotide correlates between two PFMs). Motifs within the same cluster are then arranged using the hierarchical clustering with cluster flips to place similar motifs near each other.²⁷ Then, the PFM for the entire cluster is estimated as the weighted average of member PFMs using local information content at each position p

where f_ki is the element of PFM, multiplied by motif abundance as a weight. Finally, a sequence logo²⁸ is generated from the PFM.

As an alternative criterion for clustering, the CisFinder also uses co-occurrence of word instances in the test sequences. This method is generally less accurate than the similarity-based method because of the limited number of word pairs in the sequence set. We, therefore, designed the program to use the correlation-based clustering method as a default. However, the co-occurrence method may help to cluster PFMs with a high level of self-similarity (after shifting a position by 1–4 bp), because their relative positions cannot be uniquely identified based on the correlation. Further details of the algorithm implementation are available in Supplementary Text S1 and online (http://lgsun.grc.nia.nih.gov/CisFinder).²⁹

2.3. Implementation of additional tool to search for motifs that match to PFMs

Once PFMs are estimated by the CisFinder or given in the literature, it is often necessary to find DNA sites that match a specific PFM in a given sequence (e.g. in promoters of certain genes). This task is computationally intensive if a matching score is estimated sequentially at each position of the sequence as in MatInspector or MATCH.^30,31 We implemented as additional tool in the CisFinder website, a faster method to identify DNA sites, which is based on a lookup table. For each motif represented by a PFM, we selected the most informative stretch of eight nucleotides, which is used as a core. Then, a lookup table is generated that specifies all PFMs from the list whose cores match sufficiently well to each possible 8-mer word. The length of 8 bp is selected for the core because the number of all 8-mers is small enough to keep the lookup table in the computer memory, and 8-mer words are specific enough to be linked with only a few PFMs that match them. A match score is defined as log likelihood that a specific sequence matches a matrix and is equal to the sum of those elements of the PWM (log-transformed PFM) that corresponds to nucleotides at each position of the sequence. The match score for the full matrix, T_full = T₈ + T_resid, where T₈ is the match score for 8-mer core and T_resid is the match score for the residual of the matrix. The program finds the threshold value R₈ for the match score T₈, which ensures that the match score for the full matrix exceeds the given threshold R_full with probability 0.999 if T₈ > R₈:

e6

where F is the cumulative probability distribution of T_resid when matching to a random sequence. The value of F⁻¹(0.999) is estimated by Monte-Carlo simulation. A PFM is included into the lookup table for the 8-mer core word if T₈ > R₈. The query sequence is scanned sequentially, and for each position, only those matrices are tested that are in the lookup table for the specific 8-mer word that starts at this position. Although this method may miss up to 0.1% of matching sites, we consider it a reasonable trade-off for the increase in computation speed by several orders. On the basis of Equation (e6), these missed sites always have a poor match to the core motif. Although the match score of missed sites formally exceeds the threshold, the quality of these sites is low from a biological point of view because of the poor match to the core motif.

2.4. Data sets used in this study

CisFinder was tested using published ChIP-seq data on binding of 14 TFs [CTCF, ESRRB, KLF4, MYC, POU5F1 (also known as OCT4 or OCT3/4), SMAD1, SOX2, STAT3, TCFCP2L2, ZFX, P300, NMYC, NANOG, E2F1] in ES cells⁹ (Supplementary Table S1). We also used a deliberately selected low-quality subset of ChIP-PET data¹⁰ on binding of POU5F1 to test if CisFinder can process sequences with low enrichment of binding motifs. We used genome locations with 2 (N = 19 803) and 3 ditags (N = 3361) from POU5F1 ChIP-PET that did not include loci with additional NANOG ditags to avoid indirect binding effects (Supplementary Table S2). All binding regions were mapped to the latest mouse genome (mm9, NCBI/NIH) using the UCSC coordinate conversion tool (http://genome.ucsc.edu/cgi-bin/hgLiftOver).

3. Results and discussion

3.1. CisFinder algorithm and its main features

The proposed CisFinder algorithm, which is implemented as an online software tool,²⁹ is described in detail in Section 2. In brief, CisFinder has the following features.

1. CisFinder algorithm is based on detecting over-represented short words (i.e. nucleotide sequences) in a sequence and clustering them. Unlike oligo-analysis (RSAT)²⁶, which is also based on the same concept but clusters exact words, CisFinder clusters PFMs that represent binding motifs more accurately than exact words.

2. CisFinder algorithm analyzes words with gaps and expands PFMs over the gaps and flanking regions.

3. CisFinder uses real control sequences to compare against test sequences. This helps to process repeat regions, because motifs that are specific to repeat sequences are expected to be equally abundant in the test and control sets of sequences [thus, the difference of motif frequencies (e1) is close to zero]. Because mammalian functional TF binding sites are often located in repeat regions,³² the ability to search for motifs without removing repeat sequences is useful. An option to use randomized model sequence (a third-order Markov process with probabilities extracted from the test sequences) as control is also provided.

4. CisFinder is designed to carry out exhaustive searches for all over-represented DNA motifs in a single run. It combines motifs only at the clustering step, and users can adjust the correlation threshold used for clustering to make clusters bigger or smaller.

5. CisFinder includes auxiliary functions: comparison of DNA motifs with databases of known binding motifs of TFs,^33,34 search for motifs that match to PFMs, visualization of sequences and TF binding motifs with a CisView browser³⁴ and UCSC genome browser,³⁵ and extraction of sequence fractions and subsets of sequences.

3.2. CisFinder algorithm accurately identifies PFMs of TF binding motifs

To test the performance of the new algorithm, we used ChIP-seq data for 12 TFs associated with the pluripotent state of ES cells.⁹ We extracted 200 bp sequence segments centered at TF binding locations identified with ChIP-seq and compared them with control sequences (i.e. 500 bp sequence segments starting from nucleotide positions 400 bp away from both ends of 200 bp test sequence segments). Clustering of PFMs generates highly consistent TF binding motifs that were independent from the correlation threshold used for clustering (Fig. 2A). In contrast, clustering over-represented 8-mer words using the RSAT²⁶ resulted in long aberrant motifs because of the chain effect of clustering. All 12 motifs identified with CisFinder matched well with motifs found by Chen et al.⁹ with Weeder (Fig. 2B), indicating that the quality of results is comparable. Unlike other existing tools, CisFinder has also generated PFMs for additional over-represented motifs at the same time. Utility of such additional motifs will be presented and discussed below (Sections 3.3–3.5).

Figure 2.

Testing CisFinder algorithm. (A) Binding motifs of POU5F1 generated by clustering of PFMs (with CisFinder) and over-represented 8-mer words. Binding motifs of TFs in ES cells identified with CisFinder. (B) Comparison of TF binding motifs generated by Chen et al.⁹ using Weeder and motifs generated with CisFinder. (C–E) Binding motifs of POU5F1, ESRRB, and CTCF, respectively, identified with CisFinder.

Computation time for all steps of the CisFinder algorithm ranged from 5 to 120 s (Supplementary Table S1), with median time 38 s needed to process a 7.5 Mb sequence (sum of test and control sequences). Our estimate is that our software works >1000 times faster than both MEME¹⁵ and Weeder³⁶ and >100 times faster than RSAT.²⁶ The MDscan²⁰ works fast; however, it is designed to process a small number of sequences (from 20 to 400, see http://ai.stanford.edu/~xsliu/MDscan), and the online version of the software accepts only 200 sequences.

Taken together, the data indicate that CisFinder works faster than existing tools without sacrificing sensitivity. It is, however, difficult to make a fair comparison between tools for sensitivities and calculation speeds because each tool was designed to process different types of data. CisFinder was developed to process ChIP-seq or ChIP-chip data, which typically include several thousands of sequences (i.e. a few megabase) and cannot be effectively processed by probabilistic methods (e.g. MEME and Weeder). On the other hand, the probabilistic methods works efficiently on relatively small numbers of sequences (e.g. a typical benchmark sequence set is <32 kb¹³), as they are designed to process a small data set by selecting only high-scoring sequences. However, the reduction in the data set often leads to the loss of useful information, as we describe below (Section 3.3).

3.3. Cisfinder algorithm detects alternative binding motifs

Eukaryotic transcription regulation is extremely complex, and most TFs have multiple binding motifs, which correspond to direct binding of single TFs, tandems of identical TFs in various orientations and spacings, binding with various co-factors, and finally, indirect binding via protein–protein interactions with other TFs. Analysis from 50 to 200 high-score binding sites (which is a typical data size for MEME or Weeder) is usually sufficient to extract the main motif, but it is often not sufficient to examine alternative motifs. For example, Chen et al.⁹ used Weeder³⁶ and reported only a single motif for each TF. In contrast, using the same data set, CisFinder was able to find multiple motifs for each TF, e.g. POU5F1 (also known as OCT4 or OCT3/4), ESRRB, and CTCF (Fig. 2C–E).

For the POU5F1, predicted alternative binding motifs included several palindromes (Fig. 2C, b–f). Previous studies have already shown that these motifs are also functional: (b) is a ‘MORE’ motif,³⁷ (e) is a ‘PORE’ motif,³⁸ and (c) is a part of two motifs identified by Tantin et al.³⁹ On the other hand, CisFinder could not detect a well-known OCT–3N–SOX composite motif with a 3 bp spacer between OCT and SOX motifs, which is located in the enhancer of Fgf4.⁴⁰ To investigate this issue, we searched for this motif in ChIP-selected sequences using a PFM derived from the regular OCT–SOX composite motif after adding a 3 bp spacer. Because OCT–SOX and OCT–3N–SOX motifs are similar, we counted sites only if they matched more strongly to OCT–3N–SOX than to OCT–SOX motif. We found that the OCT–3N–SOX motif was indeed present in ChIP–POU5F1 sites (Supplementary Fig. S1), but its abundance was too low (20-fold less abundant than OCT–SOX motif) to be detected de novo with a statistical confidence.

For the estrogen-related receptor beta (ESRRB), CisFinder predicted 12 alternative binding motifs (Fig. 2D), all of which represented different repeat configurations of the same elementary motif AGGTCA. In direct repeats (i.e. repeats in the same orientation) (a–g), monomers were spaced by either 0, 1, 2, 3, 4, or 5 bp. In inverted repeats, the spacing between monomers was less flexible. When the first monomer had a positive orientation (h–j), then inverted repeats were spaced by either −3, 0, or 3 bp (−3 means 3 bp overlap). However, when the first monomer had negative orientation (k and l), then motifs were spaced by either 2 or 6 bp. Akter et al.⁴¹ tested 12 paired motifs (direct and inverted) with the competitive EMSA and found the increased binding of estrogen-related receptors to direct repeats with 0, 2, and 4 bp spacing and to inverted repeats with 0 and 3 bp spacing. Thus, the in vivo ChIP-seq data confirmed in vitro EMSA data by Akter et al., although the motifs (h), (k), and (l) found in the ChIP-seq data (Fig. 2D) were not tested by Akter et al. Our results indicate that ESRRB can bind in vivo to direct repeats spaced by 1, 3, and 5 bp despite weak competitiveness in EMSA, presenting the largest set of alternative binding motifs detected for the ESRRB.

For the CTCF (an insulator in the regulation of transcription⁴²), several alternative binding motifs were detected. The main DNA motif enriched in ChIP–CTCF loci (Fig. 2E, a) matched well to the motifs identified in earlier studies^43–45 (Supplementary Fig. S2). Furthermore, CisFinder identified several alternative binding motifs for CTCF (b–e), including three palindromes (b–d). However, further experimental validation is needed to prove that these motifs are indeed functional.

3.4. CisFinder algorithm detects binding motifs of potential co-factors

Genome locations identified with ChIP for a specific TF often do not carry the primary or alternative binding motifs, but are enriched with binding motifs for other TFs (cofactors). The most likely interpretation of this phenomenon is that the TF used for the immunoprecipitation binds to DNAs indirectly through binding to a co-factor that directly binds to DNA. Thus, the analysis of co-factor binding motifs may help to infer potential mechanisms of transcription regulation.

To explore this issue, we first selected 22 motifs that were over-represented in ChIP loci for single or multiple TFs reported by Chen et al.⁹ and used the corresponding PFMs generated by CisFinder to search for these motifs in 200 bp DNA segments centered at ChIP loci (Fig. 3). Some of these motifs were well characterized and supported the bindings of known TFs (e.g. ESRRB, GABP, ATF1, and TEF). A motif MIT-008 was shown to be over-represented in mammalian promoters,⁴⁶ although a TF binding to these sites remains unknown. We also found a novel motif (AP4-L) which is similar to the V$AP4_01 binding motif in TRANSFAC.⁴⁷ The YY1 motif may correspond to ZFP42 (=REX1) binding because both TFs have nearly identical motifs.^48,49

Figure 3.

Motifs of TFs and their co-factors over-represented in ChIP-seq (data from Chen et al.⁹) distal binding sites (200 bp segments centered at binding sites and located 500–100 000 bp away from transcription start sites) compared with flanking regions 500–1000 bp away from binding sites. Motifs were selected if they were over-represented by >2-fold for at least one TF; search was done with CisFinder using the option of one false positive match per 10 kb. Groups of TFs and binding motifs with high over-representation rate are outlined.

Next, we compared the abundance of these motifs in the 200 bp DNA segments centered at ChIP loci with the control sequences (i.e. 500 bp sequence segments starting from nucleotide positions 400 bp away from both ends of 200 bp test sequence segments). To obtain a homogeneous data set, we used only the ChIP loci that were located at >500 bp away from the transcription start sites of genes (distal ChIP loci). Another reason to focus on the distal ChIP loci was that pluripotency-related TFs, such as POU5F1 and NANOG, are active mostly at distal locations rather than at proximal promoters.¹⁰ We then tabulated the motif abundance data and found that TFs and corresponding binding motifs formed three distinctive groups (Fig. 3, Supplementary Table S3). The first group (group #1) included the major pluripotency-related TFs (POU5F1, SOX2, and NANOG) as well as SMAD1 and P300. As expected, the strongest binding motif in this group was the OCT–SOX composite motif. OCT motif alone was associated mostly with POU5F1 binding, whereas SOX2 motif alone, which was known previously as SOX9 (V$SOX9_B1) in TRANSFAC,⁴⁷ was associated mostly with binding of SOX2, NANOG, and SMAD1. A novel motif AP4-L was associated with binding of all TFs in the group #1, but the association was strongest for SMAD1 and NANOG. A TEF motif was most abundant in P300 binding locations. The second group (group #2) included STAT3, KLF4, ESRRB, and TCFCP2L1. The third group (group #3) included MYC, NMYC, ZFX, and E2F1 (Fig. 3). Although it is tempting to speculate that these TFs in each group form a protein complex, drawing such a conclusion requires further evidence for the presence of such protein complexes in the ES cells.

We also noticed that some DNA motifs were negatively associated with binding of some TFs, which may indicate the inhibition of DNA binding. For example, the major OCT4 palindrome motifs, OCT4-GCGC and OCT4-MORE, were strongly under-represented in many ChIP loci including binding sites of pluripotency-related TFs (NANOG, SOX2, STAT3, KLF4) (green color), except for POU5F1 that bound to these motifs (Fig. 3). This suggests that palindrome POU5F1 motifs are likely to be involved in a different cellular function than supporting ES cell pluripotency. The OCT–SOX and SOX2 motifs alone were negatively associated with the binding of SUZ12, which may explain why Polycomb protein complexes cannot inactivate pluripotency-related genes in ES cells.

3.5. CisFinder algorithm can find motifs with a low level of enrichment

We tested whether the CisFinder algorithm was robust enough to identify motifs that were only slightly enriched in the set of DNA sequences. According to Loh et al.,¹⁰ ChIP loci with at least 4 ditags (ChIP-PET data) were reliable enough to infer binding of POU5F1 and NANOG. Thus, we used ChIP loci with 2 or 3 ditags for POU5F1 as examples of data with a low level of motif enrichment. To evaluate the over-representation of binding motifs, we searched for the OCT–SOX motif in 200 bp test DNA segments centered at ChIP loci and in control sequences (i.e. two 500 bp sequence segments starting from nucleotide positions 400 bp away from both ends of 200 bp test sequence segments). To avoid a circular reference, we took the PFM for the OCT–SOX motif from an independent source, where the PFM was estimated on the basis of ChIP-PET loci with at least 4 ditags for POU5F1.¹⁰ The over-representation ratios of the OCT–SOX motif density were only 1.57 and 0.99 in ChIP-PET data sets with 3 and 2 ditags, respectively (Supplementary Fig. S3). They were substantially lower than the over-representation ratio (7.10) of the OCT–SOX motif in the ChIP-seq data, which confirms the low level of motif enrichment. The CisFinder algorithm was successful in finding the OCT–SOX composite motif ATTGTTATGCAAAT as the top-scored consensus sequence for the set of 3361 ChIP loci with 3 ditags. Similarly, in the set of 19 803 genome loci with 2 ditags for POU5F1, CisFinder identified a canonical POU-motif ATGCAAAT.⁵⁰ However, this motif was not the top-scored one (rank = 11), which may be the result of a large proportion of false positives in the data set. The OCT–SOX composite motif was not found, which can be explained by no enrichment of this motif (over-representation ratio = 0.99) (Supplementary Fig. S3). Thus, we hypothesized that the weak binding of POU5F1 does not require SOX2 as a co-factor. Top-scored motifs over-represented in ChIP loci with 2 ditags were also meaningful: they corresponded to NRF1 and KLF motifs, which were associated with POU5F1 binding as shown above (Fig. 3) and reported in the literature.⁵¹ In comparison, neither MEME¹⁵ nor Weeder³⁶ found any meaningful motifs in both data sets with 3 or 2 ditags of POU5F1.

3.6. Other potential applications and limitations of CisFinder

Although CisFinder was designed specifically for the analysis of ChIP experiments on TF binding, it can be used for other purposes. For example, it can be used to find over-represented motifs in promoters of co-regulated genes, in introns of alternatively spliced genes, or in 3′-untranslated regions of genes with high or low rates of mRNA degradation. The search for over-represented motifs can be improved by limiting the search to evolutionarily conserved regulatory regions because functional sequences have a tendency to be conserved during evolution.⁵² [However, recent findings indicate that many regulatory regions are located in transposable elements, which are usually not conserved.³²]

Because of its high processing speed, CisFinder can be used interactively by adjusting parameters of motif detection. Also, it can be utilized effectively as a component of systems for reconstructing gene regulatory networks. For example, Reiss et al.⁵³ used de novo motif discovery in promoters of co-regulated genes, which were clustered using the data on gene expression in various conditions. Because the identification of motifs is repeated many times in this analysis, the use of CisFinder algorithm can increase the processing speed.

The main limitation of CisFinder algorithm is that its performance decreases if the input sequence is too short. For example, if the length of sequence is 32 kb, then it contains only one 8-mer word on average (based on the random model). In this case, the CisFinder can detect only highly over-represented motifs (e.g. with >10-fold enrichment) and, thus, other software (e.g. MEME¹⁵) should be used instead.

3.7. Conclusion

CisFinder implements an express method for de novo identification of over-represented DNA motifs and is specifically designed to process ChIP-chip and ChIP-seq data. It is a complementary method to existing motif-finding tools, which are highly efficient in processing short input sequences. Unique features of CisFinder are: (i) it extracts all over-represented motifs in a single run and describes them with PFMs; (ii) it can effectively process large sequences (up to 50 Mb); (iii) because of its high processing speed, it can be used in an interactive manner by running the analyses multiple times after re-adjusting parameters; and (iv) it can process data with a low-level enrichment of DNA motifs.

Supplementary data

Supplementary data are available at www.dnaresearch.oxfordjournals.org.

Funding

This research was supported entirely by the Intramural Research Program of the NIH, National Institute on Aging.