Rank of Correlation Coefficient as a Comparable Measure for Biological Significance of Gene Coexpression

Abstract

Information regarding gene coexpression is useful to predict gene function. Several databases have been constructed for gene coexpression in model organisms based on a large amount of publicly available gene expression data measured by GeneChip platforms. In these databases, Pearson's correlation coefficients (PCCs) of gene expression patterns are widely used as a measure of gene coexpression. Although the coexpression measure or GeneChip summarization method affects the performance of the gene coexpression database, previous studies for these calculation procedures were tested with only a small number of samples and a particular species. To evaluate the effectiveness of coexpression measures, assessments with large-scale microarray data are required. We first examined characteristics of PCC and found that the optimal PCC threshold to retrieve functionally related genes was affected by the method of gene expression database construction and the target gene function. In addition, we found that this problem could be overcome when we used correlation ranks instead of correlation values. This observation was evaluated by large-scale gene expression data for four species: Arabidopsis, human, mouse and rat.

1. Introduction

The function of every gene depends on that of another gene(s). To predict gene partnerships, gene coexpression databases can be used, because coexpressed genes are generally expected to be involved in related cellular functions.¹ Many technical improvements have been achieved in microarray measurements, and thus coexpression databases are now widely used for various experimental objectives, such as gene targeting, regulatory investigations and/or identification of potential partners in protein–protein interactions.^2,3 In addition to target-specified research, gene coexpression data provide a fundamental basis for omics studies such as the metabolome or phenome.^4,5 To easily extract pertinent information from gene coexpression data, gene coexpression databases with various analysing tools have been constructed for model organisms.^6–14

In these databases, gene coexpression data, which are similarities of expression patterns of gene pairs over a number of samples, have been calculated using publicly available gene expression data produced using the Affymetrix GeneChip system, most of which are stored in primary databases such as GEO,¹⁵ TAIR¹⁶ and NASCArray.¹⁷ Calculation of gene coexpression can be divided into the following three general steps: (i) selection of microarray samples, (ii) normalization of gene expression data and (iii) calculation of gene coexpression. In many coexpression databases, the MAS5 algorithm¹⁸ is used for GeneChip summarization, and Pearson's correlation coefficients (PCCs) are used to measure gene coexpression. In this paper, we especially focus on coexpression measure for construction and usage of large-scale gene coexpression databases.

PCC is one of the most convenient measures to evaluate gene expression similarities¹ because it is easy to calculate and is familiar to experimental biologists; still, certain caveats have been reported. Yona et al.¹⁹ assessed five coexpression measures based on four types of yeast microarray data. The ‘mass–distance’ measure, which they proposed, showed stably higher performance than others, although the most effective measure differed between data sets. Hardin et al.²⁰ reported the insufficiency of PCC against outliers using a small data set based on 25 microarray slides. de la Fuente et al.²¹ proposed the use of a partial correlation coefficient with PCC to improve causal properties. Although these studies are valuable for the calculation of gene coexpression, it is difficult to directly apply the results to large-scale database construction, because of its extremely high calculation cost for large-scale collections of gene expression data. Condition-independent gene coexpression data are constructed based on hundreds or thousands of GeneChip data to generalize specific experimental conditions; for example, for Arabidopsis, 1310, 1779 and 1388 GeneChips are used for PED,¹⁰ CressExpress¹² and ATTED-II,¹⁴ respectively. To balance high performance and easy calculation for database construction, we re-examined coexpression measures using large-scale gene expression data. Note that we did not specially focus causal relationship, but effective retrieval of coexpressed genes to find functional partner of a gene(s) of interest.

To retrieve coexpressed gene sets, users have to set a threshold of coexpression value, because coexpression databases basically return continuous values indicating how strong the two genes of interest are coexpressed in selected samples. Aoki et al.²² specified a minimal PCC value (0.55–0.66) for coexpressed gene retrieval to minimize false gene function relationships. Because the calculation was based on downloadable coexpression data from ATTED-II,¹⁴ this estimation is valuable for the users of this database. However, experimental biologists can now use many coexpression databases that were constructed using different samples and different normalization procedures. In addition, some databases provide their own options for sample selection and/or for coexpression measures other than PCC. Moreover, comparison of coexpression data among different species has been a powerful approach to investigate functional modules.²³ A question arising from this situation is whether users can apply a particular threshold (e.g. PCC = 0.6) to retrieve coexpressed genes for any databases with any options as pointed out by Manfield et al.⁹ Another question is whether the PCC threshold can be applied to any genes for various functions such as direct interactions for protein complex formation, successive reactions by enzymes in a particular metabolic pathway or gene regulatory relationships. The number of coexpressed genes under a particular PCC threshold follows a power-law distribution.²⁴ Namely, a small number of genes are coexpressed with thousands of other genes, whereas a large number of genes are not coexpressed with any (or only a few) other genes. Although PCC is a convenient measure of expression similarity between gene pairs of interest, it may not directly indicate the strength of gene functional relationships. The fundamental question we address here is how the strength of gene functional relationships is affected by calculation procedures or gene functions. For simplicity, we hereafter refer to the strength of a gene functional relationship as ‘biological significance’.

In this study, we first investigated characteristics of PCC as a measure of gene coexpression. The problems we found for PCC fall into two categories, both of which lead low comparability of PCC value. The first case is derived from the construction of gene expression data, which includes the selection of microarray samples (a specific condition or a mixture of various conditions) and of GeneChip summarization methods [RMA,²⁵ GCRMA,²⁶ MAS5¹⁸ or PLIER (Affymetrix Technical Note, http://www.affymetrix.com/support/technical/technotes/plier_technote.pdf)]. The second case is derived from the variety of cellular functions that the gene of interest concerned. The biological significance of a PCC value depends on each type of coexpression data, and thus users cannot directly compare PCC values obtained from different types of coexpression data. To obtain a comparable coexpression measure, we tested several measures and found that correlation rank could normalize these differences and can be used as the comparable measure. Four model species—Arabidopsis, human, mouse and rat—were used to confirm that the correlation rank was useful to directly compare the coexpression level among different genes, conditions and species.

2. Materials and methods

2.1. Data source of microarray experiments

To calculate condition-independent gene coexpression data, we constructed gene expression profiles using as many genes and samples as possible. Towards this end, we selected the GeneChip platforms shown in Supplementary Table S1. Because some samples were manually omitted due to different GeneChip usage, e.g. ChIP-on-chip or heterohybridization of close species, we used the following number of GeneChips; 1388 for Arabidopsis, 5188 for human, 2226 for mouse and 632 for rat. The samples used are shown in the Supplementary data. GeneChip summarizations were performed for each experiment using BioConducter packages.²⁷ PLIER was run with quantile normalization, and an offset of 10 was added to expression values of PLIER and MAS5. If these options were not applied, GO prediction performance in this study significantly decreased (data not shown). All the expression values used in this study were in base-2 logarithm. For each experiment, an average expression level for each gene was subtracted to normalize differences in basal expression levels between experiments. Finally, all experiments were combined into one large expression matrix, which was constructed for each summarization method and for each species.

2.2. Calculation of gene-to-gene PCC for gene coexpression

Even if technical replications are normalized, some data (e.g. a large series of time-course experiments under a single biological condition) are biologically redundant and result in unfairly biased gene expression data. Because these unexpected biases will affect the PCC values, we used a gene-to-gene PCC weighted by the following sample information scores W_S. The weighted PCC has been applied to evaluate the relationships between two variables with data samples by unbalance manner, and also used for microarray analyses.^28,29 The weight W_Sa for a sample Sa of interest was derived from the sample-to-sample similarity J_Sa,Sx between the sample Sa and anyone of the sample Sx, which was calculated as PCC between the two samples. To focus on significantly similar samples, we introduced the cut-off threshold C. If the sample similarity J_Sa,Sx is smaller than the cut-off threshold C, J′_Sa,Sx is set to 0. On the other hand, if J_Sa,Sx is larger than C, J′_Sa,Sx= (J′_Sa,Sx − C)/(1 − C), so that the range of sample-to-sample similarity J′_Sa,Sx becomes 0 to 1. We roughly optimized the cut-off threshold C and used 0.4. We did not carry out a fine optimization because the results were not sensitive to this parameter. The sample redundancy J_Sa for the sample Sa is calculated as the summation of the J′_Sa,Sx, namely 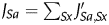. Because a large J_Sa value indicates highly redundant and thus a poorly informative sample, weight of the sample Sa, W_Sa, was defined as the inverse of the square root of the sample redundancy J_Sa. This procedure is analogous to the calculation of the standard error from the standard deviation, where the number of samples corresponds to the sample redundancy. If the sample S is replicated four times without experimental error, the reliability of the data for the sample S is doubled. Finally, the weighted PCC was calculated between two probes, according to the formula of weighted PCC²⁸ with the weight described here. This weighted PCC was used as PCC in this study. Negative PCC values were used as is, namely treated as weaker relationships than zero PCC value, because negative correlations did not promote gene function prediction in our data (see also Fig. 2C, where red dots indicating the same GO annotation to each of the reference gene did not significantly appear in right-bottom anti-correlation region). The effectiveness of the weight was not fully evaluated and it can be different with data set. In our data set, the weighted PCC gave slightly better performance than non-weighted PCC, but the differences were not so large in our data set.

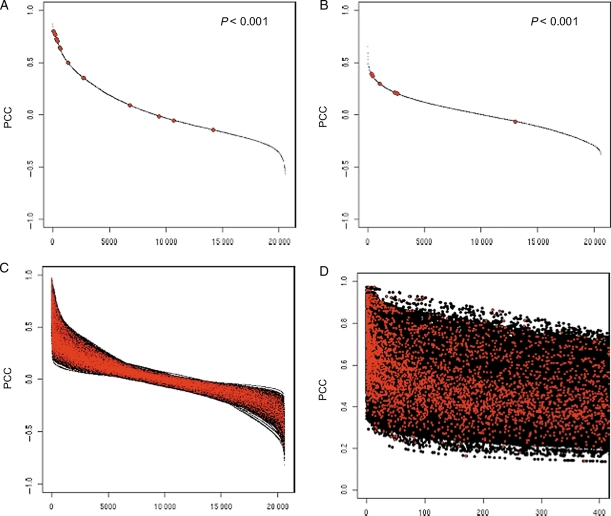
Figure 2.

Relationships of PCC values and GO term agreement. Decay curves of PCC values for gene coexpression are shown for Arabidopsis genes. Decay curves of PCC values of coexpressed genes from two particular genes: At3g20000 (A) and At5g06140 (B). Red dots indicate genes that have the same annotations of GO BP terms as the reference gene. Statistical significance of non-random distribution of the red dots was established by the Kolmogorov–Smirnov test. (C) The same curves in A and B are overlaid for all Arabidopsis genes. (D) Detailed view of the 0–400 range of C.

In the case of Arabidopsis, genes with a single probe set are used, so that a probe-to-probe correlation directory indicates gene-to-gene correlation. For human, mouse and rat cases, the probe-to-probe correlations are transformed to gene-to-gene correlations using the maximum correlation value between all pairs of probes between the two genes, because most of genes in these three species are supported by multiple probe sets.

2.3. Calculation of PCC rank and mutual rank for gene coexpression

When we focus one gene of interest, we can obtain coexpressed gene list sorted by PCC values between the gene of interest and all other genes on the microarray. ‘PCC rank’ used in this study is the rank of the gene in the PCC-ordered gene list. When gene A is third strongly coexpressed genes for gene B, PCC rank of gene A to gene B is 3. This PCC rank was used as one of coexpression measures. Since PCC rank between two genes of interest can be different, we introduced another coexpression measure, mutual rank (MR), by taking a geometric average of the PCC rank from gene A to gene B and that of gene B to gene A. The reason why we used ‘geometric average’ rather than arithmetic average is that we think that the difference of PCC ranks will change as logarithmic manner. For example, the impact of the difference of 1 and 3 in PCC rank can be similar with that of 100 and 300. Actually, the geometric-averaged MR showed slightly better gene prediction performances than arithmetic-averaged MR (data not shown).

2.4. Extraction of GO terms for the assessment of gene coexpression

Each of the three categories of Gene Ontology (GO) Annotation,¹⁶ namely biological process (BP), cellular component (CC) and molecular function (MF), was used to annotate gene function. Because GO terms have hierarchical topology with different importance, we selected appropriate GO terms to represent gene function. The selection was conducted based on the information content of GO terms.³⁰ All annotations were first mapped to all upper GO terms up to the root terms. Because terms that are associated with too many genes have less informative annotations, and thus could not be used to construct new experiments, we used GO terms associated with >4 and <20 genes. As a result, 729 BP terms, 147 CC terms and 391 MF terms were selected on average for the four species. Although we chose this range of gene numbers (i.e. >4 and <20) based on the characteristics of the randomized coexpressed gene lists to be AUC = 0.5 (see next section for AUC), we reached the same conclusion even using other ranges. The statistics of the selected GO terms are shown in Supplementary Table S2.

2.5. Prediction of gene function

We iteratively applied the nearest neighbour approach to predict GO annotations for each reference gene. The actual procedure was conducted as follows. First, we applied it to GO annotations of the most strongly coexpressed gene to the reference gene. Then, the GO annotations of the second-most strongly coexpressed gene were applied. In the same way, GO annotations of all coexpressed genes were iteratively applied. One of the characteristics of this prediction method is that it does not require parameter optimization. Another characteristic is that we can introduce any thresholds to define valid coexpressed genes. Using the predicted result on various thresholds, we generated receiver operating characteristic (ROC) curves, which is a plot of true-positive rate [TP/(TP + FN)] against false-positive rate [TN/(FP + TN)] with all possible threshold values, where TP, FN, TN and FP are the number of true positives, false negatives, true negatives and false positives, respectively. In gene function prediction, the number of positive gene-to-function relationships is far smaller than that of negative relationships. To evaluate such unbalanced data, evaluation measure such as overall accuracy, the Mathews correlation coefficient and F-measure is not adequate. A representative ROC curve is shown in Supplementary Fig. S1. Because the ROC curves produced in this analysis showed standard convex-upward shapes, we simply showed the area under the ROC curve (i.e. AUC) to compare the effectiveness of the coexpression data. For example of BP in Arabidopsis, 376 GO annotations for 2280 genes were tested (Supplementary Table S2), where all possible associations were 857 280, and positive associations were 3705. We calculated true- and false-positive rates for all possible thresholds (857 280) to draw the ROC curve, and then AUC were obtained as the average of the true-positive rates for the false-positive rate ranging from 0 to 1 by 0.0001 steps.

3. Results and discussion

3.1. Problems with PCC values

We first used the PCC value as a measure of coexpression but found that the inferred biological significance varied depending on the type of coexpression data. This problem can be attributed to two main factors: (i) different gene expression data and data treatments were used in each database, and (ii) different kinds of cellular functions require differences in the strength of gene coexpression. Examples of these two possibilities for Arabidopsis are shown in Figs 1 and 2, respectively.

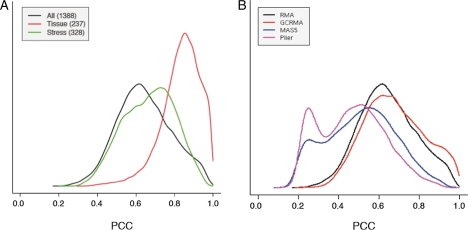
Figure 1.

Distributions of PCC values between each gene and its strongest coexpressed gene in Arabidopsis. (A) Distribution of PCC values calculated from 1388 GeneChip slides (black), 237 slides (red) and 328 slides (green), both of which were summarized by RMA. (B) Distribution of PCC values calculated from 1388 GeneChip slides summarized by four methods (RMA, GCRMA, MAS5 and PLIER).

The first factor is related to the expression data construction. Specifically, it depends on the choice of sample set (Fig. 1A) and the choice of normalization method for the expression data (Fig. 1B). Figure 1 shows the distribution of the gene-to-gene PCCs between each gene and the most strongly coexpressed gene. In Fig. 1A, the black line shows the distribution of the PCC values calculated from the 1388 Arabidopsis GeneChip slides downloaded from TAIR,¹⁶ and the red line was calculated from the 237 samples related to developmental experiments (TAIR-ME00319) and the green line was calculated from the 328 samples related to abiotic stresses (from TAIR-ME00325 to ME00330), both of which were a subset of the 1388 samples containing various experimental conditions. As seen in the figure, the red- and green-line distributions are shifted to the right compared with the black-line distribution, indicating that high coexpression around PCC = 0.8 was commonly observed in the PCCs from the developmental samples, whereas high coexpression pairs were rarely observed in the unselected samples (black-line distribution). Two possible reasons—one biological and the other mathematical—can account for the differences in PCC values. The biological reason is that gene expression changes among developmental samples were far larger than those elicited in response to environmental stresses. Such large changes in gene expression amplitude can decrease experimental noises that decrease any gene correlations. Therefore, absolute values of the PCC obtained from developmental experiments will be higher than those from experiments with unselected samples. On the other hand, the mathematical reason is that a smaller sample number tends to produce larger amplitude of correlation values between any two genes as discussed previously.¹² This can easily be understood by considering an extreme case using only two microarray slides, for which all the PCC values between the most highly coexpressed gene pair should be 1.0 from the definition of PCC. The mathematical issue can be resolved by using statistical significances of the PCC values. In fact, some coexpression databases, such as ACT,⁹ CSB.DB⁷ and CressExpress,¹² calculate the statistical significance of every PCC value. In the later part of this paper, we introduced rank of PCC. For a given expression matrix, the effect of rank is identical to PCC and to its P-value, because the order of PCC and its P-value of PCC were identical.

In the same way, the choice of the normalization method of microarray data affects the PCC values. Figure 1B shows that distributions of the highest PCCs from RMA- and GCRMA-summarized data manifested as a single peak, whereas those of MAS5 and PLIER were bimodal. The peak around PCC = 0.2 observed in MAS5 and PLIER was derived from genes with low expression level (data not shown), where noises in microarray experiments may strongly affected the observed expression patterns to calculated gene coexpression. Similar to Fig. 1A, high PCC values (e.g. PCC = 0.8) were more frequently observed in RMA- and GCRMA-summarized data, whereas those values were less frequently observed in MAS5- and PLIER-summarized data.

Gene function is another factor causing differences in biological significance of a PCC value. In Fig. 2A and B, two examples show relationships between PCC values and gene function. The black line in Fig. 2A indicates PCC values of coexpressed genes to a gene, At3g20000 (mitochondria outer membrane protein TOM40), in descending order. Genes with the same function by GO BP annotation as the reference gene (At3g20000) are highlighted by red dots. Because genes with the same cellular function can be expected to be coexpressed, it is reasonable that the red dots accumulated at the top-left area in the graph. Figure 2B is another example with a different reference gene, At5g06140 (PHOX domain-containing protein). Good accumulation of genes with the same function was again observed in the top-left area. However, the absolute PCC values of the red dots were different in these two graphs. Most of red dots in Fig. 2A accumulated around PCC = 0.6, whereas most red dots in Fig. 2B accumulated around PCC = 0.3. This observation suggested that the required strength of gene coexpression might be different for each reference gene. At3g20000 (Fig. 2A) requires stronger gene coexpression than At5g06140 (Fig. 2B) to realize its function. To check the generality of this observation, the correlation curves for all genes were overlaid in Fig. 2C and D (Fig. 2D is a close-up view of Fig. 2C). If the absolute value of PCC directly indicates biological significance, these red dots should accumulate in the upper area in these graphs. This was not the case, however, as they accumulated in the left-most region. Especially in the region of the top-most 20 genes, there is almost no relationship between the PCC values and functional relationship. These results suggest that the rank of PCC is a more effective measure of coexpression (to identify functionally related genes) than the PCC value itself. In the following sections, we focus on the characteristics of the rank of PCC value for each reference gene, which we call ‘PCC rank’ against normal ‘PCC value’, hereafter.

3.2. PCC rank can normalize inconsistencies caused by different sample compositions or different GeneChip summarization methods

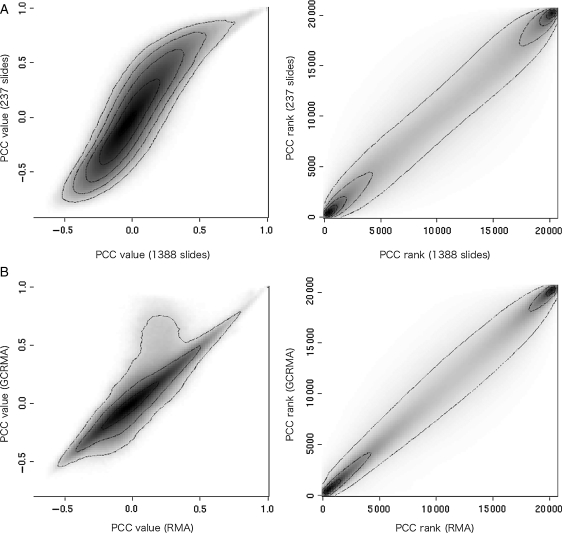
From the analyses of the relationship between PCC value and gene function, we proposed that the PCC rank might be a good measure of coexpression. Next, we assessed how PCC rank is affected by differences in expression data observed in Fig. 1. We observed the distribution between developmental samples and all samples for PCC values (Fig. 3A, left) and PCC ranks (Fig. 3A, right), and that between RMA- and GCRMA-summarized data for PCC value (Fig. 3B, left) and PCC rank (Fig. 3B, right). The left panel of Fig. 3A is a density plot between PCC values calculated from 1388 Arabidopsis GeneChips on the x-axis and PCC values calculated from 237 developmental samples on the y-axis. Each original dot was calculated for all gene pairs and shown as a density plot in logarithmic scale. The distribution was a broad S-shape, indicating weak correspondence of the two types of PCC values. On the other hand, when we used PCC rank instead of PCC value, the distribution aligned on the diagonal (Fig. 3A, right panel), meaning there was a linear correspondence of PCC ranks between the different samples. Notably, the genes in the highest (bottom-left) and the lowest (top-right) rank regions were highly populated between the two types of coexpression data, indicating that PCC ranks, as opposed to PCC values, were robust with respect to different sample compositions when the correlation was relatively high in each reference gene. In the same way, differences in PCC values caused by different GeneChip summarization methods shown in Fig. 1B can be normalized by PCC rank (Fig. 3B). Although it was generally well correlated in both panels, some gene pairs showed exceptionally high values for GCRMA in PCC value (Fig. 3B, left) as was the case in Fig. 1B. Again, these PCC ranks showed very good agreement (Fig. 2B, right). This result indicated that PCC rank was more stable than PCC value with respect to the selection of GeneChip summarization methods, and thus is suitable as a comparable coexpression measure. Correspondence between RMA-MAS5 and MAS5-PLIER showed similar results (Supplementary Fig. S2). Our observation that PCC values obtained after GCRMA summarization were higher than those obtained after RMA summarization is consistent with the report for GCRMA problems by Lim et al.,³¹ and thus these problematic characteristics of GCRMA may be a general feature.

Figure 3.

Inconsistency of the PCC values and consistency of the PCC ranks for differently constructed expression data. Degree of coexpression is compared using PCC value (left panels) or PCC rank (right panels). (A) The x-axes indicate coexpression calculated from 1388 Arabidopsis GeneChip slides, whereas the y-axes indicate coexpression calculated from 237 developmental slides. (B) The x-axes indicate coexpression calculated from RMA-summarized data, whereas the y-axes indicate that from GCRMA-summarized data. All distributions are represented by density plots in logarithmic scale.

PCC values and its distribution on a given set of experiments can also be affected by the quality of microarray data, where more noise in microarray experiments causes lower PCC values. On the other hand, we can neglect the original PCC values and its distributions by taking the rank of the PCC values. This may be one of the reasons why rank-based values can compare different coexpression data. As inextricably linked aspect of this comparability, rank-based values do not include any information to estimate the quality of original microarray data. This phenomenon is quite similar with RMA summarization of GeneChip compared with MAS5, where the rank of probe intensity is used to reconstruct common distribution.

3.3. Large-scale assessment of PCC rank and MR

For large-scale assessment of PCC rank, we predicted gene function using coexpressed gene lists sorted by PCC value or by PCC rank and compared the results, because many recent studies used gene coexpression data to identify gene function (see review²²). After constructing a coexpressed gene list for each gene, we predicted GO annotations assigned to the reference gene using the following procedure (see Section 2 for details). First, the GO annotations for the gene that was most strongly coexpressed with the reference gene were applied as the first prediction. Then, the GO annotations of the second-most strongly coexpressed gene were applied, and so forth until all coexpressed genes under a given threshold of coexpression were applied. On the basis of ROC curves of this prediction, the AUCs were compared as prediction performance. AUC = 1.0 indicates a perfect prediction, whereas AUC = 0.5 means random prediction. We evaluated the performance for each GO category, i.e. BP, CC and MF.

We compared the performance of the GO annotation prediction based on PCC values and PCC ranks (Fig. 4). In all the cases for GO BP, CC and MF predictions, PCC rank was more effective than PCC value. This result agreed well with the result in Fig. 2D, which showed that genes with same GO BP annotation accumulated in the high PCC rank region (the left-most region in Fig. 2D) rather than the high PCC value region (top region in Fig. 2D). Note here that we introduced ‘MR’ by taking a geometric average of the PCC rank from gene A to gene B and that of gene B to gene A, because the two ranks between genes A and B are usually different and thus are not convenient to use like a PCC value. The performance of MR was almost the same as or slightly better than PCC rank (Fig. 4). To further confirm the statistical significance of the difference between PCC value and the other two measures, we randomly selected half of the entire genes, and constructed PCC table and calculated PCC rank and MR, and then AUCs of gene function predictions were obtained as the same procedure in this study. This procedure was repeated 100 times and calculated the standard deviation of the difference of AUCs. The result showed clear difference in performances between PCC value and the rank-based measures (Supplementary Table S3). Note that no difference between PCC rank and MR was observed.

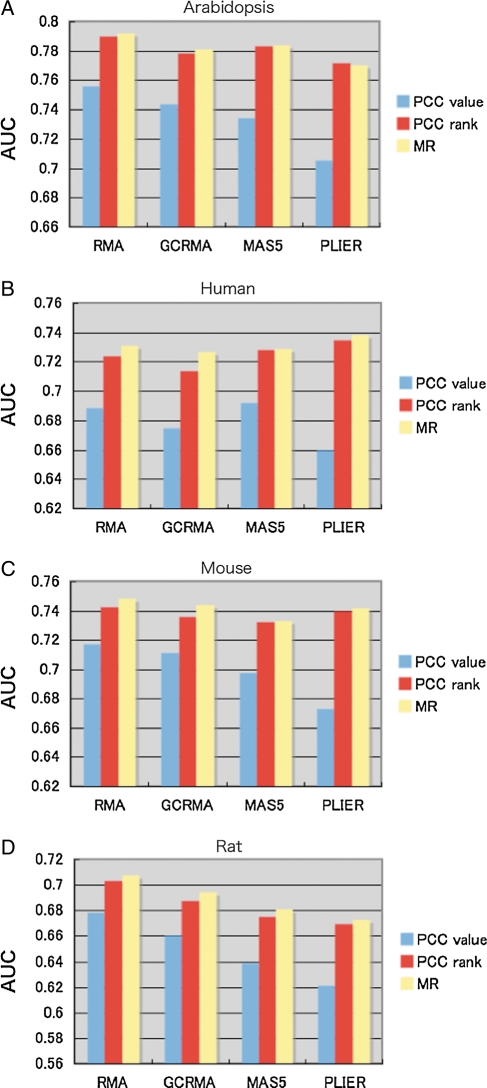
Figure 4.

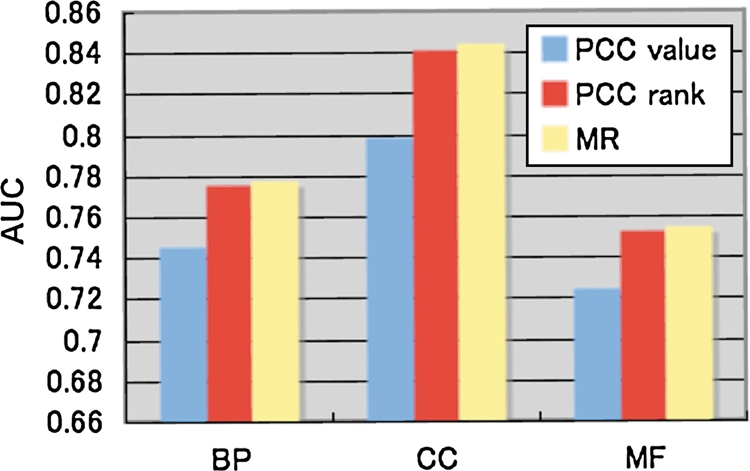
Effect of rank-based coexpression measures to predict GO annotations. The y-axis indicates AUCs to predict three types of GO annotations (BP, CC and MF) from gene coexpression data represented by PCC value, PCC rank and MR. Note that the AUCs on the y-axis do not start from 0.5, which corresponds to random prediction, because we focused on differences in AUCs rather than the absolute value of AUCs. BP, biological process; CC, cellular component; MF, molecular function.

Our observation that PCC value was less effective for predicting gene function than PCC rank is probably a consequence of the different requirements of coexpression for different biological functions. When we consider genes for a protein complex, strength of required gene coexpression may depend on the stability of monomers. Strong coexpression should be required for unstable monomers, whereas loose coexpression may be sufficient for stable monomers, the half-life of which may be regulated by phosphorylation and/or protein subcellular localization. In the same way, when we consider genes for enzymes of a particular metabolic pathway, strength of required gene coexpression may depend on the stability or toxicity of the metabolites. If the intermediate metabolite(s) between any reactions is unstable or toxic, strong coexpression of the enzyme genes will be required.

PCC is not the only measure of gene coexpression. For example, Spearman's correlation coefficient (SCC), mutual information content and partial correlation have also been used in gene coexpression studies.^21,31,32 According to our results, the performance of PCC and SCC values was almost the same for GO term prediction (Supplementary Fig. S3). Although PCC may still have limitations with respect to outliers, as reported previously,²⁰ the outlier effect was smaller in large-scale microarray data. Compared with the difference between SCC and PCC values, PCC rank is very different from PCC value. It may be understood by considering that SCC value as well as PCC value is two-body relationship whereas PCC rank is multi-body relationship, i.e. PCC value can be calculated from just two genes of interest, and PCC rank reflects the distribution of PCC value around the two genes of interest. In this sense, the relationship between SCC and PCC values was more similar than that of PCC value and PCC rank. This viewpoint was also supported by our preliminary observation that SCC rank had a similar effect to PCC rank (data not shown).

3.4. Performance of PCC rank and MR in other species

Although to this point we have focused solely on Arabidopsis data, we also tested the effectiveness of PCC rank and MR with respect to gene coexpression in other species to evaluate the generalities of PCC rank. We used RMA-summarized data for Arabidopsis (Fig. 4), and here we show the results with different GeneChip summarization methods (GCRMA,²⁵ MAS5¹⁸ and PLIER) for different model species (human, mouse and rat), which have been used in several gene coexpression databases. Because the pattern of the results was almost the same for the BP, CC and MF categories of GO (Fig. 4), we show only the average AUC values for the other species and other normalization methods (Fig. 5). Figure 5A shows the results of the gene function prediction in Arabidopsis. AUC values on the y-axis were compared for three coexpression measures (PCC value, PCC rank and MR) and for four GeneChip summarization methods (RMA, GCRMA, MAS5 and PLIER). For all four GeneChip summarization methods, PCC rank and MR showed higher prediction efficiency than PCC values. Figure 4B–D shows the results for human, mouse and rat, respectively. Although the gene expression data for the four species were completely different with respect to sample size and sample composition and the quality or density of GO terms is quite different in each species, PCC rank and MR were consistently more effective at predicting gene function than PCC value, strongly suggesting that the relatively higher performance of PCC rank is a general feature.

Figure 5.

Effect of summarization methods for GO predictions. The four types of summarization methods were assessed for their ability to predict GO annotations. The y-axes indicate average AUC values of the ROC curves to predict GO BP, CC and MF. Note that the AUCs on the y-axis do not start from 0.5, which corresponds to random prediction, because we focused on differences of AUCs rather than the absolute value of AUCs.

3.5. Effects of PCC rank with respect to different summarization methods of GeneChip data

Figure 5 shows the performance of different GeneChip summarization methods. The selection of the GeneChip summarization method is one of the most analysed issues of GeneChip data. Although many studies have compared GeneChip summarizations, there has been no general consensus. For example, Irizarry et al.³³ showed superiority of GCRMA, whereas relatively low performance of GCRMA was shown by titration experiments.³⁴ Srinivasasainagendra et al.¹² discussed RMA superiority compared with GCRMA and MAS5 based on their unpublished result using redundant probeset pairs, which should be separated from the probeset pairs randomly selected. This disagreement is partially caused by different assessment systems. The focus of our assessment was to obtain more information from gene coexpression data. From this point of view, Lim et al.³¹ reported MAS5 superiority and the requirement for GCRMA modification when using human GeneChip data. Although our results do not support the inferiority of GCRMA, MAS5 showed the highest performance for humans and, in that sense, supports the results by Lim et al.³¹ As for basic properties of GeneChip summarization methods, MAS5 returns relatively high accuracy of gene expression values, but reproducibility of the value is relatively low compared with other summarization methods.³³ Because the number of human samples was larger (5188 samples) than that for the other species (1388, 2226 and 632 samples for Arabidopsis, mouse and rat, respectively), the shortcoming of low reproducibility using MAS5 summarization may be overcome by a large number of samples. In fact, when we used 500 randomly selected human samples instead of all 5188 samples, MAS5 showed lower performance than RMA (data not shown). However, MAS5 still has merits to construct coexpression data, because it can be applied to a single GeneChip slide and because the number of available data from MAS5 in public database is larger than that from other methods which requires raw data registrations. Note that we did not use detection call of MAS5 (Present, Marginal and Absent), which provides significance of expression against background noise. Although the effectiveness of detection call of MAS5 has been reported,³⁵ we did not use it to avoid managements of missing values. This probably caused lower performance of MAS5.

3.6. Gene coexpression data for Arabidopsis are more powerful than those for mammalian species

The AUC of GO term prediction for Arabidopsis genes was higher than for the mammalian genes (Fig. 5). This may be because Arabidopsis has a simpler morphology and gene structure than mammals, i.e. Arabidopsis has fewer tissues and a lower degree of tissue differentiation. For example, flowering plant tissues have totipotency, and thus the developmental programme for each tissue can be maintained independently, e.g. cutting the bulb is not lethal. On the other hand, Arabidopsis has many paralogous genes to increase the variation of transcripts instead of using an alternative splicing strategy that is common in mammals.³⁶ This characteristic in Arabidopsis probably results in a more accurate measurement of the gene expression pattern, because gene expression microarrays cannot distinguish between splicing variants. Also, the sample variety of GeneChip data might be higher in Arabidopsis. The GeneChip data for Arabidopsis include many time-course experiments for external stimuli in addition to precise tissue samples collected by AtGenExpress,^37–39 whereas this type of experiment may be more difficult to obtain for mammalian species. In fact, gene coexpression data are extensively used for gene targeting in Arabidopsis research, whereas this is not a major approach used in mammalian studies.

3.7. MR effects on hierarchical clustering

To evaluate the effect of MR on multiple reference genes, we conducted hierarchical clustering using PCC or MR as the metric; (1 − PCC) was used as the PCC metric. Since the result of hierarchical clustering depends on a selected linkage rule, we applied seven methods available in ‘hclust’ function of statistical package R (http://www.r-project.org). To assess hierarchical clustering result, we counted the number of junction whose nodes are filled with a single GO annotation, i.e. the nodes with the same function (Supplementary Fig. S4A). As a result, MR metric showed generally better performance than PCC metric, and the difference between MR and PCC was remarkable for single, centroid and median linkage methods (Supplementary Fig. S4B–D). It may be noteworthy that MR showed very stable performance for every linkage method compared with the variable performances in PCC values. This result may suggest that MR already included some effects caused by multiple gene reference induced by some linkage rules as average, mcquitty, ward and complete, where all pairs of the cluster members are considered to calculate the distance between clusters.

3.8. Conclusion

In this study, we investigated the characteristics of PCC (value and rank) as a coexpression measure. The biological significance of PCC could be altered by expression data construction and gene function. We found that PCC rank could normalize differences in biological significance, and we propose a new measure for coexpression analysis, MR, because a single index for a pair of gene is more convenient. MR is easy to calculate from PCC and can be directly compared among different coexpression data. This universality of MR enabled us to introduce a common threshold to all reference genes and to calculate average distances among multiple genes. As a consequence, hierarchical clustering and a combined coexpressed gene list for multiple reference genes can be available more effectively. Tools for these functions based on MR are available in our databases.^13,14

Although selection of the GeneChip summarization method strongly affected the performance of coexpression data, MR could reduce the difference. This result applies directly to coexpression database construction, because much of the GeneChip expression data have been stored in public repositories as MAS5-summarized data. Our results provide a standard calculation procedure for condition-independent gene coexpression data to elucidate gene-to-gene functional relationships.

The generalities and easy calculation of PCC rank or MR will enable the users to directly compare results obtained from different coexpression databases, and this will strongly promote comparative transcriptomics using public databases. Searching conserved coexpression is one of the possible important applications, which is also provided in our databases.^13,14 In this study, we did not pay attention to anti-correlation. To analyse anti-correlation using rank-based measures, some normalization such as taking percentile of PCC rank or MR may be useful to standardize the measures from zero to one.

3.9. Data availability

Coexpression data represented by the PCC value and the MR based on RMA-summarized GeneChip data used in this study are available at (http://atted.jp/download.shtml) for Arabidopsis and (http://coxpresdb.jp/download.shtml) for human, mouse and rat.

Supplementary data

Supplementary data are available at www.dnaresearch.oxfordjournals.org.

Funding

This work was supported by a grant-in-aid from the Institute for Scientific Research on Priority Areas from the Ministry of Education, Culture, Sports, Science and Technology of Japan to K.K. and by the Global COE Program (Center of Education and Research for Advanced Genome-Based Medicine), MEXT, Japan to T.O.