Volumetric Interpretation of Protein Adsorption: Kinetics of Protein-Adsorption Competition from Binary Solution

Abstract

The standard solution-depletion method is implemented with SDS-gel electrophoresis as a multiplexing, separation-and-quantification tool to measure competition between two proteins (i and j) for adsorption to the same hydrophobic adsorbent particles (either octyl sepharose or silanized glass) immersed in binary-protein solutions. Adsorption kinetics reveal an unanticipated slow protein-size-dependent competition that controls steady-state adsorption selectivity. Two sequential pseudo-steady-state adsorption regimes (State 1 and State 2) are frequently observed depending on i, j solution concentrations. State 1 and State 2 are connected by a smooth transition, giving rise to sigmoidally-shaped adsorption-kinetic profiles with a downward inflection near 60 minutes of solution/adsorbent contact. Mass ratio of adsorbed i, j proteins (m_i m_j) remains nearly constant between States 1 and 2, even though both m_i and m_j decrease in the transition between states. State 2 is shown to be stable for 24 hours of continuous-adsorbent contact with stagnant solution whereas State 2 is eliminated by continuous mixing of adsorbent with solution. In sharp contrast to binary-competition results, adsorption to hydrophobic adsorbent particles from single-protein solutions (pure i or j) exhibits no detectable kinetics within the timeframe of experiment from either stagnant or continuously-mixed solution, quickly achieving a single steady-state value in proportion to solution concentration. Comparison of binary competition between dissimilarly-sized protein pairs chosen to span a broad molecular-weight (MW) range demonstrates that selectivity between i and j scales with MW ratio that is proportional to protein-volume ratio (ubiquitin, Ub, MW = 10.7 kDa; human serum albumin, HSA, MW = 66.3 kDa; prothrombin, FII, 72 kDa; immunoglobulin G, IgG, MW = 160 kDa; fibrinogen, Fib, MW = 341 kDa). Results are interpreted in terms of a kinetic model of adsorption that has protein molecules rapidly diffusing into an inflating interphase that is spontaneously formed by bringing a protein solution into contact with a physical surface (State 1). State 2 follows by rearrangement of proteins within this interphase to achieve the maximum interphase concentration (dictated by energetics of interphase dehydration) within the thinnest (lowest volume) interphase possible by ejection of interphase water and initially-adsorbed proteins. Implications for understanding biocompatibility are discussed using a computational example relevant to the problem of blood-plasma coagulation.

1. Introduction

A widely-held belief within the biomaterials community is that adsorbed protein catalyzes, mediates, or moderates the biological response to artificial materials [1–10]. In light of this seemingly incontrovertible fact, it is self evident that responsible proposition of evidence-based biochemical mechanisms for the biological response to materials requires quantitative knowledge of the exact composition of protein that becomes adsorbed to biomaterials in contact with complex biological mixtures such as blood. This composition must be known both in terms of protein identity and concentration. It also seems self evident that prospective materials engineering for various medical applications requires detailed knowledge that relates biomaterial properties to protein adsorption. Otherwise, structure-property relationships cannot be formulated, leaving biomaterials engineering dependent on design-directed or trial-and-error approaches [11]. Thus, the entirety of biomaterials surface science seems critically dependent on a thorough understanding of protein adsorption.

Our work in protein adsorption is aimed at experimental resolution of some fundamental aspects of protein adsorption, motivated by the expectation that clarification of the physical chemistry of adsorption will ultimately lead to a predictive basis for cardiovascular biomaterials design. These fundamentals include the reversibility/irreversibility of protein adsorption, mechanism of the so-called Vroman effect [1, 17, 20, 24–43], capacity of proteins to adsorb in multilayers [6, 38, 44–60], energetics of protein adsorption [6, 14, 22, 43, 45, 49–51, 61–63], and the applicability of thermodynamic/computational models [47]. In particular, we have focused on obtaining energy [6, 14, 22, 43, 50, 51, 61–63] and mass [44, 45, 47] balance for the adsorption of a wide variety of purified blood proteins to a broad span of materials with different surface chemistry/energy. Results of this survey have been illuminating (see brief review in the introduction of ref. [45]) and strongly implicate a controlling role for water in the adsorption process. In very brief summary, experimental results have led us to adopt the classical Guggenheim interphase model of the surface region [64, 65] and interpret protein adsorption as a partitioning between bulk solution and a three-dimensional (3D) interphase region that separates bulk solution from the physical adsorbent surface. The 3D interphase paradigm is hardly new to surface science but has not been widely applied in the study of protein adsorption, or to the general problem of adsorption for that matter. Significant advantages of the interphase paradigm are retention of the concept of chemical activities (concentrations) essential for a complete understanding of adsorption energetics and consistency with standard surface thermodynamics [48]. Importantly, the interphase model easily accommodates multilayer-protein adsorption that has been shown to occur by a number of investigators using a variety of experimental methods over the last twenty years or so [6, 38, 49–60]. This so-called ‘volumetric interpretation’ of adsorption has it that proteins are expelled from aqueous solution to the interphase by what amounts to be the hydrophobic effect. Expelled protein can partition into the interphase if-and-only-if it is energetically favorable to displace a volume of interphase water equal to that of the adsorbing hydrated protein [51]. In this way, water-wettability substantially controls adsorption because it requires more energy to displace water from the interphase of relatively hydrophilic surfaces than from the interphase of more hydrophobic counterparts [45]. Efforts to understand competition between two proteins adsorbing from mixed solution [43, 46] based on this overarching mechanism have been less satisfactory because, for reasons detailed herein, we have failed to fully appreciate the role that adsorption kinetics plays in protein-adsorption selectivity.

It has been widely (but not universally) assumed that protein adsorption occurs over a relatively long timeframe that is directly related to tens-of-minutes-to-hours change in interfacial energetics observed when a protein solution is brought into contact with a surface [6, 14, 22, 43, 50, 51, 61]. Furthermore, it is popularly held that selective adsorption of certain proteins from a mixture is due, at least in part, to a time-dependent adsorption-displacement phenomenon involving proteins engaged in adsorption competition (a.k.a Vroman Effect). Recent work shows that the former perspective is substantially incorrect for concentrated (mg/mL) protein solutions [48, 66]. This finding, in turn, suggests that the interpretation of the Vroman effect is also problematic. A more correct view seems to be that protein molecules rapidly diffuse into an inflating interphase volume that is initially formed upon contact of an adsorbent with concentrated protein solution [48]. Through this process, the interphase captures a fixed mass of protein in proportion to solution concentration. Mass transport from concentrated solution is effectively complete within seconds, if not milliseconds, but certainly well before the tens-of-minutes-to-hours associated with interfacial energetic changes. Indeed, protein-adsorption kinetics are difficult to follow unless solution concentrations are quite low in the μg/mL range. This initially-formed interphase slowly shrinks in volume by efflux of interphase water, causing interphase protein concentrations to increase and interfacial tensions to concomitantly decrease over the aforementioned tens-of-minutes-to-hours time scale. Unfolding of proteins (changing occupied volume, denaturation) at a surface [67] can also lead to concentration of protein within the interphase region.

Curious to understand ramifications of the above-described adsorption kinetics on protein-adsorption competition from mixed-protein solutions, we adapted the standard solution-depletion method to measure adsorption competition [46] between two proteins as a function of time, ranging from 5 minutes to 90 minutes and, in one test case, 24 hours. Herein we show that adsorption competition is very rapid, leading to unanticipated selectivity that persists long after the initial burst of protein arriving at the adsorbent surface. This outcome has significant ramifications in understanding both protein adsorption and how protein adsorption controls the biological response to materials.

2. Methods and Materials

2.1 Proteins, Adsorbent Particles, and Solution-Depletion Measurements

Proteins were used as received from the vendor without further purification. Table 1 lists relevant details. SDS-PAGE of purified protein solutions yielded single bands. These proteins were selected as representatives of a broad molecular weight range that could be clearly separated on the same type of electrophoresis gel. Selected pairs of proteins were mixed together in phosphate buffer solution (PBS; Sigma; 0.14 M NaCl, 3mM KCl prepared in 18 MΩ water) at concentrations specified in column 3 and 4 of Tables 2A,B that correspond to specific competitive-adsorption Cases 1–5 further discussed in Section 3.2.

Table 1.

Purified Protein Used in Competitive Adsorption Experiments

Name of Protein (Acronym)	Molecular Weight (kDa)	As-received form	Purity (Electrophoresis) or Activity	Vendor
Ubiquitin (Ub)	10.7	Powder	98%	Sigma Aldrich
Human Serum Albumin (HSA)	66.3	Powder	96–99%	Sigma Aldrich
Prothrombin (FII)	72	Powder	> 95%	Enzyme Research
Human IgG (IgG)	160	Powder	> 95%	Sigma Aldrich
Fibrinogen (Fib)	341	Powder	80% Clottable Protein	Sigma Aldrich

Table 2.

Table 2A: Protein-Adsorption Kinetics from Binary Solution to Octyl Sepharose Particles (OS)
					State 1			State 2
Protein Pairs	Condition	${(W_{B_i}^o)}_{i,j}$ (mg/mL)	${(W_{B_j}^o)}_{i,j}$ (mg mL)	$\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$	(Di)i,j mg/mL, (N)	(Dj)i,j mg/mL, (N)	$\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$	(Di)i,j mg/mL, (N)	(Di)i,j mg/mL, (N)	$\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$	Transition Period (min)	Si,j, (N, R2)
HSA (i) + Fib (j)	Case 1	1.25	1.25	1.00	0.66 ± 0.05, (9)	0.46 ± 0.05, (9)	0.70 ± 0.09	0.53 ± 0.05, (3)	0.28 ± 0.03, (3)	0.53 ± 0.08	55–75	0.80 ± 0.02 (5, 0.99)
	Case 2	2.00	3.00	1.50	0.98 ± 0.06, (9)	1.21 ± 0.08, (9)	1.23 ± 0.11	0.60 ± 0.01, (3)	0.74 ± 0.01, (3)	1.23 ± 0.03	45–80
	Case 3	4.00	2.00	0.50	1.61 ± 0.09, (9)	0.60 ± 0.03, (9)	0.37 ± 0.02	1.11 ± 0.09, (6)	0.45 ± 0.04, (5)	0.41 ± 0.05	35–70
	Case 4	2.00	6.50	3.25	0.96 ± 0.05, (9)	2.60 ± 0.11, (7)	2.71 ± 0.18	0.62 ± 0.05, (4)	2.01 ± 0.03, (4)	3.24 ± 0.26	50–75
	Case 5	4.00	6.50	1.62	2.34 ± 0.07, (6)	2.86 ± 0.13, (5)	1.22 ± 0.26	1.57 ± 0.05, (5)	2.14 ± 0.04, (3)	1.36 ± 0.05	35–80
HSA (i) + IgG (j)	Case 1	1.25	1.25	1.00	0.56 ± 0.03, (9)	0.52 ± 0.03, (8)	0.94 ± 0.07	0.36 ± 0.02, (4)	0.35 ± 0.02, (3)	0.97 ± 0.08	40–80	0.88 ± 0.03 (5, 0.99)
	Case 2	2.08	5.00	2.40	1.12 ± 0.06, (8)	2.20 ± 0.14, (8)	1.96 ± 0.16	0.90 ± 0.05, (4)	1.58 ± 0.11, (4)	1.76 ± 0.16	40–75
	Case 3	4.17	5.00	1.20	2.21 ± 0.09, (6)	2.02 ± 0.16, (6)	0.91 ± 0.08	0.64 ± 0.10, (3)	0.75 ± 0.04, (3)	1.17 ± 0.19	25–80
	Case 4	2.08	10.00	4.81	0.92 ± 0.04, (7)	4.04 ± 0.17, (7)	4.39 ± 0.26	0.69 ± 0.01, (4)	2.75 ± 0.08, (4)	3.98 ± 0.13	35–80
	Case 5	4.17	10.00	2.40	2.26 ± 0.22, (9)	4.35 ± 0.15, (5)	1.92 ± 0.20	0.92 ± 0.14, (3)	2.10 ± 0.23, (4)	2.28 ± 0.43	50–85
HSA (i) + Ub (j)	Case 1	1.33	1.25	0.94	0.67 ± 0.02, (7)	0.66 ± 0.01, (9)	0.98 ± 0.03	0.55 ± 0.00, (3)	0.48 ± 0.01, (5)	0.87 ± 0.02	50–75	1.09 ± 0.04 (3, 0.98)
	Case 3	5.00	2.08	0.42	2.29 ± 0.09, (9)	1.00 ± 0.06, (8)	0.44 ± 0.03	1.30 ± 0.03, (4)	0.60 ± 0.03, (5)	0.46 ± 0.02	40–75
	Case 5	5.00	5.00	1.00	2.18 ± 0.29, (8)	2.49 ± 0.12, (5)	1.14 ± 0.16	0.96 ± 0.09, (4)	0.86 ± 0.10, (6)	0.90 ± 0.13	25–65
IgG (i) + Fib (j)	Case 1	3.00	1.50	0.50	1.22 ± 0.06, (13)	0.55 ± 0.03, (13)	0.45 ± 0.03	0.94 ± 0.04, (4)	0.41 ± 0.02, (4)	0.43 ± 0.03	65–80	0.90 ± 0.01 (3, 1.00)
	Case 3	10.00	2.50	0.25	4.02 ± 0.37, (10)	0.97 ± 0.06, (10)	0.24 ± 0.03	2.60 ± 0.14, (3)	0.71 ± 0.01, (3)	0.27 ± 0.02	55–80
	Case 5	10.00	7.00	0.70	4.89 ± 0.22, (9)	3.06 ± 0.14, (9)	0.63 ± 0.04	3.33 ± 0.22, (3)	2.27 ± 0.10, (3)	0.68 ± 0.05	45–80
FII (i) + Fib (j)	Case 1	1.50	1.25	0.83	0.74 ± 0.04, (11)	0.55 ± 0.03, (11)	0.74 ± 0.06	0.31 ± 0.03, (4)	0.25 ± 0.04, (4)	0.81 ± 0.15	65–75	0.96 ± 0.06 (3, 0.96)
	Case 3	6.00	2.50	0.42	3.05 ± 0.18, (17)	1.04 ± 0.10, (17)	0.34 ± 0.11	No State 2			No State 2
	Case 5	6.00	7.00	1.17	2.35 ± 0.10, (10)	2.79 ± 0.11, (10)	1.19 ± 0.07	1.40 ± 0.19, (4)	1.86 ± 0.03, (4)	1.33 ± 0.18	50–75
FII (i) + IgG (j)	Case 1	1.50	1.50	1.00	0.64 ± 0.04, (18)	0.70 ± 0.04, (18)	1.09 ± 0.09	No State 2			No State 2	0.97 ± 0.06 (3, 0.96)
	Case 3	6.00	3.00	0.50	2.60 ± 0.11, (15)	1.17 ± 0.09, (17)	0.45 ± 0.04	No State 2			No State 2
	Case 5	6.00	10.00	1.67	2.46 ± 0.15, (8)	3.81 ± 0.20, (8)	1.55 ± 0.12	1.10 ± 0.08, (6)	2.01 ± 0.15, (6)	1.83 ± 0.19	40–65

Table 2B: Protein-Adsorption Kinetics from Binary Solution to Octadecyltrichlorosilane-Treated Glass Particles (OTS)
					State 1			State 2
Protein Pairs	Condition	${(W_{B_i}^o)}_{i,j}$ (mg/mL)	${(W_{B_j}^o)}_{i,j}$ (mg/mL)	$\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$	(Di)i,j mg/mL, (N)	(Dj)i,j mg/mL, (N)	$\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$	(Di)i,j mg/mL, (N)	(Dj)i,j mg/mL, (N)	$\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$	Transition Period (min)	Si,j, (N, R2)
HSA (i) + Fib (j)	Case 2	2.00	2.00	1.00			0.89 ± 0.18	0.10 ± 0.01, (3)	0.13 ± 0.01, (3)	1.30 ± 0.17	45–75	1.09 ± 0.06 (4, 0.95)
	Case 4	2.00	4.00	2.00	0.35 ± 0.04, (8)	0.80 ± 0.07, (8)	2.28 ± 0.34	0.08 ± 0.02, (4)	0.13 ± 0.07, (4)	1.62± 0.96	45–70
	Case 5	4.20	6.00	1.43	1.13 ± 0.09, (9)	1.77 ± 0.16, (9)	1.56 ± 0.19	0.18 ± 0.04, (3)	0.56 ± 0.01, (3)	3.11 ± 0.69	40–75
HSA (i) + IgG (j)	Case 2	2.00	4.00	2.00	0.51 ± 0.03, (11)	0.86 ± 0.07, (11)	1.68 ± 0.18	0.28 ± 0.05, (4)	0.44 ± 0.06, (4)	1.57 ± 0.36	60–80	0.91± 0.04 (4, 0.86)
	Case 3	5.00	8.00	1.60	1.80 ± 0.09, (10)	2.81 ± 0.22, (10)	1.56 ± 0.14	0.91 ± 0.07, (5)	1.72 ± 0.03, (3)	1.89 ± 0.16	55–80
	Case 5	5.00	12.00	2.40	1.76 ± 0.15, (10)	4.00 ± 0.50, (10)	2.27 ± 0.34	0.22 ± 0.05, (4)	0.79 ± 0.10, (3)	3.59 ± 0.95	55–80

Notes: See text for symbology and Section 3.2 for discussion of experimental conditions Cases 1–5.

Octyl Sepharose^™ 4 Fast Flow adsorbent (OS) was obtained from Amersham Biosciences (75% by volume of 90 μm nominal-diameter sepharose-based particles dispersed in 20% aqueous ethanol solution). The actual surface area of these hydrogel particles was not measured because accurate knowledge of adsorbent surface area is not necessary in volumetric analysis of protein adsorption [44–46]. Also, analytical difficulties encountered in working with relatively low-nominal-surface-area, hydrated-hydrogel particles precluded accurate surface-area determinations at a size scale relevant to proteins. Glass particle adsorbents used in this work were 106 μm nominal diameter glass particles (Sigma Aldrich) in either cleaned or silanized form. Surface area measured by the Brunauer–Emmett–Teller (BET) method (Micromeritics ASAP 2000 using nitrogen as the probe gas) was 0.38 ± 0.09 m²/g. OS adsorbent was freshly prepared just before each depletion experiment by 3X washing in PBS (to remove ethanol) using a sequential centrifugation/resuspension protocol (40 RPM for 1 min in a Hettick microtube fixed-rotor centrifuge, VWR) that processed 1 mL of as-received suspension (750 μL beads, 250 μL fluid). After each of 3 centrifugations, 1 mL of supernate was replaced with 1 mL PBS, ending with a 75:25 v/v stock suspension in PBS. Glass particles were rendered hydrophobic by silanization with octadecyltricholorosilane (OTS). A glass cover slip (Fisher 22 × 30 × 0.1mm) witness sample was carried through the silanization with particles, providing a substrate suitable for reading PBS contact angles. Glass particles and cover slips were first treated with piranha solution (a hot mixture of 30% H₂O₂ and concentrated H₂SO₄) by immersion for 30 min followed by 3X sequential washes in each of 18 MΩ de-ionized water and 100% ethanol. Piranha-solution oxidized glass was air dried and subsequently oxidized by air-plasma treatment of a single layer of particles (or coverslip) held in a 15 mm Pyrex glass petri dish (10 min at 100 W plasma; Herrick, Whippany, NY) directly before use in silanization procedures or adsorption measurements. This process yielded fully water-wettable “clean” glass surfaces. Clean-glass particles and cover-slip witness samples were silanized by 1.5 hr reaction with 5% OTS dissolved in chloroform. OTS-silanized samples were 3X rinsed with chloroform before curing in a vacuum oven at 110 °C for 12 hr.

For each depletion experiment with OS, 20 μL stock (5 μL fluid, 15 μL beads) was pipetted into a 0.5 mL microtube (Safe-lock micro centrifuge tubes, Eppendorf; approximately 2 cm² internal surface area). Adsorption experiments employed ~ 65 cm² adsorbent (geometric) surface area or a 97:3 adsorbent-to-tube surface area ratio. OS particles were re-suspended by gentle pipette aspiration in 25 μL protein solution prepared in advance to the desired protein composition or concentration so that the final depletion volume V_B = 30 μL. Depletion experiments with OTS glass particles were carried out similarly using 22 mg of adsorbent weighed into individual microtubes on an analytical balance and suspended in a final depletion volume V_B = 30 μL. Adsorption experiments were performed as specified below in either sessile or continuously-mixed protein solutions in contact with adsorbent particles. In the mixed case, microtubes were attached to an inverting hematology mixer and continuously turned for the duration of the kinetic experiment. In all cases, particle-free supernate was sampled by either allowing particles to settle to the bottom of the conical test tube after mixing with protein solution (sessile experiments) or by pelleting by brief centrifugation (40 RPM for 1 min in a Hettick microtube fixed-rotor centrifuge, VWR). Experimental details for the SDS-electrophoresis implementation of the depletion method have been disclosed elsewhere [44–46]. In a typical kinetic experiment, 18 identical tubes containing adsorbent and solution mixture were setup and supernates sampled every 5 min. for 90 min. Supernates were held for analysis on SDS-PAGE electrophoresis as described below.

2.2 SDS-PAGE Electrophoresis

26 lane NuPAGE® Novex Tris-Acetate precast gels (Invitrogen; 500 kDa capacity) were used to separate and quantify protein pairs with MW > 30 kDa. NuPAGE® Novex Bis-Tris gels were used for experiments involving ubiquitin. Electrophoresis was carried out for 70 min. at 150 V (Tris-Acetate) or 35 min. at 220V (Bis-Tris) using an XCell SureLock^™ Cell (Invitrogen). Gels were stained with SimplyBlue^™ SafeStain (Invitrogen) for 1 hour and destained with de-ionized (18 MΩ) water for several hours while mixing on a standard hematology rocker. Band intensity was quantified using the Gel-doc system (Bio-Rad Laboratories) that employed a highly-sensitive CCD camera to read optical density (OD). A standard curve was prepared for each protein and each gel using the first 6–8 lanes by applying solutions of known concentration of the probe protein(s). Linear calibration curves were obtained (R² > 95%) within the concentration range of interest for all proteins. Each different protein required a separate calibration curve on the same gel to account for differences in staining density.

2.3 Computational and Statistical Methods

Computational and statistical methods have been disclosed in detail in ref. [44]. Briefly reiterating essential details for the purposes of this paper, amount of the i^th protein adsorbed was calculated by difference D_i in weight/volume (w/v, mg/mL) protein-solution concentrations before $W_{B_i}^o$ and after W_Bi adsorption to particulates ( $D_i\equiv \left(W_{B_i}^o-W_{B_i}\right)$, see further Section 3.1). In the absence of particulate adsorbent, D_i < 0.1 mg/mL for all proteins at surface-saturating bulk-solution concentrations ${\left(W_{B_i}^o\right)}^{max}$ and decreased in proportion to decreasing $W_{B_i}^o$. This background adsorption, due to all sources of protein loss to tubes and pipette tips in handling procedures, represented less than 1–2% of experimental D_i measured in the presence of particulate adsorbent. Thus, it was concluded that background correction of depletion measurements was unnecessary within the $W_{B_i}^o$ range explored in this work [44].

Error in depletion values listed in Tables 2A,B was estimated by standard propagation-of-error in experimental determination in $W_{B_i}^o$ and W_Bi associated with calibration curves (error in slope of calibration curves). Likewise, error estimates in parameters calculated from depletion measurements such as depletion ratios listed in Table 2A,B and Table 3A,B were computed by propagation-of-error in individual depletion measurements. Computational details for the model of Section 4.2.1 is given in Appendix A.

Table 3.

Table 3A: Selectivity Factors for Reversed i,j Adsorption Competition to Octyl Sepharose Particles (OS)
Reversed Protein Pairs(from Table 2)	Experimental Condition	S̄i,j (N,R2)	Si,j (N,R2)
HSA (j) + Fib (i)	Case 1	1.35 ± 0.03 (5, 0.99)	0.80 ± 0.02 (5, 0.99)
	Case 2
	Case 3
	Case 4
	Case 5
HSA (j) + IgG (i)	Case 1	1.18 ± 0.06 (5, 0.95)	0.88 ± 0.03 (5, 0.99)
	Case 2
	Case 3
	Case 4
	Case 5
HSA (j) + Ub (i)	Case 1	0.94 ± 0.02 (3, 1.00)	1.09 ± 0.04 (3, 0.98)
	Case 3
	Case 5
IgG (j) + Fib (i)	Case 1	1.06 ± 0.02 (3, 0.99)	0.90 ± 0.01 (3, 1.00)
	Case 3
	Case 5
FII (j) + Fib (i)	Case 1	1.19 ± 0.06 (3, 0.98)	0.96 ± 0.06 (3, 0.96)
	Case 3
	Case 5
FII (j) + IgG (i)	Case 1	1.07 ± 0.05 (3, 0.98)	0.97 ± 0.06 (3, 0.96)
	Case 3
	Case 5

Table 3B: Selectivity Factors for Reversed i,j Adsorption Competition to Octadecyltrichlorosilane-Treated Glass Particles (OTS)
Reversed Protein Pairs(from Table 2_OTS)	Experimental Condition	S̄i,j(N,R2)	Si,j(N,R2)
HSA (j) + Fib (i)	Case 2	1.03 ± 0.08 (4, 0.91)	1.09 ± 0.06 (4, 0.95)
	Case 4
	Case 5
HSA (j) + IgG (i)	Case 2	1.09 ± 0.05 (4, 0.79)	0.91 ± 0.04 (4, 0.86)
	Case 3
	Case 5

Notes: See text for symbology and Section 3.2 for discussion of experimental conditions Cases 1–5. Column 4 is repeated from Table 2 for convenience of comparison.

3. Results

Proteins listed in Table 1 were used in various combinations in binary protein-adsorption competition experiments using either hydrophobic octyl sepharose (OS, a sepharose-based hydrogel) or octadecyltrichlorosilane treated glass particles (OTS, an impermeable ceramic). Similarity of results obtained with these two very different particulate adsorbents helped assure that the unique adsorption-competition kinetics observed were not specific to a particular kind of adsorbent but rather a general phenomenon involving protein interactions with hydrophobic adsorbents. Five adsorption-competition cases outlined in Section 3.2 represent the full range of possible combinations. Adsorption competition to OS was tested for all of these cases (6 protein pairs, 22 competition experiments) supplemented with 3 cases for OTS (2 protein pairs, 6 competition experiments). Tables 2–4A,B summarize adsorption parameters derived from an extensive experimental program involving different protein pairs (i and j) competing for adsorption to the same hydrophobic adsorbent particles (either octyl sepharose or silanized glass) immersed in binary-protein solutions at different initial concentration ratios. Experimental data plotted for experiments selected from these tables in Figs. 1, 4–5 represent the full spectrum of different competition behaviors observed for all protein/adsorbent pairs investigated. The following sections organize these detailed experimental results in a way that reveals the surprising complexity of adsorption competition between just two proteins, as compared to adsorption of either protein from purified solution. This complexity nevertheless collapsed into a systematic pattern that allowed prediction of competitive-adsorption outcomes between any two proteins. Section 3.1 first discusses the solution-depletion method in the measurement of protein-adsorption kinetics and serves as background to Section 3.2 disclosing application of solution depletion to probe binary protein-adsorption kinetics. Section 3.2 further reveals that selectivity between two proteins engaged in adsorption competition scales smoothly with the ratio of molecular weights (MW, proportional to relative size). Results are qualitatively and quantitatively interpreted in Section 4.

Table 4.

Table 4A.: Characteristic Parameters obtained from Binary Protein Adsorption Kinetics to Octyl Sepharose (OS)
				State 1		State 2
Protein Pairs	Experimental Condition	Di (mg/mL)	Dj (mg/mL)	$\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$	$\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$	$\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$	$\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$
HSA (i) + Fib (j)	Case 1	0.65 ± 0.04	0.66 ± 0.02	1.02 ± 0.10	0.70 ± 0.08	0.82 ± 0.09	0.42 ± 0.05
	Case 2	1.16 ± 0.07	1.64 ± 0.06	0.84 ± 0.07	0.74 ± 0.06	0.52 ± 0.03	0.45 ± 0.02
	Case 3	2.20 ± 0.13	1.08 ± 0.08	0.73 ± 0.06	0.56 ± 0.05	0.50 ± 0.05	0.42 ± 0.05
	Case 4	1.16 ± 0.07	3.36 ± 0.17	0.83 ± 0.07	0.77 ± 0.04	0.53 ± 0.05	0.60 ± 0.02
	Case 5	2.20 ± 0.13	3.36 ± 0.17	1.06 ± 0.07	0.85 ± 0.05	0.71 ± 0.05	0.64 ± 0.02
HSA (i) + IgG (j)	Case 1	0.65 ± 0.04	0.55 ± 0.07	0.86 ± 0.07	0.94 ± 0.13	0.55 ± 0.04	0.64 ± 0.09
	Case 2	1.21 ± 0.07	2.31 ± 0.29	0.92 ± 0.07	0.95 ± 0.13	0.74 ± 0.06	0.68 ± 0.10
	Case 3	2.20 ± 0.13	2.31 ± 0.29	1.00 ± 0.07	0.87 ± 0.13	0.29 ± 0.05	0.32 ± 0.04
	Case 4	1.21 ± 0.07	4.44 ± 0.57	0.76 ± 0.05	0.91 ± 0.12	0.57 ± 0.03	0.62 ± 0.08
	Case 5	2.20 ± 0.13	4.44 ± 0.57	1.03 ± 0.12	0.98 ± 0.13	0.42 ± 0.07	0.47 ± 0.08
HSA (i) + Ub (j)	Case 1	0.70 ± 0.04	0.33 ± 0.03	0.96 ± 0.06	2.00 ± 0.31	0.78 ± 0.03	1.45 ± 0.14
	Case 3	2.20 ± 0.13	1.22 ± 0.10	1.04 ± 0.07	0.82 ± 0.08	0.59 ± 0.04	0.49 ± 0.05
	Case 5	2.20 ± 0.13	2.19 ± 0.18	0.99 ± 0.14	1.14 ± 0.11	0.44 ± 0.05	0.39 ± 0.06
IgG (i) + Fib (j)	Case 1	1.37 ± 0.17	0.80 ± 0.03	0.89 ± 0.12	0.69 ± 0.04	0.69 ± 0.09	0.51 ± 0.03
	Case 3	4.44 ± 0.57	1.36 ± 0.05	0.90 ± 0.18	0.71 ± 0.05	0.58 ± 0.11	0.52 ± 0.02
	Case 5	4.44 ± 0.57	3.36 ± 0.17	1.10 ± 0.20	0.91 ± 0.06	0.75 ± 0.14	0.68 ± 0.04
FII (i) +Fib (j)	Case 1	0.12 ± 0.01	0.66 ± 0.02	6.17 ± 0.61	0.83 ± 0.05	2.58 ± 0.33	0.38 ± 0.06
	Case 3	2.01 ± 0.12	1.36 ± 0.05	1.52 ± 0.13	0.76 ± 0.08	No State 2
	Case 5	2.01 ± 0.12	3.36 ± 0.17	1.17 ± 0.08	0.83 ± 0.06	0.70 ± 0.10	0.55 ± 0.03
FII (i) + IgG (j)	Case 1	0.12 ± 0.01	0.66 ± 0.08	5.33 ± 0.56	1.06 ± 0.14	No State 2
	Case 3	2.01 ± 0.12	1.37 ± 0.17	1.29 ± 0.09	0.85 ± 0.12	No State 2
	Case 5	2.01 ± 0.12	4.44 ± 0.57	1.22 ± 0.10	0.86 ± 0.12	0.55 ± 0.05	0.45 ± 0.07

Table 4B: Characteristic Parameters obtained from Binary Protein Adsorption Kinetics to Octadecyltrichlorosilane-Treated Glass Particles (OTS)
				State 1		State 2
Protein Pairs	Experimental Condition	Di (mg/mL)	Dj (mg/mL)	$\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$	$\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$	$\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$	$\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$
HSA (i) + Fib (j)	Case 2	0.53 ± 0.04	1.62 ± 0.19			0.19 ± 0.02	0.08 ± 0.01
	Case 4	0.53 ± 0.04	2.50 ± 0.30	0.66 ± 0.09	0.32 ± 0.05	0.15 ± 0.04	0.05 ± 0.03
	Case 5	1.50 ± 0.12	2.50 ± 0.30	0.75 ± 0.08	0.71 ± 0.11	0.12 ± 0.03	0.22 ± 0.03
HSA (i) + IgG (j)	Case 2	0.53 ± 0.04	0.67 ± 0.08	0.96 ± 0.09	1.28 ± 0.18	0.53 ± 0.10	0.66 ± 0.12
	Case 3	1.50 ± 0.12	1.95 ± 0.24	1.20 ± 0.11	1.44 ± 0.21	0.61 ± 0.07	0.88 ± 0.11
	Case 5	1.50 ± 0.12	2.71 ± 0.34	1.17 ± 0.14	1.48 ± 0.26	0.15 ± 0.04	0.29 ± 0.05

Notes: See text for symbology and Section 3.2 for discussion of experimental conditions Cases 1–5.

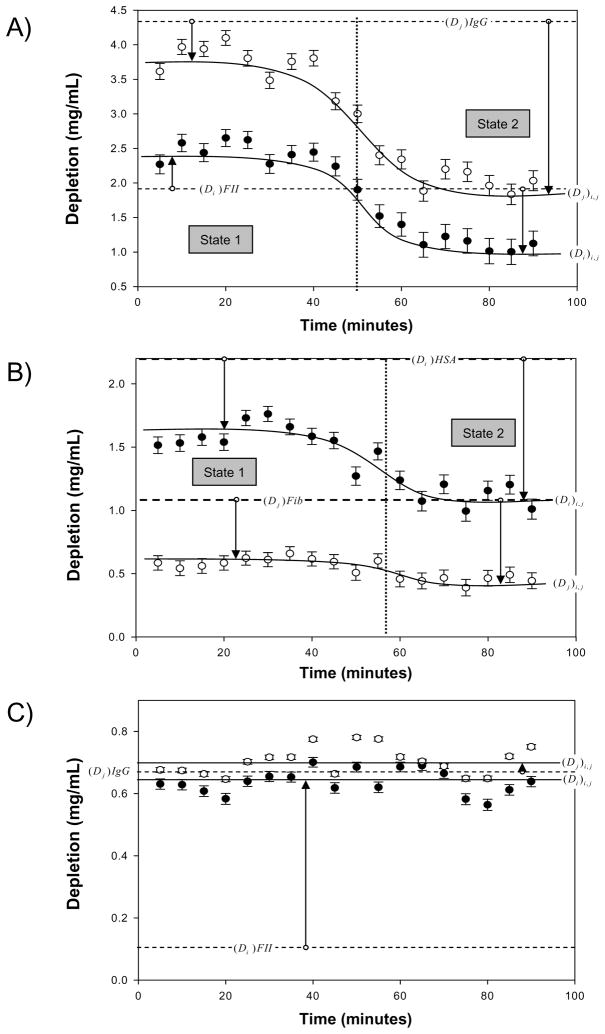
Figure 1.

Adsorption-competition kinetic profiles plotting amount of proteins i and j adsorbed to the same hydrophobic octyl sepharose (OS) adsorbent from stagnant binary-protein solutions. Similar adsorption-competition outcomes were observed for octadecyltrichlorosilane treated glass particles (OTS). Adsorption is measured as solution depletion (D_i)_i,j and (D_j)_i,j (see text for nomenclature). Simultaneous adsorption competition between i, j proteins exhibit different kinetic profiles that depend on relative competing-protein size (molecular weight) and relative solution concentration (see Tables 2A,B). Panel A (i = FII and j = IgG) and Panel B (i = HSA and j = Fib) illustrate experimental circumstances (Cases 5 and 3, see Section 3.2) wherein two pseudo-steady-state adsorption regimes (State 1 and State 2) were observed (solid lines are guides to the eye). State 1 and State 2 were connected by a smooth transition lasting for 20 to 30 minutes (vertical dotted lines note the approximate half-maximum transition time). The State 1 → State 2 transition for HSA in Panel B was just detectable above experimental uncertainty. Panel C (i = FII and j = IgG) illustrates an experimental circumstance (Case 1) where only a single steady-state adsorption of both i, j proteins were observed. For comparison, dashed horizontal lines indicate the depletion D_i or D_j adsorbing from a single-protein solution at the concentration used in the binary competition experiment. Vertical arrows indicate loss or gain of adsorption in binary competition compared to adsorption from single-protein solution.

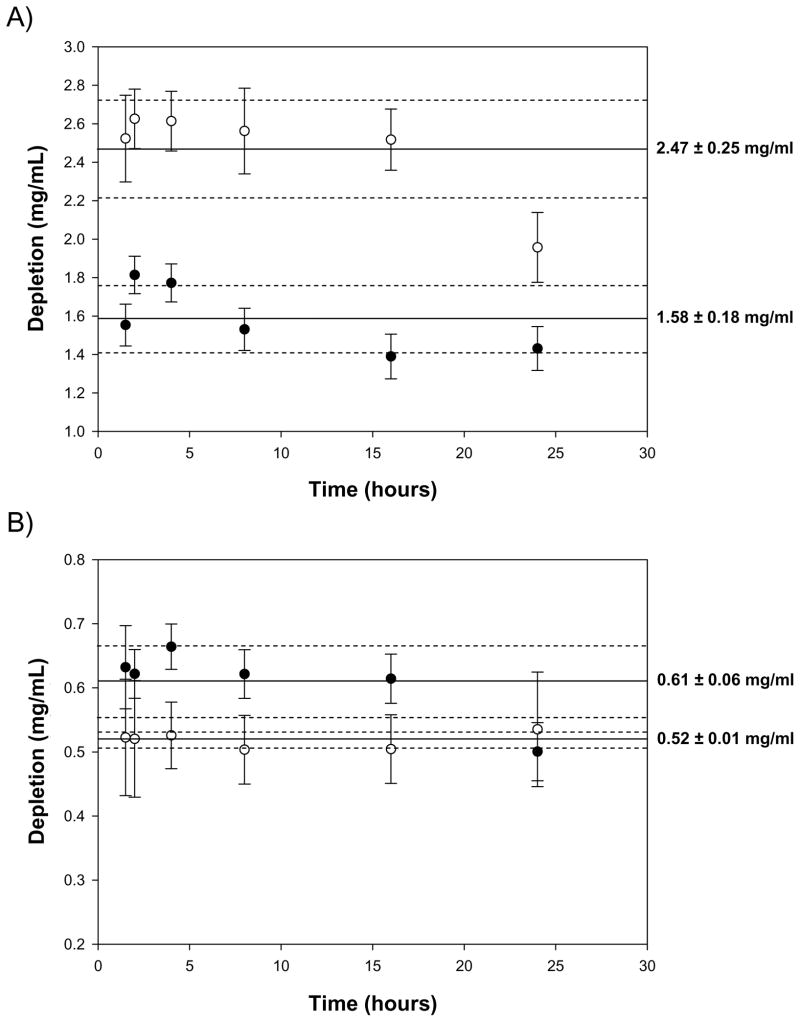
Figure 4.

Stability of State 2 to long-term (24 hour) adsorption competition between HSA (closed circles) and Fib (open circles) for the same hydrophobic octyl sepharose (OS) adsorbent from stagnant binary-protein solutions. Panels A and B correspond to competition Case 5 and Case 1, respectively (see Tables 2A,B). State 2 is stable within experimental error but final data points are suggestive of a slow change in relative amounts of HSA and Fib adsorbed to OS. Solid lines represent the mean of all depletion values for HSA and Fib, respectively, and dashed lines represent standard-deviations of those mean values.

Figure 5.

Comparison of adsorption competition between HSA (closed circles) and Fib (open circles) for the same hydrophobic octyl sepharose (OS) adsorbent from either stagnant (Panel A) or continuously-mixed (Panel B) binary-protein solutions. Panels A and B correspond to competition Case 5 whereas Panels C and D correspond to competition Case 1 (see Tables 2A,B). Continuous mixing of adsorbent with protein solution blurred an otherwise clear State 1 → State 2 obtained under stagnant-solution conditions and appeared to extend duration of State 1 or eliminate State 2 altogether (compare to Figs. 1, 4).

3.1 Solution Depletion Measurement of Protein Adsorption

The venerable solution-depletion method is among the most unambiguous measures of protein adsorption and is (or can be) essentially free from experimental artifacts or cumbersome interpretive theory. In particular, solution depletion allows assessment of protein adsorbed from solution without removing adsorbent from solution or otherwise perturbing the interfacial dynamic. The basic idea behind the depletion method was to measure the w/v concentration (mg/mL) of protein in solution before ( $W_{B_i}^o$) and after (W_Bi) contact with adsorbent particles (OS and OTS). Loss in solution concentration at any time t due to adsorption was calculated by difference (mass balance) as the solution depletion $D_i\equiv \left(W_{B_i}^o-W_{B_i}\right)$, where D_i is expressed as protein-mass-adsorbed-per-unit-volume bulk solution V_B (mg/mL). The actual adsorbed mass m_i = D_iV_B (V_B = 30 μL in all cases). Solution depletion occurred because protein adsorbed from solution into the interfacial region surrounding adsorbate particles (a.k.a. interphase, see Section 1). According to our so-called “volumetric interpretation” of adsorption from a single-protein solution [44, 45, 48], this interphase had a discrete volume V_Ii (mL) related to the dimensions of the i^th protein and a concentration W_Ii (mg/mL) so that $D_i=\left[W_{I_i}\left(\frac{V_{I_i}}{V_B}\right)\right]$ at steady state. When solution contained two proteins i and j, depletion of individual proteins D_i and D_j were measured. At steady-state, the mixed interphase concentration (W_I)_i,j = [(W_Ii)_i,j + (W_Ij)_i,j] occupied an interphase volume (V_I)_i,j; where the “i,j” subscript denotes a binary protein mixture. The relationships among (V_I)_i,j, V_Ii, and V_Ij are dependent on the complexities of packing two dissimilar-shaped proteins within the interphase [46].

SDS-gel electrophoresis was used as a multiplexing, separation-and-quantification tool to measure protein adsorption as described in Section 2. Implementation of the depletion method using electrophoresis met the need for a single method that could be applied to both single- and multiple-protein solutions in a way that was free of experimental artifacts related to solute labeling, rinsing/drying, or complicated instrumentation. The experimental method applied herein has been shown to be sensitive to about 0.1–0.2 mg/mL (estimated to be equivalent to 0.3 mg/m² [45] with approximately 10% CV), which was adequate for studying protein adsorption from mg/mL solutions. Previous work “certified” method and interpretive mass-balance theory applied to steady-state adsorption (t → 1 hr.) by first studying adsorption of a broad range of single proteins to hydrophobic [44] surfaces (OS and silanized glass) from purified aqueous-buffer solution. These results comported with thermochemically-measured free energies of adsorption and interfacial energetics measured by tensiometry (contact angle and wettability methods). Subsequently, HSA adsorption to silanized-glass adsorbent particles with incrementally-increasing hydrophilicity was measured [45], showing here that mass and energy balances for HSA adsorption were in full agreement. Consistent mass-and-energy balance obtained using very different analytical methods engendered confidence that this gel-electrophoresis implementation of the depletion method provided internally-consistent and accurate results for proteins adsorbing to surfaces from both stagnant and continuously-mixed solutions at steady state. We have also demonstrated utility of the depletion method in studying protein-adsorption competition to the same adsorbent surface immersed in multi-component solutions [46]. Standard radiometric methods have been used as a further check on the electrophoresis method described above [48] and electrophoresis results obtained with purified proteins agreed with spectrophotometry (not shown).

3.1.1 Adsorption Kinetics by Solution Depletion

The above-described methods were used to measure adsorption kinetics by setting up 18 identical depletion experiments as outlined in Section 2 and serially sampling solution from one of these identical microtubes at increasing time intervals. Methods outlined in Section 2 could not be reliably executed by our hands in less than about 3 min., yielding a minimum reproducible elapsed-time resolution of about 5 minutes; which was small compared to the 0–60 min. time span over which significant adsorption kinetics was observed using tensiometry [6, 14, 22, 43, 50, 51, 61] and the 60–90 min. time span over which competition kinetics were experimentally observed by the depletion method (see below and section 4). Protein solutions and adsorbents were either subjected to continuous mixing on a rotating hematology rocker or allowed to rest unperturbed in a tube rack. Using the above kinetic implementation of the depletion method, we found in this and previous work that there was no detectable adsorption kinetics to either OS or OTS from single purified protein buffer solutions at any concentration studied, either from stagnant solution or continuously-mixed solutions [48]. That is to say, D_i was a constant proportion of solution concentration with time up to saturation of the adsorbent surface that occurred at a characteristic solution concentration ${\left(W_{B_i}^o\right)}^{max}$. However, mixing was observed to affect adsorption-competition kinetics, as described separately below for stagnant solutions and continuous-mixing conditions.

3.2 Binary Adsorption Competition

Five general cases for adsorption competition between two different proteins i, j with MW_i ≠ MW_j were identified on the basis adsorption of single proteins from buffer solution [46]. These general cases were related to the bulk-solution concentrations of various purified proteins required to saturate adsorbent surface area (OS or OTS). Saturating bulk-solution w/v concentrations (mg/mL) were designated as either ${\left(W_{B_i}^o\right)}^{max}$ or ${\left(W_{B_j}^o\right)}^{max}$; where the “B” subscript differentiated bulk solution from the interphase “I” and the “o” superscript denoted initial concentration of either purified protein “i” or “j” identified by subscripts enclosed in parentheses. The total binary-solution concentration was designated as ${\left(W_B^o\right)}_{i,j}$, where the “i, j” subscript has been used throughout this work to denote a binary mixture. Initial binary-solution concentrations were prepared by mixing protein i at ${\left(W_{B_i}^o\right)}_{i,j}$ with protein j at ${\left(W_{B_j}^o\right)}_{i,j}$, where superscripts and subscripts are as specified above.

Case 1: Proteins i, j neither individually nor collectively at bulk-solution concentrations sufficient to saturate the adsorbent surface. Total binary-solution concentration ${\left(W_B^o\right)}_{i,j}$ was prepared by mixing protein i at ${\left(W_{B_i}^o\right)}_{i,j}\ll {\left(W_{B_i}^o\right)}^{max}$ with protein j at ${\left(W_{B_j}^o\right)}_{i,j}\ll {\left(W_{B_j}^o\right)}^{max}$ (see Tables 2A and Appendix B for details).

Case 2: Proteins i, j at bulk-solution concentrations insufficient to independently saturate the adsorbent surface but collectively sufficient to saturate the adsorbent surface. Total solution concentration ${\left(W_B^o\right)}_{i,j}$ prepared by mixing protein i at ${\left(W_{B_i}^o\right)}_{i,j}<{\left(W_{B_i}^o\right)}^{max}$ with protein j at ${\left(W_{B_j}^o\right)}_{i,j}<{\left(W_{B_j}^o\right)}^{max}$ (see Tables 2A,B and Appendix B for details).

Case 3: Protein i at bulk-solution concentration sufficient to independently saturate the adsorbent surface mixed with protein j at bulk-solution concentrations insufficient to independently saturate the adsorbent surface. Total solution concentration ${\left(W_B^o\right)}_{i,j}$ prepared by mixing protein i at ${\left(W_{B_i}^o\right)}_{i,j}\ge {\left(W_{B_i}^o\right)}^{max}$ with protein j at ${\left(W_{B_j}^o\right)}_{i,j}<{\left(W_{B_j}^o\right)}^{max}$. Same as Case 4 but with reversed saturating protein (see Tables 2A,B).

Case 4: Protein j at bulk-solution concentration sufficient to independently saturate the adsorbent surface mixed with protein i at bulk-solution concentrations insufficient to independently saturate the adsorbent surface. Total solution concentration ${\left(W_B^o\right)}_{i,j}$ prepared by mixing protein j at ${\left(W_{B_j}^o\right)}_{i,j}\ge {\left(W_{B_j}^o\right)}^{max}$ with protein i at ${\left(W_{B_i}^o\right)}_{i,j}<{\left(W_{B_i}^o\right)}^{max}$. Same as Case 3 but with reversed saturating protein (see Tables 2A,B).

Case 5: Proteins i, j each at bulk-solution concentrations sufficient to independently saturate the adsorbent surface. Total solution concentration ${\left(W_B^o\right)}_{i,j}$ prepared by mixing protein i at ${\left(W_{B_i}^o\right)}_{i,j}\ge {\left(W_{B_i}^o\right)}^{max}$ with protein j at ${\left(W_{B_j}^o\right)}_{i,j}\ge {\left(W_{B_j}^o\right)}^{max}$ (see Tables 2A,B and Appendix B for details).

In summary, two broad categories of adsorption competition were studied; total-mixed-solution concentration presumed (on the basis of pure-protein adsorption characteristics) to be insufficient to saturate the adsorbent surface (Case 1) and total-mixed-solution concentration presumed to be sufficient to saturate the adsorbent surface (Cases 2–5). Case 5 differed from surface-saturating Cases 2–4 in that both competing proteins were at total-mixed-solution concentrations well in excess of the amount needed to saturate available adsorbent. At least one of the competing proteins was at under-saturating solution concentrations in Cases 2–4.

3.2.1 Adsorption-Competition Kinetics from Stagnant Solution – Component Analysis (Tables 2A,B)

Adsorption-competition kinetics from stagnant solution between two different proteins selected from those listed in Table 1 gave rise to different competition behaviors that depended on protein identities and initial-solution concentrations. Tables 2A,B collects data for experimental pairs tested (column 1) under some-or-all of the 5 adsorption cases identified in the preceding section (column 2) prepared by mixing proteins i, j at the specific concentrations listed in columns 3–4 such that ${\left(W_B^o\right)}_{i,j}=\left[{\left(W_{B_i}^o\right)}_{i,j}+{\left(W_{B_j}^o\right)}_{i,j}\right]$.

Fig. 1 represents the full range of competition behaviors observed in experiments summarized in Tables 2A,B for both OS and OTS adsorbents. Cases 4 and 5 always exhibited two sequential pseudo-steady-state regimes (see State 1 and State 2 annotations) connected by a smooth transition, giving rise to sigmoidally-shaped adsorption-kinetic profiles (illustrated by Fig. 1 Panel A; Case 5 with i = FII and j = IgG). Steady-state depletions (D_i)_i,j and (D_j)_i,j corresponding to State 1 and State 2 were taken to be the mean ± standard deviation of the first N measurements of State 1 or last N measurements of State 2, respectively, and are sequentially collected in columns 6–7 and 9–10 of Tables 2A,B along with N for each case.

Cases 1 and 3 did not always give rise to a detectable State 1 → State 2 transition and sometimes a transition was just detectable above experimental error. Panel C of Fig. 1 illustrates a circumstance where no State 1 → State 2 transition was observed (Case 1 with i = FII and j = IgG). Panel B illustrates as case wherein the transition is just detectable (Case 3 with i = HSA and j = Fib). Tables 2A,B indicates competitive-protein pairs and conditions in which State 2 was not detectable above 1σ error limits with a “No State 2” entry. For convenience, when no State 1 → State 2 transition was observed, it was assumed that the steady-state corresponded to State 1, although this assumption had no impact on conclusions drawn from this work. The transition period between states (mid range indicated by dotted vertical line in Panels A, B of Fig. 1) was surprisingly long, between 25 to 80 minutes of solution/adsorbent equilibration transition time (column 12 of Tables 2A,B).

Detailed inspection of Tables 2A,B revealed that, when a transition was observed, (D_i)_i,j and (D_j)_i,j corresponding to State 1 was always greater than State 2, meaning that the State 1 → State 2 transition always involved ejection of initially-adsorbed mass of both competing proteins from the interphase. Columns 8 and 11 of Tables 2A,B compute the depletion ratios $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$ (equivalent to mass ratio $\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)$) obtained for i, j proteins at State 1 and State 2. Comparison of entries in column 8 to column 11 revealed that the mass ratio of adsorbed proteins in State 1 and State 2 were statistically identical at the 2σ confidence interval and different at the 1σ interval only for 4 cases out of 27 studied (OS: Case 4 for HSA/Fib and HSA/IgG and Case 1 for HSA/Ub; OTS: Cases 2,5 for HSA/Fib). It was concluded that the State 1 → State 2 transition always involved ejection of adsorbed mass of both competing proteins from the interphase in the same mass ratio as initially adsorbed in State 1.

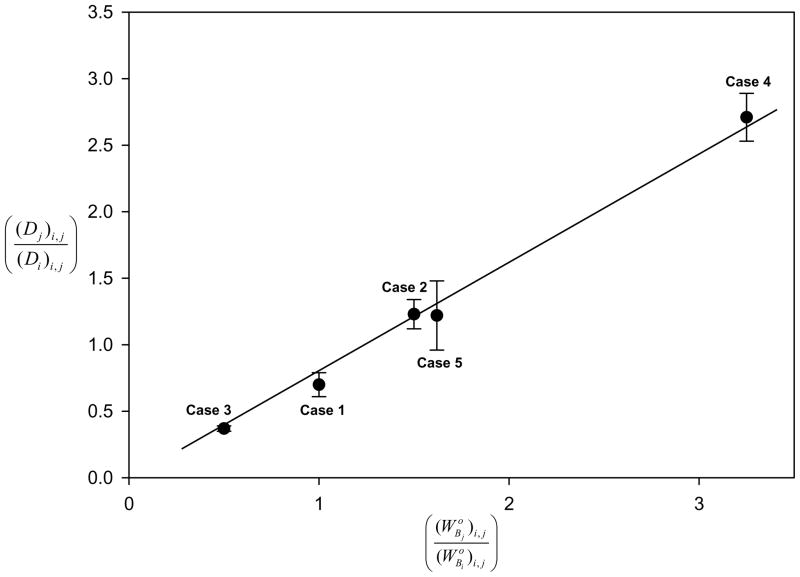
Fig. 2 plots the State 1 depletion ratio $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$ against solution concentration ratio $\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$ used in the competition experiments between HSA and Fib, with annotations indicating the corresponding adsorption cases. Similar plots were obtained for all other competitive-protein pairs on each adsorbent (OS and OTS, not shown) for either State 1 or State 2 (because ${\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)}_{\mathit{State}1}={\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)}_{\mathit{State}2}$ within experimental error, see above). Different adsorption cases identified on the basis of adsorption behavior of purified proteins did not align with any perceivable regularity, suggesting that $\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$ dominated competition. Column 13 of Tables 2A,B collects slope values S_i,j and statistics of linear-best-fit to the equation ( $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)=S_{i,j}\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$) for all tested pairs and conditions (linear regression for N = 3 cases was regarded as only an estimate). In certain competitive situations, was detectably less than unity (more protein i adsorbed than protein j). In other competitive situations, S_i,j was equal-or-nearly-equal to unity (nearly the same mass of proteins i, j adsorbed). As a consequence, S_i,j was interpreted as a selectivity factor that measured adsorption discrimination between competitive-protein pairs at the solution concentration tested (Cases 1 – 5). Fig. 3 scales S_i,j by the molecular weight ratio $\left(\frac{{MW}_j}{{MW}_i}\right)$, where open circles correspond to data of column 13 of Tables 2A,B and the closed circles correspond to data of column 3 of Tables 3A,B discussed below (data point represented by a star corresponds to the hypothetical circumstance i = j for which $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)=\left(\frac{{MW}_j}{{MW}_i}\right)\equiv 1$).

Figure 2.

Linear relationship between the measured State 1 depletion ratio $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$ and initial solution-concentration ratio $\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$ for 5 conditions of adsorption competition between HSA and Fib (Cases 1–5, see Section 3.2). Line through the data represents the best fit to $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)=S_{i,j}\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$ (R² = 0.99). The slope S_i,j is interpreted as a selectivity factor measuring adsorption discrimination between competitive i, j protein pairs (see also Eq. 5 of Appendix A). Notice that there is adsorption discrimination between HSA and Fib for all 5 adsorption-competition conditions, including Case 1 wherein adsorbent surface area does not limit adsorbent capacity.

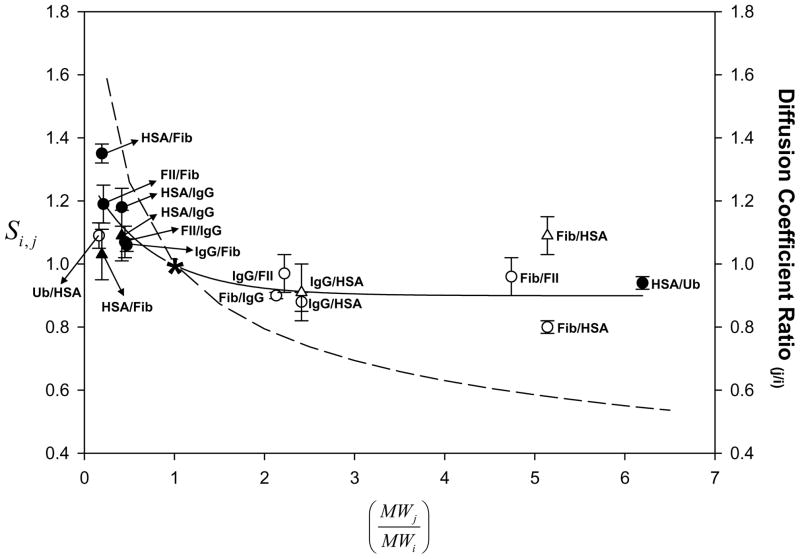
Figure 3.

Curvilinear relationship between the adsorption selectivity factor S_i,j (left ordinate, see also Fig. 2) and molecular-weight ratio $\left(\frac{{MW}_j}{{MW}_i}\right)$ for i and j proteins in adsorption competition for the same hydrophobic adsorbent from stagnant binary-protein solutions (open and closed circles = octyl sepharose OS; open and closed triangles = silanized glass OTS). Star data point represents the hypothetical competition between two identical proteins (i = j for which $S_{i,j}=\left(\frac{{MW}_j}{{MW}_i}\right)\equiv 1$). Open symbols correspond to S_i,j and closed symbols correspond to the reversed-selectivity factor S̄_i,j (see Sections 3.2.2 and 4.1.2). Solid line through the data is a guide to the eye. Dashed line (right ordinate) is the ratio of diffusion-coefficients calculated from the Stokes-Einstein-Sutherland equation for two dissimilar-sized proteins with radius scaling as MW^1/3 (see Section 4.1.2). Similarity in trends and magnitude between experiment and theory suggests that adsorption selectivity could arise from a difference in protein diffusion rates that preferentially fills the surface region with smaller proteins.

3.2.2 Adsorption-Competition Selectivity Based on Size (Tables 3A,B)

S_i,j measurements collected in Tables 2A,B were supplemented by measuring adsorption competition under Cases 1 – 5 between pairs with reversed i, j identity (protein i used as protein j and vice versa; compare Column 1 of Tables 2 to Tables 3A,B). Column 3 of Tables 3A,B collects the reversed-selectivity factor S̄_i,j obtained for comparison to S_i,j in column 4 (repeated from Tables 2A,B for convenience). Interestingly, ${\overline{S}}_{i,j}=(1/S_{i,j})$ for all cases (at 2σ or less) and these experimental S̄_i,j values filled in an exponential-decay-like curve when co-plotted with S_i,j in Fig. 3 (solid circles).

3.2.3 Adsorption-Competition Kinetics from Stagnant Solution – Comparison to Adsorption from Purified-Protein Solution (Tables 4A,B)

Columns 3 and 4 of Tables 4A,B list the solution depletions D_i and D_j obtained with pure i and j solutions, respectively, for the concentrations specified in columns 3–4 of Tables 2A,B (corresponding to the adsorption cases given in column 2 of either table). Columns 5–8 of Tables 4A,B compute the ratios $\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$ and $\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$ that compared the amount of i, j proteins adsorbed under State 1 and State 2 competitive conditions to the amount adsorbed from pure protein solutions. Dashed horizontal lines shown in Fig. 1 correspond to D_i and D_j for visual comparison of competition to adsorption from pure solution. Inspection of Fig. 1 and Tables 4A,B for State 1 revealed that, in some cases, competition caused more protein to adsorb than obtained from pure solution at the tested concentration (see vertical arrow for FII, Panel A for example). In other cases, competition caused less protein to adsorb than obtained from pure solution at the tested concentration (see vertical arrow for IgG, Panel A for example).

In a few Case 1 trials, $\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$ or $\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$ were ≥ 2 (see HSA/Ub, FII/Fib, and FII/IgG of Tables 4A,B, State 1). Remarkably, both $\left(\frac{{(D_i)}_{i,j}}{D_i}\right)$ and $\left(\frac{{(D_j)}_{i,j}}{D_j}\right)$ were within 10% of unity for all Case 5 (State 1) tested. Thus, according to the data of Tables 4A,B (State 1), competition between i, j proteins each at initial solution concentrations sufficient to independently saturate the adsorbent surfaces (Case 5) led to co-adsorption of a mass of protein i sufficient to independently saturate the adsorbent surface together with 90–100% of the mass of protein j required to independently saturate the adsorbent surface. In other words, adsorbent capacity was much greater when two proteins engaged in adsorption competition from Case 5 saturating solutions than under identical experimental circumstances using only one of the competing pairs in solution.

3.2.4 Stability of State 2

Competition kinetics reviewed in the preceding sections revealed that State 1 was a transient pseudo-steady state. Time stability of State 2 in stagnant solution was tested by measuring HSA/Fib competition periodically for 24 hours for Case 5 (Panel A of Fig. 4) and Case 1 (Panel B of Fig. 4). Average values over this testing interval could not be confidently distinguished from shorter-term measurements collected in columns 9 and 10 of Tables 2A,B. However, data corresponding to Fib in Panel A and HSA in Panel B was suggestive of a downward trend, possibly indicating that State 2 was also a pseudo-steady state, but one of much longer duration than State 1. Other complicating experimental factors such as solution evaporation from sealed-cap polymer microtubes, protein unfolding/denaturation at adsorbent surfaces [67], or even growth of bacteria in non-sterile solutions complicated unambiguous interpretation of these results as definitive evidence for a beginning of a hypothetical State 3. For the purposes of this work, State 2 was treated as a final equilibrium (lowest-energy) adsorption condition for all adsorption cases exhibiting competition kinetics. Assuming otherwise did not affect overall conclusions drawn from this work.

Again using HSA/Fib competition as a single test protein pair, results of protein-adsorption competition under stagnant or continuous solution/adsorbent mixing were compared in Fig. 5 (stagnant-solution competition correspond to Panels A, C; mixed-solution competition correspond to Panels B, D for Cases 5 and 1, respectively). This comparison revealed that mixing blurred an otherwise clear transition between State 1 and State 2 obtained under stagnant-solution conditions and appeared to extend State 1 in time or eliminate State 2 altogether. State 2 was clearly sensitive to fluid mixing.

4. Discussion

The primary experimental finding of this work is that adsorption competition between two proteins i, j competing from stagnant binary solution for the same hydrophobic adsorbent surface (either octyl sepharose, OS; or silanized glass particles, OTS) exhibits surprisingly complex kinetics that depend on relative i, j protein size and solution concentrations (Section 3.2.1). Two sequential pseudo-steady-state adsorption regimes are typically observed (State 1 and State 2). State 1 and State 2 are connected by a smooth transition lasting 20–30 minutes, giving rise to sigmoidally-shaped adsorption-kinetic profiles over 90 minutes of observation. In sharp contrast to competition kinetics, protein adsorption from single-protein solutions to OS or OTS adsorbents under otherwise identical experimental conditions exhibits no measurable protein-mass-adsorption kinetics [48]. State 2 is effectively eliminated when the binary solution is continuously mixed with adsorbent particles whereas mixing has no measurable effect on amount adsorbed from single-protein solutions [44, 45, 47, 48].

State 1 is apparently not the minimum-energy arrangement of proteins within the thinnest (lowest volume) interphase possible. Consequently, proteins within the State 1 interphase slowly reorganize into a thinner (and presumably more ordered) State 2 interphase by ejection of water and a portion of initially-adsorbed protein (see further Section 4.1). For reasons that are not yet fully understood, i, j proteins are ejected at the same mass ratio $\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)$ as initially adsorbed from solution (Section 3.2.1). Hence, it is quite evident from competition kinetics that at least some State 1 proteins are not irreversibly adsorbed. This observation supplements our conclusion based on previous studies that protein adsorption is not an inherently irreversible phenomenon [22, 47, 48, 63], as is sometimes otherwise contended in the protein-adsorption literature. Continuous solution/adsorbent mixing prevents or substantially slows attainment of State 2 (Section 3.2.4) apparently by perturbing a delicate exchange dynamic between solution and interphase that is qualitatively consistent with the shear-sensitive viscoelasticity of blood proteins adsorbed at the liquid-vapor interface [49].

Under certain State 1 conditions, much more protein adsorbs from binary solution than from surface-saturating solutions of either single protein of the competing i, j pair (Case 5, see Section 3.2.3). Effectively, all of the purified i that can possibly adsorb to OS adsorbent from single-protein solution co-adsorbs with nearly all of the purified j that can possibly adsorb from single-protein solution, leading to “doubly saturated” OS adsorbent. This consistently-observed result for 6 different i, j pairs and two different hydrophobic adsorbents shows that maximum adsorbent capacity depends on solution concentration, not just on surface area. Since adsorbent saturation with adsorbed single proteins leads to monolayer- or multilayer-surface coverage depending on protein size [44, 51], the co-adsorption of surface-saturating masses of both i, j proteins must form multilayers. As such, adsorption-competition results are completely inconsistent with monolayer protein adsorption and entirely consistent with multilayer protein adsorption. Multilayer adsorption is itself inconsistent with the popular idea that protein adsorbs to surfaces primarily through protein/surface interactions because proteins within second (or higher-order) layers are too distant from the adsorbent surface to be held surface bound by strong forces in close proximity. Multilayer adsorption observed herein corroborates the conclusion drawn by a number of investigators using a variety of experimental methods over the last twenty years or so [6, 38, 44, 46, 49–60] that proteins can, in fact, adsorb from concentrated solutions in multiple layers; especially if surfaces bear ion-exchange functionalities [47]. Quite apparently, interactions other than just between protein and surface are important in protein adsorption to hydrophobic surfaces [45, 47].

Globular-blood proteins are oblate spheroids in solution with volume proportional to molecular weight (molecular-packing radius for globular proteins closely follows r_v= 6.72×10⁻⁸MW^1/3 in cm for MW expressed in kDa; see refs. [68–74] for basic information regarding spherical dimensions and molecular packing of proteins). As a consequence, protein volume is proportional to MW with a concomitantly conserved partial specific volume v^o falling with the range 0.70 ≤v^o ≤0.75 cm³/g protein [75]. In light of this fact, we take systemization of otherwise quite perplexing adsorption-competition results (Tables 2A, B) on the basis of relative protein molecular weight (Sections 3.2.2 and 3.2.3, Fig. 3) as strong evidence for adsorption selectivity based substantially on a size-based discrimination (see further Section 4.1.2).

4.1 Volumetric Interpretation of Protein Adsorption and Protein-Adsorption Competition

Our physical explanation of the experimental findings of this work is based on the idea that protein adsorbs into a 3D interphase region and, in so doing, adsorbing protein displaces an equivalent volume of interfacial water; as briefly discussed in Section 1. Complete justification of this so-called ‘volumetric interpretation’ of protein adsorption is beyond the intended scope of this paper, so let it suffice only to say that we find this theory adequately explains both energy-and-mass balance of adsorption of a wide variety of proteins adsorbing to surfaces spanning the full range of observable surface energy [6, 14, 22, 43–51, 61, 63, 76–78]. In particular, multilayer protein adsorption is a natural outcome of the volumetric theory.

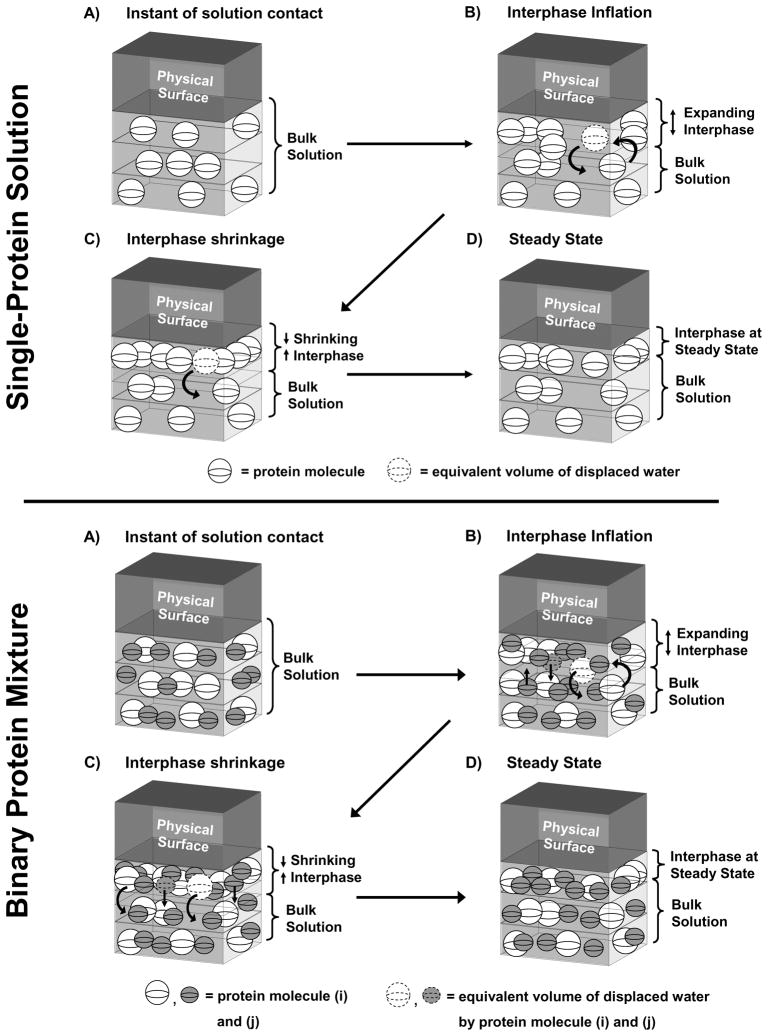
Fig. 6 illustrates core interpretive concepts applied to adsorption from single-protein (top group of panels) and binary-protein solutions (bottom group of panels). Panels A–D represent snap-shots of the hypothetical arrangement of proteins at different times in the adsorption process. Fig. 6 is intended only to present qualitative features of the volumetric interpretation of protein adsorption and should neither be interpreted literally nor accepted as substitute for a quantitative kinetic model of binary competition that has yet to be developed. However, we hasten to point out in this latter regard that adsorption kinetics from purified-protein solution has been modeled [48]. The related computational example of Section 4.2.1 emphasizes importance of binary competition in understanding biocompatibility.

Figure 6.

Graphical illustration of the volumetric interpretation of single-protein adsorption (top panel group) and binary-adsorption competition between i, j proteins for the same hydrophobic adsorbent (bottom panel group). Essential steps depicted in both cases are: (Panel A) instantaneous creation of a thin interface between adsorbent (Physical Surface) and protein solution (Bulk Solution); (Panel B) rapid diffusion of proteins from solution into an inflating interphase region with concomitant displacement of interphase water; (Panel C) reorganization and concentration of protein within an interphase that is shrinking by expulsion of either interphase water (top panel group) or both interphase water and initially-adsorbed protein (bottom panel group); and (Panel D) attainment of steady-state interphase protein concentration by entrapment of initially-adsorbed protein in a minimal volume interphase (see Section 4.1 for detailed discussion).

4.1.1 Diffusion into an Inflating Interphase

Each panel of Fig. 6 diagrams the same unit area of physical adsorbent surface in contact with a solution containing proteins. Proteins are drawn here as spheres consistent with the oblate-spheroidal dimensions of blood proteins (see citations in Section 4) and for ease of representation. At the first instant of surface-solution contact (A Panels, top and bottom groups), there has been no time for the system to respond to the significant energetic perturbation caused by creation of a (in this case) hydrophobic interface [48]. In the fleeting moments after interface formation, however, there is wholesale movement of water and ions in response to this imposed interface [5, 23]. A thin interphase is created that is depleted in proteins relative to bulk-solution concentration. This concentration (chemical potential) gradient drives diffusion of protein into the newly-created interphase. The interphase necessarily inflates to accommodate arriving proteins (B Panels, top and bottom groups) [48]. But two objects cannot occupy the same space at the same time and, as a consequence, arriving hydrated proteins must displace a volume of interfacial water equal to the protein volume (curved arrows and dashed spheres, B Panels). Displacement of interfacial water is referred to as “interphase dehydration” [44, 45, 51, 63].

4.1.2 Adsorption Selectivity Imposed by Diffusion

It is apparent from Fig. 2 that the relative adsorbed mass of competing i, j proteins $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)=\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)$ is linearly related to relative solution concentrations $\left(\frac{{(W_{B_j}^o)}_{i,j}}{{(W_{B_i}^o)}_{i,j}}\right)$. We observe that the slope of this linear relationship S_i,j is not typically unity (Tables 2A, B). Non-unity S_i,j means that, for a given pair of competitive proteins, there is a modest adsorption bias for one protein over another, even if adsorbent surface area is not limiting (Case 1 in Fig. 2 for example). This bias scales smoothly with relative protein size as measured by $\left(\frac{{MW}_j}{{MW}_i}\right)$ (Fig. 3). The effect of competing-protein size is emphasized by experiments described in Sections 3.2.1 and 3.2.2 in which protein identity is switched for particular adsorption cases, causing measured selectivity ${\overline{S}}_{i,j}=(1/S_{i,j})$ within experimental error. This adsorption bias apparently arises during the initial diffusion of proteins into the inflating State 1 interphase and persists into State 2 by ejection of i, j proteins at the same mass ratio( ${\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)}_{\mathit{State}1}={\left(\frac{{(m_j)}_{i,j}}{{(m_i)}_{i,j}}\right)}_{\mathit{State}2}$, Section 3.2.1).

A first-level approximation is that two proteins diffuse as independent particles from solution toward the same adsorbent surface against individual (not net) concentration gradients. The diffusion coefficient D (not to be confused with depletion) for each protein is related to protein radius r and solution viscosity η by the well-known Stokes-Einstein-Sutherland (SES) equation $D=\left(\frac{k_{B}T}{6\pi \eta r}\right)$, where k_B T is the product of the Boltzmann constant and Kelvin temperature. Using the relationship r_v = 6.72×10⁻⁸MW^1/3 mentioned above for the radius of i, j proteins, it is evident that the diffusion-constant ratio follows ${\left(\frac{{MW}_i}{{MW}_j}\right)}^{1/3}$. This relationship predicts that the rate-of-diffusion of the smaller protein through an observation plane from any point in solution will exceed that of the larger protein. There are many reasons to expect that this relationship will not be exact for real proteins. Firstly, proteins are not exactly spherical and hence volume scales only approximately with molecular weight (v^o = 0.77 cm³/g for a perfectly-spherical protein rather than the observed 0.70≤v^o≤0.75 range; see Appendix C). Secondly, proteins arriving at the interphase encounter previously-adsorbed proteins and crowding would slow mass transport relative to that occurring in free solution. Nevertheless, SES should predict the general trend and order-of-magnitude of a purely diffusion-based size bias. As shown in Fig. 3, the SES line is systematically offset from experimental data, over predicting selectivity S_i,j at low $\left(\frac{{MW}_j}{{MW}_i}\right)<1$ and under predicting at $\left(\frac{{MW}_j}{{MW}_i}\right)>1$, but the general trend and magnitude is in rough agreement with experiment. This leads us to speculate that State 1 protein-adsorption selectivity is substantially due to the relative rates at which i, j proteins arrive at the inflating interphase region (B Panels, Fig. 6). This interpretation is consistent with the observation that there is adsorption selectivity even in Case 1 wherein surface area does not present a limitation (surface is not saturated) and cannot, therefore, impose any selectivity based on available space within the interphase. It is clear, however, that the SES does not quantitatively reproduce experimentally-measured adsorption selectivity, so it can be concluded that relative diffusivity does not entirely explain adsorption selectivity. Perhaps factors mentioned above such as molecule-packing restrictions also influences adsorption competition.

This relative-diffusion-rate rationalization of adsorption selectivity is quite different than the classical time-dependent-adsorption-displacement interpretation of the Vroman effect mentioned in Section 1. Here, we attribute adsorption selectivity to relative i, j diffusion rates and not to any adsorption-displacement effect. Furthermore, diffusion-rate selectivity occurs over the short time span required to fill the interphase, which is experimentally found to occur in less than 5 minutes and is expected theoretically to be over within milliseconds for mg/mL solution concentrations [48].

4.1.3 Protein Entrapment within the Interphase

Mass transfer from bulk solution quickly comes to a halt as interphase concentration rises to a fixed proportion of solution concentration (see Appendix D). Back diffusion of protein out of the interphase must overcome energy barriers related to rehydration of the interphase (replacing water originally displaced by adsorbing protein) and the undoing of either-or-both protein/protein and protein/surface interactions that may have formed upon arrival within the interphase. The fact that protein concentration within the interphase can be 100–500X bulk-solution concentrations at steady-state [23, 44] is testimony that back diffusion is not energetically favored. Hence, the initial mass of protein transported to the interphase is effectively captured within the interphase by an energetic preference for the adsorbed state. However, the initially-swollen interphase formed at the end of the protein-diffusion stage (B Panels of Fig. 6) is not the thinnest possible that can contain all of the protein supplied by diffusion in the preceding step. As a consequence, the interphase shrinks in volume (thickness) by expulsion of either just water, or both water and protein. It is this latter distinction, expulsion of water or water and protein, that seems to be a fundamental difference between adsorption from single-protein solution and adsorption competition from binary solutions, as separately detailed below in continued reference to Fig. 6.

4.1.4 Adsorption from Single-Protein Solution

We find from previous work that protein mass adsorbed from a single-protein solution remains a constant proportion of solution concentration even though interphase protein concentration increases with time [48]. We conclude, therefore, that interphase thickness decreases by expulsion of only interphase water (not protein) to arrive at the minimal interphase volume containing a single-protein type (Panel C, upper panel group of Fig. 6). This minimal-interphase volume is related to protein dimensions and number of layers occupied by adsorbed protein. More specifically, Fig. 6 (upper panel group) models the interphase as consisting of M slabs with thickness δ _i, the characteristic size of the protein molecule under study (in cm). The total interphase thickness (in cm) is Ω=Mδ _i and volume V_Ii = AΩ = AMδ _i (in cm³); where A is the interfacial area (cm²) and M is an integer number of slabs that may be fully or partially filled [44]. As solution concentration rises, diffusion adds proportionately greater number of protein molecules to the interphase that serially fill unoccupied space within the first-formed layer and, if necessary, successive layers. As a consequence, relatively-simple Henry-type adsorption isotherms result wherein adsorbed amount increases in direct proportion to bulk-solution concentration for a wide range of proteins and adsorbent surface chemistries [44, 45, 47]. Of course, the stratified-layer model depicted in Fig. 6 is but one of a number of possible protein arrangements within the interphase that might actually occur. Hence Fig. 6 should be accepted as only illustrative of more general packing possibilities. Face centered cubic (or hexagonal) packing of hydrated protein spheres represents the maximum conceivable packing within a very highly-ordered interphase [44, 51].

Protein captured within an interphase that has shrunk to V_Ii establishes the equilibrium interphase concentration W _Ii (Panel D of the upper panel group of Fig. 6). W _Ii is related to the concentration remaining in bulk solution after adsorption, W _Bi, by the partition coefficient $P_i\equiv \left(\frac{W_{I_i}}{W_{B_i}}\right)$. P_i is itself related to slopes of adsorption isotherms mentioned above [44]. However, diffusion cannot bring indefinitely-increasing mass of protein to the interphase. Instead, it is experimentally observed that a fixed adsorbent surface area saturates at a specific solution concentration ${\left(W_{B_i}^o\right)}^{max}$ related to adsorbent surface energy (water-wettability) [44–46].

The volumetric interpretation of protein adsorption asserts that there is a maximum w/v (not molar) maximum interphase concentration (W_I)^max that is controlled by the energetics of interphase dehydration, as more fully discussed in refs. [44–47]. According to this theory, (W_I)^max is a material property related to the adsorbent water-wettability but unrelated to the specific identity of protein(s) adsorbing to that material. We estimate that (W_I)^max = 300±60 mg/mL for OS adsorbent used herein for any protein or protein mixture [44]. Protein size (MW) determines how many adsorbed layers are required to reach (W_I)^max and the w/v solution concentration ${\left(W_{B_i}^o\right)}^{max}$ required by the i^th protein to saturate a given adsorbent surface area. A natural outcome of this process is that maximal adsorbed mass (maximum depletion $D_i^{max}$) increases with increasing protein size because the interphase volume increases with size ( $m_i^{max}=D_i^{max}{V}_B=W_I^{max}{V}_{I_i}$). As a consequence, the depletion method is relatively difficult to implement for small proteins such as lysozyme [44].

4.1.5 Adsorption from Binary-Protein Solution

Competitive-protein adsorption is more complicated than single-protein adsorption from the outset because diffusion transports two proteins into the inflating interphase (Panel B, lower panel group of Fig. 6) in proportion to i, j solution concentrations, with only modest selectivity between i, j proteins based on size (see Section 4.1.2). For this reason, State 1 can contain more total protein than adsorbs from corresponding single-protein solutions (especially for Case 5, see Section 3.2.3). As in the single-protein circumstance just discussed, the interphase at the end of the diffusion process is not the thinnest possible and consequently shrinks. Continuous shrinkage of the State 1 interphase concentrates the mixed interphase to a limit that triggers the observed State 1 → State 2 transition to achieve yet higher-efficiency packing of i, j proteins. Unlike the single-protein circumstance, however, this transition expels both water and protein to achieve this best-packing limit (Panel C, lower panel group). The final State 2 is stable for at least hours (Panel D, lower panel group; see also Section 3.2.4) and probably represents the energy minimum under ambient sessile-solution conditions.

4.2 Summary and Implications for Understanding Biocompatibility

There can be no doubt that understanding protein adsorption from a multi-component solution under various conditions of flow encountered in vivo is essential to prospective biomaterials design for the reasons outlined in Section 1. Although understanding how two proteins compete for the same adsorbent surface is but a small step toward understanding adsorption from biological milieu such as blood, five outcomes of this and previous work [48] on protein-adsorption kinetics seem to have broad implications for understanding biocompatibility and warrant summary here. A simple illustrative computational example is offered in closing to emphasize impact of these factors on understanding hemocompatibility of cardiovascular biomaterials.

1. Immersion of a hydrophobic material into a concentrated, multi-component protein solution (such as blood) leads to rapid diffusion of protein molecules from the proximal fluid phase. Diffusing proteins partition into an inflating interphase that separates the physical surface from bulk solution. There is little reason to suspect that the proximal solution is significantly depleted by adsorption [6], especially in light of the facts that: (i) surface capacity for protein is actually quite small (typically in the range of 2–3 mg/m² or μmoles/m² for kDa-size proteins), (ii) the total blood-protein concentration is large (50–60 mg/mL, [79, 80]), and (iii) proteins exhibit surprisingly little difference in adsorption energetics across a broad range of blood protein types (3 decades in molecular weight, see refs. [14, 22, 43–46, 49–51, 61, 63] for more discussion).

2. Individual proteins diffuse into an inflating interphase in proportion to individual (not collective) bulk-solution concentration. Proteins diffusing into the interphase become effectively trapped by an energetic preference for the adsorbed state. As a consequence, the interphase can contain much more protein than otherwise estimated from single-protein studies. Under conditions of flow (mixing in lab experiments or possibly flow in vivo), this state of excess persists for many hours, perhaps indefinitely. Mixing apparently prevents or inhibits establishment of the most efficiently-packed 3D interphase region rather than facilitating mass transport to-and-from the interphase, as might otherwise seem consistent with ordinary physical intuition. Evidently, adsorption measurements from single-protein solutions or static mixtures are not necessarily good indicators of adsorption from flowing fluids (although relevant to understanding the physical chemistry of adsorption).

3. Simultaneous diffusion of two proteins into an adsorbing interphase causes a modest size selectivity that appears to be partly due to relative rates of diffusion. Hence, relative adsorbed masses of proteins engaged in adsorption competition strongly resembles that of the bulk solution from which adsorption occurs so that “…in mixtures such as blood, the proteins would be adsorbed simply in proportion to their surface collision frequency or concentrations…”; as argued by Brash and Lyman in the early 1960’s [16]. Relative diffusion rates leads to a number discrimination against larger proteins such that a greater number of smaller proteins adsorb from a mixture of larger-and-smaller proteins [46]. A disproportionately higher number of small proteins such as enzymes at a surface can have significant consequences on the biological response to materials (see following section).

4. The popular qualitative explanation for the Vroman Effect [1, 17, 20, 24–43] based on the idea that lower-molecular-weight proteins arriving first at a surface are displaced by higher-molecular-weight proteins arriving later seems untenable in view of the above, at least for binary-protein competition. Diffusion from concentrated protein solutions is too rapid [48], only modestly selective (item 3 above), and proteins traverse only short distances from concentrated solutions to arrive at a rapidly-filling surface region (item 1 and ref. [48]). Hence, there seems simply too little time-and-space for mass transfer to exert a significant adsorption-discrimination effect from concentrated protein solution. Rather, it appears that a Vroman-like discrimination is substantially due to a purely-physical process unrelated to protein biochemistry other than size.

5. Proteins adsorbing within the interphase necessarily displace interphase water. Energetics of this “interphase dehydration” controls maximum adsorbent capacity. Maximum adsorbent capacity is consequently observed to be related to adsorbent water wettability [22, 23, 44, 45, 63, 76–78] (with the notable exception of surfaces bearing ion-exchange functionalities [47]). Maximum adsorbent capacity scales with w/v (not molar) solution concentration [44, 51] and is a material property unrelated to the specific identity of protein or proteins adsorbing from purified or mixed solution, respectively. At any particular interphase w/v concentration, there is naturally higher-number of lower-molecular-weight proteins than higher-molecular-weight proteins.

4.2.1 Modeling the Adsorption-Dilution Effect on Contact Activation of Plasma Coagulation

Material contact activation of blood factor XII (FXII, Hageman factor) is widely thought to be a primary cause of poor hemocompatibility (see ref. [81] and citations therein). We have discovered that this so-called “autoactivation” reaction ( $\text{FXII}\stackrel{\text{surface}}{\to }\text{FXIIa}$, a.k.a. autoactivation) is not specific for anionic surfaces, as proposed by the generally-accepted surface biophysics involved in contact activation of blood-plasma coagulation [82]. Rather, it is found that autoactivation in the presence of plasma proteins leads only to an apparent specificity for anionic-hydrophilic surfaces that is actually due to a relative diminution of the $\text{FXII}\stackrel{\text{surface}}{\to }\text{FXIIa}$ reaction at hydrophobic surfaces [83, 84]. We refer to this phenomenon as an “adsorption-dilution effect” whereby adsorption competition dilutes FXII contact with procoagulant surfaces, sharply reduces frequency of FXII/surface interactions that lead to autoactivation, and renders hydrophobic surfaces nearly inert to plasma coagulation [81]. Nevertheless, it is observed that hydrophobic surfaces retain measurable activation properties [85–87], which is thought to be due to persistent contact of FXII with activating surfaces in the presence of a plethora of blood proteins [81].

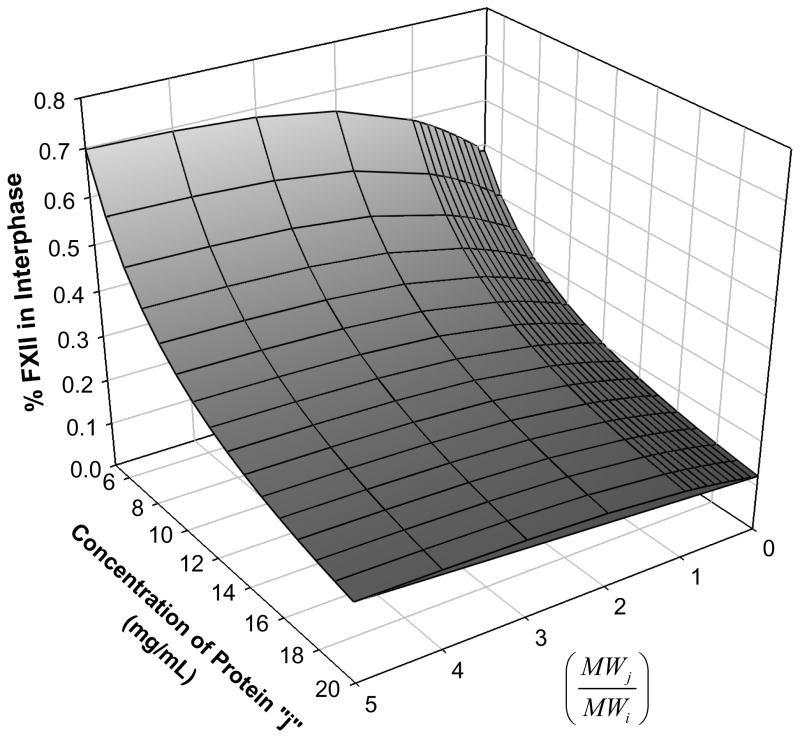
The adsorption-dilution effect is modeled by reducing the problem to a hypothetical binary competition between FXII (protein i at physiological blood concentration ~ 30 μg/mL, [81]) and a protein j ranging in size from smaller than FXII (low relative molecular weight) to larger than FXII (high relative molecular weight). The adsorbent is hydrophobic octyl sepharose (OS) surfaces for which the adsorption selectivity factor is estimated from Fig. 3. Computational details are given in Appendix A for the specific circumstance that OS adsorbent is saturated with protein j for all circumstances considered (Cases 2–4, Section 3.2).

Fig. 7 compiles computational results in a 3D surface plotting FXII surface composition (in %) as a function of protein j solution concentration and relative molecular weight $\left(\frac{{MW}_j}{{MW}_i}\right)$. Inspection of Fig. 7 reveals that high relative concentrations of protein j is indeed effective in diluting FXII from the surface. This effect is becomes especially pronounced as at lower $\left(\frac{{MW}_j}{{MW}_i}\right)$. But even high concentrations of smaller proteins smaller than FXII ( $\left(\frac{{MW}_j}{{MW}_i}\right)<1$) fail to compete away all FXII at the surface. Residual FXII in contact with the surface can undergo autoactivation, releasing FXIIa into solution to propagate coagulation. Thus, results of this computational model qualitatively reproduces general aspects of the adsorption-dilution effect on FXII autoactivation at hydrophobic surfaces [82, 83] in that it is observed that autoactivation depends on the protein composition of the fluid phase. These results help understand the small-but-measurable residual activation properties of hydrophobic surfaces immersed in blood plasma [81]. Fig. 7 is in essential agreement with computational modeling previously reported by us in ref. [46] in that a number bias for adsorption of low-molecular-weight proteins was predicted. However, because [46] assumed that binary-adsorption competition between proteins came to steady state within 1 hour of solution/adsorbent contact, it failed to take into account the State 1 → State 2 transition that this work observed. Modeling theory employed did not account for adsorption specificity between two proteins discovered by this work and mass balance equations are consequently in error.

Figure 7.

Binary-competition model of the “adsorption-dilution effect” on blood Factor XII (see Appendix A for computational details). FXII (protein i) at physiological concentration competes with a hypothetical protein j with variable molecular weight measured by the ratio $\left(\frac{{MW}_j}{{MW}_i}\right)$. Solution concentration of FXII is fixed but protein j concentration is variable. The computed surface shows that high relative concentrations of protein j is effective in diluting FXII from the surface, especially for lower $\left(\frac{{MW}_j}{{MW}_i}\right)$ representing j proteins that are smaller than FXII. But even high concentrations of smaller proteins ( $\left(\frac{{MW}_j}{{MW}_i}\right)<1$) fail to compete away all FXII at the surface. Residual adsorbed FXII can hypothetically undergo autoactivation ( $\text{FXII}\stackrel{\text{surface}}{\to }\text{FXIIa}$) even in the presence of an overwhelming concentration of other proteins, possibly accounting for the observed sluggish coagulation of blood plasma in contact with hydrophobic procoagulants.

5. Conclusions

Kinetics of protein-adsorption competition from binary solution to the same hydrophobic adsorbent exhibits surprising complexity related to the way dissimilarly-sized, hydrated molecules diffuse into a 3D interphase region that separates the physical adsorbent surface from bulk solution. Experimental results are consistent with reversible, multilayer adsorption and thereby inconsistent with the assumption of irreversible adsorption into a single monolayer used by certain protein-adsorption theories. Multilayer adsorption is itself inconsistent with the popular idea that protein adsorbs to surfaces primarily through protein/surface interactions because proteins within second (or higher-order) layers are too distant from the adsorbent surface to be held surface bound by strong forces in close proximity.

Proteins diffuse from binary solution into a rapidly inflating interphase in proportion to individual solution concentration with a modest size selectivity between competing proteins. This initially-formed interphase shrinks in volume by expulsion of both water and proteins to minimize system energetics. The diffusion-based adsorption selectivity persists by ejecting adsorbed proteins in the same mass ratio as initially adsorbed. Adsorption-competition kinetics has important ramifications in the interpretation of biocompatibility and emphasizes an important role of water in protein adsorption.

Table A1.

Surface-Saturating Bulk-Solution Concentrations

Name of Protein (Acronym)	${\left(W_{B_i}^o\right)}^{max}$ mg/mL
Ubiquitin (Ub)	2.99 ± 0.35
Human Serum Albumin (HSA)	3.53 ± 0.21
Prothrombin (FII)	4.05 ± 0.50
Human IgG (IgG)	9.53 ± 0.37
Fibrinogen (Fib)	6.07 ± 0.22

Notes: Solution concentrations required to saturate surface area of OS adsorbent used in this work.

Appendices

Appendix A: Computational Details for the Adsorption-Dilution Effect on Contact Activation of Plasma Coagulation

Equation (1a–d) gives mass balance requirements for adsorption from single- and binary-protein solutions, respectively:

$$\begin{array}{c}{W}_{I_i}=\frac{m_{I_i}}{V_{I_i}}=\frac{D_i{V}_B}{V_{I_i}}(a)\\ W_{I_j}=\frac{m_{I_j}}{V_{I_j}}=\frac{D_j{V}_B}{V_{I_j}}(b)\\ \text{and}\\ {(W_{I_i})}_{i,j}=\frac{{(m_{I_i})}_{i,j}}{{(V_I)}_{i,j}}=\frac{{(D_i)}_{i,j}{V}_B}{{(V_I)}_{i,j}}(c)\\ {(W_{I_j})}_{i,j}=\frac{{(m_{I_j})}_{i,j}}{{(V_I)}_{i,j}}=\frac{{(D_j)}_{i,j}{V}_B}{{(V_I)}_{i,j}}(d)\end{array}$$ (1)

where subscripts I and B refer to interphase and bulk-solution phases, respectively. The subscripts i and j differentiate between two different proteins with adsorbed masses m and m that may be in either pure solution or in a mixture denoted by the “i, j” subscript. W _Ii and W _Ij are w/v concentrations of i, j proteins such that (W_I)_i,j = [(W_Ii)_i,j + (W_Ij)_i,j] which is to be read as the sum of individual contributions to the i, j binary mixture. In pure solution, each protein occupies a characteristic volume V_Ii orV_Ij. The volume of the binary mixture is denoted (V_I)_i,j which is not necessarily the sum of individual characteristic protein volumes due to packing constraints of mixing two dissimilar-sized proteins with the mixed interphase. It is readily apparent from Eq. (1) that:

$$\left(\frac{{\left(W_{I_j}\right)}_{i,j}}{{\left(W_{I_i}\right)}_{i,j}}\right)=\left(\frac{{(D_j)}_{i,j}{V}_B/{(V_I)}_{i,j}}{{(D_i)}_{i,j}{V}_B/{(V_I)}_{i,j}}\right)=\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)$$ (2)

In view of the experimental finding that $\left(\frac{{(D_j)}_{i,j}}{{(D_i)}_{i,j}}\right)=S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)$ (Section 3.2.1), it is apparent that $\left(\frac{{\left(W_{I_j}\right)}_{i,j}}{{\left(W_{I_i}\right)}_{i,j}}\right)=S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)$. Using the relationship (W_I)_i,j =[(W_Ii)_i,j + (W_Ij)_i,j], Eq. (2) can be solved for either i or j contributions to the total (W_I)_i,j:

$$\begin{array}{c}{(W_I)}_{i,j}=\left[{(W_{I_i})}_{i,j}+S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right){(W_{I_i})}_{i,j}\right]=\left[1+S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)\right]{(W_{I_i})}_{i,j}\\ \text{or}\\ {(W_{I_i})}_{i,j}=\frac{{(W_I)}_{i,j}}{\left[1+S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)\right]}\end{array}$$ (3)

Eq. (3) permits calculation of the i contribution if (W_I)_i,j happens to be known. In fact, (W_I)_i,j is known for the circumstance when the adsorbent surface area is saturated with adsorbate and ${(W_I)}_{i,j}=W_I^{max}$ (Cases 2–5, see Sections 3.2.1 and 4.1.1). We estimate that (W_I)^max=300 ±60 mg/mL for OS and OTS adsorbents used herein [44]. Accordingly,

$$\begin{array}{c}{(W_{I_i})}_{i,j}=\frac{300}{\left[1+S_{i,j}\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)\right]}\\ \text{and}\\ {(W_{I_j})}_{i,j}=300-{(W_{I_i})}_{i,j}\end{array}$$ (4)

The selectivity factor S_i,j was fitted (Fig. 3) with an arbitrary three-parameter exponential-decay function yielding:

$$S_{i,j}=(0.9\pm 0.04)+(0.4\pm 0.09)e^{-\left[(1.4\pm 0.82)\left(\frac{{MW}_j}{{MW}_i}\right)\right]}(R^2=0.76)$$ (5)

Eq. (5) permitted estimation of a protein selectivity for any competitive i, j protein pairs with molecular-weight ratio $\left(\frac{{MW}_j}{{MW}_i}\right)$. Combining Eqs. (4) and (5) leads to:

$$\begin{array}{c}{(W_{I_i})}_{i,j}=\frac{300}{\left[1+\left(0.9+0.4e^{-(1.4)\frac{{MW}_j}{{MW}_i}}\right)\left(\frac{{\left(W_{B_j}^o\right)}_{i,j}}{{\left(W_{B_i}^o\right)}_{i,j}}\right)\right]}\\ \text{and}\\ {(W_{I_j})}_{i,j}=300-{(W_{I_i})}_{i,j}\end{array}$$ (6)

Eq. (6) permitted calculation of the concentration of FXII (at 0.03 mg/ml FXII physiological blood concentration ~ 30 μg/mL, [81]) adsorbed within the interphase in competition with a hypothetical protein j with variable $\left(\frac{{MW}_j}{{MW}_i}\right)$ under the conditions of surface saturation. Results shown in Fig. 7 are reported in percent interphase concentration by:

$$\%\mathit{FXII}=\left[\frac{{(W_{I_i})}_{i,j}}{300}\right]\times 100$$ (7)

Appendix B: Surface-Saturating Bulk-Solution Concentration

Bulk-solution concentrations that saturate adsorbent surface area employed in this work was obtained from depletion adsorption isotherms measured for proteins used in this work, as summarized in Table A1.

Appendix C: Arithmetic of the Spheres

Molecular volume of a hypothetical protein sphere $V_p=4/3\pi r_v^3$ where r_v is molecular radius in cm/molecule. Consequently, molar volume ${\overline{V}}_p=4/3\pi r_v^3{N}_A$ in cm³/molecule if N_A is the Avogadro number. The specific volume v^o = V̄_p · MW · 10³) in cm³/g, where MW is molecular weight in kDa. Using the relationship r_v = 6.72×10⁻⁸ MW^1/3, it is apparent that $v^o=4/3\pi N_A\left[\frac{\left({(6.72\times {10}^{-8}M{W}^{1/3})}^3\right)}{{10}^{3}MW}\right]=\left(\frac{4\pi {(6.72\times {10}^{-8})}^3}{3\times {10}^3}\right)(6.02\times {10}^{23})=0.77{\text{cm}}^3/\text{g}$ (see citations in section 4.1.2).

Appendix D: Protein Diffusion into the Interphase

Varoqui and Pefferkorn’s classic treatment of diffusion to a semi-reflecting interface [88] improved upon classical Fickian diffusion [89] by incorporating the idea of an energy barrier to adsorption (see ref. [48] for more discussion including historical context). This energy barrier accounts for the fact that surfaces have a finite capacity for adsorbate. As a consequence, not every solute encounter with a surface leads to adsorption over the entire timeframe of adsorption. In Varoqui and Pefferkorn’s treatment, the surface is construed to be a semi-adsorbing or reflecting plane, as opposed to a perfectly-adsorbing sink [88]. This energy barrier to adsorption increases as the surface region fills with adsorbate. The basic premise of this work was to couple the Langmuir adsorption equation with standard diffusion theory by proposing that rate-of-change in surface concentration $\left(\frac{d{c}_s}{dt}\right)$ is controlled by a forward rate that was a function of unoccupied surface area and a reverse rate that was itself a function of surface concentration c_s (molecules/area), such that:

$$\frac{{dc}_s}{dt}=K_1\delta c(0,t)(1-\sigma c_s)-K_2{c}_s$$ (8)

where c(x, t) is solution concentration at position x at time t (molecules/volume), δ is a characteristic size (length), K₁ is a forward rate constant, and K₂ is a reverse rate constant. Eq. 1 was coupled with standard diffusion theory through $\frac{dc(x,t)}{dt}=D\left(\frac{{\partial }^{2}c(x,t)}{\partial x^2}\right)$; where D is the diffusion constant and for which the boundary conditions c(x, t) = c₀ for x = ∞, t >0 and c = c₀, x > ∞, t >0 apply. Eq. 8 cannot be solved explicitly but short- and long-time asymptotic solutions can be readily obtained. We focus on the long-time limit because it is experimentally found that protein mass adsorption to a surface is complete within minutes for mg/mL solution concentrations [48] and the time scale of protein competition is of the order of hours. The long-time asymptotic solution reads [88]:

$$\begin{array}{c}{c}_s(t)=\frac{K_1\delta }{K_2+K_1\delta \sigma c_0}c(0,t)\\ \text{or}\\ m_I(t)=\frac{K_1\delta A}{(K_2+K_1\delta \sigma c_0)}c(0,t)\end{array}$$ (9)

where time-dependent surface concentration c_s(t) has been converted to time-dependent mass adsorbed within the interphase m_I(t) (in molecules/interphase volume) by multiplying by adsorbent area A. Application of the above-mentioned boundary conditions leads to the conclusion that:

$$m_I=\left(\frac{K_1\delta A}{K_2+K_1\delta \sigma c_0}\right)c_0=\chi c_0$$ (10)

Eq. (10) uses the fact established by Varoqui and Pefferkorn that K₂ ≫ K₁δσc₀ (see Eqs. 43–47 of ref. [88]) to show that mass adsorption is proportional to solution concentration near steady state (c(0,t)= c₀, t →∞). Applied to binary-protein adsorption leads to the conclusion $\left(\frac{{\left(m_{I_j}\right)}_{i,j}}{{\left(m_{I_i}\right)}_{i,j}}\right)=\frac{{\chi }_j}{{\chi }_i}\left(\frac{{\left(c_{0_j}\right)}_{i,j}}{{\left(c_{0_i}\right)}_{i,j}}\right)$, meaning that the mass ratio of two proteins diffusing to a surface is proportional to the ratio of solution concentrations, as is observed experimentally.