Abstract
The idea that enzymes catalyze reactions by dynamical coupling between the conformational motions and the chemical coordinates has recently attracted major experimental and theoretical interest. However, experimental studies have not directly established that the conformational motions transfer energy to the chemical coordinate, and simulating enzyme catalysis on the relevant timescales has been impractical. Here, we introduce a renormalization approach that transforms the energetics and dynamics of the enzyme to an equivalent low-dimensional system, and allows us to simulate the dynamical coupling on a ms timescale. The simulations establish, by means of several independent approaches, that the conformational dynamics is not remembered during the chemical step and does not contribute significantly to catalysis. Nevertheless, the precise nature of this coupling is a question of great importance.
Keywords: adenylate kinase, coarse-grained model, renormalization, simplified model, enzyme catalysis
The origin of the enormous catalytic power of enzymes has remained one of the key secrets in biology. Although it is clear that electrostatic effects play a major role in stabilizing the transition states of enzymatic reactions (see refs. 1 and 2), it is important to explore the impact of other factors and, in particular, the interesting possibility that the dynamics of conformational transitions make a major contribution to enzyme catalysis (e.g., 3–6). It was also recently argued that there exists a hierarchy of motions, which play a crucial role in enzyme catalysis (e.g., 7).
Although the dynamical idea has been expressed in various incarnations, it clearly implies that motions along conformational coordinates play an important role in the chemical step. However, support for this proposal comes from indirect considerations, particularly from the observation that in some cases, the conformational motions are on the same timescale as that of the chemical step (6, 8, 9). This does not, however, provide concrete evidence for the idea that the conformational dynamics are coupled to the chemistry and that there are inertial motions that are not completely dissipated during the conformational motion (so that they can be transferred to the chemical coordinate).
It must be emphasized that NMR experiments such as those in refs. 4–6 are highly valuable, providing remarkable detail about the conformational dynamics in the different steps of the enzyme's cycle. However, such experiments have not provided direct information about the coupling between the chemical and conformational dynamics, whereas simulation techniques that have been used to examine the magnitude of the dynamical effects have indicated that these effects do not contribute significantly to catalysis (1, 9, 10). Furthermore, studies of free energy surfaces have pointed out that the coupling between the two motions is unlikely to lead to large catalytic effects (9, 10). Nevertheless, the existing computational studies were unable to address this problem in a direct way due to the enormous amounts of computer time needed for simulating (at least) ms processes. One could try running downhill trajectories from the transition state (TS) and exploring the time reversal of the activated trajectories (see figure 6 in ref. 9), but, although preliminary studies produced mode randomization, they are not convincing, as the trajectory needs to be extended to a much longer timescale to disprove the dynamical proposal.
Fig. 6.
The effect of introducing additional fast relaxation components to the conformational dynamics on τfp in the 2-D model. The notation for the different configurations is the same as that used in Fig. 1. The figure demonstrates that drastic qualitative changes in the features of the landscape along the conformational coordinate have almost no effect on the first passage time for the chemical barrier.
Recent studies have allowed for progress in exploring the free energy surface in the conformational and chemical space, particularly with the use of coarse-grained (CG) models (10), but this did not include dynamical studies. Another important advance has been made in the use of CG simulations to explore the dynamics of protein structural changes (11), but these works have not explored the coupling to the chemical process.
Here, we report simulations that actually explore the dynamical idea by bridging the timescale needed to examine the dynamical coupling between the conformational and chemical motions. This study is accomplished by developing a multiscale approach that allows us to explore the dynamical nature of enzyme catalysis in the ms timescale. Our study shows that the kinetic energy of the conformational motion associated with the closing of the active site lid (due to the binding of the substrate) is completely dissipated before the chemical step and cannot affect the time of the chemical process. This dissipation trend will hold for as long as the chemical barrier is higher than a few kcal/mol. Thus, we conclude that protein conformational changes do affect catalysis by changing the active site preorganization (12), but that this reflects the shape of the free energy landscape and is not a result of time-dependent effects. Therefore, our study, which actually explores the dynamical coupling between chemistry and protein structural fluctuations, found that once the chemical barrier is greater than a few kcal/mol (which is the case in enzymatic reactions), there exists basically no coupling.
Renormalizing the Landscape and Dynamics of Enzymatic Reactions.
In this study, we chose the enzyme adenylate kinase (ADK) as our model system for exploring the dynamical proposal, as this enzyme has been the subject of extensive experimental studies of this proposal (3, 5, 6). The chemical reaction catalyzed by ADK is shown in Fig. S1. Here we focus on the second step of this reaction, where the bound AMP and ATP move together upon the closure of the protein lid (see Fig. S1 and Fig. S2 for details of the reaction mechanism, Fig. S3 for an overlay of the two conformations of ADK, and Figs. S4 and S5 for the surfaces obtained using ab initio and EVB, respectively) and a phosphoryl group is transferred from the ATP to the AMP, yielding 2 ADP.
Proper examination of the dynamical proposal in ADK in general requires one to simulate the catalytic process on a very long timescale. To accomplish this challenging task, we have introduced a renormalization approach that transforms the energetics and dynamics of the explicit all-atom enzyme to an equivalent low-dimensional system. The full details of this approach are described in the SI Text, and only the main points are outlined in this section.
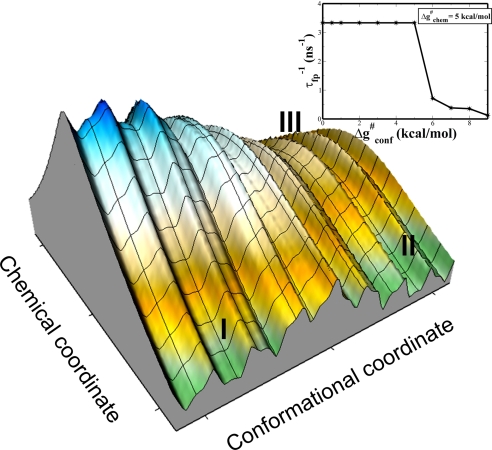
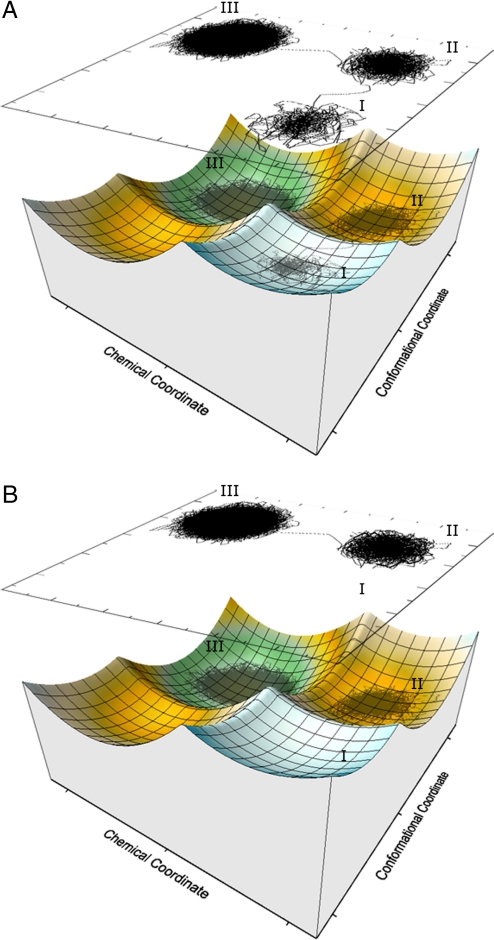
The renormalization process involved the use of three models: an explicit all-atom model (model A), a simplified CG model (13) in which each side chain is represented by a sphere (model B), and a two-dimensional (2-D) simplified model (model C). To get equivalent energetics, we started by generating an empirical valence bond (EVB) surface for model A, generating the catalytic landscape from the EVB profile at the closed, half-open, and open conformations (see ref. 10 for a related approach and the SI Text for the calibration process). A similar procedure was implemented with the CG model. Finally, we fitted the 2-D model to the landscape obtained from model A, resulting in the surface of Fig. 1.
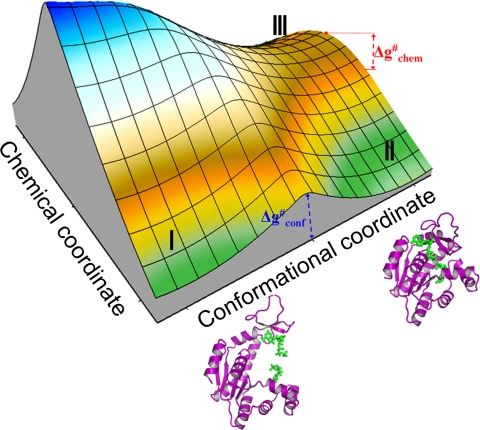
Fig. 1.
The effective 2-D free energy surface for the ADK system. Here, I, II, and III denote the reactant state (RS) in the open conformation, the RS in the closed conformation, and the product state (PS) in the closed conformation respectively.
In the subsequent step, we forced the short timescale Langevin Dynamics (LD) of both the conformational and chemical coordinates of the lower-dimensionality models (i.e., the CG and 2-D models) to represent the corresponding dynamics of the full model. First, we introduced a special renormalization treatment, by forcing the longer timescale dynamics of the CG model to represent the conformational dynamics of the full model, under the influence of strong constraints (see Fig. S6). We further refined the dynamical properties of the short timescales of the CG and 2-D models by calculating the corresponding autocorrelation functions (ACFs) of the conformational coordinates for several different friction constants, in order to identify the constants that give the best agreement with the ACF of the full explicit model (see Fig. S7). Finally, we also forced the short-timescale dynamics of the chemical coordinate of the three models to be similar by ensuring that the autocorrelations of the energy gap are similar. The resulting short timescale of the chemical coordinate of the three models is given in Fig. S8. As discussed in the SI Text, the agreement between the short timescale dynamical properties of the three models is reasonable but not perfect. Better agreement could in principle be obtained, but this is not needed here because, as will be seen in this section, we will change the dynamical properties of the 2-D model in a very wide way while looking for our general conclusions. The final stage of our renormalization approach involved refining the 2-D model to reproduce the findings from NMR studies of the mesophile Escherichia coli (14), where it was estimated that kclose and kopen are ≈1,500 s−1 and 300 s−1, respectively. Additionally, we considered the finding of FRET and NMR studies (6) that estimated the kopen and kclose of the ligand-free ADK to be ≈6,500 s−1 and 2,000 s−1, respectively. This renormalization step was performed by forcing the long timescale conformational dynamics of the 2-D model (without the constraint) for the apo-enzyme to reproduce the experimentally observed values of kopen and kclose (obtaining kclose from kopen by using a detailed balance). The simulated motion was subsequently mapped onto the CG model, and is depicted in Movie S1.
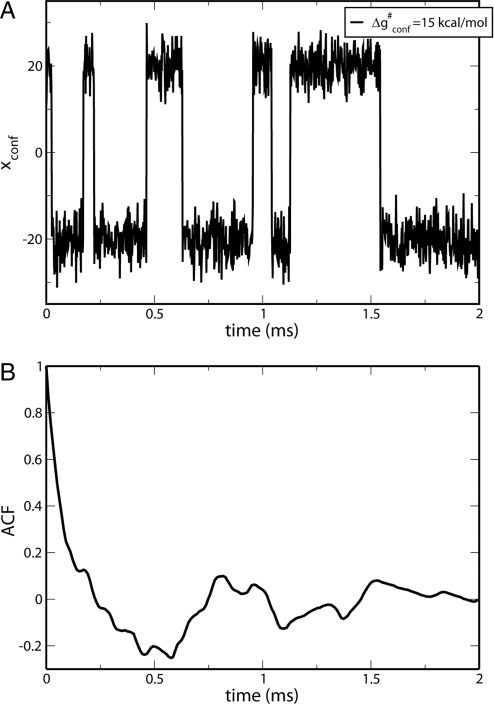
The main factor in the fitting of the long timescale features appears to be the barrier for the motion from the open to the closed configuration rather than the friction used (as is clear from ref. 15, in the high-barrier limit the correlation time is exponentially dependent on the barrier height). Fig. 2 describes the time dependence of the trajectories in the 2-D model and the ACF of the conformational motion. For simplicity, this simulation was performed with ΔG0 = 0. The observed experimental rate (kopen) of 6,500 s−1 is reproduced with a barrier of 14–15 kcal/mol for the conformational coordinate (the precise barrier being dependent on the friction used in the calibration process). A direct comparison to the FRET studies is not simple (16) and is left to subsequent studies.
Fig. 2.
A long-timescale trajectory along the conformational coordinate, showing (A) the time dependence of and (B) the corresponding ACF for the conformational coordinate in the 2-D model.
Next, we introduced the effect of the ligands, by changing ΔG0 for the open to closed motion to ≈2 kcal/mol and increasing the barrier that corresponds to kclose by 1 kcal/mol, so that the corresponding rate is ≈1,500 s−1. We also adjusted the chemical barrier to be 14.3 kcal/mol, such that k2 (our kchem) corresponds to the observed value of 260 s−1 at 300K (14) (with the assumption that k2 is equal to the observed kcat).
Exploring the Idea That Dynamical Coupling Contributes to Catalysis.
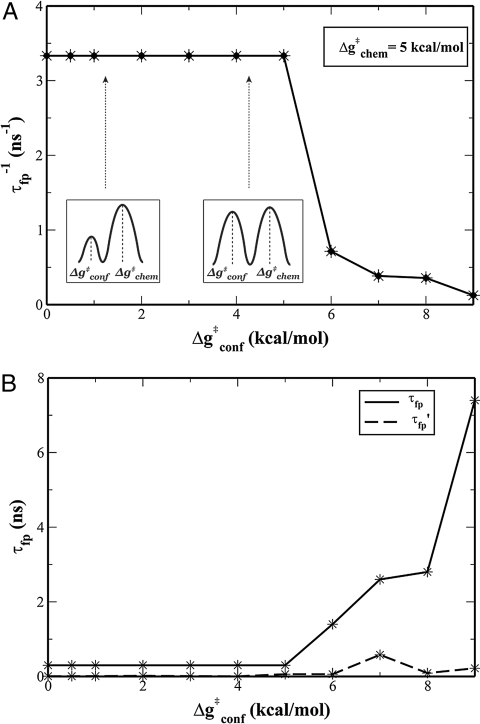
The renormalized 2-D model allows us to finally explore the coupling between the conformational and chemical coordinates. This was done while focusing on the key question, namely that of whether the dynamical information from the conformational motion is remembered during the chemical step (for further clarification of this issue, see Fig. S9, where the diffusive and inertial models define the two limiting cases). In order to resolve this issue, we started from the open structure without the constraint and ran LD up to the ms timescale. The simulations were used to determine the average first passage time, τfp (i.e., the time required to reach the chemical TS and then the product state for the first time). We started the simulations by running several trajectories on the 2-D surface, with barriers of 14.0 and 14.3 kcal/mol for the conformational and chemical motions, respectively. Here, it appeared that the overall time for reaching the product state was ≈0.5 ms, and the system spent significant time in the reactants region before crossing to the product region (this trend will be quantified in this section below). However, more general conclusions could be obtained while using lower barriers and thus shorter runs (see Fig. 3 and the associated discussion in the figure legend). Thus, we explored the dynamical proposal by using Δgchem≠ = 5 kcal/mol, while gradually changing the conformational barrier, Δgconf≠. The results of these simulations are summarized in Fig. 3A, where it can be seen that τfp is independent of the conformational barrier, as long as this barrier is smaller than the barrier that determines kchem. This clearly indicates that there is no significant dynamical coupling between the conformational and chemical coordinates.
Fig. 3.
The relationship between the first passage (fp) time, τfp, over the chemical barrier, and the height of the conformational barrier (for the case where Δgchem≠ = 5 kcal/mol). The calculations represent the average from several runs. The figure considers two correlations: The inverse fp time, (τfp)−1, as a function of the conformational barrier, where it is shown that the crossing time of the chemical barrier is independent of the characteristic time of motion along the conformational coordinate as long as kconf > kchem (A), and τfp and τfp′ (which is the fp time when we start the counting from the moment the trajectory reaches the RS) (B). It can be seen that even when kconf < kchem, the time of crossing the chemical barrier is independent of the conformational landscape.
Additionally, Fig. 3B displays τfp′, which is the fp time, as calculated from the moment a trajectory reaches the bottom of the chemical barrier. Here we see that even in the cases where the conformational barrier is higher than the chemical barrier, the change in τfp′ is rather small and might reflect sampling effects.
To establish the generality of our finding, we repeated the above protocol for a somewhat higher barrier (i.e., Δgchem≠ = 7 kcal/mol) and obtained the same trend as in Fig. 3. Thus, this behavior is expected to be reproducible in the barriers range that corresponds to ADK. However, performing the relevant simulations would require significantly longer time, making it harder to reach stable results. Moreover, the conclusions obtained at small barriers are clearly valid for higher barriers where frictional effects are less important.
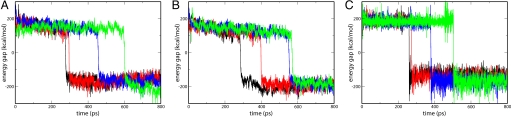
In the next step, we proceeded to examine the intriguing proposal that the chemical reaction is partly driven by the kinetic energy that is associated with the conformational change, which is in turn triggered by the binding of the substrate (17). This study started by taking the 2-D model and artificially increasing the energy of the open state, thus simulating a very exothermic binding process. Fig. 4 shows the results of the corresponding LD simulation, where even in the case of very large excess binding energy, the kinetic energy of the trajectories is dissipated before it can be used to drive the chemical process. Fig. 4 also indicates that inertial effects do not couple the conformational and chemical coordinates because the 2-D trajectory involves random motions in the Michaelis Complex.
Fig. 4.
Exploring the possible effect of excess binding energy on the chemical step in the 2-D effective model. (A and B) The figure shows the following two situations: a hypothetical case where the trajectory starts from a high energy open state (I), rapidly moves to the closed RS (II), and finally crosses to the PS (III) (A), and a case where the simulations start at the closed RS (II) and move to the PS (III) (B). In both cases, the trajectory appears to be randomized in the closed reactant state.
To ensure that the results of Fig. 4 do not reflect an underestimation of the friction by the 2-D model, we validated the above hypothesis by using the full CG model (model B). It was not practical to directly apply this model by using the actual chemical barrier of ADK due to the very long simulation times required, but it is sufficient to prove our point by using a lower chemical barrier, as randomization effects increase with the height of the chemical barrier. Thus, we used the case with a very low (several kcal/mol) barrier so that it could be crossed rapidly (within ≈100 ps). The simulations were done by starting from a partially open conformation and applying a constraint that pushed the system toward the closed conformation (by using a type of potential similar to the one used in Fig. S6). The strength of this constraint represents the excess binding energy. The calculations were performed with (i) no constraint (starting immediately from the closed structure), (ii) a weak constraint (K = 0.5 kcal mol−1Å−2), and (iii) a strong constraint (K = 5.0 kcal mol−1Å−2). The results of these simulations (see Fig. 5) demonstrate that the excess kinetic energy does not help accelerate the chemical reaction: The time required to cross the chemical barrier was not shortened in the case of a large constraint, i.e., large initial kinetic energy.
Fig. 5.
Obtaining the first passage time for different trajectories in the CG model. The system starts at the closed structure (A), the partially open structure with a weak constraint (0.5 kcal mol−1Å−2) with a minimum at the closed configuration (this pushes the system to the closed state) (B), and the partially open structure with a strong constraint (5 kcal mol−1Å−2) (C). The chemical TS is reached when the energy gap changes sign. For simplicity, we describe the reaction by considering only the two first EVB states, and assuming a one-step mechanism. The resulting figures describe the time dependence of different trajectories starting with different initial conditions and demonstrate that having excess kinetic energy that drives the system toward the closed form does not lead to a shorter time for the chemical process.
It is important to clarify that using the CG and full models leads to a very complex landscape, the random search along which is a part of the transmission factor (in combination with the activation free energy) that determines the rate, kconf. Thus, the magnitude of kconf reflects the timescale of the search for the Michaelis Complex. However, our critical finding is that the excess energy associated with motion along the conformational coordinate is “forgotten” and thus dissipated before the generation of the first productive trajectory that can pass the TS. This situation is expected to continue for as long as the chemical barrier is higher than a few kcal/mol, regardless of whether the conformational step is rate-determining or not.
We have also explored the idea that the existence of multiple timescales is relevant to catalysis (7). Of course, enzymes have multiple correlation times with contributions from a wide variety of timescales (18), but the same is true for any solution reaction. Thus, it is hard to see why such relaxation times should have any special significance in enzymes. Nevertheless, our approach allows us to explore this issue by generating drastically different relaxation times for the conformational motion. These relaxation times were achieved by changing the surface (see Fig. 6), and, by doing so, introducing additional fast components to the ACF. This appears to have no effect on the chemical rate (see Fig. 6). In other words, here we used a consistent model with contributions from relaxation times in different timescales, and this did not lead to detectable changes in the coupling between the conformational and chemical steps. The reason for this is that the specific memory of the fast motions is dissipated long before the time needed to overcome the chemical barrier.
Finally, one may argue that dynamical effects are only relevant when the chemical barrier is lower than the conformational barrier. In analyzing this idea, we start by noting that once the conformational barrier becomes rate-limiting, it not useful to enhance the speed of the chemical step. Nevertheless, we also note that Fig. 3B has established that the first passage time (evaluated starting from the Michaelis Complex) does not change significantly, even when the conformational barrier is higher than the chemical barrier. Thus, even in the case where kon < kchem, the dynamical effects are quite small. The situation does change, however, when the chemical barrier is very small (i.e., Δgchem≠ < 3 kcal/mol) and the first passage time lies on the ns scale. In such cases, we find that the energy of the conformational motion may perhaps be used to pass the second barrier. However, we are not aware of enzymatic systems where the chemical barrier is much lower than 9 kcal/mol, because there is no evolutionary reason to reduce the chemical barrier below the diffusion limit.
Conclusions
The idea that dynamical coupling between the conformational and chemical coordinates contributes to enzymatic rate enhancement has been a cause of much excitement in recent years (3–5, 7, 19, 20). Although circumstantial evidence such as similar timescales for both motions has been pointed out (6), direct experimental findings of coupling between these motions are not available. This issue can, in principle, be explored by simulation approaches, but such simulations could not be extended to the relevant timescales.
Here, we have provided the first simulation-based analysis of the proposed dynamical coupling on a ms timescale. Our simulations were based on renormalizing lower-dimensionality models so that they capture the energetics and dynamics of the full reacting protein system. We have also provided additional relevant analysis by use of a CG model. The simulations have used the catalytic reaction of ADK as a benchmark and have been applied to a general protein model with different types of conformational motions.
It was found that no significant dynamical coupling exists between the chemical and conformational trajectories and that the inertial part of the conformational motion decays in less than a ns, whereas the rest of the process is guided entirely by the free energy surface and the corresponding Boltzmann probability. In other words, the chemical process has no significant “memory” of the dynamics of the conformational motion. We would like to emphasize that despite the seemingly simple nature of the 2-D model, not only does it capture the energetics and dynamics of the full model, but we have also established the validity of our findings by varying the friction over any reasonable range. Furthermore, we were able to fully support our conclusions through our use of the CG model (see Fig. 5). It might also be stated for those who consider this work to be a collection of incomplete proofs that it is clearly a far more in-depth study than any of the opposing evidence provided by the proponents of the dynamical proposal.
It is important to emphasize that we are not in any way claiming that the experimental findings are wrong, but merely that their dynamical interpretation is problematic because it is not based on solid proof that the conformational motion transfers energy to the catalytic process. In fact, we argue that our study can actually provide a basis for the molecular interpretation of the NMR and FRET observations, as far as the coupling between conformational changes and catalysis is concerned.
At this point, we can also address the idea that the existence of a hierarchy of timescales contributes to catalysis (6). That is, it has been proposed that the conformational transitions occurring at the timescale of the catalytic turnover are “facilitated” by much faster motions (7). However, although the fast motions are real, they do not seem to affect the behavior of the system on the ms timescale. In other words, the slow motions follow random fluctuations, whose amplitudes obey the Boltzmann distribution, without remembering the fast motions. As seen from our simulations, we clearly have motions that reflect multiple timescales, but regardless of the “spectrum” of the autocorrelation we obtain the same overall catalytic effect (see Fig. 6).
Finally, we would like to emphasize that exploring enzyme dynamics on different timescales, as well as reproducing single molecule experiments, is a fascinating and potentially very important challenge. There are clearly dynamical effects that play a major role in ultrafast biological reactions (9, 21). However, although these studies are quite elegant, they do not automatically imply that that there is coherent coupling between the slow productive trajectories that overcome the chemical barrier and the conformational motions in enzyme catalysis.
Methods
Our study first thoroughly characterized the reaction mechanism in solution by constructing the appropriate ab initio 2-D free energy surface (see the SI Text for full details). Next, we calibrated an EVB surface on the ab initio solution surface by using the resonance structures shown in Fig. S5 and then used the (unchanged) calibrated parameters to examine the catalytic landscape of ADK. This was achieved by EVB simulations of the full model in the open, closed, and intermediate configurations.
Once the catalytic landscape of the full model had been characterized, it was possible to move to the reduced representations. Here, the multilevel hierarchical “renormalization” approach introduced in Renormalizing the Landscape and Dynamics of Enzymatic Reactions was applied. This approach maps the full-atom protein+solvent explicit system with the coordinate set r onto a CG simplified protein model with the coordinate set q, in which each side chain is represented by a sphere (13) (this model allows one to explore the system on a longer timescale while still keeping most of the relevant multidimensional physics of the protein). Then the full system was also mapped onto a 2-D simplified model (model C), with the coordinates Q1 and Q2 (this model projects the energetics and dynamics onto a 2-D space, while still representing the chemical and conformational features of the full system). The mapping procedure included a “fine tuning” of the dynamical properties of the three models at different timescales by forcing the relevant ACF to behave similarly in all three models, to capture the dynamics of the full model in the reduced models. The relaxation times were manipulated by applying strong constraints to the system, which allows the full model to undergo the conformational changes on a short timescale (see the SI Text for further information). Finally, once the model had been reasonably calibrated, it was possible to explore the long-timescale motions by use of the 2-D model (without any constraints), as it had been ensured that the 2-D model is behaving in the same way as the full explicit system, and thus that we are not compromising accuracy by use of the simplified model. Additionally, we were also able to use the CG model in simulations at intermediate timescales to prove some of the conclusions obtained by the 2-D model (see Fig. 5). Full details of the simulations (including comprehensive theoretical background) are provided in the SI Text.
Supplementary Material
Acknowledgments.
This work was supported by National Institutes of Health Grant GM24492, and all calculations were performed by using the University of Southern California High Performance Computing and Communication Center cluster.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0909150106/DCSupplemental.
References
- 1.Warshel A, et al. Electrostatic basis for enzyme catalysis. Chem Rev. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 2.Hansson T, Nordlund P, Åqvist J. Energetics of nucleophile activation in a protein tyrosine phosphatase. J Mol Biol. 1997;265:118–127. doi: 10.1006/jmbi.1996.0716. [DOI] [PubMed] [Google Scholar]
- 3.Akke M. Out of hot water. Nat Struct Mol Biol. 2004;11:912–913. doi: 10.1038/nsmb1004-912. [DOI] [PubMed] [Google Scholar]
- 4.Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science. 2006;313:1638–1642. doi: 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
- 5.Eisenmesser EZ, et al. Intrinsic dynamcs of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 6.Henzler-Wildman KA, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 7.Henzler-Wildman KA, et al. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 8.Akke M. NMR methods for characterizing microsecond to millisecond dynamics in recognition and catalysis. Curr Opin Struct Biol. 2002;12:642–647. doi: 10.1016/s0959-440x(02)00369-x. [DOI] [PubMed] [Google Scholar]
- 9.Olsson MHM, Parson WW, Warshel A. Dynamical contributions to enzyme catalysis: Critical tests of a popular hypothesis. Chem Rev. 2006;106:1737–1756. doi: 10.1021/cr040427e. [DOI] [PubMed] [Google Scholar]
- 10.Roca M, Messer B, Hilvert D, Warshel A. On the relationship between folding and chemical landscapes in enzyme catalysis. Proc Natl Acad Sci USA. 2008;105:13877–13882. doi: 10.1073/pnas.0803405105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen J, Dima RI, Thirumalai D. Allosteric communcation in dihydrofolate reductase: Signaling network and pathways for closed to occluded transition and back. J Mol Biol. 2007;374:250–266. doi: 10.1016/j.jmb.2007.08.047. [DOI] [PubMed] [Google Scholar]
- 12.Liu H, Warshel A. The catalytic effect of dihydrofolate reductase and its mutants is determined by reorganization energies. Biochemistry. 2007;46:6011–6025. doi: 10.1021/bi700201w. [DOI] [PubMed] [Google Scholar]
- 13.Levitt M, Warshel A. Computer simulation of protein folding. Nature. 1975;253:694–698. doi: 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- 14.Wolf-Watz M, et al. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat Struct Mol Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 15.Perico A, Pratolongo R, Freed KF, Pastor RW, Szabo A. Positional time correlation function for one-dimensional systems with barrier crossing: Memory function corrections to the optimized Rouse-Zimm approximation. J Chem Phys. 1993;98:564–573. [Google Scholar]
- 16.Torres T, Levitus M. Measuring conformational dynamics: A new FCS-FRET approach. J Phys Chem B. 2007;111:7392–7400. doi: 10.1021/jp070659s. [DOI] [PubMed] [Google Scholar]
- 17.Min W, Xie S, Bagchi B. Two-dimensional reaction free energy surfaces of catalytic reaction: Effects of protein conformational dynamics on enzyme catalysis. J Phys Chem B. 2008;112:454–466. doi: 10.1021/jp076533c. [DOI] [PubMed] [Google Scholar]
- 18.Nienhaus GU. How do we explore the energy landscape for function. In: Frauenfelder H, Deisenhofer J, Wolynes PG, editors. Simplicity and Complexity in Proteins and Nucleic Acids. Berlin: Dahlem Univ Press; 1999. pp. 39–57. [Google Scholar]
- 19.Benkovic SJ, Hammes GG, Hammes-Schiffer S. Free-energy landscape of enzyme catalysis. Biochemistry. 2008;47:3317–3321. doi: 10.1021/bi800049z. [DOI] [PubMed] [Google Scholar]
- 20.Vendruscolo M, Dobson CM. Dynamic visions of enzymatic reactions. Science. 2006;313:1586–1587. doi: 10.1126/science.1132851. [DOI] [PubMed] [Google Scholar]
- 21.Engel GS, et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature. 2007;446:782–786. doi: 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.