Abstract
Purpose
To develop, implement, and evaluate a novel post-processing method for enhancing the spectral resolution of in vivo Magnetic Resonance Spectroscopic Imaging (MRSI) data.
Materials and Methods
Magnetic field inhomogeneity across the imaging volume was determined by acquiring MRI datasets with two differing echo times. The lineshapes of the MRSI spectra were derived from these field maps by simulating an MRSI scan of a virtual sample whose resonance frequencies varied according to the observed variations in the magnetic field. By deconvolving the lineshapes from the measured MRSI spectra, the linebroadening effects of the field inhomogeneities were reduced significantly.
Results
Both phantom and in vivo proton MRSI spectra exhibited significantly enhanced spectral resolutions and improved spectral lineshapes following application of our method. Quantitative studies on a phantom show that, on average, the full width at half maximum of water peaks was reduced 42%, the full width at tenth maximum was reduced 38%, and the asymmetries of the peaks were reduced 86%.
Conclusion
Our method reduces the linebroadening and lineshape distortions caused by magnetic field inhomogeneities. It substantially improves the spectral resolution and lineshape of MRSI data.
Keywords: magnetic resonance spectroscopic imaging, spectral resolution, field inhomogeneity, field mapping, deconvolution
INTRODUCTION
Spectral resolution defines the ability to distinguish two closely spaced peaks in a spectrum. It is one of the most important determinants of the quality of Magnetic Resonance Spectroscopy (MRS) data (1–3). Low spectral resolution can obscure the information available from a spectrum of tissue metabolites, hindering the detection and quantification of some or all of those metabolites. This is especially true for in vivo proton MRS (1H MRS) of the brain, for several reasons. First, the differences in the chemical shifts of brain metabolites are relatively small (i.e., the spectral peaks are close to one another), and the line splitting caused by J-coupling further reduces the separation of the peaks in the spectrum. Consequently, some spectral lines overlap intrinsically and cannot be easily distinguished. Second, inhomogeneities of the magnetic field caused by the spatial variation of the external field, B0, and by the local differences in magnetic susceptibility of different tissues, produce line broadening and distortion of the lineshape, thereby reducing spectral resolution. Consequently, some lines that are intrinsically separated may overlap. Third, motion of the tissue being imaged may produce line broadening and reduce spectral resolution.
Many techniques have been developed to improve the spectral resolution of in vivo MRS. These techniques generally fall into one of two classes, depending on whether they are employed during the acquisition or the processing of spectral data. The most commonly employed strategy for improving spectral resolution during data acquisition is to improve the homogeneity of the main magnetic field, B0. Fast, high-order shimming techniques (4) have been implemented on modern scanners, yet these methods cannot eliminate variations in the local magnetic field across the imaging volume that are caused by differing magnetic susceptibilities of the various tissues that are interposed within the body. Another strategy to increase spectral resolution is to acquire data at higher magnetic field strengths, which increases the signal-to-noise ratio (SNR) of the MRS data.
Theoretically, doubling the field strength should double the differences in chemical shifts and therefore the separations of peaks in the metabolic spectrum. Unfortunately, the benefit of higher field strengths in improving spectral resolution is much lower than theoretically predicted. Several recent studies have shown, for example, that scanning at 3 or 4 Tesla (T) increases spectral resolution only marginally compared with spectral resolution obtained at 1.5 T. Use of scanners with higher magnetic field strengths compromises spectral resolution because those scanners usually have poorer magnetic field homogeneity. Higher field scanners must contend with shorter and increased susceptibility effects, both of which increase spectral linewidths (2,5–9). Moreover, scanning at higher magnetic field strengths does not eliminate the adverse effects that distortion of line shape can have on spectral resolution. Additionally, the upper limit on field strength, and therefore on the benefits that higher field strengths confer on spectral resolution and SNR, is constrained by both practical and safety considerations.
Techniques that permit the rapid acquisition of MRSI (Magnetic Resonance Spectroscopic Imaging) data can reduce total scan time and thereby reduce the likelihood that the person being scanned moves, and reducing motion artifact will indirectly reduce linebroadening (10,11). Rapid data acquisition, however, often comes with other scanning artifacts and reduced SNR. Additional acquisition-based techniques that are designed to improve spectral resolution include higher spatial resolution MRSI (12) and 2 dimensional (2D) J-resolved MRSI (13), both of which require longer scan times.
Most software-based methods that have been developed to improve spectral resolution are either borrowed or modified from those commonly used in processing conventional Nuclear Magnetic Resonance spectra (14). These methods, however, usually produce only marginal improvement in spectral resolution of in vivo MRS data. The method of Positive Exponential Multiplication (PEM), for example, multiplies the free induction decay (FID, the time-varying MR signal) by a positive exponential function. Although this operation can increase spectral resolution, it also increases noise in the signal and reduces overall SNR, a cost that usually cannot be afforded with in vivo data, given that the SNR of in vivo MRS data is typically already poor. A method similar to PEM is the Double Exponential Multiplication (DEM), which transforms the Lorentzian lineshape to Gaussian with a narrower linewidth at the base of a peak. When employing carefully selected exponential factors, DEM can improve spectral resolution while largely preserving the SNR (14). Because the lineshape of in vivo MRS is often more Gaussian than Lorentzian, however, and because metabolite peaks may overlap far above their bases, DEM has limited applicability for in vivo MRSI. Another processing-based method is spectral deconvolution using the isolated singlet of water as a reference (15,16). This approach assumes that the water peak and metabolite peaks have identical lineshapes, which is not always true for in vivo MRSI, because the distribution profiles and chemical shift displacements of water and metabolite peaks can differ (17). Moreover, acquiring an MRSI dataset for water typically doubles MRSI scan time, which is highly undesirable and usually impractical in many clinical and research applications. Because of these inherent difficulties, processing-based methods have limited utility for improving the spectral resolution of in vivo MRSI data.
Recently, the effects of field inhomogeneity on the linewidth of MRSI spectra that were reconstructed using SLIM (18), a non-Fourier-based MRSI technique, were investigated (19,20). The field inhomogeneity was derived from magnetic field mapping and was incorporated into the algorithm of SLIM reconstruction. The performance of this approach was demonstrated using data from a 2D phantom (19) and 1D in vivo MRSI (20). The results showed that this method significantly improved the SLIM technique in terms of the reduced signal contamination within compartments and narrowed spectral linewidth. The field mapping technique was also employed in FFT-based MRSI to measure field inhomogeneity (21), and this information was directly incorporated into the spectral analysis to improve quantification of metabolites (22).
We present a method for enhancing spectral resolution of in vivo 1H MRSI data. The technique is based on the deconvolution of spectra using as references the lineshapes derived from magnetic field mapping (23). At any given field strength, spectral resolution is related to the linewidth of the spectrum, which is in turn determined jointly by the natural (or intrinsic) linewidth and by linebroadening that is caused by inhomogeneity of the magnetic field. Microscopically, the linewidth of a metabolite spectrum from a volume of the sample being scanned can be regarded as a combination of many spectral lines originating from tiny sub-volumes of the sample. Each of these spectral lines has its natural linewidth, but frequencies are altered slightly by the small variation in strength of the local field where the sub-volume is located (17,20–22). Mathematically, this combination of spectral lines from sub-volumes is described as a convolution of the natural linewidth and the profile of the lineshape for the metabolite signal originating in different sub-volumes. For in vivo MRSI, the profile of the lineshape, or the lineshape function, is determined largely by the linebroadening that is caused by inhomogeneity of the static magnetic field. Therefore, the lineshape function can be derived from the summation of spectral lines that have infinitely narrow linewidths. By deconvolving the measured spectra from the lineshape function that is derived from field mapping, we can significantly reduce the linewidth of the spectrum and thereby enhance the spectral resolution of MRSI data. We have designated this method “Spectral Resolution Amelioration by Deconvolution” (SPREAD). In the following sections, we will first describe the theory and methods of SPREAD, then apply it to the proton MR spectra of both phantom and human brain, and finally conclude with a discussion of its performance.
THEORY
A phase encoded signal in MRSI can be expressed as:
| [1] |
where is the spin density of the tissue at location with an MR frequency f, SW is the spectral bandwidth of the receiver, R is the excited spatial volume of interest (VOI), is the spatial-frequency vector corresponding to a point in k-space that represents a phase encoding step, {td }= t1, t2, …, tD are time points of the acquisition, and Δf is the frequency dispersion caused by the field inhomogeneity, ΔB:
| [2] |
where γ is the gyromagnetic ratio of the nucleus.
In the case of conventional 2D MRSI,
where Nx and Ny are the numbers of PE steps in x and y directions, respectively. The Nx × Ny phase encoded signals will be a 3D matrix in k-space: with two spatial dimensions and one spectral dimension in time domain (with ND data points). A 2D spatial Fourier transform translates these k-space signals into spatial signals in the Nx × Ny grids or matrix of voxels, with the signal in each voxel, Sv, given by,
| [3] |
Here ⊗ stands for convolution integration and is the point spread function (PSF), whose 1D form is given by,
where FOVx is the field of view in the x dimension.
We explain the physical meaning of Eq. [3]. The variable is in the coordinate system of the high-resolution anatomical MRI. The integration runs across all individual voxels, {Vi}, in the MRSI grid, which ideally should produce spectra for all elements in the Nx × Ny matrix. However, the limited number of data points in the Fourier transform produce signal contamination across voxels, so that the signal in voxel Vi will have contributions from other voxels. This phenomenon is described in Eq. [3] by the convolution integration of the PSF with the ideal matrix of spectra. Clearly, variables and x in the convolution are within the MRSI coordinate system and run across the whole MRSI grid. Note further that in order to suppress the long-range contamination due to the PSF, spatial filtering is routinely applied to the MRSI dataset in k-space prior to reconstruction using the 2D spatial Fourier transform, but at the price of increased bleeding of signal among immediately adjacent voxels. This spatial bleeding decreases the actual spatial resolution of the MRSI dataset. Accordingly, identical spatial filtering must be applied when reconstructing the lineshapes for the MRSI voxels, as described in Field Mapping and Lineshape Reconstruction in the next section.
We now simplify Eq. [3] to derive an analytical relationship between the ideal spectrum and the actual spectrum in an inhomogeneous field. First, we suppose that the term is constant within each Vi. The above equation can be simplified as
| [4] |
where is the time domain equivalent of , the ideal signal in a volume Vi with intrinsic frequencies and linewidths. Then we ignore inter-voxel contamination by replacing the PSF in Eq. [4] with a δ function:
which gives,
| [5] |
The phase terms in Eq. [5] that are induced by field inhomogeneities within voxel V will cause accelerated and distorted decay in the time domain signal s̃V(td) and, consequently, will produce an increased linewidth and a distorted lineshape in the frequency-domain spectrum. We thereby refer to this term as the lineshape profile of the spectrum for that voxel, without considering the PSF:
| [6] |
The ideal signal can be recovered from the measured signal, sV(td), by dividing point-wise by the lineshape profile:
| [7] |
[Eq. 5–Eq. 7] are valid only for single voxel MRS or an ideal MRSI that is not contaminated by the effects of the PSF. In reality, the voxel’s spectrum sV(td) in the Fourier-transform reconstructed MRSI will automatically incorporate the PSF effect. Therefore the effects of the PSF must also be taken into account in the lineshape profile of the voxel’s spectrum:
| [8] |
This can be realized by simulating the MRSI with a virtual sample whose spin density is unity and whose frequencies are .
The ideal signal can then be recovered from the measured signal sV(td) by again dividing point-wise by the lineshape profile LV(td):
| [9] |
This is a deconvolution in the time domain.
The preceding is a theoretical outline of our proposed algorithm. Several points warrant mention.
The amount of frequency dispersion in Eq. [2] can be measured from using magnetic field maps, which can be derived from high-resolution MR images that are acquired using two different gradient echo times (TEs) (23). Therefore, if is known, the linebroadening and lineshape distortions caused by field inhomogeneities can be reduced significantly, and spectral resolution can be significantly improved, using Eq. [9].
The calculated lineshape also depends on the resonance frequency of water, which was set to 0 with respect to the system frequency f0(B0).
The low spatial resolution of MRSI relative to the spatial resolution of the field maps causes partial volume effects for some voxels at the edge of the MRSI or near the cerebral ventricles, where metabolites are absent. In practice, these partial volume effects should be excluded when using Eq. [8] to calculate lineshape profiles, lest the calculated lineshapes deviate from the actual lineshapes of the metabolites in those voxels.
Various practical problems must be addressed during the implementation of SPREAD. For example, the lineshape profiles were not calculated using Eq. [6] or Eq. [8], but were derived by using a scheme of MRSI simulation that automatically accounts for the PSF effects. In addition, spikes at points of zero-crossing in the denominator and amplification of noise at the ends of the signal can occur when recovering the ideal signal using Eq. [9] (24). These practical problems will be addressed in the Materials and Methods section below.
MATERIALS AND METHODS
Data Acquisition
We acquired MRI and MRSI data both on a phantom and on human volunteers using a whole-body 3T scanner (Signa 3.0T, GE Healthcare, Waukesha, WI) equipped with a single-channel volume coil for transmission and a standard quadradure head coil for receiving radiofrequency signals. Scout images in three orthogonal planes were first acquired for the localization of both MRSI and field mapping images. MRSI data were acquired using a multi-planar MRSI pulse sequence (25). Image slices were placed in transaxial planes parallel to the AC-PC (anterior commissure-posterior commissure) line. The parameters used for data acquisition included: FOV = 24×24 cm2; Number of slices = 4; Nominal number of phase encoding (PE) steps = 16 × 16 data sampled in an inscribed circle of diameter of 16 in k-space, producing 180 PEs; Number of signal averages for each PE = 1; Slice thickness = 10 mm with 2 mm spacing. The nominal voxel size was therefore 2.25 cm3. Repetition time (TR) = 2300 ms; Echo time (TE) = 144 ms; Spectral width = 2000 Hz; An asymmetric full echo with a longer tail was acquired with 512 complex data points. The outer volume lipid signal was suppressed using operator-placed saturation bands. Water suppression was realized by CHESS pulses imbedded in the sequence (26).
Immediately following the MRSI scan, high resolution MR images for field mapping were acquired using the commercial 3D MRI sequence, “Incoherent Radio Frequency Spoiled Gradient Echo” (SPGR). The slices of the 3D SPGR image were exactly parallel to those of the MRSI data. The volume of the 3D SPGR image was slightly larger than that of the MRSI. The TEs of the two sets of MR images were 8 and 10.5 ms, respectively. Other imaging parameters for the field mapping MRI sequence included: FOV = 24×24 cm2; Slice thickness = 2 mm; Spacing = 0; Number of slices = 28; In-plane resolution = 256×256, Nominal spatial resolution = 1.7 mm3; TR = 20 ms; Flip angle = 110; SW = 15.6 kHz. Therefore the scan time for an MRI scan was approximately 2.3 minutes. Each MRSI slice covered 5 high-resolution MRI slices. Without considering the PSF effect, each nominal MRSI voxel consisted of approximately 1280 nominal high-resolution MRI voxels.
To ensure identical field homogeneity during the one MRSI and two sets of MRI scans, first-order shimming was performed for the MRSI acquisition, and the same shim values were retained for the MRI scans. The same parameters were applied in the phantom scans as in the human scans. We first performed an automated prescan for first-order shimming and to optimize transmitter and receiver gains. We then destroyed the shimming by manually changing the shim value in the Y-direction to produce a field with pronounced inhomogeneity, and then we acquired one set of MRSI data and two sets of MRI data with these shim values. All k-space data for MRI were saved in complex form, in addition to the conventional magnitude mode in the DICOM (Digital Imaging and Communications in Medicine) format, to facilitate generation of the field maps.
A spherical spectroscopy phantom filled with homogenous water solutions of the major brain metabolites (GE Medical Systems) was used in the phantom study. The labeled concentration of N-acetylaspartate (NAA), creatine (Cr), and choline (Ch) was 12.5, 10 and 3 mM, respectively. Three healthy adult volunteers participated in the in vivo study. The protocol was approved by the local Institutional Review Board.
Field Mapping and Lineshape Reconstruction
MR images in the complex format were reconstructed from raw k-space data using a 2D spatial filter with a Hamming window function followed by a spatial Fourier transform. The phase unwrapping procedure was performed using a program provided by Dr. S. Peled (27). For computational efficiency and robustness, however, we used the complex conjugate multiplication of the paired MR images with differing TEs as the input instead of the individual images (28). We then converted these unwrapped phase images into field maps represented by the frequency deviations across the slices.
From these field maps we calculated the lineshape profiles in the voxel matrix of a 2D MRSI slice, as follows:
We synthesized echo signals with the form of for MRI voxels in an MRI slice, where {Δfi} were obtained from the field maps according to Eq. [2] and where {td} began from a negative value synchronized with the beginning of data acquisition, to form echoes at time point td = 0. This yielded a 3D dataset, with two spatial dimensions having the same resolution as the high-resolution MRI, and one spectral dimension having the same spectral resolution as the actual MRSI dataset.
We repeated the above procedure for all MRI slices and added together the datasets corresponding to an MRSI slice to form a single 3D dataset for each MRSI slice.
We multiplied the 3D dataset obtained from step 2 by the term, where (knx, kny) is a spatial-frequency vector corresponding to the PE step n and (xi, yi) is the position vector of the voxel i. Then we summed the products across all voxels in the FOV (e.g., 256×256 voxels).
We repeated the above procedures for all , corresponding to the PE steps in a real MRSI scan. These procedures provided a computer simulation of the real-world MRSI scan described in Eq. [1], with resonance frequency f set to 0 and Δf given by Eq. [2].
Just as the same as we did on the MRSI data acquired by the scanner, we performed a spatial filtering on the simulated k-space data and a half-voxel shift, followed by a 2D spatial Fourier transform. We thus obtained the lineshape profiles for the MRSI.
Spectral Deconvolution
Spectral deconvolution was performed in the time domain based on Eq. [5]. Ideally, this should eliminate the linebroadening caused by field inhomogeneities to provide spectra with their natural linewidths. However, the amplitude of the time-domain lineshape profile in the denominator may decay below the noise level of the signal, thereby amplifying noise, or it may approach zero at some time points, producing spikes in the deconvolved signal. To suppress the noise at the ends of the echo, we applied a modified Gaussian-Wiener filtering window to the signal, yielding the following deconvolution:
| [10] |
where w(td) is the time domain-modified Gaussian-Wiener window function. The term w(td) is given as:
| [11] |
where G is the Gaussian function, α is a scaling constant, KV is defined as (29),
| [12] |
and σ2 is the noise power calculated by
| [13] |
The scaling constant α is calculated as α = Lv,max / Sv,max. The widths of the windows were determined using the linewidths of the original spectra and the linewidths of the objective spectra. We selected the widths of the windows to be 50–70% of the linewidths of the original spectra. To eliminate the spikes near zero-crossing points, we replaced the values of the denominator in Eq. [10] by 1 when the ratio of sv/Lv larger than 8 (24). We note that alternative methods, such as QUECC (30), can also be used to suppress the spikes, which is specially useful for short TE MRSI data.
Data Processing
The measured phantom or human k-space MRSI data were Fourier transformed into the spatial domain following a Hamming window filtering and a half-voxel shift. We then used the SVD-based Matrix Pencil Method to remove the water residue in the spectrum of each voxel (31), because it allows us to eliminate water components without phase distortion. The resulting signal for voxel V was|sV(td)|. 3D lineshape signals having two spatial dimensions at the same in-plane resolution as the MRSI and with a single spectral dimension were constructed from field maps within each MRSI slice, as described above. The resulting lineshape signal for the voxel V, one in the Nx × Ny matrix, is|LV(td)|.
The spatial MRSI data in the time domain after water removal were submitted to the deconvolution procedure. Following deconvolution, the time domain data were zero-padded to either 2048 or 4096 points and then transformed to the frequency domain for further analysis.
All programs used for implementing SPREAD were written in Matlab® (The MathWorks, Inc, Natick, MA). The most time-consuming procedure in SPREAD is the reconstruction of lineshapes from the field maps. For an MRSI slice consisting of 5 field mapping slices having a 256 × 256 in-plane resolution, the reconstruction of the lineshapes with 512 complex data points for 16 × 16 voxels required approximately 80 seconds on a PC equipped with a 4G Hz processor.
Evaluation Methods
We evaluated the performance of SPREAD by measuring spectral linewidths and the asymmetry of spectral lineshapes for the phantom MRS signals before and after application of SPREAD. We also compared the spectral fitting of in vivo MR spectra before and after SPREAD.
Spectral Linewidths
Spectral linewidth is a measure of spectral quality. Linewidth in MRS is conventionally defined as the Full Width at Half Maximum (FWHM), a definition that suffices when spectral lineshapes are symmetric, such as lineshapes described by Lorentzian or Gaussian functions. When lineshapes are severely distorted, however, as they often are for in vivo MR spectra when magnetic fields are highly inhomogeneous, the FWHM definition is not sufficient. For example, two spectra with the same FWHM may have quite different linewidths at the base of the spectra, and hence they may have differing spectral resolutions. We therefore introduce a second definition of spectral linewidth, the Full Width at the Tenth Maximum (FWTM). We used both FWHM and FWTM to characterize the spectral linewidth and to evaluate the performance of SPREAD.
Asymmetry of Spectral Lineshape
The asymmetry of spectral lineshape can be defined in several ways. Herein we define asymmetry as the absolute difference of the left half and the right half areas of a pure absorption peak (i.e., the real part of a peak of a perfectly phased complex spectrum, or a peak in a magnitude spectrum if the time domain data were acquired in the full echo mode), evaluated as a ratio of total peak area:
| [14] |
where aL and aR are the left and right half areas, respectively, when dividing the spectral line from the top of the peak. Therefore, the value of η is 0 for a symmetric peak and 1 for a completely asymmetric one. This definition has the advantage that the irregular lineshape distortions on both sides are taken into account. The areas were calculated by numerical integration of the spectral data using Simpson’s algorithm (32).
Spectral Fitting
Spectral fitting was performed in the frequency domain (FD). Because the time domain data were acquired in the full echo mode, we used a simplified Voigtian function to fit the FD spectrum in the magnitude mode, which has a perfect zero phase. The Voigtian function is the linear combination of Lorentzian and Gaussian lineshapes with a zero phase:
| [15] |
| [16] |
where mP, fP, and WP are the magnitude, frequency, and FWHM of peak P, respectively, {i} are the data points in the spectrum, and c is the weighting factor for the Lorentzian lineshape. Spectral parameters, which include the magnitudes, frequencies, linewidths, and the weighting factors of the Lorentzian and Gaussian portion of the function, were determined using a non-linear least squares algorithm. Fitted spectral data were reconstructed from the parameters using Eq. [15] and Eq. [16].
RESULTS
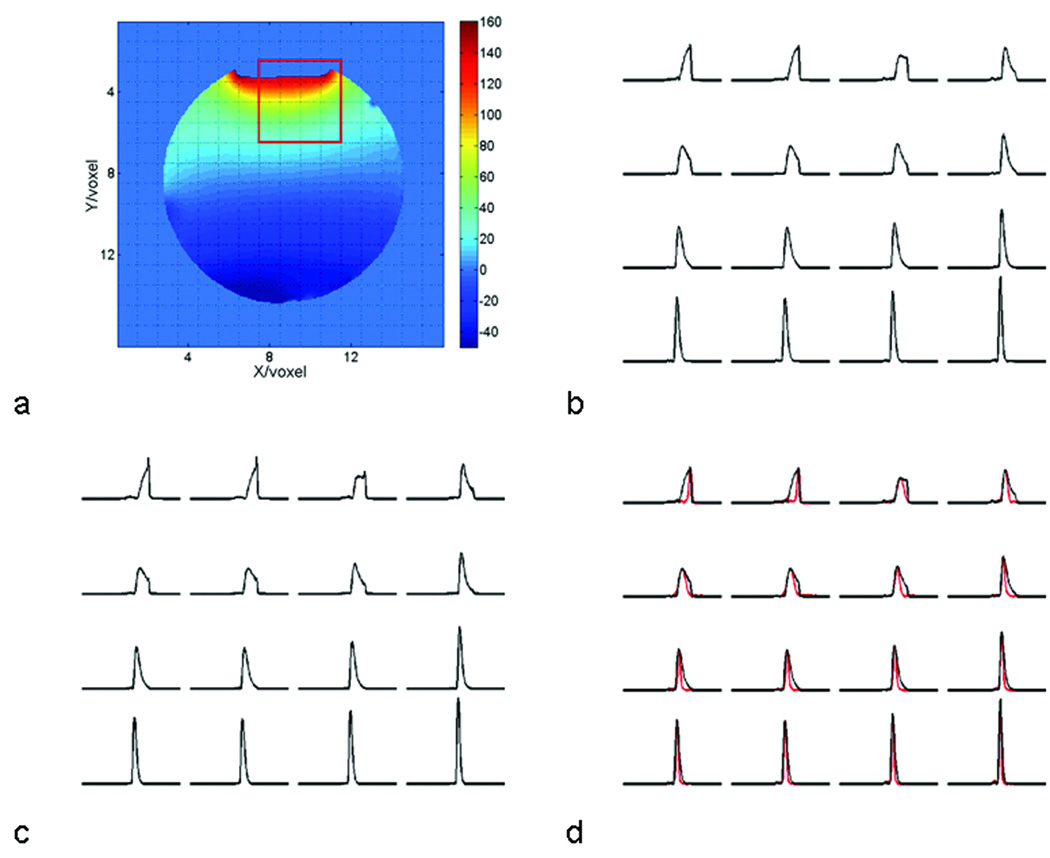
The performance of the lineshape reconstruction based on field mapping was demonstrated by the spectra of water measured on a spectroscopy phantom, because the concentration of water is spatially homogenous, and its lineshape was only altered by the spatial variation of the magnetic field. Field homogeneity was deliberately destroyed in the Y-direction, producing severe field inhomogeneity in the interface between liquid and air (Fig. 1a). Consequently, the lineshapes of water in the voxels adjacent to the liquid-air interface were severely distorted, and linewidths were broadened (Fig. 1b). Note that these lineshapes cannot be described by Lorentzian, Gaussian, or Voigtian functions, thus posing a challenge for spectral fitting. The reconstructed lineshapes (Fig. 1c) were identical to those of water (Fig. 1b), ensuring significant line narrowing and improvement in lineshape using SPREAD (Fig. 1d).
Figure 1.
Examples of lineshape reconstruction based on field maps. (a) An example of field maps for a spherical phantom, with the color bar on the right coding the field strength variation in Hertz. The magnetic field is highly inhomogeneous at the interface of liquid and air. Overlaid on the field map is the grid representing the MRSI voxels. (b) These are the lineshapes of the measured water signals in the voxels within the red square of Fig.1a. (c) Shown here are the reconstructed lineshapes in the corresponding voxels obtained from the field maps. The areas of the spectra in the first row in both Fig. 1b and Fig. 1c are normalized to remove partial volume effects. (d) The spectra following application of SPREAD (red lines) are shown overlaid with the spectra in Fig. 1b (black lines) for comparison. The deconvolved spectra are normalized to the peak heights of water. The width of all spectra is 6.1 ppm, or 781 Hz at 3T.
Further quantitative studies evaluated performance of SPREAD in terms of improvements in line narrowing and lineshape. As shown in Table 1, the FWHMs of water peaks were reduced 30–65% (mean± standard deviation (S.D.) = 42±11%), and FWTMs were reduced 3–55% (38±18%). The asymmetries of the peaks were reduced 75–99% (86±7%) (Table 2). These findings demonstrate the ability of SPREAD to eliminate linebroadening and lineshape distortion caused by variations of the static magnetic field and differences of in magnetic field susceptibility.
Table 1.
Spectral linewidths (Hz) in the 16 voxels shown in Fig. 1.
| Voxel | Before SPREAD | After SPREAD | ||
|---|---|---|---|---|
| FWHM | FWTM | FWHM/ (δ%*) | FWTM/ (δ%**) | |
| 1 | 62.50 | 92.28 | 22.5/ (64.0) | 43.9/ (52.4) |
| 2 | 62.99 | 92.28 | 22.0/ (65.1) | 52.2/ (43.4) |
| 3 | 87.9 | 115.7 | 61.0/ (30.6) | 112.8/ (2.5) |
| 4 | 57.1 | 116.7 | 39.0/ (31.7) | 73.2/ (37.3) |
| 5 | 92.8 | 112.3 | 60.5/ (34.8) | 109.4/ (2.6) |
| 6 | 92.8 | 113.3 | 60.0/ (35.3) | 110.4/ (2.6) |
| 7 | 72.8 | 117.7 | 38.6/ (47.0) | 74.7/ (36.5) |
| 8 | 47.9 | 108.9 | 24.4/ (49.1) | 51.7/ (52.5) |
| 9 | 48.8 | 101.0 | 22.0/ (54.9) | 42.0/ (58.4) |
| 10 | 49.3 | 102.1 | 24.4/ (50.5) | 46.4/ (54.6) |
| 11 | 43.5 | 91.8 | 24.4/ (43.9) | 47.4/ (48.4) |
| 12 | 32.7 | 68.9 | 21.5/ (34.3) | 41.5/ (39.8) |
| 13 | 30.3 | 60.6 | 20.0/ (33.3) | 35.6/ (41.3) |
| 14 | 31.3 | 61.5 | 20.5/ (34.5) | 36.6/ (40.5) |
| 15 | 27.8 | 56.2 | 18.0/ (35.3) | 32.7/ (41.8) |
| 16 | 23.0 | 44.4 | 16.1/ (30.0) | 28.8/ (35.1) |
FWHM: Full With at Half Maximum; FWTM: Full Width at Tenth Maximum; δ = (B-A)/B% is the percentage reduction in linewidth
The mean (standard deviation) of the δ for FWHM is 42.1% (11.7%)
The mean (standard deviation) of the δ for FWTM is 36.9% (18.3%).
Table 2.
Spectral asymmetries in the 16 voxels shown in Fig. 1.
| Voxel | Before SPREAD | After SPREAD |
|---|---|---|
| Asymmetry | Asymmetry/ (δ%*) | |
| 1 | 0.7123 | 0.084/(88.21) |
| 2 | 0.7326 | 0.100/ (85.98) |
| 3 | 0.1876 | 0.030/ (84.01) |
| 4 | 0.4229 | 0.009/(84.01) |
| 5 | .3075 | 0.002/(99.35) |
| 6 | .2825 | 0.013/(95.40) |
| 7 | .3776 | 0.049/(87.02) |
| 8 | .4049 | 0.083/(79.50) |
| 9 | .3875 | 0.081/(79.10) |
| 10 | .3601 | 0.074/(79.45) |
| 11 | .3719 | 0.072/(80.64) |
| 12 | .3596 | 0.088/(75.53) |
| 13 | .2557 | 0.039/(84.75) |
| 14 | .2616 | 0.015/(94.27) |
| 15 | .2782 | 0.028/(89.94) |
| 16 | .1987 | 0.0016/(99.19) |
Asymmetry is defined in Equation 12; δ = (B-A)/B% is the percentage of asymmetry
The mean (standard deviation) of δ is 86.28% (7.14%).
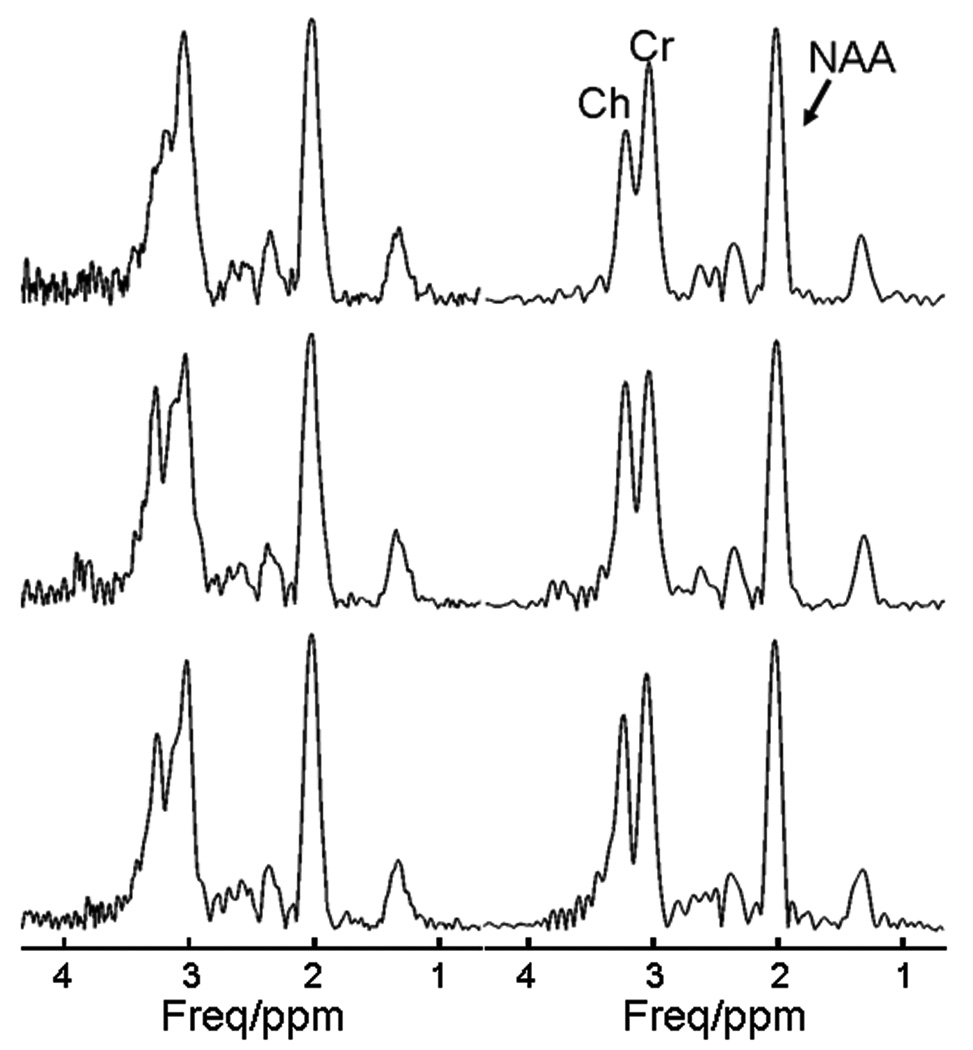
To demonstrate the effects of SPREAD, we assessed three phantom spectra from voxels in the regions with poor field homogeneity, in which the peaks of Cr (at 3.04 ppm) and Ch (at 3.24 ppm) severely overlapped and could not otherwise be resolved (Fig. 2). Following the application of SPREAD, these two peaks were clearly separated and could be resolved easily (Fig. 2).
Figure 2.
Examples of phantom spectra before and after SPREAD. Before SPREAD (left panel), the peaks of creatine (Cr) and choline (Ch) overlap to form a single peak with a distorted lineshape that cannot be resolved. Following SPREAD (right panel), linewidth narrowing and lineshape correction permit separation of the peaks. Because of severe lineshape distortion, the residue of water signal was not completely removed using a high-pass filter. The spectra are in magnitude mode.
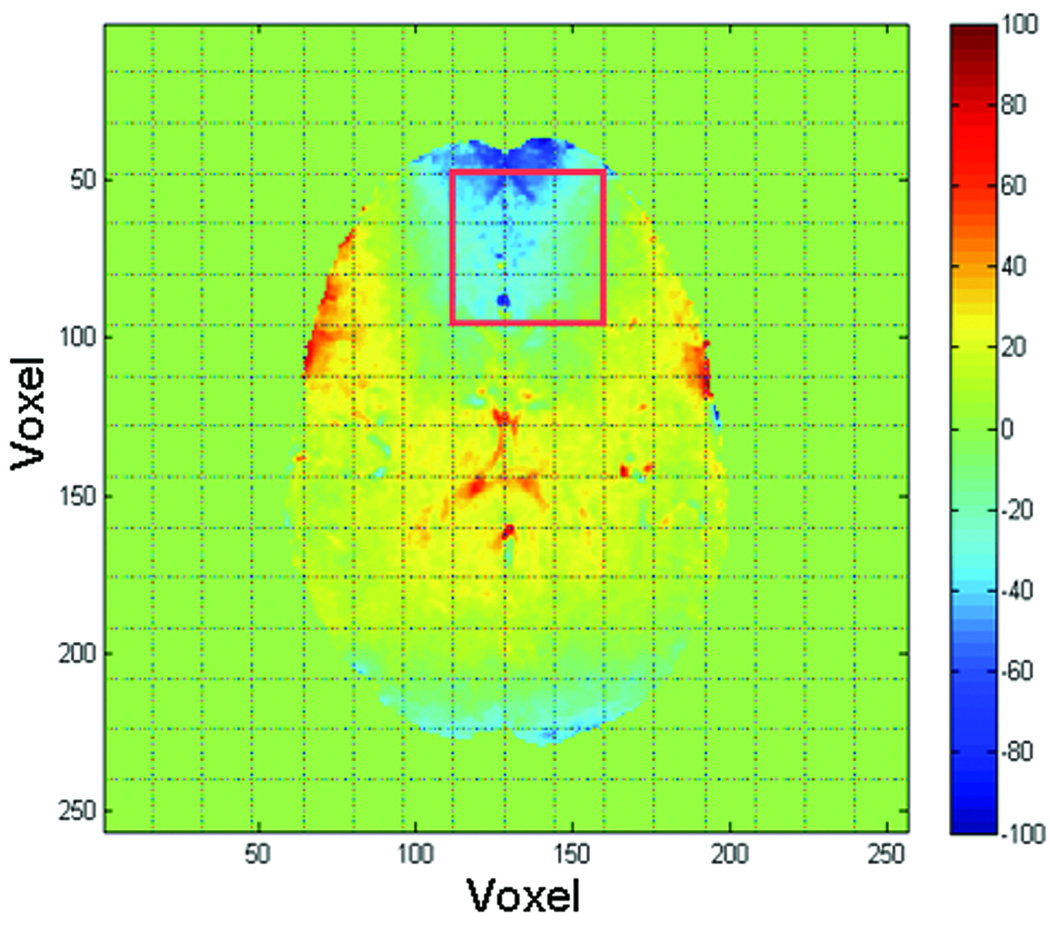
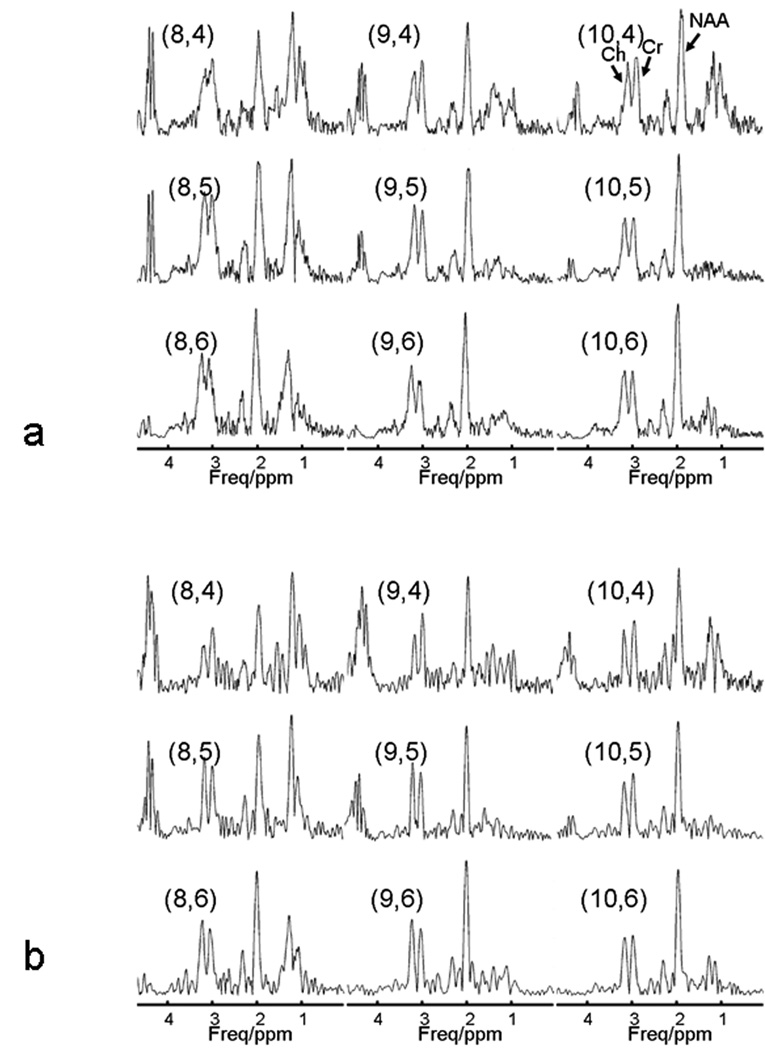
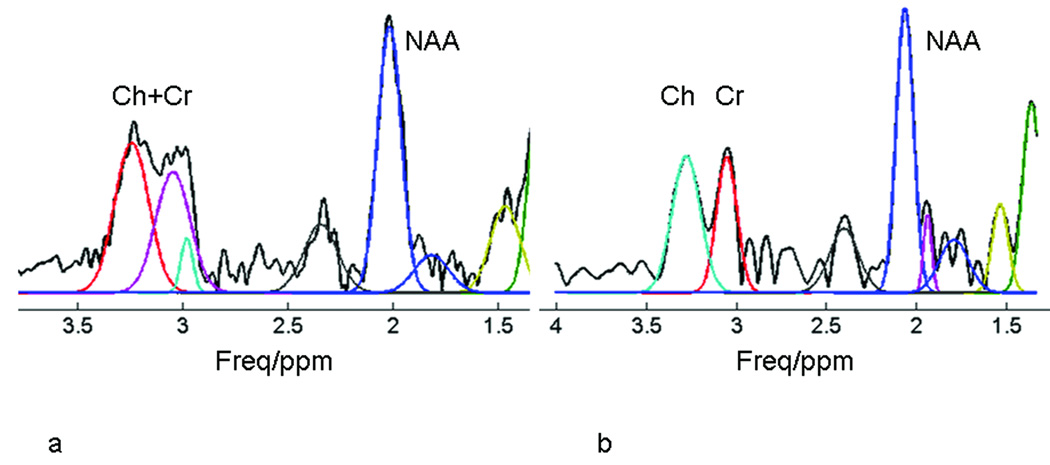
The magnetic field in the human brain is much more inhomogeneous than the field when using a spectroscopy phantom (Fig. 3). The metabolite spectrum exhibits severe spectral overlap, lineshape distortion, and linebroadening in regions close to the frontal sinuses (Fig. 4a). Consequently, the severe distortion of lineshape impairs resolution not only of the overlapping Cr and Ch peaks, but also accurate fitting of the singlet NAA peak (Fig. 5). Following deconvolution by SPREAD, the adjacent Cr and Ch peaks are well separated, lineshape distortion is corrected (Fig. 4b), and the spectrum can be more accurately fit (Fig. 5).
Figure 3.
An example of field mapping in the human brain. The magnetic field in the prefrontal region is highly inhomogeneous because of its proximity to the frontal sinuses. The red square inset indicates the matrix of voxels whose spectra are shown in Fig. 4.
Figure 4.
Application of SPREAD in vivo. (a) In vivo 1H MR spectra from the region shown in Fig. 3, with the pairs of numbers in parentheses indicating the indexes of the voxels. Peak assignments are shown in the upper right panel. The quality of some of the spectra is poor in terms of spectral resolution and lineshape. (b) Following the application of SPREAD, spectral resolution is enhanced and lineshape is improved.
Figure 5.
Automatic spectral fitting before and after SPREAD. Because of poor spectral resolution and distorted lineshape, the peaks of creatine (Cr) and choline (Ch) were not accurately or correctly detected (note the two peaks near 3.0 ppm in the left panel). The discrepancy of the measured and fitted peaks for N-acetylaspartate (NAA) caused by lineshape distortion is obvious. Following the application of SPREAD (right), the Cr and Ch peaks are well resolved and the measured and fitted peaks agree well compared with spectra before the application of SPREAD (left).
DISCUSSION
Our theoretical analysis and experimental findings show that SPREAD improves spectral resolution both by narrowing the linewidth and by correcting lineshape distortion. Unlike the strategy for improving spectral resolution that invokes acquiring MRSI data at higher magnetic field strengths, SPREAD effectively increases the separation between spectral peaks without increasing their absolute differences in frequency. Our preliminary findings show that SPREAD can increase spectral resolution by more than 30%. This improvement in spectral resolution is considerably greater than the improvement provided by increasing the magnetic field strength from 1.5T to 3T, as the increased linewidth at higher fields can almost entirely negate the increase in chemical shifts that the higher field strength provides (5–9). Another advantage of SPREAD over the measuring of MRSI data at higher field strengths is that SPREAD improves the lineshape of the spectrum (Fig. 4 & Fig. 5), yielding better agreement between the lineshape-corrected and model-based fitted spectra (Fig. 5). SPREAD also avoids the greater SAR (specific absorption rate), the more prominent chemical shift artifacts, and the increase in B1 inhomogeneity that accompanies scanning at higher field strengths (33).
Nevertheless, scanning at higher field strengths does provide either a moderate increase in SNR (albeit less than expected based on the theoretical linear relationship of field strength and SNR) or an increase in spatial resolution for a given SNR, which will in turn also improve spectral resolution. The use of multichannel coils can improve SNR further, and the higher SNR can be traded to improve spatial and spectral resolution (34). Of course SPREAD can also be used to improve the spectral resolution of MRSI data acquired at higher field strengths, just as it improves data acquired at lower field strengths.
For improving spectral resolution, SPREAD has several advantages over the long-standing technique that employs spectral deconvolution using measured spectroscopic water signal as a reference. (1) The lineshape of unsuppressed water signal depends not only on spatial variation of the magnetic field B0, but also on the distribution of water within the imaging volume. When multiple tissue types that have differing water content are present within a single MRS voxel, as is the case at the boundary of gray and white matter in the human brain, the lineshape of the water signal will differ from the lineshape distortion that is caused solely by local inhomogeneity of the static magnetic field (17). In this case, using water as a reference for deconvolution cannot remove linebroadening or lineshape distortion entirely. SPREAD, in contrast, can eliminate linebroadening and lineshape distortion caused solely by local field inhomogeneities because its lineshape functions are derived from field maps. (2) The T2 relaxation time of tissue water is shorter than that of most metabolites and, therefore, the signal from water decays in the time domain more rapidly than do signals from tissue metabolites. Consequently, noise amplification and spike artifacts can occur at both ends of the deconvolved signal, where the water signal can be smaller than the metabolite signals. Therefore, the gain in resolution when using water as the reference for deconvolution can come at the cost of reduced SNR. In contrast, the T2 relaxation time of the reconstructed lineshape signal is virtually infinite, and the lineshape signal decays slower than do any metabolite signals, subject only to the errors in field mapping caused by noise in the MR images. Therefore, noise amplification and spike artifacts can be smaller when using SPREAD than when using deconvolution with water signal as a reference (24). (3) Measurement of the internal water signal typically requires acquisition of a water MRSI dataset in addition to the metabolite data, thereby doubling total MRSI scan time, an often impractical requirement in most human imaging protocols. Although this increase in scan time can be avoided by using pulse sequences that interleave the acquisition of metabolite and water signals (35,36), these sequences are not yet widely available. In contrast, the time required to obtain field maps that SPREAD needs is only a small portion of the time required for an MRSI scan. (4) Measurement of the water signal is sensitive to inhomogeneities in the radiofrequency field, B1, whereas the use of SPREAD is not.
In addition to its use as a reference for deconvolution of lineshape, the measured spectroscopic signal from water can also be used to derive information about lineshape, and that information can be incorporated directly into spectral analyses to improve the quantification of metabolite concentrations (22). SPREAD, in contrast, can be regarded as a preprocessing step that enhances the resolution and lineshape of FFT-reconstructed MRSI spectra. These spectra can be analyzed further using other software, such as LCModel (37) or AMERES (38), or by home-built programs. In this regard, SPREAD is similar to the approach that incorporates the information of field inhomogeneity into the reconstruction of MRSI spectra using SLIM (19,20).
The performance of SPREAD in enhancing spectral resolution depends on accurate field mapping and, therefore, on the accurate reconstruction of the experimental lineshape. The field in the region of the water-air interface in our phantom experiment was not mapped accurately (Fig. 1) because field inhomogeneities produced a loss of signal in the MR images. In addition, errors in field mapping produced small spikes in the reconstructed lineshapes (Fig. 1). In general, however, acquiring field maps of higher spatial resolution or higher SNR will improve their accuracy, albeit at the expense of a longer scan time. We found that the experimental lineshape reconstructed from 10 2D field maps having 1 mm thickness was not superior to that reconstructed from five field maps of 2 mm thickness, with the constraint that scan time and in-plane resolution of each slice were identical. The comparability of the lineshapes of these datasets likely derived from the mitigating effects that the disadvantage of lower SNR had on the benefits of scanning at higher spatial resolution. A 3D MRI sequence is preferred for high-resolution field mapping, as it can generate MR images having higher SNR than in comparable 2D sequences.
Although deconvolution without Wiener filtering can theoretically recover spectra with their natural linewidths, its performance is vulnerable to the effects of noise and to the zero-crossing effects at the end of the time domain signal. Our findings show that Gaussian-Wiener filtering can improve the performance of the deconvolution in terms of suppressing spike artifacts and reducing noise amplification. If the first few points of the time domain signal are corrupted by the switching of the Analog-to-Digital Converter, a cosine window function can be applied to the signal to increase the robustness of SPREAD. Because signals at the ends of the echo are small, the cosine factor of the windowing function has little effect on the lineshape of the spectrum following deconvolution. As is true with other time-domain, deconvolution-based techniques (24), however, filtering reduces noise and spike artifacts at the expense of spectral resolution. Therefore, improvement in spectral resolution competes with the effects on SNR when using SPREAD.
Synchronization of the time domain signals (i.e., aligning the peaks of the echoes) prior to deconvolution is important to avoid distortion of phase and lineshape in the signal and reduction in spectral resolution. The position of the peak for each echo should be calculated from the timing of the pulse sequence and, if needed, it can be adjusted by measuring the echo of the water signal acquired in a single voxel MRS using the same pulse sequence and timing, but without phase encoding. Once its position is determined, the corresponding value of the peak can be used in forming the lineshape signals according to the field maps for all MRSI data acquired with the same timing parameters.
The distribution of metabolite concentration within the voxel V is not considered in Eq. [8], in which the lineshape function was derived under the assumption that the spin density is constant in V. This assumption is clearly not always true, especially in voxels consisting of multiple tissue types. In practice, therefore, the lineshape will be a function of both the field inhomogeneity and the concentrations of metabolites. However, the contribution of field inhomogeneity to the linewidth and lineshape is dominant, and the effects of spatial variation in the concentration of metabolites within the voxel are small. After deconvolution, therefore, the major contribution to the distortion in lineshape that is caused by field inhomogeneities will be corrected, and the final lineshape, rather than representing the ideal lineshape, will be concentration–weighted.
SPREAD has additional limitations. The effects of eddy currents on lineshape are not included in the model and therefore cannot be corrected (16,39). This may limit the application of SPREAD when using very short TEs, when eddy current effects are pronounced. This limitation, however, is of little concern when using modern scanners that are equipped with active shielding and that use the pre-emphasis technique to reduce eddy currents dramatically. Moreover, QUECC and other techniques can be used to correct for residual eddy current effects (30). Unlike measuring water signals as a reference for deconvolution, SPREAD requires phase unwrapping to reconstruct field maps, an additional post-processing task that is fast and trivial using modern techniques. The method is thus far implemented only for a standard quadrature coil, however. Finally, SPREAD should be improved to account for partial volume effects on lineshape reconstruction and to suppress noise and spike artifacts more optimally. Rigorous and comprehensive evaluations of the effects of SPREAD on noise and the accuracy of spectral fitting are needed, although these are beyond the scope of the present report.
In conclusion, we have described a technique that efficiently and effectively enhances the resolution and lineshapes of MRSI spectra. Its performance using both phantom and in vivo data was excellent. Although the examples used 1H MRSI data from the human brain acquired at 3T, we expect that the technique can be applied to MRSI data acquired at other field strengths and from other nuclei, such as 31P and 13C, and to MRSI data from other parts of the human body and from other species. As an example, we envision that a dual-tuned coil will be necessary when applying this method to nuclei (we denote X) other than 1H, thus the field mapping will be based on 1H MRI. Some fairly trivial modifications will be required, such as scaling the frequency deviations caused by field inhomogeneities by the factor γx/γh, where γx and γh are gyromagnetic ratios of X and 1H, respectively.
ACKNOWLEDGEMENT
The authors thank Dr. Feng Liu and Ms. Satie Shova for their help with data acquisition.
Contract grant sponsor: National Institute of Mental Health (NIMH); Contract grant numbers: MH068318, MH36197, and K02-74677;
Contract grant sponsor: National Institute on Drug Abuse; Contract grant number: DA017820.
REFERENCES
- 1.Macri MA, Garreffa G, Giove F, et al. In vivo quantitative 1H MRS of cerebellum and evaluation of quantitation reproducibility by simulation of different levels of noise and spectral resolution. Magn Reson Imaging. 2004;22(10):1385–1393. doi: 10.1016/j.mri.2004.10.021. [DOI] [PubMed] [Google Scholar]
- 2.Bartha R. Effect of signal-to-noise ratio and spectral linewidth on metabolite quantification at 4 T. NMR Biomed. 2007;20(5):512–521. doi: 10.1002/nbm.1122. [DOI] [PubMed] [Google Scholar]
- 3.Kreis R. Issues of spectral quality in clinical 1H-magnetic resonance spectroscopy and a gallery of artifacts. NMR Biomed. 2004;17(6):361–381. doi: 10.1002/nbm.891. [DOI] [PubMed] [Google Scholar]
- 4.Gruetter R. Automatic, localized in vivo adjustment of all first-and second-order shim coils. Magn Reson Med. 1993;29(6):804–811. doi: 10.1002/mrm.1910290613. [DOI] [PubMed] [Google Scholar]
- 5.Dydak U, Schar M. MR spectroscopy and spectroscopic imaging: comparing 3.0 T versus 1.5 T. Neuroimaging Clin N Am. 2006;16(2):269–283. doi: 10.1016/j.nic.2006.02.002. [DOI] [PubMed] [Google Scholar]
- 6.Bartha R, Drost DJ, Menon RS, Williamson PC. Comparison of the quantification precision of human short echo time (1)H spectroscopy at 1.5 and 4.0 Tesla. Magn Reson Med. 2000;44(2):185–192. doi: 10.1002/1522-2594(200008)44:2<185::aid-mrm4>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 7.Gonen O, Gruber S, Li BS, Mlynarik V, Moser E. Multivoxel 3D proton spectroscopy in the brain at 1.5 versus 3.0 T: signal-to-noise ratio and resolution comparison. AJNR Am J Neuroradiol. 2001;22(9):1727–1731. [PMC free article] [PubMed] [Google Scholar]
- 8.Barker PB, Hearshen DO, Boska MD. Single-voxel proton MRS of the human brain at 1.5T and 3.0T. Magn Reson Med. 2001;45(5):765–769. doi: 10.1002/mrm.1104. [DOI] [PubMed] [Google Scholar]
- 9.Kim JH, Chang KH, Na DG, et al. Comparison of 1.5T and 3T 1H MR spectroscopy for human brain tumors. Korean J Radiol. 2006;7(3):156–161. doi: 10.3348/kjr.2006.7.3.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dreher W, Leibfritz D. A new method for fast proton spectroscopic imaging: spectroscopic GRASE. Magn Reson Med. 2000;44(5):668–672. doi: 10.1002/1522-2594(200011)44:5<668::aid-mrm2>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 11.Ebel A, Dreher W, Leibfritz D. A fast variant of (1)H spectroscopic U-FLARE imaging using adjusted chemical shift phase encoding. J Magn Reson. 2000;142(2):241–253. doi: 10.1006/jmre.1999.1936. [DOI] [PubMed] [Google Scholar]
- 12.Ebel A, Maudsley AA. Improved spectral quality for 3D MR spectroscopic imaging using a high spatial resolution acquisition strategy. Magn Reson Imaging. 2003;21(2):113–120. doi: 10.1016/s0730-725x(02)00645-8. [DOI] [PubMed] [Google Scholar]
- 13.Kim DH, Margolis D, Xing L, Daniel B, Spielman D. In vivo prostate magnetic resonance spectroscopic imaging using two-dimensional J-resolved PRESS at 3 T. Magn Reson Med. 2005;53(5):1177–1182. doi: 10.1002/mrm.20452. [DOI] [PubMed] [Google Scholar]
- 14.Claridge TDW. High-resolution NMR techniques in organic chemistry. Oxford: Pergamon Press; 1999. p. 382. [Google Scholar]
- 15.Morris GA. Compensation of instrumental imperfections by deconvolution using a internal reference signal. J Magn Reson. 1988;80(3):547–552. [Google Scholar]
- 16.Klose U. In vivo proton spectroscopy in presence of eddy currents. Magn Reson Med. 1990;14(1):26–30. doi: 10.1002/mrm.1910140104. [DOI] [PubMed] [Google Scholar]
- 17.Soher BJ, Maudsley AA. Evaluation of variable line-shape models and prior information in automated 1H spectroscopic imaging analysis. Magn Reson Med. 2004;52(6):1246–1254. doi: 10.1002/mrm.20295. [DOI] [PubMed] [Google Scholar]
- 18.Hu X, Levin DN, Lauterbur PC, Spraggins T. SLIM: spectral localization by imaging. Magn Reson Med. 1988;8(3):314–322. doi: 10.1002/mrm.1910080308. [DOI] [PubMed] [Google Scholar]
- 19.Khalidov I, Van De Ville D, Jacob M, Lazeyras F, Unser M. BSLIM: spectral localization by imaging with explicit B0 field inhomogeneity compensation. IEEE Trans Med Imaging. 2007;26(7):990–1000. doi: 10.1109/TMI.2007.897385. [DOI] [PubMed] [Google Scholar]
- 20.Bashir A, Yablonskiy DA. Natural linewidth chemical shift imaging (NL-CSI) Magn Reson Med. 2006;56(1):7–18. doi: 10.1002/mrm.20917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Webb P, Spielman D, Macovski A. Inhomogeneity correction for in vivo spectroscopy by high-resolution water referencing. Magn Reson Med. 1992;23(1):1–11. doi: 10.1002/mrm.1910230102. [DOI] [PubMed] [Google Scholar]
- 22.Spielman D, Webb P, Macovski A. Water referencing for spectroscopic imaging. Magn Reson Med. 1989;12(1):38–49. doi: 10.1002/mrm.1910120105. [DOI] [PubMed] [Google Scholar]
- 23.Willcott MR, 3rd, Mee GL, Chesick JP. Magnetic field mapping in NMR imaging. Magn Reson Imaging. 1987;5(4):301–306. doi: 10.1016/0730-725x(87)90008-7. [DOI] [PubMed] [Google Scholar]
- 24.Metz KR, Lam MM, Webb AG. Reference deconvolution: a simple and effective method for resolution enhancement in nuclear magnetic resonance spectroscopy. Concept in Magnetic Resonance. 2000;12(1):21–42. [Google Scholar]
- 25.Duyn JH, Gillen J, Sobering G, van Zijl PC, Moonen CT. Multisection proton MR spectroscopic imaging of the brain. Radiology. 1993;188(1):277–282. doi: 10.1148/radiology.188.1.8511313. [DOI] [PubMed] [Google Scholar]
- 26.Haase A, Frahm J, Hanicke W, Matthaei D. 1H NMR chemical shift selective (CHESS) imaging. Phys Med Biol. 1985;30(4):341–344. doi: 10.1088/0031-9155/30/4/008. [DOI] [PubMed] [Google Scholar]
- 27.Saad N, Peled S. Easy 3D phase unwrapping; Miami. 13th Annual Meeting of ISMRM; 2005. p. 2251. [Google Scholar]
- 28.Meyer C, Irarrazabal P Board of Trustees of the Leland Stanford Junior University, assignee. Magnetic field inhomogeneity correction in MRI using estimated linear magnetic field map. 5617028. United States patent. 1997
- 29.Bhat H, Sajja BR, Narayana PA. Fast quantification of proton magnetic resonance spectroscopic imaging with artificial neural networks. J Magn Reson. 2006;183(1):110–122. doi: 10.1016/j.jmr.2006.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bartha R, Drost DJ, Menon RS, Williamson PC. Spectroscopic lineshape correction by QUECC: combined QUALITY deconvolution and eddy current correction. Magn Reson Med. 2000;44(4):641–645. doi: 10.1002/1522-2594(200010)44:4<641::aid-mrm19>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 31.Lin Y-Y, Hodgkinson P, Ernst M, Pines A. A novel detection-estimation scheme for noisy NMR signals: applications to delayed acquisition data. J Magn Reson. 1997;128:30–41. [PubMed] [Google Scholar]
- 32.Atkinson KA. An Introduction to Numerical Analysis. New York: John Wiley &Sons; 1989. [Google Scholar]
- 33.Marzola P, Osculati F, Sbarbati A. High field MRI in preclinical research. Eur J Radiol. 2003;48(2):165–170. doi: 10.1016/j.ejrad.2003.08.007. [DOI] [PubMed] [Google Scholar]
- 34.Xu D, Chen AP, Cunningham C, Osorio JA, Nelson SJ, Vigneron DB. Spectroscopic imaging of the brain with phased-array coils at 3.0 T. Magn Reson Imaging. 2006;24(1):69–74. doi: 10.1016/j.mri.2005.10.019. [DOI] [PubMed] [Google Scholar]
- 35.Thiel T, Czisch M, Elbel GK, Hennig J. Phase coherent averaging in magnetic resonance spectroscopy using interleaved navigator scans: compensation of motion artifacts and magnetic field instabilities. Magn Reson Med. 2002;47(6):1077–1082. doi: 10.1002/mrm.10174. [DOI] [PubMed] [Google Scholar]
- 36.Ebel A, Maudsley AA. Detection and correction of frequency instabilities for volumetric 1H echo-planar spectroscopic imaging. Magn Reson Med. 2005;53(2):465–469. doi: 10.1002/mrm.20367. [DOI] [PubMed] [Google Scholar]
- 37.Provencher SW. Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med. 1993;30(6):672–679. doi: 10.1002/mrm.1910300604. [DOI] [PubMed] [Google Scholar]
- 38.Vanhamme L, van den Boogaart A, Van Huffel S. Improved method for accurate and efficient quantification of MRS data with use of prior knowledge. J Magn Reson. 1997;129(1):35–43. doi: 10.1006/jmre.1997.1244. [DOI] [PubMed] [Google Scholar]
- 39.de Graaf AA, van Dijk JE, Bovee WM. QUALITY: quantification improvement by converting lineshapes to the Lorentzian type. Magn Reson Med. 1990;13(3):343–357. doi: 10.1002/mrm.1910130302. [DOI] [PubMed] [Google Scholar]