Dynamic Contrast Enhanced MRI Parameters Independent of Baseline T₁₀ Values

Abstract

A baseline T₁₀ value is typically needed for dynamic contrast-enhanced (DCE-) MRI studies. However, an assumed baseline T₁₀ has to be used when T₁₀ measurements for patients are not available. In this work, we systematically investigate the dependence on T₁₀ of the commonly used DCE-MRI parameters (K^trans, k_ep, v_e and IAUC) as well as several new-defined parameters (the normalized ratios of k_ep, K^trans and v_e, which are measures of relative changes in these parameters between two time points) for a spoiled gradient echo pulse sequence using simulations and in vivo studies. Effects of various factors on the T₁₀-dependence, such as the true T₁₀ value, flip angle and the potential changes in T₁₀ due to treatment were also assessed using simulations. We found that DCE-MRI parameters, k_ep and the normalized ratio of k_ep, are largely independent of T₁₀, especially when larger flip angles are used (e.g. 30–40°). Their estimations therefore do not require any knowledge of T₁₀. The normalized ratios of K^trans, v_e and IAUC also exhibit independence to T₁₀, but only when T₁₀ remains constant between pre- and post-treatment. The estimation of parameters themselves (K^trans, v_e and IAUC) are highly dependent on the T₁₀ value.

1. Introduction

Dynamic contrast-enhanced- (DCE-) MRI is a technique by which images are acquired during intravenous injection of a gadolinium contrast agent to assess the vascular characteristics of tissues. DCE-MRI is commonly used in cancer diagnosis, in which DCE-MRI-based measures correlate well with tumor angiogenesis [1–6]. DCE-MRI is also used to assess cancer drug efficacy by comparing findings from imaging acquired before and after therapy [7, 8]. DCE-MRI has also been applied in assessing cerebral [9] and cardiac [10] ischemia.

Although DCE-MRI is growing in importance in many clinical applications, repeatability is a major limiting factor preventing it from being used in wider applications and clinical trials [11–13]. One factor that drastically limits repeatability is the intrinsic baseline T₁₀. A T₁₀ is generally required for quantitative [14] and semi-quantitative analyses [15] to determine DCE-MRI kinetic parameters, and any error in T₁₀ measurement can be magnified in the resulting parameters.

There are several techniques available for assessing T₁₀. One accurate method is the inversion recovery (IR) technique, but IR methods for T₁₀ assessment often require long scan times, particularly when large volume coverage is desired [16]. A more efficient technique is the variable flip angle method, which uses a set of gradient recalled-echo images with different flip angles [17–19]. However, errors caused by radiofrequency field inhomogeneity or uncertainty can be significant when using this method [19]. Even though the actual flip angle could be measured to correct for field inhomogeneity to some extent [20], T₁₀ measurement is still problematic due to other factors, such as imperfect slice profile. In large clinical studies, T₁₀ measurements for some patients may also not be reliable or available due to either motion or other factors. An assumed T₁₀ value has to be used in DCE-MRI analyses when a measured T₁₀ is not available.

Given the difficulty of assessing the baseline T₁₀, Haacke et al. [13] recently presented a parameter, NR50, which is independent of T₁₀. NR50 represents the relative change in the median of the initial area under the signal-time curve (IAUC) for assessing drug effectiveness by comparing pre- and post-treatment findings. T₁₀ independence of NR50 assumes that T₁₀s are unchanged pre- and post-treatment. But this assumption may not be generally true when treatment is involved.

DCE-MRI kinetic parameters (K^trans, k_ep, v_e and IAUC) are commonly used in cancer diagnosis [14, 15, 21, 22]. The computation of K^trans, v_e and IAUC requires T₁₀ [14, 15]. The computation of k_ep, however, does not require T₁₀ when linearity between signal enhancement and concentration could be assumed using T₁-weighted spin-echo or saturation/inversion recovery approaches [23–27]. Currently, the spoiled gradient echo pulse sequence is widely used in DCE-MRI studies to achieve good temporal resolution and volumetric coverage. However, for a spoiled gradient echo pulse sequence the signal increase with concentration is nonlinear, and T₁₀ may be required to convert the signal to a concentration and compute k_ep [27].

In this paper, we have also defined several new characteristic parameters, the normalized ratios (NR) of K^trans, k_ep, v_e and IAUC, which are measures of the relative change in parameter values between two time points (pre- and post-treatment). We evaluate the assumed T₁₀ independence of these parameters, K^trans, k_ep, v_e, IAUC and its NRs for a gradient echo pulse sequence using simulations. T₁₀-independent properties of all the parameters and several potentially influencing factors are also investigated using simulations and in vivo human studies.

2. Methods

In DCE-MRI, the tracer concentration in the tissue, C_t, also called tissue enhancement curve (TEC), can be described by Tofts' model [28], one of the modified Kety models [29].

$$\begin{array}{c}\hfill C_t\left(t\right)={\upsilon }_p{C}_p\left(t\right)+K^{\mathit{trans}}{C}_p\left(t\right)\otimes e^{-\frac{K^{\mathit{trans}}t}{{\upsilon }_e}}\hfill \\ \hfill ={\upsilon }_p{C}_p\left(t\right)+K^{\mathit{trans}}{C}_p\left(t\right)\otimes e^{-k_{\mathit{ep}}t}\hfill \end{array}$$ (1)

where C_p is the tracer concentration in the blood plasma, v_p is the blood plasma volume, K^trans is the volume transfer constant between the blood plasma and tissue, v_e is the volume of the extravascular extracellular space per unit volume of tissue, k_ep = K^trans/v_e is the rate constant between extravascular extracellular space and blood plasma, and ⊗ represents a convolution. C_b = C_p·(1-Hct) is the tracer concentration in the blood, also called AIF (arterial input function). The hematocrit (Hct) is typically assumed to equal to 0.42 [30]. v_b = v_p/(1-Hct) is the whole blood volume and was assumed to be 0.05.

While absolute values of the above DCE-MRI kinetic parameters may be of some interest in cross-sectional studies, the relative change in these parameters subsequent to therapy may be an additional pertinent measure of treatment effects in serial studies. For this purpose, analogous to the definition of NR50 [13], which is the normalized ratio of IAUC, three new parameters, the normalized ratios (NR) of k_ep, K^trans, and v_e, were defined as the following:

$$\mathit{NR}=\frac{P^{\mathit{pre}}-P^{\mathit{post}}}{P^{\mathit{pre}}}$$ (2)

where P represents perfusion parameters (k_ep, K^trans, and v_e) and superscripts designate pre- and post-treatment values. For comparison purposes, the NR of IAUC-60 (the integration of TEC across 60 seconds) was also computed.

2.1 Simulation Studies

A series of simulations were performed to investigate how the parameters (k_ep, K^trans, v_e and IAUC) and the newly defined parameters (NRs of k_ep, K^trans, v_e and IAUC) depend on the baseline T₁₀ and which factors, among true T₁₀ values, flip angles, and T₁₀ changes caused by treatment affected this relationship when using standard gradient echo pulse sequences.

An AIF was generated according to the experimentally derived functional form [30], which is based on a population-averaged high-temporal-resolution AIF measurement:

$$C_b\left(t\right)=\frac{\alpha e^{-\beta t}}{1+e^{-s(t-\tau )}}+\sum _{n=1}^2\frac{A_n}{\sqrt{2\pi }}{e}^{-\frac{{(t-{\tau }_n)}^2}{2{\sigma }_n^2}}$$ (3)

where α is 1.05 mmol; β is 0.1685 min⁻¹; s is 38.078 min⁻¹; τ is 0.483 min; A₁ is 14.3694 mmol; A₂ is 2.5 mmol; τ₁ is 0.17046 min; τ₂ is 0.365 min; σ₁ is 0.0563 min; and σ₂ is 0.132 min [30]. TECs were generated according to Eq. (1) using various K^trans and v_e or k_ep values.

The tracer concentration in the tissue, C_t, was then generated using this AIF and given kinetic parameters (K^trans, v_e, and v_b) according to equation (1). The tracer concentration (C_t or C_b) is linearly proportional to the change in the relaxation rate (ΔR₁) [31, 32]. The change in the relaxation rate can be converted to the normalized signal intensity according to the spoiled gradient-echo signal equation (4).

$$S\left(t\right)=\frac{M_0\sin \theta (1-e^{-\mathit{TR}(R_{10}+\Delta R_1\left(t\right))})}{1-\cos \theta e^{-\mathit{TR}(R_{10}+\Delta R_1\left(t\right))}}$$ (4)

where R₁₀ = 1/T₁₀ is the baseline relaxation rate and M₀ is equilibrium magnetization. TR = 4 ms and θ = 15° were used in this conversion with a given true T₁₀ (= 800ms, unless otherwise noted). The normalized signal intensity curves were then converted back to tracer concentration curves using equation (4) with assumed T₁₀ values from 200 to 2000 ms. Kinetic parameters were subsequently computed using these tracer concentration curves according to equation (1).

In our simulation, T₁₀ independence of K^trans, k_ep, v_e and IAUC-60 was first investigated for the spoiled gradient echo pulse sequence, and the relationship between the RF flip angle θ and the nonlinearity of signal with the relaxation rate change (ΔR₁) was examined. Second, T₁₀ independence of NRs of K^trans, k_ep, v_e and IAUC-60 was identified. Finally, the effects of three key factors (true T₁₀ values, flip angles and T₁₀ changes caused by treatment (ΔT₁₀=T₁₀_pre-T₁₀_post)) on T₁₀ independence were investigated.

2.2 Human Studies

For in vivo studies, DCE-MRI data from six pediatric patients aged from 11 to 16 with osteosarcoma treated on a phase II trial of multi-agent chemotherapy acquired previously from 1999 to 2008 were utilized. Prior institutional review board approval and informed consent were obtained. DCE-MRI images were acquired on a 1.5 T Siemens Symphony scanner at presentation (before chemotherapy, week 0) and at week 12. After selection of the single slice that best showed the tumor, images were acquired before, during, and after bolus injection into a central line of a 0.1 mmol/kg dose of Gd-DTPA, followed by a saline flush. Thirty sequential FLASH images (TR[TE=23/10 ms, 40°flip angle, xres/yres = 256/256, 10 mm thickness, 40–50 cm FOV, 2 acquisitions) were collected over a 6.5 minute period. Tumor regions of interest (ROIs) for all patients were drawn by an experienced radiologist. A measured AIF was not available for these patients and AIF shown in Eq. (3) was used for the computation of K^trans and v_e.

The baseline T₁₀ was measured prior to the DCE-MRI scan using the optimized IR method [16]. A turbo inversion recovery (TIR) pulse sequence was used to acquire four images with different TIs, 100, 500, 900 and 2400 ms. The TIR protocol was as follows: single slice with 10 mm thickness; TR/TE = 2500/60 ms; xres/yres = 256/192; 40–50 cm FOV the same as DCE-MRI images; echo train length was 11; ~45 seconds for each acquisition. Occasionally, IR images were corrupted by large patient movements which caused the slice position to shift dramatically and T₁₀ could not be computed.

3. Results

3.1 Simulation Studies

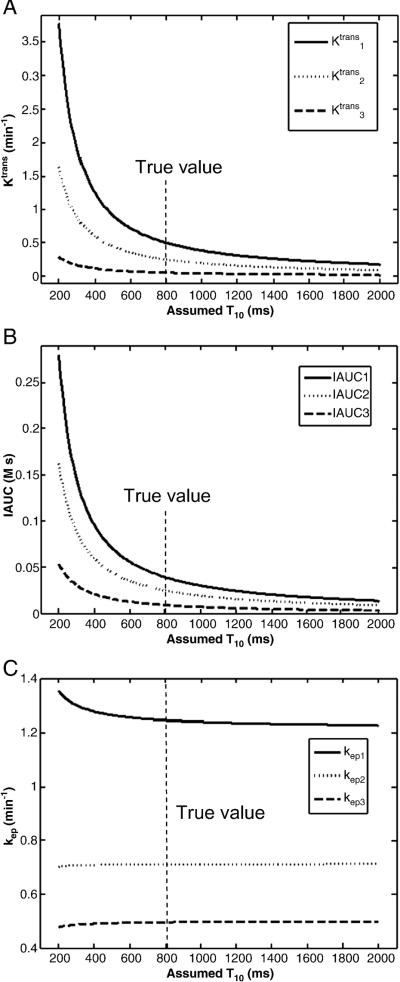
Figure 1 shows the simulation results of the baseline T₁₀ dependence of K^trans, k_ep and IAUC-60 for three different true values. K^trans and IAUC-60 shown in Fig. 1 (a, b) were highly dependent on the assumed T₁₀ value and they approach the true values only when the assumed T₁₀ was near the true T₁₀ (800 ms). However, k_ep was nearly independent of T₁₀ shown in Fig. 1c, and any assumed T₁₀ within a large range (500 to 2000 ms) can give accurate k_ep estimation. v_e, which is equal to K^trans/k_ep, had the same pattern of T₁₀ dependency as K^trans and was thus not shown here.

Fig. 1.

Plots of K^trans (a), IAUC (b) and k_ep (c) vs. assumed baseline T₁₀ when the true T₁₀=800 ms. The y-axis represents the computed K^trans (or IAUC or k_ep) values when an assumed T₁₀ (x-axis) is used. For each plot, the three curves represent results for three different true values as follows: True K^trans values are 0.5, 0.25 and 0.05 min⁻¹, respectively; true IAUC are 0.039, 0.025 and 0.009 M·s, respectively; and true k_ep values are 1.25, 0.7143 and 0.5 min⁻¹, respectively.

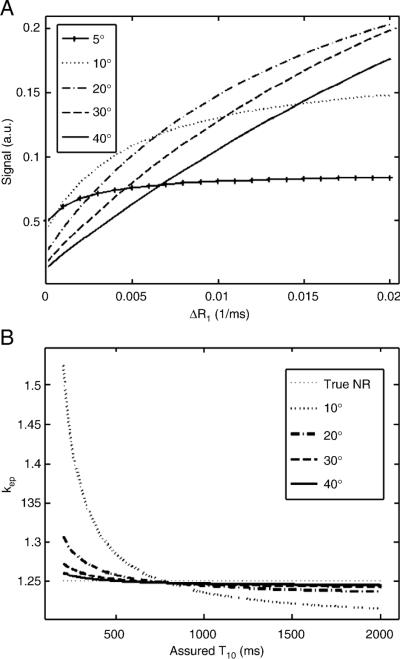
The nonlinear relationship between the signal and the change of the relaxivity rate (ΔR₁) (i.e. the concentration) for different flip angles using a spoiled gradient echo pulse sequence is shown in Fig. 2. The results in Fig. 2a show that there existed strong nonlinearity between the signal and ΔR₁ for small flip angles; however, the relationship became more linear as the flip angle increased. When the signal is linearly proportional to the concentration, k_ep is independent of T₁₀ [23, 25]. This was consistent with the results shown in Fig. 2b, in which k_ep appeared independent of the assumed T₁₀ at larger flip angles, e.g. 40°. But even with smaller flip angles, k_ep was nearly constant when the assumed T₁₀ was larger than 500 ms.

Fig. 2.

Nonlinearity changes as flip angle. (a) The relationship between the signal amplitude and ΔR₁ becomes more linear as flip angle becomes larger; (b) k_ep is less dependent on T₁₀ at larger flip angles. TR of 4 ms was assumed.

Fig. 3 shows that the normalized ratios (NRs) of k_ep, K^trans, v_e and IAUC were largely independent of the assumed T₁₀ when the true T₁₀s were assumed to be the same for pre- and post-treatment, i.e. the chemotherapy does not change T₁₀. Within a large range from about 500 to 2000 ms, any assumed T₁₀ can yield accurate parameter estimation when the true T₁₀ is 800 ms.

Fig. 3.

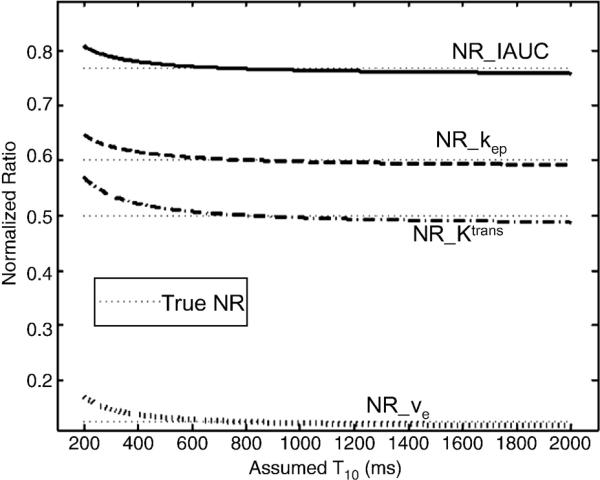
Plots of the normalized ratios of IAUC, k_ep, K^trans and v_e. True NRs are 0.77, 0.6, 0.5 and 0.125, respectively (dotted lines). The same true T₁₀ (800 ms) was assumed for both pre- and post-treatment.

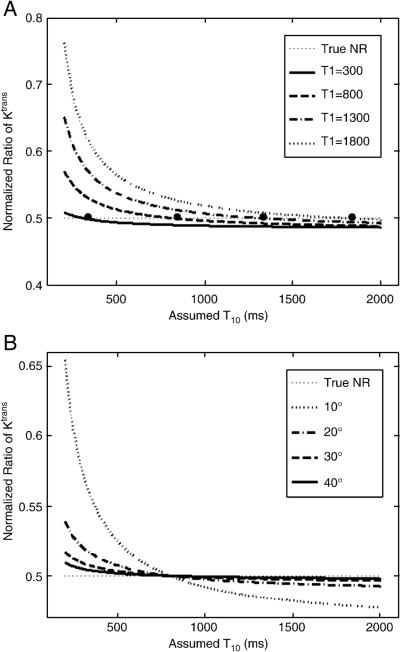
T₁₀ independence of the normalized ratios could vary with the true T₁₀. Fig. 4a shows the independence of the normalized ratio of K^trans for four different true T₁₀s (300, 800, 1300 and 1800 ms). NR with smaller true T₁₀ had better T₁₀ independence, while larger true T₁₀ values led to larger errors when low T₁₀ values were assumed. However, assuming a T₁₀ larger than the true T₁₀ (e.g. 1000–1500 ms) can give more accurate estimations. Another factor, the flip angle, will also affect T₁₀ independence of the normalized ratios. NRs of K^trans for four different flip angles are shown in Fig. 4b, where T₁₀ independence was higher for larger flip angles. The normalized ratios of k_ep, v_e and IAUC generally behave similarly as NR of K^trans, and therefore are not shown here.

Fig. 4.

Plots of the normalized ratios of K^trans for the different true T₁₀ values (a) and flip angles (b). The true NR of K^trans is 0.5. The same true T₁₀s were assumed for both pre- and post-treatment. The large dots are the true NRs for the different true T₁₀s. The normalized ratios of k_ep, v_e and IAUC also have similar relationships as the normalized ratio of K^trans and are not shown.

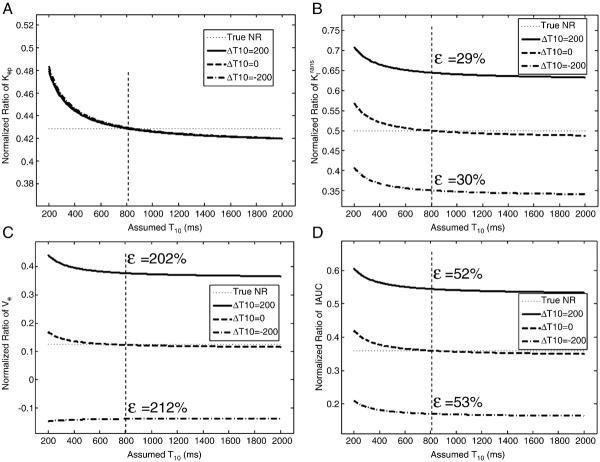
Baseline T₁₀s for pre- and post-treatment were often assumed to be the same when T₁₀ measurements were not available. However, this assumption may generally not be valid. Table 1 shows average T₁₀ values within whole tumor ROIs from the six osteosarcoma patients without motion. According to the table, chemotherapy treatment can lead to substantial changes in T₁₀, e.g. over 300 ms change between pre- and post-treatment in some cases. Effects of T₁₀ changes on the normalized ratios were investigated using simulations and the results are shown in Fig. 5. The normalized ratio of k_ep was insensitive to this T₁₀ change as shown in Fig. 5a. However, this T₁₀ change could cause much larger errors in the normalized ratios of K^trans, v_e and IAUC as shown in Fig. 5 (b–d). Figure 6 shows that the error in the NR of k_ep was almost constant while the errors of the three normalized ratios (K^trans, v_e and IAUC) changed significantly with the percentage change in T₁₀. These results indicate that unless it is known that T₁₀ does not change following treatment, the normalized ratios of K^trans, v_e and IAUC cannot be reliably utilized using an assumed value.

Table 1.

Averaged baseline T10 values for pre- and post-treatment from six Osteosarcoma patients.

Patient	T10_pre (ms)	T10_post (ms)	ΔT10 (ms)
1	1326	960	366
2	1359	1001	358
3	1300	1190	110
4	1154	1066	88
5	1434	1465	31
6	1157	1197	30

Fig. 5.

Effects of changes in baseline T₁₀ following treatment. Plots of the normalized ratios of k_ep (a), K^trans (b), v_e (c) and IAUC (d) with different pre- and post-treatment baseline T₁₀ values. True NRs are 0.0.429, 0.5, 0.125 and 0.36, respectively. A change in T₁₀ between pre- and post-treatment is calculated as ΔT₁₀=T₁₀_pre-T₁₀_post. A true T₁₀ = 800 ms was assumed for pre-treatment. ε represents the percentage error at assumed constant T₁₀ = 800 ms.

Fig. 6.

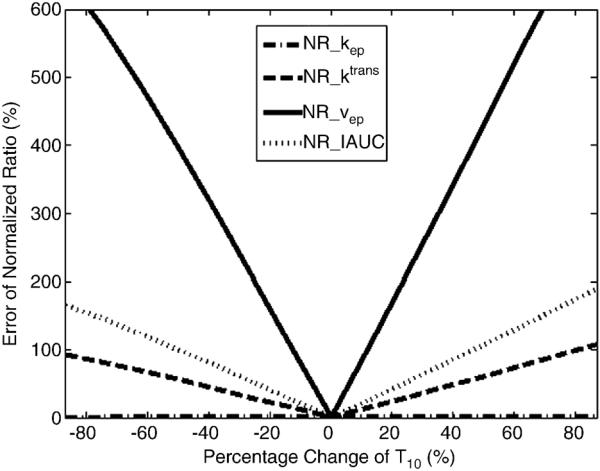
Plots of the error of normalized ratios vs. percentage change of T₁₀. The true T₁₀_pre is fixed to 800 ms. The percentage change of T₁₀ is equal to (T₁₀_pre-T₁₀_post)/T₁₀_pre.

3.2 Human Studies

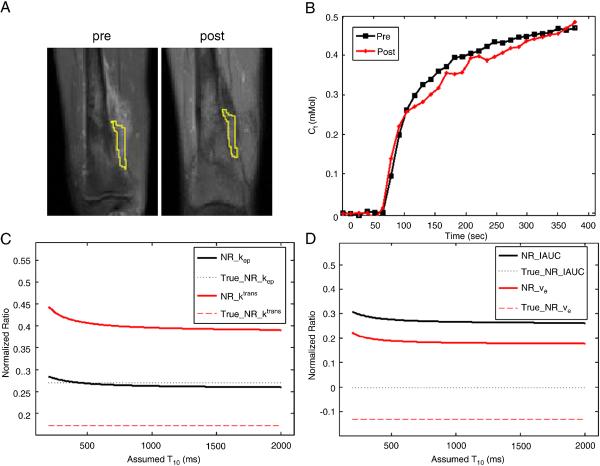
Results from one of the osteosarcoma patients without motion are demonstrated in Fig. 7. Fig. 7a shows the pre- and post-treatment post-contrast images near the knee with tumor ROIs outside the bone. Even though the shape of tumor outside the bone has slightly changed, two similar ROIs were selected in a relative homogeneous region. Average T₁₀ and kinetic parameters (k_ep, K^trans, v_e and IAUC) were computed for the two ROIs. Average T₁₀ values within the selected ROIs were 1512.6 and 1136.3 ms, respectively for pre- and post-treatment yielding ΔT₁₀ of 376.3 ms. Fig. 7b shows the average concentration curves for the ROIs, and Figs. 7c and 7d show the normalized ratios of k_ep, K^trans, v_e and IAUC. The solid lines represented the results assuming T₁₀s for pre- and post-treatment were the same; the dotted lines represented the results using actual measured baseline T₁₀s.

Fig. 7.

Results from one of the osteosarcoma patients. (a) Similar tumor ROIs on pre- and post-treatment images were used. (b) Mean concentration curves computed using measured baseline T₁₀ for both ROIs in (a). Plots of the normalized ratio of k_ep and K^trans (c) and of IAUC and v_e (d) with the same assumed T₁₀ for pre- and post-treatment in comparison with true NR using measured T₁₀.

4. Discussion

Baseline T₁₀ is necessary to obtain accurate lesion kinetic parameters in DCE-MRI studies. However, physiologic or voluntary motion can often cause large errors or even corrupt T₁₀ measurements, especially for 3D volume measurements. Errors in the flip angle and imperfect slice profiles can yield large uncertainties in T₁₀ measurements as well when using the variable flip angle (VFA) method. K^trans, k_ep, v_e and IAUC are commonly used in cross-sectional DCE-MRI studies [14, 15], and accurate T₁₀ values were required for the computation of these parameters. However, accurate k_ep could be estimated without T₁₀ measurements using assumed values, and its accuracy is improved when larger flip angles were utilized. On the other hand, SNR of pixel-wise k_ep calculations could be improved by forcing all measured T₁₀ values from the selected ROI to be equal to a fixed value close to that the actual measured T₁₀ value according to a recent study [13].

Normalized ratios of k_ep, K^trans, v_e and IAUC could be used to estimate the treatment effects of the chemotherapy in longitudinal DCE-MRI studies if the change of T₁₀ during therapy is negligible. While the normalized ratios were largely T₁₀-independent when T₁₀ values for pre- and post-treatment were assumed to be the same, any changes in T₁₀ due to treatment could generate large errors in normalized ratios of K^trans, v_e and IAUC. On the other hand, the normalized ratio of k_ep was almost completely independent of T₁₀ and its change between pre- and post-treatment.

The actual T₁₀ value and flip angle affected the T₁₀-independent property of normalized ratios of k_ep, K^trans, v_e and IAUC. While T₁₀-independence almost held for variations in actual T₁₀ values and flip angles, the computed normalized ratios could still be significantly different affected by different flip angles and assumed T₁₀s. Therefore, additional care must be taken to control for these factors. For example, a larger assumed T₁₀ than the possible true one (e.g. 1000ms for muscle) could be used to compute normalized ratios; and a larger flip angle could be used to keep a better T₁₀-independence to reduce the error for all normalized ratios.

When the relationship between Gd concentration (and thus ΔR₁) and signal is approximately linear, k_ep could be determined without any T₁₀ measurement using a spin echo pulse sequence according to Brix's model [23]. For a spoiled gradient echo pulse sequence, the relationship between ΔR₁ and signal is approximately linear for a large flip angle as shown in Fig. 2a, and k_ep became more T₁₀-independent as shown in Fig. 2b. This result was consistent with Brix's observation [23]. But even with small flip angles, the computed k_ep is still approximately constant when the assumed T₁₀ is larger than a certain T₁₀ value (e.g. 500ms for a true T₁₀ of 800 ms).

In conclusion, we have demonstrated with simulations and in vivo experiments that DCE-MRI parameters k_ep and the normalized ratio of k_ep are independent of the baseline T₁₀ for a gradient echo pulse sequence utilizing a large flip angle (e.g. 30°). Thus, these two parameters could be accurately computed using an assumed T₁₀ value in the absence of a T₁₀ measurement, even when T₁₀ changes following treatment. Normalized ratios of K^trans, v_e and IAUC are largely independent of T₁₀ only when there is no T₁₀ change between pre- and post-treatment caused by the chemotherapy. In contrast, the absolute values of K^trans, v_e and IAUC are highly dependent on the baseline T₁₀ value.