Sub-millimeter resolution 3D optical imaging of living tissue using laminar optical tomography

Abstract

In-vivo imaging of optical contrast in living tissues can allow measurement of functional parameters such as blood oxygenation and detection of targeted and active fluorescent contrast agents. However, optical imaging must overcome the effects of light scattering, which limit the penetration depth and can affect quantitation and sensitivity. This article focuses on a technique for high-resolution, high-speed depth-resolved optical imaging of superficial living tissues called laminar optical tomography (LOT), which is capable of imaging absorbing and fluorescent contrast in living tissues to depths of 2–3 mm with 100–200 micron resolution. An overview of the advantages and challenges of in-vivo optical imaging is followed by a review of currently available techniques for high-resolution optical imaging of tissues. LOT is then described, including a description of the imaging system design and discussion of data analysis and image reconstruction approaches. Examples of recent applications of LOT are then provided and compared to other existing technologies.

By measuring multiply-scattered light, Laminar Optical Tomography can probe beneath the surface of living tissues such as the skin and brain.

1. Introduction

Medical imaging modalities rely on in-vivo contrast that is specific to their particular form of imaging radiation. X-rays visualize bones because of the higher atomic numbers, and therefore higher x-ray attenuation, of the constituents of bones compared to soft tissue. Magnetic Resonance Imaging (MRI) is sensitive to the different electromagnetic environments experienced by hydrogen atoms in water molecules in different tissues. Both of these modalities can also utilize contrast agents to allow enhanced imaging of particular structures or parameters such as blood flow. X-ray imaging uses elements with higher atomic numbers than tissue, such as iodine or barium as contrast agents, and MRI most commonly uses highly paramagnetic gadolinium.

Optical imaging utilizes light to image the body, and so is sensitive to compounds and structures in tissue that provide optical contrast. Optical contrast mechanisms include absorption, fluorescence, luminescence and scattering [1]. Many substances present in the body have optical contrast, most notably the oxy- and deoxy-hemoglobin (HbO₂ and HbR) in blood is highly absorbing, as is melanin in skin. A wide range of intrinsic substances fluoresce, including collagen, elastin, keratin, tryptophan, nicotinamide adenine dinucleotide (NADH) and flavin adenine dinucleotide (FAD) [2]. Exogenous absorbing and fluorescent optical contrast agents, and transgenic methods for introducing optical contrast are also continually being developed [3–5]. Unlike in MRI and X-ray imaging, compounds with optical contrast are often small and biologically compatible, making them highly suited to in-vivo use. Substances with strong optical contrast can be manipulated and functionalized, allowing the development of targeted optical contrast agents with specific in-vivo behavior (such as the ability to adhere to a cancerous tumor). Intrinsic absorbers and fluorophores are also often linked to tissue physiology and metabolism (e.g. HbO₂ and HbR, and NADH and FAD). Optical imaging can therefore offer ‘functional contrast’ capable of measuring dynamic, real-time processes in the living body, for example changes in the oxygenation level of blood [1]. No other medical imaging modality can offer such a broad range of distinctive in-vivo contrast mechanisms. Both the growing toolkit of available exogenous contrast agents, and the wide range of intrinsic absorbers and fluorophores make optical imaging very attractive as an in-vivo imaging modality.

Scattering of light can also provide valuable contrast in living tissues, since the behavior of scattered light is a function of the size, density and shape of the particles causing the scattering [9–11]. However, scattering also represents the most significant obstacle for in-vivo optical imaging. Light interacts with so many constituents of tissue, that it is quickly attenuated. X-rays typically travel in straight lines through the body, so they provide crisp images and can be used to create detailed 3D images via computed tomography. However, optical imaging of living tissues must confront and overcome the problems of light scattering in order to access and exploit the rich range of absorption and fluorescence contrasts available. As a result, ‘in-vivo optical imaging’ as a field spans a wide range of different tools and approaches, each utilizing different methods to exploit, address or suppress the effects of scattering.

In microscopy, detected light has only been minimally scattered, leading to very high-resolution imaging but with only shallow penetration depths (a few hundred microns). This is not a problem for imaging thin tissue sections ex-vivo, but can be limiting for in-vivo imaging of intact tissues. At the other end of the scale is diffuse optical tomography (DOT), a technique similar to x-ray computed tomography, which utilizes light to image large tissue volumes such as the breast or brain [12]. DOT must rely on a model of light scattering within the tissue to compensate for the statistically uncertain paths of photons as they have traveled through the tissue. This uncertainty manifests as blurring in the reconstructed images, such that resolutions between 5–10 mm are typical. DOT most often uses near infra-red wavelengths of light, since tissue is significantly less absorbing and scattering in this range compared to visible wavelengths (see Fig. 1). However, this also limits the ability of DOT to detect many of the body's intrinsic fluorophores, as well as exogenous contrast agents whose absorption and emission spectra are generally at lower wavelengths [2].

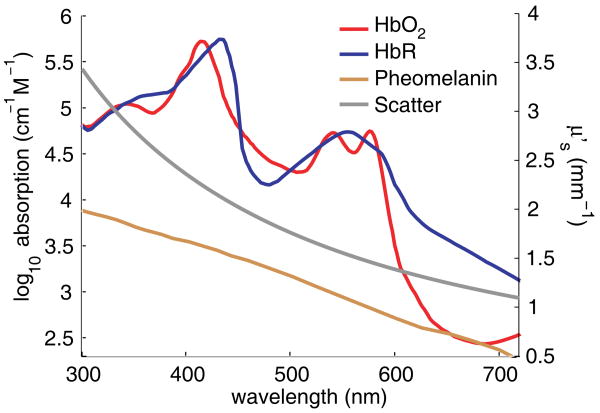
Figure 1.

(online color at: www.lpr-journal.org) Optical contrast in living tissue. The three major absorbers of light in tissue are oxy- and deoxy-hemoglobin (HbO₂ and HbR) and melanin (shown on log scale, from [6] and [7]). Reduced scattering coefficient (linear right-hand axis) is estimated as ${\mu }_s^{\prime }=A{\lambda }^{-b}$ where A = 1.14 × 10⁻⁸ and b = 1.3 for tissue [8].

In-between these two extremes lies a wide range of ‘mesoscopic’ optical imaging techniques seeking to harness the value of optical contrast while accommodating the effects of scattering and maximizing resolution and penetration depth. In general, mesoscopic imaging is limited to applications where tissues of interest are superficial; such as the skin, eye and oral mucosa. However, mesoscopic optical imaging of internal organs can sometimes be achieved via endoscopic, intraluminal or intrasurgical imaging configurations.

Several technologies for mesoscopic imaging have been developed in recent years. This article focuses on Laminar optical tomography (LOT), a non-contact laser-scanning imaging technique which harnesses scattered light to probe both absorbing and fluorescent contrast in living tissues, to depths of several millimeters [13–15]. We begin with a review of other existing mesoscopic imaging technologies including laser scanning microscopy, camera-based imaging, optical coherence tomography and photoacoustic tomography. We then describe the basic principles of LOT, its system design, considerations for data analysis and interpretation, and then review examples of its current and prospective applications.

2. Overview of mesoscopic imaging approaches

Mesoscopic imaging approaches can be separated into two distinct categories. One subset aims to reject light that has been scattered, the other incorporates or even exploits the effects of scattering. In the former category are laser scanning microscopy (including confocal and two-photon microscopy), and optical coherence tomography. Camera-based imaging and LOT photo-acoustic imaging fall into the second category. The mechanisms of each of these techniques are illustrated in Fig. 2.

Figure 2.

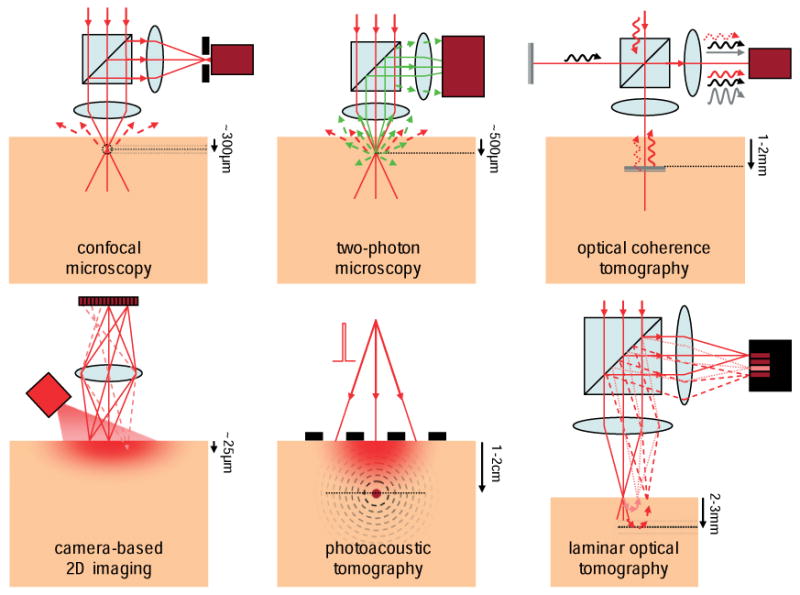
(online color at: www.lpr-journal.org) Mesoscopic Optical Imaging techniques. Confocal microscopy isolates reflected or fluorescent light from the focus of a scanning laser beam using a pinhole (black) in front of a detector (dark red). Two-photon microscopy exploits non-linear excitation of fluorescence at only the focus of a pulsed near infra-red laser beam. Optical coherence tomography compares the phase of a reference beam (black) to reflected light (red) to isolate signal reflecting from specific depths. Camera-based 2D imaging is sensitive only to superficial layers and contains insufficient information to create images of deeper tissues. Photoacoustic tomography uses a pulse of laser light to generate thermo-elastic waves from absorbers, which can be detected using ultrasound transducers (black). Laminar optical tomography measures light that has scattered to different depths within the tissue.

In general, those approaches that seek to reject scattered light lack sensitivity to the absorption properties of tissue. This is because the effect of absorption on the intensity of light is exponential with the distance that the light has traveled through the absorber, as given by the Beer-Lambert law:

$$I=I_0{e}^{-{\mu }_{a}x}$$ (1)

where I₀ is the intensity of the incident light, I is the intensity of the detected light, μ_a is the absorption coefficient of the absorber (units of mm⁻¹), and x is the pathlength of light through the absorber. By limiting the amount of scattered light that is detected, such mesoscopic imaging techniques isolate only photons that have traveled straight into, and straight out of the tissue without scattering, and which therefore have the shortest pathlengths and have been influenced the least by tissue absorption.

Confocal microscopy reduces the amount of scattered light detected by isolating signal from the focus of a scanning laser beam. As the focused beam is scanned around in tissue, the signal detected from its focus is used to build up a high-resolution (<1 micron) image of the tissue [16, 17]. If fluorescence contrast is present, and a suitable filter is used to isolate light at the fluorophore's emission wavelength, confocal microscopy contrast will be a function of the concentration of the fluorophore within each image voxel. If ‘reflectance’ confocal is being performed, where the intensity of light emerging at the incident wavelength is measured, image contrast is governed predominantly by back-scattering (e.g. refractive index mismatches in the tissue that cause almost direct reflection of the light). The focus of visible light in tissue cannot be maintained to depths of more that around 300 microns, whereupon the likelihood of scattering events occurring becomes too great. So while a high-resolution 3D image can be obtained by scanning the depth-position of the beam's focus, confocal images become blurred once the focus of the beam is positioned too deeply.

Two-photon microscopy works in a similar way to confocal microscopy, but uses longer-wavelength pulsed laser light capable of inducing a non-linear fluorescence excitation at only the very focus of the laser beam [18]. For example, 800 nm light with sufficient flux can excite a fluorophore that would otherwise excite at around 400 nm (because two photons are absorbed at virtually the same instant). The fluorophore then emits at its usual emission wavelength (e.g. 500 nm). As the two-photon laser beam is scanned in 3D within tissue, all of the 500 nm light emerging from the tissue must be originating from the very focus of the beam (where the flux is high-enough to cause two-photon excitation). Longer wavelength light can travel more deeply into tissue because it does not scatter or absorb as much as visible light, so a tighter focus can be maintained to deeper depths. Two-photon microscopy can therefore image more deeply into tissue (500-600 microns), with higher resolution (<1 micron) than confocal microscopy. Also, it does not matter that emitted light scatters on the way out of the tissue, if its position of origin is known. This means that unlike confocal microscopy, two-photon microscopy does not need light to be de-scanned, nor does it require the use of a pinhole. Two-photon typically can only image fluorescence contrast.

Optical coherence tomography exploits the interference properties of light to reject light that has been multiply scattered [19]. In its simplest form, an interferometer-based detection system isolates light that constructively interferes with a reference beam that has been bounced off a mirror whose position can be modulated. As the mirror's position moves further away, only the light emerging from deeper tissues at an equivalent distance from the interferometer will have the same phase and will constructively interfere. Light that has scattered from shallower or deeper regions will be out of phase with respect to the reference beam. By moving the mirror back and forth, and the illuminating beam from side to side, it is possible to build up a 3D image of the tissue. This method is much more effective at rejecting scattered light than confocal microscopy, and OCT imaging can reach depths of 1–2 mm in living tissue with 1–10 micron resolution [20]. However, just as with reflectance-mode confocal microscopy, the rejection of scattered light means that only light with the shortest pathlengths is isolated. This means that OCT's main contrast mechanism is back-scattering or back-reflection from interfaces within the tissue, rather than absorption. Furthermore, the reliance of OCT on the coherence of the detected light means that it is unsuitable for fluorescence imaging.

Mesoscopic imaging techniques that do not seek to reject scattered light share the common feature that they are much more sensitive to the absorption properties of tissue. This is very important for looking at hemoglobin concentration and oxygenation properties, and makes them very attractive for in-vivo functional imaging applications.

2D camera-based imaging of tissue uses just a simple light source to illuminate the tissue surface, and a lens creates a focused image of the surface onto the camera's sensor. While the plane of the tissue that is at the focal point of this lens will be clearest, signal from deeper tissues will also be detected. This out-of-plane signal will not be in focus, but it will add to the overall image, causing the recorded signal in each pixel to be a superficially weighted sum of signals from shallower and deeper layers. Even light from positions adjacent to the detection point can be detected within a pixel, since light can enter the surface of the tissue and scatter laterally before emerging and being detected [14]. It is possible to slightly vary the depth of the lens's focus to bring deeper tissue into focus, but this is ineffective beyond a few tens of microns whereupon the whole image will become blurred. This is because light entering and leaving the tissue becomes more and more likely to have encountered a scattering event on its path to and from the focal plane, such that it will arrive at the wrong position on the imaging sensor.

However, since the light detected consists of all of the light that has back-scattered within the tissue, some of it has traveled a long pathlength and so contains rich information about the absorption properties of the tissue (weighted most strongly towards the more superficial tissue) [1]. The limitations of quantitation for camera-based imaging stem from the contributions of scattered and out-of-plane light to the detected signal, such that the Beer-Lambert law (Eq. (1)) cannot be used directly since the pathlength x of light is an unknown distribution. These effects can be overcome to a certain extent by using a mathematical model of light transport to estimate the mean pathlength of the detected light. Monte Carlo models based on estimates of the tissue's background absorption and scattering properties are most commonly used [21, 22]. The calculated pathlength values are then incorporated into the Modified Beer Lambert law to calculate μ_a for each wavelength of light using:

$$I=I_0{e}^{-{\mu }_a\text{DPF}x+G}$$ (2)

where DPFx is the simulated mean pathlength of light, and G is a geometry-dependent factor which accounts for the fact that only a fraction of the scattered light is usually detected. The resulting values of μ_a can then be converted into estimates of the concentrations of a mixture of n absorbers using Beer's law,

$${\mu }_a(\lambda )=\sum _n{\xi }_n(\lambda )c_n$$ (3)

where ξ(λ) is the specific absorption coefficient of the absorber in the mixture (e.g. measured previously in a pure sample), and c is the absorber's concentration. Given the number of unknowns in Eq. (2), it is common to calculate changes in concentration from one time to another (or referenced to a standard or other region of tissue) yielding:

$$\begin{array}{c}\text{In}\left(\frac{I\left(t,\lambda \right)}{I\left(t_0,\lambda \right)}\right)=\left({\mu }_a\left(t_0,\lambda \right)-{\mu }_a\left(t,\lambda \right)\right)\text{DPF}x(\lambda ),\\ \Delta {\mu }_a=\frac{\Delta \text{In}\left(I\right)}{\text{DPF}x}.\end{array}$$ (4)

So for the case of measurements at two or more wavelengths where oxy- and deoxy-hemoglobin are the dominant absorbers, measurements can be converted into concentrations by solving:

$$\left(\begin{array}{c}\Delta {\mu }_a{\lambda }_1\\ \Delta {\mu }_a{\lambda }_2\\ ⋮\\ \Delta {\mu }_a{\lambda }_n\end{array}\right)=\left(\begin{array}{c}{\xi }_{{\text{HbO}}_2,{\lambda }_1}\\ {\xi }_{{\text{HbO}}_2,{\lambda }_2}\\ ⋮\\ {\xi }_{{\text{HbO}}_2,\lambda n}\end{array}\begin{array}{c}{\xi }_{\text{HbR},{\lambda }_1}\\ {\xi }_{\text{HbR},{\lambda }_2}\\ ⋮\\ {\xi }_{\text{HbR},\lambda n}\end{array}\right)\left(\begin{array}{c}\Delta c_{\text{HbO}}\\ \Delta c_{\text{HbR}}\end{array}\right).$$ (5)

It should be noted that the pathlength of light in scattering tissue is wavelength-dependent, and that DPFx does not cancel when looking at changes in absorption (or concentration) [23]. Also, while such calculations can allow improved estimates, they cannot account for tissue heterogeneity, and the differing penetration depths of light of different wavelengths. These methods also cannot explicitly produce 3-dimensional images of the tissue [1].

Tissue fluorescence can also be evaluated using camera imaging, by illuminating with one wavelength of light, and detecting the light emerging at a longer wavelength [24]. Similar problems as for absorption imaging are faced if quantitative values of fluorophore concentration are to be derived from simple 2D camera images.

Photoacoustic tomography (PAT) is a hybrid optical/acoustic mesoscopic imaging technique. To acquire PAT data, a pulsed laser such as an optical parametric oscillator (OPO) is used to create pulses of light that enter tissue and get absorbed by strong absorbers (such as blood vessels). When the pulse of light is absorbed, it causes the absorbers to momentarily expand, creating an elastic wave which radiates through the tissue outwards from the site of the absorber. This wave is similar to ultrasound radiation, so its passage through tissue is linear and unaffected by optical scattering. The wave can be detected using ultrasound transducers on the tissue's surface, and an image can be reconstructed using hybrid optical/ultrasound inversion techniques [25, 26]. As long as sufficient incident light can reach absorbers within the tissue (and is not irregularly attenuated by other structures) PAT can produce images with resolution equivalent to ultrasound, but with sensitivity to optical absorption (and therefore hemoglobin concentration and oxygenation) [27]. The penetration of PAT can exceed a few centimeters into tissue (limited by optical attenuation), and resolution can reach 20-50 microns [28, 29]. However, PAT is limited because it is primarily sensitive to the absorption contrast of the tissue. While fluorescent probes could be used, only their absorption properties would be measured, and these would need to be separated from the effects of strong background absorbers such as hemoglobin. PAT also requires acoustic matching between the tissue and the acoustic sensor and can be limited by the slow repetition rates of the OPO lasers that are currently available.

Laminar optical tomography overcomes many of the difficulties faced by the preceding mesoscopic imaging techniques; being a non-contact device which is sensitive to both absorption and fluorescence contrast, while also being able to image beyond the scattering limits of tissue to depths of several millimeters. While the resolution of LOT cannot rival mesoscopic imaging techniques that reject scattered light, its benefits are significant for a range of applications. The basic principles of LOT imaging are described below.

3. Basic principles of Laminar Optical Tomography

LOT uses laser-scanning instrumentation similar to a confocal microscope. However, LOT achieves sensitivity to both absorption and fluorescence by selectively measuring the scattered light emerging from the tissue at different distances (between 0 to 3 mm) from the laser beam's focus [13]. Whereas camera-based imaging suffers from the overlapping contributions of light from different regions of the tissue, LOT serially injects light, and detects emerging light at multiple discrete positions on the tissue's surface. The wider the distance between the ‘source’ position and the ‘detector’ position, the deeper on average the detected light has traveled. This results in a dataset which contains rich information about the depth-resolved properties of the tissue. Because the detected light has scattered within the tissue, its pathlength is much longer than the light detected in confocal microscopy and OCT, and therefore is sensitive to absorption changes. LOT can also readily measure fluorescence.

In order to interpret the measured LOT data, it is necessary to employ mathematical models of light propagation to determine the likely paths that the light has taken through the tissue [30]. This model relies on an estimate of the background scattering and absorbing properties of the tissue. However, if the model is sufficiently accurate, it can be used to reconstruct 3D images of the depth-resolved absorption and fluorescence contrast within the tissue [13–15]. The resolution of these images will degrade as a function of depth, reflecting the fact that the path of photons becomes more uncertain as they scatter further (and deeper). However, since scattered light is not being rejected, there is no explicit ‘scattering limit’ as encountered in confocal microscopy, so imaging of even deeper tissues can feasibly be achieved if wider source-detector separations are used, and lower image resolution is acceptable. In the limit of wider source-detector separations, the physical measurements that LOT acquires are equivalent to reflectance-geometry diffuse optical tomography [12, 31]. The significant difference however is that, with narrower source-detector separations, the light detected by LOT has been scattered and attenuated less, and as such can yield higher resolution images with better signal to noise. In addition, LOT instrumentation is very different to DOT, which typically uses optical fibers positioned in a grid pattern on the tissue's surface [31–33]. LOT uses non-contact laser-scanning, allowing rapid frame-rate, multi-spectral imaging with a highly adaptable field of view and measurement density. The basic design of LOT instrumentation is described below.

4. LOT instrumentation

The design of an LOT system was first described in 2004 [13]. The original system used a single wavelength of light, and measured only absorption contrast. Since then, many improvements to this design have been made, to incorporate three simultaneously acquired wavelengths of laser light, both fluorescence and absorption detection, and very high frame-rate imaging. The general layout of an LOT system is shown in Fig. 3.

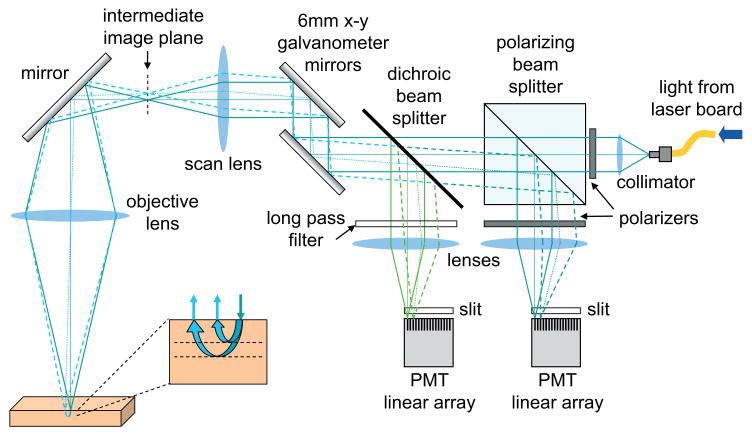
Figure 3.

(online color at: www.lpr-journal.org) Design of a Laminar Optical Tomography system. Linear photomultiplier tube (PMT) arrays detect fluorescence or reflectance light emerging from the tissue. The incident light is scanned using galvanometer mirrors, which also de-scan the returning light. The different detector elements on the PMT arrays detect light emerging from different distances away from the scanning spot. The wider these distances, the deeper, on average, the light has traveled into the tissue.

The incident light is shown as solid lines, and originates from a polarization maintaining fiber into which three lasers are combined and focused. This incident light passes through a polarizing beam splitter, a dichroic mirror, and off two galvanometer mirrors. These mirrors are electronically controlled to raster scan the beam in x and y directions, and in our configuration they modulate the angle of the incoming collimated laser beam. This beam then passes through a scan lens, which converts this angular deviation into a lateral translation of the scanning spot. The raster scanning spot at the intermediate image plane of the scan lens can then be imaged onto the tissue surface using an objective lens arrangement. On scattering tissue, this spot will appear to have a bright center, with a glow of light around it corresponding to the light that has entered and scattered deeper and more laterally within the tissue before emerging.

Light originating from the very center of the spot on the tissue will travel back through the optical system in exactly the same way as the incident light. However, on its way back, any fluorescent light (of a wavelength other than the incident light) will reflect at 90° from the dichroic mirror. This light will be focused by the ‘fluorescence channel’ lens and will form a focused spot in the detector plane. The polarizing beam splitter will also reflect a significant fraction of the returning light of the same wavelength as the incident light, making a similar focal point on the ‘absorption arm’ detector plane. In a confocal microscope, these detection arms would include a pinhole at the detector plane, and a single detector. As the galvanometer mirrors deflect the incident light, causing it to pan back and forth over the tissue, the returning light will always trace the same path back through the system, being de-scanned by the galvanometer mirrors such that the focus of the scanning spot will always be imaged back to the center of the detection plane (where the confocal pinhole would normally be). In essence, the direction change that the galvanometers cause in the forward direction is undone when the light reflects off them on the return path.

However, LOT does not contain a pinhole in the detector plane, instead it contains a linear array of detectors that allow it to selectively detect scattered light that has emerged from the tissue at different distances from the beam's focus. This is shown by the dotted lines in Fig. 3 which follow the path of light emerging from the tissue at a position laterally displaced from the focus of the incident beam. This light also travels back through the system and is de-scanned by the galvanometer mirrors. As this light reflects off the dichroic mirror (for fluorescence) or the polarizing beam splitter (for absorption), it focuses to a point adjacent to the focal point of light from the very center of the scanning beam. Essentially, the system creates an image of the scanning spot at the detection plane, consisting of both the spot's bright center and its more diffuse surround. As with the confocal light, no matter where the galvanometers scan the focused beam, the light emerging from the tissue at some distance away from the spot's focus will be imaged onto a detector that is similarly displaced from the center of the scanning spot in the detector plane. It is this scattered surround of light that provides information about the deeper layers of the tissue. Each detector in the linear array therefore separates light emerging at specific distances from the focus. The depth-resolved spatial sensitivity of these measurements can be simulated using Monte Carlo modeling as described later and as shown in Fig. 4.

Figure 4.

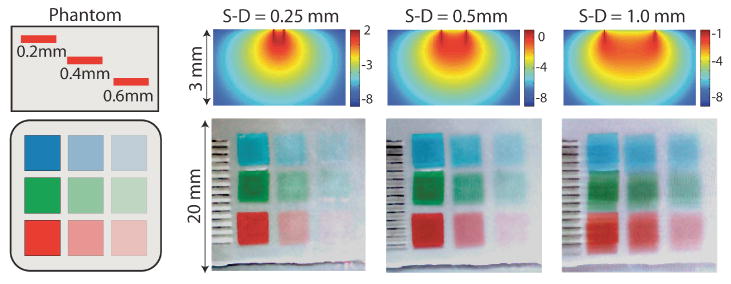
(online color at: www.lpr-journal.org) LOT Raw data and sensitivity functions. (top) Simulated sensitivity functions for LOT showing the log(sensitivity) of a change in measurement ΔM to a change in absorption Δμ_a for three source-detector separations. Images below show raw LOT data acquired using the same source-detector separations on a multicolor, multilayered phantom. All three colors were acquired simultaneously and data is shown as a red-green-blue merged bitmap. For the narrowest source-detector separation, the most superficial absorbing regions have the darkest contrast, and the deepest absorbers can barely be seen. For the wider separation, the deeper absorbers have more contrast. Lines to the left are millimeter ruler makings. Note also the shadow on these lines and the objects for the wider source-detector separations. The phantom was composed of colored acetate squares embedded in a homogenous background medium consisting of agarose, intralipid, and bovine hemoglobin. The optical properties of the background medium were: μ_a = 0.2 mm⁻¹ and ${\mu }_s^{\prime }=1{\text{mm}}^{-1}$ at 532 nm, while the red, green and blue squares had μ_a values of 5.3, 1.2, and 0.9 mm⁻¹ at 532 nm, respectively. Figure modified from [37]

Besides the linear-array detectors, there are several other special features of LOT instrumentation that are not common to other laser scanning modalities such as confocal microscopy. The most important feature is that the distances between the optical elements to the proximal (right) side of the galvanometers (as shown in Fig. 3) must be carefully optimized. This is because the scattered light in the system travels at angles on its return path, unlike the confocal light which always remains along the axis of the optical path. As a result, if there is excessive distance between the optical elements, or they are too small in size, this valuable scattered light will be apertured and will not reach the detector. It is also very important to carefully align the system, particularly to ensure that the distance between the scan lens and the galvanometer is equal to the focal length of the scan lens. This ensures that the maximum amount of scattered light is captured by the galvanometers on its way back to the detectors. The working distance of an LOT system can be quite long, and the numerical aperture of the incident beam can be as low as 0.05. The lower the numerical aperture, the more forward-facing the incident beam becomes, meaning that light penetrates more deeply into the tissue (although this does not directly mean that depth-resolution improves).

The system illustrated in Fig. 3 is drawn with 1× magnification, such that the scan lens and the lenses in front of the detectors have the same focal lengths, and the objective lens is a single lens creating 1× magnification. In this configuration, the physical separation between the detector channels on the linear PMT array will equal the absolute distance between the source and detector positions at the tissue. This is not always desirable, since most PMT arrays have an element pitch of ∼ 1 mm, yet we would like to detect light emerging from the tissue in increments of several hundred microns. However, we also want to maintain the system's ability to scan a wide field of view (up to 3 cm) relatively quickly. We can therefore adjust the magnification of the system in two distinct ways. If we change the magnification of the objective lens, both the field of view, and the relative separations between the ‘source’ and ‘detector’ positions will vary. If we change the ratio of the focal lengths of the scan lens, and the detector lenses, we can scale only the separation between the source and detector spacings, independently of the field of view. In practice, this is how our current system is configured, with approximately 4× magnification on the detection side of the system, such that a 1 mm pitch between elements of the PMT maps to a 250 micron separation at the tissue surface.

Another interesting aspect of the system is the use of polarization. A polarization maintaining fiber is used to deliver laser light to the system. The polarizations of the lasers are aligned so that all contribute P-polarized light, and so predominantly P-polarized light enters the optical system. This light is passed through a polarizer and then the polarizing beam splitter, ensuring that only P polarized light will reach the tissue. As the light scatters within the tissue, it gradually loses its P polarization, such that emerging light is a combination of both S and P polarized light. Detrimental specular reflections, such as may occur from the surface of the tissue or from intermediate lenses will maintain their P polarization. In a fluorescence confocal microscope, these reflections are overcome because all light at the incident wavelength will be removed by emission filters. However in LOT, by using a polarizing beam splitter, we deliberately reject all returning P-polarized light from out absorption detection arm. This effectively blocks specular reflections, while also preferentially selecting photons that have scattered more deeply (and therefore lost more of their P polarization). If the system were implemented using a simple 50:50 beam splitter, only 25% of all available light could ever reach the detector. If polarization were to be controlled in an equivalent way, only 12.5%, rather than 50% of returning S polarized light would be detectable.

LOT has many advantages compared to DOT-like imaging geometries where multiple source and detector fibers are placed in contact with, or imaged onto the tissue [33–35]. For LOT, it is only necessary to have as many detector elements as the number of source-detector separations required, and only one light source (for a given wavelength) is needed. Fiber-based tomographic systems are typically arranged in an array pattern, with the source position varied by either using a fiber-switch to route source light into each fiber, or using multiple light sources that can be switched on and off, each attached to its own source fiber. Each detector fiber is generally attached to its own detector. Detector fibers close to an illuminated source fiber will see high light intensities, but the same detector will see much lower intensities when the source is positioned at another point in the grid. As a result, a fiber-based grid system consisting of 8 sources and 8 detectors could acquire only 64 measurements per image, at a single wavelength, and each detector's dynamic range would have to be sufficient to detect all 8 different signal amplitudes corresponding to each separation. Fiber switches are often slow, and requiring 8 separate laser sources would significantly impact system cost. Measurements would suffer from uncertainty in the relative positioning of each fiber, and problems with coupling of light into and out of the tissue. Using LOT however, the number of ‘sources’ can be increased by simply moving the laser beam to more positions. It is therefore possible for a LOT system to acquire 100 × 100 grid of source positions, with 8 or more source-detector separations per position, yielding 80,000 measurements per image in as little as 22 ms. Further, each detector in LOT is positioned to detect light for only one given source-detector separation. The detectors at wider source-detector separations can be configured to have higher gain than the closer detectors. As the source position changes, the relative positions of these detectors do not change, so they are not required to have the very high dynamic range required for fiber-based systems. This is also beneficial for reducing cross-talk and digitization errors in LOT.

One final aspect of our more advanced LOT system is the ability to achieve simultaneous multi-spectral imaging. Acquiring data at multiple wavelengths is very valuable for spectroscopic evaluation of the absorbers in the tissue. However, in the system configuration shown, images at different wavelengths must be acquired serially, with shutters turning different lasers on and off between each frame. This imposes a significant restrictions on the imaging speed achievable, since shutters are typically slow. It also means that spectroscopic analysis would need to assume that the data acquired at each wavelength represented exactly the same distribution of absorbers, which would not be true for imaging of dynamically changing physiological parameters. We therefore recently added an extension to the system which incorporates a dispersive element into the absorption arm of the system, and an 8 × 8 PMT square array detector, rather than a linear detector array. This design is described in more detail in [36] and [37]. This approach means that light from up to 8 lasers (but in our case 3) can be detected simultaneously, since the scattered light is resolved at 8 positions along one dimension of the detector array, and wavelength is resolved along the other. Once shutters are not required, this system can run continuously, acquiring 200 × 200 source-position raw image data at 23 frames per second, or 40 × 40 source-position data at 100 frames per second.

Signals from all the PMTs are converted into voltages, and read using fast, simultaneous sampling data acquisition boards. These boards also control the synchronized scan pattern of the galvanometer mirrors.

5. LOT modeling, data interpretation and image reconstruction

The raw data produced by such an LOT system consists of a stream of measurements acquired as the laser beam scans over the tissue's surface. The z-position of the objective is never varied, and all depth-specific information is acquired in a single raster scan of the tissue being imaged. The first step in visualizing this raw data is to reshape it into a series of square images, corresponding to the galvanometer mirrors' raster scan, where each image consists of data from a channel with a different source-detector offset (or a different wavelength, or fluorescence).

These raw images contain a great deal of information, and can be examined by eye to infer information about the depth of structures within scattering media. For example, ‘raw’ LOT images for three source-detector separations, acquired on a multi-color tissue phantom are shown in Fig. 4. As the source-detector separation gets farther apart, the contrast of the deeper structure becomes stronger compared to the contrast of the shallower structures. It should be noted that this data does not represent true depth-sectioning of the tissue (as you would get from confocal imaging), but rather an image that is a weighted sum of signal from shallower and deeper layers. While this was also the case for camera-based imaging, the difference here is that there are 8 raw LOT images to describe a single area of tissue, each corresponding to a different source-detector separation, and therefore showing a different set of weightings between shallow and deep structures. This weighting can be quantified using a model of light propagation to generate ‘sensitivity functions’ for each source-detector separation as shown in Fig. 4. It is also possible to see shadows of the absorbers in the 0.5 mm and 1 mm separation images (cast downwards). These shadows are predicted by the sensitivity functions and occur because the LOT system will detect contrast equally, both when the source and the detector scan over the object. The shape and intensity of these shadows are a function of the depth and thickness of the absorber, and are an important part of LOT's ability to generate 3D images [38].

These ‘raw’ LOT images have excellent dynamic range and signal to noise characteristics (owing to the use of sensitive PMT detectors) as well as the ability to be rapidly acquired, with variable resolution and field of view and with simultaneous acquisition of both multi-wavelength and fluorescence data with a single co-registered system. As such, they compare very favorably to the 2D imaging performance of high-end CCD camera imaging systems. However, while raw LOT data images resemble those from a camera, unlike for camera imaging, it is also possible to extract quantitative information about the depth-resolved contrast within each image, and even to convert these raw images into true 3D renderings of the absorbing or fluorescent structures within the tissue.

The LOT image reconstruction process can be expressed in the following way:

$$\Delta M_{n,m}=J_{n,m}\left(r\right)\Delta {\mu }_a\left(r\right),$$ (6)

$$\Delta {\mu }_a={\text{J}}^{\text{T}}{\left(\text{J}{\text{J}}^{\text{T}}+\alpha I\right)}^{-1}\Delta \text{M}.$$ (7)

Eq. (6) shows the linearized form of the imaging problem, the Born Approximation, which predicts the small change in measurement ΔM between source position n and detector position m that will result from a small change in absorption Δμ_a at position r. These two changes are related by J, which represents the spatial sensitivity of the measurements to changes in absorption. J could be measured empirically by moving a small object around r within the scattering medium and observing the effect that it has on measurements between different points n, m on the surface [38, 39]. However, since this is not practical for in-vivo applications, this spatial sensitivity J can instead be predicted using a model of light propagation. Such a simulation needs to be based on the approximate background scattering and absorbing properties of the tissue. A typical Monte Carlo-generated set of J's (or ‘sensitivity functions’) was shown in Fig. 4.

In practice, it is sometimes preferable to formulate the problem as shown in Eq. (8) (so-called ‘Normalized Born’), where the measured signal is normalized by M₀, representing the signal measured before a perturbation. The right hand side of the equation then needs to be similarly divided by Φ₀ representing the simulated signal that would be expected to emerge from the tissue in the absence of the perturbation. This approach can be very useful for cancellation of systematic errors, both related to measurements (such as variations in gain between each detector) and the forward model, as well as increasing the influence of the wider source-detector separations on the reconstructed solution [13, 40, 41].

$$\frac{\Delta M_{n,m}}{M_{0_{n,m}}}=\frac{J_{n,m}\left(r\right)}{{\varphi }_{0_{n,m}}}\Delta {\mu }_a\left(r\right).$$ (8)

Once J has been calculated, it is possible to invert Eq. (6) (or (8)) to yield the image of Δμ_a (r) that corresponds to a given set of measurements ΔM_n,m. This image reconstruction approach is equivalent to X-ray computed tomography (CT); where information about the direction and position of each measurement are used to infer the 3D cross-sectional structure that resulted in the measured projection data. However, while in X-ray CT, the projections are transillumination measurements through non-scattering objects, for LOT, we instead have a probability distribution J representing the likely paths that the scattered photons have taken on their way into, and back out of the tissue. One way to perform this inversion is to use Tikhonov Regularization as shown in Eq. (7) where αI is a regularization factor which varies how strongly the image reconstruction requires the data (ΔM) to fit the model (JΔμ_a). Regularization is required to ensure that the image reconstruction tolerates small mismatches between the real data and the forward model, which could result from systematic errors or noise and inaccuracies in the light propagation model. If α = 0 were chosen, the reconstruction would likely over-fit the data and the resulting images would have significant high-frequency artifacts. Large values of α will generate superficially-weighted smooth images with underestimated quantification. All forms of optical tomography face the same challenge of selecting suitable regularization to yield reliable and accurate image reconstruction results, and reflectance-geometry optical tomographic image resolution and accuracy will always degrade as a function of depth [42].

Instead of Monte Carlo modeling, LOT image reconstruction could use different models of light propagation such as the radiative transport equation (RTE) [43], or the diffusion approximation to the RTE [12] (although for the small source-detector separations typically used with LOT, the diffusion approximation is invalid and will not provide accurate results [44]). If reciprocity relations are to be used for generation of J, for reconstructions of absorption contrast it is essential to account for the directionality of the photons at shallow depths [13, 30]. Image reconstruction can also be achieved in different ways, such as by using different inversion schemes, or by using non-linear algorithms that do not rely on the Born approximation, but instead iteratively seek a solution for Δμ_a that fits the measured data [45]. It is also, in principle, possible to reconstruct images of the scattering properties of the tissue, although whether both absorption and scattering properties can be extracted uniquely from just measures of intensity is not yet clear [30, 46–48]. For LOT results to date, we have used only homogenous forward models for generation of J. However, anticipated heterogeneities in the background optical properties (such as large blood vessels, layers or a large lesion) could feasibly be incorporated into the forward model to allow improved fitting between the data and the model [40, 42]. Constraints and priors can also be incorporated into the reconstruction [49, 50], as can reconstruction of fluorescence contrast [15, 51]

All of the above approaches seek to generate quantitative information about the change in absorption coefficient Δμ_a at a given wavelength, as a function of x, y, and z. These values can then be converted into the concentrations of known absorbers using an equation of the form of 3. This conversion can also be incorporated into the reconstruction by substituting 3 into Eq. (6) [42,49] to yield:

$$\begin{array}{c}\left(\begin{array}{c}\Delta M_{{\lambda }_1}\\ \Delta M_{{\lambda }_2}\\ ⋮\\ \Delta M_{{\lambda }_n}\end{array}\right)=\left(\begin{array}{cccc}{J}_{{\lambda }_1}& 0& \cdots & 0\\ 0& J_{{\lambda }_2}& & \\ ⋮& & \ddots & \\ 0& & & J_{{\lambda }_n}\end{array}\right)\left(\begin{array}{cc}{\xi }_{{\text{HbO}}_2,{\lambda }_1}& {\xi }_{\text{HbR},{\lambda }_1}\\ {\xi }_{{\text{HbO}}_2,{\lambda }_2}& {\xi }_{\text{HbR},{\lambda }_2}\\ ⋮& ⋮\\ {\xi }_{{\text{HbO}}_2,{\lambda }_n}& {\xi }_{\text{HbR},{\lambda }_n}\end{array}\right)\\ \times \left(\begin{array}{c}\Delta c_{\text{HbO}}\\ \Delta c_{\text{HbR}}\end{array}\right).\end{array}$$ (9)

Formulating the reconstruction in this way constrains the solution to have some consistency between the measurements at different wavelengths which is based upon the known spectra of the absorbers in the tissue.

Performing a full reconstruction to calculate Δμ_a (or concentrations) is very different to the camera-based imaging strategy described above in Sect. 2, where it was necessary to make an estimate of the average pathlength of all of the detected light combined in order to estimate some depth-averaged μ_a. Each LOT source-detector separation represents a discrete set of pathlengths, and the forward model for each measurement can be adjusted to compensate for differences in the absorbing and scattering properties of light at different wavelengths (hence J_λn). As a result, LOT actually compensates for the differences in the sampling depths of different wavelengths of light, something that camera-based imaging cannot do. This means that LOT allows much more complete modeling of light in tissue, and hence can provide better quantitative estimates of absorber or fluorophore concentrations than camera-based imaging, while also being able to resolve depth-specific changes. The one difficultly shared between both LOT and camera-based analysis is the need for an accurate estimate of the ‘background’ absorbing and scattering properties of the tissue being imaged.

For fluorescence LOT imaging, the reconstruction takes a similar form but requires different considerations. Firstly, for absorption contrast, it is assumed that detected photons scatter along a random walk path from the source to the detector. Each interaction with a scatterer results in a direction change that is governed by the anisotropy of the scatterers within the tissue. In most tissues, this scattering is predominantly in the forward direction, such that each scattering event changes the direction of the photon by a relatively small amount (see Fig. 5A). However, when a photon interacts with a fluorophore, it is absorbed and then re-emitted at a longer wavelength. This process is incoherent, so the photon loses all knowledge of its previous direction and the photon can be emitted in any direction (see Fig. 5B). Therefore, for fluorescence LOT, all detected emission light has undergone an isotropic scattering event within the tissue, and as such the modeling of light propagation needs to accommodate this. Another important aspect of fluorescence imaging is the need to compensate for the different optical properties that will be experienced by photons of different wavelengths. Since fluorescence emission will always be at a longer wavelength than excitation light, photons will propagate differently depending on whether they have experienced an interaction with a fluorophore yet.

Figure 5.

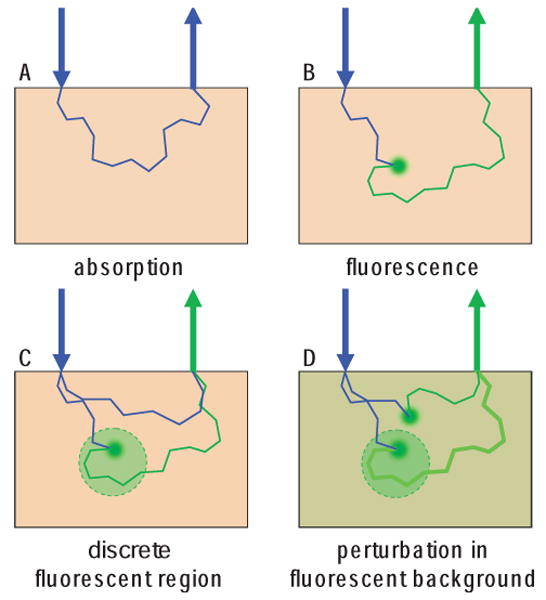
(online color at: www.lpr-journal.org) Modeling absorption and fluorescence interactions. A Absorption imaging detects light that has not been absorbed. Each photon scattering event maintains some directionality. B Fluorescence imaging detects only light which has been emitted from a fluorophore after absorption of an incident photon. This interaction results in isotropic emission, and a change in wavelength of the light. C For discrete fluorescence perturbations, light detected at the fluorescence emission wavelength can only have originated from within the fluorescent area. D For fluorescence perturbations in a fluorescent background, the fractional change in fluorescence can be measured.

Another aspect to consider for fluorescence imaging is that there exist two different scenarios: 1) Where a tissue initially has no fluorescence, and the perturbation is created by the appearance of a discrete fluorescent region (this would be the case for small animal molecular imaging of a targeted dye [51]) (see Fig. 5C). 2) Where a large volume of the tissue is already fluorescent, and the perturbation sought is a local increase (or decrease) in the fluorescence of a discrete region (this would be the case for voltage or calcium sensitive dye imaging in the brain or heart, for example [15]) (see Fig. 5D).

In case 1, all of the light at the emission wavelength that is detected must have come from the region containing the fluorophore. However, in case 2, fluorescence is detected from all regions of the tissue, with additional fluorescence being detected from the region where fluorescence has increased. In case 2, signal to noise and dynamic range can become a problem, since the total fluorescence detected will be dominated by signal from shallower layers, with the deeper perturbation signal representing a small change on this large background. However it is possible to measure ΔF/Fo, the percentage change in fluorescence before and after the perturbation. Case 2 therefore effectively reduces to the same perturbation problem as for absorption, only that J needs to be modeled appropriately: J^F must account both for the isotropy of the fluorescence interactions, and the different absorbing and scattering properties that the excitation and emission light will experience in the tissue, such that Eq. (8) becomes:

$$\frac{\Delta F_{n,m}}{F_{0_{n,m}}}=\frac{J_{n,m}^F(r)}{{\varphi }_{0_{n,m}}^F}\Delta p(r)$$ (10)

where

$$p_{x,m}(r)={\epsilon }_x(r)c(r){\eta }_m(r)$$ (11)

where ε_x is the extinction coefficient of the dye (a function of the excitation wavelength), c is the concentration of the dye, and η_m is the quantum efficiency of the dye's fluorescence (a function of the emission wavelength). Note that different ‘active’ dyes (such as calcium and voltage sensitive dyes) have different mechanisms leading to their change in fluorescence, such that changes in all three of the elements of p may vary [15]. Eq. (10) is shown normalized by F₀ (the fluorescence detected before the perturbation) and ${\varphi }_0^F$, (the expected fluorescence simulated on a homogeneous medium) [15].

For case 1, the only measurement available is F₁ the fluorescence from the fluorescent region. Prior to the perturbation, no light will be detected at the emission wavelength, the only light emerging will be excitation light, which has traveled through the tissue. F₁ is still technically the result of a change in p, from zero to some finite value, so it is still possible to formulate the problem as:

$$(F_{n,m}-0)=J_{n,m}^F(r)(p(r)-0).$$ (12)

However, it is not possible to normalize each side of this equation. In practice, this means that case 2 measurements can provide better depth sensitivity, since the detected signal can be amplified to fill the system's dynamic range. However, without the ability to utilize normalized measurements, systematic effects such as the gains of each detector channel, must be compensated for via a separate calibration, which can reduce the accuracy of reconstructed images.

Instead of performing image reconstructions to create 3D renderings of sub-surface structures, another way to analyze LOT data is to simply examine the raw data. Analogous to multi-distance measurements often made with fiberoptic probes [52-55], LOT measurements contain sufficient information, at every detection point, to allow simplified estimates of tissue optical properties [56-58]. This can be achieved by comparing measurements to a range of forward model predictions. A ‘lookup table’ approach is valuable for cases where a simplified geometry can be assumed (e.g. in skin imaging where the depth, thickness and contrast of a lesion could be assumed to be the only unknowns), or for situations where the Born approximation doesn't hold (e.g. lesions with very high absorption, or low scattering). This can easily be implemented by generating a ‘white’ [59] or ‘scalable’ [60] Monte Carlo model, and iteratively adjusting the absorption properties in discrete regions. If the tissue is known to be composed of layers, the depth, absorption concentration and/or thickness of those layers could be determined [37]. If the sample is known to be homogenous within the limits of depth sensitivity, LOT's multi-distance measurements could also potentially even yield both the absorbing and scattering properties of the tissue [56-58]. The benefits of using LOT for these measurements is that very dense grids of source-position measurements can be made very rapidly and in a non-contact geometry. This means that measurements can be selected from anywhere in the ‘raw’ image, and analyzed pixel-by-pixel, or as groups of pixels, to provide mutually consistent data. This approach is only limited by the assumption that a given set of source-detector separation measurements are all sampling the same axially symmetric tissue volume.

To date, we have focused our studies on perturbations in absorption, assuming that scattering properties do not change before and after the perturbation of interest. We have, however, incorporated scattering heterogeneity into the baseline Monte-Carlo forward model in cases where significant scattering differences are expected, such as in the layers of the skin, or when imaging the brain through thinned skull [14]. We are continuing to develop these various approaches to analyzing and interpreting LOT data, based on each specific application for which LOT is being developed.

6. LOT applications

In this section, we provide three examples of LOT in-vivo imaging applications; neuroimaging, cardiac imaging and dermal imaging. Each application highlights a different aspect of LOT's advantages for in-vivo imaging.

LOT for in-vivo neuroimaging

LOT can allow depth-resolved optical imaging of the hemodynamic response to forepaw activation in the in-vivo exposed rat cortex [14]. Camera-based optical imaging of the exposed cortex has been used for many years to record the changes in blood flow, volume and oxygenation that occur in the brain when a region is active [61-66]. However, as described in Sect. 2, camera-based imaging requires wavelength-dependent estimates of the pathlength of the detected light to allow conversion of raw images of attenuation into quantitative maps of ΔHbO₂, ΔHbR, and ΔHbT (ΔHbT = ΔHbO₂ + ΔHbR). This conversion is always going to suffer from the effects of light of different wavelengths scattering to different depths within the tissue (partial volume effects), as well as the fact that light is predominantly probing superficial layers [1]. Camera-based 2D imaging cannot resolve the depth at which changes are occurring.

The cortex of the brain is intrinsically layered, with each layer being composed of different neuron sub-types and different input or output connections to other regions of the central nervous system. The blood supply to the cortex is also unusual in that most large vessels course over the surface of the brain, with narrower diving vessels penetrating almost perpendicularly to the surface to feed dense networks of capillaries in deeper layers [67]. These capillary beds deliver blood to the parts of the cortex that are most metabolically active during neuronal firing. The signals observed in superficial arteries and veins are related to the in-flow and out-flow of blood to these capillary beds, and can have very different spatial and temporal behavior compared to the capillaries. However, the extent and behavior of the capillary responses are most interesting, because they are expected to be most closely related to the functional behavior of responding neurons. Camera-based imaging has limited sensitivity to changes occurring in the deeper capillary beds, and does not allow any separation of signals from deeper and shallower regions, such that a large deep change cannot be distinguished from a shallow small change.

We have demonstrated that LOT can be used to capture the hemodynamic response to stimulus throughout the layers of the rat cortex [14]. In this experiment LOT data was acquired at around 8 frames per second, with interlaced illumination at 473 nm and 532 nm. Seven source-detector separations were acquired spaced 0 to 2 mm apart. Data were acquired in a 50×50 source-position grid over a 3.5 mm square area. Each rat was anesthetized and had the somatosensory part of its cortex exposed by retracting the scalp and gently thinning the skull. LOT data were acquired for around 140 repetitions of a four second electrical forepaw stimulus delivered at 3 Hz. The resulting dual wavelength data was block-averaged and interpolated onto the same time-base. Images of Δμ_a(x,y,z,t) were then reconstructed for each wavelength using Eq. (8) and Tikhonov regularization, and then combined using Eq. (5) to yield time-varying images of ΔHbO₂, ΔHbR, and ΔHbT.

Fig. 6 shows some of the results from this study. The camera image shows the region that was imaged using LOT, as indicated by the white box. The inset shows an x-y map of the LOT ΔHbO₂ response at a depth of 200 microns, 0.6 seconds after cessation of the stimulus. The red areas indicate regions of increased HbO₂ concentration relative to the period before the stimulus. Shown below are cross-sectional x-z maps of the same HbO₂ response through the planes indicated by (i) and (ii). Plane (i) transects a superficial vein, which can be seen as a discrete, shallow region. Plane (ii) transects the deeper capillary response. The depth-resolved time-courses of the ΔHbO₂, ΔHbR and ΔHbT responses through the midline of these venous and capillary responses are shown to the right and reveal distinctive functional signatures for the two different vascular compartments (for example, note that no ΔHbT response is discernable in the region of the superficial vein).

Figure 6.

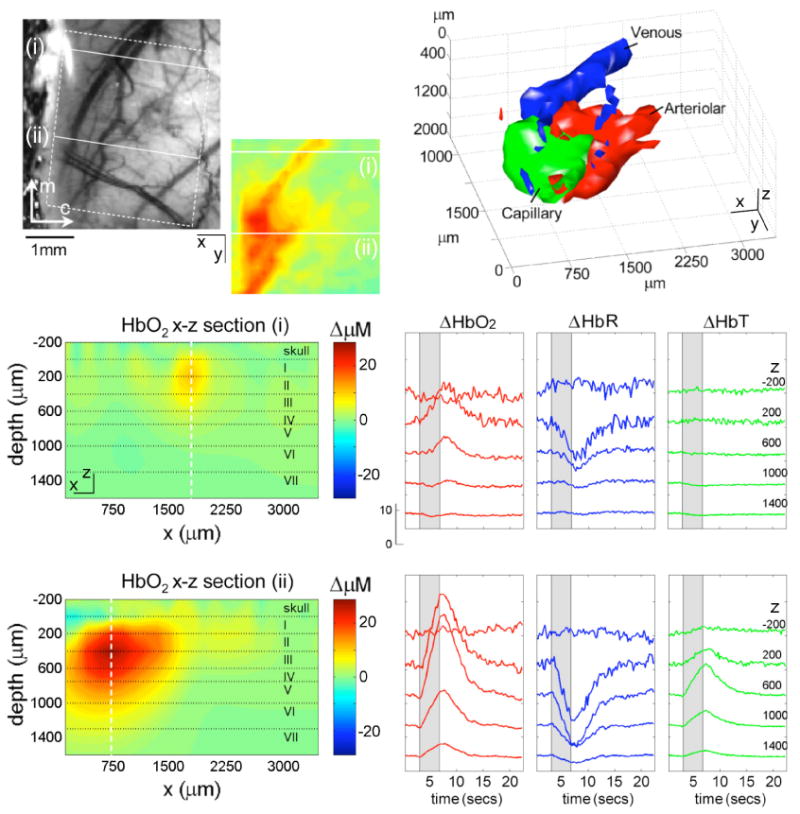
(online color at: www.lpr-journal.org) Laminar Optical Tomography of the cortical hemodynamic response to forepaw stimulus in rat. (top left) photograph of field of view showing superficial veins and dural vessels (the skull was thinned but intact). Inset: reconstructed x–y LOT image of HbO₂ response at 200 micron depth at 0.6 secs after cessation of 4 second stimulus. Below: x–z planes of the same 3D HbO₂ reconstruction showing a cross-section through the surface vein (top, region i), and the deeper capillary response (bottom, region ii). Lower right: time-courses of hemodynamic response at each depth for the center of the surface vein (top) and the capillary response (bottom). Top right: isosurface rendering of hemodynamic response resolved into arterial, capillary and venous compartments based on their distinctive temporal behaviors. Modified from [14].

The four-dimensional data set produced by LOT can be analyzed and displayed in many different ways. Based on the distinctive differences between the dynamic behavior of the arteriolar, capillary and venous responses observed within our data, we demonstrated that it is possible to segment the LOT response into regions with those specific dynamic behaviors [14, 68]. The result is shown in Fig. 6 as a 40% isosurface. We validated these results using vascular casts and high-speed in-vivo two-photon microscopy (see Hillman et al, Neuroimage 2007 for more details [14]).

Analogous to Fig. 4, Fig. 7 shows a sample of the raw LOT data corresponding to the reconstructed results in Fig. 6. The ‘absolute’ signals for the 0 micron source-detector separation show the rough surface of the thinned skull, while wider source-detector separations reveal the pial vessels and sample the parenchyma. The Δ% images show changes in the detected light intensity at the two wavelengths. The 0 micron separation detects almost no changes in attenuation, yet the wider separations detect stronger signals from the pial vessels and capillary beds. The 473 nm signal is more sensitive to HbO₂ changes, and therefore reveals different vessel shapes to the images at 532 nm, which are more sensitive to HbT changes.

Figure 7.

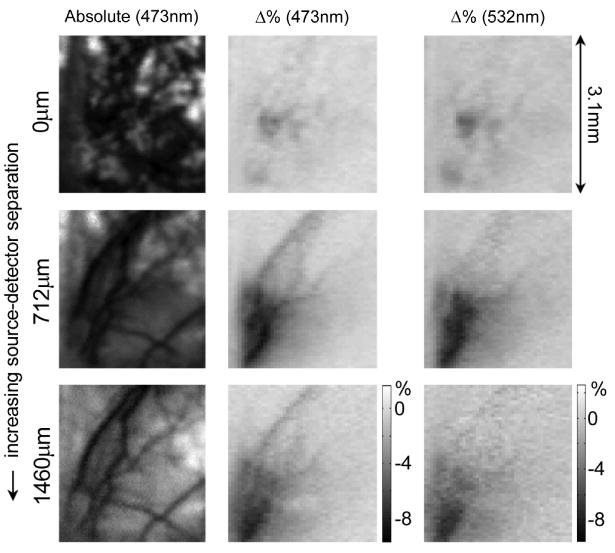
Raw LOT data acquired on rat brain. Prereconstruction data is shown for three different source-detector separations: 0, 712, and 1460 microns. Left column shows absolute data, center and right columns show fractional change (100 × ΔM/Mo) 0.6 seconds after cessation of stimulus for 473 nm (center) and 532 nm (right) wavelengths. 473 nm is more sensitive to HbO₂ changes, whereas 532 nm is sensitive to HbT. The narrowest source-detector separation shows the rough surface of thinned skull, and only small changes in signal from uppermost layers. Wider separations reveal pial vessels, and deeper responses. This same data set was reconstructed to generate the images shown in Fig. 6.

For this application, LOT added a depth-dimension to traditional camera-based optical imaging of the cortex. By incorporating the anticipated wavelength-dependent optical properties of the brain into the light-propagation forward model, we also account for ‘partial volume’ effects and do not require a pathlength-correction. Imaging frame rates for this study are similar to those used in camera-based studies, and our recently completed second generation LOT system can acquire equivalent data at 3 wavelengths at over 100 frames per second [36, 37]. Our second generation system also includes the ability to simultaneously measure the fluorescence properties of the tissue at the same time as measurements of absorption changes. Fluorescent voltage and calcium sensitive dyes can generate fluorescence intensity changes in the presence of changes in membrane potential and intracellular calcium respectively, thereby providing an optical read-out of neuronal activity [1, 24, 69].

Other studies that have sought to perform depth-resolved optical imaging of the hemodynamic response in the rodent cortex have used either coarse fiber-bundle probes placed in contact with the head [33, 34], or ‘projection-based’ approaches [35]. The latter used a grid of 12 source and 4 detector fibers which was imaged onto the surface of the thinned skull using a camera lens. Each detector fiber was connected to its own avalanche photodiode detector, and three laser diodes (of different wavelengths) were serially coupled into each of the 12 source fibers using a fiber switch. The separations between the sources and detectors ranged from 2.7 to 10mm. To acquire each ‘image frame’, a mechanical fiber switch was used to change the position of each laser source to each of the 12 source positions. As such, very coarse sampling consisting of 48 measurements (4 detectors, 12 sources) took around 30 seconds per frame [70]. Imaging resolution was insufficient to resolve superficial vessels.

In comparison, by effectively scanning the image of a source, and a line of adjacent detectors over the surface of the cortex, LOT can measure with source-detector separations up to 3mm (sufficient for sampling the 2mm thick cortex) at rates exceeding 100 frames per second, with each frame capturing 3 wavelengths, and 12,800 measurements (40×40 source positions, with 8 detectors per position). For functional imaging of the brain, this dramatically increased speed and resolution is ideal for capturing fast neuronal and hemodynamic events.

Other mesoscopic imaging technologies that have been applied to imaging of the rodent cortex include two-photon microscopy [69, 71], OCT [72, 73] and PAT [74]. Two-photon microscopy, while valuable for looking at blood flow and cellular-level function, can only image to depths of less than 500 microns, and is not generally sensitive to oxy- and deoxy-hemoglobin changes. OCT studies of the exposed cortex have shown changes in signal that relate to stimulus, but whose origins are poorly understood and are thought to be related to changes in scattering due to either neuronal swelling or movements of red blood cells. PAT imaging of the mouse brain was achieved through intact scalp and skull, and revealed fine vessel structure and functional reactivity. However, measurements to date have been too slow to resolve the dynamics of activation [1]. In summary, LOT offers a unique toolkit for functional brain imaging that is highly complementary to other mesoscopic imaging approaches.

LOT for cardiac imaging

Just as voltage and calcium sensitive dyes can provide an optical read-out of neuronal activity, so too can they provide functional contrast for other electrical tissues such as heart muscle [75]. Imaging of electrical activity in the living heart allows normal and abnormal cardiac activity to be studied in detail, including the effects of ischemia, physical damage and pharmacologic interventions.

Cardiac imaging is traditionally performed on perfused, excised hearts. This means that the heart is removed from an animal, but kept alive by providing a continuous flow of warm perfusate containing all of the necessary electrolytes, glucose and oxygen required for continued beating. In this controlled environment, it is possible to image, stimulate and measure the heart for up to several hours [76, 77]. However, until now voltage sensitive dye imaging of the heart has been limited to studies of the heart's surface using camera-based measurements. As a result, although electrical wave propagation patterns across the surface of the heart have be studied, it has not been possible to capture the intramural dynamics of electrical waves within the heart wall. More complex patterns of wave propagation that can occur during arrhythmias cannot be well characterized.

Beyond the complexity of the cardiac perfusion paradigm, cardiac imaging presents another significant imaging challenge: the need for very high frame rates. The rat heart beats at around 6 times per second. Each beat represents one complete cycle of electrical propagation, and transmural propagation is expected to occur in less than 10 ms. High frame-rate cameras are typically used for cardiac studies, running at over 100 frames per second [75], however even higher frame rates are required to study transmural propagation, in addition to the need to be able to visualize the depth-resolved electrical activity within the cardiac wall.

We developed an LOT technique to allow us to capture the transmural propagation of electrical waves in a Langendorf perfused rat heart [15]. We were able to achieve effective frame rates of 667 Hz by acquiring repeated line-scans synchronized with a regularly paced heart loaded with Di-4-ANEPPs voltage sensitive dye excited at 532 nm. A 540 nm short-pass dichroic filter was included into the system, and a 610 nm long-pass emission filter was placed in front of the LOT detectors.

Rat hearts were removed perimortem and placed into ice-cold cardioplegic solution, which temporarily arrests the heart. As shown in Fig. 8, a glass cannula was then inserted into the aorta, such that it forced perfusate into the coronary vessels which feed the heart muscle. Once cannulated, additional cardioplegic solution was pushed through the heart to wash out any remaining blood. An electrode was then inserted into the right ventricle to allow endo-cardial stimulation. An electrocardiogram (EKG) electrode was sutured onto the heart to provide continuous recording of the heart's electrical response to pacing. Once the cannula is connected to a flow of perfusate and the heart is lowered into a bath of the same warmed perfusate (Tyrode's solution), the heart recommences beating. After successful pacing of the heart was established (by providing a small pulsed current to the endo-cardial electrode) the heart was paralyzed using diacetyl monoxime, which acts as an electromechanical decoupler. This means that the heart stays still enough for imaging without motion artifacts, while the electrical activity remains (as confirmed by EKG monitoring). The voltage sensitive dye was then added to the in-flowing perfusate to stain the heart muscle prior to imaging.

Figure 8.

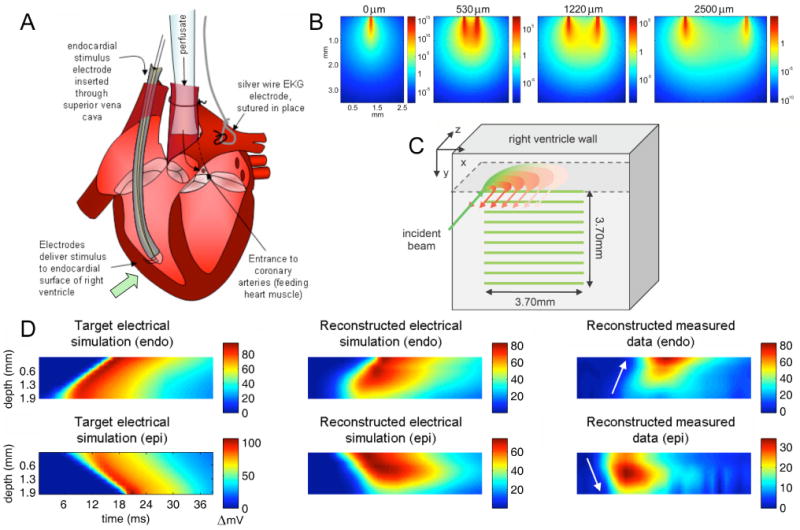
(online color at: www.lpr-journal.org) Laminar Optical Tomography of Voltage Sensitive Dyes in perfused rat heart. A) The rat heart was cannulated and Langendorf perfused. An electrode was positioned within the right ventricle, LOT imaging was performed on the outer wall of the right ventricle. B) Sensitivity functions (log scale) for fluorescent voltage sensitive emission are asymmetrical owing to the different optical properties experienced by incident and detected light. C) Data was acquired in the form of serial x-direction line-scans as illustrated. D) Results are shown as average signal plotted as a function of depth and time. Left: Data simulated with a model of electrical propagation shows wave traveling from endo-cardial to epi-cardial surface (top) or epi-cardial to endo-cardial surface (bottom). Center: Reconstructed results using LOT forward model and reconstruction of simulated electrical propagation data. Signal is distorted for deeper layers, but direction and speed of propagation can be discerned. Right: Reconstructions of measured data for endo and epi-cardial stimulation. Direction of propagation can be determined. Figure modified from [15].

Sets of 800 horizontal line-scans were acquired on the outer surface of the right ventricle for bursts of 1.2 seconds, triggered to coincide with the endo-cardial stimulus frequency (5–6 Hz). Each of these bursts therefore acquired signal for 5–6 heart beats. The vertical position of the scanning beam was then moved to a position 0.37 mm below the initial line, and a further 800 line scans were acquired. This process was repeated for 10 vertical steps to cover a 3.7 × 3.7 mm area (see Fig. 8C). This acquisition process was repeated 4 times. The same data was then acquired for the case where a stimulation electrode was positioned on the epicardial surface of the right ventricle.

All of this data was then block-averaged to create a data set representing the evolution of the response from a single heartbeat. The data were reconstructed using Tikhonov regularization and a forward model generated to accommodate the isotropic effects of fluorescence emission and the different optical properties experienced by the excitation light (532 nm) and the emission light (∼ 620 nm). An extra normalization factor was included into the image reconstruction to help to accentuate the contributions from deeper layers. We found that this was necessary by also reconstructing data that was generated using a mathematical model of the anticipated electrical propagation of a wave traveling transmurally. Having optimized our image reconstruction parameters such that the dynamics of these simulated waves were reproduced satisfactorily, we used the same parameters to reconstruct our measured data. The results are shown in Fig. 8D. We were able to clearly discern the direction of propagation of electrical waves originating either from the endo-cardial or epi-cardial surface of the heart. We performed additional, more quantitative comparisons of these dynamics using both raw and reconstructed LOT data, the details of which can be found in [15].

LOT imaging of the perfused heart allowed observation of transmurally propagating electrical signals in living heart tissue at an effective frame rate of 667 Hz. To our knowledge, no other depth-resolved optical imaging technique can provide this combination of depth-sensitivity and speed, in addition to sensitivity to both fluorescence and absorption contrast.

LOT for dermal imaging

LOT holds significant potential as a tool for quantitative depth-resolved optical imaging of superficial living tissues. Its capacity for multi-spectral absorption and fluorescence imaging and non-contact, rapid acquisition make it applicable to a wide range of biomedical applications such as imaging of oral mucosa [55], cervix [78], retina [79, 80], intrasurgical imaging [81], and a wide range of dermal imaging applications including skin cancer, wound healing, burn evaluation and for staging and evaluation of response to treatment for diseases such as psoriasis [82–85]. Many of these applications have already been the target of multi-spectral imaging, fluorescence imaging and point-by-point spectroscopic investigation using fiber probes [86]. LOT combines many of the advantages of these techniques with the ability to resolve depth-dependent features.

We are currently evaluating the efficacy of LOT for imaging of benign and malignant skin lesions. Our current system has a field of view that can extend to over 3 cm and has a flexible imaging head optimized for clinical data acquisition. Fig. 9 shows ‘raw’ LOT images of a benign mole (on the hand) acquired using LOT. Data were acquired by positioning the hand under the objective of the LOT system and acquiring at 488 nm, 532 nm, and 636 nm in a 100 by 100 source-position grid over a ∼ 6 mm square area. Signal was simultaneously detected at 7 different offset detector positions, such that a single image ‘frame’ consists of 21 raw data images (7 offsets, 3 wavelengths). The data acquired at three of these offsets are shown in Fig. 9, with each ‘raw image’ shown as a red-green-blue merge of the data at the three wavelengths.

Figure 9.

(online color at: www.lpr-journal.org) Laminar Optical Tomography of Skin. (left) Photograph of benign mole on the back of the hand. (right) Raw LOT reflectance images acquired using 488 nm, 532 nm, and 635 nm lasers. (above) simulations of sensitivity functions for each source-detector separation (S-D) (optical properties: μ_a = 0.7 mm⁻¹ and ${\mu }_s^{\prime }=5.1{\text{mm}}^{-1}$ at 532 nm). The narrowest source-detector separation accentuates superficial folds of the stratum corneum. Wider separations reveal folds in the epidermis, and sub-surface structures of the mole. Modified from [36].

These images represent the raw LOT signal and are equivalent to Figs. 4 and 7. They are not ‘depth-sections’ of the tissue per se, because the measurement will always be sensitive to the superficial tissue directly under the source and detector positions. However, the wider separations have a larger component of signal from deeper tissues than the signal from narrower separations. This is illustrated by the sensitivity functions shown for each separation in Fig. 9 (note that the shape of these sensitivity functions differs from those shown in Fig. 4, owing to the higher scattering coefficient expected in skin compared to the heart or brain tissue).

As described in Sect. 5, this raw data can be analyzed and interpreted in many ways. Just examining the data by eye reveals a lot of information: The 0.2 mm separation data shows the superficial folds in the stratum corneum. The bluish tint to the image corresponds to the higher level of back-scattering experienced by blue light compared to red light. For the wider separations, it becomes possible to see the deeper folds in the epidermal-dermal junction, and the rounded shape of the mole. The brown color of the mole corresponds to melanin absorption, while the pink color of the surround is due to hemoglobin absorption [36].

This data could also be reconstructed to show a 3D rendering of the absorbing contrast at the three wavelengths. This would require the raw data to be down-sampled to a coarser grid of source positions to reduce the size of the matrix that would need to be inverted using Eq. (7). It would also be necessary to identify a reference area to allow generation of images of Δμ_α with respect to this area from measurements of ΔM. Reconstructing would reduce the amount of high-frequency information available within the images, but could be used to evaluate the sub-surface shape of the structures containing melanin, HbR, HbO₂, and HbT. Alternatively, each pixel could be analyzed and interpreted independently. Each of the pixels in the first image has 20 additional associated measurements (3 wavelengths for 7 separations) that contain quantitative information about the absorbing and scattering properties of the underlying tissue (fluorescence was not measured in this case). This means that this data could feasibly be interpreted initially through examination by eye, and then followed by point-and-click analysis of each area to determine the absorbing, depth and thickness properties of the underlying structures [37]. We are currently working to investigate all of these approaches to LOT data analysis by performing comparative trials between in-vivo LOT imaging of malignant skin lesions, and comparing our results to ex-vivo histology of the same lesions.

Non-contact, laser-scanning optical imaging methods have previously been reported, and include a ‘flying spot’ approach [87] and a swept, spectrally resolved linescanner [88]. Both of these approaches include some of the parallisation advantages of LOT, however, neither used additional offset detectors to add a depth-dimension to their measurements. Another similar system, designed for intraocular imaging uses a linear array of laser light sources, each illuminated in turn to allow ‘offset confocal’ measurements of the retina [80, 89]. It was noted that data with wider offsets accentuated signal from deeper layers, providing valuable measures for evaluation of age-related macular degeneration, although data were not converted into 3D renderings. LOT would be more suitable for this application, since it is able to acquire data for all source-detector separations (and wavelengths) in a single high-speed scan.

Another method that is similar to LOT, and could find analogous applications to those described above is ‘Spatially Modulated Imaging’ [48]. This technique acquires multiple images with a camera while the tissue is illuminated with stripes of light of different widths or relative positions. This approach is equivalent to the spatial Fourier transform of LOT, in that LOT scans a focused spot (a delta function) over the tissue and plots seven measures of the tissue's point spread function response to this input. Modulated imaging puts different spatial frequencies of light into the tissue and measures the tissue's modulation transfer function. Whereas in LOT, wider source-detector separations yield information about deeper tissues, in modulated imaging illuminating with wider spatial frequencies provides information about deeper tissues. Modulated imaging uses much simpler instrumentation than LOT and can image larger areas of tissue. However, where LOT simultaneously acquires all spatially-resolved measurements at multiple wavelengths (and fluorescence) in parallel, Modulated Imaging faces scaled multiplexing problems since each ‘frame’ must consist of multiple images with different spatial frequencies, different relative phases and different wavelengths. LOT may also have signal to noise and dynamic range advantages owing to its use of PMT detectors with gains optimized for each offset channel, compared to modulated imaging, which must acquire all information within the dynamic range and sensitivity of a single camera chip. In general, each technique has advantages and disadvantages when compared, and we expect that LOT and Modulated Imaging will prove to be complementary modalities for a wide range of different applications.

7. Summary

In summary, we have described recent developments in optical mesoscopic imaging techniques for biomedical applications, with particular emphasis on Laminar Optical Tomography (LOT). Details of the design of an LOT system, as well as the range of ways that LOT data can be analyzed and interpreted were described. Examples of recent applications of LOT were then given, and LOT performance was compared to other existing techniques. We demonstrate that LOT is an important new technique for in-vivo optical imaging, providing a unique set of advantages over existing methods including non-contact, high-speed, quantitative, depth-resolved imaging of both absorption and fluorescence contrast.

Biographies

Elizabeth Hillman is an Assistant Professor of Biomedical Engineering and Radiology at Columbia University in the City of New York. She completed her undergraduate and graduate training in Physics and Medical Physics respectively at University College London, UK. Her graduate work focused on the development of optical tomography techniques for imaging the premature infant brain. Dr. Hillman then spent a year working in industry developing optical spectroscopy methods for measurement of analytes in-vivo, and subsequently performed post-doctoral work at Massachusetts General Hospital (MGH) and Harvard Medical School, reaching the faculty level of Instructor. Her work at MGH focused on the development of new approaches for high-resolution optical imaging of the exposed rodent brain. Dr. Hillman's group at Columbia University specializes in the development and application of novel in-vivo optical imaging approaches. These range from multi-spectral, high-speed in-vivo two photon microscopy to small animal molecular imaging. Dr. Hillman constructed and demonstrated the first Laminar Optical Tomography system in 2003. She is continuing to develop and optimize the technique for a range of applications as described in this article.

Sean Burgess is a PhD student at Columbia University in the Department of Biomedical Engineering. He is working with Dr. Elizabeth Hillman to develop multi-spectral laminar optical tomography for dermal and brain imaging applications. Sean obtained his undergraduate degree in Bioengineering from the University of Washington, Seattle WA, where he also performed research into applications of therapeutic ultrasound with Shahram Vaezy and Vesna Zderic. Sean served in the US Navy from 1996–2002 as a Nuclear Electronics Technician.