A meanfield approach to the thermodynamics of a protein-solvent system with application to the oligomerization of the tumor suppressor p53

Abstract

The thermodynamic stability and oligomerization status of the tumor suppressor p53 tetramerization domain have been studied experimentally and theoretically. A series of hydrophilic mutations at Met-340 and Leu-344 of human p53 were designed to disrupt the hydrophobic dimer–dimer interface of the tetrameric oligomerization domain of p53 (residues 325–355). Meanfield calculations of the free energy of the solvated mutants as a function of interdimer distance were compared with experimental data on the thermal stability and oligomeric state (tetramer, dimer, or equilibrium mixture of both) of each mutant. The calculations predicted a decreasing stability and oligomeric state for the following amino acids at residue 340: Met (tetramer) > Ser Asp, His, Gln, > Glu, Lys (dimer), whereas the experimental results showed the following order: Met (tetramer) > Ser > Gln > His, Lys > Asp, Glu (dimers). For residue 344, the calculated trend was Leu (tetramer) > Ala > Arg, Gln, Lys (dimer), and the experimental trend was Leu (tetramer) > Ala, Arg, Gln, Lys (dimer). The discrepancy for the lysine side chain at residue 340 is attributed to the dual nature of lysine, both hydrophobic and charged. The incorrect prediction of stability of the mutant with Asp at residue 340 is attributed to the fact that within the meanfield approach, we use the wild-type backbone configuration for all mutants, but low melting temperatures suggest a softening of the α-helices at the dimer–dimer interface. Overall, this initial application of meanfield theory toward a protein-solvent system is encouraging for the application of the theoretical model to more complex systems.

The accurate prediction of protein stability and relative stability of mutants of a given protein would be a very useful tool in biotechnology. Such a calculation must necessarily include protein-solvent interactions. Protein-solvent systems have been studied on the atomistic level (refs. 1, 2, and refs. thererin), or on a hierarchical level that starts with a coarse-grained approach that is refined at the atomistic level (e.g., refs. 3 and 4). Both approaches can reveal quite accurate dynamics, but these calculations are limited to small proteins and/or short simulation times (the time step for one integration is of the order of 1 fs). Approaches that use a coarser model for the protein structure commonly use a dielectric function to describe the solvent (5, 6). However, use of the meanfield inhomogeneous Flory–Huggins model (7), originally developed for polymer-solvent interactions, may provide a more accurate description of solvation.

Here we use a meanfield theory to calculate the free energy of a static experimentally determined protein structure. The tetramerization domain of the tumor suppressor p53 (p53tet) was chosen because it has a quaternary structure that can be altered by site-directed mutagenesis and can be readily assessed experimentally (8). p53 is the most frequently mutated protein found in human cancers (9–11). It functions as a transcription factor that regulates genes involved in the control of the cell cycle in response to DNA damage (reviewed in refs. 12 and 13). In approximately half of all human cancers, it exists in a dysfunctional mutant form, but it can also be inactivated by the products of cellular or viral oncogenes. p53 normally functions as a tetramer held together by a short sequence of 30 amino acids near its C terminus. Oligomerization deficient mutants of p53 are also defective in many of p53's important biochemical activities (14, 15), and the tetramerization domain of p53 can also help mutant inactive p53 to sequester active wild-type (WT) p53 into inactive heterotetramers (16, 17). Thus, knowledge of the structure and stability of the tetramerization domain is important for our understanding of normal and abnormal function of p53.

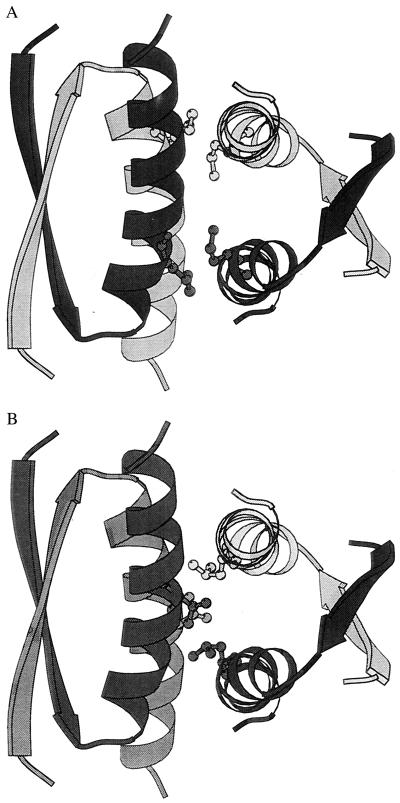
Fig. 1 shows the three-dimensional structure of p53tet (18). The tetramer is a dimer of dimers with three orthogonal axes of symmetry. Each dimer consists of an antiparallel β-sheet (one strand from each subunit) and a pair of antiparallel α-helices that interact with each other and the β-sheet via hydrophobic side chains. The two dimers associate with one another in a roughly orthogonal orientation via an extensive hydrophobic surface formed by the antiparallel helices of each dimer. Mutations that introduce a hydrophilic functionality into the hydrophobic dimer–dimer interface are expected to destabilize the tetramer and stabilize the solvated dimer. In this work, we report the design, preparation, and biophysical characterization of a series of mutations at the dimer–dimer interface of p53tet and compare these results to the meanfield theoretical prediction of their stability and oligomeric state.

Figure 1.

The p53 tetramerization domain (18) showing the association of the two primary dimers: black/gray and black/gray. The amino acid targeted for mutagenesis at the dimer–dimer interface is shown for each subunit: (A) Met-340; (B) Leu-344.

Materials and Methods

Plasmid Preparation and Protein Purification.

The sequence-encoding residues 310–360 of WT human p53 were subcloned into the pET15b vector (Noragen, Mississauga, Ontario, Canada) by using standard techniques (19). The resulting plasmid, pET-p53(310–360), expresses six histidine residues followed by a linker containing a thrombin cleavage site and a His-Met dipeptide immediately N terminal to the p53 sequence. The p53 mutations at either Met-340 or Leu-344 were created by oligonucleotide-directed mutagenesis on pET-p53(310–360) by using the Quick-Change mutagenesis kit (Stratagene) and were subsequently verified by DNA sequence analysis. Escherichia coli BL21(DE3)-[pLys-S] harboring the desired plasmid was grown in 2-liter batches of Luria broth at 37°C, and protein production was induced with 1 mM isopropyl-thiogalactose at an optical density of 0.6–0.7 at 600 nm. Three hours after induction, cells were harvested by centrifugation at 6,000 × g for 30 min. His-tagged protein was purified from cell lysate by nickel affinity chromatography as described by Johnson et al. (20). The yield of purified protein was 10–20 mg/liters of culture. Before experiments, samples were dialyzed for 24 h at 4°C against 4 liters of buffer (25 mM sodium phosphate/100 mM NaCl, pH 7.0 or 7.4) by using Spectrapor 3,000 molecular weight cutoff dialysis membrane. Protein concentration was determined by using the extinction coefficient ɛ₂₇₅ = 1,475 M⁻¹⋅cm⁻¹ per solvent exposed tyrosine residue in unfolding conditions of 6.5 M guanidine-HCl.

Circular Dichroism (CD).

CD spectra were recorded on an Aviv 62A DS CD spectrometer (Aviv Associates, Lakewood, NJ) equipped with a thermoelectric temperature controller. Measurements were made by using a 0.1-cm cuvette at a sample concentration of 40–50 μM. Thermal unfolding was followed by monitoring ellipticity at 222 nm as a function of temperature every 2°C allowing 4 min for sample equilibration and a signal average of 100 s for each data point. Melting temperatures were assigned to the midpoint of the fraction of unfolded protein (F_U) as determined by the relationship F_U(θ) = (θ − θ_N)/(θ_U − θ_N), where θ is the ellipticity at a given temperature, and θ_N and θ_U represent the ellipticity values at temperatures where the protein is fully folded or unfolded, respectively.

Laser Light Scattering.

Molecular weight determinations by using light-scattering techniques were performed on a Dawn F multiangle laser light-scattering photometer, manufactured by Wyatt Technology, Santa Barbara, CA, according to the methodology described in the Dawn F instrument manual. The complete instrumental setup consists sequentially of a vacuum solvent degasser, HPLC pump equipped with pulse dampener and in-line 0.22- and 0.1-μm filters, manual injector, Pharmacia Superose 12 gel filtration column, Dawn F, and Wyatt Optilab 903 Interferometric Refractometer.

Determinations of molecular weights were performed by injecting an aliquot of the sample into the gel filtration column and monitoring the scattering intensity and refractive index (RI) signal of the eluting peaks. The RI signal was used to calculate the protein concentration by using an assumed value of 0.185 for the refractive index increment (∂n/∂c). For each measured data slice across a peak, a Debye plot was produced [RQ/(K⋅c) vs. sin²Θ/2], in which the intercept of the extrapolation of scattering intensities to zero angle yields the molecular weight. The apparent weight-average molecular weight across the whole peak was then calculated from the individual slices.

Sedimentation Equilibrium Analysis.

A Beckman Model E Analytical Ultracentrifuge (Beckman Coulter) equipped with electronic speed control, RTIC temperature control, Rayleigh interference optics, and titanium rotor was used for all runs. Measurements of photographic plates were performed at a Nikon model 6C microcomparator at ×50. Determinations of the molecular weight of Lys-340 were made by using the meniscus depletion sedimentation equilibrium technique (21). For conventional runs, fringe counts were first performed on the samples to determine the initial concentrations. An average refractive increment of 4.1 fringes/mg/ml was assumed according to Babul (22). One hundred ten microliters of each sample was then loaded into 12-mm double-sector charcoal-filled Epon cells equipped with sapphire windows. Identical cells and sample volumes were used for meniscus depletion runs. The sedimentation equilibrium runs were performed for approximately 48 h before equilibrium photographs were taken. Molecular weight calculations were carried out by using a computer program in which the ln y vs. r² data were fitted to a second-degree polynomial equation by using the least-squares technique. The apparent weight-average molecular weight values were calculated from the slopes of the resulting plots. The partial specific volume for each sample was calculated from the amino acid composition according to the methodology of Cohn and Edsall (23). To determine a K_d value for the dimer-tetramer equilibrium of Lys-340, concentration vs. radial distance data were fit to various association state models by using a nonlinear least-squares technique (24).

Theory.

For simplicity, we coarse grain the protein by introducing two effective atoms for each amino acid: one at the C_α position representing the backbone, the other at the side chain center-of-mass position representing the side chain and its properties (e.g., hydrophobicity). This coarse-graining procedure is motivated by the approach of Kolinski et al. (25, 26), who used it for studying protein folding and oligomer equilibria. However, instead of confining the coarse-grained protein model to a discrete lattice, we introduce a continuum approach where the coordinates of each of the effective atoms as well as the solvent are represented by a density distribution. Applying a meanfield model to the system allows us to express the free energy of the system in a simple analytic form (27).

The advantages of this approach are: (i) A reduction of the degrees of freedom allowing for a faster sampling of the possible conformations. It also smoothes the energy landscape, which makes it easier to move between conformations close to the global free energy of the system. (ii) The field theoretic approach allows for a self-consistent search of the optimum conformation in a properly weighted ensemble of possible states. It also allows the straightforward introduction of the protein-solvent interactions similar to the inhomogeneous Flory–Huggins model (7).

The stability of proteins is assessed by calculating the free energy of a static protein conformation starting from a known experimentally derived structure. In particular, we use a structure of the p53tet domain obtained by three-dimensional NMR and minimize its energy with a molecular dynamics algorithm [by using Cerius2 with the dreiding 2.21 (Molecular Simulations, San Diego, CA) force field]. The resulting structure is very similar to the original one (the rms deviation is about 1 Å), but it shows better agreement with the expected 3-fold symmetry of the domain. By allowing small changes in this conformation, we can probe for stable structures, which are recognized by a local minimum in the free energy. In particular, if we consider the stability of oligomers, in a first approximation we assume the backbones of the different polypeptide subunits to be rigid and calculate the free energy with the individual subunits at different separations.

The free energy in the meanfield approximation is given by using the polymer-solvent system analogue (28),

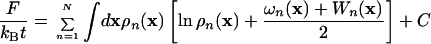1

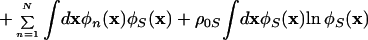where the density distributions ρ_n(x), the meanfields ω_n(x), and the volume fractions φ_n(x) are defined by

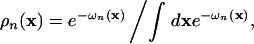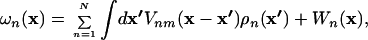2

respectively, C is a constant representing the kinetic energies of all of the particles in the system, and ρ_0S is the solvent bulk density. The kernel K_n(x) is defined as

3

The densities ρ_n(x) describe the possible fluctuations of the respective effective atoms around their zero-temperature position. The mapping from these densities ρ_n(x) to the volume fractions φ_n(x) projects these fluctuations onto the outer shell of the effective atoms.

Because we use a similar coarse-graining approach for the protein as Kolinski et al. (25, 26), we use tabulated force fields reported by the same authors for calculating the interactions between the different effective atoms within the protein. These force fields are temperature dependent and the tabulated values are given in units of k_BT. For the present problem, we kept the backbone conformation fixed and used only one- [W_n(x)] and two-body [V_nm(x − x′)] interactions, neglecting the higher order interactions, which were introduced by Kolinski et al. to enhance the formation of secondary structures.

So far we have included no bond length and bond angle constraints. In a first approximation, we assume that the center-of-mass position of each amino acid side chain n remains at the same position R_0n (relative to its neighbors) as in the WT configuration (whereas its distribution function may change with the separation of the two dimers from each other), i.e., we add to Eq. 2 the constraint

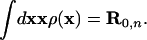4

Because the side chains of the mutant amino acids differ in size from the WT amino acid, we must relax this constraint. However, we know that the side chains can exist only in a finite number of conformations (the so-called rotamers or rotameric states) because of geometric constraints (29, 30). Using tabulated torsion angles for the amino acid side chains (31, 32) and well-known values for the bond lengths and angles for each of the 20 amino acids, we construct a table of center-of-mass positions for all the rotamers and include a proper bias function into the free energy functional Eq. 1 (28) for each of the mutant amino acids.

The side chain volume fraction φ_n(x) is obtained by mapping the ρ_n(x) onto a sphere just big enough to fit in side chain n. Because of the incompressibility of the system, i.e.,

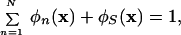5

the protein-solvent interactions in Eq. 2 yield nonzero contributions only where φ_n(x) and φ_S(x) overlap, i.e., at their mutual interface.

In our model, the interactions between the solvent and the amino acid side chains are characterized by parameters χ_n (Eq. 2), which describe the hydrophobic character of amino acid n. Hydrophobic indices χ_F(n) have been estimated by Fauchère et al. (33) by comparing the distribution coefficients of amino acid amides in water and n-octanol and fixing the absolute scale such that χ_F (Gly) = 0. Eisenberg and McLachlan (34) used these values to estimate solvation free energies χ_E = 2.3 RTχ_F (kcal/mol). For application of this method to p53tet, we are interested mainly in the change in the free energy during exposure of the hydrophobic dimer–dimer interface to the surrounding solvent. Therefore, we have included only the interface amino acid side chains in the meanfield calculations, while keeping all other amino acid side chains (as well as all backbone C_αs) fixed at their experimentally observed positions. Free energies are then calculated for different distances between the two dimers when separated along the normal of their mutual mirror plane. Starting from an initial guess for the densities ρ_n(x) and meanfields ω_n(x), we solve Eq. 2 self consistently up to a desired accuracy. The calculation of the free energy of a single configuration required approximately 20 min on a Sun Ultra Sparc 2 (Sun Microsystems, Mountain View, CA) workstation. An increase of the number N of amino acids included in the meanfield calculation scales approximately linearly with N because of the finite range of the interprotein and protein-solvent interactions.

Results and Discussion

Met-340 and Leu-344 were chosen as sites of mutation because they are involved in hydrophobic interactions across the dimer–dimer interface but are not major determinants of the folding of the dimer itself. Therefore, mutation of either Met-340 or Leu-344 to a hydrophilic residue should destabilize the quaternary structure of the tetramer but preserve and help solvate the three-dimensional structure of the dimer. A series of amino acids with increasing hydrophilicity (34) were selected to replace Met-340: His, Ser, Gln, Glu, Asp, and Lys. These six amino acids were also chosen because they have relatively strong helical propensities, so that they are less likely to disrupt the α-helix, thereby preserving the structure of the dimer. Similarly, Leu was replaced with by Ala, Arg, Gln, and Lys at position 344.

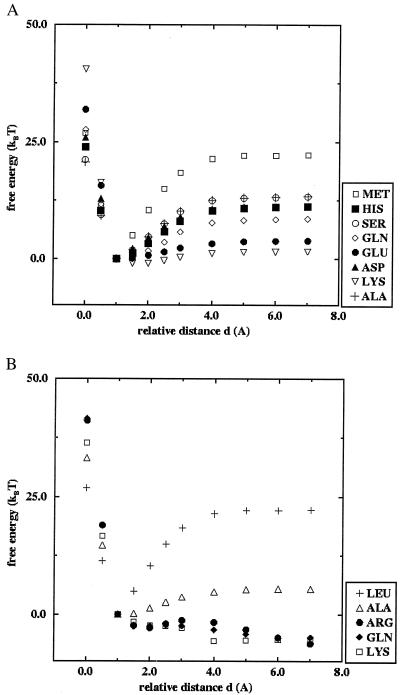
Fig. 2 shows the calculated relative free energies of the p53tet mutants as function of the dimer–dimer distance obtained from the meanfield calculations. The relative interdimer distance measures the separation of the two dimers along the axis perpendicular to the dimer–dimer interface (see Fig. 1). A separation of zero (d = 0) corresponds to the experimentally observed dimer–dimer distance for WT p53.

Figure 2.

Calculated free energies as function of the relative dimer–dimer distance for p53tet mutants: (A) mutations at site 340; (B) mutations at site 344. See text for more details.

Fig. 2a shows results of free energy calculations for mutations at site 340. The WT structure shows a pronounced minimum in free energy in agreement with the observed stable tetramer. All of the considered mutations at site 340 also show a free energy minimum near the WT dimer–dimer distance, although their binding energy is consistently smaller (up to 50%) than that of the WT (Table 1). According to our calculations, the mutant with Lys-340 is the least stable, with about 10% of the binding energy of the WT.

Table 1.

Theoretical and biophysical data for p53tet

Amino acid	Molecular weight*	Molecular weight apparent†	Sigma	N‡	Tm§	ΔE¶	Hydrophobicity‖
Mutations at residue 340
Met (WT)					85**	22.2	1.68
Ser	8,103	32,370	3,000	4.0	59	13.3	−0.05
Gln	8,144	33,730	3,250	4.1	62	8.6	−0.30
Ala**				4	55	13.4	0.18
His	8,153	27,790	2,350	3.4	58	11.1	0.18
Lys	8,144	30,440	2,830	3.4	66	2.5	−1.35
Glu	8,145	16,630	1,000	2.0	34	3.8	−0.87
Asp	8,131	15,870	1,000	2.0	38	11.3	−1.05
Mutations at residue 344
Leu (WT)					85**	22.2	1.68
Ala	6,080‡‡	15,840	2,500	2.6	49	5.4	0.18
Ala**				2	47	5.4	0.18
Gln	8,880	19,260	2,500	2.2	50	N/A	−0.30
Arg	8,910	17,970	2,700	2.0	43	N/A	−0.05
Lys	8,880	18,240	2,050	2.1	48	N/A	−1.35

^*Theoretical molecular weight of the monomeric protein. The difference between the 8.8- and 8.1-kDa proteins is in the size of the polyhistidine tag. 

^† Apparent molecular weight (Da) as determined by laser light scattering at concentrations of 200–500 μM. Sigma is one standard deviation in Da. 

^‡ N is the apparent molecular weight divided by the monomeric molecular weight and for proteins that are a single oligomeric state, N is equal to the oligomeric state. 

^§ Melting temperature in °C at 100 μM protein concentration as described in Materials and Methods. 

^¶ ΔE is the depth of the energy minima, i.e., the difference between the free energy at infinite separation minus the minimal possible energy of the tetramer. 

^‖Hydrophobicity index of Eisenberg and McLachlan (34), determined at a concentration of 57 μM. 

^**Melting temperature in °C at 10 μM protein concentration, from ref. 8. 

^‡‡This mutant was soluble only with the polyhistidine tag removed, thus the lower molecular weight. 

Fig. 2b shows similar free energy results for mutations at site 344. The calculations suggest that all of the mutations considered are less stable than the WT protein. Only the mutant with Ala has a well-defined minimum in the free energy that is comparable to the weakest bound mutants at site 340. For the mutants with Arg, Gln, and Lys, the free energy decreases with increasing dimer–dimer distance.

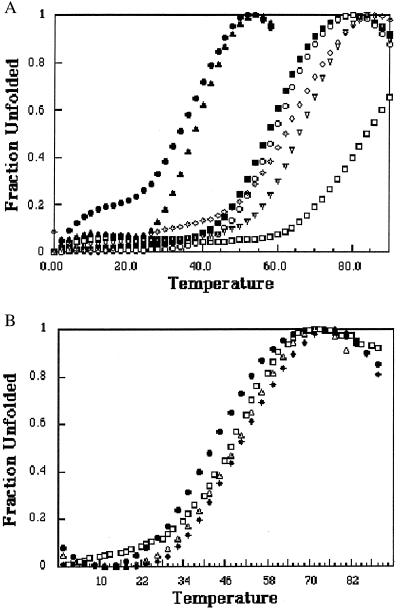
Fig. 3 shows the thermal melting curves for the six mutants, and the corresponding melting temperatures (T_m) are summarized in Table 1. The thermal stabilities of the Met-340 mutants fall into two clusters with the two small negatively charged residues, Glu-340 and Asp-340, being the least stable and the other four mutants being intermediate between WT and Glu/Asp. Although the circular dichroism spectra provide information about the amount of folded secondary structure, they do not provide a direct measure of the oligomeric state.

Figure 3.

Thermal stability of the p53tet mutants plotted as the fraction of unfolded protein vs. temperature at a total protein concentration of 100 μM (monomer). (A) Mutations at site 340 (WT, □; Lys, ▿; Gln, ◊; Ser, ○; His, ■; Glu, ●; Asp, ▴); (B) mutations at site 344 (Ala, ▿; Arg, ●; Gln, ⧫; Lys, □).

Multiangle laser light scattering was used to determine the oligomeric state of p53tet mutants, and the results are summarized in Table 1. Glu-340 and Asp-340 mutants were found to be dimeric, which would explain their lower thermal stability. The dimer–dimer interface of WT p53tet has a buried surface area of 1,006 Ų, corresponding to a free energy of −23 kcal/mol (18). Thus, dimers would be expected to have significantly lower stability relative to a tetramer. Gln-340 and Ser-340 were found to be tetrameric at the concentrations used here, whereas Lys-340 and His-340 were mixtures of dimers and tetramers. Meniscus depletion sedimentation equilibrium analysis at a loading protein concentration of 0.4 mg/ml was used to determine an apparent dissociation constant of 26 μM for the tetramer to dimer equilibrium of Lys-340. Thus, all mutants are oligomeric and retain a similar amount of secondary structure relative to the WT protein, suggesting that the dimeric mutants are likely to be “half tetramers” and are appropriate for comparison with the theoretical results.

The calculations predict a decreasing stability of the tetrameric state for the following amino acids at residue 340: Met (tetramer) > Ser, Asp, His, Gln > Glu, Lys, whereas the experimental results gave the following order: Met(tetramer) > Ser > Gln > His, Lys > Asp, Glu (dimers). For residue 344, the calculated trend was Leu (tetramer) > Ala > Gln, Arg, Lys (dimer), and the experimental trend was Leu (tetramer) > Ala, Arg, Gln, Lys (dimer). It appears that the inclusion of protein-solvent interactions, which play an important role in the tetramer-dimer dissociation, compensate for the coarse-grained description of the protein structure used in the meanfield calculations. The only major discrepancy between the simulation results and the experiments involves the Asp mutation at side 340: whereas the experiments show that this mutant dissociates into dimers, the meanfield calculation predicts a stable tetrameric configuration. However, for the numerical calculations, we assume that all mutants retain the WT backbone structure, which might no longer be true for this mutant as indicated by its low melting temperature and molecular dynamics calculations (Jürgen Wendling, personal communication). We also find a discrepancy between the theoretical results and the experiments involving the Lys mutation at residue 340, which is the least stable mutant according to the calculations. This may be because lysine has a rather long and flexible side chain with both hydrophobic and hydrophilic character. This dualism is not captured by our model, which describes each amino acid side chain by a single point coordinate and a potential function.

We also note that the calculations describe a system in infinite dilution (a single tetrameric molecule). Self association of proteins is highly concentration dependent and the relatively high concentrations used for circular dichroism and light scattering will drive the dimer–tetramer equilibrium toward the tetrameric state.

It is interesting to note that, whereas the trends in the oligomeric state determined by the meanfield calculations agree well with experiment, they do not directly correspond to the hydrophobicity index (34). For example, His has a relatively high value on the hydrophobicity index (0.18) (compared with other mutations), yet His-340 is predicted to be more dimeric than Ser-340, which has a hydrophobicity value of −0.05. This trend is also observed experimentally, where His-340 is more dimeric than Ser-340 and Gln-340. In the case of His, the important feature is likely the relatively large and rigid shape of the His side chain, which is not as easily accommodated at the dimer–dimer interface as a Ser or Gln. Because each side chain within the meanfield calculation is treated as a single effective atom, side chain geometrical constraints are not fully captured in the calculated free energy. However, the meanfield approach is still able to incorporate the multiple properties of amino acid side chains in many cases.

A comparison of the values in Table 1 suggests that p53tet is more sensitive to changes at residue 344 than at residue 340. For example, Lys-344 is a dimer with T_m = 48°C, but this same mutation at residue 340 has a T_m of 66°C and exists as an equilibrium mixture of dimers and tetramers. This difference in sensitivity can be rationalized by noting that the side chains of residue 344 from all four subunits are closer to one another than residue 340 (Fig. 1), which results in more charge repulsion at the dimer–dimer interface for Lys-344 than for Lys-340. The solvation of this interface in the dimer would reduce the charge–charge repulsion between the two Lys side chains in the dimer. It is also possible that the side chains of Lys-340 can adopt a conformation such that the hydrophobic portion of the side chain associates with the opposite dimer, whereas the charged portion has access to the solvated surface of the tetramer.

In the present study, we have applied our meanfield approach to a protein where the interactions between the different parts of the quaternary structure are purely hydrophobic. Vieth et al. studied the quaternary structure of coiled coils by using the GCN4 leucine zipper protein (3, 4). A hierarchical approach starting from a coarse-grained lattice Monte Carlo method and refining the results with molecular dynamics study at the atomistic level including solvent showed promising results for the assembly of dimers (3). However, the extension of this hierarchical approach to trimeric and tetrameric coiled-coil structures was not possible at the time because of the computational requirements. Instead, Vieth et al. (4) calculated the stability of the different possible quaternary structures of coiled coils in the GCN4 leucine zipper protein by using a coarse-grained Monte Carlo approach starting from estimated quaternary structures. The application of our meanfield approach to these systems would provide a good test for extending its use beyond purely hydrophobic interactions.

In conclusion, we have shown that a meanfield representation of a solvent-protein system can predict the major features of a self-associating protein system with reasonable accuracy. The results presented here are encouraging for the application of the meanfield method to more complicated protein-solvent systems.

Abbreviation

WT

wild type