Effects of electrical stimulation on isolated rodent gastric smooth muscle cells evaluated via a joint computational simulation and experimental approach

Abstract

Gastric electrical stimulation (GES) involves the delivery of electrical impulses to the stomach for therapeutic purposes. New GES protocols are needed that are optimized for improved motility outcomes and energy efficiency. In this study, a biophysically based smooth muscle cell (SMC) model was modified on the basis of experimental data and employed in conjunction with experimental studies to define the effects of a large range of GES protocols on individual SMCs. For the validation studies, rat gastric SMCs were isolated and subjected to patch-clamp analysis during stimulation. Experimental results were in satisfactory agreement with simulation results. The results define the effects of a wide range of GES parameters (pulse width, amplitude, and pulse-train frequency) on isolated SMCs. The minimum pulse width required to invoke a supramechanical threshold response from SMCs (defined at −30 mV) was 65 ms (at 250-pA amplitude). The minimum amplitude required to invoke this threshold was 75 pA (at 1,000-ms pulse width). The amplitude of the invoked response beyond this threshold was proportional to the stimulation amplitude. A high-frequency train of stimuli (40 Hz; 10 ms, 150 pA) could invoke and maintain the SMC plateau phase while requiring 60% less power and accruing ∼30% less intracellular Ca²⁺ concentration during the plateau phase than a comparable single-pulse protocol could in a demonstrated example. Validated computational simulations are an effective strategy for efficiently identifying effective minimum-energy GES protocols, and pulse-train protocols may also help to reduce the power consumption of future GES devices.

gastric electrical stimulation (GES) involves the delivery of extrinsic electrical pulses to the stomach, in an attempt to manipulate normal or abnormal electrophysiological functions. GES has shown therapeutic potential in the treatment of gastroparesis, where the aim is to enhance gastric emptying and/or manage symptoms, and also in obesity, where the aim is to delay gastric emptying and/or enhance satiety (26, 28). However, despite a substantial research focus on GES, few devices have become commercially available, and the efficacy of those devices has not yet been well established clinically (21, 26). There is a need for the optimization of stimulation protocols for different applications.

There are a large number of variables that must be considered when developing GES dosing protocols. The principal parameters are the stimulation pulse width, pulse amplitude, pulse frequency, and the on-off cycle timing of the stimulation device. In general, two types of GES protocols are typically described and differentiated on the basis of the pulse width and the frequency of the stimulation protocol used: short pulse (typically in the order a few hundred microseconds; typically at high frequencies) and long pulse (typically 10–600 ms; often at lower frequencies). In addition, trains of pulses (short or long, with programmed on-off timing) have been employed (28).

Existing implantable devices typically deliver short-pulse stimulation protocols, since they have been technically adapted from existing cardiac pacemakers or neural stimulators, which deliver stimuli of less than 1-ms pulse width. For example, the Enterra neurostimulator (Medtronic, Minneapolis, MN) is a device that has been granted Humanitarian Exemption by the United States Federal Drug Administration Agency for use in the treatment of gastroparesis that employs a high-frequency short-pulse protocol (amplitude 5 mA, pulse width 330 μs, frequency 14 Hz, cycle on time 0.1 s, cycle off time 5.0 s) (21, 28). The typical implantable stimulators that have been trialed in obesity management have also employed high-frequency short-pulse protocols (e.g., amplitude 6–10 mA, pulse width 300 μs, frequency 40 Hz, cycle on time 2 s, cycle off time 3 s) (29). Although these existing devices can successfully modulate cardiac myocyte or neural functions, long pulses or trains of long pulses are required to effectively modulate gastrointestinal smooth muscle cell (SMC) functions (28). Development of a new generation of implantable GES devices capable of administering longer pulses is therefore an identified research priority (26).

Long-pulse stimulation requires greater energy, and a central research challenge in developing new GES devices lies in achieving desired clinical outcomes, such as improved motility, at a suitably low level of energy consumption (18, 26, 28). Although one study has previously employed a long-pulse stimulation protocol in gastroparetic patients (amplitude 4 mA, pulse width 300 ms, frequency 10% higher than intrinsic slow-wave frequency), this study required external battery-powered stimulators too large to be implanted (19). Identifying new protocols that achieve desired clinical outcomes at low energy has proven to be a tedious and demanding task, since trial protocols must be selected from a vast parameter space involving many variables, as listed above (18, 28). To date, trial and error has been the dominant research strategy to evaluate potential protocols, requiring laborious animal model testing (13, 18). Defining promising protocols is further complicated by the recent advent of multichannel gastric pacing, which may be an important strategy to improve the efficacy and energy efficiency of GES devices (7). In multichannel stimulation, the electrical pulses are delivered to multiple localized regions of stomach, and the current doses must be individualized yet coordinated, with optimal positioning of the pacing electrodes.

Computational simulations have been proposed as a means to improve the efficiency of GES research, by employing advanced mathematical models that reduce the vast parameter combinations of all potential protocols to a much more refined pool of protocols (9, 12). Previously, a limited number of gastrointestinal mathematical models have been used in pursuit of this purpose. Mintchev and colleagues (20, 25), for example, have developed a conical dipole model of gastric electrical activity to calculate the effects of GES, focusing on high-frequency bipolar stimulation that targets neuromuscular pathways. At the cellular level, the Aliev cell model has been used to represent the gastric electrical activity in three-dimensional anatomical models of the stomach, via a multiscale integrated approach (2, 6, 8). Although these multiscale models have not yet been used to examine the effects of GES, they have been successfully employed to determine the effects of electrical uncoupling on electrogastrography (5).

Detailed descriptions of the ion channels and intracellular activities of SMCs have recently led to development of a biophysically based SMC model (the Corrias & Buist SMC model) (10). This is significant, since a biophysically based SMC model allows for the quantitative evaluation of ion currents, individually or collectively, under the effects of defined physical parameters such as temperature, ion concentration, and electrical stimulation currents. The development of this model therefore allows the possibility of undertaking a comprehensive predictive analysis of different stimulation protocols on SMCs, without relying exclusively on experimental animal studies.

SMC modulation is an important potential target for improved GES applications. However, the mechanisms by which SMCs respond to an electrical pulse have previously been investigated in few studies (3, 27). In this study, we adapted the Corrias & Buist SMC model and subjected it to a range of electrical stimulation protocols, in conjunction with experimental validation, to identify the effects of the protocols on the transmembrane potential and intracellular calcium concentration ([Ca²⁺]_i) of SMCs. The aim of this study was to develop a comprehensive description of the effects of stimulation protocols on SMC electrophysiology, as a basis for improving both the efficiency and efficacy of future GES devices.

METHODS

Smooth Muscle Cell Modeling Methods

The Corrias & Buist SMC model is a biophysically based smooth muscle cell model integrating classical Hodgkin-Huxley-type mathematical equations of eight ion conductances, in accordance with mammalian experimental data (10). In the present study, the Corrias & Buist SMC model (Fig. 1, Eqs. 1 and 2) was parameterized to match the membrane potential of rat gastric SMCs.

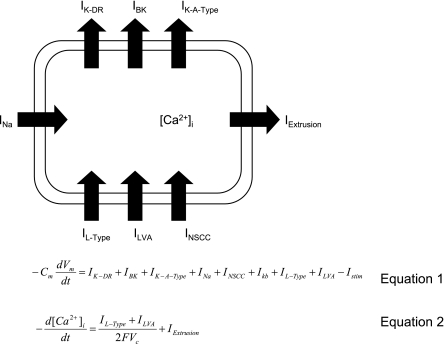
Fig. 1.

The Corrias & Buist smooth muscle cell (SMC) model incorporates a number of ion conductances: I_K-DR, delayed rectifier potassium channels; I_BK, large conductance calcium-activated potassium channels; I_K-A-Type, A-type potassium channels; I_Na, sodium channels; I_L-Type, low-voltage activated calcium current; I_LVA, low-voltage activated calcium channels; I_NSCC, nonselective calcium channels. Equation 1 describes the relationship between the rate of change of membrane potential (V_m) and ion channels. C_m represents the membrane capacitance, and I_stim represents the stimulus current; Eq. 2 describes the relationship between the rate of change of intracellular calcium concentration, [Ca²⁺]_i, and ion channels where I_Extrusion represents the extrusion rate of Ca²⁺. F, Faraday's constant; V_c, total cytoplasmic volume.

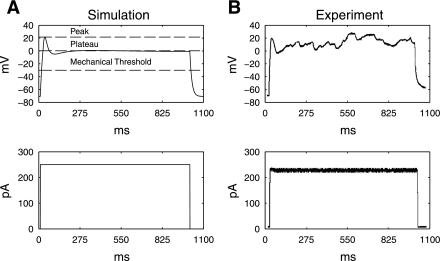
A number of parameters in the SMC model were changed to reproduce the rat SMC membrane potential. Table 1 details the specific model parameters that were adjusted, on the basis of the following rationale. From a previous study, sodium channels were not identified in rat smooth muscle cells (14), and therefore sodium conductance was set to 0 mS to eliminate Na⁺ current in the model. The cell membrane capacitance, extracellular K⁺ concentration, extracellular Ca²⁺ concentration, intracellular K⁺ concentration, and experimental temperature were adjusted to match one set of preliminary experimental measurements of the membrane potential of a rat SMC. The maximum conductance values of different channels are listed in Table 1. These values were adjusted systemically on the basis of a comparison between the membrane potential (V_m) output of the model with a preliminary set of experimental data of 4 cells in which the isolated rat SMCs were injected with a 250 pA pulse with 1-s duration (Fig. 2). The root-mean-square error between the experimental V_m response to the 250-pA stimulus (Fig. 2A) and the simulated V_m response to the same stimulus (Fig. 2B) was minimized by using the fminsearch function in Matlab (Version R2007b). The combination of G_Ltype, G_BK, G_bk, G_ka, G_kr, and G_NSCC that resulted in the minimal global error was chosen as the new values for those conductances. By these parameters, the simulated resting membrane potential of the model was −71 mV, comparable to experimental measurements of −77.4 ± 3.2 mV; the simulated peak potential was 28 mV, compared with experimental measurements of 28.25 ± 7.5 mV; the simulated plateau potential was 0.73 mV, comparable to experimental measurements of 3.1 ± 3.3 mV; and the simulated upstroke was 3.26 mV/ms, comparable to experimental measurements of 4.1 ± 1.2 mV/ms.

Table 1.

Parameters adjusted of the smooth muscle cell model to replicate the rat smooth muscle membrane potential

Parameter	Description	Default Value	Value
GNa	Maximum Na+ conductance	9 nS	0 nS
Cm	Cell membrane capacitance	77 pF	52 pF
Ko	Extracellular K+ concentration	5.9 mM	5 mM
Cao	Extracellular Ca2+ concentration	2.5 mM	2 mM
Ki	Intracellular K+ concentration	164 mM	140 mM
Texp	Experimental temperature	310 K	300 K
GL-type	Maximum L-type Ca2+ conductance	65 nS	5.2 nS
Gbk	Maximum background K+ conductance	0.014 ns	0.021 nS
Gkr	Maximum delayed rectifier K+ conductance	35 nS	3.5 nS
GBK	Maximum Ca2+-activated K+ conductance	45.7 nS	0.05 nS
Gka	Maximum A-type K+ conductance	9 nS	4.95 nS
GNSCC	Maximum nonselective ion conductance	50 nS	30 nS

Fig. 2.

A: simulated V_m, measured in mV (top), in response to a virtual stimulus of 250 pA and 1-s duration (bottom). The resting membrane potential is −71 mV, the peak potential is 28 mV, and the plateau potential is 0.7 mV. The mechanical threshold was defined to be −30 mV. B: experimental recording (top), based on the stimulus shown at bottom, that was used to parameterize the cell model.

Methods of Stimulation Studies and Model Validation

The reparameterized Corrias & Buist SMC model was applied in a series of virtual stimulation studies to evaluate its response to a range of pertinent stimulation protocols. The stimulation parameters that were evaluated were pulse amplitude (in pA), pulse-train frequency (in Hz), pulse width (in ms), and on-off time (in ms). These variables are important because they collectively determine the energy that is delivered during stimulation. The response to the virtual stimulations was described in terms of the peak potential (V_peak) and plateau amplitude (Fig. 2A).

The threshold for a successful SMC activation (i.e., the mechanical threshold) for this study was chosen on the basis of the work of Ozaki et al. (23), who described the SMC mechanical threshold to be between −40 and −30 mV during the plateau phase of depolarization. The upper limit of this range (−30 mV) is a threshold value of likely significance for mechanical activation of SMC (23). Gastric SMC depolarization above this threshold is thought to achieve significant Ca²⁺ entry and therefore to initiate contraction. In particular, sustained depolarization above this threshold leads to the sustained entry of Ca²⁺ and the intracellular accumulation of Ca²⁺ ([Ca²⁺]_i) then activates the contractile elements, although the relationship between the area under the slow-wave plateau, calcium influx, and tension generated is not linear (23). The use of a single mechanical threshold in this study is somewhat simplistic, because the contractile apparatus within in vivo SMCs is regulated by factors that may substantially alter the force generated for a given change in [Ca²⁺]_i (24). However, a single representative value was deemed to be sufficient for the purposes of this isolated SMC study.

Simulation Protocols

The first set of simulations replicated the response of the SMC model to a single 250-pA stimulus of varying duration (range: 0–400 ms in 25-ms increments). The second set of simulations replicated the response of the model to a single constant 1-s stimulus of varying amplitude (range: 0–200 pA in 25-pA increments). The third set of simulations replicated the response of the model to a train of 250-pA, 10-ms pulse width at varying frequencies (range: 0–100 Hz in 10 Hz increments), and of pulse train of 250 pA, 40 Hz at varying pulse widths (range: 0–10 ms in 2-ms increments). These ranges of protocol parameters were selected because previous work in our laboratory has identified them as having the potential to modulate SMC electrophysiology. The [Ca²⁺]_i was also quantified for a single-pulse stimulation protocol (pulse width 2,000 ms) and a frequency-train protocol with equal on time (2,000 ms) to the single-pulse width.

To validate the modeled results, corresponding patch-clamp stimulation experiments were performed at selected protocols. The first set of experiments tested a series of stimulation protocols using a 250-pA amplitude stimulus at 10-, 50-, and 100-ms duration. The second set of experiments tested a series of stimulation protocols of 1,000-ms duration at amplitudes of 160, 180, and 200 pA. The third set of experiments tested a stimulation protocol of 250 pA and 10-ms duration with stimulation train frequencies of 20, 40, and 80 Hz.

Patch-Clamp Experimental Methods

Animal and single cell preparation.

The experimental study was approved by the Institutional Animal Care and Use Committee at the Veterans Affairs Medical Center, Oklahoma City, Oklahoma and the International Guiding Principles for Biomedical Research Involving Animals were followed. All chemicals were purchased from Sigma (St. Louis, MO) unless indicated. Seven male rats (∼250–350 g) were used in this study. Smooth muscle cells were isolated via enzymes by using modified procedures as previously described (17). Following cervical dislocation under anesthesia, the stomach of each rat was dissected along the lesser curvature and pinned to a dissecting plate with the mucosal side down. Strips of gastric smooth muscle were removed by sharp dissection under anatomical microscope vision and were then finely sectioned. The sectioned pieces were first incubated for 30 min at 4°C in a low-calcium solution (in mM: 10 HEPES; 140 NaCl; 5 KCl; 0.05 CaCl₂; 2 MgCl; 10 glucose) with the pH adjusted to 7.4 with NaOH. The muscle sections were then transferred to a low-calcium physiological solution containing enzymes (in mg/ml: 2 collagenase IA; 2 papain; 2 BSA; 2 trypsin inhibitor) and incubated for a further 15 min at 35°C. Following the second period of incubation, the sectioned muscle strips were washed several times in an enzyme-free low-calcium physiological solution and gently agitated to create a cell suspension. Isolated cells were stored at 4°C for whole-cell current-clamp recording within 8 h.

Whole-cell current clamp recording and stimulation.

The experiments were performed on relaxed single gastric smooth muscle cells with smooth appearance and spindle shape by using the conventional whole-cell configuration of the patch-clamp technique (15). The myocytes were first superfused with HEPES solution (in mM: 10 HEPES, 140 NaCl, 5 KCl, 2 CaCl₂, 2 MgCl₂, 10 glucose), with the pH adjusted to 7.4 with NaOH. The patch pipettes (borosilicate glass, WPI) were pulled with a Flaming Brown P-97 micropipette puller (Sutter Instruments) and their tips were fire polished. The resistances of the pipettes were on average 5 MΩ when filled with internal high-potassium HEPES solution (in mM: 30 KCl, 100 potassium gluconate, 5 EGTA, 1 CaCl₂, 1 Na₂ATP, 2 Na₃GTP, 0.5 Na₃GTP, 1 MgCl₂) with the pH adjusted to 7.2 with KOH. The temperature of the preparation was maintained at 20°C. The membrane potentials of the single myocytes were recorded by using an Axopatch amplifier (Axopatch 200B, Axon Instruments). Data acquisition and analysis were performed with pClamp software (version 9.0, Axon Instruments).

The resting membrane potential of the SMCs dialyzed with potassium gluconate ranged between −40 and −60 mV. Cells were hyperpolarized to −60 to −80 mV by a constant negative current injection. The stimulation current that generated via Ditdata1200 analog/digital interface (Axon USA) was administered to the SMCs via the same pipette used for recording membrane potential.

Data and Statistical Analyses

Rate of upstroke (in mV/ms), peak potential (mV), plateau potential (mV), resting membrane potential (mV), and duration (ms) were calculated over five events for each stimulation protocol and expressed in means ± SE. Power consumption was calculated in mA·ms.

RESULTS

Effects of Pulse Width

The simulated SMC response to a range of pulse widths (0–400 ms in 25-ms increments), at constant amplitude of 250 pA, is as shown in Fig. 3. For a stimulation amplitude of 250 pA, the minimum pulse width for a single-pulse stimulation protocol that was required to achieve the mechanical threshold was 65 ms, as shown in Fig. 3A. For pulse durations shorter than 65 ms, a distinct plateau-phase could not be identified. These protocols were therefore deemed not able to activate the SMC model. Figure 3B, for example, demonstrates that there was a lower V_peak response and gradual repolarization to a short pulse width (10 ms). For pulse widths >65 ms, the potential of the plateau phase was 27.5–30.8 mV above the mechanical threshold (−30 mV). The length of the plateau phase that was maintained in the SMC was directly related to the length of the pulse width, with longer pulses causing a longer plateau phase (Fig. 3B).

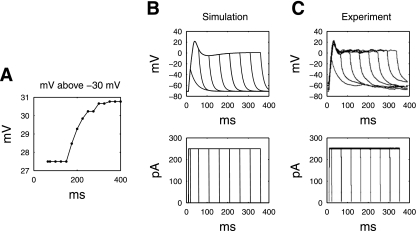
Fig. 3.

A: simulated plateau potential above the mechanical threshold (a series of stimuli of 250 pA, and widths from 0 to 400 ms in 10-ms increments); B: simulated membrane potential response of the SMC model under a series of stimulation protocols (250 pA, at 10, 50 to 300 ms in 50-ms increments), compared with experimental measurements under the same simulation protocols (C).

The simulated results were in good agreement with the validation patch-clamp studies (Fig. 3C). The highest simulated peak potential was 21.6 mV, compared with experimental value of 17.3 ± 7.5 mV. The simulated plateau potential was −0.66 mV, compared with an experimental value of 3.1 ± 3.3 mV. The simulated rate of upstroke was 3.3 mV/ms compared with the experimental value of 5.6 ± 0.7 mV/ms. The experimental results showed that pulse widths shorter than 65 ms were unable to sustain a substantial plateau phase and that a strong rapid upstroke response and plateau was consistently achieved at pulse widths greater than 50 ms. Longer pulse widths again resulted in a longer plateau phase of the SMC response.

Effects of Pulse Amplitude

The simulated SMC response to a range of pulse amplitudes, at a constant width of 1,000 ms, is shown in Fig. 4. With constant pulse width (1,000 ms), an increasing pulse amplitude (range: 25–250 pA in 25-pA increments) induced a graded response of the membrane potential of the SMC model (Fig. 4A). Stimulation amplitudes less than 75 pA was found to be unable to elicit a significant upstroke depolarization response of the membrane potential of the SMC (Fig. 4B). For pulse amplitudes greater than 75 pA, a supramechanical threshold response was achieved. The V_peak and plateau potential of the membrane potential showed a graded response to the amplitude of the simulated pulse, with higher amplitudes inducing a higher V_peak and plateau.

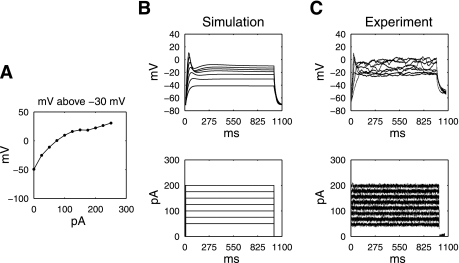
Fig. 4.

A: simulated difference between plateau potential and the mechanical threshold (stimuli of 1,000-ms pulse width, amplitude range 0–250 pA in 25-pA increments). B: simulated membrane potential of the SMC model under a series of stimulation protocols (50–200 pA in 25-pA increments), compared with experimental measurements under the same simulation protocols (C).

The simulated results were generally in agreement with the experimental validation studies (Fig. 4C), with increasing pulse amplitudes (pulse width constant at 1,000 ms, pulse amplitude range 50–250 pA) leading to a higher V_peak in the rat SMCs. The simulated potential and plateau potential were compared with the experimental recordings in the following tables (Tables 2 and 3).

Table 2.

Simulated peak amplitude compared to experimental measurements at different level of stimulation amplitudes, a single 1,000-ms pulse

Amplitude, mA	Simulation, mV	Experiment, mV	Absolute Difference, mV	Relative Difference
200	10.4	22.1±5.8	11.7	−0.53
150	−4.4	−13.8±2.7	9.4	−0.68
100	−20.4	−20.0±2.3	0.4	0.02
50	−40.4	−38.8±4.7	1.6	0.03

Table 3.

Simulated plateau amplitude compared to experimental measurements at different level of stimulation amplitudes, a single 1,000-ms pulse

Amplitude, mA	Simulation, mV	Experiment, mV	Absolute Difference, mV	Relative Difference
200	−9.9	−19.5±3.6	9.6	−0.49
150	−16.2	−27.8±1.7	11.6	−0.42
100	−23.2	−32.1±2.9	8.9	−0.28
50	−38.2	−43.9±2.6	5.7	−0.13

A 50-pA stimulus also failed to elicit a substantial rapid upstroke depolarization in the experimental study, as occurred in the simulation, whereas pulse amplitudes of 75 pA or greater did achieve a rapid upstroke response. However, the simulated and experimental data did deviate in terms of the amplitude of the membrane potential (Table 2) and plateau potential ( Table 3). For example, at 200-pA stimulation amplitude, the simulated result was on average 10 mV lower in both the peak amplitude and potential amplitude compared with experimental data. On other hand, at 50-pA stimulation amplitude, the simulated result produced a better match to the experimental data (matching peak amplitude and 5 mV lower in the plateau potential).

Effects of Pulse-Train Frequency

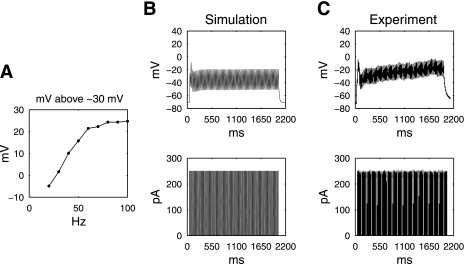
The simulated SMC response to a range of pulse-train frequencies, at a constant pulse width of 10 ms and pulse amplitude of 250 pA, is shown in Fig. 5. Between 10- and 100-Hz pulse-train frequencies, the amplitude of the simulated SMC membrane potential above the mechanical threshold increased in relation to the increasing stimulation frequency (Fig. 5A). Stimulation frequencies below 30 Hz could not maintain the plateau phase and therefore were deemed unsuccessful in activating the SMC model. Simulations demonstrated that although a single pulse of width 10 ms and amplitude of 250 pA had been unable to elicit a normal V_peak and sustain a plateau phase (as detailed above), a train of 10-ms-wide stimuli at 40-Hz frequency could induce a full depolarization of the SMC model (Fig. 5B).

Fig. 5.

A: simulated plateau potential above the mechanical threshold following a series of stimuli of 10-ms pulse width, 250 pA, 2,000/3,000 ms on-off time (0–100 Hz in 10-Hz increments). B: simulated membrane potential of the parameterized SMC model under a pulse train (40 Hz, 250 pA, 10-ms pulse width, 2,000/3,000-ms on-off time), compared with experimental measurements under the same simulation protocols (C).

The experimental validation studies demonstrated a close accord with the simulation study (Fig. 5C). The peak potential was 2.2 mV, compared with experimental value of −0.8 ± 3.2 mV. The simulated plateau potential was −20.7 mV, compared with experimental value of −21.7 ± 2.7 mV. The simulated upstroke was 5.8 mV/ms compared with experimental value of 4.1 ± 1.2 mV/ms. Additional simulations and experiments were performed at 40- and 80-Hz frequencies, and plateau potentials are presented in Table 4.

Table 4.

Simulated plateau amplitude compared to experimental measurements at different stimulation frequencies

Amplitude, mA	Simulation, mV	Experiment, mV	Absolute Difference, mV	Relative Difference
20 Hz	−34.9	−30.3±1.9	4.6	0.15
40 Hz	−20.7	−21.7±2.7	0.98	−0.05
80 Hz	−5.7	−6.9±2.4	1.2	−0.17

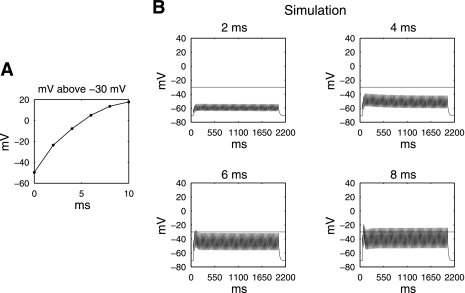
A series of further theoretical simulations were conducted to identify the effects of altering the pulse width during constant high-frequency pulse-train stimulation, since prior animal experiments used stimulation protocols with pulse widths between 0 and 10 ms, and showed these to be effective protocols in altering gastric motility (29). Results (Fig. 6A) showed that with an increasing pulse width, at constant stimulation frequency of 40 Hz, pulse widths between 4 and 6 ms approached closely to the mechanical threshold (−7.9 mV and 5.0 mV below and above the mechanical threshold, respectively).

Fig. 6.

A: simulation identifying the necessary pulse width required to achieve supramechanical threshold response at 250 pA, 40 Hz, 2,000/3,000-ms on-off time. B: simulated cell model responses at selective pulse widths (2 and 4 ms).

Simulated Effects of Stimulation on [Ca²⁺]_i

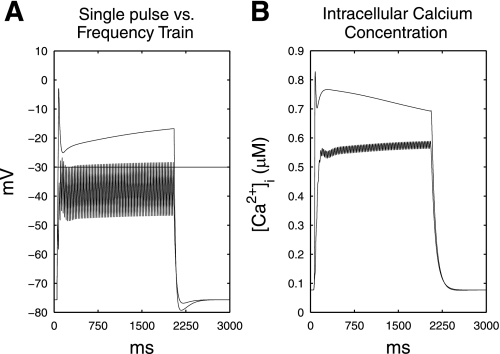
A simulated quantitative comparison between [Ca²⁺]_i following a single-pulse protocol and stimulation via a frequency train is demonstrated in Fig. 7. The [Ca²⁺]_i accumulation at the minimum amplitude required to activate the SMC model above the mechanical threshold at 40 Hz, 10-ms pulse width, 2,000-ms on time (i.e., 150 pA; Fig. 5) was compared with [Ca²⁺]_i following a single-pulse stimulation protocol with equal amplitude, but 2,000-ms pulse width. The V_peak of the single-pulse protocol was 27.4 mV higher than the plateau phase potential of the frequency-train protocol. The resting [Ca²⁺]_i for both stimulation protocols was 0.06 μM. The single-pulse protocol achieved an initial simulated Ca²⁺ influx of 0.87 μM, compared with 0.55 μM for the frequency-train protocol. During the plateau phase, the [Ca²⁺]_i was 0.77 μM for the single-pulse protocol and 0.53 μM for the frequency-train protocol. The single-pulse protocol required a power consumption of 300 mA·ms, whereas the frequency-train protocol required a 60% lower power consumption of 120 mA·ms.

Fig. 7.

A: simulated membrane potential response to a single-pulse stimulus of 2,000-ms pulse width, 145 pA, and a frequency train, 10-ms pulse width, 145 pA, 40 Hz, 2,000/3,000 ms on-off time. B: simulated intracellular calcium concentration to the same 2 simulation protocols in A; the single-pulse protocol achieved a higher initial Ca²⁺ influx, as well as [Ca²⁺]_i accumulation during the plateau phase than the frequency train.

DISCUSSION

We have evaluated the responses of rodent gastric smooth muscle cells to a variety of electrical stimulation protocols, through a joint experimentation and simulation methodology. The simulations employed an adapted biophysically based cell model (10) to evaluate a large range of stimulation parameters, and experimental validations of selected stimulation protocols were in satisfactory agreement with the simulated results. The joint computational simulation and experimental approach was then used to identify a range of minimum-energy stimulation protocols capable of effectively invoking a supramechanical threshold response (−30 mV) from isolated SMCs. Both single-pulse protocols and pulse trains were evaluated, and pulse trains were found to be a further potentially useful strategy to improve the power efficiency of GES protocols.

Computational simulations have previously been identified as a potential tool for increasing the efficiency of GES protocol research (9). This study proves this strategy is effective, by demonstrating that a large range of stimulation parameters may be evaluated in a combined simulation and experimental approach, without exhaustive experimental efforts. Simulations therefore can substantially reduce the material and time cost associated with tissue extraction, preparation, and experimentation. Importantly, experimental validation of simulated results should be conducted to prove their accuracy. In this study, the Corrias & Buist SMC model was parameterized on the basis of four sets of preliminary stimulation data, requiring adjustment of ten parameters (six of which were set according to experimental conditions), and these modifications successfully resulted in satisfactory quantitative agreement with the subsequent experimental studies (Fig. 2). Some discrepancies were noted with respect to the peak amplitude and plateau potential of the SMC membrane potential in some instances; however, such discrepancies are partly expected because of the innate deterministic nature of the model, which does not reproduce the stochastic variation that is encountered during empirical measurements. The fitting procedure was also performed using only one stimulation protocol (250-pA pulse with 1 s) only, whereas comparisons were made across multiple stimulation protocols. In addition, the maximum conductance values were optimized to fit the initial set of membrane potential measurements, rather than determined individually from experiments. The relative sensitivity of the conductance values was highly nonlinear and therefore the optimized fit might represent only one of the many combinations of the conductance values that could reproduce the experimental data. In future, with the accumulation of more experimental data to inform model refinement, it may be possible to further improve the agreement between the stimulation and experimental results.

There have been few studies examining the effects of an electrical stimulus on SMC electrophysiology, and none to the best of our knowledge that have focused on the minimum effective stimulation doses. This study presents a number of significant findings. In our first series of experiments, we found that a minimum single-pulse width could be identified for activating SMCs beyond a mechanical threshold of −30 mV (65 ms at 250 pA). In our second set of experiments, we identified a minimum pulse amplitude required to sufficiently activate an SMC (75 pA at 1,000-ms pulse width), and simulations demonstrated that the amplitude of the invoked membrane potential above the mechanical threshold was proportional to the amplitude of the stimulus. The current generation of commercially available GES devices mostly operates in the short-pulse range (typically around 300 μs) (1, 28), delivering stimuli of pulse widths below that required to directly depolarize SMCs. A new generation of long-pulse devices capable of directly modulating SMC electrophysiology has been proposed (26), and the validated simulation approach established in this study should facilitate the design of such devices by helping to define minimum-energy effective electrical doses.

Long-pulse stimulation protocols that activate gastric SMCs require a high amount of energy, which may lead to possible tissue damage due to electrical stimulation, even when amplitude and pulse width are kept to a minimum. Minimizing energy demand has prompted the idea of using a high-frequency train of stimuli instead of single long pulses, using substantially less energy (28). In our third series of experiments, we purposely employed a short-duration stimulus (10 ms), which we had shown was in itself incapable of activating an effective SMC response. Interestingly, at pulse-train frequencies higher than 30 Hz, the 10 ms pulse-width protocol employed (250 pA) was able to sustain the plateau phase and bring the membrane potential above the mechanical threshold (Fig. 5B). This pulse-train protocol requires 60% less power consumption than the comparison (minimum-energy) single-pulse protocol requires. We also found a positive correlation between stimulation frequency (at 10 ms pulse width) and the supramechanical threshold potential reached, as well as between the stimulation amplitude and the supra mechanical threshold potential reached (Fig. 4).

A simulation-based analysis was also used to predict the [Ca²⁺]_i accumulation accrued during the pulse-train protocol, compared with the [Ca²⁺]_i accumulation accrued during the single-pulse protocol. This analysis showed that the single-pulse protocol achieved a 37% higher initial Ca²⁺ influx and a 31% higher Ca²⁺ influx during the plateau phase, compared with the pulse-train protocol (Fig. 7). In gastric SMCs, calcium influx during the plateau phase of the response, and the resultant accrual of [Ca²⁺]_i, is thought to be primarily responsible for the prolonged SMC excitation-contraction coupling (24). The natural duration of gastric slow waves is ∼10 s (10). The simulation analysis above suggests that although pulse trains may effectively achieve a supramechanical threshold response at substantially lower power than single pulses, a tradeoff will be presented by the somewhat reduced accrual of [Ca²⁺]_i during the stimulation. The implications of this are not straightforward, however, because the relationship between the area under the slow-wave plateau, calcium influx, and tension generated is understood to be indirect (23). Further experimental studies, potentially aided by future biophysically based modeling of SMC excitation-contraction dynamics, would be needed to determine the exact implications of the differences in [Ca²⁺]_i influx between single-pulse and pulse-train protocols.

In vivo, gastric motility is coordinated by the interplay of multiple cooperating mechanisms, and in particular by the coordination of myogenic, neuronal, and hormonal factors (16). An electrical stimulus will potentially impact simultaneously on more than one of these elements apart from SMCs, including the enteric nervous system and the interstitial cells of Cajal (ICCs). For example, long-pulse stimuli may entrain ICC slow-wave activity, with important implications for the coordinated depolarization of gastric SMCs (4). Although SMCs are the effectors of peristaltic force and tone in the gut, isolated SMC analyses only provide one component of the total equation necessary for the rational design of efficient and efficacious long-pulse stimulation devices.

A number of further studies will therefore be necessary to translate the results and modeling methods described in this study to clinical utility. For example, future work will need to confirm that minimum-energy effective stimulation protocols identified through this work are also effective in vivo and to evaluate whether motility outcomes can be achieved. It will also be necessary to determine how the identified GES protocols modulate the electrophysiological properties of SMCs across and between the gastric muscle layers and to determine the effects of the stimuli on ICC entrainment and ICC-SMC network functions. We anticipate that the role of multiscale gastric electrophysiology simulations will expand in this research field to support these complex experimental efforts (9). For example, a gastric tissue model has recently been developed and validated through high-resolution mapping, incorporating a continuum description of SMC tissue layers and an ICC entrainment algorithm (12). In future work, more sophisticated multiscale models of this type could be applied to predict the physiological effects of stimulation protocols from cell to organ levels (9) and thereafter employed to identify effective protocols for incorporation into new clinical stimulation devices. Improved tools have recently been developed to facilitate more accurate measurements of human gastric electrical activity, which will allow for the experimental validation of these models (11, 22).

In conclusion, we have presented a simulation-assisted study of the response of rat gastric smooth muscle cells to a range of stimulation protocols. Defining minimum-energy effective stimulation protocols and the use of pulse trains are identified as important potential strategies for improving the power efficiency of implantable long-pulse GES devices that seek to modulate SMC electrophysiology. The simulated results in this study suggest that effective and efficient stimulation protocols include trains (40 Hz) of short pulse width (3–6 ms). Customized and validated computational simulations are shown here to be a worthwhile tool in improving the efficiency of GES research, and we anticipate a growing use of this research strategy in future.

GRANTS

This work is partially supported by grants from the National Institutes of Health (R01 DK64775), New Zealand Society of Gastroenterology, and the New Zealand Health Research Council (CDA08/078); a University of Auckland Doctoral Scholarship; and a research grant (to J. D. Z. Chen) from the Veterans Research and Education Foundation at the VA Medical Center, Oklahoma City, Oklahoma.