When are person tradeoffs valid?

Abstract

The person tradeoff (PTO) is commonly used in health economic applications. However, to date it has no theoretical basis. The purpose of this paper is to provide this basis from a set of assumptions that together justify the most common applications of the PTO method. Our analysis identifies the central assumptions in PTO measurements. We test these assumptions in an experiment, but find only limited support for the validity of the PTO.

1. Introduction

The Person Tradeoff (PTO) method was first devised by Patrick, Bush & Chen (1973) (they call it “the equivalence [of numbers] technique”) and later promoted by several other researchers as a means of mitigating fairness concerns in health allocation (Nord, 1995; 1999; Murray and Lopez, 1996, Pinto-Prades, 1997; Baron & Ubel, 2002; Ubel et al., 2000). The PTO method has been used in important health policy applications. For example, the World Bank uses the PTO in the estimation of the quality weights in its burden of disease studies.

Despite its long history and popularity, the PTO has, to our knowledge, no theoretical basis to support its use. As of yet, it is unknown under which conditions the PTO adequately reflects societal preferences over allocations of health. The purpose of this paper is to identify and test these conditions. The identification of these preference conditions will facilitate an understanding of the rules that govern societal health allocation decisions when the PTO is employed. It will thus help clarify assumptions associated with applications of PTO values in modeling and analysis (e.g., cost-effectiveness and cost-value analysis). Further, identifying preference conditions will allow for empirical testing of the validity of the PTO. Towards the end of this paper we report the results of a first empirical test of the conditions underlying the PTO. The experiment sheds light on the question of whether or not using the PTO is justified. The enterprise of testing the validity of the PTO is of significant importance for the obvious reason that if we ignore the preference implications of the PTO, we may end up recommending policies that conflict with society’s best interests.

Person Tradeoff Formulas

Patrick et al. (1973) is consistent with the following:

1. Assume four health state improvements “w to x”, “y to z”, “w to w” and “y to y” (for brevity we denote these by (w, x), (y, z), (w, w) and (y, y) respectively) and natural numbers m and n.

2. Policy 1 is such that m persons receive (w, x) and n persons are left untreated (i.e., they receive (y, y)).

3. Policy 2 is such that m persons receive (w, w) (i.e., they are left untreated) and n persons receive (y, z)).

4. Policy 1 is equivalent to Policy 2 if and only if $\frac{n}{m}=\frac{V\left(x\right)-V\left(w\right)}{V\left(z\right)-V\left(y\right)}$, where V is a function that assigns a numeric value to health states.

In the Patrick et al. (1973) analysis, z is “optimal functioning” and assigned a value of 1, y and w are both set equal to death, which is (implicitly) given a value 0. Finally, x is some suboptimal health state which is to be assigned a value between 0 and 1. So for example, by the Patrick et al. (1973) measurement scheme a decision maker is indifferent between the following policies:

• Policy A = “Save 500 lives (m), but these people are left with blindness (x)”, and

• Policy B = “Save 100 lives (n), returning all one hundred to full health (z)”

if and only if $\frac{n}{m}=\frac{V\left(x\right)-V\left(w\right)}{V\left(z\right)-V\left(y\right)}$ or $\frac{100}{500}=\frac{V\left(x\right)-0}{1-0}$ or $V\left(x\right)=\frac{1}{5}$.Since the work by Patrick et al. (1973), the general method given in (1) to (4) above has been used numerous times as a means of evaluating person tradeoffs (see for example, Nord, 1999; Murray and Lopez, 1996; Pinto-Prades, 1997; Baron & Ubel, 2002). Ubel et al. (2000) have objected to (4) above, because it treats health state improvements as value differences. While Ubel et al. (2000) did not state an alternative formula for expressing health state improvements as a combination of health state utilities, their position is consistent with a more general approach given here as (4′):

• 4′) Policy 1 is equivalent to Policy 2 if and only if $\frac{n}{m}=\frac{U(w,x)}{U(y,z)}$.

Thus using our previous example, the value ⅕ under (4′) is not the value of blindness as it is when (4) is assumed, but rather may only be interpreted as the ratio of the value of moving from death (w) to blindness (x) to the value of moving from death (y = w) to full health (z). If we assume that moving from death to full health equals 1 (i.e. U(y, z) = 1), which, as we will see later, is allowed under the properties of U, then ⅕ gives the utility of moving from death to blindness (i.e. U(w, x) = ⅕). Ubel et al. (2000) point out, using specific examples, how fairness concerns on the part of the respondent may be accommodated by assuming (4′) instead of (4). The downside of (4′), of course, is that, because it is more general, it is a less efficient means of computing the value of health state improvements; the value of each health state improvement must be elicited directly and cannot be inferred by subtracting health state values. Thus, simple and efficient tables given by Nord (1999) (see for example Tables 14 and 15 of Nord (1999)) or values elicited for the global burden of disease (Murray and Lopez, 1996), each being an example of values derived using Step 4, are not permissible if Step 4′ is substituted.

In this paper, we identify the assumptions underlying (4) and (4′). The comparison of assumptions will permit better insight into how much more restrictive (4) is than (4′). Several empirical studies have examined implications of the PTO formula (Damschroder et al., 2004; Dolan & Green, 1998; Dolan & Tsuchiya, 2003) and generally obtained negative results. Unfortunately, it is not clear from these studies why PTO measurements give inconsistent results, because several assumptions are tested simultaneously. The advantage of our approach is that it allows for exact tests of (4) and (4′) and their difference, in the sense that no confounding assumptions have to be made. Hence, our analysis defines a new empirical framework for testing the validity of PTO measurements. We discuss this framework in Section 5. Finally, this analysis provides insight into the issue of bias in PTO measurement. Theorems 4.1 and 4.2 offer a full understanding of the preference conditions implied by PTO formulas. Thus, when a preference condition is violated we are assured that PTO measurement yields biased results.

Person Tradeoffs and Risky Choice

Most PTO exercises are carried out in a riskless context. This means that the respondent makes decisions between two alternatives that deliver health state improvements to a cohort with certainty. However, it is clear that health policy decisions inherently involve risk or uncertainty (Doctor & Miyamoto, 2005). We know, for example, that policy makers face uncertainty as to the number of persons who will be afflicted with disease or injury in any given year. Therefore, PTO exercises draw from a subset of a larger (and perhaps more realistic) set of policy decision making scenarios that involve risk. It behooves us then to model person tradeoffs in the most general way possible so as to accommodate potential future modifications that might involve risky choices. Therefore, in what follows we describe the basic preference objects with which the policy maker is confronted as risky policies. The outcomes of these risky policies are distributions of health state improvements and the goal of the policy maker is utility maximization of health state improvements. The model we develop governs preferences over riskless policies as well, as we will explain in the next section. Thus, current practice is a special case of our approach.

2. Background

Let C_i be the set of all possible health state improvements that are experienced by the ith person in society over some pre-specified period of time (e.g., 1 year)¹ and n the number of individuals in society affected by a particular health program. The set of health state improvements, C, is a set of n-tuples of the form c = 〈c₁, c₂, ... , c_n〉, where c_i denotes the change in health of the i-th person. A health state change c_i is composed of two dimensions: pre-policy health status, x_i, health before the policy decision, and post-policy health status y_i, health after the policy decision. That is, c_i is given by the ordered pair (x_i, y_i), where each x_i and y_i are health states. We restrict these pairs such that they are always health improvements. The set of all possible health states is denoted by H. The notation 0_j is used to denote that person j’s health does not change, i.e., for all health states x, and persons j, (x_j, x_j) ≡ 0_j.

By (p:c¹; c²) we denote the health policy that gives health state improvement c¹ with probability p and health state improvement c² with probability 1-p. In what follows, we only need health policies involving at most two distinct outcomes and, hence, for ease of exposition, we will restrict attention to these. We will denote the set of all possible health policies by G. The set G contains not only risky health policies but also riskless ones, i.e. policies for which p is equal to 0 or 1 or for which c¹= c². It is for this reason that we wrote in the previous section that our analysis comprises current practice as a special case.

We consider a social planner who has preferences over health policies. The social planner’s preference relation (over health policies in G) is denoted by ≥. The social preference relation ≥ is interpreted to mean “at least as preferred as” and is a weak order. Weak orders are transitive (if a ≥ b and b ≥ c then a ≥ c) and complete (for every a and b, a ≥ b, or b ≥ a). Strict preference, ≥, and indifference, ∼, are defined in the usual manner.² We assume that preferences over health policies are governed by expected utility (von Neumann & Morgenstern, 1944). We will relax this assumption to accommodate non-expected utility models in Section 5.

When for all g and g’ ∈ G, g ≥ g’ if and only if U(g) ≥ U(g’), we say that a utility function U represents preferences over policies in G. The relation ≥ governs preferences over distributions of health changes by restricting attention to riskless health policies. Under expected utility the utility function that represents preferences over risky policies is an interval scale: Unique up to multiplication by a positive constant and addition of a real constant. We impose that persons for whom health does not change have no effect on preference. In other words, adding any number of persons with constant health to a population does not either improve or reduce the desirability of the policy.

For simplicity, we assume that a person tradeoff equivalence always exists. That is, for every improvement (w, x) and (y, z) in H × H there exist positive integers m, n such that for policies c¹ = 〈(w₁, x₁), ... , (w_m, x_m), 0_m+1, ... , 0_m+n〉 and c² = 〈0₁, ... , 0_m, (y_m+1, z_m+1), ... , (y_m+n, z_m+n)〉, we have c¹ ∼ c².

Let us summarize the assumptions made so far.

STRUCTURAL ASSUMPTION 1

A preference relation ≥ governs preferences over health policies. The relation ≥ satisfies expected utility. A person tradeoff equivalence always exists. For any outcome of a health policy, adding any number persons in constant health does not affect the desirability of the policy.

3. Definitions

We now provide definitions that will provide a formal justification for the use of person tradeoff measurement.

DEFINITION 1

Marginality (Fishburn, 1965)

(½:c¹;c²) ∼ (½:c³;c⁴) whenever c¹, c², c³, c⁴ ∈ C, and any c_i ∈ C_i that appears once (twice) in (½:c¹;c²) also appears once (twice) in (½:c³;c⁴) and vice versa.

Marginality says that preferences depend only on marginal probability distributions over health state improvements. As an illustration, consider the following two policies (Table 1) involving two equal-sized groups of patients.

Table 1. Example Marginality I.

	Probability
	½		½
Patient groups	1	2	1	2
Policy A	(poor, good)	(poor, good)	(poor, poor)	(poor, poor)
Policy B	(poor, good)	(poor, poor)	(poor, poor)	(poor, good)

Policy A results with probability ½ in a situation where both groups of patients go from poor health to good health and with probability ½ in a situation where both groups of patient(s) remain in poor health. Under health policy B one group of patients goes from poor health to good health with the other remaining in poor health. Under both policies, each patient has a ½ probability of an improvement to good health. Thus, the marginal probability distributions of health changes are the same for each patient under both policies. Put another way, both policies offer each patient exactly the same expected health benefit; when this is the case then marginality says that policies A and B are equivalent.

It is conceivable that the social planner is not indifferent between policies A and B. For instance, under A the possibility exists that everyone in society remains in poor health, a possibility that may be considered undesirable and lead to a preference for B. On the other hand, under B there will always be inequality in final health between patients. This may be a ground for a policy maker to prefer policy A. Ultimately, empirical testing will have to decide the descriptive appeal of marginality as a preference condition. We will report such a test in Section 7.

Because marginality is such a crucial condition let us consider another example (see Table 2). Both policies A and B offer the same expected benefit to each patient and thus they are equivalent if marginality holds. However, notice that policy A will never forsake (a group of) patients in worse health to give health to (a group of) patients better off; whereas there is a ½ probability under policy B that (the group) of patients starting in fair health will achieve good health while (the group of) patients starting in “poor health” will remain in “poor health”. Thus, it could be argued that policy A is preferred to policy B on the grounds of concern for fairness, because under all states (of the world) policy A, while providing the same expected benefit as policy B, will never allow those better off to achieve even greater health at the dereliction of those worse off. Yet, marginality prohibits a policy maker from exercising such fairness preferences. Under policy B, we see that it offers a ½ probability of attaining equity (with the policy every one gets “fair health”) which may be a highly valued goal when expected benefits are equal. However, this is at the risk (also a ½ probability) of a great disparity in health. In sum, marginality has difficulty accommodating decisions that are governed by specific equity and fairness principles.

Table 2.

Example Marginality II

	Probability
	½		½
Patient groups	1	2	1	2
Policy A	(fair, good)	(poor, fair)	(fair, fair)	(poor, poor)
Policy B	(fair, good)	(poor, poor)	(fair, fair)	(poor, fair)

DEFINITION 2

Anonymity

For all cⁱ = 〈c₁, c_i , _..., c_n〉 ∈ C and permutations π on {1, ..., n} such that c^j = 〈c_π(1), c_πi , _..., c_π(n)〉 we have cⁱ ∼ c^j.

Anonymity says that the identity of the recipient of a health state change does not affect the desirability of the distribution of health state improvements. Basically, it says that the social planner is only interested in changes in health. Other factors like race, sex, whether the recipient is a war veteran or not, etc. play no role. Under anonymity, the policy 〈(poor health, good health), (poor health, poor health)〉 is equivalent to the policy 〈(poor health, poor health), (poor health, good health)〉. In both policies there is one person whose health improves from poor health to good health and one person who stays in poor health. Hence, the policies are equivalent because the decision maker exercises no favoritism as to whether it is the first patient or the second patient whose health improves. Anonymity seems a plausible condition for social choice, particularly when the task is to value health state improvements, and it is indeed commonly assumed in evaluations of social welfare.

DEFINITION 3

Additivity

For all x, y, z in H, n in $\mathbb{N}$, and 〈(x₁, y₁), ..., (x_n, y_n), (y_n+1, z_n+1), ..., (y_n+n, z_n+n)〉, 〈(x₁, z₁), ..., (x_n, z_n)〉 ∈ C, we have 〈(x₁, y₁), ... , (x_n, y_n), (y_n+1, z_n+1), ..., (y_n+n, z_n+n)〉 ∼ 〈(x₁, z₁), ..., (x_n, z_n)〉.

Additivity, loosely speaking, says that health changes may be added together. It implies, for example that 〈(fair health, good health), (poor health, fair health)〉 is equivalent to 〈(fair health, fair health), (poor health, good health)〉. The example shows that additivity may be construed as a controversial assumption. One obvious reason why a policy maker would not be indifferent in the above example is that in the first policy everyone gets some improvement in health, whereas in the second case this is not true.

The following two Lemmas are useful in proving our main result.

LEMMA 4.1

Suppose Structural Assumption 1 holds. For all c in C, Marginality (Definition 1) and Anonymity (Definition 2) imply U(c) = U(c₁) + U(c₂) + ... U(c_n).

LEMMA 4.2

Suppose Structural Assumption 1 holds. For all x, y in H, Marginality (Definition 1) and Anonymity (Definition 2) imply U(x, x) = U(y, y) = 0.

4. Main Result

The following theorem characterizes statement 4′, the PTO model suggested by Ubel et al. (2000).

THEOREM 4.1

Suppose Structural Assumption 1 holds. Then for all health improvements (w, x) and (y, z) in H × H, for all positive integers m and n, and for all policies c¹ = 〈(w₁, x₁), ... , (w_m, x_m), 0_m+1, ... , 0_m+n〉 and c² = 〈0₁, ... , 0_m, (y_m+1, z_m+1), ... , (y_m+n, z_m+n)〉 in C for which c¹ ≥ c², the statements (i) and (ii) are equivalent:

1. The preference relation, ≥, satisfies Marginality (Definition 1) and Anonymity (Definition 2).

2. There exists a positive real function U on H × H such that c¹ ≥ c² if and only if $\frac{n}{m}\ge \frac{U(w,x)}{U(y,z)}$.

With Theorem 4.1 the utility function over health state improvements takes an additive form (Fishburn, 1965; Keeney & Raiffa, 1993). The additive form can accommodate some concerns about inequality (Atkinson, 1970), but not all (Bleichrodt, Crainich & Eeckhoudt, 2008). We next characterize a person tradeoff for which preference for health state improvements is represented by health state value differences, i.e. Eq. (4), the model proposed by Patrick et al. (1973) and Nord (1995), which is most commonly used in practice.

THEOREM 4.2

Suppose Structural Assumption 1 holds. Then for all health improvements (w, x) and (y, z) in H × H, for all positive integers m and n, and for all policies c¹ = 〈(w₁, x₁), ... , (w_m, x_m), 0_m+1, ... , 0_m+n〉 and c² = 〈0₁, ... , 0_m, (y_m+1, z_m+1), ... , (y_m+n, z_m+n)〉 in C for which c¹ ≥ c², the statements (i) and (ii) are equivalent:

1. The preference relation, ≥, satisfies Marginality (Definition 1), Anonymity (Definition 2), and Additivity (Definition 3).

2. There exists a positive real-valued function V such that c¹ ≥ c² if and only if $\frac{n}{m}\ge \frac{V\left(w\right)-V\left(x\right)}{V\left(y\right)-V\left(z\right)}$.

The following theorem characterizes the uniqueness of the function U in Theorem 4.1 and the function V in Theorem 4.2:

THEOREM 4.3

If U’ is any other positive real-valued function that satisfies part (ii) of Theorem 4.1 then U’ = αU, for some positive real α. If V’ is any other positive real-valued function that satisfies part (ii) of Theorem 4.2 then V’ = αV + β, for some positive real α and some real β.

Theorem 4.3 shows that U is a ratio scale and V is an interval scale. The uniqueness results are not obvious from the PTO formulas and are a consequence of the assumptions in Theorems 4.1 and 4.2. Note that Theorems 4.1 and 4.2 allow the functions U and V to be concave to express inequality aversion.

Person tradeoff research often emphasizes the use of matching (equivalence) judgments to infer relations among health state preferences. Therefore, we note the following for clarity.

REMARK 4.1

For any PTO equivalence, Theorem 4.1 implies $\frac{n}{m}=\frac{U(w,x)}{U(y,z)}$ and Theorem 4.2 implies $\frac{n}{m}=\frac{V\left(x\right)-V\left(w\right)}{V\left(z\right)-V\left(y\right)}$.

Proof of Theorems 4.1 - 4.3 and Remark 4.1 are given in Appendix A.

5. Extension to Non-Expected Utility

Thus far we have assumed that the social decision maker behaves according to expected utility. Our main motivation to do so was that social policy is normative in nature and expected utility is still the dominant normative theory of decision making. However, if we want to test whether people, when put in the role of a social planner, actually make choices that are consistent with the PTO, a problem arises. Testing preference conditions is a descriptive activity and there exists abundant evidence that expected utility is descriptively invalid: people deviate systematically from expected utility. One important reason for these deviations is probability weighting. People do not evaluate probabilities linearly, as expected utility assumes, but are more sensitive to changes in probability close to 0 (impossibility) and 1 (certainty) than to changes in the middle range. Most people perceive a change in probability (e.g. the reduction of a cancer risk) from 0.01 to 0 (the elimination of the risk) or from 0.99 to 1 (the certainty of the risk) as more meaningful than a change from, say, 0.54 to 0.53.

In this Section we will explain how our main result can be extended to non-expected utility. We will relax the assumption that expected utility holds. Without loss of generality we assume that the notation (p:c¹;c²) implies that c¹ ≥ c², i.e. health policies are rank-ordered, the first mentioned health state improvement is always considered at least as good as the second. This of course is not a restriction as any policy may be expressed with outcomes in rank-order. Rank-ordering is crucial in what follows. As with expected utility, we assume that the utility of a risky policy is a weighted average of the utilities of its outcomes. However, we no longer assume that the weights are equal to the probabilities. Instead, we assume that preferences ≥ over prospects (p:c¹;c²) can be represented by:

$$\pi \left(\mathrm{p}\right)\mathrm{U}\left({\mathrm{c}}^1\right)+(1-\pi \left(\mathrm{p}\right))\mathrm{U}\left({\mathrm{c}}^2\right),$$ (1)

where the decision weights π depend on p but need not equal p. The function π satisfies π(0) = 0 and π(1) = 1 and we assume that for some p* in [0,1], π(p*) = ½. Eq. (1) is obviously more general than expected utility. It includes expected utility as a special case, but also most other models of decision under risk that are currently used in the literature. Most importantly, it includes prospect theory (Kahneman and Tversky 1979, Tversky and Kahneman 1992), the most influential descriptive theory of decision under risk today.

Let us now redefine marginality.

DEFINITION 1′

Let p* be the probability such that at p*, π(p*) = ½. (p*:c¹;c²) ∼ (p*:c³;c⁴) whenever c¹, c², c³, c⁴ ∈ C, and any c_i ∈ C_i that appears once (twice) in (p*:c¹;c²) also appears once (twice) in (p*:c³;c⁴) and vice versa.

Definition 1′ is very similar to the definition of marginality except that now we do not use probability ½ but a probability p* that has a decision weight of ½. The probability p* can be any number between 0 and 1. It can but need not be equal to ½. We can now restate our main results.

THEOREM 5.1

If we replace in Structural assumption 1 expected utility by Eq. (1) then Theorems 4.1, 4.2, and 4.3 still hold when marginality is replaced by Definition 1′.

One question remains

how can we elicit the probability p* so that we guarantee a decision weight, π(p*) = ½? We will briefly outline a procedure to do so. We start by choosing three health state improvements c⁰ ≥ c^M ≥ c^m and an arbitrary probability p. Then we determine c¹ such that the decision maker is indifferent between (p:c¹;c^m) and (p:c⁰;c^M). Applying Eq. (1) this indifference implies that

$$\pi \left(\mathrm{p}\right)\mathrm{U}\left({\mathrm{c}}^1\right)+(1-\pi \left(\mathrm{p}\right))\mathrm{U}\left(c^m\right)=\pi \left(\mathrm{p}\right)\mathrm{U}\left(c^0\right)+(1-\pi \left(\mathrm{p}\right))\mathrm{U}\left(c^M\right)$$

or

$$U\left(c^1\right)-U\left(c^0\right)=\frac{1-\pi \left(p\right)}{\pi \left(p\right)}U\left(c^M\right)-U\left(c^m\right).$$

We next elicit c² such that the decision maker is indifferent between (p:c²;c^m) and (p:c¹;c^M). Applying Eq. (1) again this indifference implies that

$$U\left(c^2\right)-U\left(c^1\right)=\frac{1-\pi \left(p\right)}{\pi \left(p\right)}U\left(c^M\right)-U\left(c^m\right).$$

And thus, U(c²) - U(c¹) = U(c¹) - U(c⁰). Finally, we ask for the probability p* such that c¹ for sure is considered equivalent to (p*:c²;c⁰). By Eq. (1) this indifference yields:

$$\mathrm{U}\left(c^1\right)=\pi \left({\mathrm{p}}^{\ast }\right)\mathrm{u}\left({\mathrm{c}}^2\right)+(1-\pi \left({\mathrm{p}}^{\ast }\right))\mathrm{U}\left(c^0\right)$$

or π(p*) (U(c²) - U(c¹)) = (1-π(p*))(U(c¹) - U(c⁰)). Because U(c²) - U(c¹) = U(c¹) - U(c⁰), it follows that π(p*) = ½.

Proof of Theorems 5.1 is given in Appendix A.

6. Experiment

Design

We used the above theory in an experimental test of the validity of the two versions of the PTO, (4) and (4′). The experiment tested the following four questions:

1. Assuming expected utility, does marginality hold?

2. Does additivity hold?

3. Is the assumption of expected utility appropriate or do people deviate from expected utility in choosing between health policies?

4. if people deviate from expected utility, does the generalization of marginality, Definition 1′ hold?

Of the 113 subjects in the experiment 30 were graduate students from the University of Southern California and 83 undergraduate students from Erasmus University Rotterdam. The experiment was web-based. Subjects performed the experiment by clicking on a link which took them to the webpage of the experiment. A copy of the experimental questions is in the Appendix B. Before the actual experiment, we pilot-tested several versions of the experiment using other university students.

Table 3 summarizes the experimental questions. The experiment started with two tests of marginality. These two tests constituted of the examples discussed in Tables 1 and 2. Subjects were told that there are two equally-sized groups of patients and two health policies. In the first question all patients started off in poor health. Under policy A there was a 50% chance that both groups of patients would move to good health and a 50% chance that both groups of patients would stay in poor health. That is, policy A = (½: 〈(poor,good), (poor,good)〉; 〈(poor,poor), (poor,poor)〉). Under policy B there was a 50% chance that the first group of patients would move to good health but the second group of patients would stay in poor health and a 50% chance that the first group of patients would stay in poor health but the second group of patients would move to good health. That is, policy B = (½: 〈(poor,good), (poor,poor)〉; 〈(poor,poor), (poor,good)〉). Subjects were asked to choose between these two policies. Indifference, the option predicted by marginality, was allowed. In the second test of marginality, the patients differed in initial health. Subjects were asked to choose between policies A = (½: 〈(fair,good), (poor,fair)〉; 〈(fair,fair), (poor,poor)〉) and B = (½: 〈(fair,good), (poor,poor)〉; 〈(fair,fair), (poor,fair)〉). Again, marginality predicts indifference between A and B.

Table 3.

Experimental Questions

Test	Policy
Marginality I	A	(½: ((poor,good), (poor,good)); ((poor,poor), (poor,poor))
	B	(½: ((poor,good), (poor,poor)); ((poor,poor), (poor,good))
Marginality II	A	(½: ((fair,good), (poor,fair)); ((fair,fair), (poor,poor))
	B	(½: ((fair,good), (poor,poor); ((fair,fair), (poor,fair))
Additivity	A	((fair,good),(poor,fair))
	B	((fair,fair),(poor,good))
Probability Weighting I	A	(½: 100 lives; 80 lives)
	B	(½: T1 lives; 70 lives)
Probability	A	(½: T1 lives; 80 lives)
Weighting II	B	(½: T2 lives; 70 lives)
Probability Weighting III	A	(p* T2 lives; T0 lives)
	B	T1 lives
Eq. (1)′	A	(p*: ((poor,good), (poor,good)); ((poor,poor), (poor,poor))
	B	(p*: ((poor,good), (poor,poor)); ((poor,poor), (poor,good))

The third question tested was additivity. Subjects were asked to choose between A = 〈(fair, good), (poor, fair)〉 and B = 〈(fair,fair), (poor,good)〉. Additivity predicts indifference.

The next questions tested to what extent subjects deviated from expected utility in social choice questions. We sought to determine the probability p* with decision weight ½. We used number of lives saved (moving from death to full health) as number of health improvements. This was done to simplify the experimental tasks. We learned in the pilots that subjects found these questions complex and this simplified the task in estimating p*.

We started with a practice question. Then we determined the number of life-years T¹ such that subjects were indifferent between policies A = (½: 100; 80), i.e. equal chances of saving 100 lives and of saving 80 lives, and B = (½: T¹; 70). In the notation of Section 4, this means that c⁰ = 0, c^M = 80, and c^m = 70. We then determined the number of life-years T² such that subjects were indifferent between A = (½: T¹; 80) and B = (½: T²; 70). Finally, we asked for the probability p* which established indifference between A = T¹ years for sure and B = (p*: T²; 100). As shown in Section 5, under Eq. (1) this probability has decision weight ½.

In the final question, we used the above-elicited probability p* to compare policies A = (p*: 〈(poor,good), (poor,good)〉; 〈(poor,poor), (poor,poor)〉) and B = (p*: 〈(poor,good), (poor,poor)〉; 〈(poor,poor), (poor,good)〉). That is, we repeated the first question but now with probability p* instead of ½. Under Definition 1′ subjects should be indifferent between A and B. A and B are rank-ordered due to anonymity. In Section 5, we pointed out that rank-ordering is crucial for Eq.(1). We could not repeat question 2 with probability p* instead of probability ½ because for policy B the rank-order might vary by subject.

7. Results

Marginality

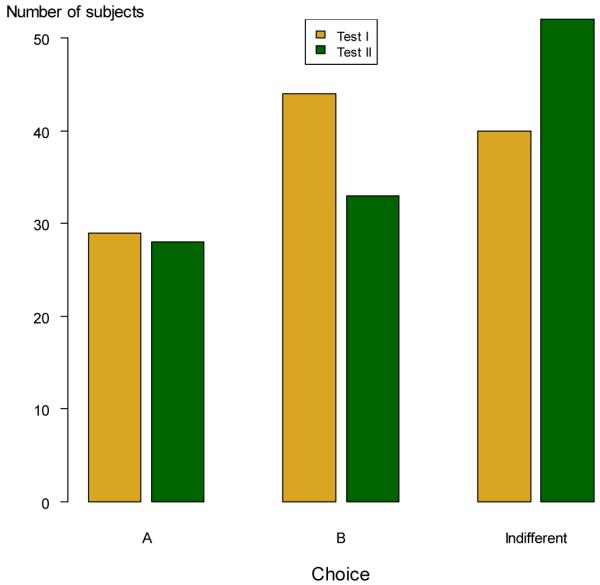
Figure 1 shows the results for the two tests of marginality. Remember that marginality predicts indifference. Approximately 40% of the subjects are indifferent in each test separately. Seventy percent of the subjects who satisfy marginality in the first test also satisfy marginality in the second test. Consequently, about 25% of the subjects satisfy marginality in both tests. Recall that Theorems 4.1 and 4.2 require that marginality holds in both tests.

Figure 1.

Results Marginality

Among the subjects who strictly prefer one of the two options, most chose B. Apparently, subjects do not want to risk that none of the groups obtains a health improvement. Note that this conflicts with a preference for an equal distribution of health. Under A both groups are always in equal health, whereas under B inequality in health exists. The preference for B is particularly pronounced in the first test. The difference between the proportion of subjects choosing A and the proportion of subjects choosing B is not significant, however (binomial test, p=0.10 in the first test and p=0.61 in the second test).

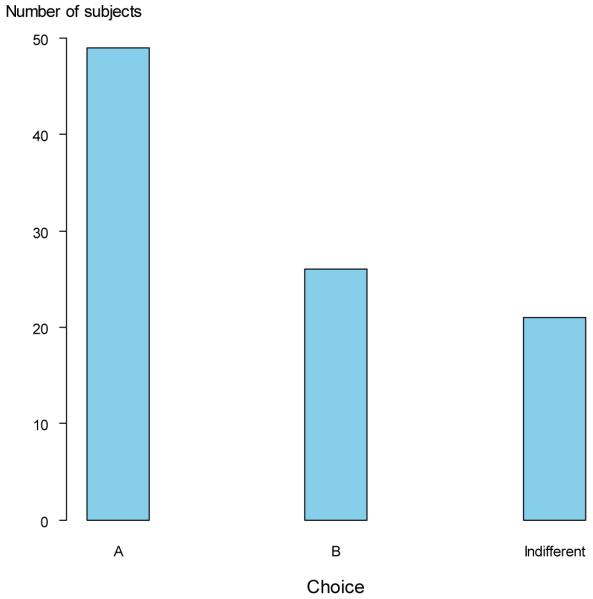
Additivity

Figure 2 shows the results for additivity. Additivity predicts indifference, but, as is clear from Figure 1, this does not obtain. A majority of subjects chooses option A. The proportion of subjects choosing A is significantly higher than the proportion of subjects choosing B (p < 0.001). In terms of final outcomes A and B are equal in the sense that one group of patients is in fair health and the other group in good health. The difference is that in A it is the first group who is in good health and in B the second. It is unlikely that subjects care which group of patients is in good health and which group in fair health. However, under policy A both groups of patients get an improvement in health, whereas under policy B only the first group benefits. Apparently, this matters.

Figure 2.

Results Additivity

Probability Weighting

In the tests of marginality reported above we assumed that subjects behaved according to expected utility. Table 4 shows the results of the test of this assumption. Seventeen subjects were removed from this analysis, because they either reported values of T¹ or T² less or equal than 100 or a value of T² less than T¹. In these cases, policy A dominated policy B. We interpreted these responses as reflecting confusion on the part of the subject and, therefore, we exclude these subjects. Many subjects reported T¹ = 110 and T² = 120 implying risk neutrality in societal decisions involving lives saved.

Table 4.

Test of Expected Utility

	Mean (st. dev.)	Median (IQR)
T1	111.9 (7.5)	110 (110,110)
T2	126.5 (30.5)	120 (120,122.8)
p*	0.55 (0.25)	0.50 (0.50,0.70)

The important results are the results for p*. Were subjects to behave according to expected utility then they should report a value of p* equal to 0.50. Table 4 shows that a substantial proportion of our subjects do not deviate much from expected utility. The median value of p* is in fact 0.50. The mean was 0.55, slightly higher than 0.50 and indicating that there was some tendency in our sample to underweight probabilities around 0.50.³ The interquartile range (IQR) shows that the distribution of responses of p* was skewed to the right, confirms this tendency. Underweighting of probabilities around 0.50 is consistent with findings from the literature on decision under risk (Gonzalez and Wu 1999, Abdellaoui 2000, Bleichrodt and Pinto 2000), except that the degree of underweighting that we observed is somewhat less in comparison. Because probability weighting is more pronounced at the ends of the probability scale, these results are not too surprising—we would expect the weight for 0.5 to be close to 0.5. The findings should not interpreted to mean that our subjects were expected utility maximizers at all probabilities. However, the findings do indicate that our tests of marginality (at p = 0.5) are robust.

In total, there were 30 subjects for whom p* was exactly equal to 0.50, i.e. they were fully consistent with expected utility. The data for these subjects, the EU maximizers, allow a test of the consistency in responses. For the EU maximizers, question 8 was identical to the first question and, consequently, we would expect the choice in both questions to be the same. Eighty percent indeed made the same choice, 20 percent changed preference. Inconsistency rates up to 30% are common in choice experiments (e.g. Starmer and Sugden 1989, Hey and Orme 1994, Ballinger and Wilcox 1997, Loomes and Sugden 1998). Those who made a different choice always changed from strict preference to indifference or from indifference to strict preference. No subject changed from a strict preference for A to a strict preference for B or vice versa. The consistency of the data seems satisfactory.

The EU maximizers behaved more in line with marginality than the rest of the sample. Slightly over 50% of them satisfied marginality in both tests. Those EU maximizers who violated marginality were distributed evenly over choosing A and choosing B. The EU maximizers violated additivity and, just like the rest of the sample, tended to prefer A, the policy in which both groups of patients benefit. The latter finding is of relevance for the interpretation of the data of the EU maximizers. One reason why they behaved according to EU could be the minimization of cognitive effort: reporting p* = 0.50 is an easy response strategy. Likewise, reporting indifference is an easy response strategy. There was no EU maximizer who was always indifferent, however, suggesting that behavior consistent with EU was not due to a minimization of cognitive effort.

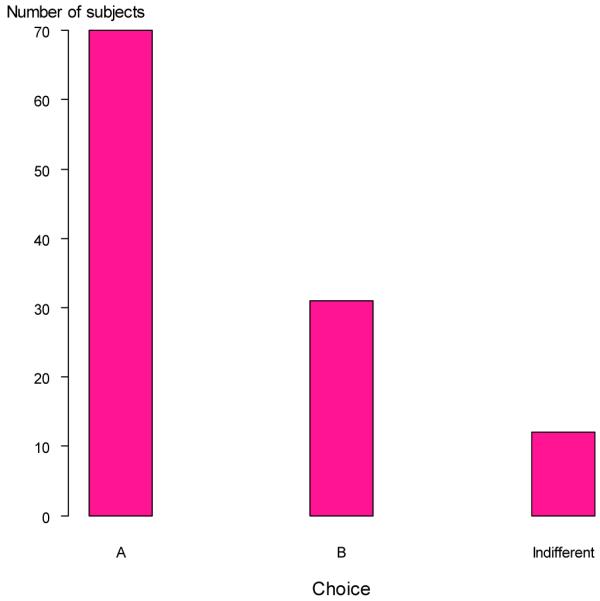
Definition 1′

Let us finally turn to the results of the test of marginality under non EU, Definition 1′. Figure 3 shows that after controlling for violations of expected utility, the support for marginality decreases. Most subjects now prefer policy A. Because there was a slight tendency to underweight probabilities with decision weight 0.50, there were more (41) subjects for whom p* > 0.50 than subjects for whom p* < 0.50 (24). For subjects who underweighted probability (those for whom p* < 0.50), the probability that both groups of patients gain was greater than 0.50 in Policy A. Thus, the better outcome in choice A had a larger decision weight in the second test than it did in the first test when p was set equal to 0.50. Apparently this is sufficient to offset the risk that no-one gains: 32 out of these 41 subjects preferred A and only 4 preferred B. For subjects who overweighted probability (p* < 0.50) the situation is reversed. The risk of no-one gaining exceeds the chance of both groups gaining. Fourteen out of 24 now prefer B. Still, 9 of these subjects prefer A.

Figure 3.

Results Definition 1′

8. Discussion

It is worth evaluating critically the preference conditions that give rise to PTO measurement so as to determine the appropriate (and valid) scope of its use. If the assumptions outlined in Theorem 4.2 hold, then the results obtained from PTO measurements would not conflict with the objectives of CEA. Indeed such measurements of health state values were the original intent of Patrick et al. (1973). Beyond use of the PTO formula given by Patrick et al. (1973) for valuation of outcomes in CEA, the preference conditions that justify the use of PTO may be controversial when it comes to the mitigation of equity and fairness concerns. Of particular concern is marginality which equates policies for which the expected benefit to each patient is the same. Marginality underlies both versions of the PTO model that have been proposed in the literature. As we discussed, marginality is to some degree unavailing with respect to addressing inequalities in health. We discussed situations where expected benefits of programs are the same, but where the public may have strong opinions about how health is distributed that cannot be captured with the PTO method. Because PTO responses require interpersonal comparisons, several researchers have conjectured that these responses capture distributional concerns (e.g., Nord (1999), p. 90, first paragraph; Damschroder et al. 2005, p. 2 fifth paragraph; Salomon & Murray (2004), p. 284, second paragraph). The results presented in this paper make clear that due to marginality, the PTO is prohibited from accommodating specific distributional concerns.

We tested the conditions underlying the PTO in an experiment. The results strongly reject additivity and, hence, the type of PTO model most commonly used. The evidence on marginality is more ambiguous. Most subjects do not satisfy marginality exactly, but prefer one of the two options presented to them. Controlling for expected utility violations, somewhat more subjects prefer the policy that offers both patient groups the prospect of both receiving an improvement in health even when this is at the risk of no improvement for either group.

The findings on marginality are of more general interest for research on equity in health. In the literature on health inequality it is commonly assumed that people dislike inequality in health and always want to reduce this. Our findings reveal a more subtle picture. People care also, and perhaps even more, about equality of opportunity i.e., each group having an opportunity to improve under all states (of the world). Whether this result stands up to further testing is a topic for future research. Further, because of small sample sizes and a sizeable proportion of foreign students in the American sample, comparing equity preferences across different nationalities (Dutch and U.S.) was not possible, but is an important future line of research.

We obtained some evidence that people deviated from expected utility in making social choices. The deviation was limited, however, and less than what is commonly observed in choice under risk. Whether people are indeed more consistent with expected utility in social choices than in decision under risk is a topic worthy of future exploration.

When we allowed for violations of expected utility, the support for marginality decreased. Then, most subjects preferred the policy leading to equal final health outcomes. We are inclined to interpret this result with caution. To be able to design a test of marginality that is robust to violations of expected utility, we had to ask four questions. One potential concern is cumulating of error as questions proceed; however, this concern would predict a greater difficulty in finding a violation of marginality with the non-expected utility test and we were able to detect such a violation.

Summing up, our experimental study casts some doubt on the validity of the PTO, especially the most common form of it. It should be kept in mind that the number of tests that we performed was limited and that the results on marginality under non expected utility should be treated with care. Our empirical study was primarily intended as an illustration of how the PTO can be tested and to give some first insights as to its validity as an outcome measure in cost effectiveness analysis. Clearly, more evidence is needed.

9. Concluding Remarks

We began this paper with the question, “When are person tradeoffs valid?” The answer, we have shown, is that they are valid when respondents are indifferent to social choices for which the expected benefit to each person in society is the same (i.e., marginality, see Definition 1), when decisions are not affected by a persons identity (i.e., anonymity, see Definition 2), and when health improvements are additive in preference (i.e., additivity, see Definition 3). As we explained, marginality excludes certain kinds of equity and fairness considerations. To allow for future testing we have explained how the various conditions can be tested and provided some initial findings. These findings put in doubt the most common form of the PTO and provide limited support for a more general form. We hoped that this paper will help to clarify what is involved in using the PTO and will foster future empirical research into its validity.

Appendix A. Proofs

In the proofs we will employ the abbreviation (x, y)_jcⁱ to indicate that for some specific distribution, cⁱ, health state change (x_j, y_j) is substituted for person j, i.e., cⁱ = 〈c₁, ..., c_j = (x_j, y_j), ... , c_n〉 for a fixed 1 ≤ j ≤ n.

PROOF OF LEMMA 4.1

Fishburn (1965) Theorem 3 showed that when ≥ is a weak order, expected utility and the marginality condition (Definition 1) together imply U(c₁, c₂, ..., c_n) = U₁(c₁) + U₂(c₂) + ... + U_n(c_n). If (U₁, U₂, ... , U_n) is an array of representing additive individual utility functions then by anonymity so are (U₂, U₃, ... , U_n, U₁), (U₃, U₄, ... , U_n, U₁, U₂), ... , (U_n, U₁, ... , U_{n - 1}). Define Σ_iU_i as the sum of each U_i, then it is clear that because for the aforementioned arrays, each U_i occurs at each array position once, we may construct an array (Σ_iU_i, Σ_iU_i, ... , Σ_iU_i) that also is representing. This shows that the additive individual utility functions can be chosen as identical. Let U equal one of these additive utility functions and this yields the desired result.

PROOF OF LEMMA 4.2

We must show both that Structural Assumption 1 together with Definitions 1 and 2 imply that for all b in H, U(b, b) = 0. Choose any health states a, b ∈ H and n > 0 in the natural numbers, $\mathbb{N}$. Let c¹ = 〈(a, b)〉 and c² = 〈(a₁, b₁), (b₂, b₂)..., (b_n, b_n)〉. Because constant health does not affect desirability of the policy (Structural Assumption 1), c¹ ∼ c². By Lemma 1, U(a, b) = U(a, b) + nU(b, b), or, 0 = nU(b, b), dividing by n we see that for all b in H, U(b, b) = 0. Q.E.D.

PROOF OF THEOREM 4.1

To prove the theorem, we must show that, (i) if and only if (ii). Clearly (ii) implies (i), so we show that (i) implies (ii). Choose any (w, x) and (y, z) in H × H and any m and n > 0 in the natural numbers, $\mathbb{N}$, such that if c¹ = 〈(w₁, x₁), ... , (w_m, x_m), 0_m+1, ... , 0_m+n〉 and c² = 〈0₁, ... , 0_m, (y_m+1, z_m+1), ... , (y_m+n, z_m+n)〉 in C then c¹ > c². Applying the result of Lemma 4.1 and noting that by Lemma 4.2 constant health has zero utility, we see that this directly yields (ii). Therefore, (i) implies (ii).

PROOF OF THEOREM 4.2

To prove the theorem, we must show that, (i) if and only if (ii). Clearly (ii) implies (i), so we show that (i) implies (ii). Define $v:H\to \mathbb{R}$, such that v(z*) = 1 and if x is in H and x ≠ z* then v(x) = 1 - U(x, z*). Let (x, y)_jc denote a finite health change distribution whereby a fixed person gets health change (x, y). Choose any such fixed health change distribution c ∈ C. Because ≥ is a weak order and a property of weak orders is that they are reflexive, (x, y)_jc c ∼ (x, y)_jc. By Marginality (Definition 1), Anonymity (Definition 2), Additivity (Definition 4) and Lemma 4.2, U((x, y)_jc) = U(x, y) + k, where k is the sum of the utility of health state improvements for all other persons not specified. If y = z*, then U(x, y) = U(x, z*) = 1 - (1 - U(x, z*)) = v(y) - v(x). Suppose now that y ≠ z*. We observe that Lemma 4.1 and Additivity (Definition 3) guarantees that U(x, y) + U(y, z*) = U(x, z*). So U(x, y) = U(x, z*) - U(y, z*) = (1 - U(y, z*)) - (1 - U(x, z*)) = v(y) - v(z). Thus, choosing any health state change (x, y) for a fixed person, we have, U((x, y)_jc) = U(x, y) + k = v(y) - v(x) + k, or, U(x, y) = v(y) - v(x), where $v:H\to {\mathbb{R}}^{+}$. We have proven the theorem.

PROOF OF THEOREM 4.3

Suppose U’ is any other function that satisfies (ii) of Theorem 4.1, then $\frac{n}{m}\ge \frac{U(w,x)}{U(y,z)}=\frac{U^{\prime }(w,x)}{U^{\prime }(y,z)}$. Let (x, y) be fixed then U’ = αU, where α = U’(x, y)/U(x, y). Thus U is a ratio scale. Suppose now that Theorem 4.2 holds such that U(x, y) = v(y) - v(x), where $v:H\to {\mathbb{R}}^{+}$ and that v’ is any other function that is representing for v. Let U’(x, y) = v’(y) - v’(x) and v(y) - v(x) = U(x, y), we know that [v’(y) - v’(x)] = α[v(y) - v(x)]. Fix y = y*. It follows that, for all x in H, v’(x) = αv(x) + β, where β = v’(y*) - αv(y*). Thus, v is an interval scale. We have proved Theorem 4.3.

PROOF OF REMARK 4.1

The proof is straightforward. Assuming a PTO equivalence and (ii) of Theorem 4.1, c¹ ≥ c² if and only if $\frac{n}{m}\ge \frac{U(w,x)}{U(y,z)}$ and c² ≥ c¹ if and only if $\frac{n}{m}\le \frac{U(w,x)}{U(y,z)}$, hence, a PTO equivalence (Structural Assumption 1) and Theorem 4.1 (i) implies $\frac{n}{m}=\frac{U(w,x)}{U(y,z)}$ By Theorem 4.2, U(x, y) = v(y) - v(x), where $v:H\to {\mathbb{R}}^{+}$ and then $\frac{n}{m}=\frac{v\left(x\right)-v\left(w\right)}{v\left(z\right)-v\left(y\right)}$ Q.E.D.

PROOF OF THEOREM 5.1

Follows from the proof of Theorems 4.1 and 4.2 in Fishburn (1965) by substituting Eq. (1) for expected utility and p′ for ½.

Appendix B. Experimental Questions*

* bracketed text [] indicates that a previous answer was inserted dynamically as text in the question.

Marginality I

Q1: Imagine two groups of patients of the same size, Group 1 and Group 2. Each group starts out in poor health. And, each has a 50% chance of some health outcome. A 50% chance is like a fair coin flip: Choose a policy, flip a coin, and if the coin lands on heads, then some outcome happens. If the coin lands on tails, then another outcome will happen. Below are two risky health policies, POLICY A and POLICY B. After choosing Policy A, if an imaginary coin lands on heads, then Policy A offers a 50% chance of moving both groups of patients from poor health to good health. Otherwise, if the coin lands on tails, then everyone will stay in poor health. After choosing Policy B, if an imaginary coin lands on heads, Policy B offers a 50% chance of moving Group 1 patients from poor to good health, but Group 2 patients stay in poor health. Otherwise, if the coin lands on tails, Group 1 patients stay in poor health and Group 2 patients move from poor health to good health. Please examine the table below and choose the health policy that you consider best.

	50% chance (heads)	50% chance (tails)
POLICY A:	Group 1: Poor to Good Group 2: Poor to Good	Group 1: Poor to Poor Group 2: Poor to Poor
POLICY B:	Group 1: Poor to Good Group 2: Poor to Poor	Group 1: Poor to Poor Group 2: Poor to Good

Which do you prefer?

• _ I prefer Policy A

• _ I prefer Policy B

• _ Equally good

Marginality II

Q2: Imagine two groups of patients of the same size, Group 1 and Group 2. Group 1 starts in fair health. Group 2 starts in poor health. And, each has a 50% chance of some health outcome. Please examine the table below and choose the health policy that you consider best.

	50% chance (heads)	50% chance (tails)
POLICY A:	Group 1: Fair to Good Group 2: Poor to Fair	Group 1: Fair to Fair Group 2: Poor to Poor
POLICY B:	Group 1: Fair to Good Group 2: Poor to Poor	Group 1: Fair to Fair Group 2: Poor to Fair

Which do you prefer?

• _ I prefer Policy A

• _ I prefer Policy B

• _ Equally good

Additivity

Q3: Consider again the patients described in question 2. Group 1 and Group 2 are the same size. This time, however, no risk is involved. A certain outcome will happened when you choose a policy. Consider the following two policies. Policy A moves Group 1 patients from fair health to good health and Group 2 patients from poor health to fair health. In Policy B Group 1 patients stay in fair health while Group 2 patients move from poor health to good health.

	100% chance
POLICY A:	Group 1: Fair to Good Group 2: Poor to Fair
POLICY B:	Group 1: Fair to Fair Group 2: Poor to Good

Which do you prefer?

• _ I prefer Policy A

• _ I prefer Policy B

• _ Equally good

Probability weighting I

Q4: Please state the number of lives saved (greater than 100 and less than) that makes the following two policies equivalent:

Table	Chance:	50% (heads)	50% (tails)
	Policy A	100 lives	80 lives
	Policy B	?=_	70 lives

Enter your answer here:? = _(T¹)

Probability weighting II

Q5: Please state the number of lives saved that makes the following two policies equivalent:

Table	Chance:	50% (heads)	50% (tails)
	Policy A	T1 lives	80 lives
	Policy B	?=_lives	70 lives

Enter your answer here:? = _ (T²)

Probability Weighting III

Q6: Table 1 shows two policies A and B. Policy A has a 100% chance of saving lives and a 0% chance that 100 lives are saved. Policy B saves [T¹] lives for sure. As indicated by the check mark “X” Policy A is better because it saves more lives than Policy B.

In Table 2, notice the probabilities are reversed. We have marked the check “X” so that Policy B is better because Policy B saves more lives than Policy A.

Table 1	Chance:	100%	0%
	X Policy A	[ T2] lives	100 lives
	_ Policy B	[ T1] lives	[ T1] lives
Table 2	Chance:	0%	100%
	X Policy A	[ T2] lives	100 lives
	_ Policy B	[ T1] lives	[ T1] lives

Please indicate the probability (e.g., 0.10... 0.35, 0.50, 0.65, ...0.90) that you believe would make Policy A and Policy B equally good.

Enter your answer here:? = _(p*)

Marginality non-expected utility (see Eq. (1′))

Q7: Imagine two groups of patients of the same size, Group 1 and Group 2. Each group starts out in poor health. A Below are two risky health policies, POLICY A and POLICY B. Please examine the table below and choose the health policy that you consider best.

	[p*] chance	1 - [p*] chance
POLICY A:	Group 1: Poor to Good Group 2: Poor to Good	Group 1: Poor to Poor Group 2: Poor to Poor
POLICY B:	Group 1: Poor to Good Group 2: Poor to Poor	Group 1: Poor to Poor Group 2: Poor to Good

Which do you prefer?

• _ I prefer Policy A

• _ I prefer Policy B

• _ Equally good