Dissecting the Impact of Matrix Anchorage and Elasticity in Cell Adhesion

Abstract

Extracellular matrices determine cellular fate decisions through the regulation of intracellular force and stress. Previous studies suggest that matrix stiffness and ligand anchorage cause distinct signaling effects. We show herein how defined noncovalent anchorage of adhesion ligands to elastic substrates allows for dissection of intracellular adhesion signaling pathways related to matrix stiffness and receptor forces. Quantitative analysis of the mechanical balance in cell adhesion using traction force microscopy revealed distinct scalings of the strain energy imparted by the cells on the substrates dependent either on matrix stiffness or on receptor force. Those scalings suggested the applicability of a linear elastic theoretical framework for the description of cell adhesion in a certain parameter range, which is cell-type-dependent. Besides the deconvolution of biophysical adhesion signaling, site-specific phosphorylation of focal adhesion kinase, dependent either on matrix stiffness or on receptor force, also demonstrated the dissection of biochemical signaling events in our approach. Moreover, the net contractile moment of the adherent cells and their strain energy exerted on the elastic substrate was found to be a robust measure of cell adhesion with a unifying power-law scaling exponent of 1.5 independent of matrix stiffness.

Introduction

Exogenous cues are known to trigger cell-fate decisions during embryogenesis, homeostasis, and regeneration. Signals associated with the extracellular matrix (ECM) include ligand density, matrix stiffness, ligand conformation, ligand anchorage, and lateral ligand distribution. These signals control stem cell differentiation (1–3), as well as apoptosis, proliferation, and differentiation of other cell types (4–6), or cell assembly in 3D tissues (7). It has recently been demonstrated that mechanical features of cells and their matrices, i.e., matrix stiffness, global cell force balance, and cell shape, play a key role in proliferation and differentiation by affecting different cell signaling events from protein phosphorylation to the epigenetic level (1–3,6,8,9). Unveiling the underlying mechanisms will clearly open up exciting new options for exerting control over cells in vitro or in vivo and is therefore one of the current priorities in cell biology, biophysics, and biomaterials science.

Along these lines, many details about the signaling molecules involved have been explored. Proteins such as focal adhesion kinase (FAK), vinculin, and p130Cas have been suggested to regulate and transmit adhesion-related signals primed by integrins. Activation of binding sites by phosphorylation and triggering of cluster formation are thought to be involved in the signaling process. Currently, stress-sensitive stretching and unfolding of protein domains, and positioning thereby of phosphorylation and binding sites at a certain distance, are subjects of intensive research (9–11). It is well known that in downstream signaling pathways, other proteins, such as RhoA, Cdc42, Rac1, and ROCK, regulate intracellular stress levels, which are built up in the actin cytoskeleton by myosin motors (11). Those events could be shown to affect cell proliferation and differentiation even further downstream (4,12). Although the mentioned signaling molecules are thought to be some of the key players in cell adhesion signaling, they act in a highly complex network, which is far from being understood (10,13,14). On the other hand, many attempts have been made to correlate those intracellular biochemical signaling events to specific exogenous cues including substrate stiffness, prestrain, external forces, and ligand density and distribution (8,15–20). Although several pathways could be revealed, the inherent complexity of intracellular signaling often makes it difficult to modulate any selected cue while keeping other regulators constant.

In a biophysical context, models have been suggested to explain how cells respond locally or globally to the mechanical properties of their extracellular microenvironment. These investigations include treatments of cells in the framework of linear elastic theory (21,22), as soft glassy materials (23), or as mechanical tensegrity structures (12). Adhesion formation and force development have been investigated as cooperative springs of single bonds (24–26), as stretch-dependent clustering of single molecules (24,26–28), and even considering the dynamics of the formation of individual contacts (29–31). These models could indeed describe many experimental observations and provide invaluable insights into possible mechanisms.

However, the efficacy and robustness of cellular communication manifests itself in the inherent convolution and cross-talk of intracellular signals (10). For instance, in the context of stiffness-dependent cell response, cellular force levels are known to become upregulated with increased substrate stiffness, which does not allow for a dissection of signaling events with respect to stiffness or receptor force, although both are similarly important (15,19). Owing to this complexity, experimental approaches and theoretical models frequently fail to quantitatively unravel the resulting connection of distinct features as occur, for instance, in the regulation of local cell adhesion forces in conjunction with overall cytoskeletal stress. To address this challenge, we introduce here a novel design strategy to control cell adhesion forces independent of the stiffness of the underlying substrate. Based on earlier studies on the modulation of anchorage of adhesion ligands to polymer substrates (32–34), we have developed, evaluated, and applied a functional substrate platform that allows the control of ligand anchorage and substrate stiffness independent of each other. The obtained set of materials is shown to be instrumental for the decoupling of distinct physical properties associated with the presentation of ECM components and for the subsequent dissecting of biophysical and biochemical signaling events in cell adhesion.

Materials and Methods

Substrate preparation and characterization

Maleic acid copolymer (MACP)-coated polyacrylamide (PAAm) gel samples were prepared based on the method of Wang and Pelham (15). First, the preparation of the PAAm layers was performed in the standard way. Briefly, coverslips were freshly oxidized (35) and surface-modified with (3-acryloxypropyl)trimethoxysilane (ABCR, Karlsruhe, Germany). PAAm were synthesized using stock solutions of 80% acrylamide (PlusOne Acrylamide PAGE, Amersham Biosciences, Piscataway, NJ) and 1% bis-acrylamide solutions (Amersham Biosciences), and fluorescent microbeads (Fluoresbrite YG microspheres, 0.50 μm, Polysciences, Warrington, PA). To adjust the layer thickness, coverslips modified with (heptadecafluoro-1,1,2,2-tetrahydrodecyl)dimethylchlorosilane (ABCR) were placed on top during gel formation. For details, see the Supporting Material.

The gel films were washed for 30 min in deionized water, then dried at room temperature under vacuum for 30 min. Next, monomolecular films with MACP on top of PAAm hydrogels were prepared. Poly(styrene-alt-maleic anhydride) (PSMA, 20,000 mol wt, special product of Leuna-Werke, Leipzig, Germany) and poly(ethene-alt-maleic anhydride) (PEMA, 125,000 mol wt, Sigma Aldrich, Deisenhofen, Germany) were spin-coated (RC5, Suess Microtec, Garching, Germany) using 0.14% PSMA and 0.3% PEMA copolymer solutions in tetrahydrofuran (Fluka, Deisenhofen, Germany) or acetone/tetrahydrofuran (1:2, w/w, Acros Organics, Geel, Belgium), respectively. Entanglement of the water-soluble MACP chains with the cross-linked PAAm hydrogel and chain attachment via residual radicals from hydrogel synthesis allow for a gentle surface modification.

A glass ring (1 cm in diameter) was stuck to the coated coverslips using silicone vacuum grease. Before use, the polymer-coated coverslips were equilibrated for 24 h in phosphate-buffered saline (Biochrom, Berlin, Germany) at pH 7.4 to ensure complete hydrolysis of the anhydride groups of the maleic anhydride copolymers to carboxylic acid groups (36) and removal of nonbound polymer molecules, as well as a full reswelling of the PAAm gels under physiological buffer conditions. The final gel films were 70–100 μm thick, as determined by confocal laser scanning microscopy (SP1, Leica Microsystems, Bensheim, Germany) using a 40× immersion oil objective.

Fibronectin (FN) (purified from adult human plasma (37)) was anchored on the substrate by adsorption from a 50-μg/ml solution in phosphate-buffered saline for 1 h at 37°C. The surface concentrations, anchorage strength, and cellular reorganization were determined by using ¹²⁵I-labeled FN or 5-(and-6)-carboxytetramethylrhodamine (Invitrogen, Carlsbad, CA), respectively. For details see the Supporting Material.

Gel stiffness was determined by scanning force spectroscopy (Bioscope BS2-Z, Veeco, Santa Barbara, CA) of PAAm films with three different bis-acrylamide concentrations. The Young's modulus, E, was obtained using a Hertz cone model (38) with a fitting of the first 10–200 nm of indentation profiles using the freely available software PUNIAS (39). The exact spring constants (∼0.01 N/m) of the pyramid-tipped SiNi cantilevers (Microlevers, ThermoMicroscopes, Sunnyvale, CA) were determined by the thermal noise method (40). The Poisson ratio of PAAm was assumed to be 0.48, as published elsewhere (41). The measurements of the three different bis-acrylamide concentrations were fitted by a second-order polynomial function as introduced by Engler et al. (8). From the fitted curve, the Young's moduli for other bis-acrylamide concentrations were calculated.

Cell culture

Human endothelial cells from the umbilical cord vein were collected according to the procedure suggested by Weis et al. (42) and grown to confluence in endothelial cell growth medium (Promocell, Heidelberg, Germany) containing 2% fetal calf serum. After one to four passages, 2 × 10⁴ cells/cm² were seeded on the FN-coated hydrogel substrates and grown for 60 min before analysis.

Traction force microscopy

Microscopy of adherent cells was performed on an inverted microscope (Axiovert 200M, Carl Zeiss MicroImaging, Jena, Germany) equipped with an AxioCam MRm camera (Zeiss), a 40×/0.75 objective (EC Plan-Neofluar, Zeiss), a moveable stage (SCAN IM 120 × 100, Märzhäuser, Wetzlar-Steindorf, Germany) with controller (MAC500, Ludl Electronic Products, Hawthorne, NY), and a heating stage P and incubator S (PeCon, Erbach, Germany) with controller (Tempcontrol 37-2 digital, CTI Controller 3700 digital, PeCon) to achieve constant cell culture conditions (37°C, 5% CO₂, 60–70% relative humidity). For fluorescence imaging, a Hg lamp and filter sets for FITC and rhodamine were attached.

In each experiment, images of bead positions in the uppermost vertical layer were taken for single adherent cells (3–5 cells/sample) with a pixel size of 0.1586 μm using the FITC filter set. The positions of the cells were memorized by the Mark&Find module of AxioVision software (Zeiss) and the moveable stage to gather images before and after detaching the cells by treatment with trypsin-EDTA (Sigma-Aldrich) for 10 min. Cell spreading and FN fibrillogenesis were visualized by phase contrast and fluorescence microscopy using the rhodamine filter set, respectively.

The image set (with and without the cell) was analyzed by the Fourier-transform traction cytometry method introduced by Butler et al. (41), with improvements published elsewhere (43,44). Briefly, after adjustment of slight misalignments of both images using the StackReg (45) tool of the freely available software ImageJ (46), bead displacements were calculated using the cross-correlation algorithm (44), with thresholding, averaging, and Gaussian filtering implemented by MATLAB software (The MathWorks, Natick, MA). From the displacement fields, traction fields were calculated (41,43) by the unconstrained approach (without a pinned cell circumference) to avoid artifacts from an improper definition of the cell border (47). From the traction fields, the maximum traction stress per cell, T_max, the strain energy exerted by the cell, U, and the net contractile moment of the cell, M_net (41), were determined.

Western blot analysis

FAK phosphorylation was analyzed after 60 min of cell culture on the MACP-PAAm substrates with three different concentrations of bis-acrylamide. Western blot analysis was performed as described elsewhere (11) using primary antibodies FAK (FAK 3285, Cell Signaling Technology, Danvers, MA), phospho-FAK pTyr397 and pTyr861 antibody (FAK pY397 and FAK pY861 PAb, Invitrogen), and GAPDH antibody (GAPDH (FL-335) HRP, Santa Cruz Biotechnology, Santa Cruz, CA). Densitometric analysis was carried out using a Lumi-Imager F1Workstation with LumiAnalyst 3.0 software (Roche, Nutley, NJ). The blots were analyzed using ImageJ software (46) by normalizing total FAK and phospho-FAK intensities to the internal standard GAPDH and calculating the phosphorylation ratio (phospho-FAK divided by total FAK). For details see the Supporting Material.

Results

Combinatorial variation of substrate stiffness and ligand anchorage

PAAm hydrogels with different cross-linking densities were coated with thin films of MACP, i.e., PSMA and PEMA. This surface-selective modification did not affect the elastic properties of the hydrogel surface layer, as the MACP chains are soluble in an aqueous environment (36). Stiffness measurements by nanoindentation using scanning force microscopy (Fig. 1 A) confirmed this assumption.

Figure 1.

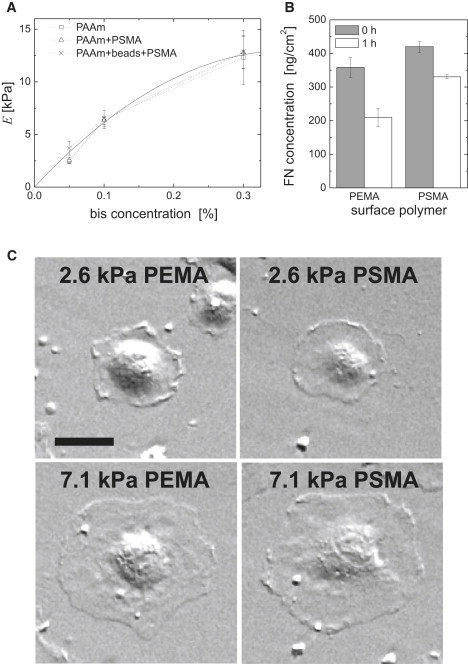
MACP-PAAm hydrogels as composite materials with combinatorial variation of substrate stiffness and ligand anchorage. (A) Dependence of the Young's modulus, E, of PAAm hydrogel films on bis-acrylamide concentration indicated that the MACP surface modification had no impact on hydrogel stiffness. The data have been fitted by the second-order polynomial $y=\mathrm{71,000}x-\mathrm{97,000}{x}^2$. (B) FN amounts adsorbed on PEMA- or PSMA-coated PAAm hydrogels represent about a monolayer of protein coverage. Differences in FN displacement after 1 h in 500 μg/ml of bovine serum albumin demonstrate the variation of FN-substrate anchorage. Error bars indicate the standard deviation. (C) Phase-contrast images of adherent endothelial cells after 1 h of cell culture. Spreading of endothelial cells was dependent on substrate stiffness but not on the type of MACP coating. Scale bar, 30 μm.

Earlier experiments with MACP thin films on stiff glass supports showed that differences in the polarity and hydrophobicity of the MACP translate into a variation of the anchorage of matrix molecules such as FN, leading to strong anchorage on PSMA and weak anchorage on PEMA (34). Adherent endothelial cells were found to respond to this gradation in anchorage by differences in focal and fibrillar adhesion patterns on the micro- and nanometer scales, which were hypothesized to be correlated to differences in cell receptor forces (32,33).

The behavior of graded ligand anchorage on MACP was preserved on MACP-PAAm substrates. FN surface concentration and its characteristics of displacement by bovine serum albumin were comparable to those in experiments performed on hard glass substrates (33,34,48), as seen in Fig. 1 B. The high ligand surface density (∼7 × 10¹¹ cm²) was reflected in the absence of observable differences in cell spreading on the two different MACP coatings (Fig. 1 C). The spreading of endothelial cells after 1 h depended only on substrate stiffness, with an increased spreading on stiffer substrates, which is in agreement with earlier findings (8,15). The type of MACP surface coating did not affect the overall cell shape, because cell spreading does not depend on small differences in ligand density in the range of high ligand densities of FN used in the experiments herein (8,16). This well-known fact is generally explained in terms of the dependence of cell spreading and migration on the number of receptor-ligand bonds formed, which is governed by the number of available cell-surface receptors in the case of high ligand densities. We further found fibrillar FN reorganization to be more pronounced on the more polar MACP-substrate (PEMA) in comparison to the PSMA coating in the case of stiff PAAm hydrogels, as expected from earlier experiments on rigid glass substrates (33). Due to the lack of focal adhesions on soft (2.6 kPa) substrates (20), FN fibrils were negligible in those cases, as FN fibrillogenesis crucially depends on directed integrin-FN transport along actin stress fibers out of focal adhesions (49).

Modulation of traction force by ligand anchorage

Incorporation of fluorescent beads into the PAAm hydrogels permitted quantitative measurement of endothelial cell tractions on MACP surfaces by unconstrained Fourier transform traction cytometry (41,43,44). Using the unconstrained approach, artifacts from an improper definition of the cell border could be omitted (47). The analysis clearly confirmed the regulation of cell traction forces by the graded anchorage of FN to the MACP surfaces. The maximum traction stress, T_max, and the net contractile moment, M_net, of single cells were evaluated: a high mean T_max of $\overline{T_{\max }}=700\pm 290$ Pa and a high mean M_net of $\overline{M_{\text{net}}}=-9.5\pm 7.5$ pNm were determined on PSMA, compared to a low $\overline{T_{\max }}=300\pm 190$ Pa and $\overline{M_{\text{net}}}=-3.7\pm 2.8$ pNm on PEMA. High T_max and |M_net| indicated the strong FN anchorage to PSMA surfaces and low T_max and |M_net| demonstrated the weak FN anchorage to PEMA. In addition, the observation of a direct correlation of T_max with M_net is in good agreement with earlier investigations by Wang et al. (50) on intracellular stress behavior, suggesting that both parameters are good measures of cellular traction. It is important to note that the maximum traction stress was not significantly affected by the stiffness of the substrates, as had been envisaged for our approach. Hence, the ligand-substrate anchorage is sensed by the cell adhesion apparatus and translated into a modulation of receptor forces in cell adhesion.

Strain energy depicts active force dipole behavior

Fourier transform traction cytometry furthermore allowed us to evaluate the strain energy, U, that the cell imparts on the substrate. The mean strain energy, $\overline{U}$, was found to decrease with increasing stiffness (Fig. 2 A). This observation somehow contradicts common thinking and earlier reports of elevated U at higher Young's moduli, E (51). However, as discussed below, those studies rely on a covalent ligand immobilization, which drives an important difference in the cell response in comparison to our setup.

Figure 2.

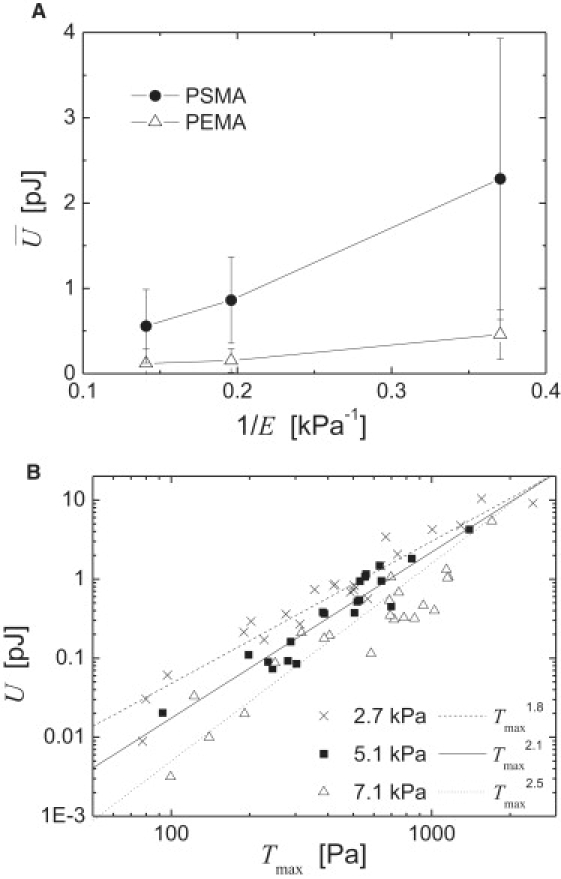
Strain energy, U, exerted by endothelial cells on MACP-PAAm substrates. (A) Mean values of U plotted versus 1/E for the two different MACP coatings. An almost linear dependence is observed. Error bars indicate the standard deviation. (B) U plotted versus the T_max for each single cell irrespective of the type of MACP coating. An almost ideal T_max² scaling is observed for intermediate substrate stiffness, whereas lower or higher stiffness results in an exponent for T_max that is diminished or increased, respectively.

On the other hand, our results are supported by applying one basic idea of the active force dipole model recently introduced by Schwarz and Bischofs (21). This model was established to describe the dependence of “durotaxis”, cell polarization, and multicell alignment on the stiffness of the cellular microenvironment in two and three dimensions. Based on an optimization principle using linear elasticity, the authors predicted an inverse dependence of U on Young's modulus, E. Our findings perfectly agree with this prediction: not only is U proportional to 1/E, but, further, it gathers the right prefactor scaling with its quadratic dependence on the cellular dipole moment, which in our case was calculated as M_net. The ratio of the square roots of the slopes of the plots of $\overline{U}$ versus 1/E for PSMA and PEMA is 2.2 (Fig. 2 A), which compares well with the ratio of $\overline{M_{\text{net}}}$ values for these two surface coatings of 2.6. This comparison clearly supports the above statement on the quadratic prefactor scaling. In a similar way, the ratio of $\overline{T_{\text{max}}}$ values is found to be in the same range, at 2.3. Thus, our results show a successful application of the active force dipole model to quantitatively explain the elastic energy imparted by adherent cells.

Stiffness-dependent variation of traction force scaling

The scatter of data in Fig. 2 A primarily originates from the inherent populational variance of primary endothelial cells. However, this variance reveals at the same time a feature of the system that cannot be accommodated by the assumptions of the active force dipole model. This property comes to the fore when plotting U versus T_max for each single cell, irrespective of the type of MACP coating (Fig. 2 B). In a double-logarithmic representation, the data of each substrate stiffness fall on separate straight lines, implying a power-law behavior. Furthermore, the plot indicates exponents in the range of 2. Such exponents resemble roughly the already discussed scaling of $U\sim T_{\max }^2$ originating from linear elasticity theory. Again, we found higher values of U for the same T_max with decreasing E, as discussed above for Fig. 2 A. However, a closer look at how variation of the power-law exponent depends on substrate stiffness revealed a distinct deviation from linear elastic behavior. For a low substrate stiffness of 2.7 kPa, an exponent of 1.8 was observed, whereas for a high substrate stiffness of 7.1 kPa, an exponent of 2.5 was determined. At an intermediate stiffness, an almost ideal exponent was achieved with 2.1. This finding suggests that there is an additional mechanism active in the cell adhesion process that is not accommodated in a linear elastic framework like the active force dipole model. It calls for a stiffness-dependent signaling mechanism on top of a linear elastic response of the cellular adhesion apparatus.

Dissection of site-specific FAK phosphorylation

The observed modulation of traction stress and strain energy suggests a selective biochemical response of signaling pathways of the cell adhesion apparatus. Accordingly, as an exemplar, we investigated FAK Tyr³⁹⁷ and Tyr⁸⁶¹ phosphorylation as prominent signaling events in traction force and stress signaling of adherent cells (11). We found a selective response in the dependence of site-specific phosphorylation on substrate stiffness and ligand anchorage. Although FAK Tyr³⁹⁷ phosphorylation in endothelial cells increased with increasing substrate stiffness, the degree of phosphorylation was independent of the ligand anchorage and, thus, of traction force level (Fig. 3). In contrast, FAK Tyr⁸⁶¹ phosphorylation was found to be independent of substrate stiffness, but the phosphorylation levels were higher on substrates with lower ligand anchorage strength and, thus, lower traction forces. Our results on FAK Tyr³⁹⁷ phosphorylation agree with previous reports on substrates with varying degrees of stiffness using covalently attached adhesion ligands, as those reports showed that phosphorylation levels were dependent on substrate stiffness but remained constant upon disruption of microtubules, which was correlated to a change in forces at the adhesion sites (17). However, the distinctively different phosphorylation pattern of the two tyrosines on FAK clearly emphasizes the usefulness of our approach for controlling ligand anchorage and receptor forces independent of matrix stiffness. Obviously, FAK is already one candidate for the adhesion signaling pathway, which exhibits a site-specific response to substrate stiffness and traction force.

Figure 3.

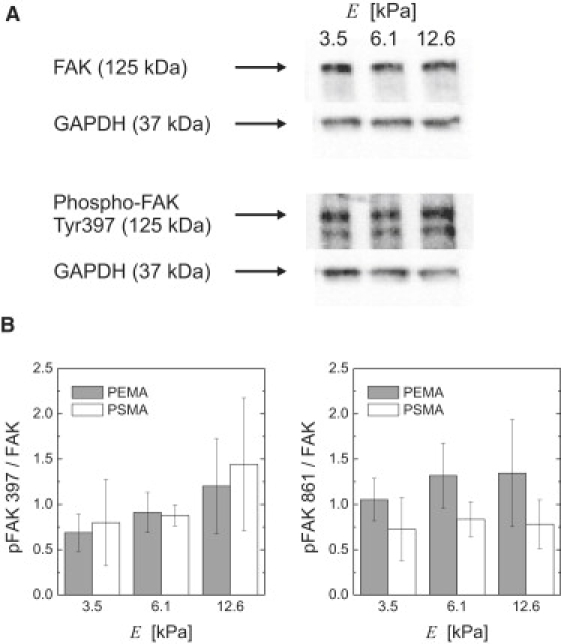
Phosphorylation of FAK Tyr³⁹⁷ and Tyr⁸⁶¹ in endothelial cells depends on substrate stiffness and MACP coating. (A) Western blots of FAK and phospho-FAK Tyr³⁹⁷ on PSMA-PAAm with three different Young's moduli. GAPDH was used as the housekeeping protein for normalization. (B) Mean phosphorylation levels in three to six independent experiments. Error bars indicate the standard deviation.

Net dipole moment, M_net, with unifying scaling

Finally, we report on a finding that may pave the way for an even more generalized view of cell-matrix adhesion. It emerges from a characterization of the cell adhesion process according to the net contractile moment, M_net, of the adherent cells. When U is plotted versus the |M_net| (Fig. 4 A, using the data presented in Fig. 2 B), all data points fall on a single line in a double-logarithmic representation, indicating a new power-law dependence with a unifying scaling exponent of 1.5. This observation suggests that cell adhesion can be described in a biophysical context by $U\sim {\left|M_{\text{net}}\right|}^{1.5}$ independent of additional activation mechanisms by matrix stiffness, as we observed for T_max.

Figure 4.

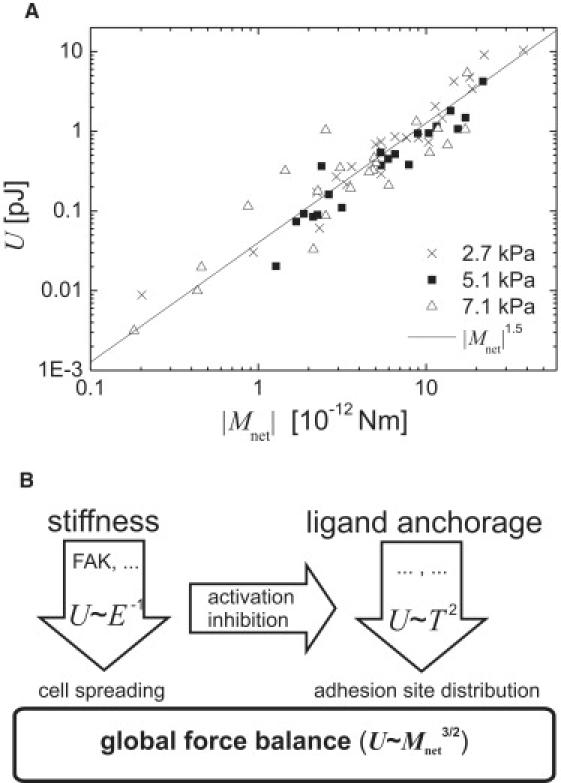
Generalized biophysical framework of cell adhesion signaling. (A) Unifying representation of strain energy, U, exerted by endothelial cells on MACP-PAAm substrates of varying stiffness and ligand anchorage. The fitted line indicates a power law dependence on the absolute net contractile moment, |M_net|, with an exponent of 1.5. (B) Scheme and biophysical description of the impact of the exogenous cues matrix stiffness and ligand anchorage on cell adhesion signaling.

Discussion

We presented what to our knowledge is a new approach to the control of exogenous cues of the extracellular microenvironment in cell adhesion signaling. Numerous investigations have gathered a wealth of information on intracellular signaling pathways, which not only demonstrate a rather high complexity of their cellular response (10,14), but also emphasize their impact on cell proliferation and differentiation (1–5,12). Detailed studies have revealed the regulation of physical cellular stress and forces, and it has been demonstrated that different exogenous cues control the related signaling events inside the cell. Among those, elasticity of the extracellular environment, density of adhesion ligands, spatial distribution of adhesion ligands, and externally applied forces were convincingly shown to function as regulators in cell adhesion signaling (8,15,16,19,20). By combining a variation of material stiffness and adhesion ligand anchorage in a composite polymer hydrogel material, we have here independently modulated, for the first time that we know of, two force-related extracellular parameters that offer detailed insights into cell adhesion signaling.

Noncovalent ligand anchorage regulates receptor force

Starting with the understanding gained from the mentioned previous studies, we could add another dimension of exogenous control in cell adhesion. As ECMs usually exhibit a highly dynamic formation and disassembly, we hypothesized that noncovalent ligand anchorage is a relevant cue for regulating cell adhesion and cell function in vitro and in vivo. Switching from a covalent ligand anchorage to a noncovalent ligand anchorage of varying strength was found to trigger the formation of focal and fibrillar adhesions, as well as cell differentiation (6,32,33). In the work reported here, we show that the graded variation of ligand-substrate anchorage is directly reflected in the maximum traction force of adherent cells. Those local forces are directly related to the net contractile moment of the cells (50), hence providing there the same substrate-dependent trend. Obviously, the cells can sense via their adhesion receptors the variation in the strength of the ligand anchorage to the substrate. Accordingly, they adjust their intracellular stress and force levels. Such a behavior fits well with previous reports on cellular response to other exogenous cues, such as externally applied forces (19).

At this stage, we cannot provide quantitative measures of the ligand anchorage strength that are directly comparable to the cellular receptor forces. However, protein displacement experiments (34,48) have qualitatively revealed the graded anchorage strength of the immobilized ligands, i.e., FN on the MACP surfaces. The experiments revealed rates of displacement of FN by bovine serum albumin on PSMA to be ∼½ the same rate observed on PEMA, which is also obvious from the surface concentration measurements presented in Fig. 1 B. (Protein displacement experiments are valuable in this context, as large biopolymers such as FN don't show considerable desorption in pure buffer, whereas displacement experiments using other proteins provide a relevant means to probe for differences in substrate anchorage or affinity (52).) Furthermore, Monte Carlo simulations of nanometer-scale FN fibrillogenesis using relevant estimates of binding energies suggest effective binding energies in the range of 1–3 kcal/mol for the FN-substrate interaction under cell culture conditions (28), which is in line with thermodynamic estimates of protein adsorption (53).

It is interesting to ask how the graded anchorage strength is translated into differences in cellular receptor force. A possible mechanism concerns a frictional force component originating from the dynamics of the intracellular force apparatus. Thereby, the activity of the myosin motors acting on the actin filaments would be transmitted to receptor-linked ligands leading to sliding of these ligands along the substrate. Recent molecular dynamics simulations of small peptides point to the possibility of such forces, as well as their relevant magnitude (54). Furthermore, the kinetics of the diffusionlike movement of the FN-integrin complexes in the Monte Carlo simulations (28) mentioned previously might be correlated to this frictional origin. Experimental studies on the mobility of ligands during cell adhesion are currently in progress to investigate those phenomena in greater detail.

Noncovalent ligand anchorage reveals ideal active force dipole behavior

Variation of the anchorage strength of the adhesion ligand FN by the newly introduced noncovalent anchorage scheme allowed us to control the traction stress level of adherent cells. By regulating this key element, we were able to observe an almost ideal active force dipole behavior, with $U\sim 1/E$ and a prefactor scaling of $U\sim T_{\max }^2$.

This observation is interesting, as it is in contrast to earlier reports showing that the strain energy imparted by cells to the substrate increases with an increase in substrate stiffness (51). This contradiction might originate from the fact that cellular forces tend to be regulated in response to different exogenous cues in the case of covalent ligand attachment. For an active force dipole, the effect of force upregulation in response to an increase in substrate stiffness would lead to a variation of cellular dipole moment and environmental stiffness at the same time, which would make a pure observation of stiffness response impossible. Similar effects can be expected for the superposition of signaling events with respect to ligand density or ligand patterns/cell spreading (8,16,20,55). Those phenomena share common features, such as a direct correlation of cell spreading area and cell traction forces, with higher forces at larger areas, which suggests that the underlying mechanisms are similar. At the same time, it points to a strong convolution of those signaling events.

In this context, our approach of noncovalent ligand anchorage provides a valuable tool to regulate receptor forces independent of substrate stiffness and ligand density. By doing so, we can adjust the cells to certain traction force levels and reveal a pure response to substrate stiffness. Cells may exhibit a similarly pure response to substrate stiffness if their intracellular force regulation apparatus is pushed to its limit by any other activation, thereby causing constant force levels independent of substrate stiffness. This idea is awaiting future experimental verification, and in the next section, we provide arguments supporting an opposing view. However, our setup is certainly advantageous, as it permits the regulation of force at much lower levels without shifting intracellular signaling to nonphysiological limits.

Furthermore, it might be interesting to use the regulation of traction force in investigations on the temporal pattern of force and strain energy development in the initial stages of cell adhesion, during migration, or in the case of inhibition of specific intracellular signaling events.

Dissection of biophysical and biochemical signaling mechanisms

The conceptual difference between noncovalent and covalent ligand anchorage not only serves to prove the linear elasticity concept of an active force dipole in cell adhesion, but can be applied to provide more detailed insights into biophysical and biochemical signaling mechanisms in cell adhesion.

At first, the stiffness-dependent deviations of the $U\sim T_{\max }^2$ scaling hint at an additional active response of elements of the cytoskeleton of cells and their intrinsic properties (23). Such special features cannot be described by the linear elastic framework of the active force dipole model. However, the observation fits quite well to the well-known cell-type- or tissue-type-specific response to extracellular elastic properties (2) and the adaptation of the cytoskeletal stiffness to the extracellular stiffness (56). It means that there exists, probably, a cell-specific range of elastic properties where a cell acts in an ideal manner that even might be describable by linear elastic models. For environments of other mechanical constituents, e.g., stiffness, the active elements of the cell adhesion apparatus inside the cell (e.g., stress fiber assembly, myosin motors, or phosphorylation levels) will be up- or downregulated, leading to nonideal behavior. One would expect that such a response, i.e., to stiffness, has to approach an upper limit. Looking at the data in Fig. 2 B, one could draw such a limit at ∼2 kPa, where all three fitted lines intersect with each other. It is of interest that this amount of traction stress agrees well with the traction stress data reported for endothelial cells after similar adhesion periods on substrates with a covalent ligand anchorage (57). Such a comparison would support the earlier-mentioned idea that covalent ligand attachment drives a maximization of the cellular response. In addition, it suggests a disappearance of the stiffness-dependent cell response in U at such constant maximized force levels. It should be noted that such a statement would only be valid for a constant force, which was not the case in earlier studies using covalently attached ligands, as traction forces tend to be upregulated in response to increasing stiffness. Furthermore, this hypothesis would be in contrast to the argument in the previous section regarding a purely elastic response with $U\sim 1/E$ for a cell stimulated maximally. Hence, this issue deserves further detailed investigations to clarify to what extent and in which situations simple biophysical models can account for the response of cells during adhesion.

The comparison demonstrates the advantage, in the experimental setup introduced here, of a variable, noncovalent ligand anchorage to modulate cell adhesion forces. In our approach, covalent ligand anchorage would have to be treated as only one specific case leading to a maximization of the applied forces in a cell-type-specific manner.

Second, the reported experiments allowed us to dissect biochemical adhesion signals. Phosphorylation of FAK as a very important signaling molecule was shown to provide site-specific effects in response to different exogenous cues. As our setup allows dissection of the impact of receptor forces and substrate stiffness, we could clearly relate an increase in FAK Tyr³⁹⁷ phosphorylation to an increase in substrate stiffness, as has also been reported by other groups (17,18). In some of those experiments, the impact of other cues, such as receptor force, cannot be completely excluded. However, our statements are supported by experiments in which traction forces were indirectly varied by disruption of microtubules. In those experiments, an unchanged FAK Tyr³⁹⁷ phosphorylation behavior was observed (17). We further extend the depth of information by showing that receptor force specifically affects a different phosphorylation site of FAK, namely Tyr⁸⁶¹. It is interesting to note that we find a lower phosphorylation at higher force levels. This finding at first contrasts earlier reports linking Tyr⁸⁶¹ phosphorylation to the number of ligand-receptor bonds without a link to bond enforcement (58). Certainly, it supports our initial statement that minor differences in ligand density on the two different copolymer surfaces exert a negligible influence. A possibly slightly higher ligand density on PSMA would be reflected by a higher Tyr⁸⁶¹ phosphorylation level, whereas the opposite is the case. Although the observed difference might be attributed to a cell-type-specific behavior, we believe it indicates a distinct response to traction force levels. However, another explanation might combine both findings with interpreting our results as an indication that different numbers of integrin receptors and adhesion sites are involved in the cell adhesion process. This idea was mentioned earlier in reference to our findings on stiff substrates (33), namely, that there are fewer focal adhesions on substrates with a stronger ligand anchorage and, we hypothesize, fewer adhesion sites with stronger traction forces for substrates with strong ligand anchorage.

Based on our findings, further experiments are planned that will examine other important molecules of the signaling cascade, such as RhoA, Cdc42, vinculin, or p130Cas. Those experiments could address the question of whether certain pathways are regulated by receptor force or stiffness. Since it is known already that both exogenous cues are tightly convoluted, one might propose that, for example, RhoA should be solely regulated by stiffness and vinculin by receptor force. It would be especially interesting to see if distinct effects of substrate stiffness and receptor force, as modulated in our approach, could be observed in signaling events further downstream, up to epigenetic levels affecting cell proliferation and differentiation.

In a similar way, the biophysical models currently available could be addressed more specifically in our setup, i.e., by modulating active components of the cell adhesion apparatus, such as myosin motors, vinculin recruitment to focal adhesion (26,27), or RhoA activation, with inhibitors in a dose-dependent manner. The cellular response in such experiments could be compared to that seen in experiments using exogenous controls such as receptor forces and substrate stiffness. Hence, a direct correlation of the characteristics of intracellular elements to extracellular components could be established.

The net contractile moment as a robust measure in cell adhesion

Besides the interesting findings on the dissection of signaling pathways in cell adhesion, our results suggest a generalized view of cell-matrix adhesion. The plot of the strain energy, U, versus the net contractile moment, M_net (Fig. 4 A), revealed a power-law behavior with a unifying scaling exponent of 1.5, a characteristic not previously reported, to the best of our knowledge. Obviously, M_net accommodates all responses on matrix stiffness and ligand anchorage of the cells and appears as a very robust measure of the cellular response in cell adhesion. Although we have no theoretical model at hand to describe this finding, we suggest the following interpretation of the occurrence of the observed correlation (see Fig. 4 B). The relation may originate from the superposition of two different mechanisms. We suggest a linear elastic behavior locally for single cellular elements such as the adhesion sites with the linked ECM and the intracellular stress fibers. This local mechanism might trigger processes such as size and distribution of adhesion sites, as suggested earlier (33). The second mechanism concerns the global spreading of adherent cells, and its stiffness dependence (8), which we would place in this context on a higher level than the first (local) mechanism in the hierarchy of cell signaling. For the globally acting net contractile moment, M_net (≙force × distance), the superposition of both mechanisms might cause the higher spreading of cells on stiff substrates to counterbalance the stronger activation of the local response on the adhesion sites (U(T_max)). This mechanism could originate from an integrating mechanism acting over the whole cell, with a possible connection to the cytoskeleton. Although the arguments presented above can provide only some reasoning to explain our findings, we hope to stimulate further theoretical developments by our results. Nevertheless, we conclude that analyzing cell adhesion in terms of U and M_net offers interesting new options for exploring the impact of different matrix environments and variations of signal activation levels (Fig. 4 B) in a generalized framework, as M_net is proposed as a robust measure that accommodates all dependences on matrix stiffness and ligand forces.

In summary, our findings reveal what to our knowledge are new opportunities for the physicochemical modulation of engineered ECMs. The anchorage of adhesion ligands provides a means of adjusting the traction stress of adherent cells that is independent of matrix stiffness. The approach allows dissection of biophysical and biochemical signaling pathways in cell adhesion, and we suggest that it be applied in further investigations of cell adhesion signaling. Finally, we report on a new unifying scaling behavior of the net contractile moment of an adherent cell, which is concluded to be a robust measure in cell adhesion.

Supporting Material

Details on substrate preparation and characterization and Western blot analysis are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01311-3.