Reinterpreting the Anomalous Mole Fraction Effect: The Ryanodine Receptor Case Study

Abstract

The origin of the anomalous mole fraction effect (AMFE) in calcium channels is explored with a model of the ryanodine receptor. This model predicted and experiments verified new AMFEs in the cardiac isoform. In mole fraction experiments, conductance is measured in mixtures of ion species X and Y as their relative amounts (mole fractions) vary. This curve can have a minimum (an AMFE). The traditional interpretation of the AMFE is that multiple interacting ions move through the pore in a single file. Mole fraction curves without minima (no AMFEs) are generally interpreted as X displacing Y from the pore in a proportion larger than its bath mole fraction (preferential selectivity). We find that the AMFE is also caused by preferential selectivity of X over Y, if X and Y have similar conductances. This is a prediction applicable to any channel and provides a fundamentally different explanation of the AMFE that does not require single filing or multiple occupancy: preferential selectivity causes the resistances to current flow in the baths, channel vestibules, and selectivity filter to change differently with mole fraction, and produce the AMFE.

Introduction

Theory can offer insights into how proteins work, as well as guide the interpretation of experiments. For ion channels, the presence or absence of an anomalous mole fraction effect (AMFE) is commonly used to infer how the pore operates. In the classic mole fraction experiment, a mixture of ion species X and Y is in the baths with their total concentration ([X] + [Y]) kept constant and the current (or conductance) is measured as the mole fraction [X]/([X] + [Y]) of X is varied. An AMFE exists when the conductance versus mole fraction curve has a minimum. This was first identified by Takeuchi and Takeuchi (1) and Hagiwara and co-workers (2,3).

The commonly accepted explanation of the AMFE (4) presented in textbooks (5) is that an AMFE indicates that multiple ions are moving through the pore in a single file. This explanation is often used to infer whether a channel has a single-file, multi-ion pore. A superficial search in PubMed and the calcium channel literature shows how common this interpretation is in the literature (6–12).

Recently, this interpretation has been challenged. Nonner et al. (13) first suggested that neither single filing nor multiple ions are necessary for an AMFE; in principle, a pore occupied (on average) by less than one ion can have an AMFE. They proposed that localized binding of ions produce depletion zones of low ion concentrations that reduce current of one ion species. These depletion zones act as high-resistance elements, just like low concentrations reduce conductivity in a salt solution. These high-resistance elements—connected in series with other low-resistance elements along the pore—limit conductance through the pore of that particular ion species. Nonner and co-workers (14,15) showed that this explained the classic Ca²⁺ block of Na⁺ current AMFE of the L-type calcium channel (16,17).

Gillespie et al. (18) later generalized this resistors-in-series theory to explain AMFEs in synthetic nanopores in plastic. These nanopores were ∼50 Å wide and thus there was no possibility of single filing or correlated ion motion. These experiments demonstrated that neither of these properties—both integral to the textbook theory—are necessary for an AMFE. Instead, they showed that the AMFE was due to preferential binding of Ca²⁺ over monovalent cations within the pore (i.e., the proportion of Ca²⁺ in the smallest part of the pore is larger than its mole fraction in the baths). This preferential binding caused the resistance to current flow for each ion species to change nonlinearly with mole fraction in the center of the pore (which is highly Ca²⁺-selective), but linearly at the edges of the pore, producing the AMFE.

Subsequently, Gillespie and Boda (19) analyzed AMFEs in a model L-type calcium channel with Monte Carlo simulations. The resistors-in-series model explained the classic Ca²⁺ block of Na⁺ current AMFE, confirming previous work (14,15). It also explained the apparently conflicting measurements of the Ca²⁺ versus Ba²⁺ AMFE (6).

The traditional textbook and resistors-in-series theories predict very different origins of the AMFE phenomenon. This is not that surprising since they use very different descriptions of how ions move through the pore. The traditional theory uses a chemical kinetics model to describe ions in a single file hopping over static energy barriers between binding sites, each of which can only hold a single ion. The resistors-in-series model describes ions as moving by electrodiffusion, where barriers and wells are created and destroyed on the atomic timescale as ions move (20). In steady state, barriers, and wells (potentials of mean force) depend on the concentration and types of ions in the baths (21,22); they are not fundamental properties of the pore (14,23).

Which explanation for the AMFE is applicable for a particular channel then depends on which theory best describes the physics of ions moving through that particular pore. Thus, a measured AMFE should not immediately be interpreted as an unambiguous marker of a multi-ion pore, especially if there is no other evidence for single filing. The traditional model can give a misleading impression about the inner workings of the channel because, instead, the AMFE may reflect the preferential binding of one ion species over another, as we show in this article for the ryanodine receptor (RyR).

RyR is a calcium channel with millimolar Ca²⁺ affinity (24) that releases Ca²⁺ from the sarcoplasmic reticulum (SR), an intracellular Ca²⁺ storage organelle. It has proven to be a useful test case for understanding selectivity in calcium channels because it lends itself to relatively easy single-channel recordings. Additionally, a model of ion permeation through RyR has been developed that reproduces all the known experimental permeation and selectivity data (21,25,26). Moreover, it predicted AMFEs in RyR before experiments confirmed them (21,25). Here we confirm new AMFE predictions with experiments.

In this article, we explore the origin of AMFE in single RyR channels using this model. Our analysis indicates that the resistors-in-series model not only explains whether an AMFE is present or absent in cation mixtures, but also the AMFEs' voltage and concentration dependences. Because the RyR model of permeation not only reproduces experimental AMFEs, but also predicts them without adjusting any model parameters, this study provides the strongest evidence so far that the cause of the AMFE in some channels is the resistors-in-series mechanism. Moreover, because the RyR model does not include single filing of ions, this study also provides further evidence that single filing is not necessary for an AMFE.

Theory and Methods

AMFE experiments

SR microsomes were prepared from rat ventricular muscle according to published methods (27). Microsomes were stored in liquid nitrogen, quickly defrosted, kept on ice, and used within 5 h. Planar lipid bilayers were formed from a 5:3:2 mixture of phosphatidylethanolamine, phosphatidylserine, and phosphatidylcholine (50 mg/mL in decane) across a 100-μm hole in a 12-μm-thick Teflon partition. The solution on one side had HEPES-Ca²⁺ (10 mM Ca²⁺, pH 7.4) and was grounded by the patch-clamp amplifier. The luminal side of the RyR2 channel always faced this solution (28). The cytosolic side had a HEPES-TRIS solution (114 mM TRIS, pH 7.4), 500 mM Cs-methanesulfonate, 2 mM CaCl₂, and 5–15 μg of SR microsomes. Once single-channel activity was observed, the solutions in both compartments were exchanged at a rate of 4 ml/min for 5 min to establish the specific test conditions detailed in Results. All test solutions contained 10 mM HEPES (pH 7.4). No calcium buffers were used. Listed [Ca²⁺] indicate added Ca²⁺ beyond the 1–4 μM contaminant [Ca²⁺] (as determined by a calcium electrode). Zero added Ca²⁺ is plotted as 1 μM [Ca²⁺].

All recordings were made at room temperature. Single-channel currents were digitized at 10 kHz and filtered at 1–2 kHz using an A/D converter and amplifier (Axon CMS, Molecular Devices, Downingtown, PA). Acquired data were analyzed using pClamp (Axon CMS, Molecular Devices). Unit current amplitudes were determined from Gaussian fitting of all-points histograms.

These experiments were performed on the native cardiac isoform (RyR2). These native channels may have endogenous regulatory proteins like the negatively-charged calsequestrin attached to them. Such proteins were not present with the purified RyR2 channels (25,29,30) that were used to develop the PNP/DFT model (described below). This may contribute to the larger discrepancies between theory and experiment here than those described previously (21,25). Nevertheless, the model is in very good agreement with experiments.

We use the added-salt mole fraction protocol (16,17) where Ca²⁺ is added to a fixed concentration of monovalent cation X⁺. This is similar to the classic mole fraction experiment described in the Introduction because [Ca²⁺] << [X⁺]. Moreover, we added Ca²⁺ only on the luminal side because millimolar cytosolic Ca²⁺ significantly decreases RyR open probability (31).

This protocol is different than that of Tomaskova and Gaburjakova when searching for AMFEs in RyR (32). They placed mole fraction mixtures on the luminal side only and LiOH on the cytosolic side. Besides the complicating effect of a third cation, their results are difficult to interpret because with a 5:1 concentration ratio of LiOH they report a reversal potential of 46 ± 2 mV (as expected for a perfectly cation-selective channel), but in a 12:1 concentration ratio they measured only 10 ± 5 mV—far from the expected ∼60 mV for a highly cation-selective channel. However, Tomaskova and Gaburjakova do show AMFEs for mixtures of Na⁺ and Cs⁺ and of Li⁺ and Ca²⁺, consistent with our results.

Model of RyR

We use a previously published model of ion permeation through a single, open RyR pore with no changes to any parameters (21). The pore is modeled as only the five conserved, charged amino acids previously shown to affect RyR selectivity and permeation (29,30): Asp-4899, Glu-4900, Asp-4938, Asp-4945, and Glu-4902 in the RyR1 numbering scheme. The model pore and amino acid locations are shown in Fig. 1 of Gillespie (21).

Figure 1.

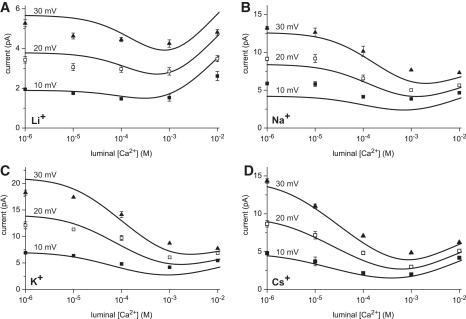
Comparing the AMFE predictions of the model (lines) to experiments (symbols). Ca²⁺ is added to the luminal bath while both baths contain 100 mM X⁺ for different monovalents X⁺: (A) Li⁺, (B) Na⁺, (C) K⁺, and (D) Cs⁺. The currents at 10, 20, and 30 mV are shown. Experimental error bars smaller than the symbol are not shown. The 20 mV curves in panels B and D were published previously (21).

Ion current is modeled with one-dimensional Nernst-Planck theory,

$$-J_{\text{i}}=\frac{1}{kT}{D}_{\text{i}}\left(x\right)A\left(x\right){\rho }_{\text{i}}\left(x\right)\frac{d{\mu }_{\text{i}}}{dx},$$ (1)

where ρ_i and μ_i are the concentration and electrochemical potential, respectively, of ion species i throughout the pore and baths. J_i is the flux of ion species i. A(x) is the area of the equi-chemical potential surfaces that is estimated as previously described (14). In the pore, it is the cross-sectional area. D_i is the diffusion coefficient.

The ions are charged, hard spheres whose chemical potentials μ_i are computed with density functional theory (DFT) of electrolytes. The DFT generalizes the Poisson-Nernst-Planck (PNP) theory of point ions so this model is called the PNP/DFT model of RyR. Note that the PNP/DFT theory only describes how ions move through the pore and is not a theory of the AMFE; that is the resistors-in-series model described below.

Corry et al. showed that Nernst-Planck approaches (Eq. 1) can fail in narrow channels like the K⁺ channel, especially for point-charge ions (33). However, they also showed that the Nernst-Planck equation is valid if the pore radius is larger than two screening (Debye) lengths. Because the RyR selectivity filter contains four negative Asp-4899 side chains at very high concentration, permeant cations are screened very effectively and the screening length is always <1.8 Å, putting our 4 Å radius pore within the diffusive limit. Moreover, the DFT eliminates the point-ion approximation that is clearly problematic in narrow pores and correctly computes ion-ion correlations of charged, hard spheres (21,34). This gives us confidence that Eq. 1 can be used to compute current through RyR.

This PNP/DFT model has reproduced the current/voltage relations (–150 to +150 mV) of wild-type and three mutant RyR channels in >70 published ionic solutions (21,25,26) and at least another as-yet unpublished 66 solutions (D. Gillespie, L. Xu, and G. Meissner, unpublished). The model also predicted—before the confirming experiments were done—previously unknown AMFEs (21,25) and other experimental data (e.g., Figs. 1, 2, and 4) in >75 ionic solutions. The quantitative prediction of large quantities of unexpected results without changing any parameters gives us confidence that this model correctly captures the essential physics of ion selectivity and permeation in RyR.

Figure 2.

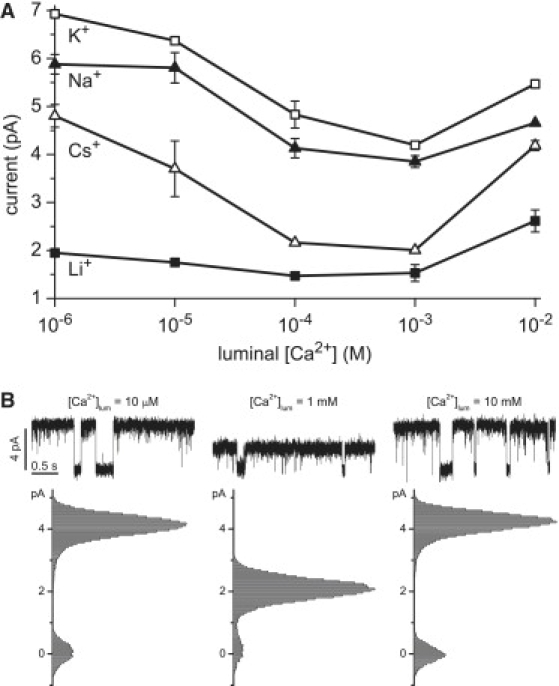
(A) The experimental data for Li⁺, Na⁺, K⁺, and Cs⁺ at 10 mV from Fig. 1. (B) Representative current recordings and histograms at 10 mV for 100 mM Cs⁺ and the indicated concentration of luminal Ca²⁺.

Figure 4.

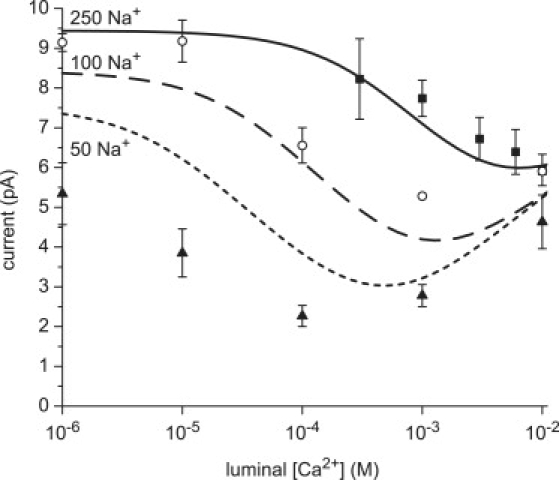
The effect of bath Na⁺ concentration on the AMFE. The current at 20 mV is shown for added luminal Ca²⁺ with symmetric 250 mM (squares), 100 mM (circles), and 50 mM (triangles) Na⁺. Symbols are experimental results and lines are the model's predictions. The discrepancies between the experiments and PNP/DFT model are larger for 50 mM Na⁺ because at low concentrations the model overestimates the affinity of RyR for monovalents. Twenty millivolts was chosen to have sufficient signal/noise ratio for the 50 mM measurements.

Ionic pathways in parallel, resistors in series

Equation 1 can be rewritten to describe ion currents as currents through an electrical circuit. In this way, we can describe the AMFE in terms of the resistors in a circuit and how their resistances change with mole fraction. To do this, we integrate Eq. 1 from bath to bath across the channel,

$$J_{\text{i}}\int \frac{dx}{D_{\text{i}}\left(x\right)A\left(x\right){\rho }_{\text{i}}\left(x\right)}=\frac{z_{\text{i}}e}{kT}\left(V-V_{\text{i}}^{\text{Nernst}}\right),$$ (2)

where e is the fundamental charge, z_i is the valence of species i, and V is the applied voltage. The cytosolic side is grounded and positive fluxes are from the SR lumen to the cytosol. The Nernst (equilibrium) potential is

$$V_{\text{i}}^{\text{Nernst}}=\frac{kT}{z_{\text{i}}e}\left[\ln \left(\frac{{\rho }_{\text{i}}^{\text{cyt}}}{{\rho }_{\text{i}}^{\text{lum}}}\right)+\frac{\mathrm{\Delta }{\mu }_{\text{i}}^{\text{ex}}}{kT}\right],$$ (3)

where ${\rho }_{\text{i}}^{\text{cyt}}$ and ${\rho }_{\text{i}}^{\text{lum}}$ are the bath concentrations on the cytosolic and luminal sides, respectively, and $\mathrm{\Delta }{\mu }_{\text{i}}^{\text{ex}}$ is the difference in the excess chemical potentials between the cytosolic and luminal baths. Then the current is

$$I=e\sum _{\text{i}}{z}_{\text{i}}{J}_{\text{i}}=\sum _{\text{i}}\frac{V-V_{\text{i}}^{\text{Nernst}}}{R_{\text{i}}}$$ (4)

with electrical resistances

$$R_{\text{i}}=\frac{kT}{z_{\text{i}}^2{e}^2}\int \frac{dx}{D_{\text{i}}\left(x\right)A\left(x\right){\rho }_{\text{i}}\left(x\right)}\text{.}$$ (5)

Equation 4 is formally identical to the equation used to describe the current through an electrical circuit with parallel pathways; the analogy is exact if it is an electrochemical circuit (i.e., the current across each resistor is proportional to the electrochemical potential drop, instead of the voltage drop, across the resistor). The parallel pathways represent movement of different ion species i. Each branch has a resistor with resistance R_i in series with a battery at the Nernst potential of species i.

Although this circuit description is well known (5), we note that each resistance R_i depends on the geometry (through A(x)) and the diffusion coefficient and ion concentration profiles, D_i(x) and ρ_i(x). Anything that changes these terms changes the resistance. For example, a conformational change or loss of a regulatory protein can change the pore geometry (and the diffusion coefficients), possibly causing a decrease in current when ion mole fraction changes.

The concentration profile along the pore, however, is the most likely to change the resistance with mole fraction because it depends on the bath concentrations, the applied voltage, and the kinds of other ions present. An example of how dramatically concentration profiles depend on the bath composition has been demonstrated in RyR (21). With a 1 mM Ca²⁺ and 100 mM Li⁺ or Cs⁺ in the baths, the selectivity filter contains five times more Li⁺ than Cs⁺. Therefore, the resistances R_i depend on the physical properties of all ion species, as well as their amounts. In other words, the resistances R_i are not constant and not known a priori, but rather must be computed by the model.

We will consider how the ion-specific resistances within different regions of the pore change with mole fraction. This can be done by breaking the integral in Eq. 5 into integrals over smaller regions,

$$\begin{array}{c}\frac{z_{\text{i}}^{\text{2}}{e}^2}{kT}{R}_{\text{i}}=\underset{\begin{array}{c}\text{bath to}\\ \text{bath}\end{array}}{\int }{\left[D_{\text{i}}\left(x\right)A\left(x\right){\rho }_{\text{i}}\left(x\right)\right]}^{-1}dx\\ =\underset{\begin{array}{c}\text{cytosolic}\\ \text{bath}\end{array}}{\int }+\underset{\begin{array}{c}\text{cytosolic}\\ \text{vestibule}\end{array}}{\int }+\underset{\begin{array}{c}\text{selectivity}\\ \text{filter}\end{array}}{\int }+\underset{\begin{array}{c}\text{luminal}\\ \text{vestibule}\end{array}}{\int }+\underset{\begin{array}{c}\text{luminal}\\ \text{bath}\end{array}}{\int },\end{array}$$ (6)

where the integrand [D_i(x)A(x)ρ_i(x)]⁻¹ is not explicitly written. For each ion species i, each region is then a resistor in series with the other four resistors. The resistance of each region of the pore changes differently with mole fraction to produce the AMFE, giving the resistors-in-series model of the AMFE its name (19).

For the results shown in this article, we divide the system as follows: the cytosolic bath; the cytosolic vestibule containing Asp-4945 and Asp-4938; the selectivity filter with Asp-4899; the luminal vestibule with Glu-4900; and the luminal bath.

Resistors-in-series model of the AMFE

Previous work on the resistors-in-series model showed that the combination of three elements was identified as necessary to generate an AMFE (18,19):

• 1.Higher binding affinity of one ion species X over another species Y. This causes X to be present in the selectivity filter in a proportion higher than in the bath. This is preferential selectivity of X over Y.
• 2.Resistance to current flow in other regions of the pore (e.g., cytosolic and luminal vestibules) changes differently with [X] than in the selectivity filter. This is because the rest of the pore has a lower affinity for X; if not, these regions would be the selectivity filter. This means that the concentrations of X and Y—and their resistances by Eq. 5—vary differently with [X] in different regions of the pore.
• 3.The endpoint currents/conductances (i.e., the currents/conductances in mixtures with the smallest and largest [X]) should be approximately equal. If the endpoints are very far apart, the current must be depressed far more to generate a minimum than if the endpoints are equal.

Gillespie and Boda (19) showed (if the endpoint conductances were equal) that both preferential selectivity and the resistances outside the selectivity filter were essential to an AMFE; without either, there was no AMFE. That work built on the experiments by Gillespie et al. (18) in synthetic nanopores, that showed that the more similar the endpoint conductances, the deeper the AMFE. Below we will show that the AMFEs in RyR are consistent with these principles.

Results

First, we show predicted and measured AMFEs in different mixtures of Ca²⁺ and monovalent cations. Second, we analyze these AMFEs, focusing on mixtures of Ca²⁺ and Cs⁺ or Li⁺ because these produce the largest and smallest AMFEs in RyR. Third, we analyze the classical mole fraction experiments where mixtures of Na⁺ and Cs⁺ generate an AMFE in RyR, while other mixtures of monovalent cations (e.g., Li⁺ and K⁺) do not.

Experiments in mixtures of Ca²⁺ and monovalent cations

We performed experiments to determine the conditions under which RyR2 has AMFEs in mixtures of Ca²⁺ and monovalent cations. The results are shown in Figs. 1 and 2 (symbols). Fig. 1 also shows the currents computed with the PNP/DFT model (lines). In these experiments, 100 mM X⁺ (X⁺ = Li⁺, Na⁺, K⁺, and Cs⁺) is in both baths and Ca²⁺ is added to the luminal bath. The cytosolic bath contains ∼1 μM Ca²⁺. The experimental data for 10 mV applied voltage are replotted in Fig. 2 A to clearly show the AMFEs. Fig. 2 B shows exemplar current traces and histograms in Cs⁺. To test the predictive power of the model, the calculations were done before the experiments.

Mixtures of Ca²⁺ and Cs⁺ have the largest AMFEs; there is a distinct minimum up to 30 mV. Na⁺ and K⁺ have smaller AMFEs at 10 and 20 mV. The AMFEs are no longer evident by 30 mV in all these mixtures except Cs⁺. Li⁺ did not generate significant AMFEs at any of the voltages we studied, although at each voltage there was a small depression of current compared to 1 μM Ca²⁺ as [Ca²⁺]_lum was increased (see Fig. 3 C). The PNP/DFT model exaggerates this depression of current at 20 and 30 mV, but when the model results are considered collectively, the model predicts all the general trends with very good quantitative agreement.

Figure 3.

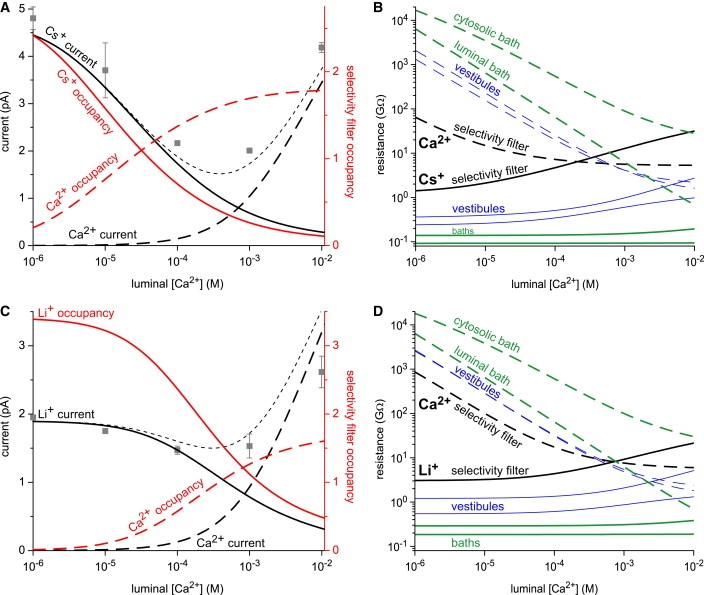
(A) Ca²⁺ and Cs⁺ current (black lines, left axis) and number of Ca²⁺ and Cs⁺ in the selectivity filter (red lines, right axis) as [Ca²⁺]_lum is increased. The net current is shown with the dotted line and the experimental results are shown with gray squares. (B) The resistances of Cs⁺ (solid lines) and Ca²⁺ (dashed lines) in the selectivity filter (black lines), the cytosolic and luminal vestibules (blue lines), and the baths (green lines). (C and D) Same as panels A and B with Li⁺ substituted for Cs⁺. The applied voltage is 10 mV.

Ca²⁺ block of monovalent cation current

Preferential selectivity and resistances

To analyze the Ca²⁺/monovalent cation AMFE (Figs. 1 and 2), we first consider the case of 100 mM symmetric Cs⁺ with added Ca²⁺ (Fig. 1 D). We start by considering preferential selectivity. Since RyR is a calcium channel, one would expect it has preferential selectivity for Ca²⁺ over any monovalent cation. This is shown in Fig. 3 A (red lines, right axis) where the number of Ca²⁺ and Cs⁺ ions calculated to be in the selectivity filter are plotted as luminal Ca²⁺ concentration [Ca²⁺]_lum is increased. Even micromolar [Ca²⁺]_lum displaces Cs⁺ from the selectivity filter and with ∼30 μM [Ca²⁺]_lum there is one Ca²⁺ and one Cs⁺ (intersection of the red lines).

Fig. 3 A also shows that Cs⁺ current (black solid line) is approximately proportional to the number of Cs⁺ in the selectivity filter (red solid line). Cs⁺ occupancy (and current) decreases because it is being replaced in the pore by Ca²⁺. For Ca²⁺ the situation is very different; the increasing Ca²⁺ occupancy does not initially translate into significant Ca²⁺ current (black lines, left axis); the Ca²⁺ current (black dashed line) reaches 0.5 pA only when [Ca²⁺]_lum is elevated to 400 μM. Note that at this point Ca²⁺ occupancy (red dashed line) in the selectivity filter is almost saturated. This suggests there is a large resistance to Ca²⁺ current somewhere outside of the selectivity filter. In other words, Ca²⁺ passing through the selectivity filter is not the rate-limiting step.

Fig. 3 B shows that this resistance comes from the baths surrounding the pore (green dashed lines), especially the regions at the pore entrances (data not shown). The high resistance arises because the very low Ca²⁺ concentrations in the baths give the baths very small Ca²⁺ conductivity. At these low concentrations, the vestibules also have very high resistances to Ca²⁺ current (blue dashed lines) (35). It is not until [Ca²⁺]_lum reaches the millimolar level that the bath becomes the very low resistance element that it is usually assumed to be and is in this case for Cs⁺ (solid green and blue lines). Therefore, even though Ca²⁺ occupancy is high within the pore, there is very little Ca²⁺ current because of the very high resistance outside the selectivity filter. Note that although Ca²⁺ is only added on the luminal side, adding Ca²⁺ symmetrically does not change our findings; in that case, both bath resistances (green dashed lines) are identical and those resistances still prevent Ca²⁺ flux and still produce an AMFE, as shown previously (19).

So why is there little or no AMFE when Ca²⁺ is added to Li⁺ (Fig. 1 A), even though Li⁺ should intuitively behave similarly to Cs⁺? In fact, Li⁺ seems to fulfill all the criteria for an AMFE: the pore selects Ca²⁺ over Li⁺ (21), the Ca²⁺ resistance outside the selectivity filter is as large as with Cs⁺ (Fig. 3, B and D), and the endpoint currents are equal (Figs. 1 A and 2 A). The reason is that RyR has a much higher affinity for Li⁺ than for Cs⁺ (21), as shown in Fig. 3: at micromolar [Ca²⁺]_lum, there are ∼3.5 Li⁺ in the selectivity filter (solid red line in Fig. 3 C), but only ∼2.5 Cs⁺ (solid red line in Fig. 3 A). This is because each Li⁺ ion has only 6% the volume of a Cs⁺ ion so more Li⁺ ions can fit into the crowded selectivity filter (15,19,25,36). Moreover, it takes ∼0.8 mM [Ca²⁺]_lum to displace enough Li⁺ so that there is one Li⁺ and one Ca²⁺ in the selectivity filter (intersection of red lines in Fig. 3 C)—27 times the amount of Ca²⁺ needed with Cs⁺. This affinity for Li⁺ causes the Li⁺ current to decrease at much higher [Ca²⁺]_lum than for Cs⁺, but at those concentrations the Ca²⁺ current is increasing. As a result, the net current (dotted black line) is relatively constant and any minimum is much smaller than for Cs⁺. This shows that it is incorrect to infer that the absence of an AMFE indicates the absence of preferential selectivity; only the presence of an AMFE is significant (18,19).

The resistance to current flow for the monovalents Cs⁺ and Li⁺ change differently as more Ca²⁺ is added compared to the resistance of Ca²⁺, especially in the selectivity filter. This is shown in Fig. 3, B and D (black lines). As the monovalent is replaced in the pore by Ca²⁺, its concentration decreases and so its resistance increases (solid black lines). Ca²⁺ resistance, on the other hand, decreases as its concentration increases, but then it saturates as Ca²⁺ occupancy saturates (dashed red lines in Fig. 3, A and C). Moreover, the selectivity filter is the highest resistance element for the monovalents (as expected), while for Ca²⁺ it is the lowest resistance element until [Ca²⁺]_lum is ∼1 mM. This keeps Ca²⁺ current small even though Ca²⁺ occupancy of the selectivity filter is high.

Concentration and voltage dependence of the AMFE

The difference in affinity of RyR for Li⁺ and Cs⁺ has significant consequences on the AMFE because it is harder for Ca²⁺ to displace Li⁺ from the selectivity filter. This then presents a testable prediction: the easier it is for Ca²⁺ to displace a monovalent, the more the minimum (if there is one) should move to lower [Ca²⁺]_lum. One way to increase Ca²⁺ binding in the RyR pore is to decrease the monovalent cation concentration in the baths (21). We test this prediction in Fig. 4 and find that, indeed, less [Ca²⁺]_lum is required to generate a minimum as [Na⁺] is decreased from 250 mM to 50 mM. As for Fig. 1, the calculations were done before the experiments.

The figure also shows that, as [Na⁺] decreases, the endpoint currents become more equal and the AMFE becomes deeper. This is consistent with the predictions of the resistors-in-series model (19) and the AMFE experiments on synthetic nanopores (18). The relationship between endpoint conductances and AMFE depth is also seen in the voltage dependence of the depth of the AMFE in Fig. 1. In the experiments (symbols), all the monovalents except Li⁺ have a minimum in the current at 10 mV, but only Cs⁺ still has one at 30 mV. This loss of the AMFE mirrors the increase in the difference between the endpoint currents (i.e., the currents at [Ca²⁺]_lum = 10⁻⁶ and 10⁻² M). The difference in the endpoint currents increases with voltage because the monovalents have significantly larger conductances (200–800 pS) compared to Ca²⁺ (100–150 pS). Therefore the same increase in voltage disproportionately increases the monovalent current at [Ca²⁺]_lum = 10⁻⁶ compared to the Ca²⁺ current at [Ca²⁺]_lum = 10⁻² M, moving the endpoint currents apart and decreasing the depth of the AMFE (or eliminating the AMFE altogether).

Classic mole fraction experiments

Analyzing the AMFE for mixtures of monovalent cations is more difficult because the effect is much smaller (<10% for Na⁺/Cs⁺ mixtures). Still, we show that preferential selectivity, resistances outside the selectivity filter, and equal endpoint conductances combine to make an AMFE possible. We analyze two mole fraction experiments, one in mixtures of Na⁺ and Cs⁺ which has an AMFE and one in mixtures of Li⁺ and K⁺ which does not (Fig. 5 A).

Figure 5.

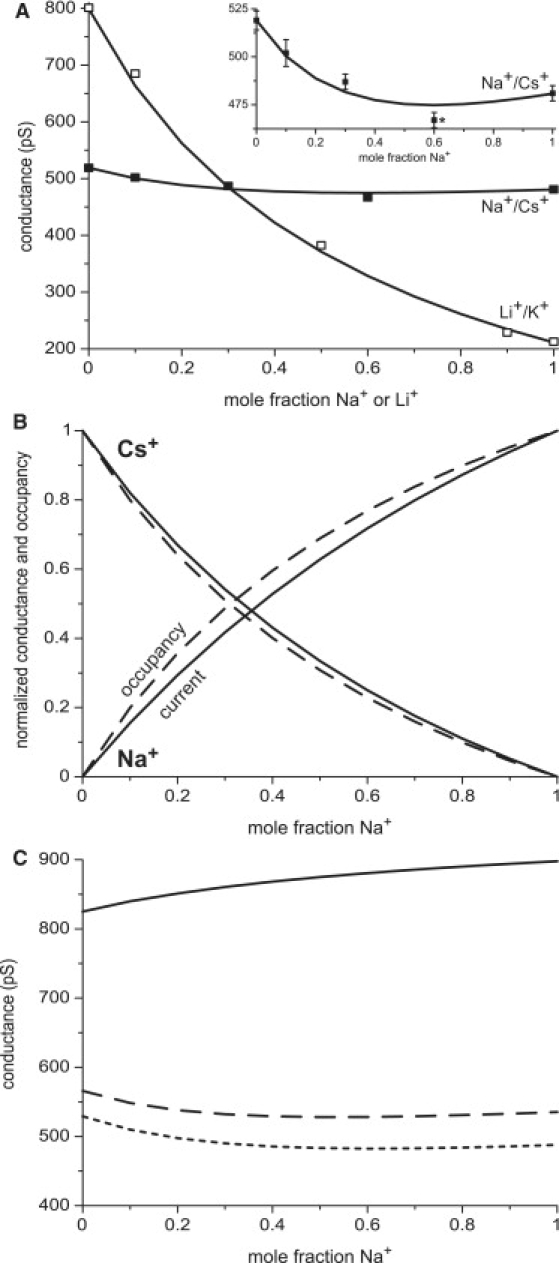
(A) Mole fraction experiments in mixtures of Na⁺ and Cs⁺ and mixtures of Li⁺ and K⁺. The experimental results (symbols) and the theoretical results (lines) have been previously published (21,25,38). The inset shows a close-up of the Na⁺/Cs⁺ curve. (B) Normalized selectivity filter occupancies (dashed lines) and individual ion species conductances (solid line) of Na⁺ and Cs⁺ are shown as the mole fraction of Na⁺ is increased. [Na⁺] + [Cs⁺] = 250 mM. (C) The conductance in Na⁺/Cs⁺ mixtures calculated with only the resistances of Na⁺ and Cs⁺ in the selectivity filter (solid line), in the entire pore (dashed line), and in the entire pore and the baths (dotted line).

For the Na⁺/Cs⁺ mixtures, normalized selectivity filter occupancy and currents are shown in Fig. 5 B. Na⁺ is preferentially selected over Cs⁺; the proportion of Na⁺ in the selectivity filter is larger than its mole fraction in the bath while the proportion of Cs⁺ is less. Cs⁺ current is approximately proportional to Cs⁺ occupancy (the Cs⁺solid and dashed lines are almost the same). For Na⁺, however, the two curves are more dissimilar, with Na⁺ current proportionately smaller than Na⁺ occupancy (the Na⁺solid line is below the dashed line).

This pattern is similar to what happened with Ca²⁺: the cation (Na⁺ or Ca²⁺) that is displacing Cs⁺ from the pore has a current that is proportionately smaller than its occupancy in the selectivity, but it was much more pronounced for Ca²⁺. The same is true for the small Li⁺ ions which RyR prefers over the larger K⁺ ions (21); Fig. 5 B is nearly identical for the Li⁺/K⁺ mixtures when the mole fraction of Li⁺ is the x axis (data not shown). That is, for these normalized variables, the replacement of K⁺ in the pore by Li⁺ is very similar to the replacement of Cs⁺ in the pore by Na⁺. So why do Na⁺/Cs⁺ mixtures have an AMFE while Li⁺/K⁺ mixtures do not? The answer lies in the endpoint conductances which are nearly identical for Na⁺ and Cs⁺ (∼500 pS), but very different for Li⁺ and K⁺ (211 pS vs. 800 pS) (Fig. 5 A).

To start the analysis, assume for simplicity that the sum total number of both Na⁺ and Cs⁺ in the filter is constant and that the pure Na⁺ and Cs⁺ endpoint conductances are equal. Both are approximately true; in RyR, there are 3–3.8 monovalents in the selectivity filter (i.e., Na⁺ plus Cs⁺ or Li⁺ plus K⁺). If the Na⁺ and Cs⁺ conductances were both proportional to their occupancies, then the total pore conductance would be constant as mole fraction changed because the total occupancy of Na⁺ plus Cs⁺ is constant and because the endpoint conductances are equal. However, the Na⁺ current is not proportional to its occupancy, and so the total current is not constant. In fact, because the conductance (solid) line for Na⁺ is less than its occupancy (dashed) line in Fig. 5B, the total pore conductance dips below the endpoint conductances to make the AMFE. At <10% this effect is not substantial when the endpoint conductances are as far apart as they are for Li⁺/K⁺ mixtures; for Li⁺/K⁺ mixtures, ∼75% of the K⁺ current would have to be depressed by a small amount of Li⁺ to be experimentally observable.

The reason that the Na⁺ conductance line is less than its occupancy line is that there is an extra resistance for Na⁺ outside the selectivity filter (like for Ca²⁺ earlier). This is illustrated in Fig. 5 C, where the pore conductance in Na⁺/Cs⁺ mixtures is calculated in different ways. The solid line computes the conductance by using only the resistances of Na⁺ and Cs⁺ in the selectivity filter. It does not have an AMFE. Only when the resistance of the entire pore is included is there an AMFE (dashed line). This demonstrates that it is not sufficient to include only the selectivity filter in the calculation because the AMFE is due to how the resistances both inside and outside the selectivity filter change with mole fraction.

Discussion

Resistors-in-series model

Nonner et al. (13) were the first to show that the AMFE requires neither single filing of ions nor multiple ions in the pore. Their model described the AMFE as coming from localized depletion zones, located adjacent to binding sites, where ion concentration is low and therefore conductivity is low or, equivalently, resistance is high. In models of the L-type calcium channel, these localized depletion zones were indeed found to generate the Na⁺ versus Ca²⁺ AMFEs (14,15,19). Therefore, localized depletion zones are one way to generate an AMFE. However, this article and recent work (described below) demonstrate that a generalization is necessary; the resistances of all regions in the system—and how they change with mole fraction—must be considered:

• 1.Experiments found AMFEs in synthetic nanopores in plastic (18). These pores have a uniform negative surface charge along their entire 12-μm length and therefore there is no localized binding site for the ions and consequently no localized depletion zones. However, the 50 Å-wide center of the pore is highly Ca²⁺-selective while the 1500–4000 Å-wide ends of the double-conical pore are not. This causes the resistances in those two regions to change very differently with mole fraction, producing the AMFE.
• 2.There are no obvious depletion zones in the density profiles of ions with the same charge. This was shown for the Ca²⁺ versus Ba²⁺ AMFE in the L-type calcium channel (19). It is also what makes analyzing the Na⁺ versus Cs⁺ AMFE in RyR challenging; there are no areas of localized high resistance to current flow for either ion species (data not shown) like there are for Ca²⁺ (Fig. 3, B and D).

Intuitively, the baths, the pore vestibules, and the selectivity filter must have different resistances to current flow; each region has different ion concentrations and, like any salt solution, has a concentration-dependent conductivity. The selectivity filter, in particular, must have a very different resistance than the rest of the pore because it must have a very different ion composition. For example, it has previously been shown that in RyR the Ca²⁺ concentration in the selectivity filter will be higher than the K⁺ concentration, but not so in the rest of the pore (21). Moreover, the ion concentrations—and therefore resistances—in the selectivity filter and the rest of pore must change differently with mole fraction because each region has a different affinity for ions like Ca²⁺—and, by definition, the selectivity filter has the highest affinity. An AMFE results because these resistors are in series and the ion species behave as if they move along parallel electrical pathways (19).

Different inferences from different theories

One common interpretation of an AMFE due to the textbook theory is that multiple ions are moving through the pore in a single file. This single-file, multi-ion origin of the AMFE has understandably become deeply engrained (6–12) because it was not until 10 years ago that an alternative theory was even proposed (13). Because these two theories describe ion permeation very differently, it is important to reexamine the inferences drawn from each.

Single filing

The classic barrier model describes ion permeation as ions hopping over energy barriers that separate binding sites that contain at most one ion (single filing) at a time (4). The resistors-in-series model describes ion permeation as diffusion of ions down their electrochemical potential gradients with no assumption of single filing. Both can theoretically explain the origin of AMFE. However, the experimentally measured AMFEs in the 50 Å-wide synthetic nanopores unequivocally show that single filing is not necessary for the AMFE (18). In this article, we have shown that a number of AMFEs can be predicted (before confirming experiments were done) with a PNP/DFT theory that does not include correlated, single-file motion of ions because it does not include the momentum conservation necessary to model that (37). Therefore, this article provides further evidence that single-filing of ions is not necessary to produce an AMFE.

Multi-ion pore

Because of the long history of the textbook theory, “AMFE” has become almost synonymous with “multi-ion pore.” However, in the resistors-in-series model, an AMFE can be explained even with <1 ion in the pore on average (13). In RyR, there are indeed multiple ions in the selectivity filter (Fig. 3), but this is not the reason there is an AMFE. There are multiple ions in a calcium channel because of basic electrostatics: the four negative glutamates or aspartates in the selectivity filter attract cations in similar numbers (approximately four monovalents or approximately two divalents).

Ca²⁺ blocks the pore

Ca²⁺ block of monovalent current in the textbook model is just that: Ca²⁺ occludes the pore because it is in a deep energy well and monovalent cations cannot pass at the occupied well (the single filing constraint). Momentum conservation would be required to model the physical block of the pore, which the Nernst-Planck approach does not include. Therefore, it is not the physical occlusion of the pore by Ca²⁺ per se that stops monovalent current in the resistors-in-series model. This is seen in the AMFEs of the synthetic nanopores where there is clearly no flux coupling (18). With increasing [Ca²⁺], Ca²⁺ increasingly occupies the center of the nanopore, but there is no occlusion of the 50 Å-wide pore by Ca²⁺; Ca²⁺ is just present in higher proportions because of the selectivity properties of the pore. In the same way, the Ca²⁺ in a calcium channel statistically occupies the pore more often, reducing the monovalent concentration and therefore the monovalent current (Fig. 3).

Preferential selectivity

The resistors-in-series model predicts that an AMFE reflects the preferential selectivity of ion species X over species Y; that is, a small amount of X replaces a disproportionate amount of Y from the selectivity filter. This has been described and experimentally tested previously (18,19). It is also seen in this article in the preferential selectivity of Ca²⁺ over monovalent cations (Fig. 3), Na⁺ over Cs⁺, and Li⁺ over K⁺ (Fig. 5 B). Preferential selectivity is necessary for the AMFE in the resistors-in-series model, but it is not enough by itself. For example, because the endpoint conductances are very different for Li⁺ and K⁺, the preferential selectivity of Li⁺ over K⁺ is not sufficient to make an AMFE (Fig. 5). However, the preferential selectivity does make the nonlinearity of the curve; a small amount of Li⁺ displaces K⁺ and moves the conductance closer to the pure Li⁺ conductance. Preferential selectivity also explains why there is no AMFE for Ca²⁺ and Li⁺; RyR has a relatively high affinity for Li⁺ compared to the other monovalent cations so there is low relative preferential selectivity of Ca²⁺ over Li⁺.

Presence or absence of an AMFE

The Ca²⁺/Li⁺ case illustrates that in the resistors-in-series model the absence of an AMFE does not mean the absence of preferential binding: Ca²⁺ is preferentially bound over Li⁺, but there is no AMFE because Ca²⁺ current makes up for the decrease in Li⁺ current (Fig. 3 C). It is actually true in both models that only when an AMFE is actually present can conclusions be drawn. In the textbook model, some multi-ion pores do not exhibit an AMFE (4). Therefore, even if no AMFE is measured under many conditions, one should not conclude that it is a single-ion pore. In fact, RyR was thought to be a single-ion pore, in part because no AMFEs had been observed—until the PNP/DFT permeation model predicted one in Na⁺/Cs⁺ mixtures (25).

Conclusion

We have used the PNP/DFT model of ion permeation through RyR to evaluate the AMFEs in RyR. The predictive power of the PNP/DFT model indicates that it describes the physics of both selectivity and permeation well. Our analysis suggests that the AMFEs in RyR are not due to the correlated motion of single-filing ions; the physics needed to describe this is not in the PNP/DFT equations.

The resistors-in-series idea explains both the origin of the AMFEs in RyR when they are present in some mixtures and why they are not present in others. Resistors-in-series also reproduces AMFE experimental data in the L-type calcium channel (14,15,19) and Ca²⁺-selective synthetic nanopores (18). Collectively these studies show that the AMFE is a natural consequence of electrodiffusion through highly-selective pores and that therefore the resistors-in-series theory may be applicable to many ion channels: an AMFE is likely to be measured in any channel that has a clear preference for one ion species over another when the endpoint conductances are similar. Moreover, the preferential selectivity underlying the resistors-in-series model is the interpretation of the nonlinear conductance versus mole fraction curves that do not have minima, like for Li⁺/K⁺ mixtures in RyR (Fig. 5 A). Preferential selectivity then provides a unifying concept for all the properties of conductance versus mole fraction curves.

The success of the resistors-in-series model demonstrates that it is a viable alternative theory of the AMFE. It also demonstrates that any interpretation of the AMFE is at best model-dependent. Consequently, observation of an AMFE is no longer enough to infer a multi-ion pore. Without independent evidence for single filing, it is not possible—in any channel type—to know whether the cause of the AMFE is correlated ion motion or preferential ion selectivity.