A Projection Pursuit Algorithm to Classify Individuals Using fMRI Data: Application to Schizophrenia

Abstract

Schizophrenia is diagnosed based largely upon behavioral symptoms. Currently no quantitative, biologically based diagnostic technique has yet been developed to identify patients with schizophrenia. Classification of individuals into patient with schizophrenia and healthy control groups based on quantitative biologically-based data is of great interest to support and refine psychiatric diagnoses. We applied a novel projection pursuit technique on various components obtained with independent component analysis (ICA) of 70 subjects’ fMRI activation maps obtained during an auditory oddball task. The validity of the technique was tested with a leave-one-out method and the detection performance varied between 80% and 90%. The findings suggest that the proposed data reduction algorithm is effective in classifying individuals into schizophrenia and healthy control groups and may eventually prove useful as a diagnostic tool.

1 Introduction

Schizophrenia is a disease that involves a disruption of a variety of cognitive functions such as memory, perception, executive function and emotion. It can be characterized by disturbances in thought, disorganized speech with poor content, delusions, hallucinations and causes impairment of personal/occupational relationships, poor self-care and impersistence at work (Liddle, 1987). Currently, diagnoses for major psychiatric disorders like schizophrenia are based solely on clinical manifestations and observed psycho-social impairments (World Health Organization, 1993). Biological indices, if they can be discovered, would be beneficial in providing more objective methods of classification.

There have been several efforts to use neuroimaging data to classify subjects into schizophrenia patients and healthy control groups. Shinkareva et al. (2006) presented an automated method that used a measure of temporal dissimilarity (RV-coefficient) in the fMRI data to identify the voxels with highly discriminating features. They used preprocessed time series for the whole brain volume, extracted spatiotemporal features that best distinguish the groups and classified subjects based on the similarity at the selected voxels. They used 14 subjects (7 healthy controls and 7 patients with schizophrenia) to test their method and average classification accuracy was 85.71% with a leave-one-out approach.

Ford et al. (2003) used Fisher Linear Discriminant (FLD) analysis on the fMRI brain activation maps to extract spatial characteristics and classify healthy controls and patients for schizophrenia, Alzheimer’s disease, and mild traumatic brain injury (MTBI). They applied FLD to find a linear projection of a training set of n classes onto n – 1 new dimensions to maximize a discriminability index. Kontos et al. (2004) used Hilbert space filling curves to map the 3D volumes to 1D and then projected them back to the 3D space with an inverse mapping procedure to detect discriminatory spatial patterns. They applied a Neural Networks based approach to classify patients with Alzheimer’s disease and healthy controls using the patterns from fMRI data. Hilbert space filling curves were also employed by Wang et al. (2004) on fMRI activation maps and the mapped 1D data was employed in time series analysis techniques for classification purposes.

Structural MRI images have also been used in the same effort applying different techniques. Nakamura et al. (2004) used MRI for morphological assessments and indicated that schizophrenia patients had structural deviations in multiple brain regions and these abnormalities were not limited to just one or a few clearly delimited brain regions. They applied discriminant function analysis to investigate the discriminative ability of combinations of brain anatomical variables and classified individuals into schizophrenia and healthy control groups. Kawasaki et al. (2007) applied discriminant function analysis using the multivariate linear model (MLM) and voxel based morphometry. They hypothesized that gray matter changes in schizophrenia patients would help discriminate them from healthy controls. MLM analysis was used to identify the eigenimages to represent inter subject variability. They used a set of 60 subjects (30 male healthy subjects and 30 male schizophrenia patients) to obtain a statistical model and the obtained model was tested using the same 60 subjects. Utilization of the first eigenimage representing most of the variance gave 90% detection performance on the same set that the statistical model was obtained (training and test sets were the same), and the performance decreased to 75% with Jackknife approach. Then they used these 60 subjects as the training set and a test group of 32 subjects (16 male healthy subjects and 16 male schizophrenia patients) was generated. The performance dropped to 80%

Fan et al. (2005) used a correlation map on the high dimensional morphological measurements obtained from brain MR images and applied a support vector machine - recursive feature extraction (SVM-RFE) to the features computed from extracted regions to determine the most important feature set. They applied a nonlinear SVM classifier to classify healthy controls and schizophrenia patients among female participants.

Other researchers have applied independent component analysis (ICA) to fMRI data in order to separate data into maximally independent groups and identified the networks most related to schizophrenia (Calhoun et al., 2004;Garrity et al., 2007). Calhoun et al. (2004) applied ICA to identify maps of task-uncorrelated synchronous fMRI activity and suggested that aberrant patterns of coherence in temporal lobe cortical regions are abnormal in schizophrenia patients. Garrity et al. (2007) identified the default mode component, which is thought to reflect the resting state of the brain, and examined the differences in the spatial and temporal aspects of the default mode. Healthy subjects and schizophrenia patients showed significant spatial differences in the default mode component.

Detection of schizophrenia with fMRI presents several challenges. Dependency of BOLD effect on the magnetic susceptibility differences cause perturbations in the magnetic field experienced by tissues near air/water interfaces in the human head. These can lead to artifacts like geometric image distortion and signal loss (Miller et al., 2007). Moreover, the signal intensity change is small and fMRI data is very high in dimension including tens of thousands of voxels with hundreds of time points. Efficient algorithms are needed in order to extract the robust spatial and spatiotemporal features in the data identifying regions in the brain that best discriminate the classes.

Jimenez and Landgrebe (1998) demonstrated that high dimensional space is mostly empty and pointed out that the useful information can be extracted more easily in a lower-dimensional subspace using Projection Pursuit (PP) algorithms (Jimenez and Landgrebe, 1999). PP is a proposed solution for problems where the classification is not accurate due to the limited number of training samples in a high dimensional space. It is defined as picking “interesting” low-dimensional projections of a high-dimensional point cloud by numerically maximizing an objective function called the “projection pursuit index” (Huber, 1985). A spatiotemporal PP algorithm was applied on multiple variables to predict the outcome of the tropical cyclones that go through extratropical transition to decrease the computational complexity of the analysis and to design a more effective classifier (Demirci et al., 2007; Demirci, 2006; Demirci et al., 2006). The designed technique is novel, adaptive, very efficient in detecting the differences between classes and computationally effective.

We are applying a similar PP technique on the activation networks of 70 individuals using the fMRI data obtained during an auditory oddball task. Then we classify the individuals objectively as either schizophrenia patients or healthy controls using a leave-one-out approach. In this paper, first we describe the fMRI experimental protocol and give information on the data that was used in Section 2. Section 3 presents the PP algorithm in detail. We present the detection performance of the technique and analyze the results in Section 4. Concluding remarks are given in Section 5.

2 Data and fMRI Experiment

We applied our PP algorithm on fMRI data that were collected at the MIND Institute, Albuquerque, NM as a part of the MIND Clinical Imaging Consortium. The consortium was established to understand the course and neural mechanisms of schizophrenia and was composed of four different sites (New Mexico, Harvard, Iowa and Minnesota) to obtain relatively large samples of data with a cooperative team approach. In this paper, we will focus on only the data from New Mexico site and present the results obtained with them as an initial test of our method.

In this study, fMRI data from 70 subjects were investigated. There were 34 patients with schizophrenia and 36 healthy controls in the group. Schizophrenia patients in the data set were limited to patients with a DSM-IV diagnosis of schizophrenia on the basis of a structured clinical interview and review of the case file (First et al., 1995). The healthy volunteer subjects were recruited from the community through newspaper advertising and carefully screened using a structured interview to rule out medical, neurological, and psychiatric illnesses, including substance abuse. Subjects with history of neurologic or psychiatric disease other than schizophrenia, head injury resulting in prolonged loss of consciousness and/or neurological sequelae, skull fracture, epilepsy, except for childhood febrile seizures, prior neurosurgical procedure, and IQ less than or equal to 70, based on a standard IQ test or the ANART were excluded from the study. All subjects were fluent in English. Patients with schizophrenia were receiving stable treatment with atypical antipsychotic medications (aripiprazole(7), olanzapine(2), risperidone(1), ziprasidone(1), clozapine(1)). 28 subjects in each class were males. There were no significant between-group differences in age. The healthy controls ranged in age from 18 to 54 years (mean=28.9, SD=12.3). The patients ranged in age from 18 to 60 years (mean=31.4, SD=11.6). All participants provided written, informed, IRB approved consent at the MIND Institute and were paid for their participation.

An auditory oddball task was employed. Participants wore sound-insulated earphones (Avotec, Stuart, FL) that presented the auditory stimuli while shielding from gradient amplifier noise. Subjects were expected to respond and press a button with their right index finger every time they heard a target stimulus and not to respond to a series of standard and novel sounds. The same auditory stimuli were used and found to be effective in differentiating healthy controls from schizophrenia subjects (Kiehl and Liddle, 2001; Kiehl et al., 2005). Standard stimuli occurred with a probability of p = 0.82 and were represented with 1 kHz tones. Target and novel stimuli were infrequent and each occurred with a probability of p = 0.09 (Fig. 1). Target stimuli were represented with 1.2 kHz tones and novel stimuli were computer generated, complex sounds. Each stimulus was presented with a pseudorandom order and last for 200 ms. The interstimulus interval changed randomly in the interval 550-2050 ms and the mean was 1200 ms. A total of four runs were acquired per session and each run was comprised of 90 stimuli. The sequences for target and novel stimuli were exchanged between runs to balance their presentation and to ensure that the activity evoked by the stimuli were not because of the type of the stimulus used. Scans were acquired at the MIND Institute, Albuquerque, NM on a Siemens Sonata 1.5T dedicated head scanner equipped with 40mT/m gradients and a standard quadrature head coil. The functional scans were acquired using gradient-echo echoplanar-imaging with the parameters: repeat time (TR)= 2s, echo time (TE)= 40ms, field of view= 22cm, acquisition matrix= 64 × 64, flip angle= 90°, voxel size= 3.44 × 3.44 × 4 mm³, gap= 1 mm, 27 slices, interleaved acquisition.

Fig. 1.

Auditory Oddball Experiment. Three different stimuli are represented with different colors and unevenly spaced to indicate the pseudorandom generation.

FMRI data were preprocessed using the software package SPM5. Images were realigned using INRIalign a motion correction algorithm unbiased by local signal changes (Freire et al., 2002). Data were spatially normalized into the standard Montreal Neurological Institute space (Friston et al., 1995), spatially smoothed with a 9 × 9 × 9 mm³ full width at half-maximum Gaussian kernel. The data (originally acquired at 3.44 × 3.44 × 4 mm³) were slightly sub-sampled to 3 × 3 ×3 mm³, resulting in 53 × 63 × 46 voxels.

3 Method

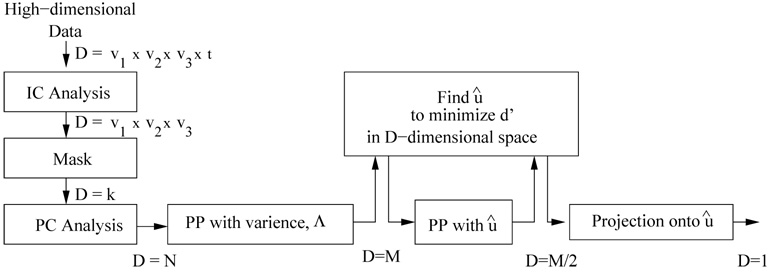
Finding an effective classifier is difficult in a high dimensional space where each subject is represented with a large set of voxels (υ₁ × υ₂ × υ₃) whose activation patterns change in time (t time points). We apply various data reduction techniques to decrease the dimensionality of the data while trying to minimize the loss of discriminability information between the healthy controls and schizophrenia patients. The steps involved in our classifier algorithm are summarized in Fig. 2.

Fig. 2.

Organization of the classifier algorithm with projection pursuit stages.

Previous research suggests that there are significant differences in the activation patterns of independent components obtained using fMRI data between patients with schizophrenia and healthy controls (Calhoun et al., 2004; Garrity et al., 2007). As an initial step, we employ a group independent component analysis (group ICA) to extract the functionally connected networks in the brain in time for different runs (Calhoun et al., 2001; GIFT, 2007). In group ICA, single-subject images in time are concatenated and used in an ICA estimation. The single subject results are then determined by projecting the single subject data onto the subject-specific mixing matrix. Application of group ICA provided less noisy components and eliminated the necessity of sorting them for each subject analysis. The dimensionality of the data for each subject is decreased from υ₁ × υ2 × υ₃ × t to υ₁ × υ₂ × υ₃ during the application of ICA. Each of the subjects is represented with one or more independent components and these components are used either separately or together as input to the algorithm (Fig. 2).

A different mask, possibly with different number of elements (k_c), was generated for each component and applied to eliminate the voxels that demonstrated indifferent activation patterns between the two classes. A stepwise method was employed. At each step, 10 patients with schizophrenia and 10 healthy controls were selected randomly among their groups and the voxels showing higher activation for either schizophrenia patients or healthy controls were retained considering the difference between the averages of the two subsets. The random selection was repeated and the voxels showing higher activation for schizophrenia or healthy subjects consistently were determined using the intersection of the voxels in each iteration till the number of voxels were less than 6000. This approach with subgroups has been followed in order to avoid overfitting the data. The obtained mask was applied to all subjects and each subject was represented with the remaining k voxels in a D = k dimensional space.

The set of remaining voxels for each subject can be arranged into a single vector (k × 1) that is denoted by x_i. These vectors corresponding to N subjects are rearranged into an (k × N) data matrix,

$$\mathrm{X}=\left[({\underset{¯}{x}}_1-\underset{¯}{\hat{\mu }})({\underset{¯}{x}}_2-\underset{¯}{\hat{\mu }})\dots ({\underset{¯}{x}}_N-\underset{¯}{\hat{\mu }})\right],$$ (1)

where $\widehat{\underset{¯}{\mu }}$ is the mean vector defined as $(\underset{¯}{\hat{\mu }}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\underset{¯}{x}}_i)}$. The (k × k) dimensional covariance matrix of the random variable X is estimated as

$${\hat{\mathrm{C}}}_{xx}=\frac{1}{N-1}\mathrm{X}{\mathrm{X}}^T=\frac{1}{N-1}{\displaystyle \sum _{i=1}^N({\underset{¯}{x}}_i-\underset{¯}{\hat{\mu }}){({\underset{¯}{x}}_i-\underset{¯}{\hat{\mu }})}^T,}$$ (2)

and it contains the covariance between any pair of voxels from subject to subject. There are k random variables and the diagonal elements of the covariance matrix are the corresponding variances $({\sigma }_i^2)$. Note that even though ${\hat{\mathrm{C}}}_{xx}$ is (k × k), the matrix has only rank N with the assumption that the N subject scans are linearly independent.

We find the linear combination of all the variables that explains maximum variance. This gives us the eigenvalue decomposition of the covariance matrix,

$${\hat{\mathrm{C}}}_{xx}=\mathrm{Q}\Lambda {\mathrm{Q}}^{-1}=\mathrm{Q}\Lambda {\mathrm{Q}}^T.$$ (3)

In Equation 3, Q⁻¹ can be replaced by Q^T and ${\hat{\mathrm{C}}}_{xx}$ is symmetric and positive semi-definite as we are assuming that columns of the matrix X are independent (Strang, 1986). It is guaranteed that eigenvalues are real, nonnegative N of which are nonzero) and k eigenvectors are orthogonal and form a set of bases (Q^TQ = I_NxN) (Strang, 1986). When we form the transformed data matrix P_N×N = Q^TX, we see that the covariance matrix of the transformed variable is diagonal,

$${\hat{\mathrm{C}}}_{pp}=\Lambda .$$ (4)

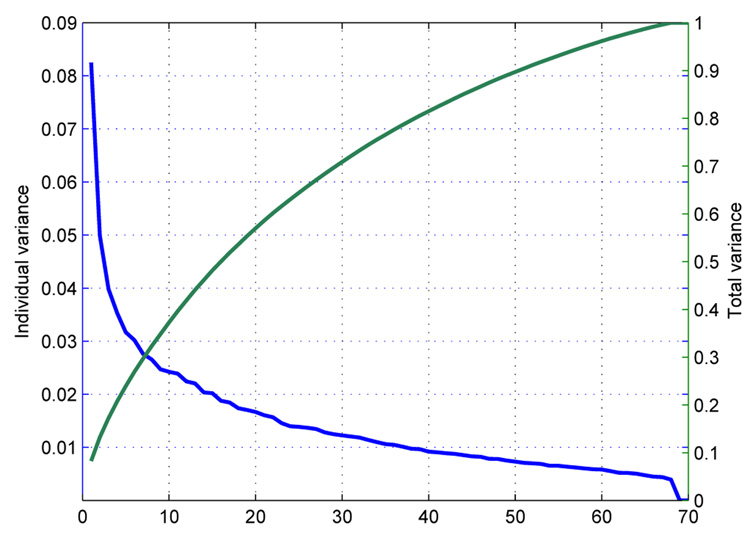
Equation 4 indicates that columns of the transformed data matrix P are spatially uncorrelated. The i^th column of Q is the i^th eigenvector, q_i, of ${\hat{\mathrm{C}}}_{xx}$ and corresponds to the i^th largest eigenvalue, λ_i. Each eigenvalue λ_i gives the measure of the fraction of the total variance in ${\hat{\mathrm{C}}}_{xx}$ explained by that particular q_i, and this fraction is the ratio of the λ_i to the sum of all eigenvalues (trace of Λ). The individual variance each q_i represents, λ_i, and the total variance represented by the largest m q_i’s are depicted in Figure 3. We can multiply the q_i’s with the coefficients in P and obtain the approximates of the subjects. This relation can be summarized by,

$${\underset{¯}{\hat{x}}}_i={\displaystyle \sum _{j=1}^N{\mathrm{P}}_{ij}{\mathrm{q}}_j}$$ (5)

where ${\underset{¯}{\hat{x}}}_i$ is the i^th subject, q_j is the j^th eigenvector rearranged into a column, P_ij is the j^th principal component (PC) of the i^th subject.

Fig. 3.

Eigenvalue spectrum for one of the independent components, Temporal Lobe.

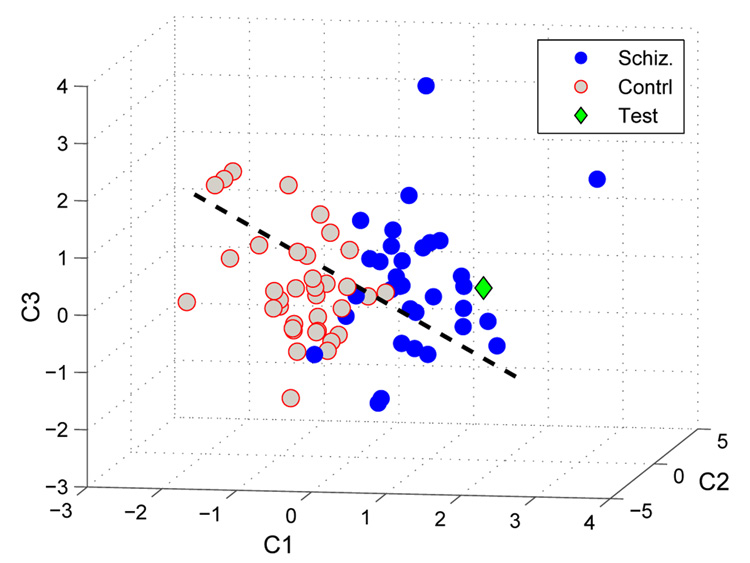
The subjects (either patient or healthy control) can now be transferred into an N dimensional space after being projected onto a lower-dimensional space using the PCs obtained in Equation 5 and applying a whitening transformation (P_ω = Λ^−1/2P). The axes in this space correspond to the eigenvectors q_1,…,N and the subjects’ coordinates are the PCs, columns of P_ω. This reduces the dimensionality of the data from k to the number of subjects, N, utilizing the eigenvectors associated with the N PCs. The rest of the eigenvectors are in the nullspace of the system and they can be represented using the first N eigenvectors with the assumption that the N subjects are independent. In Fig. 4, we can see the distribution of the subjects with schizophrenia and healthy controls in a 3-dimensional space where each of the subjects represented using the first three PCs for visualization purposes. The blue dots indicate that the subject has been diagnosed with schizophrenia. Gray dots indicate that subject is from the healthy control group. The dashed line shows the direction that maximizes the separation of the schizophrenia and healthy control subject distributions. A test subject not included in the training set can also be projected onto the same space for an objective decision. The green diamond represents the test subject in this space.

Fig. 4.

Distribution of Patients with Schizophrenia, Healthy Controls and Test subjects in 3-dimensional space where they are represented by the first three components. The dashed line represents the direction which maximizes the separation of subjects with schizophrenia and healthy controls. Subjects with schizophrenia are represented with blue points and healthy controls are represented with gray points. The green diamond represents the test subject which was projected onto the space spanned by the training subjects (blue and gray).

There is a trade-off between the number of PCs to use and detection performance that can be achieved. Although each additional PC and the corresponding eigenvector brings extra information to the system, this will increase the computational load and result in overfitting to the training data by emphasizing the information that is not important, e.g. noise. The original data can be represented with a smaller set of M (M < N) eigenvectors corresponding to the largest M eigenvalues as approximation to the data set. The optimum number of PCs (M) to be used should be determined for best detection performance. This step decreasing the dimensionality of the data from N (number of subjects) to M is called projection pursuit with variance as the elimination of the eigenvectors is based on the eigenvalues and thus the variance they include. In this paper, the results corresponding to various choices of M are presented.

We use an optimization algorithm to find the direction that maximizes the separation of schizophrenia and control subject distributions in the M dimensional space. The axes u₁,…,u_M represent the first M eigenvectors considered. The algorithm examines different directions projecting coordinates of the subjects onto the candidate directions in the M-dimensional space with a dot product operation. The projection distances of a set i is defined as,

$$x_i=P_i·{\hat{u}}_0$$ (6)

where P_i is the PC matrix whose columns are the components of the subjects from the set i. The optimization algorithm tries candidate directions, ${\hat{u}}_0$, to maximize the cost function,

$$d\prime =\frac{\sqrt{2}|{\mu }_s-{\mu }_c|}{\sqrt{{\sigma }_s^2+{\sigma }_c^2}}.$$ (7)

The role of the whitening transformation in the representation of the subjects is crucial in the analysis as we are looking for a unit length vector as a criterion for further reduction (Demirci et al., 2007). The whitening operation takes into account the whole group variance in different directions and treats each eigenvector as equally important whereas the normalization in Equation 7 considers just the class variances.

In Equation 7, µ and σ² are the means and the variances of the projection distance distributions for schizophrenia and control sets, x_i, on a particular direction, ${\hat{u}}_0$, respectively. In an M dimensional space, the direction maximizing the separation of the schizophrenia and control subject distributions is found and called ${\hat{u}}_A$. We considered the components of the unit length vector ${\hat{u}}_A$ as a measure of separability in M different directions and kept only the directions which gave us better separation between the classes. These directions (eigenvectors) correspond to the components of ${\hat{u}}_A$ with larger absolute values.

The M/2 eigenvectors corresponding to the M/2 components with the larger absolute values were kept and the remaining eigenvectors were eliminated. The step is a projection from M dimensional space onto an M/2 dimensional space and subjects are represented with only M/2 PCs with a better separability in the projected space. The axes u_j1,…,u_jM/2 (j ={1,…, M}) represent the eigenvectors that provide better separability among the first M eigenvectors. The same optimization step is repeated in the M/2-dimensional space to find another direction that maximizes the separation of schizophrenia and control subject distributions. The direction is represented with the unit length vector ${\hat{u}}_B$. Subjects that are represented with M/2 PCs are projected onto ${\hat{u}}_B$ and then represented with only a scalar each. Representing the subjects in the reduced (M/2)-dimensional space rather than the initial M-dimensional space improves the optimization that is involved in finding ${\hat{u}}_0$ and classification accuracy (data not shown). The extra step smooths the dimensionality reduction and minimizes the discriminating information loss.

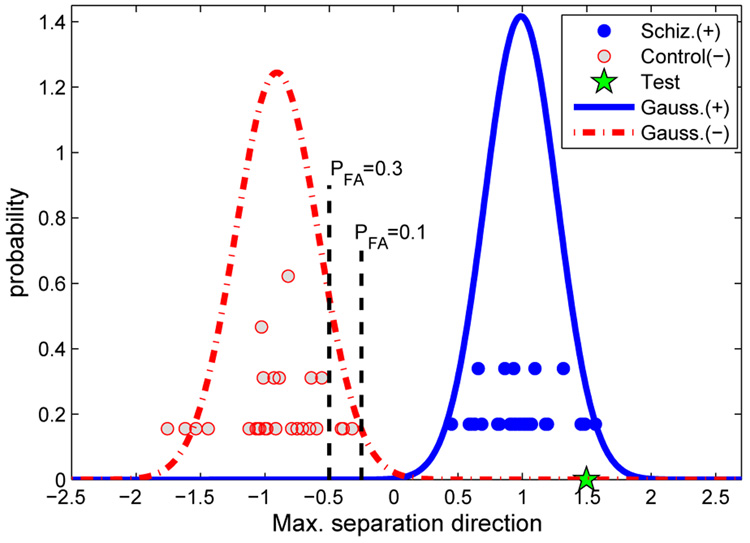
The distribution of the projection distances of the schizophrenia and control subjects on ${\hat{u}}_B$ in the M/2 dimensional space are shown in Fig. 5. The histograms are approximated with Gaussian distributions. The x-axis corresponds to the direction ${\hat{u}}_B$. 69 subjects were used in the analysis and the 70th subject was projected onto the space for a classification based on the training set. In Fig. 5, subjects with schizophrenia are represented with filled points and control subjects are represented with the empty points. The histograms were approximated with Gaussian distributions using the mean and variances of the two distributions. The test subject is also projected onto the same direction and projection distance is compared with a predicted false alarm rate (P_FA) obtained using the Gaussian approximations for an objective classification. Fig. 5 shows a test subject that is classified as a schizophrenia subject as it falls to the right side of the P_FA = 0.3 threshold.

Fig. 5.

Histogram for the projection distances of the schizophrenia and control subjects on ${\hat{u}}_B$. Distributions are approximated with Gaussian curves. The test subject is projected onto the same direction for an objective classifier.

4 Results and Discussion

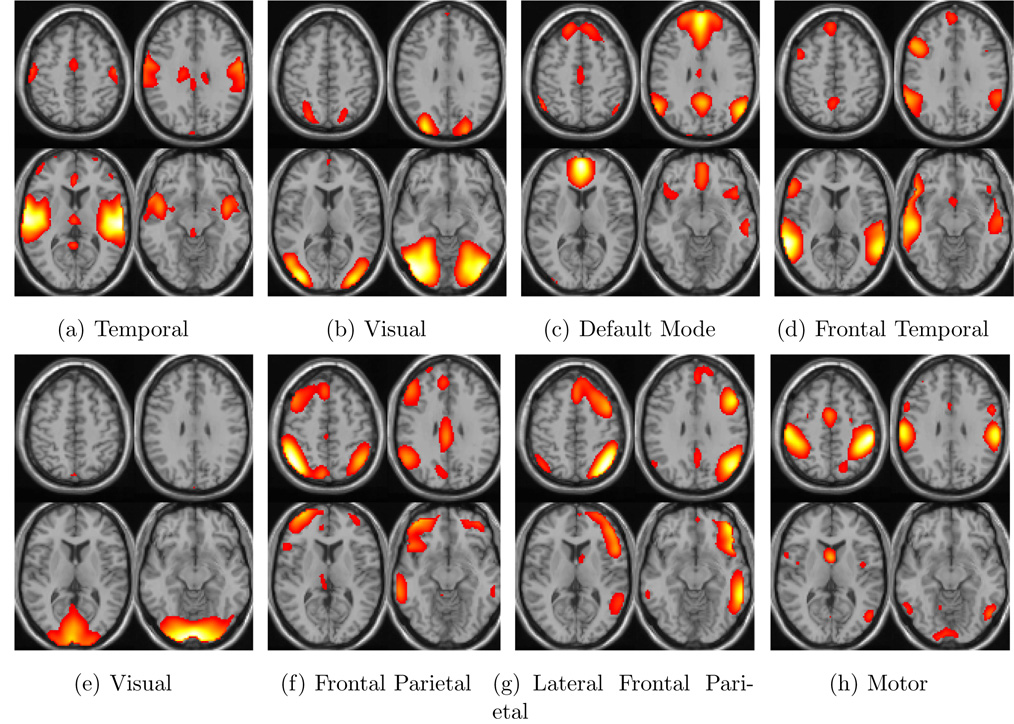
The effectiveness of the PP algorithm has been investigated with varying parameters like predicted P_FA thresholds, number of PCs and independent components. Independent components (temporal mode, visual mode, default mode, e.g.) obtained with an application of ICA on the fMRI data have been used either separately or together as input to the algorithm. Four sample slices from eight different independent components and the corresponding activated regions are shown in Fig. 6. The eight independent components were selected as preferred by Beckmann et al. (2005). The number of PCs considered after the PP step with variance, M, have been changed to see its effect on the performance. We followed a leave-one-out approach and used each of the N individuals as the test subject where the rest of the individuals, N – 1, were used as the training set in N separate analyses. The detection performance of the PP algorithm has been recorded using four different thresholds employing the predicted false alarm rates of P_FA = 0.1, P_FA = 0.2, P_FA = 0.3 and P_FA = 0.4. These thresholds were obtained using Gaussian approximations to the histograms on the ${\hat{u}}_B$ direction based on the distribution of the training subjects. The area under the control group Gaussian curve to the right of the chosen threshold is the predicted P_FA rate (Fig. 5). These thresholds are arbitrarily chosen and serve as a tool to measure performance. They can be thought of as samples on the ROC curve.

Fig. 6.

Four slices from eight different activation networks that were obtained by ICA and averaged over all subjects. The highly activated regions in the brain are indicated.

P_D (probability of detection: deciding a schizophrenia patient is a schizophrenia patient, number of correctly diagnosed schizophrenia patients divided by number of all schizophrenia patients, sensitivity), P_FA (probability of false alarm: deciding a healthy control subject is a schizophrenia patient, number of incorrectly diagnosed healthy controls divided by the number of all healthy controls, (1-specificity)) and P_all (probability of deciding correctly considering all subjects, both healthy controls and schizophrenia patients, number of correctly diagnosed subjects divided by number of all subjects) were listed in Table 1 for varying number of M and for different independent components and thresholds used. The performances in Table 1 are based on the test subjects.

Table 1.

Detection performance of the PP technique with 4 different masks with varying number of PCs (M/2,M). Probability of detection (P_D), probability of false alarm (P_FA), and the detection performance considering both schizophrenic and healthy subjects (P_All) are presented for predicted P_FA = 0.1, P_FA = 0.2, P_FA = 0.3 and P_FA = 0.4 obtained using Gaussian distribution approximations.

			Temporal (27)				Default (21)				Visual (16)				Frontal Temporal(17)				Visual (29)				Frontal, parietal (23)				Lateral, Frontal par(18)				Motor (8)				All
		PFA	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%	10%	20%	30%	40%
Number of Components Used	(25,50)	PD	0.97	0.97	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.97	0.97	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.91	1.00	1.00	1.00	0.91	0.97	0.97	0.97	1.00	1.00	1.00	1.00
		PFA	0.39	0.67	0.72	0.81	0.36	0.53	0.64	0.72	0.36	0.50	0.56	0.58	0.56	0.61	0.64	0.72	0.53	0.58	0.64	0.72	0.47	0.67	0.69	0.75	0.33	0.50	0.61	0.75	0.39	0.50	0.56	0.64	0.56	0.67	0.75	0.89
		Pall	0.79	0.64	0.63	0.59	0.81	0.73	0.67	0.63	0.81	0.74	0.71	0.70	0.70	0.67	0.67	0.63	0.73	0.70	0.67	0.63	0.76	0.66	0.64	0.61	0.79	0.74	0.69	0.61	0.76	0.73	0.70	0.66	0.71	0.66	0.61	0.54
	(20,40)	PD	0.97	0.97	1.00	1.00	1.00	1.00	1.00	1.00	0.97	1.00	1.00	1.00	0.97	0.97	0.97	0.97	0.94	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.94	1.00	1.00	1.00	0.88	0.97	0.97	0.97	1.00	1.00	1.00	1.00
		PFA	0.36	0.56	0.67	0.75	0.28	0.44	0.58	0.67	0.31	0.44	0.56	0.58	0.50	0.58	0.64	0.72	0.33	0.47	0.53	0.64	0.31	0.47	0.61	0.67	0.22	0.44	0.61	0.72	0.31	0.47	0.58	0.64	0.44	0.64	0.72	0.86
		Pall	0.80	0.70	0.66	0.61	0.86	0.77	0.70	0.66	0.83	0.77	0.71	0.70	0.73	0.69	0.66	0.61	0.80	0.76	0.73	0.67	0.84	0.76	0.69	0.66	0.86	0.77	0.69	0.63	0.79	0.74	0.69	0.66	0.77	0.67	0.63	0.56
	(15,30)	PD	0.97	0.97	1.00	1.00	1.00	1.00	1.00	1.00	0.97	0.97	1.00	1.00	0.97	0.97	0.97	0.97	0.94	1.00	1.00	1.00	0.97	1.00	1.00	1.00	0.94	1.00	1.00	1.00	0.88	0.97	0.97	0.97	1.00	1.00	1.00	1.00
		PFA	0.28	0.53	0.61	0.72	0.25	0.42	0.53	0.69	0.22	0.36	0.44	0.50	0.39	0.56	0.67	0.69	0.19	0.42	0.50	0.56	0.31	0.47	0.58	0.64	0.22	0.33	0.64	0.64	0.25	0.44	0.53	0.61	0.36	0.53	0.67	0.81
		Pall	0.84	0.71	0.69	0.63	0.87	0.79	0.73	0.64	0.87	0.80	0.77	0.74	0.79	0.70	0.64	0.63	0.87	0.79	0.74	0.71	0.83	0.76	0.70	0.67	0.86	0.83	0.67	0.67	0.81	0.76	0.71	0.67	0.81	0.73	0.66	0.59
	(10,20)	PD	0.97	0.97	1.00	1.00	1.00	1.00	1.00	1.00	0.97	0.97	1.00	1.00	0.97	0.97	0.97	0.97	0.85	0.97	1.00	1.00	0.91	1.00	1.00	1.00	0.94	0.97	1.00	1.00	0.85	0.94	0.97	0.97	1.00	1.00	1.00	1.00
		PFA	0.17	0.47	0.67	0.75	0.19	0.31	0.47	0.56	0.19	0.28	0.42	0.50	0.31	0.39	0.50	0.64	0.17	0.36	0.50	0.56	0.19	0.31	0.44	0.61	0.17	0.31	0.53	0.64	0.19	0.31	0.44	0.58	0.28	0.47	0.56	0.67
		Pall	0.90	0.74	0.66	0.61	0.90	0.84	0.76	0.71	0.89	0.84	0.79	0.74	0.83	0.79	0.73	0.66	0.84	0.80	0.74	0.71	0.86	0.84	0.77	0.69	0.89	0.83	0.73	0.67	0.83	0.81	0.76	0.69	0.86	0.76	0.71	0.66
	(7,14)	PD	0.97	0.97	1.00	1.00	0.91	1.00	1.00	1.00	0.97	0.97	1.00	1.00	0.97	0.97	0.97	0.97	0.85	0.91	0.94	1.00	0.94	0.97	1.00	1.00	0.91	0.97	1.00	1.00	0.85	0.88	0.94	0.97	1.00	1.00	1.00	1.00
		PFA	0.08	0.19	0.42	0.58	0.19	0.22	0.50	0.53	0.19	0.22	0.33	0.44	0.19	0.39	0.44	0.56	0.17	0.22	0.36	0.56	0.19	0.31	0.39	0.53	0.08	0.22	0.50	0.61	0.19	0.28	0.47	0.50	0.25	0.42	0.50	0.67
		Pall	0.94	0.89	0.79	0.70	0.86	0.89	0.74	0.73	0.89	0.87	0.83	0.77	0.89	0.79	0.76	0.70	0.84	0.84	0.79	0.71	0.87	0.83	0.80	0.73	0.91	0.87	0.74	0.69	0.83	0.80	0.73	0.73	0.87	0.79	0.74	0.66
	(5,10)	PD	0.91	0.97	1.00	1.00	0.88	0.97	1.00	1.00	0.97	0.97	1.00	1.00	0.91	0.97	0.97	0.97	0.88	0.91	0.94	0.97	0.91	1.00	1.00	1.00	0.91	0.97	1.00	1.00	0.79	0.88	0.94	0.97	1.00	1.00	1.00	1.00
		PFA	0.08	0.22	0.39	0.58	0.19	0.28	0.44	0.58	0.19	0.25	0.31	0.36	0.19	0.33	0.42	0.53	0.19	0.25	0.33	0.47	0.22	0.28	0.39	0.47	0.11	0.22	0.42	0.64	1.17	0.28	0.44	0.47	0.22	0.39	0.47	0.64
		Pall	0.91	0.87	0.80	0.70	0.84	0.84	0.77	0.70	0.89	0.86	0.84	0.81	0.86	0.81	0.77	0.71	0.84	0.83	0.80	0.74	0.84	0.86	0.80	0.76	0.90	0.87	0.79	0.67	0.81	0.80	0.74	0.74	0.89	0.80	0.76	0.67
	(3,6)	PD	0.97	0.97	1.00	1.00	0.82	0.97	1.00	1.00	0.91	0.97	0.97	0.97	0.94	0.97	0.97	0.97	0.88	0.91	0.91	0.94	0.97	1.00	1.00	1.00	0.94	0.97	1.00	1.00	0.85	0.88	0.91	0.97	1.00	1.00	1.00	1.00
		PFA	0.11	0.25	0.42	0.58	0.11	0.25	0.39	0.50	0.17	0.22	0.33	0.39	0.19	0.36	0.42	0.53	0.17	0.22	0.31	0.39	0.25	0.28	0.36	0.42	0.08	0.22	0.44	0.61	0.17	0.25	0.44	0.56	0.17	0.33	0.50	0.58
		Pall	0.93	0.86	0.79	0.70	0.86	0.86	0.80	0.74	0.87	0.87	0.81	0.79	0.87	0.80	0.77	0.71	0.86	0.84	0.80	0.77	0.86	0.86	0.81	0.79	0.93	0.87	0.77	0.69	0.84	0.81	0.73	0.70	0.91	0.83	0.74	0.70
	(2,4)	PD	0.94	0.97	1.00	1.00	0.82	0.97	1.00	1.00	0.85	0.94	0.97	0.97	0.79	0.91	0.97	0.97	0.56	0.85	0.91	0.91	0.91	1.00	1.00	1.00	0.85	0.94	1.00	1.00	0.85	0.88	0.91	0.97	1.00	1.00	1.00	1.00
		PFA	0.06	0.25	0.44	0.53	0.11	0.19	0.33	0.50	0.11	0.25	0.31	0.39	0.25	0.31	0.39	0.44	0.14	0.22	0.36	0.47	0.19	0.25	0.33	0.44	0.11	0.22	0.36	0.56	0.11	0.19	0.36	0.56	0.17	0.33	0.47	0.58
		Pall	0.94	0.86	0.77	0.73	0.86	0.89	0.83	0.74	0.87	0.84	0.83	0.79	0.77	0.80	0.79	0.76	0.71	0.81	0.77	0.71	0.86	0.87	0.83	0.77	0.87	0.86	0.81	0.71	0.87	0.84	0.77	0.70	0.91	0.83	0.76	0.70

The results indicate that the performance decreases as we increase the predicted false alarm rate threshold. P_FA = 0.1 threshold results are higher than the others. This indicates that the schizophrenia patient and healthy control distributions are quite separated on the maximum separation direction ${\hat{u}}_B$. Normally the prediction performance decreases with decreasing predicted false alarm rates (Demirci et al., 2007). Smaller choice of predicted P_FA’s would cause the opposite behavior to be observed.

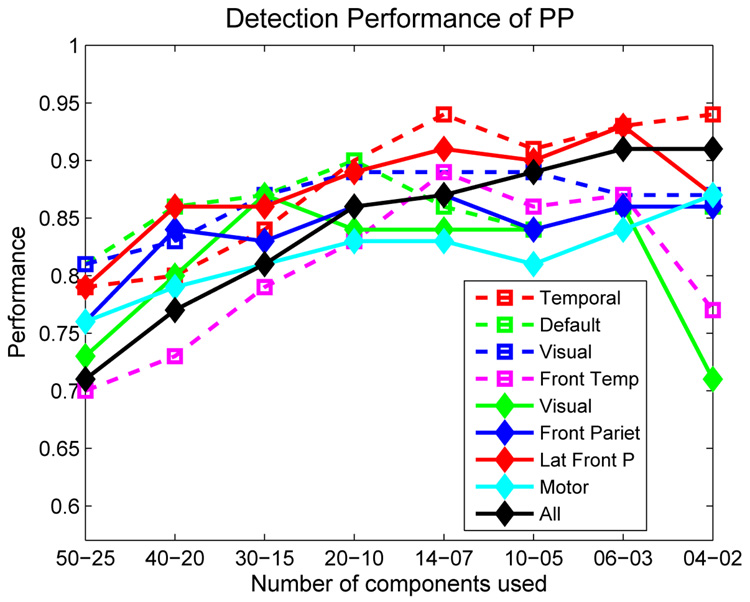
P_All performances, which is a measure of detection performance considering all subjects, for P_FA = 0.1 thresholds have been combined and plotted in Fig. 7 for better comprehension and comparison. The performances increase for almost all independent components with decreasing number of PCs considered till M=20 or M = 14. The performances decrease slightly with further decrease in the number of PCs. The optimum number of PCs to be used are either 20 or 14. This is in fact in accordance with the variance that the eigenvalues represent individually. The eigenvectors after the first 20 or 14 represent less than 2% variance (Fig. 3) and usage of these patterns in the optimization emphasizes the information that is not actually important. Including 45% or 60% of the total variance with the use of 20 or 14 PCs seem to be enough for reliable detection (Fig. 3).

Fig. 7.

Comparison of the performance of the PP algorithm using different independent components and number of PCs for P_FA = 0.1.

The results point out that temporal lobe and lateral frontal parietal mode (Fig. 6(a) and Fig. 6(g)) give better separability between schizophrenia patients and healthy controls. The performance with all 8 independent components combined is also presented in Table 1 and Fig. 7. Including all independent components together in the algorithm provide more stable results when less than 20 PCs are used and 0.85–0.90 detection performance can be achieved using all components together even with only M = 4 or M = 6. The performance obtained when all independent components are combined is lower than some of the performances obtained with individual components. This is because the data include information from components with lower individual performance and considers these equally important. The high performance obtained with temporal mode is in accordance with previous findings (Calhoun et al., 2004).

The obtained detection performance is high enough to support the effectiveness of the PP technique although almost one third of the schizophrenia patients are on medication. This paper is only an early step towards the use of imaging information in psychiatric decision making. Since disease prevalence is low (schizophrenia occurs with a probability of only 1%) there will be an increased number of false alarms. However, this is preferable to the alternative since it provides a guide for which individuals should be evaluated further. Prevalence will be less an issue for issues like treatment response or differential diagnosis within psychopathology. Another issue which needs to be studied is the impact of medication, since it is possible we are simply detecting a medication effect. Ongoing studies of prodromal subjects and first episode patients will help address this important question. There was not a clear clustering among the first episode and chronic schizophrenia patients and the subclassification of these groups will be investigated in a future paper.

5 Conclusion

We have applied a novel projection pursuit algorithm to classify 70 subjects as either patients with diagnosed symptoms of schizophrenia or healthy controls using independent components obtained with ICA. The results are presented with varying number of PCs and indicate a great potential for future clinical application.

Thus far, our investigations have been limited to differentiating healthy controls from patients with schizophrenia. We are planning to further refine these studies to perform subclassification of subjects with schizophrenia, possibly discriminating specific symptom type (positive and negative symptoms for example). More than just one component could be used together possibly with different number of voxels. Applying SVD combining information that is available from other networks will help us incorporate the information from various components. Other possible improvements might be obtained using the time course information for the independent components and expanding the data to multiple sites.

Our results using the present data set suggest that the projection pursuit method is a promising technique for fMRI research and appears to be an effective tool for classification of patients with mental illness using fMRI data.