Kinesin's step dissected with single-motor FRET

Abstract

The motor protein Kinesin-1 drives intracellular transport along microtubules, with each of its two motor domains taking 16-nm steps in a hand-over-hand fashion. The way in which a single-motor domain moves during a step is unknown. Here, we use Förster resonance energy transfer (FRET) between fluorescent labels on both motor domains of a single kinesin. This approach allows us to resolve the relative distance between the motor domains and their relative orientation, on the submillisecond timescale, during processive stepping. We observe transitions between high and low FRET values for certain kinesin constructs, depending on the location of the labels. These results reveal that, during a step, a kinesin motor domain dwells in a well-defined intermediate position for ≈3 ms.

Conventional kinesin, Kinesin-1, drives intracellular transport of vesicles and organelles along microtubules (MT) (1). As a result of the concerted action of its two identical motor domains, kinesin moves in 8-nm steps, hydrolyzing one ATP per step (2). The velocitiy of the motor is ATP dependent, follows Michaelis–Menten kinetics, and is 600–800 nm/s at saturating ATP-concentrations, which corresponds to ≈10 ms per step. The motor domains step in a “hand-over-hand” manner, each moving 16 nm in turn (3–5). Kinesin is a processive motor, making hundreds of steps before detaching from the MT. It is thought that processivity is achieved by keeping the ATP-hydrolysis cycles of both motor domains out-of-phase, by a gating mechanism, operated via tension on the linkage between the two motor domains (6, 7). It is not fully understood whether gating prevents ATP binding to the leading motor domain, ADP release from the trailing one, or both (6, 8). Tension might also be required to release the trailing, ADP-bound motor domain from the MT (6, 7).

Stepping occurs between configurations with both motor domains strongly bound to the MT and 8-nm apart, the “two-head-bound” state, which has been observed in single-motor Förster resonance energy transfer (FRET) (9) and fluorescence polarization studies (10). It is not very well understood what happens during a step between two subsequent two-head-bound states and what fraction of the time the motor domains spend in such configuration. At high ATP concentrations, optical trapping experiments with a time resolution of 50 μs, showed that a bead attached to kinesin's tail makes instantaneous steps and no intermediates could be resolved (11). However, substeps have been predicted on the basis of models for kinesin's mechanism (12). At low ATP concentrations, kinesin spends substantial time in the “ATP-waiting state,” before making a step. In this state, one motor domain is MT-bound and “waiting” for ATP, whereas the position of the other motor domain, containing ADP, is currently under debate. Some studies have indicated that the latter motor domain is MT-bound, similar to the two-head-bound state (5, 10, 13). In contrast, more recently, it was proposed on basis of electron microscopy data that the ADP-bound motor domain is docked on the nucleotide-free one and positioned slightly in front (14). In another study, using single-molecule FRET, the ADP-bound motor domain was also proposed to be not attached to the MT, but behind the nucleotide-free one (9). In this latter study, which had a time resolution of 10 ms, such a one-head-bound state was not detected at physiological, saturating ATP concentrations. So far, experiments that can directly resolve the motion of individual motor domains on the submillisecond time scale during processive motion have been lacking. Here, we apply a single-motor motility assay combining confocal fluorescence microscopy (15) with FRET to achieve this time resolution.

Results

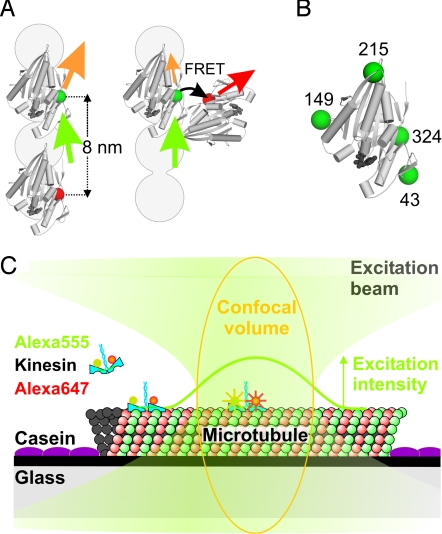
To sense distance changes between kinesin's motor domains using FRET, we generated four homodimeric kinesin constructs with single cysteine residues in different positions on both motor domains (Fig. 1). To these cysteines we attached Alexa Fluor 555 as donor and Alexa Fluor 647 as acceptor fluorophore. This FRET pair has a Förster distance of 5.1 nm (Molecular Probes). We anticipated that FRET would not occur for donor–acceptor labeled kinesins when both motor domains are bound to subsequent binding sites 8-nm apart. FRET would, however, occur in a potential intermediate with only one domain MT-bound and the other closer (Fig. 1A). We chose constructs with cysteines on position 324, 215, 43, or 149 (Fig. 1B), since it had been reported that these constructs are functional (16), which we confirmed by their unaltered velocity and processivity. FRET had been measured before, using a similar 324 construct (9).

Fig. 1.

Schematic representation of the kinesin constructs and the single-motor confocal fluorescence microscopy assay. (A) Two kinesin motor domains (PDB code 2kin) in a two motor domains MT bound state, too far apart for FRET, and a potential intermediate with motor domains close enough for FRET. The gray circles represent a single MT protofilament, plus-end pointing upwards. Green, orange, red, and black arrows represent excitation light, donor emission, acceptor emission, and FRET, respectively. (B) The four positions where cysteines were introduced for specific labeling (green spheres). (C) Experimental assay with fluorescently-labeled kinesin landing on a MT and walking through the confocal volume (orange), where it senses a Gaussian-shaped excitation intensity profile (green curve). Drawing not to scale; FWHM of the profile is ≈250 nm, corresponding to ≈30 kinesin steps.

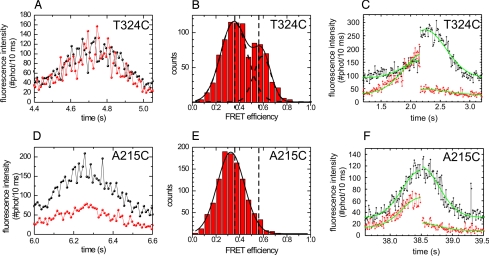
To detect short-lived stepping intermediates, a single-motor fluorescence assay with submillisecond time resolution is required, because kinesin's stepping cycle takes on average ≈12 ms at saturating ATP concentrations (17). To overcome the limited time resolution of wide-field fluorescence approaches (18), we have developed a confocal fluorescence microscopy assay allowing measurement of fluorescence intensity fluctuations on walking kinesins on time scales down to 100 μs (15). Here, we use this assay to measure variations in FRET efficiency by positioning the focused laser beam on a MT and collecting photons emitted by a single labeled motor walking through (Fig. 1C). Photons are separated by wavelength into two channels, detected and time tagged with 12.5-ns accuracy. Due to the motor's constant velocity and the Gaussian excitation profile, its fluorescence intensity time trace has a Gaussian shape (Fig. 2 A and D and Fig. S1 A and D). The width of this Gaussian is a direct measure of kinesin's velocity (15). The donor and acceptor fluorescence intensities directly reflect the labeling stoichiometries. We have restricted our analysis to events arising from kinesins labeled with one donor and one acceptor and that could be fitted well with a Gaussian [in many cases truncated by photo bleaching, attachment or detachment of the motor from the MT in the confocal spot (15)]. In time traces of A215C and S149C obtained at a saturating ATP concentration (2 mM), the acceptor intensity is much lower than the donor intensity, whereas both signals have similar intensity in traces of T324C and S43C (Fig. 2 and Fig. S1). In addition, intensity fluctuations appear anticorrelated for these latter two constructs. To investigate whether these observations are due to FRET occurring only in the latter constructs, we calculated the apparent FRET-efficiency (acceptor intensity divided by sum of donor and acceptor intensities; calculated only for the limited number of time traces that were not affected by photo bleaching or landing in the central 200 ms). The efficiency of T324C and S43C shows two populations (Fig. 2B and Fig. S1B). In contrast, for A215C and S149C, only one population can be distinguished (Fig. 2E and Fig. S1E) similar in efficiency to the low-FRET population of T324C and S43C. In the occasional events where the acceptor photo-bleached, the instantaneous drop of acceptor signal was accompanied by a rise of the donor signal for T324C and S43C, but not for A215C (Fig. 2 C and F, and Fig. S1C; note that these events were taken at ATP concentrations different from 2 mM). Taken together, these results indicate that during processive movement, the T324C and S43C kinesins switch between low and high-FRET states. In contrast, no high-FRET state is observed for the A215C and S149C constructs.

Fig. 2.

FRET is observed for donor—acceptor-labeled T324C kinesin and not for A215C. ATP concentration: 2 mM, unless stated differently (C and F). (A) T324C fluorescence intensity time trace binned over 10 ms showing large fluctuations. Black, donor fluorescence intensity; red, acceptor fluorescence intensity. (B) Apparent-FRET-efficiency histogram of T324C [I_A/(I_A + I_D), binned over 2 ms, central 200 ms of 6 events (other events were not taken into account for this analysis, because they were affected by landing or photo bleaching within this time interval)] showing two peaks (at FRET efficiencies of 0.353 ± 0.009 and 0.59 ± 0.01, obtained from double Gaussian fit). (C) Intensity time trace of a single T324C event. The green lines represent global fits with two Gaussians (one for the donor and one for the acceptor channel) with a common width, offset, and centre position and with an amplitude step at the moment of acceptor photo-bleaching. The fitted amplitudes show that after acceptor photo bleaching (at ≈2.2s) the donor intensity increased by a factor of 2.6 ± 0.2. For this trace the ATP concentration was 20 μM. (D) A215C fluorescence intensity time trace. The intensity fluctuations appear lower than in A. (E) Apparent-FRET-efficiency histogram of A215C (5 events). Only one peak, corresponding to the low FRET one in B, is observed (FRET efficiency = 0.325 ± 0.003). (F) Intensity time trace of a single A215C event. After acceptor photo bleaching (at ≈38.5 s), the donor intensity is hardly affected (increase of a factor 1.07 ± 0.05). For this trace, the ATP concentration was 50 μM.

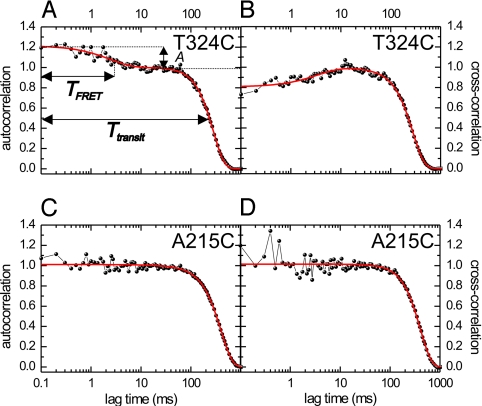
To further confirm the occurrence of FRET and determine the timescale of FRET fluctuations, we analyzed the fluorescence time traces using correlation techniques (15), similar to fluorescence correlation spectroscopy (19). The fluorescence intensity autocorrelation at time lag, τ, is proportional to the probability of detecting a photon at time t + τ, after one has already been detected at t. The autocorrelation calculated from a donor fluorescence time trace of a single T324C event, ranging from 0.1–1,000 ms (Fig. 3A), has two contributions (15): (i) a Gaussian with half-width ≈ 250 ms, reflecting the transit time through the confocal spot, and (ii) an exponential decay on the millisecond scale. To test whether this fast component is due to FRET, we calculated the cross-correlation between donor and acceptor signals. The cross-correlation (Fig. 3B) shows the same two contributions, the fast one having, however, negative amplitude. This negative amplitude indicates that the fast fluctuations are anticorrelated in donor and acceptor signal, a clear sign of FRET (20). A similar approximately millisecond FRET component was observed in the cross- and autocorrelations of S43C, but not of A215C and S149C (Fig. 3 and Fig. S2).

Fig. 3.

Millisecond-intensity fluctuations due to FRET are observed for T324C and not for A215C. ATP concentration: 2 mM. (A) Autocorrelation of the “cover neck bundle” donor fluorescence intensity time trace of Fig. 2A (T324C). Shown is a fit (red curve) of the data with Eq. 2, consisting of a Gaussian (transit through confocal spot) and an exponential (FRET) component. The FRET component has an amplitude, A, of 0.22 ± 0.01 and a decay time, T_FRET, of 2.5 ± 0.3 ms. (B) Cross-correlation of donor and acceptor intensity time traces of the same T324C event. The FRET-related correlation decay has an amplitude of −0.20 ± 0.01 and a decay time of 3.6 ± 0.6 ms. (C) Autocorrelation of the fluorescence intensity time trace of the A215C event of Fig. 2D. No decay of the autocorrelation on the approximate ms timescale can be discerned. (D) Cross-correlation of donor and acceptor intensity time traces of the same A215C event. No decay of the correlation is observed on the approximate ms timescale, indicating that no fluctuations occur due to changes in FRET.

For further quantitative analysis, we focus on donor autocorrelations only, since donor-signal fluctuations are a direct measure of the FRET efficiency, not affected by cross talk between donor and acceptor (21). Cross-correlation curves were only used as an additional quality check: None of the events used showed a positive cross-correlation on the approximately millisecond timescale. Fitting the T324C autocorrelations (n = 16, in total ≈500 steps; see Fig. S3 for additional curves) with Eq. 2 yielded an amplitude of 0.18 ± 0.02 (average ± SEM) and a decay time of 2.4 ± 0.4 ms for the exponential FRET contribution. The average step time was 15.0 ± 1.6 ms, as obtained from a Gaussian fit to the time traces (15). For S43C (n = 19) we found an amplitude of 0.17 ± 0.02, a decay time of 2.5 ± 0.3 ms, and a step time of 12.1 ± 0.7 ms (see Fig. S4 for additional curves). The decay time of the FRET contribution is substantially shorter than the step time, indicating that switching between different FRET states occurs within one step. A kinetic model is required to convert the amplitudes and decay times into FRET efficiencies and lifetimes of distinct states. In the simplest, two-state kinetic scheme, kinesin switches from a no-FRET state with both motor domains MT-bound, to a FRET state and back, completing an 8-nm step. Using this model (Eq. 3 in Material and Methods), we calculate that kinesin T324C (S43C) switches between a no-FRET state with lifetime 12 ± 2 ms (7.9 ± 0.8 ms), and a FRET state with lifetime 3.0 ± 0.9 ms (3.7 ± 0.6 ms) and FRET efficiency 0.88 ± 0.12 (0.69 ± 0.06). These values indicate that kinesin's stepping cycle includes a so-far-unresolved intermediate state with both motor domains in close proximity, lasting ≈3 ms at saturating ATP concentration.

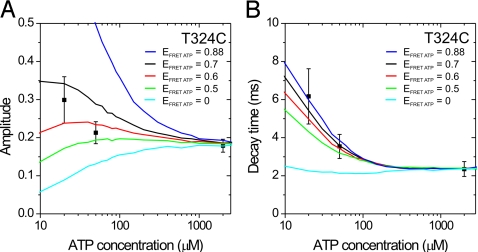
Next, we determined how the FRET signals of kinesin S43C and T324C depend on ATP concentration. From intensity time traces, we calculated apparent FRET efficiencies and observed these to increase with decreasing ATP concentration for both constructs (Fig. S5), in agreement with earlier results on a similar 324 construct (9). We calculated autocorrelations of the donor signals, fitted them (Figs. S3 and S4) and calculated lifetimes and FRET efficiencies using the two-state kinetic scheme. Note that to calculate lifetimes and FRET efficiencies from this model, the motor's stepping time is required as an input parameter (Table S1): It is not a full chemo-mechanical model that also describes the ATP-concentration dependence of the rates. Using this approach, the lifetimes of both FRET and no-FRET state change with ATP concentration (Table S1). ATP-binding is rate limiting at low concentrations (22), and one would have expected that the lifetime of only one of the states is ATP dependent. This contradiction indicates that a chemo-mechanical model incorporating the ATP-concentration dependence of the rates should be more complex and include additional states. Our data are intrinsically noisy due to the limited number of photons detected. More elaborate models create several challenges: Their autocorrelations are in many cases more complex than single exponential (23) and additional free parameters are required. To circumvent these challenges, we considered a constrained three-state cyclic chemo-mechanical model (see Materials and Methods), with two states identical to the two-state model used above: a no-FRET state, with both motor domains MT-bound and a FRET state, the intermediate. The third state has an ATP-dependent lifetime, calculated using Michaelis–Menten kinetics (Eq. 4 in Materials and Methods). This state is the ATP-waiting state characterized in refs. 9 and 14. At 2 mM ATP, its lifetime is negligible and the model reduces to two states. Only the FRET efficiency of this state was a free parameter. Lifetimes and FRET efficiencies of the other two states were taken from the two-state modeling (at saturating ATP) and kept constant. Autocorrelations were calculated from time traces generated using Monte-Carlo simulations, fitted with a single exponential (Fig. S6), and the resulting decay times and amplitudes were compared with the experimentally obtained ones. A good description of the experimentally obtained parameters was achieved using FRET efficiencies of 0.6 ± 0.1 (0.40 ± 0.15) for the ATP waiting state of T324C (S43C) (Fig. 4 and Fig. S7). Note that simulations with a FRET efficiency of the ATP-waiting state equal to that of the high-FRET or no-FRET state are inconsistent with our experimental data, indicating that the ATP-dependent state is a separate state, structurally distinct from the no-FRET and high-FRET states. Taken together, our data and analysis indicate that kinesin's stepping at different ATP concentrations can be described with a three-state model, with (i) a no-FRET state with ≈12-ms lifetime, (ii) a medium-FRET state with ATP-dependent lifetime, and (iii) a high-FRET state with ≈3-ms lifetime.

Fig. 4.

A three-state model describes the ATP dependence of the FRET signals of kinesin T324C. Amplitudes (A) and decay times (B) of the FRET autocorrelation decay. Symbols represent the values obtained from the autocorrelations of the measured time traces [mean ± SEM, n = 16 (2 mM ATP), 9 (50 μM ATP), 5 (20 μM ATP)]. The lines represent Monte-Carlo simulations with five different values for the FRET efficiency of the ATP-waiting state (E_{FRET ATP}). All other parameters were kept fixed (T_{NO FRET} = 12.0 ms, E_{NO FRET} = 0, T_{HIGH FRET} = 3.0 ms, E_{HIGH FRET} = 0.88, K_M = 19 μM).

Discussion

How do the three states fit in kinesin's chemomechanical cycle? Autocorrelation analysis is invariant to the order of the states. We believe, however, that the ≈3-ms, high-FRET intermediate state follows ATP binding to the nucleotide-free motor domain and precedes ADP release from the other motor domain, because its lifetime corresponds to that of ADP release after an ATP chase (3.3 ms) (24). In addition, it is widely accepted that ATP binding is followed by a fast change to a “closed” conformation enabling hydrolysis (25, 26) and docking of the neck linker (27). The new state now formed might correspond to the high-FRET intermediate we have observed. This intermediate state [3] (Fig. 5) is followed by forward displacement and attachment of the unbound motor domain to the MT, releasing ADP. In the resulting state [1], with both motor domains MT-bound, lasting ≈12 ms, ATP is hydrolyzed and phosphate released from the trailing motor domain. Next, the motor is in the ATP-waiting state [2] with a medium FRET efficiency, indicating that only one motor domain is tightly bound to the MT, consistent with some earlier studies (9, 14). In addition, the intermediate FRET value suggests that the ADP-bound motor domain alternates between configurations [1] and [3], or that it is tethered and can freely move within several nanometers. In this state, the flexibility of the ADP-bound motor domain could be relatively large, since both neck linkers, which together form the link between the motor domains, are most likely undocked (27, 28). On the basis of our results, we cannot distinguish between the tethered motor domain being in a rather fixed, intermediate position or being mobile. Recent studies using single-molecule fluorescence polarization (29) and optical trapping of a microsphere attached directly to one of the motor domains (30) have provided evidence for the tethered motor domain being flexible. Next, upon ATP binding, the neck linker of the tightly MT-bound motor domain docks, followed by formation of the cover-neck bundle, pulling the ADP-bound motor domain closer, returning to the high-FRET state [3] (27, 31). We have only observed FRET using kinesin labeled on the 324 and 43 positions, and not 149 and 215. This finding suggests that, in the high-FRET state [3], only one motor domain is MT-bound and the other one is oriented and translated in such a way that the 324–324 and 43–43 distances are shorter than ≈4.5 nm, whereas the 149–149 and 215–215 distances are larger than ≈6 nm (SI Text). These distance constraints are fulfilled by configurations with both neck-linker bases relatively close together and motor-domain fronts pointing apart (Fig. S8). The FRET efficiency in state [3] is higher than in the ATP-waiting state [2], indicating that, on average, the motor domains are closer together, in agreement with the neck linker of the ATP-bound motor domain being docked, shortening the tether between both motor domains (27, 31).

Fig. 5.

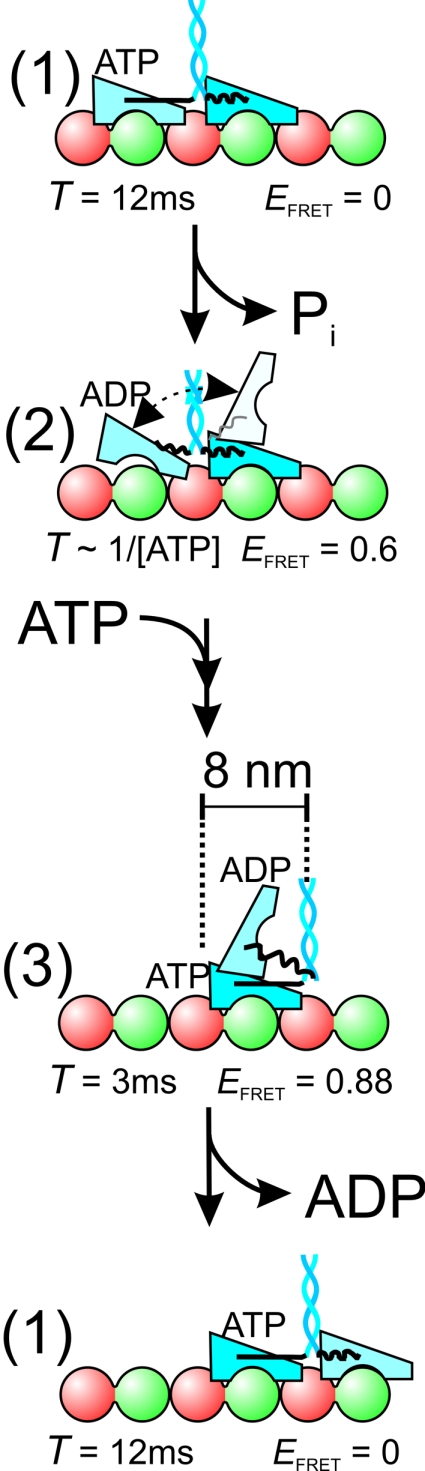
Chemo-mechanical interpretation of the three-state model. In the no-FRET state [1], both motor domains are tightly MT-bound and 8-nm apart. ATP is hydrolyzed and phosphate released from the trailing motor domain, leading to the ATP-waiting state [2], with intermediate FRET efficiency, one motor domain tightly bound, and the other tethered. Subsequent binding of ATP to the forward motor domain causes docking of its neck linker, moving kinesin's tail 8-nm forward, leading to a high-FRET intermediate state [3]. In this state, only one motor domain is MT-bound, and the other one is close, such that FRET can occur. After this intermediate state, the unbound motor domain (light blue) moves forward to the next binding side on the MT releasing ADP. Lifetimes (T) and FRET efficiencies (E_FRET) of the T324C construct are indicated.

In wide-field single-molecule fluorescence studies employing nanometer localization of individual motor domain (5, 7), no stepping intermediates have been resolved, most likely due to limited time resolution. In a recent wide-field single-pair FRET study using similar constructs to ours (9), it was shown that, in the ATP-waiting state, only one motor domain is MT bound and the other is within FRET distance, in agreement with our results. This study lacked, however, the time resolution to resolve the 3-ms high FRET state we observe here. They argued that at high ATP concentrations, kinesin makes rapid transitions from one two-motor-domain-bound state to the next, without intermediates. In contrast, our data indicate that, at saturating ATP concentrations, kinesin spends a substantial amount of time (20–30%) in a one-motor-domain-bound state (see below). We favor a model in which, at all ATP concentrations, ATP binding to the leading motor domain can only occur after the trailing, ADP-bound motor domain has released from the MT, releasing strain between the motor domains (8). After ATP binding, the ADP-bound motor domain stays loose from the MT for 3 ms, before binding to the next binding site.

In contrast to our data, no substeps have been observed in optical trapping experiments, measuring the displacement of a microsphere attached to kinesin's tail with 50-μs time resolution (11, 32). This apparent contradiction might indicate that transitions in the location of the motor domains do not lead in all cases to motion of the motor's tail. Our data does not provide direct evidence to discriminate between the 8-nm step of kinesin's tail occurring after ADP release (from [3] to [1]) or immediately after ATP binding (from [2] to [3]). However, strong support for the latter view has been provided in other studies (8, 27, 32). In addition, recent molecular dynamics simulations have shown that ATP-binding is followed by docking of the neck linker and subsequent formation of a β-strand involving residues of neck linker and N-terminal cover strand (the cover-neck bundle) (33). Optical trapping experiments have provided support for the idea that kinesin stepping is powered by the formation of this cover-neck bundle (29). Such a mechanism, with an 8-nm displacement induced by an ATP-driven, large-scale conformational change, is in line with our findings. To conclude, single-motor FRET experiments based on confocal fluorescence microscopy have provided us the observable parameter and time resolution to discern an up-till-now hidden intermediate in Kinesin-1's stepping cycle. This intermediate configuration might play a key role in directing the stepping motor domain forward, toward the plus-end of the MT, to the next binding site.

Materials and Methods

Single-Molecule Experiments.

Four single-cysteine homodimeric kinesin constructs were prepared, starting from a cysteinless (cys converted to ala), 560-aa long, ubiquitous human kinesin construct (15). Cysteins were introduced on positions 324, 43, 215, and 149 (Entelechon), verified by sequencing. Kinesins were expressed, purified, and labeled with a fivefold excess of both Alexa555 and Alexa647 (Invitrogen) as described in ref. 15. The experimental setup and assay (15) was modified to simultaneously detect donor and acceptor fluorescence. After passing through a 550DCLP dichroic mirror (Chroma), the fluorescence was split into two channels by a second dichroic mirror, 645DCXR (Chroma), and filtered by emission filters HQ575/50 or HQ675/50 (Chroma). Instead of 4 mM DTT, we used 5 mM TROLOX (Sigma–Aldrich) in the sample mix and no taxol was added. An ATP regeneration system was used at all ATP concentrations (15, 34).

Data Analysis.

Fluorescence intensity time traces (with 10-ms time bins) of single kinesins passing through the confocal spot were fitted with a Gaussian to obtain the amplitude, width, and offset. The data were restricted to ≈100-ms background signal on both sides of the event for fitting and further analysis. The fitted offset (dark counts and background fluorescence) was used for background correction, and the amplitudes of the donor and acceptor channels were used to select events that had both labels present. Also, events in which the signal vanished due to bleaching or detachment were included in the analysis, only when they traversed more than half the confocal volume. For these, the same criteria were applied, except that the fluorescence intensities after detachment or photobleaching were not taken into account. Background-corrected fluorescence intensity traces of the donor, x_i, and the acceptor, x_j, were binned at Δt = 0.1 ms and were cross- (i ≠ j) and autocorrelated (i = j) using:

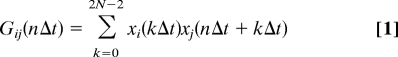where N denotes the total number of time bins of an event. The cross- and autocorrelations obtained using Eq. 1 are not normalized and decay to zero for large time lags. Correlations obtained in this way were fitted with:

where T_FRET is the decay constant and A the relative amplitude of the decay due to FRET, N is the amplitude of the correlation, α is a factor that describes the width of our confocal volume [we fixed to α = 760 (= 4 * σ_spot)], and T_step is the average step time. The term involving T_T is an empirical term added to correct for distortions from the ideal Gaussian shape of time traces, due to photo bleaching, landing, detachment, and the stochastic nature of stepping (15). All correlation curves were normalized by dividing the correlation values by the amplitude, N. Note that we have switched to a continuous lag time variable, τ, here. At a given condition, values of the decay time (T_FRET) and amplitude (A) of the FRET contribution, obtained from the fits to the autocorrelations were averaged. These average values were used for further analysis using a two- and three-state model (see below).

The Autocorrelation of a Stochastic Two-State Kinetic Scheme.

The theoretical description of the autocorrelation of a model where the donor fluorescence intensity cycles between a state without FRET (NF) and a state with FRET (F) is given by the following equations [adopted from Torres et al. (20)]:

where k_NF and k_F are the rates out of the No-FRET and FRET state respectively, E_F is the FRET efficiency of the FRET state, k_step is the step rate, and T_step is the average step time of the passing motor. Here, the FRET efficiency of the No-FRET state, E_NF, is set to zero. In our experiments, we expected a state with both motor domains MT-bound and 8-nm apart. We calculated that for such a state a FRET efficiency of <0.05 is expected [assuming a Förster distance of 5.1 nm for the FRET pair, Alexa Fluor 555 and 647 (Molecular Probes)]. Furthermore, we set the sum of the lifetimes of both states equal to the average step time (Eq. 3c).

Calculation of the Two-State Model Parameters from Experimental Autocorrelations.

From the average decay time (T_FRET) and amplitude (A) obtained from fits to the experimental autocorrelations, rates and FRET efficiencies were calculated using Eq. 3 a–c. In this way, two sets of solutions were obtained. The two solutions differ in their time-averaged relative donor intensities. The “correct” solution was selected after comparing the relative donor intensities of the two solutions with experimentally obtained values. The experimental values were determined by dividing the average donor intensity of events due to kinesins labeled with both donor and acceptor by the intensity of events due to kinesins labeled with only one donor.

Monte Carlo Simulations of the ATP Dependence of the FRET Signals Using a Cyclic Three-State Chemo-Mechanical Model.

We assumed a cyclic, three-state model without backward reactions. To limit the number of free parameters we fixed the dwell times and intensities of two of the states to those obtained with the two-state model at 2 mM ATP concentrations. We allowed the lifetime of the third state to vary with ATP concentration (such that its lifetime was negligible at 2 mM ATP), and only left the FRET efficiency of this ATP-waiting state as a free parameter. The lifetime of the ATP-waiting state, T_ATP-waiting, was obtained from the following derivative of the Michaelis–Menten equation:

where k_cat is the motor's maximal stepping rate, K_M is the concentration at which the motor moves with half the velocity, and [ATP] is the ATP concentration. The Michaelis constant (K_M = 19 ± 8 μM) was obtained from a fit to the combined average velocities of both constructs (T324C and S43C).

Using this model, we generated donor intensity time traces with simulation software written in LabVIEW (National Instruments), based on the Monte-Carlo approach. Typically, 15,000 cycles through the model were generated. Traces were generated for 20 ATP concentrations and different FRET efficiencies of the ATP-waiting state. From the simulated time traces, autocorrelations were calculated, which were fitted with an exponential function, yielding an amplitude and decay time.