The influence of target sensory modality on motor planning may reflect errors in sensori-motor transformations

Abstract

Multi-sensory integration studies have shown that combining heterogeneous signals can optimize motor performance by reducing errors inherent to any single modality. However, it has also been suggested that errors could arise from erroneous transformations between heterogeneous coordinate systems. Here we investigated the effect of visuo-proprioceptive integration on the control of multi-joint arm movements by manipulating target modality. When the target was visual, movement control required the integration of visual target signals with proprioceptive signals about limb configuration. In contrast, when the target was the unseen fingertip, movement control relied solely on proprioceptive signals since visual feedback of hand position was precluded. We hypothesized that a faulty integration of visual target signals with proprioceptive arm signals would result in a less accurate planning of visually-targeted movements with respect to proprioceptively-targeted movements. Different inter-joint coordinations patterns were tested by varying starting hand position. Results showed larger initial trajectory deviations from target direction for visually-targeted movements involving substantial shoulder and elbow motions. Inverse dynamic analysis revealed that these deviations were associated with less efficient intersegmental coordination. The control of visually-targeted movements thus appeared sub-optimal compared to proprioceptively-targeted movements when considering theoretical models of motor planning assuming kinematic or dynamic optimizations. Additional experiments further highlighted the effect of target position, and visual feedback of starting hand position, on motor planning for proprioceptively- and visually-targeted movements. Our findings suggest that the integration of heterogeneous sensory signals related to hand and target positions introduces errors in motor planning.

1. Introduction

To reach toward a visual target, the initial visual input in eye-centered coordinates must be transformed in a motor output coded in limb-centered coordinates (Andersen et al., 1997; Desmurget et al., 1998). The planning of visually-targeted arm movements is known to depend on visual information of target position (Gielen et al., 1985; Henriques et al., 2002) and starting hand position (Prablanc et al., 1979; Rossetti et al., 1995; Bagesteiro et al., 2006). It is also well established that motor planning relies on proprioceptive information to estimate limb configuration and account for intersegmental dynamics (Sainburg et al., 1995; Brown et al., 2003; Sober and Sabes, 2005). However, it remains unclear how visual and proprioceptive signals of target and hand positions are used to plan goal-directed arm movements (Desmurget et al., 1997; Graziano et al., 1999; Boulinguez and Rouhana, 2008; for a review, Sarlegna and Sainburg, 2009).

Multi-sensory integration studies have shown that combining visual and proprioceptive signals related to hand position can yield performance advantages for visually-targeted movements over conditions providing a single source of sensory information (van Beers et al., 1999; Maravita et al., 2003; Smeets et al., 2006). It has also been suggested that coordinate transformations of visual and proprioceptive signals can introduce substantial errors into the planning of visually-targeted movements (Soechting and Flanders, 1989; Sober and Sabes, 2005). This apparent controversy might in fact depend on task sensory conditions and on the studied control processes. For example, the neural processes underlying arm trajectory control have recently been reported to differ from those ensuring endpoint accuracy (Kurtzer et al., 2005; Schaefer et al., 2007). This supports the idea that final position accuracy is one goal for reaching movements while another goal is to optimize trajectory parameters such as movement kinematics (Atkeson and Hollerbach, 1985; Flash and Hogan, 1985) and/or dynamics (Uno et al., 1989; Nakano et al., 1999). We designed the present study to assess whether visuo-proprioceptive integration could influence final position achievement and intersegmental coordination for trajectory control during targeted arm movements. Because the nature of the controlled parameters remains unclear (Todorov and Jordan, 2002; Scott, 2004; Morrow et al., 2007), the task was designed to allow hand kinematics, joint kinematics and inverse dynamics analyses.

Here we manipulated visuo-proprioceptive integration by asking subjects to reach with their unseen hand for visual and proprioceptive targets. Reaching toward a visual target required the integration of visual signals about the target position with proprioceptive signals about the hand position while reaching toward a proprioceptive target (the unseen, contralateral hand) relied solely on proprioceptive signals of the pointing and target hands. We predicted that if visuo-proprioceptive integration introduces errors in motor performance, these should be evident for visually-targeted movements compared to proprioceptively-targeted movements. Previously, no differences were found between single-joint, elbow rotations toward visual and proprioceptive targets under normal conditions (Sarlegna and Sainburg, 2007). Here we investigated the effects of visuo-proprioceptive integration on the control of double-joint, elbow and shoulder movements by varying movement direction and thus interjoint coordination requirements. Movement direction was varied by changing the starting position in the main experiment or by changing target position in two control experiments. We hypothesized that the effects of visuo-proprioceptive integration on motor performance would be magnified by the intersegmental coordination requirements. These requirements were further manipulated by employing a mass-adaptation paradigm (Krakauer et al., 1999; Sainburg et al., 1999) to investigate the effect of visuo-proprioceptive integration in a novel dynamic environment.

2. Experimental procedures

Subjects

Seven neurologically intact adults (mean ± SD=24 ± 6 years) participated in the main experiment. All subjects (six males, one female) were right-handed, as indicated by laterality scores on a 10-item version of the Edinburgh Inventory (p. 112, Oldfield, 1971). Subjects were naive to the purpose of the experiment. Informed consent was solicited prior to the paid experiment, which conformed with the Declaration of Helsinki and was approved by the Biomedical Institutional Review Board of the Pennsylvania State University (IRB # 15084).

Experimental set-up

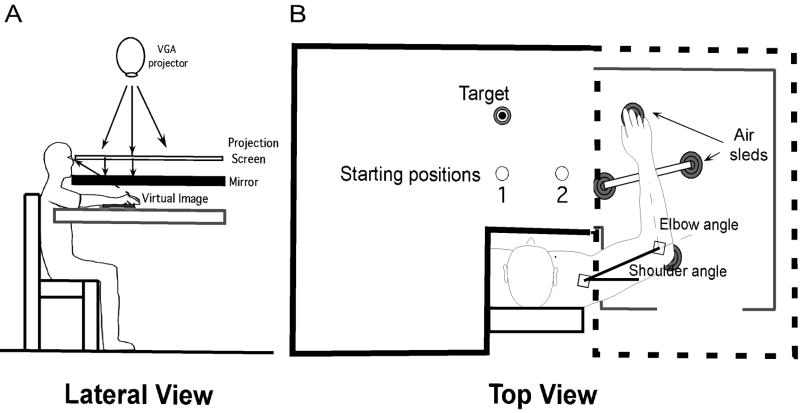
Figure 1A illustrates the set-up used for this study, which was designed to allow inverse dynamic analysis and thus reveal the coordination of muscle actions with intersegmental dynamics. Subjects sat with the right arm supported by an air-jet system positioned just below shoulder height. The air-sled glided over a horizontal surface on a cushion of air to minimize the effects of friction on arm movements. A splint was used to immobilize the wrist joint and to maintain the right index finger in an extended position. Position and orientation of each limb segment were sampled using the Flock of Birds® (Ascension Technology, Burlington, VT) electro-magnetic six degree of freedom recording system (sampling frequency: 103 Hz). A sensor was attached to the upper-arm segment via an adjustable cuff, while another sensor was fixed to the air-sled where the forearm was fitted. The sensors were positioned approximately at the center of each arm segment. A stylus rigidly attached to a sensor was used to digitize the positions of the distal phalange of the right index finger, the lateral epicondyle of the humerus, and the acromion, directly posterior to the acromio-clavicular joint. Custom computer algorithms for experiment control and data analysis were written in REAL BASIC^™ (REAL Software, Inc.), C (CodeWarrior^™) and IGOR Pro^™ (WaveMetrics, Inc.).

Figure 1.

(A) Experimental set-up. (B) Target position was constant while starting hand position varied. Part of the projection screen is omitted here for illustration. Subjects could not see their arm. Subjects could only see the target and the starting position in visual target conditions. Visual feedback of the moving limb was not available.

A visual display was projected on a horizontal back-projection screen located above the arm. A mirror, positioned parallel to and below this screen, reflected the projection to give the illusion that the visual display was in the same horizontal plane as the pointing hand. The recorded coordinates of the right index fingertip were used to project a cursor onto the screen (refreshing rate: 85 Hz) when subjects had to position their right hand at the starting location before reaching for a visual target. Calibration of the set-up ensured that the projection was veridical (Sainburg and Wang, 2002).

Experimental task

Subjects were asked to reach without visual feedback of the moving hand toward targets. The experiment consisted of four blocks of 25 trials, i.e., 100 reaching movements toward a visual or a proprioceptive target, from one of two starting positions. The order of the blocks was counter-balanced: subjects either started to reach for a visual or a proprioceptive target and, within the visual or proprioceptive blocks, the order of starting location was also counter-balanced. Target position was always the same: the target was located at 90º (compared to the fronto-parallel plane) and 18.5 cm from starting position 1, the movement being designed to require elbow motion and a small amount of shoulder motion. The target was located at 127º and 23.2 cm from starting position 2, as the arm movement was designed to require a similar amount of elbow extension but more shoulder flexion with respect to the movement starting from position 1.

In visual target conditions, a green start circle (2.0 cm diameter) was displayed to indicate starting position (Figure 1B). A 1.0 cm diameter, cross-hair cursor, providing visual feedback about the right index fingertip position, had to be positioned in the start circle. The cursor was visible within a 6 cm radius around the start circle during the initial positioning phase and was blanked after 2.2 s in the start circle, that is when the subject had to reach the visual target. The visual target, a 2.0 cm diameter circle, and the start circle were visible throughout the trial.

In proprioceptive target conditions, subjects did not see the target, the cursor or the start circle. Subjects were asked to reach without hand visual feedback of their right index fingertip toward their unseen left index fingertip. The left (target) index finger of the subject was guided by an experimenter toward a tactile landmark (corresponding precisely to the target position used in visual conditions) placed below the mirror. Once the left arm was released by the experimenter, the subject had to actively maintain the contact between the left index fingertip and the landmark. Then, the right (pointing) index fingertip was positioned at the start location by the experimenter.

After 2.2 s in starting position, subjects received an auditory “go” signal indicating that they had to reach for the (visual or proprioceptive) target. Subjects were instructed to reach the target “as fast and as accurately as possible”. No explicit instructions about the hand path were given. Note that when subjects reached with their unseen right hand toward their unseen left fingertip, the two hands never came into contact. No knowledge of results was thus available in visual or proprioceptive conditions and pilot testing showed no learning effect on performance measures over up to 100 trials per experimental condition. Subjects were asked to look at the target position as this natural behaviour has been shown to optimize endpoint accuracy both for visual and proprioceptive targets (Neggers and Bekkering, 1999). Subjects were given approximately ten practice trials to comply with task requirements, and the experimenter stood near the subject throughout the session to verify and remind task conditions.

Kinematic analysis

The positions of the right index fingertip, elbow, and shoulder were calculated from sensor data. These data were low-pass filtered at 8 Hz (third order, no-lag, dual-pass Butterworth), and differentiated to yield velocity and acceleration values. Movement onset was defined by the last minimum (last zero-line crossing in the acceleration profile, below 8% of the peak in the tangential hand velocity profile) prior to the maximum in the hand’s tangential velocity profile. Movement offset was defined as the first minimum following peak velocity (first zero-line crossing in the acceleration profile, below 8% peak velocity).

End error was defined as the 2D distance between the target and the hand (fingertip) at movement offset. Movement distance was calculated as the 2D distance between start and actual hand location. Distance errors thus reflected the difference between actual movement distance and the distance between start and target positions. The straight line between the starting hand position and the hand position at movement offset represented the major axis of the hand path. The maximum perpendicular distance between the hand and the line between start and stop positions represented the minor axis of the hand path. Hand path curvature index was defined as the ratio of the minor axis by the major axis. Movement direction was determined as the angle between the vectors start-target positions and start-hand positions, counterclockwise deviations being associated with negative values. Finger, elbow and shoulder kinematics were computed from movement onset to peak acceleration, peak velocity, peak deceleration and movement offset. The ratio of elbow-to-shoulder motion consisted of dividing the amount of elbow rotation by the amount of shoulder rotation.

Inverse dynamic analysis

To analyze the dynamic efficiency of the reaching movements, the terms of the equations of motion were partitioned into three main components: net torque, interaction torque, and muscle torque. The net torque is directly proportional to joint acceleration, inversely proportional to limb inertia, and is equal to the combined muscle and interaction torques (Sainburg et al., 2003; Zajac and Gordon, 1989). The interaction torque represents the rotational effect of the motion of the adjacent segments. Finally, the joint muscle torque primarily represents the rotational effect of muscle forces acting on the segment.

Torques were computed for the shoulder and elbow joints as detailed in Sainburg et al. (2003). The arm was modeled as two interconnected rigid links (upper-arm and arm) with the proximal end (shoulder point) free to move and frictionless joints at the shoulder and elbow. Limb segment inertia, center of mass and mass were computed from regression equations using subjects’ body mass and measured limb segment lengths (Winter, 1990). The inertia (0.0247 kg.m²) and mass (0.58 kg) of the forearm support were taken into account in the arm model.

To assess the contribution of elbow muscle torque to the initiation of movement execution, we computed the initial elbow muscle torque impulse by summing positive (torque related to elbow flexion) and negative (torque related to elbow extension) impulses from movement onset to the time of peak tangential hand acceleration. We also quantified the contribution of elbow muscle torque to net elbow torque using the following method. Intervals during which the muscle torque component acted in the same direction as the net torque were considered to contribute to a positive muscle torque impulse, and vice-versa. All positive and negative integrals were summed to yield a single muscle torque contribution for the initial phase of motion, from movement onset to peak acceleration.

Dependant measures were submitted to 2 × 2 [Start position (SP1, SP2) × Target (Visual, Proprioceptive)] analyses of variance (ANOVAs) with repeated measures. For all data analyses, statistical significance was tested using an alpha value of 0.05 and Tukey’s method was used for post-hoc analysis.

3. Results

Hand kinematics: target modality affects movement trajectory

Subjects reached without online visual feedback of hand position toward visual and proprioceptive targets, from two different starting positions. The most striking finding of the study, illustrated in Fig. 2, was the difference in the hand path as a function of the experimental conditions. The right panel of Fig. 2A shows that the initial trajectory of the movements from starting position 2 toward the visual target exhibited a directional, counterclockwise deviation compared to movements directed toward the proprioceptive target. In contrast, the left panel shows that trajectories toward the visual and the proprioceptive target were similar for movements from starting position 1. These results were consistent across all seven subjects. To assess the planned movement direction, we analyzed movement direction at the time of peak acceleration as peak acceleration occurred within the first 70 ms of the rapid movements and likely reflected planning processes (Gielen et al., 1985; Sarlegna and Sainburg, 2007). Peak acceleration was similar across conditions: Table 1 shows that peak acceleration as well as time to peak acceleration were not significantly affected by any experimental factors. Moreover, movement distance at peak acceleration (mean=1.9 cm) was not significantly affected by target modality (p>0.82) or starting position (p>0.62) and there was no significant interaction effect (p>0.14). The analysis of the mean directional deviation (compared to the straight line between start and target positions) at peak acceleration revealed an interaction between target sensory modality and starting position (F_{1, 6}=14.0; P<0.01). The bar plot of Fig. 2B shows that the initial movement deviation of the fingertip was largest for the visually-targeted movements starting from position 2 compared to the three other experimental conditions, which did not differ statistically.

Figure 2.

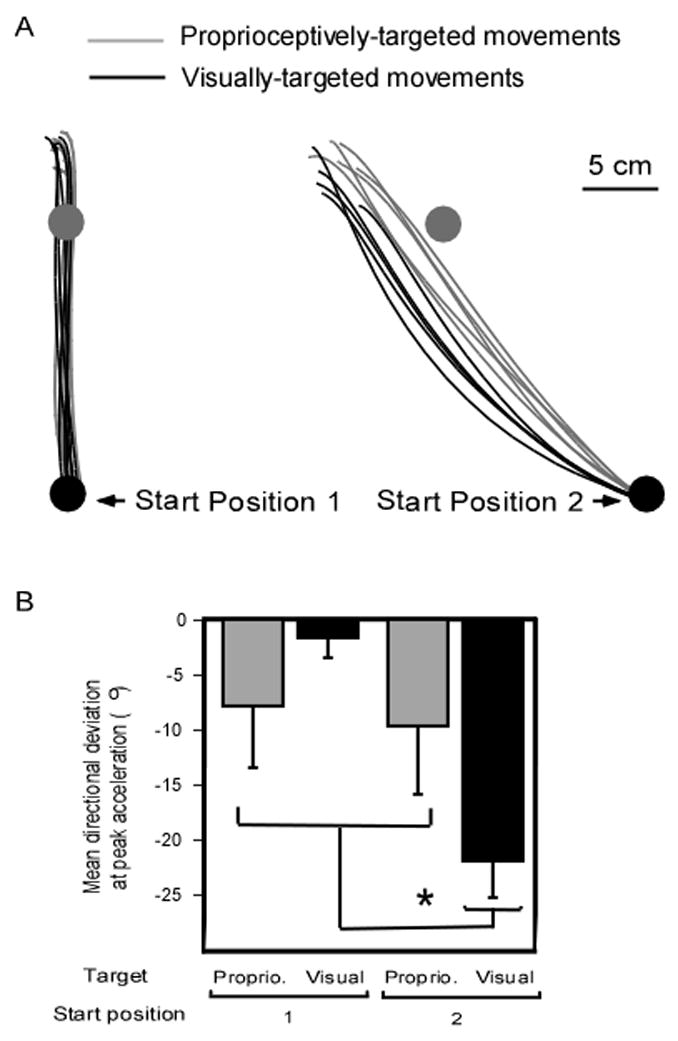
(A) Top view of representative unseen arm movements toward the proprioceptive and visual target from two starting positions, for the same subject. Although target position remained constant throughout the experiment, movements from the two starting positions are presented in two distinct panels for the sake of clarity (B) Bar plot of averaged initial movement direction (with respect to target direction) as a function of experimental conditions. Negative values represent counterclockwise deviations. Error bars represent standard errors. The asterisk indicates a significant difference at post-hoc analysis.

TABLE 1.

Kinematic data of reaching movements

Target modality	Proprioceptive	Visual	Proprioceptive	Visual	Statistical analysis
Starting Position	SP1	SP1	SP2	SP2	Target modality	Starting position	Interaction
Constant end error (cm)	5.7	6.9	5.8	7.8	-	-	-
Variable end error (cm)	1.8	2.4	1.8	1.8	-	-	-
Movement duration (ms)	408 ± 81	451 ± 86	457 ± 85	502 ± 85	p=0.01	p<0.01	-
Peak acceleration (m/s/s)	16.1 ± 3.2	15.2 ± 3.9	14.8 ± 2.7	13.3 ± 2.4	-	-	-
Time to peak acceleration (ms)	64 ± 19	75 ± 30	66 ± 13	62 ± 23	-	-	-
Peak velocity (m/s)	1.4 ± 0.2	1.5 ± 0.3	1.4 ± 0.2	1.5 ± 0.2	-	-	-
Time to peak velocity (ms)	151 ± 25	171 ± 27	167 ± 23	194 ± 28	p<0.01	p=0.01	-
Peak deceleration (m/s/s)	−14.1 ± 3.6	−15.4 ± 4.4	−11.9 ± 2.7	−12.2 ± 2.7	-	p<0.05	-
Time to peak deceleration (ms)	222 ± 34	248 ± 35	249 ± 30	282 ± 32	p<0.01	p<0.01	-

Movements in the four experimental conditions showed similar accuracy and speed as final position error, peak velocity and peak acceleration were not statistically different (Table 1). Final errors were large as neither visual feedback of the moving limb nor knowledge of results was available to enhance the accuracy of reaching movements (Soechting and Flanders, 1989; Adamovich et al., 1998; Smeets et al. 2006). Endpoint errors did not significantly differ between conditions in terms of constant errors (mean=6.6 cm) and variable errors (mean=2.0 cm). Moreover, we did not find any significant differences for directional error and variability (mean=−3.8 ± 4.0º) and distance error and variability (mean=5.2 ± 2.3 cm) at the end of the movement. There was no significant effect of the experimental conditions on peak velocity (mean=1.4 ± 0.2 m/s), peak acceleration (mean=14.9 ± 3.0 m/s²) or time to peak acceleration (mean=67 ± 21 ms). However, movement duration was longer for visually-targeted movements (mean=478 ± 91 ms) compared to proprioceptively-targeted movements (mean=434 ± 89 ms; F_{1, 6}=6.7; P<0.05). The interaction effect was not significant but movement duration was longer for movements from starting position 2 (mean=480 ± 85 ms) compared to starting position 1 (mean=430 ± 84 ms; F_{1, 6}=19.2; P<0.01), a finding consistent with the greater distance covered by movements from starting position 2 compared to starting position 1 (28.7 ± 2.1 and 23.3 ± 2.6 cm, respectively; F_{1, 6}=22.7; P<0.01).

Joint kinematics: target modality affects intersegmental coordination

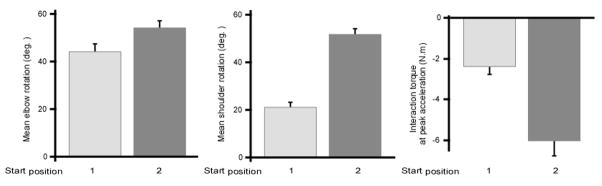
As expected from the similar final position errors, there was no significant effect of the sensory nature of the target (visual or proprioceptive) on the amounts of final elbow extension and shoulder flexion. In fact, the final amount of elbow extension was only affected by the starting position (F_{1, 6}=16.0; P<0.01). Figure 3A shows that movements from starting position 1 elicited 43.9 ± 6.1º of elbow extension while movements from starting position 2 used 53.9 ± 5.3º of elbow extension. According to task design, movements from starting position 2 involved more shoulder flexion (mean=51.5 ± 4.3º) than movements from starting position 1 (mean=21.0 ± 3.3º; F_{1, 6}=292.4; P<0.001). With the large shoulder motion associated with elbow motion, intersegmental dynamics between upper-limb segments were thus larger for movements from starting position 2 compared to starting position 1 (Fig. 3).

Figure 3.

Kinematic and dynamic differences of movements from distinct starting positions (A) Bar plot of elbow excursion. (B) Bar plot of shoulder excursion, which was greater for movements starting from start position 2. (C) Bar plot of interaction torque, which was greater for movements starting from start position 2 (F_{1, 6}=48.0; P<0.001).

We reported that the direction, speed and accuracy of visually- and proprioceptively-targeted movements were not statistically different when starting from position 1. In contrast, when movements started from position 2 and elicited large intersegmental dynamics, visually-targeted movements deviated more from the target direction than proprioceptively-targeted movements. Considering the hypothesis that arm movements are planned to be directly oriented toward the target (Flash and Hogan, 1985; Morasso, 1981; Shadmehr and Mussa-Ivaldi, 1994), this deviation in the visual condition reflects larger errors in movement planning compared to the proprioceptive condition. On the other hand, this deviation could be optimal in terms of control of intersegmental dynamics as a study of Sainburg and Kalakanis (2000) showed that curved movements can be more torque-efficient than straighter movements. We thus focused the subsequent analyses on movements from starting position 2 to investigate whether the initial deviation observed for visually-targeted movements might have been planned for an optimized coordination of muscle torques with interaction torques.

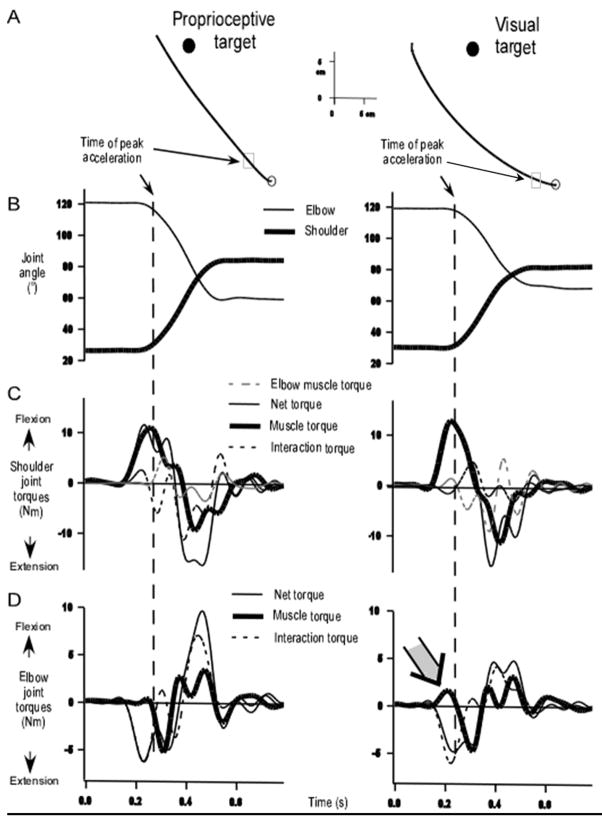
Figure 4 shows two representative trials of a participant reaching without online visual feedback for a visual or proprioceptive target from start position 2: these trials were matched in terms of speed and final accuracy. This reflected the mean data, as reaction time (mean=168 ms; t ₆=2.1; P=0.08), peak velocity (mean=1.5 m/s; t ₆=0.6; P=0.55), movement duration (mean=480 ms; t ₆=2.1; P=0.09) and end error (mean=6.8 cm; t ₆=1.4; P=0.20) were not statistically different in visual and proprioceptive conditions. A MANOVA also revealed no significant differences in x and y final hand coordinates between conditions (Lambda Wilkinson=0.8; F(_{2, 11})=1.1; P>0.35). The left column of Fig. 4 shows a typically straight movement toward the proprioceptive target and the right column shows a typically curved movement toward the visual target. The analysis of the initial movement direction showed that visually-targeted movements were biased counterclockwise compared to that of proprioceptively-targeted movements (mean=−22.0 and −9.6º, respectively; t ₆=3.2; P<0.05). Movements toward the proprioceptive target were thus more linear than movements toward the visual target (mean curvature index=0.07 and 0.09, respectively; t ₆=4.2; P<0.01).

Figure 4.

Arm movements made from starting position 2. (A) Representative hand paths. (B) Representative joint displacements profiles corresponding to the hand path shown in A. (C) Corresponding shoulder joint torque patterns. (D) Corresponding elbow joint torque patterns: in the left panel, net torque and interaction torques are almost undistinguishable from movement onset to peak acceleration.

The representative joint excursion profiles of Fig. 4 indicate that the initial upper-limb configuration was essentially the same in both experimental conditions. A MANOVA revealed no significant differences in x and y start coordinates between conditions (Lambda Wilkinson=0.9; F(_{2, 11})=0.9; P>0.44). Shoulder start angle was not statistically different in visual and proprioceptive conditions (mean=25.1º; t_{1, 6}=0.8; P=0.48), while elbow start angle differed slightly (means=117.6 and 116.0º, respectively; t ₆=3.4; P<0.05). In these conditions, the different hand path curvatures reflect different elbow and shoulder joint coordination patterns. Figure 5A shows that the elbow and the shoulder were coordinated differently in visual and proprioceptive conditions from the beginning of the reach. Indeed, in the initial phase of the movement (from movement onset up to peak acceleration), the ratio of elbow-to-shoulder motion was lower in visual condition (mean=0.87) than in proprioceptive condition (mean=1.21; t ₆=2.7; P<0.05). This indicates that in visual condition, elbow extension was reduced for a given shoulder flexion. The reduced rate of elbow excursion relative to shoulder excursion, up to peak velocity, was related to the initial deviation of finger trajectory. While the difference between the ratios in visual and proprioceptive conditions was significant early in the movement, the difference was reduced along the trajectory and did not reach significance from the time of peak deceleration (t ₆=1.1; P=0.33) to movement offset (t ₆=0.48; P=0.65).

Figure 5.

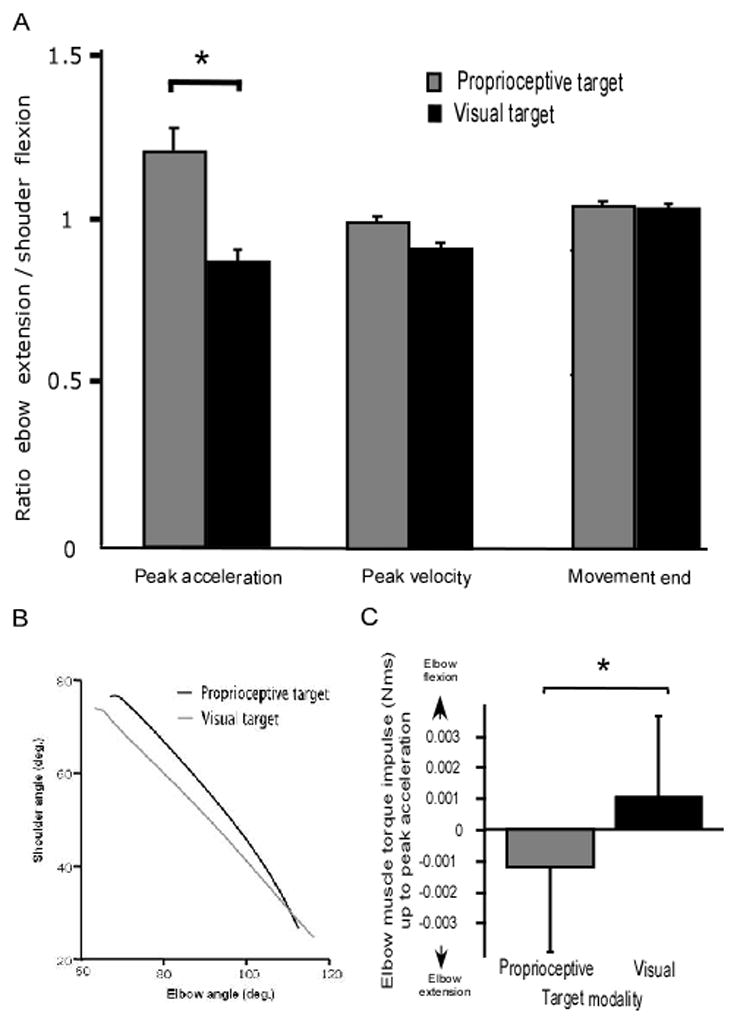
(A) Bar plot of the time course of the elbow extension to shoulder flexion ratio. Error bars represent standard errors. (B) Visually- and proprioceptively-targeted movements in joint space. (C) Bar plot of the peak elbow muscle torque between movement onset and peak acceleration. Error bars represent standard errors. Elbow muscle torque contributes to elbow flexion when reaching for the visual target, while the task requires elbow extension. The asterisk indicates a significant difference at post-hoc analysis.

Figure 5B shows that there was a strong correlation between elbow and shoulder motions for both visually- and proprioceptively-targeted movements. In other words, both types of movements were straight in joint space. This was highlighted by the correlation coefficient obtained with a linear regression. When these R values were normalized for statistical comparison (z scores obtained with Fischer transformation), a t-test revealed that there were no significant differences between visually- and proprioceptively-targeted movements.

Inverse dynamic analysis: proprioceptively-targeted movements are more torque-efficient

Multi-joint movements toward the visual and the proprioceptive target required elbow extension and shoulder flexion. In the left panel of Fig. 4, the shoulder joint torque profile for the movement toward the proprioceptive target indicates that shoulder motion, as reflected by shoulder net torque, was determined predominantly by shoulder muscle torque up to peak acceleration. The right panel shows that for the more curved trajectory toward the visual target, shoulder motion was also determined mainly by shoulder muscle torque. The difference in torque efficiency between visually- and proprioceptively-targeted movements is apparent in the bottom panel (Fig. 4D). For the straight movement toward the proprioceptive target, the initial phase of elbow extension was almost entirely driven by the interaction torque, i.e., by the effects of forces arising from the motion of the shoulder joint. Therefore, elbow muscle torque did not contribute substantially to elbow motion. In contrast, the movement toward the visual target was initiated with elbow muscle torque, in the flexion direction. This early flexor torque is related to the relatively smaller elbow extension during movement initiation and to the medial deviation of the hand path.

These kinetic differences between proprioceptively- and visually-targeted movements were significant as we found that elbow muscle torque differed qualitatively between conditions, even though it did not differ quantitatively in the initial phase of motion. Indeed, the amount of initial muscle activity at the elbow joint, as revealed by the root mean squared muscle torque from movement onset to peak acceleration, did not differ statistically between the two conditions (mean=1.7 N.m.s; t ₆=0.8; P=0.47). However, Fig. 5B shows that elbow muscle torque impulse, from movement onset to peak acceleration, was greater in the visual target condition (mean=1.1 10⁻³ N.m.s) than in the proprioceptive condition (mean= − 1.2 10⁻³ N.m.s; t ₆=4.1; P<0.01). The positive value of the elbow muscle torque impulse in visual conditions indicates that elbow muscle activation produced elbow flexion, even though elbow extension was required to achieve the target. This was further supported by the results of elbow muscle torque contribution to net torque, a measure of the dynamic efficiency of the torque strategy (Sainburg and Kalakanis, 2000). Indeed, the effect of target modality on the initial contribution of muscle torque was significant (t ₆=2.0; P<0.05). When reaching for the proprioceptive target, elbow muscle torque (mean=1113 10⁻⁶ N.m) acted synergistically with interaction torque to accelerate the elbow into extension. In contrast, under the visual target conditions, muscle torque counteracted the interaction torque producing elbow flexor acceleration (mean= − 92 10⁻⁶ N.m). Therefore, these analyses show that movements toward the proprioceptive target exploited more efficiently the intersegmental dynamics than those toward the visual target.

In conclusion, we varied target modality and start position and found that proprioceptively-targeted movements were more efficiently controlled than visually-targeted movements for one particular direction, the direction with the greatest interjoint coordination requirements. We conducted two control experiments to determine the generalization of our findings by using a center-out reaching task with distinct target locations in the workspace. In a first control experiment, we used the same set-up as in the previous experiment and the main procedural difference was that we used an additional mass to modify the upper-arm dynamics (Atkeson and Hollerbach, 1985; Krakauer et al., 1999; Sainburg et al., 1999). Here we sought to determine whether an experimental alteration of the upper-arm dynamic characteristics would enhance the differences between movements toward visual and proprioceptive targets. We hypothesized that proprioceptively-targeted movements would be less affected than visually-targeted movements by such a dynamic perturbation. We employed a typical mass-adaptation paradigm (Krakauer et al., 1999; Sainburg et al., 1999) which also allowed us to examine whether adaptation to novel inertial conditions is affected by visuo-proprioceptive integration requirements. In addition, we modified the layout of the targets and the availability of visual information about start position, and we asked subjects to actively position the left arm as the proprioceptive target to address questions about the effects of these factors on the results shown in our first experiment.

4. Control experiment 1: Experimental procedures

Ten subjects (eight males, two females; age=30 ± 4 years) were asked to reach without visual feedback of the moving limb toward visual or proprioceptive targets. The main difference with the main experiment was that in this experiment, we presented one start position and three target positions that required different excursions at the shoulder and elbow joints. Targets were located at 60, 90 and 120º (with respect to the fronto-parallel plane) and 20 cm away from starting position. Movements toward the 60º target required little shoulder joint motion, while movements toward the 120º target required the greatest coordination between elbow and shoulder motion (Sainburg et al., 1995). Targets were presented in random order. We displayed the start circle in visual target conditions and we used a tactile landmark in proprioceptive target conditions such that in both conditions, subjects could actively position their right hand in starting position. In the proprioceptive target conditions, subjects actively positioned their left hand at target position.

We employed a typical adaptation procedure such that, after a set of 36 baseline reaching movements (12 trials × 3 targets), a 1 kg mass was attached 25 cm lateral to the forearm and 72 trials (24 trials × 3 targets) were performed before the mass was removed in a 36-trial post-test. It has previously been established that this is an adequate number of trials for adaptation to novel limb dynamics (Lackner and DiZio, 1994; Krakauer et al., 1999; Sainburg et al., 1999). To capture the changes related to the modification in limb dynamics, we selected, like Lackner and DiZio (1994), the last six trials of the baseline session, the first and last trials of adaptation, and then the first “after effect” trials. Mean and standard deviation of the mean of each dependant measure were submitted to 2 × 3 × 4 [Target modality (Visual, Proprioceptive) × Target direction (60, 90, 120) × Adaptation Condition (Pretest, Early Adaptation, Late Adaptation, Post-test)] ANOVA.

5. Control experiment 1: Results

As predicted, the effect of the mass was largest on the movements toward the 120° target, the movements designed to elicit most interjoint coordination requirements. As described in detail elsewhere (Sainburg et al., 1999), the initial movements with the lateral mass were deviated clockwise with respect to baseline. Subjects then adapted to the novel limb dynamics and when the mass was removed, after-effects were observed. The Adaptation condition effect (F=2.7; P<0.05) and the interaction Adaptation condition × Target direction (F=9.4; P<0.001) showed that adding a mass had a significant effect on initial movement direction. Post-hoc decomposition of the interaction revealed that only for movements toward the 120° target, initial movement direction significantly differed between the early adaptation trials (mean=1.2°) and post-test trials (mean=−14.7°).

Target modality also influenced initial movement direction, as revealed by the interaction Target modality × Target direction (F=9.4; P<0.001). Post-hoc analysis showed that the initial movement direction differed between visually-targeted movements toward the 120° (mean=1.2°) and 60° target (mean=−7.8°), movements with the greatest and lowest interjoint coordination requirements, respectively. There were no significant differences in initial movement direction between visually- and proprioceptively-targeted movements directed toward the same targets.

Peak acceleration was not significantly affected by Target modality but was affected by Adaptation condition (F=10.8; P<0.001) as it was lower in the early-mass trials (mean=8.8 m/s²) with respect to the late-mass trials (mean=10.4 m/s²) and post-test trials (mean=12.2 m/s²). Peak acceleration was also affected by Target direction (F=13.7; P<0.001): peak acceleration was greater for the movements toward the 60° target (mean=12.1 m/s²) than for those toward the 90° target (mean=10.1 m/s²) and 120° (mean=9.2 m/s²). This analysis of peak acceleration was consistent with the analysis of movement duration: movement duration was only affected by Adaptation condition (F=9.9; P<0.001) and Target direction (F=20.1; P<0.001). Movements lasted longer when a mass was added, i.e., in the early-mass trials (mean=511 ms) and late-mass trials (mean=473 ms), than in the pre-test trials without any mass (mean=416 ms). The early-mass trials also differed from the post-test trials (mean=425 ms). Moreover, movement duration increased as target direction increased (mean=403 ms for 60°; 454 for 90° and 512 for 120°). Final accuracy error (mean=6.8 cm) was not significantly affected by any experimental condition.

The analysis of joint kinematics showed that the different target directions elicited different elbow-shoulder coordination patterns. Indeed, target direction influenced shoulder excursion (F=423.4; P<0.001) which, as predicted, increased with target direction (mean=16.4° for 60°; 31.2° for 90° and 43.2° for 120°). Since target direction did not significantly influence elbow excursion (mean=42.2°), inter-joint coordination requirements were greatest for the 120° target.

In this control experiment, manipulating intersegmental coordination requirements by adding an inertial load did not allow to maximize differences between proprioceptively and visually-targeted movements. With respect to the first experiment, this suggests that the integration of visual and proprioceptive signals related to target and hand positions is better evidenced when contrasting movements performed with different interjoint coordination patterns. To further assess the generalization of our findings, we conducted another experiment directly contrasting movements with small and large interjoint coordination requirements by, using a different set-up, testing movements toward four targets largely distributed across the workspace.

6. Control experiment 2: Experimental procedures

Five subjects (three males, two females; age=29 ± 4 years) were asked to reach in complete darkness toward visual or proprioceptive targets. On a horizontal board, at waist level, a tactile landmark indicated starting hand position, in body midline. Visual targets (red light-emitting diodes, 3 mm in diameter) were positioned on a 20 cm radius circular array at 45, 135, − 45 and −135° with respect to the fronto-parallel plane (Fig. 7). Tactile landmarks were positioned at the same location as visual targets, beneath the pointing board, to position the left hand in proprioceptive target conditions. An infrared active marker was taped to the right index fingertip whose position was sampled at 200 Hz using an optical motion tracking system (Codamotion C×1, Charnwood Dynamics Ltd, Leicestershire, UK). Subjects performed 12 trials per experimental condition, in blocks. Subjects reached toward visual or proprioceptive targets. Targets at 45 and −135° required less interjoint coordination than targets at 135 and − 45° (Sainburg et al., 1995; Gottlieb et al., 1997; Dounskaia et al., 2002). Targets at 135 and −135° were located in the left hemispace and targets at 45 and −45° were located in the right hemispace. Dependant measures were submitted to 2 × 2 × 2 [Target modality (Visual, Proprioceptive) × Interjoint coordination requirements (Small, Large) × Target hemispace (Left, Right)] ANOVA.

7. Control experiment 2: Results

Figure 6 shows representative movement trajectories toward all four targets in the visual and proprioceptive conditions. For movements toward targets at 135° (upper left) and −45° (lower right) requiring substantial coordination of the elbow and shoulder joints, the initial direction of visually-targeted movements was more variable than that of proprioceptively-targeted movements. In contrast, movements toward targets at 45 and −135°, requiring mostly elbow motion, had similar trajectories. This was reflected by the significant interaction Target modality × Interjoint coordination requirements × Target hemispace (F_{1, 4}=31.1; P<0.01). For the multi-joint movements toward the lower right target (−45°), the initial direction of visually-targeted movements was more variable than that of proprioceptively-targeted movements (P<0.01). For the multi-joint movements toward the upper left target (135°), the difference was marginally significant (P=0.08).

Figure 6.

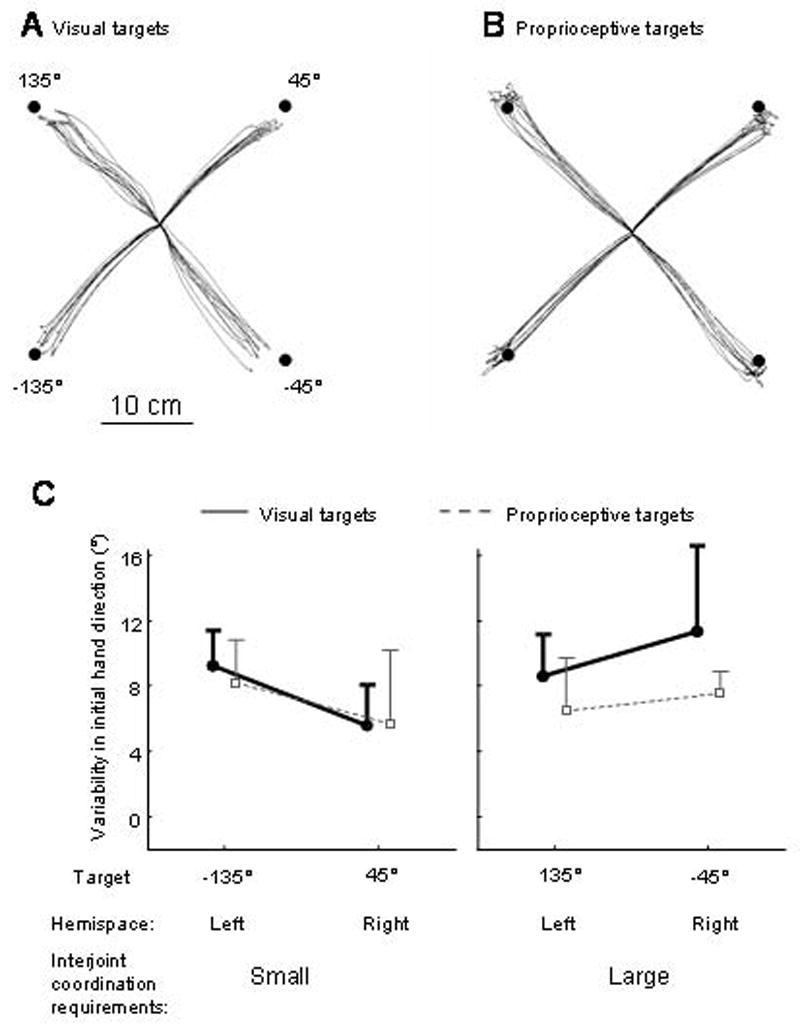
(A) Top view of representative unseen arm movements toward the visual targets. (B) Top view of representative unseen arm movements toward the proprioceptive targets. (C) Averaged initial movement direction’s variability as a function of experimental conditions.

Table 2 summarizes the kinematics of the reaching movements. Overall, movements with large interjoint coordination requirements had straighter trajectories and lasted longer than movements with smaller coordination requirements. Initial direction errors, assessed at peak acceleration, averaged 6.2° for movements with large coordination requirements while they averaged −19.4° for movements involving mostly elbow motion. Movement duration of movements with large interjoint coordination requirements (mean=479 ms) was longer than that of movements with smaller coordination requirements (mean=406 ms; F_{1, 4}=17.8; P=0.01). This is consistent with the fact that for movements with small interjoint coordination requirements, peak acceleration (mean=17.8 m/s²) was higher than for movements with larger coordination requirements (mean=10.7 m/s²; F_{1, 4}=17.8; P=0.01). A similar finding was observed for peak velocity (means=1.3 and 1.0 cm/s, respectively; F_{1, 4}=26.2; P<0.01).

TABLE 2.

Kinematic data of reaching movements

Target modality	Visual	Visual	Visual	Visual	Proprioceptive	Proprioceptive	Proprioceptive	Proprioceptive	Statistical effect
Movement type	‘Single-joint’	‘Single-joint’	Multi	Multi	‘Single-joint’	‘Single-joint’	Multi	Multi
Target Hemispace	Left	Right	Left	Right	Left	Right	Left	Right
Initial direction (deg.)	−26.4	−16.5	7.1	3.9	−17.5	−17.3	9.7	4.3	Interjoint coordination
Constant end error (cm)	0.9 ± 0.4	1.5 ± 0.9	1.0 ± 0.8	1.4 ± 0.5	1.6 ± 0.7	1.1 ± 0.8	1.3 ± 0.4	1.5 ± 0.6	-
Movement duration (ms)	421 ± 61	457 ± 105	482 ± 67	545 ± 125	369 ± 70	376 ± 72	441 ± 50	448 ± 61	Interjoint coordination
Peak acceleration (m/s/s)	18.4 ± 3.9	16.8 ± 2.9	11.2 ± 2.4	9.4 ± 1.6	18.8 ± 3.7	17.3 ± 3.1	11.7 ± 2.3	10.4 ± 2.4	Interjoint coordination
Peak velocity (m/s)	1.4 ± 0.1	1.3 ± 0.2	1.0 ± 0.1	1.0 ± 0.1	1.4 ± 0.2	1.3 ± 0.1	1.0 ± 0.1	1.0 ± 0.1	Interjoint coordination

In summary, the main finding of this second control experiment is that for movements requiring substantial interjoint coordination, movement direction at peak acceleration is more variable for visually-targeted movements than for proprioceptively-targeted movements. This supports the idea that motor planning is less efficient for movements toward visual targets as compared to movements toward proprioceptive targets, an idea further discussed below.

8. Discussion

Multi-sensory integration affects motor planning

The present study examined how visuo-proprioceptive integration affects the efficiency of trajectory and final position control for targeted arm movements. Subjects reached toward visual and proprioceptive targets without visual feedback of the moving limb/cursor. Reaching toward visual targets requires the integration of visual and proprioceptive signals about limb configuration and target position (Desmurget et al., 1998; van Beers et al., 1999; Sober and Sabes, 2003; Bagesteiro et al., 2006). In contrast, reaching toward an unseen proprioceptive target with the unseen hand may not require such cross-modal integration as the movement between the proprioceptively-felt target hand and the proprioceptively-felt pointing hand could be defined in a single, proprioceptive map. We hypothesized that if errors in movement planning arise from visuo-proprioceptive integration of hand and target signals, performance errors should be greater for visually-targeted movements. Different movement directions were employed to manipulate interjoint coordination requirements, as we predicted that errors in visuo-proprioceptive integration would be most pronounced for movements with greater intersegmental coordination requirements. This is because visual information about target position should be integrated with proprioceptive information about limb configuration to accurately predict the arm movement and the intersegmental dynamics (Sainburg et al., 1995, 2003; Brown et al., 2003).

In the main experiment, initial movement direction differed strikingly between the two target modalities when movements required substantial interjoint coordination. Proprioceptively-targeted movements were straighter than visually-targeted movements. Moreover, inverse dynamic analysis revealed that movements toward the proprioceptive target were performed with a more efficient coordination strategy by taking advantage of intersegmental inertial interactions. Therefore, proprioceptively-targeted movements were more linear and more torque efficient than visually-targeted movements. Considering theoretical models of motor planning that are based on kinematic (Atkeson and Hollerbach, 1985; Flash and Hogan, 1985) and dynamic optimizations (Uno et al., 1989; Nakano et al., 1999), we suggest that the larger initial deviations from target direction of the visually-targeted movements, associated with less efficient torque strategies, reflect errors in motor planning.

The analysis of movements requiring substantial interjoint coordination showed distinct initial directions for visually- and proprioceptively-targeted movements, supporting the idea that distinct planning processes underlie visually- and proprioceptively-targeted movements (Sober and Sabes, 2005; Bernier et al., 2007; Sarlegna and Sainburg, 2007). It should be emphasized that in the first experiment of the present study, visual and proprioceptive targets were located at the same position and that final accuracy did not significantly differ between modalities in our three experiments. It is thus unlikely that our results could be due to systematic differences in perceptual factors between the visual and proprioceptive target conditions (for a discussion of these factors, see Baud-Bovy and Viviani, 2004; Simmering et al., 2008). Since movement speed, initial and final arm configurations did not differ between conditions in the first experiment, motor-related differences such as a speed-accuracy tradeoff are not likely to account for our findings. We rather suggest that the trajectory deviations characterized for visually-targeted movements resulted from an inaccurate integration of heterogeneous visual and proprioceptive signals related to hand and target positions.

The modality-dependent trajectory differences observed for movements requiring large shoulder and elbow motions were not significant for movements that did not require substantial motion at both joints, a finding consistent with previous analysis of unaltered, single-joint elbow rotations (Flanders and Cordo, 1989; Sarlegna and Sainburg, 2007). Studies on multi-joint movements showed that accurate prediction of the intersegmental dynamics is critical to enable a torque-efficient and well-coordinated movement trajectory (Sainburg et al., 1995; Gribble and Ostry, 1999; Scott, 2004). The present study thus suggests that errors in visuo-motor transformations are amplified when initial movement plans must account for the complex dynamics of rapid, multi-joint movements. Interestingly, when de Graaf et al. (1994) studied the initial direction of slow, multi-joint movements toward visual and proprioceptive targets, no major differences were noticed.

Multi-sensory integration and coordinate transformations for motor planning

Sensory signals from different modalities are likely represented in different coordinate systems, reflecting the characteristics of the sensory channels. It thus appears that multi-sensory integration for motor planning requires neural computations akin to coordinate transformations (Johnson et al., 2001; Kakei et al., 2001). Currently, visually-targeted movements are thought to be planned in visual coordinates (Flanagan and Rao, 1995; Wolpert et al., 1995; Buneo et al., 2002), based on the visually-defined starting hand and target positions (Sainburg et al. 2003; Sober and Sabes, 2005). In fact, it has been suggested that, to plan a visually-targeted movement, information about initial hand position is transformed into visual coordinates even when the hand can only be felt through proprioception (Beurze et al., 2006). Thus, the kinematics of movements toward visual targets appear to largely depend on visual-based processes (Desmurget et al., 1998; Henriques et al., 2002).

Substantial evidence suggests that accounting for limb dynamics is necessary to plan arm movements (Atkeson and Hollerbach, 1985; Lackner and DiZio, 1994; Shadmehr and Mussa-Ivaldi, 1994; Gribble and Ostry, 1999; Scott, 2004). Studies in both healthy and deafferented participants have demonstrated the critical role of proprioception in transforming a kinematic goal into a control strategy that effectively accounts for intersegmental dynamics and limb inertia (Gordon et al., 1995; Sainburg et al., 1995, 2003; Sarlegna et al., 2006, in press). Thus, while a task-level plan of movement appears to rely heavily on visual information, transforming this plan into an efficient dynamic strategy is largely dependent on proprioceptive information (Krakauer et al., 1999; Brown et al., 2003; for a review, Sarlegna and Sainburg, 2009). This type of planning process was recently operationalized by Sober and Sabes (2003, 2005) in a computational model of planning. To summarize this model, the planning of visually-targeted movements starts within an extrinsic, mainly visual, coordinate system to specify desired movement kinematics. This kinematic plan is then combined with body configuration information to account for limb dynamics and compute motor commands in intrinsic coordinates.

In our first experiment, visually-targeted movements with large interjoint coordination requirements were initially directed counterclockwise, a bias consistent with previous studies which highlighted the influence of initial arm configuration and target direction on movement trajectories (Ghilardi et al., 1995; de Graaf et al., 1994). In contrast, the trajectories of proprioceptively-targeted movements were substantially more accurate in terms of initial direction and reflected an efficient dynamic strategy. It is possible that proprioceptively-targeted movements were more accurate because the planning of movement kinematics and dynamics could be performed within a single, intrinsic coordinate system (Darling and Miller, 1993; Adamovich et al., 1998; Simmering et al., 2008). This is consistent with previous studies suggesting that movements toward proprioceptive targets are planned in an intrinsic reference frame (Tillery et al., 1991; Bernier et al., 2007). On the other hand, the planning of reaching movements toward visual targets relies on the integration of visual and proprioceptive signals, in extrinsic and intrinsic reference frames (Sober and Sabes, 2003). We thus suggest that the planning errors observed for visually-targeted movements could result from errors in extrinsic-to-intrinsic transformations. Alternatively, the planning errors could result from errors in transformations between heterogeneous, possibly misaligned, visual and proprioceptive coordinate systems (Smeets et al., 2006; Malfait et al., 2008). Further work will be necessary to distinguish between these explanations but either way, the current results are consistent with the idea that transformations of sensory signals between coordinate systems can impair motor performance (Soechting and Flanders, 1989; McIntyre et al., 2000; Sober and Sabes, 2005; Schlicht and Schrater, 2007).

In the three experiments reported here, we showed that target modality and target position influenced initial movement direction. However, subtle differences were found between experiments, which slightly differed in sensory feedback conditions. For instance, when vision of the starting hand position was precluded in all conditions (control experiment 2), the variability of the initial direction of visually-targeted movements was affected with respect to proprioceptively-targeted movements. When vision of the starting hand position was available in visual target conditions but not in proprioceptive target conditions (main experiment), the average initial direction of visually-targeted movements was affected. These observations point at the importance of visual feedback of starting hand position for the planning of reaching arm movements, a finding previously well characterized (Desmurget et al., 1998; Sober and Sabes, 2005; Sarlegna and Sainburg, 2009). The differences in initial trajectory features led us to suggest that motor planning may be affected by visuo-proprioceptive integration requirements. In contrast, the final accuracy of reaching arm movements was not significantly affected as the different initial trajectories for visually- and proprioceptively-targeted movements converged on similar final position accuracies through different, yet apparently smooth, movement trajectories. Therefore, our results support recent evidence that initial trajectory features and final position achievement are mediated by distinct neural mechanisms (Kurtzer et al., 2005; Schaefer et al., 2007; Scheidt and Ghez, 2007). It is unclear whether the trajectory of visually-targeted movements reflect pure feedforward mechanisms or reflect also feedback mechanisms. It has been shown that movement-dependent feedback can be used to rapidly adjust descending control signals and thus compensate for errors in motor planning (Cordo et al., 1995; Danion and Sarlegna, 2007; Gordon and Ghez, 1987; Desmurget et al., 2005; Saunders and Knill, 2005). Based on this line of work, we speculate that online processes may have continuously guided the limb toward the visual target during movement execution.