Abstract
Cells serve as basic units of life and represent intricate biological molecular systems. The vast number of cellular molecules with their signaling and regulatory circuitries forms an intertwined network. In this network, each pathway interacts non-linearly with others through different intermediates. Thus, the challenge of manipulating cellular functions for desired outcomes, such as cancer eradication and controlling viral infection lies within the integrative system of regulatory circuitries. By using a closed-loop system control scheme, we can efficiently analyze biological signaling networks and manipulate their behavior through multiple stimulations on a collection of pathways. Specifically, we aimed to maximize the reactivation of Kaposi's Sarcoma-associated Herpesvirus (KSHV) in a Primary Effusion Lymphoma cell line. The advantage of this approach is that it is well-suited to study complex integrated systems; it circumvents the need for detailed information of individual signaling components; and it investigates the network as a whole by utilizing key systemic outputs as indicators.
Introduction
Cellular bio-molecules such as receptors, enzymes, and RNA/DNA, interact and organize into a complex network system with inherent robustness and flexibility.1 The analysis and understanding of biological processes often lead to vital life science and therapeutic applications, however, it is difficult to predict overall cellular behaviors by scale-up analyses of their components due to the nature of their emerging complexity of interactions. Furthermore, cellular functions are results of non-linear interactions among pathways; therefore, the effects of local molecular interactions often do not translate linearly, damped or amplified, into the global system functions. Cellular processes are dynamic in nature, sometimes stochastic with levels of randomness, and adaptive to their environments. Fundamental issues such as variations in cellular responses, communication between cellular pathways, cell-to-cell interactions, and stochasticity of gene expression are difficult to address in traditional biology experimental studies.2,3
Insight, innovation, integration.
The example of combinatorial drug treatment towards HIV indicates that multiple therapeutic stimulations applied to the cellular network can be much more effective than the application of single drugs. A challenge of this approach is to identify the best drug cocktail dosages from a huge collection of possibilities to direct the biological system towards a desired phenotype. In this work, we demonstrated that a feedback system control technique can rapidly search for the optimal drug cocktail from 1 000 000 possible drug-dosage combinations towards Kaposi's Sarcoma-associated Herpesvirus (KSHV) reactivation. This result can lead to a new front in facilitating the exploration of cellular regulatory network responses from an integrative biological system point of view.
Extensive efforts have been spent in exploring the chain reactions of bio-molecules making up the signaling pathways; however, the vast range of molecular machineries and regulatory circuitries forms an intertwined network that has yet to be completely mapped out.4 Analytical methods such as high-throughput bioinformatics, genomics/proteomics, and systems investigative techniques have made major advances in studying complex biological systems, but they are often labor intensive and time consuming in their data deciphering processes. On the other hand, various analytical and integrative approaches have been developed to study complex systems in the field of engineering and mathematics. For instance, closed-loop system control schemes have been often used in engineering for global system optimization and system performance analysis.5-8 In these systems, the optimizer may not have full understandings of the interrelationships of its parts and components but focuses mainly on information retrieved from the system before and after the introduction of stimuli.
Wong et al. have applied the integrative systems control approach to study the cellular response and potential therapeutically application.9 In many cases, combination drug therapy has been shown to be more effective than single drugs.10-12 However, to identify optimal drug combinations in a mixture using a trial-and-error method is challenging due to large number of possible combinations. With a closed-loop feedback control optimization system, they found a mixture of effectors to activate the nuclear factor kappa B (NFκB) pathway in 293T cells. Wong et al. was able to use the feedback control platform to find likely optimal combinations in less than 30 test cases out of a possible one million combinations. In this study, we want to explore whether this engineering closed-loop search platform can be extended to a very different biological system. We, therefore, explore the validity of system control scheme to rapidly identify the optimal mixture of six drugs to reactivate Kaposi's Sarcoma-associated Herpesvirus (KSHV) in vitro. KSHV is a recently discovered oncogenic human herpesvirus.13 It has become the most common AIDS associated cancer and is one of the major contributors to mortality in these patients.14 KSHV can establish two different kinds of infection: productive lytic replication or quiescent latent infection. Both phases are important for viral transmission and related tumorigenesis. Lytic replication is essential for initiate new infections within an individual or among individuals. Latent infection is critical for the virus to evade immune responses and to establish lifelong persistent infection. The virus can reactivate from latent infection and re-enter productive lytic replication phase and to infect other cells. Thus the reactivation process is central in the life cycle of herpesvirus, and is controlled by many cellular signaling pathways.15 Therefore, it will be interesting to identify the most effective drug cocktails to stimulate multiple pathways and achieve the optimal reactivation of this biological system.
KSHV latently infects mostly B cells and endothelial cells, in which, the virus exists as a multiple copy circular episomal DNA in the nucleus.16 Studies have shown that the R trans-activator (RTA) is the principle molecular switch and is expressed very early before other genes during lytic replication or reactivation process.17,18 The expression of RTA is necessary and sufficient to reactivate KSHV lytic cycle. However the expression and activity of RTA is regulated by a variety of cellular signaling pathways. However the mechanism is not fully understood. Primary Effusion Lymphoma (PEL) is caused by KSHV infection of B cells. The transformed B cells can be isolated from patients and found to contain KSHV in latency. The latency can be disrupted by activation of several cellular pathways which leads to the expression of RTA. Thus, the reactivation of KSHV lytic replication represents an output of cellular signaling network, and provides a model system for us to develop the method. Furthermore, RTA activates KSHV early lytic genes, including virus-encoded interleukin 6, polyadenylated nuclear (PAN) RNA, and small viral capsid antigen.19 Repression of RTA can up-regulate their promoters in transient assays. The activation of RTA causes a 3.7–53-fold increase in the expression of PAN RNA.21 The up-regulation of PAN promoter is directly linked to the up-regulation of RTA and indicative of KSHV reactivation.19-22
In our approach, we treat the cell as an integrated complex system that processes and responds to various cellular inputs. By using a closed-loop feedback control scheme, we aim to enhance particular cellular responses based on quantifiable output information received from the cells. Here we report our search for drug combinations that more effectively reactivate KSHV in B cells.
Materials and methods
Cell culture
We have developed a fluorescent reporter Primary Effusion Lymphoma cell line (BC-3-G) in which the expression of green fluorescent protein (GFP) is controlled by the polyadenylated nuclear (PAN) promoter, a KSHV lytic promoter.19-22 RTA (replication and transcription activator) is an immediate early gene product of KSHV that disrupts latency and drives lytic replication.23 RTA has been shown to activate the expression of PAN RNA of KSHV in a reporter system using destabilized GFP.15 Cells were incubated at 37 °C with 5% CO2. BC-3-G cells were maintained in RPMI 1640 medium supplemented with 10% fetal bovine serum (FBS) and antibiotics (penicillin and streptomycin). Experiments were conducted with a cell concentration of approximately 1 × 105 cells/ml.
Plasmid construction
The pPAN-122-d2EGFP construct was generated by replacing the promoter region in the nNFκB-d2EGFP vector (Clontech, CA) with PAN promoter region spanning nt −122 to +14 from the pGL3-8b construct.22 pTW40 containing the puromycin-resistant gene in pcDNA3 vector was generated. The BC-3-G cell line was established by cotransfecting pPAN-122-d2EGFP and pTW40 plasmids into BC-3 cells and selected with 1.5 μg/ml puromycin.23
Stochastic search algorithm
The stochastic search algorithm is an essential component of the closed-loop feedback control scheme. However, different kinds of algorithms can be used in the control scheme, each with different search properties. For our studies we used a direct search algorithm called the Gur Game to quickly locate an optimal concentration region for the drugs in combination.8 The Gur Game has been modified to cover a wide range in the search field and uses one test case per iteration.9 After the range of concentration has been established for each drug in the combination, a more refined search is conducted using a parallel search algorithm, the differential evolution (DE) algorithm,24 to find the optimal drug combination candidate for KSHV reactivation.
Gur Game algorithm
Direct search algorithms have been successfully used to solve large-scale optimization problems in the field of Engineering.25,26 Gur Game aims for self-optimization and self-organization of distributed systems and has been applied for the optimization of stiffness distribution and duty cycles of an unsteady flapping wing in a micro-air vehicle.27 It is based on a biased random search technique that aims to reach optimal system performance. Using the analogy of climbing a hill, Gur Game aims to reach the hill's summit while avoiding being trapped in local valleys and peaks.28 The essence of Gur Game is a biased random walk of multiple finite state automata towards a high system performance, which is defined by a reward function. The key concept in Gur Game is the global figure of merit which measures the performance of the system as a whole. The reward function maps the system state from 0 to 1, with higher system performance corresponding to values closer to 1. At each iteration through the control loop, the reward function is evaluated. Then the drug concentrations are changed probabilistically based on the reward function value. The advantage of Gur Game algorithm is that it does not require a pre-assumed model of the system and is robust to random changes in the system. The reward function can be multi-modal, non-linear, and discontinuous.
Differential Evolution algorithm
Differential Evolution is a population-based, parallel search, stochastic function minimizer that is equipped to solve real-valued test functions.24 Genetic algorithms are inspired by evolution biology in which inheritance, mutation, recombination, and selection are implemented to evolve the system to its optimum state. In the DE method, a population of solution vectors is successively updated by addition, subtraction, and component swapping, until the population converges to the optimum. This method requires few control variables, is easy to implement, robust, and converges with high accuracy in parallel computation. However, since this is a parallel search algorithm, more than one test case is used for each iteration. A larger number of test cases require more experimental expenditures but provide better accuracy and a better convergence rate.
Experiment implementation
The search algorithms were coded using MatLab (MathWorks, MA). For each test case, drugs were added to BC-3-G cells in 96 wells tissue culture plates (Corning, NY) and incubated for 24 h. GFP fluorescent intensity levels were collected using an inverted microscope (Nikon TE 2000-U, Japan) and the CoolSnap ES, CCC Camera (Photometrics, AZ). The GFP intensity levels were analyzed and fed into the search algorithm to determine a new test case (Gur Game) or set of test cases (Differential Evolution) for the next iteration.
Experiment set-up
To stimulate the reactivation of KSHV in vitro, we picked six drugs, Dexamethasone, sodium butyrate (NaB), Valproate, Ionomycin, 12-O-tetradecanoylphorbol 13-acetate (TPA), and Trichostatin A (TSA) that are able to upregulate the PAN promoter. Each drug was individually shown to stimulate GFP expression in BC-3-G cells (data not shown).
For the initial concentration range search using the Gur Game algorithm in the feedback control scheme, the range of individual concentrations (either in mM, μM or nM) were determined from single drug study that produced favorable GFP expression. The search was conducted with 10 discrete concentrations for each of the six drugs (0, 0.25, 0.5, 0.75, 1, 2.5, 5, 7.5, 10, 20 mM/μM/nM). The Gur Game algorithm was initiated with all drug values at the center of the concentration scale at 1 mM, 1 μM or 1 nM. The units are millimolar (mM) for drugs NaB and Valproate, micromolar (μM) for drugs Dexamethasone, Ionomycin and TSA, and nanomolar (nM) for drug TPA. GFP response from each experimental run were recorded and fed into the Gur Game algorithm that determined if the concentration of each drug was increased or decreased. After the concentration range for each drug is established using the Gur Game-based feedback control scheme we conducted a feedback control experiment using the DE algorithm to find the optimal combination of drugs to reactivate KSHV in vitro.
Results
Gur Game search to determine drug concentration range
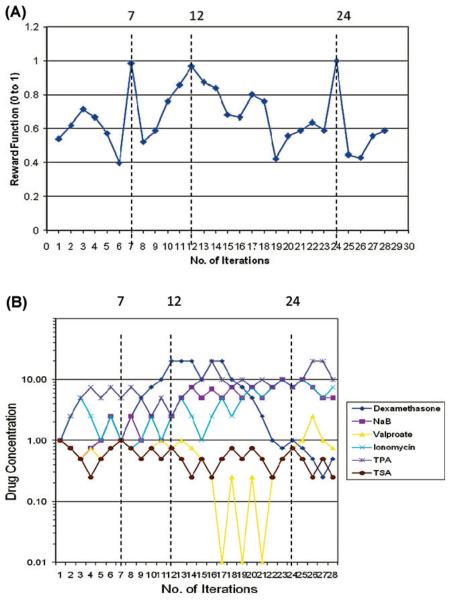
Using the Gur Game algorithm in the feedback control scheme, we conducted a total of 28 iterations over a period of two weeks. Each iteration used one experimental test case that has a mixture of six reactivation drugs. The first test case started with all six drugs in the middle of the concentration range (1 mM, 1 μM or 1 nM, depending on the drug). For the following iterations, each drug moved up or down in concentration as defined by the algorithm. Maximum intensities were reached at iteration 7, 12 and 24 (Fig. 1). Each mixture that provided the maximum intensity consisted of a different combination of reactivation drugs. Therefore, a total of 18 discrete concentrations were revealed in this study. Out of this group, 72% of them were between 0 and 2.5 concentration units. Therefore, from this experiment, we determined a working concentration range of 0–2.5 (mM, μM or nM, depending on the drug) to be used to find the optimal drug combination for viral reactivation using the DE algorithm.
Fig. 1.
Gur Game algorithm based feedback control search. (A) Reward function value against the number of iterations. The dotted lines represented iterations that generated the maximum reward function at iteration 7, 12 and 24. (B) Individual drug concentration in each of iterations of the Gur Game algorithm search. The dotted lines represented iterations that generated the maximum reward function at iteration 7, 12 and 24 (corresponds to A)
Differential evolution search to find optimal drug combination
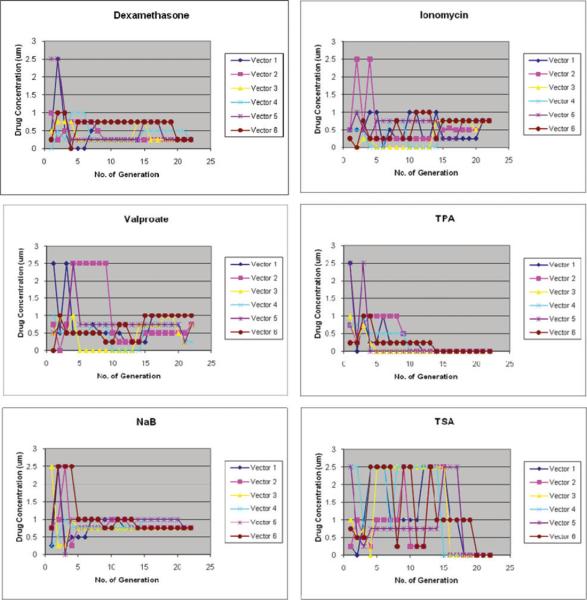
Each generation in the DE-based feedback control scheme consisted of a set of six test cases. The concentration range for each drug in the mixture determined from the Gur Game search was between 0–2.5 mM for NaB and Valproate; 0–2.5 μM for Dexamethasone, Ionomycin and TSA; and 0–2.5 nM for TPA. Each concentration range is assigned 6 discrete concentrations (0, 0.25, 0.5, 0.75, 1, 2.5 mM/μM/nM). In the first iteration of the DE search, drug concentrations in each of the six test cases were picked at random. In the following iterations, the concentrations of each drug in each of the six test cases, moves through discrete concentrations established by the algorithm. DE began to show signs of convergence to a likely combination candidate by generation 16. By generation 21, two drugs, NaB and Ionomycin converged to a single concentration of 0.75 mM and 0.75 μM respectively, for all six test cases. Dexamethasone converged to 0.25 μM in all five test cases except for one that is at 0.5 μM. TPA and TSA, were completely removed from the drug cocktails by generation 20. All drugs except TSA moved within a small range of concentrations by the 10th generation and only Valproate failed to converge to a single discrete concentration. By generation 23, almost all six test cases converged to the same combination of drugs (Fig. 2).
Fig. 2.
Differential evolution based feedback control Search. Individual drug convergence in DE search over 23 generations. Each graph maps out the drug concentrations for all six test cases (vectors 1–6) in each generation throughout the search process. NaB and Ionomycin converged to 0.75 mM and 0.75 μM, respectively; dexamethasone converged to 0.25 μM; Valproate converged to a range between 0.25 mM and 0.75 mM; TPA and TSA, converged to zero.
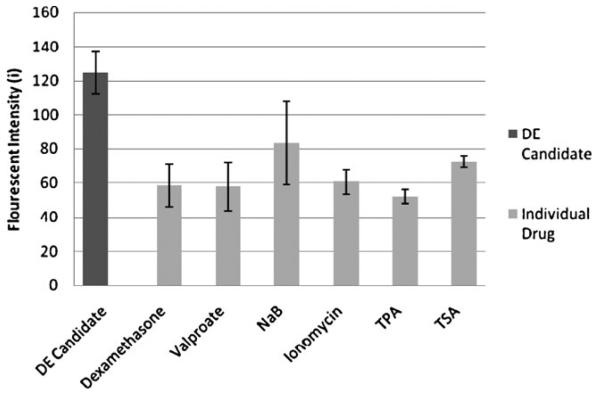
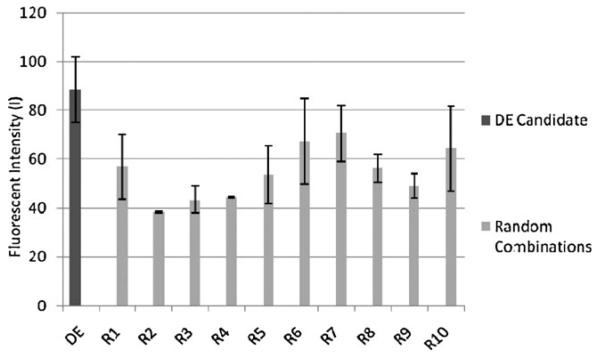
The optimized drug mixture attained from the DE-based feedback control scheme is labeled as the DE-candidate. Fig. 3 shows the GFP fluorescent intensity achieved by the DE-candidate compared to the highest GFP fluorescent intensities achieved by individual drug treatments. For the single treatment of each individual drug; highest GFP intensity were achieved at concentration 2.5 μM for Dexamethasone; 2.5 μM for Valproate; 0.5 mM for NaB; 0.5 μM for Ionomycin; 0.5 nM for TPA; and 2.5 μM for TSA. DE-candidate attained a GFP intensity of 124.5 units of fluorescence compared to 83.5 units of the best performing single drug, NaB. The lowest performing single drug is TPA at 52 units of fluorescence. Furthermore, we compared the GFP fluorescent intensity of the DE-candidate with 10 other random drug combinations of the six reactivation drugs (Fig. 4). The DE-candidate outperformed all 10 randomly generated drug combinations for the reactivation of KSHV. In Fig. 4, the DE-candidate achieved a GFP intensity of 89 units of fluorescence and the highest random combination achieved 71 units of fluorescence. The lowest performing random combination has 39 units of fluorescence.
Fig. 3.
Fluorescent intensity of the DE-candidate and the maximum fluorescent intensity achieved by single drug treatment. The single drug treatments are the maximum fluorescent intensity achieved in an individual drug treatment study.
Fig. 4.
Comparison of the performance of DE-candidate (DE) with 10 other randomly selected drug combination of the six drugs (R1–R10).
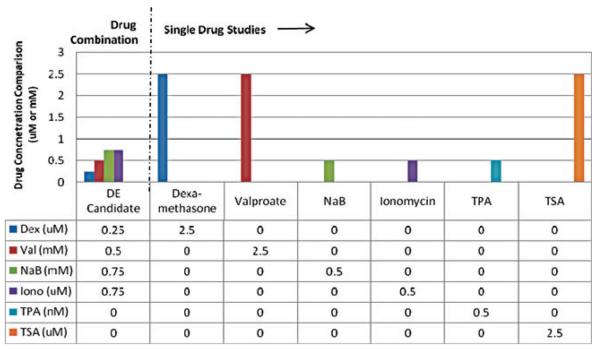
Fig. 5 presents the concentration of drugs used in the DE-candidate compared to the drug concentration needed for maximal GFP expression in the single drug study shown in Fig. 3. In the DE candidate, the concentrations of Dexamethasone and Valproate were 0.25 μM and 0.5 mM, which were lower than their concentrations needed for optimal GFP expression in the single drug study, 2.5 μM and 2.5 mM, respectively. In the single drug study, optimal concentration for TPA and TSA were 0.5 nM and 2.5 μM, respectively. These two drugs were completely removed in the DE-candidate. Only NaB and Ionomycin were slightly higher in concentration in the DE-candidate when compared to their optimal single drug concentration. NaB at 0.75 mM and Ionomycin at 0.75 μM were used in the DE-candidate and their optimal concentration as single drugs were 0.5 mM and 0.5 μM, respectively.
Fig. 5.
Concentrations of reactivation drug used in the DE-candidate vs. optimal drug concentration for KSHV reactivation in single drug studies. Dexamethasone, Ionomycin, and TSA are in μM; NaB and Valproate are in mM; TPA is in nM. The concentrations for the drugs were in discrete concentrations of 0, 0.25, 0.5, 0.75, 1 and 2.5 mM/μM/nM. For the DE-candidate, the concentrations for Dexamethasone and Valproate were four concentration levels lower than the concentration needed for each drug to reactivation KSHV in the individual drug study. TPA and TSA were completely removed in the drug mixture. NaB and Ionomycin were one concentration level higher than in the individual study.
Discussion
The Gur Game algorithm is a direct search algorithm that has high search efficiency based on a greedy criterion that aims to move the system towards better overall performance. We used a modified version of Gur Game that has a high search rate over a large search space.9 This game has no memory cells and moves rapidly through different automatons. This method is advantageous because it has the ability to move rapidly through the search space with low numbers of iterations. Experimentally, this translates to low number of test cases when performing the feedback control scheme. However, in the experimental set-up studying biological systems, the Gur Game-based feedback control scheme has certain constraints.
First, the highest reward output (GFP intensity) from the system has to be assigned to the maximum value initially, as only then can the reward from each iteration be compared. As a result, the highest GFP intensity has to be estimated from the results of single drug studies. However, due to the non-linear and dynamic responses of cells, this estimation using single drugs may not accurately represent the highest reward that can be reached by the drug combination. In cases where the reward happens to go higher than the arbitrary set number during the experiment; the experiment has to be repeated with the higher reward value set to maximum. Second, the Gur Game algorithm analyzes the responses in all iterations and determines the optimal performing combination from that group. The best mixture is chosen by comparing experimental responses over a predetermined set of iterations. We limited Gur Game to a total of 28 iterations in this study. The Gur Game algorithm can be successfully applied to a stable system that is consistent with its responses without large variation between each iteration. However, in biological systems, cellular responses are affected by various external and internal factors. The health of the cells, their stages in their life cycle, their sensitivity to their environment all affect their overall responses to drugs. In this study, we found that cell batch-to-batch variability is severe. Certain batches of cells express GFP in higher or lower levels than others in the same condition with the same amount of stimulation and drug treatment. This variability was easily visible during the course of the experiment. This type of variability in the system poses a challenge whenever the system response needs to be compared between different iterations.
Due to these reasons, we employed the Gur Game-based feedback scheme to initially locate the range of concentrations that the optimal drug mixture might reside. The rapid search was able to give us a workable range of concentrations that we used for a more precise search using a parallel search algorithm that is more accurate but also experimentally more expensive to perform. During the Gur Game experiments, maximum intensities were reached at three separate iterations. Each iteration test case consisted of a different concentration of reactivation drug in which 72% of them were between 0 and 2.5 units in concentration. Therefore, we determined a working concentration range (0–2.5 mM/μM/nM) of drug concentrations and reduced the amount of searching that the DE algorithm has to go through to find the optimal combination of drugs.
In the DE-based feedback control search study, a set of six test cases were ran in parallel for each iteration of the DE search algorithm. GFP intensities from each test case were fed back into the DE algorithm to generate new sets of six test cases. When an optimal test case is reached with the highest performance of the group, all the other test cases in the set begin to converge to it unless a better performing test case emerges in the set. Therefore, by using this algorithm, an optimal combination is reached when all six test cases reach the same mixture of drugs. No arbitrary maximum has to be set for DE and the system under study is allowed to move higher in response without limitation of the algorithm. Another important feature of the DE algorithm in this study is that as a parallel search algorithm, DE compares the response of six test cases within each iteration, unlike Gur Game which compares responses between iterations. In a biological/cellular system that has intrinsic variability, this feature is highly advantageous as it removes the error that arises from cell batch-to-batch variability by only comparing values within the same batch of cells.
Using the differential evolution algorithm in the feedback control platform, a total of 23 iterations were performed before reaching a likely combination candidate (DE-candidate). The GFP intensity achieved by the DE candidate significantly outperforms single drug treatments by up to a factor of 2.39 in the case of DE candidate vs. drug TPA and no less than a factor of 1.49 in the case of DE candidate vs. drug NaB (where TPA is the weaker performing drug and NaB is the strongest performing drug in the single drugs study).
Individually, all six drugs have the ability to reactivate KSHV in vitro and produce a quantifiable GFP signal. However, in the DE candidate, two of the reactivation drugs (TPA and TSA) were completely removed from the combination. Furthermore, the concentrations of two drugs (Dexamethasone and Valproate) in the DE candidate were less than the optimal reactivation concentrations of these drugs in single drug studies. Dexamethasone was four discrete concentration levels lower in the drug mixture (2.5 μM down to 0.25 μM) and Valproate was three levels lower (2.5 μM down to 0.5 μM). The concentrations of the remaining two drugs, NaB (0.75 mM) and Ionomycin, (0.75 μM) were one level higher than their optimal concentration in single drug studies (0.50 mM for NaB and 0.50 μM for Ionomycin). This result demonstrates the advantages of drug combination therapies in that in a synergistic drug mixture, concentrations of certain drugs may be lower to achieve a similar or better outcome. To verify that the DE candidate is not simply a random combination of six drugs but a product of a directed search through the sample space of possible combinations, 10 random combinations were tested against the DE candidate. The results showed that DE candidate consistently outperformed the randomly selected combination of drugs by up to a factor of 2.30 (DE-candidate compared to R2) (Fig. 5) and no less than a factor of 1.25 (DE-candidate compared to R7).
The approach of using a feedback control scheme to search for combinatory drugs to determine specific biological/cellular outcomes offers various advantages: first, it takes a holistic methodology to the study of behaviors and responses of biological cells. The knowledge revealed by this technique may lead to a better understanding of the dynamics of this integrative biological system. Second, we are able to optimize and manipulate the biological system with few key pieces of information without complete mapping of the molecular and signaling interconnections driving cellular networks. Third, this is a generic approach that can be applied to find optimal drug mixture to tackle biological systems that have important and pertinent therapeutic consequences. However, it should be mentioned that even though stochastic search algorithms such as DE offer robustness and high success rates during convergence, there is a possibility that local maxima are reached during the search. The likeliness of reaching local maxima depends on the overall profile of the cellular response and is highly system specific. In cases where local maxima are reached, further iterative searches have to be conducted to move towards the global maxima.
Conclusion
Therapeutic compounds act in such a way that their activity is commonly exerted among several pathways which drives broad cyto-regulatory control. Drug-induced multi-pathway impact towards a unified outcome (e.g. skin cancer targeting, inflammatory suppression, etc.) has been shown to produce amplified efficacy in comparison to single pathway targeting with multiple drugs. As such, an integrative, system control-mediated combinatorial approach coupled with the multi-pathway impact of each drug can collectively result in a broadly efficacious treatment strategy. For example, Dexamethasone, which served as one of the system control drug compounds in this study has been shown to regulate NFκB and AP-1 in rat liver macrophages.29 Additional foundations for Dexamethasone-induced activity in a wide variety of other tissues were demonstrated by its induction of a Ras superfamily gene Dexras1, the first Ras super-family gene to be induced in response to steroids.30 TPA, another therapeutic employed in this study has been shown to induce PTEN expression in the context of decreasing carcinoma latency in skin tumor progression.31 Furthermore, TPA administration has also been shown to activate protein kinase C (PKC) which in turn resulted in negative regulation of Akt activity in studies involving insulin-like growth factor (IGF-1) protection against UV-induced apoptosis in mouse keratinocytes.32 Therefore, it is clear that drug activity influences a collection of pathways and cellular signaling elements. Strategies to coordinate drug efficacy in an integrative fashion through the use of algorithm-defined concentrations for optimal dosing are thus potentially powerful solutions towards cellular control.
The challenge is that a small number of drugs, say six in this study, with 10 potential dosages result in one million potential choices. We illustrate that the effective search scheme allowed us to find the optimized combinatorial drugs from a large number of possibilities within a manageable number of tests. Specifically, we were able to use the closed loop feedback control scheme incorporating the Gur Game and Differential Evolution to direct the KSHV reactivation model towards higher reactivation levels using combinatorial drugs. Our results showed that within tens of iterations, we were able to reach an optimal state of the system under the given six drug stimulations that performed better than any single drug stimulation. Furthermore, the optimized drug mixture was able to perform significantly better than the highest reactivation individual drug and other randomly generated drug mixtures. The optimized drug mixture were able outperform the single drug treatments and random mixtures by up to a factor of 2.4 times better. Furthermore, not only does the optimized drug mixture perform better than their single drug counterparts, the concentrations of four out of six drugs were lower in the drug mixture.
This approach has quantitative method of controlling cellular outcomes by multi-parametric stimulation from a systemic approach vs. individualized pathway manipulation. This platform strategy thus opens up doors to dissect cyto-regulatory pathway activity and cross-pathway correlation which will serve as a powerful tool towards enhanced cellular and molecular insight. Quantitative interactions at the genetic level in yeast chromosomal biology have provided important information that cannot be easily derived from protein–protein interaction studies.33 These large-scale gene interaction studies known as epistatic miniarray profiles (E-MAPs) provide comprehensive mapping of pathway organization and multi-component analysis of how signaling processes are interconnected. The application of E-MAP has been shown to reveal functional relationships and interactions between genes and proteins.33,34 Furthermore, the complexity of the machinery that drives cellular genotypic and phenotypic outcomes drives the need for continued extensive efforts towards illuminating all of the interactive relationships between cellular components. To date, the mechanism from KSHV latency-to-lytic cycle is not completely understood. However, various signaling pathways that regulate the reactivation process in KSHV have been identified through a genome-wide cDNA library screen with 26 000 full-length cDNA expression constructs.15 The next step, we will start to apply cDNA library screen technique to study KSHV reactivation under optimal combinatory drug, such that signaling pathway intricacies and network interconnectivity in KSHV reactivation can be effectively revealed and identified. By using analysis tools such as cDNA library screen and E-MAPs, we may be able to reveal pathway interactions and relationships resulting in higher reactivation levels. Furthermore, the use of the closed loop feedback control scheme is broadly applicable to different systems and this technique can be applied to further the understanding of nonlinear interactions in different kinds of biological and therapeutic systems.
Our study was carried out in vitro. The method will be applied to measurement in vivo in the near future. As KSHV reactivation can be measured in vivo using PET scanning, it is thus possible to use this approach to optimize the reactivation directly in vivo and generate clinical benefit.35
Acknowledgements
This work is supported by NIH nanomedicine program (Center for Cell Control, PN2EY018228).
References
- 1.Ottino JM. Complex Systems. AIChE J. 2003;49:292–299. [Google Scholar]
- 2.Raser JM, O'Shea EK. Noise in gene expression: origins, consequences, and control. Science. 2005:2010–2013. doi: 10.1126/science.1105891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Weng G, Bhalla US, Iyengar R. Complexity in Biological signaling systems. Science. 1999;284:92–96. doi: 10.1126/science.284.5411.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boyer LA, Lee TI, Cole MF, Johnstone SE, Levine SS, Zucker JP, Guenther MG, Kumar RM, Murray HL, Jenner RG, Melton DA, Gifford DK, Jaenisch R, Young RA. Core Transcriptional Regulatory Circuitry in Human Embryonic Stem Cells. Cell. 2005;122:947–956. doi: 10.1016/j.cell.2005.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pannetier J, Bassasalsina J, Rodriguezcarvajal J, Caignaert V. Prediction of Crystal-Structures from Crystal-Chemistry Rules by Simulated Annealing. Nature. 1990;346:343–345. [Google Scholar]
- 6.Bonabeau E, Dorigo M, Theraulaz G. Inspiration for optimization from social insect behaviour. Nature. 2000;406:39–42. doi: 10.1038/35017500. [DOI] [PubMed] [Google Scholar]
- 7.Tung B. Distributed Control Using Simple Automata. University of California; Los Angeles: 1994. PhD thesis. [Google Scholar]
- 8.Tung B, Kleinrock L. Using finite state automata to produce self-optimization and self-control. IEEE Trans/Parallel Distributed Syst. 1996;7:439–448. [Google Scholar]
- 9.Wong PK, Yu F, Shahangian A, Cheng G, Sun R, Ho CM. Closed-Loop Control of Cellular Functions Using Combinatory Drugs Guided by a Stochastic Search Algorithm. Proc. Natl. Acad. Sci. U. S. A. 2008;105(13):5105–5110. doi: 10.1073/pnas.0800823105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sawyer CL. Mixing Cocktails. Nature. 2007;449:993–996. doi: 10.1038/449993a. [DOI] [PubMed] [Google Scholar]
- 11.Feldmann M, Steinman L. Design of effective immunotherapy for human autoimmunity. Nature. 2005;435:612–619. doi: 10.1038/nature03727. [DOI] [PubMed] [Google Scholar]
- 12.De Francesco R, Migliaccio G. Challenges and successes in developing new therapies for hepatitis C. Nature. 2005;436:953–960. doi: 10.1038/nature04080. [DOI] [PubMed] [Google Scholar]
- 13.Verma SC, Robertson ES. Molecular biology and pathogenesis of Kaposi sarcoma-associated herpesvirus. FEMS Microbiol. Lett. 2003;222:155–163. doi: 10.1016/S0378-1097(03)00261-1. [DOI] [PubMed] [Google Scholar]
- 14.Ahmed A, Isa MS, Garba HA, Kalayi GD, Muhammad I, Egler LJ. Influence of HIV infection on presentation of Kaposi's sarcoma. Trop. Doct. 2001;31:42–45. doi: 10.1177/004947550103100119. [DOI] [PubMed] [Google Scholar]
- 15.Yu F, Harada JN, Brown HJ, Deng H, Song MJ, Wu T-T, Kato-Stankiewicz J, Nelson CG, Vieira J, Tamanoi F, Chanda SK, Sun R. Systematic identification of cellular signals reactivating Kaposi Sarcoma-Associated Herpesvirus. PLoS Pathog. 2007;3:e44. doi: 10.1371/journal.ppat.0030044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cesarman E, Moore PS, Rao PH, Inghirami G, Knowles DM, Chang Y. In vitro establishment and characterization of two acquired immunodeficiency syndrome-related lymphoma cell lines (BC-1 and BC-2) containing Kaposi's sarcoma-associated herpesvirus-like (KSHV) DNA sequences. Blood. 1995;86:2708–2714. [PubMed] [Google Scholar]
- 17.Boshoff C, Schulz TF, Kennedy MM, Graham AK, Fisher C, Thomas A, McGee JO, Weiss RA, O'Leary JJ. Kaposi's sarcoma-associated herpesvirus infects endothelial and spindle cells. Nat. Med. 1995;1:1274–1278. doi: 10.1038/nm1295-1274. [DOI] [PubMed] [Google Scholar]
- 18.Lukac DM, Kirshner JR, Ganem D. Transcriptional activation by the product of Open Reading Frame 50 of Kaposi's Sarcoma-Associated Herpesvirus is required for lytic viral reactivation in B cells. J. Virol. 1999:9348–9361. doi: 10.1128/jvi.73.11.9348-9361.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sun R, Lin S-F, Gradoville L, Yuan Y, Zhu F, Miller G. A viral gene that activates lytic cycle expression of Kaposi's sarcoma-associated herpesvirus. Proc. Natl. Acad. Sci. U. S. A. 1998;95:10866–10871. doi: 10.1073/pnas.95.18.10866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Song MJ, Brown HJ, Wu TT, Sun R. Transcription activation of polyadenylated nuclear rna by rta in human herpesvirus 8/Kaposi's sarcoma-associated herpesvirus. J. Virol. 2001;75:3129–3140. doi: 10.1128/JVI.75.7.3129-3140.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sun R, Lin SF, Gradoville L, Miller G. Polyadenylylated nuclear RNA encoded by Kaposi Sarcoma-Associated Herpesvirus. Proc. Natl. Acad. Sci. U. S. A. 1996;93:11883–11888. doi: 10.1073/pnas.93.21.11883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Song MJ, Li XD, Brown HJ, Sun R. Characterization of interactions between RTA and the promoter of polyadenylated nuclear RNA in Kaposi's Sarcoma-Associated Herpesvirus/Human herpesvirus 8. J. Virol. 2002:5000–5013. doi: 10.1128/JVI.76.10.5000-5013.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Song MJ, Brown HJ, Wu TT, Sun R. Transcription activation of polyadenylated nuclear RNA by Rta in human herpesvirus 8/Kaposi's Sarcoma-Associated Herpesvirus. J. Virol. 2001:3129–3140. doi: 10.1128/JVI.75.7.3129-3140.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997;11:341–359. [Google Scholar]
- 25.Kirkpatrick S, Gelatt CD, Vecchi MP., Jr Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 26.Forrest S. Genetic algorithms: Principles of natural selection applied to computation. Science. 1993;261:872–878. doi: 10.1126/science.8346439. [DOI] [PubMed] [Google Scholar]
- 27.Ho S, Nassef H, Pornsin-Sirirak N, Tai YC, Ho CM. Unsteady aerodynamics and flow control for flapping wing flyers. Prog. Aerospace Sci. 2003;39:635–681. [Google Scholar]
- 28.Tsetlin ML. Finite automata and the modeling of the simplest forms of behavior. Usp. Mat Nauk. 1963;8:1–26. [Google Scholar]
- 29.Tran-Thi TA, Decker K, Baeuerle PA. Differential activation of transcription factors NFkP and AP-1 in rat liver macrophages. Hepatology. 1995;22(2):613–619. doi: 10.1002/hep.1840220235. [DOI] [PubMed] [Google Scholar]
- 30.Kemppainen RJ, Behrend EN. Dexamethasone rapidly induces a novel Ras superfamily member-related gene in AtT-20 cells. J. Biol. Chem. 1998;273(6):3129–3131. doi: 10.1074/jbc.273.6.3129. [DOI] [PubMed] [Google Scholar]
- 31.Mao J-H, To MD, Perez-Losada J, Wu D, Del Rosario R, Balmain A. Mutually exclusive mutations of the Pten and ras pathways in skin tumor progression. Genes Dev. 2004;18:1800–1805. doi: 10.1101/gad.1213804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li LW, Sampat K, Hu N, Zakari J, Yuspa SH. Protein kinase C negatively regulates Akt activity and modifies UVC-induced apoptosis in mouse keratinocytes. J. Biol. Chem. 2006;281(6):3237–3243. doi: 10.1074/jbc.M512167200. [DOI] [PubMed] [Google Scholar]
- 33.Collins SR, Miller KM, Maas NL, Roguev A, Fillingham J, Chu CS, Schuldiner M, Gebbia M, Recht J, Shales M, Ding H, Xu H, Han J, Ingvarsdottir K, Cheng B, Andrews B, Boone C, Berger SL, Hieter P, Zhang Z, Brown GW, Ingles CJ, Emili A, Allis CD, Toczyski DP, Weissman JS, Greenblatt JF, Krogan NJ. Functional dissection of protein complexes involved in yeast chromosome biology using a genetic interaction map. Nature. 2007;446:806–810. doi: 10.1038/nature05649. [DOI] [PubMed] [Google Scholar]
- 34.Collins SR, Schuldiner M, Krogan NJ, Weissman JS. A strategy for extracting and analyzing large-scale quantitative epistatic interaction data. Genome Biol. 2006 doi: 10.1186/gb-2006-7-7-r63. 7/7/R63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fu D-X, Tanhehco Y, Chen J, Foss CA, Fox JJ, Chong J-M, Hobbs RF, Fukayama M, Sgouros G, Kowalski J, Pomper MG, Ambinder RF. Bortezomib-induced enzyme-targeted radiation therapy in herpesvirus-associated tumors. Nature Med. (N. Y., NY, U. S.) 2008:1118–1122. doi: 10.1038/nm.1864. [DOI] [PMC free article] [PubMed] [Google Scholar]