The role of fluctuations and stress on the effective viscosity of cell aggregates

Abstract

Cell aggregates are a tool for in vitro studies of morphogenesis, cancer invasion, and tissue engineering. They respond to mechanical forces as a complex rather than simple liquid. To change an aggregate's shape, cells have to overcome energy barriers. If cell shape fluctuations are active enough, the aggregate spontaneously relaxes stresses (“fluctuation-induced flow”). If not, changing the aggregate's shape requires a sufficiently large applied stress (“stress-induced flow”). To capture this distinction, we develop a mechanical model of aggregates based on their cellular structure. At stress lower than a characteristic stress τ*, the aggregate as a whole flows with an apparent viscosity η*, and at higher stress it is a shear-thinning fluid. An increasing cell–cell tension results in a higher η* (and thus a slower stress relaxation time t_c). Our constitutive equation fits experiments of aggregate shape relaxation after compression or decompression in which irreversibility can be measured; we find t_c of the order of 5 h for F9 cell lines. Predictions also match numerical simulations of cell geometry and fluctuations. We discuss the deviations from liquid behavior, the possible overestimation of surface tension in parallel-plate compression measurements, and the role of measurement duration.

Cell aggregates (1) (Fig. 1 A and B), also called multicellular spheroids, are made of either a single cell type, or mixtures of different types; for a review, see refs. 2 and 3. They have become a classical tool for studies on morphogenesis (4), cancer invasion, and tissue engineering (2).

Fig. 1.

Shape of aggregates. (A) Top view, two-photon microscopy image of the middle plane of a F9 aggregate at a 27% compression rate between parallel plates (see also Fig. S1). (Scale bar, 50 μm.) Cells are alive and moving (SI Text and Movie S1). (B) Side view, in a stereomicroscope (SI Text). (Scale bar, 125 μm.) (C) Simulation of three successive compressions.

One century ago, it was discovered that two different cell types, when mixed, can sort out (5), like several two-phase physical systems do to minimize energy. Such cell sorting can be interpreted through cell adhesion differences: Motile cells rearrange to minimize the overall energy of the aggregate (6). By compressing an aggregate between two parallel plates (7), measuring its pressure and curvatures determines its surface tension (assuming that Laplace's law holds) (3, 7, 8). Comparing the surface tension values obtained for different cell types enables one to predict their sorting behavior (9). Thus, equilibrium configurations of aggregates display analogies with the shape of liquid drops (4).

When put in contact, two aggregates can fuse, and the resulting aggregate rounds up (10, 11) (Movie S2), yielding quantitative measurements of an effective aggregate viscosity (SI Text and Fig. S2) (12). Hence even out of mechanical equilibrium, aggregates have analogies with liquids: More precisely, they flow like complex (non-Newtonian) fluids (13–15). Their behavior depends on the time scale and duration of the measurement. For instance, Leghorn embryo cell aggregates subjected to brief centrifugation periods (8–16 min) flatten quickly (cell shapes flatten too), and round up quickly (in <2 min) once centrifugal forces are removed, reaching a shape very similar to the initial one, like an elastic solid (16). In contrast, during prolonged centrifugation (1 day), the same aggregates continue to flatten more slowly (while cells gradually reassume their original shapes) (17, 18); once centrifugal forces are removed, these aggregates round up slowly (in ≈1 d), like a viscous liquid.

Existing models usually involve a phenomenological viscoelastic description (13, 15–17). However, aggregates are space-filling assemblies of deformable cells and thus belong to the class of biological or physical cellular materials (19) like liquid foams (20). As such, they can display viscous, elastic, and plastic behaviors (21). Here, we develop a model based on their cellular structure that captures the complexity of their triple mechanical behavior. We compare its predictions with large-amplitude compression experiments (Fig. 1 A and B) and corresponding simulations (Fig. 1C). With two-photon microscopy, we image in situ cell shapes (Fig. 1A and Fig. S1), cell shape changes, and rearrangements (Movie S1).

Model

Global Description of the Aggregate.

At a scale much larger than the cell size, the aggregate can be characterized by its state of deformation and stress (“continuous medium” description).

In a parallel-plate compression experiment, we quantify the aggregate deformation by its relative height change, ε_tot = (h_ag − h)/h_ag. Here, h_ag is the aggregate's initial height (i.e., diameter), corresponding to the plate separation at the time of first contact; h is its current height (h < h_ag). During compression, h is equal to the current plate separation h_comp; during free decompression h increases.

The force exerted by the aggregate on the plates is the cross-section area S of the aggregate through its midplane times the internal stress of the compressed aggregate (see SI Text for the tensorial description):

Here, p is the hydrostatic pressure and τ the elastic contribution to the stress, which we study here. In the case of a drop made of a simple liquid (τ = 0) with surface tension σ, at equilibrium, p would be balanced by the drop mean curvature κ [Laplace law: p = σκ (8)].

Local Description at the Cell Level.

We assume the cell deformation (monitored by the relative cell size change, ε_cell) and the stress are small enough to be proportional:

where E is a stiffness (elastic modulus).

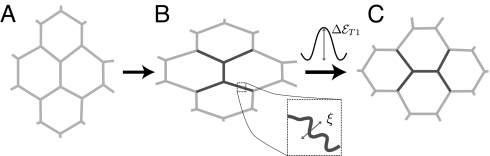
Within aggregates of inert objects such as drops (emulsions) or bubbles (foams), a “T1” (20) occurs when the local stress is high enough to overcome the energy barrier, Δℰ_T1 (Fig. 2), which depends on the interfaces' tension and length. It marks the transition from a reversible (elastic) object shape change to an irreversible (plastic) rearrangement, after which energy is dissipated (21). The energy barriers are biased and easier to overcome in the direction of the stress (21): Rearrangements accumulate and result in a continuously increasing material deformation, noted ε_rea, analogous to a flow. Because ε_rea does not correlate with each object's individual deformation, it has no direct elastic contribution to stress (and we neglect the contribution to the stress arising from each object's internal viscosity).

Fig. 2.

A neighbor swapping [“T1” topological rearrangement (20)]. (A) Sketch of initially relaxed cells. (B) Flattened cells, with a deformation ε_cell due to stress. (Inset) (Upper) Energy barrier Δℰ_T1 to overcome for a T1 to occur. (Inset) (Lower) Membrane fluctuations with amplitude proportional to ξ. (C) After a T1: The cell arrangement has changed, and the cell shapes relax, dissipating energy.

Unlike inert objects, living cells overcome some energy barriers, with large membrane shape fluctuations (Movie S1). These fluctuations are active and associated with cytoskeleton dynamics, as is evidenced by studies on cells treated with cytochalasin-B (an actin depolymerizing drug) (22, 23). An effective temperature or, equivalently, a thermal energy scale ξ (also noted kT in the literature) (23), describes not only the amplitude of these interface fluctuations (23, 24) but also the diffusion of a cell throughout an aggregate (25).

Mechanical Behavior of the Aggregate.

To capture the main physical ingredients that determine the aggregate's liquid behavior, we simplify its description. We consider here that all energy barriers have the same height, that of a T1. We take the total deformation to be:

In the absence of stress, fluctuation-induced rearrangements switch back and forth, with no flow on average. According to the Eyring model (26), the probability of rearrangement in the direction of stress (i.e., a T1 that reduces stress) is favorable: f⁺ = fexp{(−Δℰ_T1 + τVδε)/ξ}. Here, f is the inverse of a time (“attempt frequency”): It is a phenomenological quantity that characterizes how often fluctuations occur, only a fraction of which are actually able to jump over energy barriers; τV is the work gained during a rearrangement in the direction favored by the stress (V is of the order of a cell volume) and δε the deformation associated with a rearrangement.

In the direction opposing stress, the probability of a rearrangement is less favorable: f⁻ = fexp{(−Δℰ_T1 − τVδε)/ξ}. The flow rate ε̇_rea results from the difference between favored and unfavored rearrangement probabilities:

Here, both τ* and η* are continuous medium parameters (related to cell properties, see Discussion). The characteristic stress τ* = ξ/Vδε is determined by the fluctuation amplitude and cell size. The characteristic viscosity η* = ξexp(Δℰ_T1/ξ)/2fVδε² depends on τ* and energy barriers (but not on the internal viscoelasticity of cells).

Two Regimes.

Eq. 4 relates the aggregate's deformation and the applied stress; together with Eqs. 2 and 3, it fully describes the aggregate's mechanical response, i.e., the time evolution of the flow for any given configuration (“constitutive equation”). The characteristic stress τ* separates two regimes: that of fluctuation- and stress-induced flows.

If the stress τ is much smaller than τ*, the flow is due to fluctuations. The viscous stress and the flow rate are proportional to each other, τ ≃ η* ε̇_rea (Eq. 4). The associated time scale over which stress disappears is: t_c = η*/E ∼ exp{Δℰ_T1/ξ}. If t_c is smaller than or comparable with the duration of the measurement, at large scale, the aggregate relaxes the stress like a simple (Newtonian) fluid of viscosity η* (Fig. S2). Conversely, if t_c is much larger than the duration of the measurement, the flow is not measurable, and the aggregate seems to display a solid (plastic) behavior.

In contrast, if the stress τ is larger than τ*, it overcomes energy barriers. According to Eq. 4, the ratio of the viscous stress to the flow rate defines an effective viscosity η_eff, that is smaller than η*, by a factor η_eff/η* = (τ/τ*)/sinh(τ/τ*). The aggregate thus behaves like a “shear-thinning” fluid in which viscosity decreases at higher τ.

Compressions: Predictions.

Eq. 4 applies to compressions or decompressions. In a compression (Fig. 1), the distance h between plates is decreased in a stepwise manner, then is kept constant to h = h_comp, so that ε_tot = ε_comp, and ε̇_tot = 0. This creates an initial elastic stress τ₀ = Eε_comp. Eqs. 2–4 then yield a first-order differential equation. Its solution is the relaxation of stress with time t (Fig. 3):

Initially, the flow is in the stress-induced regime: The stress decreases faster than exp(−t/t_c). When the stress reaches τ*, the flow enters the fluctuation-induced regime, where the stress decreases like exp(−t/t_c).

Fig. 3.

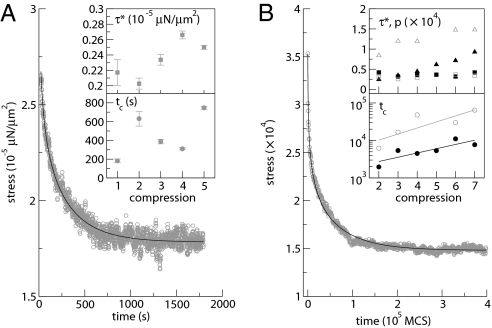
Stress relaxation while the compression plate is quickly displaced then kept fixed (constant distance h: “step-strain”). (A) Experiments showing the immediate force relaxation of an aggregate (initial diameter 500 μm) for the first compression. Gray circles, measured stress; solid line, fit from Eqs. 1 and 5 after subtraction of the asymptotic plateau value p (3). (Inset) Characteristic stress τ* and stress relaxation time t_c fitted to five (n = 1–5) successive compressions. (B) Simulations of long-term cell rearrangements. Gray circles, measured stress, here with γ_CC = 6.78 × 10⁵; solid line, fit from Eqs. 1 and 5. (Inset) Fitted parameters for cell–cell tension γ_CC = 1.13 × 10⁵ (black filled symbols) or 6.78 × 10⁵ (gray open symbols). Squares, τ*; circles: t_c; triangles, asymptotic plateau value p. The initial contact (n = 1) does not correspond to any measurable force. In the Lower Inset graph, note the log scale of the vertical axis; linear fits are drawn to guide the eye.

In principle, after a sufficiently long compression time (t_comp ≫ t_c) all elastic stresses ultimately disappear (Eq. 5). At this stage, the plates would only measure the constant contribution arising from the hydrostatic pressure generated by the aggregate surface tension. On the contrary, if t_comp is smaller (or not much larger) than t_c, the aggregate still stores some residual stress, like a plastic solid.

Experimental and Numerical Tests

Compression Experiments.

When an aggregate is compressed between plates (Fig. 1 A and B), the stress is initially high then decreases (Fig. 3A). The shape of the relaxation curve is well fitted by our model. During successive compressions the characteristic stress remains approximately constant, τ* ≃ 2.4 Pa (Fig. 3A Inset). In the curve of Fig. 3A, the initial stress is 9 Pa above the asymptotic plateau value: τ₀/τ* ≃ 3.8; hence, we estimate that initially η_eff/η* ≃ 0.2. The characteristic time t_c is of the order of a few 10² s. To understand the small value of this time scale (which might be associated with cytoskeletal dynamics, see Discussion), in what follows we distinguish the contributions from subcellular and cell levels to the dynamics.

Compression Simulations.

First, we simulate the collective cell behavior, i.e., the global flow, in a compressed aggregate (Fig. 1C) without subcellular structure. We only use cell-level ingredients: cell shapes and rearrangements, internal pressure, cell–cell interface tension and fluctuations. The stress relaxation agrees with Eq. 5 (Fig. 3B).

At low cell–cell tension (closed symbols in Fig. 3B Inset), the asymptotic plateau value compares well to the measured static pressure, p = σκ, as in a simple liquid. As expected (since in the model it is mostly determined by the fluctuation amplitude) τ* is constant through successive compressions of the same aggregate. The characteristic time t_c, which depends on Δℰ_T1, strongly increases during successive compressions. This increase might be related to the existence of energy barriers with different values (see Discussion): Low energy barriers are passed first, higher barriers later.

Simulations with larger cell–cell tensions (open symbols in Fig. 3B Inset) yield a similar τ* and a slower t_c (larger viscosity), as expected. The deviation from the liquid behavior is larger (see also Fig. S4): The asymptotic plateau value is higher; hence, a residual elastic stress contaminates the measurements of hydrostatic pressure (see Discussion).

Compression–Decompression Cycle Experiments.

Second, we perform measurements at a much larger time scale, during free relaxation (see also fusion, SI Text and Fig. S2). An aggregate is compressed at a fixed height h_comp (corresponding to a deformation ε_comp) during a time t_comp; then the upper plate is removed and the aggregate is left free (Fig. S3, Movie S3). The aggregate height relaxes quickly ≃10² s, then more slowly (Fig. S3).

In our model, during the compression time t_comp, rearrangements contribute to the aggregate flow, and a rearrangement deformation ε_rea builds up (Eq. 4). At the end of the compression, these rearrangements have relaxed the stress down to the value τ(t_comp), predicted by Eq. 5. The stored elastic deformation therefore decreases from ε_comp to ε_cell = τ(t_comp)/E. Because the total deformation is kept constant, we have (Eq. 3) ε_tot = ε_comp = ε_cell(t_comp) + ε_rea: The decrease in elastic deformation is exactly compensated by the rearrangement deformation. The arrangement of cells has been modified irreversibly. Upon removal of the compression plate, the aggregate surface tension drives rounding. At time scales shorter than hours h does not come back to its original value h_ag. The residual deformation, equivalent to an apparent plasticity (see figure 5 of ref. 13) ε_plastic = ε_rea is:

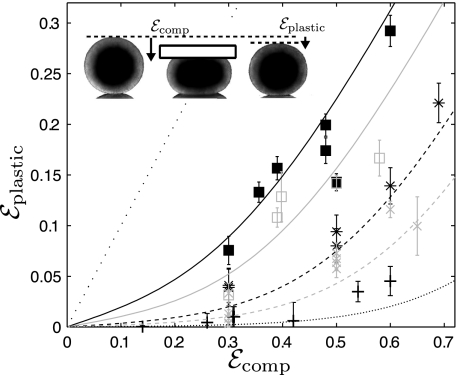
For several values of ε_comp and t_comp, the model agrees (Fig. 4) with the experimental residual deformation. We measure it at a time long enough for internal elastic stresses to have relaxed: We fix it by convention here at 440 s (Fig. S3). The relaxation time is t_c = 5 h. The characteristic deformation is ε* = τ*/E = 0.13: It means that the characteristic stress τ* is reached if the aggregate is quickly compressed to an amplitude of at least 0.13.

Fig. 4.

Apparent plasticity. An aggregate is compressed at a fixed height h_comp during a time t_comp and then the upper plate is removed and the aggregate is left free to relax (Movie S3). We define and measure h_p as the height h measured by convention after 440 s (Fig. S3). Symbols indicate t_comp: black +, 1 min; gray ×, 5 min; black *, 10 min; gray open squares, 30 min; filled squares, 60 min. Lines: prediction of Eqs. 5 and 6 plotted with t_c = 5 h and τ*/E = 0.13; thin straight dotted line: prediction with t_comp = ∞, i.e., ε_plastic = ε_comp. (Inset) Images of aggregates before compression (h_ag), during compression (h_comp), and after decompression (h_p); ε_comp = (h_ag − h_comp)/h_ag, ε_plastic = (h_ag − h_p)/h_ag.

Discussion

Energy Barriers and Nonreleased Elasticity.

Elasticity and plasticity arise from contributions of cell bulk (cytoskeleton and organelles) and surface (actomyosin-rich cortex). Adhesion and cortical contraction contribute to create a cell–cell interfacial tension [not to be confused with the aggregate surface tension (19, 27)] and, thus, energy barriers.

We study the combined effect of stress and active fluctuations to overcome energy barriers. Model and simulations suggest that higher interfacial tensions, by increasing the energy barriers, give rise to a higher viscosity. Our model captures the main features of compression experiments and simulations, as well as free relaxations, and distinguishes two flow regimes. Fits to the data (Fig. 3) determine τ*, t_c, and an asymptotic plateau value.

To interpret the values of these parameters, it is necessary to take explicitly into account not only cell rearrangements, but also the subcellular (cytoskeleton) dynamics. If the model were also developed for cell internal reorganization, Eq. 5 would be well suited to fit both types of force relaxations. A future extension of our single energy barrier model might include a more realistic distribution of energy barriers, some of which can be passed by fluctuations, whereas others are not passed within the experiment duration.

Time Scales.

The slow time scale t_c = 5 h (Fig. 4) can be interpreted as the relaxation time due to rearrangements, visible on Movie S1. Rearrangements-induced flow starts when aggregates are out of mechanical equilibrium, e.g., compressed. Rearrangements continue over hours until the complete equilibration of the aggregate. This interpretation agrees with the cell shape relaxation observed after 24 h in a centrifuged aggregate (16). It also agrees with orders of magnitude extracted from the fusion of two F9 aggregates and the rounding of the resulting aggregate, driven by surface tension, which takes 6 h (Fig. S2, Movie S2); we estimate η* = 4.4 10⁵ Pa·s: Combined with the above relations τ* = 0.13E and E = η*/t_c this yields τ* = 3.2 Pa, which is the same order of magnitude as in compression (Fig. 3A Inset).

We observe a much shorter time scale (≈10² s) in force relaxation experiments (Fig. 3A), confirmed by height recovery after compression (Fig. S3). We believe that it is due to internal release of cell elasticity, not included in the model nor in the simulations. It is compatible with the internal cell viscosity, probably hundreds of times smaller (28) than η*.

Aggregates are not always able to fuse and round up within the time of experiments or simulations [CHO cell aggregates barely fuse even after 1 week (11)]. In addition, even after relaxation, their shape sometimes displays a strong deviation from that of a liquid drop (22, 23) (Fig. S4). This suggests that the energy barriers are too high: Both the aggregate's surface tension and the fluctuations are insufficient to relax the elastic stress over the duration of the experiment. Our simulations at high cell–cell tension (open symbols, Fig. 3B Inset; Fig. S4) confirm that a plateau is sometimes reached before full stress relaxation.

Effect on Measured Surface Tension.

In compression–decompression cycle experiments, at a given relaxation time, the longer or the stronger the compression, the larger the number of rearrangements, and thus the stronger the apparent irreversibility, in good agreement with Eqs. 5 and 6.

For the assessment of surface tension, the time between two successive compressions is usually between 30 min and 2 h (7, 11). An equilibrium force seems to be attained 2–10 min after compression. We believe that this time is large enough to relax internal contributions; but, unlike what is assumed by ref. 13, only a limited number of rearrangements have taken place. Residual elastic contributions could lead to an overestimation of surface tension. This questions the validity of the application of Laplace's law in past surface tension measurement experiments.

A likely hypothesis would explain the remaining stored elasticity in our experiments by an active response of the cell. When compressed, cells could actively release a part of the elasticity stored in the compressed cytoskeleton; when decompressed, the surface tension drives the relaxation of the global aggregate shape, and cells could actively regain part of the elasticity. This hypothesis is compatible with the rate, 1–10 μm/min, at which single cells reorganize their cytoskeleton (29). It could be tested by two-photon imaging of cell contours and simultaneous force measurements recording while modifying the dynamics of actin (using drugs such as latrunculin and jasplakinolide) microtubules, or intermediate filaments.

If this hypothesis is correct, the elastic energy stored in deformed cells will be less than we assume in our model and simulations, and the overestimation of the surface tension in compression experiments will be smaller. This will explain why published measurements of surface tension are usually robust and do not depend on compression magnitude and duration, nor on aggregate size (3, 7, 9, 13).

Materials and Methods

Cell Line and Aggregates Preparation.

Mouse embryonal carcinoma F9 cell line was a generous gift from A. Nagafuchi (Kumamoto University, Japan) (30). Cells were maintained in DMEM (41965-039; GIBCO) supplemented with 10% fetal bovine serum (2902 P-232310; Biotech GmbH). For the aggregate formation, cells were dissociated and reassembled in 15-μL hanging drops containing between 1,000 and 8,000 cells (3). After 2 days, the newly formed aggregates were transferred to cell culture plates (24 wells) containing fresh medium and then put on a gyratory shaker for two more days. For the compression measurements, the cell aggregates were transferred to CO₂-independent medium (18045-054; GIBCO).

Compression–Decompression Experiments.

Each aggregate was compressed, by successive steps of 50 μm, between two glass plates. The lower one (2-mm-thick borosilicate glass) is located at the bottom of a CO₂-independent medium chamber that is moved in the x,y,z directions by a micromanipulator (MP285; Sutter Instrument). The upper one (cover glass) is fixed to a rigid pipe, except in Fig. 3A, that uses the force sensor described in ref. 3. The whole setup is embedded in a thermally isolated chamber maintained at the desired temperature by a resistance traversed by a current that is modulated by a temperature controller (331; Lakeshore). The chamber in which aggregates are deposited for the experiment is open to air to facilitate displacements and choice of aggregates; the free surface is covered with a thick mineral oil layer to prevent evaporation. Glass surfaces are carefully cleaned with soap and pure water (sonicated 30 min with 2% Microson detergent; Fisher Bioblock). They are made hydrophobic by silanization with perfluorosilane (F06179; ABCR) and covered with Pluronic F-127 (Sigma) at 10 mg/mL for 5 min and then rinsed briefly with water and dried. This treatment ensures that the aggregate adhesiveness remains small. For details see ref. 3 and SI Text.

In Fig. 3A, the error bar on fitted parameters is the 95% confidence interval of the nonlinear curve fit: All fitted parameters have errors <10% of the estimated value and smaller than the data dispersion. In Fig. 4, each error bar is estimated on only one aggregate decompression experiment as the uncertainty on the optical measurement of h_ag, h_p and h_comp; it depends on image resolution and aggregate roughness as well as the possible slight aggregate rotation and translation after decompression.

Two-Photon Microscopy.

Two-photon laser scanning microscopy is performed on an Olympus BX50WI microscope coupled to a Bio-Rad MRC 1024 scan head with a nondescanned detector to increase the observation depth. An 800-nm excitation beam from a Tsunami femtosecond Ti:Saphire laser (Millenia V; Spectra-Physics) is focused on the surface of the aggregate by using a magnification ×20 water-immersion objective (0.95 N.A., Xlum Plan Fl; Olympus). The beam scans the xy plane to acquire 512 × 512-pixel images in 0.9 s. Variation of the observation depth (z-scan) is realized by moving the motorized objective vertically. We have developed a compression apparatus similar to that described in ref. 11 mounted on the stage of the two-photon microscope with a thermostatted circulating water bath to control temperature at 37 °C. The soluble dye sulforhodamine B (SRB), injected at a concentration of 8 μg/mL in the culture medium, quickly diffuses inside aggregates and stains the extracellular space with an intensity comparable with the SRB present outside of the aggregates.

Cellular Potts Model Simulations.

The cellular Potts model (31, 32) is a standard algorithm to simulate multicellular structures (and cell packing) from individual cells of variable shape and size (32). Each cell is defined as a certain set of pixels, here in 2D [tests in 3D yielded similar results (33)]; their number defines the cell area A. The aggregate energy has two terms (31).

First, the interfacial energy between cells is the sum of the energy costs between pixels that form the border between different cells (all cells here are of the same type, noted C), as well as between one cell and the medium (M) or the plate (P). A pair of two pixels i and j at such a border has an associated energy cost γ_ij, with, here, the following combinations: γ_CC, γ_CM, γ_CP, or γ_MP. These are inputs of the simulations and are constant [making them variable (33) does not significantly change the results presented here)]. We account for the proportionality factor between energy and perimeter, here 11.3 (33), due to the average number of pixel pairs included in the evaluation of energy.

Second, the elastic energy for each cell is the sum over cells of λ_A(A_c − A_0c)²: A_c is the area of a cell c, A_0c its target area (minimum-energy area), and λ_A an area compression modulus. This term enforces the cell area conservation. The pressure p is defined and measured from −2λ_A(A_c − A_0c), averaged over all cells.

The theoretical value of the aggregate surface tension is calculated as: σ = γ_CM − γ_CC/2 (19). We checked (33) that for a liquid drop D, which in the cellular Potts model is represented by a single cell with constant interfacial tension γ_DM, the surface tension σ is equal to γ_DM.

During one Monte Carlo time step, each pixel at a cell–cell interface is considered for update once, in a random order. If the pixel update diminishes the total aggregate energy, we accept it; and if the update increases the total energy by Δℰ, we accept it with probability P = exp(−Δℰ/ξ), where the “fluctuation allowance” ξ leads to fluctuations of membrane positions (22).

Plates are used as force sensors, with a stiffness k adapted to that of the aggregate. The potential energy of the plate surface is ℰ_C = ½k(〈z〉 − z₀)², where 〈z〉 is the averaged vertical position of the plate interface, and z₀ the plate's zero-energy vertical position (33). The force F on the plate is defined and measured as F = k∣〈z〉 − z₀∣ .

To simulate a compression experiment, the zero-energy positions z₀ of the plates are approached by a step of 0.1 h_ag. Cell shapes, total force and aggregate radius are recorded during 10⁵ Monte Carlo steps (33). This is iterated until the aggregate height reaches 0.3 h_ag (70% compression rate). In Fig. 3B and Fig. S4, parameters are: γ_CM = 5.65 × 10⁵, γ_CP = 6.78 × 10⁵, γ_MP = 1.13 × 10⁵, λ_A = 1.0 × 10³, A₀ = 200, ξ = 4 × 10⁴, k = 2 × 10³. The lattice size is 250 × 800 pixels, with 240 cells.