Simulations of a protein crystal: Explicit treatment of crystallization conditions links theory and experiment in the streptavidin-biotin complex

Abstract

A 250ns molecular dynamics simulation of the biotin-liganded streptavidin crystal lattice, including cryo-protectant molecules and crystallization salts, is compared to a 250ns simulation of the lattice solvated with pure water. The simulation using detailed crystallization conditions preserves the initial X-ray structure better than the simulation using pure water, even though the protein molecules display comparable mobility in either simulation. Atomic fluctuations computed from the simulation with crystallization conditions closely reproduce fluctuations derived from experimental temperature factors (correlation coefficient 0.88, omitting two N-terminal residues with very high experimental B-factors). In contrast, fluctuations calculated from the simulation with pure water were less accurate, particularly for two of the streptavidin loops exposed to solvent in the crystal lattice. Finally, we obtain good agreement between the water and cryo-protectant densities obtained from the simulated crystallization conditions and the electron density due to solvent molecules in the X-ray structure. Our results suggest that detailed lattice simulations with realistic crystallization conditions can be used to assess potential function parameters, validate simulation protocols, and obtain valuable insights that solution-phase simulations do not easily provide. We anticipate that this will prove to be a powerful strategy for molecular dynamics simulations of biomolecules.

Molecular simulations of proteins and other biomolecules in aqueous environments are now routinely performed at atomic detail on time scales of tens to hundreds of nanoseconds. To date, molecular dynamics simulations have been useful for predicting drug binding sites not available in protein X-ray structures (1,2), elucidating the origins of drug specificity (3,4), computing binding energies for peptides and small molecules to proteins (5–7), and even informing coarser molecular modeling techniques (8).

Despite the power of molecular simulations to model chemical processes in detail, validation of the simulations has lagged. One thing impeding the validation is the disparity between simulated and experimentally observed structures. Most simulations are initiated by extracting coordinates for a biomolecule from an X-ray crystal structure, omitting some or all unobserved components of the system, and solvating the system in a bath of pure water with counterions to neutralize excess charge. Removal of packing constraints as the biomolecule is taken from the crystal lattice into the solution phase is often cited as a source of differences between the atomic fluctuations obtained from crystallography and simulations (9,10), but this point has received little quantitative testing and certainly varies for different biomolecules. Studies have also found that the overall magnitudes of atomic fluctuations, when computed from simulations on the scale of 1–10 ns, are smaller than those observed in experiment, consistent with the conclusions of previous works (11,12) that these simulations did not adequately sample the natural conformational space.

One means of bridging the gap between solution-phase simulations and experimentally observed structures is the comparison of simulated biomolecules with structure constraints derived from NMR experiments. In this regard, molecular simulations have enjoyed some success. The NMR structure of the Trp cage protein (13) has been derived by purely computational methods (14,15), but it is unclear whether the tests were truly independent because the NMR structure was refined using the same force field as the structure prediction simulations (16) and other studies using different force field models did not achieve as high a level of accuracy (17).

Another strategy to bridge the gap between molecular dynamics and experimentally observable structures is to use the versatility of the simulations to reproduce a biomolecular crystal lattice. This approach enjoys several advantages from a purely computational point of view. Debate exists as to whether the periodic boundary conditions commonly used in solution phase molecular dynamics simulations introduce significant artifacts (18,19), but they should be more appropriate in the context of lattice simulations. Because the solvent accounts for 80% or more of the particles in a solution-phase simulation (20) but as little as 30% of the particles in a protein crystal (21), more computing time can be devoted to simulating the protein of interest rather than its solvent environment. Furthermore, structural relaxation is expected to be minimal for a high-resolution X-ray structure if the simulation force field is accurate; therefore, the computing time needed to obtain a specific level of statistical convergence in simulations of biomolecular crystal lattices may be lower than that of solution-phase simulations.

In spite of several technical advantages, lattice simulations have their own drawbacks, most of which have to do with the nature of the crystallization solution. These solutions typically have very high ionic strengths, which are hard to treat without invocation of atomic polarizability (22). The amount of solution needed to properly solvate the crystal lattice is also uncertain, as the lattice may favor the inclusion of certain ions more than others in its interstices (23). The preferential binding of certain nonpolar reagents could also be important (24,25), and the degree to which water itself is constricted on a protein surface is a subject of debate (26,27).

To date, there are only a few reports of biomolecular simulations in a crystal lattice. Pioneering simulations of bovine pancreatic trypsin inhibitor in its crystal lattice (28) and a later study of the same protein (12), constrained the unit cell volume explicitly and solvated the protein with only the crystallographically observed water molecules. A more recent study involved thousands of simulations of protein crystal lattices to reoptimize the AMBER forcefield for agreement with high-resolution X-ray structures (10), but these simulations again bypassed hurdles related to the crystallization solution by using a pure water solvent and strictly maintaining the unit cell dimensions.

In this work, we test the ability of atomistic, fixed-charge molecular mechanics models to reproduce X-ray crystallographic results by simulating a biotin-liganded streptavidin crystal with complete reproduction of the experimental crystallization conditions and a variable box volume. In addition, we simulate the lattice solvated with water alone, and identify differences in the resulting protein structures and dynamics obtained with either solvent. We include detailed protocols and Supporting Information for the lattice simulation setup, in order to encourage and facilitate use of this strategy to study other proteins and biomolecular complexes.

Methods

Unit cell preparation

The 1MK5 crystal structure (29) for the streptavidin-biotin complex was used to generate the lattice simulation model. This structure was chosen from many possible candidates because of its reasonably high resolution and the fact that it was crystallized at pH 4.5, the same as a streptavidin structure without bound biotin (PDB accession code 1SWA (30)), which we plan to analyze in future studies. The 1MK5 structure crystallized in the I222 space group, and its asymmetric unit (ASU) is a dimer of biotin-liganded streptavidin subunits across what is known as the tetrameric “tight” interface (31). Streptavidin tetramers assemble in the crystal with one of their molecular two-fold symmetry axes coincident with a crystallographic symmetry axis. The crystallographically unique portion of the crystal contains a dimer of two streptavidin subunits; eight of these dimers and thus four tetramers are present in the unit cell.

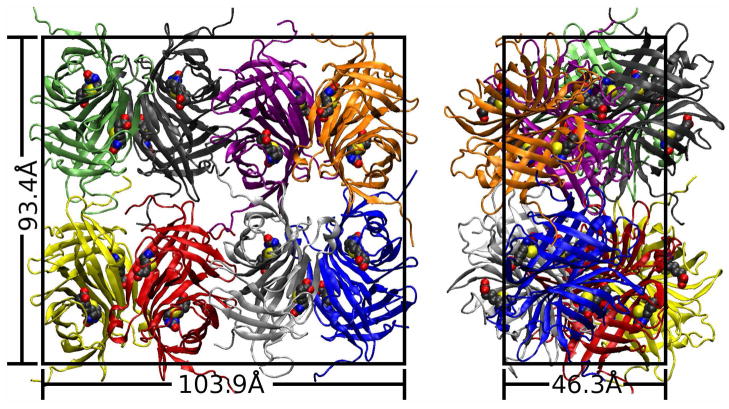
The crystallographic unit cell was modeled for simulations using the I222 space group symmetry operations and the crystal cell dimensions given in structure 1MK5, as shown in Figure 1. The amino acid sequence of the proteins in the 1MK5 structure begins AEAG, but the first one to two of these residues are unobserved in each monomer. The missing Ala and Glu residues were reconstructed by alignment with structure 2IZF (32), a streptavidin:biotin complex crystallized at pH 4.0 in the I222 space group and diffracted to 1.58Å. Similarly, the proteins in the 1MK5 structure terminate with the sequence VKPSAAS, but the final four or five residues are unobserved in each monomer. The unobserved residues at the C-terminus of the second subunit were reconstructed by alignment with the 1.55Å resolution structure 1MOY (33), the only structure in which these residues were observed. To satisfy crystal packing constraints, the C terminal tail of the first streptavidin subunit was reconstructed manually and the Tyr22 side chain was modeled alternately in either of its two observed conformations in different ASUs. Any other side chains with multiple observed conformations were modelled in the highest occupancy conformation. Consistent with the pH of the 1MK5 crystallization solution, histidines in the structure were modeled in the protonated form. All crystallographic waters were retained. Protonation of the proteins was performed using the tleap module of AMBER9 (34). The orthorhombic cell measured 46.3 by 93.4 by 103.9Å and its biotin-liganded protein component had zero net charge.

Figure 1.

Two views of the 1MK5 unit cell. All-atom simulations were performed on the lattice shown above, with either a pure water solvent or a model of the solution used in X-ray diffraction of the crystal. Protein backbone elements of the eight asymmetric units (ASUs) are shown in different colors; bound biotin molecules are shown in space-filling form. The eight ASUs are related by crystallographic symmetry operations, and each ASU itself contains two nearly symmetric biotin-liganded streptavidin monomers. Pairs of ASUs come together to form the biologically active tetramer (i.e. red and yellow, black and green).

Proteins in the unit cell were modeled with the AMBER ff99 force field (16,35), with improvements suggested by Simmerling and co-workers (15). Parameters for biotin were obtained from previous work by Israilev and co-workers (7). To resolve local steric clashes and optimize the initial orientations of the (now protonated) crystallographic water molecules, steepest descents energy minimization for all added hydrogen atoms and reconstructed terminal residues was performed for 2000 steps with 1000 kcal/mol-Ų harmonic position restraints on all crystallographically observed protein atoms. An additional 2000 steps of minimization were performed with no restraints. All force computations for these energy minimizations were performed with a 9.0Šcutoff on direct interactions, particle mesh Ewald long-range electrostatics (36), and tail corrections for Lennard-Jones interactions.

Cryosolution preparation

In order to solvate the 1MK5 crystal lattice in a model of the solution used in X-ray diffraction, we assumed that the mole fractions of all solution components in the crystal were the same as that of the mother liquor after the addition of cryoprotectant. This solvent for the crystal lattice is hereafter referred to as the “cryosolution.” For the actual diffraction experiments, 1 mL of the cryosolution was made by combining 350μL glycerol, 350 μL saturated ammonium sulfate solution, 200 μL 1.0 M sodium chloride, and 100 μL 1.0 M sodium acetate, titrated to pH 4.5 (29). (Larger volumes were made by scaling up these ratios; the final volume of the mixture may have changed slightly upon mixing the different components. The mass of a known volume of the cryosolution was taken to determine its true density.) To reconstruct this solution computationally, the mole fraction of water was determined by consulting the CRC Handbook of Chemistry and Physics (37) for density data on the individual salt solutions. Molar ratios of the cryosolution components are given in Table 1; parameters use to model these compounds in our simulations are given in Table S1 of the Supporting Information.

Table 1. Construction of cryosolution to fill lattice interstices.

Initially, the model unit cell consisted of the material observed in the crystal unit cell, 16 biotin-liganded streptavidin monomers and 1912 water molecules, plus reconstructed protein residues. The model unit cell was completed by adding solvent molecules in the order given above. The placement procedure for new solvent molecules is described in Methods: Unit cell preparation and the first section of the Supporting Information.

Molecular formula	Molar ratio in real cryosolution	Order of addition	Number of particles added	Initial value of Rsolv, Å
SO42−	0.0474	1	166	8.0
NH4+	0.0949	2	332	4.0
CH3COO−	0.0033	3	12	4.0
Na+	0.0100	4	35	4.0
Cl−	0.0067	5	23	4.0
CH2OHCHOHCH2OH	0.1600	6	561	2.0
H2O	1.0000	7	1593	1.5

Unit cell solvation

To add new solvent molecules to the crystal unit cell, the “AddToBox” program was written to place new solvent molecules in the interstices of the protein lattice at a distance of at least R_pro from all protein atoms and R_solv from each other. Details of this program are given in the first section of the Supporting Information.

To place cryosolution uniformly but only in the crystal interstices (any volume of the unit cell not occupied by streptavidin or biotin), R_pro was set to 3Å. Table 1 gives the precise order and protocol for solvating the system. Briefly, ions were added first to distribute them evenly throughout the crystal interstices, followed by large glycerol molecules and finally small water molecules. Although data are not presented, we found this method to be far superior to tiling a pre-equilibrated solvent box as is often done in molecular dynamics protocols. (If a box tiling method is used, larger solvent molecules are often removed due to steric clashes, meaning that they must be replaced by a secondary program such as AddToBox to maintain the proper solvent ratios. The exclusions also frustrate efforts to distribute the solvent components evenly throughout the box. In contrast, the strategy outlined above succeeds easily–see Results: Solvent Structure.) The exact amount of solvent needed was determined by repeatedly solvating the system, relaxing it as described below, and then running dynamics for up to 20ns in the constant pressure ensemble.

5000 steps of steepest descents minimization with 1000 kcal/mol-Ų restraints on all crystallographically observed protein atoms were used to relax the added solvent before beginning dynamics.

Unit cell dynamics

To relax the solvated unit cell, dynamics were performed with the unit cell fixed at its crystallographic dimensions at the crystal growth temperature of 293K and a 1.0fs integration time step, with noted exceptions. Force computations followed the protocol used in energy minimization (see Methods: Unit cell preparation). Water molecules were held in a rigid internal geometry with the SETTLE algorithm (38); all other bonds involving hydrogen atoms were constrained with SHAKE (39).

Molecular dynamics was run for 25ps with a 0.5fs time step and 1000 kcal/mol-Ų restraints on all crystallographically observed protein atoms. Restraints were then reduced to 250 kcal/mol-Ų for 50ps of dynamics, then to 62.5 kcal/mol-Ų for another 50ps of dynamics. Next, with 62.5 kcal/mol-Ų restraints on observed protein atoms, dynamics were propagated for 500ps at 500K, to aggressively sample conformations of the unobserved residues and ions. Restraints were maintained and the temperature was reduced back to 293K for another 50ps of dynamics. Restraints were then iteratively reduced by a factor of four with additional 50ps segments of dynamics until the restraint force fell below 0.0625 kcal/mol-Ų.

Unrestrained production dynamics on the unit cell were propagated in the constant pressure ensemble with isotropic position scaling at a temperature of 293K using a 1.5fs time step. A Langevin thermostat (40) with collision frequency of 3ps⁻¹ was used to maintain the temperature. Trajectories were recorded every 1.5ps for analyses. A total of 250ns of dynamics was generated for the cryosolution-solvated crystal lattice (the “cryo-solvated lattice”).

Comparison of water- and cryo-solvated unit cells

To determine the effects of the high ionic strength and significant fraction of glycerol in our model cryosolution, the 1MK5 lattice was solvated in a total of 6404 water molecules (this number includes crystallographic waters) and equilibrated as described above. Dynamics of the water-solvated lattice were propagated for a total of 250ns.

Computation of atomic fluctuations and lattice disorder

Alignment of two sets of coordinates is commonly done using quaternions (41). This method was used to compute root-mean squared deviations (RMSDs) for individual streptavidin dimers and tetramers as well as RMSDs for specific segments of each streptavidin polypeptide chain. However, to align the lattice as a whole, we restricted ourselves to removing global translations of the lattice, use of the eight I222 space group symmetry operations, and normalization of translations in these symmetry operations to compensate for minute fluctuations in the simulation cell volume. The unit cell origin was defined for each snapshot in our trajectory as the point which, after crystallographic symmetry operations were applied, minimized the mass-weighted squared deviations in atomic positions for the eight ASUs. This method of alignment, which better approximates the data obtained in X-ray diffraction studies, was also used for determining atomic fluctuations.

It must be noted that X-ray diffraction data for the 1MK5 crystal were collected after flash-freezing with liquid nitrogen, but our simulations were conducted at the crystal growth temperature of 293K. Because the AMBER ff99 force field is not known to be valid at cryogenic temperatures, we did not have an adequate method to simulate the freezing process. All atomic fluctuation and lattice RMSD measurements were therefore done with coordinates extracted directly from the simulations at 293K.

Results

Cryosolution modeling

Most of the challenges in simulating protein crystal lattices relate to modeling the crystallization solution. Therefore, we will describe our efforts to validate this aspect of our simulations at some length. The crystallization solution used to prepare the biotin-liganded streptavidin crystal contained roughly 4.8 M ionic particles, more than ten times the physiological concentration. The solution used for crystallographic data collection (the “cryosolution”) contained 35% glycerol by volume as a cryprotectant (see Table 1). Simulation of ammonium sulfate by atomistic, fixed-charge force fields is, to our knowledge, without precedent, and few examples of simulations with such high ionic strengths are available. Also, though the glycerol model we chose was designed for use with AMBER fixed-charge potential functions, the combination of this model with the SPC/E water model has not been tested before.

Thermodynamic data such as heat capacities or isothermal compressibilities for aqueous solutions of the various cryosolution components are seldom available. However, specific gravities for all these solutions are known in detail (37). We therefore collected density data from simulations of each cryosolution component in water at a range of concentrations. Each simulation consisted of at least 512 water molecules with one cryosolution additive, and the simulation protocol matched that used in dynamics of the crystal lattices (see Methods: Unit cell preparation and Unit cell dynamics). The results are given in Figure S1 of the Supporting Information. Briefly, the density curve for aqueous glycerol solutions is reproduced correctly but densities of concentrated ionic solutions are overestimated by up to 18%, the worst case being a saturated ammonium sulfate solution. From another perspective, the constriction of water by electrolytes is overestimated by 20% to 70%, depending on the types of ions. Overall, however, error in the complete cryosolution is much lower. Experimentally, the density of the cryosolution was 1.21 ± 0.01 g/mL (the uncertainty was extrapolated from uncertainties of measuring pipets used to construct the solution, assuming independence of errors in mass and volume measurements), while a 20ns simulation of the cryosolution at constant pressure gave a density of 1.236 ± 0.001 g/mL (the uncertainty was determined by block averaging over the final 5ns of simulation).

Reproduction of the densities of binary mixtures does not guarantee that two models are compatible. By erroneously forming two separate phases in a simulation, two fluids could reproduce a linear density curve like the one for water and glycerol in Figure S1. To check the miscibility of our water and glycerol models and to assess the solubility of our ammonium sulfate model in SPC/E water, we ran simulations of 2048 water molecules and enough glycerol or ammonium sulfate to meet the cryosolution composition. As shown in supplemental data, these simulations demonstrated that the glycerol and water models are miscible in the amounts used to make the cryosolution; however, simulations of 35% saturated ammonium sulfate showed that the salt formed amorphous aggregates in SPC/E water, suggesting that it had precipitated.

Although SPC/E does not behave well in conjunction with ammonium sulfate, it is one of a limited number of water models compatible with the long-range electrostatics corrections used in our simulations and it reproduces thermodynamic properties of pure water quite well (42). To compare SPC/E to another water model, we tried similar tests with TIP3P Ewald parameterization F (43) (results in Supporting Information). These tests showed very little glycerol:water miscibility; instead, separate glycerol and water phases were formed. Simulations of ammonium sulfate in TIP3P-F resulted in the formation of even more tightly constricted aggregates, suggesting that the salt was even less soluble in TIP3P-F than in SPC/E. The original TIP3P model (44) also proved miscible with glycerol, but it was no more effective as a solvent for ammonium sulfate than SPC/E; more importantly, Ewald electrostatics are detrimental to its reproduction of pure water properties (43). We therefore concluded that, although not ideal, the SPC/E water model was a reasonable choice to use with the other major components of the model cryosolution.

As mentioned above, a 20ns simulation of a sample of the complete cryosolution (over 17,000 atoms) was performed to assess its structure and density. The lengthy simulation time was necessary to arrive at an equilibrium structure for this mixture. In the equilibrated cryosolution sample, ammonium sulfate formed an aggregate in the water and glycerol mixture, with sodium cations condensed on the surface of the aggregate (see Figure S6 in the Supporting Information). Chloride and acetate ions were found throughout the cryosolution, indicating that they are much more soluble in the glycerol and water. In summary, the ammonium sulfate was no more soluble in a glycerol:water solution than in pure water, but the SPC/E water still mixed with glycerol in the presence of the highly polar surface of the ammonium sulfate aggregate and other soluble ions. To examine how soluble the various salts really are once glycerol is added to the crystallization solution, we created a series of cryosolutions with the same salt concentrations but different percentages of glycerol. We found that glycerol could constitute more than 50% of the volume of the real cryosolution before precipitating salt crystals; however, replacing 45% or more of the water in a 50% saturated ammonium sulfate solution did precipitate salt (data not shown).

We also wanted to quantify the dynamics of the model cryosolution. Because the majority of the ions in the cryosolution formed an amorphous aggregate, however, and because diffusion coefficients are not known for the complete cryosolution, we only measured the mobility of water molecules in a 35% glycerol solution as well as the self-diffusivity of the model glycerol in its pure form. To compute these diffusion coefficients, we simulated a solution of 1024 water molecules and 136 glycerol molecules and a separate solution of 256 glycerol molecules alone in the constant volume, constant-energy ensemble with a mean temperature of 298K. The correct volume for each simulation, as well as an equilibrium starting configuration, was determined by prior simulations at constant temperature and pressure. The mobility D of water was computed by the Einstein diffusion equation (Equation 1) in three dimensions, where r_i(t) represents the position of the center of mass of particle i at time t:

$$D=\frac{{\displaystyle \sum _i}{({\mathbf{r}}_i(t+\mathrm{\Delta }t)-{\mathbf{r}}_i(t))}^2}{6\mathrm{\Delta }t}$$ (Equation 1)

The SPC/E water model is known to have a very accurate self-diffusion constant of 2.43 ×10⁻⁵ cm²/s (42) at 298K. While the computed glycerol self diffusion coefficient, 0.031 × 10⁻⁵ cm²/s, was more than an order of magnitude higher than the true value of 0.00126 × 10⁻⁵ cm²/s (45), it was nonetheless very small in comparison to that of water. The mobility of water molecules decreased by nearly a factor of three in solution with the glycerol, to 0.87 × 10⁻⁵ cm²/s (we could not find a suitable experimental value for comparison).

Simulating the multicomponent cryosolution was indeed a challenge, and there are clearly some unresolved problems that remain to be addressed. Despite some difficulty reproducing the ionic solution densities, however, the overall simulation error in the cryosolution density was only 3%. The two most significant components of the cryosolution, water and glycerol, appear to be compatible to the extent we have tested them. The outstanding problem of ammonium sulfate precipitation will be addressed in the context of our simulations of the crystal lattice.

Trajectory stability

Stability of the simulated cryosolution- and water-solvated crystal structures (hereafter, the “cryosolvated” and “water-solvated” lattices) was assessed at four levels: convergence of simulation cell volume, mass weighted backbone atom root mean squared deviation (bkRMSD) of the eight individual ASUs (asymmetric units; biotin-liganded streptavidin dimers as shown in Figure 1), bkRMSD of the four tetramers (each composed of two ASUs), and bkRMSD of the entire lattice. For bkRMSD calculations and other analyses of the trajectory, we considered only those atoms observed in the 1MK5 structure; none of the reconstructed pieces of each protein entered our calculations except via the indirect effects that their presence may have had on the protein atoms observed in the 1MK5 structure.

During our simulations, the volume of the simulation cell was allowed to fluctuate under a constant external pressure of one atmosphere as shown in Figure 2. This was done to avoid the formation of vacuum bubbles or internal stresses that could accumulate over the lengthy simulation time, but maintenance of the correct unit cell volume was also an essential part of our simulation setup.

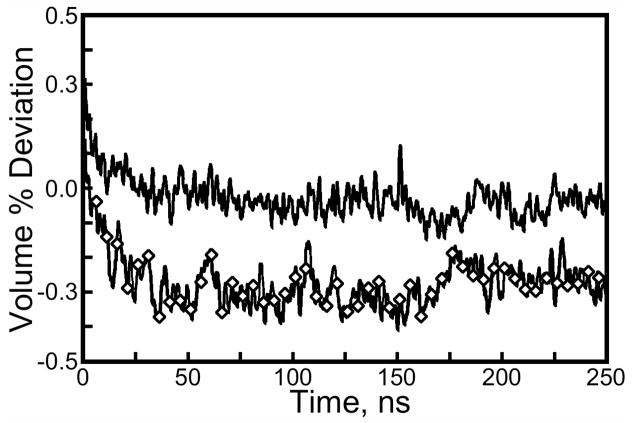
Figure 2.

Volume of the lattice simulations as a function of time. Volume is plotted as a percentage deviation from the experimental box volume, 46.3Å by 93.4Å by 103.9Å. Line with diamonds: cryosolvated lattice; plain line: water-solvated lattice. Isotropic rescaling of the volume was used to simulate each lattice in the constant pressure ensemble. Comparison of isomorphous streptavidin crystals (see Results: Trajectory stability) gives an estimate of 0.5% for the experimental uncertainty of the box volume. The volume of both simulations takes roughly 40ns to stabilize.

After the beginning of dynamics in the constant-pressure ensemble, both simulations showed a slight rise in volume followed by a slow collapse. Even with numerous trial runs with varying amounts of solvent (data not shown), it was difficult to maintain the correct simulation volume due to the long equilibration time of this parameter. After 40ns of simulation, the volume of the cryo-solvated lattice settled at 0.3% below the unit cell volume given in the crystal structure. Put simply, the isotropic box rescaling made the longest (103.9Å) edge of the unit cell 0.1Å shorter as the volume equilibrated; the 1500ų disparity between simulation and experiment is roughly equal to the volume of 30 water molecules, 5 glycerol molecules, and one ammonium sulfate molecule. To estimate the experimental uncertainty in unit cell volume, we computed the unit cell volume standard deviation for isomorphous streptavidin crystals 1MK5, 1LUQ, 2F01, 2GH7, and 1DF8: this deviation comes to 0.5% of the mean, larger than the error obtained from our simulation. The water-solvated lattice settled at nearly exactly the experimental volume, in roughly the same amount of time as the cryo-solvated lattice.

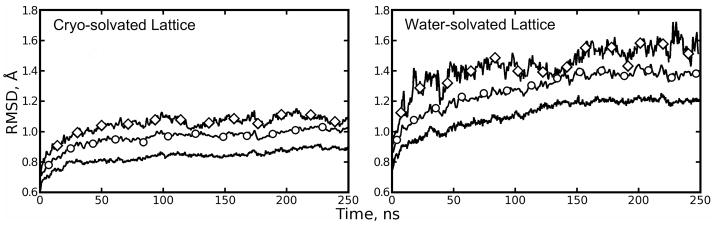
It was also important to monitor convergence of the distribution of microscopic structures in each simulation. For the dimers and tetramers, bkRMSD was measured using quaternion alignments of each dimer or tetramer to the X-ray structure configuration. However, bkRMSD of the entire lattice was measured using crystal symmetry operations for alignment as described in Methods: Computation of atomic fluctuations and lattice disorder. The results of these three analyses are shown in Figure 3. In both simulations, the bkRMSD of the tetramers is slightly greater than that of their component dimers, and the lattice bkRMSD is greater than that of the tetramers by roughly the same amount. When compared to the water-solvated lattice, the cryosolvated lattice shows 30% lower bkRMSD for dimers and tetramers, and 20% lower bkRMSD for the lattice as a whole.

Figure 3.

Backbone root mean squared deviations (bkRMSDs) of lattices and lattice components relative to the 1MK5 structure. Plain line: average bkRMSD for each lattice’s eight asymmetric units (ASUs). Line with circles: average bkRMSD for four streptavidin tetramers (2 ASUs per tetramer). Line with diamonds: bkRMSD for the lattice as a whole. Quaternion alignment was used to determine RMSDs for ASUs and tetramers. A more restricted alignment procedure was used to compute the RMSD of each lattice as a whole (see Methods: Computation of atomic fluctuations and lattice disorder). The cryo-solvated lattice shows much lower overall RMSD than the water-solvated lattice; the differences may increase with further simulation.

Although the cryosolution may have taken many nanoseconds to equilibrate (see Results: Cryosolution modeling) versus the ps correlation times of pure SPC/E water (46), the cryo-solvated lattice reaches its equilibrium volume as rapidly as the water-solvated lattice. The three measures of bkRMSD appear to have stabilized for both lattices. Despite the flaws noted in Results: Cryosolution modeling, the model cryosolution appears to stabilize the 1MK5 crystal structure, better than a pure water alternative, on many levels. We next examined whether this stability is maintained as the proteins fully sample their accessible conformational space or if the cryosolution simply slows protein movement to give the illusion of stability.

Sampling efficiency of each lattice

Given the reduced mobility of water molecules in glycerol solutions and the high concentration of ions in the cryosolution (see Results: Cryosolution modeling), analysis of protein mobility in the cryo-solvated lattice is essential.

However, because we expect the protein to move very little in its crystal lattice, a small range of motion would not immediately suggest that the proteins in the lattice were artificially restricted. Rather, three questions must be answered, all of them concerning the lattice’s ASUs, which again are its symmetry-related chains, dimers of biotin-liganded streptavidin proteins. First, how rapidly do the ASUs sample local regions of conformational space if the lattice is solvated with cryosolution as opposed to pure water? Second, how far do the ASUs’ conformations diverge from their own conformations in some length of time Δt? Third, do the ASUs move as far from each other as they do from their own initial conformations?

To address these questions, we first reduced the data set by extracting snapshots at 250ps intervals starting from 25ns to the end of each trajectory.

To answer the first and second questions, we calculated the quantity Γ, given by Equation 2 where i runs over the eight asymmetric units, j runs over all crystallographically observed backbone atoms of an ASU, r denotes position and m denotes mass:

$$\mathrm{\Gamma }(\mathrm{\Delta }t)=\frac{1}{8}\sum _{i=1}^8\sqrt{\frac{1}{\sum _{j=1}^N{m}_j}\sum _{j=1}^N{m}_j{\left[{\mathbf{r}}_j(t_0+\mathrm{\Delta }t)-{\mathbf{r}}_j(t_0)\right]}^2}$$ Equation 2

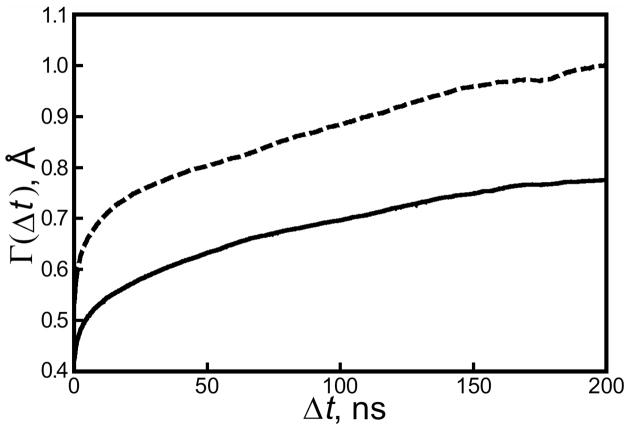
In essence, Γ measured the average bkRMSD accumulated by ASUs in some length of time Δt. As shown in Figure 4, neither the cryo-solvated nor the water-solvated lattice has reached the limiting value of Γ within the length of time of our simulations. However, Figure 4 does show that ASUs in the cryo- and water-solvated lattices can be expected to eventually accumulate at least 0.75 or 0.95Å bkRMSD, respectively, starting from any time in the simulation. Both of these values approach but are lower than average bkRMSD accumulated by ASUs since the beginning of each trajectory, given in Figure 3.

Figure 4.

Accumulated backbone RMSD for the buffer- and water-solvated crystal lattices. Backbone RMSDs were computed for asymmetric units of each lattice using their conformations from 250ps snapshots in the trajectory as reference structures (solid line: cryo-solvated lattice; dashed line: water-solvated lattice). The value of, Γ defined in Equation 2, shows the average bkRMSD of an asymmetric unit relative to some reference state in the simulation after a length of time Δt. Figure 3 gives an estimate of 0.9Å for the maximum divergence of the cryo-solvated lattice from the 1MK5 structure, but neither simulation is yet long enough to estimate the maximum divergence of either lattice from an arbitrary point in its trajectory.

To answer the third question, we computed the average bkRMSD of all ASUs with respect to their neighbors as a function of time (see Figure S7 of the Supporting Information). The cryo-solvated ASUs tended to diverge more from one another than they did from their own initial conformations, whereas in the water-solvated lattice this situation is reversed. It is also possible to compute an average structure for all ASUs over a large portion of the trajectory in each simulation, and use that to determine the spread of conformations. The mean bkRMSD of all ASUs to the average structure was 0.45Å in the cryo-solvated lattice and 0.56Å in the water-solvated lattice.

These results suggest that the water-solvated lattice does sample atomic positions faster than the cryo-solvated lattice, but only in absolute terms. The ratio of Γ values for each lattice at some time Δt, given in Figure 4, is comparable to the ratio of the lattices’ deviations from the 1MK5 structure shown in Figure 3, as well as to the ratio of their deviations from an average structure, meaning that both protein lattices sample atomic positions at the same rate relative to the sizes of their conformational spaces. The fact that ASUs diverge more from one another than from their initial conformations if they are solvated with the heterogeneous cryosolution, but not if they are solvated with pure water, raises a question of whether the cryosolution retains significant inhomogeneity throughout the simulation, despite our efforts to distribute it evenly (see Methods: Unit cell solvation). This issue is addressed in Results: Solvent structure.

Completeness of the protein trajectory

In 1995, Clarage and co-workers reported that ns-scale molecular dynamics simulations are likely sufficient to sample the average positions of atoms but not to sample higher moments of their distributions (11). Later studies (9,10) noted that the isotropic atomic fluctuations obtained from their simulations were lower than those obtained experimentally, implying that not even atomic position distributions were adequately sampled in ns-scale MD simulations. To follow on these previous studies and potentially settle some of the questions, we computed isotropic atomic fluctuations for backbone C_α atoms to measure the sampling of atomic positions. We also performed principal component analysis (PCA) (47) for the protein C_α atoms of each asymmetric unit to investigate convergence of the trajectories.

Atomic root mean squared (RMS) fluctuations were measured by aligning the eight asymmetric units of the simulation cell as described in Methods: Computation of atomic fluctuations and lattice disorder. We chose to measure RMS fluctuations and compare to the square roots of crystallographic isotropic B-factors because the unit of RMS fluctuation, length, corresponds to our measurements of bkRMSD. The conversion is simply (48):

$$F=\sqrt{\frac{3}{8{\pi }^2}B}=\sqrt{\frac{B_a+B_b+B_c}{8{\pi }^2}}$$ Equation 3

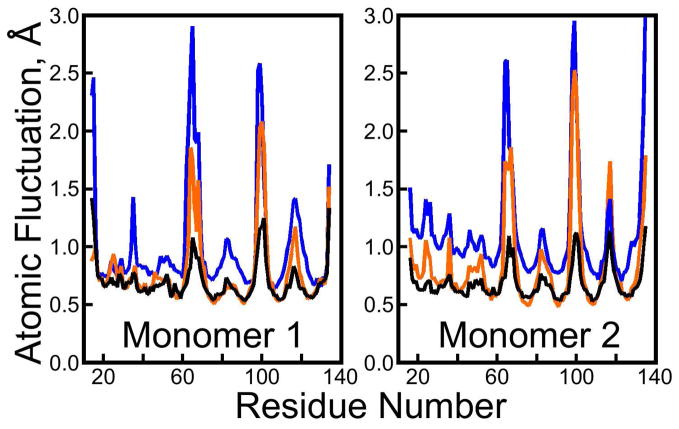
where F is the atomic RMS fluctuation and B is the isotropic B-factor obtained by averaging the anisotropic B-factors denoted B_a, B_b, and B_c, which are themselves eigenvalues of the atomic distribution tensor obtained from X-ray diffraction studies. To analyze our simulations, fluctuations were computed only for segments of trajectory with a reasonably convergent value of bkRMSD for the entire lattice (see Figure 3): 50ns onward in each simulation, and for atoms observed in the 1MK5 structure (no fluctuations were analyzed for unobserved segments of the structure, although these atoms were reconstructed by alignment with other streptavidin crystal structures as described in Methods: Unit cell preparation). As shown in Figure 5, isotropic RMS fluctuations obtained from the cryo-solvated lattice are correlated with root isotropic B-factors from the 1MK5 crystal structure (Pearson correlation coefficient 0.82). The correlation increases to 0.88 if residues Glu 14 and Ala 15 are omitted; these N-terminal residues are not highly active in the cryo-solvated lattice but have among the highest B-factors in the 1MK5 structure. Contrary to previous studies, the magnitudes of atomic fluctuations observed in the cryosolvated simulation are nearly identical to those seen experimentally in the most stable regions of the protein, and somewhat greater in the flexible loop regions. One contribution to the fluctuations not present in a solution-phase simulation (9) is the “lattice disorder,” which arises because the lattice is not ideal in the positions and orientations of each ASU nor in terms of the conformations of individual ASUs (see Figure 3 and Figure S7 of the Supporting Information). We were careful to use only the symmetry operations of the I222 space group to align the ASUs for computing atomic fluctuations; had we followed the protocol used in solution phase simulations (to align them optimally against one another and perform quaternion rotations), the fluctuations in the most stable regions of the protein would have been somewhat smaller. The greater fluctuations observed in this study as opposed to previous lattice simulations (10) may arise from the use of a larger lattice and longer simulation times.

Figure 5.

Isotropic atomic root mean squared fluctuations from crystallography versus simulations. Atomic RMS fluctuations are plotted for crystallographically observed C_α atoms in the 1MK5 structure. Black line: experiment; orange line: lattice simulation with cryosolution; blue line: lattice simulation with pure water solvent. Experimental isotropic RMS fluctuations were obtained by dividing crystallographic B-factors by 8π²/3 and taking the square root. The cryo-solvated lattice shows better reproduction of the atomic fluctuations, but both simulations predict the most active loops of the streptavidin to fluctuate much more than is evident from 1MK5 structure.

RMS fluctuations obtained from the water-solvated lattice simulation are not as highly correlated with values in the 1MK5 crystal structure (correlation coefficient 0.78). This correlation is worsened by omission of terminal residues, all of which were highly active. Generally, fluctuations of the most stable core regions of the protein are larger in the water-solvated lattice, but as shown in Figure S8 of the Supporting Information these β-barrel cores of each streptavidin monomer (see Figure 1) are equally stable in both simulations. The higher fluctuations of stable regions in the water-solvated lattice instead reflect a higher degree of lattice disorder.

As shown in Figure 1, the ASU contains two biotin-liganded streptavidin monomers; in terms of backbone structure, crystal packing, and solvent exposure, the environment of each monomer is practically identical (result not shown), but asymmetry still exists between the two halves of the ASU in the 1MK5 crystal structure. Residues 117 to 122, a loop region sitting next to a short α-helix and bearing the Trp120 residue that strengthens the interaction between streptavidin proteins in the biologically active tetramer, display higher B-factors in the second monomer than in the first. The cryosolvated lattice recovers the correct asymmetry, but the water-solvated lattice gives identical RMS fluctuations for this loop region in each monomer. Figure S13 illustrates some of the movements that contribute to the asymmetric fluctuations.

It must be acknowledged that regions of the protein displaying high B-factors in the 1MK5 structure tend to display much greater RMS fluctuations in either simulation than are seen experimentally, though most of these regions are less active in the cryo-solvated lattice than the water-solvated lattice. As shown in Figures S10, S11, S12, and S13 of the Supporting Information, these regions are all loops and exposed to solvent in the crystal lattice.

In X-ray diffraction studies, it is not possible to discern whether the microscopic fluctuations contributing to a particular B-factor were small and frequent, large and rare, or something in between. The temperature difference between our simulations and the X-ray diffraction studies could also play a role: our simulations were conducted at 293K while the X-ray data collection was performed at cryogenic temperatures. We have assumed the crystal reached an equilibrium set of conformations before flash-freezing, and that flash-freezing generally has no effect on the protein conformations, although there is evidence against the second assumption (49). To investigate this further, we examined seven other streptavidin crystals isomorphous with 1MK5 to compare four structures from X-ray diffraction at 100K to four at room temperature. The results in Figure S9 of the Supporting Information show that, while there is a slight increase in the fluctuations of these three loops if the data collection is done at room temperature, fluctuations obtained from the simulation are still somewhat higher. We can therefore reasonably conclude that, while our inability to simulate flash freezing does account for some of the discrepancy in the atomic fluctuations of loop regions, other factors (including inaccuracies of the underlying model) must also play a role.

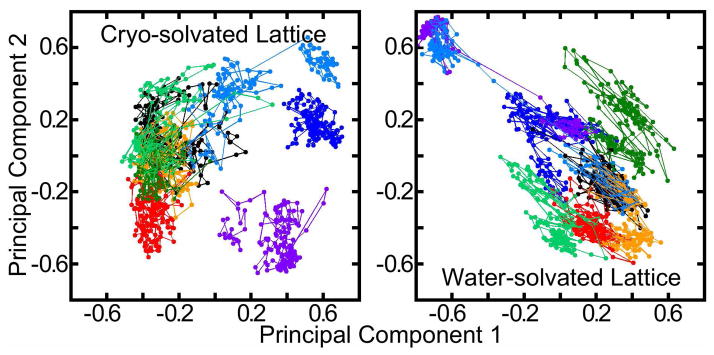
Beyond measurements of atomic distributions and fluctuations, the covariance of atoms can be analyzed to provide new tools for decomposing the motions of molecular structures. Principal component analysis (PCA) was performed by extracting crystallographically observed C_α atoms for each of the eight ASUs from 25ns onward in the trajectories of the cryo- or water-solvated lattices. This defined eight separate trajectories, all of which were pooled to obtain a common set of principal components for each lattice. Projection of the principal component vectors onto the molecular coordinates showed, as expected, that the motions represented by the largest principal components occurred primarily in the solvent-exposed loop regions (see Figures S14 and S15 of the Supporting Information). The evolution of each ASU along the first and second of these principal components is plotted in Figure 6.

Figure 6.

Principal component analysis for eight lattice asymmetric units (ASUs). Projections of the trajectories of the cryo- and water-solvated ASUs onto their first and second principal components are shown in different colors. Principal components were computed for all eight ASUs of each lattice simultaneously for snapshots at 15ps intervals from 25ns onward in each trajectory. For clarity, projections are averaged over 100 consecutive snapshots. Displaying projections from all snapshots would widen the spread of each trajectory; this plot may understate the degree of overlap between trajectories of the eight ASUs.

Based on time-resolved Mössbauer studies of protein crystals, Clarage and co-workers (11) estimated 100ns as the maximum time period for a protein crystal lattice trajectory to “orbit back” on itself in principal component space and “begin defining a Boltzmann distribution of conformations.” Indeed, with nearly 2 μs of pooled data for either lattice, we find numerous overlaps between trajectories of two or more ASUs, suggesting that both systems’ trajectories have begun to converge. However, we stress that these two principal components represent only 26% of the motion in either lattice; in higher dimensions the degree of overlap is certainly not as good. The non-convergent values of Γ in Figure 4 coupled with the convergent values of backbone RMSD in Figure 3 suggest that the degree of overlap between the trajectories of ASUs in either lattice will continue to grow if the simulations continue.

Solvent structure

The only solvent particles observed in the 1MK5 crystal structure are water molecules, despite the highly ionic nature of the crystallization solution and the glycerol content of the cryosolution. The crystal structure contains 239 water molecules, or 1912 when symmetry-related copies are included; this accounts for nearly 55% of the water molecules in our simulation. Moreover, as noted in Results: Cryosolution modeling, the ammonium sulfate precipitated from our model water:glycerol solution. It is therefore worthwhile to analyze the distributions of solvent particles obtained from our simulations to see whether they are consistent with the experimental observations. Furthermore, although we did not find evidence that the initial simulation setup biased the trajectories of individual ASUs, it is worthwhile to explicitly check for solvent inhomogeneity over the course of the simulation.

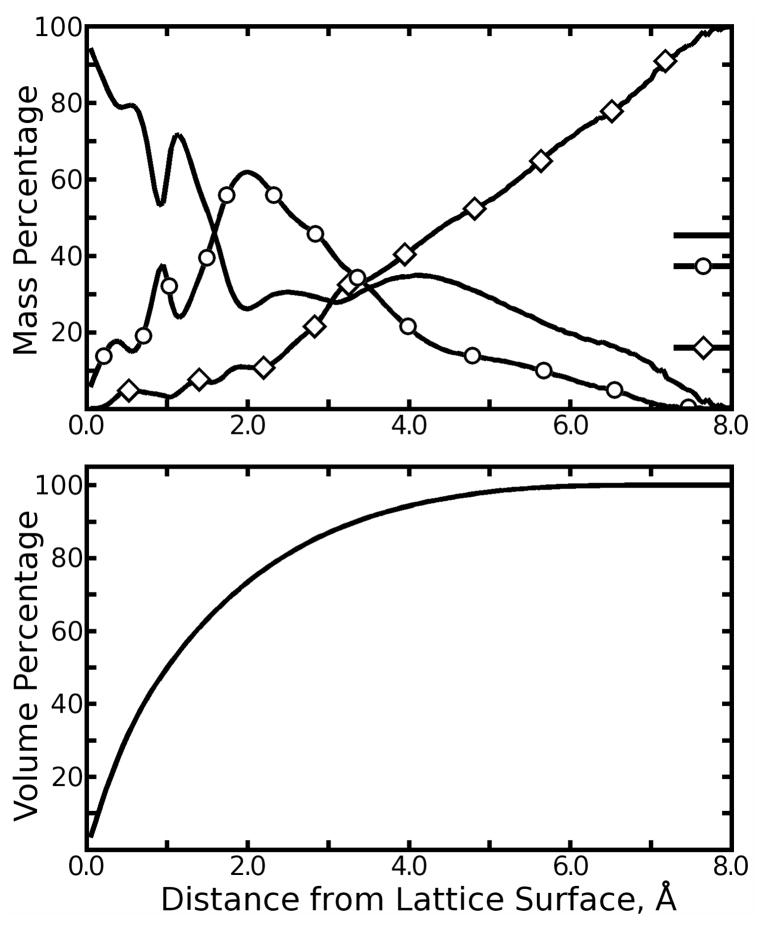
As was done in a previous study (50), the surface of the protein lattice can be defined by the Lennard-Jones σ parameters for all biotin and streptavidin atoms. Plotting the mass fraction of individual cryosolution components as a function of distance from the lattice surface, as shown in Figure 7, suggests three major layers in the cryosolution, dominated by water, glycerol, and ammonium sulfate, respectively. Cryosolution within 1.7Å of the protein surface was disproportionately composed of water with some glycerol; this layer contained roughly 70% of the water in the entire simulation. The next layer, 1.7 to 3.6Å from the protein surface, accounted for over 50% of the glycerol in the simulation. The final layer, further than 3.6Å from the lattice proteins, contained increasing concentrations of ammonium sulfate; beyond 4.6Å from the protein surface, ammonium and sulfate accounted for more than half of the solvent by mass. For reference, the proportion of the total interstitial volume within some distance r of the lattice surface is also plotted in Figure 7.

Figure 7.

Mass distributions for major cryosolution components. In the top panel, the total mass of solvent at a particular distance from the biotin/streptavidin surface was computed and then separated into contributions from all crysolution components (only the most significant three are plotted). Water: plain line; glycerol: line with circles; ammonium sulfate: line with diamonds. The mass of each component as a percentage of the solvent as a whole is marked on the right vertical axis. In the bottom panel, the total percentage of interstitial volume within some distance of the lattice proteins’ surface is plotted to reveal how much of the entire solvent each segment of the plots in the top panel respresents.

To assess the total amounts of cryosolution components around each ASU, we defined polyhedra consisting of the union of Voronoi polyhedra (51) for all protein atoms of each ASU, so that the unified polyhedron of each ASU contained very nearly one eighth of the volume of the simulation cell (all points closer to some atom of protein in that ASU than to protein atoms in any other ASU). We then counted the number of particles of each solvent species lying in each ASU’s polyhedron throughout the cryo-solvated lattice simulation. To quantify differences, we considered random, independent assignment (RIA) of N objects to eight identical bins and computed a mean standard deviation for the number of objects to fall in each bin, as well as a standard deviation for the standard deviation as an error bound; any counts above the error bound for RIA were considered asymmetries in the solvent distribution. The results in Table 2 show that, initially, only water was partitioned asymmetrically. By the end of the simulation, no species showed asymmetric partitioning and glycerol was more evenly distributed than RIA would predict. This may reflect the tendency of SPC/E water to mix with glycerol as shown in Results: Cryosolution modeling or perhaps ordering of the solvent by the individual ASUs.

Table 2. Cryosolution Partition Among the Eight Asymmetric Units.

Solvent particles were assigned to the nearest asymmetric unit (ASU) as described in the main text. The mean number of particles per ASU is trivially the total number of particles given in Table 1 divided by eight.

Species	Mean STD, First 10nsa	Mean STD, Final 10ns	Expected STD
Water	33.2 ± 2.5	24.0 ± 3.2	20.2 ± 5.5
Glycerol	8.0 ± 0.8	5.8 ± 1.0	8.1 ± 2.2
NH4+	4.7 ± 0.3	6.7 ± 0.6	6.2 ± 1.7
SO42−	2.2 ± 0.3	3.5 ± 0.7	4.4 ± 1.2
Na+	1.8 ± 0.3	1.7 ± 0.1	2.0 ± 0.5
Cl−	1.4 ± 0.1	1.3 ± 0.3	1.6 ± 0.4
CH3COO−	1.4 ± 0.2	0.8 ± 0.1	1.2 ± 0.3

^aStandard Deviation of the number of particles per ASU; the standard deviations of the standard deviation is given for the error of measurement.

^bThe expected standard deviation for random, independent assignment of N objects to identical bins.

To characterize the cryosolution’s water and glycerol distributions at a higher level of detail, we computed the solvent density surrounding the ASU. After each of the eight ASUs from any 1.5ps snapshot was aligned directly against the coordinates from the 1MK5 crystal cell, the positions of water and glycerol atoms were mapped to grids by trilinear interpolation, weighting each atom by its atomic number. This created a three-dimensional histogram to approximate the electron density expected given the solvent distribution in the cryosolvated lattice simulation. This density is shown from three perspectives in Figures S16, S17, and S18 of the Supporting Information. From these images, it is clear that water and glycerol tend to occupy distinct regions near the protein surface, and that water does occupy numerous sites in the simulations where it was observed in the crystal. However, some of the crystallographic water positions correspond to regions of high glycerol density in our simulations. The best view of glycerol binding to any streptavidin protein in this crystal space group is provided by a recently completed structure of a circular permutation mutant (unpublished results, 1.00Å resolution, R=0.117, R_free=0.143). Three glycerol molecules (two unique, one disordered) are located near the protein surface. Therefore, while some glycerol may penetrate into the protein’s first solvent layer, crystallographic results do not support the extent of penetration seen in our simulations. Other crystallographic water sites are not highly populated with either water or glycerol, but these tend to be clustered around the highly active loops (see Results: Completeness of the protein trajectory); the higher fluctuations in these regions of the protein likely smear out the surrounding solvent density so that neither water nor glycerol can become concentrated at particular sites.

To quantify the amounts of water or glycerol near crystallographic water sites, we computed the mean density of each cosolvent within 1.4Å of each site. We compared these densities to the average density of each cosolvent throughout the ASU’s first solvent layer, the region of space within 3Å of the ASU’s van-der Waals surface. As shown in Figure S19, more than 80% of the crystallographic water sites corresponded to elevated water density in our simulations. Conversely, the simulated glycerol density was depressed in more than 50% of the crystallographic water sites.

In summary, the crysolution takes on a complex structure around the protein lattice, even though most of the solvent was partitioned randomly at the beginning of the simulation. The asymmetric partitioning of water at the outset of the simulation may have pushed the cryo-solvated ASUs into different regions of the principal component space (see Figure 6). However, because 20 water molecules represent only 4% of all the water around each streptavidin dimer, the initial imbalance was not severe. Given the questions surrounding the unexpectedly large fluctuations in certain loops of the protein, any imbalances in our initial setup would seem much less problematic than the possible sources of these fluctuations discussed in Results: Completeness of the protein trajectory. The distribution of solvent relative to the protein surface is macroscopically consistent with crystallographic results in that the bulk of the water is found near the lattice proteins, and also consistent microscopically in that most crystallographic water sites do correspond to regions of elevated water density in our simulations.

Discussion

Cryosolution modeling

The purpose of this study was to simulate a protein crystal with an atomistic forcefield and atomistic representation of the cryosolution used to solvate the crystal during X-ray diffraction. Our results show that modeling complex solvent mixtures can be quite challenging. We also examined three candidate water models for the cryosolution simulation; each gave different results for properties of pure water and showed different propensities to dissolve glycerol and ammonium sulfate (see results in the Supporting Information). Even the best of these water models, SPC/E, still performed poorly in terms of reproducing the known densities of ionic solutions (see Figure S1 of the Supporting Information). However, the complete model cryosolution, with a considerable fraction of glycerol, displayed only a 3% error in the simulated solution density versus experiment.

Many qualitative results suggest that, despite the difficulties noted in Results: Cryosolution modeling and the Supporting Information, the model cryosolution performs well as a solvent for the protein lattice. The layering of solvent with respect to the protein (see Figure 7) reflects experimental observations that proteins are preferentially hydrated rather than glycerated (24), but that some glycerol may still bind to the protein surface (25). In the 1.4Å 1MK5 structure, water and glycerol could not be distinguished with confidence, even though glycerol does appear in lower resolution structures in the Protein Data Bank. While higher resolution structures of the biotin:streptavidin complex do not support the amount of glycerol found near the protein surface in our simulations, water was concentrated at the majority of the crystallographic water sites. Furthermore, the fact that ammonium sulfate is concentrated in the lattice interstices may not be unrealistic. As noted in Results: Cryosolution modeling, adding glycerol does reduce the solubility of ammonium sulfate in water. The process of precipitating proteins with ammonium sulfate rests on the fact that ammonium sulfate also competes with proteins for contact with water molecules in aqueous solutions. In general, crystals form as protein solutions slowly pass saturation. Therefore, while the precipitation of ammonium sulfate in pure water and in the model cryosolution was incorrect, its aggregation in the crystal interstices might only be unrealistic in that the tendency to aggregate was too strong, driving the formation of salt “crystals” rather than a dynamic equilibrium of transient salt clusters.

Our results also illustrate some of the challenges that remain for parameterizing accurate and reliable potential functions for water and other solvents. Much research in molecular mechanics is devoted to binding energy calculations (4,5,7), and parameter development for the underlying potential functions has often focused on reproducing binding or hydration energies for immersion of solutes from a gas-phase reference state. It may be an equally important task from the standpoint of parameterization, but more computationally tractable due to vastly improved sampling, to attempt to compute heats of mixing for binary solutions. Explicit treatment of electronic polarization is one means of improving the transferability of molecular models (see discussion below). Other solution-based force fields, based on Kirkwood-Buff theory for binary mixtures, are also in development (52).

Furthermore, it should be pointed out that the overwhelming majority of protein simulations solvate polypeptides in pure water and take a stable protein as one indication of the reasonableness of the model. In such cases, two distinct phases, water and protein, are defined from the beginning of the simulation, but it could easily be that the water and protein models are energetically imbalanced and merely remain in two phases separated by an unrealistic amount of energy throughout the simulation. Work by Shirts and colleagues (53) provides some reassurance that amino acid hydration free energies can be obtained accurately with current molecular mechanics models, finding in fact that the original TIP3P, when used with long-range corrections, is among the best. However, those studies took an isolated solute as the reference state for computing the hydration free energy. It remains to be seen whether many molecules of some highly soluble amino acid such as alanine would mix with water, give the correct hydration free energy and heat of dilution, and reproduce the densities of solutions with a range of concentrations. In sum, the field of molecular mechanics has succeeded many times in performing stable and informative simulations on systems that are expected to remain biphasic, but our results clearly show that challenges remain to properly simulate systems which are required to mix.

Implications of lattice trajectory results for molecular dynamics

Although previous studies of protein crystals have used only water to solvate the proteins, our results in Figures 3 and 5 clearly show that this is not an equivalent approach to modeling the solution used in X-ray diffraction. This study presents only one example, but it is encouraging that a more rigorous representation of the experimental conditions in our simulations yields results that are in much better agreement with experimental data.

Crystal lattice simulations with rigorous reproduction of the experimental conditions could help guide the parameterization of molecular force fields, in the same way that NMR studies of the “Trp cage” protein helped improve the AMBER ff99 force field (15). Previous work along these lines (10) focused on pure water solvents and adjusting many parameters simultaneously with thousands of simulations. Use of the model cryosolution in this study appears to have provided significantly more improvement than optimization of force field parameters without attention to details of the solvent. Furthermore, our results show that very lengthy simulations are needed to obtain convergent values of backbone RMSD and lattice disorder; any efforts to parameterize force fields using crystal simulations should therefore be guided by small numbers of thorough simulations on carefully selected crystal structures (i.e. diffraction at physiological temperature and solvent conditions that can be accurately reproduced). Regarding Figure 5, a challenging goal would be to reproduce experimental structures with high accuracy while simultaneously obtaining the correct isotropic fluctuations, particularly in cases of protein loops with high B-factors. The delicate balance of energy states needed to solve such a problem may be fundamental to protein folding and function.

Towards more accurate lattice simulations

This study presents, to our knowledge, the most detailed simulation of a protein crystal lattice to date. Overall, it appears that our effort to reproduce the crystallization conditions was worthwhile, since the model cryosolution stabilized protein conformations nearer to the 1MK5 structure, gave better reproduction of the atomic fluctuations, and produced more convergent sampling of the conformational space than a pure water solvent. Still, our crystallographic unit cell model is based on a number of approximations that deserve closer scrutiny, and future simulation studies will be needed to test these approximations as computational resources permit.

First, the dimensions of the unit cell were permitted to fluctuate, but only isotropically such that the aspect ratios found in the 1MK5 structure were maintained. Primarily, this was done to ensure that the correct amount of solvent had been included, so that neither vacuum bubbles nor unusually high pressure could develop over the course of the lengthy simulation. The effect of anisotropic fluctuations is likely to be small in comparison to artifacts that could be created by failing to include precisely the right amount of solvent to properly fill the volume of a rigid unit cell. However, it is conceivable that some additional lattice disorder might develop with anisotropic rescaling.

Next, we assumed that one unit cell per simulation is enough. Although the unit cell contained roughly 50,000 atoms, 16 streptavidin proteins comprised more than 55% of all atoms. Early in this study, we experimented with a simulation cell comprising two crystallographic unit cells such that the initial box dimensions were 92.6Å by 93.4Å by 103.9Å (data not shown). After 8ns of production dynamics, we decided that “rounding out” the box dimensions in this manner did not affect the final volume or overall backbone RMSD of the structures to an extent that our studies could detect. However, given the long relaxation times of these parameters, the debate concerning the effect of Ewald electrostatics in systems with high ion concentrations (18,19), and the fact that several of our model cryosolution’s ionic species are hardly more numerous than the streptavidin monomers of the lattice, it is worth investigating whether symmetry breaking between multiple unit cells in a simulation might change the average structures or dynamics of the lattice’s asymmetric units.

Perhaps the most fundamental assumption of our model is that this system, particularly its highly ionic cryosolution, can be accurately represented without explicit charge polarization. Our results in Results: Cryosolution modeling and the Supporting Information clearly show that the SPC/E water model does not reproduce the densities of these ionic solutions. The water is highly over-constricted upon addition of ions to the solution, and the solubility of these ions in the water model, particularly the ammonium sulfate, is questionable. Results presented in the Supporting Information suggest that other fixed-charge water models offer no improvement in these respects. Polarizable models for water-ion interactions may overcome these problems, and also may offer enough transferability to allow explicit treatment of the cryogenic conditions used in many X-ray diffraction studies. Polarizable models for proteins are in development (54). Once these new forcefields do become available, the combination of smaller time steps and iterative calculations for polarization effects will drive the computational cost of simulations upwards by a factor of 10 to 20. However, ongoing advances in computer hardware are likely to make the timescales explored in this work accessible with polarizable models in the near future.

The approximation that cryosolution composition in the crystal interstices is equal to its composition in the droplet surrounding the crystal may be the most difficult of all to test. However, given observations that the composition of solutions changes significantly at fluid interfaces (55,56) and particularly at the surface of proteins (25), this approximation is perhaps the simplest to challenge. While computing the cryosolution mass distribution functions in Figure 7, we observed that 70% of the volume of the crystal interstices lay within just 2Å of the protein surface. Clearly, if the lattice proteins discriminate among species in their first solvent layer, as is apparent from other results presented above, this would significantly alter the composition of the cryosolution in the crystal unit cell. In their current state, molecular dynamics calculations are not accurate or precise enough to probe the chemical potentials of cryosolution species in these interstices. However, in time one could envision a grand-canonical Monte-Carlo scheme (57) in which the populations of buffer components vary throughout the simulation, or perhaps a study with integral equations (58) to suggest better proportions for each component.

In the introduction to this paper, we noted that prior simulations of protein crystals had been performed in rigid containers. In closing, it is appropriate to note that the simulations presented here, while they do take steps toward a more rigorous treatment of the crystal environment, are still rigidly constrained in many ways. As we explore the impact of the approximations discussed above and perform protein crystal lattice simulations with increasingly realistic environments, we will be able to make more direct comparisons with X-ray diffraction results. This in turn will allow us to address increasingly detailed questions about protein structures and fluctuations, and should also provide a powerful metric for evaluation of potential energy functions and molecular dynamics simulation protocols.

Abbreviations

ASU

asymmetric unit

MD

molecular dynamics

SPC/E

Simple Point Charge/Extended

TIP3P

Transferable Interaction Potential, 3-Point

RMS

root mean-squared

RIA

random independent assignment