Low-Frequency Mode Activity of Heme: Femtosecond Coherence Spectroscopy of Iron Porphine Halides and Nitrophorin

Abstract

The low-frequency mode activity of metalloporphyrins has been studied for iron porphine-halides (Fe(P)(X), X = Cl, Br) and nitrophorin 4 (NP4) using femtosecond coherence spectroscopy (FCS) in combination with polarized resonance Raman spectroscopy and density functional theory (DFT). It is confirmed that the mode symmetry selection rules for FCS are the same as for Raman scattering and that both Franck-Condon and Jahn-Teller mode activities are observed for Fe(P)(X) under Soret resonance conditions. The DFT-calculated low-frequency (20-400 cm^-1) modes, and their frequency shifts upon halide substitution, are in good agreement with experimental Raman and coherence data, so that mode assignments can be made. The doming mode is located at ~80 cm^-1 for Fe(P)(Cl) and at ~60 cm^-1 for Fe(P)(Br). NP4 is also studied with coherence techniques, and the NO-bound species of ferric and ferrous NP4 display a mode at ~30-40 cm^-1 that is associated with transient heme doming motion following NO photolysis. The coherence spectra of three ferric derivatives of NP4 with different degrees of heme ruffling distortion are also investigated. We find a mode at ~60 cm^-1 whose relative intensity in the coherence spectra depends quadratically on the magnitude of the ruffling distortion. To quantitatively account for this correlation, a new “distortion-induced” Raman enhancement mechanism is presented. This mechanism is unique to low-frequency “soft modes” of the molecular framework that can be distorted by environmental forces. These results demonstrate the potential of FCS as a sensitive probe of dynamic and functionally important nonplanar heme vibrational excitations that are induced by the protein environmental forces or by the chemical reactions in the aqueous phase.

Introduction

Investigations of the internal dynamics of proteins are essential for understanding the molecular mechanisms that underlie their diverse range of functions. Although diffusive, collective fluctuations of an entire protein effectively sample between large-scale conformational substates,^1-5 the sub-Angstrom motions that take place on subpicosecond timescales at a protein active site are crucial in facilitating chemical reactions that involve electronic state changes. Common examples include photoisomerization,^6,7 electron transfer,^8-10 and bond cleavage or formation.^11-14 Within the protein interior, these rapid and small length-scale fluctuations are often under-damped and are best described as low-frequency molecular vibrations. Thus, the analysis of the thermally accessible (≤200 cm^-1) vibrational modes of a protein active site and their interaction with the surrounding amino acids is key to determining the chemical reaction mechanisms of proteins and to understanding how dynamic structures relate to protein functions.

Heme proteins form a large and interesting class of proteins that are involved in a wide variety of biological functions such as ligand transport, electron transfer, catalysis, and signal transduction. The active site of this class of proteins consists of a heme chromophore (iron protoporphyrin IX, FePPIX), with the iron atom covalently linked to the protein through axial ligand(s). One of the major issues in understanding heme proteins concerns how they tune the structural and functional properties of the heme group to efficiently carry out their widely varied biological functions. Although axial ligation and the hydrogen bonding network surrounding the heme are undoubtedly important, distortions of the heme plane are also associated with heme functionality.^14-18 Through systematic computational analysis of X-ray structures of heme proteins, it has been found that the proteins belonging to the same functional class share the same types of nonplanar heme distortions.^18-20 Such nonplanar distortions are energetically unfavorable for the heme, and their evolutionary conservation implies that the protein-induced out-of-plane (OOP) distortions of the heme have biological significance.

Two OOP heme vibrational modes have been reasonably well-characterized and correlated with protein functions. One mode that is clearly important is the heme doming mode, which involves iron and porphyrin nitrogen motion toward the proximal ligand.²¹ The functional importance of this mode can be seen in the classic T-R allosteric transition of hemoglobin (Hb).^22,23 Recently, heme model compounds were used to show that, even in the absence of the surrounding protein, doming is a key reaction coordinate for binding diatomic ligands to the heme.¹⁴ For example, the rebinding kinetics of CO are retarded by the doming distortion because thermally induced heme fluctuations are needed to move the iron into the porphyrin plane, vacating the d_z² orbital.^14,24 Another important OOP heme mode is ruffling, which involves a pyrrole-ring twisting about the Fe-N bond. The ruffling distortion tilts the p_z orbitals of the porphyrin nitrogens away from the heme normal and allows overlap of the porphyrin π and iron d_xy orbitals. Consequently, the ferric oxidation state can be stabilized through partial filling of the half-empty d_xy orbital in the (d_xz,d_yz)⁴ (d_xy)¹ electronic configuration, interfering with reduction.^25,26 This turns out to be important for NO transport in nitrophorins^26-28 and for electron transfer in c-type cytochromes,^18-20,29 both of which are known to contain significantly ruffled hemes.

Generally, functionally important modes, such as heme doming and ruffling, involve many nuclei and lie in the low-frequency region below 200 cm^-1. Conventional vibrational spectroscopies (e.g., infrared (IR) and Raman) cannot access this low-frequency region in the aqueous phase, so the nature of the thermally accessible modes of biomolecules remains obscure. On the other hand, with the recent advance in solidstate femtosecond laser sources, time-domain techniques, such as femtosecond coherence spectroscopy (FCS)^6-13,30-48 have made it possible to probe the low-frequency spectral density in aqueous solution. FCS is a pump-probe spectroscopy that utilizes the broad bandwidth of femtosecond laser pulses to induce and monitor coherent low-frequency motions in the sample due to the nonequilibrium modulation of its third order polarization. When electronic resonance is involved (e.g., excitation at the Soret band of heme), the vibrational states that are coupled to the electronic excitation are driven strongly into coherent superposition, so that the low-frequency modes of a resonant chromophore within an aqueous protein environment can be selectively and sensitively probed, in analogy to resonance Raman spectroscopy.

Using Soret band excitation, we have previously investigated the low-frequency modes of a variety of heme proteins (myoglobin (Mb),^35,43-45 Hb,⁴⁴ Campylobacter globin (Cgb),⁴⁶ horseradish peroxidase (HRP),⁴⁶ cytochrome c,^44,47 cytochrome P450,⁴⁸ chloroperoxidase,⁴⁸ CooA⁴⁵), and we have observed dramatic redistributions of frequencies and amplitudes that depend on the surrounding protein matrix. Notably, even proteins having identical heme spin, oxidation, and coordination states reveal very different low-frequency spectra,⁴⁶ in contrast to the high-frequency resonance Raman spectra. The low-frequency “soft” modes of the heme (<200 cm^-1) are most easily distorted from equilibrium by the protein surroundings. These modes (and the resulting distortions) usually involve nonplanar heme geometries and are most likely to be function-ally significant because of their thermal accessibility. The high frequency modes have “hard” force constants and are much less likely to respond to subtle environmental perturbations. As a result, the low-frequency coherence spectrum is suggested to be a unique structural probe that reports directly on the surrounding protein environment and its effect on the thermally active heme modes.⁴⁶

In this work, FCS is used in combination with polarized resonance Raman spectroscopy and density functional theory (DFT) to make low-frequency (20-400 cm^-1) mode assignments for ferric iron porphine-halides (Fe(P)(X), X = Cl, Br). These are the simplest model compounds that enable accurate analysis and assignment of the low-frequency modes of the heme core. Significant frequency shifts are observed upon exchanging the axial halide ions, so that doming, as well as other low-frequency modes, can be successfully identified. The present work also investigates the low-frequency activity in nitrophorin 4 (NP4), a NO-transport heme protein discovered in the blood-sucking insect Rhodnius prolixus.⁴⁹ A ruffling heme distortion occurs in NP4 due in part to close contacts between the heme and distal leucine residues.^27,28 Spectral comparison of the NP4 derivatives with varying degrees of the ruffling distortion reveals a mode near 60 cm^-1 that is conspicuously sensitive to this distortion. Importantly, the intensity of this mode is found to depend “quadratically” on the magnitude of the ruffling distortion. To quantitatively account for this behavior, we present a novel Raman enhancement mechanism for “soft-modes” that correlates the nonplanar heme distortions with the normally forbidden OOP mode activity observed in the coherence spectra.

Experimental Section

Sample Preparation

Fe(III) porphine chloride (Fe(P)(Cl)) and Fe(III) porphine bromide (Fe(P)(Br)) were purchased as powder from Frontier Scientific Inc. and dissolved in benzene without further purification. Ferric aquo NP4 (NP4-H₂O) was expressed and purified as described previously^50,51 and dissolved in the appropriate buffer (0.08 M citrate-phosphate buffer at pH 5.6 or 0.1 M phosphate buffer at pH 7.0). The cyano complex at pH 5.6 and 4-iodopyrazole (4IPzH) complex at pH 7.0 were obtained by adding small aliquots of concentrated (1 M) potassium cyanide (KCN) solution and saturated (<1 M) 4IPzH solution, respectively, to the ferric sample. The ferric NO sample at pH 5.6 was obtained by bubbling NO gas through the degassed ferric sample for approximately 1 min, whereas the ferrous NO sample at pH 5.6 was prepared by adding a small aliquot of concentrated (1 M) sodium nitrate (Na₂NO₂) solution after reducing the degassed ferric sample with a slight excess of freshly prepared sodium dithionite (Na₂S₂O₄) solution under argon atmosphere in a glovebox. The concentration of the model compounds and protein samples was adjusted so that the final absorbance had an optical density of approximately 1 in a 1 mm path length cell at the excitation wavelength. Absorption spectra were recorded (U-4100, Hitachi) after the preparation procedure to ensure that all chemical modifications were achieved and that they were complete. The absorption spectra were also taken after the experiments to confirm the sample integrity during exposure to laser irradiation.

Coherence Spectroscopy

The laser system consisted of a tunable (750-960 nm) Ti:Sapphire oscillator (MIRA 900F, Coherent) pumped by a 10 W diode laser (Verdi 10, Coherent). The oscillator generated 50-100 fs pulses at a repetition rate of 76 MHz with energy of ~10 nJ/pulse. To resonantly excite the samples at the Soret band, the IR output of the laser was frequency doubled in a 250 μm β-barium borate crystal and then chirp compensated by a pair of SF10 prisms to within 10% of the transform time-bandwidth limit. Subsequently, the laser light was split into a pump arm and a probe arm, with a power ratio of 2:1. The pump beam was modulated using an acousto-optic cell (Neos Technologies) driven by a lock-in amplifier (SR844, Stanford Research Systems) at 1.5 MHz. Before reaching the sample, the pump and probe beam polarizations were adjusted to be perpendicular. The time delay between the pump and probe pulses was controlled by a translation stage (Newport Klinger) in steps of 1 μm (6.66 fs in time domain). Both beams were focused into the spinning sample cell using a three inch achromatic lens in a near parallel geometry. The full width at half-maximum of the pump and probe pulses was typically ~70 fs at the sample position. After the sample, the beams were recollimated and the pump light was spatially blocked and extinguished by a polarization analyzer that only allowed the probe light to pass.

Two detection schemes allowed us to focus on different frequency ranges of the coherence signal. In the “open band” detection scheme, we employed a Si photodiode to measure the entire spectral bandwidth of the probe pulse. This scheme optimizes the detection of low-frequency modes below 100 cm^-1. The “detuned” or “dispersed” detection scheme, on the other hand, used a photomultiplier tube coupled to a monochromator to select a portion of the probe bandwidth away from the carrier frequency. Because the third order polarization oscillates at the optical carrier frequency ± vibrational coherence frequency, this configuration selectively detected higher frequency components of the signal with improved reliability in the 200-400 cm^-1 range, which allowed direct comparison with frequency domain techniques like Raman spectroscopy.

Data Analysis

The experimental data have components arising from population transfer as well as vibrational coherence. Under resonance conditions, the population transfer component is always dominant. Although this component carries important information regarding various dynamic processes (e.g., ligand rebinding, vibrational cooling, and spectral diffusion of the lineshape), it must be removed to reveal the underlying coherence signal. Due to the large amplitude of the electronic population signal (generally about 2 orders of magnitude larger than the coherence signal), special precautions had to be taken during both the digitization/recording of the signal and the fitting procedure. The digitization of the experimental signal was done in the lock in amplifier on a 24 bit scale, which offered a sufficient dynamic range even for the low amplitude coherence signal. To generate the power spectrum from the time-domain oscillatory signal, we used a linear predictive singular value decomposition (LPSVD) algorithm that can fit both the damped (cosine) oscillations and the monotonic (zero frequency) background simultaneously. As presented here, the LPSVD “power” spectrum is better characterized as the Fourier transform “amplitude” spectrum, because the oscillation amplitudes are plotted, rather than their squares. The coherence coupling spike around time zero was truncated before the fitting analysis. An alternative method of analysis involved preliminary fitting of the monotonic background by the maximum entropy method (MEM), which used a distribution of exponential rate constants. The residual oscillatory signal can then be subsequently fitted by LPSVD. When the monotonic population signal can be well described by exponential functions over the time range of interest, both the techniques essentially generated the same power spectrum for the oscillatory signal. However, because MEM can sometimes lead to over- or under-fitting of the monotonic decay, a very low-frequency (e.g., below 20 cm^-1) oscillatory residual can appear as an artifact (vibrational period > 1.7 ps). As a result, we neglected any band below 20 cm^-1 in the present study.

Given the fact that a small amount of noise is always present in the experimental data, we used Raman spectra in the region of 200-400 cm^-1 to help the LPSVD fitting analysis. We first analyzed the detuned coherence data to make sure that the controllable fitting parameters (the number of oscillations and time window of the data being fit) yielded the optimized correlation with Raman spectrum. The detuned coherence spectrum generally extends below 200 cm^-1, which is a typical lower limit cutoff for Raman spectroscopy. The open band coherence data were then analyzed and correlated with both the Raman and detuned coherence spectra in the overlapping frequency regions.

Resonance Raman Measurements

Resonance Raman spectra were obtained by employing a standard Raman setup with a 90° light collection geometry and a single grating monochromator (1870B, Spex Industries). The monochromator output was coupled to a liquid nitrogen-cooled CCD (Princeton Instruments). An optical scrambler was inserted in front of the monochromator to minimize polarization-dependent response of the grating. An interferometric notch filter (Kaiser Optical Systems) was also inserted to extinguish the laser light and to improve the system performance over the low-frequency region of Raman shifts. Samples were placed in a standard quartz cuvette (NSG Precision Cells) and excited with ~5 mW of the 413.1nm line from a krypton ion laser (Innova 300, Coherent). For polarized measurements, a polarization analyzer was placed behind the collecting lens of Raman scattered light.

Computational Methods

Geometry optimization and harmonic frequency calculations were performed by using the DFT method at the B3-LYP level implemented in the Gaussian 03 software.⁵² Ahlrich’s VTZ basis set⁵³ was employed for the iron and halide ions, whereas the moderate 6-31G(d) basis set was used for H, C, and N atoms.

Results

Iron Porphine Halides

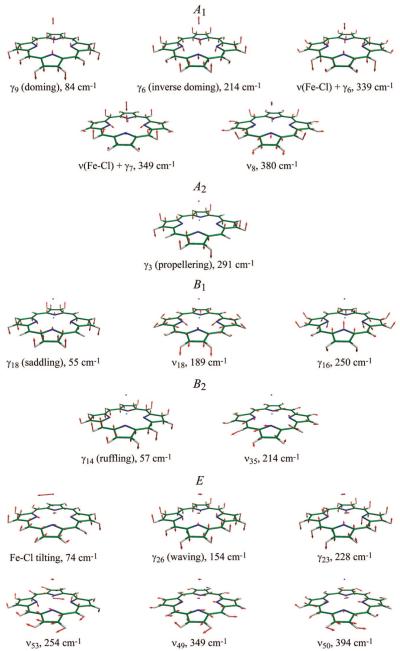
The low-frequency normal vibrational modes of Fe(P)(Cl) calculated using the DFT method are depicted in Figure 1, together with the nonscaled vibrational frequencies. Through geometry optimization under C_4v symmetry, a domed structure with an iron OOP displacement of 0.5 Å toward the Cl was obtained, and the normal modes for this energy-minimized structure are presented in the figure. The notation for each vibration is taken from ref 54 for planar Ni(II) porphine, which are designated by γ (for OOP vibrations) or ν (for in-plane (IP) vibrations), followed by the individual mode number. However, some normal modes of Fe(P)(Cl) are better expressed by a combination of OOP and IP vibrations due to mode mixing derived from the nonplanar structure. (For instance, ν₁₈ of Fe(P)(Cl) contains small amplitude of γ₁₆ motion, and vice versa.) Besides the OOP and IP mode mixing, Fe(P)(Cl) has additional modes compared to Ni(P) owing to the presence of the axial ligand, namely Fe-Cl stretching, ν(Fe-Cl), and Fe-Cl tilting, δ(Fe-Cl), both of which are mixed with porphine vibrations. Quantitative analysis of these mode mixings will be reported elsewhere (A. Barabanschikov et al., to be published).

Figure 1.

Normal vibrational modes of Fe(P)(Cl) below 400 cm^-1. The iron, chlorine, carbon, nitrogen, and hydrogen atoms are shown in light blue, pink, green, blue, and white, respectively. Eigenvectors are shown by red arrows.

Normal vibrational modes of domed (C_4v) Fe(P)(Cl) can be classified into 5 symmetry species, that is, A₁, A₂, B₁, B₂, and E. Of these, A₁ modes are known to be resonance Raman active with Soret excitation via the Franck-Condon coupling.^55-60 The lowest-frequency A₁ mode is the doming mode (γ₉) at 84 cm^-1, which is a functionally important mode involving the iron OOP motion. The inverse doming mode (γ₆) at 214 cm^-1 can also displace the iron atom from the porphine plane such that the iron moves in the opposite direction to the porphine-ring nitrogens. The next two A₁ modes at 339 and 349 cm^-1 contain ν(Fe-Cl), mixed with γ₆ and γ₇ porphine vibrations, respectively. The A₁ mode at 380 cm^-1 is Fe-N stretching (ν₈) with small contribution of ν(Fe-Cl). The B₁ and B₂ modes can also be enhanced in Soret resonance Raman spectra through the Jahn-Teller effect.^61-64 The softest modes of these symmetry types are saddling (γ₁₈) and ruffling (γ₁₄) modes at ~60 cm^-1, which are often associated with nonplanar heme distortions (vide infra). In principle, for Soret resonance Raman spectra, the A₂ and E modes cannot be enhanced through a Franck-Condon mechanism.

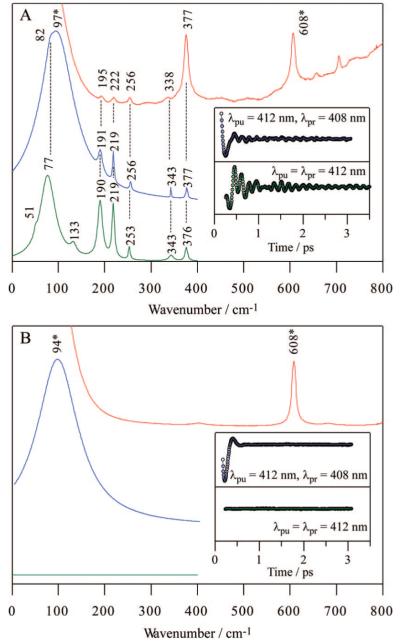
As shown in Figure 1, Fe(P)(Cl) has 5 A₁ and 5 B₁/B₂ Raman active modes below 400 cm^-1. With these Raman selection rules in mind, Raman and coherence spectra of Fe(P)(Cl) dissolved in benzene were measured, as shown in Figure 2A. The top trace represents Soret-resonance Raman spectrum (red), whereas the other two delineate detuned (blue) and open band (green) coherence spectra. The time domain oscillations are shown in the insets. Asterisks indicate benzene solvent bands, which are confirmed by the spectra of benzene only (Figure 2B). It should be noted that the open band coherence spectra (lower traces in Figure 2A and B) measure only the imaginary (dichroic) part of the third order polarization and cannot detect the nonresonant (birefringent) signal of benzene.³⁹ Thus, the open band detection scheme provides a natural way to filter out peaks associated with the transparent (nonresonant) solvent (e.g., the strong peak at 94 cm^-1 is completely absent in the open band experiment shown in the lower trace of Figure 2B). With the exception of the contribution from benzene in the detuned spectra, there are good correlations between the resonance Raman, detuned coherence, and open band coherence spectra. This demonstrates that (in the absence of photolysis) the mode selection rules for FCS are identical to Raman spectroscopy.

Figure 2.

Correlations between Raman and coherence spectra for (A) Fe(P)(Cl) in benzene and (B) benzene only. Raman spectrum (red) was measured with excitation at 413.1 nm, whereas open band (green) and detuned (blue) coherence spectra were measured at a carrier wavelength of 412 nm. The detuned coherence data were collected with a 0.5 nm spectral window, detuned 4 nm to the blue of the carrier wavelength. The inset shows time-domain oscillation data (circles) and LPSVD fits (lines) corresponding to an open band detection (green) and to a detuned detection (blue) scheme. Asterisks indicate benzene bands. Note that the open band experiments show no trace of the benzene bands as expected theoretically for a transparent fluid.

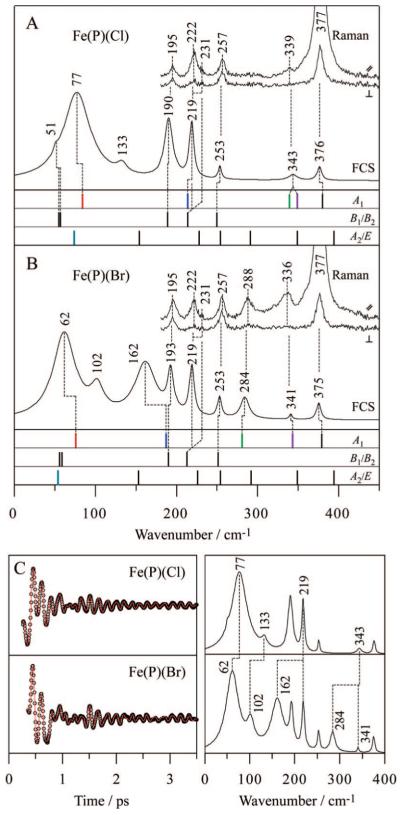
The DFT calculated frequencies are also in very good agreement with the experimentally observed frequencies, allowing us to assign the low-frequency modes of this simple model compound. Figure 3A compares the polarized Raman and open band coherence spectra of Fe(P)(Cl) with the DFT normal-mode frequencies of each symmetry type. It is evident that A₁ modes are enhanced in both of the experimental spectra, and the doming mode is clearly identified at 77 cm^-1. The two (primarily) ν(Fe-Cl) modes calculated at ~339-349 cm^-1 are observed, but not separately resolved in the experimental spectra. The enhancement of B₁/B₂ modes is also observed, as can be confirmed from the presence of depolarized bands in the Raman spectra. Both ν₃₅ (B₂) and the inverse doming mode (A₁) are expected at 214 cm^-1 by the DFT and not resolved in the coherence spectrum (219 cm^-1), but they are distinguished (222 and 231 cm^-1) by the polarized Raman measurement. The depolarization ratio measured in the Raman spectrum suggests that the shoulder at 231 cm^-1 is a better assignment for ν₃₅. The weak activity of ruffling (B₂) and saddling (B₁) modes are recognizable at 51 cm^-1 as a shoulder on the intense 77 cm^-1 peak. The experimental coherence spectrum also exhibits an extra band at 133 cm^-1 with an uncertain origin. We tentatively assign this band to the waving mode based on its DFT predicted frequency at 154 cm^-1. Although the E symmetric waving mode is formally inactive within the harmonic and Condon approximations, it could become active via a vibronic coupling mechanism. Fe(P)(Cl) displays an absorption spectrum with a marked shoulder near 365 nm on the blue side of the Soret band (Supporting Information, Figure S1). A portion of the broad 365 nm band has been assigned to a z-polarized Cl → Fe charge-transfer (CT) transition with a relatively strong intensity,^65-67 possibly due to vibronic borrowing from the (E) Soret band. Because the CT transition is z-polarized⁶⁷ and of A₁ symmetry, E modes can participate in vibronic coupling to the Soret band. This means that the E-symmetric Fe-Cl tilting mode can also be activated by a non-Condon Raman coupling mechanism and possibly contribute intensity to the broad FCS band at 77 cm^-1.

Figure 3.

Comparison of experimental spectra and calculated frequencies for (A) Fe(P)(Cl) and (B) Fe(P)(Br). Polarized Raman spectra were measured with excitation at 413.1 nm, whereas open band coherence spectra were measured at a carrier wavelength of 412 nm. The calculated frequencies are categorized into 3 symmetry groups (A₁, B₁/B₂, and A₂/E) and are shown by bars. The calculation predicts frequency shifts for 4 A₁ modes and 1 E mode when Cl is exchanged with Br, where each mode is highlighted by a different color (red, blue, green, purple, and light blue). Correspondences between the Raman bands, FCS bands, and DFT frequencies are displayed by dotted lines. (C) Open-band coherence oscillation data, LPSVD fits (left) and LPSVD power spectra (right) of Fe(P)(Cl) and Fe(P)(Br). The frequency shifts between the two samples are displayed by dotted lines.

Here it is important to note that the Raman spectrum was also measured in the high frequency region (Supporting Information, Figure S1) where a clear shoulder, or doublet structure, was detected for both the ν₂ and ν₄ modes. This is suggestive of the presence of a minority species in the solution, which we speculate to be the μ-oxo dimer, [Fe(P)]₂O. In the case of the μ-oxo dimer, the two monomer units are for the most part well-separated and very little monomer mode mixing and splitting occurs as previously seen for the Fe(TPP) (iron tetraphenylporphyrin) compound.⁶⁸ Moreover, as revealed in the same work,⁶⁸ most of the low-frequency mode frequencies of the dimer [Fe(TPP)]₂O lie close to (or completely overlap with) those of the monomer Fe(TPP)(Cl).

To help make firmer mode assignments, polarized Raman and coherence spectra of Fe(P)(Br) were also measured. The spectra are shown in Figure 3B, together with the DFT frequencies. Because Br is about twice as heavy as Cl and has different electronic properties, the DFT calculations predict frequency shifts and new mode mixing for 4 A₁ modes and 1 E mode (depicted with the color bars in Figure 3): the γ₉ doming mode (A₁) from 84 to 76 cm^-1; the γ₆ inverse doming mode (A₁) from 214 to 187 cm^-1 with γ₉ mixing; ν(Fe-L) + γ₆ (A₁) from 339 to 281 cm^-1; ν(Fe-L) + γ₇ (A₁) from 349 to 343 cm^-1 with significant reduction of the ν(Fe-L) amplitude; and the Fe-L tilting mode (E) from 74 to 54 cm^-1. Corresponding frequency shifts of the 4 A₁ modes are observed in the experimental Raman and coherence spectra. The doming mode is shifted from 77 to 62 cm^-1 and the ν(Fe-L) + γ₆ mode shifts from within the band at 343 cm^-1 down to 284 cm^-1. As predicted, the ν(Fe-L) + γ₇ mode moves only slightly from 343 to 341 cm^-1. These latter two ν(Fe-L)-containing modes can also be observed reasonably well in the Raman spectrum. The inverse doming mode is assigned by a marked frequency shift from ~220 to 162 cm^-1 in the coherence spectrum; however, part of the band intensity remains at ~220 cm^-1, as also seen in the Raman spectrum. This could be due to contamination of the μ-oxo dimer, which also has a band at ~220 cm^-1 (see Figure 2 of ref 68) but does not coordinate either Cl or Br. Thus, the residual intensity at 219 cm^-1 in the coherence spectrum is thought to arise from the 220 cm^-1 dimer mode as well as ν₃₅ (B₂), both of which are insensitive to the replacement of Cl with Br.

The frequency shifts by exchanging Cl with Br can be more clearly discerned in Figure 3C, where the coherence spectra of Fe(P)(Cl) and Fe(P)(Br) are directly compared. Note that when a significant frequency downshift takes place, it also appears to cause an increase in the band intensity. This occurs because the laser pulse bandwidth is finite and contains more field intensity near the carrier frequency than in the wings, especially in the region near 200 cm^-1 where the pulse intensity begins to drop significantly (Supporting Information, Figure S2). It is also noteworthy that the bandwidth of the doming mode is relatively broad. The bandwidth of the inverse doming mode also appears to be broad, as seen for Fe(P)(Br) (162 cm^-1), although for Fe(P)(Cl) (~220 cm^-1) the band appears to be narrower for reasons that are unclear, but possibly related to its near degeneracy with the ν₃₅ mode. The band broadening is attributed to inhomogeneity in the solution structure¹⁴ that can affect the frequency of the soft low-frequency modes. Fast homogeneous damping is also a possibility, as is solvent-induced anharmonicity, which might also be responsible for the frequencies of the doming and inverse doming modes appearing lower than the DFT calculations. The coherence spectra also reveal a frequency shift of an unassigned band at 133 cm^-1. If this is, indeed, the waving mode, it suggests that the Fe-Cl tilting motion in the waving mode is more significant in benzene than estimated in the gas-phase DFT calculation (Figure 1).

Nitrophorin 4

Raman and coherence spectra of ferric aquo NP4 (NP4-H₂O) at pH 5.6 are shown in Figure 4. Again, a good correlation is obtained between resonance Raman (red), detuned coherence (blue), and open band coherence (green) spectra. Modes below ~100 cm^-1 are resolved with the best fidelity using the open band detection scheme, while the higher frequency modes are revealed using the detuned detection. The Raman spectrum of NP4 in Figure 4 has very similar features to the spectrum reported for the homologous NP1.⁶⁹ The intensity of the depolarized ν₁₅ mode at 758 cm^-1 has been found to be sensitive to water ligation, and the observed small intensity is consistent with the presence of distal water ligand.⁴⁶ Raman bands at 309, 347, and 376 cm^-1 are assigned to γ₇, ν₈, and propionate bending δ(C_βC_cC_d) modes, respectively.^69,70 A broad band at 264 cm^-1 is assigned to ν₉, overlapping with weak ν₅₂.^69,70 A band at ~190 cm^-1 in the coherence spectra can be assigned to ν₁₈ as previously suggested for MbCN.^45,70 Below 150 cm^-1, the oscillatory activity revealed by FCS involves primarily OOP modes. A number of FCS experiments^11,44-46,48 have found that the doming mode of heme proteins is located near 40 cm^-1, which is significantly downshifted, compared to the iron porphine halides, due to the presence of the heme side chains and/or the covalent linkage of the heme iron to the protein through the axial ligand. On the other hand, far-IR synchrotron measurements have identified the inverse doming mode for an Fe(OEP) (iron octaethylporphyrin) compound at 140 cm^-1.⁷¹

Figure 4.

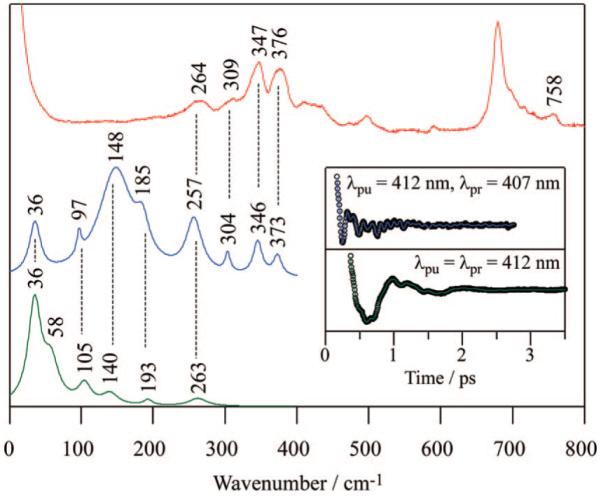
Correlations between Raman and coherence spectra for NP4-H₂O at pH 5.6. Raman spectrum (red) was measured with excitation at 413.1 nm, whereas open band (green) and detuned (blue) coherence spectra were measured at a carrier wavelength of 412 nm. The detuned coherence data were collected with a 0.5 nm spectral window, detuned 5 nm to the blue of the carrier wavelength. (Inset) Time-domain oscillation data (circles) and LPSVD fits (lines) corresponding to an open band detection (green) and to a detuned detection (blue) scheme.

It is known that, although NP4-H₂O contains a ruffled heme,^28,72 the magnitude of the ruffling distortion can be altered by selecting different distal ligands.²⁶ For instance, the heme plane is significantly more ruffled in the CN-bound form (NP4-CN),^27,72 than the more planar form induced by binding of 4IPzH (NP4-4IPzH).⁷³ Therefore, by using these different NP4 derivatives, we can systematically investigate the effect of ruffling distortion on the OOP mode activity. A quantitative connection between nonplanar heme distortions and OOP vibrational mode activity can be made by using normal-coordinate structural decomposition (NSD).^18-20 NSD is a general computational method for describing heme deformations in terms of normal-coordinate displacements. For example, it allows nonplanar distortions to be described by displacements along the softest OOP mode of each symmetry type, which are shown in Figure 1 to be the doming (A₁), propellering (A₂), saddling (B₁), ruffling (B₂), and waving (E) modes.

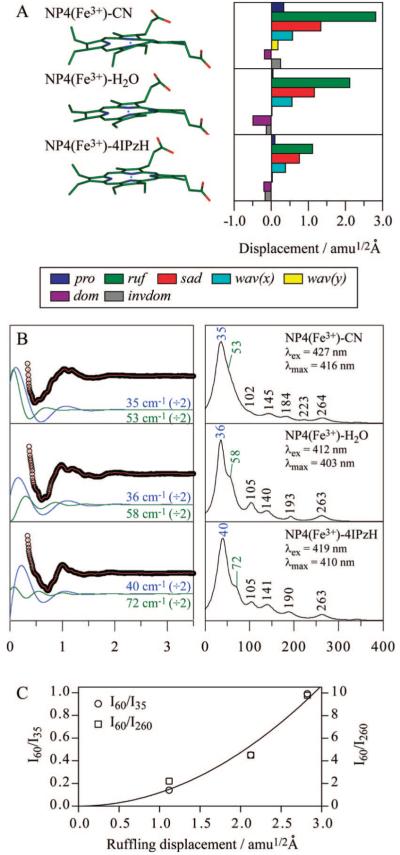
Figure 5A shows the NSD analysis for ferric NP4-CN, NP4-H₂O, and NP4-4IPzH. The NSD analysis presented here involves modifications of prior work,^18-20 which utilized the 24 skeletal atoms (4N, 20C) of Cu(P) as the stable planar reference structure and neglected the central metal. In this work, we employ the planar structure of ferric porphine, [Fe(P)]⁺, obtained by the DFT optimization under D_4h symmetry as the reference, including the iron as well as the 24 skeletal atoms. The displacement along each normal coordinate was calculated in the mass-weighted coordinate space using the scalar product (X - X₀)·Q_α, where X and X₀ are the mass-weighted atomic coordinates of the input and reference structures, respectively. The difference is found by superimposing the structures using Swiss-PdbViewer (ver. 3.7),⁷⁴ whereas Q_α is taken as the unit vector of the mass-weighted normal mode, α, of the reference structure [Fe(P)]⁺. In addition to the five lowest frequency OOP modes mentioned above, we included the inverse doming mode to more accurately model the iron OOP position, which can be roughly estimated by the sum of doming and inverse doming displacements. As a result, in the present study, the minus sign of displacement is defined only for the doming and inverse doming modes where it indicates the direction of the iron OOP displacement (+: proximal and -: distal). The NSD analysis in Figure 5A clearly shows the significant distal ligand dependence of ruffling distortion.

Figure 5.

(A) Crystal structures and NSD analysis of hemes in ferric NP4-CN, NP4-H₂O, and NP4-4IPzH. A displacement of 1 amu^1/2 Å represents that the square root of the sum of squares of the displacements of Fe and 24 porphyrin (4N, 20C) atoms is 1 amu^1/2 Å. The color coding for the modes is pro: propellering (blue), ruf: ruffling (green), sad: saddling (red), wav(x): waving_x (light blue), wav(y): waving_y (yellow), dom: doming (purple), invdom: inverse doming (gray). The minus sign of displacement is defined only for doming and inverse doming to indicate the direction of Fe displacement (+: proximal; -: distal). PDB IDs are 1EQD, 1D3S, and 1ML7 for NP4-CN, NP4-H₂O, and NP4-4IPzH, respectively. (B) Open-band coherence oscillation data, LPSVD fits (left) and LPSVD power spectra (right) of ferric NP4-CN, NP4-H₂O, and NP4-4IPzH. The pH was 5.6 for NP4-CN and NP4-H₂O and 7.0 for NP4-4IPzH, which are consistent with the X-ray crystallographic studies. The excitation wavelengths are indicated in the right panels. The ~35 cm^-1 (blue) and ~60 cm^-1 (green) oscillations in the LPSVD fits are divided by a factor of 2 and shown in the left panel, displaced from the raw data for display purposes. (C) Intensity of the ~60 cm^-1 band relative to the ~35 cm^-1 and ~260 cm^-1 bands. A solid line represents the least-squares-fitted quadratic curve passing through the origin (zero intensity at zero displacement).

FCS data of ferric NP4-CN, NP4-H₂O, and NP4-4IPzH are shown in Figure 5B. Note that we chose an appropriate excitation wavelength for each sample to ensure the same resonance condition (Supporting Information, Figure S3). The three NP4 samples display very similar low-frequency spectra with no apparent spin state dependence, except a weak additional band appearing at ~220 cm^-1 in NP4-CN. The intense band at ~35 cm^-1 is assigned to the doming mode and will be discussed in detail later. More importantly, a strong sample dependence is found for a band near 60 cm^-1, which suggests that this band is correlated to the ruffling distortion. It seems that ruffling displacement induces a downshift of this band frequency, which may be due to weakening of the macrocycle π conjugation by the OOP displacement. On the other hand, the band intensity is also seen to increase with ruffling displacement. The intensity of the ~60 cm^-1 band relative to the ~35 cm^-1 (doming) and ~260 cm^-1 (ν₉) bands is plotted as a function of ruffling displacement in Figure 5C. The band intensity appears to be enhanced proportionally to the square of ruffling displacement. Because the effect of the finite laser pulse bandwidth is negligibly small (<4%) within the range of 50 to 70 cm^-1 (Supporting Information, Figure S2), the intensity enhancement observed here cannot be attributed to the frequency shifts (due to mode softening) that take place as ruffling increases.

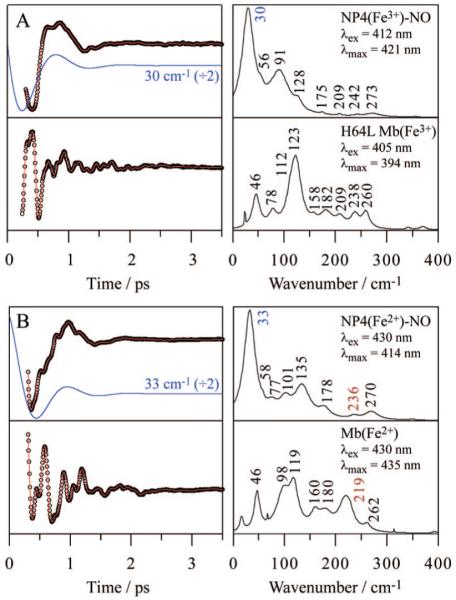
Finally, we present the coherence spectra of photoactive NO adducts of ferric and ferrous NP4 (NP4-NO) at pH 5.6, to investigate the coherence spectra of the photolyzed heme. The quantum yield of NO photolysis is 100% for ferric NP4-NO (unpublished data), but ~50% for ferrous NP4-NO by analogy to MbNO.⁷⁵ After NO is photolyzed from the heme, ~99% of it recombines geminately with a time constant of ~10 ps in both the ferric and ferrous states (unpublished data). These kinetics data will be reported elsewhere (A. Benabbas et al., to be published). Figure 6 shows the coherence spectra of ferric and ferrous NP4-NO upon NO photodissociation. The spectra of ferric H64L Mb and deoxyMb are also shown for comparison because they mimic the five-coordinate, high-spin photoproducts of ferric and ferrous NP4-NO, respectively. The ~40 cm^-1 band of the Mb systems has been well studied and assigned to the doming mode.^44-46 On the other hand, a very strong band is activated near 30 cm^-1 for the NP4 photoproducts. Since the doming distortion of the heme is not significant in ferric and ferrous NP4-NO (<1.0 amu^1/2 Å),^27,28,72 the substantial intensity of the doming mode must originate from transient forces that are induced by NO photolysis.

Figure 6.

Open-band coherence oscillation data, LPSVD fits (left) and LPSVD power spectra (right) of (A) ferric NP4-NO and H64L Mb and (B) ferrous NP4-NO and Mb. The pH employed was 5.6 for the NP4-NO samples and 7.0 for the Mb samples. Acidic pH for NP4-NO was chosen to achieve a high geminate yield (~99%) of NO rebinding, which is required in the present FCS experiments using a high-repetition-rate laser. The excitation wavelengths are indicated in the right panels. The strong ~30 cm^-1 (blue) oscillations of NP4 in the LPSVD fits are divided by a factor of 2 and shown in the left panel, displaced from the raw data for display purposes. The frequencies of ν(Fe-His) of the ferrous species are shown in red.

The weak 56 cm^-1 mode seen in the ferric NP4-NO photoproduct may be assignable to the ruffling mode, although its signal intensity is substantially less than the much stronger doming mode. The ferrous NP4-NO spectrum, on the other hand, displays two bands at 58 and 77 cm^-1, that may arise from the ~50% NO photolysis quantum yield. Since the heme in ferrous NP4-NO is ruffled to approximately the same degree as ferric NP4-H₂O,²⁸ we refer to Figure 5 (where NP4-H₂O displays a ruffling mode at 58 cm^-1) and tentatively assign the 58 cm^-1 band in Figure 6B to the ruffling mode of the unphotolyzed, vibrationally hot, NO-bound species. Accordingly, the 77 cm^-1 band in Figure 6B could arise from the five-coordinate photoproduct, and its higher frequency suggests a less ruffled heme in the photoproduct, compared to the NO-bound heme. The spectrum of ferrous NP4-NO also displays ν(Fe-His) at 236 cm^-1, a marker of the five-coordinate ferrous species (Figure 6B). The higher frequency of ν(Fe-His) in NP4, compared to Mb, is attributed to the hydrogen bonding network formed between proximal His59 and Asp70 through a water molecule, which results in an imidazolate character for His59 and a stronger Fe-His bond. Similar effects have been noted previously for HRP⁷⁶ and Cgb.⁷⁷

Discussion

In the present study, we utilize FCS to directly observe functionally important OOP modes of iron porphine model compounds in an organic solvent and FePPIX embedded in the NP4 protein matrix. Experimental (Raman and coherence) spectra and normal mode calculations are directly compared for the relatively simple iron porphines. Excellent agreement is obtained, allowing definitive new mode assignments to be made in the low-frequency region (Figure 3). The iron porphine samples show a strong halide ligand-to-metal CT band near 365 nm,^65-67 on the blue side of the Soret band (Supporting Information, Figure S1). Since this spectral feature in the Soret region of the chloride sample bears close resemblance to that of Fe(TPP)(Cl),^78-80 we conclude that the present samples are primarily Fe(P)(X). However, the CT band of the present samples is slightly distorted (somewhat larger and broader) and there appears a small extra shoulder near 336 nm, compared to the spectrum of Fe(TPP)(Cl) (see Figure 1 of ref 80). Moreover, the high frequency resonance Raman spectra exhibit secondary ν₂ and ν₄ peaks (Figure S1). These data indicate that the sample solution contains a mixture of two species. We eliminated the possibility of halide photodissociation by measuring the Raman spectra in the ν₂ and ν₄ region as a function of laser power. We found that the doublet Raman band structures were unaffected. Since oxygen solubility is rather high in benzene⁸¹ and trace water can be present, we originally thought the secondary species might be a μ-oxo dimer. However, we also found a similar doublet structure in the solid-state Raman spectra of the original powder sample. In principle, μ-oxo dimer formation in the solid powder could result from reaction with trace water; however, it is also possible that an impurity could be present in the commercially prepared material. The absorption spectrum of the μ-oxo dimer is characterized by a sharp Soret peak blue-shifted relative to the monomer and a small separate peak near 330 nm,⁸⁰ which may be overlapping with the broad feature in the Soret region of the present samples. (Note that the dimer formation discussed here should not be confused with “aggregation” known for Fe(III)PPIX in aqueous solution.) In any case, the low-frequency Raman and coherence spectra are clearly dominated by the monomer contribution. The dimer does not bind Cl or Br and the sensitivity of the spectra to the different halides demonstrates that the halide bound monomer is being probed. The important new results involve the assignment of the doming mode, and identification of modes involving ν(Fe-L) and the weak activity of the ruffling mode (Figure 3).

The correlations between Raman and coherence spectra are also noteworthy (Figures 2 and 4) because they demonstrate the common selection rules between the spontaneous and stimulated forward Raman scattering processes. Prior theoretical analysis of amplitude and phase excitation profiles in FCS³⁹ has focused on Soret excitation of the heme and those modes that are activated by a Franck-Condon mechanism. According to this theory, the electron-nuclear coupling, S = Δ²/2, is necessary to evoke wave packet oscillations via the stimulated forward Raman process. This is analogous to the “A-term” mechanism^55-60 used to describe spontaneous resonance Raman scattering. Here, Δ represents the dimensionless equilibrium position shift of the excited electronic state relative to the ground state. It should be noted that the OOP modes are Franck-Condon and Jahn-Teller inactive (Δ = 0) and thus display no linear resonance Raman coupling for an ideally symmetric (D_4h) porphine having a perfect planar geometry. However, these modes can be strongly activated in the presence of nonplanar distortions. Indeed, we confirmed this effect for domed (C_4v) iron porphines, which exhibit coherence spectra having Franck-Condon enhancement (Δ ≠ 0) of the doming mode (Figure 3).

Similarly, when the heme is subjected to the ruffling distortion within a protein matrix, the ruffling mode should be “turned on” in the coherence spectrum. Although peripheral substituents are asymmetrically attached to the heme, it is known that group theoretical arguments are still applicable in resonance Raman spectroscopy.^{57,58,70,82-88} For example, the heme has a planar structure in unfolded cytochrome c, but, when the protein is folded, the heme adopts a ruffled structure that is imposed by packing against the polypeptide chain and the covalent linkage to the protein. Consequently, Raman enhancements of several OOP modes were observed in the 400-800 cm^-1 region, which were inactive in the spectrum of the unfolded protein.^83,89 These OOP mode enhancements are due to symmetry lowering, induced by nonplanar heme distortions along low-frequency OOP mode coordinates. This “symmetry-lowering” mechanism has been studied in detail recently using heme model compounds. For example, the depolarization ratio of higher frequency (>200 cm^-1) OOP bands were measured and analyzed using group theoretical arguments.^86,88 In another study,⁸⁷ the OOP Raman intensities were simulated using the Kramers-Kronig transform approach with computationally estimated values for Δ, the Condon coupling. In the present study, we directly observe the low-frequency (<200 cm^-1) distortion coordinates using FCS and investigate a novel Raman enhancement mechanism that involves distortions along the OOP coordinates by external forces. We compare the coherence spectra of ferric NP4 under conditions of similar protein environment but different ruffling displacement of the heme (Figure 5A), and as a result, a band near 60 cm^-1 is found to be sensitive to ruffling displacement (Figure 5B), which strongly suggests that this mode is associated with the heme ruffling motion. Interestingly, the band intensity depends quadratically on ruffling displacement (Figure 5C), which is the theoretically expected result, as discussed below.

According to the effective linear response theory for stimulated forward Raman scattering in FCS,³⁹ the self-heterodyne detected signal at the delay time τ in an open band scheme is expressed by

$$S\left(\tau \right)=-{\int }_{-\infty }^{\infty }\mathrm{d}tE(t-\tau )(\partial P(t,\tau )∕\partial t)$$ (1)

with

$$P(t,\tau )={\int }_0^{\infty }\mathrm{d}s{\chi }^{\mathrm{eff}}(t,t-s)E(t-s-\tau )$$ (2)

where E(t - τ) is the probe field and P(t,τ) is the third order polarization induced by the pump and probe fields. The quantity χ^eff(t, t - s) is the effective (nonequilibrium) linear susceptibility that describes the nonstationary medium created by the pump fields. Here, tensor subscripts for the susceptibility are omitted for simplicity, assuming an isotropic medium and taking the pulse fields to be scalar quantities. In the previous work,^39,40 assuming the rotating wave approximation, we found that χ^eff(t, t - s) can be described using a correlation function C(t, t - s)

$${\chi }^{\mathrm{eff}}(t,t-s)=(i{\mid {\mu }_{\mathrm{ge}}\mid }^2∕\hslash )C(t,t-s)$$ (3)

where

$$C(t,t-s)=K\left(s\right)\exp \left[i{\omega }_0{A}_{\mathrm{g}}\Delta {\int }_{t-s}^t\mathrm{d}{t}^{\prime }{e}^{-\gamma \mid t^{\prime }\mid }\cos ({\omega }_{\nu }{t}^{\prime }+{\varphi }_{\mathrm{g}})\right]$$ (4)

Here, μ_ge represents the electronic transition dipole moment, and ω₀ and γ are the vibrational frequency and damping constant, respectively. The effective vibrational frequency of the pump induced ground-state wave packet is given by

$${\omega }_{\nu }=\sqrt{({\omega }_0^2-{\gamma }^2)}$$ (5)

whereas its amplitude and phase are found to be

$${\mathrm{A}}_{\mathrm{g}}=\sqrt{{\mathrm{Q}}_{\mathrm{g}0}^2+P_{\mathrm{g}0}^2}$$ (6a)

and

$${\varphi }_g=-{\tan }^{-1}[P_{g0}∕Q_{\mathrm{g}0}]$$ (6b)

where the initial (pump pulse prepared) first moments of the wave packet position and momentum are denoted as Q_g0 and P_g0. The equilibrium absorption correlator,⁹⁰ K(s), is connected to the susceptibility in the stationary medium χ(s) and thus to the frequency-domain Raman signal through a half Fourier transform. The nonequilibrium correlation function, C(t, t - s) in eq 4 can be viewed as the equilibrium absorption correlator modulated by the wave packet oscillation, with a modulation signal strength of ω₀A_gΔ. Since both Q_g0 and P_g0 are proportional to Δ,^39,40 the oscillatory signal amplitude is found to be proportional to Δ².

The relationship between Δ and the externally induced heme distortion, δ, along an OOP mode Q can be derived using a “compressed spring” model, as illustrated in Figure 7. The heme, distorted by the surrounding protein matrix, can be visualized as a spring compressed by an external force, F_ex. The shift in the ground-state equilibrium position (distortion from planarity), δ, is given in a dimensionless coordinate by

$$\delta =\sqrt{\frac{m\omega }{\hslash }}\frac{F_{\mathrm{ex}}}{k_{\mathrm{g}}}$$ (7)

where k_g is the force constant in the ground state. If the resonant electronic excitation alters the force constant from k_g to k_e, there is a simultaneous shift in the equilibrium position from δ to δ’ = δ(k_g/k_e). As seen in the figure, this generates “distortion-induced” displacement, Δ. Thus, we obtain a new expression for the distortion-induced Franck-Condon coupling that applies to chromophores that are sterically strained from equilibrium in their ground electronic state

$$\Delta ={\delta }^{\prime }-\delta =\delta (k_{\mathrm{g}}∕k_{\mathrm{e}}-1)$$ (8)

Because Δ is linearly proportional to the heme distortion δ, it is found that the oscillation amplitude of the coherence signal should depend quadratically on the heme distortion, which is consistent with the experimental results in Figure 5C. We also recall that the spontaneous resonance Raman cross section depends on Δ² through the Franck-Condon overlaps.^59,60 Therefore, resonance Raman intensities of distortion modes should also be enhanced quadratically if a heme distortion δ is present in the ground state.

Figure 7.

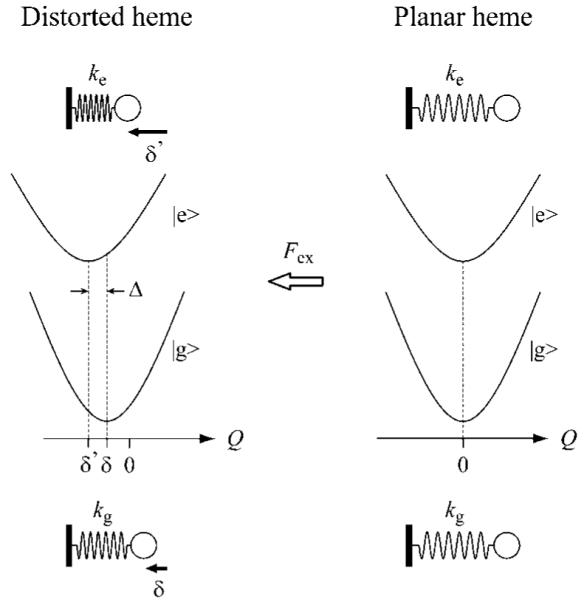
The compressed spring model for the “distortion-induced” Franck-Condon activity of OOP modes. In this model, the heme is distorted by the surrounding protein matrix and viewed as a spring compressed by an external force F_ex. The quantities k_g and k_e are the force constants of the mode Q in the ground and excited electronic states, respectively. The dimensionless equilibrium positions in the ground state δ and in the excited state δ’ are proportional to F_ex/k_g and F_ex/k_e, respectively, and accordingly, the equilibrium position shift of the excited state relative to the ground state (Δ) is obtained as Δ = δ’ - δ = δ(k_g/k_e - 1).

To our knowledge, the above Raman enhancement mechanism has not been discussed previously. A standard symmetry-lowering mechanism can also be present. The standard mechanism is based on the removal of the symmetry elements that otherwise cause the linear Condon coupling matrix elements to vanish. An important distinction between the new mechanism and the standard mechanism is the involvement of quadratic electron-nuclear coupling. If either the quadratic coupling (k_g/k_e ≠ 1) or the ground-state distortion (δ) is removed, the “Condon-like” coupling described by eq 8 will vanish. In contrast, the standard symmetry-lowering mechanism does not involve quadratic coupling, nor does it obviously connect the magnitude of the ground-state distortion to the Raman intensity.

We suggest that the mechanism described by eq 8 has not been observed previously for high frequency modes because δ is suppressed by the much larger restoring force constants k_g that scale as ω². Basically, it is the functionally important OOP modes below ~200 cm^-1, detected using FCS, which are “soft” and subject to distortion. We want to emphasize that Δ = 0 for any OOP mode of a planar heme (relaxed spring), but when the heme is distorted in a protein (compressed spring), the linear coupling Δ will no longer be zero, especially if quadratic coupling is present (k_g/k_e ≠ 1). In other words, the quadratic coupling enables the “distortion-induced” linear Franck-Condon coupling as indicated in eq 8. By way of example, for a 50 cm^-1 mode and an induced distortion of 2.8 amu^1/2 Å (see Figure 5A), a ~10% relative force constant change between the ground and excited states leads to Δ ~ 0.38 and S ~0.072. Thus, the “distortion-induced” Franck-Condon activity of low-frequency OOP modes is of the same order as the standard linear coupling that has been documented previously for higher frequency IP modes.⁹¹

A final observation that deserves discussion is the “reaction-driven” coherences, observed for the NO-bound species of NP4 (Figure 6). Reaction-driven mode enhancement differs from the distortion-induced Raman enhancement mechanism outlined above. For photoreactive samples, FCS can probe the electron-nuclear coupling forces that develop in the product state and directly detect the reaction coordinate(s). This capability (along with phase determination) differentiates FCS from its spontaneous resonance Raman scattering analog, which only probes the electron-nuclear coupling force that act on the shortest time-scales (namely the vertical photon excitation). An important example of reaction-driven coherences is the observation of the heme doming mode and ν(Fe-His) following ligand photodissociation.^35,39,43-47 The doming mode is a key reaction coordinate¹⁴ and its amplitude and phase excitation profile (carrier wavelength dependence) have been investigated previously in detail.^44,45 The results have suggested that the heme iron receives an impulsive recoil momentum when the Fe-ligand bond is broken and the ensuing heme doming oscillation occurs with a phase of π/2 or 3π/2.⁴⁵ The coherence spectra of photolabile NP4-NO also reveal a strong enhancement of the doming mode at ~30 cm^-1, the phase of which is approximately 3π/2 and 0 for the ferric and ferrous samples, respectively (Figure 6). The approximately zero phase for the doming mode in the ferrous sample is probably due to the fact that only ~50% of the sample undergoes NO photolysis. This generates a mixture of coherences in the five-coordinate photoproduct and the six-coordinate NO-bound species, yielding a complicated phase excitation profile as observed for MbNO.⁴⁴

Another photoinduced process in the heme systems that can affect the coherence spectra is ultrafast nonradiative decay.⁴⁵ Generally, the pump fields create the wave packets simultaneously on the resonant excited-state as well as on the ground-state potential surfaces. In the heme systems, however, the excited states are very short-lived, so that the wave packet in the Franck-Condon region is strongly coupled (via intermediate excited states involving the iron atom) to the ground state. This means that the rapid nonradiative decay allows the wave packet to evolve back to the ground state on timescales that are so fast (tens of femtoseconds) that very little displacement along the doming mode (vibrational period ~ 0.8 ps) takes place. Because the nonradiative decay channel is thought to involve the open shell iron d-electrons of the heme, it is likely that very strong forces act impulsively on the iron atom as the system passes through the very short-lived (d-d) excited intermediate state(s). Consequently, the doming oscillation is initiated with a ±π/2 phase in the ground state because the heme iron is subject to impulsive forces that generate momentum without a significant coordinate displacement (e.g., P_g0 ≠ 0 and Q_g0 ~ 0 in eq 6b). We are led to this hypothesis because we have observed the ±π/2 phase for doming oscillations in heme proteins even in the absence of ligand photodissociation.^44,45 In the present study, NP4-CN, NP4-H₂O, and NP4-4IPzH all exhibit the intense doming mode (Figure 5B), even though the doming distortion detected in X-ray structures is rather small (Figure 5A). Because the phases of these doming coherences are nearly π/2 (to within ± π/6), we suggest that the doming mode activation observed for these photoinert NP4 species is likely due to an impulsive momentum transfer via ultrafast nonradiative decay.

Note that we have recently suggested that the proximal His in Mb is a weaker ligand than CN and may be transiently photodissociated in the ferric MbCN complex.⁴⁵ However, the quantum yield for such a process is thought to be much lower in NP4-CN because the hydrogen bonding network increases the donor strength of the proximal His ligand. We should also note that we have observed anomalies in the doming mode enhancement in HRP and Cgb. HRP-CN has very weak activity below 50 cm^-1, whereas Cgb-CN displays strong 30 cm^-1 mode with zero phase despite a very small doming distortion.⁴⁶ Nuclear resonance vibrational spectroscopy (NRVS) measurements have suggested that the doming mode may be significantly delocalized in the protein environment;⁹² however, more recent far-IR spectroscopy and DFT calculations⁷¹ indicate that the porphyrin peripheral substituents may effectively reduce the relative iron motion and account for the diminished doming amplitude in the NRVS experiment. Further FCS studies of heme proteins and peripherally substituted model compounds are needed to enhance our understanding of the protein-dependent behavior of the doming mode activity.

Conclusion

In summary, the Soret-enhanced coherence spectra of iron porphine halides in benzene solution under C_4v symmetry are found to be consistent with predictions based on Franck-Condon and Jahn-Teller resonance Raman enhancement mechanisms. The DFT calculations and symmetry assignments agree well with the polarized frequency domain Raman spectra and, thus, give confidence to the lower frequency (<200 cm^-1) mode assignments based on the DFT calculations and the measured coherence spectra. In particular, we succeeded in using the frequency shifts induced by halide replacement to make assignments of the doming mode and the predicted combinations of γ₆ and γ₇ with the Fe-halide stretching modes. The low-frequency mode activity of the heme in NP4 is also analyzed in relation to static nonplanar heme distortions. The intensity change of the ~60 cm^-1 mode as a function of ruffling distortion indicates that it corresponds to the heme ruffling mode. The intensity enhancement is found to vary quadratically as the ruffling distortion is altered by different heme ligands. This behavior is predicted if the ground-state heme is distorted by the protein material and the resonant π-π* excitation alters the chromophore force constants. The study of the photolabile NO complex in both the ferric and ferrous states also reveals strong transient heme doming activity near 30 cm^-1. We want to emphasize that the models and analyses presented here involve a number of simplifying approximations. For example, the low-frequency modes of the heme core (porphine) must interact with the motions of its side chains and with the low-frequency density-of-states of the protein via van der Waals contacts with the surrounding amino acids. This can lead to delocalization and mixing of the vibrational excitations. To fully understand the dynamic structures and chemical reaction coordinates of heme proteins, these effects should be investigated in future work.