Characterization of protein secondary structure from NMR chemical shifts

I. Introduction

Progress in the structural biology of proteins comes from both experimental and theoretical efforts. Computational methods are capable of delivering fast structural information, ranging from low-resolution protein structural class definition to high-quality information based on homology modeling. Experimental methods that concentrate on obtaining high-resolution information are hampered by inherent time cost, and lack the capacity to provide low-resolution structural information expediently. We present a comprehensive overview of low-resolution structural determinants to correlate NMR-based chemical shift data with protein structural data in order to provide meaningful information expeditiously; i.e., prior to the intensive effort required to perform complete resonance assignments and, from these, derive three-dimensional structural information. With a historical synopsis of developments in the field, we present the underlying concepts, placing emphasis on the nuclear chemical shift, protein secondary structure, and the physical connection between them. Results from this effort have demonstrated that fast, reliable protein structural information can be obtained directly from NMR spectra prior to the complete determination of high-resolution three-dimensional structures. These methods do not provide an alternative to traditional spectroscopy-based techniques, but rather compliment them by providing low-resolution structural information very quickly. We discuss the degree to which chemical shifts of a particular nuclear species in the protein backbone can be used as a low-resolution structural parameter that correlates with a variety of protein structural parameters.

The nuclear chemical shift, first observed in nuclear magnetic resonance (NMR) spectra in 1950 by Proctor and Yu for the ¹⁴N nuclei [1] and by Arnold et al in 1957 for the ¹H nuclei [2], is among the most reliable known indicators of biomolecular structure. The development of most modern experimental pulse sequences is driven by the goal of increasing the resolution and sensitivity with which chemical shifts can be measured. In addition to structural information [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], chemical shifts provide detailed information about hydrogen bonding interactions, ionization and oxidation states, the ring current influence of aromatic residues, and the nature of hydrogen exchange dynamics[14]. Several excellent review articles describe a variety of experimental and computational methods to correlate chemical shifts with protein three-dimensional structural information [14], [15], [16], [17], [18], [19], [20]. However, these methods rely on the determination of the chemical shift of each atomic resonance in the molecule [21], which remains a challenging and time consuming procedure, despite efforts to automate the process [22], [23], [24], [25], [26], [27], [28], [29]. Moreover, it is not always possible to obtain complete assignments for a particular data set, especially for proteins undergoing conformational changes.

In addition to advances in traditional NMR-based methods, recent efforts have engendered important new approaches to investigating the structural biology of proteins. Two examples are structural proteomics and empirical correlation methods. Structural proteomics seeks to screen large numbers of proteins rapidly to identify new structural folds and to select specific sets of molecules for complete structural investigation [30], [31]. Empirical correlation methods, one example of which is homology modeling [32], [33], seek to define empirical relationships between experimental structural information and other known physio-chemical parameters in order to predict protein structure, function, and dynamics. The development of correlation methods has been fueled over the past decade both by the need for high-throughput strategies and by the advent of readily accessible, well-organized public repositories that make possible the efficient querying and mining of an unprecedented quantity of experimental information. The original, and perhaps best-known, repository of this kind is the Research Collaboratory for Structural Bioinformatics (RCSB) [34], [35], [36], [37], originally developed by Brookhaven National Laboratory, which became available to the public in 1971. Since that time, web-based repositories have become increasingly sophisticated, and are now a cornerstone of many structural biology researches.

Here, we present a comprehensive overview of empirical correlation methods whose aim is to correlate NMR-based chemical shift data with protein structural data in order to provide meaningful information expeditiously; i.e., prior to the intensive effort required to perform complete resonance assignments and, from these, derive three-dimensional structural information. We will begin with a historical synopsis of developments in the field, dating to almost 20 years ago, that includes a general discussion of fundamental, underlying concepts, placing emphasis on the nuclear chemical shift, protein secondary structure, and the physical connection between them. We will then focus on a recent effort by us to develop methods that establish and refine an empirical correlation between averaged chemical shift (ACS) and protein secondary structure content (SSC) by extensively mining chemical shift information from the BioMagResBank (BMRB) [38] and protein structural information from the PDB. We also present an overview of empirical methods for a range of applications, such as prediction of redox-state of the cystines or identification of cis-Prolines. Results from this effort have demonstrated that fast, reliable protein structural information can be obtained directly from NMR spectra prior to the complete determination of high-resolution three-dimensional structures. These methods do not provide an alternative to traditional spectroscopy-based techniques, but rather complement them by providing low-resolution structural information very quickly. This makes possible the high-throughput characterization of protein secondary structural content, and, thereby, the large-scale screening and integration of data required to accelerate efforts in fields such as structural proteomics. Further development of such empirical correlation methods for this purpose will potentially also lead to new experimental and computational protocols.

2. Empirical methods for correlating nuclear chemical shifts with protein structural data: Secondary structure index

NMR chemical shifts provide detailed information on the structure and electronic properties of biological molecules in the solution, noncrystalline and crystalline states. Chemical shifts are perhaps the most information-rich parameter obtainable from NMR; however, the physical basis for particular nuclei assuming specific chemical shift values based on the conformational state of a biomolecule is not fully understood. Although, ab initio or density functional calculations [39], [40], [41] for small peptide units provide some insight into the relevant mechanisms, at present the tools of computational chemistry remain insufficient to determine the high-resolution structure of a protein purely from chemical shifts. Consequently, we must rely upon predictive models that determine whether there exist correlations between three-dimensional structures and chemical parameters obtained from NMR. In the absence of a reliable theory, predictive models must follow semi-empirical or empirical approaches. Empirical methods use databases of previously assigned homologous molecules to predict chemical shifts of new systems. This approach is promising, particularly because the number of assigned spectra available in electronic databases continues to increase; however, it requires a reasonable level of similarity between the target and reference molecules. New combinations of semi-empirical methods have also been developed recently [42] thus paving ways to novel methods of protein structure determination from chemical shifts [43], [44], [45]. Empirical and semi-empirical methods are expected to play a significant role in NMR based structure determination in the near future.

2.1. Secondary chemical shifts in proteins

One intuitive assessment that can be made with some reliability from the chemical shift dispersion of an NMR spectrum (e.g., the ¹H spectrum of a protein) is whether the associated structure is folded or disordered. Making this determination continues to be the main goal of research efforts concerned with correlating chemical shifts and protein structure. Researchers soon learned that such straightforward and simple methods tend to predict and contribute to the final high-resolution structures. Obtaining high-quality NMR spectra is a relatively easy task, and a requisite first step toward reducing chemical shift values to a meaningful structural parameter. The empirical-statistical approach capitalizes on the vast and rapidly increasing amount of information contained in repositories of protein chemical shift data, combining these data with three-dimensional structural information to establish empirical correlations. The clear-cut trend between ‘¹H chemical shifts and secondary structure in proteins,’ which led to the definition of a ‘secondary structure shift,’ was initially recognized by Dalgarno et al. [6]. This term is also referred to as ‘conformation-dependent shift’ [46] or simply ‘secondary chemical shift.’ The secondary chemical shift $\mathrm{\Delta }{\delta }_s^i$ of a particular protein nucleus ‘i’ is defined as

$$\mathrm{\Delta }{\delta }_S^i={\delta }_S^i-{\delta }_{r.c}^i.$$ [1]

Here, ${\delta }_{\mathit{obs}}^i$ is the observed chemical shift and ${\delta }_{r.c}^i$ is the corresponding ‘random coil’ value. Though alternate definitions include a correction for ring current shifts ( $\mathrm{\Delta }{\delta }_S^i={\delta }_{\mathit{obs}}^i-{\delta }_{r.c}^i-{\delta }_{\mathit{ring}}^i$), where ${\delta }_{\mathit{ring}}^i$ is the ring current contribution [12]), the general definition expressed by Eq. [1] accounts through ${\delta }_{\mathit{obs}}^i$ for any other variations introduced by the protein.

2.2. Early efforts toward low-resolution structural information

Initial attempts to correlate chemical shift information with protein structure were carried out in the 1960s by Jardetzky and co-workers [47]. Subsequently, several groups [6], [48], [49], [50] explored the possibility of correlating protein chemical shift data with elements of regular secondary structure (helices, sheets, and turns). Szilagyi, in his comprehensive historical perspective of chemical shifts in proteins [14], credits Dalgarno et al. [6] for being the first to observe a clear-cut trend relating chemical shifts and secondary structure in proteins. On the basis of early chemical shift data from two proteins (bovine pancreatic trypsin inhibitor (BPTI) and partial assignments from hen-egg lysozyme), these authors noted that secondary chemical shifts of α-carbon protons tend to be shifted up-field for α-helical and downfield for β-sheet regions. However, progress in this area has been slow since 1987, when Jimenez et al., [51] reported secondary structure shifts of − 0.35 ppm, on average, for Hα resonances in helices, and + 0.40 ppm, on average, for Hα resonances in β-sheets based on chemical shift data from the fully assigned (¹H) spectra of five proteins. The work of Wishart and co-workers [13] provided the first extensive compilation and statistical analysis of chemical shift data in proteins, facilitating a resurgence of empirical methods for correlating chemical shifts to various structural parameters of proteins, and forming the precursor to assignment-independent NMR techniques to determine the secondary structure content of proteins. This “circular dichroism-like” (CD-like) approach has been applied successfully to a number of proteins.

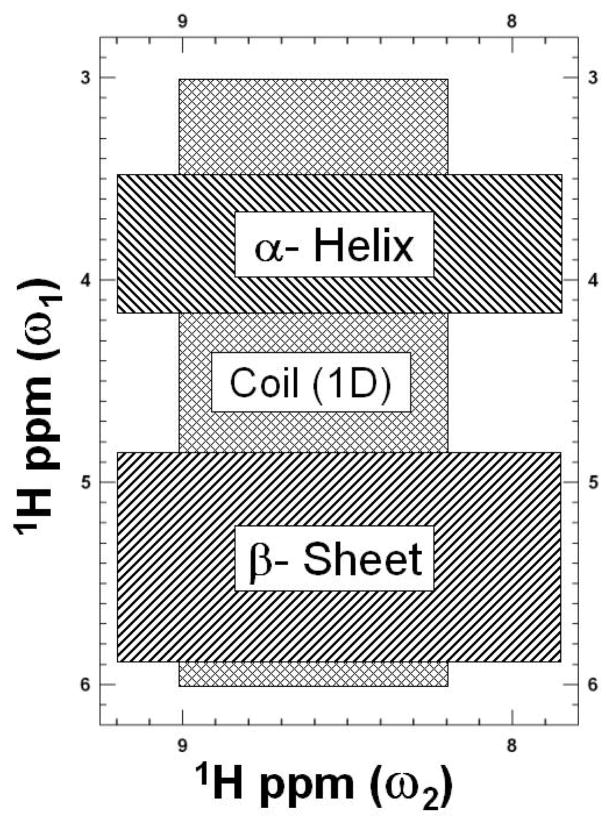
In the method developed by Wishart et al. [13], the normalized integration of amide resonances in the region between 8.20 and 9.00 ppm in a 1D proton NMR spectrum (recorded H₂O solution) provides the number of residues in coil regions of the protein (Figure 1). The number of residues in β-sheets is equal to twice the value of the normalized integral of low-field shifted resonances between 4.85 and 5.90 ppm (Figure 1,). The number of residues in a helical conformation is then obtained as the difference: = (number of β-sheet residues) − (number of coil residues). The 2D method relies on counting cross-peaks in the fingerprint (HN/Hα) region of a simple ¹H COSY or DQF (double-quantum filtered)-COSY spectrum. The number of cross-peaks (〈C〉) in the map region 8.2–9.00 ppm (ω₂) and 3.0–6.00 ppm (ω₁) is proportional to the number of residues in the random coil state; N_coil = 0.9 × 〈C〉. The number of cross peaks (〈B〉) found in the 8.20–9.00 ppm (ω₂) and 4.85–5.90 ppm (ω₁) is equal to half the number of residues in the β-sheet conformation; N_β = 2.0 × 〈B〉. The number of residues in a helical conformation can then be determined by counting cross-peaks (〈A〉) in the region 8.20–9.00 ppm (ω₂) and 3.4–4.10 ppm (ω₁). This number is to be corrected by the number of Gly residues; N_α = 2.0 × [〈A〉 − 2.0 number of Gly]. These regions are indicated in Figure 1 by various shades. It must be noted that the figure corrects for the double counting of peaks lying in overlap regions. Estimates of secondary structure elements based on this method agree surprisingly well with those from X-ray crystallography or from NOESY analysis, and it has been suggested [13] that this simple NMR ‘rule of thumb’ gives significantly better estimates than does CD or FT-IR. It is important to note that when this important work appeared in 1991, the field of structural biology was rapidly evolving. In light of the structural biology tools available today, we have reanalyzed the results of Wishart et al. [13], and present a summary of our findings in Figure 2 and Table 1.

Figure 1.

Schematic description of the peak counting method developed to determine protein secondary structure content. A typical double quantum filter COSY (DQFC) spectrum is shaded to highlight the regions of important structural information. The two hatched blocks marked by β-sheet and α-helix, correspond to the areas used to estimate the β-strand and α-helix, respectively. The hatched region marked Coil (1D) used to estimate the random coil content. Coil information is also obtained from one-dimensional NMR spectra. Some peaks appear in overlapping regions and hence are counted twice when making secondary structure estimates.

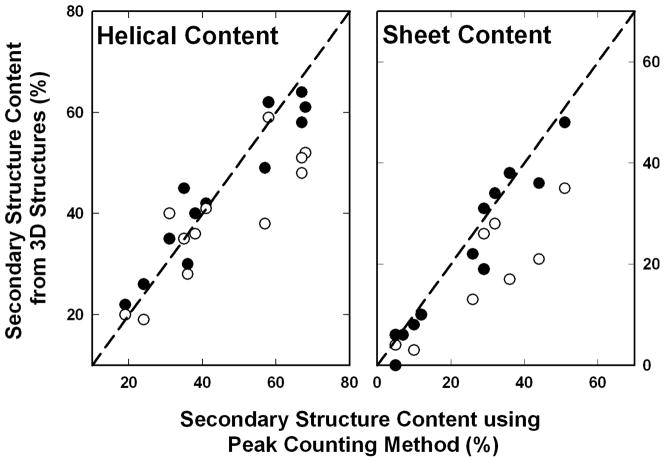
Figure 2.

Comparison of the empirical correlations derived to estimate secondary structure content from proteins by peak counting method. Filled and open circles show the secondary structure content estimated from the three-dimensional structures originally and using recent structural biology tools, respectively. The dashed lines show the ideal linear correlation.

Table 1.

Validation of the early empirical correlation methods

Protein Name	a PDB	b SSC (method 1)		b SSC (method 2)		b SSC (PROMOTIF)
		α %	β %	α %	β %	α %	β %
Acyl Carrier Protein	1ACP	61	0	68	5	52	0
α Purothionin	2PLH	35	22	31	26	40	13
BPTI	1PIT	26	36	24	44	19	21
Calmodulin	1A29	62	8	58	10	59	3
Cytochrome C	1AKK	49	6	57	7	38	0
E. Coli Thioredoxin	1XOA	40	31	38	29	36	26
HEW Lysozyme	1E8L	45	19	35	29	35	0
Human Thioredoxin	1AIU	42	34	41	32	41	28
Insulin	9INS	58	10	67	12	48	0
Parvalbumin	3PAT	64	6	67	5	51	4
Ribonuclease A	1A2W	22	48	19	51	20	35
Staph. Nuclease	1JOR	30	38	36	36	28	17

^aPDB: RCSB code of the protein

^bSSC: Secondary structure calculated using method 1 [13], method 2 [152] or PROMOTIF [52]

In 1991, it is indeed true that peak counting to determine protein secondary structure content in the absence of resonance assignments was a superior method. Based on the original estimation of secondary structure content from three-dimensional structures, a linear correlation of 0.89 and 0.94 was obtained for determining the helical and sheet content, respectively, from the peak counting method. However, using tools such as PROMOTIF [52], a generally accepted standard for secondary structure estimates, we find the correlation for estimating both helical and sheet structural contents is 0.74. Whilst the peak counting method has demonstrated utility, it has not been widely adopted; primarily it utilizes homonuclear spectra, which tend to get crowded for proteins of modest sizes. At the same time, this procedure has led to one of the most widely used methods, the chemical shift index (CSI), which utilizes both homonuclear and heteronuclear (¹³C) chemical shift information (vide infra).

Recently, Moreau et al., [53] have presented a method similar to the above mentioned approach using heteronuclear (¹³C and ¹⁵N) chemical shifts in addition to the ¹H chemical shifts. This method is called PASSNMR (Prediction of the Amount of Secondary Structure by Nuclear Magnetic Resonance). The goal of this approach and many of the other methods discussed in this article is to predict the amount of secondary structure in proteins for structural genomics applications. Overall reliability of the PASSNMR approach for helical, sheet and coiled structures are 72%, 74% and 42%, respectively and the using only the ¹⁵N-¹H data, these values drop to 49% for helix and 50% for sheets [53].

2.3. The chemical shift index method

The chemical shift index (CSI) is the first user-friendly tool for converting secondary chemical shifts to useful protein structural information [54], [55]. This method was introduced to identify the secondary structural element of each residue in a sequence-dependent manner. Prior to CSI, it was necessary to obtain the complete set of sequence-specific assignments to even get an initial glimpse of the secondary structure. The original CSI method, based on the experimental chemical shift values of a set of proteins, some empirical adjustment, and intuition, was used to develop a reference table of chemical shifts. Table 2 reproduces the values reported in the original references [55], [56]. The observed chemical shifts of the particular nuclei are then compared with the respective reference values using a set of rules. The method assigns three indices, −1, 0, or 1, depending on whether the observed chemical shift is near the average value, or at one of the extremes. Consecutive occurrences of like indices are used to identify the presence of secondary structure. To further increase accuracy, a jury system averages assignments from multiple chemical shifts (¹Hα, ¹³Cα, ¹³Cβ and ¹³C′) to arrive at a consensus assignment.

Table 2.

Chemical shift reference values used for the CSI method^a

Residue	1Hα±0.1 ppm	13Cα±0.7 ppm	13Cβ±0.7 ppm	13C′±0.5 ppm
Ala	4.4	52.5	19.0	177.1
Cys(red)	4.7	58.8	28.6	174.8
CYS(ox)		58.0	41.8	175.1
Asp	4.8	54.1	40.8	177.2
Glu	4.3	56.7	29.7	176.1
Phe	4.7	57.9	39.3	175.8
Gly	4.0	45.0		173.6
His	4.6	55.8	32.0	175.1
Ile	4.0	62.6	37.5	176.8
Lys	4.4	56.7	32.3	176.5
Leu	4.2	55.7	41.9	177.1
Met	4.5	56.6	32.8	175.5
Asn	4.8	53.6	39.0	175.5
Pro	4.4	62.9	31.7	176.0
Gln	4.4	56.2	30.1	176.3
Arg	4.4	56.3	30.3	176.5
Ser	4.5	58.3	62.7	173.7
Thr	4.4	63.1	68.1	175.2
Val	4.0	63.0	31.7	177.1
Trp	4.7	57.8	28.3	175.8
Tyr	4.6	58.6	38.7	175.7

^aAdopted from references [55], [56]

For example, a ¹Hα chemical shift that is greater or less than the CSI reference value ±0.1 ppm (Table 2) is assigned an index value of + 1 or − 1, respectively. Chemical shifts within the range ±0.1 ppm are assigned an index value of zero. Any group of four or more − 1 (not necessarily consecutive) indices uninterrupted by a + 1 identifies a helix and, likewise, any group of three or more consecutive + 1 indices identifies a β-strand. All other combinations are designated as coil. In other words, the selection criterion for secondary structure identification is set to exceed 70% of the ‘local density’ of CSIs over a window of five (for helices, 4/5 = 80%) or four (for sheets, 3/4 = 75%) residues. Termination points of helices or β– strands are defined as being either at the first appearance of a CSI value of opposite sign to an adjacent, high ‘local density’ set of values, or at the first appearance of two consecutive zero-valued CSIs. The procedure was claimed to be accurate to 90–95% after testing it on about 50 proteins [54]. Since its original description, the CSI method has been refined to account for joint probability by defining ‘consensus’ CSI values according to a simple majority rule (two out of three or three out of four) when more than two chemical shift indices are available [56]. This improvement has substantially increased the predictive power of the method.

The reliability of predictions based on the CSI method critically depends on the threshold values provided by the reference chemical shifts (Table 2). Though a quick comparison of these values with their respective random coil values might suggest approximate agreement (vide infra), some of the empirical adjustments made to provide a best fit to observed secondary structure can highly skew the distribution of chemical shifts for some residues in some structures.

2.4. Alternate methods to chemical shift index

CSI-based determination of residue-specific secondary structure is straightforward, and has become routine. NMR data processing software, such as NMRView [57], [58], allows easy implementation of these procedures following the chemical shift assignment process. In the last few years, several alternative methods have been developed that use a range of novel computational tools ranging from probability-based index identification to neural network programming. These methods include, chronologically: (1) probability-based secondary structure identification (PSSI) [59]; (2) secondary structure from chemical shift and sequence (PsiCSI) [60], (3) prediction algorithm for amino acid types with their ;secondary structure in proteins (PLATON) [61]; (4) protein energetic conformational analysis from NMR chemical shifts (PEACAN) [62], and (5) a two-dimensional cluster analysis method referred to as 2DCSi [63]. Here, we briefly describe these methods in turn, and discuss some of the advantages they offer relative to conventional CSI-based approaches.

2.4.1. Probability-based secondary structure identification (PSSI) [59]

PSSI assigns the secondary structure type (β-strand, coil, or α-helix) to each amino acid on the basis of the joint probability, derived from the observed ¹HN, ¹⁵N, ¹Hα, ¹³Cα, ¹³Cβ and ¹³C′ chemical shift data corresponding to each structure type. Based on their observed chemical shifts, nuclei are associated with particular secondary structures in a two-step process. In the first step, a joint probability is defined. Given δ_n, the chemical shift value of a particular nucleus ‘n’ in amino acid ‘i’, the secondary structure type of the amino acid is ascribed by evaluating the joint probability of the three secondary structure types, P_s,i, given by

$$P_{s,i}({\delta }_n)=F_{s,j}\prod _n{G}_{s,j}({\delta }_n),$$ [2]

Where F_s,j represents the probability for amino acid i at the secondary structure type s (s= α-helix (α), β-strand (β) or coil (C)). G_s,j is given by a Gaussian distribution

$$G_{s,j}({\delta }_n)=\frac{1}{\sqrt{2\pi {\sigma }_{n,s,i}}}exp\left(\frac{{\left({\delta }_n-{\overline{\delta }}_{n,s,j}\right)}^2}{2{\sigma }_{n,s,i}^2}\right).$$ [3]

Where, δ̄_{n,s, j} and σ_n,s,i are the center and width of the Gaussian distribution. A secondary structure type is initially assigned based on the joint probability of each type (e.g., s=α-helix, if P_α,i > P_C,i and P_α,i > P_β,i). The total probability is also set to 1 so that the residues will be in one of the three secondary structures. In the second step, which is optional, the resulting probability values are smoothed or filtered. For example, if a local density of either a β-strand or a coil exceeds one-half for a five-residue window, its secondary structure type is adjusted; ββCβC will be adjusted to βββββ (if the P value of the last residue > 0.35) or ββββC (if P < 0.35). Other rules for the end residues of a β-strand or α-helix, and short separated segments, can also be employed [59]. Global assessment of the PSSI method has suggested a significant improvement in both accuracy (~88%) and confidence over a set of 36 proteins. A JAVA interface developed by one of the authors (Y.J. Wang) is also available http://pronmr.com/yunjunwang_files/yjw_pssi.html).

2.4.2. Secondary structure from chemical shift and sequence (PsiCSI) [60]

PsiCSI combines both chemical shift-based and sequence-based methods to further increase the accuracy of secondary structure assignments [60]. In addition, it is designed to best utilize all the available data. PsiCSI begins by refining the CSI methodology; it assigns three separate potentials (scaling) ranging from 0 to 1 to reflect the relative likelihood of a given chemical shift value being associated with a given state of secondary structure (CSI assigns three indices). This approach is similar to the PSSI approach, though the actual method of calculating the potential differs. Like CSI and PSSI, PsiCSI reduces noise by polling nearby shifts. PsiCSI examines a small window of shifts (three residues) centered on the residue in question. Potentials derived from these shifts, along with the estimated residue-dependent reliabilities (i.e., probability of the assignment being correct) of these potentials, are fed into a first layer of neural networks to derive a second set of refined potentials. Multiple shifts are used to further increase accuracy. Additional information from ¹⁵N shifts and from Psipred (secondary structure prediction from protein sequence) [64], [65] predictions is also used. Rather than utilizing a simple jury system, PsiCSI trains a second layer of neural networks. Every possible combination of the available data for the residue (i.e., refined potentials from the first layer of networks and Psipred potentials) is fed into separate neural nets. Reliabilities for each combination are estimated, and the best-performing combination (for that residue type) is used to provide potentials for the next layer of neural networks. Finally, as with Psipred, a last neural net is used to take into account local interactions in a manner similar to that in which the first layer of neural nets is used to average out chemical shift noise. However, because the accuracy of the inputs at this stage is much higher, it is possible to utilize a much larger window (17 vs. 3 residues) to take into account more subtle interactions between distant residues. The most reliable outputs from the second layer, along with the estimated reliabilities, are fed into this final neural net to obtain the PsiCSI prediction.

PsiCSI achieves an accuracy of 89% (per residue), which is a significant improvement over the 82.8% (z > 12) accuracy observed for CSI. A server to use PsiCSI with sequence and chemical shift data is available from Samudrala’s group (http://protinfo.compbio.washington.edu/psicsi/).

2.4.3. Prediction algorithm for amino acid types with their secondary structure in proteins (PLATON) [61]

Prediction algorithm for amino acid types with their secondary structure, or PLATON, uses a database query approach to predict the secondary structure of a particular residue from its chemical shift values [61]. The method bases its prediction on a database consisting of reference chemical shift patterns (CSP) from the assigned chemical shifts of 51 proteins of known 3D structure. This reference CSP database is used for extracting distributions of amino acid types, along with their most likely secondary structures, for comparing single amino acid with query CSPs. The chemical shift pattern is a vector of Booleans describing relative positions of chemical shifts, and is defined by an optional combination of chemical shifts. The starting point for the definition of the CSP is the creation of an N-dimensional chemical shift space. N is determined by the kind of nuclei for which chemical shifts are available in the databases; for example, ¹³Cα, ¹³Cβ, ¹³C′, and ¹Hα, or subgroups of those. The CSP is assigned “+” or “−” elements, depending on the position of the investigated chemical shift with respect to a reference value, for all nuclei considered. The positions of the elements are defined by the axes of the chemical shift space; for example, CSP (¹³Cα, ¹³Cβ, ¹³C′) = + − +. The chemical shift value of an amino acid is compared to the value at this point. If the observed value is larger, a “+” is assigned, and if it is smaller, a “−” is assigned. Hence, for all dots in this selection, the CSP (¹³Cα, ¹³Cβ, ¹³C′) = + + + is obtained. The chemical shift space can be further subdivided by introducing reference points into the two halves of each dimension to allow for a distinction of otherwise identical CSPs. The new reference value defines another coordinate system in the upper right quadrant. Practically, the second and higher-order reference points are chosen according to a statistical analysis of all amino acid species having the same three-digit CSPs in the original coordinate.

Results obtained for the 10 investigated proteins indicate that the percentages of correct amino acid species in the first three positions in the ranking list range from 71.4% to 93.2% for the more favorable penalty function. According to the authors, the advantage of this method over those that rely on averaged chemical shift values lies in its ability to increase database content by incorporating newly derived CSPs, and therefore to improve PLATON’s performance over time. The source code for PLATON is available from one of the authors (D. Laudde, http://www.bioforscher.de/).

2.4.4. Protein energetic conformational analysis from NMR chemical shifts (PECAN) [62]

Protein energetic conformational analysis from NMR chemical shifts (PECAN) is an energy model that predicts elements of secondary structure by optimizing a combination of sequence information and residue-specific statistical energy functions to yield energetic descriptions. The energetic model presents a framework for combining the interdependent information from sequence and chemical shifts in a manner that optimizes their joint predictive potential. PECAN uses a database containing ~37,000 residues from 310 protein sequences to construct a statistical potential that is used to predict the secondary structure. An additional, non-overlapping database containing ~12,000 residues from 97 protein sequences is used to determine the model that is independent of the dataset. Equivalent unbiased criteria were used in selecting the members of each dataset, which consists of proteins with known structure and assigned chemical shifts. According to the authors, there is a marked increase in accuracy in the predicated secondary structure. The reader is referred to the original paper-describing PECAN (and supporting information) for details of the mathematical model. A web server is available at: http://bija.nmrfam.wisc.edu.

2.4.5. Two-dimensional cluster analysis method 2DCSi [63]

2D CSI (“two-dimensional cluster analyses of chemical shifts to identify protein secondary structure”) analyzes paired, two-dimensional scattering diagrams of six chemical shift data sets; i.e., six different chemical shifts (¹Hα, ¹HN, ¹³Cα, ¹³Cβ, ¹³C′, and ¹⁵NH) are used to identify the secondary structure of amino-acid residues in proteins. In a three-step approach, first the data sets of chemical shifts and protein secondary structures are collected and cross-referenced. Second, 15 cluster scattering diagrams are plotted for paired chemical shifts of the six data sets, and the clusters as a function of the secondary structure are examined. Third, score matrices created for each of 20 amino acids are used to determine the secondary structure of the residues. The probability score is estimated based on two parameters: P r(ξ| χ₁, χ₂), the probability of a ξ state for observed chemical shifts χ₁ and χ₂, and τ(χ), the sum of all 14-probability scores. The pair, (χ₁,χ₂), can take values: χ₂=c^β, χ₁=c^α, c′, n^h, h^α, or hⁿ; χ₂=c^α, χ₁= c′, n^h, h^α, or hⁿ; χ₂=c′, χ₁= n^h, h^α, or hⁿ; χ₂=n^h, χ₁= h^α, or hⁿ; and χ₂= h^α, χ₁= hⁿ. Here, c^α, c^β, c′, n^h, h^α and hⁿ are the chemical shift values of ¹³Cα, ¹³Cβ, ¹³C′, ¹HN, ¹Hα, and ¹⁵NH, respectively. In addition, ξ can be helix (H), extended In addition, ξ can be helix (H), extended structure (E), or random coil (C), defined as neither helix nor extended structure. From the two-dimensional cluster analysis, three situations of Pr (ξ| χ₁,χ₂) can arise: (i) (χ₁,χ₂) falls outside all clustered elliptical areas; (ii) (χ₁, χ₂) falls onto one and only one elliptical area; (iii) (χ₁, χ₂) falls onto an intersection area of two ellipses. A set of rules is then used to make the prediction. These rules are: (a) add up probability scores of each column in the scoring matrix to obtain the total score τ(χ) for secondary structure states, and (b) identify any secondary structural state ζ if and only if τ(χ) ≥ 0.8×λ, where 0.8 represents the decision threshold (decided based on the target data of 601 entries), λ is the total number of resonances used.

2DCSi uses a dataset containing ~40,706 residues from 336 non-redundant proteins. The performance of 2DCSi is compared [63] with that of CSI and psiCSI using a set of 45 reference-corrected proteins for the prediction accuracy of three secondary structure states. Though the authors mention web-server (http://www.ncku.2dsci.idv.tw/) is available for using 2DCSi, it is not possible to access the program.

2.4.6. Comparison of the methods

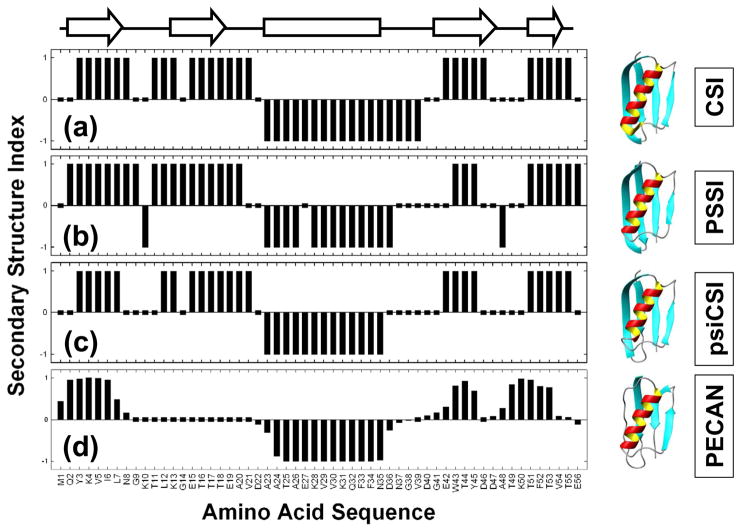
In order to compare the performance of the different methods, we calculated the secondary structure index (+1, 0 and −1, to represent β-strand, coil and α-helix, respectively) of a small protein (Protein G). Figure 3 shows the secondary structure index calculated using: (a) CSI, (b) PSSI, (c) psiCSI and (d) PECAN. We are unable to make a similar calculations using 2DCSi and PLATON as these codes were not available at the time of this study at the URLs mentioned in the respective manuscripts. The chemical shift values of protein G were obtained from the biological magnetic resonance bank (BMRB) (access number bmr5654.str). Figure 3 also shows the secondary structure estimated from an NMR-determined three-dimensional structure (the average structure corresponding to PDB ID 1GB1) using the Kabsch-Sanders algorithm in MOLMOL [66]. The secondary structures estimated by these respective methods are also superimposed on the three-dimensional structure in Figure 3. The codes for the above-mentioned programs were used with no further modification. Protein G is one of the most extensively studied proteins by either NMR or X-ray crystallography [67], [68], [69], [70]. It has 56 residues and is classified as an alpha and beta (α+β) protein [71], [72]. One important feature of the comparison is that no two methods give the same results, likely because their criteria for secondary structure identification based on the chemical shift data are inherently different. Therefore, it is important to be aware of how each method determines the secondary structure, and to exercise caution when using this information as a structural constraint upon 3D structural models. In general, the methods exhibit a broad consensus as to the location of most helix and strand core segments in protein structures; however, the termini of the segments are inconsistently defined.

Figure 3.

Plot of the secondary structure indices calculated for Protein G using four different methods, (a) CSI, (b) PSSI, (c) psiCSI and (d) PECAN. Secondary structure indices, +1, 0 and −1 correspond to α-helix, coil and β-strand, respectively. The chemical shift information is obtained from BMRB (bmr5664.str) and the programs CSI, PSSI, psiCSI and PECAN are used with their default setup. The arrows and the bar at the top of the figure are the secondary structure determined from the ensemble averaged NMR structures (RCSB file 1GB1) and the respective secondary structures are also superimposed on the 3D structure, using the molecular rendering program MOLMOL [66].

In our experience, in addition to the choice of algorithm, the choice of reference chemical shift (often referred to as the random coil chemical shift) used to determine the secondary chemical shift itself can introduce significant variation in secondary structure estimations. This issue is addressed in the following section.

2.5. Effect of reference chemical shifts on protein secondary structure estimation

Reference (random coil) chemical shifts are integral to defining the secondary chemical shifts in proteins that translate into protein secondary structure information. As discussed previously, though various techniques for estimating protein secondary structure from chemical shift data are widely employed and seem fairly reliable, at least for folded proteins, the choice of reference chemical shift values can significantly alter the outcome of secondary structure estimation. Random coil chemical shifts are the characteristic chemical shifts of the nuclei constituting the amino acid residues of disordered proteins. The effect of a particular secondary structure on the observed chemical shift known as the secondary chemical shifts are predominantly influenced by non-covalent interactions, such as secondary structural changes, hydrogen bonds, and aromatic stackings.

The primary goal of the work presented by Mielke and Krishnan [73] was to evaluate the effect on secondary structure prediction of using differing random coil chemical shift reference tables in conjunction with the CSI algorithm or, in principle, any of the alternative methods. The secondary structure content (the total percentage of helical and sheet content) of a set of 396 folded proteins was calculated using the consensus CSI method. Corresponding structural information was calculated from the three-dimensional structural coordinates of the proteins. A comparison of the results obtained using five different reference tables for CSI calculations to those obtained using a structure-based method allows a critical evaluation of the reliability of the standard protocol for evaluating secondary structure from chemical shift information using CSI.

Here we highlight some of these findings based on five different reference random coil chemical shift value sets and their respective use in estimating protein secondary structure. In general, the results show that none of the reference random coil data sets chosen for evaluation fully reproduces the actual secondary structures. Among the reference values generally available to date, most tend to be good estimators only of helices. On the basis of this, we recommend the experimental values measured by Schwarzinger et al. [74], and the statistical values obtained by Lukin et al. [75], as good estimators of both helical and sheet content.

List of reference chemical shift values

There are several reference random coil chemical shift tables in the literature, and these can be classified into two types: those measured experimentally, and those derived statistically. The complete details of these tables, including a description of the experimental conditions under which they were obtained, and their respective references, are given in Table 3. Of the various references listed in Table 3, only six different random coil chemical shift values that follow the recommendations of Wishart and Nip [20] are used for further analysis. In what follows, these five sets are identified by the initials of the first and last authors of the references as KW, WS, SD, LH, WJ and WM; Wüthrich et al. [21], [76], Wishart and Sykes [19], [77], [78], Schwarzinger et al. [74], Lukin et al. [75], Wang and Jardetzky [79], and Wang et al. [80], respectively (shown as block letters in Table 3). Of these six datasets, our study uses the first five for the analysis. Of the five chosen data sets, three were experimentally derived, while two were obtained using statistics-based approaches. We have re-referenced KW and WS, originally referenced to TMS/Dioxane, to DSS. Since reference table LH does not derive ¹Hα values, the ¹Hα reference values of Wang and Jardetzky [79] were used for structure estimation using LH. Though the experimental values of Plaxco et al. [81] are relevant for the comparison, these were not considered for the analysis due to lack of heteronuclear chemical shift values.

Table 3.

List of various reference random coil chemical shift data

Experiment- based random coil shifts
Sample	Nuclei	Solvents	Reference	T (° C)	pH	Correction	Reference
H-GG-X-A-OH	1H, 13C	D2O	TMS	35	Varied	None	[192], [193]
Apamin, BPTI	1H, 15N	90% H2O/10% D2O	TSP	50, 65	2.2–4.6	None	[194], [195]
GG-X-GG	13C	D2O/10, 20, or 30% acetonitrile or TFE	TSP	25	2.0–3.5	None	[196]
H-GG-X-A-OH (KW)	15N	90% H2O/10% D2O	TSP	35	2.0 and 5.0	Sequence- corrected	[21], [76]
H-GG-X-GG-OH	1H	90% H2O/10% D2O and TFE% varied	DSP	278–318	5.0	None	[197]
GG-X-Y-GG, Y=A, P (WS)	1H, 13C, 15N	95% H2O/5% D2O	DSS	25	5.0	Nearest neighbor	[77], [78]
Ac-GG-X-GG-NH2	1H	90% H2O/10% D2O (50mM Sodium Phosphate) 2, 3, 6, 8 M GuHCl	DSS	20	5.0	None	[81]
Ac-GG-X-GG-NH2 (X=phosphorylated amino acid)	1H, 13C, 15N	90% H2O/10% D2O	DSS	25	2.0–9.0	None	[198]
Ac-GG-X-GG-NH2(SD)	1H, 13C, 15N	90% H2O/10% D2O and 8M Urea	DSS	20	2.3	None	[74]
Ac-GG-X-GG-NH2	1H, 13C, 15N	90% H2O/10% D2O	DSS	20	2.3	Sequence- corrected	[74], [90]
Statistically derived random coil shifts
Method	Nuclei	Solvent condition	Referenced to	T (° C)	pH	Correction	Reference
Manual	1H, 13C, 15N	Aqueous solution	DSS	-	-	None	[77], [78]
Probability-based (LH)	13C, 15N	Aqueous solution	DSS	-	-	None	[75]
Probability-based (BMRB)	1H, 13C, 15N	Aqueous solution	DSS	-	-	None	[79]
Probability-based (WJ)	1H, 13C, 15N	Aqueous solution	DSS	-	-	Neighboring residue effect
Data base derived (WM)	13C,	Aqueous solution	DSS	-	-	Re—references using RefDB	[80]

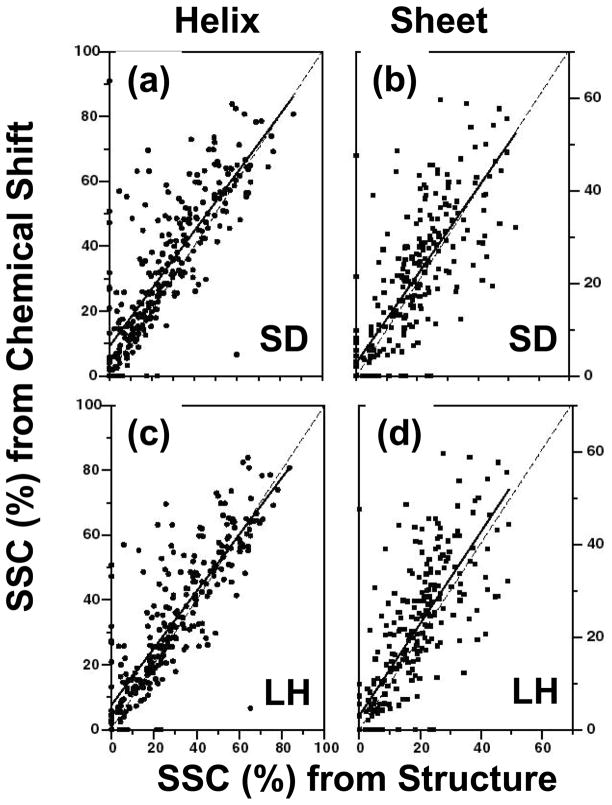
Figure 4 shows the results of estimating the percentage of helical (left panels) and sheet (right panels) content determined from the random coil chemical shift tables, SD and LH, respectively, using CSI, versus the same content calculated from relevant three-dimensional structures. The dashed lines in the figures correspond to an ideal correlation, and the solid lines to an unbiased linear regression analysis of the data. Table 4 lists the coefficients (slope and intercept) of the fit, and the correlation coefficients of the regression analysis. Chemical shift values corresponding to protein atoms were obtained from BMRB NMR-STAR files [38]. Only proteins with 50 or more amino acid residues were considered, since these are expected to contain a significant amount of secondary structure. Further, only proteins with at least 70% of their residues assigned chemical shifts were considered. As nearly all recently submitted BMRB chemical shifts are referenced using the widely accepted standard procedure recommended by Wishart [77], no re-referencing was performed. The consensus chemical shift index (CSI) of the proteins was calculated using the procedure outlined by Wishart and Sykes [55], using nuclei that are known to be highly sensitive to secondary structural changes (¹Hα, ¹³Cα, ¹³Cβ and ¹³C′). Structure files were obtained from RCSB( http://www.rcsb.org/pdb/) [35], [82]. Since most BMRB NMR- STAR files identify several corresponding PDB structures, it was necessary to examine each entry and choose by inspection the most appropriate PDB ID number. When possible, the PDB ID corresponding to the “best” NMR structure was chosen, though in some cases it was necessary to choose the best X-ray structure (resolution < 2.5 Å). A total of 396 proteins was found to be suitable, and downloaded from the Protein Data Bank. The total percentage of sheet and helix (α and 3₁₀) was determined using the program PROMOTIF (http://www.biochem.ucl.ac.uk/~gail/promotif/promotif.html) [52], which uses the atomic coordinate files obtained from the RCSB. Uncertainties in the former were obtained by a linear model bootstrapping procedure using the R statistical package (www.cran.us.r-project.org) with 512 bootstrap replicates. Based on this analysis, several distinct features are observed.

Figure 4.

Plots of secondary structure content (SSC) in percentage determined from chemical shifts and three-dimensional coordinates. Panels (a) helical and (b) sheet content for the original SD [74], [90] random coil reference values correspond to (Table 3), while (c) and (d) show the corresponding correlations for using the random coil chemical shifts of LH [75]. The dashed line corresponds to an ideal correlation, while the solid line represents the linear regression analysis results (Table 5).

Table 4.

Linear regression analysis of CSI vs. structure-based helical and sheet content estimates

Random coil reference	Helical content (%)			Sheet content (%)
	Intercept	Slope	CCa	Intercept	Slope	CCa
KW [21], [76]	5.33±0.88 − 3.45±1.02	0.91±0.02 0.82±0.03	0.82 0.77	4.56±0.59 8.11±0.58	0.95±0.02 1.03±0.03	0.77 0.67
WS [77], [78]	1.21±1.06	0.80±0.03	0.86	5.79±0.69	0.84±0.03	0.73
SD [74]	6.6±0.85	0.93±0.02	0.88	4.27±0.61	0.91±0.03	0.77
LH [75]	5.97±0.89	0.89±0.02	0.90	4.12±0.58	0.98±0.02	0.79
WJ [79]	6.92±0.77	0.94±0.02	0.88	6.6±0.61	0.96±0.03	0.73

^aCorrelation coefficient.

Figure 4 contains several significant outliers along both the abscissa and ordinate. Points along the abscissa are primarily representative of poor quality chemical shift data (inappropriate references and assignments), while points along the ordinate might represent large discrepancies between the chemical shift data and corresponding three-dimensional structures. Though removing these outliers might have affected the correlations (Table 4), they were left in the data set in order that our results reflect as accurately as possible the quality of available experimental information.

The correlations (Figure 4 and Table 4) suggest that chemical shift-based methods for predicting secondary structure content are better indicators of helical regions than sheet regions in proteins. This could be due to insufficient sensitivity of secondary chemical shifts for identifying sheets. Ambiguity in the definition of a β-sheet, by contrast with that of an α-helix, may also contribute to this error [83], [84]. In calculating the secondary structure content from three-dimensional coordinates, we have used the program PROMOTIF, which uses the DSSP (database of secondary structure assignments) algorithm of Kabsch and Sander [85]. Definitions of secondary structure by PROMOTIF [52] closely follow IUPAC convention rule 6.3, and have been widely accepted amongst crystallographers. Other commonly used programs for secondary structure determination include STRIDE (secondary structure assignment from atomic coordinates) and DEFINE (determine the secondary and first level supersecondary structure) [85]. Cuff and Barton [86] have performed a comprehensive comparison of these three methods (DSSP, STRIDE and DEFINE), and shown that DSSP and STRIDE have an overall and segment-wise agreement of 95%. As the secondary structure definitions are based on the coordinates of a model derived by X-ray crystallography or NMR, any algorithm will be affected by the quality of the underlying data. The best estimation rate varies widely depending on the choice of algorithm [86], [87], [88]. However, of the many different methods of defining secondary structure proposed, DSSP has most successfully stood the test of time, and is widely used in the field of structural biology. Consequently, using PROMOTIF to perform NMR-based secondary structure calculations seems well justified. Moreover, any variation in the secondary structure content determined from three-dimensional coordinates, though it might alter correlations with secondary structure predicted from CSI using a given reference set of random coil values, will not influence systematic variations arising from the use of different reference sets.

2.6. Note on random coil chemical shifts

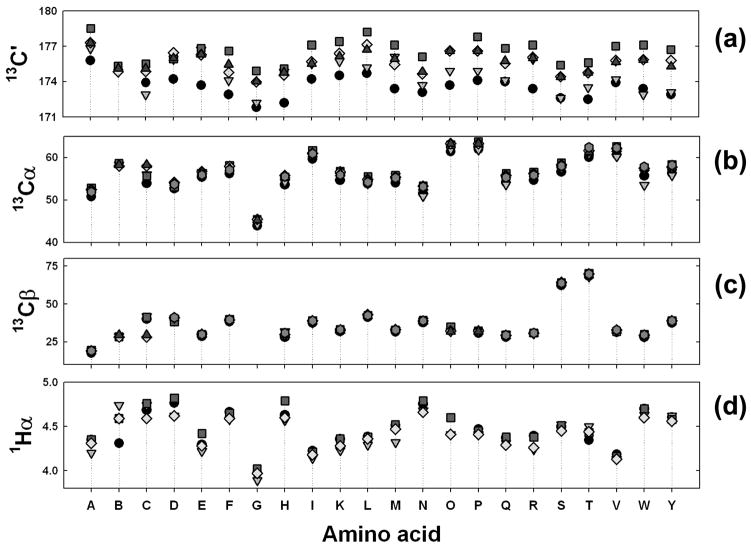
Variations in the random coil values

Reference (random coil) chemical shifts used in many of the methods for secondary structure estimation vary widely (Figure 5 and Table 5). The degree of variation in the estimated secondary structure contents using the various reference random coil chemical shift sets suggests the importance of investigating the origin of differences between the values they contain. Figure 5 shows a plot of the reference random coil shifts of ¹³C′, ¹³Cα, ¹³Cβ and ¹Hα in panels a, b, c and d, respectively, for all the amino acids. Residue types are identified by their single-letter amino acid codes, with B and O corresponding to reduced cystine and cis-proline, respectively. The largest differences in the random coil values are seen for the ¹³C′ nuclei, more modest differences for the ¹³Cα and ¹Hα spins, and the least variability for the ¹³Cβ nuclei. Visual inspection of the ¹³C′ chemical shifts (Figure 5a and Table 5) shows that in general the experimental reference values obtained in for an aqueous solution at 35 °C (reference shifts KW, marked as black circles) are lowest, and the experimental values obtained in aqueous solution with 8M Urea (reference shifts SD, marked as black squares) are the highest (see also Table 5). Values in the third experimental reference shift set (WS, filled squares) tend to be close to those in SD, while those in both statistical sets (LH and WJ, shown as stars and plus signs, respectively) fall mostly between the limits of WH and SD. Figure 5 suggests that contributions from random coil reference shifts corresponding to carbonyl nuclei, which are perhaps the most sensitive to protein structural changes, introduce the largest variability.

Figure 5.

Plots of the variation in the reference random coil values as a function of amino acid type. Panels (a), (b), (c) and (d) correspond to random coil values of ¹³C′ (carbonyl carbon), ¹³Cα, ¹³Cβ and ¹Hα, respectively. The six different reference value sets are represented by symbols: black circles (KW) [21], [76], grey triangles (WS) [77], [199], black squares (SD) [74], [90], grey diamonds (LH) [75], black triangles (WJ) and grey circles (WM) [59], [80]. Plots (b) and (c) have all the six sets and plots (a) and (b) have only 5 and 4 sets, respectively (Table 5). Amino acids along the X-axis are given in single letter codes, with ‘B’ and ‘O’ representing oxidized cystine and cis-proline, respectively.

Table 5.

List of random coil chemical shift values

AA	13C′ (ppm)						13Cα (ppm)					13Cβ (ppm)						1Hα (ppm)
	KW*	WS*	SD	LH	WJ	KW*	WS*	SD	LH	WJ	WM	KW	WS*	SD	LH	WJ	WM	KW	WS	SD	LH/OJ
A	175.8	176.8	178.5	177.3	177.3	50.8	51.9	52.8	52.4	52.5	51.9	17.7	19.0	19.3	19.0	19.0	19.1	4.3	4.2	4.4	4.3
B	--	174.8	175.3	174.8	175.1	-	58.3	58.6	58.0	58.2		-	28.6	28.3	28.2	29.5		4.3	4.7	4.6	4.6
C	173.9	172.9	175.5	174.8	175.1	53.9	56.0	55.6	58.0	58.2		40.0	41.8	41.2	28.2	29.5		4.7	4.7	4.8	4.6
D	174.2	175.9	175.9	176.5	176.0	52.7	53.2	53.0	54.1	54.0	53.7	39.8	40.8	38.3	40.8	40.8	41.1	4.8	4.6	4.8	4.6
E	173.7	176.7	176.8	176.3	176.3	55.4	56.5	56.1	56.7	56.7	55.9	28.7	29.7	29.9	30.1	29.9	29.9	4.3	4.2	4.4	4.3
F	172.9	174.1	176.6	174.8	175.5	56.2	57.5	58.1	57.9	57.5	57.1	38.4	39.3	39.8	39.3	39.4	39.6	4.7	4.6	4.7	4.6
G	171.8	172.2	174.9	174.0	174.0	43.9	44.2	45.4	45.4	45.3		-	-	-	-	-		4.0	3.9	4.0	4.0
H	172.2	174.8	175.1	174.5	174.8	53.6	54.2	55.4	55.8	55.7	55.5	28.1	32.0	29.1	29.8	29.5	30.9	4.6	4.6	4.8	4.6
I	174.2	175.5	177.1	175.7	175.5	59.6	60.6	61.6	61.0	60.8	60.9	37.5	37.5	38.9	38.9	38.4	38.8	4.2	4.1	4.2	4.2
K	174.5	175.7	177.4	176.4	176.2	54.6	55.7	56.7	56.6	56.3	55.9	31.9	32.3	33.2	32.6	32.5	33.1	4.4	4.2	4.4	4.3
L	174.7	175.2	178.2	177.2	176.7	53.8	53.9	55.5	54.8	54.8	54.2	41.2	41.9	42.5	42.8	42.1	42.4	4.4	4.3	4.4	4.4
M	173.4	176.1	177.1	175.5	175.9	54.0	55.7	55.8	55.3	55.4	55.2	31.7	32.8	32.9	33.0	32.9	32.9	4.5	4.3	4.5	4.5
N	173.1	173.7	176.1	174.7	174.8	51.5	50.9	53.3	53.2	53.0	53.1	37.7	39.0	39.1	38.7	38.4	38.9	4.8	4.7	4.8	4.7
O	173.7	174.9	--	176.6	176.6	61.4	61.8	63.0	63.3	63.2		33.0	31.7	34.8	32.1	31.8		-	4.4	4.6	4.4
P	174.1	174.9	177.8	176.6	176.6	61.9	61.8	63.7	63.3	63.2		30.6	31.7	32.2	32.1	31.8		4.5	4.4	4.5	4.4
Q	174.0	174.1	176.8	175.5	175.8	54.1	53.6	56.2	55.8	55.9	55.3	28.1	30.1	29.5	29.3	29.0	29.4	4.4	4.3	4.4	4.3
R	173.4	175.9	177.1	176.1	176.0	54.6	55.7	56.5	56.3	56.2	55.8	-	30.3	30.9	30.6	30.4	30.9	4.4	4.2	4.4	4.3
S	172.6	172.6	175.4	174.4	174.4	56.6	57.4	58.7	58.3	58.2	58.0	62.3	62.7	64.1	64.1	63.8	63.8	4.5	4.5	4.5	4.5
T	172.5	173.5	175.6	174.8	174.8	60.1	60.8	62.0	61.6	61.3	62.4	68.4	68.1	70.0	69.8	68.9	69.8	4.3	4.5	4.4	4.4
V	173.9	174.2	177.0	175.8	175.7	60.7	60.2	62.6	62.1	62.0	62.3	31.4	31.7	31.8	32.7	32.4	32.9	4.2	4.1	4.2	4.1
W	173.4	172.9	177.1	175.9	175.9	55.7	53.5	57.6	57.5	57.5	57.8	28.1	28.3	29.8	29.1	29.6	29.6	4.7	4.6	4.7	4.6
Y	172.9	173.1	176.7	175.8	175.3	56.3	55.8	58.3	57.8	57.6	58.2	37.5	38.7	38.9	38.9	38.8	38.8	4.6	4.6	4.6	4.6

AA: Single letter amino acid codes correspond to: A: Ala, R: Arg, N: Asn, D: Asp, B: Cys (reduced), C: Cys (oxidized), Q: Gln, E: Glu, G: Gly, H: His, I: Ile, L: Leu, K: Lys, M: Met, F: Phe, O: Pro (cis), P: Pro (trans), S: Ser, T: Thr, W: Trp, Y: Tyr, and V: Val.

Random coil chemical shifts obtained given by KW [21], [76], WS [77], [78], SD [74], LH [75] and WJ [79]

KW^* and WS^*: Carbon chemical shifts were originally referenced to TMS/Dioxane. These have been re-referenced to DSS in the calculations. All other chemical shifts are referenced to DSS or TSP, and are obtained from the references listed in Table 3 of the main text.

Sequence-dependent effects

According to Flory [89], a “random coil” is independent of influences from neighboring residues. However, sequence-dependent corrections of random coil chemical shifts have recently been noted using experimental [77], [78], [90] and statistical [79] methods. Schwarzinger et al. [90] have experimentally studied a subset of penta-peptides to investigate the effect of neighboring residues on the observed chemical shift, and elegantly utilized the results to determine the residual secondary structures in partially unfolded proteins. Wang and Jardetzky [79] have recently determined a statistical distribution of nearest neighbor effects from chemical shift data obtained from the BMRB. Though the nearest-neighbor effects determined by the statistical method bear a trend similar to that of the experimental results in a solution of 8M urea for random coil chemical shifts, the former approach inherently assumes that residues that are neither helical nor sheet must be “random coil.” In practice, however, it would be necessary to collect experimental data on at least 8000 different tri-peptide samples to determine nearest-neighbor effects completely. Since this would require a monumental effort, and none of the available databases provide a complete set of experimental random coil chemical shifts, we have not accounted for nearest neighbor effects.

One must be able to define what is a ‘random coil’ of a polypeptide, before addressing the question of what is a ‘random coil chemical shift’? This issue seems to have attracted considerable attention in recent literature, particularly with respect to proteins that are ‘intrinsically unstructured’ [91]. The original definition of Flory [89], corroborated by Tanford [92], defines the random coil state of a peptide as one in which the backbone dihedral angles, φ and ψ, of each amino acid residue are independent of the conformations of neighboring residues. Alternatively, a random coil is sometimes defined as a reference state in which sidechain-sidechain interactions are absent [93], which neglects the intrinsic folding propensities of amino acids. In developing a probabilistic model to estimate the random coil chemical shifts of carbon-13 chemical shifts from protein chemical shift databases (such as BMRB), Wang et al. [80] adopt the following definition: a state in which the geometry of the polypeptide ensemble samples the allowed region of (φ,ψ)-space in the absence of any dominant stabilizing interactions.

To define a secondary chemical shift, one needs first to define a reference chemical shift. In the absence of methods able ab initio to predict structural effects on measured chemical shifts, the choice of reference chemical shift assumes an important role. According to Vila et al. [94], NMR-based chemical shift methods to date have not focused on statistical coil peptides, mainly because of the intrinsic difficulties associated with the characterization of unstructured states; i.e., the experimentally-determined (NMR) chemical shift values for statistical coil peptides are not associated with a unique set of canonical dihedral angles, making a theoretical description of non-structured states difficult to achieve. Studies of the factors that affect the chemical shift are very important, because NMR methods used to determine secondary structure (e.g., CSI and others discussed earlier) rely heavily on a comparison with the chemical shifts of the so-called statistical coil, which is frequently, but erroneously, referred to as a random coil [94].

A considerable amount of effort has gone into determining random coil chemical shifts, but the specific consequences of using a particular data set to determine protein secondary structures have not been investigated in detail. Over a selected set of well-characterized protein structures, it has been suggested that CSI-based secondary structure determination is 93% accurate in comparison to X-ray structure-based determinations [19]. Our analysis of a considerable amount of raw data from the BMRB and PDB shows that CSI estimates helical and sheet structures to an accuracy of only 90% and 79%, respectively. These results do not reflect the quality of the CSI method itself, but rather the sensitivity of the method to the choice of reference chemical shifts, and the large variation inherent in chemical shift data. Our results further suggest that secondary chemical shifts are more reliable for identifying helical regions of proteins than strand regions. Sharman et al. [95] have recently proposed that long-range effects from distant amino acids are one of the dominant factors in determining experimental chemical shifts in β-sheets. The absence of a good correlation for β-sheets in the data presented here is perhaps suggestive of this. Though rigorous experimental and statistical methods have been able to estimate random coil shifts more accurately in the last decade, our findings indicate that additional experimental and theoretical developments are mandatory for an explanation of the observed deviations. The present analysis forms a critical evaluation of the current status of the reliability of secondary chemical shifts as a direct refinement parameter in structure calculations. Though caution must be advised, since this work relies only on secondary chemical shifts, it nevertheless suggests the importance of pursuing a combined experimental, theoretical, and database-driven approach to secondary structure estimation that can provide a better understanding of the factors governing both the chemical shift, and its relationship to protein structure. From a practical point of view, one might want to know what is the best set of reference (random coil or statistical coil) chemical shifts (or combination of sets) to estimate the secondary or even tertiary structure in proteins. Evaluations of the different choices of reference set have shown clear discrepancies, and suggested which choices are best for specific sets of proteins [73], [80]. However, a complete understanding of the origin of these effects, and of how well a ‘secondary chemical shift’ can be defined for purposes of accurate estimation of secondary structure, remains a challenge.

2.7. Secondary chemical shifts in DNA and RNA

In contrast to the extensive development of empirical and semi-empirical chemical shift methods for proteins, these methods are limited for DNA and, in particular, for RNAs. Though a discussion on nucleic acids might sound anomalous in an article that focuses on proteins, from the point of view of secondary chemical shifts in biopolymers in general, this section makes it complete. Lam and co-workers have extensively contributed to the measurement and categorization of random coil and B-form DNA chemical shifts [96], [97], [98], [99], while work on RNA is essentially limited to work by Cromsigt et al. [100]. Chemical shift-structure relationships in DNA can provide a quick reference guide for resonance assignments based on conventional experiments, thus facilitating solution structure studies of DNAs. These results can also provide useful information for studying structure–chemical shift relationships, identifying unstructured or right-handed double helical regions, monitoring DNA–drug or DNA–protein binding, and investigating conformational details of special features in DNA structures [101], [102], [103], [104].

Chemical shift information in DNA contains a wealth of structural information that is seldom used extensively. Over the last few years, methods have been established to predict chemical shifts of DNAs in random coil form (single stranded) [96], [97], [99] and double-helical B-form [105], [106]. These methods are based on sets of reference chemical shift values and correction factors from experimental measurements, statistical analysis or semi-empirical calculations. Shielding or deshielding contributions from nearest neighbor and/or next-nearest neighbor nucleotides have been included in these prediction methods.

To automate these prediction methods, Lam has established a web server called ‘DSHIFT’ for predicting random coil or double-helical B-DNA chemical shifts of any specific sequence (http://www.chem.cuhk.edu.hk/DSHIFT,).

Random coil chemical shifts in DNA are more sensitive to the nearest neighboring residues (contradicting the conventional definition of a ‘random coil’), and therefore a pentamer or triplet model must be defined. In the case of a triplet model, for each residue (e.g., the base ‘C’), there are 16 possible chemical shift values. For random coil proton prediction, DSHIFT uses a pentamer model: $N_2^{5^{\prime }}{N}_1^{5^{\prime }}{XN}_1^{3^{\prime }}{N}_2^{3^{\prime }}$. Here the prediction is based on the triplet chemical shift, ${\delta }_{\mathit{triplet}}\left(N_1^{5^{\prime }}{XN}_1^{3^{\prime }}\right)$, and a correction factor is invoked to account for the effects of second nearest neighbors using the expression:

$$\delta \left(N_2^{5^{\prime }}{N}_1^{5^{\prime }}{XN}_1^{3^{\prime }}{N}_2^{3^{\prime }}\right)={\delta }_{\mathit{triplet}}\left(N_1^{5^{\prime }}{XN}_1^{3^{\prime }}\right)-{\mathrm{\Delta }}_2^{5^{\prime }T}-{\mathrm{\Delta }}_2^{3^{\prime }T}+{\mathrm{\Delta }}_2^{5^{\prime }N}+{\mathrm{\Delta }}_2^{3^{\prime }N}.$$ [4]

Here, ${\mathrm{\Delta }}_2^{5^{\prime }T}$ and ${\mathrm{\Delta }}_2^{3^{\prime }T}$ are the 5′ and 3′ nearest neighbor thymine effects on the central residue (X) and ${\mathrm{\Delta }}_2^{5^{\prime }N}$ and ${\mathrm{\Delta }}_2^{3^{\prime }N}$ are the corresponding effects on X in the predicted sequence. Modifications for the terminal residues are accounted for separately in the prediction algorithm, as the 5′ and 3′ phosphate groups at the termini are absent [98], [105]. For random coil carbon chemical shifts, the prediction method is based on a trimer model, as only nearest neighbor effect has been found to be significant [97].

For prediction of double-helical (B-form) DNA, DSHIFT can use either the methods introduced by Altona et al., [105] or Wijmenga at al., [106]. In Altona’s method, proton chemical shift prediction is based on a trimer model in which an incremental scheme and statistical reference values from experimental results are used [105]. In Wijmenga’s method, the proton chemical shift of a specific nucleotide is predicted based on a set of calculated reference shift values (δ_ref) plus the chemical shift effect induced by its own base (δ_ib), as well as its 3′ (δ_3′b) and 5′ (δ_5′b) neighboring bases [106]. As noted by Lam [98], the prediction accuracy of the various methods depends mainly on DNA conformations. Since temperature and solution conditions affect stabilities of DNA structures, it is expected that these factors will also affect the prediction accuracy.

3. Empirical methods correlating averaged chemical shifts (ACS)

3.1. Basic concepts: averaged chemical shifts, protein secondary structure content, and protein structural class

3.1.1. Averaged chemical shifts

The averaged chemical shift (ACS) of a nucleus, i, is defined by:

$$AC{S}_i\equiv (1/N){\mathrm{\sum }}_{k=1,N}{\omega }_k,$$ [5]

where N is the total number of observed cross peaks (typically in a single bond-correlated spectrum, such as a heteronuclear single quantum correlation, HSQC) and ω_k is the corresponding chemical shift of the k^th resonance (referenced using recommended procedures [78]). Averaged values of chemical shifts of random coil proteins were also calculated from the respective amino acid sequences using recently published experimental values [74], [90].

3.1.2. Protein secondary structure content

Protein secondary structure content refers to the proportion of each secondary structure type constituting a given protein. Formally, it is defined as the ratio of the number of residues in a certain secondary structure to the number of total residues of a protein. According to the conventional classification by DSSP [107], there are eight secondary structure types, namely, α-helix,β-strand, β-bridge, three-turn helix, π-helix, hydrogen-bonded turn, bend, and random coil. Protein secondary structure provides fundamental information about proteins, and knowing a protein’s secondary structure content is often the first step towards more detailed knowledge of its structure and function.

Protein secondary structure content can be semi-empirically estimated using variants of spectroscopic methods, such as UV-Raman [108], CD [109], FTIR [110] and NMR [111]. However, generally speaking, these experiment-based approaches have been of questionable accuracy [112], [113]. For that reason, there have been many attempts to make ab initio predictions of secondary structure content [114], [115], [116], [117], [118], [119], [120], [121]. Among notable early attempts to do so are the multiple linear regression approach [122], [123], [124], [125], [126], [127], [128], [129], the artificial neural network approach [121], and the analytic vector decomposition approach [130], [131]. Of course, the validity of such approaches ultimately depends on the accuracy with which they predict the actual secondary structure contents of proteins, so experimental methods continue to play a significant role in these efforts.

3.1.3. Protein structural class

Classification and prediction of protein structure are essential goals of protein science, and the structural class is an important attribute used to characterize the overall folding type of a protein or its domains [132], [133], [134]. Nikashima et al. were the first investigators to suggest that protein structural class is correlated with protein secondary structural information and amino acid composition [132]. Subsequent efforts have primarily focused on designating structural classes based on amino acid composition [116], [117], [135], [136], [137], [138], [139], [140], from which folding pattern information can be obtained without addressing the complicated issue of three-dimensional structure [133], [134]. However, in the last decade, the designation of protein structural class based on secondary structure content has proven to be extremely useful from both experimental and theoretical points of view [133], [134], [140], [141], [142], [143], [144], [145], [146], [147], [148]. In the following section, we discuss a chemical shift-based structural classification method motivated by the success of secondary structure-based approaches.

3.2. Correlation between averaged chemical shift and protein structural class

This section summarizes the results of an empirical approach for estimating protein structural class directly from NMR spectra, prior to resonance assignment [149]. For a detailed discussion, see Ref. [149]. Briefly, the method seeks to correlate an empirical parameter, an averaged chemical shift (ACS) obtained by mining the BioMagResBank (BMRB) [38], with protein structural classes obtained from CATH [165,166] and SCOP [69,70,164]. This correlation permits an estimation of the classes of proteins of unknown structure based solely on the average of chemical shift values obtained from NMR.

3.2.1. Averaged chemical shifts are sensitive to protein structural class

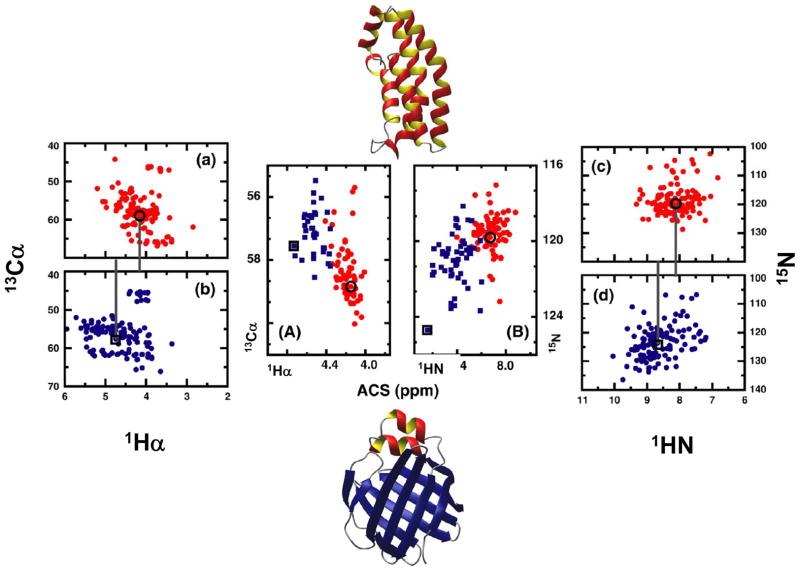
Figures 6A and 6B plot, respectively, the ¹³Cα versus ¹Hα and ¹⁵N versus ¹HN ACS values reported in Ref. [167]. Values indicated by red circles correspond to proteins deemed α-class according to CATH, and values indicated by blue squares correspond to molecules deemed β-class. As pointed out in Ref. [167], the figures are suggestive of a correlation between structural class and ACS. This is borne out by ACS values calculated from ¹³C-HSQC spectra (see Figures 6a–d) from histidine kinase (PDB code 1A0B, BMRB number 4857) [150], a predominantly α-helical protein, and from liver fatty acid binding protein (PDB code 1LFO, BMRB number 4098) [151], a predominantly β-sheet protein (the three-dimensional structures of these proteins are shown above and below Figures 6A and 6B, respectively). These values are indicated by circles for histidine kinase and squares for liver fatty acid binding protein. In both cases, the ACS values are reproduced in Figures 6A and 6B, where they are seen to lie within the appropriate cluster of α- or β-class proteins considered in Ref. [167].

Figure 6.

Representative examples to show that averaged chemical shift (ACS) is a structural parameter directly obtainable from NMR spectra. (a) and (c): simulated ¹³C and ¹⁵N-HSQC spectra of an α-helical protein (Histidine kinase, PDB code 1A0B, BMRB number 4857), respectively. (b) and (d): simulated ¹³C and ¹⁵N-HSQC spectra of a β-sheet protein (Liver fatty acid binding protein, PDB code 1LFO, BMRB number 4098). The ACS calculated from each spectrum is noted by a black circle (helical protein) and square (sheet protein). (A) and (B): representative examples of the ACS values calculated from ¹³Cα-¹Hα and ¹⁵N-¹HN correlations, respectively, for a set of proteins for which chemical shift information is obtained from BioMagResBank. The red circles and blue squares correspond to proteins that are classified as mainly-α and mainly–β, respectively, under the CATH classification scheme. ACS values from (a) and (b), and (c) and (d), are reproduced in (A) and (B), respectively. Reproduced with permission from Ref. [149].

3.2.2. Distribution of protein structural classes with respect to ACS values

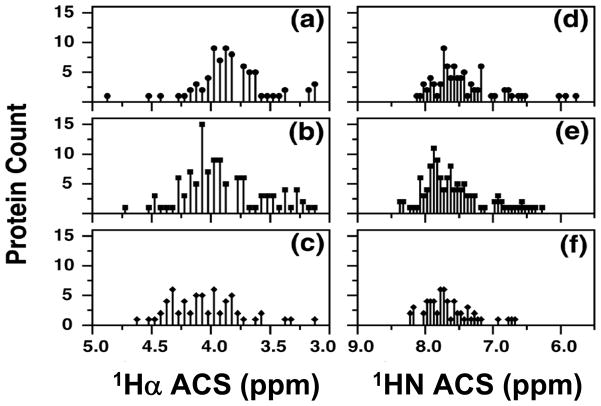
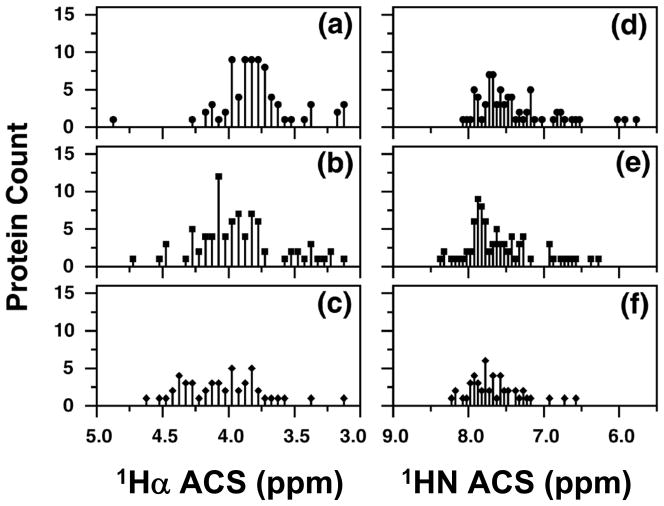
Figures 7 and 8 reproduce histograms of the protein distributions discussed in Ref. [167]. Figure 7 shows numbers of proteins, binned according to the ACS values of ¹Hα (left panels) and ¹H_N (right panels), classified by SCOP as α (panels a and d), αβ (panels b and e) and β (panels c and f). Figure 8 shows the distributions resulting from classification by CATH. Statistical information on these distributions is summarized in Table 6. As noted in Ref. [167], because they are insufficiently resolved, the distributions based on ¹HN ACS values (Figures 7,8 (right panels) and Table 6) are able to discriminate only α and “αβ/β” structural classes.

Figure 7.

ACS values vs. number of proteins in the three major structural classes defined according to the SCOP method. (a), (b), and (c) display the ¹H_α ACS values for proteins that are mainly-α, mainly-β, and a mixture of α and β (αβ) (both α/β and α+β), respectively. (d), (e), and (f) display the corresponding ¹H_N values for mainly-α, mainly-β, and αβ (both α/β and α+β), respectively. Reproduced with permission from Ref. [149].

Figure 8.

ACS values vs. number of proteins in the three major structural classes defined according to the CATH method. (a), (b), and (c) display the ¹H_α ACS values for proteins that are α, β, and αβ (both α/β and α+β), respectively. (d), (e), and (f) display the corresponding ¹H_N values for α, β, and αβ (both α/β and α+β), respectively. Reproduced with permission from Ref. [149].

Table 6.

Characterization of the statistical distribution of structural classes

SCOPa Nucleus 1Hα
Class	Totalb	Mean Chemical shift (ppm)	SDc	SDMd	2*SDM
α	88	3.83	0.34	0.040	0.072
αβ	122	3.94	0.52	0.047	0.093
β	61	4.05	0.30	0.038	0.076
Nucleus 1HN
α	87	7.54	0.64	0.069	0.14
αβ	122	7.68	0.99	0.089	0.18
β	60	7.70	0.41	0.053	0.11
CATHe Nucleus 1 Hα
α	77	3.79	0.29	0.033	0.066
αβ	83	3.93	0.32	0.035	0.070
β	49	4.05	0.30	0.043	0.086
Nucleus 1HN
α	75	7.45	0.56	0.064	0.13
αβ	83	7.62	0.48	0.053	0.11
β	49	7.69	0.43	0.061	0.12

^aSCOP (Structural Classification of Proteins),

^bTotal number of proteins,

^cSD Standard Deviation,

^dSDM Standard deviation about the mean,

^eand CATH (Class-Architecture-Topology-Homologous Superfamily) protein classification protocols.

3.2.3. Kolmogorov-Smirnov (K-S) tests

To check the statistical independence of the distributions presented in Figures 7, 8 and Table 6, Kolmogorov-Smirnov (K-S) tests were performed. Table 7 presents the results of these tests for all nuclei. As described in Ref. [167], two distributions are considered independent if the significance of the D statistic is less than or equal to 0.05. The comparisons for which this is the case are indicated by significance values in boldface type in Table 7. Only the separation of ¹Hα ACS values according to SCOP-based classes leads to three independent distributions at a 5% level of significance.

Table 7.

Results of Kolmogorov-Smirnov test

Classes Compared	SCOPa		CATHb
	K-S D Statisticc	Significanced	K-S D Statisticc	Significanced
1Hα
α ↔ αβ	0.24	0.0039	0.32	0.00042
α ↔ β	0.41	0.0000060	0.41	0.000042
αβ ↔ β	0.24	0.018	0.23	0.058
13Cα
α ↔ αβ	0.29	0.00030	0.29	0.0021
α ↔ β	0.41	0.0000090	0.34	0.0015
αβ ↔ β	0.18	0.15	0.21	0.11
1HN
α ↔ αβ	0.22	0.012	0.28	0.0029
α ↔ β	0.26	0.015	0.27	0.021
αβ ↔ β	0.11	0.65	0.092	0.94
15N
α ↔ αβ	0.082	0.88	0.10	0.79
α ↔ β	0.11	0.77	0.14	0.59
αβ ↔ β	0.13	0.47	0.13	0.65

^aProteins classified using SCOP,

^bProteins classified using CATH,

^cMaximum value of absolute difference between cumulative distribution functions,

^dSignificance: values less than/equal to 0.05 are considered significant (numbers in bold print).

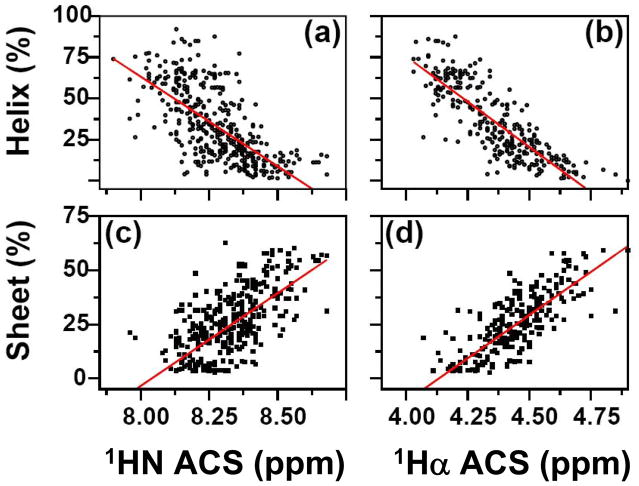
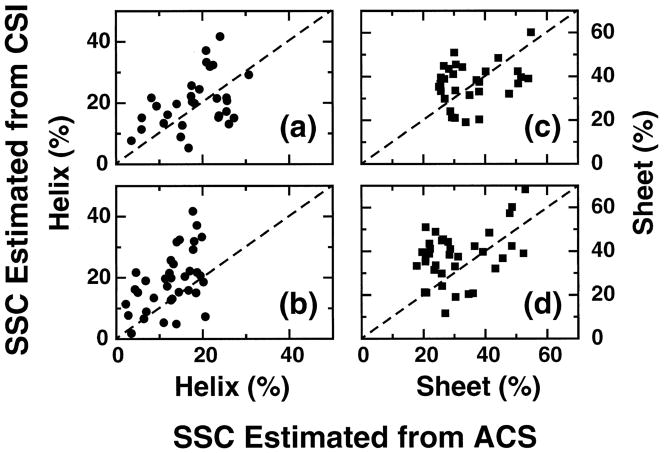
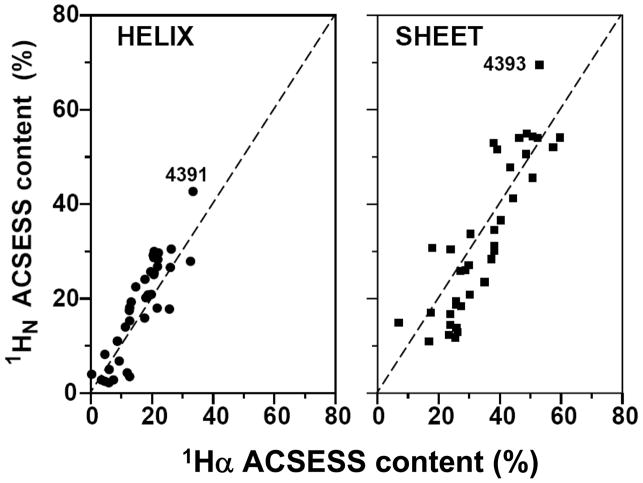
3.3. Empirical correlation between averaged chemical shifts and protein secondary structure content

It is possible to take an educated ‘guess’ by looking at the chemical shift dispersion of an ¹⁵N-HSQC spectrum to say whether it contains predominantly helical or sheet secondary structure. This is because helical proteins generally have narrow spectral dispersion in the ¹H dimension of the amide protein region, while proteins with β-sheets tend to be more dispersed. The averaged chemical shift method essentially quantifies this observation. It is based on the hypothesis that if one considers an NMR spectrum as a projection of the protein’s three-dimensional structure on a chemical shift dimension (dimensions), the distribution of the points represents some of the dominant features of the three-dimensional fold. For any distribution, the mean value—in this case the ‘averaged chemical shift’—is the first statistical quantity that distinguishes itself from other such quantities. Although the mean value in any given NMR spectrum can be calculated in a straightforward manner, there is no simple translation from this value to the three-dimensional structure. As a first step in the ‘reverse-engineering’ process one can resort to examining empirical relationships between a set of known three-dimensional structures and their respective chemical shift distributions.

In this section we address the correlation between protein secondary structure content and the average chemical shift (ACS) value for a particular type of nucleus within the protein. By using current NMR data processing software, it is fast and easy to obtain an experimentally-determined ACS value compared with obtaining complete resonance assignments. We have determined that the highest correlation with secondary structure content is found with the ¹Hα ACS value, followed by the ¹HN ACS. The empirical correlation that is derived from these relationships has been named ACSESS (averaged chemical shift to estimate secondary structure content. The application of ACSESS to determine secondary structure (helix and sheet) content under conditions where it is often difficult to obtain structural information, such as denaturing conditions, is also demonstrated. Predictions of secondary structure content obtained using ACSESS are better than those obtained using methods that rely on primary sequence, because the latter do not provide any information about conformational changes that result from different solvent conditions. Estimating changes in secondary structure content is relevant to studies of proteins, such as prions, that undergo conformational rearrangements, and to following major conformational changes of proteins in the presence of ligands or nucleic acids. It is emphasized, however, that ACSESS does not provide an alternative to other conventional NMR methods for secondary structure determination, such as the Chemical Shift Index (CSI) [19], [54]; it only provides information about overall secondary structure content prior to complete structural analysis, or in cases where it is difficult, if not impossible, to obtain such information by other means. Thus, ACSESS has several important potential applications in proteomics and protein folding studies.

3.3.1. Linear Correlations between ACS and SSC

The empirical correlation between averaged chemical shift and secondary structure content is referred as “ACSESS”. Figures 9a–d show plots of the ACS values of HN and Hα nuclei versus helix and sheet content. A total of 426 proteins was used for both ¹HN (Fig. 9a and c) and ¹Hα (Fig. 9b and d) to establish a correlation. Linear-regression analyses of the data in Figure 9 (helix and sheet structure content vs. ACS) are summarized in Table 6 (SSC = Slope × ACS + Intercept). Only ACS values corresponding to HN and ¹Hα nuclei were considered, since values associated with these nuclei are in general much more indicative of overall secondary structure content than those associated with the heavy backbone atoms [111], [152]. BMRB is the first public database to collect chemical shift information from a large number of proteins. Though highly useful, BMRB is new by comparison with three-dimensional structural databases, such as the PDB, and currently lacks a rigorous strategy for quality control. RefDB is an even newer database, assembled by Zhang et al. [153], in which chemical shift information obtained from BMRB is uniformly referenced, and unassigned or missing resonances are predicted using other empirical correlations. In addition to those obtained using BMRB data, we obtained similar correlations with secondary structure content using RefDB data (similar to Fig. 9). Table 8 lists the results of the linear correlation for both BMRB and RefDB chemical shift values. For BMRB-based chemical shifts, the coefficients of correlation between H^N ACS and helix or sheet content are −0.67 and +0.71, respectively, while the corresponding H^α values are −0.84 and +0.84. It can be seen from Table 8 that performing the analysis on the same set of proteins using RefDB-based information produces values in close agreement with these BMRB-derived values; omissions and nonstandard referencing in BMRB evidently have little impact on correlations between ACS and SSC. On the other hand, comparison of these with our earlier results [152] shows that increasing the number of proteins in the data set significantly improves the correlation. For example, the coefficients of correlation between ACS and sheet content are seen to increase from 0.75 to 0.84 for H^α, and from 0.66 to 0.71 for H^N. We note that the intercept values do not have any physical meaning, as this empirical approach is intended to show a linear correlation over a subset of chemical shifts of folded proteins only. The present results are consistent with our earlier findings that, for both H^α and H^N, the relationship between ACS and SSC are characterized by a positive correlation coefficient for sheet content and a negative coefficient for helix content. A similar correlation for the heteronuclei (¹³Cα and ¹⁵N) was also performed [152]. Correlation coefficients for the plots of ¹⁵N and ¹³Cα versus percent sheet content are 0.44 for both, while the coefficients obtained in the plots versus percent helix content are 0.40 and 0.58, respectively. Although ¹³Cα ACS values show a wider dispersion with respect to helical content than the corresponding ¹⁵N data, the correlation coefficients for the plots of heteronuclei are equally poor [152]. Overall, the best correlations were obtained with the ¹HN and ¹Hα data.

Figure 9.

Plots of the averaged chemical shift (ACS) values from experimental data versus the secondary structure content (SSC) estimated from three-dimensional structures. (a) and (c) show percent helix (circles) and sheet (squares) versus ACS for HN, whereas (b) and (d) show the corresponding plots for Hα. The continuous lines show the a linear regression analysis of the data. Reproduced with permission from Ref. [111].

Table 8.

Linear Correlation of ACS to Secondary Structure Content

Nucleus	a Helix (%)			a Sheet (%)
	b CC	Slope	Intercept	b CC	Slope	Intercept
HN	−0.67 (−0.68)	−108.7±5.7 (−109.3±5.8)	933.03±47.5 (938.0±48.7)	0.71 (0.70)	85.73±4.0 (85.3±4.2)	−689.3±33.8 (−686.2±35.4)
1Hα	−0.84 (−0.84)	−109.7±4.0 (−108.6±4.0)	514.54±17.5 (509.3±17.6)	0.84 (0.84)	79.81±2.9 (79.5±2.9)	−329.8±12.7 (−328.5±12.9)

^aSecondary structures defined based on PROMOTIF.

^bCC: Correlation coefficient from linear regression analysis.

^cSlope and intercept are defined based on a linear equation: SSC = Slope×ACS (ppm) + Intercept.

Each cell contains the analyses of chemical shift information from BMRB (RefDB).

A notable feature of these results is that the slopes of the lines for the ACS values versus helix and sheet content are opposite in sign (most clearly seen in panels a and c of Figures 6 and 9). The change in the sign of the slope indicates that changes in ACS values allow differentiation of increasing or decreasing helical or sheet secondary structural elements upon changes in environment. The ACS values increase with an increase in the total helical content and decrease with an increase in the total sheet content.

The statistical analysis of the correlation between ACS and SSC is relatively good for the ¹Hα ACS values (84%), while a moderate correlation (67%) is obtained with the ¹HN ACS values. As the number of proteins that can be added into the correlations of ACS with secondary structure increases, the correlation coefficients should improve significantly. However, certain factors may result in lowering the correlation coefficient. ACS values were based on the total number of cross-peaks that were observed, not on the total number of residues in the protein. For example, an ¹⁵N-HSQC spectrum will not contain resonances from a proline residue, which will consequently not be included in the ACS value, though it is present in the sequence. Significant contributions in lowering the correlation are expected from the residues that are present in the turns that will contribute to the ACS value as a sheet or helix. For example, residues that are part of a β-turn will be considered as β-sheet when the average values are calculated. The distribution of chemical shifts for each of the amino acids found in the BMRB database suggests that no particular amino acid dominates the ACS values; hence, the chemical shifts for a particular type of amino acid are not expected to bias the correlation. Moreover, Sharman et al. [95] have used rigorous statistical analyses of ¹Hα chemical shifts to show that there is no correlation between amino acid type and propensity to fall within helical or sheet regions. However, it is possible that certain proteins will contain a large number of one type of residue (or a preponderance of a few types of residues) that may skew the ACS value. The relatively low correlation coefficients (0.64–0.8) for the ACS versus SSC correlations may result from these and other factors.

3.4. Applications of empirical correlations of ACS

3.4.1. Identification of the protein class from ACS

Rigorous statistical analysis of the data clearly suggests that only the ¹Hα ACS values are capable of distinguishing the three different structural classes of the proteins. Based on the results of K-S test for ¹Hα chemical shifts, it is possible to define the range of ¹HαACS values corresponding to each class. For protein structural classes, α, αβ, and β, defined by SCOP, the centers of the ACS values are 3.83 ± 0.072, 3.94 ± 0.093, and 4.05 ±0.076 ppm, respectively. The corresponding values for the CATH-classified proteins are 3.79 ± 0.066, 3.93 ± 0.070, and 4.05 ± 0.086 ppm, respectively. Following this criteria, the results for a total of 37 proteins, predicted using both CATH- and SCOP-derived empirical relations, are summarized in Table 9. Only two proteins could be classified using the CATH-, but not the SCOP-based, relation (noted as NP, no prediction) and there is no cross prediction between α and β classes.

Table 9.

Prediction of structural class from NMR data for proteins of undetermined three-dimensional structure

BMRBa	ACS (1Hα)b	Protein Name	Structural Class (using CATH-based correlation)c	Structural Class (using SCOP-based correlation)d
4664	3.818	Lipocalin Q83	α	α
4688	3.899	L18	αβ	α/αβ
4698	3.846	Transforming Growth Factor β type II receptor	α	α/αβ
4722	3.823	Shikimate Kinase	α	α
4752	3.819	Gpnu1-E68	α	α
4771	3.726	Tola3	α	NP
4791	3.808	HCV NS3 RNA helicase	α	α
4792	3.778	ParD dimer	α	α
4829	3.841	Interleukin enhancer binding factor	α	α
4834	3.766	S. aureus peptide deformylase	α	α
4908	3.769	α′-domain of ERp57	α	α
5014	3.724	MyBP-C cC5	α	NP
5040	3.778	I1(I29T) monomer	α	α
5093	3.881	RbfADelta25	αβ	α/αβ
5107	3.826	Sensor & Substrate Binding Domain from Lon (La) Protease	α	α
5316	3.781	Gag	α	α
4113	3.931	Vaccinia Glutaredoxin-1	αβ	αβ
4132	4.015	Human ubiquitin-conjugating enzyme	β	αβ/β
4719	3.922	Ras binding domain of rat AF6	αβ	αβ
4802	3.968	N-terminal domain of H-NS	αβ/β	αβ
4881	3.983	Azotobacter vinelandii C69A holoflavodoxin II	αβ	αβ
4901	3.991	p62 N-terminal domain	αβ	αβ
4940	3.933	Antennal Specific Protein 1	αβ	αβ
4965	3.925	L11	αβ	αβ
5030	3.937	Honeybee antennal specific Protein 2	αβ	αβ
5093	3.881	RbfADelta25	αβ	αβ
4302	4.010	Protein disulfide isomerase a′ domain	β	αβ/β
4720	4.066	Inhibitor-2 monomer	β	β
4870	4.094	region 4.2 of sigma70 of E. coli RNA polymerase holoenzyme	β	β
4881	3.983	Azotobacter vinelandii C69A holoflavodoxin II	β	β
4901	3.991	p62 N-terminal domain	β	β
4913	4.046	cAMP-regulated phosphoprotein-19 monomer	β	β
4929	4.090	Tctex1 dimer	β	β
4956	4.013	YajQ from E. coli	β	αβ/β
4973	4.100	Saratin	β	β
4999	3.979	Nucleocapsid binding domain of the sendai virus phosphoprotein	β	β
5049	4.053	Extracellular domain of subunit 2 of the human receptor	β	β

^aBioMagResBank (BMRB) accession number (http://www.bmrb.wisc.edu/),

^bAveraged chemical shift (ACS) calculated for the ¹H_α nuclei,

^cStructural class estimation based on the empirical distribution obtained by CATH classification,

^dStructural class estimation based on the empirical distribution obtained by SCOP classification.

3.4.2. Estimation of secondary structure content from ACS

To determine the effectiveness of the ACS in estimating the SSC, we have used an independent set of proteins that are not part of the derived correlations. A set of 36 proteins obtained from the BMRB for which complete assignments of the backbone atoms are known, but the structures have not yet been determined, were used to estimate SSC by using the empirical correlation between SSC and ¹Hα or ¹HN ACS values. SSC was also calculated using the consensus chemical shift indices using the program PSSI using all the backbone atoms. In order to evaluate the secondary structure content for a set of proteins, the program Probability-based protein secondary structure identification (PSSI) was used [59] (discussed in section II.D.2). In this method, chemical shift indices (CSI) of the set of backbone atoms are used to define the probability with which the secondary structure (sheet or helix) is assigned. Secondary structure content in percentage is then calculated with respect to the total number of residues in the sequence. The list of all the proteins and their estimated SSC, using the correlation and CSI based methods are given in Table 10. There is an overall agreement between the SSC estimated between these two methods (Figure 10). Larger deviations were observed in the ¹HN ACS values compared to the ¹Hα ACS values. To compare the predictions from ¹HN and ¹Hα ACS values, Figure 11 shows the comparison. For example, the BMRB numbers 4391 (candoxin) [154] and 4393 (N-terminal domain of human spectrin including one structural domain) [155], are predicted to contain predominantly helical and sheet secondary structures, respectively. Figure 4 shows a comparison of the estimates of helical (left panel) and sheet (right panel) content for these proteins derived from either the ¹HN or ¹Hα ACS values Ideally, both ACS values should provide exactly the same values, within experimental error.

Table 10.

Estimated SSC using ACS and CSI based methods for proteins with no three-dimensional structural information.

BMRB	Protein Name	Helix (%) from			Sheet (%) from
		a ACS (1Hα)	a ACS (1HN)	b CSI	a ACS (1Hα)	a ACS (1HN)	b CSI
4840	Adenylate kinase	15.31	12.65	12.70	38.11	34.58	20.40
4834	S. aureus peptide deformylase	25.56	18.69	21.70	25.54	20.70	36.50
4825	Recombinant RC-RNase 2	27.28	18.45	15.10	25.70	19.60	39.60
4821	DcuS	17.62	15.87	20.40	33.70	30.37	19.10
4795	Human D187N gelsolin domain 2	20.83	18.67	37.10	28.73	26.01	24.10
4794	Human wild type gelsolin domain 2	25.69	19.45	20.70	25.06	20.62	35.30
4787	Apical Membrane Antigen 1	26.10	12.95	13.10	29.25	20.36	21.30
4784	Tyrosine repressor	n.a	6.38	6.60	n.a	47.90	57.40
4776	Sud dimer	14.03	11.31	19.70	40.21	36.56	42.30
4771	Tola3	8.18	4.57	21.70	50.72	45.64	36.80
4752	gpnu1-E68	11.92	4.32	16.20	51.62	39.25	39.70
4735	Olfactory marker protein	23.33	12.27	21.50	29.68	22.13	41.10
4722	Shikimate Kinase	9.34	6.80	19.00	47.78	43.28	32.10
4716	Auxilin	3.53	2.78	7.70	54.01	52.33	39.00
4712	Newt acidic FGF	16.76	10.94	5.30	30.54	26.34	45.50
4711	RNA-binding protein	n.a	13.99	31.70	n.a	36.02	20.80
4698	Transforming Growth Factor Beta type II receptor	n.a	13.86	4.90	n.a	28.66	41.00
4688	L18	22.46	14.66	32.40	34.98	23.48	31.50
4670	PIN1At	30.71	17.80	29.20	25.68	17.80	33.30
4664	Lipocalin Q83	25.54	11.77	17.20	30.01	20.71	51.00
4579	FYVE domain of EEA1	n.a	20.16	18.60	n.a	27.05	11.60
4567	Catalytic domain of yUBC1	19.30	13.23	24.50	37.21	28.38	38.40
4558	YopH-NT monomer	17.48	12.64	25.70	38.13	31.21	37.50
4463	Ras-binding domain of Byr2	21.74	18.02	31.90	30.37	23.95	33.60
4447	p23fyp	20.93	19.80	33.30	26.97	25.85	29.80
4353	p13 C-terminal domain	23.81	16.69	15.90	26.84	21.82	38.90
4335	calerythrin	5.88	2.21	11.40	54.90	48.68	60.20
4313	E2	24.09	17.73	41.70	30.19	20.94	21.10
4294	Human MBF1(57–148) core domain	5.96	4.99	15.20	50.59	48.55	42.40
4271	Calcium binding protein from Entamoeba Histolytica	11.00	8.70	13.40	44.27	41.27	48.50
4239	f29-SSB bacteriophage	23.69	14.46	15.30	28.27	21.90	43.50
4147	Cold Shock domain	14.95	6.93	8.90	32.65	27.95	44.30
4136	E. coli multidrug resistance protein E	n.a	3.46	1.80	n.a	52.96	68.20
4132	Human ubiquitin-conjugating enzyme	18.15	12.68	19.90	38.07	30.17	33.10
4027	S.aureus DHFR(F98Y)-NADPH-TMP ternary complex	17.36	17.00	22.20	26.64	25.96	44.90
1583	Micrococcal nuclease	n.a	20.59	7.30	n.a	23.89	48.90

^aSecondary structure content estimated using the correlation listed in Table 8.

^bSecondary structure content estimated using probalility based protein secondary structure identification (PSSI) [59].

n.a: not detrmined due to absence of chemical shift information.

Figure 10.

Comparison of helical and sheet content percent calculated using ¹H_α or ¹H_N ACS values to that obtained using a consensus chemical shift index based method for a set of proteins for which no three dimensional structures are available. (a) and (b) correspond to the helical content using the ¹Hα and ¹H_N ACS values, respectively, while (c) and (d) are the corresponding sheet content using the same ACS values. The dashed lines correspond to a perfect correlation between these two methods.

Figure 11.

Comparison of helical (LEFT) and sheet (RIGHT) content calculated using ACSESS with either ¹Hα or ¹H_N ACS values for a set of proteins for which no three dimensional structure are available. The numbers for two proteins are their identification codes in the BMRB database (see Table 10).

3.4.3. Averaged chemical shifts and protein folding

The utility of ACSESS as a tool to identify what structural changes occur in proteins under denaturing conditions has been demonstrated for ubiquitin. Chemical shift data acquired under a variety of conditions are available for this protein (see Table 11). Ubiquitin belongs to the αβ class according to CATH, and both chemical shift information and structures are available for three variants: multiple mutant (BMRB 4663, pdb 1C3T) [156], yeast (4769, 1UBI) [157] and core mutant (4493, 1UD7) [158]. Chemical shift information for the denatured state (BMRB 4375) is also available [159]. ACSESS- predicted sheet and helix content obtained using both ¹HN and ¹Hα ACS values from the folded forms of ubiquitin are in close agreement with secondary structure estimates obtained from their three-dimensional structures using PROMOTIF (Table 11). In the case of denatured ubiquitin, the ACSESS method estimates a loss of helical structure of approximately 6% and a gain in sheet content of the same amount, suggesting that even in the denatured state, significant residual secondary structure is present in ubiquitin.

Table 11.

Secondary structure of ubiquitin predicted by ACSESS

a BMRB	State	b ACS (ppm)	c ACSESS (%)		d PDB	e PROMOTIF (%)
			Helical	Sheet		Helical	Sheet
4663	Mutant, multiple	8.38 (1HN)	22.3±1.6	23.0±1.6	1C3T	27.6	21.1
		4.29 (1Hα)	24.9±1.4	20.4±1.0
4769	Yeast	8.37 (1HN)	21.8±1.6	23.9±1.7	1UBI	31.6	23.7
		4.54 (1Hα)	27.6±1.5	16.2±0.8
4493	Core Mutant	8.40 (1HN)	23.7±1.7	20.9±1.5	1UD7	27.6	23.7
		4.48 (1Hα)	23.7±1.1	22.3±1.1
4375	denatured	8.34 (1HN)	20.4±1.5	26.0±1.8	none
		4.37 (1Hα)	16.7±0.9	33.1±1.7

^aBMRB id number from http://www.bmrb.wisc.edu/

^bACS: Averaged chemical shift calculated form the BMRB.

^cACSESS: Averaged chemical shift to estimate secondary structure

^dPDB: Protein data back structure coordinate files from www.rcsb.org.

^ePROMOTIF estimation of secondary structure content from 3D structure.

We have demonstrated that ACSESS provides information about the denatured state of ubiquitin. Our results show that ubiquitin retains significant residual helical and sheet structure in denaturing solvents, and that the β-strand content increases relative to that of the folded state. This increase in sheet content can be attributed to the presence of additional turns in an extended conformation. The retention of helical structure, though reduced, could be due to retention of local secondary structural elements that are no longer folded into a three-dimensional conformation. This idea is consistent with the original paper by Peti et al. [159] that reported the chemical shifts of denatured ubiquitin, and compared them with chemical shifts of other denatured proteins, by assuming that all interactions in the unfolded state are local.

3.5. Some important aspects of using ACS to obtain low-resolution structural information

NMR spectroscopy plays a vital role in determining the structures of proteins in the solution state. In spite of advancement in the field during the past decade, determining the complete three-dimensional structure of any given protein remains a time-consuming proposition. Though the information content of a complete structure at atomic resolution is indisputable, in recent times several groups have begun exploring alternative methods that are faster than conventional experiments [160], [161]. Prior to collecting several days’ worth of NMR spectra for structure determination, other biophysical methods are generally adopted to infer secondary structural information about the protein of interest. In particular, circular dichroism (CD) spectroscopy is extensively used to estimate the secondary structure content of medium-sized proteins. In CD spectroscopy, deconvolution of the experimental molar ellipticity at 222 nm is used to estimate secondary structure content. In the case of NMR, chemical shifts have been used as regular indicators of a particular secondary structure. For example, an ¹Hα resonance that is shifted upfield with respect to the corresponding random coil value is considered to be α-helical, while one shifted downfield to be β-strand. This is a widely accepted procedure, and a large number of NMR studies have shown that such correlation is valid [5], [17]. However, NMR spectral information has seldom been used to obtain relatively low-resolution structural information, such as secondary structure content. In some cases, the results of CD are used to determine whether it is feasible to obtain complete, three-dimensional structural information for a particular protein, using NMR. This suggests the critical importance of evaluating whether data obtained from NMR itself can be used to estimate secondary structure content. Lee and Cao have addressed this question extensively in their comprehensive study [162], and have shown that the correlation between NMR- and CD-based secondary structure estimation is poor. Further, while CD spectroscopy is more suitable for studying relatively small proteins and polypeptides, the characterization of larger molecules requires NMR.

Computational methods often play a primary role in initial predictions of protein structure; for example, in predictions of protein structural class. These methods are typically invoked even before a protein is expressed or extracted for any biophysical characterization. Secondary structure estimations from CD are often inconsistent with such computational predictions from NMR. On the other hand, to date, estimations from NMR have required the time-consuming process of resonance assignment. A method such as that proposed here could essentially fulfill the need for an empirical, NMR-based estimator of protein structural class that is both accurate and efficient.

The results discussed above show that ¹Hα and ¹HN ACS values clearly distinguish the three different protein classes, α, mixed αβ, and β, when the proteins are classified either by CATH or SCOP, and can be used in estimating secondary structure content. The empirical correlations provide a way to determine directly the structural information of proteins in the absence of resonance assignments. They can be easily incorporated into any commercial or academic software package that employs manual or automated peak picking routines to reduce an HSQC spectrum into a single ACS value. ACS is expressed in the same unit as chemical shift (ppm). Instead of using the absolute chemical shift values to determine the averages, we have also explored definitions such as chemical shift index (CSI), which determines the relative change in the chemical shift with respect to the corresponding random coil value. CSI may better distinguish proteins that are comprised primarily of either helices or sheets; αβ proteins cannot be identified by this method, because the values of α and β segments are opposite in sign, and therefore cancel each other.

Determination of the structural classes of proteins with no available experimental three-dimensional structure information (from NMR or X-ray), using ¹Hα ACS values, provides an internal test of the reliability factor (Tables 9–11). The secondary structures of these proteins were also estimated using prediction algorithms that utilize only amino acid sequences. For many of the proteins, the sequence-based class prediction approach provided similar results for the mainly-α class, while larger differences were observed for mainly-β class proteins. However, considering the variability and confidence limits associated with such predictions (http://cubic.bioc.columbia.edu/eva/ and references therein), it is difficult to define a suitable control set for comparison. In some cases, using the sequence-based prediction method (http://www.bork.embl-heidelberg.de/SSCP/) [130], [131], we have observed large variations in the estimation of sheet and helical classes for the same amino acid sequence (data not shown).

In general, the quality of structural predictions based on specific algorithms is examined either by redistribution test or jack-knife test [163]. However, in the correlations presented here, neither of these methods was considered, for the following reasons. First, our methods are not algorithm-based; our results are strictly the outcome of an empirical correlation between known protein structural classes or SSC and averaged chemical shifts. Second, in self-consistency tests [163], it is necessary to define a training set of proteins that obey a particular criterion; for example, the resolution of three-dimensional structure. Though it is possible to define such criteria for protein classes, use of chemical shift information as the test criterion must be considered premature, as there is currently no consensus definition of the “accuracy” of such information [19].

Although we have shown that ACS values can be used to identify directly the structural classes or SSC of proteins, thereby providing a first, low-resolution structural estimate from experiments, critical questions still remain. For example, what is the reliability of the estimates? As the number of proteins that we add into our correlations of ACS with protein class or SSC increases, one can expect the reliability of the method to improve. In the empirical correlation derived between secondary structure content and ACS values, we have determined a reliability factor > 84% when ¹Hα nuclei are used. Notwithstanding the limited number of proteins in the current study, and that we have defined the relative regions of ACS values demarcating the structural classes in a conservative manner, we suggest the reliability of this method is about 80%.

Another remaining question is whether it is possible that certain amino acids bias the current estimates, since the method is based on an average of the chemical shifts. The distribution of chemical shifts for each of the amino acids found in the BMRB database suggests that no particular amino acid dominates the ACS values. In a recent paper, Sharman et al. [95] have used rigorous statistical analyses of ¹Hα chemical shifts to show that there is no correlation between amino acid type and propensity to fall within helical or sheet regions. The exact nature of the chemical shift dependence on secondary structure for a specific amino acid residue remains to be determined [95], [164]. In addition, long range and context-dependent effects on protein structural class definition are still not clearly understood [164], and may also play important roles in influencing chemical shifts.

As the estimation of structural class from NMR is directly influenced by the quality of the data used, the method is most useful in cases in which the resolution of the corresponding HSQC spectrum is excellent. Experiments based on transverse relaxation optimized spectroscopy (TROSY) [165] provide an additional advantage in applicability to large proteins. From a practical point of view, the method would be most appropriate if a sufficient number of individual cross-peaks are observed in an HSQC spectrum. Further, since calculated ACS values are based on the total number of residues in a protein, and not on the total number of crosspeaks observed, we recommend that a minimum of 70% of the total number of peaks expected be present in a given spectrum for determination of a reliable ACS value. As a final point, all amino acid residues have ¹Hα resonances (glycine has two), so these will be fully represented in any calculation of the ¹H_α ACS. In contrast, proline residues lack an amide proton resonance, and consequently are not observed in ¹⁵N-HSQC spectra; an abundance of proline-rich proteins in a data set could conceivably lead to an underestimate of amide ACS values.

It must be emphasized that ACS-based methods do not provide an alternative to conventional NMR-based experiments, and should only be considered initial predictors of protein class or secondary structure content. ACS methods might provide a novel technique for monitoring protein structural changes in real time, such as in protein folding experiments. Such methods might also be used to detect major structural changes that occur upon protein-protein, protein-DNA/RNA, and other complex formations, to provide some direct experimental structural information in situations in which other techniques are incapable of doing so (e.g., in studies of large and/or highly disordered proteins), and to facilitate initial protein fold identification in high throughput proteomics applications.

4. Other empirical correlations of chemical shift

Methods to elucidate empirical relationships between chemical shift and protein structure have been under development for decades. Examples include magnetic anisotropy [166] and methods that investigate electrostatic [167] and aromatic ring current effects [168]. In addition to methods focused on estimating the secondary structure of individual residues from a secondary structure index, and secondary structure content or structural classes from chemical shifts, a few empirical correlations have been developed to address specific features of protein structure, such as the redox state of cystines [11], [169] and Xaa-Pro peptide bond conformations [170]. In this section, we briefly review some of these methods.

4.1. Semi-empirical methods for chemical shift estimation from 3D structure

One of the earliest methods extensively to use the empirical relationship between NMR chemical shifts and protein structure is TALOS, developed by Cornilescu et al., [5]. This method is based on the observation that homologous proteins have similar secondary chemical shifts, because these correlate with local protein conformation. This relation provides a basis for searching a database for triplets of adjacent residues with secondary chemical shifts and sequence similarity that provide the best match to the query triplet of interest. Tests carried out using proteins of known structure indicate that the root-mean-square difference (rmsd) between the output of TALOS and the X-ray derived backbone angles is about 15°, and has an error rate of ~3%. TALOS is freely available (http://spin.niddk.nih.gov/bax/software/TALOS/index.html).

A range of semi-empirical methods is available to predict protein chemical shifts from three-dimensional structure and dynamics. These include: (a) SHIFTS: The first version of this program was developed by Case and co-workers [171], and has seen several subsequent improvements [18], [19], [171], [172], including a most recent version [173]. SHIFTS is available from the authors’ group page (http://www.scripps.edu/mb/case/qshifts/qshifts.htm). (b) SHIFTCALC: this method was developed by Williamson and his group, with details presented in a number of papers in the 1990s [3], [4], [174], [175], [176], [177], [178], [179]. Source code and a web-server for SHIFTCALC are available (http://nmr.group.shef.ac.uk/NMR/mainpage.html). (c) SHIFTX and SHIFTY: Wishart s group provides a wide range of software tools for correlating chemical shift with protein structure. These include: SHIFTX to predict ¹H, ¹³C, and ¹⁵N protein chemical shifts from 3D structure [180], [181] and SHIFTY to predict protein chemical shifts using only amino acid sequence [182]. In particular, Neal et al. [180], [181] have shown that accuracy for predicting chemical shifts (including amide proton shifts) can be improved by combining empirical formulas for spatial interactions with ‘hyper-surfaces’ representing local covalent interactions. (d) PROSHIFT: this neural network-based method, developed by Meiler [183], predicts the ¹H, ¹³C, and ¹⁵N chemical shifts of proteins from their three-dimensional structure as a function experimental conditions as input parameters. A webserver for PROSHIFT is available from Meiler’s group (http://www.meilerlab.org/view.php). A more recent program, Random Coil Index (RCI), predicts protein flexibility from backbone chemical shifts (¹³Cα, ¹³CO, ¹³Cβ, ¹⁵N, ¹Hα), and estimates values of model-free order parameters as well as per-residue RMSDs of NMR and MD ensembles [184], [185]. All these programs are either available to download or on a webserver at Wishart’s group (http://redpoll.pharmacy.ualberta.ca/).

Figure 12 shows a straightforward comparison of the experimental chemical shifts of protein G (BMRB 5875), represented by filled circles, with chemical shifts calculated using SHIFTX (open circles), SHIFTS (filled triangles) and PROSHIFT (open triangles). A dashed line connects the experimental points to show a visual trend. Panels (a), (b), (c) and (d) show plots of chemical shift values of the nuclei, ¹HN, ¹⁵N, ¹³Cα and ¹Hα, respectively. We were unable to perform a similar calculation with SHIFTCALC due to technical issues with the webserver. Overall, we find that all the calculations follow the experimental values, but exhibit differences with respect to specific nuclei and residues. This area sees continuing development by several groups in recent time [173], [186].

Figure 12.

Comparison of semi-empirical methods to calculate the chemical shifts of an example proteins, protein G. Panels (a), (b), (c) and (d) show the plots of chemical shifts values of the nuclei, ¹HN, ¹⁵N, ¹³Cα and ¹Hα, respectively. Experimental chemical shifts of protein G (bmr5875) in filled circles to that chemical shifts calculated using SHIFTX (open circles), SHIFTS (filled triangles) and PROSHIFT (open triangles). A dashed line is connected through a experimental points to show a visual trend.

4.2. Prediction of redox states of cysteines from chemical shifts

Disulfide bonds play a pivotal role in protein structure, function, folding, and stability. The importance of disulfide bonds has been extensively studied, but invariably involves either breaking or forming a disulfide bond. Further, it is not the disulfide bond but the effect of the disulfide bond on the rest of the structure that has been studied. Two groups have developed empirical relationship to predict the redox state; Sharma and Rajarathnam provided the first such correlation [11] and recently Wang et al., [63], [169] have developed a two-dimensional cluster approach for a similar purpose.

These results in general show that that the Cβ shift is extremely sensitive to the redox state, and can predict the disulfide-bonded state. Further, chemical shifts in both states occupy distinct groups in a XY plots of Cα, Cβ chemical shifts. The redox state chemical shifts of cysteines also sensitive to the secondary structural state of the protein. The results of Sharma and Rajarathnam are summarized in Table 12. The rules to define the empirical state with confirmed chemical shifts assignments are given in the original reference [11]. Wang et al., [169] have performed a two-dimensional cluster analysis, while the earlier method looked only Cα, Cβ correlations. This analysis showed that different clusters of (Cα, Cβ), (C′, Cβ), (HN, Cβ) and (Hα, Cβ) are helpful in distinguishing the redox state of cysteine residues. Similar to the first approach, the authors derived rules using a score matrix to predict the redox state of cysteines using their chemical shifts. The score matrix predicts the redox state of cysteine residues in proteins with 90% accuracy. Table 12 also lists the summary of the results of the most sensitive nuclei for redox state, Cβ. Table 12 shows that the results from the two methods are similar.

Table 12. Distribution of C_β chemical shifts in oxidized and reduced cysteine^a.

	Method Ia				Method IIb
	Cβ (S-S) Oxidized		Cβ (C-H) Reduced		Cβ (S-S) Oxidized		Cβ (C-H) Reduced
	α-helix	β-strand	α-helix	β-strand	α-helix	β-strand	α-helix	β-strand
Number of chemical shifts	33	49	39	35	67	79	90	86
Minimum (ppm)	32.8	35.9	23.8	25.1	32.6	34.5	24.1	25.9
Maximum (ppm)	47.4	50.9	28.8	33.3	44.6	51.2	43.7	35.1
Range (ppm)	14.6	15.0	5.0	8.2	12.0	16.7	19.6	9.2
Median (ppm)	38.8	43.2	26.6	30.2	38.9	43.0	27.0	30.4
Mean (ppm)	38.4	43.0	26.5	29.7	38.6	43.0	27.6	30.5
Std. Dev (ppm)	3.2	4.2	1.1	2.0	3.2	4.1	2.7	2.1

^aTable is adopted from Sharma and Rajarathnmam

^{a, b}are based on methods in references [11] and [169], respectively.

4.3. Prediction of Xaa-Pro peptide bond conformations

In peptides and proteins, the planar peptide bond occurs predominantly in the trans conformation [187]. In general the cis form is energetically less favorable due to the steric repulsion of the Cα/Hα atoms of the two sequential amino acids. However, in peptide bonds preceding prolines (Xaa-Pro), the Cδ/Hδ in the pyrolidine ring and the Cα/Hα atoms of the preceding residue experience a comparable repulsion and the energy difference between the cis and the trans conformation is reduced. Therefore an appreciable fraction of the Xaa-Pro peptide bonds occur in the cis form. A survey of a non-redundant database of 571 high resolution protein structures found 5.2% of all Xaa-Pro peptide bonds occur in the cis conformation, as compared to only 0.03% of all Xaa-nonPro peptide bonds [188], [189]. Earlier studies on small peptides containing prolines observed signature features of the cis conformation include an upfield change in the ¹³Cγ chemical shift and a downfield change in the ¹³Cβ chemical shift [190]. Therefore, the chemical shift difference between them, Δβγ… (δ [¹³Cβ]− δ[¹³Cγ]) is expected to be an indicator for cis or trans conformation [191]. These observations lead Schubert et al [170] to develop a chemical shift based empirical relationship. This method, also referred as POP (Prediction of Proline) conformation 304 protein entries in the BMRB, representing an overall number of 1033 prolines for the analysis.

The chemical shift difference Δβγ is a reference-independent indicator of the Xaa-Pro peptide bond conformation. Based on a statistical analysis of the ¹³C chemical shifts, a software tool was created to predict the probabilities for cis or transconformations of Xaa-Pro peptide bonds. Using this approach, the conformation at a given Xaa-Pro bond can be identified in a simple NOE-independent way immediately after obtaining its NMR resonance assignments. Table 13 lists of the results of the analysis [170]. Distribution of Δβγ were fitted a single Gaussian and the fitted parameters (average, variance and standard deviation) are used for the prediction (also listed in Table 13)). For Δβγ ιn the range from 0.0 ppm to 4.8 ppm the peptide bond conformation is predicted to be 100% trans, whereas from 9.15 ppm to 14.4 ppm it is 100% cis. In the range from 4.8 ppm to 9.15 ppm, the prediction is ambiguous and only probabilities can be given for both conformers and the results must be confirmed using the conventional NOE-based method [21].

Table 13.

Summary of the empirical analysis for the prediction of Xaa-Pro peptide bond conformation^a

	Cβ resonances (ppm)		Cγ resonances (ppm)		Δβγ (ppm)
	cis	trans	cis	trans	cis	trans
Average Value	31.75	34.16	27.26	24.52	4.51	9.64
Minimum	26.3	30.74	19.31	22.1
Maximum	35.83	36.23	33.39	27.01
Standard Deviation	0.98	1.15	1.05	1.09	1.17	1.27

^aTable adopted from [170].

5. Summary

Progress in the structural biology of proteins comes from both experimental and theoretical efforts. Computational methods are capable of delivering fast structural information, ranging from low-resolution protein structural class definition to high-quality information based on homology modeling. Experimental methods that concentrate on obtaining high-resolution information are hampered by inherent time cost, and lack the capacity to provide low-resolution structural information expediently. NMR spectroscopy is a powerful tool for obtaining high-resolution structural and dynamical details of molecules in the solution state. In order to explore new experimental methods for the fast identification of protein structures using NMR, we have presented the degree to which chemical shifts of a particular nuclear species in the protein backbone can be used as a low-resolution structural parameter that correlates with a variety of protein structural parameters.

Glossary of abbreviations

ACS

Averaged Chemical Shift

ACSESS

Averaged chemical shifts to secondary structure

BMRB

BioMagResBank

CATH

Class, Architecture, topology and homologous super family

CD

Circular Dichroism

COSY

Correlated Spectroscopy

CSI

Chemical shift index

CSP

Chemical shift pattern

DEFINE

Determine the secondary and first level supersecondary structure

DSSP

Database of secondary structure Predictions

HSQC

Heteronucelar single quantum correlation

K-S test

Kolmogorov-Smirnov test

PDB

Protein data bank

POP

Prediction of Proline

RCSB

Research collaboratory for structural bioinformatics

RefDB

Referenced database

SCOP

Structural classification of proteins

SSC

Secondary structure content

STRIDE

Secondary structure assignment from atomic coordinates