Parametrization, molecular dynamics simulation and calculation of electron spin resonance spectra of a nitroxide spin label on a poly-alanine alpha helix

Abstract

The nitroxide spin label 1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl-methanethiosulfonate (MTSSL), commonly used in site-directed spin labeling of proteins, is studied with molecular dynamics (MD) simulations. After developing force field parameters for the nitroxide moiety and the spin label linker, we simulate MTSSL attached to a poly-alanine alpha helix in explicit solvent to elucidate the factors affecting its conformational dynamics. Electron spin resonance spectra at 9 and 250 GHz are simulated in the time domain using the MD trajectories and including global rotational diffusion appropriate for the tumbling of T4 Lysozyme in solution. Analysis of the MD simulations reveals the presence of significant hydrophobic interactions of the spin label with the alanine side chains.

I. INTRODUCTION

Among the various experimental techniques probing the dynamics of proteins, site-directed spin labeling (SDSL) benefits from using a local reporter that is well tolerated at many sites on soluble and membrane proteins.¹ The observed continuous wave electron spin resonance (ESR) spectra of a spin labeled protein report about molecular motions over a wide range of time scales: from tens of picoseconds to hundreds of nanoseconds. The high sensitivity SDSL technique thus offers the potential of an extremely rich source of information about biological macromolecules. At the same time, the interpretation of the spectra in terms of detailed protein dynamics is complicated by the internal dynamics of the spin label side chain. To maximally utilize the information present in the spectra, a meticulous understanding of the spin label dynamics becomes necessary. Here we address this problem from a computational point of view.

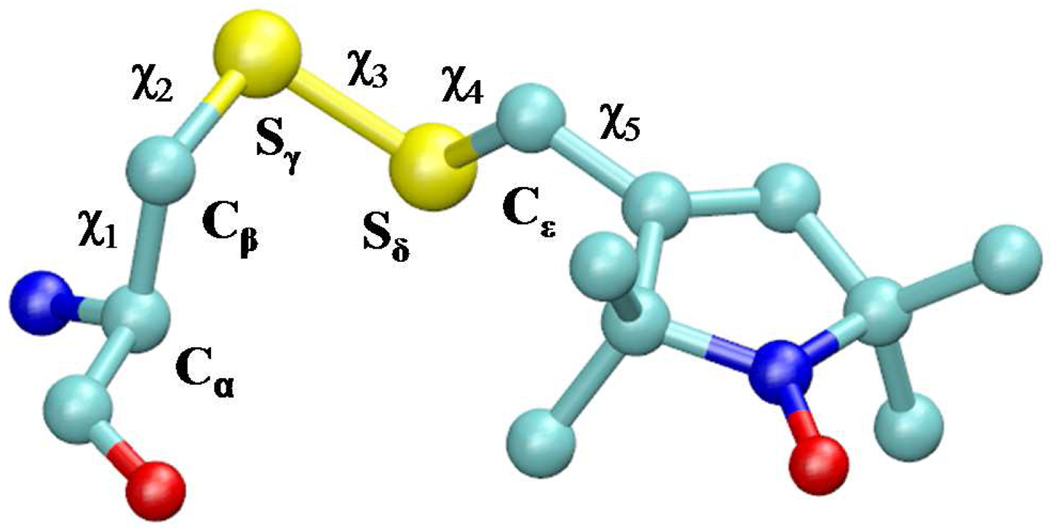
Over the last decade, Hubbell and co-workers have conducted extensive experimental studies to elucidate the factors affecting the dynamics of nitroxide spin labels on soluble proteins.^1–7 Of particular interest to this paper is the work in which 1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl-methanethiosulfonate (MTSSL) was used as a spin label. Following the general convention, we refer to the amino acid side chain resulting from the reaction of MTSSL with cysteine as R1 (Fig. 1). In the majority of the studies T4 Lysozyme (T4L) has served as a model protein system.^1–6 From this work, site 72 in T4L, situated in the middle of a long five-turn α-helix, has emerged as a prototypical solvent-exposed helix surface (SEHS) site.¹ The X-band (9 GHz) spectra of 72R1, as well as 131R1 (in the middle of a short two-turn helix), show insignificant variation upon alanine mutation of the neighboring i ± 3 and i ± 4 residues,² suggesting that at these positions R1 interacts only weakly with its neighbors.¹ In spite of this apparent lack of interactions, the spectra of both 72R1 and 131R1 indicate that the conformational freedom of the spin label at those positions is significantly restricted.^1,2 This ordering was proposed to be due the formation of hydrogen bonds between the disulfide of R1 and the hydrogen of either the backbone amide² or the backbone C_α.¹ Put together, the experimental data has been rationalized in terms of the “χ₄/χ₅ model” for the dynamics of R1 at SEHS sites that are not involved in tertiary contacts.¹ According to the model, the inter-residue immobilization of the disulfide by the backbone effectively locks the conformational transitions about the first two dihedrals, χ₁ and χ₂, of R1 (Fig. 1). Since the energetic barrier of the third linker dihedral χ₃—the disulfide torsion angle—is about 7 kcal/mol,⁸ the internal motion of R1 is assumed to be largely limited to rotations about the last two dihedrals χ₄ and χ₅, hence the name of the model.

Figure 1.

The “side chain” R1, resulting from linking MTSSL to a cysteine through a disulfide bond.

The χ₄/χ₅ model has been used to motivate quantitative spectral simulations using the MOMD^5,9–12 and SRLS^9,13 models of Freed and co-workers.^14–17 In the analytical MOMD/SRLS models, the nitroxide undergoes anisotropic rotational diffusion in an orienting potential expressed as a sum of spherical harmonics. Although such dynamics is intended to correspond to the real spin label dynamics only in an effective, “mean-field” way, a correspondence between the two diffusion coefficients of the MOMD/SRLS model (D_⊥ and D_‖) and torsions about χ₄ and χ₅ has been implied by the χ₄/χ₅ model.⁵ As a result, quantitative understanding of the dynamics of 72R1 and 131R1 in T4L has been pursued by simultaneous fits of multifrequency ESR spectra with the MOMD/SRLS model.^9,13,18

Increasing numbers of studies have recently used atomistic models to gain a deeper insight into the dynamics of R1 by performing molecular dynamics (MD) or Monte Carlo simulations.^19–25 Potentially, all-atom MD simulations with explicit solvent molecules can provide access to the detailed motion of the spin label in its heterogeneous environment. Unfortunately, exhaustively sampling the conformational space accessible to the spin label is challenging for all-atom simulations at the present time. For example, only a few transitions of the R1 dihedrals were observed during 5 and 10 ns simulations of fully solvated spin labeled T4L²¹ and Cytochrome c,²² respectively. A recent simulation of fully solvated T4L²⁵ extended for 75 ns but only conformations of R1 with χ₃ ≈ −90° were sampled, since no transition to χ₃ ≈ 90° occurred.⁶³ To reduce the system size and speed up the simulations, a large majority of the MD studies forgo explicit treatment of the solvent.^19,23,24 In addition to replacing the solvent with a continuum dielectric, Monte Carlo search of the R1 conformations,²⁶ and MD simulations at 600 K^19,23 have been used to achieve greater sampling. Though it may be designed to sample efficiently, a Monte Carlo search strategy does not contain information about the spin label dynamics. On the other hand, the dynamics and the populations of the spin label simulated at 600 K are significantly distorted. Ultimately, to assess how relevant the spin label dynamics implied by the molecular models are, ESR spectra should be calculated from the models and compared with experiment. Calculations of ESR spectra directly from trajectories require many long trajectories, far beyond what can be currently expected from routine MD simulations of solvated spin labeled proteins. Indeed, an attempt to simulate 9 and 250 GHz spectra from 10 trajectories of fully solvated T4L, between 5.5 and 6 ns each, was not successful.²¹ No such attempt has been made in the case of Cytochrome c.²² As an alternative, Steinhoff and co-workers used the MD simulations to estimate an orientational potential of mean force U(Ω), where Ω are the Euler angles mapping the nitroxide-fixed coordinate frame to the protein-fixed one.^19,23 ESR spectra were then simulated directly from trajectories of Brownian evolution in the potential U(Ω). Sale et al., on the other hand, assumed that U(Ω) can be expanded as a sum of spherical harmonics and estimated the expansion coefficients from the MD simulations.^24,27 Spectra were then simulated with the MOMD model using the expansion coefficients as input parameters.^24,27

In another, more recent study Tombolato et al. refrain from MD simulations altogether.^28,29 Building on their previous work on spin labeled lipids^30,31 they propose that the dynamics of R1 at SEHS sites can be rationalized in terms of librations in a few enumerable conformers (rotamers) and exchanges between them. This insightful observation brings the problem of the spin label dynamics to the more familiar realm of internal side chain dynamics in proteins and their manifestation in NMR, ESR and fuorescence.^32–36

In Ref. 28 the conformational dynamics of R1 on a poly-alanine α-helix was studied in detail. The absence of steric clashes between the spin label and the helix was used to identify allowed rotamers. The relative probabilities of the rotamers and the rates of exchange among them were estimated from the ab initio scans of the torsional potential energies. Based on the high energy barriers and/or large friction opposing the displacement of the bulky spin label, exchanges about χ₁, χ₂ and χ₃ were assessed to be much slower compared to the time scale of standard X-band ESR, providing independent theoretical support for the χ₄/χ₅ model. Due to its simplicity, the approach was suggested as complementary to full MD simulations when insight into the conformational freedom and dynamics of R1 at solvent-exposed sites is sought.

So far, bridging the gap between the atomistic spin label dynamics and the corresponding ESR spectra has been possible only by simplifying the atomistic model. The degree to which such approximations are justified is presently uncertain. Here, we adopt a different approach and preserve all the atomic detail that an all-atom, nonpolarizable force field like CHARMM³⁷ can offer. In an effort to simplify and reduce the problem to its most relevant aspects, we simulate a fully solvated, spin-labeled poly-alanine α-helix, hoping that the dynamics of R1 in this simple system has sufficient bearing on the experimentally well-studied spin label dynamics at SEHS sites. The behavior of the spin label in our MD simulations is expected to be informative about the simplifying assumptions that are safe to make when reduced, stochastic models of the spin label dynamics need to be constructed,^{19,23,24,26–28,38} as in the case of spin-labeled proteins, for which long, all-atom MD simulations might not be feasible.

In summary, the paper pursues two main objectives. First, to develop a reliable force field for the spin label side chain R1, calibrated by extensive comparison with ab initio calculations. Second, to characterize the “minimal,” internal dynamics of R1 on solvent-exposed, helix surface sites, by simulating the simplest such system that essentially does not exhibit additional protein backbone and side chain dynamics.

The paper is organized as follows: Our methodology is presented in Sec. II. First, the parametrization for a group of four nitroxides is discussed, with particular emphasis on their electrostatic properties. The energetics of the R1 linker are also examined carefully. Then, we give details about the MD simulations and the calculation of the ESR spectra using the MD trajectories. Section III contains our results. The conformational dynamics of R1 on a poly-alanine α-helix is analyzed and ESR spectra at 9 and 250 GHz are simulated. The discussion of the results is presented in Sec. IV and our conclusions are given in Sec. V.

II. METHODS

A. Force field parameters for four spin labels

Meaningful atomistic MD simulations require the use of accurate potential energy functions. The parameters pertaining to the nitroxide moiety that were not already present in the official set of CHARMM force field PARAM27^37,39 must be carefully determined. To ensure the more general validity of the parameters, four nitroxide model compounds with ring structures based on pyrroline (SLP), pyrrolidine (SLR), oxazolidine (SLT), and piperidine (SLH) were selected for simultaneous parametrization (Fig. 2). The first two compounds (SLP and SLR) constitute the rings of the spin labels R1² and R5,³ respectively, widely used in SDSL studies of proteins.^1,40 The third model compound (SLT) is a building block for fatty acid and phospholipid spin labels, while the last one (SLH) is itself used as the reporter group TEMPO.

Figure 2.

Structures and naming convention of the model compounds used in the parametrization.

The structures of the four model compounds were optimized with the B3LYP hybrid functional using the standard basis set 6–31G*. This level of theory has been shown to reproduce the experimental geometries of the nitroxides accurately.⁴¹ All the ab initio calculations were performed using the program Gaussian 03.⁴² The vibrational frequencies and the normal modes for the model compounds were calculated at the optimized geometries, using B3LYP/6–31G*. A global scaling factor of 0.9806 was used for the calculated frequencies, as recommended in Ref. 43. The ab initio optimized geometries, vibrational frequencies (after scaling) and vibrational modes were used as reference data in the selection of the bonded parameters for the classical force field. In their minimum energy conformations the pyrrolidin and the oxazolidine rings are not planar but prefer a puckered state (Fig. 2). Extra efforts were made to ensure that the various puckered states of those two rings and the energy barriers between them were correctly reproduced with the force field parameters (data not shown).

1. Partial charges and interaction with water

The partial charges and the Lennard-Jones parameters assigned to the atomic centers determine the nature of the direct interactions of the spin label with its surroundings (e.g. hydrogen bonding and van der Waals contacts), as well as its more global preference for certain types of environment (e.g. aqueous versus hydrophobic). Bearing in mind such considerations, the partial charges were adjusted to reproduce both the overall electrostatic properties of the molecules as well as the more specific hydrogen bonding properties. The electrostatic potential of each model compound was calculated on a grid of points at B3LYP/aug-cc-pvdz level of theory using the optimized structures. The grid points were generated on five nested Connolly surfaces with scaling factors 1.3, 2.2, 3.0, 5.0 and 6.0, with corresponding densities 2.8, 1.9, 1.3, 0.6 and 0.2 points per Ų, respectively, chosen in agreement with previous parametrization work of the CHARMM force field.⁴⁴ Once the electrostatic potential was calculated, the FITCHARGE⁴⁴ module of CHARMM was used to achieve the best fit by varying the atomic partial charges. To be consistent with the existing nonpolarizable CHARMM force field for proteins³⁷ and lipids³⁹ the charge on the nonpolar hydrogens was restricted to 0.09 in atomic units. The charge fitting was achieved in two steps. In the first step, the nonpolar hydrogens were assigned a charge of 0.09 and, to keep the molecule neutral, the adjacent carbon atoms were given a charge of −0.09 (methyne carbon), −0.18 (methylene carbon) or −0.27 (methyl carbon). The rest of the atoms were assigned zero charge. Charge fitting with a hyperbolic restraint on the charges—to prevent their unphysical increase during the fitting—was performed only for the atoms with zero initial charge. All the methyne, methylene or methyl groups, the initial charge of which was already assigned, were excluded from this fit. In the second step a parabolic restraint was applied to keep the charges close to their values of the previous step. In this case, all the atoms, except the nonpolar hydrogens, were included in the fit. The partial charges obtained from this procedure for the ring atoms of the four compounds are given in Table I. The components and magnitudes of the resulting dipole moments are compared with the corresponding ab initio values in Table II. The agreement between the two sets is satisfactory. The dipole moments of the molecules are slightly overestimated, as expected in an effective nonpolarizable force field.^37,45

TABLE I.

Partial charges for the ring atoms in atomic units.

	O	N	C2	C5	C3/O3	C4
SLP	−0.438	0.220	0.334	0.329	−0.003	−0.340
SLR	−0.433	0.249	0.245	0.267	−0.127	−0.229
SLT	−0.403	0.147	0.406	0.326	−0.336	−0.128
SLH	−0.379	0.167	0.284	-	−0.237	−0.180

TABLE II.

Ab initio vs. parametrized (in parenthesis) dipole moments (debye).

	SLP	SLR	SLT	SLH
x	1.55 (1.59)	−1.31 (−1.37)	0.78 (0.82)	0.00 (0.00)
y	2.96 (3.02)	3.07 (3.14)	−2.06 (−2.12)	3.10 (3.19)
z	0.00 (0.00)	−0.11 (−0.21)	−0.23 (−0.49)	0.15 (0.24)
tot.	3.35 (3.41)	3.34 (3.43)	2.22 (2.32)	3.11 (3.20)

In the parametrization three new atom types were introduced for the nitroxide oxygen (O) and nitrogen (N), and the doxyl ring oxygen (O3). The Lennard-Jones parameters assigned to the three new atom types were chosen based on the existing CHARMM parameters. To assess the quality of the atomic partial charges and of the Lennard-Jones parameters for the nitroxide oxygen, the interaction of the nitroxide moiety with a water molecule was examined in detail. For each of the four model compounds the relative orientation of the water molecule with respect to the nitroxide was optimized keeping the structure of the nitroxide and the structure of the water molecule fixed, the former at the B3LYP/6–31G* optimized geometry and the latter at the experimental geometry⁴⁶ (r_OH = 0.9572 Å, θ_HOH = 104.52°).⁶⁴ The optimization was performed using B3LYP/6–311++G**, a level of theory which, reportedly, is sufficient to accurately reproduce hydrogen bond geometries.⁴⁷ The energies of the optimized dimers were calculated using B3LYP/aug-cc-pvdz. The interaction energy was calculated by subtracting the energies of the individual molecules from the energy of the dimer. The resulting interaction energy suffers from basis set superposition errors (BSSEs). It is known that the BSSE is larger for MP2 and smaller for B3LYP when used with the same basis set.⁴⁸ Based on the water dimer data of Ref. 48, we estimated that the BSSE is less than 0.5 kcal/mol for the aug-cc-pvdz basis set that was used. Considering the uncertainty in the accuracy of the ab initio calculation we decided not to correct the interaction energies for the BSSE.

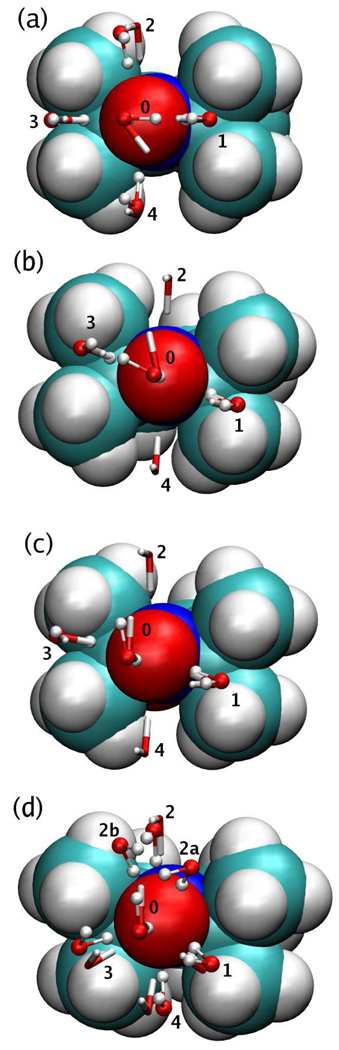
Several structural local minima were identified for each water-nitroxide dimer (Fig. 3). In the ab initio calculations, the energetically most favorable conformations are the ones in which the O–H bond of the water lies approximately along the direction of the lone pairs of the nitroxide oxygen (numbered 1 and 3 in Fig. 3). Conformations in which the water O–H bond is positioned roughly perpendicularly to the plane of the lone pairs were also found to be local minima (numbered 2 and 4). Their region of attraction is significantly smaller, but present nevertheless, especially for the symmetric nitroxides SLP and SLH. In addition, the geometry in which one of the water hydrogens is along the N–O bond of the nitroxide moiety was also examined by restricting the position of the H-bonding hydrogen to lie on the line along the N–O bond during the optimization (numbered 0). The interaction energies for each of these conformations are listed in Table III, where the distances between the H-bonding water hydrogen and the nitroxide oxygen are also shown in parenthesis.

Figure 3.

Interaction geometries with water for (a) SLP, (b) SLR, (c) SLT, and (d) SLH, optimized with ab initio (balls and thin sticks) and with the force field (thick sticks).

TABLE III.

Interaction energies with water (kcal/mol) and the O…H hydrogen bond distance (Å), shown in parenthesis, for the specified conformation.

	SLP	SLR	SLT	SLH
	ab initio
0	−4.22 (1.99)	−4.35 (1.97)	−3.88 (2.01)	−4.47 (1.97)
1	−6.23 (1.89)	−6.21 (1.90)	−5.92 (1.91)	−5.73 (1.90)
2	−5.35 (1.94)	-	-	−5.38 (1.94)
3	−6.21 (1.89)	−6.20 (1.89)	−5.98 (1.91)	−5.64 (1.91)
4	−5.35 (1.93)	-	−4.91 (1.94)	−5.40 (1.91)
2a				−5.31 (1.92)
2b				−5.35 (1.92)
	param
0	−5.38 (1.90)	−5.43 (1.91)	−4.91 (1.92)	−5.04 (1.92)
1	−6.12 (1.87)	−6.09 (1.88)	−5.77 (1.89)	−5.52 (1.90)
2	−6.08 (1.88)	−6.15 (1.89)	−5.89 (1.91)	−5.68 (1.92)
3	−6.09 (1.88)	−6.04 (1.88)	−5.75 (1.89)	−5.52 (1.90)
4	−6.08 (1.88)	−6.17 (1.89)	−5.70 (1.89)	−5.67 (1.89)

The numbers in Table III indicate that with the force field the nitroxide-water interactions are more uniform along the various directions of approach compared to the ab initio interactions. For all the model compounds, the force field correctly assigns conformation 0 to be the least favorable. At the same time, the interaction energy in this conformation calculated with our parameters is about 1 kcal/mol more favorable than the ab initio energy. The absence of explicit representation for the oxygen lone pairs in the force field makes the interaction geometries 2 and 4 as favorable as the conformations 1 and 3. This was previously observed in Ref. 41, where lone pair sites for the nitroxide oxygen were introduced in order to reproduce this structural feature with a molecular mechanics force field. Here, we choose to keep the nitroxide oxygen as a point charge and not introduce additional lone pair sites. As a result of this simplification the hydrogen bonding geometry is expected to be slightly off. Nevertheless, in the context of dynamics at ambient temperature, one might suspect that thermal agitation will render these structural effects less important since the energy differences are within one to two k_BT over the whole range of hydrogen bonding geometries.

2. Scan of the linker dihedral angles of R1

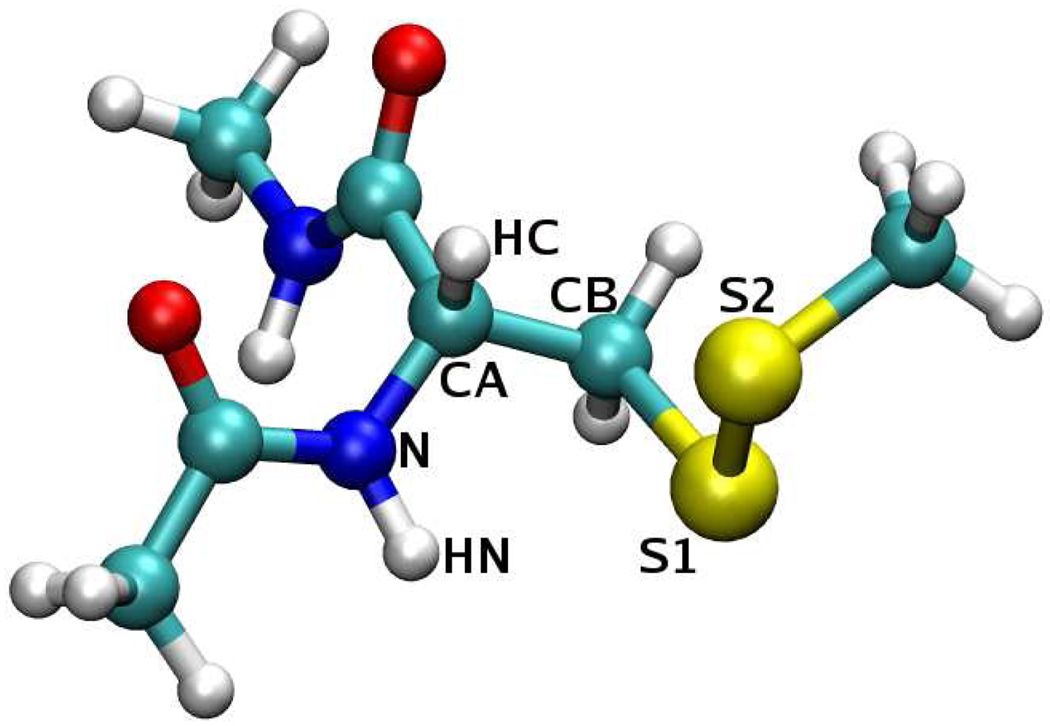
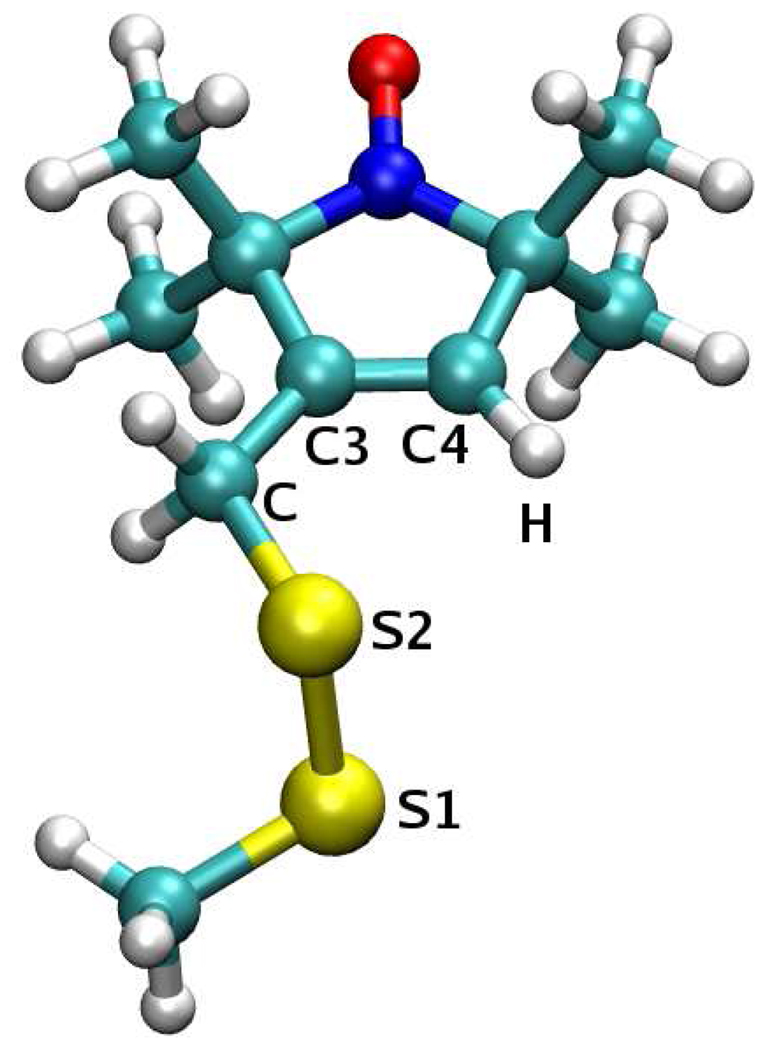
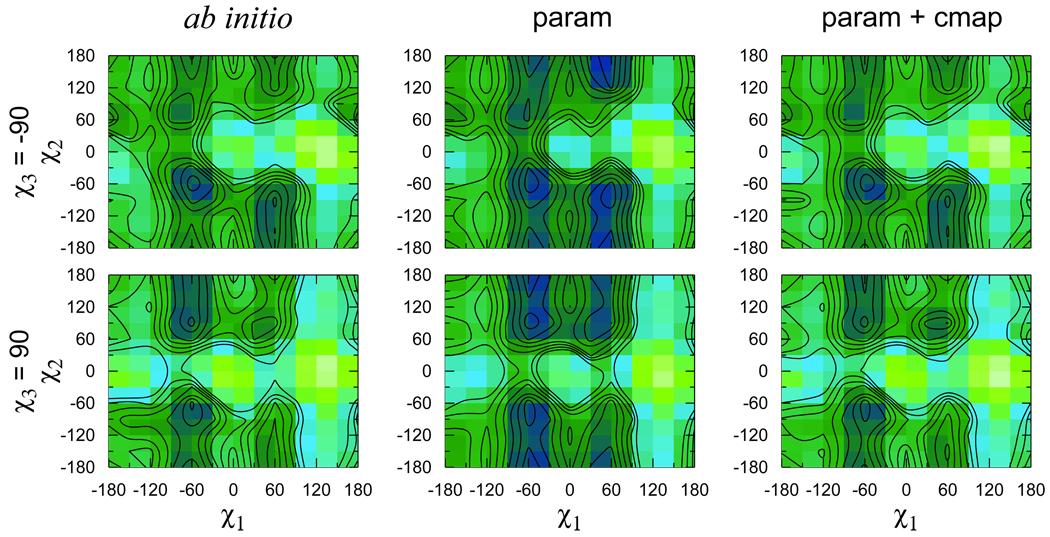
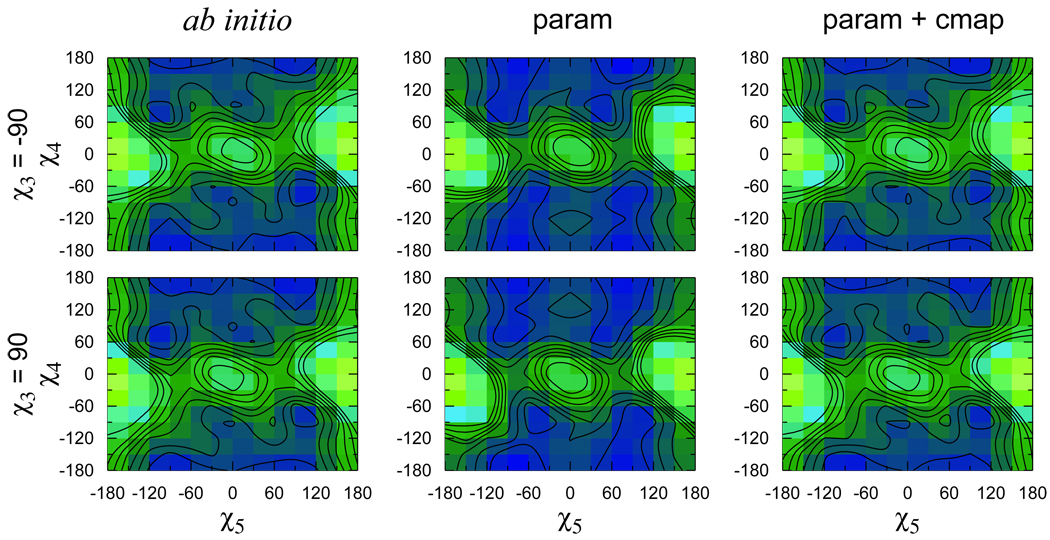
Rotations about the bonds connecting the nitroxide ring to the protein backbone constitute an intuitive way of rationalizing the dynamics of the spin label side chain R1.^2–5,28 To make sure that the simulated linker dynamics proceed on the correct energy surface, a scan of the dihedral energy was performed. Restricted optimizations and single point energy evaluations were carried at the B3LYP/6–31G* and B3LYP/aug-cc-pvdz levels of theory, respectively, for the torsion angles of interest, taking values on a two dimensional grid. The grid points were separated by 30°, in the interval (−180°, 180°). The χ₁–χ₂ energy surface was explored using the construct shown in Fig. 4. The two linker dihedrals χ₁ (N–CA–CB–S1) and χ₂ (CA–CB–S1–S2) were constrained during the optimization. In addition, the “backbone” atoms were fixed in an α–helical conformation. The procedure was carried separately for χ₃ ≈ −90° and χ₃ ≈ 90°. The χ₅–χ₄ energy surface was examined using the construct in Fig. 5. Only the values of χ₅ (S2–C–C3–C4) and χ₄ (S1–S2–C–C3) were fixed during the optimization. All the other degrees of freedom were allowed to relax. The resulting energy surfaces are shown in Fig. 6 and Fig. 7.

Figure 4.

Energetically most favorable conformation on the χ₁–χ₂ energy surface, (χ₁, χ₂, χ₃) = (−60°, −60°, −90°). The distance d_S1−HN = 2.81 Å and the angle θ_S1−N−HN = 57°. In addition, d_S2−HC = 3.03 Å and θ_S2−CA−HC = 55°.

Figure 5.

The χ₅ = 0°, χ₄ = −90°, χ₃ ≈ −90° conformation of R1. d_S2−H = 2.87 Å, θ_S2−C4−H = 62°; d_S1−H = 3.67 Å and θ_S1−C4−H = 61°.

Figure 6.

Scan of the χ₁–χ₂ potential energy surface. Low energy regions are dark, high energy regions are light. Contours are drawn for every 1 kcal/mol change in energy. The minimum energy for each surface was set to zero and used as an offset for the other energies. The corner of every small rectangle in the two plots on the left corresponds to an ab initio optimization and energy evaluation data point. The scans with the standard force field energy function, in which the energetics of each torsion are independent of the other torsions, are in the middle column (param), the ones obtained using CMAP are on the right (param+cmap).

Figure 7.

Same as Fig. 6 for χ₅–χ₄.

Figure 6 shows that the parametrization captures the positions of the minima on the χ₁–χ₂ surface rather well. The relative depths of the minima, on the other hand, are not reproduced satisfactorily. Whereas the ab initio calculation indicates that (χ₁; χ₂) = (−60°, −60°) is a global minimum for χ₃ ≈ −90°, the best that could be achieved by varying the force field parameters for the dihedrals led to two additional, almost equally deep minima at (60°, −60°) and (60°, 180°). According to the ab initio energies, these two conformations should lie, respectively, about 1 and 2 kcal/mol higher than the global minimum. The ab initio optimized structure for the global minimum is shown in Fig. 4, where one of the sulfurs (S1) is seen to be in the vicinity of the backbone amide hydrogen (HN), the other (S2), close to the hydrogen of the Cα (HC). Both of the implied sulfur-hydrogen interactions have been invoked to rationalize the apparent adsorption of the disulfide to the helix backbone.^1,2 Therefore, it is very important to account for their energetics. The absence of the sulfur lone pairs in the force field and the small partial charge of the sulfur makes it impossible to recreate these favorable interactions naturally. The tabulated spline correction map (CMAP), recently introduced in the CHARMM force field,⁴⁹ was used to impose the desired ab initio energy on the two dimensional χ₁–χ₂ energy surface, thus introducing a coupling between these two torsions. The CMAP grid was calculated by averaging the corrections necessary for the χ₃ ≈ −90° and χ₃ ≈ 90° conformations. As expected, the agreement between the ab initio energy surfaces and the ones obtained using CMAP is almost perfect (Fig. 6).

In the case of the χ₅–χ₄ energy surfaces in the first two columns of Fig. 7, the best parameters with independent χ₄ and χ₅ failed to reproduce not only the relative depths but also the positions of the minima. For χ₄ ≈ 180° the multiplicity of χ₅ is seen to be two, with minima at about −90° and ±90°. With the force field, the positions of these two minima basically persists for χ₄ ≈ ±90°, whereas according to the ab initio calculations one of the minima should shift to χ₅ ≈ 0°. The optimized structure at (χ₅; χ₄) = (0°, −90°) is shown in Fig. 5, where it is apparent that the force field fails to account for the favorable interaction between the sulfur S2 and the polar hydrogen H. The fact that this conformation has a slightly lower energy than the (0°, 180°) conformation in which S1 lies away from the nitroxide ring, is a clear indication that the lone pairs of the sulfur are involved in the interaction. As before, the sulfur representation in the force field does not allow us to take such effects into account. Using the CMAP correction for the χ₅–χ₄ energy surface led to a good agreement with ab initio (Fig. 7). All topology and parameter files are given in supplementary material.

B. MD simulation details

Simulations of R1 attached to a poly-alanine α-helix were performed using CHARMM.⁵⁰ The simulated helix consisted of 14 alanines and a single spin labeled cysteine at its central position. The helix was solvated with 686 TIP3P⁵¹ water molecules. The resulting system of of 2247 atoms filled a tetragonal simulation box with starting side lengths of 26.0, 26.0 and 34.0 Å. Periodic boundary conditions were used. The electrostatics were treated with particle mesh Ewald summation.^52,53 Pressure and temperature pistons were used to achieve an NpT ensemble at T = 297 K and p = 1 atm.⁵⁴ To prevent the unfolding of the helix in water the first five and the last five residues were harmonically restrained to their starting positions with force constants of 0.5 kcal/mol/Ų.

According to the χ₄/χ₅ model, the first three dihedrals of R1 should rarely undergo transitions. Therefore, considering their multiplicity (χ₁:3, χ₂:3, χ₃:2), we chose each of the 18 possible conformations as starting conditions for the simulations. Thus 18 systems, each one starting at a different conformation, were simulated. Below we refer to these trajectories as a1, a2, a3, etc. and b1, b2, etc., where ‘a’ and ‘b’ indicate that the trajectory was initiated with χ₃ ≈ −90° and χ₃ ≈ 90°, respectively. The initial values of χ₁ and χ₂ in each of those sets are summarized in Table IV. The simulations were equilibrated for 500 ps. During the equilibration a at bottom Saxon-Wood potential was used to restrict each of the first three dihedrals to remain in their initial state, while the last two dihedrals were free to explore different conformations. After the equilibration the Saxon-Wood potentials were removed and only the harmonic restraints on the backbone atoms of the first five and last five residues remained. Each of the 18 systems was simulated for 101 ns. The first one ns was not considered in the analysis. Snapshots of the simulations were saved every 1 ps.

TABLE IV.

Initial values of χ₁ and χ₂ (in degrees) for trajectories a1, a2, a3, etc. and b1, b2, etc.

traj. #	1	2	3	4	5	6	7	8	9
χ1	−180	−180	−180	−60	−60	−60	60	60	60
χ2	−180	−60	60	−180	−60	60	−180	−60	60

C. ESR spectra simulation details

Our recently developed numerical integrators—for the quantal spin dynamics and for the classical rotational diffusion—allow us to easily model the effect of the global protein tumbling in addition to the spin label dynamics coming from the MD simulations.⁵⁵ (For alternative numerical procedures that aim to simulate the free induction decay from trajectories see Refs. ^{56, 57} or ²⁵.) This is necessary for the qualitative comparison of the simulated spectra of R1 on a poly-alanine α-helix with the experimentally available data of T4L. For the rotational diffusion coefficient of T4L in water we used D = 18 × 10⁶ s⁻¹, which had been obtained in a multifrequency fit to spectra recorded at 22°C¹³ with the SRLS model.¹⁷ The viscosity of the nonpolarizable TIP3P water model used in the MD simulations is 2.86 times smaller than the viscosity of water,^58,59 implying that the solvent in the simulations moves about 2.5 times faster than it should. Since the spin label on the poly-alanine helix is largely solvent exposed, its dynamics are also expected to be faster to a similar degree. To correct for the low solvent viscosity, the time axis of the MD trajectories was stretched by a factor of 2.5. Because T4L is a relatively small protein, its tumbling in solution is fast enough to narrow the spectral lines at 9 GHz. To slow down the tumbling of T4L and reduce its effect on the spectra, it is a common practice to use 30 wt % sucrose solution, which is about 3.3 times more viscous than an aqueous solution with no sucrose. Since the rotational diffusion coefficient is inversely proportional to the viscosity, we estimated that D = 6 × 10⁶ s⁻¹ under such conditions. The viscosity of the solution is expected to affect not only the tumbling of the protein but also the dynamics of the spin label itself. Thus, to compare with experimental spectra in 30 wt % sucrose, the time axis of the trajectories was stretched by a factor of eight (8 ≈ 2.5 × 3.3). The stretch factors, the diffusion coefficients and the respective correlation times are summarized in Table V.

TABLE V.

Scaling factor for the time axis and rotational diffusion coeffcient of T4L used in the spectral simulations in Sec. III. The tumbling relaxation time τ = 1/6D is also shown.

solvent	stretch	D × 106 (s−1)	τ (ns)
water	2.5	18	9.3
30 (w/w) % sucrose	8.0	6	27.8

When MD trajectories are used as explicit realizations of the randomness affecting the quantum Hamiltonian, it is beneficial to average the magnetic tensors along the MD trajectories over the time step Δt appropriate for the quantum dynamics.⁵⁵ Two such time steps, suitable for B = 0.34 T (9 GHz) and B = 8.92 T (250 GHz), are given in the second column of Table VI. The snapshots from the MD simulations are available every δt = 1 ps. Dividing Δt by δt and by 2.5—the factor accounting for the larger diffusion coefficient of water in the simulations—gives the number of MD frames to be averaged over (avgN). Similarly, one can obtain the ‘avgN’ values for no stretch at all, or for a stretch by a factor of eight (both given in parentheses). It may be noted that the integration of the quantum dynamics can be initiated from different points along the MD trajectory, since the origin of time is arbitrary. The starting time instances were chosen to be separated by 2 ns, which corresponds to ‘lagN’ number of Δt steps. The last two columns in Table VI list the number of spherical grid points (sphN), used for the initial conditions of the isotropic diffusion, and the Gaussian broadening introduced in the calculation of the spectra $(T_G^{-1})$. The choice of the latter was based on the observations of Refs. ⁹ and ¹³ that the inhomogeneous broadening is larger at 250 GHz compared to 9 GHz. Small Lorentzian broadening of 0.3 G was introduced to account for the possibility of Heisenberg spin exchange.⁶⁰ The magnetic tensors,

$$\begin{array}{l}{\mathrm{g}}^{\mathrm{N}}=\text{diag}(2.00809,2.00585,2.00202)\hfill \\ {\mathrm{A}}^{\mathrm{N}}=\text{diag}(6.2,4.3,36.9),\hfill \end{array}$$ (1)

corresponding to the experimentally determined values for 72R1 on T4L,^9,13 were used in the spectral simulations.

TABLE VI.

Parameters used in the simulation of the spectra in Fig. 12 and Fig. 13. Additional Lorentzian broadening of 0.3 G was introduced in all the simulations.

field (T)	Δt (ns)	avgN	lagN	sphN	$(T_G^{-1})$ (G)
0.34	2.0	800a (250b)	1	400d	1.0
8.92	0.25	100a (250c)	8	12800d	2.0

^a2.5-fold stretch of the time axis.

^b8-fold stretch of the time axis.

^cThe time axis is not stretched.

^dTwice as many points were used for the D = 0 simulation.

III. RESULTS

A. Conformational dynamics of R1 on a poly-alanine α-helix

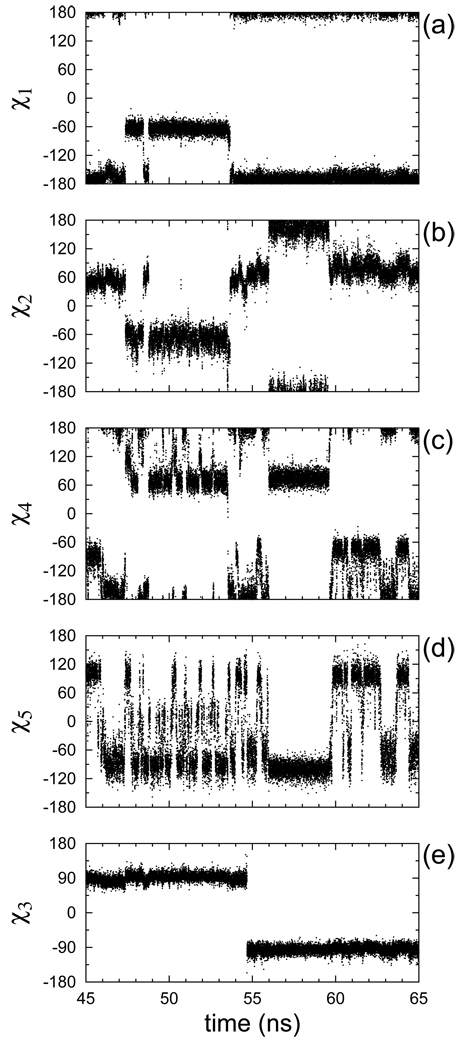
A striking feature of all the MD trajectories is the large number of transitions for each of the dihedral angles of the spin label. Even the disulfide torsion χ₃, which has the highest energy barrier among all the dihedral angles, changes its conformation ten times across all the 18 trajectories (Table VII). The two transitions in trajectories a3 and b9 are separated by 27 and 19.3 ns, respectively, and therefore, are most likely independent. (See Sec. IIB for the naming convention of the trajectories.) Figure 8 shows a 20 ns window of the evolution of the five dihedral angles of trajectory b1. This trajectory undergoes one χ₃ transition (Fig. 8(e)). The traces in Fig. 8, and all the other traces which are not shown here, indeed seem to confirm that the dynamics of R1 on a poly-alanine α-helix can be rationalized in terms of librations in discrete number of states with occasional exchange between them, as proposed by Tombolato et al.²⁸

TABLE VII.

Number of conformational transitions for χ₃ observed in the MD trajectories.

traj. #	1	2	3	4	5	6	7	8	9
a	0	0	2	0	0	0	0	0	0
b	1	0	1	1	0	1	1	1	2

Figure 8.

Evolution of dihedral angles in the time interval between 45 and 65 ns for trajectory b1.

Interestingly, in Fig. 8 we see transitions of χ₁ and χ₂ lasting from less than 1 ns to several nanoseconds—time scales which by no means are slow on the ESR time scale. In addition, the transitions of these dihedrals appear to be largely coupled. For example, the short-lived second transition of χ₁ happens simultaneously with a transition of χ₂. At the last transition of χ₁ not only χ₂ but also χ₄ changes its conformation. As expected from the low energy barriers separating its conformational minima (Fig. 7), the fifth dihedral χ₅ undergoes rapid transitions (Fig. 8(d)). At the same time, a concerted transition involving χ₂, χ₄ and χ₅, shortly after the 55th nanosecond in Fig. 8, locks the conformation of the spin label for almost 5 ns, providing an example of how in simulations extending for 5–10 ns it might be possible to have none or very few transitions of all the linker dihedrals, in spite of the low potential energy barrier of χ₅. Clearly, in this case, full account of the interactions of the spin label with its immediate environment is necessary.

Let us now try to identify the relevant rotamers of R1 and their populations. A given snapshot from the MD trajectories can be assigned to a rotamer in several different ways. One option is to define the rotamers by a set of reference dihedral angle values χi and fluctuation windows ±Δχ_i about them (1 ≤ i ≤ 5). Such reference values and fluctuation estimates were given in Ref. 28 for T = 298 K, based on the ab initio energy profiles of the R1 dihedrals, and are listed in Table VIII and Table IX. Only 3.5% of all the MD snapshots fall into the conformational volume covered by this narrow definition of rotamers. Even in this case, we find that 65 different rotamers, out of the 108 possible, are visited in the MD simulations. A larger fraction of the MD snapshots gets assigned to some rotamer when the width of the fluctuation window is increased. When 80% of the data is assigned, the trajectories visit 96 out of the 108 possible rotamers (Table IX). An alternative counting scheme is to use the reference rotamer angles from Table VIII as flagpoles and assign a given MD snapshot to the closest flagpole, according to an Euclidean distance metric. This strategy has the advantage of pairing every data point with a rotamer. According to this “minimum distance” criterion, the MD snapshots visit 102 rotamers (Table IX).

TABLE VIII.

Minima of the R1 linker dihedrals (in degrees) used to define its rotameric states in Ref. 28. The multiplicity of each torsion is in parenthesis.

χ1(3)	χ2(3)	χ3(2)	χ4(3); χ5(2)
−60, +65, 180	±75,180	±90	(±75; ±8, ∓100), (180, ±77)

TABLE IX.

Fluctuations (in degrees) about the conformations defined in Table VIII, together with their percent coverage of all the MD snapshots and the number of visited rotamers.

Δχ1	Δχ2	Δχ3	Δχ4	Δχ5	%	# rot.
8.5a	12.5a	8.5a	12.5a	(12.5a)(25b)	3.5	65
30	30	45	30	(30)(45)	59.3	90
40	40	60	40	(40)(60)	80.0	96
		minimum distance			100.0	102

^aValues estimated in Ref. 28 for T = 298 K.

^bReference ²⁸ comments that this fluctuation should be larger than 12.5° but does not specify a numerical value.

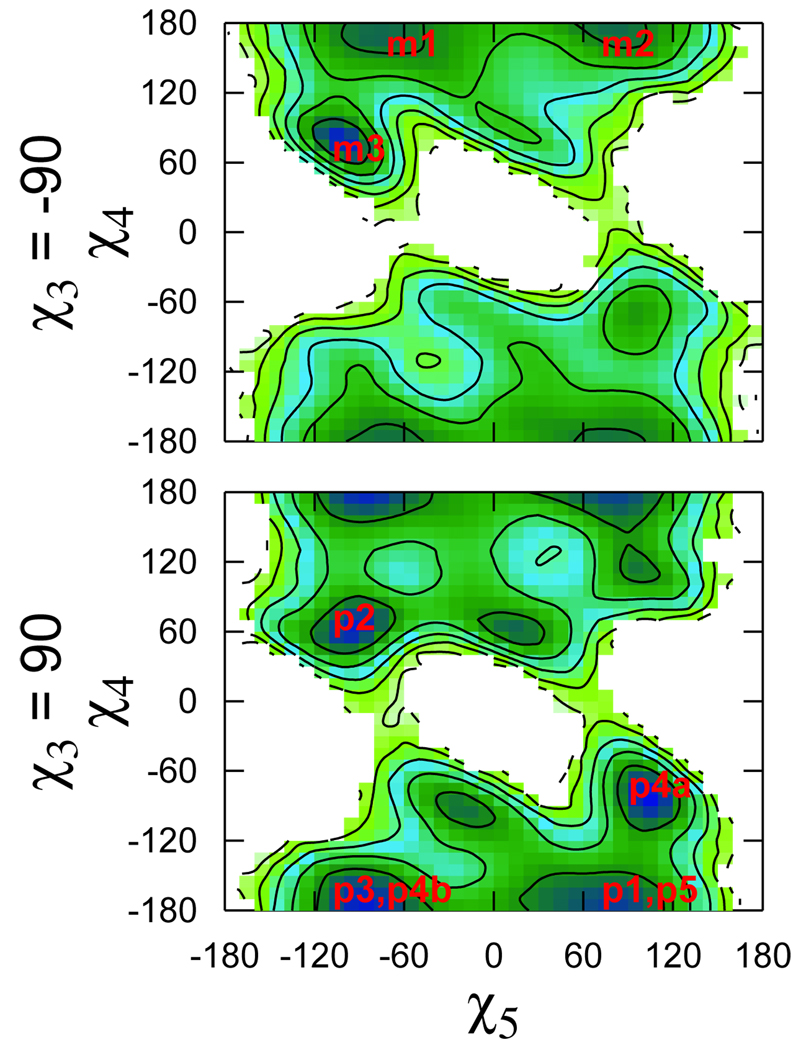
In spite of the large number of visited rotamers, it might be that the spin label visits most of these conformations only transiently and spends the more significant part of its time in a few rotamers. To evaluate this possibility we calculate the occupation probabilities of the visited rotamers using the minimum distance criterion. The 18 most populated rotamers are ranked in Table X. Indeed, the populations reveal that the spin label spends about a third of its time in only three rotamers (m1, m2 and m3), briefly visiting all the other tens of rotamers. At this point, it is important to stress that only ten transitions were observed for the dihedral angle χ₃ across all the trajectories. (For brevity, we refer to conformations with χ₃ ≈ −90° as ‘m’, and conformations with χ₃ ≈ +90° as ‘p’.) The fact that there were two p → m and eight m → p transitions suggests that the p conformer is less populated. However, the exact ratio of the two populations and the absolute ranking of the m and p rotamers in Table X is uncertain. Since more transitions were observed for the other dihedrals (for a given conformation of χ₃) it is safer to assume ergodicity in those cases. Taking into account this limitation, we analyze the two conformations of the disulfide separately. The populations of the rotamers conditioned on the state of χ₃ are given in parenthesis in Table X. From the numbers it becomes clear that the conformational freedom of the m and p states is quite different: Whereas only three rotamers (m1, m2 and m3) represent 50% of all the m conformations it takes six rotamers (p1, p2, p3, p4a, p4b, and p5) to cover the same percentage of the p states.

TABLE X.

Most populated 18 rotamers ranked according to their populations. The populations conditioned on the state of χ₃ are given in parenthesis.

rot.	χ1	χ2	χ3	χ4	χ5	prob. (%)	Ref. 28a
m1	−60	180	−90	180	−77	13.3 (20.8)	-
m2	−60	180	−90	180	77	10.3 (16.1)	-
m3	−60	−75	−90	75	−100	8.4 (13.1)	-
p1	−60	−75	90	180	77	4.5 (12.5)	-
m	180	180	−90	75	−100	3.7 (5.7)	-
p2	−60	−75	90	75	−100	3.6 (10.0)	-
m	−60	−75	−90	180	77	3.6 (5.7)	C1
m	180	75	−90	180	−77	3.0 (4.6)	-
p3	−60	180	90	180	−77	2.7 (7.6)	C6
p4a	−60	180	90	−75	100	2.6 (7.2)	-
p4b	−60	−75	90	180	−77	2.6 (7.2)	-
p5	−60	180	90	180	77	2.5 (6.9)	-
m	−60	−75	−90	180	−77	2.5 (4.0)	C2
m	180	180	−90	180	77	2.4 (3.7)	C9
m	180	−75	−90	180	77	2.0 (3.1)	-
p	−60	−75	90	75	8	1.9 (5.4)	-
p	180	75	90	−75	100	1.9 (5.3)	-
m	180	75	−90	−75	100	1.7 (2.7)	-

^aThe complete list of the 18 relevant rotamers according to Ref. 28 is given in Table XII.

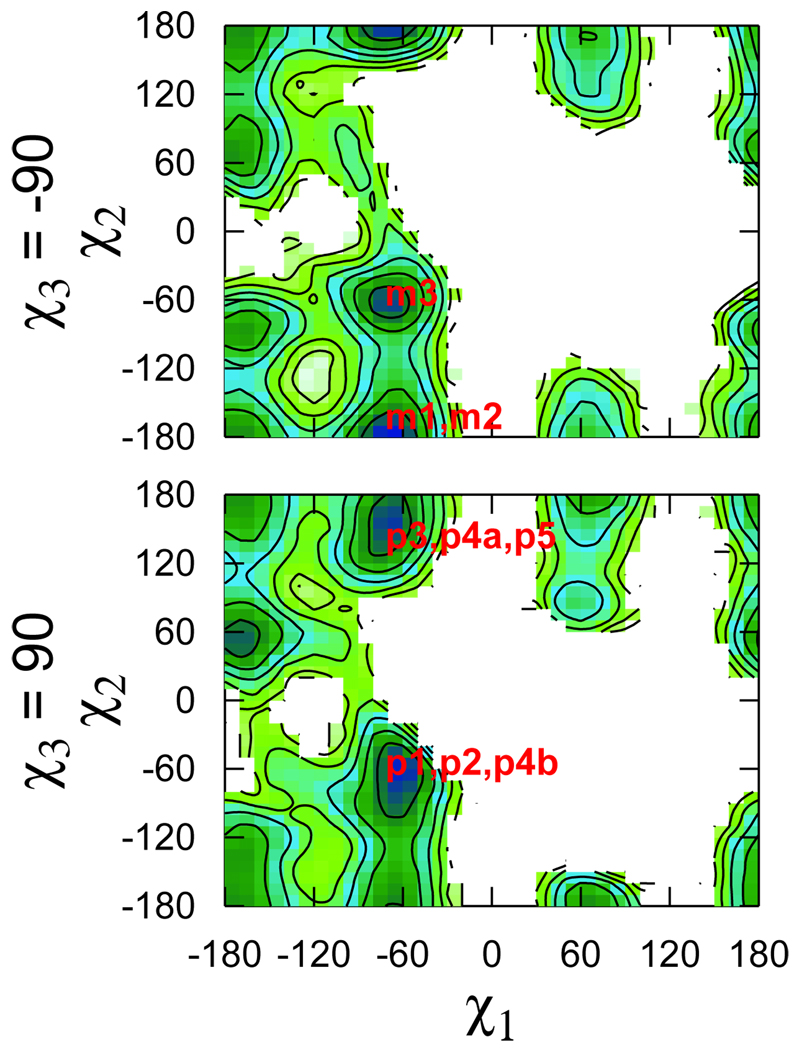
The positions of the most populated rotamers are indicated on the χ₁–χ₂ and χ₅–χ₄ free energy surfaces calculated from the trajectories (Fig. 9 and Fig. 10). The ab initio χ₅–χ₄ maps were virtually identical for the two χ₃ conformers (Fig. 7). In the context of the helix this is no longer the case (Fig. 10). The presence of the helix also restricts the conformational space accessible to the first two dihedrals (cf. Fig. 6 and Fig. 9). The (χ₁ χ₂) = (−60°, −60°) conformation was suggested as the most likely for R1, based on crystal structures of spin labeled T4L.⁴ Indeed, it was observed in four out of the six spin label conformations not involved in crystal contacts.^4,12 The free energy surfaces in Fig. 9 are in agreement with that observation. At the same time, they indicate that other minima, namely (−60°, 180°) for both m and p and (180°, 60°) for the p states only, are also very likely. In fact, the latter minimum corresponds to the other two spin label conformations observed in the crystal structures.^4,12

Figure 9.

The χ₁–χ₂ free energy surface computed from the MD trajectories for the two conformations of the disulfide dihedral. The contours correspond to an energy change of 1 kcal/mol. Regions not visited during the simulations are left white.

Figure 10.

Same as Fig. 9 for χ₅–χ₄.

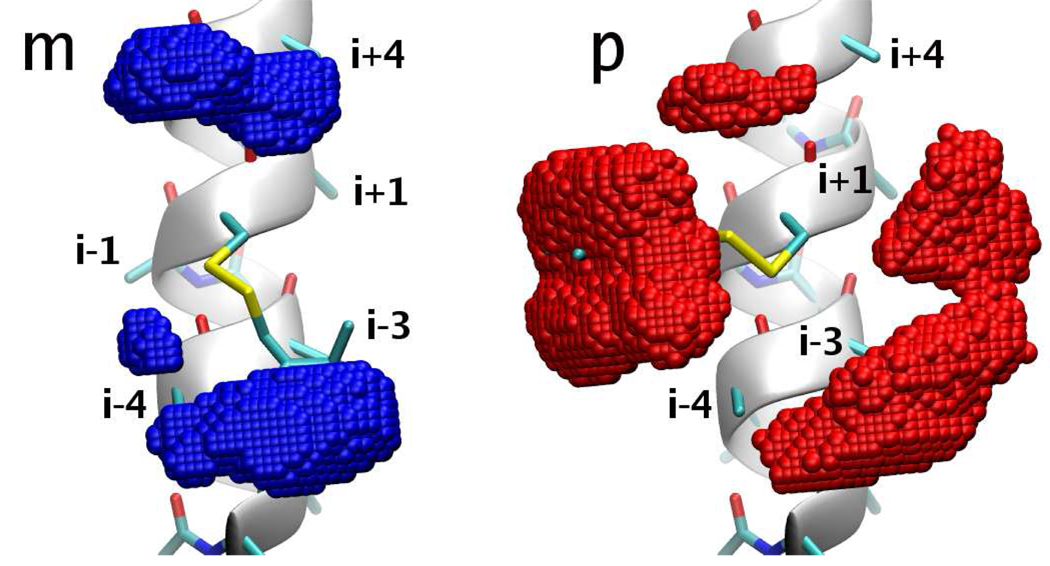
To visualize the difference in the configurational space accessible to the spin label in the two conformations of the disulfide torsion, the positions of the nitroxide N and O atoms along the trajectories were mapped onto a cubical grid. The vertices of the grid were separated by 0.3 Å. The grid cells populated by the N–O bond are shown in Fig. 11 for the m (left) and p (right) conformations. The N–O bond of the spin label spends 50% of its time within the colored volumes. The difference in the configurational volume accessible to the two conformers is striking. The spin label is seen to be much more restricted in its m states, tending to dwell as close as possible to the i − 3 and i − 4 or i + 3 and i + 4 residues of the helix. While interactions with the i − 3 and i − 4 residues appear to be as important when R1 is in the p conformations, the contacts with residue i + 4 do not seem to be as favorable. For the p states there are two additional regions easily accessible to the spin label: the broad region around residue i − 1 and the smaller region on the opposite side. For each of the most populated rotamers, we quantify the strength of the spin label-helix interaction by calculating the average van der Waals interaction energies between all the C and H atoms on the nitroxide, beyond the disulfide, and the side chain atoms of the alanines at positions i±4, i±3 and i±1 (Table XI). Although the energies of the strongest contacts are only equal to k_BT at room temperature, some rotamers are seen to establish two or three such contacts, which leads to interaction energies up to two times stronger than the thermal energy. As already suspected from Fig. 11, the energies confirm that the most considerable difference between the m and p states of the spin label is the interaction with side chains at positions i − 1 and i + 4. The former is energetically most favorable for χ₃ ≈ 90° but is irrelevant for χ₃ ≈ −90°, whereas the opposite is true for the latter. Looking at Fig. 11 and using the information in Table XI, it is hard to predict to what extent and in what direction mutations at the various neighboring sites of R1 will affect its ordering. The exact outcome will be sensitive both to the possibility of interaction with the new side chain and to the energy of that interaction.

Figure 11.

Volumes inside which the N–O bond spends 50% of its time in the m (left) and p (right) conformers of R1.

TABLE XI.

van der Waals interaction energy (kcal/mol) between R1 in the given rotamer and the side chains at positions i ± 1, i ± 3 and i ± 4. Energies larger than half k_BT at room temperature are bold.

	i − 4	i − 3	i − 1	i + 1	i + 3	i + 4
m1	−0.64	−0.61	−0.05	−0.06	−0.05	−0.06
m2	−0.64	−0.60	−0.05	−0.06	−0.05	−0.06
m3	−0.09	−0.12	−0.05	−0.13	−0.45	−0.53
p1	−0.31	−0.15	−0.44	−0.07	−0.41	−0.11
p2	−0.35	−0.11	−0.52	−0.05	−0.42	−0.08
p3	−0.25	−0.40	−0.14	−0.16	−0.16	−0.16
p4a	−0.19	−0.37	−0.13	−0.18	−0.18	−0.18
p4b	−0.32	−0.15	−0.44	−0.07	−0.38	−0.10
p5	−0.24	−0.40	−0.13	−0.17	−0.16	−0.17

B. Simulating ESR spectra using the MD trajectories

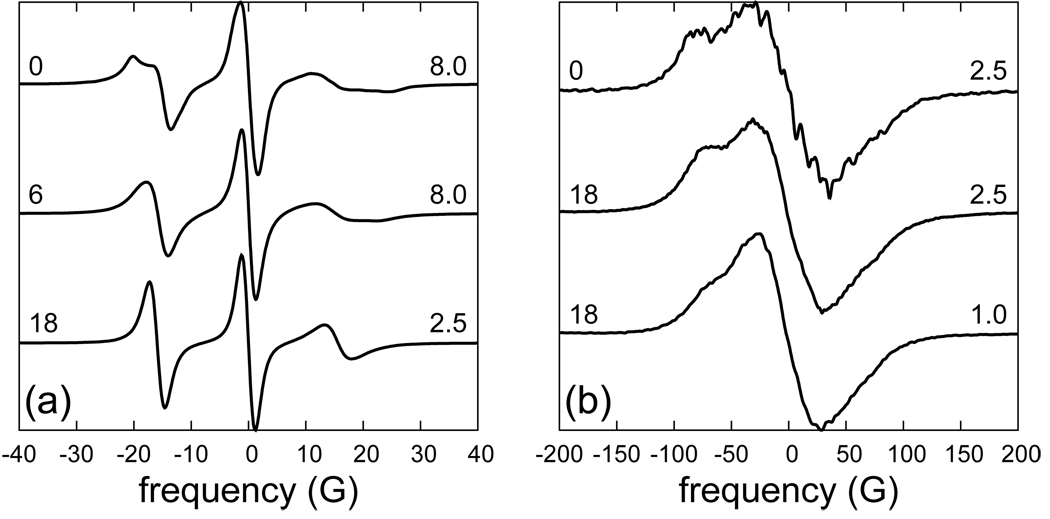
The test for the similarity of the simulated and the real dynamics of R1 is the comparison between spectra calculated using the MD trajectories and experimental spectra. Since poly-alanine does not retain perfect α-helical structure in water, any quantitative comparison with experimental spectra is not realistic. Instead, the qualitative similarities and differences of the calculated spectra with spectra from the prototypical SEHS sites 72R1 and 131R1 on T4L will be considered. Calculated spectra at B₀ = 0.34 T for three different diffusion rates are shown in Fig. 12(a). At the top is the powder spectrum for which the dynamics are entirely due to the MD trajectories (D = 0). The lower two spectra include isotropic rotational diffusion, with the specified diffusion coefficient, in addition to the dynamics coming from the MD trajectories. Both the D = 6 × 10⁶ s⁻¹ (slow) and D = 18 × 10⁶ s⁻¹ (fast) spectral lines are significantly narrower than the experimental lines for 72R1 and 131R1, recorded respectively with² or without¹³ sucrose. This indicates that R1 on a poly-alanine α-helix is less ordered and more mobile (in the time window of the 9 GHz experiment) than it is at these two positions in T4L. Comparison of the top two spectra in Fig. 12(a) demonstrates that the tumbling of T4L has a non-negligible effect on the 9 GHz spectrum, even in 30 wt % sucrose solution.

Figure 12.

(a) B = 0.34 T and (b) B = 8.92 T spectra simulated from the MD trajectories without (D = 0) and with (D = 6× and 18 × 10⁶ s⁻¹) additional tumbling. The diffusion coefficient is indicated on the left, and the scaling factor on the right hand side of each spectrum. Other simulation parameters are given in Table VI.

Spectra at higher frequencies are less sensitive to slow dynamics in the time window from a few nanoseconds to tens of nanoseconds. Instead, they become progressively more influenced by faster motions on time scales from tens of picoseconds to a few nanoseconds. At 250 GHz (8.92 T) the effect of the rotational diffusion of a protein like T4L on the spectrum is substantially diminished, as can be seen by comparing the top two spectra in Fig. 12(b). (The D = 0 spectrum is quite noisy even though twice as many stochastic+MD trajectories were used in its simulation.) As evident from the difference between the bottom two spectra in Fig. 12(b), the scaling of the time axis of the MD trajectories, used here to account for the different viscosities of the simulated and real solvent, has a substantial effect on the spectrum. What the correct scaling should be is not immediately clear in general. The situation in which R1 is almost entirely solvent exposed corresponds to one of the extremes. The other is a buried spin label for which there should be no scaling. The scaling for a partially solvent-exposed spin label should fall in between those two.

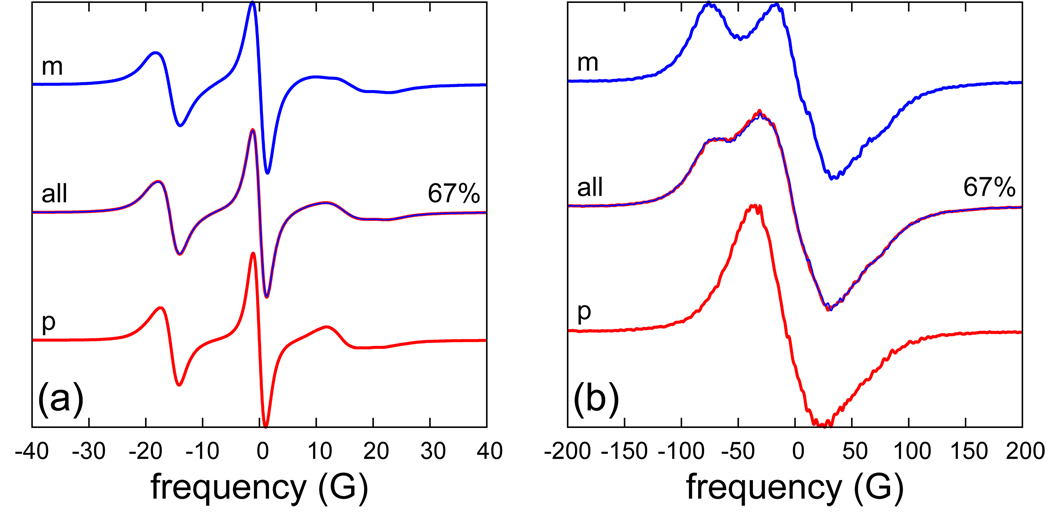
The m and p conformations of R1 on a poly-alanine α-helix were drastically different in terms of their conformational freedom. To assess the effect of this difference on the spectra, the trajectories were partitioned into segments in which R1 was either in one or the other conformation. This resulted in 17 m segments and 11 p segments of variable duration, as can be inferred from Table VII. 67% of all the snapshots fell into the first, and 33% into the second group. Spectra at 0.34 and 8.92 T, simulated using these segments, are shown in Fig. 13 (m and p), where they are compared with spectra simulated using the entire trajectories (all). Since, the m:p ratio is not necessarily represented correctly in the MD simulations, one can look at the m and p spectra as bracketing the range of spectral lines that correspond to different mixtures of the two components. Spectra of 72R1 and 131R1 in T4L at 250 GHz have been published previously (see Ref. 13, Fig. 3(a)). Qualitatively, our simulated spectra in Fig. 12(b), resemble those experimental spectra. The two humps in the m spectrum at 250 GHz are very much like the humps seen in the spectrum of 72R1, whereas the shoulder in the ‘all’ spectrum is more like the 250 GHz spectrum of 131R1.¹³ Interestingly, by going from the ‘all’ ensemble of spin labels to its more ordered subset ‘m’ we seem to go from a 131R1-like to a 72R1-like spectrum at 250 GHz.

Figure 13.

Spectra simulated using all the MD trajectories or only their m and p segments, as indicated. (a) B = 0.34 T, D = 6 × 10⁶ s⁻¹ (with an 8-fold scaling of the time axis), (b) B = 8.92 T, D = 18 × 10⁶ s⁻¹ (with 2.5-fold scaling).

Given that the exchanges between the m and p conformations are very rare, the effect of the exchange rate is expected to be insignificant both at 0.34 and 8.92 T. To test this, spectra were generated by linearly mixing the magnetizations simulated using the m and p segments in a 2.1 ratio, equal to their populations in the MD trajectories. The resulting spectra are labeled ‘67%’ in Fig. 13, where they are superimposed on the spectra from the full MD trajectories (all). As suspected, the two match perfectly. Evidently, due to the high energetic barrier of the disulfide torsion, ESR spectra of R1 in the 9–250 GHz frequency range are always a simple linear superposition of at least two slow components. Since there are no dynamic effects in the mixing of the m and p conformations, it may be feasible to simulate the two separately and determine their ratio by fitting the calculated spectrum to experiment.

IV. DISCUSSION

A. Parametrization

The partial charges for the N and O atoms of the nitroxide moiety (Table I) are in good agreement with the charges 0.17 and −0.31, respectively, recommended in Ref. 41. There, the charges were determined by a restrained fit to the ab initio electrostatic potential calculated using HF/6–31G** level of theory—a procedure very similar to the one that we followed. In the parametrization of Ref. 41, the nonpolar hydrogens have a charge of 0.06, which is typical for the AMBER/OPLS force field,^45,61 whereas we imposed the value of 0.09, in agreement with the nonpolarizable CHARMM force field. In Refs. ²⁶ and ²⁴ the charges of Barone et al. are used directly without further assessment. More recently Murzyn et al.²² determined the partial charges of the nitroxide ring of R1 by performing a restricted fit to the ab initio electrostatic potential using the AMBER/OPLS protocol. They reported partial charges of 0.118 and −0.395 for the N and O atoms of the nitroxide. Beier and Steinhoff²³ used two different sets of charges: −0.04 and −0.2, as well as 0.08 and −0.3 for the N and O atoms, respectively. In both cases the charges appear to be somewhat low, as acknowledged by the authors.²³

The dynamics of R1 is largely determined by the torsional barriers. Until now, none of the studies performing MD simulations with R1 have reported a comparison of their dihedral force field parameters with ab initio calculations of the torsional energies of the linker. In some cases, when the time traces of the dihedrals are reported, it is possible to have an idea of the multiplicity of the torsions and the approximate positions of their local minima. For example, Fig. 6 and Fig. 7 in Ref. 22 indicate that in that study χ₅ has a multiplicity of three, with preferred conformations at ±60° and 180°. Evidently, the dihedral energy barriers of the force fields used in this study were not evaluated against ab initio energy calculations.

The major problem arising from neglecting to compare the adiabatic χ₁–χ₂ energy surface of the force field used against ab initio calculations is nicely exemplified by a recent study.²⁵ When the X-band spectrum of 65R1 in T4L calculated from atomistic MD simulations did not agree with the experimental spectrum the authors were not able to eliminate the possibility that their “MD simulation protocol [i.e. force field parameters] overestimates the rotational mobility about χ₁ and χ₂.”²⁵ Our careful parametrization of both the χ₁–χ₂ and χ₅–χ₄ energy surfaces removes such an uncertainty. Even more importantly, it signals that conventional force fields (i.e. without a CMAP correction) might be incapable of reproducing the χ₁–χ₂ and χ₅–χ₄ energetics in sufficient detail.

One dimensional ab initio energy scans (performed using HF/6–31G** level of theory), in general agreement with our two dimensional energy surfaces (Fig. 6 and Fig. 7), were reported in Ref. 28. The construct used for the ab initio scan of χ₁ in that study was very similar to the one shown in Fig. 4, with the exception that the methyl group attached to S2 was replaced by a hydrogen. The model system used to scan χ₅ was exactly the same as the one shown in Fig. 5. Two additional fragments were used to scan the remaining torsional profiles: CH₃–CH₂–S–SH for χ₂ and χ₄, and CH₃–S–S–CH₃ for χ₃.²⁸ The exact positions of the two minima of χ₅ were observed to depend on the configuration of χ₄. As already discussed, this coupling between χ₄ and χ₅ is poorly captured by conventional force fields. We were able to account for it by using the CMAP correction of CHARMM. The positions of the minima for all angles determined in Ref. 28 (Table VIII) and the multiplicities of the torsions are in good agreement with our two dimensional energy surfaces (Fig. 6 and Fig. 7).

B. Conformational dynamics of R1

The adiabatic energy profiles of Ref. 28, showed that for the dihedrals from χ₁ to χ₄ the energy minima were separated by barriers ranging from about 4k_BT to more than 10k_BT, at room temperature. Based on this observation, it was concluded that the conformational dynamics of R1 can be rationalized in terms of fast librations in a finite number of stable rotamers with occasional exchanges between them. This picture of the spin label dynamics is very appealing from a conceptual point of view. To use it as a practical tool, one has to be able to identify the populations of the important rotamers and to estimate the rates of exchange between them. How to do so in practice was illustrated in Ref. 28 for a spin labeled poly-alanine α-helix. First, R1 was built in all of its 108 possible rotameric states using the reference values for the angles (Table VIII). Rotamers which led to steric clashes with the helix were eliminated. This resulted in a dramatic decrease of the allowed rotamers from 108 to 18. Second, the populations of the remaining 18 rotamers were estimated based on the energy differences between the minima of the ab initio energy profiles. For this, the potential energy was approximated to be a sum of the single bond contributions. For example, the χ₁ torsional potential (with χ₂ ≈ 180°), shown in Fig. 3A of Ref. 28, exhibits a global minimum at −60° and two local minima at +65° and 180°. Since the global minimum is about 2 kcal/mol deeper than the other two minima, rotamers in which χ₁ = −60° are more than an order of magnitude more probable than the ones in which χ₁ = +65° or 180°. The 18 relevant rotamers of Ref. 28 are shown in Table XII together with their estimated probabilities. Finally, the energy barriers separating the minima were used to estimate the rates of exchange between the rotamers. It was assumed that exchanges occur through single dihedral angle flips. Arguments about the hydrodynamic friction experienced by the spin label were invoked to argue that transitions about χ₁, χ₂ and χ₃ are rather slow on the time scale of X-band ESR and can be safely ignored. As a result, only transitions about χ₄ and χ₅ were considered, in agreement with the experimentally established χ₄/χ₅ model of spin label dynamics.

TABLE XII.

The 18 rotamers identified as relevant in Ref. 28 together with their populations.

rot.	χ1	χ2	χ3	χ4	χ5	prob. (%)
C5(C6)	−60	180	90	180	77(−77)	18.7
C1(C2)	−60	−75	−90	180	77(−77)	14.3
C8	−60	180	90	75	8	9.8
C4	−60	−75	−90	−75	−8	7.4
C7	−60	180	90	75	−100	5.9
C3	−60	−75	−90	−75	100	4.5
C9(C10)	180	180	−90	180	77(−77)	0.9
C13(C14)	180	180	90	180	77(−77)	0.9
C15(C16)	180	75	90	180	77(−77)	0.7
C12	180	180	−90	−75	−8	0.5
C18	180	75	90	75	8	0.4
C11	180	180	−90	−75	100	0.3
C17	180	75	90	75	−100	0.2

In the last column of Table X, the identity of the most populated 18 rotamers according to the MD simulations is compared with the rotamers identified as relevant in Ref. 28. It is seen that the most populated six rotamers from the MD trajectories are among the ones which were eliminated in Ref. 28 due to steric clashes. This observation highlights the difficulty in building ideal rotamers using reference values for the dihedrals determined from the minima of the ab initio energy profiles. Apparently, the spin label can easily avoid steric clashes by relaxing the geometry and still remain in the same rotamer. The fact that among the first twelve rotamers in Table X only two pass the steric clash test indicates that the structural relaxation to avoid steric clashes is more than compensated by the resulting hydrophobic contact between the spin label and the helix. As we saw, exactly such conformations in which the spin label is able to maximize its contact with the helix are the most populated ones.

It has been previously proposed^1–3 that weak hydrogen bonds between the sulfurs of the disulfide and the backbone hydrogens contribute to immobilize the χ₁ and χ₂ dihedrals on the time scale of a 9 GHz ESR experiment. Previous MD simulations report either the presence²² or the absence²³ of sulfur hydrogen bonds with the backbone Cα or amide hydrogens. In both cases, however, the force field lacks the correct ingredients to capture the energetics of such interactions (i.e. sulfur polarizability or lone pairs). In our simulation, we observed that the favorable energy gained by placing the sulfurs close to the backbone hydrogens (included effectively through the χ₁–χ₂ CMAP correction) was not sufficient to immobilize the first two linker dihedrals on the ESR time scale.

In contrast to the assumption of independent torsional dynamics, the MD simulations indicate that simultaneous transitions of several of the dihedrals are common when R1 is on a poly-alanine helix. This observation agrees with previous studies of the internal dynamics of amino acid side chains. In Ref. 34, for example, the rotameric dynamics of a lysine side chain, which like R1 has five internal torsional degrees of freedom, were studied to evaluate their effect on NMR relaxation times. It was observed that the approximation of independent internal rotations becomes less satisfactory for longer side chains, like lysine, necessitating the addition of two-bond and three-bond rotations in the set of elementary moves together with single-bond transitions.³⁴

In Ref. 22, it was proposed that the two spectral components, immobilized and mobile, often observed in the spectra of R1, might correspond to conformations with different values of χ₃. In that work, two 10 ns MD simulations of R1 attached to a site on Cytochrome c were performed. The spin label was started with χ₃ ≈ −90° in one of the simulations and χ₃ ≈ 90° in the other. It visited 3 rotamers during the former and 13 during the latter, leading the authors to conclude that the χ₃ conformation has a direct effect on the dynamics of the MTSSL moiety.²² Although our simulations are in qualitative agreement with the observations of Ref. 22 as far as the differences in the ordering and dynamics of the m and p conformations of R1 are concerned, our analysis does not point to any intrinsic property of the disulfide torsion χ₃ that will cause these differences. What orders and immobilizes the spin label are the nonspecific hydrophobic contacts with the neighboring alanine side chains.

C. Simulated ESR spectra

Very good fits to the 9 GHz and 250 GHz experimental spectra of 44R1, 69R1, 72R1, and 131R1 on T4L in water have been reported using the SRLS model to account for the dynamics of the spin label and the protein tumbling.^9,13 Excellent fits to the 9 GHz spectra of 72R1, 131R1 and more recently 115R1 and 82R1 on T4L in 30 wt % sucrose solution have also been obtained using the MOMD model, which does not account for the rotational diffusion of the protein.^5,6,12 Yet, our simulated spectra in Fig. 12(a) suggest that the tumbling of T4L has a non-negligible effect on the 9 GHz spectra, even in 30 wt % sucrose solution.

The difference in the X-band spectra of 72R1 and 131R1 in T4L, has been rationalized in terms of the difference in the magnitude of the backbone fluctuations at these two SEHS sites.^1,5,13,29 Due to the significant exibility of the linker observed in the MD simulations, the coupling of the nitroxide to the protein backbone might not be as strong as previously imagined. The fact that the ‘m’ and ‘all’ spectra in Fig. 13(b), both corresponding to R1 at a poly-alanine helix, qualitatively resemble the 250 GHz spectra of 72R1 and 131R1,¹³ respectively, suggests that factors other than the protein backbone flexibility may be responsible for the relative ordering and immobilization of the spin label at those two sites. The difference in the spectra in our case is entirely due to differences in the ability of R1 in the two ensembles to engage in hydrophobic contacts with the helix.

V. CONCLUSIONS

We studied the dynamics of R1 on a poly-alanine α-helix, which represents an “ideal” SEHS site. Force field parameters for the spin label were developed using ab initio calculations. The electrostatic properties of the spin label, in particular its dipole moment and interaction energies and geometries with water, were carefully modeled, and special attention was given to the energetics of rotation about the bonds separating the nitroxide ring from the C_α of the spin-labeled residue. These two aspects of the force field are extremely important since eventually they determine to what extent the spin label is solvated by water or “sticks” to the accessible hydrophobic patches in its vicinity, and what conformations are accessible to it.

Our MD simulations indicate that the ordering and dynamics of R1 on a poly-alanine helix result from the competition of various forces with relatively weak energies. Contrary to what is commonly believed,^1,5 the interaction of the disulfide with the backbone does not seem to lead to the immobilization of the first two dihedrals of the spin label linker on the ESR time scale. The ordering appears to be driven by the favorable van der Waals interaction of the surface of the spin label with the hydrophobic surface provided by the alanine side chains. Nonpolar interaction energies on the order of 2k_BT are present in the environment of the poly-alanine α-helix. This implies that R1 and the protein backbone are weakly and indirectly coupled. From this perspective, even a spin label attached to an isolated helix does not fit the expected behavior of an ideal noninteracting site. Sorting of the preferred R1 conformations based on the steric clashes of a rigidly built spin label is unlikely to retain the most favorable rotamers. A similar concern applies to a Monte Carlo search in which the spin label is constructed using ideal reference angles for its dihedrals. Thus, the distinction between “noninteracting” and “interacting” SEHS sites⁶ is a matter of degree, and not of fundamental qualitative difference.

The most important implication of the present results on the dynamics of R1 at noninteracting SEHS sites in T4L is the high propensity of the spin label to interact with the neighboring protein surface. When compared with our simulated spectra of R1 at 9 GHz, the experimental spectra of 72R1 and 131R1 on T4L indicate that R1 is more ordered and less mobile at these two positions than it is at the poly-alanine α-helix. Since the ordering does not seem to be due to the adsorption of the disulfide to the protein backbone, it is likely that the polypeptide surface accessible to the spin label from those two sites is more rugged than the relatively structureless surface of the poly-alanine helix.

Many questions, of course, remain unanswered: If R1 at any SEHS is expected to interact with the neighboring amino acid residues, why were such interactions not detected in the 9 GHz spectra of 72R1 and 131R1? If R1 is not necessarily a good reporter of the backbone fluctuations, what is causing the differences in the X-band spectra of 72R1 and 131R1? These, and similar questions can only be addressed by performing atomistic MD simulations of fully solvated T4L labeled at those two positions. Such simulations are currently under way.