Hofmeister Effects of Common Monovalent Salts on the Beetle Antifreeze Protein Activity

Abstract

Antifreeze proteins (AFPs) noncolligatively depress the freezing point of a solution and produce a difference between the melting and freezing points termed thermal hysteresis (TH). While the mechanism of the enhancement effect is not well understood, various low-molecular-mass solutes including neutral salts have been identified to enhance the TH activities of AFPs. Here, the effect of monovalent salts on salting out an AFP from the beetle Dendroides canadensis (DAFP-1) on the ice was treated using a simple classical theory and the relationship between the TH activity and the salt concentration was developed. The TH activities of DAFP-1 in the presence of the series of monovalent salts were assessed by differential scanning calorimetry (DSC) and the salting-out constants of DAFP-1 by these salts were determined. This study demonstrates an indirect way to determine the salting-out constants of AFPs by these salts. The results suggest that the Hofmeister effect is a potential mechanism for the TH enhancement effects of some common monovalent salts.

Introduction

Since Hofmeister first reported that the different abilities of various neutral salts to precipitate a given protein from solution in 1888, the Hofmeister effects are often referred to the relative effectiveness of specific ions on a large variety of observed biophysical phenomena including protein solubility, protein denaturation, protein aggregation, water activity coefficient, and chromatographic selectivity.¹ The recurring trend of the effectiveness of anions or cations on various physical properties is known as the Hofmeister series. The effects of anions are generally more pronounced than those of cations. Based on their decreasing abilities of interacting with water (i.e., salting-out), the anions in the typical Hofmeister series are SO₄²⁻ > HPO₄²⁻ > OH− > F⁻ > Cl⁻ > Br⁻ > I⁻ > ClO₄⁻ > SCN⁻.

Antifreeze proteins (AFPs) characterized by their ability to depress the nonequilibrium freezing point of the solution without altering the melting point have been identified in various organisms, such as Antarctic fish² and insects.³ According to the widely-accepted adsorption-inhibition mechanism of AFP action, AFPs adsorb onto the ice crystal surface at preferred growth sites and the ice crystal growth process is thereby halted by the Kelvin effect.⁴ The temperature difference between the melting point and the nonequilibrium freezing point is termed as thermal hysteresis (TH), which is usually used to assess the antifreeze activities of AFPs. In the presence of TH enhancement substances, the TH activities of AFPs can be further enhanced. Certain proteins and low-molecular-mass molecules (e.g., EDTA, trehalose, and some neutral salts) have been identified as TH enhancers, which themselves have no TH activity. The molecular mechanism of TH enhancement effect is still not well understood.^5–9

The aim of this study is to assess the contribution of the Hofmeister effects of monovalent salts on the TH enhancement of an AFP from the beetle Dendroides canadensis (DAFP-1). To address the problem, we developed an equilibrium thermodynamic model for the salting-out effect on biomolecules using the cavity model.^10–12 The derived model directly relates the TH activities of DAFP-1 in the presence of monovalent Hofmeister salts to the salt concentrations. Furthermore, we assessed the TH enhancement effects of common monovalent salts (e.g., NaCl, NaBr, and KCl) on DAFP-1 activity using differential scanning calorimetry (DSC). Combining the theoretical model and the experimental results, the salting-out constants of DAFP-1 by these salts were determined.

Theory

The unitary free energy change (ΔG⁰) in transferring DAFP-1 from a hypothetical gas phase into solution under ideal physical conditions is given by ΔG⁰ = ΔG_cavity + ΔG_{electrostatic} + ΔG_{nonelectrostatic} + RT ln (RT / PV), where ΔG_cavity and ΔG_{electrostatic} are the free energy changes for the formation of a cavity in the solvent to accommodate the solute DAFP-1 molecule and for electrostatic interactions between the solute and solvent, ΔG_{nonelectrostatic} is the free energy change for any nonelectrostatic interactions over a wide range of salt concentrations (e.g., van der Waals interactions), and RT ln (RT / PV) is the energy accounting for the change in free volume. We assume that there is no other specific interactions between DAFP-1 and the salts except for electrostatic interactions, therefore ΔG_{nonelectrostatic} = 0 and RT ln (RT / PV) = 0 and thus

$$\mathrm{\Delta }{G}^0=\mathrm{\Delta }{G}_{\text{cavity}}+\mathrm{\Delta }{G}_{\text{electrostatic}}$$ (1)

By combining the expressions of Sinanoğlu’s cavity model^{10, 12} and the surface tension of the solvent in the presence of the inorganic salts¹³ and assuming that the solute, solvent and complex are spherical shaped molecules, we obtain the energy for making a spherical cavity as

$$\mathrm{\Delta }{G}_{\text{cavity}}=[\mathit{\text{NS}}+{\mathit{\text{aN}}}^{1/3}(k_0-1)V^{2/3}][1-f(T)]{\gamma }^0+[\mathit{\text{NS}}+{\mathit{\text{aN}}}^{1/3}(k_0-1)V^{2/3}][1-f(T)]\tau m$$ (2)

where N is Avogadro’s number and a is a constant equal to (36 π)^1/3, S is the molecular surface accessible area, γ⁰ is the surface tension of the pure solvent, k₀ is the ratio between the energy requirements for forming a spherical shaped cavity and expanding the same surface area into a planar surface in pure solvent, V is the molar volume of the pure solvent, T is the absolute temperature, τ is the molar surface tension increment constant, which depends on the nature of the salt, and m is the molality of the salt, which is independent of the temperature. In addition, f (T) in Eq. 2 is the energy requirement for expanding the planar surface of the solvent by the same surface area that can be expressed as a function of temperature: f (T) = (1 − k’/k)[(d ln γ)/ (d ln T) + (2/3)(cT)] , where c is the liquid coefficient of the thermal expansion for the species, k is the ratio between the energy requirements for forming a spherical shaped cavity and expanding the same surface area of the solvent, and k’ is the corresponding entropy production when the cavity is made. Usually, k and k’ approach to be equal¹² and thus the value of f (T) approaches to zero.

The Debye-Hückel expression of activity coefficient can only be used for very dilute solutions.¹⁴ Much effort has been made to extend Debye-Hückel theory to higher concentrations. Hückel extended the application of the Debye-Hückel theory to solutions at moderately high concentrations by including a term describing the change of dielectric constant, but the extended theory fails at high ionic strengths.¹⁵ Stokes and Robinson introduced the effect of ion solvent interaction in the term of hydration with the assumption that this interaction is significantly larger than kT.^16,17 This hydration theory can be successfully applied to high ionic strengths, say up to 4, for most 1:1 and 2:1 electrolytes. According to the hydration theory of Stokes and Robinson^16,17 and assuming osmotic coefficient is 1 for m ≤ 1.5 m, ΔG_{electrostatic} can be expressed as

$$\mathrm{\Delta }{G}_{\text{electrostatic}}=\mathit{\text{RT}}\ln f_i{C}_i=\mathit{\text{RT}}[-({\mathit{\text{Am}}}^{1/2})/(1+\mathrm{\alpha }{\mathit{\text{Bm}}}^{1/2})+0.036\mathit{\text{nm}}-0.018\mathit{\text{vm}}]+\mathit{\text{RT}}\ln C_i$$ (3)

where f_i and C_i are the activity coefficient and the concentration of solute i, A and B are constants in the Debye-Hückel equation, α is the electrolyte size parameter, n is the hydration number for one mole of electrolyte, v is moles of ions per mole of electrolyte, and m is the molality of the electrolyte.

At the solvation equilibrium state, the molar hydration energy of DAFP-1 is a function of its mole fraction, x, besides the molar hydration energy of its thermodynamic standard state, ΔG⁰

$$\mathrm{\Delta }{G}_{\text{DAFP}-1}=\mathrm{\Delta }{G}^0+\mathit{\text{RT}}\text{ln}x$$ (4)

where x is the mole fraction of DAFP-1. The molecule weight of DAFP-1 is 8969.4 Da⁶ and the solubility of DAFP-1 can be expressed by the weight of DAFP-1 in grams per 1000 mL of water, w, thus ln x = ln w − 13.12 (x ≪ 1).

By combining Eq. 1–Eq. 4, we find the simplified relationship between DAFP-1 solubility and the salt concentration at the temperature T as

$$\text{ln}w=\text{ln}{w}_0-\text{ln}\mathrm{c}+\beta -{\mathrm{K}}_{s}m=\beta ’-{\mathrm{K}}_{s}m$$ (5)

where w₀ is the solubility of DAFP-1 in pure water, c is the temperature coefficient of solubility (is assumed equal or larger than 1.0 in the experimental temperature range), the Stokes and Robinson term approaches to a constant, β, in our experimental salting-out region, β = (Am^1/2)/ (1 + αBm^1/2) ≈ −ln f, β’ = ln w₀ + β, and K_s is the salting-out constant for DAFP-1. Eq. 5, thus becomes the salting-out relationship reported by Green.¹⁸

According to the adsorption inhibition mechanism of AFPs,⁴ the TH activity of DAFP-1 can be expressed as

$$\text{TH}={\mathrm{k}}_{\text{TH}}{S}_{\text{coverage}}$$ (6)

where TH is the measure of the antifreeze activity of DAFP-1 in °C, k_TH is a constant, and S_coverage is the surface coverage of the ice. We assume that all precipitates of DAFP-1 are on the surface of the ice, that is no DAFP-1 inside the ice. The precipitated AFP is believed to be monolayerly adsorbed on the growing surface of the ice crystal.⁴ No experimental evidence suggested that self-aggregation of DAFP-1 exists, even in the presence of salts.^7–9 Thus the total weight of DAFP-1 is given as the sum of the weight of DAFP-1 in solution and that on the ice surface

$$w+{\mathrm{K}}_{\text{coverage}}{S}_{\text{coverage}}=w_0$$ (7)

where K_coverage is a constant to express S_coverage into the weight of DAFP-1 in grams per 1000 mL water and K_coverage can be defined when the ice melts into water. Combining Eq. 6 and Eq. 7 and applying the logarithm, as most DAFPs are in the solution at sub-millimolar concentrations and K_coverageTH / (k_TH w₀) is very small, finally we obtain

$$\text{log}w=\text{log}{w}_0-[{\mathrm{K}}_{\text{coverage}}\text{TH}/(2.303{\mathrm{k}}_{\text{TH}}{w}_0)].$$ (8)

Eq. 8 predicts that the TH value of the system increases linearly with the salt concentration. By substituting Eq. 5 into Eq. 8, we obtain ln c + ln f + K_s m = K_coverageTH / (2.303 k_TH w₀) = K_total TH, where K_total = K_coverage / (k_TH w₀). The relationship between TH and the salt concentration is thus derived as

$$\text{TH}={\mathrm{K}}_{s}m/{\mathrm{K}}_{\text{total}}+(\text{ln}\mathrm{c}+\text{ln}f)/{\mathrm{K}}_{\text{total}}.$$ (9)

In the absence of the salts, the experimental TH activity of the DAFP-1 solution, TH₀, is log c / K_total. In the small range of concentrations of electrolytes, the activity coefficient, f, can be assumed as a constant and Eq. 9 thus describes a linear dependence of TH activity with molality, m.

Experimental Materials and Methods

The sodium, potassium, and rubidium monovalent salts with reagent grade or higher were purchased from Sigma-Aldrich (St. Louis, MO) and used without further purification. The sample solutions were prepared using fresh Milli-Q water with a minimum resistivity of 18 MΩ·cm. The purified DAFP-1 was prepared as described previously.⁷

The measurements of TH activities of DAFP-1 alone and DAFP-1 in the presence of these common Hofmeister monovalent salts were carried out using a DSC 823e (Mettler Toledo, OH) with an HSS7 high sensitivity sensor and a Julabo FT900 intracooler chiller (Julabo Company, PA) as described previously.⁷ The concentration of DAFP-1 used in all the measurements was 453 µM. The activity of DAFP-1 was measured in the presence of the following common monovalent Hofmeister salts, respectively: (a) NaCl, NaBr, NaI, NaClO₄; (b) KCl, KBr, KI; (c) RbCl, RbBr, RbI. Each sample solution was prepared at least twice and measured for three times. The averages were plotted in Figure 1–Figure 3 and the standard deviations were between ±0.01 and ±0.02 °C.

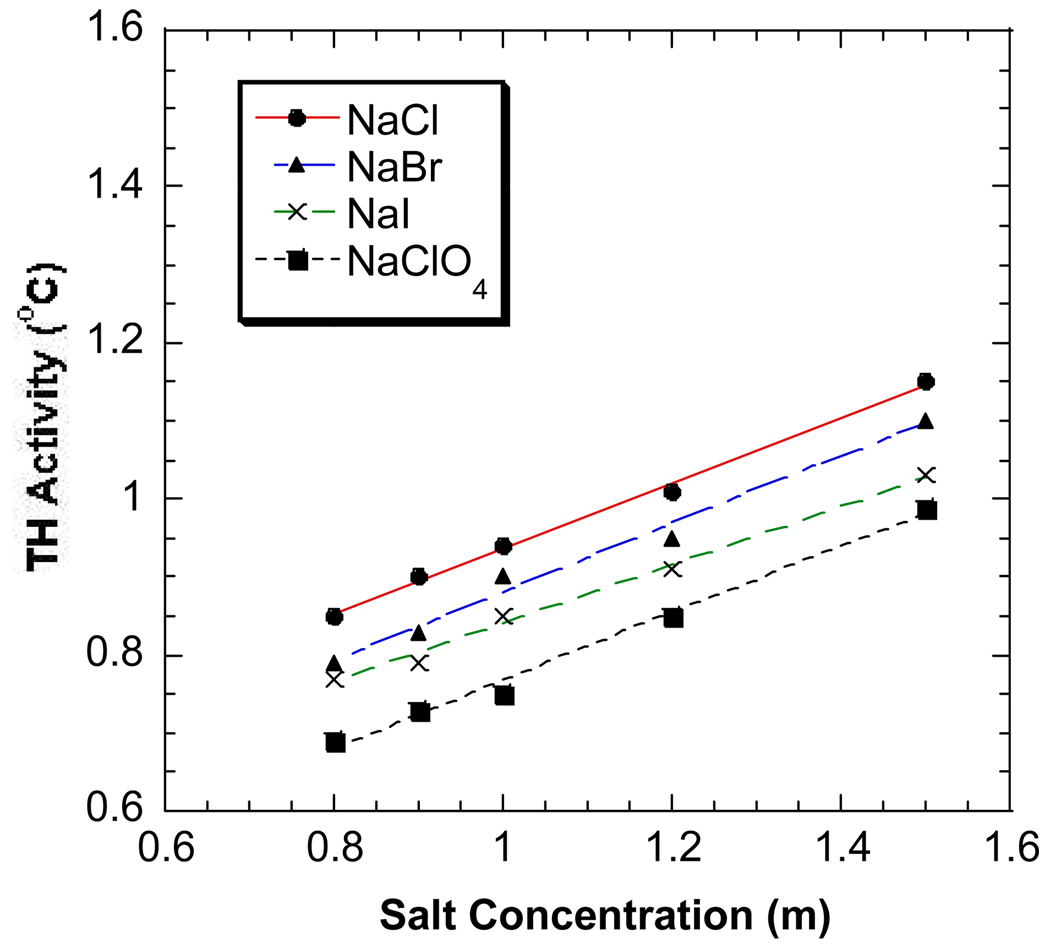
Figure 1.

The antifreeze activities of DAFP-1 in the presence of NaCl (●), NaBr (▲), NaI (×), and NaClO₄ (■) at 0.8 – 1.5 M. The curve fitting lines are plotted.

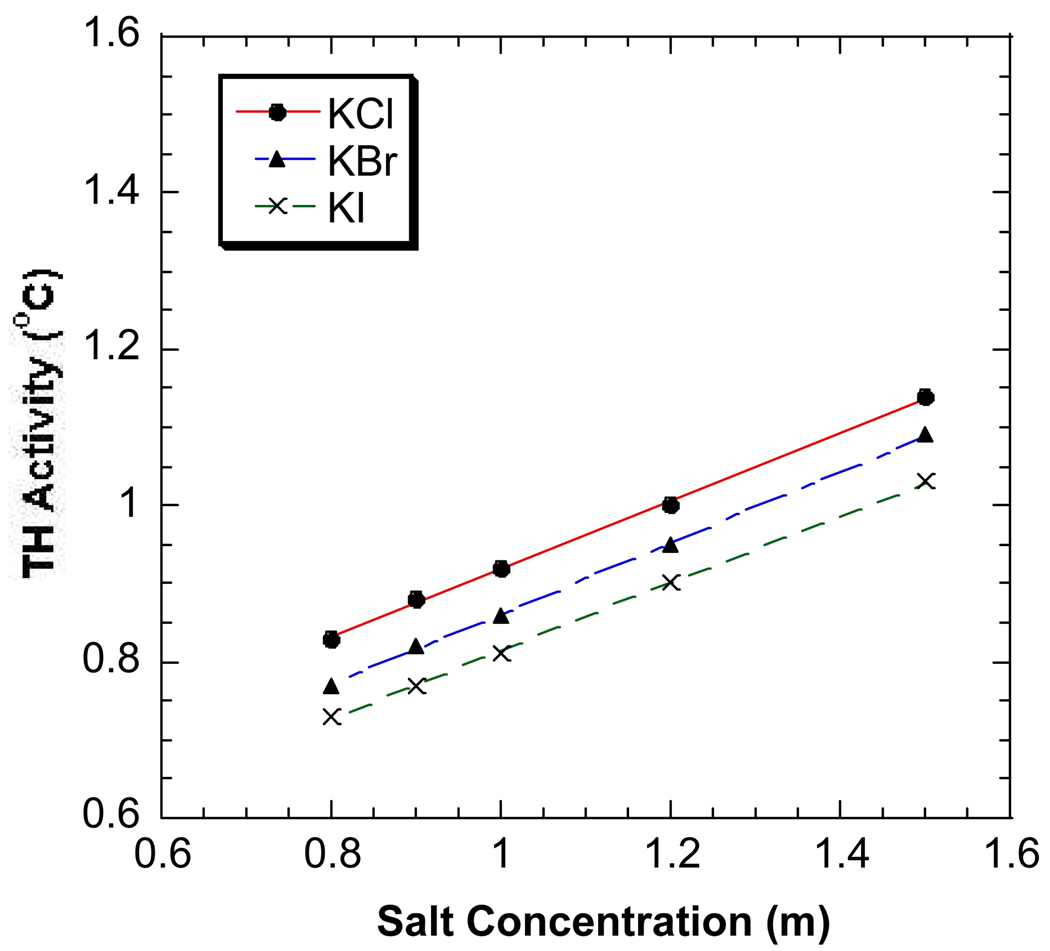
Figure 3.

The antifreeze activities of DAFP-1 in the presence of RbCl (●), RbBr (▲), and RbI (×) at 0.8 – 1.5 M. The curve fitting lines are plotted.

Results and Discussion

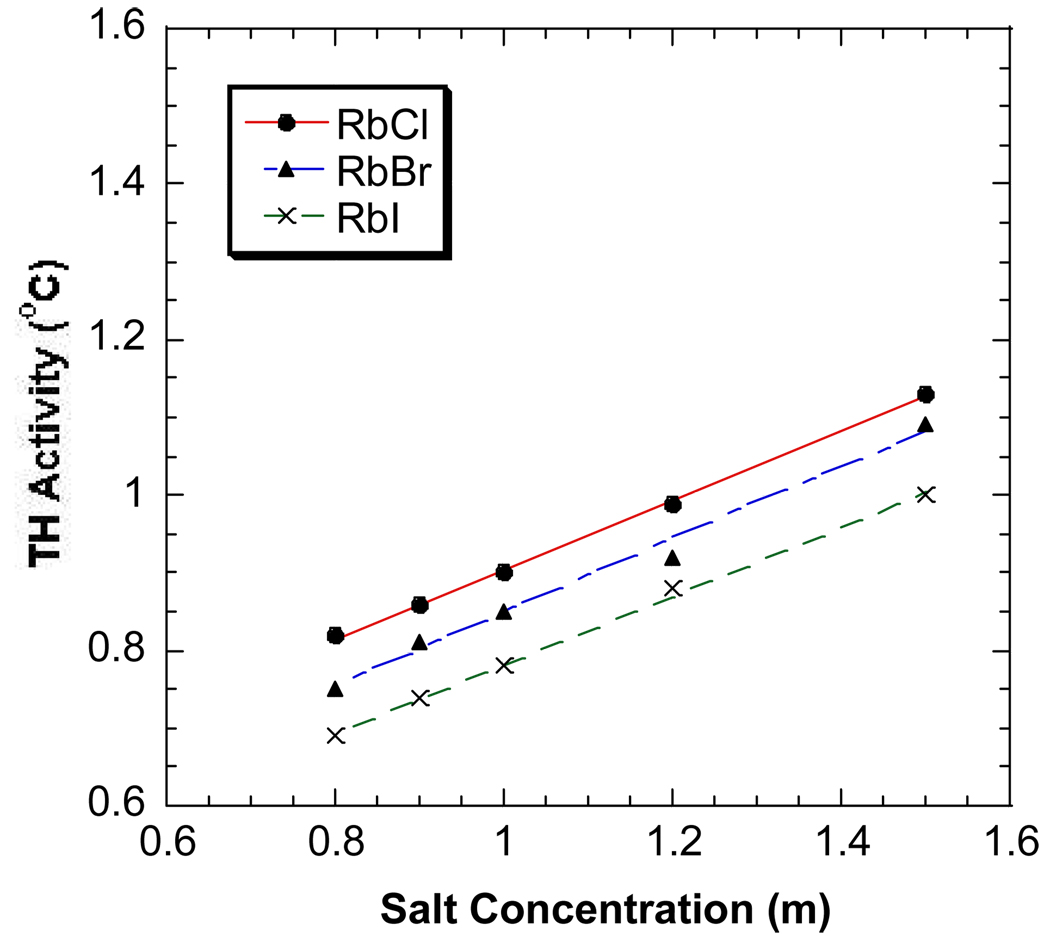
The salting-out effects of anions are generally more pronounced than those of cations. Very similar results were observed for the common monovalent sodium, potassium and rubidium salts with the same anions and the TH activity of DAFP-1 appears to increase linearly with increasing salt concentration (Figure 1–Figure 3). The salting-out constants of DAFP-1 in the presence of these common monovalent salts were obtained by applying Eq. 9 to the experimental results. The obtained salting-out constants are well comparable to the known salting-out constants for proteins (Table 1) indicating there is no apparent difference between AFPs and other proteins in terms of the Hofmeister effects of these common monovalent salts.^19–21

Table 1.

The salting-out constant (K_s) of DAFP-1 by some common monovalent salts^a

Ks	Cl−	Br−	I−	ClO4−
Na+	1.42	0.88	0.67	0.64
K+	1.34	0.91	0.71	---
Rb+	1.28	0.94	0.78	---

^aThe activity coefficients used in the calculations of K_s are obtained from the Handbook of Chemistry and Physics (the 89^th Edition, 2008–2009). The TH activity of DAFP-1 alone (453 µM) is 0.64 °C (i.e., TH₀ = log c / K_total = 0.64 °C). The values of K_s were obtained by linearly fitting the curves in Figure 1–Figure 3.

Various AFP enhancers have been identified, however, the detail mechanism of AFP enhancers is still lacking.⁶ DAFPs have been proposed to produce antifreeze activity by the adsorption inhibition mechanism.^22–24 At least two general mechanisms by which salts may function as TH enhancers: (1) salts lead to an increase in the coverage of AFPs on the ice surface (the salting-out effect); (2) salts influence the binding between AFPs and the ice surface. The salting-out effects of the Hofmeister salts with a reasonable range of concentrations uniformly obey Eq. 5, while it should be noted that Eq. 5 is a simplified result depends on many assumptions and some data still cannot be explained quantitatively or qualitatively.^6,7,9 At very low concentrations, salts have salting-in effects on proteins. The TH activity would decrease if the salting-in effects are the main mechanism, however, the decrease in TH activity of DAFP-1 was not seen in our experiments or reported in any other literature.^6,7,9 At very high salt concentrations, the effect of solution viscosity and the effect of the crystallization velocity of water need to be considered in the derivation.

The TH activity of DAFP-1 in the presence of the simple monovalent Hofmeister ions appears to obey our simple model as suggested in Eq. 9. Therefore, the salting-out effect may act as the sole mechanism of the TH enhancement for these common monovalent Hofmeister salts. These ions may facilitate the precipitation of DAFP-1 on the ice surface and increase the coverage of DAFP-1 on the ice surface, by which the TH activity may increase linearly with salt concentration. In contrast, complex enhancers, such as polycarboxylates, polyhydroxy compounds, and proteins, may have more than one mechanism to enhance the TH activity of DAFP-1.^6,7,8 For examples, both (NH₄)₂SO₄ and Na₂SO₄ would be good TH enhancers according to the Hofmeister series, however, Na₂SO₄ inhibits the TH activity of DAFP-1,⁹ which cannot be explained only using the Hofmeister effects. The Hofmeister effects should be applied carefully to multivalent salts and other complex enhancers.

In summary, the Hofmeister effects may be used to explain the enhancement effect of some monovalent salts on TH activity of DAFP-1. We developed a quantitatively relationship between the TH activity and the salt concentration using a simple classical theory and experimentally determined the TH activities of DAFP-1 in the presence of some common monovalent salts. The salting-out constants of DAFP-1 by some common monovalent salts were determined through applying the developed relationship to the experimental data. This method may be used to determine the salting-out constants of AFPs by monovalent salts. The limitations of using the Hofmeister effects to account for the TH enhancement of salts were also discussed.

Figure 2.

The antifreeze activities of DAFP-1 in the presence of KCl (●), KBr (▲), and KI (×) at 0.8 – 1.5 M. The curve fitting lines are plotted.