Summary
Generalized linear models with serial dependence are often used for short longitudinal series. Heagerty (2002, Biometrics 58, 342–351) has proposed marginalized transition models for the analysis of longitudinal binary data. In this article, we extend this work to accommodate longitudinal ordinal data. Fisher-scoring algorithms are developed for estimation. Methods are illustrated on quality-of-life data from a recent colorectal cancer clinical trial.
Keywords: Fisher scoring, Generalized linear models, QOL
1. Introduction
Quality-of-life (QOL) data in clinical trials is generally obtained repeatedly over time using questionnaires that can be completed by the patient without direct supervision. We will analyze QOL data from a recent colorectal cancer clinical trial (Goldberg et al., 2004). The main objective of this trial was to find a “better” treatment for colorectal cancer. However, given that the toxicity profiles were quite different on the three treatment arms, it was of interest to see if there was a negative impact of “better” treatments on patients’ QOL. In this article we compare the QOL on the three treatments. We will introduce a new regression model to answer this question using a full likelihood-based approach.
Generalized linear models for longitudinal data can be classified into directly specified (marginal) models and indirectly specified (conditional) models. In marginal models, the population-averaged effect of covariates on the longitudinal response is directly specified (Liang and Zeger, 1986; Fitzmaurice and Laird, 1993). In conditional models, the effect of covariates on responses is specified conditional on random effects or previous history of responses. Therefore, the population-averaged effect of covariates is indirectly specified (Zeger and Karim, 1991; Breslow and Clayton, 1993). Here, we focus on marginal models.
Marginalized likelihood-based models describe the correlation among observations by embedding the marginal mean structure within a complete multivariate probability model with dependence, modeled via random effects or a Markov structure. We will extend the previous work using a Markov structure (Azzalini, 1994; Heagerty, 2002) to ordinal categorical data. Related models for binary data can be found in Heagerty (1999) and Miglioretti and Heagerty (2004). This class of likelihood-based directly specified marginal models has several advantages over conditional models. First, the interpretation of regression coeEcients is invariant with respect to specification of the dependence in the model unlike in conditional models. In addition, they can be much less susceptible to bias resulting from random effects model misspecification (Heagerty and Zeger, 2000; Heagerty and Kurland, 2001).
Next, we provide a brief review of models for ordinal data on which our work will build. McCullagh (1980) proposed the cumulative logit model for independent ordinal data. A general overview of models for ordinal categorical data can be found in Liu and Agresti (2005). Most of the models for correlated ordinal data fall into two classes: those modeling dependence using the global odds ratio (GOR) (Dale, 1986) and those modeling dependence via random effects. The GOR is an extension of the simple odds ratio for a 2 × 2 contingency table formed when adjacent rows and columns of a K × K contingency table (K > 2) are collapsed into a 2 × 2 table. Molenberghs and Lesaffre (1994) specified the joint probability of multivariate observations through the first-and higher-order marginal parameters. Williamson, Kim, and Lipsitz (1995) developed marginal mean regression techniques based on the GORs as a measure of association and also considered the latent variable models and the maximum likelihood estimation (MLE) for bivariate ordinal responses. Heagerty and Zeger (1996) proposed marginal regression models for clustered ordinal data by specifying marginal means and marginal pairwise GORs and used estimating equations and alternating logistic regressions for inference. In terms of random effects, Gibbons and Hedeker (1997) developed random-effects ordinal regression models for the probit and logistic links. Todem, Kim, and Lesaffre (2006) and Liu and Hedeker (2006) proposed models for multiple ordinal outcomes in longitudinal settings using random effects.
All these approaches to modeling dependence have a goal of reducing the number of dependence parameters, thereby implicitly reducing the number of probabilities that need to be estimated. For example, a saturated model (with no covariates) for a five-category ordinal response measured at six occasions would require the estimation of 15,625 multinomial probabilities. Our approach to reducing this estimation problem will be to introduce a proportional odds model for the marginal means (probabilities) and a Markov transition structure for the temporal dependence. The use of a likelihood-based approach will have advantages for longitudinal data that are missing at random (MAR) and in particular, ignorable. Likelihood-based inference is valid under ignorability and the missing data mechanism (mdm) need not be explicitly specified. Semiparametric generalized estimating equation (GEE) approaches require explicit specification of the mdm for MAR. In addition, the re-weighting based approaches (based on the mdm) to handle MAR in GEEs only “impute” missing values at the observed data points. Likelihood-based approaches do not have this restriction and allow “imputation” of values outside the range of the observed data points via parametric distributional assumptions.
The article is arranged as follows. In Section 2, we briefly review marginalized transition models (MTMs) for longitudinal binary data. In Section 3, we consider two MTMs for the longitudinal ordinal data. Methods are illustrated in the QOL data in Section 4.
2. Review of Marginalized Transition Model
In this section, we review Heagerty’s marginalized model for the analysis of longitudinal binary data (Heagerty, 2002). Let Yi = (Yi1, …, Yini) be binary data observed on subject i = 1, …, N at times t = 1, …, ni. We assume that associated exogenous but possibly time-varying covariates, xit = (xit1, …, xitr ), are recorded for each subject at each time. Define . We assume that the regression model properly specifies the full covariate conditional mean such that E(Yit | Xit ) = E(Yit | Xi1, …, Xini). The pth-order MTM(p) can be expressed through the pair of regressions
| (1) |
| (2) |
where is the conditional mean, are dependence parameters describing serial dependence by quantifying how strongly the immediate past predicts the present, zit is a subset of xit, and the subject-time-specific intercept in the conditional model, Δit, is determined implicitly by Xi, β, and α.
The mean parameter β describes changes in the average response as a function of covariates. Using a logistic link for the transition model, (2), implies that the parameters αj are unconstrained. For a given mean model, (1), and dependence model, (2), the intercept Δit is fully constrained and must yield the proper marginal expectation when is averaged over the distribution of the history. Therefore, a unique Δit can be identified that satisfies both the transition model and the marginal mean assumptions given any finite-valued dependence model and probability distribution for the history.
This model has several desirable features. First, the mean model is specified separately from the dependence model. As a result, the interpretation of the regression parameter β is invariant as we modify assumptions regarding the dependence in equation (2). This is not true for classical transition models, which parameterize directly as a function of covariates. Second, the MTM can be used with data where subjects have variable lengths of follow-up, permitting likelihood analysis in settings where data may be MAR.
Given β and α, Δit for an MTM(p) is computed based on the following relationship between the marginal and conditional means,
where . Further details are given in Heagerty (2002).
3. Marginalized Transition Models for Longitudinal Ordinal Data
In this section, we propose two MTMs for longitudinal ordinal data, a simple extension of the MTM (OMTM) and an improved extension of the MTM (IOMTM).
Let Yi = (Yi1, …, Yini) be a vector of longitudinal K-category ordinal responses on subject i = 1, …, N at times t = 1, …, ni (ni ≤ T ). We assume that associated exogenous but possibly time-varying covariates, xit = (xit1, …, xitr ), are recorded for each subject at each time and that the regression model properly specifies the full covariate conditional probability such that P(Yit = yit | Xit ) = P (Yit = yit | Xi1, …, XiT ).
The simple extension of MTM of order p, an OMTM(p), is specified using the following two regressions,
| (3) |
| (4) |
where β is the r × 1 vector of regression coefficients, β01 < β02 < … < β0K−1, , zit is a q × 1(subset of xit), , k = 1, …, K − 1, and Yi,t−m,l is the set of K − 1 indicators with Yi,t−m,l = 1 if Yi,t−m = l; Yi,t−m,l = 0 otherwise for l = 1, …, K − 1; m = 1, …, p. Model (3) is a cumulative logit model, a common model for ordinal data. However, the link function in the conditional probabilities (4) is a multinomial logit because we expect the K − 1 conditional probabilities to have different coefficients depending on k and if cumulative logits were used as in the marginal probabilities (3), the monotonicity property of the cumulative conditional probabilities would be difficult to satisfy as it involves Δitk.
The dependence model (4) based on the multinomial logit link function models the probability of moving from category k at time t to category k′ at time t + 1 under p = 1. This is a natural and interpretable way to model the dependence for longitudinal data. An alternative approach would be to model dependence using GORs (Dale, 1986; Heagerty and Zeger, 1996) as discussed in the introduction, which also allows the interpretation of marginal mean parameters to be invariant with respect to specification of the dependence and allows for parsimonious specification of dependence. However, GOR does not directly represent the change over time for a subject, unlike the OMTM, and that is why we choose to specify the dependence using a Markov transition structure.
Because this model is a straightforward extension of the MTM for binary data, it shares many of the same advantages including having the attractive characterization of serial dependence that a transition model provides combined with a marginal regression structure. However, it does have some drawbacks. First, there are a lot of dependence parameters. For example, if p = 2, K = 4, and q = 1 (zit = 1), we need p × (K − 1)2 × q = 18 dependence parameters. Second, the ordering of the categories is not exploited in the conditional probabilities (4). For these two reasons, we propose a modified version in which (4) is replaced with
| (5) |
where c(·) is a smooth function of yit−1, …, yit−p parameterized by α(k). For our methods here, we chose an additive structure for c(·;α(k)), i.e., c(yit−1; α (k)) + c(yit−2; α(k)) + … + c(yit−p; α(k)) and quadratic polynomials for each c(yit−l; α(k)):l = 1, …, p. The quadratic polynomials should be adequate to explain the smooth change of the conditional probabilities and we hypothesize that there is no dramatic change in conditional probabilities that would necessitate higher-order polynomials or other smooth functions; we discuss a more general specification in the Discussion. Implicit in this specification is the “scoring” of the response in the dependence model, which is not an issue in the (proportional odds) mean models. For example, a quadratic model could be made more reasonable for a data set by changing the values of the responses (but not changing their order). We replace (5) by
| (6) |
where and . We call the model given by equations (3) and (6) an improved extension of MTM of order p, an IOMTM(p). The IOMTM(p) has fewer dependence parameters than the OMTM(p). For example, an OMTM has 18 dependence parameters for K = 4, p = 2, and q = 1, whereas an IOMTM(2) has p × 2 × (K − 1) = 12 dependence parameters. In general, for an OMTM(p), the number of dependence parameters increases quadratically with K, the number of categories, whereas in an IOMTM, the number increases linearly in K. The IOMTM also exploits the ordering of the categorical responses in the conditional model (6).
Clearly, for models (3)–(6) to form a coherent probability model, the Δitk will be constrained. Constraints are needed for (3), (4), and (6) to be a valid probability model. Specifically, Δitk is found using the following identity
| (7) |
In this article, we consider only first- and second-order (I)OMTM’s. Higher-order models are possible but require more dependence parameters and larger sample sizes.
3.1 First-Order Models: OMTM(1) and IOMTM(1)
In this subsection, we provide some details for OMTM(1) and IOMTM(1), which are often sufficient for short time series. The dependence models for marginalized first-order transition models [OMTM(1) and IOMTM(1)] are specified using the following two regressions,
| (8) |
| (9) |
Note that (9) is only valid for t ≥ 2 because there are no history data available for the initial state (t = 1).
For both the IOMTM(1) and OMTM(1), mean and dependence parameters are orthogonal as given in the following theorem and corollary.
Theorem 1
The marginal mean parameters, (β0, β) are orthogonal to the dependence parameters, α in the OMTM(1).
Corollary 1
The marginal mean parameters, (β0, β), are orthogonal to the dependence parameters, α in the IOMTM(1) when c(y; α) is a polynomial in y.
Fitzmaurice and Laird (1993) showed consistency of marginal mean parameters regardless of the dependence structure. This was used by Heagerty (2002) in binary MTM’s. The following theorem gives the equivalent result for ordinal MTM’s.
Theorem 2
The maximum likelihood estimate, (β̂0, β̂), remains consistent for (β0, β) even if the dependence model is incorrectly specified.
Proofs of these results can be found in the Web Appendix.
3.2 Maximum Likelihood for the First-Order Models
The maximum likelihood algorithm for these models is described next. Define the marginal cumulative probabilities, for i = 1, …, N; t = 1, …, ni ; k = 1, …, K and conditional probabilities, for i = 1, …, N ; t = 2, …, ni ; k = 1, …, K. The OMTM(1) likelihood function consists of two components, conditional probabilities for time >1 and marginal probabilities at time 1,
where . We propose a Fisher-scoring algorithm to find the MLE of the parameters of interest in the OMTM(1). For estimation of the K − 1 intercepts β0k(k = 1, …, K − 1), r covariate coefficients β, and (K − 1)2 dependence parameters α, we rewrite the log likelihood as
| (10) |
where Ri1k = Yi11 + … + Yi1k, and g(a) = log{1 + exp(a)}. Here we have used the notation from McCullagh (1980) for the log-likelihood function for the cumulative logit model for the ordinal data, log L(1).
To evaluate the likelihood, we need to evaluate both the contribution from the initial state, L(1), and the subsequent contribution from each transition probability, L(2). Let θ = (β0, β, α) be the vector of parameters. We obtain
The K − 1 + r + (K − 1)2q-dimensional likelihood equations and details on the Fisher-scoring algorithm used to solve the likelihood equations can be found in Supplementary Materials.
Estimation for the IOMTM(1) is similar.
3.3 Second-Order Models: OMTM(2) and IOMTM(2)
For the initial states, we assumed a marginal model for t = 1, as we did for the first order models, and an OMTM(1) and IOMTM(1) for t = 2. The marginal models for OMTM(2) and IOMTM(2) are the same as (3) and the dependence models for the OMTM(2) and the IOMTM(2) are given by (4) and (6), respectively, with p = 2. Unlike the first-order OMTM and IOMTM, the orthogonality of marginal and dependence parameters no longer holds (i.e., cannot write it in canonical log-linear form). Thus, consistent estimation of the marginal mean parameters requires correct modeling of the dependence (though marginalized models of this form often offer some robustness; see Heagerty and Kurland, 2001). Details on MLE for the second-order models can be found in Supplementary Materials.
3.4 Missing Data
When the data are incomplete due to dropout that is associated with observed outcomes (i.e., MAR), the orthogonality of marginal mean and dependence parameters in the (I)OMTM(1) no longer holds. Thus, the consistency of the marginal mean parameters under MAR relies on correctly specifying the dependence structure; otherwise, the score functions for the mean parameters can be biased.
3.5 Simulation Study
We conducted several simulation studies to examine robustness to misspecification of dependence model when there is ignorable (MAR) dropout. We set T = 8 and N = 500 with an approximately equal sample size for each of the three (treatment) groups. We considered two different marginal mean models, (3), one with an unstructured mean over time with design vector of the form, , where the 1 is in the tth slot, and one with a linear trend over time, , where groupji is an indicator of whether the subject was in group j. The two different mean models were included to see if any bias in the presence of dropout differed between the unstructured and structured (over time) means.
For each simulation, we considered the following MAR dropout model,
We simulated data using (9) with , m = 1, 2, (α10, α11, α20, α21) = (−1.0, 0.5, −0.5, 0.1) and fit the model assuming .
Table 1 presents the point estimates and the percent relative bias. Percent relative biases in the coefficients were small, the largest being about 3%. The coefficients of time-varying covariates in the structured mean model appeared to be more robust to misspecification of dependence and MAR missingness than in the unstructured mean model.
Table 1.
Bias of the IOMTM(1) MLEs when data are MAR. Displayed are the average regression coefficient estimates and the percent relative bias, 100 × (β̂ − β)/β
| Unstructured marginal mean |
Structured marginal mean |
||||||
|---|---|---|---|---|---|---|---|
| Para. | Truth | Mean | Bias (%) | Para. | Truth | Mean | Bias (%) |
| int1 | −1.00 | −1.00 | 0.0 | int1 | −1.00 | −1.00 | 0.0 |
| int2 | 0.70 | 0.70 | 0.0 | int2 | 0.70 | 0.70 | 0.0 |
| int3 | 2.00 | 2.01 | 0.5 | int3 | 2.00 | 2.00 | 0.0 |
| grp1 | 0.10 | 0.10 | 0.0 | grp1 | 0.10 | 0.10 | 0.0 |
| grp2 | −0.50 | −0.50 | 0.0 | grp2 | −0.50 | −0.50 | 0.0 |
| vis1 | 0.10 | 0.10 | 0.0 | vis | −0.50 | −0.49 | −2.0 |
| vis2 | −1.50 | −1.51 | 0.7 | ||||
| vis3 | 1.20 | 1.20 | 0.0 | ||||
| vis4 | −0.40 | −0.39 | −2.5 | ||||
| vis5 | 0.80 | 0.80 | 0.0 | ||||
| vis6 | −0.30 | −0.29 | −3.3 | ||||
| vis7 | −1.00 | −1.03 | 3.0 | ||||
We performed several similar simulations using the same models for the marginal means, but simulating data under an IOMTM(2) and then fitting an IOMTM(1) with and without MAR dropout. In the presence of dependence misspecification and MAR dropout, we saw considerable bias, with relative biases as large as 74% for the unstructured mean (see Supplementary Materials for the results of these simulations). Under dependence misspecification with no dropout, the biases were quite small despite the orthogonality of the mean and dependence parameters being lost in the IOMTM(2). These simulations further emphasize the importance of correctly specifying the dependence in the presence of missing data. We also did simulations (not shown) to examine small sample bias in the MLE’s with complete data. The bias in the mean parameters was negligible. These results can be found in Lee (2007).
4. Example
We use the models proposed in Section 3 to analyze QOL data from the clinical trial of metastatic colorectal cancer introduced in Section 1. A total of 795 patients with colorectal cancer were randomly assigned to one of the three treatments [FOLFOX, IFL(Control), IROX] between May 1999 and April 2001 (Goldberg et al., 2004). We focus on one QOL measure, fatigue. Fatigue is measured on a five-point ordinal scale (1: I am usually not tired at all; 2: I am occasionally rather tired; 3: There are frequently periods when I am quite tired; 4: I am usually very tired; 5: I feel exhausted most of the time). Because very few patients reported category 5, we collapsed category 4 and 5 into one category. For numerical reasons, we rescaled the response as −0.9, −0.3, 0.3, and 0.9. in the dependence model; the re-scaling was not needed for the marginal mean model.
To examine treatment differences in fatigue levels, we included type of treatment (ARM1 = 1 for FOLFOX; ARM2 = 1 for IROX) and visit number (TIME = 0.0, 0.1, …, 0.5) again re-scaled. The Akaike Information Criteria (AIC; Akaike, 1974) and likelihood ratio tests were used as the model selection criteria.
We assumed the missing responses (mostly due to dropout) were MAR in our initial analysis. In Section 4.2, we more carefully handled the dropouts related to the reason for dropping out (including death).
The Fisher-scoring algorithm is not trivial computationally due to the need to obtain an estimate of Δit for all subjects and at all times, within each Fisher-scoring step. However, in our data set, with 795 patients, a four-category ordinal response and six visit times, the computational burden was not high. Each Fisher-scoring step (in which all the Δit are computed) on a Pentium with a 1.6 GHz processor took about 10 and 30 seconds for the IOMTM(1) and the IOMTM(2), respectively. In addition, using good initial values based on fitting an independent proportional odds model in standard software results in a minimal number of iterations until convergence.
4.1 Models Fit
We fitted and compared seven models. Three were IOMTM(1)’s, three were IOMTM(2)’s, and the other was an OMTM(1). IOMTM(1)-1 and IOMTM(2)-1 were the simplest models, with time homogeneous dependence, . IOMTM(1)-2 and IOMTM(2)-2 allowed the dependence coefficients to depend on Time, . IOMTM(1)-3 and IOMTM(2)-3 had dependence parameters depending on treatment, . The OMTM was an OMTM(1) with time homogeneous dependence model, for j = 1,2,3.
Table 2 presents MLEs for all seven models. Point estimates and standard errors for marginal mean parameters for the OMTM were similar to those for the IOMTM(1) and IOMTM(2). To compare the fit of the models, in particular, the dependence structure, we computed the AIC. The AIC for OMTM was 3800.700 and for IOMTM(1)-1 3876.306, indicating that IOMTM(1)-1 fit better than OMTM. Comparison of deviances for IOMTM(1)-1, IOMTM(1)-2, and IOMTM(1)-3, which are nested, yields , p-value = 0.015 on 6 d.f and , p-value = 0.246 on 12 d.f. The AIC’s for IOMTM(1)-2 and IOMTM(1)-3, which were not nested, were 3872.450 and 3885.380, respectively. These comparisons indicated that IOMTM(1)-2 was the better-fitting model among IOMTM(1)’s and OMTM. Similarly, we had IOMTM(2)-2 as better fitting among IOMTM(2)’s by comparison of deviances and the AIC’s ( , p-value = 0.036 on 12 d.f.; , p-value = 0.917 on 24 d.f.; AIC for IOMTM(2)-2 = 3825.910, AIC for IOMTM(2)-3 = 3861.820). Again, we compared deviances for IOMTM(1)-2 and IOMTM(2)-2 (ΔD22 = 54.540, p-value < 0.0001 on 12 d.f.) and concluded that IOMTM(2)-2 was the best-fitting model.
Table 2.
MLEs of models fit
| Marg. para. | IOMTM(1)-1 Coef. (SE) | IOMTM(1)-2 Coef. (SE) | IOMTM(1)-3 Coef. (SE) | IOMTM(2)-1 Coef. (SE) | IOMTM(2)-2 Coef. (SE) | IOMTM(2)-3 Coef. (SE) | OMTM Coef. (SE) |
|---|---|---|---|---|---|---|---|
| Intercept 1 | −1.099* (0.124) | −1.094* (0.122) | −1.104* (0.124) | −1.082* (0.123) | −1.084* (0.121) | −1.095* (0.123) | −1.099* (0.124) |
| Intercept 2 | 0.844* (0.121) | 0.841* (0.120) | 0.836* (0.119) | 0.849* (0.120) | 0.841* (0.117) | 0.832* (0.119) | 0.844* (0.121) |
| Intercept 3 | 2.318* (0.143) | 2.316* (0.142) | 2.301* (0.142) | 2.319* (0.143) | 2.317* (0.141) | 2.293* (0.143) | 2.319* (0.143) |
| Visit | −0.290 (0.675) | −0.427 (0.683) | −0.235 (0.678) | −0.455 (0.617) | −0.484 (0.600) | −0.124 (0.651) | −0.265 (0.676) |
| Arm1 | −0.066 (0.167) | −0.070 (0.164) | −0.060 (0.166) | −0.086 (0.164) | −0.088 (0.161) | −0.070 (0.164) | −0.065 (0.167) |
| Arm2 | 0.036 (0.165) | 0.036 (0.163) | 0.043 (0.165) | 0.025 (0.163) | 0.055 (0.160) | 0.036 (0.162) | 0.037 (0.166) |
| Visit * Arm1 | −0.647 (1.013) | −0.458 (1.027) | −0.767 (1.006) | −0.346 (0.926) | −0.160 (0.906) | −0.815 (0.937) | −0.687 (1.014) |
| Visit * Arm2 | −1.593 (0.985) | −1.579 (0.996) | −1.637 (0.984) | −1.507 (0.897) | −1.847* (0.874) | −1.835 (0.888) | −1.606 (0.986) |
| Max. loglik | −1924.153 | −1916.225 | −1916.690 | −1900.033 | −1888.955 | −1886.910 | −1923.350 |
| AIC | 3876.306 | 3872.450 | 3885.380 | 3840.660 | 3825.910 | 3861.820 | 3880.700 |
Indicates significance under 95% confidence level.
4.1.1 Graphical assessment of the dependence model
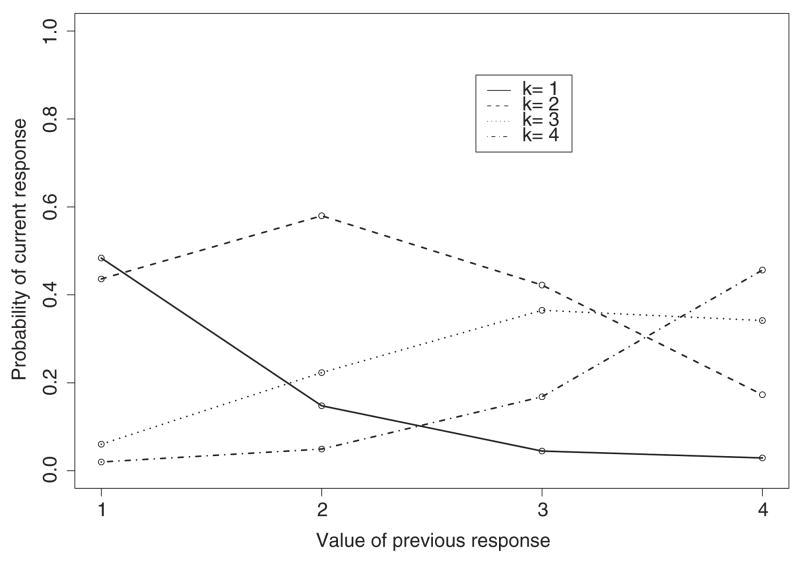
Figure 1 presents conditional probabilities given previous values for the OMTM(1) given in (8). We arbitrarily chose one subject and visit because the shapes of conditional probabilities are the same across subjects (the intercepts Δitk only shift the trajectories up or down). The trajectories of conditional probabilities change quadratically with previous responses. Thus, the quadratic model given in (9) appears adequate to explain the change in the conditional probabilities as a function of the previous response. We were unable to get an OMTM(2) to converge to obtain a similar plot for first- and second-order dependence.
Figure 1.
Conditional probabilities for category k given previous response under the OMTM(1).
4.1.2 Inference on regression coefficients
In the IOMTM(2)-2, the β coefficient of Visit * Arm2 was significant with an estimate of −1.847 and SE of 0.874. This indicated that the level of fatigue increased over time on the IROX arm and this was significantly greater than for patients on the IFL (control) arm. The β coefficient of Visit * Arm1 was not significant. This indicated that the level of fatigue did not change over time on the FOLFOX arm and there was no significant difference of fatigue over time between the IFL and the FOLFOX arms. The cumulative probabilities for the IROX arm decreased more steeply over time compared to the FOLFOX arm and the IFL arm. Thus, for this particular measure of QOL, fatigue, the worst treatment was not the one that provided the longest time to progression and best overall survival (FOLFOX).
4.2 Dropout Due to Progression/Death
A large number of subjects dropped out due to tumor progression or death (40.5%). Thus, the analysis in Section 4.1 is problematic as among other things, it implicitly imputes missing values for the dropouts due to death. Imputing such values for subjects who died is not a sensible approach. We would argue for QOL data, that imputing these QOL values for those who dropped out due to their disease progressing is not sensible either.
Table 3 summarizes the reasons for dropout in the three treatment arms. The dropout rates due to progression/death were marginally higher in the IFL and the IROX arms. To deal with events due to progression/death, we used a mixture model for the joint distribution of longitudinal measures and progression/death times (Hogan and Laird, 1997) similar to previous work by Pauler, McCoy, and Moinpour (2003) and Kurland and Heagerty (2005). For this data set, we had the actual progression/death times for subjects who dropped out due to progression/death and also for those who dropped out for other reasons. Table 4 summarizes the visit window in which patients progressed/died for all three treatments. Note, for some subjects, this is past the time they actually dropped out.
Table 3.
Completers and dropouts by treatment groups. Proportions in parentheses
| Reason for dropout |
||||
|---|---|---|---|---|
| Treatment | Completer | Progression/death | Other | Total |
| IFL | 10 (0.043) | 117 (0.498) | 108 (0.460) | 235 |
| FOLFOX | 4 (0.017) | 68 (0.292) | 161 (0.691) | 233 |
| IROX | 4 (0.017) | 101 (0.423) | 134 (0.561) | 239 |
| Total | 18 (0.025) | 286 (0.405) | 403 (0.570) | 707 |
Table 4.
Progression/death windows by treatment groups. Proportions in parentheses
| Progression/death window |
|||||||
|---|---|---|---|---|---|---|---|
| Treatment | 1 | 2 | 3 | 4 | 5 | 6a | Total |
| IFL | 35 (0.149) | 32 (0.136) | 38 (0.162) | 26 (0.111) | 18 (0.077) | 86 (0.366) | 235 |
| FOLFOX | 16 (0.069) | 28 (0.120) | 24 (0.103) | 17 (0.073) | 19 (0.082) | 129 (0.554) | 233 |
| IROX | 22 (0.092) | 33 (0.138) | 36 (0.151) | 27 (0.113) | 16 (0.067) | 105 (0.439) | 239 |
| Total | 73 (0.103) | 93 (0.132) | 98 (0.139) | 70 (0.099) | 53 (0.075) | 320 (0.453) | 707 |
Window 6 means “after study.”
Define S to be the progression/death time. We specify the ordinal MTM models conditional on progression/death time, S. Due to the small sample sizes when conditioning on individual times, we assumed the parameters were the same for S = 1, …, 5 (those who progressed/died before the end of the study) but different for those who did not, S = 6. This approach implicitly assumes that for a given progression/death time (pattern), that missing data before the progression/death time is MAR (conditional on pattern); this situation occurs if dropout is not due to progression/death.
Within this framework, the probability of fatigue for patients who progressed/died beyond time k is given by
| (11) |
where Tx is treatment and P(Yt > c | S = j, Tx) is only de-fined for t < j. In our analysis here, our target probabilities are (11) evaluated at k = 5; that is, those who did not progress/die before the end of the study. Table 5 presents the estimated target probabilities on the three treatment arms. The probabilities of high fatigue for the IROX and the FOLFOX arm increased over time, whereas that for the IFL arm was more stable. However, there were no significant differences between the treatment arms. Thus, we conclude that patients’ fatigue was not affected by treatment unlike in the models under MAR.
Table 5.
MLEs of P(Yt > c | S > 5, Tx) (and standard errors) where S is progression/death time
| Visit(t) |
|||||||
|---|---|---|---|---|---|---|---|
| Tx | c | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0.756 (0.037) | 0.754 (0.033) | 0.752 (0.037) | 0.751 (0.047) | 0.749 (0.060) | 0.747 (0.075) | |
| IFL | 2 | 0.281 (0.039) | 0.279 (0.025) | 0.277 (0.039) | 0.275 (0.050) | 0.273 (0.063) | 0.271 (0.078) |
| 3 | 0.076 (0.017) | 0.076 (0.016) | 0.075 (0.017) | 0.074 (0.020) | 0.074 (0.024) | 0.073 (0.028) | |
| 1 | 0.744 (0.032) | 0.759 (0.028) | 0.773 (0.034) | 0.786 (0.044) | 0.799 (0.055) | 0.811 (0.066) | |
| FOLFOX | 2 | 0.268 (0.032) | 0.284 (0.030) | 0.300 (0.039) | 0.316 (0.055) | 0.333 (0.075) | 0.351 (0.097) |
| 3 | 0.072 (0.014) | 0.077 (0.014) | 0.083 (0.018) | 0.089 (0.024) | 0.096 (0.031) | 0.103 (0.041) | |
| 1 | 0.741 (0.035) | 0.761 (0.030) | 0.779 (0.035) | 0.797 (0.044) | 0.813 (0.053) | 0.829 (0.062) | |
| IROX | 2 | 0.265 (0.034) | 0.286 (0.032) | 0.308 (0.042) | 0.330 (0.058) | 0.354 (0.079) | 0.378 (0.102) |
| 3 | 0.071 (0.015) | 0.078 (0.015) | 0.086 (0.019) | 0.095 (0.025) | 0.104 (0.035) | 0.114 (0.046) | |
5. Conclusions and Discussion
We proposed two MTMs for longitudinal ordinal data that directly model marginal probabilities as a function of covariates while accounting for the longitudinal correlation via a Markov structure. The IOMTM has fewer dependence parameters than the OMTM and exploits the ordering of previous responses. Parameter estimation was based on maximum likelihood using a Fisher-scoring method. We showed that the ML estimates for the (I)OMTM(1) were consistent regardless of specification of (8) when there was no missing data. Simulation studies indicated that marginal mean parameter estimates were robust to the dependence model being incorrectly specified in (I)OMTM(1)’s under MAR dropout. However, IOMTM(2)’s were much less robust to dependence model misspecification under MAR dropout.
Calculations and analyses in this article are based on first-and second-order (I)OMTMs. Extension to higher orders is also possible. However, such models introduce more dependence parameters and more complex computing and constraints; such models are workable for larger data sets. An alternative formulation would be to introduce random effects instead of, or in addition to, previous response to model the longitudinal dependence. This is ongoing work.
As discussed in Section 4, about 40% of the patients dropped out due to tumor progression or death. We adjusted for this using a pattern mixture approach with patterns defined based on the observed progression/death times. To obtain the causal effect of treatment while accounting for progression/death, a principal stratification approach (Frangakis and Rubin, 2002) could be developed, which would condition on progressing/dying past a given time on all three treatment arms. This is also ongoing work.
In (5), we specified a very general formulation for pth-order Markov dependence and then simplified it to an additive structure with quadratics for the individual components. Using the more general formulation is possible and would allow for more flexible dependence; for example, removing the additive restriction and allowing interactions. Computationally, this would create no additional burden. We are currently exploring such generalizations.
6. Supplementary Materials
Web Appendices, detailed calculations, tables, and figures referenced in Section 3 are available under the Paper Information link at the Biometrics website http://www.tibs.org/biometrics.
Supplementary Material
Acknowledgments
We would like to thank Dr Daniel Sargent and Ms. Erin Green of the Mayo Clinic for providing the data and for their help in data collection and clarifying issues with data and the study, including dropout. The authors gratefully acknowledge the associate editor and a referee for helpful comments on the manuscript. This project was supported by NIH grants CA85295 and HL079457.
Contributor Information
Keunbaik Lee, Department of Statistics, University of Florida, Gainesville, Florida 32611, U.S.A.
Michael J. Daniels, Department of Epidemiology and Biostatistics, Department of Statistics, University of Florida, Gainesville, Florida 32611, U.S.A.
References
- Akaike H. A new look at the statistical model identification. IEEE Transactions Automatic Control. 1974;19:716–723. [Google Scholar]
- Azzalini A. Logistic regression for autocorrelated data with application to repeated measures. Biometrika. 1994;81:767–775. [Google Scholar]
- Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88:125–134. [Google Scholar]
- Dale JR. Global cross-ratio models for bivariate, discrete, ordered responses. Biometrics. 1986;42:909–917. [PubMed] [Google Scholar]
- Fitzmaurice GM, Laird NM. A likelihood-based method for analysing longitudinal binary responses. Biometrika. 1993;80:141–151. [Google Scholar]
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbons R, Hedeker D. Random effects probit and logistic regression models for three-level data. Biometrics. 1997;53:1527–1537. [PubMed] [Google Scholar]
- Goldberg RM, Sargent DJ, Morton RF, Fuchs CS, Ramanathan RK, Williamson SK, Findlay BP, Pitot HC, Albets SR. A randomized controlled trial of fluorouracil plus leucovorin, irinotecan, and oxaliplatin combinations in patients with previously untreated metastatic colorectal cancer. Journal of Clinical Oncology. 2004;22:23–30. doi: 10.1200/JCO.2004.09.046. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ. Marginally specified logistic-normal models for longitudinal binary data. Biometrics. 1999;55:688–698. doi: 10.1111/j.0006-341x.1999.00688.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ. Marginalized transition models and likelihood inference for longitudinal categorical data. Biometrics. 2002;58:342–351. doi: 10.1111/j.0006-341x.2002.00342.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ, Kurland BF. Misspecified maximum likelihood estimates and generalised linear mixed models. Biometrika. 2001;88:973–985. [Google Scholar]
- Heagerty PJ, Zeger SL. Marginal regression models for clustered ordinal measurements. Journal of the American Statistical Association. 1996;91:1024–1036. [Google Scholar]
- Heagerty PJ, Zeger SL. Marginalized multilevel models and likelihood inference (with discussion) Statistical Science. 2000;15:1–26. [Google Scholar]
- Hogan JW, Laird NM. Mixture models for the joint distribution of repeated measures and event times. Statistics in Medicine. 1997;16:239–257. doi: 10.1002/(sici)1097-0258(19970215)16:3<239::aid-sim483>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- Kurland BF, Heagerty PJ. Directly parameterized regression conditioning on being alive: Analysis of longitudinal data truncated by deaths. Biostatistics. 2005;6:241–258. doi: 10.1093/biostatistics/kxi006. [DOI] [PubMed] [Google Scholar]
- Lee K. PhD thesis. University of Florida; 2007. Marginalized regression models for longitudinal categorical data. [Google Scholar]
- Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- Liu I, Agresti A. The analysis of ordered categorical data: An overview and a survey of recent developments. Test. 2005;14:1–73. [Google Scholar]
- Liu LC, Hedeker D. A mixed-effects regression model for longitudinal multivariate ordinal data. Biometrics. 2006;62:261–268. doi: 10.1111/j.1541-0420.2005.00408.x. [DOI] [PubMed] [Google Scholar]
- McCullagh P. Regression models for ordinal data. Journal of the Royal Statistical Society, Series B. 1980;42:109–142. [Google Scholar]
- Miglioretti D, Heagerty P. Marginal modeling of multilevel binary data with time-varying covariates. Biostatistics. 2004;5:381–398. doi: 10.1093/biostatistics/5.3.381. [DOI] [PubMed] [Google Scholar]
- Molenberghs G, Lesaffre E. Marginal modeling of correlated ordinal data using a multivariate Plackett distribution. Journal of the American Statistical Association. 1994;89:633–644. [Google Scholar]
- Pauler DK, McCoy S, Moinpour C. Pattern mixture models for longitudinal quality of life studies in advanced stage disease. Statistics in Medicine. 2003;22:795–809. doi: 10.1002/sim.1397. [DOI] [PubMed] [Google Scholar]
- Todem D, Kim K, Lesaffre E. Latent-variable models for longitudinal data with bivariate ordinal outcomes. Statistics in Medicine. 2006;26:1034–1054. doi: 10.1002/sim.2599. [DOI] [PubMed] [Google Scholar]
- Williamson JM, Kim K, Lipsitz SR. Analyzing bivariate ordinal data using a global odds ratio. Journal of the American Statistical Association. 1995;90:1432–1437. [Google Scholar]
- Zeger SL, Karim MR. Generalized linear model with random effects: A Gibbs sampling approach. Journal of the American Statistical Association. 1991;86:79–86. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.