Point Mutation Rate of Bacteriophage ΦX174

Abstract

The point mutation rate of phage ΦX174 was determined using the fluctuation test. After identifying the genetic changes associated with the selected phenotype, we obtained an estimate of 1.0 × 10⁻⁶ substitutions per base per round of copying, which is consistent with Drake's rule (0.003 mutations per genome per round of copying in DNA-based microorganisms).

MUTATION rates in DNA microorganisms range over 10⁻¹⁰–10⁻⁶ mutations per base per round of copying (m/b/r), whereas the rate varies by less than threefold around a mean value of 0.003 mutations per genome per round of copying (m/g/r), a result known as Drake's rule (Drake 1991). RNA viruses show higher mutation rates (10⁻⁶–10⁻⁴ m/b/r and 0.03–3 m/g/r) than DNA viruses (Drake and Holland 1999; Duffy et al. 2008) and hence deviate from Drake's rule. The rate of the molecular evolution of RNA viruses is also high (10⁻⁴–10⁻² substitutions per site per year) (Jenkins et al. 2002), and RNA viruses have been traditionally considered the fastest-evolving entities (Holland et al. 1982). However, this view has been challenged by recent work showing that some single-stranded DNA (ssDNA) viruses, such as parvoviruses (Shackelton et al. 2005; Shackelton and Holmes 2006), anelloviruses (Umemura et al. 2002), and geminiviruses (Duffy and Holmes 2008), can match the evolutionary rates of RNA viruses. One possible explanation for these findings is that the mutation rates of ssDNA and RNA viruses might be more similar than previously thought.

Although many mutation rate estimates are available for RNA viruses (Drake and Holland 1999, Duffy et al. 2008), few have been reported for ssDNA viruses. The genomic mutation rate of bacteriophage M13 is 0.005 m/g/r and thus fits Drake's rule (Drake 1991). The replication fidelity of ΦX174 has also been studied (Denhardt and Silver 1966; Fukuda and Sinsheimer 1976; Fersht and Knill-Jones 1981, 1983; Raney et al. 2004), and it has been hypothesized that, since ΦX174 spends a larger fraction of its infection cycle in the form of ssDNA, its mutation rate might be higher (Duffy et al. 2008). Here, we estimate the mutation rate of ΦX174 using the Luria–Delbrück fluctuation test (Luria and Delbrück 1943; Zheng 1999).

Phage ΦX174 was plaque purified in Escherichia coli C permissive cells and used to infect 216 liquid cultures (divided in nine blocks of 24 cultures) with N_i = 231 ± 9 (standard error) particle-forming units (pfu). An average of N_f = (3.3 ± 0.2) × 10⁵ pfu per culture was released to the supernatant after 50 min of incubation at 37°. Supernatants were plated onto the nonpermissive strain gro87, bearing a mutation in the DNA helicase gene rep that blocks stage III single-stranded DNA synthesis and hence prevents phage maturation (Tessman and Peterson 1976; Ekechukwu et al. 1995). This allowed us to score spontaneous mutants with the ability to grow on these cells (ogr phenotype). We obtained 0, 1, 2, 3, 4, 5, 6, 11, and 50 ogr plaques in 113, 57, 30, 7, 3, 1, 2, 2, and 1 cultures, respectively. Taking the nine experimental blocks as replicates, the fraction of cultures showing no ogr phages was P₀ = 0.52 ± 0.05. On the basis of the principle that the number of mutational events per culture follows a Poisson distribution (Luria and Delbrück 1943), we estimated the mutation rate to the ogr phenotype as 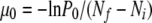for each replicate (null-class method), yielding an average of μ₀ = (2.3 ± 0.3) × 10⁻⁶. Alternatively, the entire distribution of the number of mutants per culture can be used. This distribution is Luria–Delbrück for strictly binary replication and Poisson for strictly linear or “stamping-machine” replication (Chao et al. 2002; Furió et al. 2005) provided that mutations are selectively neutral and, in the latter case, that only one infection cycle has been completed. The maximum-likelihood estimates, obtained as detailed in Furió et al. (2005), were 1.7 × 10⁻⁶ and 3.4 × 10⁻⁶ for the Luria–Delbrück and Poisson models, respectively.

To calculate the mutation rate per base, we sought to identify the mutations leading to the ogr phenotype. Previous work has shown that these map to the N-terminal region of protein A (an endonuclease involved in DNA synthesis) and, putatively, to protein F (the major capsid component) (Tessman and Peterson 1976; Ekechukwu et al. 1995; Raney et al. 2004). We thus sequenced the A and F genes of 47 ogr mutant clones picked from different cultures. All clones showed mutations in one of three codons in a six-amino-acid region of the N-terminal region of gene A, whereas no changes were found in gene F. Seven different base substitutions were identified (Table 1) after sequencing 12 clones, whereas no additional mutations were found in the remaining 35 clones. Hence, we conclude that these seven substitutions probably represent the vast majority of point mutations leading to the ogr phenotype. For each of these substitutions, the mutation rate was calculated (Table 1) and, averaging these values, the estimated rate is μ_b = (1.0 ± 0.3) × 10⁻⁶ m/b/r or, equivalently, since the genome size is 5386 bases, 0.005 ± 0.002 m/g/r.

TABLE 1.

ΦX174 mutations detected on E. coli gro87

Base substitutiona	Amino acid substitution (protein A)	No. of observations (%)	Mutation rate for the substitutionb
4210 A → T	77 His → Leu	2 (4.3)	9.9 × 10−8
4218 G → A	80 Ala → Thr	9 (19.1)	4.5 × 10−7
4218 G → C	80 Ala → Pro	7 (14.9)	3.5 × 10−7
4219 C → Tc	80 Ala → Val	4 (8.5)	2.0 × 10−7
4225 A → C	82 Asp → Ala	5 (10.6)	2.5 × 10−7
4225 A → G	82 Asp → Gly	17 (36.2)	8.5 × 10−7
4225 A → T	82 Asp → Val	3 (6.4)	1.5 × 10−7

^aRelative to the genome sequence with GenBank accession no. GQ153915. Genes F (positions 1001–2284) and A (positions 3981–5386 and 1–136) were sequenced for 47 independent ogr plaques. The nucleotide sequence for codons 75–84 is GACGGCCATAAGGCTGCTTCTGACGTTGTG.

^bBased on the relative contribution of each mutation to the total phenotypic mutation rate (μ₀ = 2.3 × 10⁻⁶). The average of these seven values was multiplied by three to obtain the average per-site mutation rate to any of the three possible substitutions, giving μ_b = 1.0 × 10⁻⁶ m/b/r (see text).

^cAn additional substitution (4126A → G) was found in two clones in combination with this mutation.

This assay did not allow us to detect insertions or deletions. However, since the latter constitute only 15–20% of the total mutations in most organisms (Drake 2009), the value obtained for base substitutions should be close to the total mutation rate per round of copying. Finally, the mutation rate per infection cycle should be approximately twice the rate per round of copying, because the single-stranded genomic DNA is first copied to form double-stranded DNA, which is then used to make progeny genomes through the rolling-circle mechanism. Although there might be additional rounds of copying, analysis of the distribution of the number of mutants per infection cycle indicates that most progeny are made from the same template (Denhardt and Silver 1966).

A different E. coli host with a mutation in the rep gene, gro89, has been used previously to measure the mutation rate of ΦX174 (Raney et al. 2004). Using mutant frequencies instead of the fluctuation test, the authors reported a phenotypic mutation rate of 7.4 × 10⁻⁶. In the assays used to obtain this estimate, 13 base substitutions were found in mutants with the ability to grow on gro89 and their relative contributions to the overall phenotypic mutation rate were also determined. This yields a mutation rate estimate of (1.9 ± 1.8) × 10⁻⁶ m/b/r, which is essentially the same as our finding. Further, our results neatly match amber mutation reversion frequencies (1.1 × 10⁻⁶, 1.7 × 10⁻⁶; Denhardt and Silver 1966; 1 × 10⁻⁶, Fukuda and Sinsheimer 1976; 1.0 × 10⁻⁶, Bernal et al. 2004). Therefore, evidence from different approaches supports a mutation rate of ∼1 × 10⁻⁶ m/b/r. Similar in vitro error rates (1–7 × 10⁻⁶ per base in a single gap-filling replication round) have been found during replication of M13 and E. coli genes with DNA polymerase III holoenzyme (Schaaper 1993; Mo and Schaaper 1996; Pham et al. 1998). This suggests that the mutation rate observed in ogr mutation screens and in stop codon reversion assays could be fully explained by polymerase error and lack of efficient proofreading.

Both ssDNA viruses that have been studied obey Drake's rule. This means that their genomic mutation rates are very similar to those of double-stranded DNA viruses, bacteria, and unicellular eukaryotes, but, on the other hand, their small genome sizes imply that they have the highest per-site mutation rates of all DNA-based systems. However, these rates are still at least an order of magnitude lower than those of most ssRNA viruses. The fact that ssDNA viruses obey Drake's rule while RNA viruses do not suggests that the factors governing mutation rate evolution in these two groups are fundamentally different. Yet, for these differences to be well established, mutation rate estimates for eukaryotic ssDNA viruses would be required. Data available from RNA viruses have revealed no substantial differences between phages and eukaryotic viruses, but it is unclear whether the same generalization could be applied to ssDNA viruses. For example, it is conceivable that replication of eukaryotic ssDNA viruses is mediated by host DNA polymerases that are more error prone than the prokaryotic ones. Further, editing of viral DNA by APOBEC-like cytidine deaminases has not been shown in bacteria. It is also possible that DNA damage due to free radicals might be more frequent in eukaryotes than in prokaryotes (Baker et al. 1996).