Abstract
Markov state models (MSMs) are a powerful tool for modeling both the thermodynamics and kinetics of molecular systems. In addition, they provide a rigorous means to combine information from multiple sources into a single model and to direct future simulations∕experiments to minimize uncertainties in the model. However, constructing MSMs is challenging because doing so requires decomposing the extremely high dimensional and rugged free energy landscape of a molecular system into long-lived states, also called metastable states. Thus, their application has generally required significant chemical intuition and hand-tuning. To address this limitation we have developed a toolkit for automating the construction of MSMs called MSMBUILDER (available at https:∕∕simtk.org∕home∕msmbuilder). In this work we demonstrate the application of MSMBUILDER to the villin headpiece (HP-35 NleNle), one of the smallest and fastest folding proteins. We show that the resulting MSM captures both the thermodynamics and kinetics of the original molecular dynamics of the system. As a first step toward experimental validation of our methodology we show that our model provides accurate structure prediction and that the longest timescale events correspond to folding.
INTRODUCTION
For a molecular system, the distribution of conformations and the dynamics between them is determined by the underlying free energy landscape. Thus, the ability to map out a molecule’s free energy landscape would yield solutions to many outstanding biophysical questions. For example, structure prediction could be accomplished by identifying the free energy minimum,1 leading to insights into catalytic mechanisms of proteins that are difficult to crystallize. Intermediate states, such as those currently thought to be the primary toxic elements in Alzheimer’s disease,2 could also be identified by locating local minima. As a final example, protein folding mechanisms could be understood by examining the rates of transitioning between all the relevant states.
Unfortunately, the free energy landscapes of solvated biomolecules are extremely high dimensional and there is no analytical means to identify all the relevant features, especially when one is concerned with molecules in which small molecular changes yield significant perturbations of the system, such as amino acid mutations in proteins. Therefore, a theoretical treatment requires sampling the potential, generally using Monte Carlo or molecular dynamics (MD), and then inferring information about the states in the free energy landscape from the sampled configurations. Moreover, if one is interested in kinetic properties, one must go further and sample kinetic quantities (e.g., rates) of interconversion between these thermodynamic states.
Mapping out a molecule’s free energy landscape can be broken down into three stages: (1) identifying the relevant states and, in particular, the native state, (2) quantifying the thermodynamics of the system, and (3) quantifying the kinetics of transitioning between the states. Each of these stages builds upon the preceding stages. In fact, this hierarchy of objectives is evident in the literature. For example, in the structure prediction community it is common to plot the free energy as a function of the RMSD to the native state.3 Such representations allow researchers to quickly assess whether or not their potential accurately captures the most experimentally verifiable state, the native state. However, they provide little information on the presence of other states, their relative probabilities, or the kinetics of moving between them.4 Projections of the free energy landscape onto multiple order parameters, on the other hand, may capture multiple states and their thermodynamics.4, 5 The main limitation of these representations is that they depend heavily upon the order parameters selected.5 If the order parameters are not good reaction coordinates, then important features may be distorted or even completely obscured.5, 6 Furthermore, barring the selection of a perfect set of reaction coordinates, such projections only yield limited information about the system’s kinetics due to loss of information about other important degrees of freedom.7
Clustering techniques are a promising means of overcoming these limitations as they allow the automatic identification of the relevant degrees of freedom.8 However, most clustering techniques are based solely on geometric criteria9 so they may fail to capture important kinetic properties. To illustrate the importance of integrating kinetic information into the clustering of simulation trajectories, one can imagine two people standing on either side of a wall. Geometrically these two individuals may be very close but kinetically speaking it could be extremely difficult for one to get to the other. Similarly, two conformations from a simulation data set may be geometrically close but kinetically distant and, therefore, a clustering based solely on a geometric criterion would be inadequate for describing the system’s dynamics.
Markov state models (MSMs) fit nicely into this progression as they provide a natural means to achieve a complete understanding of a molecule’s free energy landscape—a map of all the relevant states with their correct thermodynamics and kinetics.10, 11, 12, 13, 14 The critical distinction between MSMs and other clustering techniques is that an MSM constitutes a kinetic clustering of one’s data.10, 11, 12, 14 That is, conformations that can interconvert rapidly are grouped into the same state while conformations that can only interconvert slowly are grouped into separate states. Such a kinetic clustering ensures that equilibration within a state, and therefore loss of memory of the previous state, occurs more rapidly than transitions between states. As a result, the model satisfies the Markov property—the identity of the next state depends only on the identity of the current state and not any of the previous states.
MSMs are better able to capture the stochastic nature of processes such as protein folding than traditional analysis techniques, allowing more quantitative comparisons with and predictions of experimental observables. Thus, they will allow researchers to move beyond the traditional view of MD simulations as molecular microscopes. An MSM also provides a natural means of varying the resolution of one’s model. For example, consider a protein folding process that occurs on a 10 μs timescale. Using a cutoff of 1 ns to distinguish a fast transition from a slow one would yield a high resolution model that may be difficult to interpret by eye. Using a cutoff of 1 μs, however, would likely yield a high-level model capturing the essence of the process in a human readable form. MSMs provide a rigorous means to combine data from multiple sources and can be used to extract information about long timescale events from short simulations.15 Finally, there are a number of ways of exploiting MSMs to minimize the amount of computation that must be performed to achieve a good model for a given system.16
Unfortunately, constructing MSMs is a difficult task because it requires dividing the rugged and high dimensional free energy landscape of a system into metastable states.11 A good set of states will tend to divide phase space along the highest free energy barriers. More specifically, none of the states will have significant internal barriers. Such a partitioning ensures the separation of timescales discussed above—intrastate transitions are fast relative to interstate transitions—and, therefore, that the model is Markovian. States with high internal barriers break the separation of timescales and introduce memory. To illustrate this situation, imagine a state divided in half by a single barrier that is higher than any barrier between states. Besides breaking the separation of timescales by causing transitions within this state to be slow relative to transitions between states, trajectories that enter the state to the left of the internal barrier will also tend to leave to the left while trajectories that enter on the right will tend to leave to the right. Thus, the probability of any possible new state will depend both on the identity of the current state and the previous state, breaking the Markov property. Avoiding such internal barriers has generally required a great deal of chemical insight and hand tuning;17, 18 thus, the application of MSMs has been limited.
To facilitate the more widespread use of MSMs we have developed an open source software package called MSMBUILDER that automates their construction (now available at https:∕∕simtk.org∕home∕msmbuilder).14MSMBUILDER builds on previous automated methods11 by incorporating new geometric and kinetic clustering algorithms. It also provides a command-line interface built on top of an object oriented structure that should allow for the rapid incorporation of new advances. In summary, MSMBUILDER works as follows: (1) group conformations into very small states called microstates and assume the high degree of structural similarity within a state implies a kinetic similarity, (2) validate that this state decomposition is Markovian, and optionally (3) lump the microstates into some number of macrostates based on kinetic criteria and ensure that this macrostate model is Markovian. There are also a number of tools for analyzing and visualizing the model at both the microstate and macrostate levels.
In this work we demonstrate that MSMBUILDER is able to construct MSMs for full protein systems in an automated fashion by applying it to the villin headpiece (HP-35 NleNle).19, 20 Unlike the peptides that have been studied with automated methods in the past,11 villin has all the hallmarks of a protein, such as a hydrophobic core and tertiary contacts. It is also fast folding, so it is possible to carry out simulations on timescales comparable to the folding time.21
Our hope is that this work will serve as a guide for future users of MSMBUILDER. Thus, we will discuss failed models, the insights these models gave us, and how these insights led to the final model. We will also discuss some of the remaining limitations in the automated construction of MSMs. In addition, we will demonstrate that our model yields accurate structure prediction and that the longest timescales correspond to folding. However, our main emphasis will be on the methodology of building MSMs that faithfully represent the raw simulation data. In particular, we will focus on the microstate level as this is the finest resolution and bounds the performance of lower resolution models. The full biophysical implications of the model and their relation to experimental results will be discussed more thoroughly in a later work.
METHODS
Simulation details
The data set used in this study was taken from Ensign et al.21 and is described briefly below. It consists of ∼450 simulations ranging from 35 ns to 2 μs in length and is publicly available at the SimTK website (https:∕∕simtk.org∕home∕foldvillin).
First, the crystal structure (PDB structure 2F4K)19 was relaxed using a steepest descent algorithm in GROMACS (Ref. 22) using the AMBER03 force field.23 The resulting structure was placed in an octahedral box of dimensions 4.240×4.969×4.662 nm3 and solvated with 1306 TIP3P water molecules. Nine 10 ns high temperature simulations (at 373 K), each with different initial velocities drawn from a Maxwell–Boltzmann distribution, were run from this solvated structure. The final structures from each of these unfolding simulations were then used as the initial points for ∼450 folding simulations at 300 K.
Folding simulations were preceded by 10 ns equilibration simulations at constant volume with the protein coordinates fixed. For all MD simulations, the SHAKE (Ref. 24) and SETTLE (Ref. 25) algorithms were used with the default GROMACS 3.3 parameters to constrain bond lengths. Periodic boundary conditions were employed. To control temperature, protein and solvent were coupled separately to a Nosé–Hoover thermostat26 with an oscillation period of 0.5 ps. The system was coupled to a Parrinello–Rahman barostat27 at 1 bar, with a time constant of 10 ps, assuming a compressibility of 4.5×10−5 bar−1. Velocities were assigned randomly from a Maxwell–Boltzmann distribution. The linear center-of-mass motion of the protein and solvent groups were removed every ten steps. A cutoff at 0.8 nm was employed for both the Coulombic and van der Waals interactions. During these simulations, the long-range electrostatic forces were treated with a reaction field assuming a continuum dielectric of 78, and the van der Waals was treated with a switch from 0.7 to 0.8 nm. The neighborlist was set to 0.7 nm for computational performance.
MSM construction
All the MSMs used in this paper were constructed with MSMBUILDER,14 the relevant components of which are reviewed below. A significant modification of the code was the introduction of sparse matrix types, which allows the construction of MSMs with many more states than previously possible by making more efficient use of the available memory. Sparse matrices will be included in the next release of MSMBUILDER.
Clustering
An approximate k-centers clustering algorithm was used to generate the microstates in all the MSMs used in this study.28, 29 The algorithm works as follows: (1) choose an arbitrary point as the first cluster center, (2) compute the distance between every point and the new cluster center, (3) assign points to this new cluster center if they are closer to it than the cluster center they are currently assigned to, (4) declare the point that is furthest from every cluster center to be the next new cluster center, and (5) repeat steps 2–4 until the desired number of clusters have been generated. The computational complexity of this algorithm is O(kN) where k is the number of clusters and N is the number of data points to be clustered. The algorithm is intended to give clusters with approximately equal radii, where the radius of a cluster is defined as the maximum distance between the cluster center and any other data point in the cluster. Given that MD simulations are Markovian,10 it should be possible to generate a Markov model for simulation dynamics by constructing sufficiently small (or numerous) states. However, the size of a given data set will limit how many clusters can be generated because reducing the number of conformations in each state will eventually result in an unacceptable level of statistical uncertainty.
Based on the Boltzmann relationship, we can calculate the free energy of a state as −kT log(p), where p is the probability of being in the state. Though small variations in the radii of microstates may imply quite large variations in their volumes due to the high dimensionality of the phase space of biomolecules, empirically we find that assuming the clusters have equal volume is useful. In particular, we find that interpreting lower free energy microstates as having higher densities and evaluating models based on the correlation between the free energy and RMSD of each microstate agrees with other measures of the validity of an MSM, such as implied timescales plots as discussed below. Because this relationship is not guaranteed to hold the correlation between microstate free energy and RMSD should never be used as the sole assessment of a model. As discussed in the Sec. 3, it is quite useful for identifying potential shortcomings of a given model. These issues are not a concern at the macrostate level.
All clustering in this work was based on the heavy-atom RMSD between pairs of conformations. However, we note that pairs of atoms in the same side chain that are indistinguishable with respect to symmetry operations were excluded from the RMSD computations. Representative conformations from some clusters are shown using VMD.30
Transition probability matrices
Transition probability matrices are at the heart of MSMs.10 Row normalized transition probability matrices are used in this study. The element in row i and column j of such a matrix gives the probability of transitioning from state i to state j in a certain time interval called the lag time (τ).
The transition probability matrix serves many purposes. For example, a vector of state probabilities may be propagated forward in time by multiplying it by the transition probability matrix.
| (1) |
where t is the current time, τ is the lag time, p(t) is a row vector of state probabilities at time t, and T(τ) is the row normalized transition probability matrix with lag time τ.
The eigenvalue∕eigenvector spectrum of a transition probability matrix gives information about aggregate transitions between subsets of the states in the model and what timescales these transitions occur on.10 More specifically, the eigenvalues are related to an implied timescale for a transition, which can be calculated as
| (2) |
where τ is the lag time and μ is an eigenvalue. The corresponding left eigenvector specifies which states are involved in the aggregate transition. That is, states with positive eigenvector components are transitioning with those with negative components and the degree of participation for each state is related to the magnitude of its eigenvector component.10
Implied timescales plots
Implied timescales plots are one of the most sensitive indicators of whether or not a model is Markovian.31 These plots are generated by graphing the implied timescales of an MSM for a series of lag times. If the model is Markovian at a certain lag time then the implied timescales should remain constant for any greater lag time. The minimal lag time at which the implied timescales level off is the Markov time, or the smallest time interval for which the model is Markovian. The implied timescales for a non-Markovian model tend to increase with the lag time instead of leveling off. Unfortunately, increasing the lag time decreases the amount of data and, therefore, increases the uncertainty in the implied timescales. Thus, implied timescales plots can be very difficult to interpret.
In this study error bars on implied timescales plots were obtained using a bootstrapping procedure. Five randomly selected subsets of the available trajectories were selected with replacement and the averages and variances of the implied timescales for each lag time were calculated.
Time evolution of observables
The time evolution of the mean and variance of any molecular observable can be calculated from an MSM. Calculating the time evolution of an observable X requires calculating the average of X in each state i (Xi) and the average of X2. In this study we took averages over five randomly selected conformations from each state. An initial state probability vector may then be propagated in time as in Eq. 1. At each time step the mean and variance can be calculated as
| (3) |
| (4) |
where N is the number of states, pi(t) is the probability of state i at time t, σ is the standard deviation and
| (5) |
RESULTS AND DISCUSSION
An initial model
Given the computational cost of running extensive MD simulations an important consideration in constructing an MSM is to maximize one’s use of the available data. Of course, one’s hardware always sets hard upper limits on the amount of data that may be used at each stage of building an MSM. In particular, it may not always be possible to fit all of the available conformations into memory for the initial clustering phase of constructing an MSM with MSMBUILDER. A convenient way of overcoming this bottleneck is to use a subset of the available data to generate a set of clusters. Data that was left out during the clustering phase may then be assigned to these clusters.
To maximize the use of our data while satisfying the memory constraints of our system we first subsampled our data set by a factor of 10 and clustered the resulting conformations into 10 000 states. Snapshots were stored every 50 ps during our MD simulations, which will henceforth be referred to as the raw data. Thus, the effective trajectories used during our clustering consisted of snapshots separated by 500 ps. The remaining 90% of the data was subsequently assigned to this 10 000 state model. Fortunately, it is possible to parallelize this assignment phase because the cluster definitions are never updated after the initial clustering.
As discussed in the introduction, the first criterion for assessing the validity of our model is whether or not it is capable of capturing the native state. The next criterion is whether or not the thermodynamics of the model are correct. An initial assessment of these two criteria may be obtained from a scatter plot of the free energy of each state as a function of the RMSD of the state center from the native state.
There is some correlation between the free energy of a microstate and the RMSD of its center from the crystal structure in this model, as shown in Fig. 1a. However, the most nativelike RMSD of any of the state centers is 4.15 Å, whereas the simulations reach conformations with RMSD values as low as 0.52 Å. This discrepancy is a first indication that there may be significant heterogeneity within the states of this model. In particular, more near-native conformations must have been absorbed into one or more other states. Highly heterogeneous states are likely to violate the assumption that the degree of geometric similarity within a microstate implies a kinetic similarity, preventing the construction of a valid MSM. This conclusion is supported by the fact that the average distance between any conformation and the nearest cluster center is over 4.5 Å.
Figure 1.
Scatter plots of the free energy of each microstate (in kcal∕mol) vs its RMSD. (a) The initial 10 000 state model, (b) the 30 000 state model, (c) the final 10 000 state model, and (d) the final 10 000 state model except that the average RMSD across five structures in each state is used instead of the RMSD of the state center.
Final confirmation of the imperfections of the current 10 000 state model comes from examining the implied timescales as a function of the lag time. If the division into microstates were fine enough to ensure the absence of any large internal barriers the largest implied timescales should be invariant with respect to the lag time for any lag time greater than the Markov time.31 Figure 2 shows that the implied timescales for this model continue to grow monotonically as the lag time is increased. While the growth is not too severe it should be possible to improve upon this model given the amount of sampling in the data set.
Figure 2.
Top ten implied timescales for the initial 10 000 state model.
Besides the structural and kinetic heterogeneity within states, the monotonic growth of the implied timescales may also be due to the low number of counts in some states and the resulting uncertainty in transition probabilities from these states. For example, there are less than 10 data points in over 100 of the states at the smallest lag time. Even for a state with ten data points no transition probability can be resolved beyond a single significant digit. Increasing the lag time will reduce the number of data points in every state, having particularly deleterious effects on estimates of transition probabilities from states with low counts in the first place.
More states are not always better
As a first attempt at improving our original model we increased the number of states from 10 000 to 30 000. Our objective in doing so was to avoid internal barriers by dividing phase space into smaller states. In addition, we hoped to find more near-native states by pulling low RMSD conformations into their own clusters.
Clustering the data into more states did indeed result in more near-native states, as shown in Fig. 1b. The most nativelike state center in the 30 000 state model has an RMSD of 3 Å and there is still a general correlation between low free energy and low RMSD. The average distance between any conformation and its nearest state center was also reduced from 4.5 to 3.5 Å.
However, increasing the number of states also had some negative effects on the model. In the 10 000 state model about 1% of the states had 10 or less conformations in them, whereas in the new 30 000 state model 6% of the states have 10 or fewer conformations. Thus, the uncertainty in the transition probabilities from many states will be greater. In addition, while increasing the number of states did create a handful of more near-native states, it also more than doubled the number of states with an RMSD over 10 Å. These phenomena are consistent with the fact that the approximate k-centers clustering algorithm used in this work tends to create clusters with approximately equal radii.28, 29 When adding more clusters, this property will tend to result in most of the new clusters appearing in large sparse regions of phase space in the tails of the distribution of conformations. As a result of these shortcomings, the 30 000 state model was found to have monotonically increasing implied timescales similar to those for the 10 000 state model and, therefore, is not significantly more Markovian than the previous model (data not shown).
Disregarding outliers during clustering yields a Markovian model
One approach to dealing with outliers would be to use all the data during the clustering phase and then discard those clusters that behave in unphysical ways, such as clusters that act as sinks. However, such an approach could discard legitimate trapped states. In addition, the tendency of our approximate k-centers algorithm to select outliers as cluster centers could easily result in a large fraction of clusters being discarded.
To deal with the limitations of our clustering algorithm we reverted to using 10 000 states and increased the amount of subsampling at the clustering stage from a factor of 10 to a factor of 100, which is equivalent to using trajectories with conformations stored at a 5 ns interval for this data set. This change compensates for the tendency of our approximate k-centers algorithm to select outliers as cluster centers by reducing the number of available data points in the tails of the distribution of conformations at the clustering stage. Thus, increasing the degree of subsampling at our clustering stage focuses more clusters in dense regions of phase space where more of the relevant dynamics are occurring. The remaining data can then be assigned to these clusters, so no data is thrown out entirely. Incorporating the remaining data in this manner will tend to enlarge clusters on the periphery of phase space because they will absorb data points in the tails of the distribution of conformations. More central clusters, on the other hand, will tend to stay approximately the same size. The number of data points in every cluster should increase though, allowing better resolution of the transition probabilities from each state.
A very simple kinetically inspired clustering scheme could be implemented by subsampling to select N evenly spaced conformations (in time) as cluster centers. In this case a large number of clusters would appear in dense regions of phase space while there would be very few clusters in sparse regions. Our current approach is an intermediate between such a kinetically inspired clustering and the purely geometrically defined clustering used in our first two models. It is intended to have some of the strengths of both approaches—i.e., fine resolution everywhere as in the geometric approach but even more so in dense regions of phase space as in the kinetic approach.
In fact, subsampling more at the approximate k-centers clustering stage and then assigning the remaining data to these clusters does improve the structural, thermodynamic, and kinetic properties of the model. Based on our experience with this data set and a few others (RNA hairpins and small peptides, data not shown) a good starting point is to subsample such that 10N conformations are used to generate N clusters and conformations used during the clustering are separated by at least 100 ps. The remaining data should then be assigned to these clusters. The degree of subsampling and number of clusters may then be adjusted to improve the model as necessary as the optimal parameters will depend on the system. In particular, the optimal strategy may be quite different for much smaller or larger systems.
Structural agreement: Fig. 1c shows that our new model has state centers with RMSDs as low as 3.4 Å, which is somewhat higher than the 30 000 state model but better than the original model. Examination of randomly selected structures from a number of states revealed that the microstate center is not always a good representative of the state. In particular, some near-native states have a dense pocket of very low RMSD conformations and a handful of outliers. In such cases our approximate k-centers clustering algorithm will select a conformation in between the dense pocket of low RMSD states and the outliers28 when really a structure from the denser region would be more representative of the state. A further improvement in the structural characterization of the model is made possible by calculating the average RMSD over five randomly selected conformations from each state instead of just the state center, as shown in Fig. 1d. This analysis reveals that the most nativelike state has an average RMSD of about 1.8 Å. To illustrate the agreement between this state and the crystal structure Fig. 3a shows an overlay of three randomly selected conformations from this state with the crystal structure. An interesting future direction would be to further validate near-native states by comparing them directly with the experimental data rather than the model thereof.
Figure 3.
Three representative structures for (a) the lowest RMSD state in the final model and (b) the most probable state in the final model overlaid with the crystal structure (red). The phenylalanine core is shown explicitly for each molecule.
Thermodynamic agreement: As discussed in the introduction, we cannot calculate the equilibrium distribution of villin analytically so we do not have an absolute reference point to judge our model against. However, there are some promising features of the thermodynamics of the model that lend it credibility. The most populated state has about 4% of the total population and has an average RMSD of 2.3 Å. Figure 3b illustrates the agreement between three random conformations from this state and the crystal structure. The state with the lowest average RMSD also has the fifth highest population, which is about 2% of the total population, and about 12% of the conformations are in states with average RMSD values less than 3 Å. There is also a reasonable correlation between the RMSD and the free energy, as shown in Fig. 1d. Our results seem to be robust with respect to the method used for calculating the equilibrium distribution as well, as discussed in Appendix A. Finally, the populations from the MSM are consistent with those from averaging over the raw data in successive windows of the simulation time, indicating that the MSM thermodynamics are in agreement with the underlying potential if not experiment (data not shown).
Here it is important to note that none of the simulations were started from the native state. While this is not formally a blind prediction (since the crystal structure has been previously reported20), it is promising that so many simulations folded under the given potential, allowing one to not merely reach the folded state but predict its structure ab initio. It will be interesting to see if this procedure can yield similar results in a blind prediction, or at least when structural criteria are not used as a basis for adjusting the model as in this work.
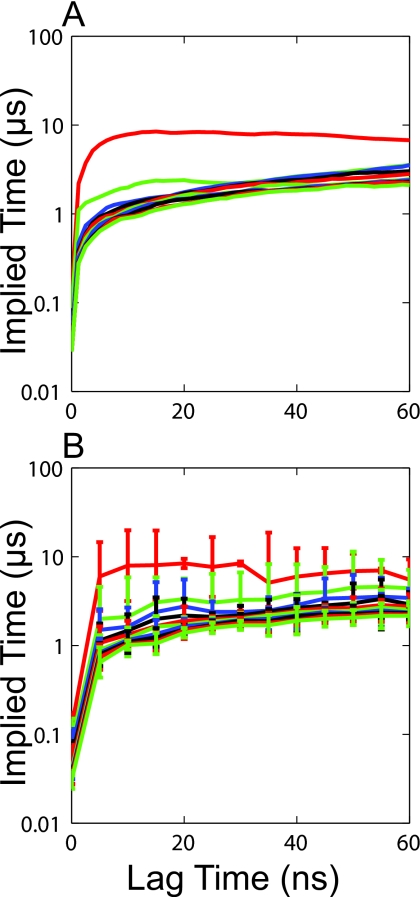
Kinetic agreement: Another promising feature of this model is that there are no fewer than 12 data points in every state, indicating that this model may be able to better resolve the transition probabilities for most states. In fact, the implied timescales for this model do seem to level off as the lag time is increased. Figure 4a shows that the longest timescales level off at a lag time of about 15 ns but increase moderately at longer lag times. Figure 4b, however, shows that the implied timescales are level within error from 15 to 60 ns. After about 35 ns there is an increase in the statistical uncertainty in the implied timescales, explaining their apparent growth in Fig. 4a. After 60 ns the statistical uncertainty becomes enormous so implied timescales beyond this point are not shown. Thus, this model appears to be Markovian at lag times of 15 ns and beyond.
Figure 4.
Top ten implied timescales for the final model. (a) The implied timescales at intervals of 1 ns. (b) The implied timescales with error bars obtained by doing five iterations of bootstrapping at an interval of 5 ns.
The longest implied timescale for this model is about 8 μs. While this is quite long relative to the experimentally predicted folding time of 720 ns at 300 K,19 it is consistent with previous simulation work suggesting that the experimental measurements may be monitoring structural properties which relax faster than the complete folding process.21 In that study, the authors found that a surrogate for the experimental observable was consistent with the experimental measurements but that longer timescales on the order of 4 μs were present when monitoring the relaxation of a more global metric for folding. Ensign et al.21 also found timescales as high as ∼50 μs by applying a maximum likelihood estimator to a subset of the data with little folding. While this timescale is much longer than any of the implied timescales in our MSM, it is not inconsistent with our model because the rates for transitioning between some states in an MSM, when fit using a two-state kinetics assumption, may be slower than the implied timescales. Ensign et al.21 likely identified one of these slow rates by focusing on a subset of the data. For a more detailed discussion of this topic with a simple example see Appendix B.
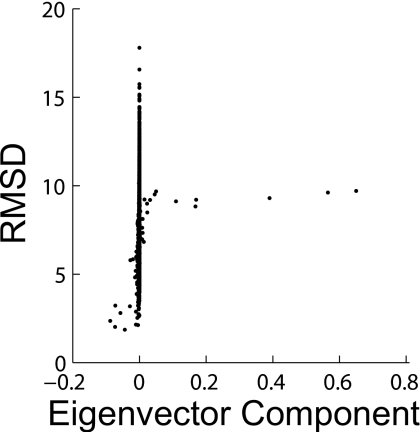
The components of the left eigenvector corresponding to the longest timescale give information about what is occurring on this timescale. That is, states with positive eigenvector components are interchanging with states with negative components and the degree of participation in this aggregate transition is given by the magnitude of the components.10 Figure 5 demonstrates that the longest timescale in our model does correspond to folding by showing that it corresponds to transitions between high and low RMSD states. Numerous states do not participate strongly in this transition, explaining the streak of points with eigenvector components near zero.
Figure 5.
The average RMSD of each state in the final model vs its left eigenvector component in the longest timescale transition showing that this transition corresponds to folding.
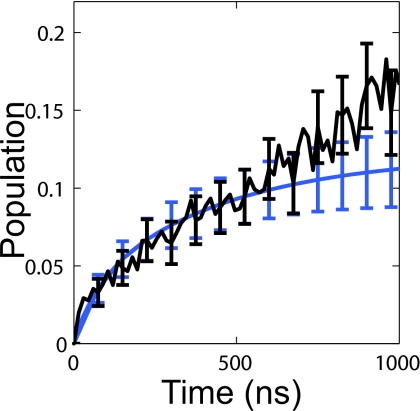
For further confirmation that the MSM is an accurate model of the simulation data we compared the predicted time evolution of the population of the native state with the raw simulation data, where the native state was defined as all microstates with an average Cα RMSD to the crystal structure less than 3 Å. Figure 6 shows that there is good agreement between the MSM and raw data.
Figure 6.
Comparison between the time evolution of the native population in the MSM (blue) and the raw data (black) for the entire data set. The error bars represent the standard error.
While the time evolution of state populations is a good test of our MSM, often we will want to compute the time evolution of some observable to make comparisons with and predictions of experiments. As an example we compare the predicted time evolution of the Cα RMSD to the actual time evolution of the RMSD in the raw data for each of the nine initial configurations. The means by which we calculated the RMSD from the MSM is described in the Sec. 2. Measuring the time evolution of the RMSD from the raw data is simply a matter of measuring the average RMSD over the simulations started from the given initial structure at every time point. We also included a reduced representation of the raw data in this comparison. In the reduced representation each trajectory is represented as a series of states rather than a series of conformations. The average RMSD at a given time point is then calculated by averaging the RMSD of the states each of the relevant trajectories is in. It is important to note that we used the average RMSD across five randomly selected conformations (and the variance thereof) for each state rather than the RMSD of the state centers in these comparisons. Just using the RMSD of the state centers resulted in poor comparisons since they are not truly representative of the state, as discussed above.
Very good agreement (i.e., within the uncertainties of the observables) was found between all three representations for seven of the nine starting configurations, an example of which is shown in Fig. 7a. In these cases the MSM was found to capture both the mean and variance of the time evolution of the RMSD to high precision. The agreement was less strong for the two remaining starting conformations, as shown in Fig. 7b. In these cases the reduced representation agreed well with the raw data, showing that our states are structurally sufficient to capture the correct behavior. The mean RMSD from the MSM does not agree as well with the other two representations, though the true mean is still within the variance of the prediction from the MSM. Note that this variance, as well as all the other variances shown in Fig. 7, are just due to the variance in the RMSD within each state and do not include any of the statistical uncertainty in the model. Their large magnitude is an indication of the heterogeneity of villin folding.
Figure 7.
Comparison between the time evolution of the RMSD in the MSM (blue), the reduced representation (yellow), and the raw data (black) for (a) an example of good agreement and (b) an example of the worst case scenario. The error bars represent one standard deviation in the RMSD.
The discrepancy between the MSM predictions and the other two representations for two of the starting structures indicates that our model still has some subtle memory issues in a subset of the states. Interestingly, the two conformations where the MSM agreed less well with the raw data were found to be faster folding than the other seven initial configurations in a previous study.21 It would appear that the slower folding trajectories are dominating the equilibrium distribution, causing all the MSM predictions to level off at about 6 Å, which is too high for the two fast folding initial configurations. Similar results were found with other observables, such as the distance between the Trp23 and His27 residues that was previously used as a surrogate for the experimental observable used to measure the folding time21 (data not shown).
Remaining issues
The most probable cause of any subtle memory issues in our model is the existence of internal barriers within some states. As discussed previously, a state with a sufficiently high internal barrier could cause transition probabilities from that state to depend on the identity of the previous state. In particular, simulations started from one initial configuration could tend to enter and exit a state in one way while simulations started from a different initial configuration could tend to enter and exit the same state in a completely different way.
To test for the existence of internal barriers we calculated independent MSMs for each initial configuration. Each of these MSMs used the same state definitions, however, only simulations started from the given starting conformation were used to calculate the transition probabilities between states. All of these models agreed well with the raw data. For example, Fig. 8 shows good agreement for the starting structure previously used as an example of the poorest agreement between the full model and the raw data [shown in Fig. 7b].
Figure 8.
Improved agreement between the MSM and raw data for the example of poor agreement from Fig. 7b obtained by building the transition probability matrix from simulations started from this starting structure alone. The error bars represent one standard deviation in the RMSD.
This improved agreement indicates that some states do indeed have internal barriers. Moreover, the seven conformations for which the full model best reproduced the raw data probably have the same behavior in these states while the two initial configurations with poorer agreement between the full MSM and the raw data have a different behavior in these states. The discrepancy then occurs because transition probabilities for these states in the full MSM will be a weighted average of the two types of behavior. The two starting conformations that contribute less heavily to this weighted average are then captured less well by the full MSM.
In an attempt to address this problem we tried increasing the number of states to 30 000. This model may have had some structural advantages and given a slightly lower Markov time, however, it still suffered from the same subtle memory issues as the 10 000 state version (data not shown). Models with even more states were not attempted as they would greatly increase the number of states with very few counts and, therefore, increase uncertainty in the model. These issues may be resolved by identifying those states with internal barriers and splitting them further. However, such hand-tuning is beyond the scope of this work, which focuses on the performance of automated procedures for constructing MSMs.
CONCLUSIONS
Our analysis of the villin headpiece shows that the automated construction of MSMs using MSMBUILDER is now at a point where it can be applied to full protein systems, a step beyond the small peptides that have been studied in the past.11, 32 This advance was made possible by the proper application of our approximate k-centers clustering algorithm. A naïve application of this algorithm to a molecular simulation data set may result in a mediocre state decomposition because outliers in sparse regions of phase space are likely to be selected as cluster centers. To compensate for this tendency, one can subsample at the clustering stage, effectively disregarding many of the outliers and focusing the clusters in more relevant regions of conformational space. Data not included in the clustering phase may then be assigned to the resulting model to maximize the use of the available data. General guidelines for applying this result are given in Sec. 3C.
To demonstrate that our MSM is a reasonable map for villin’s underlying free energy landscape, we showed that it is capable of accurate structure prediction and its thermodynamics and kinetics are consistent with the raw simulation data. Thus, we have laid a foundation for implementing an automated adaptive sampling scheme capable of constructing models with the minimum possible computational cost. The fact that our model captures both the mean behavior and heterogeneity of villin folding will also allow for more accurate comparisons with experiments and predictions of other experimental observables in a future work on the biophysics of villin folding. By applying this methodology to multiple systems we hope to understand general principles of protein folding. Of course, there is still room for improvement. Future work on estimating reversible transition matrices from simulation data, clustering, adaptive sampling, and exploring the connections between MSMs and transition path sampling18, 33 could extend the accuracy and applicability of MSMBUILDER.
ACKNOWLEDGMENTS
Many thanks to D. Ensign for giving us access to his villin simulation data and to Sergio Bacallado and John Chodera for their input on MSMs. This work would not have been possible without the support of the Folding@home users. This work was also supported by NIH Grant No. R01-GM062868, NIH Roadmap Grant No. U54 GM072970, and NSF Award No. CNS-0619926. G.B. was funded by the NSF Graduate Research Fellowship Program.
APPENDIX A: ESTIMATING TRANSITION MATRICES AND EQUILIBRIUM DISTRIBUTIONS
Given our simulation data and assignments thereof to states, it is necessary to estimate the transition probability matrix and the corresponding equilibrium distribution. We have experimented with a number of such methods, all of which give results that are similar to within error for this data set. However, this property should not be assumed of other data sets a priori.
First, we show the standard method for estimating the transition probability matrix T(τ) (or just T for simplicity). The entries of T are the probabilities of transitions from state i to state j in time τ, that is, Tij=P(i→j). To estimate this, let Cij=C(i→j) be the number of observed transitions from i to j. Then a reasonable estimate (a maximum likelihood estimate) is Tij=Cij∕Ci, where
| (A1) |
is the number of observed transitions starting in state i.
To estimate the equilibrium distribution of T, one merely has to find the stationary eigenvector of T. Under ideal conditions (if the model is ergodic and irreducible),34 the stationary eigenvector e is unique and can easily be computed by repeated multiplication of some initial probability density by T, as in Eq. 1. Similarly, one could use standard eigenvalue routines to find the eigenvector corresponding to an eigenvalue of 1.
A possible problem with the standard estimate for T is that the resulting model might not satisfy detailed balance
| (A2) |
where ei is the equilibrium probability of state i. The naïve solution to this is to symmetrize the count matrix by adding its transpose, which amounts to including the counts that would have arisen from viewing the simulations in reverse. Clearly this procedure is inappropriate for situations not at equilibrium; nonetheless, we sometimes find this procedure useful for equilibrium data due to its ease. Furthermore, if the underlying count matrix is symmetric, one can show that the equilibrium distribution can be obtained simply by dividing the number of observations in each state by the total number of observations.
A somewhat more complicated procedure to ensure reversibility is using a maximum likelihood estimate constrained to the set of models satisfying detailed balance. To achieve this, assume that we are given the observed count matrix C. By exploiting the equivalence between this count matrix and a random walk on an edge-weighted undirected graph,35 we then estimate an additional count matrix, X, which we require to be symmetric. We compute X by maximizing the likelihood of X given C; this assumption gives a set of equations that allow the self-consistent calculation of X. More formally, if C is the observed counts, and X is a symmetric matrix that approximates C, then the likelihood is
| (A3) |
Maximizing the likelihood yields the following equation, which we solve by self-consistent iteration,
| (A4) |
where Ci and Xi are defined as the row sums of C and X, respectively, as in Eq. A1. In our experience, this method works but it can be slow for the large matrices we consider. Furthermore, statistical noise in the count data can dominate the resulting equilibrium distribution and even cause the self-consistent iterations to diverge.
A final method is that of Bacallado et al.,36 which uses Bayesian inference with a prior on the space of matrices satisfying detailed balance. This method is formally the most sound, as it uses Bayesian inference and includes a powerful prior. However, it is much more computationally demanding than the other methods. Thus, this method was also applied to the data in order to assess the validity of the simpler methods.
We find that the four methods mentioned above give similar results for the underlying equilibrium distribution of this data set, indicating that we have achieved equilibrium sampling. As such, we have used the naïve method of symmetrizing the matrix due to its computational efficiency (and the fact that we have so much data that our data set is very close to having reached equilibrium). However, in general, we stress that either the maximum likelihood or Bayesian methods should be used.
APPENDIX B: THE POSSIBILITY OF LONGER TIMESCALES THAN THE IMPLIED TIMESCALES
Here we show a simple model demonstrating that the rates for transitioning between some states in an MSM under a two-state assumption (as used in the maximum likelihood approach of Ensign et al.21) may be slower than the implied timescales. First we define a four state system that satisfies detailed balance
This system is depicted in Fig. 9a.
Figure 9.
Graph depiction of the model system defined in Appendix B with edges labeled by (a) their probability and (b) their average timescale under a two-state assumption.
The eigenvalues of this system are 1, 0.997, 0.95559, and 0.94141 and we will assume a lag time of 1 in arbitrary units. Thus, disregarding the eigenvalue of one corresponding to the equilibrium distribution, there are three implied timescales: 332.785, 22.0139, and 16.5627.
We can write the probability of transitioning between two states as
| (B1) |
where ω is the average timescale for the transition (this notation deviates from the standard notation of τ but avoids confusion with the lag time). Rearranging, we find
| (B2) |
Plugging our transition probabilities into this equation we arrive at the average timescales for transitioning between each pair of states shown in Fig. 9b. Many of these timescales are as high as 1000 units, much greater than the largest implied timescale of ∼332 units. In principle, one could monitor these average timescales, resulting in apparent timescales longer than the implied timescales of the system.
References
- Anfinsen C. B., Haber E., Sela M., and F. H.White, Jr., Proc. Natl. Acad. Sci. U.S.A. 47, 1309 (1961). 10.1073/pnas.47.9.1309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein W. L., W. B.Stine, Jr., and Teplow D. B., Neurobiol. Aging 25, 569 (2004). 10.1016/j.neurobiolaging.2004.02.010 [DOI] [PubMed] [Google Scholar]
- Simons K. T., Kooperberg C., Huang E., and Baker D., J. Mol. Biol. 268, 209 (1997). 10.1006/jmbi.1997.0959 [DOI] [PubMed] [Google Scholar]
- Bowman G. R. and Pande V. S., Proteins 74, 777 (2009). 10.1002/prot.22210 [DOI] [PubMed] [Google Scholar]
- Krivov S. V. and Karplus M., Proc. Natl. Acad. Sci. U.S.A. 101, 14766 (2004). 10.1073/pnas.0406234101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis P. G., Dellago C., and Chandler D., Proc. Natl. Acad. Sci. U.S.A. 97, 5877 (2000). 10.1073/pnas.100127697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du R., Pande V. S., Grosberg A. Y., Tanaka T., and Shakhnovich E. S., J. Chem. Phys. 108, 34 (1998). 10.1063/1.475393 [DOI] [Google Scholar]
- Bowman G. R., Huang X., Yao Y., Sun J., Carlsson G., Guibas L. J., and Pande V. S., J. Am. Chem. Soc. 130, 9676 (2008). 10.1021/ja8032857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karpen M. E., Tobias D. J., and C. L.BrooksIII, Biochemistry 32, 412 (1993) 10.1021/bi00053a005 [DOI] [PubMed] [Google Scholar]; Shao J. Y., Tanner S. W., Thompson N., and Cheatham T. E., J. Chem. Theory Comput. 3, 2312 (2007). 10.1021/ct700119m [DOI] [PubMed] [Google Scholar]
- Schutte C., Habilitation thesis, Department of Mathematics and Computer Science, Freie Universitat Berlin, 1999. [Google Scholar]
- Chodera J. D., Singhal N., Pande V. S., Dill K. A., and Swope W. C., J. Chem. Phys. 126, 155101 (2007). 10.1063/1.2714538 [DOI] [PubMed] [Google Scholar]
- Noe F. and Fischer S., Curr. Opin. Struct. Biol. 18, 154 (2008). 10.1016/j.sbi.2008.01.008 [DOI] [PubMed] [Google Scholar]
- Dill K. A., Ozkan S. B., Shell M. S., and Weikl T. R., Annu. Rev. Biophys. 37, 289 (2008). 10.1146/annurev.biophys.37.092707.153558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman G. R., Huang X., and Pande V. S., “Using generalized ensemble simulations and Markov state models to identify conformational states,” Methods (in press). [DOI] [PMC free article] [PubMed]
- Chodera J. D., Swope W. C., Pitera J. W., and Dill K. A., Multiscale Model. Simul. 5, 1214 (2006) 10.1137/06065146X [DOI] [Google Scholar]; Sriraman S., Kevrekidis L. G., and Hummer G., J. Phys. Chem. B 109, 6479 (2005) 10.1021/jp046448u [DOI] [PubMed] [Google Scholar]; Yang S., Banavali N. K., and Roux B., Proc. Natl. Acad. Sci. U.S.A. 106, 3776 (2009). 10.1073/pnas.0808261106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinrichs N. S. and Pande V. S., J. Chem. Phys. 126, 244101 (2007) 10.1063/1.2740261 [DOI] [PubMed] [Google Scholar]; Roblitz S., Habilitation thesis, Department of Mathematics and Computer Science, Freie Universitat Berlin, 2008 [Google Scholar]; Huang X., Bowman G. R., Bacallado S., and Pande V. S., “Rapid equilibrium sampling initiated from nonequilibrium data,” Proc. Natl. Acad. Sci. U.S.A. (in press). [DOI] [PMC free article] [PubMed]
- Jayachandran G., Vishal V., and Pande V. S., J. Chem. Phys. 124, 164902 (2006). 10.1063/1.2186317 [DOI] [PubMed] [Google Scholar]
- Buchete N. V. and Hummer G., J. Phys. Chem. B 112, 6057 (2008). 10.1021/jp0761665 [DOI] [PubMed] [Google Scholar]
- Kubelka J., Chiu T. K., Davies D. R., Eaton W. A., and Hofrichter J., J. Mol. Biol. 359, 546 (2006). 10.1016/j.jmb.2006.03.034 [DOI] [PubMed] [Google Scholar]
- Chiu T. K., Kubelka J., Herbst-Irmer R., Eaton W. A., Hofrichter J., and Davies D. R., Proc. Natl. Acad. Sci. U.S.A. 102, 7517 (2005). 10.1073/pnas.0502495102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ensign D. L., Kasson P. M., and Pande V. S., J. Mol. Biol. 374, 806 (2007). 10.1016/j.jmb.2007.09.069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J. C., Vanderspoel D., and Vandrunen R., Comput. Phys. Commun. 91, 43 (1995) 10.1016/0010-4655(95)00042-E [DOI] [Google Scholar]; Lindahl E., Hess B., and van der Spoel D., J. Mol. Model. 7, 306 (2001). [Google Scholar]
- Wang J. M., Cieplak P., and Kollman P. A., J. Comput. Chem. 21, 1049 (2000). [DOI] [Google Scholar]
- Ryckaert J. P., Ciccotti G., and Berendsen H. J. C., J. Comput. Phys. 23, 327 (1977). 10.1016/0021-9991(77)90098-5 [DOI] [Google Scholar]
- Miyamoto S. and Kollman P. A., J. Comput. Chem. 13, 952 (1992). 10.1002/jcc.540130805 [DOI] [Google Scholar]
- Hoover W., Phys. Rev. A 31, 1695 (1985) 10.1103/PhysRevA.31.1695 [DOI] [PubMed] [Google Scholar]; Nose S. and Klein M. L., Mol. Phys. 50, 1055 (1983). 10.1080/00268978300102851 [DOI] [Google Scholar]
- Nose S., Mol. Phys. 52, 255 (1984) 10.1080/00268978400101201 [DOI] [Google Scholar]; Parrinello M. and Rahman A., J. Appl. Phys. 52, 7182 (1981). 10.1063/1.328693 [DOI] [Google Scholar]
- Gonzalez T., Theor. Comput. Sci. 38, 293 (1985). 10.1016/0304-3975(85)90224-5 [DOI] [Google Scholar]
- Dasgupta S. and Long P. M., J. Comput. Syst. Sci. 70, 555 (2005). 10.1016/j.jcss.2004.10.006 [DOI] [Google Scholar]
- Humphrey W., Dalke A., and Schulten K., J. Mol. Graph. 14, 33 (1996). 10.1016/0263-7855(96)00018-5 [DOI] [PubMed] [Google Scholar]
- Swope W. C., Pitera J. W., and Suits F., J. Phys. Chem. B 108, 6571 (2004). 10.1021/jp037421y [DOI] [Google Scholar]
- Schultheis V., Hirschberger T., Carstens H., and Tavan P., J. Chem. Theory Comput. 1, 515 (2005). 10.1021/ct050020x [DOI] [PubMed] [Google Scholar]
- Bolhuis P. G., Chandler D., Dellago C., and Geissler P. L., Annu. Rev. Phys. Chem. 53, 291 (2002). 10.1146/annurev.physchem.53.082301.113146 [DOI] [PubMed] [Google Scholar]
- Brzezniak Z. and Zastawniak T., Basic Stochastic Processes: A Course Through Exercises (Springer, New York, 1999). [Google Scholar]
- Cover T. M. and Thomas J. A., Elements of Information Theory, 2nd ed. (Wiley, Hoboken, 2006). [Google Scholar]
- Bacallado S., Chodera J. D., and Pande V., J. Chem. Phys. 131, 045106 (2009). 10.1063/1.3192309 [DOI] [PMC free article] [PubMed] [Google Scholar]