Skip to main content
NCBI home page
The Review of Scientific Instruments logoLink to The Review of Scientific Instruments
. 2009 Sep 22;80(9):093708. doi: 10.1063/1.3227836

Measurement of the spectral directivity of optoacoustic and ultrasonic transducers with a laser ultrasonic source

André Conjusteau 1, Sergey A Ermilov 1, Richard Su 1, Hans-Peter Brecht 1, Matthew P Fronheiser 2, Alexander A Oraevsky 1
PMCID: PMC2766411  PMID: 19791945

Abstract

Comprehensive characterization of wideband ultrasonic transducers and specifically optoacoustic detectors is achieved through the analysis of their frequency response as a function of the incident angle. The tests are performed under well-defined, repeatable operating conditions. Backillumination of a blackened, acoustically matched planar surface with a short laser pulse creates an acoustic impulse which is used as a wideband ultrasonic source. Upon illumination with a short laser pulse, the bandwidth of our source shows a −6 dB point of 12 MHz and a low-frequency roll-off around 300 kHz. Using proprietary software, we examine thoroughly the planarity of the emitted wave front within a specified amplitude cutoff and phase incoherence. Analysis of the angular dependence of the frequency response yields invaluable directivity information about the detector under study: a necessary component toward accurate optoacoustic image reconstruction and quantitative tomography. The laser ultrasonic source we developed is the main feature of our directivity measurement setup. Due to its simplicity, it can easily be adapted to various calibration devices. This paper focuses on the development and characterization of the flatness and the bandwidth of our wideband ultrasonic source.

INTRODUCTION

Optoacoustic imaging is a rapidly evolving technique showing great promise for high-resolution visualization of vasculature and blood distribution in tissues, including microvasculature of tumors in humans1, 2, 3 and laboratory animals.4, 5, 6, 7 It involves optical generation of acoustic pressure transients in tissues, which carry information on distribution of optically absorbing objects. Following data acquisition, the reconstruction of images is performed using radial back projection of the processed pressure transients.8, 9, 10 The effect of finite spatial dimension of receiving transducers on the shape of the optoacoustic signals emanating from spherical targets had been studied previously.11 Through numerical simulations, it was concluded that significant distortions in the pressure transients occurred, and that the effect was a greatly decreased resolution in the reconstructed images. Furthermore, image reconstruction is affected by off-axis low-frequency signals that overwhelm the high-resolution information generated by the objects of interest, such as blood vessels.12 It is therefore necessary to introduce the directivity of the elements, which can be defined as the angular dependence of their impulse or frequency response, into image reconstruction algorithms. Thus, understanding the directivity along with the impulse response allows one to: (1) properly reconstruct the images by backprojecting amplitudes of each signal sample only to the spherical surfaces which contributed to the detected signal and applying the appropriate weighting factor, (2) properly filter the detected signals by keeping the relevant ultrasonic frequency band, and (3) lowering the noise floor by rejecting the low acoustic frequencies incident to the transducer originating from locations outside the volume of interest.

The standard way of characterizing transducers involves emitting from an element of the array and receiving with a neighboring element the signal reflected off a metallic plate or cylinder.13, 14 The frequency response obtained from such a procedure is the convolution of the element’s transmit and receive properties. It is valid for acoustic signals impinging normally the surface of the transducer and does not address the spatial properties of the acoustic wave front. While this information may be sufficient in pure ultrasound studies, we found that it is incomplete for accurate image reconstructions from optoacoustic signals. The use of ideal point transducers in simulations generates unrealistically rendered images.15 The purpose of this work is to enable one to fully characterize optoacoustic transducers in their natural mode of operation and obtain information about their spectral directivity. Sections 2, 3 describe the source we have developed, its design considerations, and results of the evaluation of its performance.

METHODOLOGY

Instead of relying on a tunable source of acoustic waves, the system we developed generates an optoacoustic impulse which translates into a broadband signal in the frequency domain. The Fourier analysis of the impulse response of the transducer generates the response over the whole frequency band. An additional feature of our source is that it generates a plane wave, minimizing the occurrence of acoustic diffraction intrinsic to spherical wave sources at small distances. This last feature also permits operation at a wide range of distances separating the source and the transducer, thereby easing the analysis of irregularly shaped detectors.

The concept is simple: A short burst of light hits a highly absorbing surface and generates a pressure pulse.16 Energy absorption at the surface generates an acoustic transient that is sensed by the detector. In order to devise a truly general method of detector characterization, it is imperative that the source produces a signal with the flattest response over the widest possible band of ultrasonic frequencies. From the properties of the Fourier transform, it is known that a constant function in the frequency domain originates from a delta function in the time domain.17 Therefore an ideal laser ultrasound source should produce delta pulses.

Laser pulse duration and bandwidth

The laser pulse duration determines the maximum bandwidth achievable with the current system. Under laser illumination conditions of temporal pressure confinement, an acoustic impulse generated in an absorbing layer of sufficient thickness will replicate the profile of the absorbed energy, and the generated ultrasound band is inversely related to the penetration depth of the light.18 In a case where acoustic pressure is not confined in the course of laser energy deposition, the generated acoustic spectrum is inversely proportional to the laser pulse duration.19 The former was the case for our laser ultrasound source. The temporal profile of our laser system, a Quanta System SpA Ti:sapphire laser operating at 764 nm (delivering up to 65 mJ∕pulse at 10 Hz) yields a −6 dB high-frequency corner of about 50 MHz, the full width at half maximum (FWHM) of the laser pulse being 8 ns. Although not absolutely necessary, emitter response flatness is desirable as it ensures an optimal signal-to-noise ratio (SNR) upon deconvolving the calibrated hydrophone’s response from the measured source output. The characteristics of our laser system ensure the development of a device able to characterize detectors operating in a wide frequency band.

Delta pulse formation and propagation

Upon generating the acoustic impulse, different factors can alter, or mar, the response of the transducer. These situations must be controlled, or at least be fully characterized in order to determine the limitations of the system.

Spatial distribution of laser energy

The absorber is uniform in absorbance and of even thickness as the generated acoustic wave front does mimic the spatial distribution of laser absorption. However, if the laser energy profile is not spread out sufficiently over the active area of the absorber, then diffraction effects will alter the waveform sensed by the transducer. Effectively, as the laser spot is reduced in size, differentiation of the acoustic signal may increase (depending upon transducer size). This would cause the signal to become bipolar and shift the entire band toward high frequencies. Although seemingly desirable in situations calling for higher frequencies, this effect can only be used for transducers of very small effective area as diffraction also curves the wave front which yields to signal integration over large transducers, thereby reducing the bandwidth and nullifying the effect. Our source design is based upon the largest possible laser beam size producing a wide and flat acoustic wave front.

Acoustic boundary effects

The occurrence of acoustic reflections at interfaces does alter negatively the impulse by extending it in time and introducing resonances that cause unwanted oscillations in the impulse response. To ensure near-theoretical performance, the boundary effects must be avoided. As we perform all tests in water, we used Rexolite, a polymer acoustically well matched to water, to minimize the possibility of reflections at the source-water interface. Additionally, the thickness of the absorbing layer is kept to a minimum for the same reason.

Experimental setup

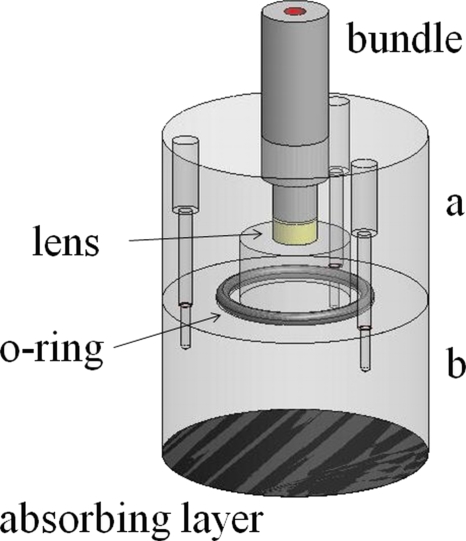
The source we have developed and built is comprised of two sections: an optical part and an acoustic part. It is hermetically sealed (both halves are held against an o-ring) and is thus fully submersible. It is 98 mm long and 77 mm in diameter. A schematic representation is presented in Fig. 1.

Figure 1.

Figure 1

Open in a new tab

Optoacoustic delta-pulse source. In the first part (a), the laser light travels in air through expanding optics. Then, in the second half of the source (b), light travels through Rexolite until it converts into sound on a highly absorbing layer.

The pulsed radiation from our Quanta Ti:sapphire laser is coupled to the source via an off-the-shelf 3∕8 in. (9.5 mm) aperture fiber bundle (Dolan-Jenner Industries). This ensures flexibility in positioning and greatly reduces the possibility of laser misalignment. The bundle is rigidly attached to the body of the source and the joint is sealed to ensure water resistance: It is primordial that light propagates in air to benefit the characteristics of dielectric coated optics. At few millimeters from the bundle face, light propagates through a 12.7 mm diameter biconcave lens with a focal length of −15 mm. The light is then transmitted into the source body where it travels through Rexolite. Finally, the light hits the absorbing layer which consists of three light coats of high-gloss black plastic paint (Krylon Fusion for Plastics). The surface underneath the paint is machined precisely perpendicular to the light propagation axis and then highly polished to ensure the creation of a distortion-free plane wave.

RESULTS AND DISCUSSION

With a fast charge coupled device camera, the laser beam was imaged on the emitter face prior to painting. Despite the high index of refraction of Rexolite, the beam does expand as much as can be calculated from the specifications of the negative lens used in the device. A final beam size of 40 mm (FWHM) is obtained, and although significantly smaller than the full size of the source’s face (77 mm), it has shown to be sufficient as will be presented below. Procedures to further expand the beam through appropriate shaping of the back side of the Rexolite block are under investigation.

Using the delta source with our Quanta Ti:sapphire laser under the normal operating conditions mentioned above, we obtain the acoustic impulse shown in Fig. 2, as sensed by our Onda GL 0200 calibrated hydrophone and following 17 dB amplification (SEA A17 dB Hydrophone Preamplifier, 7.1 v∕v into 50 Ω from 0.005 to 25 MHz). It is estimated that 30 mJ per pulse is propagated through the system under these conditions, and with the Onda hydrophone, our broadest band but least sensitive detector, we reliably observe a SNR in excess of 50 (Fig. 2 shows a SNR of 63).

Figure 2.

Figure 2

Open in a new tab

Optoacoustic delta-pulse source impulse measured with GL 0200, amplified 7.1 times.

The impulse shown in Fig. 2 is monopolar and features minimal low-frequency overshoot (see broad structure around 700 ns). The FWHM is 21 ns, which is more than twice the laser shot duration. In order to identify the limitations of the system, tests were also run with 8 ns 1064 nm pulses (pump radiation from the Quanta unit) and also 16 ns 1064 nm pulses [Quantel Brilliant B Nd:YAG (yttrium aluminum garnet) laser]. Neither frequency nor wavelength measurably affected the high-frequency corner of the impulse response. This suggests that neither light penetration nor pulse duration is the limiting factor in our setup. To confirm, the use of an absorbing layer with increased absorbance was fabricated, inspired by a recent literature article.20 Again no measurable change in the bandwidth of the emitted wave was observed. The most likely cause of bandwidth narrowing was thus assumed to be the temporal distribution of the laser Gaussian pulse, and this assumption was confirmed by numerical simulations. Modifying the temporal profile of the laser spot is thereby warranted and possible modifications to our system are being investigated. Nevertheless, as can be seen in Fig. 3, the −6 dB frequency roll-off occurs around 12 MHz, which is beyond the high-frequency roll-off of most common ultrasound probes and optoacoustic detectors.

Figure 3.

Figure 3

Open in a new tab

Frequency content of the optoacoustic delta-pulse source impulse. The −6 dB point occurs around 12 MHz.

The next step in characterizing the source is to measure the flatness of the wave front. To proceed, it is essential to use a transducer with an effective area as small as possible. We used our GL 0200 calibrated hydrophone (circular element of 200 μm diameter) attached to a high precision, computer driven, three-axis translation stage to scan the whole area of the source at a few distances. At each step of the scan, an impulse is acquired over 2500 samples on the digitizing oscilloscope (Tektronix TDS 2024B) at a sampling rate of 1 GHz.

Through the use of proprietary software developed with MATLAB, a reference signal was chosen (highest amplitude, usually at the center of the probe). In the second step, the second and third most intense impulses are identified, and the three points are used to define a plane. Then, successively, neighboring data points are considered (in order of decreasing amplitude) and fitted to the plane. Each point must fit the plane equation within the predetermined phase incoherence parameter (i.e., a time delay expressed as a fraction of the acoustic period). The procedure is terminated when a point does not satisfy the coherence restriction: All the rejected data are zeroed.

In the initial test, we defined the wave front as flat if the signal amplitude was within 6 dB of the reference signal. We also determined that the temporal position of the impulse (for each physical location within the area of interest) must fall within an allowed phase incoherence of 15% at a frequency of 10 MHz. Two slices were chosen. One, close to the source at 0.5 mm, shows near field characteristics of the wave front. The second one shows far field performance at a distance of 50 mm from the source. The results are shown in Figs. 45. The two-dimensional plots represent a map of flatness for the source. Superimposed over the gray scale rendition of the entire dynamic range is a contour that represents the area where the intensity of the signal falls within a specified amplitude parameter (here, −6 dB).

Figure 4.

Figure 4

Open in a new tab

Planarity of the acoustic wave front 0.5 mm from the source. The contour indicates the area inside of which the amplitude of the signal is within a 6 dB window. The phase incoherence is limited to 15% at 10 MHz.

Figure 5.

Figure 5

Open in a new tab

Planarity of the acoustic wave front 50 mm from the source. The contour indicates the area inside of which the amplitude of the signal is within a 6 dB window. The phase incoherence is limited to 15% at 10 MHz.

The purpose of the delta source is to generate a plane wave that can be used to determine the directivity of optoacoustic transducers. With a conventional emitter, it is often challenging to fully control the angle of incidence of the acoustic field impinging upon a transducer under study. This is due often to the presence of side lobes or the nonplanarity of the emitted wave front. With our setup, thanks to the large effective area of the source (see Figs. 45), it is easy to locate the transducer of interest into the very center of the plane wave. Rotational motion of the detector can be performed without altering the original alignment and risking falling off the plane wave area.

The acquisition of an impulse is achieved with a digitizing oscilloscope (Tektronix TDS 3014) and the data are transferred to a PC via GPIB interface with OPENCHOICE DESKTOP V1.5. A sampling rate of 1.25 GHz ensures the faithful digitization of frequencies far higher than the physical limit imposed by the laser parameters. With the help of a custom-made protractor-mounted fixture, the sensitive area of the detector is located precisely at the center of rotation: Angle adjustments do not change the effective distance between the transducer and the source. A drawing of our directivity fixture is presented in Fig. 6. The data acquisition can then be performed reliably and reproducibly for different angles. The spectral directivity of the transducer can be determined by simply analyzing the Fourier transform of the acquired impulses and observing their variation with incident angle. To illustrate, the directivity of the GL 0200 detector is shown in Fig. 7. The high frequencies are increasingly attenuated as the angle of incidence decreases due to integration against the spatial profile of the transducer.

Figure 6.

Figure 6

Open in a new tab

Schematics of the directivity setup. The whole assembly is placed on top of a water tank in a way to fully immerse the detector. The mounting block is designed to allow positioning of a variety of detectors exactly onto the axis of rotation. The source is then held in place, also under water, centered onto the sensitive area of the transducer. The detector can then be rotated and the angle of incidence, with respect to the face of the source, is read on the protractor.

Figure 7.

Figure 7

Open in a new tab

Directivity data for our GL 0200 detector. The source’s intrinsic response was deconvolved from the measured impulse, and the curves were normalized individually to emphasize the frequency roll-off.

CONCLUSIONS

We have designed, built, and analyzed an optoacoustic source that produces well-defined acoustic impulses upon illumination from short (10 ns) laser pulses. It provides a flat acoustic wave front over a large area. Due to the laser intensity profile, frequencies up to about 10 MHz are generated. Combined with a protractor-based pivoting fixture, the optoacoustic source allows measuring accurately and reproducibly the spectral directivity of acoustic transducers.

ACKNOWLEDGMENTS

This work was supported in part by grants from the National Cancer Institute (Nos. 5R44CA110137, 4R44CA096153, and 3R44CA128196). We thank the engineering teams of the Fairway Medical Technologies and Seno Medical Instruments for technical assistance.

References

  1. Oraevsky A. A., Andreev V. G., Karabutov A. A., Fleming D. R., Gatalica Z., Singh H., and Esenaliev R. O., Proc. SPIE 3597, 352 (1999). 10.1117/12.356829 [DOI] [Google Scholar]
  2. Manohar S., Vaartjes S. E., van Hespen J. C. G., Klaase J. M., van den Engh F. M., Steenbergen W., and van Leeuwen T. G., Opt. Express 15, 12277 (2007). 10.1364/OE.15.012277 [DOI] [PubMed] [Google Scholar]
  3. Ermilov S. A., Khamapirad T., Conjusteau A., Leonard M. H., Lacewell R., Mehta K., Miller T., and Oraevsky A. A., J. Biomed. Opt. 14, 024007 (2009). 10.1117/1.3086616 [DOI] [PubMed] [Google Scholar]
  4. Wang X., Pang Y., Ku G., Stoica G., and Wang L. V., Opt. Lett. 28, 1739 (2003). 10.1364/OL.28.001739 [DOI] [PubMed] [Google Scholar]
  5. Kolkman R. G., Klaessens J. H., Hondebrink E., Hopman J. C., de Mul F. F., Steenbergen W., Thijssen J. M., and van Leeuwen T. G., Phys. Med. Biol. 49, 4745 (2004). 10.1088/0031-9155/49/20/006 [DOI] [PubMed] [Google Scholar]
  6. Zhang E. Z., Laufer J. G., Pedley R. B., and Beard P. C., Phys. Med. Biol. 54, 1035 (2009). 10.1088/0031-9155/54/4/014 [DOI] [PubMed] [Google Scholar]
  7. Brecht H. -P., Su R., Fronheiser M., Ermilov S. A., Conjusteau A., and Oraevsky A. A., “Whole body three-dimensional optoacoustic tomography system for small animals,” J. Biomed. Opt. (submitted). [DOI] [PMC free article] [PubMed]
  8. Kruger R. A., Liu P. Y., Fang Y. R., and Appledorn C. R., Med. Phys. 22, 1605 (1995). 10.1118/1.597429 [DOI] [PubMed] [Google Scholar]
  9. Oraevsky A. A., Andreev V. G., Karabutov A. A., and Esenaliev R. O., Proc. SPIE 3601, 256 (1999). 10.1117/12.350007 [DOI] [Google Scholar]
  10. Xu M. and Wang L. V., Phys. Rev. E 71, 016706 (2005). 10.1103/PhysRevE.71.016706 [DOI] [PubMed] [Google Scholar]
  11. Andreev V. G., Ponomarev A. E., Karabutov A. A., and Oraevsky A. A., Proc. SPIE 4618, 153 (2002). 10.1117/12.469860 [DOI] [Google Scholar]
  12. Ermilov S., Fronheiser M., Brecht H. -P., Su R., Conjusteau A., Mehta K., Otto P., and Oraevsky A. A., Proc. SPIE 7177, 717703 (2009). 10.1117/12.812192 [DOI] [Google Scholar]
  13. Light E. D., Davidsen R. E., Fiering J. O., Hruschka T. A., and Smith S. W., Ultrason. Imaging 20, 1 (1998). [DOI] [PubMed] [Google Scholar]
  14. Caliano G., Carotenuto R., Cianci E., Foglietti V., Caronti A., Iula A., and Pappalardo M., IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 2259 (2005). 10.1109/TUFFC.2005.1563268 [DOI] [PubMed] [Google Scholar]
  15. Oraevsky A., in Photoacoustic Imaging and Spectroscopy, edited by Wang L. (Taylor & Francis, New York, 2009). [Google Scholar]
  16. Chen Q. X., Dewhurst R. J., Payne P. A., and Wood B., Ultrasonics 32, 309 (1994). 10.1016/0041-624X(94)90011-6 [DOI] [PubMed] [Google Scholar]
  17. James J. F., A Student Guide to Fourier Transform (Cambridge University Press, Cambridge, 2002). [Google Scholar]
  18. Oraevsky A. A., Jacques S. L., and Tittel F. K., Appl. Opt. 36, 402 (1997). 10.1364/AO.36.000402 [DOI] [PubMed] [Google Scholar]
  19. Karabutov A. A., Savateeva E. V., Podymova N. B., and Oraevsky A. A., J. Appl. Phys. 87, 2003 (2000). 10.1063/1.372127 [DOI] [Google Scholar]
  20. Hou Y., Ashkenazi S., Huang S. W., and O’Donnell M., IEEE Trans. Ultrason. Ferroelectr. Freq. Control 54, 682 (2007). 10.1109/TUFFC.2007.292 [DOI] [PubMed] [Google Scholar]

Articles from The Review of Scientific Instruments are provided here courtesy of American Institute of Physics

RESOURCES