Temporal multiplexing radiography for dynamic x-ray imaging

Abstract

All current x-ray imaging devices acquire images sequentially, one at a time. Using a spatially distributed multibeam x-ray source we recently demonstrated the feasibility for multiplexing x-ray imaging, which can significantly increase the data collection speed. Here we present a general methodology for dynamic x-ray imaging of an object in cyclic motion with temporal multiplexing. Compared to the conventional sequential imaging technique, where 2N−1 phase images are required and N exposures are needed for a single phase image, a temporal multiplexing of dimension 2N−1 can reduce the imaging time by a factor of N while maintaining the temporal resolution.

INTRODUCTION

In many x-ray imaging applications including medical diagnosis and industrial inspection, it is often necessary and informative to obtain dynamic images of an object undergoing cyclic motions, such as human respiration and cardiac motions. Motion-induced blurs degrade the image quality resulting in significantly deteriorated imaging resolution. The current practice of reducing motion blurs is to use fast frame readout from x-ray detectors or short x-ray exposure from x-ray sources. However because of technological constraints, the frame rate of current x-ray detectors is limited by the speed from detector readout electronics and the x-ray exposure time is limited by the flux from a given x-ray tube. To reduce the imaging blur induced by a cyclic motion, it is common to gate the x-ray exposure and the image acquisition to the cyclic motion. This method can reduce the blur but significantly increase the imaging time because only one image is taken within one motion cycle.

Multiplexing¹ refers to the simultaneous collection of multiple data sets, and has been applied successfully in areas such as telecommunication and analytical instrumentations^{2, 3} to increase the data acquisition rate. Multiplexing using coded aperture⁴ has previously been considered for x-ray imaging. Using the newly developed technology for carbon nanotube (CNT) based spatially distributed multibeam x-ray source, we have recently demonstrated the feasibility of multiplexing x-ray imaging with either frequency multiplexing⁵ or spatial binary multiplexing.⁶ By simultaneous collection of multiple x-ray images, both multiplexing approaches can significantly increase the data collection speed when compared to the conventional sequential imaging mode.

In the dynamic x-ray imaging of an object in cyclic motion, multiple phase images (i.e., multiple images corresponding to different phases) along the motion cycle are required. In the conventional sequential imaging mode, each phase image is acquired from synchronizing the x-ray exposure and the detector readout with the motion cycle. And within one motion cycle, only one image can be acquired. Furthermore, when the flux within the short exposure from a given x-ray tube is limited, each phase image needs to be averaged from multiple frames acquired at the same phase for the phase image to have a sufficient signal-to-noise ratio (SNR). This leads to prolonged imaging time.

To overcome this limitation, we propose a novel temporal multiplexing method for dynamic x-ray imaging of an object in cyclic motion. Similar to the previously reported spatial multiplexing methods, this process has the same effect in terms of reduction in data collection time but requires only a single-beam x-ray source and multiplexing is performed through the temporal domain. The general idea of temporal multiplexing is to speed up the multiple-frame-averaged dynamic x-ray imaging process by acquiring multiple images of the object at different phases within a single motion cycle, and then deconvolute the images by demultiplexing to recover the individual phase image. In the following, we first describe the temporal multiplexing concept in general and then demonstrate the feasibility of this method by the dynamic x-ray imaging of a mechanical rotating wire phantom with temporal multiplexing. Lastly, we discuss the potential benefits and limitations of the temporal multiplexing method.

TEMPORAL MULTIPLEXING

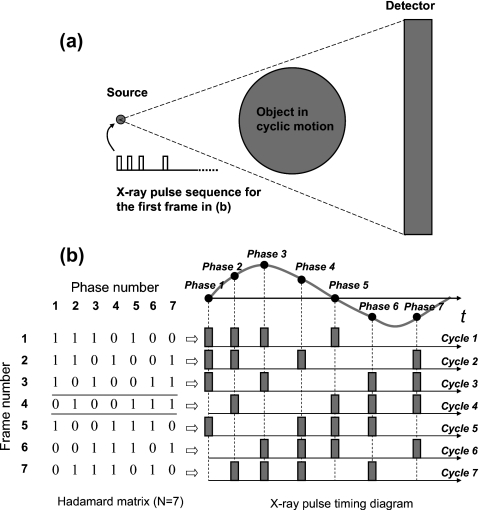
The temporal multiplexing concept is illustrated in Fig. 1. What we considered here is a generalized x-ray imaging system consisting of a single-beam x-ray source, a digital area detector, and an object undergoing cyclic motion. Here “cyclic” refers to a motion profile that is repeatable but not necessarily periodic, such as the contraction∕expansion of a human heart. The x-ray source can be programmed so that the x-ray exposure can be synchronized with the detector readout and the motion. When the motion speed is fast, the x-ray exposure needs to be sufficiently shorter than the detector integration time in order to reduce the imaging blur. At this short exposure, suppose the x-ray flux from the source is limited so that multiple-frame averaging is required for the dynamic x-ray imaging of the object in sequential imaging mode. With this generalized system, we will demonstrate that temporal multiplexing can reduce the imaging time significantly while maintaining the high temporal resolution.

Figure 1.

(a) Generalized x-ray imaging system using a single-beam x-ray source and detector pair with temporal multiplexing scheme to image an object in cyclic motion. (b) The correlation between a multiplexing matrix and the x-ray pulse timing diagram. The columns of the matrix are associated with each phase; the rows are associated with each recording frame. A 1∕0 at a location indicates that the x-ray pulse for that phase is turned on∕off for that recording frame. The highlighted row is shown with four x-ray pulses on at four different phases as an example.

To image the object in N phases with temporal multiplexing, the first step is to construct a multiplexing matrix. Similar to spatial multiplexing,^{5, 6} there are many possible ways of achieving multiplexing. For convenience here we chose the Hadamard binary matrix.^{7, 8} The second step is to acquire N composite x-ray frames. Each composite frame is triggered by the trigger signal synchronized to the beginning of a motion cycle and exposed by an x-ray pulse sequence defined by a row of the Hadamard multiplexing matrix. After all composite images are acquired, demultiplexing is done by applying inverse Hadamard matrix^{5, 6} to recover the x-ray phase images corresponding to the N phases of a motion cycle. To simplify the explanation, let N be 7. Figure 1b shows the seven phases along one motion cycle, the Hadamard multiplexing matrix, and the corresponding x-ray pulse timing diagram. The columns of the matrix correspond to phases and the rows of the matrix correspond to output recording frames, i.e., the composite frames. In a single row of the matrix, a 1 in a particular column indicates that the x-ray pulse corresponding to that phase is on for that composite frame. Likewise, a 0 indicates that the x-ray pulse corresponding to that phase is off for a given composite frame. Each of the seven composite frames is exposed by four x-ray pulses according to the corresponding row of the Hadamard matrix. From those seven composite images, we can recover the seven phase images corresponding to the seven phases of the motion cycle through demultiplexing.

Please notice that the temporal resolution of the imaging method is determined by the individual x-ray pulse width and it is not necessary for all pulses to have the same pulse width as long as the pulse width is the same for a given phase of cyclic motion. This could be a potential advantage when applying temporal multiplexing to objects that have complex cyclic motion. In a complex motion, different phases could have different motion speeds, such as the contraction and expansion of a heart and lung. A higher motion speed requires a higher temporal resolution to limit the motion blur. The flexibility in temporal multiplexing to choose different x-ray pulse widths for difference phases of a complex cyclic motion can lead to the better handling of motion blurs, resulting in sharper imaging quality.

PHANTOM EXPERIMENT AND RESULTS

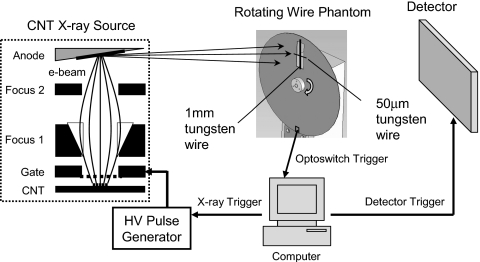
To demonstrate the feasibility of this method, we applied temporal multiplexing to the dynamic x-ray imaging of a mechanical rotating wire phantom with a CNT-based x-ray source and a flat panel x-ray detector, as illustrated in Fig. 2. A CNT x-ray source was chosen because of its flexibility in electronic switching. In principle, any other types of x-ray sources with easy programmable switching mechanisms can be used. The CNT x-ray source was developed in house and its details can be found in our previous works.^{9, 10, 11} For this experiment, the CNT x-ray source was operated at 45 kVp, 0.9 mA peak tube current, and 100 μm effective focal spot size. The x-ray detector is a complementary metal-oxide semiconductor flat-panel sensor with a CsI scintillator plate directly deposited on a photodiode array (model C7940DK-02, Hamamatsu). It has 2k×2k pixels with a nominal pixel size of 50 μm.

Figure 2.

Schematics for the experimental setup to image a rotating wire phantom with temporal multiplexing.

The phantom was made of a 1-mm-thick aluminum disk driven by a stable rotor. The disk has a radius of 115 mm, with a 20×60 mm² rectangular cut-out section near its edge. Mounted radially across this cut-out section is a tungsten wire of 1 mm diameter. Perpendicular to the 1 mm wire at midpoint there is a 50 μm tungsten wire. On the disk’s edge opposite to the 1 mm wire is a 3×5 mm² notch, which serves as the optoswitch trigger point. The phantom was placed close to the detector so that the magnification was nearly one. The phantom was rotating at a speed such that the linear velocities of the 1 mm wire were 6.0 cm∕s (bottom) and 7.5 (top) cm∕s for the part of the wire within the cut-out section. When the wires passed through the detector field of view (FOV), a generic optoswitch coupled below the edge of the disk would generate a transistor-transistor logic pulse, which was used to trigger the x-ray pulse sequences and the composite image acquisitions.

This rotating wire phantom was imaged with seven-phase temporal multiplexing. All seven phases were equally spaced to each other, with the first phase triggered by the optoswitch trigger without delay. Each phase (hence the corresponding x-ray pulse τ) was 10 ms in duration. The delay between two neighboring phases∕pulses was 10 ms. Therefore, the seven phases∕pulses were separated from the optoswitch trigger by 0, 20, 40, 60, 80, 100, and 120 ms, respectively. The multiplexing matrix was the one shown in Fig. 1b. In a single row of the matrix, a 1 in a particular column indicates that a 10 ms x-ray pulse corresponding to that phase is on for that composite frame. Likewise, a 0 indicates a 10 ms x-ray pulse corresponding to that phase is off for a given composite frame. After acquiring the seven composite images over seven motion cycles, demultiplexing was applied on those composite images to recover the seven demultiplexed phase images.

Figure 3a shows the seven composite images. The composite images show a good correlation to the x-ray pulse sequences. As the wires moved across the detector FOV from left to right, four out of seven phases of this motion were captured in a composite image by the corresponding four x-ray pulses; a phase was recorded if and only if the corresponding x-ray pulse for that phase was on for that composite image. By demultiplexing the composite images pixel by pixel, clear images for the seven phases can be extracted and are shown in Fig. 3b.

Figure 3.

(a) Seven composite images acquired over seven motion cycles. (b) Seven demultiplexed phase images from the seven composite images in (a). (c) Seven sequential phase images acquired at the same dose as the demultiplexed images in (b).

To assess the quality of the seven demultiplexed phase images, the same seven phase images were also obtained in the sequential imaging mode. In this mode, each phase image was averaged from four x-ray images that were acquired over four motion cycles at the same phase and the same imaging conditions (kilovolts, milliamperes, detector configuration, and geometry), except that each image was exposed by a single 10 ms x-ray pulse. Thus the doses for the sequential images and the demultiplexed images were same, except that the sequential images took four times longer to obtain. The seven sequential phase images are shown in Fig. 3c. The two sets of images in Figs. 3b, 3c appear to have good phase coregistration, which indicates no loss of temporal resolution.

DISCUSSION AND CONCLUSION

Compared to sequential imaging, temporal multiplexing imaging enables the imaging system to squeeze more x-ray photons within a motion cycle without loss of temporal resolution, thus reducing the imaging time. In general, given a sequential dynamic imaging of an object in cyclic motion where 2N−1 phases are required and each sequential phase image is averaged from N frames∕cycles, a temporal multiplexing of dimension 2N−1 would reduce the total number of motion cycles required for image acquisition by a factor of N without loss of the temporal resolution. This reduction in data collection time becomes significant when N is large.

Like other multiplexing approaches, the temporal multiplexing method may not be able to achieve the full benefit of the increased dose as measured in SNR. SNR in the sequential images in Fig. 3 appears to be better when qualitatively compared to the corresponding multiplexed images. SNR from multiplexing depends on many factors including the selection of multiplexing matrix, and the relative ratio of different types of noises in the imaging system such as photon noise and electronic noise.¹² More detailed SNR analysis will be carried out and its results will be reported in future publications.

To conclude, we have described a general method of reducing the imaging time for dynamic x-ray imaging of an object in cyclic motion by using temporal multiplexing x-ray (TMX) imaging. The method has been tested with the dynamic x-ray imaging of a rotating wire phantom and showed very good results. Compared to sequential imaging, TMX can achieve high temporal resolution of dynamic objects in multiple phases with imaging time significantly reduced. We expect TMX imaging to find applications in both biomedical imaging and industrial nondestructive testings.