Color Tuning in Short Wavelength-Sensitive Human and Mouse Visual Pigments: Ab initio Quantum Mechanics/Molecular Mechanics Studies

Abstract

We have investigated the protonation state and photoabsorption spectrum of Schiff-base (SB) nitrogen bound 11-cis-retinal in human blue and mouse UV cone visual pigments as well as in bovine rhodopsin by hybrid quantum mechanical/molecular mechanical (QM/MM) calculations. We have employed both multireference (MRCISD+Q, MR-SORCI+Q, and MR-DDCI2+Q) and single reference (TD-B3LYP and RI-CC2) QM methods. The calculated ground-state and vertical excitation energies show that UV-sensitive pigments have deprotonated SB nitrogen, while violet-sensitive pigments have protonated SB nitrogen, in agreement with some indirect experimental evidence. A significant blue shift of the absorption maxima of violet-sensitive pigments relative to rhodopsins arises from the increase in bond length alternation of the polyene chain of 11-cis-retinal induced by polarizing fields of these pigments. The main counterion is Glu113 in both violet-sensitive vertebrate pigments and bovine rhodopsin. Neither Glu113 nor the remaining pigment has a significant influence on the first excitation energy of 11-cis-retinal in the UV-sensitive pigments that have deprotonated SB nitrogen. There is no charge transfer between the SB and β-ionone terminals of 11-cis-retinal in the ground and first excited states.

1. Introduction

Visual pigments are seven transmembrane α-helical proteins. Although all visual pigments in their dark states use 11-cis-retinal (see Figure 1) bound covalently to Lys296 as the chromophore, the absorption maximum of 11-cis-retinal in their UV–visible electronic spectra varies in a wide range (350–630 nm).^1,2 Compared with the gas-phase spectrum (610 nm),^3,4 Glu113 counterion (see Figure 1), which is common in all vertebrate visual pigments, has been shown in recent hybrid quantum mechanical/molecular mechanical (QM/MM) studies^5–7 to account for most of the pigment effects on the first absorbing state of 11-cis-retinal in bovine rhodopsin (RH, 500 nm^1,2).

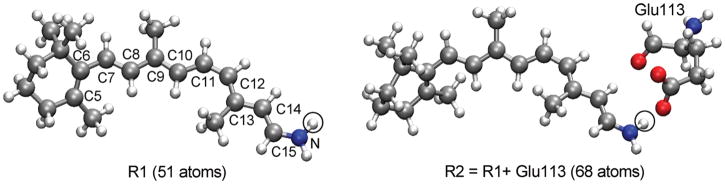
Figure 1.

QM models, R1 and R2, and atom numbering of PSBR. SBR corresponds to removing the circled hydrogen (gas phase) or transferring it to Glu113 carboxylic oxygen.

In short wavelength-sensitive type 1 (SWS1) visual pigments, the absorption maximum of 11-cis-retinal is at ~420 nm (violet) or at ~360 nm (UV).^1,8–11 It is unclear what makes these pigments UV- or violet-sensitive despite some experimental indications; differential intensities of infrared bands of some UV-sensitive SWS1 pigments at the 1100–1500 cm⁻¹ region relative to the E113Q (Glu → Gln) mutants are significantly smaller than those of violet-sensitive ones and RH.^12,13 Hence, the mechanism of color tuning in violet-sensitive pigments should be different from UV-sensitive pigments and E113Q mutants but similar to RH. Furthermore, E113Q mutants of the SWS1 pigments appear always UV-sensitive in absorption spectral studies at neutral pH irrespective of the color sensitivity of the native pigments.^10,14 This arises probably from the lack of residue that donates proton to the retinal at site 113 in the E113Q mutant. Therefore, UV- and violet-sensitive SWS1 pigments should have deprotonated and protonated Schiff-base retinals (SBRs), respectively.^10–14

In this study, we investigate mouse-UV (MUV, 359 nm^9,10) and human-blue (HB, 414 nm^9,10) pigments with QM/MM calculations in order to elucidate the mechanism of color tuning along with the role of retinal protonation in UV- and violet-sensitive SWS1 pigments. Based on the above indirect experimental evidence,^10–14 only IR spectra calculations were performed previously for MUV in the dark state,¹³ and the previous absorption spectra calculations on HB considered only protonated SBR (PSBR).^15–17 The present study allows us to investigate MUV and HB electronic spectra with a consistent methodology and to compare high-level computational results with previous experimental and theoretical findings.

2. Computational Details

2.1. Setup of the Systems

HB and MUV crystal structures are not resolved yet. However, their amino acid sequences are known and 45% identical to that of bovine RH.^9,10 Therefore, we obtained the coordinates of amino acids in MUV with homology modeling¹⁸ by taking the crystal structure of bovine RH (pdb code: 1U19; chain A)¹⁹ as a template. For HB, we took the previous homology-modeled structure (pdb code: 1KPN).²⁰ The missing coordinates of 11-cis-retinal and water molecules in the homology-modeled structures were included by overlapping backbone atoms of the modeled structures with those of bovine RH (pdb code: 1U19). The number of water molecules included in HB and MUV is 16 and 14, respectively.

In the following, we will follow the amino acid numbering system of bovine RH. When protonating the resulting solvated homology-modeled structures, standard protonation states were used for all amino acids, with the following exceptions. Met1 was acetylated and C terminal was used for Asn348 (HB) and His348 (MUV). Disulfide bond-forming cysteines were not protonated. All histidines were singly protonated, consistent with their local environments.

It has been shown recently that Glu181 and its protonation state do not have any significant effect on the calculated absorption spectrum of bovine RH.^6,21,22 However, calculated ground- and excited-state dipole moments of 11-cis-retinal in bovine RH are only consistent with the experimental value when Glu181 is protonated (neutralized).²² In addition, our PROPKA²³ pK_a calculations on the homology-modeled structures of HB and MUV as well as on RH suggest protonated Glu181. Therefore, we assign Glu181 to be protonated for all pigments.

It was also suggested²⁴ on the previous homology-modeled structures by comparing the calculated ground-state energies of the structures with deprotonated and protonated Glu181 that Glu181 is deprotonated with deprotonated SBR (concluded on MUV), while it is protonated with PSBR. However, our calculations on MUV show that the structure with protonated Glu181 has lower energy when no restraint is applied during geometry optimizations. The same authors already pointed out in their previous study¹³ for the same homology-modeled structure of MUV²⁴ that they could not align Glu181 side chain properly with partial geometry optimizations and called readers to caution on their structure around Glu181. Therefore, it is apparent that this previous study²⁴ has a computational artifact for the protonation state of Glu181 as a result of constrained geometry optimizations.

In a recent CASPT2/AMBER study on bovine RH,²⁵ the calculated first excitation energy has been found the same as the experimental absorption maximum when Glu181 is deprotonated, while it is 35 nm red-shifted with protonated Glu181. However, earlier studies at the same computational level^26,27 found 20 nm blue-shift relative to experiments when Glu181 is protonated. Thus, the earlier^26,27 and recent²⁵ CASPT2/AMBER studies with protonated Glu181 differ for the first excitation energy by 55 nm, arising probably by the use of different initial X-ray coordinates. Surprisingly, almost all pigment atoms (including the coordinates of Glu113 counterion and Glu181) were fixed during geometry optimizations in these CASPT2/AMBER studies.^25–27 Only the coordinates of PSBR, Lys296, and two water molecules were optimized in these studies.^25–27 Therefore, these CASPT2/AMBER studies seem to suffer from partial geometry optimizations, especially from unbalanced electrostatics due to partially screened side chains. The magnitude of such errors is expected to be different when starting from different X-ray coordinates. The effect of the QM method used in these studies for geometry optimizations (CASSCF)^25–27 will be discussed in the Results section.

2.2. Force Field Calculations

AMBER96 all-atom force field and TIP3P water model,²⁸ implemented in the Gaussian03 program package,²⁹ were used for both pure MM and hybrid (QM/MM) calculations. All available force field parameters and charges were taken from the AMBER library.^28,29 The missing charges and parameters in the AMBER library for the lysine (Lys296) bound protonated and deprotonated 11-cis-retinals were taken from our previous study (see the Supporting Information of ref 6). First of all, the positions of only water molecules in the homology-modeled HB and MUV structures were optimized at the AMBER level. Then, the positions of backbone C_α atoms were kept fixed while optimizing the coordinates of all the rest to remove close contacts due to flexible side chains. Finally, the entire systems were fully optimized at the AMBER level. The resulting structures were further optimized fully at the QM/MM level in the ONIOM scheme as described below. The seven-transmembrane α-helices were well conserved during these geometry optimizations.

2.3. QM/MM Calculations

In the present ONIOM(QM/MM) calculations,^6,30–32 we evaluated electrostatic interactions between QM and MM layers both classically at the MM level (mechanical embedding, ME) and quantum mechanically (electronic embedding, EE).^6,30–33 ONIOM-EE geometry optimizations were performed by using ESP charges of the QM region updated at each optimization step, while fixed AMBER charges were used during ONIOM-ME geometry optimizations. As the QM method, the B3LYP/6-31G* method^34,35 was employed for geometry optimizations. The bonds cut at the QM/MM boundaries were saturated by hydrogen link atoms.³³

Two QM models (R1 and R2; see Figure 1) were mainly employed in QM/MM calculations. R1 model includes the full retinal along with covalently bound N (NH) moiety of Lys296 for deprotonated (protonated) SB linkage. R2 model includes the R1 model and full Glu113. Either 11-cis-retinal or Glu113 is protonated in the R2 model, corresponding to PSBR or SBR, respectively. In this study, the R1 model was used unless stated otherwise. To assess the effects of pigment environments, we compared the QM/MM results with the gas-phase single-point QM results on the bare R1 and R2 models at the QM/MM geometries (QM-none).

Vertical excitation energies were calculated at the fully optimized ONIOM(B3LYP/AMBER)-EE geometries by using three complete active space self-consistent field³⁶ (CASSCF)-based multireference configuration interaction (MRCI) methods (see below). The active space used in our standard 3-root MR calculations is comprised of six electrons in six orbitals. In this study, only the active space of the cost-effective 6-root DDCI2+Q calculations (see below) comprises 12 electrons in 12 orbitals. The number of roots has no influence on the calculated excitation energies of PSBR and SBR.⁷ In our previous study,⁷ we have also shown for MRCI+Q methods that the error introduced by the use of 6/6 cost-effective active space is only ~15 nm (~0.06 eV) red-shift and ~30 nm (~0.38 eV) blue-shift for PSBR and SBR, respectively. In addition to our previous study,⁷ we here further discuss the accuracy of time dependent (TD)-B3LYP³⁷ reference to MRCI results. TD-B3LYP has already been shown reliable for the effects individual amino acids on excitation energies.⁷ For HB, we also used the approximate coupled cluster singles doubles method with the resolution of the identity approach (RI-CC2)³⁸ by using TURBOMOLE program package³⁹ to test the accuracy of single reference correlated methods on the excitation energies.

The simplest MRCI method applied is the difference dedicated DDCI2 method that includes double excitations involving either two particles in the inactive empty orbitals or two holes in the inactive occupied orbitals in addition to all single excitations.^40–42 This method with +Q correction⁴³ has a blue shift error of ~65 nm for the first vertical excitation energy of PSBR and SBR.⁷ However, it reproduces spectral shifts very well.⁷ Therefore, this method was only used to investigate the effect of Glu113 counterion rather than to predict absolute values of the excitation energies. As a more extensive MRCI method, spectroscopy oriented CI (SORCI)⁴¹ was performed. SORCI can be considered as an individually selecting approximation to the iterative DDCI3 method,⁴⁰ which includes active-space configurations only with two holes and one particle or two particles and one hole, in addition to DDCI2 excitations. The most straightforward MRCI method applied here includes all single and double excitations (MRCISD).^44,45 The effects of excitations higher than doubles were included in all the MRCI excitation energies with the MR-Davidson +Q corrections.⁴³ Computational efficiencies of the MRCI calculations were increased with previously defined T_nat (only for SORCI), T_pre and T_sel thresholds set to 10⁻⁶, 10⁻⁴, and 10⁻⁶ E_h, respectively.^{7,41,42,46,47} Core orbitals with energies of less than −4 E_h were frozen. A level shift of 0.4 E_h was applied in all perturbative treatments.

All B3LYP and MRCI calculations were performed with the 6-31G* basis set.⁴⁸ This basis set was previously shown⁷ in DDCI2+Q calculations to give the first excitation energy of PSBR (SBR) blue-shifted only by about 5 (15) nm compared with the results of a larger and more flexible ANO basis set. Auxiliary basis set SV/C⁴⁹ was used to speed-up MR calculations.

All geometry optimizations and TD-B3LYP excitation energies were performed with a development version of Gaussian03 program package,²⁹ whereas all MR calculations were carried out with ORCA 2.6.19 program package.⁵⁰ Further details of our computational strategy are as given in refs ⁶ and ⁷. All calculated geometry parameters and excitation energies of bovine RH given in this study were taken from refs ⁶ and ⁷ for comparing them with the results on HB and MUV.

3. Results

3.1. Geometry of the 11-cis-Retinal

Incorporation of dynamical correlation in the QM method is essential to obtain proper geometries for retinal excitation energy calculations. For example, CASSCF method (incorporating only static correlation) overestimates the single/double bond alternation (BLA) of the polyene chain of the retinal.² Therefore, the first excitation energy calculated at the CASSCF geometries is artificially red-shifted up to 100 nm.^7,47 MRCI ground-state energies of retinal at B3LYP geometry (incorporating dynamical correlation) are significantly lower than those at CASSCF geometry, indicating that B3LYP geometries are more balanced than CASSCF geometries.⁷ Moreover, B3LYP geometries are almost the same as more sophisticated MP2 and CASPT2 geometries on some small or full PSBR models.^2,51–54 Therefore, we optimized all structures with the cost-effective B3LYP method. The calculated bond and dihedral angles along the polyene chain of SBR and PSBR in HB and MUV are very similar to those in RH.⁶ Hence, we only discuss BLA in the following.

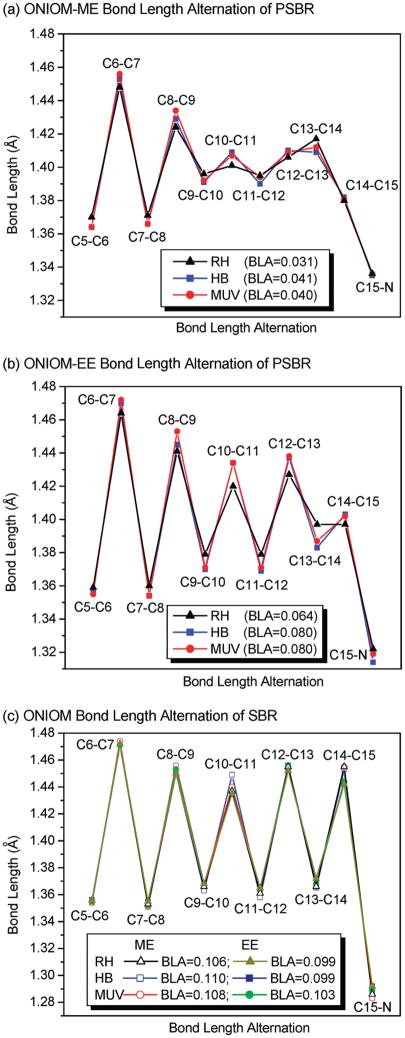
When the electrostatic interactions between QM and MM layers are calculated at the MM level, that is, the ONIOM-ME scheme, polyene chain of PSBR in proteins has a similar BLA pattern as in the gas phase (see Figure 2a). When the effects of MM charges are included in the QM Hamiltonian, that is, the ONIOM-EE scheme, polyene chain of PSBR presents a more pronounced BLA pattern (see Figure 2b). This suggests that the weakening and strengthening of single and double bonds in the pigment environments, respectively, arise mainly from the polarization of the QM wave function. As a result of this polarization effect, the average BLA (or in short BLA) of the C5-N moiety of PSBR, defined as the average single bond distance minus the average double bond distance (in Å), increases twice. These trends obtained on HB and MUV are the same as those obtained previously on bovine RH⁶ (see also Figure 2). However, the BLA pattern of PSBR in HB and MUV are more pronounced than that in RH; in the polarizing field of pigment environments, the BLA of PSBR in HB and MUV is 0.02 Å larger than that in RH. This BLA difference is expected to affect excitation energies significantly (see below).^6,46

Figure 2.

Calculated bond length alternation along the polyene chain of the SB and PSB 11-cis-retinal chromophore for RH, HB, and MUV. Average BLA is also given.

The difference between ONIOM-ME and ONIOM-EE geometries is related to the positive charge density distribution of PSBR (+1) along its C5-N moiety. Because of no net charge (see Figure 2c), SBR geometry is almost identical in the gas phase and pigment environments, irrespective of the ONIOM embedding scheme (ME and EE).

3.2. Nature of S₀ and S₁ States

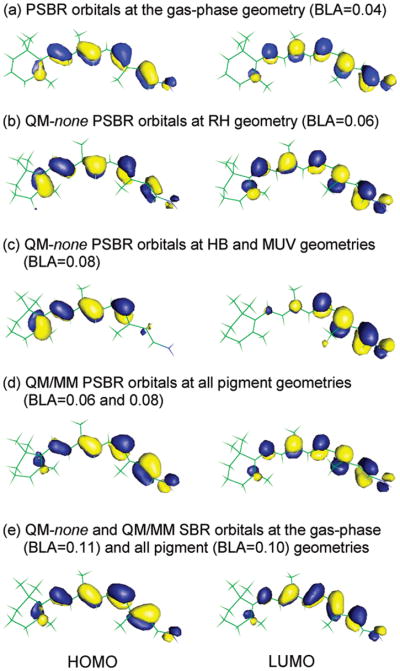
CASSCF and MRCI (DDCI2+Q, SORCI+Q, and MRCISD+Q) charge densities of S₀ and S₁ states are similar. Therefore, we will not differentiate state densities with the method name in the following. Since the first singlet vertical excitation (S₀ → S₁) is dominated by the HOMO to LUMO transition, we will also discuss the nature of HOMO and LUMO obtained at CASSCF and CASSCF/MM levels. All CASSCF/MM orbitals and state densities were calculated with the EE scheme. In our previous study,⁷ the calculated nature of the orbitals and state densities appeared irrespective of the active space size used, that is, 6/6 versus 12/12.

At B3LYP geometries, about half of the positive charge of PSBR in S₀ and S₁ states is in general located on the C15-NH₂ moiety, whereas the remaining charge is located at the carbon atoms of the polyene chain adjacent to methyl groups. Thus, the β-ionone ring has almost no net charge. However, at unbalanced CASSCF geometries with significantly overestimated BLA, about half of the positive charge is transferred to β-ionone ring upon S₁ excitation.⁷

At B3LYP geometries with or without pigment environment (see Figure 3), there is no significant charge transfer between the SB and β-ionone ring terminals of PSBR in HOMO and LUMO except for the HB and MUV geometries in the absence of pigment environments. At these geometries (Figure 3c), the electron density of PSBR is accumulated around the β-ionone ring in HOMO and around the SB terminal in LUMO because polarizing fields of these pigments induce BLA increase. However, this does not mean that the S₀ and S₁ states are as of charge transfer type. MR wave functions do not show any such charge transfer for the S₀ and S₁ states at any pigment geometries, irrespective of the presence or absence of pigment environments. Similar to PSBR (+1 charge), there is no intramolecular charge transfer in HOMO and LUMO as well as S₀ and S₁ states of neutral SBR (see Figure 3e). For both PSBR and SBR, B3LYP and TD-B3LYP methods properly describe HOMO and LUMO orbitals and S₀ and S₁ state densities, respectively, as in the MR methods.

Figure 3.

HOMO and LUMO of the SB and PSB 11-cis-retinals calculated at the CASSCF level in the gas phase (labeled as QM-none) and at the CASSCF/AMBER level with RH, HB, and MUV pigment environments. Average BLA is given in parentheses.

3.3. Stability of Protonation States of Schiff-Base Nitrogen

To investigate relative stabilities of PSBR and SBR, it is necessary to include Glu113 in the QM part, leading to the R2 model (see Figure 1). Ground-state ONIOM-EE energies with the R2 QM model were calculated at the ONIOM-EE geometries obtained with the R1 QM model. Because MRCI calculations require a very large active space to follow a continuous energy path for migrating a proton between the retinal SB nitrogen and the Glu113 carboxylic oxygen (see Figure 1), we only used the cost-effective B3LYP as the QM method in this section.

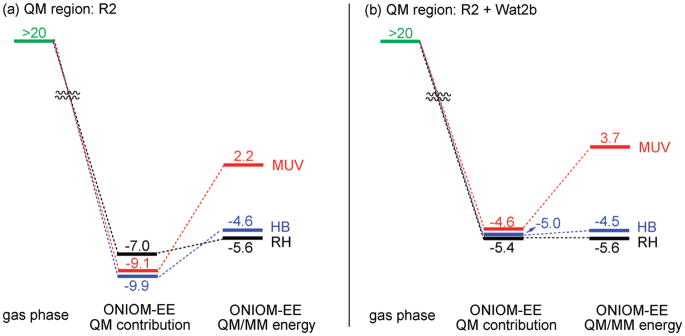
The bare 11-cis-retinal is protonated at the SB terminal (PSBR) in the gas phase.^3,4 As noted previously,^55,56 when a Glu counterion is introduced in the gas phase near the SB terminal (R2 model), PSBR becomes unstable and the proton transfers to Glu. This can be rationalized by the increased BLA induced by electrostatic and polarizing fields of the Glu counterion. Increased BLA leads to the accumulation of a more positive charge around the SB terminal in the gas phase. Therefore, the Coulombic repulsion between the increased positive charge of the SB nitrogen and its proton causes deprotonation of the retinal. At all ONIOM-ME geometries (RH, HB, and MUV), optimized with the R1 QM model, the isolated R2 with PSBR is ~20 kcal/mol above the isolated R2 with SBR (see the left side of energy diagram in Figure 4a). Therefore, if we converged to PSBR in the gas phase, it would be more than 20 kcal/mol (the value at ONIOM-ME protein geometry) but less than 87 kcal/mol (the value at infinite separation) above SBR. Here it should be noted that ONIOM-ME calculations always converge artificially to SBR with the R2 QM model, as in the gas phase, because these calculations ignore polarization of the retinal by the pigment environments (see below).

Figure 4.

B3LYP and B3LYP/MM ground-state energies (kcal/mol) of PSBR relative to SBR [QM model: (a) R2 and (b) R2 + Wat2b] in the gas phase and in RH, HB, and MUV pigment environments at the ONIOM-EE structures optimized with R1.

When the effects of both electrostatic and polarization are included in the geometries (ONIOM-EE geometries), the energy separation of isolated R2 with PSBR and SBR reduces by ~4 kcal/mol (to ~16 kcal/mol), favoring still SBR. However, in the presence of these two effects in the QM wave function, PSBR is more stable than SBR (~7–9 kcal/mol in each pigment environment; see QM contribution of ONIOM-EE energy in Figure 4a). This is a consequence of localization of the positive charge more on the SB nitrogen in the pigment environments. As seen in Figure 4a, the MM contributions to the polarized R2 regions destabilize the pigment with PSBR. In bovine RH and HB, this destabilization arises nearly completely from the electrostatic of a water molecule (Wat2b) H-bonded to the carboxylic OE2 atom of Glu113 as realized when Wat2b is included in the QM model (compare Figure 4a and 4b, and see Figure 5). In MUV, Wat2b is not the sole factor explaining the difference in the QM/MM energy and its QM contribution. The extent of the MM contribution to the QM/MM energies determines the stability order of a given pigment with PSBR and SBR. This contribution is large enough in only MUV to make the pigment with SBR more stable (see Figure 4), arising from structural changes accompanied with the change of protonation state of retinal.

Figure 5.

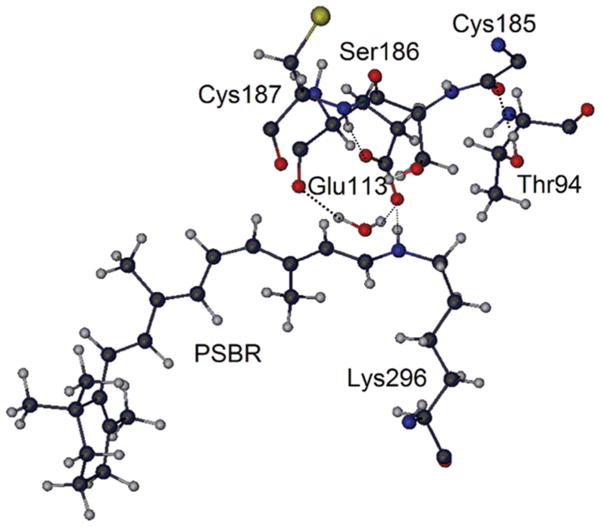
Some important amino acid sites around SB nitrogen. Coordinates taken from RH.

Although it has been discussed which amino acids stabilize PSBR in bovine RH for some gas-phase model systems at HF and density functional levels, different conclusions have been reached.^55,56 In one such study,⁵⁶ Ser186 and Cys187 (the latter H-bonded to carboxylic OE1 atom of Glu113; see Figure 5) do not have any significant influence on the stability of PSBR, whereas Thr94 and Wat2b stabilize PSBR by around 5 and 3 kcal/mol (total of 8 kcal/mol), respectively. In this previous gas-phase study,⁵⁶ Thr94 forms a H-bond with the carboxylic OE2 atom of Glu113 (as in low resolution X-ray structures of bovine RH⁵⁷) during molecular dynamics (MD) simulations even if the initial structure of MD contains no such H-bond (as in high-resolution X-ray structures of bovine RH^19,58). Actually, this gas-phase model study⁵⁶ ignores Cys185, whose C terminal is H-bonded to the OH moiety of Thr94 in high-resolution X-ray structures.^19,57 In the presence of Cys185 and other amino acids around Thr94, side chain rotation of Thr94 to form a H-bond with Glu113 seems unlikely. At some low resolutions, crystallographic assignments of groups that have the same number of electrons (in the case of Thr: OH and CH₃ side chains) may be erroneous.⁵⁹ The early low-resolution X-ray structures⁵⁷ suffer possibly from such artificial assignments. In the absence of the H-bond of Thr94 with Glu113, another previous gas-phase⁵⁵ and our B3LYP/MM calculations with charges turned off find a small contribution of 2 kcal/mol from Thr94 to the stability of PSBR. Therefore, the effect of Thr94 on the stability of PSBR in RH is overstated in one of the previous studies.⁵⁴ Site 94 is occupied by a Val in HB and MUV, which has little effect (less than 1 kcal/mol) on the stability of PSBR.

In B3LYP/MM (QM model = R2) calculations, by turning off the charges of the amino acid whose effect is investigated, Wat2b appears to stabilize PSBR by ~8 kcal/mol in all pigments. Because the Wat2b effect is overestimated with the R2 model by ~4 kcal/mol (see Figure 4), its actual effect should be ~4 kcal/mol. In HB, Ser90 forms a H-bond with carboxylic OE2 atom of Glu113 (see Figure 5) and stabilizes PSBR by 3 kcal/mol. Ser186 and Cys187 (the latter H-bonded to carboxylic OE1 atom of Glu113) are conserved in RH, HB, and MUV. Each of them stabilizes PSBR by ~3 kcal/mol in all pigments, in agreement with a previous gas-phase model study on bovine RH.⁵² Each of the remaining amino acids around the 4 Å vicinity of retinal and Glu113 has an effect of less than ±1 kcal/mol on the stability of PSBR. Therefore, one can conclude that the largest contributions come mostly from the groups near the carboxylic oxygens of Glu113.

The effect of individual contributions to the stability of PSBR is almost perfectly additive in the present QM/MM calculations, in agreement with the previous gas-phase study on bovine RH.⁵⁵ The sum of the effects of Wat2b, Ser186, Cys187, Thr94 (only in RH), and Ser90 (only in HB) on PSBR stability with R2 is ~16 kcal/mol. Because this effect is larger than the value in the pigment environments (see Figure 4), the remaining protein environment must overall destabilize PSBR.

3.4. Vertical Excitation Energies

In this section, we discuss the calculated S₁ vertical excitation energy of RH, HB, and MUV (see Table 1) for both protonation states of retinal at ONIOM-EE geometries obtained with R1 QM model. The QM/MM excitation energies were calculated only with the EE scheme.

TABLE 1.

Calculated S₁ Vertical Excitation Energy (nm) of RH, HB, and MUV with PSBR and SBR at ONIOM-EE Geometries in the Gas Phase (QM-none) and in the Presence of Pigment Environments (QM/MM) with QM Model R1 and 6-31G* Basis Set^a

pigment (experiment)	retinal protonation	method	TD-B3LYP	SORCI+Q(6/6)b	MRCISD+Q(6/6)b
RH (500 nm)	PSBR	QM-none	560	616	626
		QM/MM	503	495	499
	SBR	QM-none	408	328	319
		QM/MM	429	336	324
HB (414 nm)	PSBR	QM-none	634	556	546
		QM/MM	488	424	448
	SBR	QM-none	382	304	295
		QM/MM	402	318	304
MUV (359 nm)	PSBR	QM-none	596	550	541
		QM/MM	469	430	447
	SBR	QM-none	396	328	322
		QM/MM	409	335	321

^aS₁ and S₂ vertical excitation energies of SBR are very close to each other. Only the absorbing state of SBR is given for relating the calculations with the experiments. The calculated oscillator strengths of the first absorbing state are 1.2–2.0 for both PSBR and SBR.

^bEstimated errors in SORCI+Q and MRCISD+Q vertical S₁ excitation energies with the present computational settings (see ref 7) are 15 nm red shift for PSBR and 50 nm blue shift for SBR.

As shown previously,⁷ the first SORCI+Q and MRCISD+Q vertical excitation energies have a red-shift error of only 15 nm for PSBR and a blue-shift error of 50 nm for SBR with the present computational settings. Irrespective of the inclusion of these error estimates, the S₁ MRCI/MM (including both SORCI+Q/MM and MRCISD+Q/MM) excitation energies are consistent with the experiments only if the retinal in RH and HB is protonated and the retinal in MUV is deprotonated (see Table 1), in agreement with the QM/MM ground-state energetics.

The S₁ MRCI excitation energy of PSBR blue-shifts going from RH to HB and MUV by ~60–70 nm in both gas phase (at protein geometry: QM-none) and in the pigment environment (QM/MM). Therefore, this shift must solely arise from the structural changes in the PSBR geometry (i.e., BLA increase of 0.02 Å along the polyene chain) induced by electrostatic and polarization effects of the pigment environments. It has already been shown previously that the first vertical excitation energies of retinal proteins correlate with the BLA.^6,46 The corresponding experimental^9,10 blue shift (86 nm) going from RH (500 nm) to HB (414 nm) agrees very well with the computational MRCI results (~60–70 nm).

TD-B3LYP estimates ~70 nm red shift going from RH to HB geometry in the gas phase contrary to the blue shift of ~60–70 nm in MRCI calculations discussed above. The corresponding blue shift in protein with TD-B3LYP/MM is also underestimated by ~70 nm. Therefore, TD-B3LYP should not be used with R1 in the gas phase. However, previous calculations have been shown that it can be used in QM/MM calculations to estimate the effects of amino acids on the excitation energies for a given pigment.^6,7 The use of the R2 model corrects TD-B3LYP excitation energies significantly.⁷ Interestingly, the S₁ SACCI/MM excitation energies with R1 (496 nm) and R2 (435 nm) QM models¹⁶ are very similar to the corresponding TD-B3LYP/MM energies (488 and 453 nm).

The difference in the gas phase (MRCI) and pigment (MRCI/MM) S₁ excitation energies of all the pigments with PSBR is ~120 nm (see Table 1). It has been shown on bovine RH that this pigment effect comes almost solely from Glu113 at CASPT2(12/12)⁵ and DDCI2+Q(12/12)⁷ levels when using B3LYP geometries. Although the pigment effect is also equal to the effect of Glu113 at TD-B3LYP level for bovine RH,⁶ TD-B3LYP should not be used to predict its amount because the reference S₁ excitation energy of R1 in the gas phase is misleading (see above).

CASPT2/MM calculations at CASSCF geometries suggest for bovine RH that the effect of Glu113 is counteracted by the remaining protein partially or fully.^25–27 First of all, MRCI ground-state energies of PSBR are significantly lower at B3LYP geometries than at CASSCF geometries.⁷ Second, PSBR absorbs at around 600 nm in both gas-phase experiments^3,4 and calculations (SORCI+Q,⁷ MRCISD+Q,⁷ and CASPT2⁵) at B3LYP geometries. However, the S₁ energy of PSBR is calculated ~530 nm at the above computational levels at the gas-phase CASSCF geometries.^7,47,60 Similarly, PSBR absorption in the presence of Glu113 is at ~500^5,7 and ~390^25–27 nm at B3LYP and CASSCF geometries obtained in the pigment environment of bovine RH, respectively. Therefore, the S₁ excitation energy is significantly blue-shifted at CASSCF geometries (~100 nm) compared with experiments and calculations at more-balanced B3LYP geometries. The S₁ energy of PSBR is corrected significantly by the electrostatic and polarizing fields of pigment environments and calculated for bovine RH to be ~500 nm at both CASSCF and B3LYP geometries, in agreement with experiments.^5,7,25–27 Therefore, the mechanisms regarding the effect of Glu113 and the remaining pigment proposed based on CASSCF geometries are apparently artificial. Below we further investigate the Glu113 effect in HB by using B3LYP geometries.

Although the inclusion of Glu113 in the QM model does not affect the S₁ QM/MM excitation energy in bovine RH,^6,7 it blue-shifts the S₁ excitation energy of HB by 35 nm at the TD-B3LYP/MM level, including 8 nm blue-shift effect of geometry optimization with Glu113 in the QM model (R2). The present DDCI2+Q(12/12)/MM calculations find a similar effect of 29 nm (with R1, 378 nm → with R2, 349 nm), whereas the previous SACCI/MM calculations¹⁶ find a larger effect of 61 nm (with R1, 496 nm → with R2-like model, 435 nm). The QM effect of Glu113 arises probably from the fact that Glu113 in HB has more H-bonding partners than that in RH. Therefore, they should have larger electrostatic and polarization effects in HB. DDCI2+Q-none excitation energies of HB with R1 (524 nm) and R2 (351 nm) differ by 173 nm. The S₁ DDCI2+Q/MM excitation energy with the R2 QM model (349 nm) is almost the same as the gas-phase DDCI2+Q-none energy of R2 (351 nm). Therefore, the net pigment effect of HB on the S₁ excitation energy is the result of Glu113, as in the bovine RH.⁷ However, it blue-shifts the S₁ excitation energy by ~30 nm more in HB than in RH. The S₁ excitation energy of SBR is nearly independent of the inclusion of Glu113 in the QM model and of the presence of pigment environments at given geometries. Therefore, the S₁ excitation energy of MUV with SBR in its ground state is not affected much by the presence of Glu113.

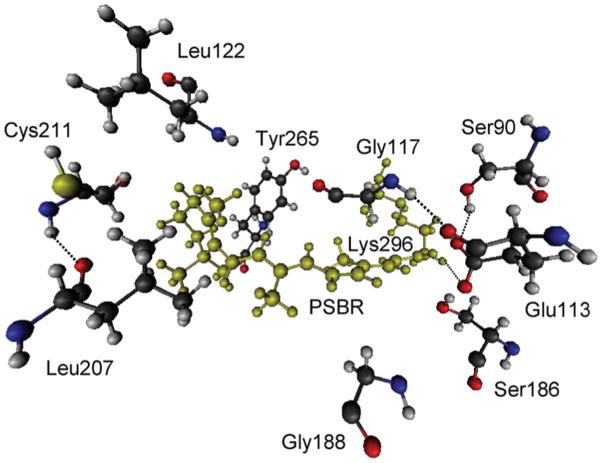
Although the inclusion of environmental amino acids in the QM model does not affect the calculated S₁ excitation energy much in bovine RH,⁶ almost all amino acids within 4 Å of retinal and Glu113 in HB affect the S₁ excitation energy when we include them one by one in the QM model. Such single-point QM/MM excitation energy calculations with large QM regions were performed only with TD-B3LYP. The inclusion of Wat2b in the QM model does not affect the S₁ excitation energy. When Ser90 or Ser186 (both H-bonded to Glu113) is singly included along with Glu113, each serine blue-shifts the S₁ excitation energy by ~20 nm. They together, however, blue-shift the S₁ excitation energy by 20 nm (not 40 nm). When any of Gly117, Leu122, Gly188, Leu207, Cys211, and Tyr265 amino acids (see Figure 6) is introduced to the large R2 + Ser90 + Ser186 QM region, the effects of the remaining amino acids within 4 Å of retinal and Glu113 disappear if they are smaller than the effect of the selected amino acid among those six. Because the effect of any of the remaining amino acids is not larger than the effect of Gly117 or Gly188, they do not contribute to the overall polarization effect of the pigment environment in HB. These six specific amino acids together red-shift the S₁ excitation energy by 86 nm. Their single red-shift effects are Gly117, 20 nm; Leu122, 9 nm; Gly188, 25 nm; Leu207, 11 nm; Cys211, 7 nm; Tyr265, 9 nm (total of 83 nm).

Figure 6.

Amino acids that show strong polarization effect on the S₁ excitation energy of HB. PSBR and Lys296 bound covalently to each other are shown in green.

To sum up these TD-B3LYP/MM polarization contributions, Gly117, Leu122, Gly188, Leu207, Cys211, and Tyr265 red-shift the S₁ excitation energy of HB by 86 nm; Ser90 and Ser186 blue-shift it together by 20 nm; the blue-shift effect of Glu113 is 35 nm. The overall effect of the environmental polarization in HB is, thus, a red shift of 31 nm at B3LYP/MM level. There is already an expected red-shift error of 15 nm in the S₁ MRCI excitation energies with the present settings.⁷ Hence, the bare S₁ MRCI/MM excitation energies calculated with the R1 QM model (see Table 1) appear already appropriate enough without applying any correction.

Whereas the ESP charge distribution around the SB nitrogen indicates that Tyr268 in HB with PSBR blue-shifts the S₁ excitation energy significantly in a previous SACCI/MM study,¹⁶ it does not have any effect at the HF and CIS levels.¹⁵ The present S₁ TD-B3LYP/MM excitation energy is not affected much when we turn off the charge of this amino acid (blue shift of 2 nm) or include it in the QM region (red shift of 6 nm, which disappear including Tyr268 in the QM region with any of the above six important amino acids). Therefore, our calculations support the previous HF and CIS results for the role of Tyr268.

Recently, it has been shown that RI-CC2 method estimates the S₁ vertical excitation energy of retinal in vacuo very well when a large basis set (def2-TZVPP) is used.⁵¹ To probe if this method reacts properly to the electrostatic and polarizing fields of the pigment environments, we calculate the S₁ RI-CC2 vertical excitation energies of PSBR (R1) in HB at the QM-none and QM/MM levels. For these calculations, we switch from 6-31G* and SV/C to def2-TZVPP basis set because CC2 singlet excitation energies are mostly not converged with small basis sets.⁶¹ The S₁ QM-none and QM/MM excitation energies of PSBR in HB with RI-CC2 (578 and 427 nm) are consistent with the SORCI+Q (556 and 424 nm) and MRCISD+Q (546 and 448 nm) energies. Therefore, the RI-CC2 method can also be used in calculating the S₁ excitation energy of retinal proteins, although it is a little computationally demanding because it requires larger basis sets.

4. Discussion and Conclusions

We have investigated the protonation state of the SB nitrogen of 11-cis-retinal in bovine RH, HB, and MUV as well as the absorption spectra of these pigments by QM/MM calculations. Both multireference (MRCISD+Q, SORCI+Q and DDCI2+Q) and single reference (TD-B3LYP and RI-CC2) QM methods were employed in the QM/MM calculations.

The S₁ SORCI+Q/MM and MRCISD+Q/MM vertical excitation energies are only consistent with the experiments when RH and HB have PSBR, while MUV has SBR, in agreement with the calculated B3LYP/MM ground-state energetics and indirect experimental conclusions.^10–14 Therefore, UV (~360 nm) and violet (~420 nm) sensitivities of the SWS1 pigments arise from the use of SBR and PSBR as the chromophore, respectively.

The most significant individual contributions to the stability of PSBR come from the amino acids around Glu113. However, the overall effect of the remaining pigment environments is still large and against the stability of PSBR.

Although both RH (500 nm) and HB (414 nm) have PSBR, the absorption maximum of HB is blue-shifted by 86 nm. The present MRCI and MRCI/MM calculations show that this blue-shift comes from an increase in BLA of the polyene chain of the retinal induced by the polarizing field of the pigment environment of HB. When Glu113 is included in the QM model, the S₁ DDCI2+Q vertical excitation energy of PSBR in RH or HB is unchanged with and without the remaining pigment environment. Therefore, the main counterion in color tuning is Glu113 in both RH and HB.

The overall effect of environmental polarization on the S₁ excitation energy of R1 in HB is a blue shift of 35 nm at TD-B3LYP/MM level. Because this effect is around the estimated error of our MRCI results with R1 (~15 nm), the cost-effective MRCI/MM excitation energies calculated with the R1 region are considered to be reliable. Because SBR excitation energies are not very sensitive to the pigment environments, MUV with SBR in its ground state has no significant polarization effect on the S₁ excitation energy.

In summary, the present calculations enhance significantly our understanding on spectral tuning mechanisms in retinal proteins by exploring the role of different pigments not only on the excitation energies but also on the stability of retinal-Glu system.