Physical Binding Pocket Induction for Affinity Prediction

Abstract

Computational methods for predicting ligand affinity where no protein structure is known generally take the form of regression analysis based on molecular features that have only a tangential relationship to a protein/ligand binding event. Such methods have limited utility when structural variation moves beyond congeneric series. We present a novel approach, based on the multiple-instance learning method of Compass, where a physical model of a binding site is induced from ligands and their corresponding activity data. The model consists of molecular fragments that can account for multiple positions of literal protein residues. We demonstrate the method on 5HT1a ligands by training on a series with limited scaffold variation and testing on numerous ligands with variant scaffolds. Predictive error was between 0.5 and 1.0 log units (0.7–1.4 kcal/mol), with statistically significant rank correlations. Accurate activity predictions of novel ligands were demonstrated using a validation approach where a small number of ligands of limited structural variation known at a fixed time point were used to make predictions on a blind test set of widely varying molecules, some discovered at a much later time-point.

Introduction

Small molecule activity prediction for the purpose of lead optimization in drug discovery remains an important and challenging problem. Physics-based approaches for affinity prediction exist in cases where a reliable, high-resolution structure of the protein target is available. While there have been some encouraging reports of success (1), the problem remains unsolved, with prediction methods suffering from a lack of accuracy and high computational cost (2; 3; 4). Also, for large classes of pharmaceutically relevant targets, high-resolution protein structures are only rarely available (e.g. ligand-gated ion channels, membrane transporters, and membrane spanning G-protein coupled receptors). Advances in techniques for protein crystallography have begun to tackle some of these types of protein targets (5), but derivation of such structures is far from routine (6). Increasingly, homology models have become used in place of experimentally derived structures (7).

For these reasons, constructing predictive models of ligand activity based purely on structure activity data is a long-studied problem. It is a classic machine-learning problem, that of model induction from training data, and it not amenable to a direct physics-based approach. A crucial challenge is that one does not know the relevant poses of ligands under study. Either one must make use of an alignment-independent method, where molecular features used for model induction and activity prediction are unrelated to molecular pose, or some approach must be used to identify conformations and alignments of ligands. The 3D QSAR arena is dominated by an approach introduced in the 1980’s: Comparative Molecular Field Analysis (CoMFA) (8). CoMFA employs grid-based field computations on a fixed alignment of ligands to yield features related to the 3D shape and electrostatic character of the ligands. Partial-least-squares is employed to developed a regression model based upon the activities of training ligands. Later approaches introduced in the 1990s included multi-point pharmacophoric modeling (9; 10; 11; 12; 13). Our own work in 3D QSAR yielded an approach that was sensitive to the detailed shape and polarity of molecular surfaces and which constructed models in which ligand pose choice was embedded as part of the learning procedure (14; 15; 16).

Each of these approaches shares a common feature: there is a direct link between the representation of molecular structure and the physical events that govern binding of a ligand to a protein. However, each approach has a distinct limitation. The CoMFA approach relies upon a fixed choice of ligand poses, and the choice is generally made using structural commonality among ligands (e.g. a shared ring system or substructure) as opposed to being driven by the way in which ligand poses fit the model. Alignments in such approaches can be productively driven by docking or molecular similarity (17; 18), but treatment of ligand pose as being model independent is still not ideal. The pharmacophoric approach identifies a set of geometric constraints that are likely to represent necessary conditions for ligand activity, and they can be used to produce ligand poses subject to the constraints. This represents an improvement in the sense that the model can be used to predict the relative poses of ligands in a way that is well-defined and related to activity. But pharmacophoric constraints are generally not sufficient conditions for binding. In particular, variations in the hydrophobic shapes of ligands are not captured well, yet such subtleties can be critical in determining the affinity of an interaction. The Compass approach offered solutions to both the pose problem and the detailed shape problem, but the models themselves were abstract, being similar to neural networks. The models could be physically unrealizable, and this led to difficulties in interpretation and visualization.

One key contribution of the Compass work, also employed here, was an approach to deriving a virtual binding pocket at the same time as the precise relative poses of training ligands were identified. The process iterated between model refinement and pose refinement, where the model itself was used to choose the poses. Compass was the first to make use of this iterative model refinement paradigm (14; 15; 16). A formalization of this early work, termed multiple-instance learning (19), has found applications in many areas of machine learning, and we have also used it in scoring function development for molecular docking (20; 21; 22).

The approach we report here builds upon the Compass approach by constructing physical models of a protein binding site based upon ligand binding data. The result is a binding site composed of molecular fragments that can be treated as a target for molecular docking. The binding site model consists of molecular fragments that can account for multiple positions of protein residues. It is not a literal reconstruction of a single configuration of protein residues. New molecules are docked directly into the binding site, with their highest scoring poses serving as the prediction of binding geometry and the corresponding score being the predicted affinity. In deriving a virtual binding pocket at the same time as we identify the relative poses of ligands, the key analogy is that one can treat a computational model of a binding site as one treats a protein binding pocket. We seek the optimal fit of ligands into the binding site. One begins with a guess as to the initial alignment of ligands, then constructs a model of activity that depends on the ligands’ poses. The model can be thought of as a virtual receptor (technically it need not have a physical manifestation). Next, one seeks poses for each ligand that optimize their interaction with the virtual receptor. Then, the virtual receptor is refined, making use of the new ligand poses, and the process iterates between pose refinement and virtual receptor refinement. As the virtual receptor evolves, the changes in ligand scores due to pose optimization decrease. When the iterative process converges, the final poses of the ligands are optimal with respect to the final virtual receptor. The software implementing the algorithms for pocket construction and ligand activity prediction constitute a new module within the Surflex platform, called Surflex-QMOD (Quantitative Modeling). The virtual binding pockets constructed are called “pocketmols.”

We focused on derivation of a binding site model for the 5HT1a receptor, which was the subject of an earlier Compass study (16). The training ligands consisted of just 20 molecules from two chemical series with pK_d spanning 6.0 to 10.0, an activity range of practical interest in lead optimization. One binding site model (pocketmol) induced from these data was tested on three different sets of new ligands: 1) the set of 35 holdout molecules from the original study; 2) a set of 32 highly structurally divergent 5HT1a ligands; and 3) a set of 23 beta adrenergic drugs. We also compared the pocketmol to a model of 5HT1a derived using a recently solved structure of the human beta-2 adrenergic receptor as a template.

The structural variation among the 35 holdout ligands was limited but representative of typical medicinal chemistry lead optimization. The prediction task was subtle, reflecting significant changes in activity based on one or two-atom modifications or variations in scaffold chirality. The 32 structurally diverse ligands were curated from the G-Protein-Coupled Receptor Database (GPCRDB) (23) and PubChem (24) by an individual with no role in model derivation. The mean error of prediction was between 0.5 and 1.0 log units (0.7–1.4 kcal/mol), and highly significant rank correlations were obtained with both of these sets. Given two test ligands whose experimentally determined pK_d was one log unit or more apart, predictions of relative rank were correct 75–85% of the time. With test ligand pairs two or more logs different in activity, predicted ranks were correct nearly 95% of the time. The test of beta adrenergic drugs for prediction of off-target affinity for the 5HT1a receptor correctly identified pindolol and several others as having pharmacologically important serotonergic effects. The ligand-induced binding site model showed important similarities to the modeled receptor structure, which provides a degree of validation and also suggests that hybrid approaches combining formal machine learning methods with protein structure modeling may be fruitful.

Methods and Data

The present study makes use of four groups of molecules used for training, validating, and testing learned models of activity for the 5HT1a receptor. In machine-learning studies, where data are used for model induction, care must be taken in order to avoid information leakage from training procedures into testing procedures. Here, we employed a training set of molecules along with a holdout set to assess the effects of training procedures. Then, a completely independent blind prediction was made on two new groups of molecules. The following describes the molecular data sets, computational methods, detailed computational procedures, and quantification of performance.

Molecular Data Sets

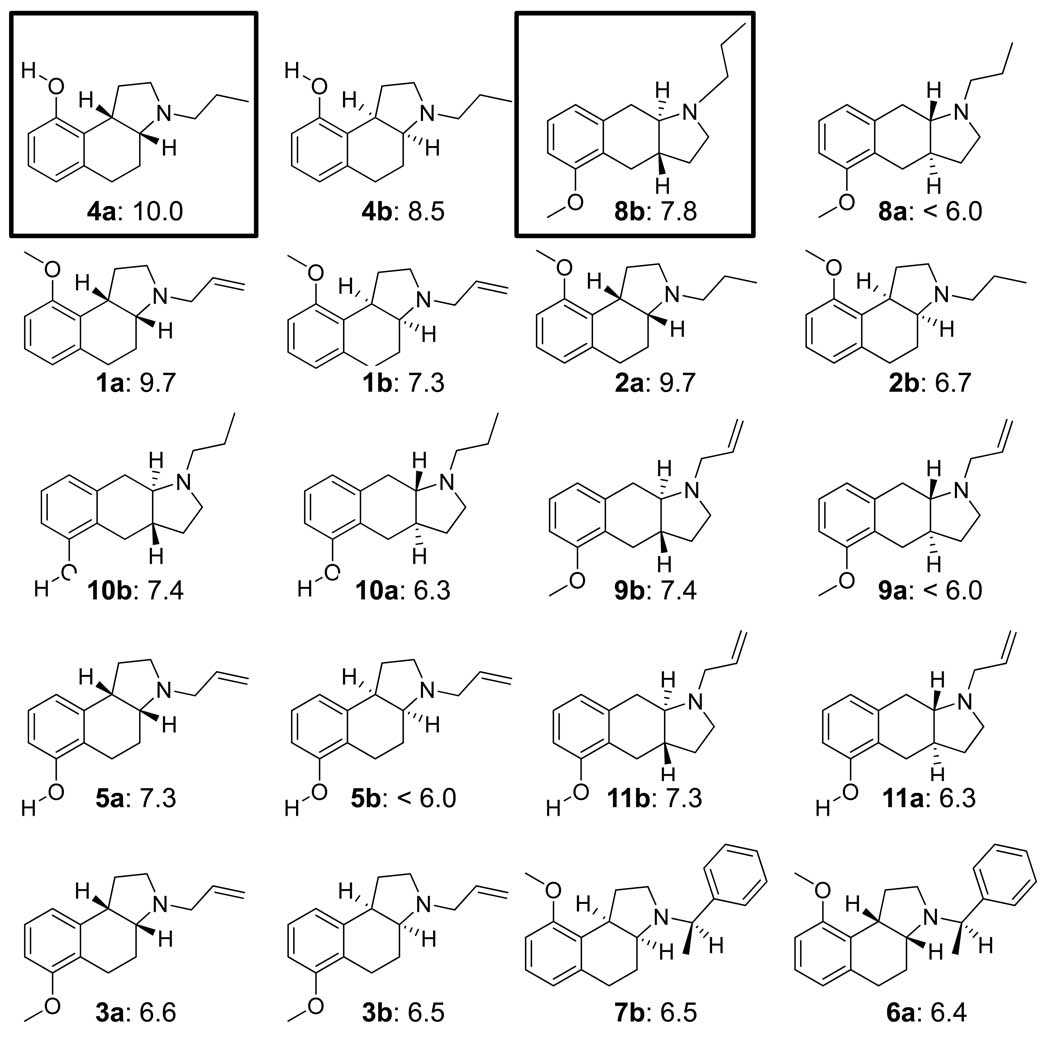
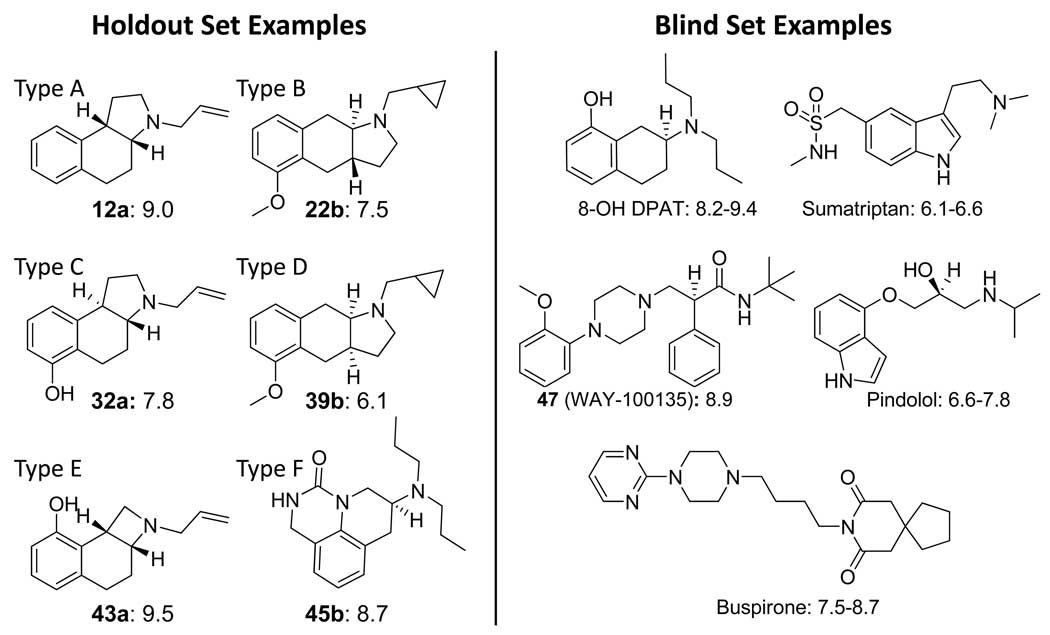
Two sets of ligands, a training set of 20 molecules and a holdout set of 35 molecules, came from a previous 3D QSAR study using the Compass method (16). These structures had been published by a group from Upjohn in 1993 (25; 26; 27). Figure 1 shows the structures and 5HT1a activity for each of the 20 training molecules, which consist of two chemical series of angular and linear tricyclic compounds each with an amino-tetralin substructure. The angular series with the cis ring fusion will be referred to as body type A, and the linear series with the trans fusion will be referred to as body type B. The 35 holdout molecules consisted of five different body types, illustrated in Figure 2a. The holdouts contained 13 racemic mixtures of body types A and B, with different substitution patterns. Also included were 9 compounds with an angular trans configuration (body type C) and 9 with a linear cis configuration (type D). Two examples of the angular cis configuration were present with a four-membered ring containing the nitrogen (type E) as well as two urea-based tricyclics (type F). All structures are detailed in the original Compass paper (16), and they are part of the data archive associated with this paper. Of note, there was no correlation between molecular weight and pK_d in either the training or holdout sets.

Figure 1.

Structures and experimentally determined pK_d of training ligands for 5HT1a. The molecules are shown as enantiomeric pairs, with a/b designating the isomers. The boxed ligands in the top row were the most active of the two scaffold types and were used to guide initial alignments for pocket induction (see Figure 3). The remaining molecules are shown by decreasing potency of the more active isomer. The differences in potency among isomers range from nearly 2 log units to zero. There is a complex interaction between sidechains, scaffold, and chirality that is difficult to model without contemplation of a full 3D model. Compounds numbers are as in ref 16.

Figure 2.

Example structures and activities of holdout ligands (left) and blind testing ligands from the Organon set (right). The body types A–D indicated for the former describe, respectively, the angular cis, linear trans, angular trans, and linear cis ring configurations. Type E describes a variant of type A in which the nitrogen-containing ring has four members, and type F describes a cyclic urea scaffold. The Organon set contained diverse scaffolds, which included the prototypical amino-tetralin 8-OH-DPAT, multiple aryl-piperazines, as well as drugs such as pindolol and sumatriptan. Compound numbers are as in ref 16.

The 35 molecule set from our previous work was known, well studied, and also formed a test for which we knew a priori that a Compass-like method could yield an excellent predictive result. As such, it did not form a suitable challenge for a true test of prediction accuracy. Additionally, since 16 years have elapsed since the original publication of the structures used for model induction, a number of new and structurally quite divergent serotonergic agents have been discovered. We identified all ligands with human 5HT1a assay data from Organon in GPCRDB (23) for which we could unambiguously identify chemical identifiers and 3D structures from PubChem (24). The curation was undertaken after the final model had been constructed, and it was done by an individual not involved in algorithm development or model refinement (author AEC). There was no possibility of contaminating knowledge of this test set influencing the model nor of the characteristics of the model influencing curation of the test set. The process yielded a list of 32 molecules, ranging in activity from approximately a K_d of 30 µM (paroxetine) to multiple ligands near 1 nM potency (e.g. 8-Hydroxy-N,N-dipropyl-2-aminotetralin (8-OH-DPAT) and buspirone). A number of these were published after 1993 when the structures and activities of the training compounds became public. Apart from two amino-tetralin compounds, these represent very different scaffolds from the training compounds. Figure 2b shows examples of molecules from the Organon set.

The Organon set included a number of approved drugs whose primary therapeutic targets were not the 5HT1a receptor. Of these, the most active was pindolol, whose primary target is the beta adrenergic receptor. While pindolol has been identified as a competitive antagonist at the 5HT1a binding site, other adrenergic ligands (e.g. timolol) have been established as non-binders. We identified 23 approved drugs which target the beta adrenergic receptor for their primary therapeutic benefit from two previous studies of drugs and their targets (28; 29). They included both agonists and antagonists: albuterol, bitolterol, carteolol, carvedilol, dipivefrin, ephedrine, epinephrine, isoetharine, isoproterenol, labetalol, levalbuterol, levobunolol, metaproterenol, metipranolol, nadolol, penbutolol, pindolol, pirbuterol, propranolol, ritodrine, sotalol, terbutaline, and timolol. Of these, five (carteolol, labetalol, penbutolol, pindolol, and propranolol) are known to bind the 5HT1a receptor at pharmacologically relevant concentrations, but only one (timolol) is known not to do so (30; 31; 32; 33). The majority have not been part of published studies of 5HT1a binding. This set was used to assess whether our predictive model could be exploited in assessing off-target effects.

All ligand structures as well as preparation protocols are available for download (see http://www.jainlab.org for details). Additional details regarding computational procedures for training ligand alignment, model induction, and testing of novel ligands follows.

Computational Methods

The core computational methods for molecular alignment based upon molecular similarity have been reported in previous papers and will be described only briefly here. The methods for binding site model induction will be presented in detail. Overall, there are five steps to construct and employ a physical binding pocket for activity prediction (a “pocketmol”):

1. Generation of an initial set of alignments for each training ligand.

   1. Input: Structures of ligands, with 2 or 3 chosen to serve as the seed alignment hypothesis.

   2. Output: At least one pose for each training ligand, all of which are plausible ithin the same mutual alignment.

2. Generation of an initial set of molecular probes to form the binding pocket.

   1. Input: One particular pose for each active training ligand, selected from the pool from Step 1.

   2. Output: A large set of molecular probes surrounding the ligands, where each probe makes a near-optimal interaction with at least one active ligand’s pose.

3. Selection of an optimal minimal pocketmol followed by augmentation to provide spatial coverage.

   1. Input: The set of probes from Step 2, a single identified pose for each training ligand (actives and inactives), and activity values for each ligand specified as exact values or inequalities.

   2. Output: A minimal set of probes such that nominal interaction scores against this set lie within a specified accuracy (using the fixed single poses) along with a set of additional probes that “cover” exposed areas of space.

4. Refinement of the pocketmol by modifying probe positions interleaved with refining ligand poses.

   1. Input: The initial pocketmol from Step 3, the full set of ligand poses for all training ligands, and the molecular activities.

   2. Output: A refined pocketmol with refined ligand poses such that further local optimization of ligand poses against the pocketmol yields little change in scores and where the final scores are close to the experimentally measured ones.

5. Testing of new putative ligands within the pocketmol:

   1. Input: A new molecular structure, the final pocketmol, and a selection of training molecules for use in alignment generation.

   2. Output: Predicted score and pose alternatives for the new ligand using a procedure analogous to docking ligands into a protein active site.

The following several paragraphs describe in detail the algorithms and computational procedures used for model building and testing. However, the process can be comprehended by readers less interested in technical details based on the description above and with Figure 3–Figure 7.

Figure 3.

The highest scoring mutual alignment of 4a (atom color) and 8b (blue carbons) is shown, with the panel at right being the view from the bottom of the panel at left. The procedure seeks to maximize joint molecular similarity while minimizing overall volume. Despite significant differences in the underlying scaffolds, the procedure is able to identify joint poses where the steric envelopes are remarkably similar, with the charged amines tightly aligned, and the oxygens of both ligands being able to accept hydrogen bonds from the same part of space.

Figure 7.

The overall procedure begins with an initial alignment hypothesis, as shown in Figure 2, which is used to generate initial alignments of all training ligands, possibly using multiple approaches (panel A shows a single alignment for each active training ligand). The initial alignments of active ligands are used to produce a large number of molecular probes that interact well with at least one pose of one active ligand (panel B, with hydrophobic probes shown without hydrogens for clarity). A subset of the probes are chosen to optimize concordance with activity (panel C, thick sticks). These identify the known pharmacophore, characterized by interactions with a donor (blue arrow), a charged acceptor (red arrow), and hydrophobic interactions (gray arrows). Additional probes are added back in order to provide “coverage” of the entire possible pocket (probes shown with thin sticks). Panel D shows the final optimized pocket (atom color) along with the initial probe positions (blue).

Initial Alignment

Initial alignment of training ligands proceeds in two stages. First, a small number of molecules (usually 2 or 3) are selected from which to build an alignment hypothesis. The methods used for this procedure have been described in previous papers and consist of the morphological similar- ity algorithm (34) along with the ligand-based structural hypothesis algorithm that depends upon it (35). The former is a method to compute molecular surface similarity (both shape and polar aspects) between two molecules along with algorithms to enable rapid optimization of conformation and alignment of molecule onto a specific pose of another. The latter uses this procedure in order to produce a joint superimposition of multiple ligands that simultaneously maximizes mutual similarity while minimizing overall volume. Our previous work has shown that such superimpositions can yield biologically relevant relative poses and that such joint superimpositions can be used effectively as surrogates for protein structures in virtual screening, even in cases where molecular flexibility is substantial (34; 35; 28; 29). Note that it is also possible to select protonation and tautomeric states in this procedure if they are ambiguous.

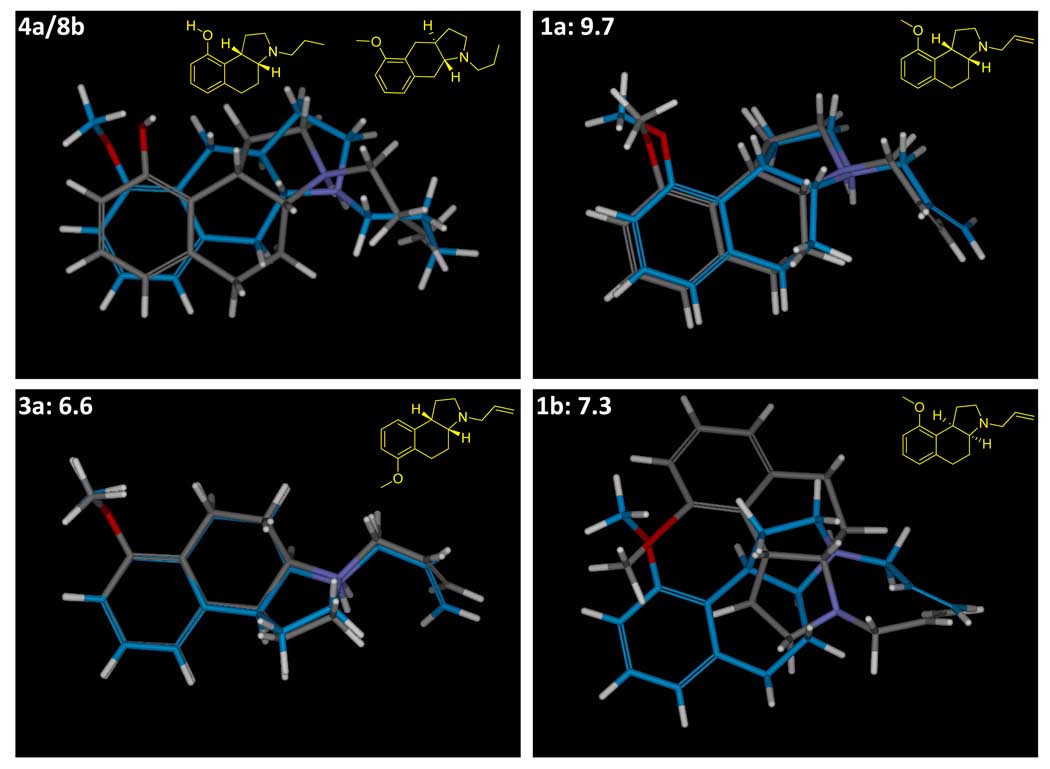
Figure 3 shows the highest-scoring alignment hypothesis of the boxed pair of ligands from Figure 1, which served as the seed alignment for the model-building here. While making use of a more sophisticated approach for alignment optimization, the resulting joint poses looked remarkably similar to those derived in the original Compass work on 5HT1a (16). The protons of the charged amines of the two ligands were in tight alignment, with the acceptors presented by the hydroxyl and methoxy both aligned such that they could interact with a common putative hydrogen bond donor. The hydrophobic envelopes of the two ligands were also concordant. Figure 5 depicts the quantitative differences and similarities between these two molecules as computed by the morphological similarity method. The differences included the lack of a donor on 8b, minor changes in the steric envelope (primarily from the additional methyl group), and some subtleties in the precise position of the acceptor functionality. The depiction of the similarities shows strong surface concordance over the entire ligands.

Figure 5.

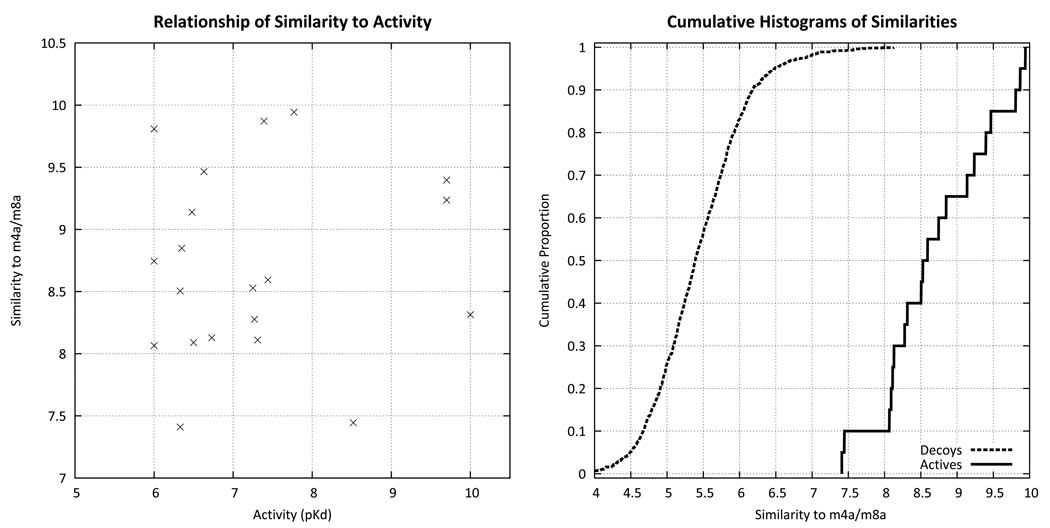
Using the alignment of Figure 3 as a target, the similarity of all training molecules from Figure 1 are plotted against experimentally measured activity (left). There is no correlation between similarity and activity, either by rank or by linear correlation. However, as shown on the right, the similarity computation yields highly separable distributions of scores for random screening compounds (dotted line) compared with the training ligands (solid line). Over 99% of the screening compounds had scores of 7.3 or less, but all of the training compounds met or exceeded that threshold. Lead optimization is typified by quantitative distinctions between 6.0 and 10.0 pK_d, which exceeds the accuracy of pure unweighted molecular similarity. However, virtual screening requires enrichment of active ligands in a background of completely inactive ligands, which requires much less in terms of quantitative accuracy.

This initial seed hypothesis served as a template for generation of multiple alternative poses for all training ligands. Since the similarity computation makes no use of activity data, and the relative importance of specific molecular features is not known a priori, the gross balance of the importance of shape vs. polar characteristics is also not known. The learning paradigm chooses ligand poses as the model of activity is developed, so the issue at the outset is to have a pool of poses for each training ligand that covers the reasonable possibilities. The procedure aligns each training ligand to each of the molecules in the seed hypothesis, using M different weightings of the relative strength of polar versus steric surface features (default weightings: 1.0 and 0.1).

For each training ligand, N poses are generated (default 100), which include the N/M highest joint similarity values to the alignment seed hypothesis for each of the M different weighting choices. We have shown previously that the numerical scores of joint similarity to an alignment hypothesis is effective in virtual screening (35; 28). This amounts to a distinction between ligands with measurable activity (roughly pK_d > 6.0) and non-ligands (roughly pK_d < 4.0) that is sufficiently quantitative to yield an enrichment of active compounds at the top of a ranked list. Figure 5 shows that similarity to the seed hypothesis yields distributions of similarity scores for random compounds much lower than for the 20 compounds from Figure 1, as expected. However, the relationship was not sufficiently accurate to rank ligands in a lead-optimization exercise, where distinctions of a single log unit can be important. In fact, there was no significant correlation between computed similarity and activity for the 20 training compounds.

The poses generated in this manner do provide an adequate pool from which to derive a more detailed model of activity. Note that when model construction begins, a particular ligand may have very different alternative poses in the initial pool. Figure 6 shows the alignments of training ligands arising from different weights for polar surface features. For molecules 1a and 3a, the optimal alignments under the different weightings were very similar to one another. But for 1b (the enantiomer of 1a), the two different alignments were very different. The pose shown in gray carbons resulted from the equal polar weighting, which yielded an excellent alignment of the amine and acceptor functionality of 1b onto the joint superimposition of 4a and 8b. The pose shown with blue carbons was much more concordant in the steric envelope, but the amine was poorly oriented. At this stage, one cannot distinguish which of the two poses is preferable, since no activity data have come into play. It is possible that the amine is geometrically tightly constrained by a specific interaction with a non-flexible pocket element and the steric envelope of the pocket is large and forgiving. It is also possible that the pocket itself is tight, with flexibility in the functionality that interacts with the amines of the ligands.

Figure 6.

The parent alignment (upper left) is shown along with three examples of training molecules. Molecule 1a is a minor variation of 4a (propyl to allyl and hydroxyl to methoxy). Molecule 3a moves the methoxy of 1a, resulting in vastly decreased potency. In both of these cases, alignment with full weighting of polar features (gray carbons) and alignment with a 90% reduction in the polar component of the similarity function (blue carbons) yielded concordant top-scoring poses. However, molecule 1b (the enantiomer of 1a) shows highly discordant alignments, depending on whether the steric envelope dominates (blue carbons) or the precise orientation of the charged proton on the nitrogen dominates (gray carbons). The union of poses resulting from both alignment strategies are used in learning.

Pocketmol Probe Generation

Our procedure must accommodate a multiplicity of choices for what the ultimate pocket will look like. In general, we should expect that multiple solutions are possible, all of which may yield equally good fits to the training data. Our approach is to generate a large number of potential probe positions, any of which may be selected and refined in subsequent steps of the procedure. Figure 7 illustrates the procedure. We choose a single pose for each active training ligand (defined here as those ligands with pK_d ≥ 7.0) using the highest scoring alignment from the polar surface feature weighting of 1.0 (Figure 7a). For each ligand, we tessellate its surface using probes of three types: hydrophobic (methane), donor (N-H), and acceptor (C=O). These probes are precisely those used in the Surflex-Dock “protomol” approach for characterizing protein cavities (36). As in that approach, the probes are subjected to local optimization using the Surflex-Dock intermolecular scoring function, and probes having high scores are retained unless they are redundant with another probe that has already been accepted. Figure 7b shows the resulting probes (with the methane probes devoid of hydrogen atoms for clarity) along with the alignments of 4a and 8b. The positions of the probes represent reasonable possibilities as to where an interaction from a pocket may lie, but they are too numerous to form a reasonable pocket in a physical sense.

Pocketmol Initialization

At this point, we have a pool of poses for each training ligand, both active and inactive, as well as a pool of pocketmol probes. Thus far, activity information has been used only minimally (e.g. by using only the active ligands for probe generation). To select a small set of probes that makes use of the activity data, both active and inactive ligands in the training set are used. We construct a matrix of scores between a pose for each ligand and each of the pocket probes generated. Given such a matrix, selection of a subset of probes that yields scores close to experimental activities can be treated as a mathematical programming problem, since the predicted activity for a molecule is simply the sum of its scores against a set of chosen probes. For this work, we used the SCIP 1.1.0 (Solving Constraint Integer Programs) solver (37) to select a minimal subset of probes that would yield a Surflex-Dock score for each of the ligands within 0.5 log units of the experimentally measured activity. For the probe selection, we used the top scoring poses from the polar weighting of 1.0 (as described above). Note that the requirement of identifying single poses stems from the use of this constraint satisfaction method. We are exploring approaches where the initial probe set may be chosen using the full pool of ligand poses, which are used in any case in the subsequent model refinement process.

The resulting small set of probes is shown with thick sticks in Figure 7c. This parsimonious set of probes (highlighted with arrows) captures the key interactions that have been described in numerous pharmacophoric representations of the requirements for 5HT1a activity (e.g. (27)). Pocket probes complementing the acceptor, the charged amine, and multiple hydrophobic elements were automatically selected based upon the requirement to match the activity pattern of the molecules. The small set of selected probes leaves large gaps in the pocket surface, so additional probes from the larger pool are added back to fill in sparse areas. This requirement is a consequence of using the multiple-instance learning approach. Since ligand poses will change in order to optimize activity relative to the model, overly sparse models allow too much freedom in alignment adaptation. For example, a ligand that is inactive due to a large steric protrusion can adapt to occupy empty space with its extra bulk. To allow the model freedom to cover all parts of space surrounding the training molecules, probes are added back from the larger pool iteratively, including new probes not near any existing ones. In this work, the tolerances for nearness were 4.5 for steric probes and 3.0 for polar probes, measured using RMSD in Angstroms. Figure 7c shows the added-back probes with thin sticks.

Pocketmol Refinement

At this point, we have a pool of poses for each training ligand and an initial pocketmol consisting of donor, acceptor, and steric probes (roughly 30 total in the 5HT1a case). The problem now involves local optimization of both the probes and the ligand poses. The goal is a binding site model in which computed activity is close to experimentally measured activity (while allowing for ligands to optimize their poses within the model). We optimize the probe positions in order to minimize the mean-squared-error (MSE) of computed vs. actual activity across all ligands. We employ a steepest descent procedure based on the gradient of the MSE with respect to probe positions. Activity is computed for each molecule using the Surflex-Dock scoring function. A single step of gradient descent requires computation of the change in MSE across all ligands with respect to probe position and orientation for each probe in the pocketmol. This gradient computation is made using the maximally scoring pose for each ligand, where the procedure maintains a set of the poses of each ligand explored during model refinement (this is called the pose cache). Gradient steps for the probes are made simultaneously for all probes, using a step size that ensures small movements (less than 0.1Å).

After 100 steps of gradient optimization of probe positions (or if the computed MSE is less than 0.05), the positions are fixed as the current model. Then, using the current model, each of the ligands’ pose caches are optimized. Poses for each ligand are subjected to all-atom optimization to maximize the Surflex-Dock scoring function. Note that the function contains both intermolecular as well as intramolecular terms, so ligand internal strain is quantitatively traded for interaction with the binding pocket. The processes are repeated (probe position optimization followed by ligand pose optimization). Early in learning, the scores of the ligands change substantially during pose cache optimization. In cases where the learning procedure converges, as the learning progresses, these changes decrease in magnitude, and the overall MSE reaches a plateau. We have not observed situations where ligand scores fail to stabilize during iterative refinement. The process terminates when the MSE based on ligand scores (after pose cache updating) is less than 0.05. A maximum of 50 rounds of probe and ligand optimization are used. Figure 7D shows the final pocketmol (atom colored sticks) along with the initial probe positions (blue). The changes were subtle, with the most significant rearrangements being in the positions of the acceptor probes that interact with the amines of the training ligands. The refinement procedure takes a few hours on standard desktop hardware and is the lengthiest step in the overall process.

Testing New Ligands

New ligands are simply docked into the final pocketmol and are scored as if it were a protein binding site. While the process can be carried out with Surflex-Dock directly, we have implemented a procedure to enable the direct use of training ligand poses to help guide the alignment of test ligands, which results in more reliable pose generation at a reasonable computational cost. Testing a new ligand takes less than a few minutes. The procedure is analogous to the initial alignment procedure above, with the exception that the top scoring alignments based upon similarity to the specified ligands are subject to scoring and local optimization within the pocketmol itself. The default parameters make use of two similarity weightings (1.0 and 0.1 for polar surface features), 100 best poses from each alignment to each input alignment target, and 5 final poses representing the best optimized fit to the pocketmol for each input ligand.

Computational Procedures

Detailed scripts for generating the results presented here are available in the data archive associated with this paper. Briefly, the procedures were as follows:

1. sf-sim.exe +misc_ring −misc_outconfs 10 +fp prot LigList protlig

   This command protonates and performs a ring search on the input ligand list, yielding low energy ring conformations (maximum of 10 per ligand), including nitrogen anomers. This process is applied to the training molecules and the testing molecules.

2. sf-sim.exe hypo SeedList loghypo

   Produces a set of mutual alignments of the ligands in SeedList (up to 100). The top scoring such hypothesis superimposing 4a and 8b was used for all model construction (shown in Figure 2).

3. sf-qmod.exe initalign TrainLigList hypo.mol2 logalign

   Generates initial alignments for all training ligands (hypo.mol2 from the prior step). The default parameters make use of 2 weightings of polar surface features (1.0 and 0.1) and yields up to 100 poses for each ligand.

4. sf-qmod.exe initprobes ActiveTrainPoseList outprobes

   Generates a dense set of initial probes based upon the top scoring alignments of the active ligands specified.

5. sf-qmod.exe makesolverscript TrainData outprobes

   Generates a problem definition file (pmol.zpl) for input to the SCIP solver. TrainData contains file paths and corresponding activity data for the input molecules. The SCIP solver is then run on the problem definition file pmol.zpl, and it generates a solution file soln.scip if a feasible solution is found.

6. sf-qmod.exe readsolveroutput TrainData outprobes soln.scip

   Reads the solver output and writes a file subsetList describing the probes that comprise the minimal subset.

7. sf-qmod.exe probeaddback TrainData outprobes subsetList

   Adds probes back to the subset pocketmol in areas whose coverage is sparse and writes the resulting set of probes to startingProbes.

8. sf-qmod.exe refinepocketmol TrainData startingProbes

   Refines the pocketmol and the ligand poses using gradient optimization in the multiple-instance learning paradigm.

9. sf-qmod.exe scorepocketmol TestLigList align-targets.mol2 pocket-mol.mol2 logscore

   Scores the ligands in TestLigList based upon alignments guided by the poses provided in align-targets.mol2, scored against the pocketmol specified in pocketmol.mol2. Scores are listed for each molecule in logscore, with the final poses in logscore-results.mol2. This procedure makes use of the all-atom optimization procedure implemented within Surflex-Dock, so ligand strain enters into the pose optimization process explicitly and prevents excessive deformation of ligands. The final scores represent the intermolecular interaction energy along with the entropic fixation terms and do not include internal strain directly.

The data and scripts required to replicate these procedures are available from www.jainlab.org.

Structural Model of 5HT1a

In addition to pocketmol induction and scoring, we generated a protein structural model of human 5HT1a based on the recently solved structure of the beta-2 adrenergic receptor bound to timolol (PDB code 3D4S (5)). Models of 5HT1a were produced using the software MODELLER (38). The experimentally determined structure for the adrenergic receptor was an engineered fusion protein, so the sequence alignment of 5HT1a to the protein sequence of 3D4S was done by hand. It was based upon the relationship between human 5HT1a and beta-2 adrenergic sequences from the multiple sequence alignment of the amine GPCR family in GPCRDB (23). The top twenty models from MODELLER were retained in order to ensure adequate representation of alternate conformations of the ligand binding site. Models were assessed using two metrics of model quality: DOPE and GA341 (39). Both of the metrics returned favorable results (GA341 > .99 and negative DOPE scores) for all 20 models created, yielding confidence that they are a reasonable representation of the human 5HT1a structure.

Results and Discussion

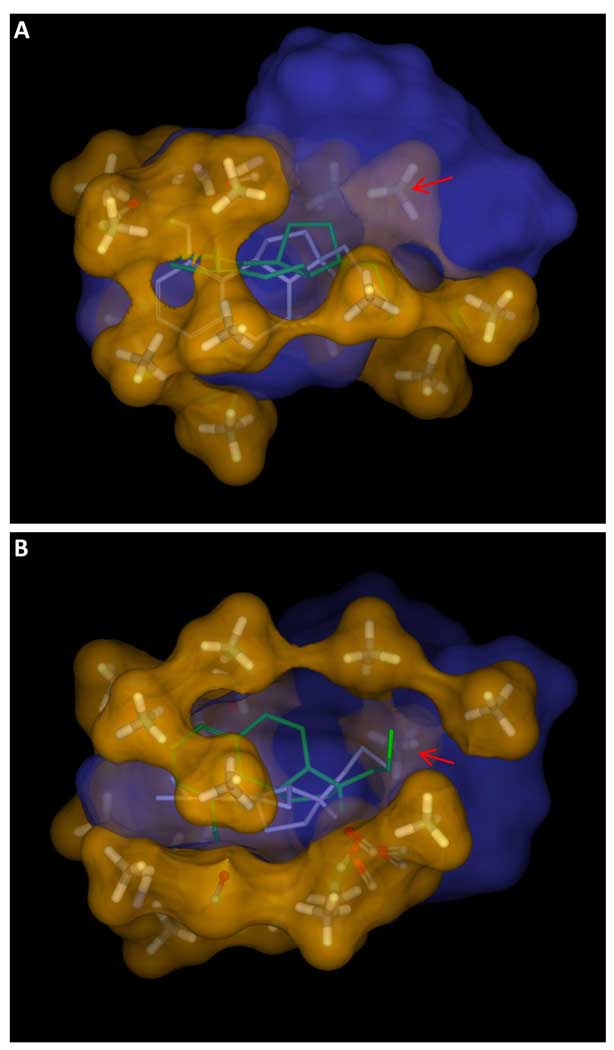
At a minimum, the goal of QSAR approaches is to make accurate predictions of ligand activity. Preferably, the methods should also yield predictions of relative binding modes, be amenable to visualization, and offer some guidance as to the confidence associated with specific predictions. Figure 8a depicts the final learned pocketmol (atom-colored sticks with a translucent surface) along with the solvent-accessible surface explored by the final optimal poses of the training ligands that had measureable activity (solid orange surface). The overall pocket was well enclosed, except for the bottom and upper right. These open areas accommodated the phenyl groups of molecules 6a and 7b (see Figure 1), both of which had sub-micromolar activity and whose pendant phenyls required extra space (one ligand preferred the phenyl up and one down).

Figure 8.

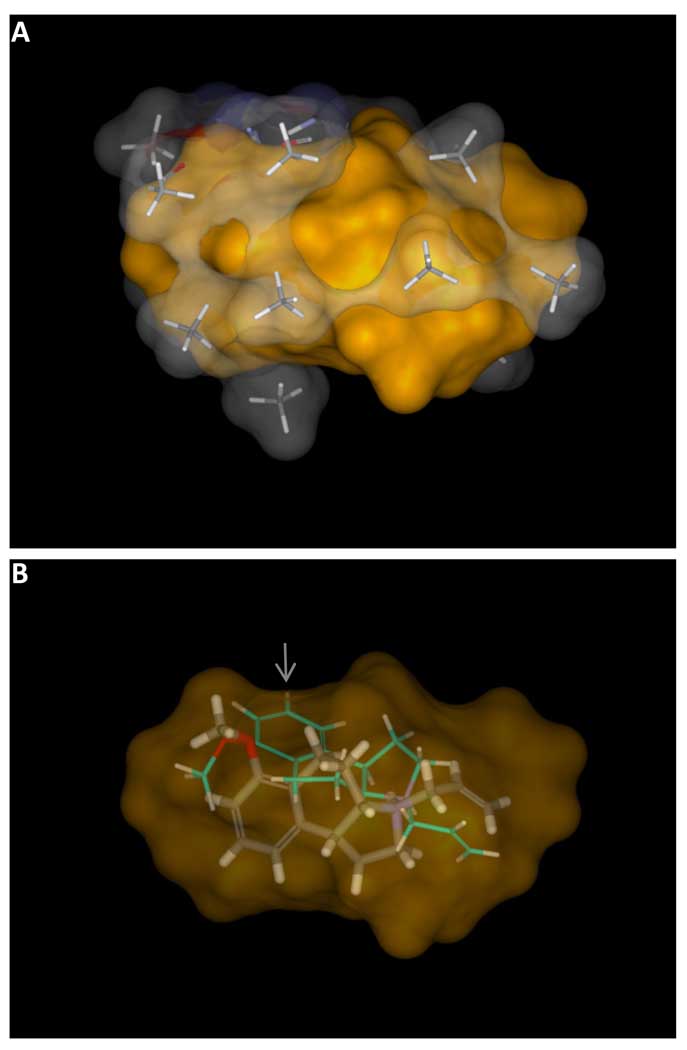
The final pocket, depicted in sticks with a translucent atom colored surface, encloses the volume of the final poses of the active training ligands, depicted with a solid orange surface (Panel A). In some cases, the final optimal pose of a training ligand changes significantly from the initial one, illustrated in Panel B with molecule 3b. The initial pose (thin sticks with cyan carbons) was chosen based purely on molecular similarity to the initial alignment hypothesis. The final pose (thick sticks in atom color) was selected based on interaction with the virtual binding pocket. Note that the initial pose extended slightly beyond the active envelope (gray arrow).

The interplay between the evolving pocket and the ligand poses was generally subtle, with most ligands showing only minor movement when comparing the initial preferred poses to the final optimal poses. However, for some ligands, the final optimal pose was very different, resulting from one of the 100 initial poses available. Figure 8b shows the initial preferred pose of 5a (cyan carbons), a compound with 50 nM K_d, along with its final pose (atom color). The initial pose fit an underspecified “pharmacophore” for 5HT1a (the amine, acceptor, and hydrophobic cleft), but it was not concordant in steric shape with the most active ligands, and it protruded slightly beyond the active envelope (gray arrow). The initial preferred pose did not make favorable interactions with the pocket probes that surrounded the aromatic component of the training ligands. The final optimal pose traded off a suboptimal amine orientation for a much improved fit to the pocket. Other methods that do not allow for rigorous pose selection during model induction must adjust model parameters to accommodate errors in initial ligand alignment, which leads to inaccuracies in prediction.

Performance on the Holdout Set: Comparison to Compass

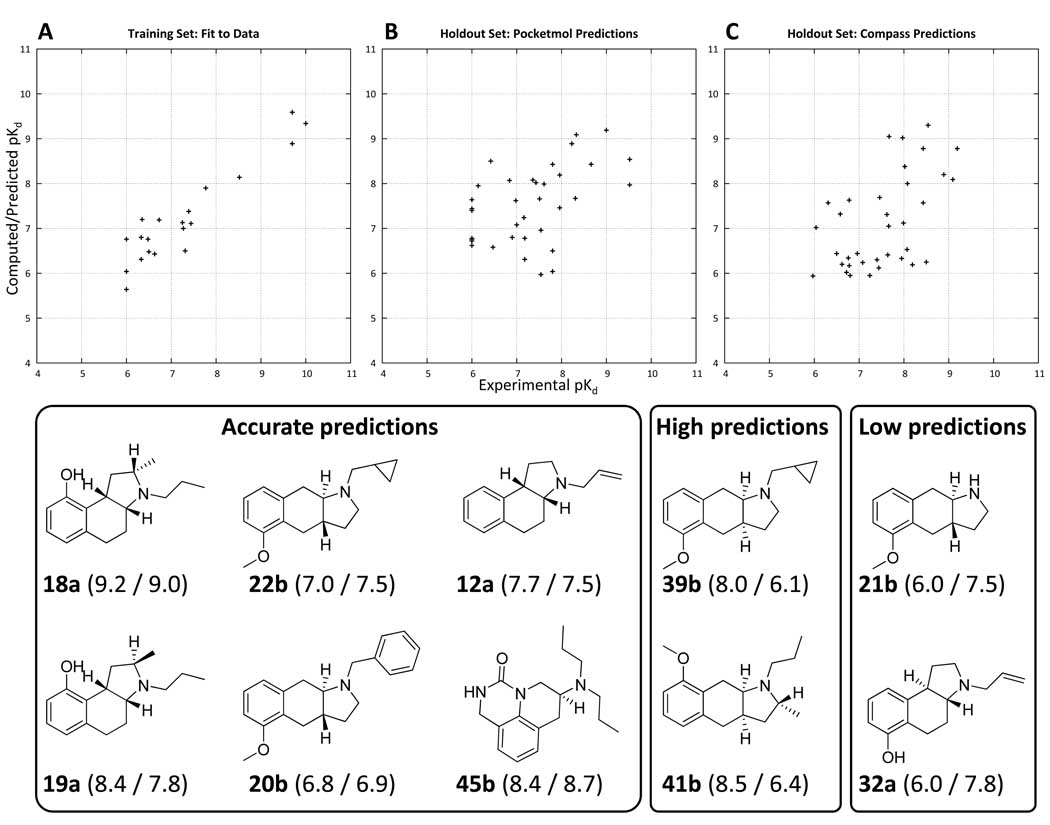
Figure 9 shows plots of experimental vs. computed pK_d for the 20 molecule training set using the final pocketmol. Predictions are shown for the 35 molecule holdout set from the pocketmol and from Compass (16). Note that plot A reports the fit to the data, whereas plots B and C report predictions on ligands not used in model induction. For both the pocketmol and Compass predictions, the activity of racemic mixtures was reported as the maximum pK_d of either enantiomer less log₁₀(2) (there is an extensive discussion of some subtleties involving this issue in the original paper (16)). It is not surprising that the fit to the data was excellent. Nominally, there were roughly 180 parameters to estimate (6 translation and rotation parameters for each of 30 molecular probes) given just 20 training ligands. However, it is important to recall that each training ligand had a manifold of different poses, the best scoring of which was involved in the reported score. Comparing parameter count to data set size is not straightforward in multiple-instance learning, so overfitting may or may not be a problem here and must be judged by careful model testing.

Figure 9.

Plots of experimental (X-axis) versus computed/predicted pK_d for the final optimized binding pocket for the 20 molecule training set (Panel A) and the 35 molecule holdout set (Panel B). Predictions from Compass on the same holdout set (using the same training molecules) are shown in Panel C. Mean error of fit for the training set was 0.4 pK_d units. Prediction error on the 35 molecule holdout set was 0.8 units, with a Kendall’s tau rank correlation of 0.34 (p < 0.01 by permutation). The Compass predictions had a mean error of 0.6 units, with a Kendall’s tau rank correlation of 0.36 (p < 0.01 by permutation). The differences between the prediction quality for the pocketmol and for Compass were not statistically significant. However, the pocketmol predictions tended to be high for inactive molecules, and the Compass predictions were low for mid-range actives, apparently reflecting a significant difference in the bias of the learning approaches. Examples of structures with accurate, low, and high predictions from the pocketmol are shown (predicted/actual pK_d are shown in parentheses with molecule names). Note: there is a slightly negative but insignificant correlation between molecular weight and pK_d for the 35 holdout molecules.

The pocketmol predictions averaged 0.8 log units of error, with Compass yielding 0.6. The average error magnitudes were not statistically different by t-test (p > 0.05). The pocketmol predictions yielded a Kendall’s tau rank correlation of 0.34, with Compass yielding a correlation of 0.36. Both rank correlation values were statistically significant (p < 0.01), but they were not statistically different from one another. While the statistical model quality measures were very similar, the character of model prediction errors was quite different, with the pocketmol yielding higher scores for less active holdouts and Compass yielding lower scores for holdouts with mid-range activities. The difference between pocketmol score and Compass score was rank-correlated with actual activity, with p < 0.01 by Kendall’s tau. Table I details the experimental and predicted values for the holdouts. Learning systems have different biases in transforming input data into models. The bias of the pocketmol regime we have used is to form a minimal physical model, where missing data will tend to lead toward a literal vacuum. The bias of the Compass approach was to form a tightly enclosed virtual pocket around all training molecules, due to the manner of construction of the neural network that implemented the virtual receptor model. These differences were reflected in the errors observed in the holdout set.

Table 1.

Performance of the virtual binding pocket on a holdout set of 35 molecules (compound numbers as in ref 16).

Molecule	Body	Experimental	Predicted	Error
16	A	9.5	8.5	1.0
18	A	9.0	9.2	0.2
19	A	7.8	8.4	0.6
12	A	7.5	7.7	0.2
14	A	7.4	8.0	0.6
15	A	7.0	7.1	0.1
13	A	6.0	6.8	0.8
17	A	6.0	7.6	1.6
21	B	7.5	6.0	1.6
22	B	7.5	7.0	0.6
23	B	7.2	7.2	0.1
24	B	7.0	7.6	0.6
20	B	6.9	6.8	0.1
26	C	8.3	9.1	0.8
31	C	8.3	7.7	0.6
25	C	8.0	7.5	0.5
27	C	7.8	6.5	1.3
32	C	7.8	6.0	1.8
29	C	7.4	8.1	0.7
28	C	7.2	6.3	0.9
30	C	7.2	6.8	0.4
33	C	6.5	6.6	0.1
42	D	8.0	8.2	0.2
40	D	6.8	8.1	1.2
41	D	6.4	8.5	2.1
39	D	6.1	8.0	1.8
34	D	6.0	7.4	1.4
35	D	6.0	6.8	0.8
36	D	6.0	6.7	0.7
37	D	6.0	7.4	1.4
38	D	6.0	6.6	0.6
43	E	9.5	8.0	1.6
44	E	8.2	8.9	0.7
45	F	8.7	8.4	0.2
46	F	7.6	8.0	0.4

Experimental, Predicted, and Error values are in units of pK_d.

In Figure 9, two molecules that typified the pocketmol’s high predictions of relatively inactive molecules were 39b and 41b, both of body type D. These were linear tricyclic compounds with a cis ring fusion, a scaffold not seen in the training set. The pocketmol was permissive toward variations in that part of the ligands, having had no significant variation in the bodies of the training ligands on which to establish physical boundaries. Conversely, in the case of 21b (an underprediction), the training ligands had significant variation in the nitrogen substituents, but all of the ideal substituents were roughly the size of a propyl group. No smaller groups were observed in the training data, and larger ones tended to be less active. The low prediction for 21b reflected an overgeneralization of a preference for propyl-sized substituents from the limited variation in the training set. Molecule 32a, another underprediction, was of body type C (a trans fused angular tricyclic), again illustrating that a lack of variation in geometry among the training ligands can lead to limitations in predictive ability. Overall, accuracy for holdout molecules of body types A and B (13 molecules) was 0.6, but for body types C and D (18 molecules) was 1.0, with the difference being weakly significant (p = 0.05 by t-test).

Accuracy for molecules of body types E and F (just 2 molecules each) averaged 0.7, with molecules 45 and 46 (both type F) yielding predictions within 0.5 log units of the experimental values. These were the most structurally novel ligands within the 35 molecule holdout set. Their predicted alignments were as expected, with the more active isomer of 45 illustrated in Figure 10 with 4a (cyan carbons). The amines corresponded well, and the carbonyl oxygen was able to make similar interactions to those of the acceptors in the amino-tetralin series. The donor from the urea of 45 was able to mimic the interaction made by the hydroxyl proton of 4a.

Figure 10.

The predicted pose of holdout molecule 45 (thick sticks with atom color) along with the optimal pose of training ligand 4a (cyan carbons) rendered inside the surface enclosing the volume of the active training ligands. The chemical structure is novel, but the prediction is accurate (pK_d of 8.4 compared with the experimental value of 8.7).

Performance on the Organon Set

In the foregoing, we established that performance on the holdout set paralleled that of Compass, with sensible predictions of binding poses as well as affinities. However, the bulk of the holdout molecules were similar to the 20 training ligands, representing R-group variations and some variation in chemical scaffolding. It is important to note that there was no correlation between molecular weight and affinity in the holdout set, and also that the types of variations are typical of work in a medicinal chemistry lead optimization exercise. So, the prediction task was relatively subtle and was also relevant in a practical sense. However, the conformation and alignment questions posed by the holdout set were challenging only in a few cases. Perhaps more importantly, the holdout set was not truly “blind” (either for the pocketmol predictions or for Compass) since the structures of the molecules along with their activities were known at the time that the methods were being developed.

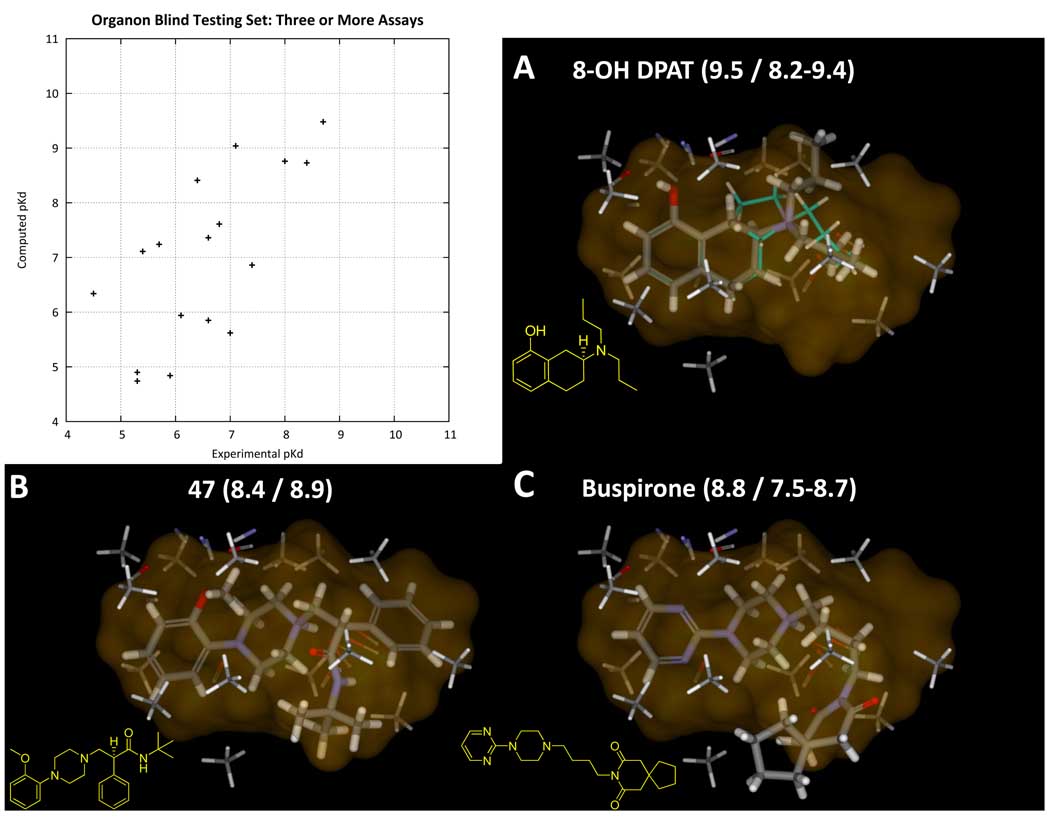
Consequently, we tested the model on a separate objectively constructed blind set (as detailed in the Methods section). The set consisted of 32 molecules total, with 17 having data from 3 binding assays or more and 15 having data from 1 or 2 assays. These compounds exhibited tremendous structural variability, including just 2 classic amino-tetralins. Multiple assay values also afforded the ability to estimate the experimental uncertainty in pK_d measurements. Among the compounds with more than 1 assay value, the mean difference between high and low pK_d values was 0.7 log units, providing a bound on reasonable expectations for computational predictions. Table II shows the experimental and predicted values for the pocketmol on the Organon set, along with information regarding number of assays. For these predictions, values that fell within the assay range were assigned an error of 0.0, and predictions that fell outside of the assay range were assigned an error in the amount of their excursion beyond the range. Computations of correlation were made using mean assay values. For the 17 ligands having 3 or more assay values, Kendall’s tau was 0.51 (p < 0.01) with a mean error of 0.6 log units. For the full set of 32 ligands, Kendall’s tau was 0.29 (p = 0.01) and the mean error was 1.0 log units. The difference in errors between the two sets of compounds was statistically significant, and we have focused our analyses on the set of compounds with 3 or more assays.

Table 2.

Performance of the virtual binding pocket on a blind set of 32 molecules.

Name	PubChem CID	Min pK	Max pK	N As- say	Average pK	Predicted pK	Error	Assay Uncertainty
5-CT (5-carboxamidotryptamine)	1809	9.2	9.6	2	9.4	6.4	2.8	0.4
47	115111	8.9	8.9	1	8.9	8.4	0.5	0.0
Lisuride	28864	8.6	8.8	2	8.7	6.5	2.1	0.2
Spiroxatrine	5268	8.6	8.6	2	8.6	7.2	1.4	0.0
Bufotenine	10257	8.4	8.6	2	8.5	8.9	0.3	0.2
UH-301 (5-F-8-OH-DPAT)	122187	7.5	7.6	2	7.6	9.4	1.8	0.1
Rauwolscine	643606	7.3	7.5	2	7.4	6.2	1.1	0.2
Pindolol	4828	6.6	7.8	2	7.2	7.5	0.0	1.2
Nefazodone	4449	6.8	6.8	1	6.8	7.6	0.8	0.0
Risperidone	5073	6.1	6.6	2	6.4	7.3	0.7	0.5
Sumatriptan	5358	6.1	6.6	2	6.4	7.4	0.8	0.5
Ketanserin	3822	5.9	6.2	2	6.1	8.7	2.5	0.3
Pirenperone	4847	5.5	5.6	2	5.6	8.4	2.8	0.1
Moclobemide	4235	5	4.9	2	5.3	7.8	2.3	0.5
Phendimetrazine	12460	4.9	4.9	1	4.9	7.1	2.2	0.0
8-OH-DPAT	1220	8.2	9.4	13	8.7	9.5	0.1	1.2
Ipsapirone	56971	8.1	8.6	3	8.4	8.7	0.1	0.5
Buspirone	2477	7.5	8.7	10	8.0	8.8	0.1	1.2
Spiperone	5265	5.9	8.4	7	7.4	6.9	0.0	2.5
Gepirone	55191	7	7.2	3	7.1	9.0	1.8	0.2
MCPP (m- chlorophenylpiperazine)	1355	6.6	7.5	7	7.0	5.6	1.0	0.9
Mesulergine	68848	5.9	8.9	11	6.8	7.6	0.0	3.0
Flumexadol	65774	5.8	7.2	3	6.6	5.9	0.0	1.4
Ritanserin	5074	5.9	7	7	6.6	7.4	0.4	1.1
Mianserin	4184	6	6.7	9	6.4	8.4	1.7	0.7
MK-212 (2-chloro-6- piperazin-1-ylpyrazine)	107992	5.7	6.8	3	6.1	5.9	0.0	1.1
Olanzapine	4585	5.6	6	4	5.9	4.8	0.8	0.4
Quipazine	5011	5	6	7	5.7	7.2	1.2	1.0
Remoxipride	54477	5.1	5.8	4	5.4	7.1	1.3	0.7
4-Iodo-2,5- dimenthoxyamphetamine	1229	4.6	5.9	4	5.3	4.9	0.0	1.3
Mirtazapine	4205	5.2	5.3	6	5.3	4.7	0.5	0.1
Paroxetine	43815	4.5	4.6	3	4.5	6.3	1.7	0.1

Figure 11 shows a plot of experimental vs. predicted pK_d for these 17 Organon ligands (r² was 0.7 with a linear fit slope of 0.92). Three examples are shown: 8-OH-DPAT, 47, and buspirone. The former is a canonical amino-tetralin (generally this is the ligand used in displacement assays for measuring 5HT1a binding). The latter two represent different aryl-piperazines, a scaffold that has received extensive study in serotonergic development. The numerical prediction and alignment for 8-OH-DPAT is not surprising, since it constitutes a straightforward ring opening (plus a carbon) of the most active ligand from the training set (4a). However, the predictions for the latter two molecules represent very significant leaps both in terms of alignment and prediction of numerical activity. Compound 47 essentially filled the entire active envelope of the model, and it made the interactions expected. The protonated amine interacted with the collection of carbonyl probes of the pocketmol, and the methoxy acted as the acceptor. Buspirone could have yielded several different options for alignment. However, the optimal fit to the pocketmol comports with our understanding of aryl-piperazine SAR, where it is the pyrimidine nitrogen that serves as the hydrogen bond acceptor (40; 41). Note that ipsapirone and spiperone were also among this group and were accurately predicted in analogous poses, but gepirone was overpredicted. It is clear from Figure 11, however, that variations in the distal moiety of such ligands extend beyond that which the model can confidently predict. The bias of the pocketmol model, to treat such excursions as reaching into a vacuum as opposed to violating an implicit constraint, seems preferable to the Compass approach. While it is not possible to test the Compass model (its parameters were not published), we believe that it would have failed in many cases where the pocketmol correctly yielded predictions of high activity for extended ligands.

Figure 11.

The plot shows fully blind predictions for the pocketmol on 17 molecules from GPCRDB’s Organon assay data where three or more assays were present for human 5HT1a receptor. Mean error was 0.6 log units, with Kendall’s tau of 0.51 (p < 0.01). Including those ligands with fewer than 3 assays (plot not shown, see Table II), the mean error was 1.0 log units and Kendall’s tau was 0.29 (p = 0.01). For those molecules with more than 1 assay value, the average assay uncertainty was 0.7 units. Panels A, B, and C show three ligands (names and predicted/actual pK_d as indicated). In the case of 8-OH-DPAT, the ligand is quite similar to those used for model construction; 4a (cyan carbons) is shown to be essentially a cyclization of a propyl group from 8-OH-DPAT. But for 47 and buspirone, the core element containing the critical amine and acceptor combination as well as the hydrophobic components are all very different. Only in the last case does the ligand extend significantly beyond the area explored by active training ligands. There is no correlation between molecular weight and pK_d for the Organon ligands (either for the full set or those with three or more assays).

Off Target Effects of Adrenergic Ligands

Among the Organon set were a number of marketed drugs, with pindolol, a beta adrenergic antagonist, being the most active against 5HT1a. Pindolol was correctly predicted by the model to have activity better than 100 nM (see Table II). Antagonist activity against the 5HT1a receptor by adrenergic ligands is an important pharmacological phenomenon that relates to the effectiveness of selective serotonin reuptake inhibitors (SSRIs). Specifically, clinical studies showed that co-administration of pindolol enhanced the antidepressant effect of SSRIs (42), and subsequent radiotracer experiments in healthy volunteers showed that, at pharmacological concentrations, pindolol displaced a potent and selective 5HT1a radioligand from its binding sites in the brain (43). The binding of pindolol in the human brain showed selectivity for the dorsal raphe nuclei (DRN) region. The DRN region is rich in serotonergic nerves, and it is the major source of serotonin innervation to the forebrain. The DRN region has very high expression levels of both the serotonin reuptake transporter and 5HT1a receptor and is a major site of action for the therapeutic effects of SSRIs (for a review, see (44)).

Within the DRN region, SSRIs increase the extracellular concentration of 5HT, but initially the 5HT binds to 5HT1a receptors present in the same presynaptic neurons in which the reuptake transporters reside. These 5HT1a receptors act in an inhibitory feedback loop, so activation of these 5HT1a receptors causes a decrease in 5HT release, thereby opposing the effects of the SSRI. With SSRI treatment alone, the inhibitory 5HT1a receptors become desensitized over a roughly 2–3 week period, whereupon there is a therapeutic benefit. However, co-administration of a 5HT1a antagonist such as pindolol markedly speeds onset of the SSRI antidepressant effects (43). Although inter-patient variability exists with respect to the benefits of pindolol antagonism of the 5HT1a receptor, pindolol represents a proof-of-concept that beta adrenergic ligands as 5HT1a receptor antagonists can enhance SSRI therapy.

We identified all beta adrenergic ligands from our previous work on comprehensive drug target modeling (28; 29). The status of 5HT1a activity for most of these compounds has not been published. However, there are clear data for six of them: five (carteolol, labetalol, penbutolol, pindolol, and propranolol) are known to bind the 5HT1a receptor at pharmacologically relevant concentrations and one (timolol) is known not to do so (30; 31; 32; 33). Of the 5 drugs with known 5HT1a activity, 3 scored better than 100 nM: pindolol, carteolol, and labetalol. Timolol (closely related to pindolol and carteolol but inactive against 5HT1a) was predicted by the model to have pK_d < 6.0. Figure 12 shows the predicted alignment of three adrenergic ligands to the pocketmol. Pindolol and carteolol exhibited similar binding modes, with the ether oxygen in their linkers providing the required acceptor functionality to interact with the donor surface of the pocketmol. Timolol was unable to adopt a pose that makes this interaction while fitting into the aromatic groove of the model.

Figure 12.

The beta adrenergic antagonist pindolol was among the accurate predictions from the Organon binding data, shown in Panel A along with 4a (cyan carbons) and the pocketmol surface colored to reflect polarity. Panel B shows the view from the bottom, without 4a. The interaction between the amine and hydroxyl to the large negative pocket surface is apparent, as is the interaction of the ether oxygen with the donor surface. Panel C shows carteolol (atom color), which mimics the binding mode of pindolol (shown in blue), and also scores greater than 7.0. The ether oxygens of pindolol and carteolol are able to act as the critical acceptor functionality within the 5HT1a pocket while making proper interactions with their protonated amines. Timolol (Panel D, atom color with pindolol in blue), by contrast, while being a structural analog, is correctly predicted to be inactive (predicted pK_d of 5.2). It appears that the additional bulk and non-planarity of the morpholine renders timolol unable to make the correct interactions. See text for additional details on adrenergic ligand predictions.

While this analysis is anecdotal due to the lack of comprehensive and comparable assay data for the adrenergics, it is encouraging that the pocketmol approach is sufficiently predictive to suggest off-target effects of ligands earlier in the development process than they are typically found at present. The effects of pindolol on the 5HT1a receptor were discovered long after marketing of the drug. Systematic computational modeling of many targets may offer information at time points in drug discovery where biological investigation of a possible off-target effect is both inexpensive and likely to modify the course of a lead optimization exercise.

Relationship to Protein Binding Pockets

The pocketmol that was developed is physical in the sense that it represents real atomic positions of molecular fragments. However, it does not correspond to a pocket that could be formed by a single protein conformation. Rather, it offers multiple positions for some interacting moieties. The group of acceptor probes that interact with the basic nitrogen in the serotonin ligands represents multiple conformations of the aspartic acid sidechain that is known to be critical in binding within aminergic GPCRs. Similarly, the donor probes that interact with the acceptor in the serotonin ligands represent multiple positions of a donor, believed by some to be a hydroxyl proton from a serine residue in 5HT1a.

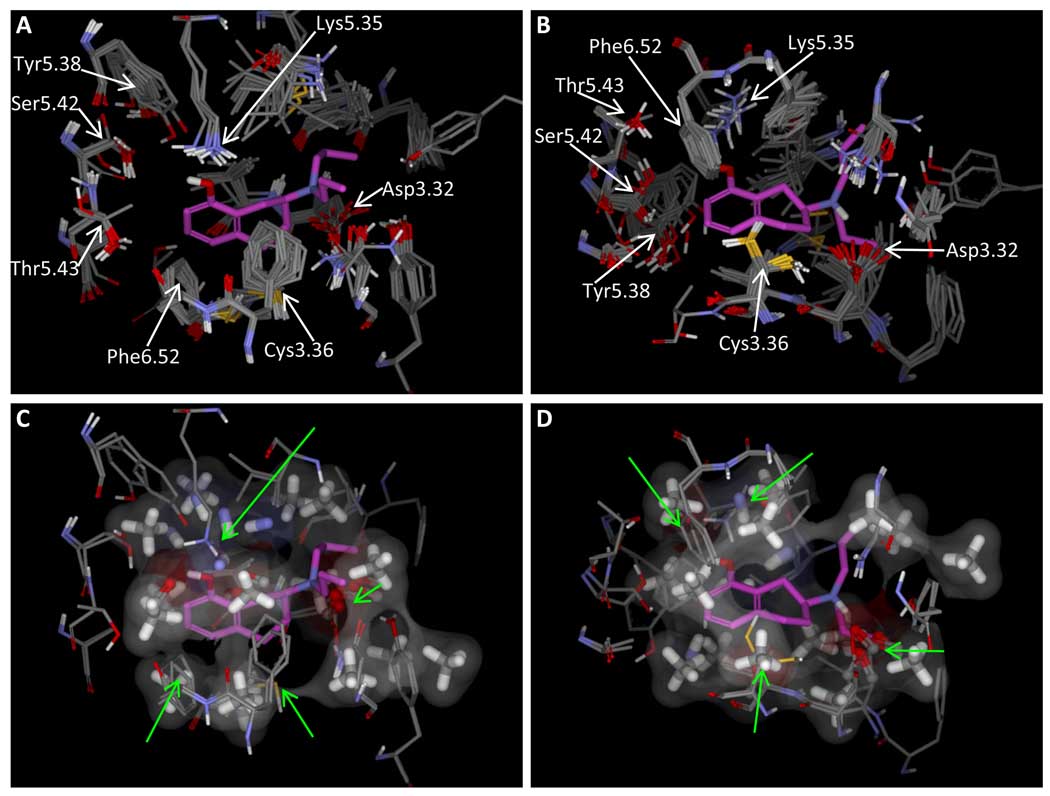
No experimental structure has been determined for 5HT1a, but the recently solved structure of the beta-2 adrenergic receptor (5) offers an excellent template. We used it to generate 20 alternative conformations of human 5HT1a receptor (see Methods). We then used the Surflex-Dock multi-structure docking protocol to dock 8-OH-DPAT to these protein conformations, followed by all-atom protein pocket refinement (45). This process yielded a single high-scoring family of related ligand poses. Figure 13 shows the different contributing protein conformations (panels A and B) along with the single best scoring pose of 8-OH-DPAT. The result was quite consistent with a recent report taking a related approach but using rhodopsin as the modeling template (7). The similarities included interaction with Asp3.32, Phe6.52, and Cys3.36 closing the bottom of the pocket (using the numbering scheme of Ballesteros and Weinstein as in (7)). Interactions with the acceptor functionality of serotonergics (here the hydroxyl oxygen of the ligand) in our model structure can be accommodated by Ser5.42 as proposed by others. However, Thr5.43, Tyr5.38, and Lys5.35 all offered the potential to interact with ligand acceptors. In our preferred binding mode, the lysine was the agent of interaction with the ligand’s acceptor. We propose that the network of hydroxyls and the lysine collectively offer a multitude of different donors and acceptors within 5HT1a. The lysine is conserved in all mammalian 5HT1a receptor sequences, and the consensus amino acid for this position among the full family of serotonin receptors is glutamine. It is possible that the true preference for the lysine is to be in solvent, in which case Tyr5.38 rotates into the binding site in our models. We have made note of the potential for a lysine binding site interaction since it may offer some insight into selectivity of ligands among the different receptor subtypes.

Figure 13.

Panel A shows a model of the 5HT1a receptor, with protein conformations chosen based on docking of 8-OH-DPAT (panel B shows the view from the bottom of A). Panels C and D show the same views, with two selected protein conformations along with the pocketmol. The pocketmol was superimposed by applying the transform that yielded a maximally similar rigid alignment of 8-OH-DPAT bound to the pocketmol to the pose shown within the protein model. The correspondence of key residues within the protein model to pocketmol probes varies somewhat, but it is striking for Asp3.32, Lys5.35, Cys3.36, and Phe6.52 (green arrows).

Panels C and D of Figure 13 show the 5HT1a pocketmol superimposed upon two conformations of the protein. The alignment transformation was derived by a rigid alignment of the preferred pose of 8-OH-DPAT in the model to that preferred in the protein structure. The family of acceptor probes nicely corresponds to Asp3.32, and the donor probes appear to correspond best with Lys5.35, but there is some correspondence with Tyr5.38. It is more difficult to visualize the relationship between the hydrophobic methane probes and the shape of the pocket, but there are clear surface correspondences for Phe6.52, Cys3.36, Asn7.49, and Ile5.33.

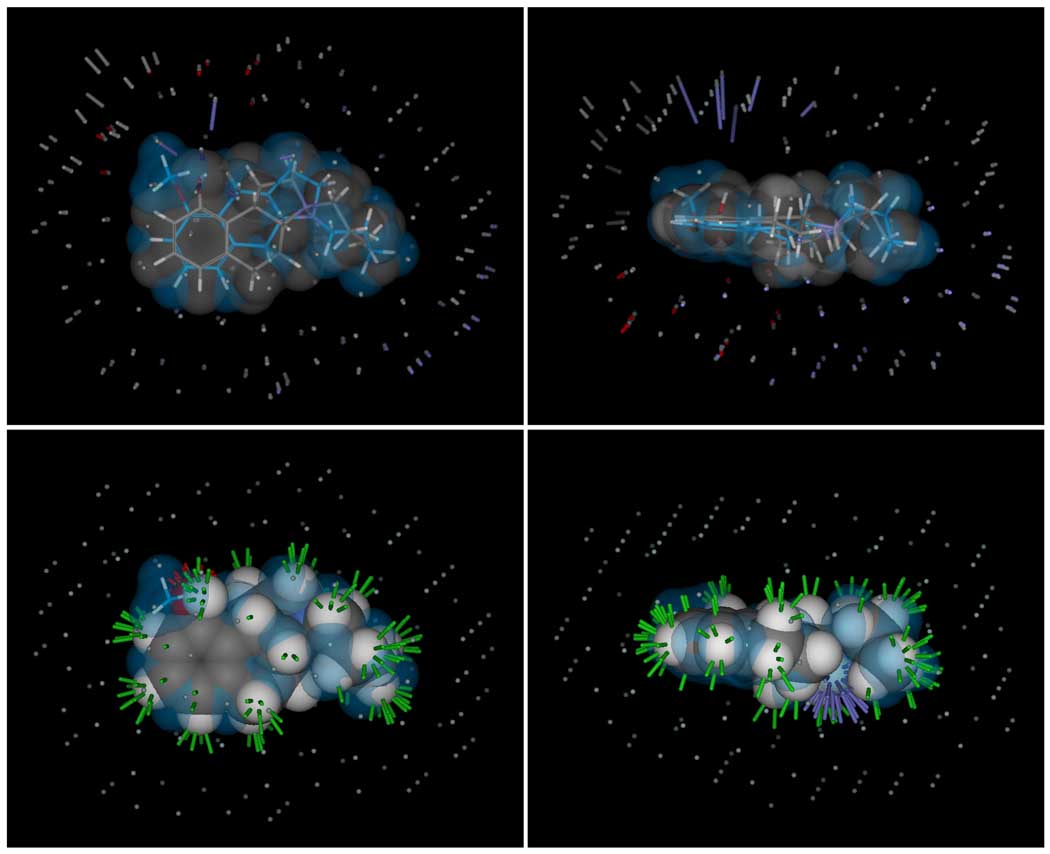
Figure 14 illustrates the surface correspondence differently. In blue is shown the solventaccessible surface of the union of all pose families of 8-OH-DPAT from the docking study, which effectively filled the model protein pocket in multiple configurations. The pocketmol with an orange translucent surface is shown with molecule 4a (pK_d of 10.0, shown with white sticks) and its enantiomer 4b (pK_d of 7.8, shown with green sticks). Except for the single methane probe inside the blue surface (red arrow), the two surfaces were complementary. The bottom panel illustrates the thickness of the pocketmol, which extended far beyond what is required to accommodate ligands such as 4a. Alternate binding modes for a number of training ligands were predicted by the model where the aromatic ring was nearly 90° rotated, including the prediction for M4b. This alternate binding mode accounts for the pocket’s girth and remarkable correspondence to the modeled protein active site.

Figure 14.

Panel A shows the pocketmol and surface (orange) is shown surrounding the union of high-scoring poses of 8-OH-DPAT in docking to the model 5HT1a receptor (blue). Panel B is the view from the bottom of A. The blue surface essentially traces the maximal volume of the protein binding pocket under the different conformations of the protein that are energetically feasible when bound to 8-OH-DPAT. The orange surface was derived purely from ligand activity data, and the blue surface reflects the ligand binding pocket of the protein structural model of 5HT1a based on the 3D4S beta adrenergic structure. Except for the marked probe (red arrows) which resides inside the blue surface, the surfaces are complementary. The poses of training molecules 4a (white sticks) and 4b (green sticks) are predicted to have alternate binding modes with a nearly 90° rotation along the body of the arenes, which explains the width of the pocketmol and the remarkable concordance of the two surfaces.

Relationship to Other Approaches

As discussed in the Introduction, the field of QSAR (even just 3D QSAR) has a long history. The widely used methods that address aspects of ligand binding in a 3D sense include field-based approaches such as CoMFA (8; 46; 47) as well as numerous variations of pharmacophoric methods (9; 10; 11; 12; 13). The field-based methods treat the ligand alignment problem as a separate procedure from model derivation or application and are facilely applied in cases where a common scaffold exists and activity variation relative to substituents is of interest. Systematic substituent analysis is beneficial in understanding SAR for lead optimization, but such methods cannot address activity modeling in the general case across multiple scaffolds. The pharmacophoric methods address the ligand pose problem directly, but the type of subtle activity variation based on hydrophobic shape studied here is beyond the capability of such sparse models. The method we report here has three advantages. First, it addresses the alignment problem as an intrinsic part of model building. Second, predictions of activity (and binding mode) take into account aspects of molecular shape and polarity at a level of detail comparable to that done with structure-based design. Third, the models themselves are physical, which makes them visualizable and leads to intuitive notions of prediction confidence.

The work done by groups to employ data fitting approaches to select and refine homology models of proteins for activity prediction is the closest in spirit to what we report here (7; 48; 49). These approaches have been applied with some success to GPCR ligand discovery. The general idea is to use template-based modeling to generate possible structures of a target and to select and refine protein conformations through consideration of docked poses of known ligands. Our approaches for addressing multiple-instances of ligands could be applied profitably to such refinement protocols. They offer a formal method to address the question of model refinement in the presence of ligand activity data and uncertainty in precise ligand pose.

In a historical sense, the present work is also related to the work of Snyder and Rao on pseudoreceptors (50), further refinements including Vedani (51), and the work of Zbinden with Vedani on PrGen (52). The pseudoreceptor idea was to construct an actual protein binding pocket based upon a hypothesized alignment of ligands that would allow prediction of binding affinities, but it required a number of manual steps. Our approach systematically addresses automated molecular alignment, iterative model and ligand pose refinement, and automated flexible docking of new ligands to predict activity. The PrGen approach made a significant improvement over earlier pseudoreceptor work by use of a “ligand equilibration protocol” which interleaved optimization of the pseudoreceptor (both for fit to ligand binding data and for internal geometry) with relaxation of the ligands in the pseudoreceptor. This formulation is analogous to the multiple instance approach that we introduced (14; 19) in the time between the early pseudoreceptor work (50) and the more refined PrGen approach (52).

We plan to explore hybrid approaches where our pocketmols make direct use of actual or modeled protein binding pockets. A slight generalization of our procedure, allowing for multiple discrete protein conformations, will probably be necessary. The pocketmols we have observed clearly show spatial variation in the preferences of receptor moieties, and the docking study against the 5HT1a model showed many plausible alternative protein conformations. While this could theoretically be treated by allowing the joint configuration of protein and ligand to represent individual instances, we do not believe that the internal energetics of protein conformation variation are easy to model. Instead, the set of protein conformations would be refined such that, when any training ligand was optimized against all of them, the best resulting score would be close to the experimental activity. It is important to note that our approach does not require a modeled structure at all though. So, for complex targets such as ligand-gated ion channels and membrane-bound transporters, where structures are still generally unavailable, the pocketmol method offers a systematic way to build predictive models.

The work being done by many groups using physics-based approaches in cases where protein structures are well-determined is, to a degree, addressing a different problem. While the nominal goal is activity prediction, an overriding concern is fidelity to physical modeling. Our focus is on functionally predictive models that have a basis in the physical binding events we are modeling, but the overriding goal is accurate and practically useful predictions. We believe that empirically derived models based on ligand-binding data offer a practical and potentially more accurate alternative to physics-based approaches. The potential for higher accuracy stems from the fact that we are addressing an easier problem. The derivation of a predictive model of activity for a particular protein target given carefully measured ligand activity data is fundamentally less challenging than deriving a general theoretical and computational protocol for calculating free energies of binding in physically realistic simulation models.

Limitations and Future Directions

The most significant limitation in what we report here is the question of generality and validation on multiple targets. This will take time, but in principle there is no barrier to inducing predictive models for which competitive non-covalent binding drives the biological activity of ligands under study. The most significant methodological limitation is that there are many models that may yield nominally equivalent performance on a set of training data. This results in two problems. First, only some of the models may be truly predictive. Second, among the models that are predictive in a numerical sense for many compounds, only a single model may have a direct correspondence to the true bioactive interactions between ligands and the binding pocket under study. The practical solution to the former issue is a common one in machine learning, where a training set is split into a subset used for model induction and a subset used for model selection. In the case of ligand activity prediction, the best way to make this split is temporally, using compounds synthesized first for model induction and subsequent molecules for model selection. The latter issue is more complex, where two models, for example, yield equally good predictions on a validation set but have quite different geometrical underpinnings. Two such models will disagree in predictions on some new molecules, but this can be taken as an advantage. The existence of two such models indicates that the known ligands do not uniquely disambiguate a particular binding site. Molecules should be tested where predictions from the two models disagree in order to identify which model is closer to being correct and refine it. For example where all known ligands share a common flexible linker, multiple models will exist that constitute variation in the conformations of the linker. Disambiguation could be done by making compounds with different partially rigid linkers that yield non-superimposable ligands.

A related issue is the case where groups of training ligands partially overlap in their true binding site. If the overlap is sufficient to exclude simultaneous occupancy, biochemical experiments will indicate competitive binding. Our seed hypothesis approach has a bias toward minimal volumes, which will tend to incorrectly align molecules in this case. Beginning from such a seed hypothesis may well yield a model with reasonable fit to activity data, and it may be predictive for ligands having either binding mode. Our hope is that in such cases model convergence will be difficult due to the incorrect alignments, but the possibility remains that models will pass nominal convergence tests. A ligand synthesized based on the apparent correspondence of parts between a pair of ligands with different binding modes will not be correctly predicted.

This highlights the importance of formal estimation of prediction confidence. A conservative approach would partially address the case just described, where high confidence would arise only in cases where a new ligand was predicted to have similar activity to a similar known ligand (in a surface-based sense). This is quite limiting though, and we need a general method to decide which parts of a pocket have explicit “support” based on actual exploration with training ligands. It is not sufficient for a part of the pocket simply to interact with some of the training ligands in their final predicted optimal poses, since the training ligands may not have varied at all in some places. Pocket probes may exist as artifacts of the learning procedure, for example providing a constant interaction value for all ligands. Instead, we need to see where molecular structure varied relative to the pocket. The idea is to compare the alignments and scores of ligands based purely on molecular similarity to those that make use of the induced binding site model. Probes in the pocket that result in sharp changes in activity among highly similar molecules exist because they are needed to explain activity and thus have explicit experimental support from assayed compounds.

Conclusions

Practical approaches for ligand activity prediction in lead optimization that do not rely upon well-determined protein structures must address predictions of ligand pose as well as ligand activity. In this study, the multiple-instance learning approach developed for Compass has been adapted for induction of physical models of binding sites. In the challenging test case on 5HT1a presented here, predictive accuracy on diverse chemical series was excellent, both in terms of numerical accuracy and in terms of geometric concordance with accepted models of serotonergic SAR. The approach appears to meet the bar required for operational use in medicinal chemistry lead optimization exercises. Important challenges remain, including validation on large numbers of targets, comparison of induced model binding sites to sites of known structure, development of rigorous approaches for model selection, and implementation of formal methods for estimation of confidence.

Figure 4.

The similarity function makes use of “observer points” (small spheres surrounding each molecule) in order to compare molecular surfaces. In the optimized alignments, the differences are very minor, resulting in a similarity of 0.82 (scale of 0 to 1). These small differences manifest as rods in the upper panels, with length proportional to the magnitude of the difference. The gray rods indicate steric differences. The longer gray rods stem from the protrusion of the methyl group on 8b relative to 4a. The blue rods indicate differences due to positive polar moieties. The longer blue rods are due to a missing hydrogen bond donor on 8b where 4a has a hydroxyl. The other differences are minor, with very slight differences in position and orientation of the acceptor functionality of both molecules, as shown by the red rods. The bottom panels illustrate similarity of the surface of 8b to the surface of 4a, with green rods indicating high shape similarity, red indicating high similarity for negative polar moieties, and blue indicating high similarity for positive polar moieties.

Abbreviations

8-OH-DPAT

8-Hydroxy-N,N-dipropyl-2-aminotetralin

GPCRDB

G-protein coupled receptor database

SSRI

selective serotonin reuptake inhibitor

DRN

dorsal raphe nuclei