Calcium buffering in rodent olfactory bulb granule cells and mitral cells

Abstract

In the mammalian olfactory bulb, axonless granule cells (GCs) mediate self- and lateral inhibitory interactions between mitral cells (MCs) via reciprocal dendrodendritic synapses. Calcium signals in the GC dendrites and reciprocal spines appear to decay unusually slowly, hence GC calcium handling might contribute to the known asynchronous release at this synapse. By recording fluorescence transients of different Ca²⁺-sensitive dyes at variable concentrations evoked by backpropagating action potentials (APs) and saturating AP trains we extrapolated Ca²⁺ dynamics to conditions of zero added buffer for juvenile rat GC apical dendrites and spines and MC lateral dendrites. Resting [Ca²⁺] was at ∼50 nm in both GC dendrites and spines. The average endogenous GC buffer capacities (κ_E) were within a range of 80–90 in the dendrites and 110–140 in the spines. The extrusion rate (γ) was estimated as 570 s⁻¹ for dendrites and 870 s⁻¹ for spines and the decay time constant as ∼200 ms for both. Single-current-evoked APs resulted in a [Ca²⁺] elevation of ∼250 nm. Calcium handling in juvenile and adult mouse GCs appeared mostly similar. In MC lateral dendrites, we found AP-mediated [Ca²⁺] elevations of ∼130 nm with a similar decay to that in GC dendrites, while κ_E and γ were roughly 4-fold higher. In conclusion, the slow GC Ca²⁺ dynamics are due mostly to sluggish Ca²⁺ extrusion. Under physiological conditions this slow removal may well contribute to delayed release and also feed into other Ca²⁺-dependent mechanisms that foster asynchronous output from the reciprocal spine.

Olfactory perception appears to be governed by both fast and slow types of temporal coding as investigated in various species and under various conditions of sensory input (review e.g. Wilson & Mainen, 2006). At the level of the olfactory bulb, a special dendrodendritic microcircuit interconnects olfactory bulb granule cells (GCs) and the lateral dendrites of principal mitral cells (MCs) and tufted cells via reciprocal GC spines. MC input causes both immediate and asynchronous GC responses, the latter occurring on a 500 ms time scale (Jahr & Nicoll, 1982; Isaacson & Strowbridge, 1998; Schoppa et al. 1998). The delayed responses are attributed to mechanisms intrinsic to GCs, such as a transient A-type potassium current (I_A) (Schoppa & Westbrook, 1999; Kapoor & Urban, 2006) or a non-selective cation current (I_CAN) that requires synaptic activation (Hall & Delaney, 2002; Egger, 2008).

However, there are additional possible sources of delay: similar to Purkinje neurons (Fierro & Llano, 1996), GCs might feature an unusually high buffering capacity since their dendritic calcium signals appear rather sluggish when monitored with calcium-sensitive fluorescent dyes (Egger et al. 2003, 2005; Pinato & Midtgaard, 2005; Zelles et al. 2006). At physiological temperatures and otherwise similar conditions, GC Ca²⁺ signals decay with a time constant of ∼400 ms versus∼100 ms in neocortical layer 5 and ∼200 ms in hippocampal CA1 pyramidal cells (Egger et al. 2003, 100 μm Oregon Green BAPTA-1 (OGB-1); Markram et al. 1995, 100 μm Calcium Green-1 (CG-1); Sabatini et al. 2002, 100 μm OGB-1). Ca²⁺ clearance is governed mainly by the endogenous buffering capacity κ_E, i.e. the ratio of bound Ca²⁺ to free Ca²⁺ at equilibrium, and the Ca²⁺ extrusion rate γ (Neher & Augustine, 1992; Helmchen et al. 1996). Strong intrinsic buffering will reduce the peak local concentration of free Ca²⁺ but prolong the time over which the free Ca²⁺ concentration will remain elevated over baseline. Now if transmitter release was very sensitive to small elevations in free Ca²⁺ concentration, a high κ_E could promote late asynchronous output. The attenuation of the peak Ca²⁺ concentration may also make release more asynchronous by leaving vesicles available for delayed release. For example there is a long-lasting, low-level component in presynaptic Ca²⁺ signals at the cerebellar granule cell to Purkinje cell synapse that is correlated to delayed release (Atluri & Regehr, 1998). Long-lasting presynaptic Ca²⁺ signals were also proposed to underlie asynchronous release from hippocampal cholecystokinin-expressing interneurons (Hefft & Jonas, 2005).

Thus here we investigate a possible contribution of intracellular Ca²⁺ handling to the slow response dynamics of rat granule cells by measuring their endogenous calcium buffering capacity and estimating the time course of their calcium transients under physiological conditions. We also studied Ca²⁺ dynamics at the reciprocal synaptic counterpart of GCs, the MC lateral dendrites. These data will both allow for future modelling studies of Ca²⁺ dynamics and release at the reciprocal synapse and serve as a control for the GC results.

While no gross differences between the mouse and rat olfactory system have been revealed so far, with even a high similarity in the respective odour maps (Soucy et al. 2009), calcium handling in mouse GCs might be different, e.g. due to a different distribution of calcium-binding proteins similar to what has been shown for the periglomerular neurons in rat and mouse (Kosaka & Kosaka, 2007). Also, there is a large variability emerging across GCs with respect to the expression of calcium-binding proteins (see Discussion), and the relative composition of these subtypes might be species specific. Mouse data play an increasingly important role in olfactory research, and thus we also investigated mouse GC Ca²⁺ dynamics.

Since regular sodium APs elicited by somatic current injection propagate throughout the entire GC dendrite where they cause robust global calcium entry (Egger et al. 2003), we used these as a fairly well-defined brief signal to elicit calcium signals in dendrites and spines (‘delta function’, Helmchen et al. 1996), that were monitored with two-photon laser scanning microscopy. Saturating AP trains at two frequencies were used to establish maximal levels of fluorescence and to estimate the resting calcium level and the peak calcium amplitude associated with single current-evoked APs (Maravall et al. 2000).

Methods

All experiments were carried out according to national and Ludwig Maximilians Universitat guidelines. Animals were briefly anaesthetized with carbon dioxide and decapitated. Sagittal olfactory bulb brain slices were prepared of juvenile Sprague–Dawley rats (thickness 350 μm; postnatal days (PNDs) 11–16; 60 animals) and B6 mice (thickness 250 μm; PNDs 16–43; 20 animals).

Neurons were visualized using infrared gradient-contrast illumination via an infra-red filter (Hoya, Tokyo, Japan) and patched with pipettes 4–8 MΩ in size. Somatic whole cell patch-clamp recordings were performed with an EPC-9 (HEKA, Lambrecht, Germany). Series resistances measured 10–40 MΩ.

The intracellular solution contained (mm): 130 potassium methylsulfate, 10 Hepes, 4 MgCl₂, 4 Na₂ATP, 0.4 NaGTP, 10 sodium phosphocreatine, 2 ascorbate, at pH 7.2. The added calcium-sensitive dye was either OGB-1 (20, 50 or 100 μm), OGB-6F (100 μm) or Fluo-5F (100 μm, combined with 25 μm Alexa 594 to visualize the neuronal morphology; all dyes from Invitrogen, Carlsbad, CA, USA). The extracellular artificial cerebrospinal fluid was bubbled with carbogen and contained (mm): 125 NaCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 20 glucose, 2.5 KCl, 1 MgCl₂ and 2 CaCl₂. Most experiments were performed at room temperature (RT; ∼21°C). To check for the effect of physiological temperatures on calcium handling we conducted a subset of experiments where the temperature was raised from 21°C to near-physiological temperatures (32–36°C; temperature control via TC-324B, Warner Instruments, Hamden, CT, USA).

GCs and MCs were identified by their morphological appearance and the shape of their current-evoked APs and firing patterns, as evoked via long depolarizing current steps (500 ms) with amplitudes increasing in steps of 10 pA and 50 pA, respectively (Egger et al. 2003; Fig. 1A, Fig. 4A). The average input resistance of the investigated GCs was in the order of 1 GΩ and their resting potential ranged from −80 to −70 mV, similar to our previous data (Egger et al. 2003; Egger, 2008). MCs had an input resistance of ∼200 MΩ and a resting potential range of −60 to −53 mV. Because of the strong expression of low-voltage activated (LVA) calcium channels in GCs (Egger et al. 2003; Pinato & Midtgaard, 2003), GCs were generally held within the range given above, whereas MCs were held at −55 to −60 mV. Leaky GCs/MCs that required more than ∼−30 pA/−100 pA of holding current (i.e. were above spiking threshold) were rejected. Action potentials (APs) were evoked by brief depolarizing somatic current injections (1 ms, 1 nA); saturating trains of APs at 50 and 80 Hz were evoked with 15 successive current injections.

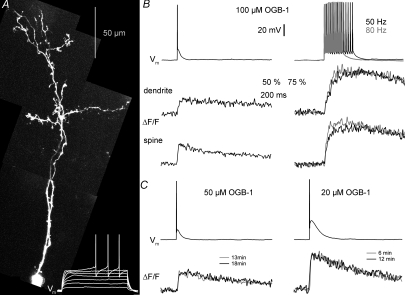
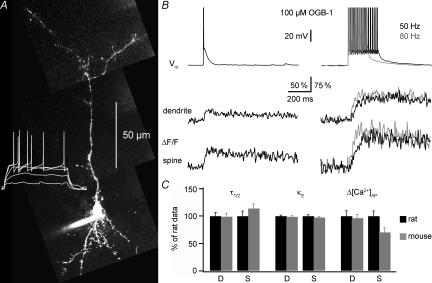
Figure 1. Fluorescence transients ΔF/F in granule cells in response to single-current-evoked APs and AP trains. Fast equilibration.

A, two-photon scan of a granule cell filled with 100 μm OGB-1 and somatic voltage recordings of this cell's response to 500 ms depolarizing pulses (white traces at the bottom). Scaling of the voltage trace similar to traces in B. B, somatic voltage recordings and corresponding averaged fluorescence transients ΔF/F imaged in line-scan mode across the proximal dendrite and a spine of the cell shown in A. The decay half-duration τ_1/2 was 650 ms in the dendrite and 430 ms in the spine. Left, responses to single APs (ΔF/F)_AP; on the right, responses to trains of 15 APs at 50 and 80 Hz, all evoked by somatic current injection. Scaling of all traces as indicated by the bars; note the condensed scaling of the ΔF/F responses to AP trains. C, examples of averaged (ΔF/F)_AP responses from two other granule cell dendrites, filled with 50 μm and 20 μm OGB-1 respectively, and recorded at the indicated times after break-in. Scaling of the voltage recordings and (ΔF/F)_AP transients similar to above.

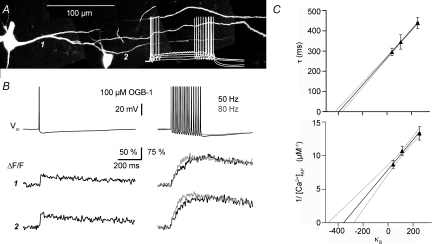
Figure 4. Ca²⁺ handling in juvenile rat mitral cells. Extrapolation to conditions of 0 added buffer.

A, two-photon scan of rat mitral cells (PND 14) filled with 100 μm OGB-1 and somatic voltage recordings of the left cell's reponse to 500 ms depolarizing pulses (white trace). Scaling of the voltage trace similar to traces in B. B, somatic voltage recordings and simultaneous fluorescence transients ΔF/F imaged across the lateral dendrite shown in A, at the positions labelled 1 and 2. Depiction as in Fig. 1B. C, data points from recordings with 20, 50 and 100 μm OGB-1. Upper graph: extrapolation of decay half-duration data vs. buffering capacity κ_B in mitral cell lateral dendrites. Lower graph: inverse of absolute Δ[Ca²⁺] per single somatic AP. Continuous lines, linear fit; dotted lines, 2σ confidence interval; dashed lines, 1σ confidence interval. These intervals do not account for the uncertainty in the data points themselves. All error bars represent s.e.m. The errors in x-direction (s.e.m. of mean κ) are very small and thus barely visible.

Imaging was performed on an Olympus Fluoview system (Olympus Europe, Hamburg, Germany), with two-photon excitation at 800 nm provided by a Ti:sapphire solid-state laser system (Mai Tai, Spectraphysics, Mountain View, CA, USA). The microscope was equipped with a × 60 Nikon fluor water immersion objective (NA 1.0; Nikon Instruments, Amstelveen, The Netherlands). Fluorescence transients in response to somatically evoked APs were imaged in line-scan mode (temporal resolution 2 ms) at different locations along the apical dendrite of GCs, usually within the external plexiform layer, and within its spines or along a lateral dendrite of a MC. Mostly we used rather proximal dendritic locations (10–100 μm from the soma) to make sure that the calcium dye concentration had equilibrated at the imaged location (see also Fig. 1C). For MCs we waited at least 30–40 min before imaging. Fluorescence transients in response to single APs were recorded at a stimulus repetition rate of 0.1 Hz. Saturating fluorescence signals in response to AP trains were imaged at yet lower rates below 0.03 Hz; otherwise, the fluorescence signals in response to the following trains would often decrease in amplitude.

Changes in calcium were measured in absolute terms f₀, f_i and for comparison between experiments in terms of ΔF/F=δf= (f_i−f₀)/f₀. The average background fluorescence was calculated from an adjacent region of the same width as the imaged structure and subtracted from f₀. Since erroneous background correction can result in considerable distortions (Sabatini et al. 2002), the possibility of such influences was analysed carefully (Fig. 5).

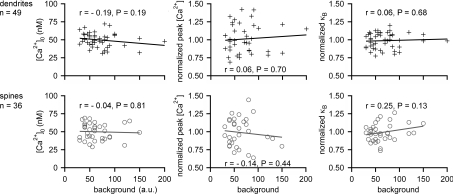
Figure 5. Influence of background levels on [Ca²⁺]₀, peak [Ca²⁺] and κ_B.

Measurements of [Ca²⁺]₀, peak [Ca²⁺] and κ_B for OGB-1 in individual locations in GC dendrites (upper row) and spines (lower row) versus the fluorescence background measured next to these locations. The lines indicate the linear fits, r the Spearman correlation coefficient and P the significance of the difference between the determined r and r= 0 (no correlation). The shown data include all GC OGB-1 measurements at 20, 50 and 100 μm; to heighten the sensitivity to possible correlations, peak [Ca²⁺] and κ_B were normalized to their average value at the concentration at hand and pooled.

Measurement of absolute Ca²⁺ according to Maravall et al. (2000)

Absolute Ca²⁺ levels were measured according to the method of Maravall et al. (2000). We used trains of 15 APs at 80 Hz and 50 Hz, respectively, to establish the saturation correction factor x (eqn (2); Fig. 1B). The K_d of OGB-1 at room temperature was assumed to be ∼200 nm, in accordance with literature values (e.g. Maravall et al. 2000; Wilms et al. 2006; Hendel et al. 2008; Stocca et al. 2008; see Results section for effects of a possible intracellular reduction in dye K_d). The intracellular dynamic range (R_f) of OGB-1 was assumed to be in the order of 6 (Maravall et al. 2000).

For Fluo-5F, K_d was assumed to be 1300 nm (at RT, 1 mm Mg²⁺: Woodruff et al. 2002).

Absolute [Ca²⁺]_i was determined from the fluorescence level f_i via

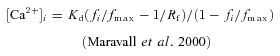(1)

with the maximal fluorescence f_max estimated via the saturating fluorescence measured at two frequencies (ν₁ < ν₂; here ν₁= 50 Hz and ν₂= 80 Hz), using the saturation factor x:

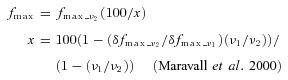(2)

The contribution to the total buffering capacity from the dye κ_B was estimated as:

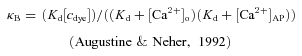(3)

The extrapolation of the measured decay time constants τ and peak amplitude changes in absolute calcium Δ[Ca²⁺]_AP to conditions of zero added buffer in a single compartment allows us to obtain two independent estimates of the endogenous buffering capacity κ_E, with:

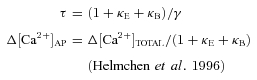(4)

The extrusion rate γ reflects the removal of Ca²⁺ from the cytosol via ionic pumps and exchangers.

While 50 Hz trains in mitral cells would always contain only full-blown APs, some mitral cells were not quite able to respond with full APs to current injections at 80 Hz even at the maximally available current, resulting in a decrease in AP amplitude within the train and thus also a reduced Ca²⁺ entry that would not surpass the plateau level at 50 Hz stimulation. In these cases, we calculated the maximal fluorescence based on the maximal fluorescence measured at 50 Hz and the saturation factor as determined from other mitral cells. Similarly, if in GCs we encountered a decrease in δf_max__ν in the course of recording several trains and/or could not obtain good measurements at both 50 Hz and 80 Hz, we would use only the first measurement and then estimate f_max based on x measured in other GCs.

Data analysis and selection

Data were analysed with custom software based on Igor (Wavemetrics, Lake Oswego, OR, USA). For kinetic analysis, we used only averaged transients with small noise levels after slight smoothing (3–5 point wide sliding window). The decay of all ΔF/F signals was determined in terms of their half-duration time τ_1/2 rather than in terms of the exponential decay time constant τ to keep them comparable to the dynamics of other GC Ca²⁺ signals that decay in a non-exponential fashion (Egger et al. 2005; Zelles et al. 2006; Egger, 2008). For the final estimate of calcium dynamics under physiological conditions (physiological temperature, no added dye), the decay time constant was calculated via τ = ln(2) ×τ_1/2.

After analysis of the absolute [Ca²⁺]_i levels in all experiments the OGB-1 data were selected for the final extrapolation according to the following criteria:

(1)δf_max > 150%. Low values of δf_max might indicate bleaching or other photodamage (Maravall et al. 2000). In our measurements from rat GCs, OGB-1 showed an average δf_max= 205 ± 27% (range 160–256; n= 85 dendrites and spines).

(2)Resting calcium [Ca²⁺]₀ < 100 nm. This criterion was meant to ensure cellular health, since we found an average [Ca²⁺]₀≈ 50 nm (see Results).

(3)κ_B no less than 20% below the average κ_B at the given indicator concentration. While incomplete equilibration was not a problem in the majority of experiments due to rapid filling of the small granule cells (see also Results, Fig. 1), sometimes the recording pipette might have become clogged, resulting in a block of further exchange of pipette solution and cytosol. Data were subjected to particular scrutiny if both κ_B and τ_1/2 were low, a hallmark of insufficient equilibration (see eqn (4)).

(4)A regular firing pattern as described in Egger et al. (2003). We also encountered cells that had the morphological appearance of GCs but bursting or fast-spiking firing patterns (n= 4 for each type). Most of these cells showed Ca²⁺ dynamics that were obviously different from those in GCs with regular firing, with much larger Δ[Ca²⁺]_AP; thus we excluded all of them from the sample (Δ[Ca²⁺]_AP on average 177 ± 117% larger than in the regularly spiking GCs, n= 20 dendrites and spines).

Estimates of the ratio of spine and parent dendritic radius

To estimate the relative diameter of spines and their parent dendrites, we used the full width at half-maximum (FWHM) of the structures in the averaged projection of the line scans onto their spatial dimension after background subtraction. Although most imaged structures are on a size scale comparable to the resolution level of our two-photon microscope (lateral resolution δr= 0.4 ×λ_exc/NA = 0.3 μm) and therefore cannot be resolved faithfully, this procedure yielded a mean radius for GC spines that is very close to the published electronmicroscopic data (0.46 ± 0.08 μm (n= 26) vs. 0.51 ± 0.07 μm from Woolf et al. 1991a). The mean ratio of spine and dendritic radius was then used to estimate their relative surface-to-volume ratios. We also estimated the radius of the MC lateral dendrites (0.86 ± 0.26 μm, n= 23).

Statistics

To assess statistical significance levels, the non-parametric Wilcoxon matched-pairs signed-ranks test was applied for comparing paired data sets. Unpaired data were compared via the Mann–Whitney U test. The significance of correlations was tested using the Spearman correlation coefficient. All averages are given ±s.d. unless indicated otherwise.

Results

Calcium signals in rat granule cell dendrites and spines

As noted previously (Egger et al. 2003), the small size of GCs promoted rapid filling with the dye via the patch pipette. Single action potentials evoked by somatic current injection resulted in detectable fluorescence increases for all dyes and dye concentrations used in this study. Usually, the fluorescence signals at locations close to the cell soma would equilibrate within less than 10 min, showing no more decrease in amplitude and simultaneous increase in decay time constants (Fig. 1C). Therefore we were not able to observe regular loading curves and extrapolate the endogenous buffering capacity for individual cell locations (as e.g. in Maravall et al. 2000); rather, we would wait for 10–15 min and then collect data for different dye concentrations, extrapolating endogenous buffer capacities and unperturbed transients for an ensemble of cells. If these data showed any indication of incomplete loading (see Methods), they were excluded from the final analysis.

The resting Ca²⁺ concentration as calculated via eqn (1) is independent of the concentration of added dye due to homeostatic mechanisms and therefore can be averaged over all data sets. GC [Ca²⁺]₀ was thus estimated to be 51 ± 11 nm in dendrites (n= 53) and 49 ± 12 nm in spines (n= 39).

To estimate the maximal possible fluorescence level f_max in a given compartment, we applied saturating trains of APs at frequencies of 50 and 80 Hz (Fig. 1B). A larger plateau fluorescence was obtained for the latter frequency, allowing us to calculate the degree of saturation x and obtain the maximal fluorescence by applying the correction f_max=f_max__{80 Hz}/x according to Maravall et al. (2000). We found a saturation factor of 85 ± 7%s.d. (n= 40 dendritic locations) for plateau levels δf_max__{80 Hz}, in close agreement with the saturation factor determined by Maravall et al. at 83 Hz (85 ± 4%s.e.m.).

A decrease in δf_max in the course of a measurement was also taken as a warning that the location might have become photodamaged, since such decreases occurred in particular upon repetitive recording and imaging of trains at short intervals. These observations lead us to use an interval of > 30 s between the recordings of AP trains and rather low illumination levels for the final measurements presented here.

Extrapolation of GC data to conditions of zero added buffer

We measured Ca²⁺ dynamics in response to single APs and AP trains in GC spines and dendrites loaded with different indicators at varying concentrations (OGB-1 at 20 μm, 11 spines and 20 dendrites in 9 cells; OGB-1 at 50 μm, 14 spines and 18 dendrites in 9 cells; OGB-1 at 100 μm, 15 spines and 15 dendrites in 11 cells; Fluo-5F at 100 μm in 15 spines and 10 dendrites in 11 cells). Representative data for each of the OGB-1 concentrations are shown in Fig. 1. The decay time constants for (ΔF/F)_AP were averaged over data from these and additional cells to reduce the inherently large standard deviation. For the OGB-1 data we also determined absolute Ca²⁺ levels at rest and at the AP peak, yielding Δ[Ca²⁺]_AP.

The Fluo-5F data did not allow for a proper measurement of absolute Ca²⁺ levels because the resting [Ca²⁺] could not be determined with this medium-affinity dye. Thus we used only the measured decay half-durations, estimating κ_B-Fluo≈ 66. Exclusion of the Fluo-5F data from the extrapolation did not significantly change the result.

Figure 2 shows the extrapolation for both dendrites and spines, for the inverse Δ[Ca²⁺]_AP and τ, respectively, plotted versus the added buffering capacity κ_B. Both x-axis intercepts yield the endogenous buffering capacity κ_E while the y-axis intercepts yield the values of Δ[Ca²⁺]_AP and τ at 0 added buffer, and the extrusion rate γ is the inverse of the slope of the fit. The results are given in Table 1.

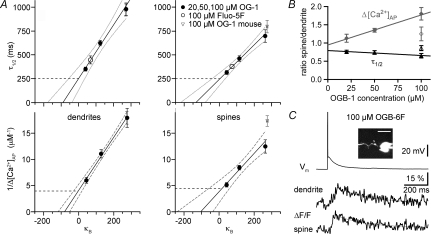
Figure 2. Extrapolation to conditions of 0 added buffer for granule cell dendrites and spines; data with low-affinity dye.

A, upper graphs: extrapolation of decay half-duration data versus exogenous buffering capacity κ_B in dendrites and spines; lower graphs: inverse of absolute change Δ[Ca²⁺] per single somatic AP. Continuous lines, linear fit; dotted lines, 2σ confidence interval; dashed lines, 1σ confidence interval. These intervals do not account for the uncertainty in the data points themselves. All error bars represent s.e.m. The errors in x-direction (s.e.m. of mean κ_B) are very small and thus not visible. B, relation of spine to dendrite Δ[Ca²⁺]_AP (grey filled diamonds) and of τ_1/2 (black filled triangles) of individual pairs of spines and their parent dendrites versus the concentration of OGB-1 (9 pairs for each data point). The open symbols represent data from mouse (16 pairs). The lines represent linear fits of the rat data, the error bars again represent s.e.m. C, representative data for the low-affinity dye OGB-6F. About 20 averaged traces for ΔF/F. The decay half-duration was τ_1/2≈ 200 ms for the dendrite and τ_1/2≈ 240 ms for the adjacent spine. The inset shows a scan of the respective granule cell with the scale bar corresponding to 10 μm; the data shown were recorded from the upper spine next to the GC soma.

Table 1.

Extrapolation results and estimate of extrusion rate in juvenile rat granule cell apical dendrites and spines

	Spine (total n= 55)		Dendrite (total n= 63)
Parameter	Mean	s.d. data fit	Mean	s.d. data fit
21°C
κE via τ	138	100	87	55
κE via Δ[Ca2+]AP	107	75	85	13
τ1/2_RT (ms)	250	90	250	120
Δ[Ca2+]AP (nm)	250	120	230	33
γ_RT (s−1)	550	340	360	150
37°C
τ0_PT (ms)	175	60	175	80
γ_PT (s−1)	870	540	570	240
γ0_PT (μm s−1)	150	90	170	70

Total numbers are given including the Fluo-5F data. The standard deviations (s.d.s) were calculated via propagation of the s.d.s of the fit parameters. The extrusion rate γ was estimated via γ= (1 +κ_E)/τ.

The estimate of τ at physiological temperatures (τ__PT) is based on the previously measured Q₁₀__τ≈ 0.63: τ__PT=τ__RT× (Q₁₀__τ)^ΔT/10 (Egger et al. 2003; see also Lee et al. 2005). If we assume that the temperature dependence of κ_E is weak (e.g. Helmchen et al. 1997), then γ__PT will increase with 1/Q₁₀__τ in relation to γ__RT. This relation is also in accordance with the temperature dependence of extrusion mechanisms. For example the Na⁺–Ca²⁺ exchanger has a Q_10-NaCa≈ 1.57 (from Shannon et al. 2004), so its inverse is 1/Q_10-NaCa≈ 0.64. The Q₁₀ of γ in other preparations was also found within a similar range (e.g. Q₁₀≈ 2, Helmchen et al. 1997; Q₁₀≈ 1.7, Stocca et al. 2008). The amplitude of Δ[Ca²⁺]_AP is likely to be fairly independent of temperature changes, except for a slight decrease in peak [Ca²⁺]_AP due to the shorter duration of the action potential (Q₁₀≈ 0.9, Markram et al. 1995; Lee et al. 2005). We verified these assumptions by measuring [Ca²⁺]₀, Δ[Ca²⁺]_AP and τ_1/2 at the same location at both room temperature and near-physiological temperatures (32–36°C; n= 5 locations in 3 GCs and n= 3 locations in 2 MCs). In both cell types [Ca²⁺]₀ was temperature independent while Δ[Ca²⁺]_AP showed a slight decrease to ∼80% of its value at room temperature and τ_1/2 decreased to ∼50%, yielding a similar Q₁₀__τ1/2≈ 0.6 as used above. Thus κ_E is weakly temperature dependent; most of the dependence is carried by extrusion. For an estimate of the intrinsic extrusion rate γ₀ see the next section.

We also performed measurements in nine GCs using 100 μm of the low-affinity dye OGB-6F (K_d≈ 2.2–3 μm, Holthoff et al. 2004; Invitrogen Handbook). Cells were bright enough at the resting potential to visualize dendrites and individual spines. While low-affinity dyes cannot detect [Ca²⁺]₀ and require substantial averaging for the measurement of small signals such as (ΔF/F)_AP, the decay time course of ΔF/F will resemble unperturbed Ca²⁺ dynamics. The averaged (ΔF/F)_AP signals yielded average decay half-durations very similar to the extrapolated time course at zero added buffer, namely τ_1/2= 270 ± 80 ms at 13 dendritic locations, and τ_1/2= 250 ± 70 ms in nine spines. An example is shown in Fig. 2C.

Granule cell spines versus dendrites

While the extrapolated Δ[Ca²⁺]_AP and τ_1/2 as shown in Table 1 are very similar in spines and dendrites, the large standard deviation might obscure a systematic difference in individual pairs of spines and their parent dendrites. The ratios of the respective values in spines vs. parent dendrites are shown in Fig. 2B. The extrapolation of the mean ratios to zero added buffer yields a ratio of 0.94 ± 0.38 for Δ[Ca²⁺]_AP and a ratio of 0.79 ± 0.19 for τ₀, indicating a similar amplitude of Δ[Ca²⁺]_AP and a slightly faster decay of the signal in GC spines versus their parent dendrites, as would be expected due to their larger surface-to-volume ratio (SVR).

The SVR is required to estimate the intrinsic extrusion rate γ₀=γ/SVR. The SVR is 3/r for a spherical spine and 2/r for a cylindrical dendrite. While GC spines are often ellipsoidal rather than spherical and highly variable in their shape, their average surfaces can be described fairly well by a sphere with an effective radius of 0.51 ± 0.07 μm based on electronmicroscopic data from mouse GCs (at PNDs 30,35; Woolf et al. 1991a). Since there is little quantitative anatomical data on the radius of GC apical dendrites (1.0–1.2 μm proximal to 0.4–0.6 μm distal, Woolf et al. 1991b), we estimated the ratio of spinous to dendritic surfaces in the spines of our data set by measuring the ratio of the apparent width of spines and their parent dendrites in the line scans, 0.85 ± 0.23 in rat (n= 26 pairs; see Methods) and 0.80 ± 0.22 in mouse (n= 13). Together with the electronmicroscopic data cited above, these data led us to assume a mean effective spine radius of 0.5 μm and a mean effective dendritic radius of 0.6 μm for both species. These assumptions yielded intrinsic extrusion rates that are roughly equal for GC dendrites and spines (see Table 1).

Juvenile and adult mouse GCs

Absolute Ca²⁺ concentrations in mouse GCs (Fig. 3) were measured as described before in two sets of cells filled with 100 μm OGB-1, the first from mice aged PNDs 16–23 and the second from mice aged PND 36–43 (10 vs. 14 cells). The two age groups were not significantly different from each other with regard to [Ca²⁺]₀, κ_E and τ_1/2, while there was a slight decrease in Δ[Ca²⁺]_AP with age in the dendrites (P < 0.05, Mann–Whitney U test, 10 vs. 9 locations). A similar but not quite significant decrease was also seen in the spines (P= 0.09). Therefore, the data from both age groups were pooled together, resulting in an average dendritic [Ca²⁺]₀= 51 ± 11 nm (n= 18) and spine [Ca²⁺]₀= 50 ± 11 nm (n= 31). For all buffer-dependent parameters, i.e. Δ[Ca²⁺]_AP, κ_E and τ_1/2, Fig. 3C shows the comparison of the respective rat data relative to the mouse data. There were no significant differences except for Δ[Ca²⁺]_AP in the mouse spines, which was on average 40% smaller than in rat at the same indicator concentration (Mann–Whitney U test, P < 0.025; see also Fig. 2B). Due to this overall similarity between rat and mouse data for 100 μm OGB-1, we did not perform additional experiments in mouse GCs at other dye concentrations.

Figure 3. Ca²⁺ handling in mouse granule cells.

A, two-photon scan of a mouse granule cell (PND 36) filled with 100 μm OGB-1 and somatic voltage recordings of this cell's reponse to 500 ms depolarizing pulses (white trace). Scaling of the voltage trace similar to traces in B. B, somatic voltage recordings and simultaneous fluorescence transients ΔF/F imaged in line-scan mode across the proximal dendrite and a spine of the cell shown in A. Depiction as in Fig. 1B. C, comparison between mouse and rat data for dendrites (D) and spines (S); all using 100 μm OGB-1. The rat data were normalized to 100%. The mouse data are shown as relative fractions and included 24 GCs of mice aged PNDs 16–43.

Rat mitral cells

To characterize Ca²⁺ handling at the opposite side of the dendrodendritic synapse, we also investigated mitral cell Ca²⁺ buffering. In addition, these data serve as a control for our results in granule cells.

For MCs we used similar concentrations of the indicator OGB-1 to those used for GCs (at 20 μm, 16 dendritic locations in 5 cells; at 50 μm, 15 locations in 4 cells; at 100 μm, 16 locations in 4 cells). The large MCs required longer filling for equilibration; even measurements next to the MC soma were made at least 30 min after break-in. Again, if MC data showed any indication of incomplete loading (see also Methods), they were not used for the final analysis. The resting Ca²⁺ concentration as calculated via eqn (1) was averaged over all data sets. [Ca²⁺]₀ thus was estimated to be 55 ± 11 nm in lateral MC dendrites (n= 44 locations). The saturation factor was x= 84 ± 7%s.d. (n= 21 dendritic locations) for plateau levels measured at 80 Hz.

Figure 4 shows a representative experiment and the extrapolation. Its results are given in Table 2. While both the MC buffering capacity and extrusion rate are considerably higher than in GCs, these changes cancel out when it comes to the extrapolated decay half-duration. Therefore, the decay of Ca²⁺ signals in GCs and MCs is likely to be similar also under physiological conditions. The mitral cell lateral dendrites in our data set had an estimated radius of 0.86 ± 0.26 μm, yielding a SVR = 2.3 μm⁻¹.

Table 2.

Extrapolation results and estimate of extrusion rate in juvenile rat mitral cell lateral dendrites

Parameter	Mean	s.d.
21°C
κE via τ	400	390
κE via Δ[Ca2+]AP	360	340
τ1/2_RT (ms)	270	90
Δ[Ca2+]AP (nm)	130	40
γ_RT (s−1)	1470	1360
37°C
τ0_PT (ms)	190	60
γ_PT (s−1)	3060	2830
γ0 (μm s−1)	1320	1220

Analysis of background influence and other sources of error and variability

The dark noise level of our detection system at the used photomultiplier tube voltage and gain was in the order of 30 arbitrary units (total dynamic range 4096). The majority of our data sets had a background no more than two times above the dark noise level (including the dark noise; background/dark noise = 2.2 ± 1.1, n= 51) and was also small in relation to the basal fluorescence level of the imaged structures (f₀/background = 6.5 ± 3.9). To control for an erroneous manipulation of the raw data by background subtraction (Sabatini et al. 2002) we tested whether there was a systematic relationship between the background level and the measured parameters [Ca²⁺]₀, κ_B and peak [Ca²⁺]_AP. To obtain a data set large enough to reveal possible correlations, the individual data for κ_B and peak [Ca²⁺]_AP for the different concentrations of OGB-1 were normalized to their mean values, yielding a total of 48 dendritic and 36 spine data points. Figure 5 shows that no significant correlations were found.

The intracellular environment is likely to lower the affinities (K_d) of the dyes, resulting in higher actual [Ca²⁺] levels that scale directly with K_d (eqn (1)). κ_B will scale inversely with K_d (eqn (3)) and thus for a given increase in K_d we obtain similar decreases in κ_E. Therefore our results for the endogenous buffering capacity κ_E represent an upper limit, while the absolute [Ca²⁺] concentrations represent a lower limit. Variations in R_f affect the results more weakly: an increase in R_f by 25% will cause a 7% reduction in buffering capacity and a 16% increase in absolute Ca²⁺ concentrations. If we used R_f= 8.5 as an upper limit (Maravall et al. 2000), κ_E would decrease by 10%.

Another potential source of variability is the existence of various subtypes of GCs (see Discussion); the observed GCs with irregular firing patterns that were excluded from the sample (see Methods) may represent correlates of such subtypes.

Discussion

Granule cell and mitral cell Ca²⁺ handling and dendritic release

The present extrapolation of GC Ca²⁺ dynamics to conditions of zero added buffer allows for two main conclusions. First, there is little difference in Ca²⁺ handling between the GC spine and the dendrite with respect to all extrapolated parameters (see below). Second, the apparently slow dynamics observed in previous measurements are not due to a particularly high GC endogenous buffering capacity. GC κ_E is within a medium range (∼100), not as low as in hippocampal or cortical pyramidal cell fine dendrites and spines (range 20–60, Maravall et al. 2000; Sabatini et al. 2002; Cornelisse et al. 2007), and not as high as in Purkinje cells (∼2000, Fierro & Llano, 1996) or cortical layer 2/3 inhibitory interneurons (∼300, Kaiser et al. 2001) and hippocampal basket cells (∼200, Aponte et al. 2008). The apparently slow decay of GC calcium signals is caused rather by a comparably low extrusion rate (γ; 600–900 s⁻¹) at physiological temperatures, whereas extrusion in most of the other mentioned neuronal types was found to be at least two times faster.

Thus GC Ca²⁺ signalling under physiological conditions is likely to occur on an intermediate time scale (τ≈ 175 ms; see Fig. 6). Isaacson & Strowbridge (1998) and Schoppa et al. (1998) measured a time constant of asynchronous release from GCs of τ_as≈ 500 ms at room temperature; its Q₁₀ was sampled in a small set of experiments as 2.3 ± 0.7 (n= 3; Isaacson & Strowbridge, 1998), yielding a physiological time scale of τ_as__PT≈ 150 ms. Thus a main conclusion from our data is that asynchronous release from the GC spine is likely to be fostered by the slow removal of Ca²⁺ from the cytosol. Delayed release may be also triggered in conjunction with mechanisms of slow Ca²⁺ entry into the GC spine, e.g. due to activation of I_CAN (Hall & Delaney, 2002; Egger, 2008).

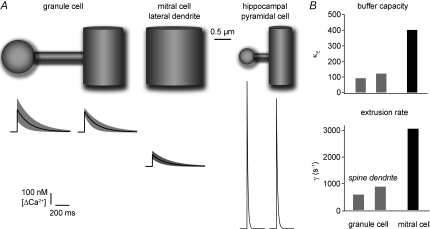
Figure 6. Estimated average Ca²⁺ dynamics under physiological conditions in granule cells, mitral cell lateral dendrites and hippocampal CA1 cells.

This figure illustrates the estimated mean dimensions and the extrapolated Ca²⁺ dynamics of the investigated structures (GC spine and dendrite, MC lateral dendrite; Tables 1 and 2) and a spine on a fine hippocampal pyramidal cell dendrite for comparison. The olfactory bulb anatomical data were in part taken from Woolf et al. (1991a; see Methods and Results). The hippocampal data were taken from Harris & Stevens (1989) and Sabatini et al. (2002; their Table 1), respectively. The black traces show the mean Ca²⁺ transient, the grey band denotes the s.d. with respect to Δ[Ca²⁺]_AP and τ. B shows the extrapolated buffering capacities and extrusion rates for GC spines and dendrites and MC lateral dendrites under physiological conditions.

Is there a general correlation between κ_E and asynchronous release, in the sense that medium to higher buffering capacities may favour delayed release? This hypothesis is difficult to test for two reasons: there is scant data available regarding κ_E at synapses with delayed release, and there are also other tightly intertwined parameters that factor into the relation between Ca²⁺ influx and release, such as the speed of buffering, the size of the relevant domain, the affinity of the calcium sensor and the degree of coupling between Ca²⁺ entry and Ca²⁺ sensor. For example, asynchronous release might be favoured by high buffering capacities (Atluri & Regehr, 1998) and/or parvalbumin expression (Collin et al. 2005); however, reduced Ca²⁺ buffering increased asynchronous release in rod bipolar cells (Singer & Diamond, 2003), and parvalbumin-expressing hippocampal interneurons are less prone to asynchronous release than cholecystokinin-expressing interneurons (Hefft & Jonas, 2005). Our own data also do not support such a relation, since MC lateral dendrites show a considerably higher κ_E than GC spines while there are no reports of asynchronous release at the dendrodendritic MC to GC synapse. Nevertheless a κ_E in the medium to high range may be necessary – but not sufficient – to sustain asynchronous release.

While we found Ca²⁺ dynamics in mitral cell dendrites to occur on a similar time scale to those in GC dendrites and spines, the underlying mechanisms operate in a quite different manner, with a rather high κ_E (∼400) and an accordingly high extrusion rate (∼3000; see Fig. 6B). Perhaps these differences contribute to the contrasting forms of short-term plasticity that were observed at the MC–GC synapse and the GC–MC synapse (Dietz & Murthy, 1995). Previous Ca²⁺ imaging data in mitral cells in the main and accessory olfactory bulb also showed fairly slow AP-mediated transients within the lateral and apical dendrites including the tuft (Xiong & Chen, 2002; Ma & Lowe, 2004; Urban & Castro, 2005; note the apparently biphasic tuft signals in Yuan & Knöpfel, 2006).

The considerable variability in the MC data is most likely due to the tapering of the MC lateral dendrites in our data set, reflected in the large standard deviation in their dendritic diameter.

GC spines and dendrites

We find that granule cell spines and dendrites have rather similar Ca²⁺ handling properties. There is no apparent specialization of the reciprocal GC spine that may be related to its input/output function as compared to the dendrite. Interestingly, the electronmicroscopic data indicate that there are varicosities on GC dendritic shafts that also bear reciprocal synapses (Woolf et al. 1991a); the density of these shaft synapses is not known. Morphologically, the dimensions of a GC spine are comparable to a 1 μm section of parent dendrite and thus GC spines and dendrites also resemble each other in this respect. However, there could be a differential distribution of mobile buffers that becomes washed out in the whole-cell configuration used here.

In hippocampal CA1 neurons, Ca²⁺ handling in spines and small, distal dendrites was also found to be fairly similar to each other (Fig. 6; Table 1 in Sabatini et al. 2002), whereas spine Ca²⁺ kinetics were faster and κ_E lower by a factor of 2 in cortical pyramidal cells (Cornelisse et al. 2007). Compared to GC spines, both hippocampal and cortical spines show a considerably higher Ca²⁺ influx. This is likely to be due to their smaller size (see e.g. Cornelisse et al. 2007): GC spines have a 6-fold larger surface and a 10-fold larger volume than hippocampal spines (Woolf et al. 1991a). Figure 6A illustrates this point by showing the relative anatomical sizes of an ‘average’ GC spine and dendrite, a mitral cell lateral dendrite and a CA1 cell spine and dendrite (Harris & Stevens, 1989) and the sizes of their average Ca²⁺ signals due to backpropagating APs.

Sources of variability

While our two data sets on τ and Δ[Ca²⁺]_AP converge quite well onto similar values of κ_E for both GC dendrites and spines and MC dendrites, there is a considerable variability of the data across cells. Some may be due to errors in the measurement process such as insufficient dye equilibration. Another possible source of variability is the existence of various GC subtypes, both with respect to the expression of Ca²⁺-binding proteins (CaBPs) and their maturational state, since GCs are subject to constant turnover (Bayer, 1985).

First, the expression of CaBPs in olfactory bulb GCs is variable and also species specific. In rodents, some GCs express calretinin, and a non-overlapping subset expresses neurocalcin. α-Ca²⁺/calmodulin-dependent protein kinase II (α-CaMKII) is heavily expressed and neuronal calcium sensor 1 (NCS-1) is also widespread among GCs, whereas calbindin is at best weakly expressed and parvalbumin was not found (e.g. Toida et al. 1996; Brinon et al. 1999; Zou et al. 2002; Treloar et al. 2005).

Second, maturation might well include changes in Ca²⁺ buffering as shown e.g. for hippocampal and cerebellar interneurons or retinal ganglion cells (Collin et al. 2005; Mann et al. 2005; Stocca et al. 2008). While the GCs in our sample appeared mature with respect to their anatomy and AP firing (Carleton et al. 2003), there might be more subtle gradations of maturation that affect Ca²⁺ handling.

Another consequence of GC turnover is the coexistence of early-born and adult-born cells. These two populations have been found to differ with respect to certain physiological properties (Lledo et al. 2008) and thus may also differ in Ca²⁺ handling. While our juvenile rat data are restricted to early-born GCs simply because of the young age of the animals, the mouse data may encompass both early-born and adult-born neurons.

Outlook and conclusion

The parameters we have measured will help to interpret measurements of population activity from olfactory bulb neurons that have been either bulk-loaded with indicator or express genetically encoded indicators (e.g. Stosiek et al. 2003; Hendel et al. 2008) and thus contribute to the analysis of in vivo observations of olfactory processing. Mathematical approaches (e.g. Borst & Abarbanel, 2007) may allow us to extrapolate unperturbed GC Ca²⁺ signals where Ca²⁺ entry – unlike in the case of backpropagating, current-evoked APs – does not resemble a δ-function, such as during low-threshold spikes or synaptic calcium entry within a spine (Egger et al. 2005; Egger, 2008).

In conclusion, GC Ca²⁺ dynamics are slow under physiological conditions, owing mostly to sluggish Ca²⁺ extrusion. This slow clearance of Ca²⁺ from the cytoplasm may contribute to delayed release and also feed into other Ca²⁺-dependent mechanisms that foster asynchronous output from the reciprocal spine. Conversely, extrusion from mitral cell lateral dendrites is relatively fast while their buffering capacity is high.

Glossary

Abbreviations

AP

action potential

CG

Calcium Green

GC

granule cell

KB

dye buffering capacity

κ_E

endogenous buffering capacity

γ

extrusion rate

MC

mitral cell

OGB

Oregon Green BAPTA

PND

postnatal day

PT

physiological temperature

RT

room temperature

SVR

surface-to-volume ratio

Author contributions

O.S. contributed to the recording and analysis of the Fluo-5F data set in rat GCs and the data set in adult mouse GCs, and to the revision of the draft.