Abstract
Structural changes in myosin motors and filaments during relaxation from short tetanic contractions of intact single fibres of frog tibialis anterior muscles at sarcomere length 2.14 μm, 4°C were investigated by X-ray diffraction. Force declined at a steady rate for several hundred milliseconds after the last stimulus, while sarcomere lengths remained almost constant. During this isometric phase of relaxation the intensities of the equatorial and meridional M3 X-ray reflections associated with the radial and axial distributions of myosin motors also recovered at a steady rate towards their resting values, consistent with progressive net detachment of myosin motors from actin filaments. Stiffness measurements confirmed that the fraction of motors attached to actin declined at a constant rate, but also revealed a progressive increase in force per motor. The interference fine structure of the M3 reflection suggested that actin-attached myosin motors are displaced towards the start of their working stroke during isometric relaxation. There was negligible recovery of the intensities of the meridional and layer-line reflections associated with the quasi-helical distribution of myosin motors in resting muscle during isometric relaxation, and the 1.5% increase in the axial periodicity of the myosin filament associated with muscle activation was not reversed. When force had decreased to roughly half its tetanus plateau value, the isometric phase of relaxation abruptly ended, and the ensuing chaotic relaxation had an exponential half-time of ca 60 ms. Recovery of the equatorial X-ray intensities was largely complete during chaotic relaxation, but the other X-ray signals recovered more slowly than force.
Skeletal muscle is activated by a transient increase in intracellular free calcium concentration, [Ca2+]i, triggered by depolarisation of the muscle cell membrane. The Ca2+ ions bind to troponin on the actin-containing thin filaments of the muscle sarcomere, causing a change in thin filament structure that allows myosin motors to bind to actin and generate force (Gordon et al. 2000). The structure of the myosin-containing thick filaments also changes on activation: the quasi-helical organisation of the myosin motors on the surface of the filaments is lost, and the axial periodicity of the filaments increases by about 1.5% (Huxley et al. 1982). The functional significance of the change in the periodicity of the myosin filaments during muscle activation is unclear.
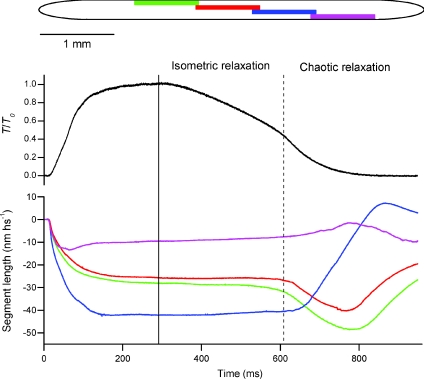
Muscle relaxation at the end of electrical stimulation is associated with a decrease in [Ca2+]i, as Ca2+ ions are re-accumulated into the sarcoplasmic reticulum. The dynamic relationship between [Ca2+]i and force during relaxation is complex, however, and its molecular basis is poorly understood. [Ca2+]i decreases relatively quickly after the end of stimulation, and is reduced to about 10% of its plateau value within 100 ms after a short tetanus in amphibian muscle at 4°C (Blinks et al. 1978; Cannell, 1986; Caputo et al. 1994; Konishi, 1998). The final 10% of [Ca2+]i recovery is much slower, however, lasting for tens of seconds in these conditions. The time course of mechanical relaxation (Fig. 1) is quite distinct from that of [Ca2+]i. After an initial lag of about 60 ms, force decreases at an almost constant slow rate for several 100 ms, a period in which [Ca2+]i has become roughly constant. Force typically declines to about half of its plateau value (T0) during this phase of relaxation, which is called isometric relaxation because the lengths of sarcomeres along the muscle fibre remain close to their tetanus plateau values (Fig. 1; Huxley & Simmons, 1970; Edman & Flitney, 1982). Isometric relaxation is terminated by the onset of redistribution of sarcomere lengths along the fibre, accompanied by a ‘shoulder’ in the force record, corresponding to an acceleration of the relaxation rate. This late phase of relaxation, called chaotic relaxation, has an approximately exponential time course and is accompanied by large changes in local sarcomere length, so that some fibre segments shorten whilst others are stretched (Fig. 1). Chaotic relaxation triggers a secondary transient increase in [Ca2+]i (Blinks et al. 1978; Cannell, 1986; Caputo et al. 1994; Konishi, 1998).
Figure 1. Changes in the length of muscle fibre segments associated with tetanic stimulation at constant fibre length.
Force (black) is normalized by its plateau value (T0). Segment length records (nm per half-sarcomere; nm hs−1) correspond to bars of the same colour in the fibre diagram. The vertical continuous and dashed lines denote the end of electrical stimulation and force shoulder, respectively.
We investigated the factors controlling the rate of isometric relaxation and the onset of chaotic relaxation at the level of structural changes in the actin- and myosin-containing filaments using X-ray diffraction from isolated single muscle fibres. Some of these X-ray signals have been recorded previously during relaxation of whole skeletal muscles (Huxley et al. 1982; Kress et al. 1986; Matsuo & Yagi, 2008), but the two phases of relaxation are not clearly resolved in multicellular preparations, and the structural changes associated with each phase have not been separated. We measured the equatorial reflections associated with movement of the myosin motors between the myosin and actin filaments (Haselgrove & Huxley, 1973; Cecchi et al. 1991), the intensity and spacing of the M3 reflection from the axial repeat of the motors along the myosin filaments (Huxley & Brown, 1967; Huxley et al. 1982), and the interference fine structure of the M3 reflection, which measures the axial movement of the myosin motors with high spatial resolution (Linari et al. 2000; Piazzesi et al. 2002; Reconditi et al. 2004). We also measured the axial and layer line reflections associated with the quasi-helical structure of the myosin filaments in resting muscle (Huxley & Brown, 1967; Huxley et al. 1982), and the ca 44 and 38 nm axial reflections associated with myosin-binding protein C and troponin, respectively (Huxley & Brown, 1967; Otsuki et al. 1967; Rome et al. 1973a,b;).
Methods
Ethical approval, muscle fibres and experimental protocol
Frogs (Rana temporaria except where noted) were killed by decapitation and destruction of the brain and the spinal cord, following European Community Council Directive 86/609/EEC, and in conformation with the UK Animals Scientific Procedures Act, 1986 (Drummond, 2009). Single fibres ca 6 mm long were dissected from the tibialis anterior muscle and mounted via aluminium foil clips attached to the tendons in a trough containing Ringer solution (115 mm NaCl, 2.5 mm KCl, 1.8 mm CaCl2, 3 mm phosphate buffer, pH 7.1). A pair of mica windows was positioned close to the fibre, about 600 μm apart, to minimise the X-ray path in solution. Sarcomere length, fibre length and cross-sectional area were measured with a ×40 water immersion objective and a ×25 eyepiece. Resting sarcomere length was set to 2.14 ± 0.02 μm. Force was measured with a capacitance transducer (Huxley & Lombardi, 1980). The length of a population of sarcomeres in a 1–2 mm segment of the fibre was measured with a striation follower (Huxley et al. 1981) in control tetani before mounting the fibre vertically at the beamline. Trains of stimuli of alternate polarity, at a frequency of 20–24 Hz, were delivered every 4 min at 4°C and via platinum electrodes on the top and bottom edges of the opposing windows to elicit fused tetani of duration 390–550 ms. The segment length and stiffness measurements in Figs 1 and 6 were made in the University of Florence using the same methods and protocols in a tibialis anterior fibre from Rana esculenta. Stiffness was determined from in-phase force changes associated with small (2 nm per half-sarcomere peak-to-peak) 4 kHz length oscillations, monitored with the striation follower in a segment near the force transducer end of the fibre.
Figure 6. Half-sarcomere and myosin motor strain during isometric relaxation.
A, force and segment length traces showing the superimposed 4 kHz oscillations used to determine half-sarcomere stiffness during the tetanus rise and isometric relaxation. The vertical full and dashed lines denote the end of electrical stimulation and force shoulder, respectively, and the insets show the oscillations close to these times on an expanded time scale. B, half-sarcomere strain (circles) and myosin motor strain (triangles) during isometric relaxation (filled symbols) and the tetanus rise (open symbols). Mean ±s.d. from 3 fibres with plateau force 155 ± 5 kPa. The continuous line was obtained by linear regression to the open circles and has slope 2.06 ± 0.09 nm/T0 and ordinate intercept 1.63 ± 0.06 nm. C, number of myosin motors attached to actin as a fraction of that at the tetanus plateau, during isometric relaxation (filled symbols) and the rising phase of a tetanus (open symbols).
X-ray data collection
The trough was sealed to prevent solution leakage, and the fibre was mounted vertically at beamline ID2 of the European Synchrotron Radiation Facility (ESRF), which provided up to 2 × 1013 photons s−1 at 0.1 nm wavelength in a beam of size ca 300 μm (horizontal, full width at half-maximum (FWHM)) and ca 100 μm (vertical) at the fibre. The beam was attenuated for fibre alignment. To minimise radiation damage, X-ray exposure was limited to the data collection period using a fast electromagnetic shutter (nmLaser Products, Inc., Sunnyvale, CA, USA) and the fibre was moved vertically by 0.1–0.2 mm between tetani. Data were collected from 40–120 tetani in each fibre with no detectable sign of radiation damage. X-ray diffraction patterns were recorded with 5 ms exposures using the FReLoN CCD-based detector with image intensifier (Narayanan et al. 2001), active area 200 × 200 mm2, mounted 10 m from the fibre. The 2048 × 2048 pixels of the CCD were binned by 16 in the horizontal direction and 2 in the vertical direction before the readout to increase the signal-to-noise ratio. X-ray data are presented from four fibres with cross-sectional area 18 000 ± 4000 μm2 (mean ±s.d.) and isometric plateau force (T0) 201 ± 12 kPa.
Data analysis
X-ray diffraction data were analysed using the SAXS package (P. Boesecke, ESRF), Fit2D (A. Hammersley, ESRF) and IgorPro (WaveMetrix, Inc.). Two-dimensional patterns were centred and aligned using the equatorial 1,1 reflections, then mirrored horizontally and vertically. The distribution of diffracted intensity along the meridional axis of the X-ray pattern (parallel to the fibre axis) was calculated by integrating from 0.012 nm−1 on either side of the meridian for the myosin-based M3 reflection, and 0.0046 nm−1 for the M2, troponin (T1) and myosin-binding protein C (C1) reflections. The first myosin layer line (ML1) was integrated in the region between 0.064 and 0.037 nm−1 from the meridional axis. Background intensity distributions were fitted using a convex hull algorithm or straight-line fitting and subtracted; the small background remaining when the convex hull algorithm had been used was removed using the intensity from a nearby region of the X-ray pattern containing no reflections. Integrated intensities were obtained from the following axial regions: M3, 0.067–0.072 nm−1; M2, 0.046–0.048 nm−1; ML1, 0.019–0.023 nm−1; T1, 0.025–0.027 nm−1; C1, 0.021–0.024 nm−1. The limits for ML1 were chosen to exclude the contribution of the first actin layer line. The cross-meridional width of the M3 reflection was determined from a Gaussian fit of the integrated intensity in the axial region 0.071–0.067 nm−1. The equatorial intensity distribution was determined by integrating from 0.0036 nm−1 on either side of the equatorial axis, and the intensities of the 1,0 and 1,1 reflections from subsequent radial integrations in the regions 0.025–0.033 nm−1 and 0.044–0.056 nm−1, respectively. The interference components of the M3 reflection were determined by fitting multiple Gaussian peaks with the same axial width to the meridional intensity distribution, and the total intensity of the reflection was calculated as the sum of the component peaks. The spacing of each reflection was determined from the weighted mean of the component peaks, and calibrated using a spacing of 14.34 nm in the resting fibre (Haselgrove, 1975). The point spread function of the FReLoN detector was ca 250 μm (FWHM), and the combined instrumental point spread function was negligible compared with the radial width of the M3 reflection.
Force, stimulus, sarcomere length and X-ray acquisition timing were collected and analysed using LabVIEW (National Instruments Co., Austin, TX, USA). The force and time at the relaxation shoulder were determined from the intersection of linear and exponential fits to the isometric and chaotic phases of relaxation, respectively.
Results
Two-dimensional X-ray diffraction patterns at rest and at the isometric tetanus plateau
The low-angle X-ray diffraction pattern from resting muscle (Fig. 2A) contains a series of reflections due to the regular organisation of the myosin motor domains on the surface of the myosin-containing thick filaments of the muscle sarcomere (Huxley & Brown, 1967). The quasi-helical arrangement of the motors is responsible for the horizontal off-axis layer lines, of which the most intense is the first myosin layer line, ML1, corresponding to the helical periodicity of 43 nm along the filament axis. On the meridian (vertical axis) of the X-ray pattern, intense reflections appear at the second and third orders of this spacing, called the M2 and M3, respectively (Fig. 2A; Fig. 2C, thick line). The M2 region contains a closely-spaced cluster of reflections, and for time course analysis we used the most intense peak, corresponding to a spacing of ca 21.5 nm. The meridional reflections around the 43 nm periodicity of the ML1 also contain several components. The most intense peaks correspond to axial spacings of ca 38 and 44 nm (Huxley & Brown, 1967), and are thought to arise from troponin in the actin-containing thin filaments and myosin-binding protein C in the thick filaments, respectively (Rome et al. 1973a,b;). These reflections will therefore be referred to as T1 and C1 (Fig. 2A and C). The T1 reflection appears as a doublet, but was considered as a single reflection for the purposes of the present experiments.
Figure 2. Low-angle X-ray diffraction pattern from isolated muscle fibres at rest (A) and at the plateau of an isometric tetanus (B).
The fibre axis is vertical. The ML1, M2 and M3 reflections arise from the axial periodicity of the myosin motors and filaments; the T1 and C1 reflections from that of troponin and myosin-binding protein C, respectively. The equatorial 1,0 and 1,1 reflections are sensitive to the mass distribution in the hexagonal lattice of myosin and actin filaments. The intensity of the regions near the equatorial and meridional axes has been digitally attenuated so that the intensity distributions can be seen in the same image as the weaker layer lines. C, meridional intensity distributions at rest (thick line) and at the tetanus plateau (thin line). The dashed lines show integration limits for individual reflections. Total exposure, 130 ms.
The equator (horizontal axis) of the X-ray pattern contains a series of reflections, arising from the hexagonal lattice of thick and thin filaments, which are indexed according to the planes of this lattice as 1,0, 1,1 etc. The 1,0 reflection is brighter than the 1,1 reflection in the resting fibre, indicating that the myosin motors are close to the myosin filament (Haselgrove & Huxley, 1973).
At the plateau of an isometric tetanus (Fig. 2B; Fig. 2C, thin line) the myosin-based ML1 and M2 reflections become very weak (Huxley et al. 1982), as does the C1 reflection (Martin-Fernandez et al. 1994; Matsuo & Yagi, 2008). The T1 reflection changes to a smaller extent (Martin-Fernandez et al. 1994; Matsuo & Yagi, 2008; Sugimoto et al. 2008). The M3 remains strong, but broadens across the meridian and moves closer to the centre of the X-ray diagram, indicating an increase in the axial spacing of the myosin filament backbone by about 1.5% (Huxley et al. 1982; Linari et al. 2000). Moreover this reflection is split into two sub-peaks of roughly equal intensity during active contraction, as a result of X-ray interference between the two arrays of myosin motor domains in each filament (Linari et al. 2000). This interference fine structure is a sensitive measure of the axial motion of the motor domains during contraction (Piazzesi et al. 2002, 2007; Reconditi et al. 2004). The equatorial 1,1 reflection broadens during the tetanus and becomes brighter than the 1,0 (Fig. 2B), signalling movement of the myosin motor domains towards the actin filaments (Haselgrove & Huxley, 1973).
We measured the time courses of the changes in the 1,0, 1,1, ML1, M2, M3, C1 and T1 X-ray reflections after the end of electrical stimulation in tetanic contractions in which fibre length was held constant in order to determine the changes in myosin and actin filament structure and the movement of the myosin motors during isometric and chaotic relaxation, and to compare the time courses of these structural changes with that of force.
Equatorial reflections
After the last stimulus of an isometric tetanus, there was a delay of ca 60 ms, then the force (Fig. 3A–C, continuous line) started to decrease at an almost constant rate. This is the isometric phase of relaxation, in which sarcomere length remains almost constant and uniform along the fibre (Fig. 1). About 400 ms after the last stimulus, when the force had decreased to about half its plateau value, the rate of relaxation suddenly increased; this is the force shoulder (vertical dashed line) marking the start of chaotic relaxation in which there is large-scale redistribution of sarcomere length along the fibre (Fig. 1). Chaotic relaxation had a roughly exponential time course, with a half-time of about 40 ms in this fibre.
Figure 3. Changes in the intensities of the equatorial reflections during relaxation.
A, D and G, intensity of the 1,1 reflection (I11); B, E and H, intensity of the 1,0 reflection (I10); C, F and I, equatorial intensity ratio I11/I10. A–C, time courses following the last stimulus in a single fibre; force is the continuous line; the vertical dashed line marks the force shoulder. D–F, relationship between equatorial intensity parameters and force during relaxation (n= 4 fibres), with linear fits to X-ray data before the force shoulder. G–I, time courses following the force shoulder (n= 3) with exponential fits (continuous lines). I10 and I11 are normalised to their resting values (horizontal dashed lines). Filled (open) circles denote X-ray data recorded before (after) the force shoulder.
The intensity of the equatorial 1,1 reflection (I11) decreased during isometric relaxation (Fig. 3A, filled circles) and the intensity of the 1,0 (I10) increased slightly (Fig. 3B, filled circles). The intensity ratio I11/I10, a parameter which is often used as a measure of the position of the myosin motors within the filament lattice, decreased (Fig. 3C, filled circles), indicating movement of the motors away from the actin filaments. All these equatorial intensity parameters changed at a roughly constant rate during isometric relaxation, like the force, and plots of each of these parameters against force for four fibres were linear during this period (Fig. 3D–F, filled circles). After the force shoulder (vertical dashed line in Fig. 3A–C), during chaotic relaxation, the rate of change of the three equatorial intensity parameters increased (Fig. 3A–C, open circles), like the rate of mechanical relaxation, and the slope of the relationship between the intensity parameters and force (Fig. 3D–F), was maintained or slightly increased during chaotic relaxation (open circles). By the end of chaotic relaxation, I10 had recovered almost completely to its resting value (Fig. 3H), but I11 recovery was not quite complete more than 1 s after the last stimulus (Fig. 3A and G). Exponential fits of the changes in I11, I10 and I11/I10 during chaotic relaxation (Fig. 3G–I) gave half-times which were not significantly different from each other, or from that of force, 61 ± 17 ms measured from the force shoulder (mean ±s.d., n= 3; Table 1).
Table 1.
X-ray parameters during mechanical relaxation
| Resting | Tetanus plateau | Pre-shoulder | Late | Isometric phase force regression | Chaotic phase half-time (ms) | |
|---|---|---|---|---|---|---|
| I11 | 1 | 2.72 ± 0.26 | 1.96 ± 0.14 | 1.23 ± 0.07 | 1.29 ± 0.35 | 120 ± 66 |
| I10 | 1 | 0.53 ± 0.04 | 0.58 ± 0.03 | 0.98 ± 0.03 | −0.16 ± 0.05 | 86 ± 32 |
| I11/I10 | 0.42 ± 0.05 | 2.30 ± 0.31 | 1.50 ± 0.22 | 0.50 ± 0.01 | 1.38 ± 0.32 | 53 ± 22 |
| SM3(nm) | 14.34 ± 0.01 | 14.57 ± 0.01 | 14.56 ± 0.01 | 14.35 ± 0.01 | 0.029 ± 0.010 | 110 ± 17 |
| wM3 | 1 | 2.74 ± 0.43 | 2.52 ± 0.26 | 0.98 ± 0.17 | 0.02 ± 0.56 | 193 ± 37 |
| IM3c | 1 | 2.09 ± 0.49 | 1.00 ± 0.27 | 0.97 ± 0.13 | 2.16 ± 0.39 | — |
| LM3 | 0.07 ± 0.03 | 0.54 ± 0.01 | 0.52 ± 0.07 | 0.08 ± 0.01 | 0.03 ± 0.05 | 118 ± 16 |
| IM2 | 1 | 0.01 ± 0.06 | 0.10 ± 0.06 | 0.88 ± 0.18 | −0.19 ± 0.06 | 311 ± 54 (205 ± 70) |
| IML1 | 1 | 0.01 ± 0.12 | 0.04 ± 0.27 | 0.80 ± 0.25 | −0.06 ± 0.25 | 87 ± 29 |
| IT1 | 1 | 0.08 ± 0.23 | 0.18 ± 0.05 | 1.03 ± 0.14 | 0.01 ± 0.15 | 290 ± 43 |
| IC1 | 1 | 0.21 ± 0.17 | 0.02 ± 0.29 | 0.81 ± 0.11 | 0.28 ± 0.20 | 296 ± 51 |
| T/T0 | 0 | 1 | 0.58 ± 0.05 | 0 | — | 61 ± 17 |
Each X-ray parameter was measured in the resting fibre, at the plateau of an isometric tetanus, just before the force shoulder in relaxation, and late in relaxation, 710–880 ms after the force shoulder. Means ±s.d. for n= 4 except late (n= 2) and chaotic relaxation (n= 3). Intensities were normalised by the value at rest. Isometric phase force regression reports the slope vs. T/T0, as plotted in the central columns of Figs 3–5, and the standard error of the slope. Chaotic relaxation half-times are from the exponential (sigmoidal for SM3 and LM3) fits plotted in the right-hand columns of Figs 3–5; the value in parentheses for IM2 was calculated after width correction using wM3.
M3 reflection
Changes in the M3 reflection from the axial repeat of the myosin motors along the filaments during relaxation were characterised by four parameters (Fig. 4): axial spacing (SM3), cross-meridional width (wM3), total intensity (IM3c), and an interference parameter (LM3). The axial spacing (SM3) was almost constant during isometric relaxation (Fig. 4A and E, filled circles), then decreased during chaotic relaxation (Fig. 4A and E, open circles; Fig. 4I). The SM3 decrease during chaotic relaxation was slower than mechanical relaxation, and the time course of SM3 was well fitted by a sigmoidal curve (Fig. 4I), with half-time 110 ± 17 ms (mean ±s.d., Table 1). This half-time is larger than that of force during this phase, 61 ± 17 ms.
Figure 4. Changes in the M3 meridional reflection during relaxation.
A, E and I, axial spacing (SM3); B, F and J, cross-meridional width (wM3); C, G and K, intensity after width correction (IM3c); D, H and L, interference fine structure parameter (LM3). A–D, time courses following the last stimulus in a single fibre. E–H, relationship between X-ray parameters and force during relaxation (n= 4 fibres), with linear fits to X-ray data before the force shoulder (black continuous lines). I–L, time courses following the force shoulder (n= 3); fits (continuous lines) are sigmoidal in I and L, exponential in J and linear in K. Circles and vertical dashed lines as in Fig. 3; horizontal dashed lines denote resting values of X-ray parameters.
The cross-meridional width of the M3 reflection (wM3) is larger at the tetanus plateau than at rest (Fig. 2A and B), indicating decreased axial alignment between neighbouring myosin filaments during contraction (Huxley et al. 1982). wM3 did not recover significantly during isometric relaxation (Fig. 4B and F, filled circles), or during the early part of chaotic relaxation (Fig. 4F, open circles). Recovery of wM3 following the force shoulder was fitted with an exponential with half-time 193 ± 37 ms (Fig. 4J; Table 1), three times greater than that of force.
The increase in the cross-meridional width of the M3 reflection associated with axial misalignment between filaments reduces the total observed intensity (IM3o) compared to that which would have been measured (IM3c) if the alignment between neighbouring filaments had been constant. IM3c is the more relevant parameter for the present study, since it is directly related to internal filament structure, and can be estimated as IM3o×wM3 (Huxley et al. 1982). IM3c decreased during isometric relaxation (Fig. 4C and G, filled circles), roughly in proportion to the force, and its value at the force shoulder, 1.00 ± 0.27 (Table 1), was the same as that at rest (Table 1). IM3c appeared to undershoot its resting value during the first 100 ms of chaotic relaxation before recovering (Fig. 4G and K, open circles).
The interference fine structure of the M3 reflection was characterised by LM3, the intensity of its lower angle peak divided by the total intensity of the reflection. LM3 was 0.07 ± 0.03 at rest (mean ±s.d., n= 4) and 0.54 ± 0.01 at the tetanus plateau (Table 1). LM3 did not decrease significantly during isometric relaxation (Fig. 4D and H, filled circles), indicating there was little axial motion of the myosin motors during this period, and recovered fully to its resting value during chaotic relaxation (Fig. 4D, H and L, open circles). As in the case of SM3, the LM3 recovery lagged that of force, and its time course was fitted with a sigmoidal curve (Fig. 4L). The half-time of LM3 recovery during chaotic relaxation was 118 ± 16 ms (Table 1), similar to that of SM3, and slower than that of force relaxation.
Myosin-based M2 and ML1 reflections
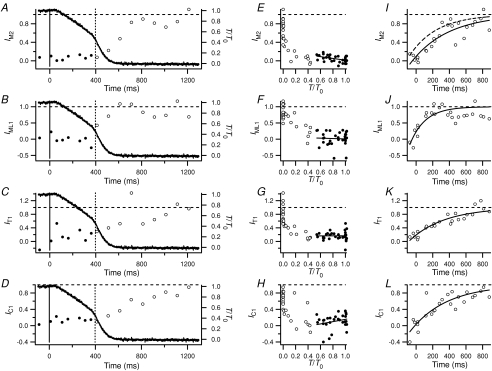
The M2 and ML1 reflections are related to the axial and helical distributions of myosin motors on the surface of the myosin filaments, and are very weak at the tetanus plateau (Fig. 2), so they can be used to assess the time course of recovery of the resting conformations of the myosin motors during relaxation. There was no significant recovery of the intensity of the M2 reflection (IM2; Fig. 5A and E) or of the ML1 reflection (IML1; Fig. 5B and F) during isometric relaxation (filled circles). The recovery of IM2 was still incomplete at the end of chaotic relaxation, and an exponential fit to the IM2 data after the force shoulder had a half-time of 311 ± 54 ms, more than five times larger than that of force. However, the time course of IM2, like that of IM3, is affected by changes in cross-meridional width, and estimates of changes in the internal structure of the filament should be obtained as IM2×wM2, analogous to the IM3c analysis in the previous section. In practice, because the M2 is very weak during the early part of relaxation, wM2 could not be measured with sufficient precision. We therefore used wM3 as the best available estimate of wM2 for this purpose, and the corrected fitted M2 time course is shown as the dashed exponential in Fig. 5I. The width correction decreased the half-time of the structural change reported by the M2 reflection to 205 ± 70 ms (Table 1). This is still longer than that reported by the intensity of the first myosin layer line IML1 (Fig. 5J, Table 1), 87 ± 29 ms, although the difference may be due to the uncertainty about M2 width correction combined with the limited signal:noise.
Figure 5. Changes in the intensities of the M2, ML1, T1 and C1 reflections during relaxation.
A, E and I, second-order myosin-based meridional (IM2); B, F and J, first myosin layer line (IML1); C, G and K, first troponin meridional (IT1); D, H and L, first myosin-binding protein C meridional (IC1). A–D, time courses following the last stimulus in a single fibre. E–H, relationship between X-ray parameters and force during relaxation (n= 4 fibres), with linear fits to X-ray data before the force shoulder. I–L, time courses following the force shoulder (n= 3) with exponential fits (continuous lines); the dashed line in I was obtained after correcting IM2 for width changes using wM3. Circles and vertical dashed lines as in Fig. 3; horizontal dashed lines denote resting values of X-ray parameters.
Troponin and myosin-binding protein C reflections
Like the M2 and ML1 reflections, the T1 and C1 reflections are weaker at the tetanus plateau than in the resting fibre (Fig. 2), so they give two further signals related to the return of the resting filament structures during relaxation. Again like M2 and ML1, the intensities of the T1 (Fig. 5C and G, filled circles) and C1 (Fig. 5D and H, filled circles) reflections did not recover significantly during isometric relaxation. In both cases, recovery was also slower than that of force during chaotic relaxation (Fig. 5K and L), and exponential fits to the T1 and C1 data after the force shoulder gave half-times of 290 ± 43 and 296 ± 51 ms, respectively (Table 1). As in the case of the M2 reflection, these half-times may be overestimated because it was not possible to measure changes in the width of the reflections with sufficient precision to make reliable corrections of the intensity time courses.
Determination of myosin motor strain during isometric relaxation from fibre stiffness
Muscle fibre stiffness during isometric relaxation was measured by imposing small sinusoidal length oscillations at a frequency, 4 kHz, that is sufficiently high to exclude mechanical contributions from the working stroke in the myosin motor. The resulting in-phase force and segment length oscillations (Fig. 6A; insets) were used to calculate the instantaneous stiffness, and thus the average strain of the half-sarcomere as a function of the decreasing average force during isometric relaxation. The slope of this half-sarcomere strain/force relationship (Fig. 6B, filled circles) was smaller than that of the corresponding relationship determined during the rising phase of the tetanus in the same set of fibres (open circles). The latter results are similar to those reported previously (Brunello et al. 2006); during the tetanus rise the variation of half-sarcomere strain with force is entirely due to the compliance of the actin and myosin filaments (Huxley et al. 1994; Wakabayashi et al. 1994; Dobbie et al. 1998; Reconditi et al. 2004), and the strain in the myosin motors is independent of force (Brunello et al. 2006). The gradient of the half-sarcomere strain/force relationship during the tetanus rise (Fig. 6B, open circles; continuous line), corresponding to the compliance of the filaments, was 2.06 ± 0.09 nm/T0, or 0.013 ± 0.001 nm kPa−1, in agreement with previous measurements. The intercept of this line with the strain axis, 1.63 ± 0.06 nm, is the motor strain which, given a constant motor stiffness, is proportional to the force per motor. Thus the force per motor is roughly constant during the tetanus rise (Fig. 6B; open triangles, dashed line). The half-sarcomere strain during isometric relaxation (Fig. 6B, filled circles) was higher than that during the tetanus rise (Fig. 6B, open circles) at the same force. The motor strain during isometric relaxation (Fig. 6B, filled triangles), calculated by subtracting the filament strain from the half-sarcomere strain using the filament compliance value given above, increased progressively from 1.63 nm at the last stimulus to slightly over 2 nm at the end of isometric relaxation, when the force had fallen to about 0.5T0. Since myosin motors are mechanically in parallel in the half-sarcomere, it follows that the number of motors attached to actin in each half-thick filament, expressed as n/n0, the fraction of those present at the tetanus plateau, declines to a greater extent than half-sarcomere force during isometric relaxation (Fig. 6C, filled circles), again in contrast to the directly proportional relationship between n/n0 and force during the tetanus rise (Fig. 6C, open circles).
Discussion
Structural changes in myosin and actin filaments during isometric relaxation
The X-ray signals described above can be grouped into two classes on the basis of their behaviour during isometric relaxation. The intensities of the equatorial and meridional M3 reflections recovered towards their resting values during this period, whereas the width, spacing, and interference fine structure of the M3 reflection, and the intensities of M2, C1 and T1 meridional and ML1 layer-line reflections essentially retained their tetanus plateau values. Such a clear distinction has not been observed during muscle activation during the rise of an isometric tetanus, although the half-times of the changes in these X-ray reflections do differ by up to 30 ms during force development (Huxley et al. 1982; Kress et al. 1986; Martin-Fernandez et al. 1994; Piazzesi et al. 1999; Brunello et al. 2006; Matsuo & Yagi, 2008).
The changes in the intensities of the equatorial reflections during isometric relaxation show that myosin motors are detaching from actin, as also indicated by the decrease in fibre stiffness during this period (Fig. 6). The decrease in the intensity of the M3 reflection (IM3c) is also consistent with motor detachment, because actin-attached motors have a greater degree of axial order than the detached motors in active muscle, and therefore a greater contribution to IM3c (Linari et al. 2000; Huxley et al. 2006b; Piazzesi et al. 2007). The observation that IM3c has already reached its resting value at the end of isometric relaxation, when force is still about half its tetanus plateau value (Fig. 4C and G), suggests that the detached motors in active muscle have a lower axial order than the detached motors in resting muscle.
The quasi-helical structure of the myosin filament characteristic of resting muscle, and signalled by the ML1 and M2 X-ray reflections, does not reappear during isometric relaxation. The axial periodicity of the myosin filament (SM3) also stays close to its tetanus plateau value as force decreases by ca 50% (Fig. 4E). The slope of the regression of SM3 against fractional force (T/T0) during this period was 0.029 ± 0.010 nm (Table 1), corresponding to a myosin filament compliance of 0.20 ± 0.06%/T0. This is close to the value, 0.26%/T0, measured previously by applying rapid load steps at the tetanus plateau (Reconditi et al. 2004). The much larger ca 1.5% spacing increase observed during the tetanus rise, and associated with a change in myosin filament structure, is not reversed during isometric relaxation. The molecular basis of the 1.5% spacing change is unknown, but the present results show that the underlying structural change is not sensitive to filament stress in the range 0.5–1.0T0, in agreement with previous results in which the stress was varied in this range by imposing shortening ramps either at the tetanus plateau or during the rising phase (Brunello et al. 2006).
The lack of significant recovery of the intensity of the T1 reflection (IT1) associated with the axial periodicity of troponin on the actin-containing thin filaments during isometric relaxation (Fig. 5C and G) is broadly consistent with previous reports from whole muscles of its delayed recovery during early relaxation (Maeda et al. 1992; Matsuo & Yagi, 2008). However, those studies showed that the time course of changes in IT1 is complex, and may be influenced by preferential binding of myosin motors to ‘target zones’ between troponin molecules on the thin filaments in addition to structural changes in troponin itself. Thus IT1 cannot be considered to be a reliable measure of the time course of structural changes in the thin filaments during isometric relaxation. A more informative X-ray indicator of these changes would be the intensity of the second actin-based layer-line reflection, which is related to the azimuthal motion of tropomyosin accompanying thin filament activation. This reflection is relatively weak and diffuse, and its time course is difficult to record precisely from a single muscle fibre. However, in whole muscles it is clear that this reflection recovers relatively early during relaxation, at a time corresponding to isometric relaxation in single fibres (Kress et al. 1986; Matsuo & Yagi, 2008). These observations suggest that the structure of the thin filament does return towards its resting state during isometric relaxation.
Axial motions of myosin motors during isometric relaxation
The interference fine structure of the M3 reflection, characterised here by LM3, provides a sensitive measure of the motion of myosin motors along the filament axis (Linari et al. 2000; Piazzesi et al. 2002, 2007; Reconditi et al. 2004). LM3 was roughly constant during isometric relaxation (Fig. 4D and H), suggesting that the average axial position of the myosin motors did not change significantly. During this period, however, there is net detachment of motors signalled by both the equatorial and M3 X-ray intensity changes (Figs 3 and 4G) and the stiffness decrease (Fig. 6). Previous X-ray interference studies in which changes in muscle length were imposed at the tetanus plateau (Piazzesi et al. 2002, 2007; Reconditi et al. 2004; Huxley et al. 2006a,b; Brunello et al. 2007) showed that the centre of mass of the attached motors is further from the midpoint of the myosin filament than that of the detached motors. These previous results imply that, in the absence of other structural changes, net motor detachment during isometric relaxation should have been accompanied by an axial shift of the motors’ centre of mass towards the midpoint of the myosin filament, signalled by an increase in LM3. The absence of an increase in LM3 during isometric relaxation therefore suggests that a compensating structural change occurs in the attached motors, in which they are progressively displaced away from the midpoint of the myosin filament, i.e. towards the start of their working stroke. Such a motion of the actin-attached motors during isometric relaxation would be consistent with the higher motor strain observed in this period (Fig. 6B, filled triangles).
Structural changes during chaotic relaxation
All the X-ray signals measured here, including those that did not change during isometric relaxation, returned towards their resting values after the force shoulder. Although the X-ray patterns were not recorded at short enough intervals to determine the precise time courses of the structural signals during chaotic relaxation, some clear differences between the time courses of the various X-ray signals were apparent. Recovery of the equatorial intensity ratio (I11/I10) had an exponential time course with a half-time (t½) of 53 ± 22 ms (Table 1), indistinguishable from that of force (61 ± 17 ms). Recovery of the first myosin layer line was rather slower, with t½ 89 ± 29 ms. The spacing and interference fine structure of the M3 reflection, SM3 and LM3, respectively (Fig. 4I and L), shared a distinct time course, with a lag of ca 50 ms after the force shoulder followed by a rapid transition to the corresponding resting values, suggesting a co-operative process with a time course similar to that of the inhomogeneous sarcomere length changes during chaotic relaxation (Fig. 1). The sarcomeres that yield during this period are presumably those that became inactivated first, so the mass distribution of myosin motors in these sarcomeres would return more quickly towards its resting state. The contribution of the shortening sarcomeres to the M3 X-ray reflection would be reduced by shortening per se (Piazzesi et al. 2007), so the expected net effect of sarcomere inhomogeneity during chaotic relaxation is to accelerate the recovery of SM3 and LM3 towards their resting values, as observed. The cross-meridional width of the M3 reflection had only half-recovered by ca 200 ms after the force shoulder (Fig. 4J, Table 1), at a time when force, I11/I10, SM3 and LM3 recovery were essentially complete, and this may also be related to continuing sarcomere length redistribution. The slow recovery of cross-meridional width affects the intensity time courses of other meridional reflections, and it is difficult to apply an accurate correction for these width changes.
Mechanism and functional significance of isometric relaxation
The isometric phase of relaxation is maintained for several hundred milliseconds in the conditions of the present experiments (amphibian muscle, 4°C). Isometric relaxation is slower after longer tetani, in which the falling phase of the [Ca2+]i transient is slower (Blinks et al. 1978; Caputo et al. 1994), but is also apparent following a single action potential in a twitch, provided that the twitch–tetanus ratio is high. The rate and duration of isometric relaxation are also affected by mechanical conditions; it is slowed by clamping the length of a central fibre segment (Huxley & Simmons, 1973) and accelerated by applying a step stretch (Lombardi et al. 1990) or ramp shortening or stretch (Caputo et al. 1994). Although some of these mechanical perturbations can alter the time course of [Ca2+]i (Cannell, 1986; Caputo et al. 1994), it seems likely that there are also direct mechanical effects on the subsequent time course of relaxation.
The present results indicate that the number of myosin motors attached to actin decreases at a roughly constant rate during isometric relaxation, but the fraction of attached motors decreases slightly faster than the force, so the force per attached motor increases, as inferred previously from the response to fast ramp stretch during relaxation (Bagni et al. 2005). The interference fine structure of the M3 reflection also shows that the average conformation of the attached motors is not constant; the catalytic domains of attached motors move progressively away from the midpoint of the myosin filament during isometric relaxation, so that the motor conformation is closer to the start of the working stroke. This can be considered as the steady-state response of the motor to the increased strain. At the nanometer scale of an attached myosin motor, ‘isometric’ relaxation is not strictly isometric. Sarcomere lengths are not precisely constant on the nanometre scale either (Fig. 1); some fibre segments shorten slightly during isometric relaxation whilst others are stretched. The X-ray signals reported above were added from segments along the fibre, and at the level of the average myosin motor the response is consistent with a stretch, pulling the motor towards the start of its stroke. A net stretch response of the motors is expected in these conditions, considering that both the fibre tendons and the myosin and actin filaments shorten elastically during relaxation in these fixed-end tetani. However, the stretch is not uniform along the muscle fibre, and we might speculate that fibre segments that are stretched to a greater extent during isometric relaxation might be those that yield during chaotic relaxation. This seems to be the case for the blue and magenta segments in Fig. 1, although the effect may be attenuated in these long (900 μm) segments, within which there may be substantial local sarcomere inhomogeneity.
The progressive decrease in the number of attached motors during isometric relaxation is presumably mediated by a reduced attachment rate, which in turn is likely to be related to a [Ca2+]i value that is intermediate between the tetanus plateau and resting values. Peak [Ca2+]i in a tetanus is 10–20 μm (Konishi, 1998), so [Ca2+]i during isometric relaxation may be 1–2 μm, close to the Kd for the calcium regulatory sites of troponin (Potter & Gergely, 1975). Thus the regulatory state of the thin filament is likely to be neither fully OFF nor fully ON during isometric relaxation, and this would be consistent with partial recovery of the intensity of the actin-based second layer-line reflection (Matsuo & Yagi, 2008), as noted above. The prolongation of motor attachment and force during isometric relaxation may also be facilitated by the myosin filament retaining its ON or tetanus-plateau structure, as shown here.
Isometric relaxation is much slower than the rising phase of a tetanus. Slow relaxation from long-lasting contractions allows force maintenance at minimal metabolic cost, in comparison with repeated short activations. On the other hand, slow relaxation seems generally incompatible with rapid and efficient control of body movements. One way in which these apparently conflicting requirements might be reconciled would be via a mechano-sensing mechanism within the muscle sarcomere which allowed isometric relaxation to be rapidly terminated by a stretch, provided in vivo by activation of an antagonist muscle. Stretching isolated muscle fibres during isometric relaxation is known to produce such an effect, as discussed above, although the mechanism is unknown. The present results suggest that maintenance of a ‘pre-relaxed’ state during isometric relaxation, in which myoplasmic free [Ca2+] and the activation state of the thin filaments are intermediate between their resting and tetanus plateau values, may be facilitated by the maintained ‘ON’ structure of the myosin filament. They also reveal a progressive change in the conformation and strain of the myosin motors during isometric relaxation that suggests that the myosin motors themselves might be the mechano-sensors that control the rate of relaxation.
Acknowledgments
We thank M. Dolfi and J. Gorini for mechanical and electronics support. This work was supported by Ministero dell’Istruzione, dell’Università e della Ricerca (Italy), Medical Research Council (UK), National Institutes of Health R01 AR049033 (USA), European Molecular Biology Laboratory and European Synchrotron Radiation Facility. E.B. acknowledges a grant from the INFM-CNR-OGG (Italy) and a grant from the European Molecular Biology Organization, Fellowship No. ASTF 75-2007.
Glossary
Abbreviations
- ESRF
European Synchrotron Radiation Facility
- FWHM
full width at half-maximum
- hs
half-sarcomere
Author contributions
All authors contributed to the conception and design of the experiments. E.B. and L.F. made the main contributions to data analysis. All authors contributed to data interpretation, drafting and critical revision of the article for important intellectual content. All authors have approved the final version to be published. All experiments were performed at ESRF except those presented in Figs 1 and 6, which were done in the University of Florence.
References
- Bagni MA, Cecchi G, Colombini B. Crossbridge properties investigated by fast ramp stretching of activated frog muscle fibres. J Physiol. 2005;565:261–268. doi: 10.1113/jphysiol.2005.085209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blinks JR, Rudel R, Taylor SR. Calcium transients in isolated amphibian skeletal muscle fibres: detection with aequorin. J Physiol. 1978;277:291–323. doi: 10.1113/jphysiol.1978.sp012273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunello E, Bianco P, Piazzesi G, Linari M, Reconditi M, Panine P, Narayanan T, Helsby WI, Irving M, Lombardi V. Structural changes in the myosin filament and cross-bridges during active force development in single intact frog muscle fibres: stiffness and X-ray diffraction measurements. J Physiol. 2006;577:971–984. doi: 10.1113/jphysiol.2006.115394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunello E, Reconditi M, Elangovan R, Linari M, Sun YB, Narayanan T, Panine P, Piazzesi G, Irving M, Lombardi V. Skeletal muscle resists stretch by rapid binding of the second motor domain of myosin to actin. Proc Natl Acad Sci U S A. 2007;104:20114–20119. doi: 10.1073/pnas.0707626104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannell MB. Effect of tetanus duration on the free calcium during the relaxation of frog skeletal muscle fibres. J Physiol. 1986;376:203–218. doi: 10.1113/jphysiol.1986.sp016149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caputo C, Edman KA, Lou F, Sun YB. Variation in myoplasmic Ca2+ concentration during contraction and relaxation studied by the indicator fluo-3 in frog muscle fibres. J Physiol. 1994;478:137–148. doi: 10.1113/jphysiol.1994.sp020237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cecchi G, Griffiths PJ, Bagni MA, Ashley CC, Maeda Y. Time-resolved changes in equatorial x-ray diffraction and stiffness during rise of tetanic tension in intact length-clamped single muscle fibres. Biophys J. 1991;59:1273–1283. doi: 10.1016/S0006-3495(91)82342-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobbie I, Linari M, Piazzesi G, Reconditi M, Koubassova N, Ferenczi MA, Lombardi V, Irving M. Elastic bending and active tilting of myosin heads during muscle contraction. Nature. 1998;396:383–387. doi: 10.1038/24647. [DOI] [PubMed] [Google Scholar]
- Drummond GB. Reporting ethical matters in The Journal of Physiology: standards and advice. J Physiol. 2009;587:713–719. doi: 10.1113/jphysiol.2008.167387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman KA, Flitney FW. Laser diffraction studies of sarcomere dynamics during ‘isometric’ relaxation in isolated muscle fibres of the frog. J Physiol. 1982;329:1–20. doi: 10.1113/jphysiol.1982.sp014287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon AM, Homsher E, Regnier M. Regulation of contraction in striated muscle. Physiol Rev. 2000;80:853–924. doi: 10.1152/physrev.2000.80.2.853. [DOI] [PubMed] [Google Scholar]
- Haselgrove JC. X-ray evidence for conformational changes in the myosin filaments of vertebrate striated muscle. J Mol Biol. 1975;92:113–143. doi: 10.1016/0022-2836(75)90094-7. [DOI] [PubMed] [Google Scholar]
- Haselgrove JC, Huxley HE. X-ray evidence for radial cross-bridge movement and for the sliding filament model in actively contracting skeletal muscle. J Mol Biol. 1973;77:549–568. doi: 10.1016/0022-2836(73)90222-2. [DOI] [PubMed] [Google Scholar]
- Huxley AF, Lombardi V. A sensitive force transducer with resonant frequency 50 kHz. J Physiol. 1980;305:15–16P. [Google Scholar]
- Huxley AF, Lombardi V, Peachey LD. A system for fast recording of longitudinal displacement of a striated muscle fibre. J Physiol. 1981;317:12–13P. [Google Scholar]
- Huxley AF, Simmons RM. Rapid ‘give’ and the tension ‘shoulder’ in the relaxation of frog muscle fibres. J Physiol. 1970;210:32–33P. [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Mechanical transients and the origin of muscular force. Cold Spring Harb Symp Quant Biol. 1973;37:669–680. [Google Scholar]
- Huxley HE, Brown W. The low-angle x-ray diagram of vertebrate striated muscle and its behaviour during contraction and rigor. J Mol Biol. 1967;30:383–434. doi: 10.1016/s0022-2836(67)80046-9. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Faruqi AR, Kress M, Bordas J, Koch MH. Time-resolved X-ray diffraction studies of the myosin layer-line reflections during muscle contraction. J Mol Biol. 1982;158:637–684. doi: 10.1016/0022-2836(82)90253-4. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Reconditi M, Stewart A, Irving T. X-ray interference studies of crossbridge action in muscle contraction: evidence from muscles during steady shortening. J Mol Biol. 2006a;363:762–772. doi: 10.1016/j.jmb.2006.08.055. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Reconditi M, Stewart A, Irving T. X-ray interference studies of crossbridge action in muscle contraction: evidence from quick releases. J Mol Biol. 2006b;363:743–761. doi: 10.1016/j.jmb.2006.08.075. [DOI] [PubMed] [Google Scholar]
- Huxley HE, Stewart A, Sosa H, Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys J. 1994;67:2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konishi M. Cytoplasmic free concentrations of Ca2+ and Mg2+ in skeletal muscle fibres at rest and during contraction. Jpn J Physiol. 1998;48:421–438. doi: 10.2170/jjphysiol.48.421. [DOI] [PubMed] [Google Scholar]
- Kress M, Huxley HE, Faruqi AR, Hendrix J. Structural changes during the activation of frog muscle studied by time-resolved x−ray diffraction. J Mol Biol. 1986;188:325–342. doi: 10.1016/0022-2836(86)90158-0. [DOI] [PubMed] [Google Scholar]
- Linari M, Piazzesi G, Dobbie I, Koubassova N, Reconditi M, Narayanan T, Diat O, Irving M, Lombardi V. Interference fine structure and sarcomere length dependence of the axial X-ray pattern from active single muscle fibres. Proc Natl Acad Sci U S A. 2000;97:7226–7231. doi: 10.1073/pnas.97.13.7226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lombardi V, Piazzesi G, Goldman YE. Following tetanic stimulation, relaxation is accelerated by quick stretches of frog single muscle fibres. J Physiol. 1990;426:38P. [Google Scholar]
- Maeda Y, Popp D, Stewart AA. Time-resolved x−ray diffraction study of the troponin-associated reflexions from the frog muscle. Biophys J. 1992;63:815–822. doi: 10.1016/S0006-3495(92)81648-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin-Fernandez ML, Bordas J, Diakun G, Harries J, Lowy J, Mant GR, Svensson A, Towns-Andrews E. Time-resolved X-ray diffraction studies of myosin head movements in live frog sartorius muscle during isometric and isotonic contractions. J Muscle Res Cell Motil. 1994;15:319–348. doi: 10.1007/BF00123484. [DOI] [PubMed] [Google Scholar]
- Matsuo T, Yagi N. Structural changes in the muscle thin filament during contractions caused by single and double electrical pulses. J Mol Biol. 2008;383:1019–1036. doi: 10.1016/j.jmb.2008.09.007. [DOI] [PubMed] [Google Scholar]
- Narayanan T, Diat O, Boesecke P. SAXS and USAXS on the high brilliance beamline at the ESRF. Nucl Instrum Methods Phys Res A. 2001;467:1005–1009. [Google Scholar]
- Otsuki I, Masaki T, Nonomura Y, Ebashi S. Periodic distribution of troponin along the thin filament. J Biochem. 1967;61:817–819. doi: 10.1093/oxfordjournals.jbchem.a128619. [DOI] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Dobbie I, Linari M, Boesecke P, Diat O, Irving M, Lombardi V. Changes in conformation of myosin heads during the development of isometric contraction and rapid shortening in single frog muscle fibres. J Physiol. 1999;514:305–312. doi: 10.1111/j.1469-7793.1999.305ae.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Linari M, Lucii L, Bianco P, Brunello E, Decostre V, Stewart A, Gore DB, Irving TC, Irving M, Lombardi V. Skeletal muscle performance determined by modulation of number of myosin motors rather than motor force or stroke size. Cell. 2007;131:784–795. doi: 10.1016/j.cell.2007.09.045. [DOI] [PubMed] [Google Scholar]
- Piazzesi G, Reconditi M, Linari M, Lucii L, Sun YB, Narayanan T, Boesecke P, Lombardi V, Irving M. Mechanism of force generation by myosin heads in skeletal muscle. Nature. 2002;415:659–662. doi: 10.1038/415659a. [DOI] [PubMed] [Google Scholar]
- Potter JD, Gergely J. The calcium and magnesium binding sites on troponin and their role in the regulation of myofibrillar adenosine triphosphatase. J Biol Chem. 1975;250:4628–4633. [PubMed] [Google Scholar]
- Reconditi M, Linari M, Lucii L, Stewart A, Sun YB, Boesecke P, Narayanan T, Fischetti RF, Irving T, Piazzesi G, Irving M, Lombardi V. The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature. 2004;428:578–581. doi: 10.1038/nature02380. [DOI] [PubMed] [Google Scholar]
- Rome E, Offer G, Pepe FA. X-ray diffraction of muscle labelled with antibody to C-protein. Nat New Biol. 1973a;244:152–154. doi: 10.1038/newbio244152a0. [DOI] [PubMed] [Google Scholar]
- Rome EM, Hirabayashi T, Perry SV. X-ray diffraction of muscle labelled with antibody to troponin−C. Nat New Biol. 1973b;244:154–155. doi: 10.1038/newbio244154a0. [DOI] [PubMed] [Google Scholar]
- Sugimoto Y, Takezawa Y, Matsuo T, Ueno Y, Minakata S, Tanaka H, Wakabayashi K. Structural changes of the regulatory proteins bound to the thin filaments in skeletal muscle contraction by X-ray fibre diffraction. Biochem Biophys Res Commun. 2008;369:100–108. doi: 10.1016/j.bbrc.2007.11.088. [DOI] [PubMed] [Google Scholar]
- Wakabayashi K, Sugimoto Y, Tanaka H, Ueno Y, Takezawa Y, Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys J. 1994;67:2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]