Probing the mechanical architecture of the vertebrate meiotic spindle

Abstract

Accurate chromosome segregation during meiosis depends on the assembly of a microtubule-based spindle of proper shape and size. Current models for spindle size control focus on reaction-diffusion based chemical regulation and balance in activities of motor proteins. While several molecular perturbations have been used to test these models, controlled mechanical perturbations have not been possible. Here we report a piezo-resistive dual-cantilever-based system to test models for spindle size control and, for the first time, examine the mechanical features, e.g., deformability and stiffness, of the vertebrate meiotic spindle. We found that meiotic spindles prepared in Xenopus egg extracts were viscoelastic and the shape was recovered to the original one in response to small compression. Larger compression resulted in plastic deformation, but surprisingly, the spindle adapted to it, establishing a stable mechanical architecture at different sizes. Our technique will also be useful for examining micro-mechanics of a variety of other cellular organelles.

Introduction

The past few decades have seen an explosion in the analysis of the components of the meiotic spindle, and clarifying contributions to spindle dynamics of microtubules, molecular motors (kinesins, cytoplasmic dyneins), chromosomes and other regulatory proteins (microtubule-associated proteins)^1-5. Seminal work provided quantitative analysis of forces that act on chromosomes during cell division in intact grasshopper spermatocytes⁶. The effects of changes in pressure and temperature have revealed the dynamicity of the metaphase spindle and also provided certain thermodynamic parameters⁷. However, the consequences of properly controlled mechanical perturbations of the spindle have not been analyzed, in spite of the fact that the force balance and its self-control are considered to be an essential factor for the spindle dynamics determining the accurate chromosome segregation.

The use of metaphase meiotic spindles assembled in Xenopus egg extracts, a powerful model system that can recapitulate many aspects of meiosis and has provided valuable insight into mechanisms underlying spindle assembly and chromosome segregation, allowed us to circumvent difficulties in directly accessing the spindle with force-measuring equipment through cell membranes. This analysis also required the development of a force-sensor that could not only make accurate measurements in the relevant force range, which had to be experimentally determined, but also accommodate the complex dynamics of the spindle. Here we describe a piezo-resistive dual-cantilever-based system with the fluorescence-microscopic imaging that makes it possible to probe the mechanical architecture of the vertebrate meiotic spindle with the application of nanoNewton forces and micron-size perturbations. Using this technique, we observed the response of the metaphase meiotic spindle to controlled mechanical force.

Results

Dual-cantilever system with fluorescence imaging

A force-measuring set-up for the spindle, an organelle floating in an aqueous solution, needs the following features: (a) a stiff structure to freely move in viscous cytoplasm⁸, (b) a surface of sufficient contact area to prevent slipping on or readily penetrating the spindle, and (c) sensitive detection and precise quantification of forces.

We examined the suitability of a piezo-resistive force-sensing cantilever for this experiment⁹. We constructed a system that has two cantilevers, a manipulating and a force-sensing cantilever, which were held in micromanipulators mounted on the microscope. Unlike the atomic force microscopy which requires a sample firmly fixed on the substrate surface, this dual-cantilever system is useful for a sample that floats in solution. The components of this system are cartooned in Fig. 1a. The cantilevers are plate-like structures between which the whole spindle can be sandwiched and manipulated (Fig. 1b). Since the electric resistance of a force-sensing cantilever changes in response to the light used for the fluorescence imaging, we took the following procedure for manipulating the spindle after the electric resistance had reached the steady level. The cantilevers were positioned at the sides of the spindle equator using micromanipulators. The manipulating cantilever was moved either perpendicular to or parallel to the pole-to-pole axis of a spindle, driven by a piezo-actuator (Figs. 1c and 3a and Supplementary Videos 1 and 2 online). We chose the period of one compression cycle (8 ∼ 30 s) so as to be much shorter than the time for complete turnover of microtubules. This approach enabled us to measure both force-dependent deformability, analyzed by time-lapse observation of the fluorescent tubulin incorporated in the spindle, and the force response determined by the force-sensing cantilever, which is a piezo-resistive strain sensor that eliminates the need for additional external detectors (e.g. for tracking cantilever deflection)⁹.

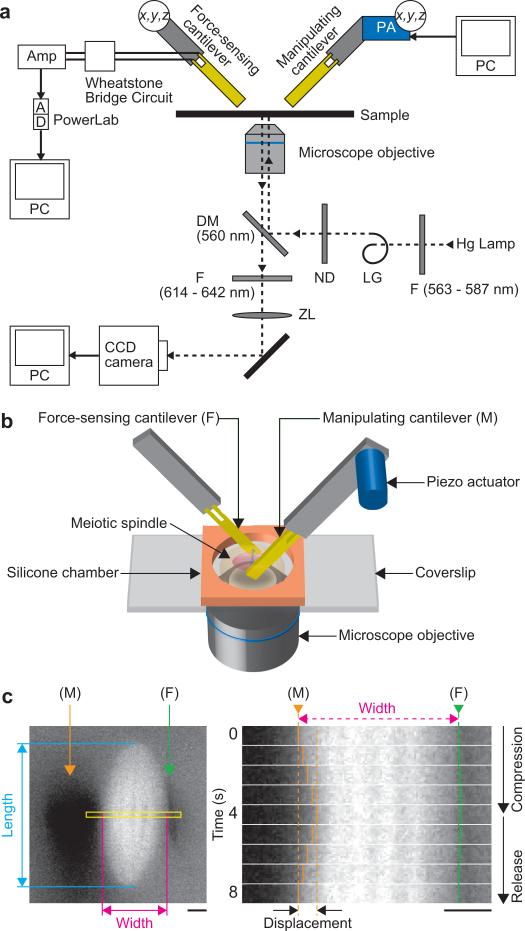
Figure 1. Force measurements using a force-sensing cantilever.

(a) Schematic diagram of the microscope imaging system with dual cantilevers. The dashed line shows the optical path for the fluorescence imaging. The microscope system includes a dichroic mirror (DM (the wavelength in parentheses indicates the wavelength of the light being reflected)), filters (F (the wavelength in parentheses indicates the wavelength of the light passing through)), a neutral density filter (ND) and a zoom lens (ZL). The output from the external Wheatstone bridge circuit connected to a force-sensing cantilever was recorded by using PowerLab data acquisition system (AD) through a hand-made instrumentation amplifier (Amp). x,y,z, micromanipulator; PA, piezo-actuator; PC, personal computer; LG, light guide. (b) Schematic showing the experimental set-up for manipulating the meiotic spindle. This illustrates how to compress the meiotic spindle perpendicular to the pole-to-pole axis (not to scale). (c) A spindle assembled in Xenopus egg extracts was sandwiched between dual cantilevers along the width direction. The width of the spindle before the compression was determined from such a fluorescence image. By moving the manipulating cantilever (M) using a piezo actuator, the spindle was compressed. The length (pole-to-pole distance) was measured from images acquired every 1 s. The applied force and the change of the spindle width were determined by monitoring the changes in its electric resistance of force-sensing cantilever (F) (see Methods for detailed description). The image of cantilever that looks black does not show its real shape and size. Scale bars are 5 μm.

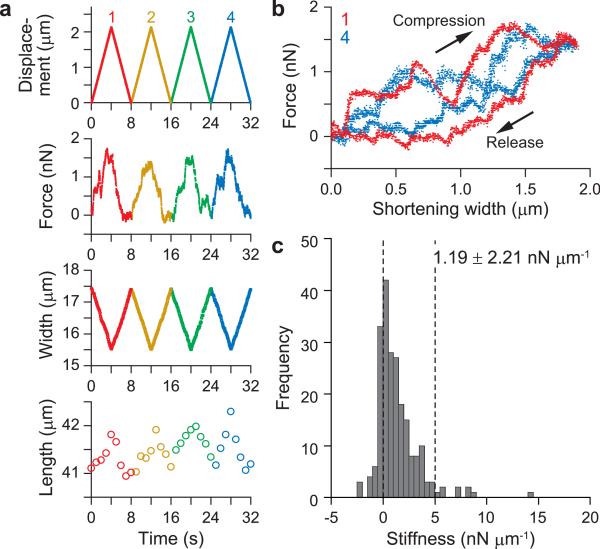
Figure 3. Elastic response of meiotic spindle to the pole-to-pole compression.

(a) A spindle assembled in Xenopus egg extracts was sandwiched between a force-sensing cantilever (F) and a manipulating cantilever (M) along the pole-to-pole direction. By moving the manipulating cantilever, the spindle was compressed along the pole-to-pole axis (Supplementary Video 2 online). The image of cantilever that looks black does not show its real shape and size. Scale bars are 5 μm. (b) The meiotic spindle was repeatedly compressed by ≤ 5% of its unperturbed length. The applied displacement, measured force, and changes in length and width are shown. (c) The force vs. compression relationship over two compression cycles (red, 1^st cycle; yellow, 2^nd cycle). (d) Histogram showing the stiffness distribution obtained for small deformation. Average stiffness = 2.69 ± 3.30 nN μm⁻¹ (mean ± s.d., n = 8 compression cycles, four different spindles).

Quantitative perturbations with dual-cantilever system

We mainly examined the mechanical properties of meiotic spindles obtained by compressing them perpendicular to the pole-to-pole axis (along the width direction). Gradual compression of the spindle along a width direction by a pair of cantilevers resulted in a reduction of the spindle width while the length (pole-to-pole distance) increased. Decrease in the external force allowed the spindle to recover the initial aspect ratio (= spindle width/length) (Fig. 2a). For a small deformation, where ΔW/W (defined as, (spindle width change)/(initial spindle width)) ≤ 0.1 and ΔL/L (defined as, (spindle length change)/(initial spindle length)) ≤ 0.03, the width vs. length relationship was reversible over several compression cycles (Supplementary Fig. 1a and Supplementary Video 1 online). Analysis of the force vs. compression relationship revealed that the compression route and the release route were different from each other. A closed loop, a so-called “hysteresis loop”, was observed (Fig. 2b and Supplementary Fig. 1b online). The area enclosed by this loop represents the energy loss associated with mechanical work performed by the external force. These data indicate that the meiotic spindle has a viscoelastic architecture, but the shape is recovered to the original one as far as the deformation is small (elastic regime). Based on our measurements, the stiffness of spindle obtained by compression along the width direction (see Methods) is estimated to be 1.19 ± 2.21 nN μm⁻¹ (mean ± s.d., n = 12 compression cycles, three different spindles, Fig. 2c). Most of the stiffness values thus determined were less than 5 nN μm⁻¹.

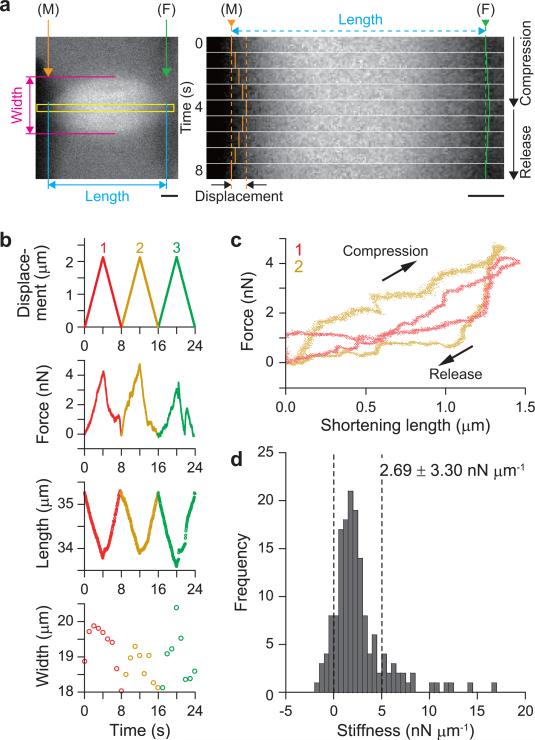
Figure 2. Elastic response of meiotic spindle to small deformations.

(a) The meiotic spindle was repeatedly compressed ≤ 10% of its unperturbed width. The applied displacement, measured force, and changes in width and length are shown. (b) The force vs. compression relationship over two compression cycles (red, 1^st cycle; blue, 4^th cycle). Additional cycles are shown in Supplementary Fig. 1b. (c) Histograms showing the stiffness distribution obtained for small deformations. Average stiffness = 1.19 ± 2.21 nN μm⁻¹ (mean ± s.d., n = 12 cycles, three different spindles, also see Supplementary Fig. 1b online).

We confirmed that the effect of viscoelasticity of the cytoplasm did not affect the force measurements of the spindle, but occasional small negative values of stiffness were probably due to fluctuations associated with flows in the cytoplasm (Supplementary Fig. 2 online). The much larger fluctuations in force-compression curves may reflect the heterogeneous internal structure of the spindle. Here, by using the microscope images to estimate the contact area (S_W) to be several tens of square μm (Fig. 1c), which was assumed to be an ellipsoid similar in shape to the spindle, the Young's modulus (E_W), i.e. a material constant independent of the size and shape, could be calculated to be several kPa (E_W = K_WW/S_W: where K_W = 5 nN μm⁻¹, W ∼ 10 μm, and S_W ≥ 10 μm², see Methods). This value coincides with the lower limit of the Young's modulus of a whole cell reported thus far¹⁰. The Young's modulus of the spindle appears to be several orders of magnitude greater than that of cytoskeletal networks (2−10 Pa) in Xenopus egg extracts⁸, suggesting that the mechanical architecture of spindle is stiffened by molecular motors that crosslink microtubules¹¹.

Pole-to-pole compression of the spindle using our system was more difficult, most likely due to the small size of the contact area at the pole. The spindle tends to ‘escape’ the dual cantilevers rapidly. We have thus far been able to obtain several satisfactory data only for small deformations (Fig. 3 and Supplementary Video 2 online). The spindle also showed a viscoelastic behavior with reversible deformability in a small deformation regime along the pole-to-pole axis (Fig. 3b,c). The average stiffness (K_L) obtained for the compression phase was estimated to be 2.69 ± 3.30 nN μm⁻¹ (mean ± s.d., n = 8 compression cycles, four different spindles, Fig. 3d), a few times larger than that for the width direction. Here, the contact area (S_L), which was assumed to be a circle, was estimated to be about one-third of that for the width direction. Therefore, taking into account that the spindle length (L) was about twice longer than the width, the Young's modulus (E_L) for the pole-to-pole axis was estimated to be at least ten fold larger than that for the width direction. Such anisotropic mechanical properties will be attributable to the microtubule orientation and the directional forces generated by molecular motors.

Next, we examined the mechanical response of the spindle to larger deformations. The spindle was compressed perpendicular to the pole-to-pole axis, in the 8 to 12-μm range in successive cycles (Supplementary Fig. 3 online). In the first cycle (8-μm compression), the spindle width responded reversibly. However, the length extended stepwise and irreversibly when the compression amplitude was increased and with repetition of the large amplitude compression cycle (Fig. 4a,b and Supplementary Video 3 online). Over the experiment, the spindle length elongated by 25%, while recovering to initial width. Thus, the aspect ratio for the elliptical spindle gradually decreased over the compression cycles (initial, 0.54, final, 0.42). These experiments show that the deformation cycles with amplitudes greater than 8 μm induce an irreversible increase in spindle length, resulting in unidirectional plastic behavior (plastic regime).

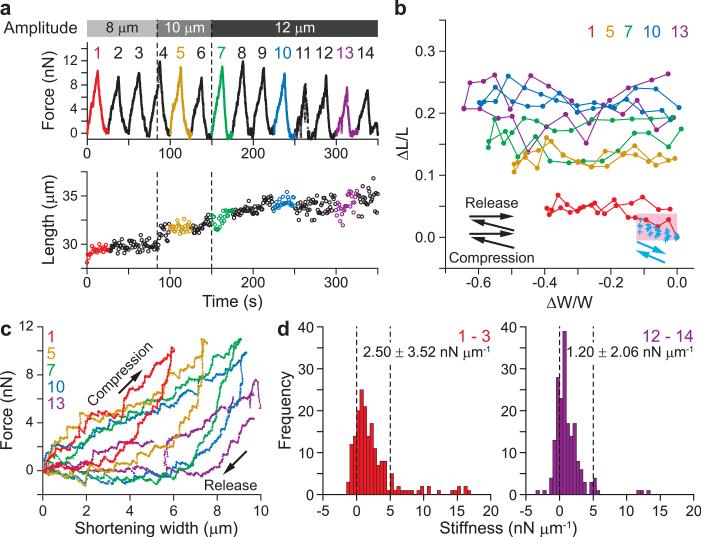
Figure 4. Irreversible changes of the meiotic spindle shape due to large deformations.

(a) The meiotic spindle (the initial length = 28.1 μm, the initial width = 15.3 μm) was compressed perpendicular to the pole-to-pole axis by moving a manipulating cantilever with 8-μm, 10-μm, and 12-μm displacement (Supplementary Fig. 3a online). Accompanied by the compression, the length increased stepwise without returning to the initial length. (b) Relationship between the proportions of length vs. width changes for large deformation (red, 1^st cycle; yellow, 5^th cycle; green, 7^th cycle; blue, 10^th cycle; purple, 13^th cycle) and a small deformation (blue crosses, 4 cycles of Fig. 2b). The length irreversibly increased after each compression cycle as shown by black arrows. Blue arrows show an elastic response observed in the range of a small deformation shown by a pink area (width change, ΔW/W ≤ 0.1; length change, ΔL/L < 0.03). (c) The force vs. compression relationships for the 1^st, 5^th, 7^th, 10^th, and 13^th cycles are shown. Additional examples are in Supplementary Fig. 3b. (d) Histograms showing the stiffness distribution obtained for 8-μm and 12-μm deformations. The average stiffness (mean ± s.d.) is shown at the upper right-hand corner in each figure. The distribution obtained in the 1^st−3^rd cycles was broad, extending larger than 5 nN μm⁻¹ (a dashed line), while that obtained in the 12^th−14^th cycles became narrower and indicated softening of the structure (P < 0.0001 compared with the 1^st−3^rd cycles) (also see Supplementary Fig. 3c online).

Analysis of the stiffness of the spindle during these large compressions revealed that the mechanical properties were also altered along with apparently irreversible changes in morphology. For the first compression of the spindle by 6 μm (∼40% of spindle width), ∼10 nN force was required (Fig. 4c and Supplementary Fig. 3a online). The slope of the compression phase gradually reduced as compression cycles were repeated. We found that a lower force could reduce spindle width to the same extent compared to earlier cycles (Fig. 4c and Supplementary Fig. 3b online). In addition, the hysteresis loop gradually became larger, indicating that the proportion of energy loss in the mechanical work done by one compression cycle increased. Most of the stiffness in the elastic regime was less than 5 nN μm⁻¹ (Fig. 2c), but higher stiffness was readily apparent in the plastic regime (Fig. 4d). The small (< 5 nN μm⁻¹) and large (> 5 nN μm⁻¹) stiffness may be attributable to different architectural components in the spindle. As a result of several compression/release cycles with large amplitude, the stiffer components gradually disappeared (Fig. 4d and Supplementary Fig. 3c online). Together, our data suggest that the elastic architectural features in the spindle are partly disrupted by these larger compressions.

Spindle architecture adapts to mechanical perturbations

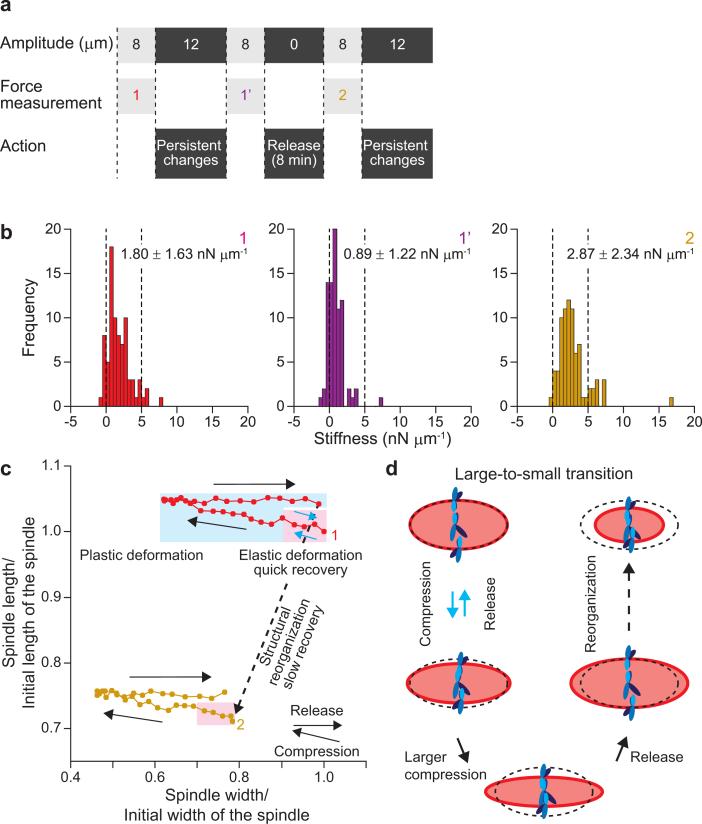
The meiotic spindle size is believed to depend on balance in forces due to activities of motor proteins and diffusible signals that are generated at chromatin. The changes in size due to mechanical perturbations, which occurred without changes in the number of chromosomes, and direct inhibition of molecular components of the spindle (e.g. motor proteins), were therefore unexpected. To examine if the ‘deformed’ spindles, resulting from compressions in the nN and μm range, recover in shape and architectural mechanics, we designed experiments that altered the timing of controlled perturbations (Fig. 5a and Supplementary Fig. 4a online). In the initial compression cycle, the spindle responded with irreversible length changes, as observed in Fig. 4b (Supplementary Fig. 4b online). To induce further changes in same spindle's morphology, higher forces were applied six times in series. The resulting ‘deformed’ spindle needed a lower force in order to reach the same compression, indicating that the spindle lost architectural strength (Supplementary Fig. 4c online). Following these compression cycles, the spindle was released from the cantilevers for 8 min to observe whether it could recover to its original morphology. We found that while both spindle width and length were reduced (width, from 16.1 to 12.6 μm; length, from 30.5 to 21.7 μm), the aspect ratio recovered to that of unperturbed spindles (from 0.53 to 0.58). In addition to the shape changes, the mechanical architecture of the spindle, which was softened through repeated compression cycles, regained stiffness that was only slightly higher than what we had measured for unperturbed spindles (Fig. 5b). It seems that the each spindle with each width has the dependence of own stiffness on the spindle size (Supplementary Fig. 4e online). Together, our data indicate that the mechanical framework of the ‘deformed’ spindle reorganized over minutes (Fig. 5c) and the spindle stabilized its mechanical architecture at different sizes in response to mechanical perturbations.

Figure 5. Transitions of meiotic spindle between different sizes driven by mechanical perturbations.

(a) Time table for the force measurements, compression and release cycles. The width of a meiotic spindle was compressed with 8-μm amplitude to induce a large deformation (Force measurement 1), and then with 12-μm amplitude for inducing persistent changes in spindle morphology. After confirming the structural softening (Force measurement 1’), the spindle was released from the compression for 8 min. Then, the spindle was subjected to the same compression cycles (Force measurement 2). These entire cycles were repeated two more times (Force measurements 3 and 4; see Supplementary Fig. 4b-d online). (b) Histograms showing the stiffness distribution obtained in the Force measurements 1, 1’, and 2. The average stiffness (mean ± s.d.) is shown at the upper right-hand corner in each figure. Paired t-tests compared with the Force measurement 1 were P = 0.0001 against the Force measurement 1’, and P = 0.001 against the Force measurement 2. (c) Width vs. length deformation relationship obtained in the Force measurements 1, and 2. Pink and blue areas, respectively, show the range of elastic and plastic deformations of the spindle. (d) Schematic representation of the shape change in the meiotic spindle describing the process of elastic and plastic deformations and the transition to a smaller size. The ellipse shown by a dashed line represents the shape of the initial spindle located at the upper-left. The shape changes are exaggeratedly expressed.

Discussion

Using quantitative perturbations with a piezo-resistive cantilever system, we found that vertebrate meiotic spindle at metaphase behaves like a viscoelastic or a plastic structure depending on the extent of applied various known load. The quick recovery from a small deformation of the spindle shape, which occurs in seconds, can be attributed to the flexural rigidity of crosslinked microtubules in the spindle. Furthermore, accounting for the ellipsoidal shape of the spindle and assuming that the circumference is constant while the minor axis (= width) is reduced, we estimate that 10% compression of the width should induce ∼3% extension in length. Our experimental results are consistent with these assumptions (Supplementary Fig. 1a online). The ratio of deformation in two perpendicular axes (Poisson ratio) should be 0.5 for a perfect elastic body that does not change volume upon compression. We find that for the spindle, the Poisson ratio is 0.2 for the compression along the width direction, implying that the spindle is quite different from a homogenous gel for which the Poisson ratio should be ∼0.45. The hysteresis in the compression cycles is also consistent with this interpretation of our measurements.

Organelle size control has been studied in different contexts. Self-assembly underlies control of certain cellular structures, such as ribosomes, that do not vary in size. Other organelles, which in principle can be of any size, adopt sizes that are highly reproducible under similar conditions, are believed to use control mechanisms that broadly fit into two classes, molecular rulers (e.g. bacteriophage tail) or balance between two opposing processes, at least one of which is length-dependent (e.g. flagella). A balance in activities of molecular motors, which can push and pull spindle microtubules and can control polymer assembly dynamics, with at least one example of length-dependent control¹², is also believed to be important for controlling metaphase spindle size¹³. Our data show that transitions between spindles of different sizes, each with similar elastic properties, can be achieved through controlled mechanical perturbations (Fig. 5d). This clearly demonstrates that the spindle architecture is controlled by self-regulatory processes that respond to external forces. The time-scale for structural reorganization we observe is slow, i.e., minutes, which may accordingly relate to what is needed for mitotic motors to move micron distances at typical velocities¹⁴ to reorganize microtubule crosslinks.

Cells in unicellular and multicellular organisms experience a variety of physical perturbations, resulting from environmental fluctuations or active processes, such as movement or growth. The mechano-sensing may control organelle architecture to allowing adaptation to forces when cells move or tissues grow. Our experimental system can be used to examine the responses of other organelles to mechanical perturbations and thereby add a new dimension to tests of models for organelle size control. Several advances have been made in the biochemical, structural and biophysical characterizations of key molecules required for meiotic spindle assembly. Magnitudes of forces generated by microtubule polymerization and individual motor proteins have been determined^15-17. Our studies provide a foundation for establishing firm links between these studies to the properties of complex macromolecular cellular machines. The present technique will be useful for combined mechanical and optical studies of a wide variety of cellular organelles.

Methods

in vitro spindle assembly

Cytostatic factor (CSF)-arrested extracts were prepared from Xenopus laevis eggs as previously described¹⁸. Meiotic spindles were assembled with demembranated X. laevis sperm nuclei in the presence of tetramethylrhodamine-labeled tubulin¹⁹. All experiments were carried out at 20 °C.

Experimental setup of force measurements using force-sensing cantilever

Force-sensing cantilevers with ultra-thin piezoresistors were produced and the calibration of their spring constant was performed as previously described⁹. Force-sensing cantilevers (200 μm long, 30 μm wide, 0.3 μm thick) used here had a spring constant of 5−7 nN μm⁻¹. On the other hand, manipulating cantilevers had the same shape except for a thickness of 15 μm. A pair of cantilevers was held in micromanipulators (Narishige Scientific Instrument Lab., Tokyo, Japan) mounted on the microscope. The egg extract containing meiotic spindles was transferred to a coverslip onto which a silicone sheet with a round cutout of 9 mm in diameter (silicone chamber) was affixed, and covered with mineral oil (Sigma-Aldrich, St. Louis, MO) to prevent the evaporation of extract (used for spindle manipulation with a pair of glass micro-needles²⁰). The cantilevers were carefully inserted into the extract at a 45 degree angle to the coverslip after a bipolar spindle was found under the microscope (see Fig. 1). The meiotic spindle was placed between the tip end areas (about 30 × 30 μm square) of the force-sensing cantilever and the manipulating cantilever, and then the position of each cantilever was adjusted such that it can push the meiotic spindle either perpendicular to or parallel to the pole-to-pole axis of the spindle. As Fig. 1 shows, external perturbation to the spindles was accomplished by moving the manipulating cantilever mounted on a piezo-actuator (PI Japan Co., Ltd., Tokyo, Japan). The electric resistance of force-sensing cantilever which is connected to the external Wheatstone bridge was amplified by a hand-made instrumentation amplifier and recorded at the sampling frequency of 1 kHz by using PowerLab data acquisition system (ADInstruments Japan Inc., Nagoya, Japan). The cantilever resistance obtained was converted to the applied force using a resistance-force calibration constant that was obtained before each experiment. The deflection of the force-sensing cantilever was calculated from the measured force using the inverse of its spring constant (0.14−0.20 μm nN⁻¹).

The relationship between the deflection signals and the spindle narrowing width (or length) is called the force-compression relationship. The narrowing width (or length) after both cantilevers made contact with the surface of the spindle was determined as the distance obtained by subtracting the deflection of the force-sensing cantilever from the displacement of manipulating cantilever. The narrowing width (or length) calculated from the distance between the two cantilevers was consistent with that measured from spindle images. The stiffness of the spindle during the compression was estimated by the equation, ΔF/Δt = K Δ(W or L)/Δt (ΔF, the increment of measured force; Δt = 0.2 s; K, stiffness of the spindle; ΔW or ΔL, the indentation of the spindle width or length), in which the changes in force and width (or length) were measured at a sampling frequency of 1 kHz, and were averaged at 5 Hz. The Young's modulus (E) was determined by the equation, ΔF/S = E Δ(W or L)/(W or L) = K Δ(W or L)/S (S, the contact area; W or L, initial spindle width or length). The contact area (S) for the compression along the width direction was estimated by assuming that it is an ellipsoid similar in shape to the spindle, and its long axis of the ellipsoid was measured from fluorescence image obtained when the spindle was compressed by 2 μm. On the other hand, the contact area for the compression along the pole-to-pole axis was estimated by assuming that it is a circle because of the symmetry of the spindle shape, and its diameter was measured from fluorescence image obtained when the spindle was compressed by 2 μm. The statistical significance, P, of the experiments was confirmed by a paired two-tailed Student's t-test.

Image acquisition and analysis

Time-lapse images of tubulin fluorescence in meiotic spindles were acquired using a Hamamatsu ORCA AG cooled CCD camera (Hamamatsu Photonics K. K., Hamamatsu, Japan) on an inverted microscope (IX70; Olympus, Tokyo, Japan) with a 40× Plan Fluor lens and a 1.5× zoom lens at 1 s intervals. Spindle width and length were estimated using Metamorph software (Molecular Devices, Sunnyvale, CA).