Abstract
The spatial extent of attention was investigated by measuring sensitivity to stimuli at to-be-ignored locations. Observers detected a stimulus at a cued location (target), while ignoring otherwise identical stimuli at nearby locations (foils). Only an attentional cue distinguished target from foil. Several experiments varied the contrast and separation of targets and foils. Two theories of selection were compared: contrast gain and a version of attention switching called an all-or-none mixture model. Results included large effects of separation, rejection of the contrast gain model, and the measurement of the size and profile of the spatial extent of attention.
Keywords: attention, filtering paradigm, spatial tuning functions, contrast gain, attention switching
The spatial extent of attention refers to the region of space in which perceptual tasks are affected by an attentional state. For example, one might cue a point in space as relevant to a task and then measure the extent to which nearby locations are also affected. If attention affects sensitivity, then one can refer to the effect of attention across space as a spatial sensitivity function, highlighting an analogy to spatial tuning functions of neurons in sensory areas of the cortex. Such spatial sensitivity functions, like tuning functions of neurons, can have different profiles for different conditions. For example, the spatial sensitivity function might be quite narrow under some conditions, with only a small region surrounding the cued location showing effects of attention, whereas under other conditions it may extend more broadly around the cued location. Also, like the spatial tuning function of neurons, the spatial sensitivity function may sometimes have relatively complex profiles such as an antagonistic center-surround structure. These issues have been investigated through a diverse range of paradigms.
In the present study, we develop a filtering paradigm to characterize the spatial extent of attention that is based on psychophysical theories. The theoretical basis of this paradigm allows a quantitative evaluation of alternative answers to multiple questions within a single theoretical framework. A goal in developing this framework is to provide a common theoretical context within which one can derive and test hypotheses about the effects of attention on human behavior and the effects of attention on the underlying neurophysiology.
Perhaps the best known approach to investigating the spatial extent of attention is to cue a location and observe how detection or discrimination performance changes with increasing separation between the cued location and the target. Sagi and Julesz (1986), for example, used a dual-task paradigm in which observers were to discriminate whether a stimulus presented at a cued location was a T or an L, while simultaneously monitoring the display for the presentation of probe dots at other locations. They found that for a cued location at an eccentricity of 4°, there was a region surrounding the cued location with a diameter of 3° that had improved detection performance relative to more distant locations. Several studies have used variations of this dual-task approach to further study the spatial extent of attention (e.g., Huang & Dobkins, 2005; LaBerge, 1983; Lee, Itti, Koch, & Braun, 1999; Zenger, Braun, & Koch, 2000).
An alternative to the dual-task approach is to use partially valid cues (e.g. response time: Shulman, Wilson & Sheehy, 1985; Moore, Lanagan-Leitzel & Fine, 2007; accuracy: Niebergall, Tzvetanov & Treue, 2005). In this paradigm, detection or discrimination performance to stimuli presented at cued locations (valid condition) is compared to performance at uncued locations (invalid condition). Shulman, et al. (1985) found, for example, that increasing the distance between the cued location and the uncued location increased the response time to the uncued location monotonically for distances of 0° to 20°.
The cueing paradigm has been modeled in different ways. Sperling and Weichselgartner (1995) did so using a theory that emphasizes gain mechanisms, which are natural specifications of the idea that the processing of stimuli at uncued locations is attenuated relative to that at cued locations (Treisman, 1960). Bahcall and Kowler modeled it as an all-or-none process whereby sometimes stimuli at the cued location are processed, but other times stimuli at an uncued location are processed instead. This is a specification of the idea that stimuli at uncued locations are filtered out from further processing (Broadbent, 1958) or as attention switching from the cued to uncued locations (Sperling & Melchner, 1978).
There are several interesting variations of the cueing paradigm. Some studies use cues that indicate the location of the target with 100% validity and study the effect of noise (e.g., Davis, Kramer & Graham, 1983; Dosher, Liu, Blair & Lu, 2004; Eckstein, Shimozaki & Abbey, 2002; Eriksen & Hoffman, 1973). Other studies introduce an array of stimuli and require the maintenance and manipulation of the attended stimuli (Intriligator & Cavanagh, 2001; Moore, Lanagan-Leitzel, Chen, Halterman & Fine, 2007). Studies of this sort (i.e., that included competing noise) have yielded estimates of the spatial extent of attention that tend to be narrower than estimates from dual-task and partially valid cueing studies. Such diversity of estimates regarding the spatial extent of attention has contributed to conclusions that the spatial extent of attention is under flexible control and that it depends on the stimulus and task (e.g. Cheal, Lyon & Gottlob, 1994; Eriksen & St. James, 1986; LaBerge & Brown, 1989).
In addition to differences in the estimates of the size of the spatial extent of attention, qualitative differences have also been observed across studies and paradigms. In particular, whereas the studies cited so far all found monotonic effects of the separation between cued and uncued locations, other studies have reported non-monotonic effects (e.g., Cutzu & Tsotsos, 2003; Steinman, Steinman, & Lehmkuhle, 1995). In these studies, the observed performance is consistent with a center-surround profile analogous to the spatially antagonistic processing of visual information that is commonly observed in early visual neurons. Performance is better for stimuli presented at the cued location than for stimuli presented at a distant baseline location. Performance is worse, however, for stimuli presented at locations nearby the cued location than for stimuli presented at the distant baseline location. Such a profile is predicted by a computational theory developed by Tsotsos and colleagues (Tsotsos, Culhane, Wai, Davis, & Nuflo, 1995; see also Trappenberg, Dorris, Munoz and Klein, 2001) in which top-down cue information is systematically combined with bottom-up stimulus processing. The center-surround profile has also received support from studies in which two items are cued and observers must process (e.g., identify) both. These studies often find reduced performance with reduced separations between the targets (Bahcall & Kowler, 1999; Becker, 2001; Cutzu & Tsotsos, 2003; Mounts, 2000; but see Sagi & Julesz, 1985).
An alternative to the cueing paradigms just reviewed is the filtering paradigm. In filtering paradigms, one must attend to some stimuli while ignoring others. For example, shadow the message in one ear while ignoring the message in the other ear (e.g. Cherry, 1953). Or, classify the size of a stimulus while ignoring the color (e.g. Gottwald & Garner, 1975). For a definition of a filtering task see Kahneman and Treisman (1984) and for a more recent discussion see the first chapter of Pashler (1998). This paradigm is also known as a gating task (Posner, 1964) or a focused attention task (Yantis & Johnston, 1990). More generally, one can find aspects of spatial filtering in masking (e.g. Baldassi & Verghese, 2005), crowding (e.g. Parkes, Lund, Angelucci, Solomon & Morgan, 2001) and surround suppression paradigms (e.g. Petrov & McKee, 2006). To make clear what distinguishes a filtering paradigm, note that a partially valid cueing task is not an example of filtering because both valid and invalid stimuli are relevant to the response. Similarly, dual-task situations (e.g., Sagi and Julesz, 1986) are not examples of filtering because both tasks are relevant to a response. The filtering task that is probably most similar to the cueing studies reviewed above and that has been used to study the spatial extent of attention is the flanker paradigm (Eriksen & Hoffman, 1973; Eriksen & Eriksen, 1974). We focus our review on this task.
In the flanker task, performance to stimuli that are presented at a single relevant location is compared across conditions in which irrelevant but potentially distracting stimuli (flankers) are presented at variable distances from the relevant location. Thus, this is a filtering task. The special feature emphasized in the flanker task is the use of a many-to-one categorization task in which multiple stimuli (typically letters) are mapped onto a single response. This mapping allows one to compare the effect of flankers that are compatible with the category of the target to those that are incompatible with the target. Such a flanker compatibility effect must be mediated by post-categorical processing because the stimuli are arbitrarily assigned to categories. Eriksen and Hoffman (1973), for example, applied this task to the question of the spatial extent of attention. They found that the identification of target stimuli presented at fixation was influenced by compatible flanking letters when those letters appeared within 1° in either direction of the target, but not when they appeared farther away. These results have been replicated in several studies (e.g. Miller, 1991; Pan & Eriksen, 1993; Yantis & Johnston, 1990) and a recent study has reported evidence for a center-surround profile (Müller, Mollenhauer, Rösler and Kleinschmidt, 2005). More recently, this flankers task has been used with non-letter stimuli (e.g. Cohen & Shoup, 1997; Mordkoff, 1998). In general, the flanker task has several distinguishing features that make it useful for studying the spatial extent of attention. It measures manipulations of the irrelevant flankers rather than manipulations of the targets. Importantly, these targets and flankers are identical except for one being at a cued location and the others being at uncued location.
To summarize this brief review of prior approaches to studying the spatial extent of attention, the large range of prior approaches has lead to a large range of results regarding at least three aspects of the spatial extent of selection: the size of the spatial extent, the profile of the spatial extent, and the mechanism from which the spatial extent derives. In particular, some found large extents of spatial attention; others much smaller extents. Some found the spatial extent of attention to have a monotonic profile; others found it to have a center-surround profile. Some found results consistent with a form of gain; others found hints of an all-or-none filter.
In this article, we develop a theoretical framework within which these aspects of the spatial extent of attention—size, profile and mechanism—as well as others, can be addressed systematically within a common context. The framework is grounded in existing psychophysical theories of sensory phenomena. The idea is that by using explicit psychophysical theory, diverse behavioral effects of attention can be related to each other. Moreover, behavioral effects of attention can be related to the underlying neurophysiological effects of attention. The theory provides a framework within which to develop explicit linking propositions between behavioral and neurophysiological mechanisms (Teller, 1984).
Overview of the spatial filtering paradigm
The basis of our approach is a particular cueing paradigm, which we refer to as spatial filtering in a visual detection task or spatial filtering for short. The central idea is to present stimuli at both a relevant and an irrelevant location and to measure detection performance as a function of the separation between these locations. We refer to the stimulus at the relevant location as the target and the stimulus at the irrelevant location as the foil. Nothing other than location—relevant versus irrelevant—distinguishes the target from the foil. Because the relevant location is specified only by an attentional cue, and the target is defined only by appearing in that location, any difference in the processing of the target and the foil can be attributed to selective attention.
To understand the spatial filtering paradigm it is useful to consider two extreme idealized conditions. If the separation between the cued location and the foil is large enough to allow perfect selection of stimuli at the cued location over stimuli at the foil location, then the foil will not be processed and performance will be based entirely on the target. If performance is then measured in terms of the foil value, it should be at chance. This follows because the value of the foil is unrelated to that of the target, and performance is based entirely on the target. At the other extreme, if the separation between the cued location and the foil location is zero so that selection of a target over the foil is impossible, then when performance is measured in terms of the foil, it must be the same as that for the target. Thus, under conditions in which the target is clearly visible and therefore allows near perfect performance, the response to the foil must range from near 100% (like the target) at small separations to random responding at large separations. This paradigm, therefore, can provide enormous effects upon which to base measurements of the spatial extent of attention.
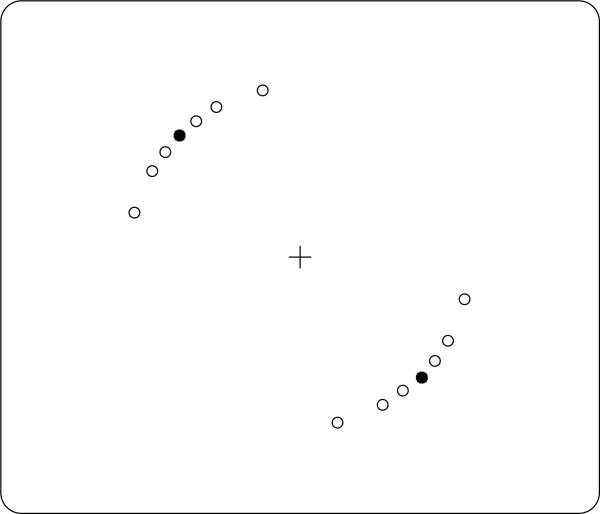
To introduce the paradigm, a simplified version of a spatial filtering experiment is illustrated in the next series of figures. First the experimenter defines a set of relevant and irrelevant locations as illustrated in Figure 1. Specifically, Figure 1 shows two relevant locations (filled symbols), one on either side of a central fixation cross, and several surrounding irrelevant locations (open symbols). The symbols are shown here only to illustrate the layout of relevant and irrelevant locations; they do not appear during the experiment itself.
Figure 1.
A schematic illustration of the arrangement of possible stimulus locations. The filled disks mark the relevant locations where a target can appear. The open disks mark the irrelevant locations where a foil can appear.
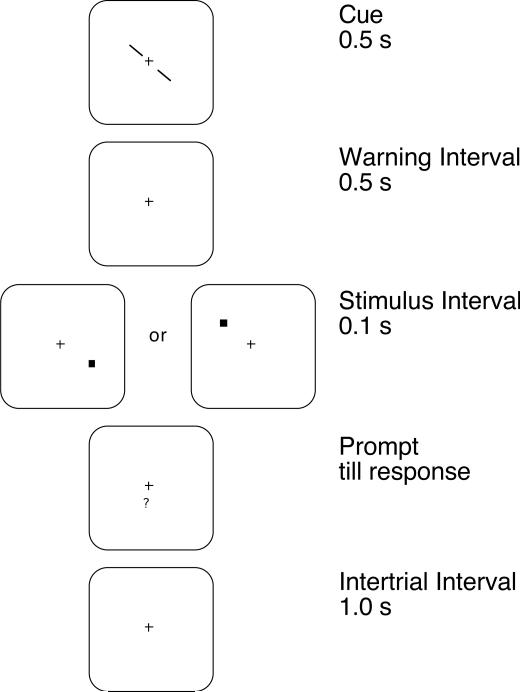
Figure 2 illustrates the trial events. Relevant locations are constant throughout a block of trials, but to facilitate observers' memory of those relevant locations, each trial begins with central pointers that indicate the relevant locations. Following a brief warning interval, a stimulus is presented in one of the two relevant locations—this is the target. The task is a two-alternative forced-choice (2AFC) detection task in which an observer indicates whether the target appeared to the left or to the right of fixation. A second stimulus—the foil—is presented in one of the twelve irrelevant locations at the same time as the target. Importantly, the location of the foil does not predict the location of the target in any way. For simplicity, foils are not shown in Figure 2. Instead, several sample displays that include both a target and a foil are illustrated in Figure 3. The arrows in Figure 3 are shown only to indicate the relevant locations for purposes of description here; they do not appear during the experiment itself.
Figure 2.
An illustration of the procedure used in all experiments. Each trial begins with a cue followed by the stimulus and then a prompt until response. The target is at one of two possible relevant locations on the left or right side of fixation. Foils are not shown.
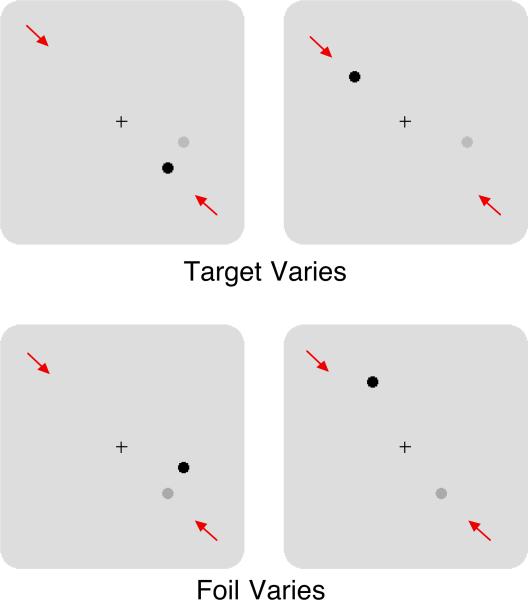
Figure 3.
An illustration of four possible stimulus displays. In the top two examples, a high contrast target is on either the right or left side of fixation. A low contrast foil remains on the right. In the bottom two examples, a high contrast foil is on either the right or left side. The low contrast target remains on the right. In the illustration, the red arrows indicate the relevant locations and were not present in the experiment.
Throughout the course of the experiment, contrast of both the target and the foil are varied, and two separate psychometric functions are obtained, one for the target based on those trials in which the foil was presented at low contrast and one for the foil based on those trials in which the target was presented at low contrast. All contrast values are intermixed from trial to trial. The psychometric function for the target is a standard function relating performance on the 2AFC task to target contrast. Again it is based on the subset of trials in which the foil contrast was low. The top two displays in Figure 3 illustrate trials that contribute to this function. The foil has a low contrast and the location of the target varies from right to left across trials. Performance is expected to be near perfect at high contrast and near chance at low contrasts, just like a standard psychometric function in which the target is the only stimulus in the display.
The psychometric function for the foil is the main innovation of this spatial filtering paradigm. It measures the proportion of trials on which the 2AFC response corresponds to the side on which the foil was presented, and is based on the subset of trials in which the target contrast was low. Analogous to the standard target psychometric function, this proportion is graphed as a function of foil contrast. The bottom two displays in Figure 3 illustrate trials that contribute to this function. The target has a low contrast and the foil varies from right to left across trials. When the foil can be clearly distinguished from the target (e.g., because it is widely separated from the cued location), the psychometric function for the foil should remain at random responding (0.5) for high foil contrast. This follows because if the foil and target can be clearly distinguished, then it is assumed that responses should be based on the target, which are on the same side as the foil half the time. In contrast, when the foil is indistinguishable from the target, the foil function should approach 1.0 for high foil contrasts. This follows because if the foil and target are indistinguishable, then observers must interpret a high contrast foil as a target, and therefore tend to respond on the side with the foil.
The motivation for this way of presenting the data underlying the foil psychometric function is worth elaborating. Again, targets and foils differ only in location. This is critical to the logic of attributing these effects to spatial attention. Similarly, the analysis of target and foil psychometric functions is equivalent. The target psychometric function is the proportion of responses on the same side as the target, presented as a function of target contrast. The foil psychometric function is the proportion of responses on the same side as the foil, presented as a function of foil contrast. Thus given the specified task, the target psychometric function reflects percent correct, whereas the foil psychometric function reflects the extent to which observers responded to the foil despite the fact that they were trying to respond to the target.
The purpose of obtaining both of these psychometric functions is that the nature of the selection process makes predictions about the relation between them. Consider once again the two extreme idealizations. At zero separation where selection of the target from the foil is impossible, the target and the foil psychometric functions must be identical. At large separations where selection of the target from the foil can be perfect, the target and foil psychometric functions must differ. Specifically, the foil psychometric function must drop to random responding. Thus, measuring the way in which these psychometric functions change as a function of separation can provide a measure of the spatial extent of attention. In order to do that, however, one must develop theory concerning how the psychometric functions relate to the underlying mechanisms of selection. This is described in the next section.
Theory
Here we consider two hypotheses specifying the mechanism of selection in the spatial filtering task. The first is a contrast gain hypothesis whereby attention acts to modulate the effective contrast of stimuli at attended locations. This model is an example of attenuation as discussed in early theories of attention (e.g., Treisman, 1960) and has been investigated in a number of recent studies, both psychophysical (e.g. Huang & Dobkins, 2005; Ling & Carrasco, 2006) and neurophysiological (e.g. Reynolds, Pasternak & Desimone, 2000; Williford & Maunsell, 2006).
The second hypothesis is an all-or-none mixture hypothesis whereby stimuli are processed either as an attended stimulus or as an unattended stimulus. This is an example of an attention switching model (Sperling & Melchner, 1978). What varies with separation is the proportion of trials on which the stimulus is attended. This model has its origins in the filter theory of Broadbent (1958), and is formally specified as the “mixture model” by Shaw (1980). Further elaborations of this model include the “single-band model” (Davis et al., 1983) and the “imprecise targeting model” (Bahcall & Kowler, 1999).
The gain hypothesis and the all-or-none mixture hypothesis predict different effects of target-foil separation on the two psychometric functions from the spatial filtering task. A summary of these predictions for each model is provided next. Formal descriptions of the two models and derivations of the predictions are provided in the Appendix.
The contrast gain model
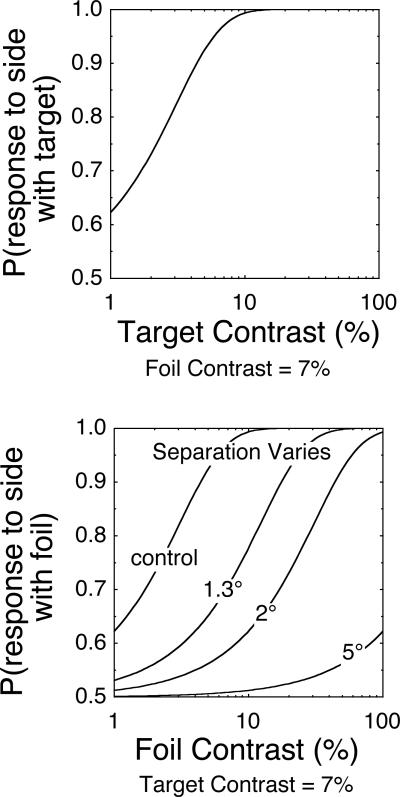
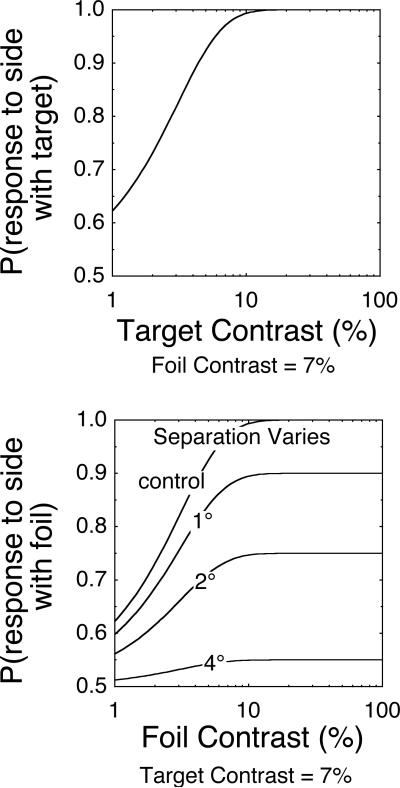
First consider a model with contrast gain as the selection process. Under such a model, the value corresponding to the representation of the relevant attribute is modulated by a multiplicative factor. For example, in contrast detection, the internal response to contrast is a function of the product of contrast and a gain parameter. This model is formalized in the Appendix and its predictions for the spatial filtering task are illustrated in Figure 4.
Figure 4.
The predictions of the contrast gain model are shown for the target and foil psychometric functions. The top panel is the target psychometric function with a typical function. The bottom panel is the foil psychometric function. Several functions are shown for different separations and for the target as a control. The contrast gain model predicts that the foil functions shift horizontally on a log contrast axis.
The top panel of Figure 4 shows a representative psychometric function for the target. A typical psychometric function relating performance to log contrast is shown with a threshold of about 2% contrast and response proportion with an upper asymptote of 1.0. Little effect of separation between the target and the foil is expected on the psychometric function for the target because the foil is always presented at low contrast on those trials that contribute to this function and it should therefore be almost as though only the target is present (see Figure 3).
The critical predictions of the model concern the effect of separation between the target and the foil on the psychometric function of the foil. this foil function is shown in the lower panel of Figure 4. This function relates the proportion of responses that corresponded to the side of the foil as a function of foil contrast, and is therefore an estimate of the influence of the foil on performance. The control curve is for the special case of zero separation where the foil cannot be distinguished from the target and so the predicted foil function is identical to the target function. The remaining family of curves represents results with increasing separation between the target and the foil and corresponding decreases in gain as applied to the foil. The predicted curves are horizontal shifts of the function on this graph of log contrast. Thus, under a contrast gain model, the effect of attention can be summarized as a change in threshold of the foil psychometric function.
The all-or-none mixture model
Next consider a model with an all-or-none selection process. Under such a model, there is a switching process such that stimuli are processed at one location or the other over time. For example, suppose there is variability in the maintenance of the relevant location from trial to trial (following Bahcall & Kowler, 1999). If so, then the same stimulus is judged as being at the relevant location on some trials and not on others. When the stimulus is judged to be at the relevant location, then the response varies with stimulus contrast. When the stimulus is judged to not be at the relevant location, then responses are random with respect to this stimulus. Consequently, the observed aggregate performance is a mixture of two states: one state corresponding to the response to the target that is influenced by contrast of the target, and one state corresponding to random responses. This all-or-none mixture model is presented in the Appendix and its predictions for the spatial filtering task are illustrated in Figure 5.
Figure 5.
The predictions of the all-or-none mixture model are shown for the target and foil psychometric functions. The top panel is the target psychometric function with a typical function. This target function is identical to that used in the previous figure. The bottom panel is the foil psychometric function. Several functions are shown for different separations and for the target as a control. The all-or-none mixture model predicts that the foil functions scale vertically.
As before, the top panel of Figure 5 shows a representative psychometric function for the target. It is the same as that for the contrast gain model (see Figure 4). As shown in the lower panel of Figure 5, the critical prediction of the model again concerns the effect of separation between the target and the foil on the psychometric function of the foil. The control curve is again for the special case of zero separation where the foil cannot be distinguished from the target and so the predicted target and foil functions are identical. The remaining family of curves represents increasing separation with corresponding decreases in the probability of attending the foil. The predicted curves show a vertical scaling of the curve for the foil. Thus under an all-or-none mixture model, the effect of attention can be summarized as the change in the upper asymptote of the foil psychometric function.
Estimating the spatial extent of attention
The spatial extent of attention can be estimated by using the most appropriate of the two models: contrast gain or all-or-none mixture. For the contrast gain model, one can plot sensitivity (1/threshold) as a function of separation. From this spatial sensitivity function, one can estimate the critical separation as having a sensitivity that is half of the maximum sensitivity to a target.
For the all-or-none mixture model, one can plot asymptotic performance as a function of separation. From this spatial asymptote function, one can estimate the critical separation as having an upper asymptote halfway between 0.5 and 1.0. Thus, both models allow one to plot analogous spatial functions and to quantify the spatial extent of attention by the critical separation.
Summary
We have considered two models of the effect of attention: contrast gain and all-or-none mixture. These models can be distinguished from each other on the basis of the psychometric function for the foil. Specifically, if there is an underlying contrast gain mechanism of selection, then performance reveals a change in the threshold of the foil psychometric function. In other words, a horizontal shift of the function. If there is an underlying all-or-none mechanism of selection, then performance reveals a change in the upper asymptote of the foil psychometric function. In other words, a vertical scaling of the function. One can then use the appropriate parameter from the foil psychometric function to estimate a spatial function that is analogous to a spatial tuning function for attention. The spatial extent of attention can then be quantified by the critical separation that describes the half-height, half-width of this spatial function. This pair of models is far from exhaustive; others are described in the General Discussion.
Overview of study
The ultimate goal of this study is to describe the spatial extent of visual attention using the spatial filtering task. To do so, however, it is necessary to first identify the underlying mechanism of selection in order to know the relevant parameter of the foil's psychometric function. The first two experiments of the study, therefore, distinguish between contrast gain and all-or-none mixture models. The second two experiments then use these results to measure something analogous to spatial tuning functions for visual attention. These functions are then used to estimate the spatial extent of attention for a given eccentricity and to determine the shape of the spatial profile of attention.
General Method
Observers
The observers were adults with normal or corrected-to-normal acuity. All were experienced in psychophysical judgments and gave written consent. JP is an author.
Apparatus
The stimuli were displayed on a flat-screen CRT video monitor (19 inch View Sonic PF790) with a refresh rate of 74.5 Hz controlled by a Macintosh G4 computer (Mac OS 9.2). The display contained 832 by 624 pixels which at a viewing distance of 60 cm subtending 32° by 24° (25.5 pixel per degree at screen center). Moderate room lights were used to reduce pupil size to facilitate eye movement recording. Display luminance was linearized using conventional methods (Cowan, 1983). Three essentially identical instruments with slightly different lighting were used over the course of the study. For Instrument A, the peak luminance was 115 cd/m2 and the black level was 6.5 cd/m2; for Instrument B, the peak luminance was 110 cd/m2 and the black level was 3.6 cd/m2; for Instrument C, the peak luminance was 98 cd/m2 and the black level was 9.0 cd/m2. The instrument used for each observer was somewhat idiosyncratic because observers participated in the experiments in different orders. In Experiment 1, JP and NP used Instrument A, the other observers used Instrument C; in Experiment 2, MK used Instrument B, SY used Instrument C; in Experiment 3, JP used Instrument A, MK and SY used Instrument B; in Experiment 4, JP and SY used Instrument A, MK used Instrument C. Stimuli were generated using the Psychophysics Toolbox version 2.44 (Brainard, 1997; Pelli, 1997) for MATLAB (version 5.2.1, Mathworks, MA). Observers were seated in an adjustable height chair in front of the display. A chin and forehead rest was set so that each observer's eyes were level with the middle of the monitor.
For most observers, eye movements were recorded using a noninvasive video system (EyeLink I, Version 2.04, SR Research, Osgoode, ON, Canada) controlled by a separate DOS computer. The EyeLink I is a binocular, head-mounted, infrared video system with 250 Hz sampling. It was controlled by the EyeLink Toolbox extensions of MATLAB Version 1.2 (Cornelissen, Peters, & Palmer, 2002). We recorded and analyzed only the right eye position. For discussions of the performance of this system, see van der Geest and Frens (2002) and Palmer, Huk and Shadlen (2005). In brief, the system has a resolution of at least 0.1° for detecting saccades and a resolution of about 1.0° for sustained eye position over many trials.
The summary statistics of the eye position for individual observers in each experiment are given in Table 1. For some cases (5 of 15 possible instances), observers did not have their eye movements measured for ease or timeliness of the measurement. All observers reported that it was very easy to maintain fixation for the displays in this experiment. In the table, the first column specifies the percent of aborted trials. They ranged from 0.3% to 2.2% with a mean of 0.5±0.2%. Most of these aborts were from blinks and equipment problems and not saccades to peripheral locations. The next two columns specify the mean eye position at the beginning of the stimulus display. Different observers showed idiosyncratic deviations that are probably due to biases in calibration. Overall the mean horizontal position was -0.1±0.2° and the mean vertical position was 0.6±0.3°. The last two columns specify the standard deviation of the eye position at the beginning of the stimulus display. Here observers were quite consistent. Overall the mean horizontal deviation was 0.7±0.1° and the mean vertical deviation was 1.3±0.1°. This variability is probably due to the imprecision in the EyeLink measurements over time (cf. Palmer, et al., 2005). In summary, observers maintained accurate fixation and essentially never made saccades to the possible target locations.
Table 1.
Eye Fixation Measurements
| Experiment and Observer | Percent Aborted Trials | Mean Horizontal Position | Mean Vertical Position | SD Horizontal Position | SD Vertical Position |
|---|---|---|---|---|---|
| Experiment 1 | |||||
| AS | 2.2% | -0.3° | 0.2° | 0.7° | 1.3° |
| JP (n/a) | |||||
| MK | 0.4% | 0.0° | -0.1° | 1.2° | 1.0° |
| MM | 1.0% | -1.2° | 1.8° | 0.8° | 1.1° |
| NP (n/a) | |||||
| SY | 0.7% | 0.5° | -0.4° | 0.5° | 1.7° |
| Experiment 2 | |||||
| MK | 0.4% | 0.1° | 0.6° | 0.6° | 1.1° |
| SY | 0.4% | 0.6° | 1.1° | 0.9° | 1.3° |
| Experiment 3 | |||||
| JP (n/a) | |||||
| MK | 0.3% | -0.4° | 0.3° | 0.7° | 1.3° |
| SY | 0.4% | 0.2° | 0.8° | 0.7° | 2.1° |
| Experiment 4 | |||||
| JP (n/a) | |||||
| MK | 0.1% | -0.2° | 0.9° | 0.6° | 1.1° |
| SY (n/a) | |||||
| Mean | 0.6±0.2% | -0.1±0.2° | 0.6±0.2° | 0.7±0.1° | 1.3±0.1° |
Note: SD denotes standard deviation.
Stimuli
The target stimuli were disks with a diameter of 0.3° presented at an eccentricity of 8°. On any trial, two stimuli always appeared. The target was located at one of two relevant locations. In most experiments, the relevant location was fixed to a pair of locations on opposite sides of fixation corresponding to clock positions of 10:30 and 4:30. The foils appeared at irrelevant locations on either side of the relevant locations. The relevant location was indicated by a high contrast peripheral cue at the beginning of each block of trials illustrated in Figure 2. Contrast was varied for both the targets and foils in a partial factorial design as specified below. Based on an expected threshold of 7% to 8%, the contrast values for most observers were 7, 10, 14, 20, and 100%.
Procedure
A 2AFC procedure was used in which a key press indicated whether a target was shown on the left or on the right side of fixation. Observers were instructed to maximize accuracy, with no speed stress, and feedback was provided following incorrect responses.
Figure 2 illustrates the trial events in a typical trial. A central fixation cross was presented continuously. Each trial began with a cue display for 0.5 s, which was followed by a 0.5 s warning interval during which the screen was blank. The stimulus display was then presented for 0.1 s, simultaneously with a medium frequency tone. Following a 0.2 s interval during which the screen was blank (not shown), a prompt display was presented until a response was made. A low frequency tone was played in the event of an error, adding 0.5 s to the end of a trial. No feedback was given following correct responses. Trials were separated by inter-trial interval of 1 s.
Design
Every trial included both a target and a foil. The only difference between targets and foils was that a target occurred at the cued locations and a foil did not. For a given trial, the combination of possible contrasts for targets and foils is shown in Table 2. Each contrast value in the design was a multiple of the estimated contrast threshold for the target alone, which was near 7% for most observers. The table specifies the conditions for describing the two psychometric functions of this spatial filtering paradigm. In particular, the leftmost column of the table shows conditions across which the contrast of the target varies while the contrast of the foil remains fixed at the lowest value. Responses indicating the side of the target for these conditions define the target function, which is just the standard psychometric function. The bottom row of the table shows the contrast of the foil varying while the contrast of the target remains fixed at the lowest value. Responses indicating the side of the foil, regardless of which side the target is on, define the foil function. This is an analogous psychometric function that describes the extent to which the foil determines the response.
Table 2.
Design for Two-Stimulus Experiment
| Target Contrast | |||||
| 100% | X |
||||
| 20% | X |
||||
| 14% | X |
||||
| 10% | X |
||||
| 7% | X | X | X | X | X |
| 7% | 10% | 14% | 20% | 100% | |
| Foil Contrast | |||||
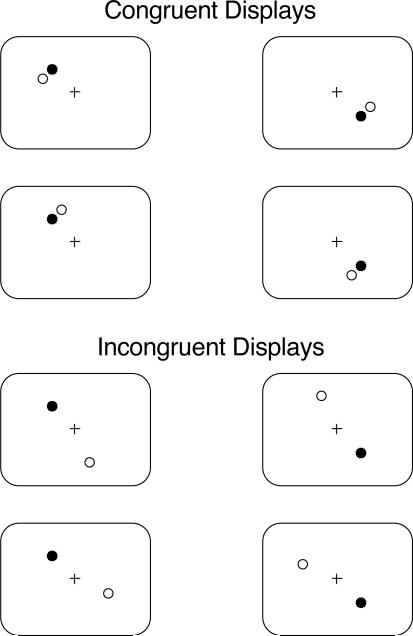
A complication of the two-stimulus design arises from whether the target and foil evoke a congruent response. For some trials, the target and foil are on the same side of fixation; for other trials, they are on opposite sides of fixation. These trials are labeled congruent and incongruent, respectively. The geometry of all possible displays of target and foil is illustrated in Figure 6. Only a single pair of contrasts at one separation is shown. In each display, a target is represented by an filled disk and a foil is represented by a open disk. The top four displays are congruent and the bottom four displays are incongruent. Displays in the left column have targets on the left side and those in the right column have targets on the right side. Finally, the remaining variation is whether the foil is on one or the other side of the target. The primary analyses of this article simply identify if the response is on the same side as the target for the target function or on the same side as the foil for the foil function. For Experiment 2, these functions are further broken down by whether the target and foil are congruent or not. This breakdown allows tests of hypotheses concerning how information from both stimuli combine to influence the response (see Appendix).
Figure 6.
All possible arrangements of the target and foil are shown for one pair of contrasts and one separation. Three binary variables are combined to form eight possible displays: congruent versus incongruent, target on left versus right side of fixation, and foil shifted counter clockwise or clockwise from the target.
Except for Experiment 2, all experiments combined this design with multiple separations between the target and foil. In the initial experiment, these were separations of 1.2°, 2.4° and 4.8°. Both contrast and separation conditions were presented in a mixed-list fashion. In some experiments, a control condition was presented in separate sessions with only the target at varying contrasts. Data were collected over multiple sessions of about 1 hour each. Several practice sessions were conducted before the beginning of each experiment.
Analysis
All psychometric functions were fit to a cumulative normal raised to a power (Pelli, 1987) using maximum likelihood methods (e.g. Watson, 1979). This method of analysis yields functions that are essentially indistinguishable from functions fit with a Weibull (Pelli, 1987). The psychometric functions were described by three parameters: the upper asymptote, a detection threshold, and an exponent. The exponent was always fixed to 3 which is typical for contrast detection experiments. The detection threshold was defined as the contrast necessary to yield a performance level that was half way between chance (.5 for the 2AFC task used here) and the estimated asymptotic performance. This definition of threshold made the threshold invariant of changes in the mixture parameter of the all-or-none mixture model. For example, if the percentage of attended trials dropped from 100% to 50%, then the upper asymptote drops from 100% to 75% but the threshold remains the same. This is because the same stimulus yields the criterion performance halfway between chance and the upper asymptote.
Experiment 1: Effect of Separation and Contrast
Methods
Spatial attention was manipulated using a cued location to define targets and foils. Contrast was varied to measure target and foil psychometric functions as described in the general methods. These measurements were made for three separations. For most observers, the contrasts were 7%, 10%, 14%, 20% and 100% and the separations were 1.2°, 2.4° and 4.8°. Two observers were presented with modified values because of their high initial performance. For Observer MK, smaller values of separations were used: 0.3°, 0.6° and 1.2°. For Observer SY, smaller values of contrasts were used: 5%, 7%, 10%, 14% and 100%. After practice, 6 observers participated in five hour-long sessions resulting in 320 trials per psychometric function for each observer
Results and Discussion
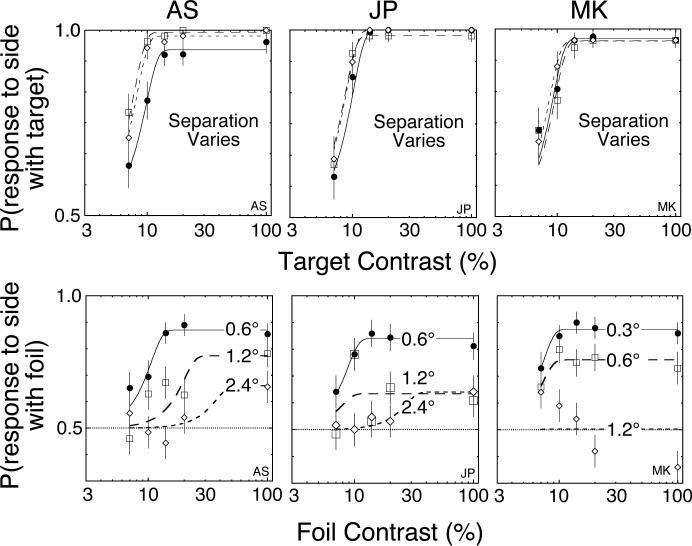
The results for 6 observers are shown in Figures 7 and 8. For each observer, the psychometric function for the target is in the top panel and the psychometric function for the foil is in the bottom panel. For the target functions, there is a little or no effect of separation on the threshold and the asymptote. These effects are quantified below.
Figure 7.
The results for Experiment 1 are shown for three observers. Each column shows a separate observer. The top panels contain a target function and the bottom panels contain a foil function. There is little or no effect of separation for the target functions. In contrast, there is a large effect of separation for the foil functions. The functions for larger separations show a reduced asymptote consistent with the all-or-none mixture model.
Figure 8.
The results for Experiment 1 are shown for three more observers. Format and results are the same as Figure 6.
Of primary interest is the effect of separation on the psychometric function of the foil that is shown in the bottom panels of the figure. For the smallest separations, the foil functions are similar to those observed for targets but with a reduced asymptote. For the larger separations, the functions show much lower asymptotes. Such vertical scaling is the pattern predicted by an all-or-none mixture and not by contrast gain.
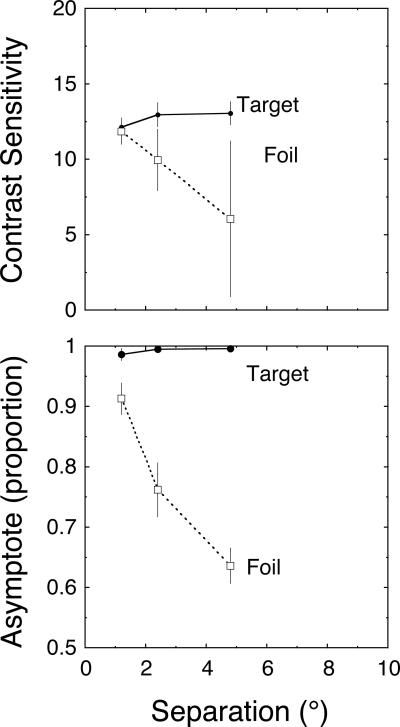
We quantified these effects using the estimated threshold and asymptote parameters. In Figure 9, the top panel shows contrast sensitivity (1/threshold) as a function of separation for the target and foil. The plotted values are averaged over the 5 observers that used a common set of separations. Contrast sensitivity for the target is constant while sensitivity to the foil drops. For the foil conditions, the standard errors on the sensitivity estimates are particularly large because only two of the five observers showed an effect on sensitivity. On average, this effect is not reliable when quantified by the slope on this graph (slope = -2.3±1.4, t(4)=1.6, p>.1).
Figure 9.
A summary of results for Experiment 1 averaged over the five observers with the same separation values. In the top panel, the contrast sensitivity (1/threshold) is plotted for different separations. There is little effect of separation on either target or foil. In the bottom panel, the estimated asymptote of the psychometric function is plotted for different separations. Asymptotes are perfect for the target functions while asymptotes fall from near perfect to near random responding for the foil functions.
The bottom panel shows the upper asymptote as a function of separation for the target and foil separately. Here the asymptote for the target is consistently perfect while the asymptote to the foil drops from close to 1.0 to nearly random responding. In contrast to sensitivity, the effect on the asymptote of the foil function is found for all observers. This effect is reliable when quantified by the slope on this graph (slope = -0.07±0.01, t(4)=7.0, p<.005).
Given the consistent drop in upper asymptote, these results rule out a model in which the effect of attention is due only to contrast gain. Instead, the results are consistent with the all-or-none mixture model of selection, in which attention modulates the likelihood of selecting a given stimulus. The results are also consistent with an additional modulation of contrast gain for some observers.
In summary, the separation of a low contrast foil from the relevant location (i.e., the location of the target) has little effect on the target psychometric function. This suggests that observers do attend the relevant location as instructed and that there is relatively little masking effect of the low contrast foil on the target. In contrast, the separation of a foil from the relevant location has a large effect on the foil psychometric function. Quantitative analyses of the sensitivity and asymptotic performance confirmed that the effect is primarily a vertical scaling of the psychometric function, with a possible additional effect on sensitivity. Thus, although attention may act to modulate the gain of the stimulus in some situations, these results rule out this model as the only mechanism of selection in this spatial filtering paradigm.
In the next experiment, we repeat a similar measurement for a single separation and increased the number of trials. This provides more detailed psychometric functions, which in turn, allow for more precise estimates of the effect of the separation on the psychometric function of the foil.
Experiment 2: Detailed Psychometric Functions
Methods
There were two observers for Experiment 2. Procedures were similar to those used in Experiment 1. The two differences were the use of only one separation and the inclusion of a separate block of control trials with targets only. The one separation was 2.4° for Observer SY and 1.2° for Observer MK. As with Experiment 1, Observer SY had contrast values starting from 5% and Observer MK had contrast values starting from 7%. The two observers participated in eight hour-long sessions resulting in 1200 trials per psychometric function for each observer. This is almost four times as many trials per function as in Experiment 1.
Results & Discussion
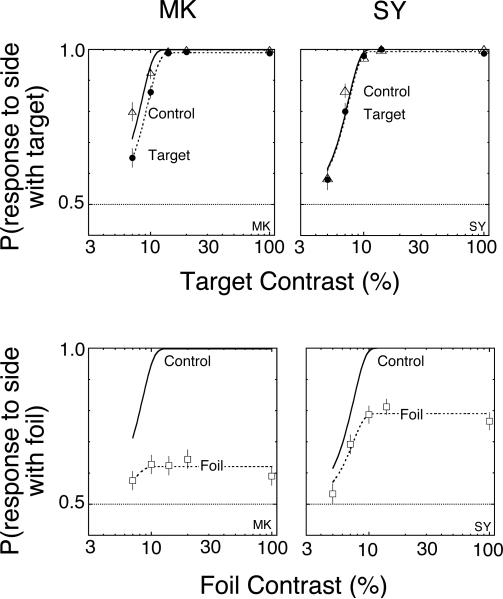
First consider the target functions in the top panels of Figure 10. The psychometric functions for target and control conditions were not very different. MK had a threshold of 8.4±0.2% for the target condition and 7.4±0.2% for the control condition. SY had a threshold of 6.7±0.2% for the target condition and 6.6±0.2% for the control condition. Measurements of asymptotic performance were also not very different: MK had a asymptote of .989±.004 for the target condition and .998±.001 for the control condition. SY had a asymptote of .993±0.003 for the target condition and 1.000±.004 for the control condition. Thus, there is a very small (MK) or no detectable difference (SY) between the target and control conditions.
Figure 10.
The results of Experiment 2 are shown for two observers. The observers are shown in separate columns with the target functions in the top row and the foil functions in the bottom row. The top panel shows little or no difference between the target condition and a blocked control with only target stimuli. The bottom panel shows the foil functions with reduced asymptotes. This larger experiment most clearly illustrates the reduced asymptotes of the foil psychometric functions for intermediate separations.
Now consider the foil psychometric functions in the bottom two panels of Figure 10. The control and foil functions are not at all similar. The obvious effect is on asymptotic performance. It was nearly 1.0 for both the control and target conditions and dropped to .62±.02 for MK and .79±.02 for SY in the foil condition. In contrast, the effects on thresholds were relatively modest: MK had a threshold of 8.4±0.2% for the target condition and 6.4±1.1% for the foil condition. SY had a threshold of 6.7±0.2% for the target condition and 6.5±0.4% for the foil condition. Thus, the small and idiosyncratic effect on thresholds is in the opposite direction from that predicted by the contrast gain model, which is an increase in threshold for the foil condition, not a decrease. Given the standard errors for the foil functions, which are understandably larger than for the target functions, we cannot rule out a small decrease in contrast gain to accompany the large decrease in the asymptote, as was suggested in the data from Experiment 1.
Congruency analysis
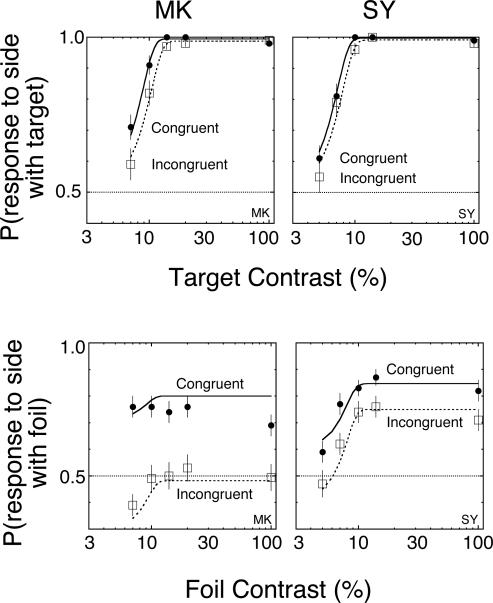
Given the larger data set of this experiment, we can ask further questions about the responses. One complication of the two-stimulus design (i.e., presenting a target and a foil on every trial) is whether the presence of two stimuli on the same side of the display has an effect relative to when one stimulus is on one side and the other is on the other side. It may be, for example, that when the target and the foil are on the same side, they provide separate cues that are combined to determine the final response. Furthermore, if there is such an effect, it might change the interaction of the foil's contrast with separation in a qualitative manner as well as a quantitative one. This possibility is discussed further in the Appendix. Such a congruency effect can be measured by distinguishing trials in which the target and foil are on the same side of fixation (congruent) or on different sides of fixation (incongruent). Figure 11 shows the results separated this way. For both observers, there is an effect of congruency on the threshold of the target function and on the asymptote of the foil function. A simple model of this effect is presented in the Appendix. Thus, although congruency does influence performance, the important point is that regardless of congruency, the primary effect of separation on the foil functions remains an effect on asymptotic performance. Therefore, while congruency must be taken into account for a quantitative analysis of this experiment, it does not change the qualitative result, which is consistent with an all-or-none mixture model.
Figure 11.
For Experiment 2, an analysis is shown of the congruency of target and foils. As with the prior figure, observers are shown in separate columns with the target functions in the top row and the foil functions in the bottom row. The new feature is to break down the target and foil functions by whether the target and foil are on the same side (congruent) or opposite sides (incongruent). There is a congruency effect for all conditions. The main point is that the reduced asymptote in the foil functions is found for both congruent and incongruent conditions.
In the Appendix, two models are developed for how information from the target and foil might be integrated. The first model combines the contrast gain model with the weighted integration model (Kinchla & Collyer, 1974; Shimozaki, Eckstein & Abbey, 2003). It predicts that congruency affects the threshold and the point of subject equality but not the asymptote of the psychometric function. Thus, it can be rejected for this situation. The second model combines the all-or-none mixture model with an attention switching account of information integration of the target and the foil (Mulligan & Shaw, 1980; Shimozaki, Eckstein & Abbey, 2003). This model is similar to probability summation (Graham, 1989). The 1-parameter model described in the appendix predicts congruency effects on both the asymptote and on the baseline of the psychometric function. The fit of this model is shown in the smooth curves of Figure 11. This model does a good job capturing the variation in asymptote. It also predicts that performance in the incongruent condition falls below .5 for low contrasts. The one weakness is for MK's foil function in the congruent condition for the lowest contrast. For this condition, the model does not predict the observed result. This failure might be remedied by combining the two integration models described in the appendix, but such detailed fitting is not pursued here. Instead we emphasize that the all-or-none mixture model is sufficient to capture the qualitative results of the congruency effects.
Identical stimulus conditions
A desirable control in attention experiments is to compare conditions that have identical stimuli. In the comparisons thus far, the targets and foils were at somewhat different locations on the display. Here, we restrict the analysis to trials in which both targets and foils occurred in only two locations (either side of 4:30 and 10:30). Thus, the stimuli contributing to these target and foil functions were identical in every way. The results from this subset of trials were essentially identical to the entire set. In Table 3, the results for both the full set and the subset with identical stimulus are listed side by side. The key comparison is the difference between the target and foil functions. For both observers, the threshold are essentially identical for targets and foils. For both observers, the asymptotes are radically different for targets and foils. Thus, this analysis with identical stimuli confirms the previous results.
Table 3.
Results from Experiment 4 for the Subset of Trials with Identical Stimuli
| Thresholds | Asymptotes | |||
|---|---|---|---|---|
| Full Set | Subset | Full Set | Subset | |
| MK: Target | 8.4±0.2% | 8.3±0.3% | .989±.004 | .992±.005 |
| MK: Foil | 6±1% | 6±2% | .62±.02 | .61±.02 |
| SY: Target | 6.7±0.2% | 6.8±0.3% | .993±.003 | .988±.006 |
| SY: Foil | 6.5±0.4% | 6.1±0.5% | .79±.02 | .81±.02 |
Summary
Experiment 2 extends the results of Experiment 1 in several ways. First, it shows that the detailed shape of the foil psychometric functions is consistent with a vertical shift. Second, the occurrence of a vertical shift is general to whether the target and foil are congruent or incongruent. Third, the vertical shift is also found for the subset of conditions with identical stimuli as targets and foils. Thus, the evidence continues to be consistent with the all-or-none mixture model.
Experiment 3: Measuring Spatial Extent
Experiments 1 and 2 established which of the two models that we have considered—contrast gain and all-or-none mixture—best captures the effect of attention in the spatial filtering pattern. The results favored the all-or-none mixture as the model accounting for most of the effect of attention. We now turn to measuring the spatial extent of attention using these methods.
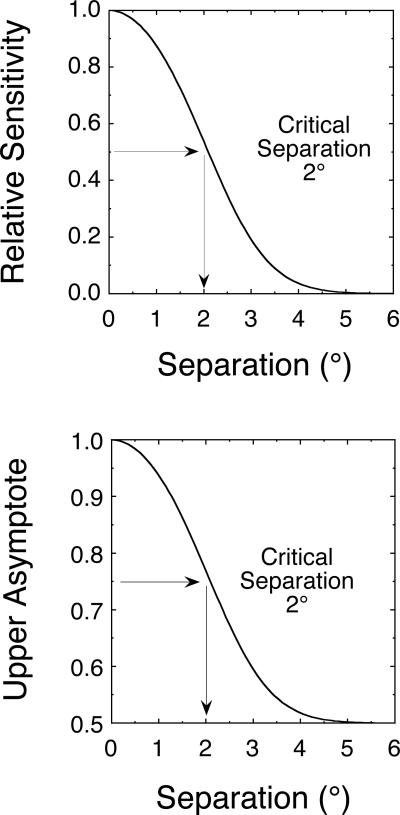
A challenge for measuring the spatial tuning function of attention given the results of Experiments 1 and 2, is that tuning functions are usually measured in the context of a contrast gain model. For example, the top panel of Figure 12 illustrates a graph of the relative sensitivity as a function of separation. This spatial sensitivity function is illustrated by a Gaussian function with a half-height, half-width of 2° (the critical separation).
Figure 12.
Functions analogous to spatial tuning functions are illustrated that are appropriate for two different models of the selection process. In the top panel, relative sensitivity is plotted as a function of separation. This is an example of a spatial sensitivity function. In the bottom panel, upper asymptote is plotted as a function of separation. This is a spatial asymptote function that is appropriate to the all-or-none mixture model.
However, for the spatial filtering task, attention to a was consistent with an all-or-none mixture process rather than through contrast gain. Therefore a somewhat different spatial function must be estimated. Specifically, we plot the asymptotic performance to the foil as a function of the separation. This spatial asymptote function is illustrated in the bottom panel of Figure 12. We summarize this function with its half-height, half-width parameter: the separation at which the upper asymptote is halfway between chance (0.5) and perfect (1.0). This way, one can define a spatial function for an all-or-none process in a way analogous to the more familiar spatial sensitivity function. Furthermore, both functions are summarized by a similarly defined critical separation.
Methods
This experiment followed the procedures of the general methods with specializations to measure a spatial asymptote function. Eight separations were measured at only one high contrast value. More specifically, for the target conditions, the target contrast was 100% and the foil contrast was 7%. For the foil conditions, the foil contrast was 100% and the target contrast was 7%. Thus, this experiment continued to use the two-stimulus design but with an extreme pairing of contrasts. Three observers participated in five hour-long sessions resulting in 160 trials per condition for each observer. The observers had somewhat different conditions. Observer JP participated in an early version of the experiment that had blocked separation conditions with somewhat different separations. The other two observers had mixed separation conditions. Observer MK showed relatively high spatial resolution so her separation values were cut in half relative to Observer SY.
As in the previous experiments, observers were instructed to be sure to detect the target. Specifically, they were told: “if you are in doubt whether the stimulus is a target or a foil, assume that it is a target”. It is possible that such instructions encouraged the observers to broaden the spatial extent of where they attended. Thus, this experiment should not be expected to reveal the narrowest possible spatial extent of attention.
Results & Discussion
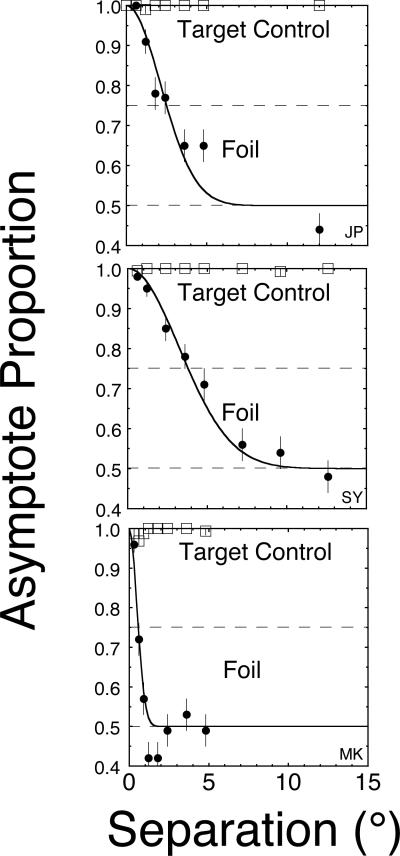
The three panels of Figure 13 show the results for each of the 3 observers. The observed performance for the 100% contrast condition is plotted as a function of separation for the target and foil condition. This performance level is interpreted as an estimate of asymptotic performance. For all three observers, the estimated asymptote is nearly 1.0 for the target control, whereas it drops with separation for the foil. For JP and SY, the functions are monotonic and are reasonably described by a Gaussian with an estimated critical separation of 2.5±0.2° and 3.8±0.3°, respectively. For MK, the function appears to be non-monotonic, showing a dip below random responding (0.5) at close separations, and the critical separation is only 0.57±0.05°.
Figure 13.
The results for Experiment 3 are shown for three observers. In each panel, the upper asymptote is plotted as a function of the separation. Observers JP and SY have monotonic functions with a critical separation of about 3°. Observer MK has a function with a center-surround profile and a critical separation of about 1°.
This experiment demonstrates that the behavioral analog of a spatial tuning function of attention can be obtained from a modest amount of data. It also reveals striking quantitative and qualitative differences among the observers. Observers JP and SY are both researchers that were intently aware of the instruction to be certain to detect the targets. In contrast, MK is an excellent observer, but only given this instruction in passing at the beginning of the experiment. Thus, we speculate that MK was using much narrower tuning functions at minimal cost to detecting the target. The following experiment is intended to reduce the observed individual differences.
Experiment 4: Revised Attention Instructions
Methods
We repeated the experiment with modified instructions and a new set of separations intended to span the range of results found for all observers. The instructions were: “…try to attend only to the relevant location and make your best guess based on that location alone. It is OK to sometimes miss the target when trying to use information from only the relevant location.” These instructions were intended to encourage observers to use as narrow tuning as possible. The same three observers participated in five hour-long sessions resulting in 160 trials per condition for each observer.
Results and Discussion
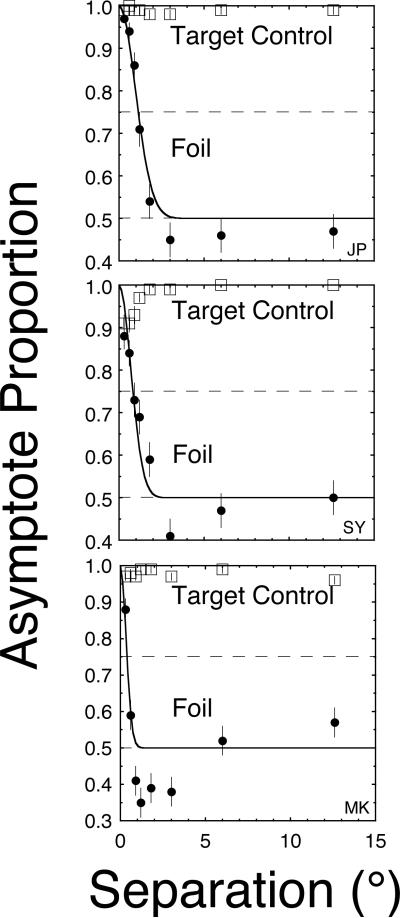
The results for the three observers are shown in Figure 14. As before, the performance for the 100% contrast condition is used as an estimate of asymptotic performance. This estimated asymptote is plotted as a function of separation for both the target and foil functions. Looking at the target data, it can be seen that observers MK and SY both missed some targets at small separations and JP missed a few targets at all separations. These results suggest that the observers complied with the instructions and sacrificed the correct selection of some targets in order to limit responses to stimuli in the relevant location (i.e., narrow their tuning functions as much as possible). Turning to the foil data, the estimated asymptote that was nearly 1.0 for the target function and drops with separation for the foil function for all three observers. Unlike Experiment 3, all three observers show some degree of non-monotonicity for the foil; only MK showed this non-monotonicity in Experiment 3. Quantitatively, the estimated critical separations are 1.14±0.09°, 0.40±0.07° and 0.83±0.07°, for JP, MK and SY, respectively. These critical separations are smaller than those found in Experiment 3.
Figure 14.
The results for Experiment 4 are shown for three observers. In each panel, the upper asymptote is plotted as a function of the separation. For this experiment with “narrow attention” instructions, all observers have functions with a center-surround profile and a critical separation of around 1°.
In summary, the revised instructions result in more similar results across observers than those obtained in Experiment 3. The three observers show more similar critical separations. Furthermore, all three observers show signs of the center-surround profile suggested by Tsotsos, et al. (1995). Any comparison to that theory must be tempered by the fact that these spatial functions are based on an all-or-none mixture rather than a contrast gain mechanism.
General Discussion
The goal of this study is to measure the spatial extent of attention using a paradigm that is based on the psychophysical theory of contrast sensitivity and that is generalizable across a variety of conditions. To do this, we introduce a particular version of a cueing task that we refer to as a spatial filtering task. In this General Discussion, we provide a summary of the results, offer a more detailed hypothesis concerning the relevant mechanisms of selection, present several alternative hypotheses, and close by discussing the larger implications of the results.
Summary of Results
The experiments reported here use a spatial filtering paradigm in which observers detected a small, brief target flash of light at one of two relevant locations, while ignoring otherwise identical foils at nearby locations. Spatial attention is manipulated by cueing the relevant location. Location—relevant versus irrelevant—is the only difference between targets and foils. This paradigm yields two psychometric functions for contrast. One is the standard psychometric function for target detection. The other is the psychometric function for the foil, which reflects the proportion of trials on which the response corresponded to the location of the foil. The foil psychometric function is the primary innovation of the present approach. When the foil is completely ignored, the foil psychometric function must be at 0.5 (i.e., chance) because the foil location and the target location are unrelated. When the foil cannot be discriminated from the target, the foil psychometric function must be identical to that for the target.
The results from our spatial filtering experiments can be summarized in three parts. First, the effect of separation between the relevant location and the foil is primarily on the response to the foil; the effect of separation on the response to the target is minimal. Because the target and foil are identical except for one being at the cued location, this effect must be due to some kind of an attentional mechanism acting differently on the target and the foil.
Second, the effect of separation on the psychometric function of the foil is on the upper asymptote. In particular as separation increased, the asymptote falls from nearly 1.0 to random responding. In contrast, for most observers, there is little effect of separation on threshold. Of the two models of attention that we have considered in detail—contrast gain and all-or-none selection—this pattern of effects rejects a process that is based entirely on contrast gain, because that model predicts a threshold effect. The pattern is instead consistent with an all-or-none selection process, which predicts an asymptote effect. It may also be consistent with certain versions of a response gain model, which is discussed below.
Third, the size of the spatial extent of attention is measured by estimating the asymptote of the foil psychometric function for many separations. These asymptotes range from near 1.0 for the smallest separations to near 0.5 for the largest separations. For instructions that emphasize detecting the target even at the cost of incorrectly basing responses on foils, most observers show wide and monotonic tuning functions (about 3° critical separation at 8° eccentricity). In contrast, for instructions that emphasize narrowing attention as much as possible (i.e., avoiding responses based on foils even at the cost of missing some targets), observers show narrower tuning functions with a center-surround profile (about 1° critical separation at 8° eccentricity). These results are consistent with flexible top-down control of the size of the spatial extent of visual attention. They are also consistent with suggestions of a center-surround profile for effects of visual attention under at least some conditions. It should be noted, however, that the center-surround profile that is found here, is as predicted by an all-or-none selection mechanism rather than by a gain mechanism as has been suggested in the past. As discussed below, it is also possible that this profile is due to an observer strategy rather than the underlying sensory mechanisms.
More Detailed Hypotheses
The hypotheses discussed thus far—contrast gain and all-or-none mixture—can be elaborated by adding details from specific models in the literature. The resulting more elaborate hypotheses can account for additional results and suggest further testable predictions.
Mandatory pooling model
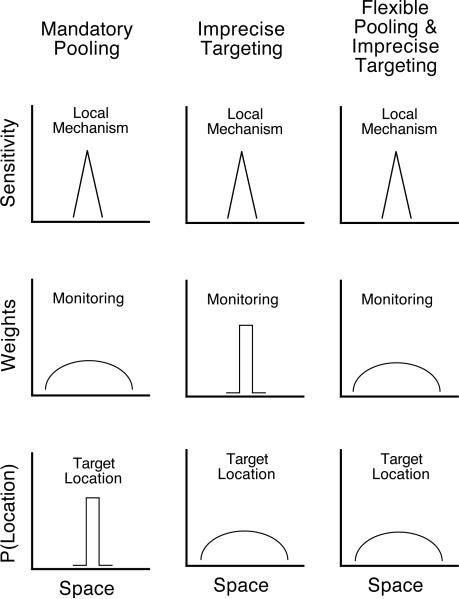
First, consider the contrast gain model as applied to the spatial filtering task. A more specific version of this general model is the mandatory pooling model developed for crowding (e.g. Levi, Hariharan & Klein, 2002; Parkes, et al., 2001; Pelli, Palomares & Majaj, 2004). Some of its properties are illustrated in the left column of Figure 15. First, assume an array of sensory mechanisms that are spatially local and that tile the visual field. This is illustrated for a single mechanism in the upper panel by a plot of sensitivity as a function of space. These mechanisms have relatively narrow tuning functions and set the stage for further processing. Second, assume that the outputs of these mechanisms are pooled across space in a weighted manner. This is represented in the middle panel by a plot of the relative weights as a function of space. For the mandatory pooling model, there is always some such pooling and it is typically assumed to increase with eccentricity. Finally, the pooled output is constructed around a specific location in visual space that has little variability from trial to trial. This lack of variability is represented in the bottom panel by a plot of the probability of sampling a location as a function of space. For this model, the distribution across space is very narrow. The mandatory pooling model predicts the same pattern of results as the contrast gain model previously discussed, because the effect of separation is due to weights that combine with contrast in a multiplicative fashion.
Figure 15.
An illustration of three spatial tuning functions for three different hypotheses. Each hypothesis is in a separate column. All hypotheses assume the same narrowly-tuned local mechanism shown in the top row. For the mandatory pooling hypothesis, there is broad pooling of the local mechanisms. This hypothesis assumes little variability in targeting of the relevant mechanisms. For the imprecise targeting hypothesis, there is little or no pooling of the local mechanisms. Instead, this hypothesis assumes significant variability in targeting of the relevant mechanisms. For the hypothesis with flexible pooling and imprecise targeting, there is both pooling of the local mechanisms and significant variability in targeting of the relevant mechanisms.
Imprecise targeting model
A more specific version of the all-or-none mixture model is the imprecise targeting model, which is illustrated in the middle column of Figure 15 (Bahcall & Kowler, 1999; Strasburger, 2005). This model assumes the same array of local mechanisms as that assumed in the mandatory pooling model (shown in the top panel). It differs in that only a single location is monitored under focused attention conditions such as those of a spatial filtering paradigm. This assumption is illustrated in the middle panel of the second column in Figure 15. The bulk of the variability in selection under the imprecise targeting model comes from trial-to-trial variability in which location is sampled for information about the stimulus. This assumption is illustrated by the wide function in the lower panel of the second column in Figure 15.
Imprecise targeting makes the same predictions about the foil psychometric functions as the more general all-or-none mixture models. Specifically, imprecise targeting predicts a decreasing upper asymptote with increasing separation. Thus, between mandatory pooling and imprecise targeting, the results from our spatial filtering experiments are more consistent with imprecise targeting.
Flexible pooling and imprecise targeting
While the largest effects found in this study are consistent with imprecise targeting, there were some effects that are consistent with some degree of pooling. Moreover, considerable evidence from prior research including some of the authors own work suggests that attention acts at least in part through a gain mechanism of some sort (e.g., Huang & Dobkins, 2005; Ling & Carrasco, 2006; Palmer, 1990; Palmer, Ames, & Lindsey, 1993; Reynolds, et al., 2000 and many more). These findings suggest the possibility of a hybrid model that combines pooling and imprecise targeting. For such a model, the mechanism that dominates depends on the task.
A hybrid model is illustrated in the right column of Figure 15. As do the other models, it assumes an array of local mechanisms (top panel). But now it is further assumed that one can flexibly pool across these local mechanisms if doing so is appropriate for the task (middle panel). Thus, this model has a pooling component, but it is flexible pooling that is mandatory only insofar as there is a limit to how narrowly one can pool. Finally like the imprecise targeting model, it is assumed that there is variability in which location is sampled for information about the target (bottom panel).
The flexible pooling component allows this model to look like a gain model or an all-or-none mixture model depending on whether the pooling is wide or narrow. In particular, if pooling is set wide enough, then the effects of pooling—revealed through threshold effects on the foil psychometric function—can dominate any effect of imprecise targeting. In contrast, if pooling is set as narrow as possible, then the effects of imprecise targeting—revealed through asymptote effects on the foil psychometric function—can dominate any effect of pooling.
Thus, for situations in which there is little reason to attend narrowly, pooling may be set wide and the pattern of results reflects a contrast gain model. The partially valid cueing paradigm is an example of such a situation. Although a single to-be-attended location is cued, targets can appear in other locations as well. The dual-task cueing paradigms are another example (e.g., Sagi & Julesz, 1986). Although the primary task concerns only stimuli at the cued location, stimuli to which a response is required can appear in other locations as well. There is no reason in either of these paradigms for observers to narrow pooling as much as possible, because doing so would risk missing stimuli that are relevant to the task.
The spatial filtering paradigm differs in that observers must ignore stimuli in the irrelevant locations in order to respond correctly. Thus under a model with flexible pooling and imprecise targeting, pooling is relatively narrow and the all-or-none effects of the imprecise targeting component can dominate. Even in this task, however, instructions may influence the width of pooling. We suspect this accounts for differences in results observed between Experiment 3 and 4. In summary, a model with flexible pooling and imprecise targeting can behave as a pooling model when the pooling is broad and behave as an imprecise targeting model when the pooling is narrow.
Alternative Hypotheses
Response gain hypothesis
An alternative hypothesis for effects of attention that has not been emphasized thus far in this paper is a response gain mechanism (e.g. Ling & Carrasco, 2006; Morrone, Denti & Spinelli, 2004). Response gain models are like contrast gain models in that they propose that selection acts by a multiplicative modulation of stimulus information. Response gain differs from contrast gain in that the modulation is of the internal response rather than of the effective stimulus. The two models are identical if the internal response is proportional to the relevant attribute of the stimulus. However, if the internal response is not proportional, such as is the case for contrast response functions that are compressive, the two models can act differently. Most relevant for current purposes is that for strong saturating signals (i.e., above threshold stimuli), response gain models make the same predictions as the all-or-none mixture model. Thus, response gain can in principle account for effects on both threshold and asymptotic performance. The question is whether a given model can systematically predict the conditions under which the two possible effects attain. To pursue this, one needs to manipulate not only attention, but also adaptation in order to probe the system at points at which a response-gain model predicts threshold effects (i.e., low levels of adaptation) and points at which it predicts asymptote effects (i.e., high levels of adaptation). Studies of this sort are just beginning to appear (Huang & Dobkins, 2005; Pestilli, Viera & Carrasco, 2007). Given that asymptote effects are predicted from a response gain model at high levels of adaptation, rather than low, we suspect that the role of response gain in yielding the asymptote effects that we observed here is limited. This is because we used a contrast detection task and conditions that minimize contrast adaptation. Nonetheless, a definitive experiment remains to be done that distinguishes between response gain and an all-or-none mixture model.
Early versus late selection
The discussion thus far has said little about where in processing the selection of information might occur. This is intentional because one can imagine both early and late selection versions of the theories described thus far. For an early selection version, one can select the spatial channels for “early vision” at the cued location and ignore those at other locations. For a late selection version, one can select fully formed perceptual objects at the cued location and ignore other objects. Distinguishing among these alternatives is very interesting but beyond this initial study.
Selection or decision
Perhaps the most radical alternative hypothesis is that we are not really studying attentional selection in this version of the spatial filtering task. In particular, perhaps the only aspect of selection that occurs is to select which location to remember on the basis of the location cue, and then all objects are localized with respect to this remembered location. Under this hypothesis, what we have been taking as effects that reflect the precision of attentional selection actually reflect the precision of memory for the relevant location and variability in the localization decision process. This is a possibility that must be explored further with additional variations of the task and stimuli. Based on our existing data, however, we suggest that this possibility cannot account for the entire pattern of results that we found across experiments. In particular, the size of the spatial extent of attention, which was measured by estimating the asymptote of the foil psychometric function across many separations, changed depending on the instructions that observers were given with regard to how to allocate their attention. If the effects that we observed in this task reflected only memory for the cued location and the decision process about the position of a stimulus relative to that location, then one would not expect them to vary with instructions about attention. This follows because the memory limitations were identical across the different instruction conditions. Nonetheless, it is clear that localization and memory for location are critical for this task and parsing out the relative contribution of those processes and attentional processes is an important direction for further work with the spatial filtering.
Implications of the Present Results
Mechanism of selective attention
A critical question concerning the effects of attention is what is the underling mechanism by which attention modulates stimulus processing? The most common mechanisms that are considered in the literature are gain mechanisms. For the case of contrast gain, an attention parameter multiplies a signal that is proportional to contrast to modify the effective contrast. Such gain models have been developed extensively in the work of Sperling and colleagues (e.g. Reeves & Sperling, 1986; Sperling & Weichselgartner, 1995) and have recently been extended using linear systems theory (Blaser, Sperling & Lu, 1999; Gobell, Tseng & Sperling, 2004) and the analysis of external noise (Dosher, et al., 2004; Eckstein, et al., 2002). Efforts are also being made to understand the neural basis of attentional modulation using gain hypotheses (e.g. Reynolds, et al., 2000; Treue & Martinez-Trujillo, 1999; Williford & Maunsell, 2006).
A highlight of the current results is evidence that an all-or-none selection mechanism may also play a role in effects of attention. For the spatial filtering experiments conducted here, the effects can be almost entirely accounted for by an all-or-none mixture mechanism rather than by contrast gain. In particular, we suggest that under these conditions performance is limited by the imprecise targeting of selective attention. All-or-none mixture models and imprecise targeting have been considered less often in the literature and to our knowledge have not been linked to the underlying neurophysiology. Given the results presented here, further investigation of all-or-none selection is a promising avenue for future consideration.
Spatial extent of selective attention
Another question concerning the effects of attention concern the measurement of the spatial extent of attention. This measurement is particularly relevant to the issue of attentional resolution (He, Cavanagh & Intriligator, 1996). In the present context, this question can be articulated as what is the narrowest tuning function of attention that can be achieved and how does that limit change across conditions? In an review of the literature related to this question, Intriligator and Cavanagh (2001) make clear that there is a large range of estimates (less than 1° to the entire visual hemifield). Related, a large number of methods have been used to measure attentional resolution and no consensus regarding which is the most appropriate for what purposes has been reached.
An advantage of the spatial filtering paradigm is that it is based a priori on psychophysical theory, and it estimates something analogous to a spatial tuning function for attention. Perhaps by building on these methods, one can test if the observed spatial extent is the narrowest possible. Such tests may allow one to find better ways to measure attentional resolution.
Spatial profiles of selective attention
A third question concerns the spatial profile of attention. What is it and how does it vary across stimulus and task conditions? The spatial profile of attention is characterized by both the size (e.g. the critical separation) and the shape (e.g., monotonic versus non-monotonic). As reviewed above, there have been several previous reports of center-surround profiles of attentional effects (e.g. Bahcall & Kowler, 1999; Cutzu & Tsotsos, 2003; Mounts, 2000; Müller, et al., 2005; Steinman, et al., 1995).
In Experiments 3 and 4, we found quite different profiles depending on instruction and observer. Specifically, the profiles were either monotonic with a critical separation of about 3° or they followed a center-surround profile with a critical separation of about 1°. This dependence on instruction indicates the existence of flexible control over visual attention. Moreover, these results raise the issue of what is the profile under conditions that require the use of the narrowest attentional selection. While the current results may still not be the narrowest possible, the appearance of the center-surround profile under the “narrow attention” instructions suggests that this pattern may reveal something about the spatial characteristics of the underlying mechanisms rather than something about task-specific demands.
While the results of Experiments 3 and 4 are consistent with underlying mechanisms that have a center-surround profile, there is another possibility. Observers report a strategy that when they see a vivid foil, they often respond on the opposite side as the foil. While this strategy is not obviously rational, it may be related to reports of a “distance advantage” in shifts of attention (Fecteau & Enns, 2005). We explicitly discouraged this strategy by pointing out that the target was equally likely to be on the same side as the foil as on the opposite side. One might argue that the return to .5 responding at larger separations indicates a spatial structure and not an overall strategy. Unfortunately, this is not true for the spatial task used here because the most distant foil locations are equally distant to the two relevant locations. Hence, responding to the “opposite side” becomes ambiguous. In summary, further experiments must be designed to distinguish whether the observed center-surround profile arises from perceptual mechanisms or strategic responses.
Conclusions
Three results stand out from these spatial filtering experiments. First, the separation between targets and foils has a large effect on responses to the foil but not the target. This suggests that attention modulates the processing of the foil. Second, the effect of separation for the foil psychometric function of contrast is primarily on the asymptote of that function, not the threshold. This is consistent with an all-or-none mixture model of attentional modulation rather than with a contrast gain model. Third, depending on instructions and observers, the spatial effect of attention is either wide and monotonic or narrow with a center-surround profile. This is consistent with a model that combines flexible pooling and imprecise targeting.
Acknowledgments
Author Notes We thank Elisabeth Hein, Nicolle Perisho, Alec Scharff, and Serap Yigit for help conducting these experiments. We also thank Roozbeh Kiani and Zelda Zabinsky for suggestions and criticisms of early versions of this article. The work was partly supported by NIH/NIMH grant MH067793 to CM.
Appendix
In this appendix, we formalize two models of attentional selection. The first is the contrast gain model which has received much recent discussion in the attention literature (e.g. Huang & Dobkins, 2005; Carrasco, Ling & Reed, 2004; Martinez-Trujillo & Treue, 2002). The second is the all-or-none mixture model is an example of an attention switching model (Sperling & Melchner, 1978) and follows closely the “mixture model” in Shaw (1980) and the “imprecise targeting model” in Bahcall and Kowler (1999). Here we derive results for an idealized one-stimulus design in which either the target or the foil is presented alone. The current two-stimulus design approximates this by keeping one of these stimuli at a low contrast. Ideally, single-stimulus trials can be embedded within a two-stimulus design to improve upon this approximation. The generalization to the two-stimulus design is presented in the second part of the appendix.
Basic Experiment
Consider a simplified version of the contrast detection task of Experiment 1. Let the target t be at one of the relevant locations and the foil f be at one of the irrelevant locations. The observer's task is to detect the presence of the target and to ignore the foil. For trials with only the target, the proportion of responses to the target is denoted pt and the target's contrast is xt; for trials with only the foil, the proportion of responses to the foil is denoted pf and the foil's contrast is xf. The separation between the target and foil is denoted s.
Contrast Gain Model
Definition
For this model, the idea is that selective attention changes the effective value of the relevant stimulus attribute. This can be interpreted as either modifying the signal-to-noise ratio or as modifying its appearance as well as its discriminability (Carrasco et al., 2004). The model is based on two assumptions. First, performance is assumed to be a monotonically increasing function of the relevant attribute of the stimulus (e.g. contrast). Second, the information about this attribute is modulated by a multiplicative factor specific to location. This multiplicative factor is what is meant by the general term of stimulus gain. When the relevant attribute is contrast, the appropriate term is the familiar contrast gain. Specifically, define gain parameters for the target gt(s) and the foil gf(s) that are both a function of separation. For example, a simple model might have the target gain to always be equal to one and the foil gain to decrease monotonically with separation. To describe a psychometric function for contrast, let Ψ be a monotonically increasing function and the responses to the target and the foil be given respectively by
| (1) |
| (2) |
In words, the stimulus values xt, xf are modulated by the corresponding gain parameters gt(s) and gf(s). The monotonicity assumption simply means that performance must increase with increasing quality of the stimulus information.
Predictions
For this model, the foil psychometric function depends on separation by only the gf(s) term. Moreover, this term multiplies the contrast. Thus, the effect of separation is equivalent to a change in the effective contrast. Because graphs of the contrast psychometric function are typically shown as a function of log contrast (here base 10), the prediction of the contrast gain model needs to be understood for these graphs. Let Ψ*(x) = Ψ(10x). One can rewrite Equation (2) as
| (3) |
This version of the equation makes explicit that changing the separation shifts the psychometric function horizontally when it is plotted on log contrast.
Next an equation is derived to estimate the gain parameter from the observed threshold for the foil. Define the threshold value of the foil as the value that yields a criterion performance level pcrit at a given separation. For this threshold stimulus, Equation (2) can be rewritten as
| (4) |
Because Ψ is monotonically increasing, the inverse of Ψ exists and can be denoted as Ψ-1. Taking this inverse yields
| (5) |
Ψ-1(pcrit) is a constant so denote it k, solve for gf(s) and one can see the relation between the gain parameter gf(s) and the threshold :
| (6) |
Thus, for this model, the gain is inversely proportional to the threshold.
The All-or-None Mixture Model
Definition
In this all-or-none mixture model, a stimulus on a given trial can either be attended or not attended. For example, in the imprecise targeting model (Bahcall & Kowler, 1999), somewhat different locations are selected as relevant on different trials. The foil is at a selected location on some trials but not on others. Thus, mean performance is a mixture of these two kinds of trials. We assume the same notation as above: xt and xf are contrast, s is the separation and pt, pf are responses to the target and foil, respectively. We also assume a similar functional representation for the psychometric function Ψ that is again monotonically increasing. The new feature is to replace the idea of gain by the proportion of trials in which a particular stimulus is attended. This mixture parameter is denoted ht(s) for the target and hf(s) for the foil. These parameters depend on separation in a fashion analogous to how the gain parameters did in the prior model. Responses to the target and the foil are given respectively by
| (7) |
| (8) |
In words, on the attended fraction of the trials, performance is determined by the usual psychometric function Ψ, and on the unattended trials performance is determined by guessing Ψ(0). The parameter hf(s) is the critical mixture parameter for the experiments described here. In summary, performance is a probability mixture of trials where a stimulus is attended and trials where it is not attended.
Predictions
From Equation (8), one can predict that the effect of separation is a scaling of the psychometric function for the foil that depends solely on the term hf(s). This mixture parameter scales the first part of Equation (8) which is the only part that depends on contrast. The second part of the equation contributes a constant Ψ(0) that defines guessing responses. Thus, all possible functions are a rescaling of the assumed psychometric function Ψ.
In this model, the psychometric function is predicted to scale with a change of separation. Thus, effect of separation can be summarized by a change in the upper asymptote of the foil psychometric function. This upper asymptote can be used to estimate the mixture parameter, hf(s). For the upper asymptote, let be the performance observed for an arbitrarily large value of the relevant stimulus attribute (xf ∞). Then, for this asymptotic stimulus, Equation (8) becomes
| (9) |
Solving for hf(s) yields:
| (10) |
For the two-choice task used here, Ψ(0) = .5 and Ψ(∞) =1, which allows one to simplify the result to
| (11) |
Thus, the mixture parameter is a simple linear function of the observed upper asymptote of the foil psychometric function.
Predictions for the Two-Stimulus Design
Up to this point, the two models have been developed with the one-stimulus idealization of the current experiments. In the experiments, this idealization was approximated by keeping the contrast of one stimulus low. In this section of the appendix, we develop explicit predictions for the two-stimulus design. These require additional assumptions about how information from multiple sources is combined (for reviews see Shaw, 1982; Shimozaki, Eckstein & Abbey, 2003).
Contrast gain and weighted integration
A natural way to extend the contrast gain model to multiple sources of information is to consider the gain as a weight in a simple additive model. This weighted integration model has long been studied in psychophysics (Kinchla & Collyer, 1974; for reviews see Shaw, 1982; Graham, 1989). Using the notation introduced previously for the contrast gain model, the inputs from the two stimuli are simply weighted and added together. Specifically, the proportion of foil responses for congruent foils and targets is
| (12) |
and the proportion of foil responses to incongruent foils and targets is
| (13) |
To simplify the model, we assume that the target information is always given a weight of 1 (gt(s) = 1). This leaves a single parameter gf for each separation.
To understand the predictions of this model, first consider two boundary conditions. If gf = 0, then the foil is successfully ignored and performance is determined by the target contrast alone. If gf = 1, then the target and foil are weighted identically and either add or subtract depending on whether they predict congruent responses. For the foil functions based on the experiments in this article, the target contrast is fixed to a low value and the foil contrast is varied. The result is a foil function equivalent to the target function but with a shift in the point of subjective equality (PSE) due to the target information.
Now consider an intermediate case with the gain term for the foil between 0 and 1. Now the psychometric function for the foil has an increased threshold inversely proportional to the gain. This prediction is the same as for the simple contrast gain model discussed above. The additional effect is a shift of the PSE that depends on the target contrast and the relative values of the target and foil gain. This model predicts no change in the asymptote of the psychometric function. Thus, this extension of the contrast gain model cannot account for the data found here where there are large effects on the asymptote rather than the threshold.
The all-or-none mixture model and probability summation
One way to extend the all-or-none mixture model is to allow independent decisions for each source of information (Mulligan & Shaw, 1982). This idea is often referred to as “probability summation” (for reviews see Graham, 1989; Shaw 1982). In the previous development, a generic detection was assumed (e.g. yes-no). For the extension, we need to be more specific and instead explicitly model the coarse two-choice localization task used here (see Shaw, 1980; Busey & Palmer, 2008).
To keep the model simple, we consider just four possible locations two for each response. Define random variables for the relevant evidence in internal states that corresponds to the possible stimuli at the four locations: T for target, F for foil, D1 for the first no-stimulus location, D2 for the second no-stimulus location. To begin, consider the simpler case of localizing a single target at one of two locations. The usual decision rule is to pick the location with the most evidence. In other words, the proportion of target responses is
| (14) |
Assume independent distributions for T and D and denote the density function by a and the cumulative distribution function by A. Then, the proportion of target responses is solved by the integral
| (15) |
(see Shaw, 1980 or Palmer, Ames & Lindsey, 1993 for more detail about such derivations).
Of interest here is the more complex case where there are two possible stimuli over 4 possible locations and the response is to categorize the locations into two sets (e.g. left versus right). Furthermore, the conditions with the target and foil on the same side (congruent) and on the opposite side must be distinguished. For the congruent case, the proportion of foil side responses is
| (16) |
where hf is the proportion of trials in which both the target and foil are attended. The target is always assumed to be attended in this simple model. For the incongruent case, the proportion of foil side responses is given by a similar expression
| (17) |
The difference in these two equations is that for the incongruent case, the high values of a foil and distractor contribute to the foil response instead of a foil and target. These equations can be used to derive integral equations similar to Equation (15).
Given any assumed family of distributions, this model has only a single parameter hf for each separate separation. We assume a shift family of Gaussian distributions with a power-function transformation as used for the psychometric functions (see Pelli, 1987). The shift between target and distractor is taken from the thresholds estimated from the control conditions of Experiment 2. This allows one to make a single parameter fit of the two congruency conditions of Experiment 2 as is shown in Figure 11.
For hf = 0, the foil is ignored and the foil function becomes flat at whatever level is determined by the target contrast. For hf = 1, the foil is treated the same as the target. Now the foil function is similar to the target function with a small shift in threshold due to the target contrast. The interesting case is for intermediate values of hf. For such values, the asymptote is reduced as found in the experiments. Furthermore, both the asymptote and baseline proportions vary with the target contrast. For Observer SY, the best fit hf is .60. The predicted asymptote is .85 for the congruent condition and is .75 for the incongruent condition. Similarly, the predicted baseline is .60 and .40, respectively. For Observer MK, the best fit hf is .28 and the predicted asymptote is .80 for the congruent condition and is .48 for the incongruent condition. The predicted baseline is .71 and .29, respectively. For Observer SY, the fit is quite good and captures all of the qualitative features of the data. For Observer MK, the fit is not as good and misses for the relatively flat foil function for the congruent condition. For this observer, the data hints at an effect on the PSE as well as the asymptote. This can be predicted if one combines aspects of the two models but such detailed fitting is not pursued here. In summary, the extension of the all-or-none mixture model predicts the primary effect of a reduced asymptote that depends on congruence.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bahcall DO, Kowler E. Attentional interference at small spatial separations. Vision Research. 1999;39:71–86. doi: 10.1016/s0042-6989(98)00090-x. [DOI] [PubMed] [Google Scholar]
- Becker L. Doctoral dissertation. Johns Hopkins University; 2001. Attending over space and objects. [Google Scholar]
- Broadbent DE. Perception and Communication. Oxford University Press; New York: 1958. [Google Scholar]
- Baldassi S, Verghese P. Attention to locations and features: Different top-down modulation of detector weights. Journal of Vision. 2005;5:556–570. doi: 10.1167/5.6.7. [DOI] [PubMed] [Google Scholar]
- Blaser E, Sperling G, Lu ZL. Measuring the amplification of attention. Proceedings of the National Academy of Science U S A. 1999;96:11681–11686. doi: 10.1073/pnas.96.20.11681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Busey T, Palmer J. Set-size effects for identification versus localization depend on the visual search task. Journal of Experimental Psychology: Human Perception and Performance. 2008 doi: 10.1037/0096-1523.34.4.790. in press. [DOI] [PubMed] [Google Scholar]
- Carrasco M, Ling S, Read S. Attention alters appearance. Nature Neuroscience. 2004;7:308–313. doi: 10.1038/nn1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheal M, Lyon DR, Gottlob LR. A framework for understanding the allocation of attention in location-precued discrimination. Quarterly Journal of Experimental Psychology A. 1994;47:699–739. [Google Scholar]
- Cherry EC. Some experiments on the recognition of speech with one and with two ears. Journal of the Acoustical Society of America. 1953;25:975–979. [Google Scholar]
- Cohen A, Shoup R. Perceptual dimensional constraints in response selection processes. Cognitive Psychology. 1997;32:128–181. doi: 10.1006/cogp.1997.0648. [DOI] [PubMed] [Google Scholar]
- Cornelissen F, Peters E, Palmer J. The EyeLink toolbox: Eye tracking with MATLAB and the psychophysics toolbox. Behavior Research Methods, Instruments & Computers. 2002;34:613–617. doi: 10.3758/bf03195489. [DOI] [PubMed] [Google Scholar]
- Cowan WB. An inexpensive scheme for calibration of a colour monitor in terms of CIE standard coordinates. Computer Graphics. 1983;17:315–321. [Google Scholar]
- Cutzu F, Tsotsos JK. The selective tuning model of attention: Psychophysical evidence for a suppressive annulus around an attended item. Vision Research. 2003;43:205–219. doi: 10.1016/s0042-6989(02)00491-1. [DOI] [PubMed] [Google Scholar]
- Davis ET, Kramer P, Graham N. Uncertainty about spatial frequency, spatial position, or contrast of visual patterns. Perception & Psychophysics. 1983;33:20–28. doi: 10.3758/bf03205862. [DOI] [PubMed] [Google Scholar]
- Dosher BA, Liu SH, Blair N, Lu ZL. The spatial window of the perceptual template and endogenous attention. Vision Research. 2004;44:1257–1271. doi: 10.1016/j.visres.2004.01.011. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Shimozaki SS, Abbey CK. The footprints of visual attention in the Posner cueing paradigm revealed by classification images. Journal of Vision. 2002;2:25–45. doi: 10.1167/2.1.3. [DOI] [PubMed] [Google Scholar]
- Eriksen BA, Eriksen CW. Effects of noise letters upon the identification of a target letter in a nonsearch task. Perception & Psychophysics. 1974;16:143–149. [Google Scholar]
- Eriksen CW, Hoffman JE. The extent of processing of noise elements during selective encoding from visual displays. Perception & Psychophysics. 1973;14:155–160. [Google Scholar]
- Eriksen CW, James JD. Visual attention within and around the field of focal attention: A zoom lens model. Perception & Psychophysics. 1986;40:225–240. doi: 10.3758/bf03211502. [DOI] [PubMed] [Google Scholar]
- Fecteau JH, Enns JT. Visual letter matching: Hemispheric functioning or scanning biases? Neuropsychologia. 2005;43:1412–1428. doi: 10.1016/j.neuropsychologia.2005.01.006. [DOI] [PubMed] [Google Scholar]
- Gobell JL, Tseng CH, Sperling G. The spatial distribution of visual attention. Vision Research. 2004;44:1273–1296. doi: 10.1016/j.visres.2004.01.012. [DOI] [PubMed] [Google Scholar]
- Gottwald RL, Garner WR. Filtering and condensation tasks with integral and separable dimensions. Perception & Psychophysics. 1975;18:26–28. [Google Scholar]
- Graham NVS. Visual Pattern Analyzers. Oxford University Press; New York: 1989. [Google Scholar]
- He S, Cavanagh P, Intriligator J. Attentional resolution and the locus of visual awareness. Nature. 1996;383:334–337. doi: 10.1038/383334a0. [DOI] [PubMed] [Google Scholar]
- He S, Cavanagh P, Intriligator J. Attentional resolution. Trends in Cognitive Science. 1997;1:115–121. doi: 10.1016/S1364-6613(97)89058-4. [DOI] [PubMed] [Google Scholar]
- Huang L, Dobkins KR. Attentional effects on contrast discrimination in humans: Evidence for both contrast gain and response gain. Vision Research. 2005;45:1201–1212. doi: 10.1016/j.visres.2004.10.024. [DOI] [PubMed] [Google Scholar]
- Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognitive Psychology. 2001;43:171–216. doi: 10.1006/cogp.2001.0755. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Treisman A. Changing views of attention and automaticity. In: Parasuraman R, Davies DR, editors. Varieties of Attention. Academic Press; New York: 1984. [Google Scholar]
- Kinchla RA, Collyer CE. Detecting a target letter in briefly presented arrays: A confidence rating analysis in terms of a weighted additive effects model. Perception & Psychophysics. 1974;16:117–122. [Google Scholar]
- LaBerge D. Spatial extent of attention to letters and words. Journal of Experimental Psychology: Human Perception and Performance. 1983;9:371–379. doi: 10.1037//0096-1523.9.3.371. [DOI] [PubMed] [Google Scholar]
- LaBerge D, Brown V. Theory of attentional operations in shape identification. Psychological Review. 1989;96:101–124. [Google Scholar]
- Lee DK, Itti L, Koch C, Braun J. Attention activates winner-take-all competition among visual filters. Nature Neuroscience. 1999;2:375–381. doi: 10.1038/7286. [DOI] [PubMed] [Google Scholar]
- Levi DM, Hariharan S, Klein SA. Suppressive and facilitatory spatial interactions in peripheral vision: Peripheral crowding is neither size invariant nor simple contrast masking. Journal of Vision. 2002;2:167–177. doi: 10.1167/2.2.3. [DOI] [PubMed] [Google Scholar]
- Ling S, Carrasco M. Sustained and transient covert attention enhance the signal via different contrast response functions. Vision Research. 2006;46:1210–1220. doi: 10.1016/j.visres.2005.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J. The flanker compatibility effect as a function of visual angle, attentional focus, visual transients, and perceptual load: A search for boundary conditions. Perception & Psychophysics. 1991;49:270–288. doi: 10.3758/bf03214311. [DOI] [PubMed] [Google Scholar]
- Moore CM, Lanagan-Leitzel LK, Chen P, Halterman R, Fine EM. Nonspatial attributes of stimuli can influence spatial limitations of attentional control. Perception & Psychophysics. 2007;69:363–371. doi: 10.3758/bf03193757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore CM, Lanagan-Leitzel, Fine EM. Attentional resolution as measured in the attentional walk task reflects limitations of control not spatial extent. 2007. Manuscript submitted for publication. [Google Scholar]
- Mordkoff JT. Between-dimension flanker effects: A clarification with encouraging implications. Psychonomic Bulletin & Review. 1998;5:670–675. [Google Scholar]
- Morrone MC, Denti V, Spinelli D. Different attentional resources modulate the gain mechanisms for color and luminance contrast. Vision Research. 2004;44:1389–1401. doi: 10.1016/j.visres.2003.10.014. [DOI] [PubMed] [Google Scholar]
- Mounts JR. Evidence for suppressive mechanisms in attentional selection: Feature singletons produce inhibitory surrounds. Perception & Psychophysics. 2000;62:969–983. doi: 10.3758/bf03212082. [DOI] [PubMed] [Google Scholar]
- Müller NG, Mollenhauer M, Rösler A, Kleinschmidt A. The attentional field has a Mexican hat distribution. Vision Research. 2005;45:1129–1137. doi: 10.1016/j.visres.2004.11.003. [DOI] [PubMed] [Google Scholar]
- Mulligan RM, Shaw ML. Multimodal signal detection: Independent decisions vs. integration. Perception & Psychophysics. 1980;28:471–478. doi: 10.3758/bf03204892. [DOI] [PubMed] [Google Scholar]
- Niebergall R, Tzvetanov T, Treue S. The spatial profile of attentional modulation of contrast detection thresholds. Talk presented at the Meeting of the Society for Neuroscience; Washington, DC. 2005. [Google Scholar]
- Palmer J. Attentional limits on the perception and memory of visual information. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:332–350. doi: 10.1037//0096-1523.16.2.332. [DOI] [PubMed] [Google Scholar]
- Palmer J, Ames CT, Lindsey DT. Measuring the effect of attention on simple visual search. Journal of Experimental Psychology: Human Perception and Performance. 1993;19:108–130. doi: 10.1037//0096-1523.19.1.108. [DOI] [PubMed] [Google Scholar]
- Palmer J, Huk AC, Shadlen MN. The effect of stimulus strength on the speed and accuracy of a perceptual decision. Journal of Vision. 2005;5:376–404. doi: 10.1167/5.5.1. [DOI] [PubMed] [Google Scholar]
- Pan K, Eriksen CW. Attentional distribution in the visual field during same-different judgments as assessed by response competition. Perception & Psychophysics. 1993;53:134–144. doi: 10.3758/bf03211723. [DOI] [PubMed] [Google Scholar]
- Parkes L, Lund J, Angelucci A, Solomon JA, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Pelli DG. On the relation between summation and facilitation. Vision Research. 1987;27:119–123. doi: 10.1016/0042-6989(87)90148-9. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Pelli DG, Palomares M, Majaj NJ. Crowding is unlike ordinary masking: Distinguishing feature integration from detection. Journal of Vision. 2004;4:1136–1169. doi: 10.1167/4.12.12. [DOI] [PubMed] [Google Scholar]
- Pestilli F, Viera G, Carrasco M. How do attention and adaptation affect contrast sensitivity? Journal of Vision. 2007;7:1–12. doi: 10.1167/7.7.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrov Y, McKee SP. The effect of spatial configuration on surround suppression of contrast sensitivity. Journal of Vision. 2006;6:224–238. doi: 10.1167/6.3.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner MI. Information reduction in the analysis of sequential tasks. Psychological Review. 1964;71:491–504. doi: 10.1037/h0041120. [DOI] [PubMed] [Google Scholar]
- Reeves A, Sperling G. Attention gating in short-term visual memory. Psychological Review. 1986;93:180–206. [PubMed] [Google Scholar]
- Reynolds JH, Pasternak T, Desimone R. Attention increases sensitivity of v4 neurons. Neuron. 2000;26:703–714. doi: 10.1016/s0896-6273(00)81206-4. [DOI] [PubMed] [Google Scholar]
- Sagi D, Julesz B. Enhanced detection in the aperture of focal attention during simple discrimination tasks. Nature. 1986;321:693–695. doi: 10.1038/321693a0. [DOI] [PubMed] [Google Scholar]
- Shaw ML. Identifying attentional and decision-making components in information processing. In: Nickerson RS, editor. Attention and Performance VIII. Erlbaum; Hillsdale, NJ: 1980. pp. 106–121. [Google Scholar]
- Shaw ML. Attending to multiple sources of information: 1. The integration of information in decision making. Cognitive Psychology. 1982;14:353–409. [Google Scholar]
- Shimozaki SS, Eckstein MP, Abbey CK. Comparison of two weighted integration models for the cueing task: linear and likelihood. Journal of Vision. 2003;3:209–229. doi: 10.1167/3.3.3. [DOI] [PubMed] [Google Scholar]
- Shulman GL, Wilson J, Sheehy JB. Spatial determinants of the distribution of attention. Perception & Psychophysics. 1985;37:59–65. doi: 10.3758/bf03207139. [DOI] [PubMed] [Google Scholar]
- Sperling G, Melchner MJ. The attention operating characteristic: Examples from visual search. Science. 1978;202:315–318. doi: 10.1126/science.694536. [DOI] [PubMed] [Google Scholar]
- Sperling G, Weichselgartner E. Episodic theory of the dynamics of spatial attention. Psychological Review. 1995;102:503–532. [Google Scholar]
- Steinman BA, Steinman SB, Lehmkuhle S. Visual attention mechanisms show a center-surround organization. Vision Research. 1995;35:1859–1869. doi: 10.1016/0042-6989(94)00276-r. [DOI] [PubMed] [Google Scholar]
- Strasburger H. Unfocused spatial attention underlies the crowding effect in indirect form vision. Journal of Vision. 2005;5:1024–1037. doi: 10.1167/5.11.8. [DOI] [PubMed] [Google Scholar]
- Teller DY. Linking propositions. Vision Research. 1984;24:1233–1246. doi: 10.1016/0042-6989(84)90178-0. [DOI] [PubMed] [Google Scholar]
- Trappenberg TP, Dorris MC, Munoz DP, Klein RM. A model of saccade initiation based on the competitive integration of exogenous and endogenous signals in the superior colliculus. Journal of Cognitive Neuroscience. 2001;13:256–271. doi: 10.1162/089892901564306. [DOI] [PubMed] [Google Scholar]
- Treisman AM. Contextual cues in selective listening. Quarterly Journal of Experimental Psychology. 1960;12:242–248. [Google Scholar]
- Treue S, Martinez-Trujillo JC. Feature-based attention influences motion processing gain in macaque visual cortex. Nature. 1999;399:575–579. doi: 10.1038/21176. [DOI] [PubMed] [Google Scholar]
- Tsotsos JK, Culhane SM, Wai WYK, Lai Y, Davis N, Nuflo F. Modeling visual attention via selective tuning. Artificial Intelligence. 1995;78:507–545. [Google Scholar]
- van der Geest JN, Frens MA. Recording eye movements with video-oculography and scleral search coils: A direct comparison of two methods. Journal of Neuroscience Methods. 2002;114:185–195. doi: 10.1016/s0165-0270(01)00527-1. [DOI] [PubMed] [Google Scholar]
- Watson AB. Probability summation over time. Vision Research. 1979;19:515–522. doi: 10.1016/0042-6989(79)90136-6. [DOI] [PubMed] [Google Scholar]
- Williford T, Maunsell JH. Effects of spatial attention on contrast response functions in macaque area v4. Journal of Neurophysiology. 2006;96:40–54. doi: 10.1152/jn.01207.2005. [DOI] [PubMed] [Google Scholar]
- Yantis S, Johnston JC. On the locus of visual selection: Evidence from focused attention tasks. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:135–149. doi: 10.1037//0096-1523.16.1.135. [DOI] [PubMed] [Google Scholar]
- Zenger B, Braun J, Koch C. Attentional effects on contrast detection in the presence of surround masks. Vision Research. 2000;40:3717–3724. doi: 10.1016/s0042-6989(00)00218-2. [DOI] [PubMed] [Google Scholar]