Reinforcement learning design for cancer clinical trials

Summary

We develop reinforcement learning trials for discovering individualized treatment regimens for life-threatening diseases such as cancer. A temporal-difference learning method called Q-learning is utilized which involves learning an optimal policy from a single training set of finite longitudinal patient trajectories. Approximating the Q-function with time-indexed parameters can be achieved by using support vector regression or extremely randomized trees. Within this framework, we demonstrate that the procedure can extract optimal strategies directly from clinical data without relying on the identification of any accurate mathematical models, unlike approaches based on adaptive design. We show that reinforcement learning has tremendous potential in clinical research because it can select actions that improve outcomes by taking into account delayed effects even when the relationship between actions and outcomes is not fully known. To support our claims, the methodology's practical utility is illustrated in a simulation analysis. In the immediate future, we will apply this general strategy to studying and identifying new treatments for advanced metastatic stage IIIB/IV non-small cell lung cancer, which usually includes multiple lines of chemotherapy treatment. Moreover, there is significant potential of the proposed methodology for developing personalized treatment strategies in other cancers, in cystic fibrosis, and in other life-threatening diseases.

1. Introduction

Discovering effective therapeutic regimens for life-threatening diseases is one of the central goals of medical research. Finding powerful and general methodologies for accomplishing this discovery is a major challenge. The prevailing approach is to develop candidate therapies in the laboratory using basic science and then to test those therapies in animals and then in human clinical trials. A major problem is that very few candidate treatments make it to human clinical trials and only about 10% of treatments making it to human clinical trials demonstrate enough efficacy to be approved for marketing [1, 2]. Typical regimens for patients with certain advanced cancers (such as breast cancer, lung cancer, and ovarian cancer) utilize a single agent in combination with some platinum-based compound, and consist of multiple stages of treatment (especially when relapse is common). For example, many studies demonstrate that three lines of treatment can improve survival for patients with advanced non-small cell lung cancer (NSCLC). For patients who present with a good performance status and stage IIIB/IV disease, platinum-based chemotherapy is the primary treatment which can offer a modest survival advantage over best supportive care alone. Approximately 40-50% of patients in recent first-line trials received second-line treatment. Some patients who maintain a good performance status and tolerate therapy without significant toxicities will receive third-line therapy [3].

A widely used approach is to give a maximum dosage of chemotherapy drug for some period of time, followed by a period of recuperation in which no drug is given. Although this therapeutic regimen can be easily clinically implemented, this may not be the best strategy for minimizing tumor burden. Such problems have motivated the vast literature on drug-scheduling strategies. In the past few years, there has been extensive research on applications of adaptive design to clinical trials. Many investigators have developed various adaptive designs to efficiently identify clinical benefits of the treatment, and demonstrated that conducting adaptive designs can be very promising in clinical development. In general, adaptive designs for multiple courses of chemotherapy allow modification of randomization schedules based on varied probabilities of treatment assignment in order to increase the probability of success. In choosing treatments for successive courses, one of the popular adaptive designs to do this is the play-the-winner-and-drop-the-loser design, which is to repeat a treatment that is successful in a given course and otherwise switch to a different treatment. Thall et al. [4] provided a statistical framework for multi-course clinical trials involving some modifications of the play-the-winner-and-drop-the-loser strategy. In their proposed design, all treatments after the first course are assigned adaptively, thus increasing the amount of information available per patient. Thall et al. [5] presented a Bayesian adaptive design for a trial comparing two-course strategies for treating metastatic renal cancer. Each patient is fairly randomized between two treatments at enrollment, and if a patient suffers disease progression (s)he is then re-randomized among three treatments not given initially. One of the common features of these adaptive designs is the use of parametric models accounting for efficacy, toxicity, or time to some events (such as survival time). By defining a probability model, it is easy to study the design's operating characteristics under a range of parameterizations and clinical scenarios. However, as a result, it will lead to all individuals being assigned to the same level and type of treatment. Therefore, the limitation is not only to ignore the heterogeneity in treatment across individuals, but also to unsuccessfully incorporate the heterogeneity needed for optimal individualized treatment across time.

In addition to the challenge of taking into account accrued information in clinical trial designs, another major challenge is the examination of the long-term benefit of treatment due to delayed effects. If we consider the larger context of the overall therapeutic strategy, in many clinical settings a regimen with a lower initial response rate still can be the best choice in the long run. This is quite plausible due to the potential for the regimen's comparatively better delayed clinical benefit. For finding new treatment regimens with this motivation, one of the most promising approaches has been referred to variously as “dynamic treatment regimes” or “adaptive treatment strategies” [6]. In contrast to classic adaptive designs, dynamic treatment regimes can allow dosage level and type to vary with time for subject-specific needs. As a consequence, the optimal strategy is able to provide information not only on the best treatment choice from the beginning but also treatment choices that maximize outcomes for a later time. Dynamic treatment regimes are recently emerging as a new paradigm for the treatment and long term management of chronic disease, and they have been utilized in some trials such as sequential multiple assignment randomized trials (SMART) [6] and drug and alcohol dependency studies [7]. However, to date, there are no clinical trial methodologies for discovering new treatment regimens for life-threatening diseases. Thus, for diseases like cancer, the use of clinical trials for evaluation and not discovery remains the prevailing paradigm.

In this paper, we present a general reinforcement learning framework and related statistical and computational methods for use in the clinical research arena. Reinforcement learning has been applied to treating behavioral disorders, where each patient typically has multiple opportunities to try different treatments [8]. Murphy et al. [9] suggest Q-learning, which is one of the most important breakthroughs in reinforcement learning, for constructing decision rules for chronic psychiatric disorders, since these chronic conditions often require sequential decision making to achieve the best clinical outcomes. Moreover, reinforcement learning has been successfully applied to the segmentation of the prostate in transrectal ultrasound images. Due to its use of knowledge obtained from the previous input image, the reinforcement learning algorithm is potentially capable of finding the appropriate local value for sub-images and extracting the prostate image [10]. However, reinforcement learning has not yet been applied to life-threatening diseases like cancer where individual patients do not have the luxury to try many different treatments. Our main aim is to illustrate the application of these methods to the discover of new treatment regimens for life-threatening diseases such as cancer. This is a paradigm shift from the standard clinical trial framework which is used for evaluating treatments but not for discovery. We consider trials in which each patient is randomized among a set of treatments at each stage and this treatment set consists of a continuous range of possibilities including, for example, a continuous range of dose levels. Therefore, rather than being constrained to a finite list of pre-specified treatments, our method allows for more general multiplicities of treatments which may include a continuum of possibilities at each stage. Reinforcement learning design has two attractive features that make it a useful tool for extracting optimal strategies directly from clinical data. First, without relying on the identification of any accurate mathematical models, it carries out treatment selection sequentially with time-dependent outcomes to determine which of several possible next treatments is best for which patients at each decision time. This feature not only helps us account for heterogeneity in treatment across individuals, but also possibly captures the best individualized therapies even when the relationship between treatments and outcomes is not fully known. Secondly, in contrast to focusing on short-term benefits, the proposed approach improves longer-term outcomes by considering delayed effect of treatments. Furthermore, we find that reinforcement learning design can extract the optimal treatment strategies while taking into account a drug's efficacy and toxicity simultaneously, which is supported by our simulation studies.

The remainder of this paper is organized as follows. In Section 2, we provide a detailed description of reinforcement learning and Q-learning. Two methods for estimating Q-functions, support vector regression (SVR) and extremely randomized trees (ERT) are presented in Section 3. The proposed “clinical reinforcement trial” method is presented in Section 4. In Section 5, we describe extensive simulation studies we conducted to discover individualized optimal treatment strategies. In Section 6, we conclude with a brief discussion that includes an important future application to NSCLC.

2. Reinforcement Learning Background

Our goal in this section is to introduce reinforcement learning theory, specifically, Q-learning, which will be used to discover individualized optimal therapies in cancer clinical trials.

2.1. Reinforcement learning

Over the last few decades, machine learning has become an active branch of artificial intelligence. Some of the fields studied in machine learning involve stochastic sequential decision processes, commonly referred to as reinforcement learning methods. The term “reinforcement” is subject to the occurrence of an event, in the proper relation to a response, that tends to increase the probability that the response will occur again in the same situation. From a computer science perspective, reinforcement learning is the first field to address the computational issues that arise when learning from interaction with an environment in order to achieve long-term goals. A detailed account of the history of reinforcement learning is given in Sutton and Barto [11].

The basic process of reinforcement learning involves trying a sequence of actions, recording the consequences of those actions, statistically estimating the relationship between actions and consequences, and then choosing the action that results in the most desirable consequence. In our reinforcement learning design, the thing a patient interacts with is called the “environment”, which may indicate the complex system consisting of the human body and more sources of error and greater restrictions on what can be measured. While these interactions continually happen, we choose a sequence of actions applied to the patient and the environment responds to those actions and provides feedback. To be specific, we use S and A to denote random variables, where S represents the set of environmental “states” and A represents the set of possible “actions”. Here “states” may represent individual patient covariates and “actions” can be denoted by various treatments or dose levels. Both variables can be discrete or continuous. Define time-dependent variables S_t = {S₀, S₁,…, S_t}, and similarly, define A_t = {A₀, A₁,…, A_t}. We also define states to possibly include past actions (i.e., S_t can include A_t−1). We use lower case letters, such as s and a, to denote the realized values of the random variables S and A, respectively. Also, for convenience, define s_t = {s₀, s₁,…, s_t}, and similarly, a_t = {a₀, a₁,…, a_t}. We assume the finite longitudinal trajectories are sampled at random according to a distribution P. This distribution is composed of the unknown distribution of each S_t conditional on previous (S_t−1, A_t−1). We denote these unknown conditional densities as {f₀,…, f_T}, and denote expectations with respect to the distribution P as E.

As a consequence of a patient's treatment, after each time step t, the patient receives a numerical reward r_t. This could be denoted as a function (possibly random), which maps to a single number the key elements: current state s_t, action a_t, and next state s_t+1. When t = 0, 1,…, T, the reward is given by

$$r_t=R\left({\text{s}}_t,{\text{a}}_t,s_{t+1}\right).$$

We also define random variable R_t = R(S_t, A_t, S_t+1). Reinforcement learning is learning what to do, how to map situations from state space S to action space A, and depending on what our goal is, how to choose a_t to maximize or minimize the expected discounted return:

$${\stackrel{\sim }{r}}_t=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots +{\gamma }^T{r}_{t+T}=\sum _{k=0}^{T-t}{\gamma }^k{r}_{t+k}.$$

In this equation, γ is the discount rate (0 ≤ γ ≤ 1). We can interpret γ as a control to balance a patient's immediate rewards and future rewards. As γ approaches 1, we take future rewards into account more strongly. In the extreme case, where γ = 1, we fully maximize or minimize rewards over the long run.

Another key element of a reinforcement learning system is an exploration “policy”, p, which maps (s_t, a_t−1) to the probability p_t(a | s_t, a_t−1) (the probability that action a is taken given history {s_t, a_t−1}). If the policy is possibly non-stationary and non-Markovian but deterministic, we denote π_t(s_t, a_t−1) = a_t. In other words, policy π_t, as a sequence of decision rules {π₁,…, π_T}, is an action. Let the distribution P_π denote the distribution of training data when the policy π is used to generate actions. We can then denote expectations with respect to the distribution P_π by E_π. Let Π denote the collection of all policies. Thus the expectations E_π range over π ∈ Π. For simplicity and without loss of generality, we mainly concentrate in this paper on the goal of discovering which treatment can yield a maximized reward for a given patient. Hence seeking the policy that maximizes the expectations with respect to the sum of the rewards over the time trajectories is our ultimate goal. To accomplish this, a “value function” is established as a function of a state. Based on the condition of history s_t, the value function represents the total amount of reward a patient can expect to accumulate over the future. That is,

$$V_t(s_t)=E_{\pi }\left[\sum _{k=0}^{T-t}{\gamma }^k{R}_{t+k}|S_t={\text{s}}_t\right].$$

According to this, the optimal value function can be simply defined as

$$V_t^{\ast }(s_t)=\underset{\pi \in \Pi }{\text{max}}{V}_t(s_t)=\underset{\pi \in \Pi }{\text{max}}{E}_{\pi }\left[\sum _{k=0}^{T-t}{\gamma }^k{R}_{t+k}|S_t=s_t\right].$$

Efficiently estimating the optimal value function is the most important component of almost all reinforcement learning algorithms. Since a fundamental property of value functions used throughout reinforcement learning is that they satisfy particular recursive relationships such as the Bellman equation [12], it is clear that the optimal policy, π*, must satisfy,

$${\pi }_t^{\ast }(s_t)\in \text{arg}\underset{a_t}{\text{max}}E\left[R_t+\gamma V_{t+1}^{\ast }(S_{t+1})|S_t=s_t,A_t=a_t\right].$$

Modern techniques in mathematical and computational areas have stimulated the developments of many methods for estimating the optimal value functions or optimal policies. Many of the existing methods can be categorized into one of the following two classes: dynamic programming or Monte Carlo method [11]. Bellman [12] first provided the “dynamic programming” term to show how these methods are useful to a wide range of problems. Minsky [13] first described the connection between dynamic programming and reinforcement learning. In classical dynamic programming methods, policy evaluation and policy improvement [12, 14] refer to the computation of the value function and the improved policy, respectively. The computation in both methods requires an interactive process. Combining these two methods together, we obtain two other methods called policy iteration and value iteration [15, 16]. Although dynamic programming can be applied to many types of problems, it is restricted to solving reinforcement learning problems under the Markov assumption. If this assumption is violated, dynamic programming may not be able to find an exact solution. Additionally, dynamic programming for solving reinforcement learning problems requires knowledge of a complete and accurate model of the environment. This is almost always unrealistic in clinical settings due to the heterogeneity in the model across individual patients.

2.2. Q-learning

Although the value function plays a fundamental role in reinforcement learning, it is usually not possible to directly compute an optimal policy by just solving the Bellman optimality equation, even if we have a complete and accurate model of the environment's dynamics. Sutton [17] claims that temporal-difference (TD) learning is an alternative method to find optimal policies without any knowledge of the dynamic model. One fundamental expression of TD-learning is the incremental implementation. Compared to Monte Carlo methods, TD-learning requires less memory for estimates and less computation. Almost any TD-learning belongs to the “eligibility traces” problem. For more details on this issue, see Sutton and Barto [11] and Kaelbling et al. [18].

One of the most important off-policy TD-learning methods is Watkins' Q-learning [19, 20]. Q-learning does not estimate the value function directly; it estimates a Q-function instead. Q-learning handles discounted infinite-horizon Markov decision processes (MDP). It requires no prior knowledge, is exploration insensitive and easy to implement, and is so far one of the most popular and seems to be the most effective model-free algorithm for learning from delayed reinforcement. In the setting where we don't have any information about the transition function or the probability distribution of the random variables, such a model-free method can be used to find optimal strategies from the unknown system. The motivation of Q-learning is that once the Q functions have been estimated, it is only necessary to know the state to determine the best action. From a statistical perspective, the optimal time-dependent Q-function is

$$Q_t^{\ast }(s_t,a_t)=E\left[R_t+\gamma V_{t+1}^{\ast }(S_{t+1})|S_t=s_t,A_t=a_t\right].$$

Note that since

$$V_t^{\ast }(s_t)=\underset{a_t}{\text{max}}{Q}_t^{\ast }(s_t,a_t),$$

it is relatively easy to determine an optimal policy, which satisfies

$${\pi }_t^{\ast }(s_t)=\text{arg}\underset{a_t}{\text{max}}{Q}_t^{\ast }(s_t,a_t).$$

One-step Q-learning has the simple recursive form

$$Q_t(s_t,a_t)=E\left[R_t+\gamma \underset{a_{t+1}}{\text{max}}{Q}_{t+1}(S_{t+1},a_{t+1})|S_t=s_t,A_t=a_t\right].$$ (1)

In learning a non-stationary non-Markovian policy with one set of finite horizon trajectories (also called a training data set)

$$\left\{S_0,A_0,R_0,S_1,A_1,R_1,\dots ,A_T,R_T,S_{T+1}\right\},$$

we denote the estimator of the optimal Q-functions based on this training data by Q̂_t, where t = 0, 1,…, T. According to the recursive form of Q-learning in (1), we must estimate Q_t backwards through time t = T,T − 1,…, 1, 0, that is, use the estimates beginning at the last time point Q̂_T recursively back to Q̂₀ at the beginning. For convenience we set Q̂_T+1 equal to 0. In order to estimate each Q_t, we denote Q_t(s_t, a_t; θ) as a function of a set of parameters θ, and we allow the estimator to have different parameter sets for different time points t. For example, Q_t(s_t, a_t; θ) may be of the form

$$Q_t(s_t,a_t;{\theta }_t)=\sum _{j=1}^k{\theta }_{tj}{\phi }_{tj}(s_t,a_t),$$

where θ_t = (θ_t1,…, θ_tk) and {φ_t1,…, φ_tk} are selected basis functions. Once the backwards estimation process is done, we save the sequence of {Q̂₀, Q̂₁, …, Q̂_T} for estimating optimal policies

$${\widehat{\pi }}_t=\text{arg}\underset{a_t}{\text{max}}{\widehat{Q}}_t({\text{s}}_t,{\text{a}}_t;{\theta }_t),$$

where t = 0, 1,…, T, and we thereafter use these optimal policies to test or predict for a new data set.

There are many other promising learning methods based on modifications or extensions of Q-learning, for example, Blatt, Murphy, and Zhu [23] proposed A-learning. However, some properties of these methods have not yet been carefully investigated. Due to the simple equations and minimal amount of computation, we restrict our attention in this paper to Q-learning for discovering effective therapeutic regimens in our clinical trial settings.

3. General Methodology

In this section, our main aim is to estimate the Q-function for finding the corresponding optimal policy. However, challenges may arise due to the complexity of the structure of the true Q-function, including the non-smooth maximization operation in equation (1), the high-dimension of the states variable S, the high-dimension of the action variable A, or having the action variable be continuous. In order to obtain the estimator of interest, many authors have considered different approaches in recent years. Murphy [24], Blatt et al. [23] and Tsitsiklis and Van Roy [25] showed that Q-learning estimation can be viewed as approximate least squares value iteration. The parameter estimators θ̂_t for the t-th Q-function satisfy

$${\widehat{\theta }}_t\in \text{arg}\underset{\theta }{\text{min}}{\mathbb{E}}_n{\left[R_t+\underset{a_{t+1}}{\text{max}}{\widehat{Q}}_{t+1}(S_{t+1},a_{t+1};{\widehat{\theta }}_{t+1})-Q_t(S_t,A_t;\theta )\right]}^2,$$

where 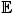_n is the empirical expectation. This is consistent with the one-step update of Sutton and Barto [11] with γ = 1, and furthermore, it is general enough to permit function approximation and non-stationary Q-functions. Another simple and standard estimating form is provided by Murphy et al. [9]. They claim that Q-learning is a generalization of the familiar regression model. When the dimension of the action space is small, linear regression methods can sometimes be adequate; but, more generally, quadratic regression or higher order regression is desirable for estimating the Q-function. In this article we apply two recent flexible techniques from the machine learning literature, support vector regression (SVR) and extremely randomized trees (ERT), as our main methods to fit Q-functions and to learn an optimal policy using a training data set.

3.1. Support vector regression

The ideas underlying SVR [26] are similar but slightly different from SVM [27] within the margin-based classification scheme. The data x_i are mapped into a feature space by a nonlinear transformation Φ, which guarantees that any data set becomes arbitrarily separable as the data dimension grows [28], then a hyperplane f(x) is fitted to the mapped data. One of the popular loss functions involved in SVR is known as the ε-insensitive loss function, which is defined as L(f(x_i), y_i) = (|f(x_i) − y_i| − ε)₊, ε > 0 [27]. Other possible loss functions include quadratic loss, Laplace loss, and Huber loss. In Q-learning, given training data ${\left\{\left(x_i,y_i\right)\in X\times Y\right\}}_{i=1}^n,$ the variable X may be replaced by {S, A} that represents states and actions information, and we define attributes x_it ∈ S_t × A_t, where i = 1,…, n, t = 0,…, T, S_t = {S₀, S₁,…, S_t} and A_t = {A₀, A₁,…, A_t}; the variable Y may be replaced by the numerical rewards, and we assign the label index y_it to each total future reward value r̂_it. The hyperplane f(x) is equivalent to the Q function.

To fit the Q functions, let f(x) = w^TΦ(x_i)+b. Then SVR solves the optimization problem:

$$\underset{w,b,\xi ,{\xi }^{\prime }}{\text{min}}\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^n({\xi }_i+{\xi }_i^{\prime }),$$

$$\begin{array}{cc}\text{subject to}\hfill & (w^T\Phi (x_i)+b)-y_i\le \epsilon +{\xi }_{i,}\hfill \\ \hfill & y_i-(w^T\Phi (x_i)+b)\le \epsilon +{\xi }_i^{\prime },\hfill \\ \hfill & {\xi }_{i,}{\xi }_i^{\prime }\ge 0,i=1,\dots ,n,\hfill \end{array}$$ (2)

where ε is the width of the tube, ξ_i and ${\xi }_i^{\prime }$ are slack variables, and C is the cost of error. C is also called the tuning parameter in the machine learning field and is determined by cross validation. By minimizing the regularization term $\frac{1}{2}{\Vert \text{w}\Vert }^2$ as well as the training error $C{\sum }_{i=1}^n({\xi }_i+{\xi }_i^{\prime }),$ SVR can avoid both overfitting and underfitting the training data. The slack variables ξ_i and ${\xi }_i^{\prime }$ allow for some data points in the feature space to stay outside the confidence band determined by ε. In other words, the goal is to find a function that has at most ε deviation from the actually obtained targets y_i for all the training data. Errors with deviation larger than ε are not acceptable. A class of functions called kernels K : ∝^m × ∝ ^m → ∝ such that K(x_i, x_j) = Φ(x_i)^TΦ(x_j) (for example, the Gaussian kernel is K(x_i, x_j) = exp (−ζ‖x_i − x_j‖²)) are used in SVR to guarantee that any data set becomes arbitrarily separable as the data dimension grows. Since the SVR function is derived within this reproducing kernel Hilbert space (RKHS) context, the explicit knowledge of both Φ and w are not needed if we have information regarding K. In this case, problem (2) is equivalent to solving an optimization dual problem equipped with Lagrange multipliers λ_i:

$$\begin{array}{c}\underset{\lambda ,{\lambda }^{\prime }}{\text{min}}\frac{1}{2}{(\lambda -{\lambda }^{\prime })}^{T}K(x_i,x_j)(\lambda -{\lambda }^{\prime })+\epsilon \sum _{i=1}^n({\lambda }_i-{\lambda }_i^{\prime })+\sum _{i=1}^n{y}_i({\lambda }_i-{\lambda }_i^{\prime }),\\ \text{subject to}\sum _{i=1}^n({\lambda }_i-{\lambda }_i^{\prime })=0,0\le {\lambda }_i,{\lambda }_i^{\prime }\le C,i=1,\dots ,n.\end{array}$$

Once the above formulation is solved to get the optimal λ_i and ${\lambda }_i^{\prime }$ the approximating function at x is given by:

$$f(x)=\sum _{i=1}^n({\lambda }_i^{\prime }-{\lambda }_i)K(x_i,x)+b.$$

Similar to SVM which calculates a hyperplane, the solution of an SVR function only depends on the support vectors [29]. Usually support vectors just represent a small fraction of the sample, therefore, the evaluation of the decision function is computationally efficient. This attractive property is especially useful when dealing with data sets with a low ratio of sample size to dimension. To achieve good performance by using SVR, some procedures such as data scaling, kernel and related parameter selection need to be examined very carefully. We discuss these procedures in more detail in the simulation studies below.

Compared to least-squares regression where ε is always zero, SVR is a more general and flexible approach for regression problems. There are several examples where SVR is successfully used in practice, and they generally perform better than other regression methods. See Chen et al. [30] and Smola and Scholkopf [31]. For a detailed exposition with a more computational discussion about SVR, refer to LIBSVM [32], which is a library for SVM.

3.2. Extremely randomized trees

The complex and unclear structure of the Q-function has also partly motivated the vast literature on nonparametric statistical methods and machine learning. Ernst et al. [33] and Geurts et al. [34] proposed an extremely randomized trees (ERT) method, which is called the Extra-Trees algorithm, for batch mode reinforcement learning. Unlike the classical classification and regression trees such as the Kd-tree or the pruned CART tree, this nonparametric method builds a model in the form of the average prediction of an ensemble of regression trees (called a random forest). Moreover, each tree built by this algorithm consists of strongly randomizing both attribute and cut-point choice while splitting a tree node. In addition to the number of trees G, this method depends on one parameter, called K, the maximum number of cut-direction tests at each node, and n_min, the minimum number of elements at each leaf required to split a node. The choice of an appropriate value of G depends on the resulting compromise between computational requirements and prediction accuracy. K determines the strength of the randomization: e.g., for K = 1, the splits are chosen totally independent of the output variable. A larger n_min yields smaller trees but higher bias. The ERT algorithm builds G trees using the training data set. To determine a test at a node for each tree, this algorithm randomly selects K attributes with K randomized cut-points. A score is calculated for each test and then the one which has the highest value is kept. The algorithm stops splitting a node when the number of elements in the node is less than n_min. The complete ERT algorithm is given in the Appendix of Geurts et al. [34].

Compared to standard tree-based regression methods, ERT successfully leads to significant improvements in precision. Additionally, it can dramatically decrease variance while at the same time decreasing bias, and it is very robust to outliers. ERT has been recently demonstrated in a simulation of HIV infection [35] and adaptive treatment of Epilepsy [36]. While this algorithm reveals itself to be very effective to extract a well-fitted Q from the data set, it has one drawback: the computational efficiency is relatively low especially with increasing numbers of patients in the training data set.

4. Clinical Reinforcement Trials

In this section, we propose a new design and analysis method for a new kind of clinical trial for life threatening diseases, “clinical reinforcement trials”. The design for these trials consists of three aspects:

First, a finite, reasonably small set of decision times is identified. These times could be either specific time points measured from trial onset or decision points in the treatment process such as the starting times of each new line of cancer treatment. For example, in the simulation study below, we create a synthetic cancer treatment setting where patients are monitored monthly for six months and treatment for each month is determined based on patient biomarker values available at the beginning of the month. As a second example, in NSCLC, it may be more appropriate to have one decision time at the beginning of the first line of treatment, a second decision time at the beginning of the second line of treatment, and possibly a third decision time at the beginning of the third line of treatment. The third line is currently only available for certain patients and there is only one FDA approved third line treatment, and so decision possibilities are severely limited at the third decision time for this example. Note that the decision time in this instance is really a stage of treatment and not a calendar time. Other decision time sets, including hybrid variants of the previous two examples, are also possible.

Second, for each decision time, a set of possible treatments to be randomized is identified. The choice of treatments can be a continuum as mentioned earlier or a finite set and can include restrictions which may be functions of observed variables such as biomarkers. For example, in our simulations we restrict the dose of chemotherapy at the first decision time to be above a threshold so that all patients are guaranteed some initial treatment. When the set of treatments is finite, the proposed design reduces to a SMART design.

Third, a utility function is identified which can be assessed at each time point and contains an appropriately weighted combination of outcomes available at each interval between decision times and at the end of the final treatment interval. In our simulation study below, we use a combination of tumor size and overall patient health as our utility function.

We now briefly describe how a study using the proposed method would be conducted. First, a clinical reinforcement trial addressing the targeted clinical disease is designed using the principles described above. This may require developing a virtual patient model as we do in the next section. Once a design has been determined, patients are then recruited into the study and randomized to the treatment set under the protocol restrictions at each decision point, outcome measures used to compute patient state and utility are obtained, and each patient is followed through to completion of the protocol or until the end of the trial. The patient data is collected and Q-learning is applied, in combination with either SVR or ERT applied at each time point as described above, to estimate the optimal treatment rule as a function of patient variables and biomarkers, at each decision time. We allow the Q-functions to differ from decision time to decision time. This yields an individualized, time varying treatment rule that can be significantly better than the standard of care, although it may be important to validate this treatment regime in an additional phase III clinical trial. We will show in the simulation study below that our proposed approach is able to generate treatment rules that lead to improved patient outcomes. One open question which we will pursue in a later paper is how to determine sample size mathematically. Fortunately, it appears from our simulation studies that the sample sizes required are similar to and not larger than the sizes required for typical phase III trials.

5. Simulation Studies

We simulate a sequentially randomized clinical reinforcement trial as a numerical example to examine the performance of the proposed design and analysis methodology. To demonstrate that the optimal therapy found using Q-learning is superior to any other regimens, the treatments at each course are specified in terms of a continuum of dose levels of a single drug, and the comparisons we consider are between the optimal regimen identified from our proposed clinical reinforcement trial procedure and various constant-dose regimens. We first present a simple mathematical model for disease and chemotherapy which we will be using for our study. We then present the specific implementation of Q-learning which we will use for the simulation. This section concludes with a presentation of the results of the simulation study.

5.1. Simple chemotherapy mathematical model

To construct a set of training data reflecting a hypothetical cancer trial, we need a simple chemotherapy mathematical model to generate virtual patients and virtual clinical trial data. The goal for such a chemotherapy mathematical model is to allow for sufficient complexity so that the model will qualitatively generate clinically observed in vivo tumor growth patterns, while simultaneously maintaining sufficient simplicity to admit analysis. Thus, the model we present must exhibit: (1) tumor growth in the absence of chemotherapy; (2) patients' negative wellness outcomes in response to chemotherapy; (3) the drug's capability for killing tumor cells while also increasing toxicity; and (4) an interaction between tumor cells and patient wellness. To obtain data which satisfy these requirements, we propose using a system of ordinary difference equations (ODE) modeled as follows:

$$\begin{array}{c}{\dot{W}}_t=a_1(M_t\vee M_0)+b_1(D_t-d_1),\\ {\dot{M}}_t=\left[a_2(W_t\vee W_0)-b_2(D_t-d_2)\right]\times 1\{M_t>0\},\end{array}$$ (3)

where time (with month as unit) t = 0, 1,…, T − 1, and Ẇ_t and Ṁ_t indicate transition functions. Note that these changing rates yield a piecewise linear model over time. Without loss of trade-off between toxicity and efficacy, the piecewise linear model can be implemented very easily. For simplicity, we here consider tumor size instead of number of tumor cells. M_t denotes the tumor size at time t, M₀ indicates the value of tumor size when the patient is at the beginning of the study. W_t measures the negative part of wellness (toxicity), similarly, W₀ indicates the initial value of patient's wellness. D_t denotes the chemotherapy agent dose level. The value of other different parameters for the model are fixed as: a₁ = 0.1, a₂ = 0.15, b₁ = 1.2, b₂ = 1.2, d₁ = 0.5 and d₂ = 0.5. The indicator function term 1{M_t > 0} in (3) represents the feature that when the tumor size is absorbed at 0, the patient has been cured, and there is no future recurrence of the tumor. Note that this model is not meant to reflect a specific cancer but to reflect a generic plausible cancer created for illustration.

Before generating simulated clinical data, it is easy to notice that the dynamic model has two state variables (W_t, M_t) and one action (treatment) variable (D_t). The state variables can be obtained via:

$$\begin{array}{c}{W}_{t+1}=W_t+{\dot{W}}_t,\\ M_{t+1}=M_t+{\dot{M}}_t,\end{array}$$

where t = 0, 1,…, T − 1 are the T decision times we will utilize in our simulated trial design. We generate a simulated clinical reinforcement trial with N = 1000 patients (replicates) with each simulated patient experiencing 6 months (T = 6) of treatment based on this ODE model. The initial values W₀ and M₀ for each patient are generated from independent uniform (0, 2) deviates. The treatment set consists of doses of a chemotherapy agent with an acceptable dose range of [0, 1], where the value 1 corresponds to the maximum acceptable dose. The values chosen for chemotherapy drug level D₀ are simulated from the uniform (0.5, 1) distribution, moreover, D₁,…, D₅ are drawn according to a uniform distribution in the interval (0, 1). Thus our treatment set is restricted differently at decision time t = 0 than at other decision times to reflect a requirement that patients receive at least some drug at onset of treatment. Various other distribution settings for the action space are possible, and clinical researchers have tremendous flexibility in utilizing this approach.

Figure 1 provides a disease progression example of one patient to show dynamic treatment results with influence of different levels of chemotherapy agent. The system is clearly sensitive to the chemotherapy dosing regimen. Note that when the dose level switches to low, the tumor size grows to a dangerous level. Moreover, the toxicity increases (decreases) once the dosage is changed to a higher (lower) level. Note that in this model we have taken a simplistic approach for illustration and have excluded a number of potentially important factors such as the distinction between reversible and irreversible toxicities.

Figure 1.

Representation of the disease progression for a patient treated from randomized chemotherapy drug. The solid curve represents the negative part of patient's wellness, the dashed curve represents the tumor size, and the dotted curve represents the randomized treatment.

5.2. Q-function estimation and optimal regimen discovery

We now return to Q-learning. Utilizing the proposed ODE model, we generate a simulated clinical trial that provides a set of simulated finite horizon trajectories (or training data),

$${\left\{S_{0i},A_{i0},R_{i0},S_{i1},A_{i1},R_{i1},\dots ,A_{i5},R_{i5},S_{i6}\right\}}_{i=1}^{1000},$$

where each two-dimensional state variable S_t consists of (W_t, M_t), and each continuous action variable A_t is a dose level D_t. Note that our model ignores, for simplicity, dose history in the state variables, even though past dose is technically part of the history. We wish to emphasize that it is not necessary to use all available data in Q-learning, and the user has tremendous flexibility in implementing this general approach. Continuing with our example, we will use Q-learning to maximize a sum of numerical rewards, which we now define, over six months. We assume each reward only depends on the states observed right before and after each action, that is, when t = 0, 1,…, 5,

$$r_t=R(s_t,a_t,s_{t+1}).$$

We decompose this reward function R_t into three parts: R_t,1(D_t, W_t+1, M_t+1) due to survival status, R_t,2(W_t, D_t, W_t+1) due to wellness effects, and R_t,3(M_t, D_t, M_t+1) due to tumor size effects. It can be described by:

$$R_{t,1}(D_t,W_{t+1},M_{t+1})=-60,\text{if patient died},$$

otherwise,

$$R_{t,2}(W_t,D_t,W_{t+1})=\{\begin{array}{cc}\hfill 5& \text{if}{W}_{t+1}-W_t\le -0.5,\hfill \\ \hfill -5& \text{if}{W}_{t+1}-W_t\ge -0.5,\hfill \\ \hfill 0& \text{otherwise},\hfill \end{array}$$

$$R_{t,3}(M_t,D_t,M_{t+1})=\{\begin{array}{ll}\hfill 15& \text{if}{M}_{t+1}=0,\hfill \\ \hfill 5& \text{if}{M}_{t+1}-M_t\le -0.5,\text{but}{M}_{t+1}\ne 0,\hfill \\ \hfill -5& \text{if}{M}_{t+1}-M_t\ge 0.5,\hfill \\ \hfill 0& \text{otherwise}.\hfill \end{array}$$

In most phase III clinical trials, the primary endpoint of clinical interest is the overall survival (OS): this is why we put −60 as a high penalty for patient death. Additionally, we assign a relative high value 15 as a bonus when a patient is cured.

We assume that survival status depends on both toxicity and tumor size. For each time interval (t − 1, t], t = 1,…, 6, we define the hazard function as λ(t), which satisfies

$$\text{log}\lambda (t)={\mu }_0+{\mu }_1{W}_t+{\mu }_2{M}_t,$$

where μ₀, μ₁, and μ₂ are constant pre-specified parameters. In particular, assigning μ₁ = μ₂ = 1 indicates that we consider wellness and tumor size to have an equally weighted influence on the survival rate. The survival function is then

$$\Delta F(t)=\text{exp}\left[-\Delta \Lambda (t)\right],$$

where $\Delta \Lambda (t)={\int }_{t-1}^t\lambda (s)d(s)$ is the cumulative hazard function. The reason the term R_{t, 1}(D_t, W_t+1, M_t+1) is expressed as a function of W_t+1 and M_t+1 is that the hazard function is only determined by the states at the end of each time interval. The conditional probability of death for each time interval is p = 1 − ΔF(t). The survival status (with death coded as 1) is drawn according to a Bernoulli distribution B(p). Overall, by letting γ = 1 (we would like to fully consider maximizing rewards in the long run), the one-step Q-learning with recursive form is utilized, with Q_t(S_t, A_t) predicting

$${\widehat{R}}_t=R_t+\underset{a_{t+1}}{\text{max}}{\widehat{Q}}_{t+1}(S_{t+1},a_{t+1}),$$

where R_t = R_t,1(D_t, W_t+1, M_t+1)+ R_t,2(W_t, D_t, W_t+1)+ R_t,3(M_t, D_t, M_t+1), t = 0,…, 5. Note that r̂_t mentioned previously is defined as a realization of R̂_t. This recursive estimation process is called SARSA (state, action, reward, next state, next action) in the reinforcement learning literature.

To obtain the estimator Q̂_t, we apply SVR and ERT respectively for fitting Q_t backward, and save the results as {Q̂₅, Q̂₄,…, Q̂₀}. Figure 2 illustrates the treatment plan and relevant Q-function estimation procedures. Because of the inner product property of the kernel in SVM/SVR, scaling the data before applying SVR is very important. Another advantage for scaling is to avoid states with greater numeric ranges dominating those with smaller numeric ranges. In our simulation studies, every variable is scaled to zero mean and unit variance, and the center and scale values are saved and used for later predictions. To do fitting of Q̂_t via SVR, we select the Gaussian kernel (or Radial Basis Function), K(x, y) = exp (−ζ‖x − y‖²), because the Gaussian kernel can nonlinearly map samples into a higher dimensional space. Consequently, it can handle the case when the relation between rewards (labels) and states and actions (attributes) is nonlinear. In the SVR approach there are two hyperparameters involved with the Gaussian kernel: ζ and the tuning parameter C. To maximize the performance of the proposed method, we apply a grid search to choose C and ζ by using cross-validation. Trying exponentially growing sequences of C and ζ is recommended as a practical method to identify good hyperparameters. Specifically, for each t in our simulated example, given a straightforward coarse grid search with C = 2⁻⁵, 2⁻³,…, 2¹⁵ and ζ = 2⁻¹⁵, 2⁻¹³,…, 2³, we apply cross-validation to each candidate pair (C, ζ), and then select the pair that yields the highest cross-validation rate. To do fitting of Q̂_t via ERT, we need to be careful with the choice of parameters G, K and n_min. Based on empirical studies, Geurts et al. (2006) suggest that the default value of K should be equal to the number of attributes in the regression problem. Thus we fix K as the dimension of state variables plus the dimension of action variables, which is equal to 3 in our case. To maintain good precision and small bias, G and n_min have been chosen equal to 50 and 2, respectively.

Figure 2.

Treatment plan and the procedure for obtaining the sequential estimator {Q̂₅, Q̂₄, …, Q̂₀}.

Based on the sequential estimators {Q̂₅, Q̂₄,…, Q̂₀}, the individualized optimal policies as a function of the state variables are estimated by maximizing over dose level (i.e., a_t):

$${\widehat{\pi }}_t(s_t)=\text{arg}\underset{a_t}{\text{max}}{\widehat{Q}}_t(s_t,a_t;{\widehat{\theta }}_t).$$

In order to evaluate how the above estimated treatment policies performed, we generated a virtual phase III clinical trial with 200 patients per each of 11 treatments consisting of the estimated optimal treatment regime and each of the 10 possible fixed dose levels ranging from 0.1 to 1.0 with increments of size 0.1. The initial values of W₀ and M₀ for the patients were randomly chosen from the same uniform distribution used in the training data.

The entire algorithm for Q-function estimation and optimal regimen evaluation is summarized as follows:

1. Inputs: a set of training data consists of attributes x (states s_t, actions a_t) and index y (rewards r_t), i.e. {(s_t, a_t, r_t)_i, t = 0,…, T, i = 1,…, N}.

2. Initialization: Let t = T + 1 and Q̂_T+1 be a function equal to zero on S_t × A_t.

3. Iterations: repeat computations until stopping conditions are reached (t = 0).

   1. t ← t − 1.
   2. Q_t is fitted with support vector regression (SVR) or extremely randomized trees (ERT) through the following recursive equation:

      $$Q_t(s_t,a_t)=r_t+\underset{a_{t+1}}{\text{max}}{\widehat{Q}}_{t+1}(s_{t+1},a_{t+1})+\text{error}.$$
   3. Use cross-validation to choose tuning parameters C and ζ if fitting Q_t via SVR with Gaussian kernel; choose plausible values of parameters K, G, n_min if fitting Q_t via ERT (K = 3,G = 50, n_min = 2 in our simulation).

4. Given the sequential estimates of {Q̂₀, Q̂₁,…, Q̂₅}, the sequential individualized optimal polices {π̂₀,…, π̂₅} for application to the virtual phase III trial are computed.

5.3. Simulation results

In the simulated phase III trial, we examine W_t, M_t and the patients' cumulative survival probability. All of these quantities were averaged over the 200 virtual patients. These averages at time t = 6 are given, along with the survival results, in Table 1.

Table I.

Summary of main simulation results

	Optimal Regimens		Constant-Dose Regimens
	RL1	RL2	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
W6	1.276	1.328	-0.411	0.129	0.669	1.217	1.783	2.375	3.016	3.705	4.421	5.141
M6	1.993	1.866	4.737	4.017	0.300	2.654	2.133	1.658	1.203	0.812	0.496	0.257
W6 + M6	3.269	3.194	4.326	4.146	3.970	3.870	3.916	4.033	4.219	4.517	4.917	5.397
CSP	0.442	0.441	0.240	0.292	0.345	0.377	0.363	0.331	0.275	0.189	0.061	0.003

Note: Results such as the wellness (W₆), tumor size (M₆), wellness plus tumor size (W₆ + M₆) and cumulative survival probability (CSP) are given for the optimal regimen using reinforcement learning methods via SVR (RL¹) and ERT (RL²), and for the constant-dose regimen which ranges from 0.1 to 1.0. All numbers are averaged over 200 patients. Entries for superior strategies are given in boldface type.

We used a sample size of 1000 for our simulated clinical reinforcement trial and estimated the optimal treatment policy using both SVR and ERT. For the sake of simplicity, unless stated explicitly otherwise, we only show results in the figures for the SVR method, since we obtain very similar results when we estimate optimal therapy using ERT. In Figures 3 and 4, trajectories (wellness and tumor size, respectively) that would have been observed by putting the patients on constant-dose regimens have been plotted. Note that the wellness measure has been inverted so that larger values represent worse health. This is to make comparisons with tumor size more direct. We test the behavior of estimated optimal regimens on 200 new simulated patients by comparing the outcomes using π̂_t from the Q̂_t (t = 0,…, 5) against the results obtained using 10 different fixed D_t levels (t = 0,…, 5) in the ODE model. As shown in both Figure 3 and Figure 4, the optimal regimens derived from Q-learning do not have better performance for either wellness or tumor size compared to some constant dosing regimens. This is not beyond our expectation. Because when a higher dose level decreases tumor size, it can yield a higher toxicity simultaneously, and vice versa. However, due to our reward functions structure, the estimated optimal policies have an appealing feature that seeks a good balance between toxicity and efficacy. Figure 5 illustrates that the estimated optimal regimen is absolutely superior to any constant-dose regimen when we combine toxicity and efficacy (W_t + M_t) into one comparison criterion. Table 1 agrees with this conclusion by respectively presenting W₆ + M₆ = 3.269 (SVR) or W₆ + M₆ = 3.194 (ERT) as the lowest number compared to the others. Most notably, although the regimen derived from simulated data shows suboptimal results in the first three months, it achieves the best performance eventually. These findings agree well with reinforcement learning's substantially powerful long-run capabilities.

Figure 3.

Plots of averaged value of “wellness” (negative part) for 10 different constant-dose regimens compared to optimal regimen. The results are based on 200 patients. Dashed curves represent the constant-dose regimens, and a solid curve represents the optimal regimen.

Figure 4.

Plots of averaged value of “tumor size” for 10 different constant-dose regimens compared to the optimal regimen. The results are based on 200 patients. Dashed curves represent the constant-dose regimens, and a solid curve represents the optimal regimen.

Figure 5.

Plots of averaged value of “wellness + tumor size” for 10 different constant-dose regimens compared to optimal regimen. The results are based on 200 patients. Dashed curves represent the constant-dose regimens, and a solid curve represents the optimal regimen.

Figure 6 provides the dynamic optimal regimen for an individual patient as well as the toxicity and efficacy values during the whole trial. This simulated patient comes into the trial with initial condition W₀ = 0.30 and M₀ = 1.05. Optimal therapy begins with a very high dose D₀ = 1.00 aimed at reducing the patient's tumor burden. The patient is then monitored for the following month and then treated with another two consecutive high doses (D₁ = 0.74, D₂ = 1.00). In the third month, the tumor size suddenly reaches 0, i.e. the patient has been cured. As expected, we find that the dosage to be administrated rapidly reduces to 0 in the following months. Patients who recover after three months will not receive high dosing anymore because the high dose will likely result in unnecessarily high toxicity. As we can see, rather than the constant dose level for each t, optimal therapy usually has an up-and-down structure due to its adaptive properties. This is an important result which demonstrates that the optimal policy can be approximated very well by reinforcement learning.

Figure 6.

Representation of the optimal treatment for a patient with W₀ = 0.30 and M₀ = 1.05. The optimal treatment sequence (D_t ∈ {1.00, 0.74, 1.00, 0.04, 0.01, 0.01}) is computed by the proposed reinforcement learning methods on clinical data generated by 1000 patients. The solid curve represents the negative part of patient's wellness, the dashed curve represents the tumor size, and the dotted curve represents the estimated optimal regimen.

Finally, compared to all fixed-level doses, Table 1 clearly shows that the therapy found using the Q-learning approach with either SVR or ERT has better performance in terms of cumulative survival probability (CSP). Both SVR and ERT appear to perform equally well with comparable computational burden.

6. Discussion

We have developed a reinforcement learning method for discovering effective therapeutic regimens in clinical trial design. To investigate the validity of such a purely data (model-free) driven approach, we have generated clinical data by relying on a set of hypothetical (and simplistic) but plausible ODE models. Based on these simulated data, we have found that reinforcement learning is indeed able to identify individualized optimal regimens in clinical trials which consist of multiple courses of treatment. Such regimens can reduce tumor burden while taking into account a drug's toxicity. Treatment delay effects, which is an important issue that must be considered for longer term outcomes, are fully assessed by this method. Another appealing feature of our approach is the incorporation of Q-learning methodology with SVR and ERT. Hence even in a data set comprised of high-dimensional attributes, our method is capable of obtaining promising results without much computational burden.

There are a number of challenges we expect to face in future research. First of all, in our study we have defined the reward as a straightforward function to map states and actions into some integer numbers (15, 5, 0, −5 and −60). This simplistic reward function construction along with Q-learning represents an attractive way for trading off efficacy against toxicity and death. However, it is unclear how changing these numbers affects the resulting optimal regimens identified during discovery of effective therapeutic strategies. Understanding the robustness of Q-learning to numerical reward choices is an interesting problem and clearly deserves further investigation. Secondly, since the choice of reward function plays a crucial role in reinforcement learning, therefore, it is very important to consider alternative rewards directly reflecting primary endpoints (such as overall survival, progression-free survival, quality-of-life adjusted survival, freedom from side effects, etc.) in clinical trial designs. One of many feasible approaches for accomplishing this is to perform retrospective analyses on existing clinical trial data to identify clinical factors that influence the outcome of patients treated with chemotherapy drugs, and to build a model that can be used in practice to predict long-term survival in this patient population. Such a model may assist us in building a more plausible reward function, and thereafter determining a regimen which is as close as possible to an optimal policy. To construct a clinically relevant reward function, we believe that close collaboration with clinical researchers is required. An interesting illustrative example of a related strategy is shown by Ernst et al. [35]. They consider discounted instantaneous costs (which is a continuous function directly associated with actions) as their reward function: the rationale behind this comes from a validated and identified HIV model [37].

In this paper, we observed that with sample size N = 1000 for a clinical reinforcement trial, using SVR or ERT leads to a reasonably low bias for estimating optimal regimens. The evidence for this is the confirmed success of the discovered treatment regimen on an independent sample of 200 simulated patients. Clearly, in many settings, this assumption may be violated due to the complexity associated with the performance of the approximation on the Q function, the high-dimensional state or action space, the horizon time T, the connection with SVR or ERT, and more importantly, estimation accuracy. Therefore, an interesting but potentially difficult question would be: how to determine the number of patients N required in a clinical reinforcement trial, utilizing SVR or ERT to fit Q, which can be guaranteed to obtain a regimen that is very close to the optimal one. All these theoretical issues are under investigation and will be presented elsewhere.

Since the work of this article is motivated by the clinical question of proper treatment for Stage IIIB/IV NSCLC, as examined by several clinical trials conducted at the UNC Lineberger Comprehensive Cancer Center (LCCC), an important future application is to refine our model to more accurately reflect NSCLC and the associated treatment issues. The goal of this future study is to compare strategies for multiple lines of treatment for patients with advanced NSCLC who have not been treated previously with systemic therapy. In our future study we will apply reinforcement learning to discover individualized optimal regimens while restricting attention to first-line and second-line only, since there is only one approved agent (Erlotinib) indicated for third-line treatment [38].

First-line treatment primarily consists of platinum-based doublets that include cisplatin, gemcitabine, pemetrexed, paclitaxel, carboplatin or vinorelbine. Numerous studies have compared these various platinum doublets, the great majority of these trials have concluded that all such regimens are comparable in their clinical efficacy. As an example, see Scagliotti et al. [39]. Their study represents the largest number of patients entered into a single phase III study using either cisplatin + gemcitabine or cisplatin + pemetrexed regimen. Noninferiority was demonstrated because the median survival time was an identical 10.3 months in each arm. In addition to platinum-based doublets, some phase III studies have examined the efficacy of various targeted therapies. Bevacizumab plus paclitaxel + carboplatin in the treatment of selected patients with NSCLC showed a significant survival benefit [40], however, with the risk of increased treatment-related deaths. Cetuximab plus cisplatin + vinorelbine demonstrated superior survival in patients with advanced EGFR-detectable NSCLC [41]. The strategies of first-line therapy are essentially based on these four targeted combination therapies, the choice depends on a number of factors, including the patient's histology type, toxicity profile, smoking history, VEGF level, EGFR expression and race [39, 40, 41].

There are three agents approved for treating patients in a second-line regimen: docetaxel, pemetrexed, and erlotinib. Similar to the first-line regimen, these agents appear to have similar efficacies in terms of response and overall survival, but have significantly different toxicity profiles. The choice of agent also depends on many factors, including the patient's number of prior regimens, response to prior chemotherapy, the risk for neutropenia, EGFR expression, and patient preference [42, 43, 44, 45].

Due to the complexity of the biomarkers and unclear toxicities, the trial described here was motivated by the desire to compare those agents in a randomized fashion, and the belief that different combinations given between first-line and second-line may have interactive effects. Another very important factor omitted from the cancer treatment model given in this paper is the potentially enormous difference between reversible and irreversible toxicity. This difference will need to be incorporated in future studies on this topic. Despite the difficulty of discovering superior therapies, another primary challenge is to determine the optimal second-line regimen's starting time, either immediate or delayed after induction therapy, having the highest overall survival probability. Although Fidias et al. [44] provided some results to suggest that an immediate transition to second-line therapy may be optimal, whether these findings are specific to docetaxel or would hold true for other common second-line options such as pemetrexed or erlotinib remains unknown. Hence, optimal timing of second-line therapy with a non-cross-resistant agent is an important issue and still remains unclear. Furthermore, including biomarkers as covariates to assess possible effects, such as biomarker treatment interactions and biomarker second-line-timing interactions, is potentially useful. In our future research, a better understanding of prognostic factors is needed, and this may lead us to discover better individualized therapies using reinforcement learning. In addition to developing new treatments for non-small cell lung cancer, there is significant potential of the proposed strategy for developing personalized treatment strategies in other cancers, in cystic fibrosis, and in other acute and chronic diseases.