The Growth of Obesity and Technological Change

Abstract

This paper presents a dynamic theory of body weight and develops its implications. We argue that technological change has induced weight growth by making home- and market-production more sedentary and by lowering food prices through agricultural innovation. In addition, we illustrate that, while exercise and food intake are complements, reductions in exercise will always raise optimal body weight, as will increases in food intake. We also characterize how body weight varies with income, both within a country, and across countries. Within a country, income may have an inverted U-shaped relationship with body weight, due to the offsetting effects of the demand for food, and the demand for an ideal body weight. This can have important implications for the body weight impacts of public transfer programs. Across countries, however, mean weight is likely to be higher in richer countries. Finally, we present descriptive empirical evidence that illustrates the inverted U-shaped relationship between body weight and income in US males, and suggests the importance of secular trends in weight gain, which are consistent with the impacts of broad-based technological changes.

1 Introduction

Policymakers and the public have been concerned about the dramatic growth in obesity seen in many developed countries over the last several decades. Close to half the US population is estimated to be over-weight and more Americans are obese than smoke, use illegal drugs, or suffer from ailments unrelated to obesity. A substantial risk factor for most of the high-prevalence, high-mortality diseases, including heart disease, cancer, and diabetes (Wolf and Colditz, 1998; Tuomilehto et al., 2001), obesity affects major public transfer programs such as Medicare, Medicaid, and Social Security. Obesity also affects wages and the overall demand for and supply of health care, a sector that itself accounts for one-sixth of the US economy.

Obesity is typically treated as a problem of public health or personal attractiveness. While it is those things, it is even more an economic phenomenon. More than many other physical conditions, obesity can be avoided through behavioral changes, which economists expect to be undertaken if the benefits exceed the costs.¹ Naturally, people may rationally prefer to be under-or over-weight in a medical sense, because weight results from personal tradeoffs and choices along such dimensions as occupation, leisure-time activity or inactivity, residence, and, of course, food intake. Given the variation in their choices about weight, being either fat or thin may be as desirable from the individual’s standpoint as adhering to the norms of weight set by doctors and the public health community.

In particular, this paper develops the argument that economic growth and technological change have created incentives for the long-run growth in weight we have observed. Although the recent rise in obesity has attracted attention, growth in weight is not a recent or short-lived phenomenon. Costa and Steckel (1997) document large secular gains in average height-adjusted weight for men in different birth cohorts over the last century, a finding deepened by Komlos et al (2009).² Indeed, the growth in weight is more pronounced in the early part of the century, although the extreme weights in the tails of the distribution may be a more recent phenomenon. Height-adjusted weight for people in their 40’s, the age group with the highest labor force attachment, has increased by nearly 4 units over this period. To put this into perspective, an increase of this magnitude in the height-adjusted weight of a 6-foot tall man would require a weight gain of approximately 30 pounds.

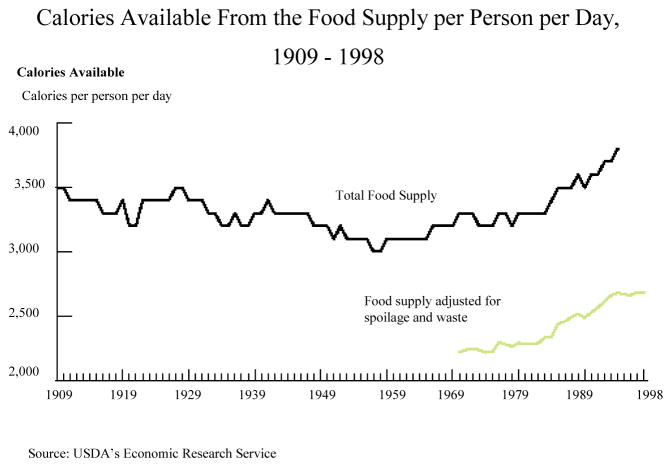
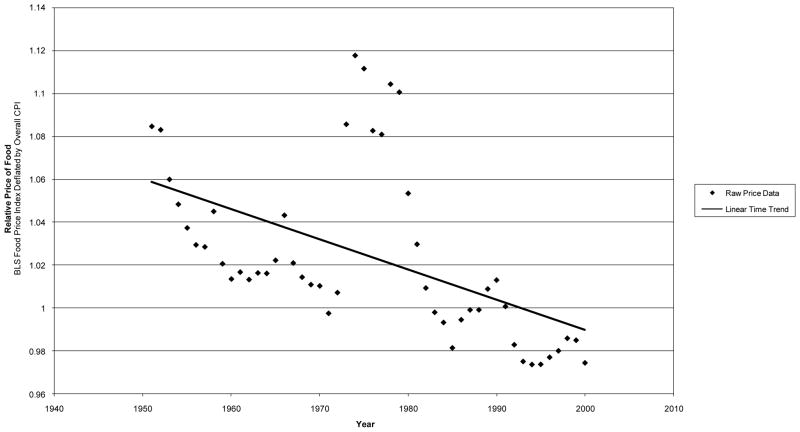
As Figure 1 illustrates, this secular growth in weight has been accompanied by only modest gains in calorie consumption.³ Indeed, the immediate postwar period witnessed substantial growth in weight and declining consumption of calories. The lack of time-series correlation between calorie intake and weight suggests that an analysis of weight must account not only for food consumption, but also for changes in the strenuousness of work, both at home and in the market, caused by economic development. This idea is made even more salient by apparent declines in the relative price of food. Figure 2 plots the relative price of food in the postwar United States.⁴ With the exception of one sharp upward movement at the time of the early 1970s oil shock, the relative price of food has been declining consistently, by about 0.2 percentage points annually. The negative price trend over time suggests that the expansion in supply of food through agricultural innovation has outpaced any increases in demand if indeed demand increased at all.

Figure 1.

Long-Run Change in Calorie Consumption.

Figure 2.

Changes in the Relative Price of Food in the US, 1951–2000.

This paper develops the implications of the hypothesis that technological change has simultaneously raised the cost of physical activity and lowered the cost of calories. It has raised the cost of physical activity by making household and market work more sedentary and has lowered the cost of calories by making agricultural production more efficient. In an agricultural or industrial society, work is strenuous and food is expensive; in effect, the worker is paid to exercise. He often must also forego a larger share of his income in order to replace the calories spent on the job. In addition, with the low levels of public welfare characteristic of these societies, the cost of not exercising could even include starvation. Technological change has freed up resources previously used for food production and has enabled a reallocation of time to the production of other goods and, in particular, more services. In a post-industrial and redistributive society, such as the United States, most work entails little exercise and not working may not cause a large reduction in weight, because food stamps and other welfare benefits are available to people who do not work. As a result, people must pay for undertaking, rather than be paid to undertake, physical activity. Payment is mostly in terms of forgone leisure, because leisure-based exercise, such as jogging or gym activities, must be substituted for exercise on the job. In addition, a smaller share of income is needed to replace the calories spent. Put simply, it was not feasible to be poor and fat historically in developed countries, and still not feasible in many developing countries today.

Our theory predicts that technological change on both the supply side, through agricultural innovation, and the demand side, through more sedentary home- and market production, are needed to explain the long-run patterns. Long-run growth in weight, falling relative food prices, and ambiguous changes in food consumption cannot jointly be predicted by technological change on the demand- or supply-side alone.

The theory has several novel predictions for prices and income as well. First, since labor involves physical activity that may differ from that of leisure, the effects of unearned- and earned income on weight may differ. This difference between unearned- and earned income effects may be important in understanding why income varies positively with weight across countries, where levels of technology and job strenuousness often vary considerably, but negatively within countries, where technology levels are more uniform. In addition, income may have an inverted U-shaped relationship with body weight, due to the offsetting effects of the demand for food, and the demand for an ideal body weight.

Moreover, we predict a negative relationship between weight growth and relative food prices, even though exercise and food intake are complementary. This prediction remains distinct from several other popular explanations of weight growth. Alternative explanations, such as a change in the “culture” of food consumption, growth in the demand for fast food,⁵ or changing social norms, all stress the importance of a rise in the demand for food and thus growth in its price.

We present some simple descriptive analysis illustrating the relationship between income and body weight in US data, along with evidence that the growth in weight is almost entirely secular in nature, rather than driven by specific demographic groups. The latter finding is broadly consistent with an explanation emphasizing cross-cutting technological change.

Our paper may be outlined as follows. Section 2 presents the theoretical framework. Section 3 develops its implications for the behavior of food prices, weight, and food intake. Section 4 presents our descriptive empirical work. Finally, Section 5 concludes with a discussion of future avenues of research suggested by our analysis.

2 Theoretical Analysis

2.1 The Dynamics of Weight Management

Suppose that an individual’s current period utility depends on food consumption, F, other consumption, C, and her current weight, W. We can write this as U(F, C, W), where U rises in food consumption and other consumption, but is non-monotonic in weight. In particular, for a given level of food and other consumption, the individual has an “ideal weight”, W₀, in the sense that, all else equal, she prefers to gain weight when her weight is below W₀, but prefers to lose weight when above it. In addition, suppose that food consumption and alternative consumption are not substitutes, in the sense that U_FC ≥ 0.

We consider an individual who manages weight according to a dynamic problem where her weight, W, is the state variable. Weight is a capital stock that depreciates over time,⁶ and can be accumulated by eating or decumulated by exercising.⁷ Denoting food consumption by F, and the strenuousness of home or market production activities as S, the transition equation relating current weight to next period’s weight, W′ can be written as:

$$W^{\prime }=(1-\delta )W+g(F,S)$$

where δ < 1, and g is continuous, concave, increasing in food consumption, and decreasing in physical strenuousness. We allow the choice of food to be bounded below by zero and above by some finite physical limit; since these bounds are never binding, we need not track them analytically. The associated value function ν for an individual is given by:

$$\begin{array}{l}v(W)={max}_{F,C,W^{\prime }}\{U(F,C,W)+\beta v(W^{\prime })\}\\ s.t.pF+C\le Y\\ W^{\prime }=(1-\delta )W+g(F,S)\end{array}$$ (1)

where Y is the income of the individual and p is the price of food. We interpret agricultural innovation on the supply side as a reduction in p, and sedentary technological change on the demand side as a reduction in S.

Provided that the utility function U is continuous, strictly concave, differentiable, and bounded, and that the transition function g is continuous and concave, we can differentiate the value function, which is continuous and strictly concave (Stokey and Lucas, 1989). This leads to the first order and envelope conditions:

$$\begin{array}{l}{U}_F(F,Y-pF,W)+\beta v^{\prime }{(W^{\prime })}^{\ast }{g}_F=p{U}_C(F,Y-pF,W)\\ v^{\prime }(W)=U_W(F,Y-pF,W)+\beta v^{\prime }(W^{\prime })(1-\delta )\end{array}$$ (2)

The first-order condition implies that the marginal utility of consumption must be equal to the overall marginal utility of food, which equals the marginal utility of eating plus the marginal value of the weight change induced by eating. The envelope condition implies that the long-run marginal value of additional weight is equal to the marginal utility of weight in the current period plus the discounted future marginal utility of weight.

This model of weight yields a unique and stable steady-state in food and weight, as long as the marginal utility of food (U_F − pU_C) is falling in weight.⁸ Rewriting the optimality condition for food,

$$v^{\prime }(W+g(F,S))=\frac{p{U}_C-U_F}{g_F}$$ (3)

This equation implicitly defines food as a function of W, Y, S, and p. The left-hand side is the marginal benefit of weight tomorrow, and the right-hand side is the marginal cost of spending resources on weight gain. Equation 3 illustrates that the optimal food policy falls in current weight W. When W rises, ν′ falls as a result of concavity, and pU_C − U_F rises, because increases in weight lower the marginal utility of food. As a result, the marginal utility of weight tomorrow falls below its cost, or $v^{\prime }<\frac{p{U}_C-U_F}{g_F}$. To restore equilibrium, the individual will eat less. This demonstrates that Φ_W (W; S, p, Y) < 0, where Φ is the optimal food policy.

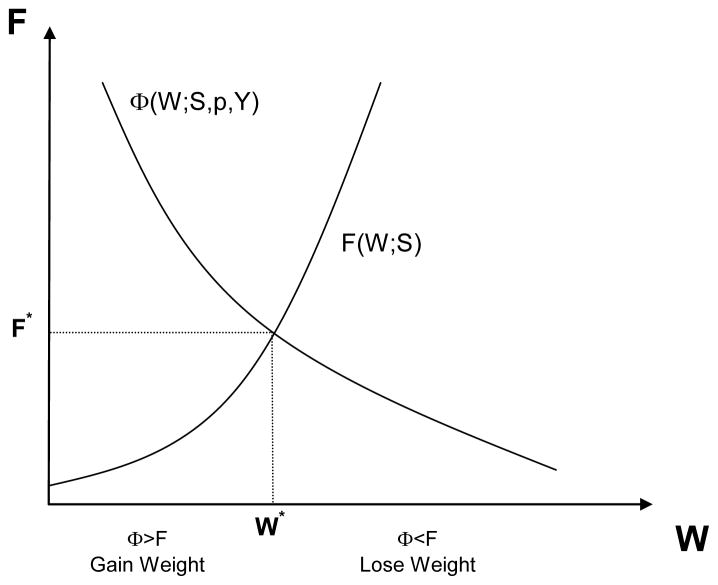
The fact that food consumption decreases in weight yields a unique and stable steady-state, as Figure 3 demonstrates. In the figure, steady-state food consumption, F (S, W), is defined implicitly according to: g(F(S, W),S) = δW. F increases in W and S. Writing the associated steady-state values as W^* and F^*, a steady-state equilibrium (W^*, F^*) exists when the steady-state curve intersects the optimal food policy Φ. This steady-state is unique, because F_W > 0, and Φ_W < 0. It is also stable, because when weight lies below this steady-state, food intake exceeds the steady-state food intake. Conversely, when weight lies above it, food intake is less than the steady-state food intake.

Figure 3.

Steady-State Weight and Food Consumption.

2.2 The Steady-State Determinants of Weight

The steady-state choice of weight is a function of physical activity, food prices, and income, as in W^*(S, p, Y). The same is true for the steady-state choice of food, F^*(S, p, Y). Equation 3 illustrates that an increase in the price of food raises the marginal cost of gaining weight, while leaving the marginal benefit unaffected. This results in the relationship Φ_p(W; S, p, Y) < 0. An increase in the price of food shifts inward the policy function of Figure 3 and lowers steady-state weight, so that $W_p^{\ast }(S,p,Y)<0$. Steady-state food consumption also falls, since we move down the F curve. This suggests that $F_p^{\ast }(S,p,Y)<0$.

2.2.1 Physical Activity

Reduction in physical activity shifts down the steady-state food curve, F(S, W). This induces a movement down the policy function Φ and causes growth in weight and reduction in food intake. The policy function itself also shifts. According to equation 3, the fall in S raises g(F, S) and thus lowers the marginal benefit of weight, ν′. The individual will respond to the lower marginal benefit of eating by reducing food intake, so that Φ_S(W; S, p, Y) > 0.⁹ The downward shift in the policy function reinforces the downward shift in F, so that steady-state food intake falls with physical activity ( $F_S^{\ast }>0$). The shift in the policy function also has an offsetting, negative impact on weight, but this can never be entirely offsetting. Suppose that it is, and that the food policy shifts inward by so much that W′ is actually lower than it was before. But if this were true, then the marginal benefit of weight (v′) is higher than it was before, and the individual should be eating more, not less. This contradiction illustrates that the reduction in physical activity will raise steady-state weight W^* overall, in spite of the offsetting effect. As a result, $W_S^{\ast }(S,p,Y)<0$.

2.2.2 Unearned Income Effects

Consider the partial effect of income on weight, $W_Y^{\ast }$. It is important to stress that this represents the effect of unearned income. Since labor may involve a level of physical activity that differs from leisure, working will tend to affect physical activity S, as well as income Y. The effect of earned income will thus be the combined effect of changes in Y and changes in S that accompany working.

$W_Y^{\ast }$ can have an inverted U-shape, so that increases in unearned income will initially raise weight, but at high levels of income, further increases could actually lower weight. Suppose that consumption and “closeness to ideal weight” are complements in the utility function. This implies that U_WC > 0 for the underweight, but that U_WC < 0 for the overweight. This has important implications for the food policy function. In equation 3, an increase in income lowers the marginal cost of gaining weight, pU_C − U_F, and it can also affect the marginal benefit of weight, ν′(W′). While it has no first-order effects on future weight, W′ = (1 − δ)W + g(F,S),it does affect the marginal value of weight, ν′, depending on whether an individual is underweight or overweight. For the underweight, an increase in income raises U_W, because it raises the marginal utility of being close to ideal weight. Therefore, according to the envelope condition in equation 2, this raises the marginal utility of weight, ν′. Since an increase in income raises the marginal utility of gaining weight and lowers the marginal cost for the underweight, Φ_Y > 0. Conversely, for the overweight, an increase in income lowers U_W, because it raises the marginal disutility of being overweight. This lowers the marginal benefit of gaining weight. As a result, it is possible that Φ_Y < 0 for the overweight.

This could lead to an inverted U-shaped relationship between income and weight. For underweight individuals, growth in income shifts out the food policy function in Figure 3, resulting in an increase in steady-state weight. In contrast, for overweight individuals, growth in income shifts inward the food policy function and reduces steady-state weight. For the underweight, $W_Y^{\ast }>0$, while $W_Y^{\ast }<0$ for the overweight.¹⁰ The effects on food intake are identical. For the underweight, income shifts out the optimal food policy, and $F_Y^{\ast }>0$. For the overweight, it shifts in the optimal policy, and $F_Y^{\ast }<0$.

Consider the example of a utility function of the form $U(F,C,W)=fF+\{Q-(\frac{h}{2}){[W-W_0]}^2\}C$, where Q is some large and positive constant. This utility function embeds the assumption of complementarity between consumption and closeness to ideal weight. To keep things simple, suppose that W′ = W+F − S; people gain weight when their food intake exceeds the strenuousness of their activity. Suppose we can differentiate the envelope condition in 2 with respect to income.¹¹ This yields the following expression:

$$\frac{\partial F}{\partial Y}={[p+\frac{\beta (1-\delta )v^{″}}{h(W-W_0)}]}^{-1}$$ (4)

Since the value function is strictly concave, this expression demonstrates that income raises food consumption (and weight) when an individual is underweight, W < W₀, but lowers it when an individual is overweight, W > W₀.

2.2.3 Earned Income Effects

The total effect of earned income has to account for the fact that earning income can affect one’s physical activity. In other words, S is a function of income earned in the labor market. The total effect of earned income on steady-state weight is given by:

$$\frac{d{W}^{\ast }}{dY}=W_Y^{\ast }+W_S^{\ast }{S}_Y(Y)$$ (5)

The total effect includes the unearned income effect, $W_Y^{\ast }$, along with the effect of earned income on physical activity.

The distinction between the earned and unearned income effects helps us understand how weight varies with income within and between countries. Within a country, income has different effects depending on whether it was earned in the labor market or not. Unearned income may come, for example, from asset markets or from the income of a spouse. If work is sedentary, an increase in earned income will have a larger effect on weight than an increase in unearned income, because earned income also reduces physical activity. If S_Y < (>)0, the effect of earned income is larger (smaller) than for unearned income. When work is sedentary, getting rich through the labor market will raise your weight more than getting rich through the asset market.

Second, within-country income effects may differ from between-country income effects. Empirically, within developed countries, there can be a non-monotonic relationship between income and weight, as we will show later on. However, across countries, income tends to be correlated with higher weight; people in less developed countries tend to be lighter than those in more developed countries. A natural way to interpret this is to argue that differences in technology are much larger between countries than within them.¹² S_Y may thus be large and positive between countries, but fairly small within countries. Within countries, therefore, the unearned income effect dominates, and this can imply an inverted U-shaped relationship between income and weight. Between countries, however, the earned income effect dominates, which implies a monotone positive relationship between income and weight.

Finally, the difference between earned and unearned income effects provides insight into the effects of income redistribution on average weight. In assessing the effects of redistribution, one needs to identify the nature of the income that is being transferred. If redistribution is in terms of unearned income—through programs like food stamps or cash transfers, and through taxes on capital gains or estates—it may raise the weight of both the rich (who become poorer) and the poor (who become richer). In contrast, if it is in terms of earned income—through programs like job training, and through taxes on earnings—the rich may become thinner by working less, while the poor may become heavier by working more. In a post-industrial society, redistributing unearned income can have larger positive effects on weight than redistributing earned income.

3 The Time Series Behavior of Weight and Its Determinants

Changes in weight over time are due to simultaneous changes in all the factors discussed above. Denote by F(t) ≡ F^*(S(Y(t)), p(t), Y(t)) the time path of steady-state food consumption, and denote by W(t) ≡ W^*(S(Y(t)), p(t), Y(t)) the time path of steady-state weight. We have analyzed the partial derivatives of F^* and W^*. We can summarize our results as: $F_S^{\ast }>0$, and $F_p^{\ast },W_p^{\ast },W_S^{\ast }<0$. For the underweight, $F_Y^{\ast },W_Y^{\ast }>0$, while $F_Y^{\ast },W_Y^{\ast }<0$ for the overweight. While these are the partial effects, the total change over time in food and weight is influenced by simultaneous changes in income, physical activity, and prices. Technological change raises income and lowers physical activity; it also lowers the supply price of food. Both these forces tend to raise weight, and lower the equilibrium price of food. However, the time path of food consumption is ambiguous.

3.1 The Time Path of Food Prices

Denote the supply of food by Z(p;A), where A represents technological change in agriculture, in the sense that Z_A > 0. The equilibrium steady-state price p(t) is determined by:

$$F^{\ast }(S(Y(t)),p(t),Y(t))=Z(p(t);A(t))$$ (6)

Using the implicit function theorem, we obtain that the change over time in the price is determined by:

$$p^{\prime }(t)=p_A{A}^{\prime }(t)+[p_S{S}_Y+p_Y]Y^{\prime }(t)=\frac{Z_A{A}^{\prime }(t)+(F_S^{\ast }{S}_Y+F_Y^{\ast })Y^{\prime }(t)}{Z_p-F_p^{\ast }}$$ (7)

Since the denominator of this expression is positive, the direction of the price change is governed by the numerator. The first term of the numerator is negative, because technological progress in agriculture will lower the price of food. The second term will also be negative, if the effect of sedentary technological change dominates the income effect, or $F_S^{\ast }{S}_Y+F_Y^{\ast }<0$. Over periods of significant technological change, therefore, we expect the price of food to fall, because sedentary technological change lowers the demand for food, while agricultural technology expands its supply.

This simple price implication differs from those of alternative explanations of the rise in weight. Many of these explanations—such as a change in attitude towards obesity, growth in the demand for fast food, or reduced parental oversight of children—may be interpreted in our framework as growth in the demand for food. However, if demand were to grow in this fashion, weight would still grow, but price would increase rather than decrease, while food consumption would unambiguously rise. According to Costa and Steckel (1997), Figure 1, and Figure 2, some periods display coincident declines in calorie intake, declines in prices, and growth in weight. These seem difficult to interpret as the result of demand growth alone. Other alternatives—such as growing portions at fast-food and other restaurants—can be interpreted as responses to growing food supply and are thus quite consistent with our explanation and the prediction of falling relative food prices.

A distinct variant on the fast-food explanation is presented by Chou, Grossman, and Saffer (2004), who argue that the increased cost of women’s time has raised the relative demand for fast food outside the home, which is made palatable to consumers through the addition of calorically dense fats and sugars. An increase in the relative demand for calorically dense food, but not necessarily an increase in aggregate food demand, is thus the cause of obesity growth. There seems little doubt that the demand for food away from home has risen and that this is connected with the rising cost of time. However, the linkages among female labor force participation, food prices, and weight growth are less clearly borne out by the data. The largest gains in female labor force participation occurred during the 1960s and 1970s (Goldin and Katz, 2000), before the recent gains in average weight, which began in 1979. Significantly, this also coincides with trends in the relative price of food away from home. From 1960 to 1973, the relative price of food away from home rose by 25 percent. In contrast, from 1973 to 2001, it actually fell by four percentage points and exhibited no trend growth.¹³ This evidence suggests that the bulk of the growth in the relative demand for restaurant food did coincide with substantial gains in female labor force participation, during the 1960s and 1970s, but that these pre-dated the recent acceleration in weight growth that began in 1979.

3.2 The Time Path of Weight

Movements in steady-state weight are governed by:

$$\frac{\partial W^{\ast }}{\partial t}=W_p^{\ast }{p}^{\prime }(t)+[W_Y^{\ast }+W_S^{\ast }{S}_Y]Y^{\prime }(t)$$ (8)

The first term is the effect of expansions in the supply of food, which always raise weight and food consumption. The second reflects changes in the demand for food that accompany changes in earned income. The second term may also be positive if the effect of earned income on weight is positive. In this case, it would reinforce the price effect and raise weight. The continued growth in weight, however, depends on whether the earned income effect remains positive. Income growth can encourage weight control and lower weight, because $W_Y^{\ast }<0$. If this effect offsets the effect of sedentary technological change ( $W_S^{\ast }{S}_Y$), weight growth could slow. Weight could even begin to decline if the earned income effect becomes so negative that it offsets the effect of declining food prices. Historically, income and weight have grown together, indicating that the price effect has dominated or been reinforced by the income effect. While this has been true in the past, it need not remain true. The future course of obesity will depend on which of the two effects dominate the time-series behavior of weight.

3.3 The Time Path of Food Intake

The change in steady-state food consumption is governed by:

$$F^{\prime }(t)=F_p{p}^{\prime }(t)+[F_Y+F_S{S}_Y]Y^{\prime }(t)$$ (9)

The first term represents the effect of supply expansions, and it is always positive. The second represents the effect of earned income growth on the demand for food. If the effect of sedentary technological change, F_SS_Y, dominates the income effect, this can be negative. That is, if physical activity declines considerably, this can offset the effect of income growth and lower the demand for food. An important point to make is that a decline in food consumption, if it occurs, will coincide with an increase in weight. Food consumption falls when the reduction in physical activity lowers the demand for food. However, such a reduction will always raise weight, as discussed in Section 2.2.

4 Empirical Analysis

The theory admits several possible relationships between income and weight—positive, negative, or inverted U-shaped—and it made the specific predictions that $W_S^{\ast }<0,W_p^{\ast }<0$. Earlier research has demonstrated the importance of strenuous job-related exercise as a form of weight control, and sedentary occupation as a factor that raises weight (Lakdawalla and Philipson, 2007). There is also a body of evidence relating declining food prices to rising weight in various contexts (Goldman et al, 2009; Chou et al, 2004). In this section, we do not attempt to duplicate these analyses, but instead seek to illustrate the importance of technological change as an explanation of growth in obesity. In particular, we present data on the relationship between income and weight, and evidence on the importance of secular trends in weight growth.

4.1 Data

4.1.1 National Health Interview Survey

The National Health Interview Survey (NHIS) contains individual-level data on height, weight, income, education, demographic variables, and occupation. It is a repeated cross-section done every year for several decades. Our analysis uses every survey year from 1976 through 1994. Prior to 1976, the NHIS did not ask respondents about their weight. After 1994, the survey switched to a much coarser occupational classification system that we found to be too coarse for our purposes. Use of the NHIS requires that we solve several measurement issues, which we address below.

4.1.2 Measuring Job-Related Exercise

To measure job-related exercise, we rate US Census occupations using consistent measures of strenuousness with the help of two additional data sets. The Dictionary of Occupational Titles, Fourth Edition, by the Department of Labor’s Bureau of Labor Statistics, contains various ratings of the strenuousness of each 3-digit occupational code from the 1970 Census. In the past, this data set has been used primarily to study Workers’ Compensation issues rather than the occupational effects stressed here.¹⁴ We use these publicly available data to rate the physical demands of each 3-digit occupational category in the 1970 US Census. We focus on two ratings in particular: a rating of strength, and a rating of other physical demands. It is important to separate strength requirements from other physical requirements, because stronger workers with greater muscle mass may weigh more than other workers, even though they are not more “overweight” in any medically relevant sense.

The strength rating is an ordinal scale from one to five, corresponding to: sedentary, light, medium, heavy, and very heavy. The physical demands measure is the number of demands present, out of the following list: climbing, reaching, stooping, and kneeling. In earlier work, we validated the DOT job characteristics measures against worker’s self-reports of how strenuous their jobs are (Lakdawalla and Philipson, 2007).

Before 1983, the NHIS uses an occupational classification scheme based on the 1970 Census; this is consistent with the DOT measures mentioned above. However, from 1983 onwards, its scheme is based on the 1980 Census. The differences between these two schemes are substantial, but the 1980 Census occupations can be rated on the same DOT job characteristics scales, using the work of England and Kilbourne (1988). England and Kilbourne use a sample of individuals from the 1970 US Census who were assigned occupational codes both from the 1970 US Census and from the 1980 US Census. They then assign strenuousness scores to each individual in the sample, based on her 1970 US Census occupational code. These strenuousness scores are averaged within each 1980 US Census code to obtain an average strenuousness score for each 1980 code. This method allows us to measure job-related exercise under both systems of occupational classification. Even though these ratings span two types of occupational classification, they are both based on a single, consistent measure of job-related exercise, taken from the Dictionary of Occupational Titles.¹⁵

4.1.3 Measurement of Weight

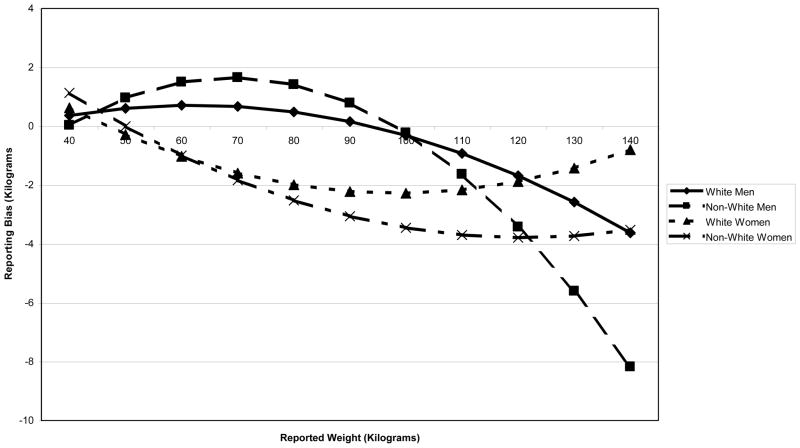
The NHIS contains self-reported data on height and weight, whose pitfalls are well-known (Cawley, 1999). To address this problem, we use data from Wave III of the NHANES, which was collected from 1988 to 1994. The NHANES is an individual-level data set containing both self-reported weight and height, and measured weight and height, for each individual in the sample.¹⁶ Following the method of Cawley (2004), we use the NHANES to correct for reporting error in the NHIS, by estimating the relationship between self-reported weight and actual weight. We regress self-reported weight and its square on actual weight. This regression is run separately for white males, white females, non-white males, and non-white females. The R-Squared for all these regressions is over 90 percent, indicating that the quadratic function fits the data quite well. The results are presented in Figure 4, which plots the predicted reporting bias against self-reported weight for the four sex-race cells used. Nearly all women tend to under-report their weight; the under-reporting is somewhat greater for non-white women than for white women. The reporting patterns of men, on the other hand, differ more by weight. Lighter men, who report weight under 100 Kg, tend to say they are heavier than they really are, while heavier men tend to understate their weight. Using the estimated relationship from the NHANES data, we predict actual weight in the NHIS from the self-reported weight data.¹⁷ All our analysis is performed using this constructed series. Correcting for reporting error improves the fit of our regressions slightly, but it does not appreciably change the quantitative results.¹⁸

Figure 4.

Reporting Bias in Weight Data, by Sex and Race.

4.1.4 Summary Statistics

Characteristics of the NHIS sample are presented in Table 1. The sample includes NHIS respondents aged 18 to 64, over all survey years from 1976 to 1994. The mean male respondent is slightly overweight, both in terms of the self-reported and predicted actual weight. The mean female respondent is at the upper end of the normal weight category. The table also illustrates the distribution of job characteristics in the sample. Not surprisingly, men engage in slightly more strenuous jobs than women.

Table 1.

Characteristics of NHIS Respondents Aged 18–64, 1976–1994.

	Males	Females
BMI	25.47 (4.01)	24.14 (5.10)
BMI (Adjusted)	25.32 (4.17)	24.57 (5.33)
Married, Spouse Present	0.67 (0.47)	0.65 (0.48)
Black	0.11 (0.31)	0.13 (0.34)
Age	38.14 (13.08)	38.27 (13.14)
# Physical Demands
Mean	1.09	0.84
1st Percentile	0.00	0.00
25th Percentile	0.60	0.42
Median	1.00	0.99
75th Percentile	1.50	1.00
99th Percentile	3.00	2.65
Measure of Strength Needed
Mean	2.24	1.90
1st Percentile	1.00	1.00
25th Percentile	1.88	1.14
Median	2.00	2.00
75th Percentile	2.87	2.09
99th Percentile	4.12	3.90

Notes: Standard deviations appear in parentheses below their mean values. All variables reported are native to the NHIS, except for the physical demands and strength measures, which are linked from the Dictionary of Occupation Titles data described in the text.

4.2 Regression Results

Using the NHIS data linked to job characteristics, we estimate the following specification¹⁹:

$$W_{it}={\beta }_0+{\beta }_1{\mathit{Year}}_t+{\beta }_2{\mathit{Muscle}}_{it}+{\beta }_3{S}_{it}+{\beta }_4{Y}_{it}+{\beta }_5({\mathit{Demog}}_{it})+{\beta }_6({\mathit{Age}}_{it})+{\beta }_7{(Ag{e}_{it})}^2+{\epsilon }_{it}$$ (10)

The dependent variable is BMI adjusted for reporting error. This variable W, along with the variable S, play the same role as in the theoretical section. Job strenuousness is separated from strength, because they are predicted to have different effects: Muscle reflects the strength requirement of a worker’s job, taken from the Dictionary of Occupational Titles. . Stronger workers will have greater muscle mass and thus greater BMI. We predict that β₂ > 0 and β₃ < 0. Y represents income, just as in the theory section, but in this regression Y will be included as a set of dummies indicating the quartile of the income distribution to which a worker belongs. There are two reasons for this. First, this specification allows for the inverted U-shaped relationship we predict. Second, the NHIS reports a person’s income category, not his actual income. It is not possible to include a continuous measure of income. The inverted U-shaped relationship is true conditional on a level of job-related exercise, but it may not be unconditionally true. Unconditionally, at higher incomes, job-related exercise could be lower and weight may be rising unconditionally. In addition, it will not be true if we condition on food intake: income initially raises weight precisely because it raises food intake. Year_t represents a vector of year dummies. Next, we allow for weight to have an inverted U-shape in age: people gain weight as they approach middle age, but they begin to lose weight as they enter old age. This means that β₆ should be positive, while β₇ should be negative.²⁰ Finally, we include a vector of demographic variables, Demog, that contains highest grade attained, an indicator for blacks, and an indicator for being married with a spouse present.²¹

The regression specified above serves two purposes. First, it illustrates the conditional variation in weight across groups with different income status at a point in time. (Income quartile is always measured in the year of observation, relative to other respondents in that year.) Second, it provides some suggestive evidence regarding the importance of technological change in the growth of weight. By estimating the empirical relationship between weight and various demographic characteristics, we can identify the growth in weight that resulted from demographic changes. The residual change is attributed to technological change, in the tradition of economic growth-accounting. This relies upon the premise that changes in technology – by altering prices, incomes, and production technologies – cut across the population. Observe that this residual change does not include changes over time in our strenuousness and strength requirements variables. These variables are based on a single ranking of occupations, performed during the 1970s. They do not include changes in strenuousness overtime. Changes in exercise within particular occupations will not be captured by these variables.

The results of estimating equation 10 for male and female workers are presented in Table 2. The table echoes the findings of previous research that workers in more strenuous jobs weigh less, while those in more strength-demanding jobs weigh more. A novel feature of the table is the analysis of BMI variation across the income distribution. For males, we see the inverted U-shaped relationship that the theory predicted was possible, as a result of the offsetting interaction between the demand for food and the demand for ideal weight. Among women, the relationship is monotonically negative, suggesting that the demand for ideal weight grows more rapidly and reaches down into the lower parts of the income distribution.

Table 2.

Regression results for NHIS respondents, 1976–1994.

	Males	Females
# of Physical Demands:0–4	−0.204*** (0.013)	−0.106*** (0.020)
Measure of Strength needed:1–5	0.223*** (0.013)	0.430*** (0.015)
Income Quartiles:
Bottom	−0.238*** (0.021)	0.290*** (0.026)
Third	0.038** (0.017)	−0.476*** (0.022)
Top	−0.057*** (0.019)	−0.887*** (0.025)
Age	0.301*** (0.004)	0.313*** (0.005)
Age-Squared	−0.003*** (0.000)	−0.003*** (0.000)
Highest Grade Attained	−0.111*** (0.003)	−0.221*** (0.004)
Black	0.123*** (0.025)	2.244*** (0.030)
Married, Spouse Present	0.650*** (0.016)	−0.018 (0.020)
Fixed- Effects	Region, Year
Observations	422640	349467
R -squared	0.08	0.12

Robust standard errors in parentheses

^*significant at 10%;

^**significant at 5%;

^***significant at 1%

Notes: Each column reports a separate regression on the sample of NHIS respondents aged 18–64, between the years 1976 and 1994.

Regressions are weighted using the NHIS sampling weights.

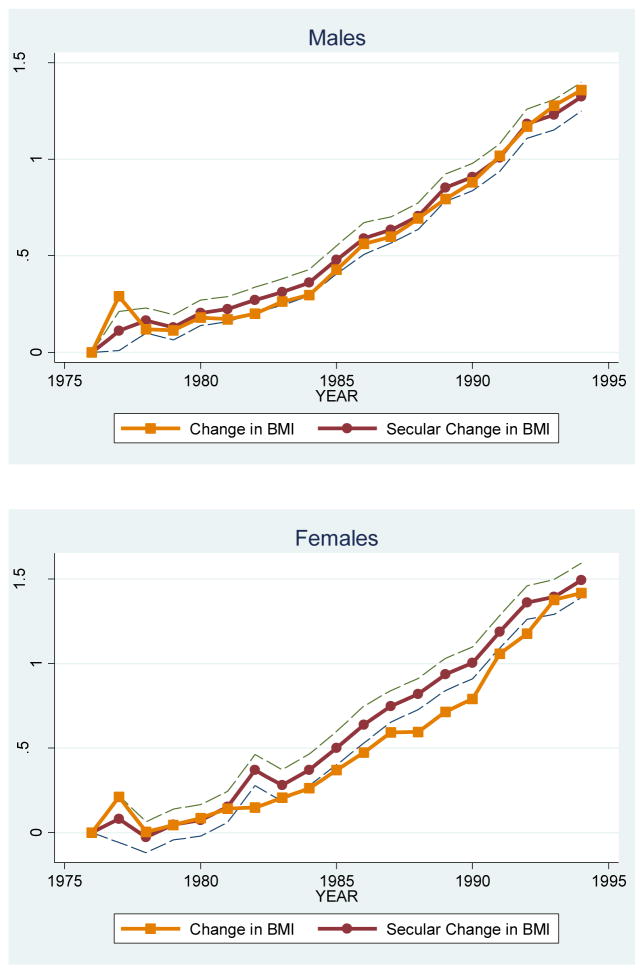
The table does not report the coefficients on all the year dummies, but these are summarized by Figure 5. The figure reports the total trend in BMI, by sex, from 1976–1994, shown by the solid line with square markers. For instance, between 1976 and 1994, BMI rose by nearly 1.5 units for both males and females. The solid line with the circular markers reports the coefficients on the year fixed-effects in the specification above. This can be interpreted as the regression-adjusted trend in weight, net of all the demographic and socioeconomic factors included in the regression. The dashed lines represent the 95% confidence interval around this estimated trend. The figures demonstrate that the total trend in BMI is statistically indistinguishable from the secular, regression-adjusted trend, indicating that the vast majority of BMI growth cuts across the population, and is not specific to particular demographic or socioeconomic groups.

Figure 5.

Secular and total trends in BMI by Sex, 1976–1994.

5 Conclusion

This paper provided a theoretical examination of the forces that have been contributing to the long-run growth in weight over time. We considered the hypothesis that technological change has led to weight growth by making home- and market-production more sedentary and by lowering food prices through agricultural innovation. We also derived the particular relationships among income, weight, and food prices that obtain in the presence of such technological change. This analysis gave rise to predicted time-series behavior for food prices, weight, food intake, and exercise. It also generated implications for the relationship between individual income and body weight, and between national income and body weight. The income distribution of body weight was also shown to have important implications for the impact of public transfer programs on the distribution of body weight.

The paper suggests several avenues of future research. First, the sources of growth in weight need to be better understood to develop better policy responses to the rising epidemic of obesity. Currently, one set of public interventions against obesity has involved education programs emphasizing the benefits of good diet and exercise. However, if technological change in production is the major factor driving the trend, information may be less of an issue than incentives. To this end, many have suggested the importance of “fat taxes” or other pricing disincentives for food intake (Nestle, 2004). Many researchers have pointed out the pitfalls of this approach, which risks regressivity, or unintended consequences (Richards et al, 2007; Schroeter et al, 2007; Drewnowski and Darmon, 2005). Since technological change is ultimately driven towards beneficial ends, attempting to reverse it always risks unintended consequences of one kind or another. However, a broader question intimated by our paper, and made explicit elsewhere (Grossman and Rashad, 2004), concerns the nature of obesity as a public or private problem. The primary externality generated by obesity occurs as a result of health insurance pools, or more specifically, as a result of failures to premium-discriminate between people with unhealthy and healthy body weights (Bhattacharya and Sood, 2006). As a result, taxation of food may be a blunt instrument for this particular type of externality. Future research should strive for a closer link between the policy instrument of choice and the nature of the obesity externality.

Second, an aspect of technological change we explored concerns the declining price of food. It remains to understand the determinants of the time-series path for the relative price of food. More detailed analysis of technological change in agricultural production seems to be the logical next step in a research agenda that aims to understand the economics of weight gain.

Third, although the analysis here stresses the impact of technological change on the quantity of food and calorie consumption, it may have affected the quality of food intake as well. In particular, technological advances may have affected the relative prices of the different sources of calories such as proteins and fats. It is interesting to note that the food diary data from the National Health and Nutrition Examination Surveys suggests that the proportion of calories from fat actually fell slightly during the 1980s. Nonetheless, a substantial increase in total calories consumed pushed up total fat intake. Therefore, it seems important to understand the interaction between quantity and quality, particularly to better understand the negative relationship between income and weight induced by high-calorie foods being less expensive.

Fourth, a better understanding is needed of the relative importance of labor versus leisure activities in the impact technological change has had in reducing activity levels. Leisure issues are particularly important for understanding the growth in child obesity that may be due to technological change, such as computers and television, which have raised the utility of consuming leisure but lowered the calories spent in doing so. Although few data sets will likely be available to do so on a population bases, one may potentially pursue the empirical strategy of identifying a control profession for which the calories spent per hour worked has not changed over time, using its weight growth as a measure of the impact of technological change in leisure on weight.

Finally, although existing data do not allow for a clean and systematic and convincing decomposition of weight growth into a food component and an exercise component, future data production aimed at collecting micro-data on occupation, demographics, and food consumption could make such analysis feasible. This would further advance our understanding of the relationship between weight and technological change.