Challenging a Paradigm: Theoretical Calculations of the Protonation State of the Cys25-His159 Catalytic Diad in Free Papain

Abstract

A central mechanistic paradigm of cysteine proteases is that the His – Cys catalytic diad forms an ion-pair NH(+)/S(−) already in the catalytically active free enzyme. Most molecular modeling studies of cysteine proteases refer to this paradigm as their starting point. Nevertheless, several recent kinetics and X-ray crystallography studies of viral and bacterial cysteine proteases depart from the ion-pair mechanism, suggesting general base catalysis. We challenge the postulate of the ion-pair formation in free papain. Applying our QM/SCRF(VS) molecular modeling approach, we analyzed all protonation states of the catalytic diad in free papain and its SMe derivative, comparing the predicted and experimental pK_a data. We conclude that the His – Cys catalytic diad in free papain is fully protonated, NH(+)/SH. The experimental pK_a=8.62 of His159 imidazole in free papain, obtained by NMR controlled titratin and originally interpreated as the NH(+)/S(−) ⇌ N/S(−) equilibrium, is now assigned to the NH(+)/SH ⇌ N/SH equilibrium.

INTRODUCTION

Cysteine and histidine form the catalytic diad in the active site of all cysteine proteases. They are thought to be present as a thiolate-imidazolium ion pair (Cys25)-S⁻/(His159)-Im⁺H (papain numbering) in the free enzyme (FE).^1–3 The thiolate anion in catalytically active free enzyme is prepared for nucleophilic attack at the carbonyl carbon of the scissile amide or ester bond. The His-Im⁺H functions as a general acid, facilitating the living group departure from the tetrahedral intermediate to produce an acyl enzyme intermediate. This widely accepted mechanistic paradigm, pioneered by Polgar and coworkers, was based on pH-dependence of the second-order rate constants of inactivation of papain and thiosubtilisin.^4–6 The acidic pK_a = 4 was assigned to the (Cys25)-SH/(His159)-Im⁺H ⇌ (Cys25)-S⁻/(His159)-Im⁺H equilibrium, and the basic pK_a = 8.4 was assigned to the (Cys25)-S⁻/(His159)-Im⁺H ⇌ (Cys25)-S⁻/(His159)-Im equilibrium. This reversed order of pK_a (Cys) < pK_a (His) in the ion pair, compaired with 6.04 for histidine and 8.37 for cysteine in solution,⁷ was interpreted to reflect mutual electrostatic stabilization of the counter ions in the thiolate-imidazolium ion pair.^1–3 Fluorescence spectroscopy⁸ and NMR^9,10 titration experiments of free papain and its SSMe derivative, in which the Cys25 thiol was blocked by methylthiolation, further supported this interpretation. The pK_a = 8.62 of free papain was assigned to histidine deprotonation from the ion-pair state. When the electrostatic influence of the thiolate anion was eliminated by the bound SMe, His pK_a was decreased to 3.39.

Some kinetic experiments led to the speculation that ion-pair formation is not sufficient to generate catalytic competence in cysteine proteases and that other ionizable residues have to be deprotonated in order to affect substrate hydrolysis.^11–16 Asp158 was considered as one such electrostatic modulating factor in papain.^11–16 On the other hand, a study of Asp158 point mutations indicated that the charge of the Asp158 carboxylate plays a minor if at all role in the observed pK_a shift in papain. The possible Asp158 influence was assigned to stabilization of the catalytic active conformation by forming local hydrogen bonds with the backbone amides of Ala136 and His159.^17,18 A recent study suggested a key role for Trp177, influencing the hydrophobic shielding of the (Cys25)-S⁻/(His159)-Im⁺H ion pair.¹⁹ Recent interpretations of the catalytic mechanism of some viral and bacterial cysteine proteases based on kinetics^20,21 and X-ray crystallography²² depart from the ion-pair mechanism.

The above experimental works provide macroscopic data derived from enzymatic kinetics and therefore they cannot directly identify the actual protonation state of the Cys-His catalytic diad in cysteine proteases. Moreover, currently there is no NMR or high resolution crystallographic 3D structure of free papain valuable for an unambiguous identification of protons position in the catalytic diad. Thus, theoretical analysis based on molecular modeling is the only way to address this issue.

A general theoretical principle regarding the role of electrostatic interactions in enzyme catalysis states that an enzyme active site can stabilize varied constellations of charges, including ion pairs and polar transition states, much better than bulk water does, by pre-oriented permanent dipoles either alone or in combination with several water molecules.²³ These ideas were further developed²⁴ and validated for various enzymes,^25–28 including the proton transfer between Cys25 and His159 in papain.^29–30 Applying molecular modeling methods calibrated on the experimental energy of the ion pair in solution using empirical valence bond model (EVB) for the reacting region and PDLD and other models for the protein, it was demonstrated that Cys25–His159 ion-pair is more stabilized in the enzyme active site than in water, i.e. the enzyme inverts the stabilization of the covalent and ionic states relative to their order in water solution.

The ion-pair paradigm dominates modern molecular QM/MM simulations of enzyme-substrate and enzyme-inhibitor interactions in the active site of cysteine protease.^31–33 A recent QM/MM study of free cathepsin B concluded that the ion pair (Cys)-S⁻/(His)-Im⁺H is significantly more stable than its neutral counterpart (Cys)-SH/(His)-Im.³⁴ A quantitative assessment of the various effects indicated that the enzyme environment stabilizes the ion pair by 40 kJ/mol in comparison with the ion pair in aqueous solution (QM region in COSMO environment). The stabilization was attributed to hydrogen bonding network involving the catalytic Cys, neighboring residues and solvent water molecules. It was observed that removal of even a single solvent water molecule destabilizes the ion pair and shifts the equilibrium to the neutral state (Cys)-SH/(His)-Im.

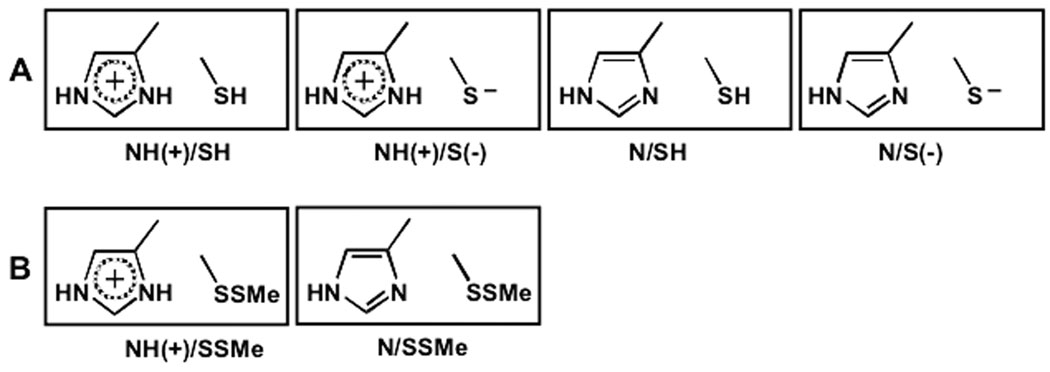
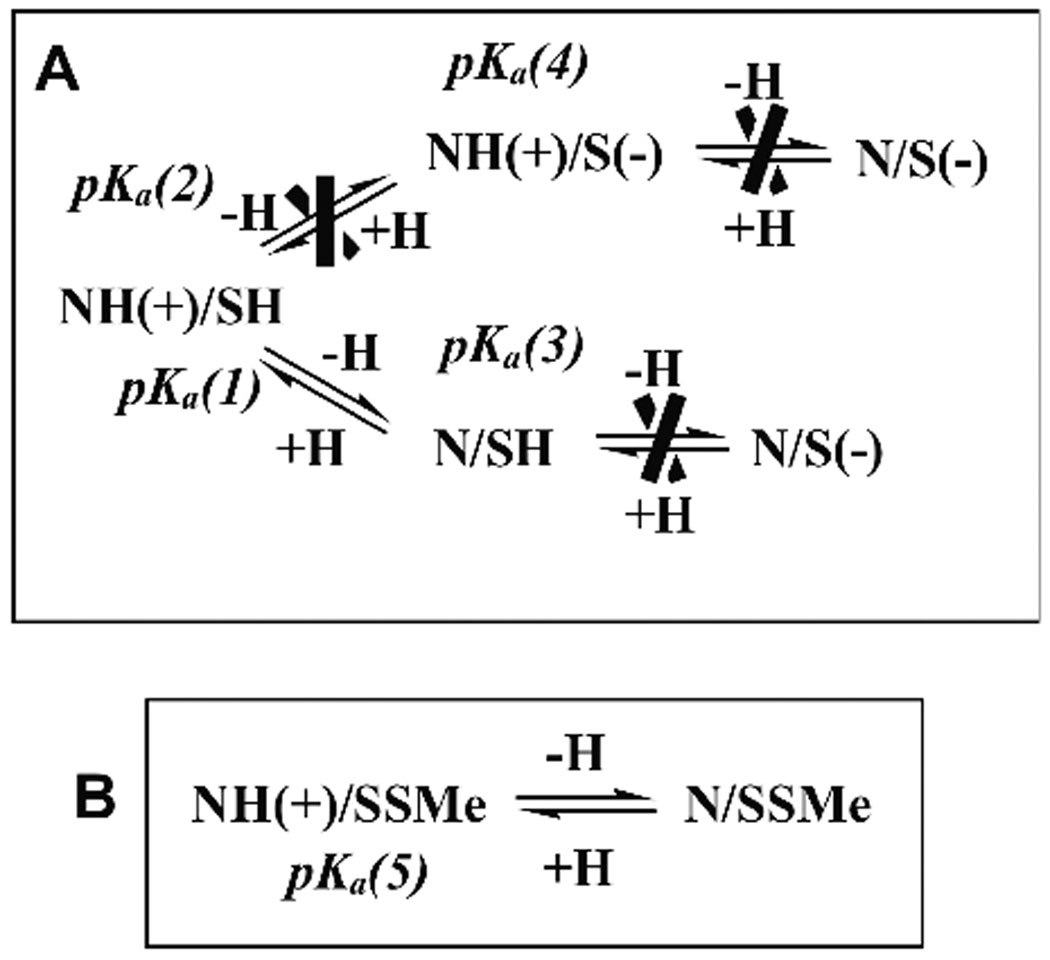
It is important to stress that the mechanistic discussions in all of the above experimental and theoretical studies circulates around Polgar’s hypothesis that the Cys–His catalytic diad in free cysteine proteases is more stable in its ion pair than in its neutral form. The idea was introduced in order to rationalize the observed pK_a values of 4 and 8.4 of the bell shaped pH-dependence of the second-order rate constant of inactivation of papain.^4–6 In the present study we shift the focus from the stability of the Cys-His ion-pair relative to the neutral form. Applying our quantum mechanical QM/SCRF(VS) molecular modeling approach³⁵ we analyze all possible protonation states of the catalytic diad in free papain (FE) and its derivative (SSMe), in which the catalytic thiol is blocked by methylthiolation (Figure 1).^9,10

Figure 1.

All possible protonation states of the Cys25—His159 catalytic diad in free papain (A), and its SMe derivative (B).

We have recently used our QM/SCRF(VS) approach for studying enzyme mechanisms,^36,37 formulation of an enzyme mechanism based CADD method,^38,39 and for the analysis of the role of active site polar interactions and bulk water solvation in modulating general acid / base catalysis in serine proteases.^35,40 Combining the homogenious solvation Born model of spherical solute cavity with a model in which this cavity is located in the border between two different dielectric media, we have formulated analytical equation that describes the dependence of the pK_a of catalytic residues on various environmental factors in the enzyme active site. These include the degree of exposure of the catalytic residue to the bulk solvent, the character of ionized groups in the enzyme active site, and the influence of the pre-oriented dipoles of the active site on the target catalytic residue.³⁵ We have used this equation for the rationalization of the experimentally observed pK_a shift of the catalytic histidine in serine proteases along the transformation from the free enzyme to the tetrahedral covalent complex, and the alterations of this His between acid and base catalytic functionality along the reaction coordinate.⁴⁰ We have further demonstrated that ligand binding in the enzyme active site plays a triggering role in catalysis by screening of the catalytic His from the bulk water, leading to a large shift in its pK_a³⁵ in agreement with experimental observations.^41,42

The ion-pair paradigm in cysteine proteases ignores a possible abrupt pK_a shift in the catalytic His upon ligand binding; the Cys/His catalytic diad is suggested to have an ion-pair structure in both the free enzyme and the enzyme/ligand Michaelis-like non-covalent complex.^{1–6, 31–34} Thus, in the present study we challenge the NH(+)/S(−) ion pair paradigm.

METHODS

Construction of the modeling system

We have considered papain in two states: free enzyme (FE) and its derivative with the Cys25 thiol blocked by methylthiolation (SSMe). The geometries of FE and SSMe were derived from the 9pap⁴³ PDB file (1.65 Å resolution). The initial X-ray structure was transformed into the two variants, SH group in free enzyme and SSMe derivative, by Maestro molecular editor.⁴⁴

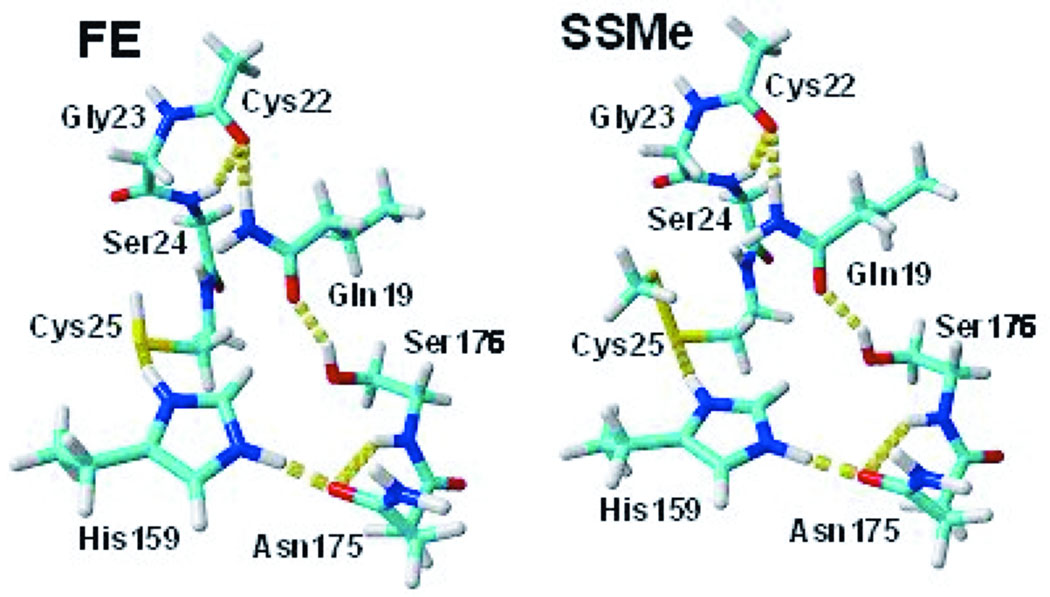
Preliminary geometry relaxation of the whole FE and SSMe protein molecules were conducted in vacuum with the backbone frozen by OPLS AA force field⁴⁵ in the Macromodel 7 package.⁴⁶ The applied cutoff was 7Å for vdW and 12Å for charge/charge interactions. All water exposed groups ionized at pH 7 (Asp, Glu, Lys and Arg) were neutralized to avoid an overestimation of ionic interactions in vacuum caused by the absence of screening water molecules and counterions. The Cys25 and His159 catalytic groups were examined in both protonated and deprotonated states. The position of the SSMe group was refined by conformational analysis on three torsional angles corresponding to rotations around C_α-C_β, C_β-S and S-S single bonds, applying 200 steps of random changes in torsional angles by MCMM algorithm^47,48 implemented in the Macromodel package. The most stable structures of FE and SSMe proteins were used to extract molecular clusters corresponding to the enzyme active site – the quantum mechanical site (QM) in our modeling. In the QM/SCRF(VS) approach QM explicitly accounts for the preorganized local polar environment in the enzyme active site influencing recharging of the ionizable groups in the Cys/His catalytic diad. Thus, our model FE and SSMe molecular clusters include the Cys25 and His159 residues in their basic (B) and acidic (A) forms, as well as residues associated with them by a net of hydrogen bonds in the active site. Asp158, the closest ionic group to the Cys25-His159 catalytic diad, has negligible electrostatic influence on the ionization of His159^17–19 (see Results and discussion) and thus was excluded from the QM site. The constructed QM molecular clusters FE and SSMe contain the Gln19, Cys22, Gly23, Ser24, Cys25, His159, Asp175, and Ser176 residues (Figure 2). Open valences of the broken covalent bonds at the “edges” of the modeling molecular clusters are capped with hydrogen atoms.

Figure 2.

The molecular clusters used for the modeling of the active site of free papain (FE), and its derivative with Cys25 covalently modified by methylthiolation (SSMe). The protonated form of His159 is illustrated. Color scheme: C - cyan, H - white, N - blue, O - red, S - yellow. H-bonds are marked as chains of yellow cylinders. Figures were prepared by the Yasara Dynamics software.

The QM/SCRF(VS) approach

In the QM/SCRF(VS) approach the water solvated enzyme is treated as a two layer system.^35–37,40 The inner layer, the quantum mechanical region, is the enzyme active site (AS) molecular cluster, explicitly calculated by DFT. The outer layer, the classical region, includes the rest of the protein and the bulk water, and is accounted for on a macroscopic level as a uniform dielectric continuum – “virtual solvent” (VS). The molecular shaped solute cavity of the AS cluster is embedded in the virtual solvent, which is characterized by an effective dielectric constant, ε_eff. The empirical parameter ε_eff is calibrated by equalizing the theoretical pK_a of the target ionizable group to the experimental value: pK_a^theor = pK_a^exp. The solute charge distribution, ρ(r), in the AS cluster (calculated in quantum mechanical Poisson-Bolzmann SCRF model implemented in the Jaguar software package⁴⁹) polarizes the surrounding dielectric medium (virtual solvent), inducing surface point charges distributed over the solute-solvent interface.^50,51 The induced surface charges give rise to an electrostatic field at the solute, called the reaction field, treated as a quantum mechanical perturbation of the solute Hamiltonian. SCRF uses an iterative self-consistent procedure until convergence in ρ(r) is achieved.

Geometries of the extracted QM molecular clusters FE and two SSMe were optimized at the B3LYP/6-31+G** level of DFT theory,^52,53 implemented in the JAGUAR 5.1 package. B3LYP/6-31+G** can successfully reproduce geometries and energies of hydrogen bonds and proton positions on ionized groups in the enzyme active site.^35–37,40 The geometries of the FE and the SSMe molecular clusters were optimized in vacuum. The C_α atoms were kept fixed during the QM optimization process in order to maintain biologically relevant molecular structures. Theoretical values, pK_a^theor, were calculated on the QM molecular clusters of the two models FE and SSMe by the QM/SCRF(VS) algorithm.³⁵ A key feature of the QM/SCRF(VS) algorithm is its validation and calibration by experimental values of gas-phase deprotonation free energies, ΔG_g, and pK_a in water of small organic molecules before the estimation of pK_a^theor in the protein. Since we concentrate on the pK_a’s of Cys25 and His159 of the catalytic diad in papain, we used training sets of five thiols and six nitrogen heteroaromatics with tabulated ΔG_g ^54,55 and pK_a ^56–59 values (Table I). Experimental pK_a’s ranged from 7.0 to 11.5 in the former set, and from 0.7 to 9.7 in the latter. pK_a^theor of the training small molecules were calculated by the same formulas used for the FE and SSMe molecular clusters and at the same level of theory. We calculated pK_a^theor by the standard thermodynamic definition:

$$p{K}_a^{\mathit{\text{theor}}}=G_{\mathit{\text{dpr}}}/\mathit{2}.\mathit{303}\mathit{\text{RT}}$$ (1)

For small molecules, used for calibration:

$$G_{\mathit{\text{dpr}}}=\Delta G_g+\Delta G_{ws}+G_{hyd}\mathit{(}{H}^{+}\mathit{)}$$ (2)

The calculation of the deprotonation free energy of the catalytic residue in the enzyme active site is analogous to Eq. 2:

$$G_{\mathit{\text{dpr}}}=\Delta G_g\mathit{(}AS\mathit{)}+\Delta G_{vs}(AS)+G_{\mathit{\text{hyd}}}\mathit{(}{H}^{+}\mathit{)}$$ (3)

In Eq. 2 and Eq. 3, Δ represents differences between deprotonated (basic, B) and protonated (acidic, A) states: the gas-phase free energy of deprotonation, ΔG_g = G_g(B) − G_g(A), and the difference of solvation free energy of the calibrating small molecules in water, ΔG_ws = G_ws(B) − G_ws(A). In Eq. 3 ΔG_vs = G_vs(B) − G_vs(A) accounts for the difference in solvation free energy of the enzyme active site in a virtual solvent that according to the QM/SCRF(VS) algorithm simulates the target catalytic residue partially water exposed. The value of −262.5 kcal/mol was used for the free energy of proton hydration G_hyd(H⁺).⁶⁰ The gas-phase deprotonation free energy of a small molecule, ΔG_g in Eq. 2, or the catalytic residue in the enzyme active site, ΔG_g(AS) in Eq. 3, is calculated explicitly by:

$$\Delta G_g=\Delta E_{\mathit{\text{tot}}}+\Delta ZPE+\Delta H-T\Delta S+G\mathit{(}{H}^{+}\mathit{)}$$ (4)

As above, Δ indicates difference between deprotonated and protonated species. The total electronic energy of the molecular cluster, zero point energy, enthalpy, and entropy (E_tot, ZPE, H, and S, respectively) were calculated in harmonic approximation by standard procedures implemented in the Jaguar package. Eq. 4 also accounts for the gas-phase translational enthalpy and entropy of the released proton calculated at T = 298K and standard pressure in the gas phase: G(H⁺) = 5/2RT − TS(H⁺) = − 6.28 kcal/mol.⁶¹ The water solvation free energies of calibrating small molecules were calculated at ε = 80, and probe radius 1.4 Å by the self-consistent reaction field (SCRF) method^50,51 implemented in the JAGUAR package.

Table I.

Experimental and theoretical gas-phase free energy of deprotonation of thiols and nitrogen heteroaromatics (in kcal/mol) and pK_a in water

Thiols	Gg expa	Gg theor	pKa expb	pKa theor
C2H5SH	348.9	352.0	10.5	10.14
C6H5SH	333.8	336.0	7.78	6.58
SH2	344.4	346.7	7.0	5.49
t-C4H9-SH	346.2	350.6	11.05	11.50
n-C4H9-SH	347.4	351.7	10.65	10.37
nitrogen heteroaromatics	Gg exp	Gg theor	pKa exp	pKa theor
4-Me-imidazole	220.0	221.2	7.45	7.49
pyridine	214.6	214.8	5.30	5.95
pyrimidine	204.4	204.3	1.30	1.04
thiazole	208.3	206.4	2.80	2.20
4-aminopyridine	226.4	226.9	9.70	9.38
pyrazine	202.3	201.2	0.70	1.10

^aRefs ⁵⁴, ⁵⁵.

^bRefs ⁵⁶–⁵⁹.

We used linear regression analysis on the training sets of the thiols and nitrogen heterocycles for the optimization of empirical corrections: pK_a^theor,corr = α pK_a^theor + β. The following values were obtained from linear regression analysis: α = 0.9940, β = 0.0427, SE = 0.52 pK_a units, R² = 0.983, F = 228.5 for nitrogen heteroaromatics, and α = 0.7085, β = 3.1506, SE = 0.19 pK_a units, R² = 0.991, F = 365.2 for the thiols.

MD simulations

All ionizable protein groups, except for Cys25 and His159, were protonated / deprotonated according to their tabulated pK_a values and the accepted pH 7. Periodic boundary cell that is 20 Å larger than the protein along each axis was used for the MD simulation. The periodic box was filled with TIP3P water molecules. The free papain was put into a box of 54.5×71.2×62.3 Å with 7162 water molecules for NH(+)/S(−) and 54.5×71.4×62.4 Å with 7163 water molecules for NH(+)/SH, and the SSMe derivative into a box of 67.0×62.8×66.5 Å with 8397 water molecules. Counter ions were iteratively placed at the coordinates with the highest electrostatic potential until the cell was neutral. To remove bumps and correct the covalent geometry, the structure was energy-minimized with the AMBER 99 force field,⁶² using a 7.86 Å force cutoff and the Particle Mesh Ewald algorithm^63,64 to treat longrange electrostatic interactions. After removal of conformational stress by a short steepest descent minimization, the procedure continued by simulated annealing (time step 2 fs, atom velocities scaled down by 0.9 every 10th step) until convergence was reached, i.e. the energy improved by less than 0.1% during 200 steps.

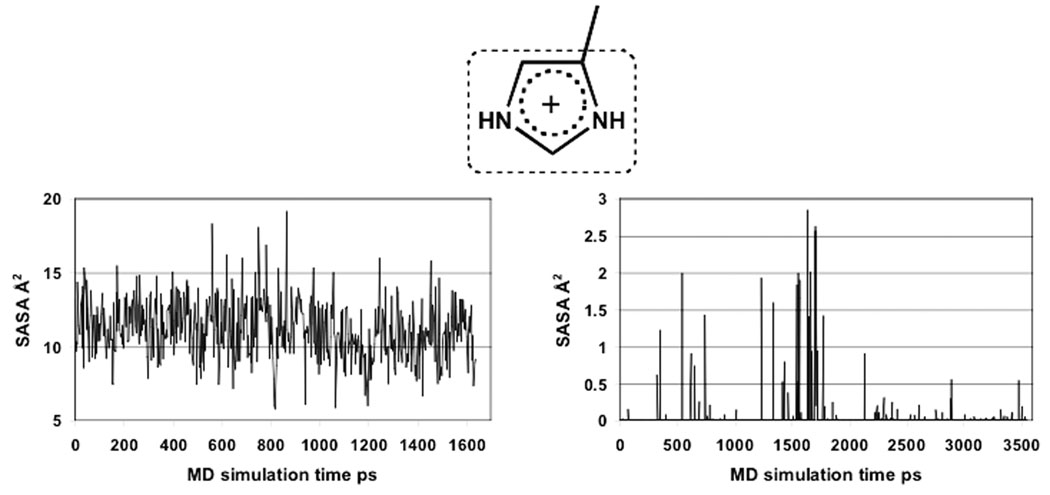
The molecular dynamics (MD) simulations were conducted with a total run time of 3.6 ns for NH(+)/S(−) and 1.6 ns for NH(+)/SH structures of free papain, and 3.5 ns for the NH(+)/SSMe derivative by the Yasara Dynamics software,⁶⁵ using AMBER 99 force field.⁶² The MD equilibrated simulations were run at 298K and constant pressure. Multiple time step was used: 1.25 fs for intramolecular and 2*1.25 fs for intermolecular forces. The cutoff for van der Waals interactions was 7.86 Å. The electrostatic interactions were calculated without cutoff by particle mesh Ewald algorithm.^63,64 Snapshots were collected every 3 ps. In the post processing analysis of the MD simulation trajectory we calculated the solvent accessible surface area (SASA) of the imidazolium cation of His159 in both free papain and its SMe derivative. The SASA calculation was done applying Gaussian approximation, and a probe radius of 1.4 Å.

¹H NMR calculations

We calculated proton NMR chemical shifts, δ, in the FE and SSMe molecular clusters for the CH_ε proton of the His159 imidazole for all studied protonation states of the catalytic diad, applying a method for gas-phase calculations of the shielding constants, σ, implemented in the Jaguar software.⁶⁶ Chemical shifts were calculated by standard formula, δ_i = σ_TMS − σ_i, relative to a calculated average proton shielding constant, 31.6443, of the TMS standard. The calculated proton chemical shift values of His159 in FE and SSMe were then corrected by a liner function: δ_i^corr = aδ_i + b. The empirical coefficients a = 0.8102 and b = 1.4896 were previously calibrated by linear regression analysis used for the correlation of experimental vs. theoretical chemical shifts of all protons in pyridine and imidazole in both basic and acidic forms. All NMR calculations were done in the B3LYP/6-31+G** level of theory. Experimental values of imidazole and pyridine chemical shifts were determined in our lab at 25°C in water solution.

RESULTS AND DISCUSSIONS

MD simulations of free papain

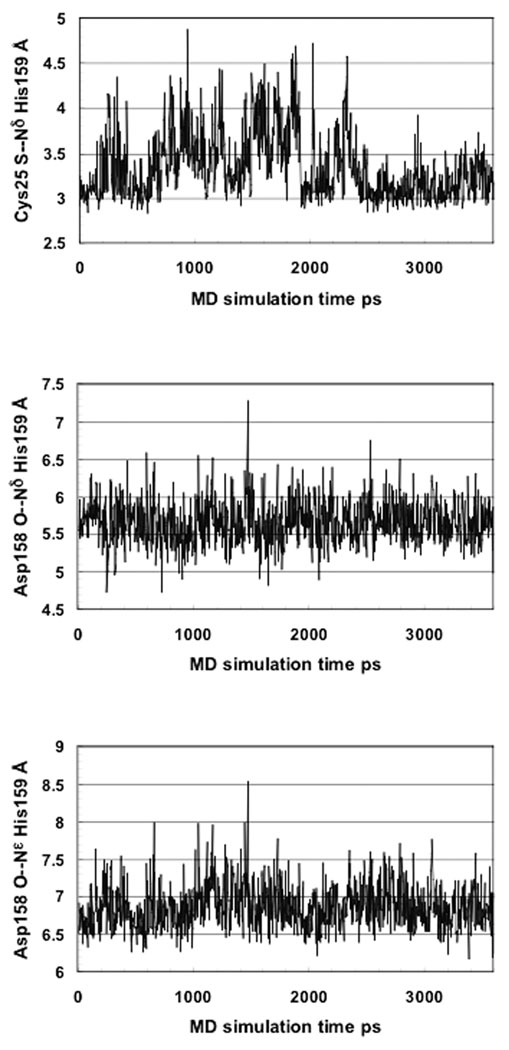
No experimentally-derived 3D structure of the catalytically active form of free papain is available. Therefore, we modeled the enzyme using molecular dynamics (MD). We carried out a 3.6 ns simulation with the suggested ion pair state.^1–6 Figure 3A presents the time dependent Cys25 S(⁻)—N_δH(+) His159 distance. The average value of 3.35Å over the whole trajectory and 3.13Å for the last 1 ns interval is too large for hydrogen bond formation. This is due to water exposure of the Cys25 thiolate and the His159 imidazolium, resulting in preferable formation of hydrogen bonds with solvent water molecules (Figure 4).

Figure 3.

Interatomic distances collected every 3ps on the MD simulation trajectory of free papain, assuming an NH(+)/S(−) ion pair state of the Cys25—His159 catalytic diad.

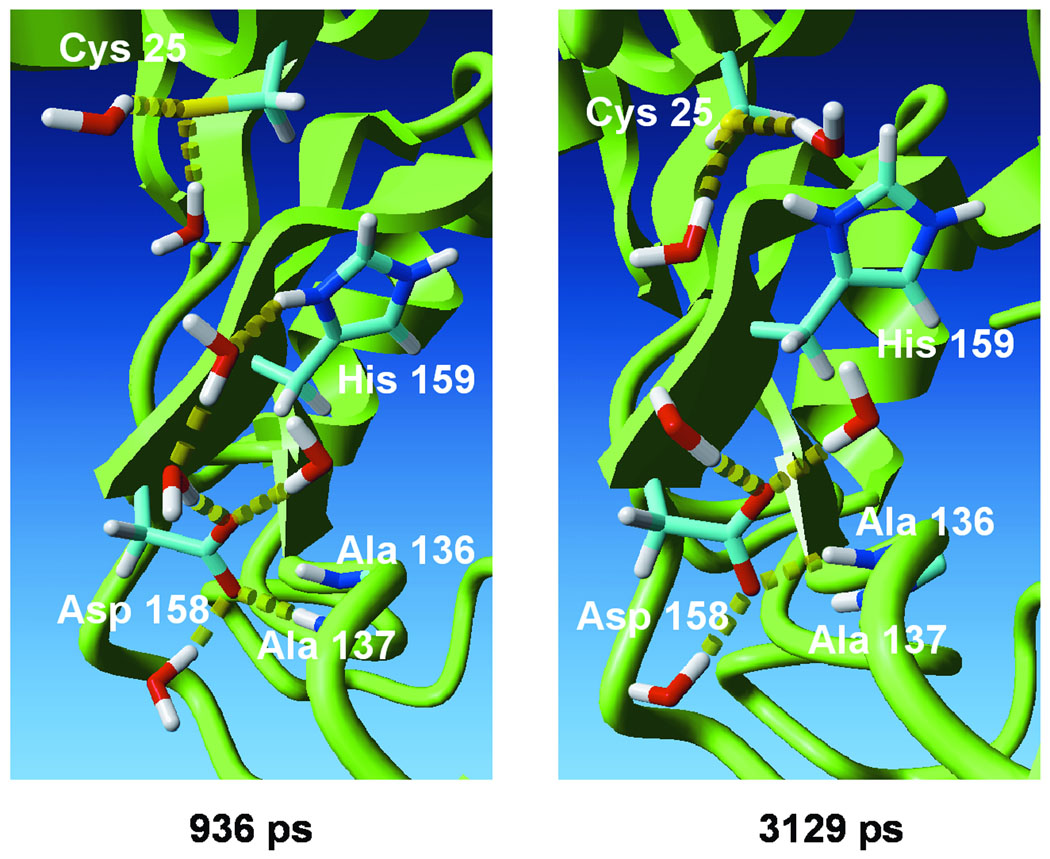
Figure 4.

MD snapshots collected at 936 ps and 3129 ps time points on the MD trajectory of the NH(+)/S(−) ion pair form of free papain. The Cys25 S—N_δ His159 distance is 4.86 Å at the first and 2.93 Å at the second time point. Residues irrelevant to the discussion and water molecules not forming hydrogen bonds with the considered residues are ommitted for clarity. H-bonds are marked as chains of yellow cylinders. Figures were prepared by the Yasara Dynamics software.

Asp158 is considered to be an electrostatic modulator of the pK_a of the catalytic His159 (10–15). Figures 3B and 3C present fluctuations of the Asp158(−) O—N_δ His159(+) and Asp158(−) O—N_ε His159(+) inter-atomic distances along the MD trajectory. The average values are 5.65 Å and 6.85 Å, respectively. The Asp158 carboxylate is highly exposed to the solvent, forming hydrogen bonds with water molecules and with the backbone amide of Ala136 or Ala137 (Figure 4). The average estimated Debye length (the distance at which the absolute value of the energy of an electrostatic interaction is ≤ RT) for solvent exposed charged groups in a protein at near physiological ionic strength (0.1M) is ~5Å.⁶⁷ Thus, Asp158 is expected to play a negligible role in the electrostatic stabilization of the His159 imidazolium, in agreement with previous interpretations of kinetic experiments on wild-type and mutant papain.^17–19

The protonation state of the catalytic diad in free papain

To study the protonation state of the catalytic diad in free papain, we applied our QM/SCRF(VS) approach.³⁵ The current assignment of the pK_a values of the catalytic Cys25 and His159 is based on comparison of two species, the free enzyme (FE) and the SMe derivative (SSMe), in which the catalytic thiol is blocked by methylthiolation.^9,10 We examined all possible protonation states of the Cys—His catalytic diad in these two enzyme forms. FE has two centers of ionization – the His159 N_δ atom and the Cys25 thiol. His159 N_δ is the only protonation center in SSMe (Figure 1). The constructed QM molecular clusters are presented in Figure 2.

Table II contains pK_a^theor(ε) values calculated over a wide interval of ε values for all hypothetically possible protonation/deprotonation equilibria for FE and SSMe (Figure 5). It thus may be used to identify ε = ε_eff for which the pK_a^theor(ε_eff) = pK_a^exp condition is satisfied in both free papain and its SMe derivative. The values of pK_a^theor were calibrated on small organic molecules – thiols and amines - solvated in water according to the QM/SCRF(VS) algorithm (see Methods). Thus, in fact Table II contains pK_a^theor,corr, but we used the pK_a^theor designation for simplicity.

Table II.

pK_a^theor of FE and SSMe, solvated in VS at different dielectric constants ε^a

ε	FE				SSMe
	pKa(1) NH(+)/SH ⇌ N/SH	pKa(2) NH(+)/SH ⇌ NH(+)/S(−)	pKa(3) N/SH ⇌ N/S(−)	pKa(4) NH(+)/S(−)⇌ N/S(−)	pKa(5) NH(+)/SSM⇌ N/SSMe
1	−13.9	0.0	41.9	44.8	−13.9
2	−2.5	6.5	31.1	32.0	−2.9
3	1.4	8.6	26.9	27.1	0.9
4	3.5	9.6	24.5	24.4	2.8
6	5.4	10.6	22.1	21.5	4.5
8	6.4	11.1	20.8	20.1	5.6
10	7.1	11.3	20.0	19.2	6.1
20	8.5	12.0	18.5	17.5	7.2
30	8.9	12.2	18.2	17.2	7.6
40	9.2	12.3	17.8	16.8	7.7

^aCalculated at 25°C

Figure 5.

All possible variants of deprotonation/protonation of the Cys25—His159 catalytic diad in free papain (A) and its SMe derivative (B). The crossed equilibria represent computational variants that could not be fitted either to the experimental pK_a or to the calculated relative stability.

We used Eq. 1–Eq. 4 in the QM/SCRF(VS) method for rigorous DFT calculations of the pK_a values presented in Table I and Table II. Nevertheless, to rationally understand how changes of environmental factors in the enzyme active site influence the trend in pK_a of catalytic residues, a more simplified model would be most helpful. We have recently demonstrated that a QM/SCRF(VS) model with molecular shaped solute cavity of the AS (QM molecular cluster) can be approximated by a spherical cavity of radius a embedded in the same VS with ε_eff.³⁵ This new model is equivalent to the same spherical solute cavity located at the interface between different dielectric media: ε_eff = 1/(1–0.9875θ), where ε_eff grows hyperbolically with the increase of the normalized value of the surface fraction of the spherical solute cavity that faces the water, θ (0 ≤ θ ≤ 1). The SASA of a catalytic group in the enzyme active site, used for the pK_a calibration in QM/SCRF(VS), changes proportionally with the values of θ and ε_eff. We have derived an approximated analytical expression for pK_a^theor:³⁵

$$p{K}_a^{\mathit{\text{theor}}}\approx \mathit{72}.\mathit{1}\frac{\mathit{(}{Q}^{\mathit{2}}\mathit{(}B\mathit{)}-Q^{\mathit{2}}\mathit{(}A\mathit{)}\mathit{)}}{RTa}\frac{\mathit{(}\mathit{1}-{\epsilon }_{\mathit{\text{eff}}}\mathit{)}}{{\epsilon }_{\mathit{\text{eff}}}}+C$$ (5)

C = [ΔG_g(AS) + G_hyd(H⁺)] / 2.303RT, where ΔG_g(AS) is the free energy of deprotonation of the target catalytic residue calculated in the active site molecular cluster in the gas-phase approximation (see Eq. 1, Eq. 3, Eq. 4, and ref. 35), and G_hyd(H⁺) is the free energy of proton hydration. Q(A) and Q(B) are the total charges of the spherical solute cavity of radius a in Å, when the target ionizable functional group is in the acidic (A) or the basic (B) form, respectively. Eq. 5 rationalizes the dependence of pK_a not only on the active site permanent dipoles (ΔG_g(AS) in the second term), but also on the partial water solvation accounted for in the first term. The first term in Eq. 5 is the approximation of the rigorously calculated (by DFT) ΔG_vs(AS) in Eq. 3. Being a combination of two functions, ε_eff (SASA) and (Q²(B) − Q²(A)), the first term of Eq. 5 accounts for the combined influence of two environmental factors on pK_a: the degree of water exposure of the target catalytic residue, ε_eff (SASA); and the dependence of the free energy of solvation on the change of the total number of the ionized groups in the enzyme active site caused by the recharging of the target catalytic group during deprotonation. Eq. 5 enables prediction (used for the interpretations purpose only, but not for quantitative calculations) of the trend of pK_a changes by knowing the value of Q²(B) − Q²(A) in the active site. If Q²(A) > Q²(B), pK_a shifts in parallel to the change in ε_eff or θ, while if Q²(A) < Q²(B), a decrease in θ or ε_eff will lead to increase in pK_a.^35,40 Examining Table II and the corresponding protonation states (Figure 1) of the basic and acidic forms of the QM molecular clusters shows that the former trend applies to pK_a(1), pK_a(2), and pK_a(5) (Q²(B) − Q²(A) = 0 − 1= −1), while the latter is represented by pK_a(3) and pK_a(4) (Q²(B) − Q²(A) = 1 − 0 = 1).

We used as a reference the experimental pK_a^exp = 9.2 at 25°C in FE (recalculated from pK_a = 8.62 measured at 45°C by titration under ¹H NMR analysis).¹⁰ Two alternative deprotonation variants of the free papain could potentially fit the experimental pK_a in FE: pK_a(1) corresponding to the equilibrium NH(+)/SH ⇌ N/SH, and pK_a(2) corresponding to the equilibrium NH(+)/SH ⇌ N/S (Table II). These could be resolved by comparison of FE with its SMe derivative. The SMe group on Cys25 in the papain derivative screens the His159 imidazole from solvent. The time-averaged values of the solvent accessible surface area (SASA) collected on the MD trajectories are 11.13 Ų in FE, and only 0.038 Ų in the SMe derivative (Figure 6). The experimental pK_a = 3.5 of His159 in SSMe at 25°C (recalculated from the measured value of 3.39 at 35°C⁹) was reproduced for the theoretical pK_a(5) at ε_eff = 4.5. Thus, accepting the pK_a(2) equilibrium, reached at ε_eff = 3.5, would indicate that the water exposure of His159 in free enzyme is smaller than in the SMe derivative, in contradiction to the above MD results. On the other hand, pK_a(1) in FE fits the experimental pK_a value at ε_eff ≥ 40, a value which is much larger than that identified for SSMe, in agreement with our theoretical findings that ε_eff is a measure of the SASA of the ionizable group used for the calibration.³⁵

Figure 6.

Calculated SASA values of the His159 imidazolium along the MD simulation trajectory for free papain, and its SMe derivative.

The remaining pK_a(3) and pK_a(4) variants of FE are far beyond the range of the experimental pK_a = 9.2 at all examined ε values (Table II). These high pK_a values seem unreliable at first glance, if compared with the experimental values of the amino acids in aqueous solution (6.04 for histidine and 8.37 for cysteine)⁷ and of other small molecules (Table I). Nevertheless, these high values of pK_a(3) and pK_a(4) can be rationalized in the QM/SCRF(VS) approach considering energy contributions of the two cooperatively acting environmental effects – the local electrostatic environment in the enzyme active site (pre-oriented dipoles), ΔG_g(AS), and the solvation of the target catalytic residue in a virtual solvent with calibrated ε_eff (partial water solvation), ΔG_vs(AS) (Eq. 3).

Let us consider the N/SH ⇌ N/S(−) equilibrium. The calculated Cys pK_a(3) = 41.9 at ε = 1 (Table II) is in fact smaller than what would be calculated without the effect of the active site environment. Indeed, the calculated gas-phase ΔG_g(AS) = 343.1 kcal/mol corresponding to Cys pK_a(3) is smaller than 348.9 kcal/mol, the analogous experimental gas-phase basicity of ethylmercaptane (Table I). The smaller value of ΔG_g(AS) reflects the stabilization effect by neighboring polar groups of the thiolate anion of Cys in the enzyme active site. pK_a(3) = 17.8 at ε = 40 is also not surprising. According to the MD simulations (Figure 4) the Cys thiolate in free papain is partially water solvated, forming several hydrogen bonds with water molecules. This observation correlates with QM/MM findings.³⁴ Nevertheless, the partial water solvation of the catalytic Cys thiolate in free papain is considerably smaller than in the case of a surface cysteine residue or small molecules fully solvated in water. In addition there are no positively charged neighboring groups in the active site of free papain that could stabilize the Cys thiolate of the catalytic diad in the N/S(−) state.

The NH(+)/S(−)⇌N/S(−) equilibrium (corresponding to pK_a(4), Table II) is commonly correlated with the experimental pK_a = 8.62 at 45°C of free papain¹⁰ or pK_a = 9.2 recalculated at 25° C in this work. This value was interpreted to reflect electrostatic stabilization in the Cys—His ion-pair in free cysteine proteases.^4–6,9–10 pK_a(4) is much larger at all considered ε values than the experimental value of 8.62 suggested for this interpretation. The calculated ΔG_g(AS) = 330 kcal/mol contributing to the corresponding pK_a(4) (Eq. 3) is much larger than the experimental gas-phase basicity of 220 kcal/mol of 4-Me-imidazole (Table I), confirming the expected stabilization of the imidazolium cation in the ion-pair. We would like to note in this context that we have previously calculated pK_a = 11.5, and the corresponding ΔG_g(AS) = 327.8 kcal/mol for the catalytic His195 in the modelling of enzyme-inhibitor covalent anionic tetrahedral complex in serine proteases, in very good agreement with the experimental value of pK_a = 11.2 recalculated to 25°C.³⁵ Thus the value of ΔG_g(AS) = 330 kcal/mol in the present study is very reasonable.

Our results are only consistent with NH(+)/SH, the structure of the Cys25—His159 catalytic diad in free papain at neutral pH – the only state satisfying the pK_a^theor = pK_a^exp condition. This conclusion directly contradicts the NH(+)/S(−) ion pair paradigm. It should be noted that the acidic pK_a value of papain was measured in kinetic experiments,^4–6 but not in the NMR titration experiment.^9,10 While the latter directly bears on the free enzyme structure, the former may be interpreted in different ways, relating to different species along the catalytic reaction. In the present study we considered only the structure of the free enzyme, while the observed acidic pK_a issue will be addressed elsewhere.

It is interesting to note that while an ion-pair structure of the catalytic diad in free papain would render the enzyme fully active and thus amenable to non-specific reactivity, the suggested fully protonated structure may serve to protect the enzyme from undesired reactions. We suggest that papain-like cysteine proteases become active only upon substrate binding. The latter event reduces the water exposure of the catalytic diad in the Michaelis complex (MC) and thus triggers the enzymatic catalysis.³⁵ Indeed, according to Eq. 5 the pK_a change in the FE → MC transformation is characterized by the Q²(B) − Q²(A) = 0 − 1= −1 trend, if FE is initially in the NH(+)/SH protonation state as found in this work. Thus, two possible protonation states could be realized in the MC: N/SH or NH(+)/S(−). The latter is the ion pair, in which the thiolate is ready for the nucleophilic attack and the His imidazolium can activate the scissile amide by general acid catalysis. If N/SH is initially formed in the Michaelis complex, an alternative mechanism is feasible, in which the SH proton is transferred to the catalytic His concurrently with the nucleophilic attack of the S atom on the substrate. This mechanism is analogous to the corresponding catalytic mechanism of serine proteases.

¹H NMR

We have also calculated chemical shifts of the CH_ε proton of His159 imidazole for all considered protonation states of the catalytic diad in both FE and SSMe molecular clusters (Table III). The theoretically calculated NMR chemical shifts nicely reproduce the experimentally observed chemical shifts and the difference between the δ values of the protonated and the deprotonated forms of His159 imidazole in free papain and its SMe derivative.^9,10 Nevertheless, within computational error the calculated CH_ε proton chemical shifts cannot differentiate between the two examined equilibria: NH(+)/SH ⇌ N/SH and NH(+)/S(−) ⇌ N/S(−). This ambiguity demonstrates that the experimental NMR chemical shifts cannot unequivocally serve to support the paradigm of the presence of an NH(+)/S(−) ion pair in free papain.

Table III.

¹H NMR chemical shifts (ppm) of CH_ε of the His159 imidazole

Diad state	Theoretical δ	Experimental δ
NH(+)/SSMe	8.79	8.52a
N/SSMe	8.08	7.74a
NH(+)/SH	8.63	8.51b
N/SH	7.77	7.67b
NH(+)/S(−)	8.71
N/S(−)	7.72

^aValues from ref. 9

^bValues from ref. 10.

CONCLUSIONS

We have studied the protonation state of the His-Cys catalytic diad in free papain and its SSMe derivative. We demonstrated that the pK_a values of catalytic residues are controlled by the cooperative effect of the active site polar local environment (pre-oriented dipoles) and the free energy of solvation of the partially water exposed target catalytic group in the active site. Based on our modeling simulations of all possible protonation states of the catalytic diad, calculated vs. experimental pK_a’s, we suggest a novel structure to the catalytic Cys25-His159 diad in free papain at neutral pH, in which both residues are protonated, rather than in the ion pair paradigm. The experimental pK_a 8.62 in free papain is now assigned to the equilibrium NH(+)/SH ⇌ N/SH. ¹H NMR chemical shift calculations demonstrated that the experimental CH_ε proton chemical shifts cannot differentiate between the two equilibria NH(+)/SH ⇌ N/SH and NH(+)/S(−) ⇌ N/S(⇌), and therefore cannot support the ion pair paradigm. Thus, it is very difficult to provide definitive experimental data for the protonation state of the Cys-His catalytic diad in free cysteine proteases. One possible solution could be very high resolution X-ray crystallography of free papain, in which protons position could be identified. Such high resolution 3D structures of serine proteases with proton positioning were previously determined for serine proteases.^68,69 Further application of the QM/SCRF(VS) approach to study the cysteine proteases mechanism is now underway.