Abstract
The ability of functional MRI to acquire data from multiple brain areas has spurred developments not only in voxel‐by‐voxel analyses, but also in multivariate techniques critical to quantifying the interactions between brain areas. As the number of multivariate techniques multiplies, however, few studies in any modality have directly compared different connectivity measures, and fewer still have done so in the context of well‐characterized neural systems. To focus specifically on the temporal dimension of interactions between brain regions, we compared Granger causality and coherency (Sun et al., 2004, 2005: Neuroimage 21:647–658, Neuroimage 28:227–237) in a well‐studied motor system (1) to gain further insight into the convergent and divergent results expected from each technique, and (2) to investigate the leading and lagging influences between motor areas as subjects performed a motor task in which they produced different learned series of eight button presses. We found that these analyses gave convergent but not identical results: both techniques, for example, suggested an anterior‐to‐posterior temporal gradient of activity from supplemental motor area through premotor and motor cortices to the posterior parietal cortex, but the techniques were differentially sensitive to the coupling strength between areas. We also found practical reasons that might argue for the use of one technique over another in different experimental situations. Ultimately, the ideal approach to fMRI data analysis is likely to involve a complementary combination of methods, possibly including both Granger causality and coherency. Hum Brain Mapp, 2009. © 2009 Wiley‐Liss, Inc.
INTRODUCTION
Understanding the temporal interactions between brain areas has clear importance for the understanding of information processing in the brain. Knowing whether activity in the supplemental motor area precedes that in the primary motor cortex during a motor task, for instance, has clear implications for theories about the functional organization of motor systems. To study such questions requires not only the use of data acquisition techniques with sufficient temporal resolution to identify time changes on scales appropriate to neural processing, and sufficient spatial resolution to distinguish brain areas of interest, but also the use of analysis techniques sensitive to these temporal and spatial differences. In humans, such studies have typically been performed using electroencephalography, magnetoencephalography, and related techniques, in which human whole brain recordings can be made with excellent temporal resolution at the expense of lesser spatial resolution. Functional MRI, on the other hand, provides a method for obtaining excellent spatial resolution at the expense of temporal resolution, due primarily to the low‐pass filtering effect of the hemodynamic response function (HRF). In the realm of temporal analysis, EEG and MEG are frequently able to take advantage of signal processing techniques dependent on excellent temporal resolution to an extent that may not be possible with fMRI. It nonetheless remains possible, however, to obtain differences in timing effects from the time series generated by fMRI data, as demonstrated by many authors [Bressler et al., 2008; Deshpande et al., 2009; Formisano and Goebel, 2003; Fuhrmann‐Alpert et al., 2007; Menon et al., 1998; Sack et al., 2008; Sun et al., 2004, 2005].
One recently‐introduced technique for determining temporal relationships in time series data is Granger causality, a method with a long history of applications in fields such as econometrics [Geweke, 1982, 1984; Granger, 1969]. The idea behind the method is relatively straightforward. For a time series of interest, a model of the data uses past time points from that same time series to predict future time points. These predictions hopefully match the data well, but invariably fit with errors that can be summarized by an error variance. Granger causality takes advantage of the fact that providing the model with more input may improve its predictions. Specifically, if augmenting the model by adding past time points from a second time series reduces variability in the prediction of the time series of interest, as measured by a reduction in the variance of the error, the second time series is said to be “Granger causal” for the first. The use of the term “causal” is based on the fact that the simple model predicts future time points, and thereby imparts temporal directionality.
Much previous work has gone into the use of Granger causality, including the aforementioned pioneering work in econometrics by Granger and others [Geweke, 1982, 1984; Granger, 1969] and, of more relevance here, in systems neuroscience, particularly in the analysis of local field potential (LFP) data from extracellular recordings [e.g., Bernasconi and Koenig, 1999; Brovelli et al., 2004; Chen et al., 2006a, b], and in EEG [e.g., Hesse et al., 2003]. The temporal resolution of these recordings was a significant boon to the analyses; thus, at face value, the need for temporal resolution would seem to be a significant hurdle for the application of this technique to functional MRI data. However, two early studies [Goebel et al., 2003; Roebroeck et al., 2005] demonstrated that Granger causality techniques could be applied to fMRI data. In each of these studies, the authors examined two subjects who performed a stimulus‐response mapping task. After demonstrating the efficacy of the technique on simulated data, the authors showed that the Granger analysis identified regions within visual, motor, and (broadly‐speaking) cognitive control areas whose activity varied with the task in which subjects were engaged. In two larger studies that followed, Abler and colleagues [ 2006] were able to identify Granger influence from auditory to motor cortices in a majority of the 11 subjects performing a simple task in which subjects squeezed a ball with either left or right hand based on the auditory cues “left” or “right”; and Rypma and colleagues [ 2006] showed that the influence of prefrontal cortex on other brain areas was greater for slow than fast learners during a speeded processing task. Subsequently, a number of interesting reports [e.g., Bressler et al., 2008; Stilla et al., 2007] have confirmed and extended the utility of Granger causality in fMRI analyses, including its ability to take advantage of multiple variables at once [Deshpande et al., 2009].
As is true for any new technique, however, understanding the use of Granger causality in fMRI analyses ideally involves a combination of two approaches. The first is to compare and contrast results of a Granger causality analysis with those from a complementary multivariate fMRI technique, as has been studied with electrophysiological data [e.g., Winterhalder et al., 2005]; another is to leverage such analyses on what has already been learned of the function of the underlying neural structures. In this article, we address both of these possibilities. We first take advantage of coherency, a method designed to characterize the relative timing of brain activity [Biswal et al., 1995; Sun et al., 2004, 2005, 2007], to provide a comparison for the results of the Granger analysis. In this method, itself also quite recent, transforming time series data from the time domain to the frequency domain segregates amplitude information from phase information; and this phase information permits calculation of a phase delay that can be used to determine the temporal offset between time series. Secondly, we choose to investigate each of these methods in the motor system, the neurophysiology of which has been well‐investigated and thereby provides a biological reference for our results. As Sun and colleagues [ 2005] argue, because electrophysiology [e.g., Ikeda et al., 1992] and previous neuroimaging [e.g., Weilke et al., 2001] suggest that the supplementary motor area (SMA) is active before primary motor cortex (M1) during performance of a motor task, and because SMA is known to be active in tasks requiring bimanual coordination and sequencing [e.g., Lee and Quessy, 2003], motor tasks provide a particularly compelling paradigm for fMRI studies interested in temporal effects.
Given that our goal is to compare these two methods, we expect both similarities and differences. In a baseline case—a linear system without feedback—the underlying mathematics demonstrate that the phase delay and the direction of Granger causality should correlate well. However, in a system with reciprocal connections, the results can diverge [Granger, 1969]. More specifically, Granger shows [Granger, 1969; page 434] that for a simple feedback system consisting of two time series, the cross spectra give rise to “coherency‐based” coherence and phase diagrams that are frequency‐dependent. He thus concludes that these diagrams are “clearly of little use in characterizing the feedback relationship.” On the other hand, the “Granger causality‐based” coherence and phase diagrams are constant with respect to frequency—i.e., their analytical expressions depend only on the parameters describing the feedback, not on the particular set of frequencies evaluated—and are thus robust to this complication.
Empirically, a case in which coherency‐based and Granger causality‐based analyses differ comes from the data of Brovelli and colleagues [ 2004] in a study of LFP recordings in the behaving macaque. They showed “no clear relation…between the time delay derived from the mean phase difference and the Granger causality,” suggesting that their recorded time series demonstrated feedback. On the other hand, as demonstrated by Roebroeck et al. [ 2005] in fMRI data, artifactual causality can be induced by the HRF and by subsampling of the BOLD activity (i.e., at the TR value). Therefore, they argued for a Granger causality measure that subtracts the influence in one direction from the influence in the opposite direction—a choice that eliminates the potential advantage of Granger causality over coherency in distinguishing bidirectional influences.
Other issues also arise. A distinction due to the implementation arises from the fact that Granger causality in most fMRI studies is implemented in the time domain [Abler et al., 2006; Goebel et al., 2003; Roebroeck et al., 2005; Rypma et al., 2006; but see Stilla et al., 2007], while coherency [Curtis et al., 2005; Miller et al., 2005; Sun et al., 2004, 2005] is implemented in the frequency domain. Therefore, comparing them in these domains is of practical importance in assessing different studies. These Granger causality values do not differentiate amplitude and phase, as coherency measurements do, and therefore do not distinguish between a shorter, stronger temporal influence and a longer, weaker temporal influence (Table I). One must also consider that temporal measures are sensitive to HRF shape, and that because coherency and Granger causality decompose the time series differently, the results with respect to HRF shape might also differ [Winterhalder et al., 2005]. Finally, the use of conditional analyses—the ability of each method to distinguish direct influences between two brain regions from those conditional upon the influence of a third area—has only been extended to fMRI data for coherence [Sun et al., 2004], although a multivariate analysis based on the directed transfer function and related to conditional Granger causality [Deshpande et al., 2009] has recently been developed. In extending Granger causality to include conditional effects, we may distinguish influences that have not yet been shown in fMRI with phase delay.
Table I.
Issues impacting the use of Granger causality and coherency
| a. Factors that may affect the correspondence between Granger causality and coherency |
| The presence of reciprocal connections between brain areas |
| Conflation of connection strength and temporal offset in the time domain |
| Differences in HRF shape between areas |
| The length of the time series available |
| b. Factors that will affect the use of both methods |
| Low‐pass filtering by the HRF |
| Sub‐sampling of the BOLD response |
| Ensuring that interactions between areas are consistent when the methods are applied |
To evaluate these methods, we performed a series of experiments. We first examined the performance of Granger causality and coherency on simulated data. Such data permitted us to manipulate parameters such as the coupling strength between time series, the latency of interactions between time series, and the data sampling rate (equivalent to the TR) to develop further intuition about the function of each technique. Next, in keeping with the early studies on Granger causality [Goebel et al., 2003; Roebroeck et al., 2005], we assessed both methods on fMRI data for single subjects performing a finger‐tapping task [Sun et al., 2005] to ensure that, as in these early studies, we could obtain plausible relationships between brain regions within an individual. Third, we extended these findings to a group of 14 subjects; and finally, we returned to both single‐subject and group fMRI data to address conditional Granger and coherence analyses to clarify the nature of the interregional interactions we uncovered. In so doing, we were able to investigate the relative advantages and disadvantages of each analytic technique, in a neurobiological system about whose workings we had previous knowledge, and to exploit the ability of functional MRI to evaluate the interaction of many brain regions at once.
METHODS
In this section, we first address the motor task itself and the initial steps in the fMRI data analysis, including preprocessing of the raw data and generation of regions of interest (ROIs) from the univariate analyses. We then address the two multivariate techniques, Granger causality and coherency, in depth. Both methods are initially discussed from a theoretical perspective, after which are described the details of the computer simulations and the application to fMRI data.
Subjects
As per Sun et al. [ 2005], 14 right‐handed subjects gave informed consent to participate in the study, per protocols approved by the University of California at Berkeley and in compliance with the Declaration of Helsinki. Four of the subjects were women; ages of the subjects varied between 19 and 29 years old (mean: 23.5). None of the subjects reported a history of neurological or psychiatric disorders, and none of them were taking any medications at the time of the study.
Experimental Paradigm
Details of the experimental paradigm are fully described in Sun et al. [ 2005]; here we briefly review the task (“random”) and rest conditions, which were presented in a pseudorandom order within a mixed block/event‐related schedule. In each task condition, subjects performed a series of motor movements under the guidance of a set of visual cues (Fig. 1). Each sequence of 8 successive visual cues was presented for a total of 5800 ms, resulting in a duration of 725 ms per cue. While a given cue was on‐screen, subjects were to respond with the corresponding finger. In the rest condition, only the central fixation cross was present; subjects were instructed not to perform or rehearse any of the motor sequences. All subjects completed a total of five 8‐min runs, each of which contained two presentations of four types of condition blocks in pseudorandom order. Only two of these condition blocks are examined here [the task/“random” and rest blocks; see Sun et al. [2007] for details about the other two conditions (the “novel” and “learned” blocks)]. All stimuli were back‐projected onto a custom screen using E‐prime presentation software (http://www.pstnet.com). Responses were collected with a pair of five‐fingered MRI‐compatible button boxes.
Figure 1.
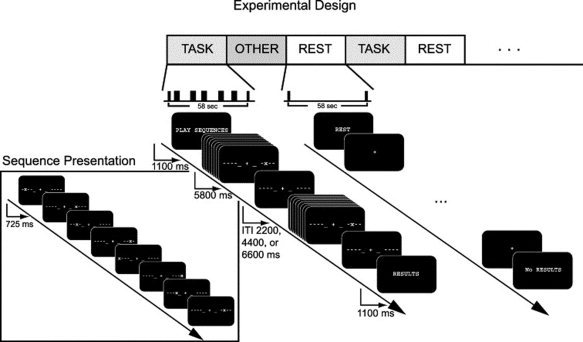
Experimental design: Subjects performed a motor task in which a cued sequence of eight finger taps (“Sequence Presentation”) was performed over 5800 ms. Each dashed line represents one of the subject's fingers (excluding the thumbs); when a “+” appeared at the corresponding position, the subject tapped that finger. A total of five finger‐tapping sequences, separated by randomized inter‐trial intervals of 2200, 4400, or 6600 ms, was performed during each task block. During the “rest” block, subjects were asked simply to maintain fixation. The conditions subsumed by the heading “other” were not analyzed in this article; refer to Sun et al. [ 2007] for details.
MRI Data Acquisition
Images were acquired with a 4‐T Varian INOVA MR scanner (http://www.varianinc.com) and a TEM send‐and‐receive RF head coil (http://www.mrinstruments.com). Functional images were acquired using a 2‐shot gradient‐echo echo‐planar image (GE‐EPI) sequence with a relatively short repetition time (TR) of 543 ms per half k‐space, during which time ten 5‐mm thick axial slices with a 0.5 mm inter‐slice gap were obtained from the top of the brain caudally. Obtaining one half k‐space per TR allowed us to increase our sampling rate at the potential expense of increased noise due to field inhomogeneities not incorporated by the subsequent interpolation to full k‐space. Images were normalized to the Montreal Neurological Institute (MNI) atlas space. Other details of the data acquisition can be found in Sun et al. [ 2005].
Preprocessing
After acquisition, functional images were reconstructed from k‐space using a linear time‐interpolation algorithm across shots of equal ordinal rank, based on sequences developed by Menon and colleagues [Menon et al., 1997] and previously published by our laboratory [Sun et al., 2004, 2005, 2007]. In this technique (J.Ollinger, personal communication), alternating halves of k‐space were acquired at each TR, and values for each half of k‐space at the intervening TR were linearly interpolated from the two neighboring time points. The resulting volumes were then corrected for slice‐timing skew using temporal sinc‐interpolation, and for movement using a rigid‐body transform. Finally, these steps were followed by spatial, but not temporal, smoothing with an 8 mm full‐width at half‐maximum (FWHM) Gaussian kernel. The task and rest conditions were analyzed separately. For each condition, and thus for each voxel in the brain, 10 data segments of 96 time points were obtained.
The issue of spatial smoothing requires particular comment. In the articles of Goebel et al. [ 2003] and Roebroeck et al. [ 2005], no spatial or temporal smoothing was performed before the Granger causality analysis. This approach avoids the potential introduction of further influences from neighboring voxels on the time series for a given voxel of interest. However, our data were simply too noisy for this approach. Without spatial smoothing, group results were significantly degraded (see Supporting Information Figure 1). For this reason, other studies that have investigated temporal influences based on this data set [Fuhrmann‐Alpert et al., 2007; Sun et al., 2005], and on which we base our use of coherency, have also relied on smoothed data. Consequently, we performed preliminary spatial smoothing, as described. Although we did not anticipate that smoothing should differentially affect coherency and Granger causality (e.g., Supporting Information Figure 1), this possibility has not been otherwise tested, given the above concerns about the unsmoothed data.
Univariate Analyses
Per standard protocols, univariate analyses were performed to identify regions with high task‐related BOLD activity. Regressors for the modified general linear model assigned each “task” sequence a unique onset time, modeled the duration of the sequence as a boxcar function of 5800 ms, and convolved these values with a canonical HRF [Josephs et al., 1997]. T‐statistics were applied to the resulting parameter (“beta”) values to identify ROIs for the subsequent analyses. Each of these ROIs met criteria for significant activation (set as P < 0.05, corrected for multiple comparisons by the family‐wise error [Nichols and Hayasaka, 2003]), and was chosen as per Sun et al. [ 2005]: within anatomical masks defining each area, the ROI consisted of the most significant voxel based on the univariate T‐maps of task‐related activity, plus all surrounding significant voxels within a 6 mm radius.
Multivariate Methods
Two different methods were used to examine networks of functional connectivity that were active in the task. We first address the mathematical underpinnings for Granger causality and coherency, then turn to the details of the implementations.
Granger Causality
For a given time t, the values at a set of points 1..n can be represented by a vector x = [x 1 , …, xn]T. Across time points 1..T, a series of vectors x(t) = [x 1(t), …, x n(t)]T generates a multivariate time series. To apply Granger causality techniques, one can model this time series by positing that the value of each vector x(t) is linearly related to the values of the vector(s) that preceded it. In other words, the vector time series can be modeled as a linear multivariate vector autoregressive (MVAR) process [Harrison et al., 2003].
 |
(1) |
where A(i) is a matrix of constants (refer to Bagarinao and Sato [ 2002] or Sato et al. [ 2006] for more complex implementation including time‐varying coefficients), p (the order) represents how far back in time we look to construct our model, and e(t) is a residual/noise vector that captures the portion of the data not fit by the MVAR. To fit the model, we need to estimate the value of both the matrix A and the parameter p.
Values for the A matrix can be determined via maximum likelihood estimation (MLE). To solve for a given time series, we construct the following matrix equation:
 |
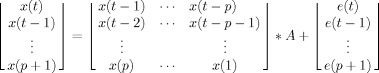(2) |
Without manipulating the equation, we substitute variable names for the above vectors and matrices.
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi x} = XA + {\bi e}$$ | (3) |
This system is in most cases significantly overdetermined. For the overdetermined system, we apply the MLE solution:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$$A = (X^T X)^{ ‐ 1} X^T {\bi x}$$ | (4) |
Once the A matrix is specified, the error terms are easy to calculate:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi e} = {\bi x} ‐ XA$$ | (5) |
where the errors e have covariance matrix Σ. Finally, we determine the optimal order p for the model. As a general rule, the model should account for as much of the variance in the data as possible, as simply as possible—i.e., the errors should be small, but the number of parameters should also be small. Consequently, the above MVAR model is fit for many different values of p, and we choose the model that minimizes the Schwartz Criterion:
 |
(6) |
where |Σ| is the determinant of the error covariance matrix for a given model, T is the number of time points used to construct the model (i.e., 96, in our example), p is the model order, and D is the model dimension. Given that we want to minimize S, the first term accounts for the fact that we want the model to fit our data well—i.e., lower values of ln(|Σ|) are better—while the second penalizes the model as its complexity increases.
To illustrate application of Granger causality, we take a simple case in which we desire to compare the time series x and y of two different voxels. We fit the following equations:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi x}(t) = \sum\limits_{i = 1}^p {{A}_ x} ({i}){\bi x}(t ‐ i) + {\bi e}_{\bi x} (t),\quad {\mathop{\rm cov}} [{\bi e}_{\bi x} (t)] = \Sigma _ x$$ | (7) |
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi y}(t) = \sum\limits_{i = 1}^p {{A}_y} (i){\bi y}(t ‐ i) + {\bi e}_{\bi y} ({t}),\quad {\mathop{\rm cov}} [{\bi e}_{\bi y} (t)] = \Lambda _ y$$ | (8) |
We then set \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}${\bi z}(t) = \left\lfloor {\matrix{ {\bi x} {(t)} \cr {\bi y} {(t)} \cr } } \right\rfloor$ and fit the model yet again:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi z}(t) = \sum\limits_{i = 1}^p {{\bi A}_z (i){\bi z}(t ‐ i) + {\bi e}_z (t),\quad {\mathop{\rm cov}} [{\bi e}_z (t)]} = \Omega = \left[ {\matrix{ {\Sigma _z } & C \cr {C^T } & {\Lambda _z } \cr } } \right]$$ | (9) |
The essence of the technique is the following: if including time series y(t) in our model of x(t), as we do by constructing z(t), helps us to improve the fit—or, in equivalent terms, helps us to reduce the variance of the error term—time series y(t) can be said to be “Granger causal” for time series x(t). Geweke [ 1982, 1984] capitalized on this model structure to define two measures describing how well the time series for one voxel predicts that of another:
 |
(10) |
In F x→y, for instance, if including time series x(t) in the model of y(t) improves the prediction, then the covariance term in the denominator will be less than that in the numerator, and F x→y will be greater than zero. The time series x(t) is therefore said to be “Granger causal” for time series y(t). Lastly, not all the influence of x(t) on y(t) will be Granger causal; some will be instantaneous. This influence is captured by the term F xy:
 |
(11) |
The total linear dependence F x,y is defined as the following sum:
 |
(12) |
For the remainder of the article, due to reasons discussed by Roebroeck et al. [ 2005] and described more fully below, we will focus on the Granger causality difference (F x→y−F y→x) for each segment, which we hereafter refer to as the Granger causality difference value (GCD). For the sake of terminology, we also refer to the Granger causality simultaneity value F xy as the “GCS.”
Conditional Granger Causality
One caveat with the analysis of Granger causality data is the interpretation of the influence measures. Take, for example, a data set in which time series x(t) helps to predict time series y(t). The etiology of this influence may truly be related to a direct effect of x(t) on y(t), but it could also be due to the fact that the processes represented by x(t) and y(t) receive a common input at different time lags. To address this problem, Geweke [ 1984] delineated the idea of so‐called “conditional” Granger causality, so defined because the interaction between the two time series of interest was “conditional” on a third. In other words, suppose that, in addition to time series x(t), with noise covariance Σx, and time series y(t), with noise covariance Λy, there is a third time series r(t) that may influence x(t) and y(t):
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi r}(t) = \sum\limits_{i = 1}^p {{ A}_r (i){\bi r}(t ‐ i) + {\bi e}_r (t)} ,\quad {\mathop{\rm cov}} [{\bi e}_{\bi r} (t)] = \Gamma _r $$ | (13) |
In this case, we set w(t) = [x(t) y(t) r(t)]T and s(t) = [x(t) r(t)]T, producing the following noise covariance matrices when we model the time series together:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$$\eqalign{ & {\mathop{\rm cov}} ({\bi e}_w ) = \Omega = \left\lfloor {\matrix{ {\Sigma _w } & {C_{xy} } & {C_{xr} } \cr {C_{yx} } & {\Lambda _w } & {C_{yr} } \cr {C_{rx} } & {C_{ry} } & {\Gamma _w } \cr } } \right\rfloor ,\,\,{\rm where}\,\Omega _{{\rm 1,2}} = \left[ {\matrix{ {\Sigma _w } & {C_{xy} } \cr {C_{yx} } & {\Lambda _w } \cr } } \right] \cr & {\mathop{\rm cov}} ({\bi e}_s ) = \Phi = \left[ {\matrix{ {\Sigma _s } & {C_{xr} } \cr {C_{rx} } & {\Gamma _s } \cr } } \right] \cr}$$ | (14) |
We can then derive, in analogy with the non‐conditional case, the following measures [Geweke, 1984]:
 |
(15) |
 |
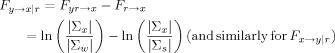(16) |
Intuitively, we perform the same type of operations as in the non‐conditional case, but always including the time series r(t) in our models.
Coherency
As discussed in detail by Sun et al. [ 2004, 2005], the principles behind coherency derive from the Fourier analysis of time signals. For a time series x(t), one obtains the frequency representation by applying the Fourier transform:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi x}(\lambda ) = \sum\limits_{t = 1}^T {{\bi x}(t){\bi e}^{2\pi i\lambda (t ‐ 1)/T} } $$ | (17) |
where λ equals the set of discrete frequencies [−T/2 … T/2]. This transform results in a series of sine waves x(λ) that are characterized by both an amplitude and a phase, rather than a series of time points x(t) that are characterized by different amplitudes; the data have not changed in any way other than their representation. The coherency R xy(λ) between two time series x(t) and y(t) is then calculated by computing the frequency‐by‐frequency product of their Fourier transforms x(λ) and y(λ), normalized by their respective power spectra (i.e., how much “amplitude” is present in each):
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi R}_{xy} (\lambda ) = {{{\bi x}(\lambda ){\bi y}(\lambda )^* } \over {\sqrt {{\bi x}(\lambda )^2 } \sqrt {{\bi y}(\lambda )^2 } }}$$ | (18) |
where y(λ)* refers to the complex conjugate of y(λ). The coherence C xy(λ) utilizes the amplitude component of the coherency to calculate the Fourier equivalent of covariance:
 |
(19) |
while obtaining the phase spectrum P xy(λ):
 |
(20) |
allows one to subsequently calculate a phase delay.
Conditional Coherence
Similarly to Granger causality, one can condition the coherence between two time series on a third. As per Sun et al. [ 2004], the coherence between two time series x(t) and y(t), conditioned on a third time series r(t), can be described as:
 |
(21) |
Simulations
As per Roebroeck et al. [ 2005], we generated simulated time series to model the interaction between two neural populations by constructing a bidimensional first‐order VAR process for which
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi A} = \left\lfloor {\matrix{ {0.82} & c \cr d \hfill & {0.82} \cr } } \right\rfloor ,\quad {\mathop{\rm cov}} [{\bi e}(t)] = \Sigma = \left\lfloor {\matrix{ 1 & 0 \cr 0 & 1 \cr } } \right\rfloor $$ | (22) |
where c and d are constants that determine how strongly to couple the two time series, and the constant 0.82 was chosen to be maximal without inducing instability for any condition (i.e., without producing a leading eigenvalue greater than 1). Because of computer memory limitations, the temporal resolution of each time step was limited to 10 ms, and the duration of each time series was set to 216 time steps, or 655.36 s, to facilitate the use of the fast Fourier transform for coherency calculations. This duration does not include an initial 2000 time steps that were discarded in order “to allow the system to enter a steady state, to introduce the delay, and to avoid boundary effects in subsequent filtering” [Roebroeck et al., 2005]. The coupling strength c from time series 2 to time series 1 varied from 0.0 to 0.5; the latency of this influence varied from 10 ms to 500 ms. For the case in which influence was bidirectional, d was set to 0.125. Next, each of the time series was convolved with a model of the HRF (via the function “spm_hrf.m” from SPM2, with time parameter 0.01 s). The resulting time series were normalized to zero mean and unit variance, after which 20% Gaussian white noise was added to simulate BOLD noise. Finally, the data were down‐sampled to simulate different TRs of 0.64 s, 1.28 s, 2.56 s, and 5.12s, and, after another renormalization, corrupted with 20% Gaussian white noise intended to represent measurement noise. Thus, despite the fact that 216 time steps were initially generated, the analyzed data comprised a significantly subsampled portion. Twenty different runs for each of the 64 combinations of connection strength, delay, and TR parameters provided the data for analysis with each of the multivariate techniques (Granger causality and coherency); a 3‐way analysis of variance was used to evaluate each technique, relative to those parameters. For coherency, analysis was restricted to frequencies from 0 to 0.15 Hz, in keeping with our previous work [Sun et al., 2004].
For the conditional coherence and Granger causality cases, we analyzed the analogous model for three time series, utilizing the following connectivity matrix:
| \font\abc=cmmib10\def\bi#1{\hbox{\abc #1}}$${\bi A} = \left\lfloor \matrix{ 0.9\,0.0\,c_{13} \hfill \cr 0.0\,0.9\,c_{23} \hfill \cr 0.0\,0.0\,0.9 \hfill \cr} \right\rfloor $$ | (23) |
where c 13 and c 23 represent the coupling strength from time series 3 to time series 1 and 2, respectively.
MRI Data
Granger causality, fMRI implementation
Preprocessing of the fMRI data gave rise to 10 sequences of 96 time points for each of the task and rest conditions. All sequences were then mean‐centered. Because most of these segments were not temporally contiguous, they were all analyzed separately. For each segment, we fit an MVAR separately for the seed ROI and for every other voxel in the brain. We removed from the analysis those voxels for which the GCS value was < 0.02, as Roebroeck and colleagues [ 2005] reported such voxels to be strongly identified with draining veins. Differences were averaged over the 10 segments to produce a single value for each voxel.
To define significant voxels in single‐subject, single‐condition maps, we compared the values for each condition to separate, “null‐distribution” values generated by bootstrapping. We generated a suitable “null” time series by transposing the first and second halves of the reference time series, thereby largely preserving the temporal dynamics of each time course but altering the relationship between time courses [Roebroeck et al., 2005]. Once the null distributions were generated for every voxel, the false discovery rate [Genovese et al., 2002] was applied to define significant activations, at a P < 0.05 level, for each subject in each condition. To compute multi‐subject maps, we applied a non‐parametric permutation analysis via SnPM99 [Nichols and Holmes, 2002] to the normalized single subject maps to account for the fact that the distribution of GCD and GCS values need not conform to Gaussian assumptions. Importantly, all calculations were performed for each subject in native space before normalizing. We ran SnPM99 using no confounding covariates, an exact number of permutations (16,384), variance smoothing of 8 mm, AnCova normalization, and no threshold masking. For the resulting GCS (but not GCD) multi‐subject maps, most voxels tended to be significant with respect to zero across subjects because the GCS measure is always zero or greater. To emphasize the structure in these multi‐subject maps (Figs. 7 and 10), we thresholded the set of significant voxels arbitrarily but consistently in all relevant figures. The corresponding unthresholded set of significant voxels can be found in Supporting Information Figure 2.
Figure 7.
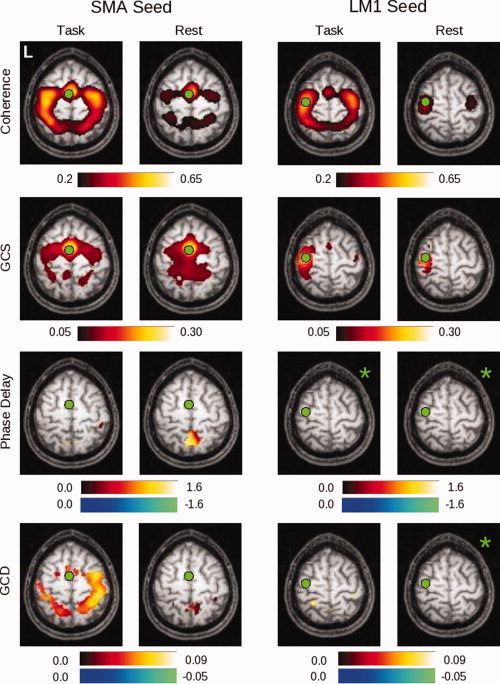
In this figure can be seen group maps thresholded at P < 0.05 (corrected) across all 14 subjects, for the range of values demonstrated by the associated color bars, for each of the analysis methods. The left two columns represent values produced for the SMA seed in both the task and rest conditions; the right two columns represent values obtained for the LM1 seed in both the task and rest conditions. Note that the slice is not identical for the two seeds (Z = 60 for the SMA seed, Z = 66 for the LM1 seed). Those images marked by a green asterisk (*) contained no voxels significant at P < 0.05, corrected. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Figure 10.
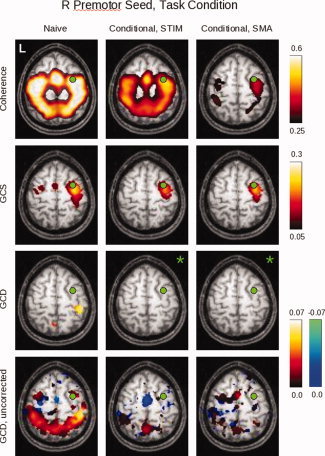
Here can be seen the results of the conditional analyses for group data obtained for the right premotor (PMC) ROI during task performance. The non‐conditional (“naive”) analysis is shown in the left column; the analysis conditioned on the stimulus is shown in the middle column; and the analysis conditioned on the SMA activity is shown in the right column (for slice Z = 58). Images in which no voxel reached a significance of P < 0.05, corrected, are denoted by green asterisks. Because such images only occur in the GCD analysis, the bottom row shows the same GCD maps for an uncorrected SnPM99 “pseudo‐P” value of 0.05 to reveal the underlying map structure. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Figure 2.
(A) Illustrates the behavior of the Granger causality difference value (GCD) as the different parameters within the simulated time series—coupling strength, latency, and sampling rate (or TR)—were varied, where each bar represents the average of 20 different time series with the same parameters but different noise inputs. Note that a particular Granger value does not uniquely specify the nature of the functional connectivity between the two time series. For a TR of 1.28 s, for example, a Granger value of ∼0.1 could represent a latency of 0.17 s with a coupling strength of 0.5, or a latency of 0.5 s with a coupling strength of 0.17. (B) Demonstrates the performance of the phase delay component of coherency on the same simulated data. Note that the phase delay measure is quite noisy when the simulated time series are uncoupled (i.e., coupling strength of zero).
To create the reference function for the conditional analyses, we generated two separate conditional time series. For the stimulus‐related conditional time series, we convolved an impulse train representing trial onset times with SPM's canonical HRF [Sun et al., 2004]. For the SMA time series, we averaged all time series within the ROI.
Coherency, fMRI implementation
After preprocessing, each of the 10 time segments was mean‐centered, windowed with a 4‐point split‐cosine bell, and concatenated with the other segments to produce a condition‐specific 960 time‐point series. Consequently, every voxel in the brain generated two concatenated time series—one for the task condition, and one for the rest condition.
The time series generated for the seed (ROI) region was then compared with every other voxel in the brain. Coherency values were obtained by applying a fast Fourier transform (Matlab 6.5, http://www.mathworks.com) to each, implemented via Welch's periodogram averaging method using a 64‐point discrete Fourier transform, Hanning window, and overlap of 32 points. Condition‐specific coherence and phase delay maps for the seed ROI were then computed using (1) the band‐averaged coherence [Sun et al., 2004] and (2) the average slope of the phase spectrum [Sun et al., 2005] within the 0–0.15 Hz frequency band.
Single‐ and multi‐subject maps for the coherency analysis were computed as described for the Granger causality case, with the following exceptions. First, the precision of the phase delay estimates for a single condition was derived by computing the root mean squared error (RMSE) of the linear fit to the phase spectrum over those values within the frequency band of interest (0–0.15 Hz). Only those areas were displayed for which the variance in the delay was less than 0.5 s with 95% confidence interval [Sun et al., 2005]. Second, to compute correlations between coherence results and those obtained by other methods for our simulations, we transformed the values by the inverse hyperbolic tangent (
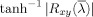) to generate an approximately normal distribution [Rosenberg et al., 1989]. Finally, for the resulting coherence (but not phase delay) multi‐subject maps, most voxels tended to be significant with respect to zero across subjects because the coherence measure ranges between zero and one. To emphasize the structure in these multi‐subject maps (Figs. 7 and 10), we thresholded the set of significant voxels arbitrarily but consistently in all relevant figures. The corresponding unthresholded set of significant voxels can be found in Supporting Information Figure 2.
RESULTS
To gain an intuition for the behavior of both Granger causality and coherency, we first investigated simulated data in which such variables as the coupling strength between regions could be explicitly manipulated. We next turned to fMRI data. We initially applied both methods to a representative subject, in keeping with previous reports [Roebroeck et al., 2005; Sun et al., 2004, 2005], before applying them to the group of subjects as a whole. These analyses were performed with respect to the bivariate case (i.e., the case in which the influence of additional time series was not considered). Finally, we repeated the analyses for a single subject and a group of subjects in the “conditional” case in which the influence of a third time series was explicitly addressed.
Simulations
To explore the Granger causality technique under different parametric conditions, we first generated multiple instances of time series from two simulated brain regions in which we systematically varied the strength of their connection (the “coupling strength” between them), the temporal delay of their connection (the “latency” between them), and the sampling rate (i.e., the TR). To facilitate comparison with previous data, we used a simple model similar to that of Roebroeck et al. ([ 2005]; refer to Methods for further explanation) and evaluated their proposed measure of Granger causality—the difference between the influence of region 1 on region 2 and the influence of region 2 on region 1 (i.e., F 1→2−F 2→1), which we subsequently refer to as the Granger causality difference, or GCD. To emphasize this connection to previous work, we first addressed both the behavior of the GCD measure itself and its correlation with the phase delay component of coherency. We then expanded our analysis to include other measures provided by Granger causality, including a measure of simultaneous influence (which we hereafter refer to as the Granger causality simultaneity measure, or “GCS”), and compared these measures to the two measures provided by coherency (i.e., coherence and phase delay) under additional conditions in which such variables as the shape of the HRF were manipulated. Finally, we attempted to account for the effect of additional influences on the two time series of interest, and to determine the amount of data necessary for our fMRI analyses.
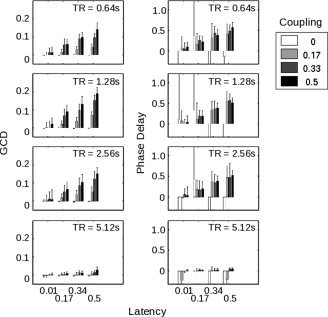
Results of the first GCD analysis are illustrated in Figure 2a. As is easily visible, the magnitude of the GCD varied strongly with the coupling between the two time series (P ≪ 10−5 by 3‐way ANOVA), as well as the latency (P ≪ 10−5) and the sampling rate/TR (P ≪ 10−5). All 2‐way and 3‐way interactions were also significant. Note that, independently of the coupling and delay parameters, the sampling rate, or TR, affected the GCD value; when the TR reached 5.12 s, the differential influence declined as the sampling became too coarse to allow identification of timing differences on the time scale of interest. On the other hand, a range of TRs from 0.64 s to 2.56 s produced robust results, and a spectrum of latencies and coupling strengths were detectable—though in all cases greater coupling strengths and longer latencies gave rise to stronger results.
These values were clearly related to those obtained by determining the phase delay of these time series (Fig. 2b). Across all latencies, and excluding the atypical sampling rate of 5.12 s, GCD and phase delay values were highly correlated (r = 0.33, P ≪ 10−5). Excluding trials in which the coupling strength was set to zero, this correlation between GCD and phase delay rose to 0.40 (P ≪ 10−5). This correlation might be stronger, were GCD values not also reflective of coupling strength (unlike the phase delay measure, which depended only on latency). For a TR of 1.28 s, for instance, Figure 2 shows that a GCD value of ∼0.10 could correspond to a coupling strength of 0.5 with a latency of 170 ms, or to a coupling strength of 0.17 with a latency of 500 ms.
To further assess the relationship of these techniques, both to simulated data and to each other, we modified the inputs and connections for the models. In Figure 3a, we show the variation of coherence, phase delay, GCS value, GCD value, and the separate components of the GCD measure for one of the baseline cases included in Figure 2. Coherence varied significantly with coupling strength (P ≪ 10−5 by ANOVA) but not with latency (P = 0.0942), whereas phase delay did not vary with coupling strength (P = 0.8509) but showed a strong relationship with latency (P ≪ 10−5) after exclusion of the extremely noisy values obtained when areas 1 and 2 were unconnected (i.e., a coupling strength of zero). In contrast, GCS varied significantly with both coupling strength and latency (P ≪ 10−5), as did GCD (P ≪ 10−5). When we decomposed the GCD value into its individual components, the influence of area 1 on area 2 mirrored the behavior of the GCD value. However, as previously discussed by Roebroeck and colleagues [ 2005], even with no neural connection from area 2 to area 1, spurious influence from area 2 to area 1 was seen in most conditions as a result of both the filtering of the neural responses by the HRF and the downsampling of the BOLD signal inherent in the discrete acquisition time (i.e., the TR).
Figure 3.
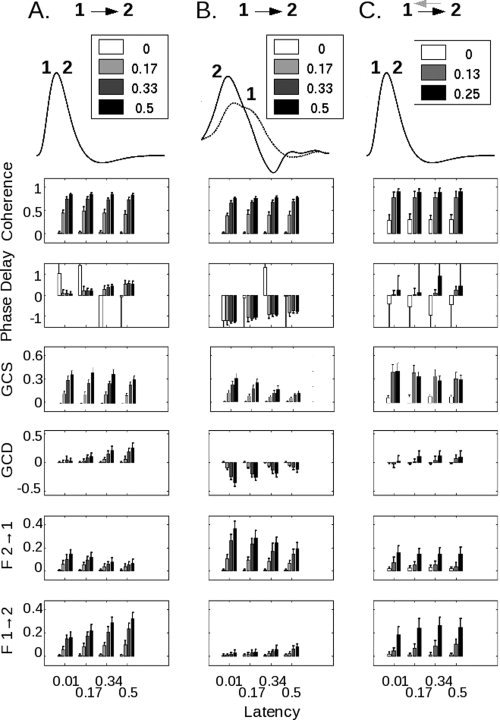
(A) In this case, a neural influence exists from area 1 to area 2, but not from area 2 to area 1. HRFs are identical (overlapping curves labeled 1 and 2). As the coupling strength (see inset) increases, the coherence increases. As the latency (see x‐axis) increases, the phase delay increases. GCS, as for coherence, varies primarily with coupling strength. GCD increases with both parameters, as do the individual components of GCD (F 1→2 and F 2→1). Note that even without any connection from area 2 to area 1, artifactual but statistically‐significant Granger influence can be noted as the latency of coupling increases. (B) In this case, the asymmetric neural influence from area 1 to area 2 remains unchanged, but the HRF for area 2 peaks earlier than that for area 1 (HRF data courtesy of Handwerker et al., 2004). Although the coherence value—which does not depend on HRF shape—remains unchanged, both the phase delay and Granger causality values reflect the shape of the HRF, not the underlying neural coupling. Moreover, as the coupling strength increases, the Granger causality value becomes progressively larger in the direction opposite the neural influence. (C) In the final case, there is a reciprocal influence between areas 1 and 2. The black arrow pointing from 1 to 2, as for (A) and (B), represents the coupling strength that is modified; the gray arrow from 2 to 1 represents a fixed coupling strength of 0.125 and a latency of 100 ms. As both the strength and the latency of the connection from 1 to 2 increase, the phase delay and GCD reflect a shift from negative to positive values.
In Figure 3b, we addressed the possibility that the HRFs from different brain regions might themselves be different in shape [Handwerker et al., 2004]. In this example, the neural influence was directed from area 1 to area 2, but the HRF for area 2 appears to peak earlier than that for area 1. Coherence remained unchanged, in keeping with the fact that it is insensitive to HRF shape [Sun et al., 2004]. However, there was a marked change in the phase delay. It was once again dependent only on latency (P ≪ 10−5), but now negative, suggesting that area 2 led area 1 and reflecting the relative timing of the HRFs rather than the underlying neural influence—even for coupling strengths (e.g., 0.5) that produced robust changes in coherence in the plot above, and robust phase delay differences in Figure 3a. For GCS, the relationship with coupling strength persisted, although there was clearly an interaction with latency as well (P ≪ 10−5). GCD maintained its relationships with both coupling and latency, but, as for phase delay, in the direction opposite the neural influence. Moreover, as the coupling between areas 1 and 2 increased, GCD became more negative—incorrectly suggesting that the influence from area 2 to area 1 was increasing, rather than that from area 1 to area 2. This relationship, while it reflects the change in coupling strength between the two areas, could potentially be misconstrued to represent a latency change. The measures of individual influence from area 2 to 1, and from area 1 to 2, confirmed the trend seen in the GCD value.
It is also possible that areas 1 and 2 might share a reciprocal coupling. In Figure 3c, the strength of the connection from area 1 to area 2 was varied in the presence of a constant coupling strength of 0.125 and latency of 100 ms from area 2 to area 1. In this case, both coherence and GCS were non‐zero at “zero” coupling strength because of the reciprocal connection from area 1 to area 2; and both phase delay and the GCD measure showed a change in the direction of influence from negative (i.e., directed from area 2 to area 1) to positive as the strength of the connection from area 1 to area 2 increased. The separate influence measures contributing to the GCD value shared a change with increasing connection strength. However, note that the data for F2 → 1 (Fig. 3c) in which a reciprocal connection was present, were not readily distinguishable from those for F2 → 1 (Fig. 3a) in which this connection was absent.
A separate question concerns the behavior of both Granger causality and coherency values in a larger network. In particular, for more than two areas, it is possible that the bivariate measures computed above could be confounded by network interactions. In one simple example, two areas could truly be coupled, or they could both only appear to be coupled because they received a common input. In either of these cases, a bivariate analysis might suggest a connection between the areas, even though, in the latter case, no such connection existed. To address this possibility, we examined a scenario in which two hypothetical ROI (“1” and “2,” in the Figure) and a third area (“3”) were variably connected. To simplify the analysis, areas were either coupled with a weight of 0.5 or not coupled at all; and the latency of the connection from area 3 to area 2 was always shorter (500 ms) than the latency of the connection from area 3 to area 1 (1000 ms). So‐called “naive” and conditional analyses were performed for GCD, GCS, and coherence, where the conditional analysis consisted of evaluating a relationship between two time series 1 and 2 while accounting for the effect of (or “conditioned upon”) the input from area 3.
Reassuringly, for both the naïve and conditional cases, the methods suggested a connection between areas 1 and 2 when a connection existed (Fig. 4, right two columns within every bar graph). Moreover, for all cases in which areas 1 and 2 did not receive a common input from area 3 (i.e., rows A–C), the naïve analyses correctly predicted their connectivity. However, in the case of interest—in which areas 2 and 1 were not connected, but both received a common, temporally‐offset input from area 3 (row D, left two columns in each graph)—the naïve methods both indicated significant coupling. Both Granger and coherence‐based conditional analyses correctly produced a significantly lower connectivity value.
Figure 4.
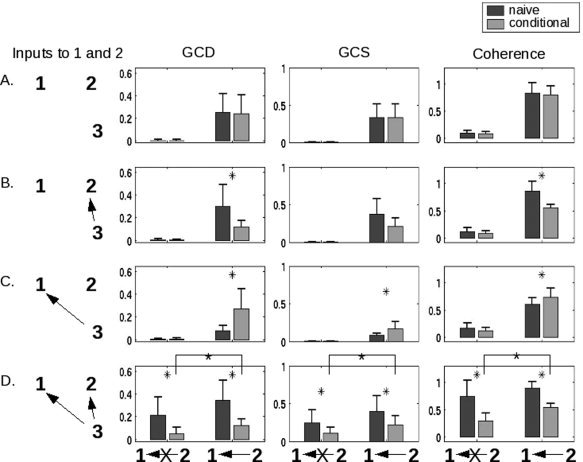
Performance of the methods in more complex networks, and the role of conditional values (for both Granger causality and coherence), are shown in this figure for a simulated interaction between two hypothetical areas “1” and “2”. The first column shows the connectivity from a hypothetical area labeled “3” that is capable of providing input to both 1 and 2. The second displays the results of a conditional GCD analysis, as compared with the non‐conditional (“naive”) analysis. The third and fourth columns plot results for conditional GCS and coherence analyses, respectively. Areas 1 and 2 are either uncoupled or coupled as indicated underneath each of the three right columns. In all cases, the presence of an arrow indicates a connection strength of 0.5; the absence of an arrow (or an arrow with an “X” through it) indicates no connection. The network is configured such that area 2 influences area 1 with a latency of 500 ms, area 3 influences area 1 with a latency of 1000 ms, and area 3 influences area 2 with a latency of 500 ms. By designing the latencies in this way, we see in row D that both techniques—Granger causality and coherence—show a link between areas 1 and 2 even when there is no connection between them (dark gray bars, leftmost in each graph). Using a conditional analysis significantly reduces this effect, but does not completely eliminate it. All comparisons between naïve and conditional bars marked by an asterisk are significant (P < 0.05, Wilcoxon rank sum test). Additionally, the differences between conditional values in row D (noted by the crossbars) are significant.
Importantly, these declines were relative. The values obtained in the conditional case for GCD, GCS, and coherence remained significantly different from zero, and thus, were more useful in comparison to the naïve analysis. This result was to be expected: as discussed by both Roebroeck and colleagues [ 2005] and Sun and colleagues [ 2004], such factors as low‐frequency filtering by the HRF and subsampling of the data lead to artifactual changes in connectivity that are unlikely to be directly addressed by this conditional approach. On the other hand, if all three areas were connected (row D, right two columns in each graph), the conditional analysis reduced the Granger and coherence values to a significantly lesser extent. Finally, one interesting aspect of these data is that the conditional analysis need not always reduce the Granger/coherence values; in the case in which area 1 received input from both areas 2 and 3, but areas 2 and 3 were not connected (row C, right two columns), the conditional analysis produced an increased connectivity value.
One final question concerns the amount of data required to apply these techniques reliably. Coherency analyses, for example, might require more time points to successfully model the low frequencies inherent in the hemodynamic response, a finding that would potentially render the current implementation of Granger causality more advantageous for shorter data sets. Figure 5 represents the results of such an analysis for simulated data sets ranging in size from 32 data points to 512 data points, across three different values of the sampling rate (TR). Coherence, GCS, and GCD appear most robust to shorter time series, while phase delay is more sensitive to the number of data points (but refer to Lauritzen et al. [ 2008] for potential methodological improvements in the phase delay measure). In the fMRI analyses below, a total of 960 data points permitted us to provide an asymptotic comparison of these methods.
Figure 5.
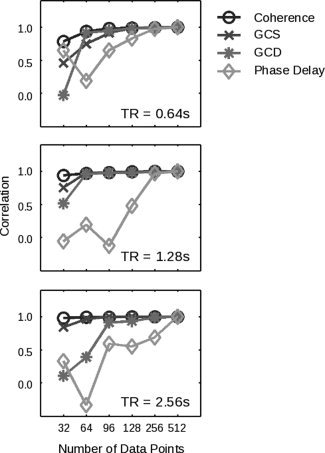
The performance of both coherency and Granger causality varies with the number of data points. On the y‐axis is shown, for each method and number of data points, the correlation of the values obtained across all nonzero coupling strengths and latencies with the data obtained for the same method in the case of 512 data points. (As a consequence, all methods show a correlation of one by construction at point 512.) Results are shown for three different TR values. In each case, phase delay requires more data before converging to asymptotic performance.
fMRI Data, Single Subject
To address the performance of Granger causality and coherency on BOLD data, and to ensure that we could obtain meaningful results in individual subjects, we examined data from a single subject performing the motor task described in Figure 1. Figure 6 presents the FDR‐thresholded maps in native space for subject 212 in the “task” compared to the “rest” condition. In the coherence map, high values (in yellow) show those areas that are coherent with the reference seed area—in this case, either the SMA or left primary somatomotor cortex (LM1). As expected, this sequential finger‐tapping task activates a number of regions within the motor network, including presumptive SMA and pre‐SMA, premotor cortex (PMC), primary somatomotor cortex, and posterior parietal (PPC) areas [Sun et al., 2004, 2005]. In the rest condition, note that the coherence values do not all become subthreshold in these areas; however, the number of suprathreshold voxels is smaller. As expected, a similar set of brain areas is coherent with the LM1 seed. A similar but more restricted set of strongly‐active regions is identified by the GCS analysis. This result may stem from the fact that GCS is sensitive (as the name implies) to simultaneous influences; as the latency between regions changes, these influences might better be captured by GCD. Coherence, however, is the spectral equivalent of covariance in the time domain, and thus captures relationships across multiple latencies.
Figure 6.
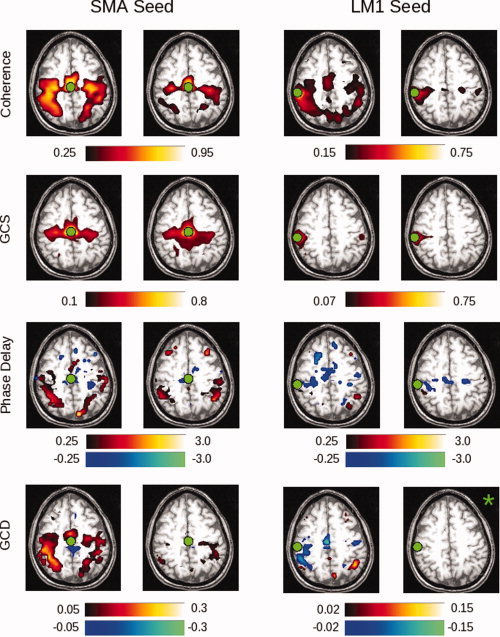
Shown in the two left columns are the results of native‐space exploratory analyses, using a seed in the SMA, for subject 212. The two right columns demonstrate results for a left M1 (LM1) seed. Areas shaded in “hot” (red–yellow) hues represent positive values; areas shaded in “cool” (blue–green) hues represent negative values. Thus, activity in a red voxel in the GCD or phase delay maps occurs after (i.e., lags) activity in the seed region. Green circles indicate the location of the SMA or LM1 ROI. Each “task” and “rest” map is created by computing the false discovery rate for a P‐value of 0.05, as determined by comparing with the null distribution (described in Methods). Those images marked by a green asterisk (*) contained no voxels significant at P < 0.05, corrected. Among other findings, the maps demonstrate that activity in the SMA leads, rather than lags, activity in the left M1 seed region. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The GCD analysis applied to the SMA seed identifies a similar network of areas. Cool/blue colors signify that those voxels are Granger causal for the seed—i.e., that those voxels are sources of influence onto the seed—while hot/red colors signify the opposite—i.e., that the seed is a source of influence onto (is “Granger causal for”) those voxels. Consistent with animal studies (e.g., [Ikeda et al., 1992]), the SMA is Granger causal for the posterior regions identified by the coherence analysis (bilateral primary somatomotor cortex and PPC). Note that the direction of this influence changes appropriately when the seed changes. For a left M1 seed, not only the SMA activity, but also activity from other areas within the precentral gyrus and central sulcus, appear to influence activity in LM1. Consistent with our simulations, the GCD values may correlate with, but are not determined by, the coherence values. With use of the left M1 seed, for example, the coherence values are qualitatively similar to those obtained with the SMA seed, while the GCD values are not.
The phase delay maps demonstrate the relative latency between the SMA and all other brain regions. As for the Granger maps, cool/blue colors indicate voxels that lead the reference region, whereas hot/red colors indicate voxels that lag the reference region. The results are similar, though not identical, to those of the GCD analysis. Activity in the SMA leads that in the primary somatomotor cortices, while activity in LM1 appears to lead activity in right PPC, at least in the task condition.
fMRI Data, Group
These relationships also appear to hold for group data across 14 subjects. Figure 7 presents the normalized, group‐averaged data for the SMA (left columns) and LM1 (right columns) seeds. The results for the coherence analysis confirm the initial indications from the single subject maps shown in Figure 6. A network of areas, including the SMA, bilateral premotor (PMC), bilateral primary somatomotor cortex, and bilateral PPC, are active during performance of the motor task, while fewer significant voxels are seen during rest. A similar, though not identical, pattern is seen for GCS.
For the SMA seed, the GCD analysis shows a significant influence originating from the SMA on posterior (PMC, M1, PPC) areas, and the phase delay analysis confirms that the SMA leads an area in the right post‐central gyrus. Interestingly, the number of suprathreshold voxels is much larger for the GCD map than for the phase delay map, potentially consistent with the fact that Granger causality also reflects coupling strength. For the LM1 seed, on the other hand, GCD shows only a significant influence from LM1 onto the left PPC. The resting maps, and both the task and rest maps for the phase delay analysis, did not give rise to any significant voxels for this seed (denoted by the green asterisks in the Figure).
For the GCD and phase delay analyses for the LM1 seed in Figure 7, the limited number of significantly active areas within both the task and rest conditions raises the question as to whether the group maps actually reflect the differences seen in the single subject map of Figure 6, or, alternatively, whether the single subject map is not representative of the group behavior. By relaxing the uncorrected significance level from P < 0.05 (corrected, via SnPM99) to P < 0.05 uncorrected (from a pseudo‐t map provided by SnPM99) in Figure 8, the underlying structure of the map becomes clearer. In keeping with the single‐subject findings, the group maps demonstrate preceding activity in the SMA, and the subsequent activity in the bilateral PPC also appears.
Figure 8.
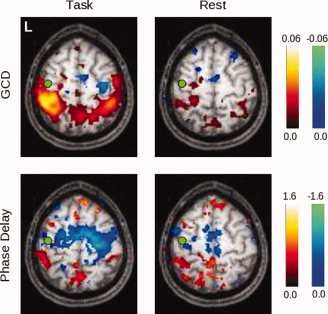
Here the threshold on significant voxels is relaxed to P < 0.05 (uncorrected), to show the pattern of values obtained for both GCD and phase delay for the left primary somatomotor cortex (LM1) seed. In the task condition, there is a non‐significant tendency for activity in the SMA, the right premotor, and the right primary somatomotor cortex to be Granger causal for activity in LM1, while the opposite is true for activity in the bilateral posterior parietal cortices. The phase delay map is grossly concordant, though it appears to be more sensitive to BOLD signals that precede those in LM1. At rest, these timing differences are less prominent. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
fMRI Data, Single Subject, Conditional Analysis
To assess the extent to which the bivariate measures might be dependent on unexamined inputs within a larger network, we next applied conditional coherence and Granger causality methods to the task period in our empirical data for subject 212 for a right premotor cortex (right PMC) ROI. This ROI was chosen because the preceding maps suggested that it both received leading and provided lagging influences, and we suspected that the existence of both types of connections would render the maps most sensitive to differences uncovered by the conditional analysis. In Figure 9, the naïve results (left column) once again highlight the network of motor areas involved in this subject's performance of the task. The coherence map appears comparable with that for the SMA seed in Figure 5, while the results for GCS are once again similar to those of coherence. The naïve GCD analysis confirms that the right PMC is influenced by activity in the area of the SMA and right precentral gyrus, and itself influences activity in the bilateral posterior parietal cortex.
Figure 9.
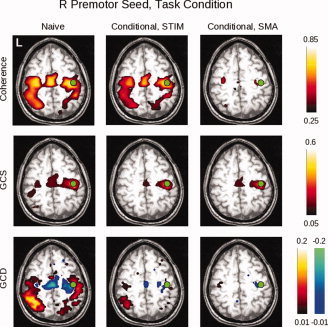
Here can be seen the results of the conditional analyses of the data obtained for the right premotor (PMC) ROI for subject 212 during task performance. The non‐conditional (“naive”) analysis is shown in the left column; the analysis conditioned on the stimulus is shown in the middle column; and the analysis conditioned on the SMA activity is shown in the right column. The slice was chosen to include the right PMC ROI (green circles). For the coherence analysis, conditioning on the stimulus does not markedly change the magnitude of the response, consistent with the fact that there remains significant coherence between motor areas even when no stimulus is present (i.e., in the rest condition); whereas conditioning on the SMA removes much of the coherent activity. These differences are less apparent for GCS. For GCD, the “leading” influence of the SMA on the right PMC remains after conditioning on the stimulus. Conditioning on the SMA, on the other hand, leaves small lagging and leading influences with bilateral motor/pre‐motor areas. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Conditioning on either the stimlus or SMA activity differentially affects these results. When conditioned on the stimulus, the coherence map remains relatively unchanged, in keeping with the findings of Sun and colleagues [ 2004]—i.e., as they showed, there remains significant coherence between motor areas even at rest, arguing that removal of the stimulus contribution would have a minimal effect. The GCS analysis shows a decline in connectivity of the R PMC seed with the homologous area on the left; and in the GCD map, a leading influence in the area of the SMA and adjacent premotor cortex persists, while the extent of influence onto more posterior areas declines. When conditioned on activity in the SMA ROI, however, there is a marked decline in the coherence values, again consistent with the existing literature on the role of the SMA in motor systems; a relative lack of change in the GCS values; and a loss of influence from R PMC on more posterior areas.
fMRI Data, Group, Conditional Analysis
The group conditional maps (Fig. 10), thresholded at P < 0.05 (corrected) via SnPM99, show broadly similar results. The coherence findings, interestingly, continue to demonstrate coherent activity when conditioned on the stimulus. The conditional GCS maps again identify a region surrounding the seed itself, while the conditional GCD maps show very little influence that reaches statistical significance—limited to areas in the right post‐central gyrus and left precuneus. However, with the level of significance relaxed to P < 0.05, uncorrected (Fig. 9, bottom row), the GCD map emphasizes the leading influence of the SMA when conditioned on the stimulus. When conditioned on the SMA, it produces a less structured map in which there are fewer clearly leading anterior and lagging posterior voxels.
DISCUSSION
In this study of a motor task, we demonstrated that two multivariate methods with components sensitive to temporal differences—Granger causality and coherency (including GCD and phase delay estimates, respectively)—produced complementary results when applied to simulated data. Whereas the GCD measure was more sensitive to both coupling strength and latency, the two components of coherency (coherence and phase) segregated the former and the latter, respectively. We demonstrated that differences in the shape of the HRF could obscure the underlying neural dynamics, and that such timing changes could be potentially misinterpreted by both methods. Moreover, in fMRI data the use of the GCD measure, while advantageous in some ways, might also diminish the theoretical advantages of Granger causality in distinguishing reciprocal or feedback connections; whereas the phase delay measure of coherency required more data to reach asymptotic values. Reflecting their bivariate nature, both GCD and coherency measures could be inaccurate when two regions within a larger network were considered, unless further steps—such as conditional analyses—were undertaken. Despite these caveats, when applied to experimental BOLD data, both GCD and coherency analyses were shown to be sensitive to latency differences in motor areas that remained even when time series data were conditioned on the stimulus.
Theoretical Considerations and Simulations
Independently of the underlying neural connectivity, Granger causality and coherency share a conceptual and mathematical foundation. As discussed in the introduction, phase delay and Granger causality produce consistent representations of the timing differences, provided the system is linear. On the other hand, phase delay and Granger causality will differ in the case with reciprocal/feedback connections, as has been shown both analytically [Granger, 1969] and, with LFP data, experimentally (e.g., [Brovelli et al., 2004]). The simulations in this article with bidirectional connections (Fig. 3c) demonstrated, however, that these differences with respect to fMRI data are possibly more apparent than real. Additionally, the need to use the GCD subtraction measure to determine the dominant direction of influence—i.e., to reduce artifactual unidirectional influence induced by the temporally‐prolonged HRF and subsampled BOLD response [Roebroeck et al., 2005]—decreased the ability of the Granger technique to detect reciprocal but lesser connections. As a result, in our hands GCD and phase delay both reflected the direction of dominant influence, consistent with the empirical results obtained from their application to the fMRI data.
Are there other ways to distinguish these two methods? They cannot be distinguished by a dependence, or lack thereof, on HRF shape—both GCD and phase delay depend on the form of the HRF. As shown in Figure 3b, both methods incorrectly determined the direction of neural influence when an epiphenomenal difference in the timing of the HRF between two areas was present. In this case, the ability of coherency to distinguish coupling strength from latency might provide a relative advantage. As the coupling strength between two areas increases, the phase delay remains constant for a given neural latency. It only becomes more positive (i.e., more reflective of the underlying neurophysiology) as the latency increases. The fact that GCD reflects both coupling strength and latency renders it more negative as coupling strength increases, a change that could be misinterpreted if ascribed to latency changes. In most experimental data, it will be unclear whether the underlying coupling, latency, or both are changing between ROI across two task conditions, and the model suggests that coherency might better clarify these relationships.
Another caveat that applies equally to both methods, and consequently does not distinguish them at face value, is the fact that both GCD and coherency are bivariate measures that depend on analysis of time periods—whether in a block, mixed, or event‐related design—in which consistent temporal relationships exist between brain ROI. They are thus susceptible to common but unconsidered influences, a problem long identified (e.g., [Perkel et al., 1967]). We have also demonstrated that conditional GCD can reduce the influence of additional inputs onto an area of interest. The conditional coherence shows a similar pattern. Thus, the ability to apply conditional Granger causality to fMRI data might be an advantage, although a future implementation/validation of conditional phase delay for BOLD data could certainly occur. Additionally, recent articles in which a multivariate version of Granger causality was used between specified ROIs [Deshpande et al., 2009; Stilla et al., 2007] point to the expansion of this technique.
Finally, the determination of statistical significance for each method raises potentially distinguishing issues. For coherency, significant values can be determined analytically by applying a Z‐transform to the coherence, and examining the root mean square error of the linear fit to the unwrapped phase spectrum. For Granger causality, to assess the significance of the GCD value, a common approach is to consider bootstrapped significance values that are determined by generating a number of null time series. (Parametric Granger causality approaches, such as those used by Rypma and colleagues [ 2006] and Bressler and colleagues [ 2008], were not developed for the difference measure). The choice of these null time series can be arbitrary. Ideally, a null time series should preserve as much of the richness of the original time series as possible (e.g., timing and amplitude information) while removing the relationship of that time series to another. Roebroeck and colleagues [ 2005] opted to generate null series by switching the two halves of the original time series, which is the approach we follow here; while Stilla et al. [2008] transformed to frequency space, randomized phase, and transformed back to the time domain. It remains unclear what approach will ultimately be preferable; but it might be considered a relative advantage of coherency to avoid this complication.
fMRI Results
As predicted from the simulations, which suggested that differences between GCD and phase delay might be minimized in BOLD data, the GCD and phase delay measures agreed quite well, both for individual subjects and for the group. As noted in Figures 6 and 8, for instance, GCD and phase delay tended to identify the same direction of influence for different areas. To the extent that the GCD maps tended to show more suprathreshold voxels, they may reflect the contribution of coupling strength to GCD values; and we noted that across both individual and group data, the most robust findings—i.e., the most suprathreshold findings—were for coherence.
A weakness of this study (and possibly of others that attempt to measure timing differences in fMRI data) is that when the data were collected, no independent measure of individual HRFs was obtained, as in Handwerker et al. [ 2004]. Of course, it is likely impossible to truly “isolate” HRFs, as even the simple tasks used by Handwerker et al. [ 2004] undoubtedly give rise to interactions between regions of (in their case) the motor system. As our simulations have shown, HRFs of differing shapes (taken from Handwerker and colleagues) can give rise to spurious GCD and phase delay differences, potentially even opposite to those of the underlying neurophysiology.
Nonetheless, even without these independent HRF data, there are measures to reduce this possibility of error. One is to examine areas for which independent timing information is available, as we have done here. In the motor system, for example, other studies in primates and humans have shown a leading influence of SMA on posterior areas, as described above. This knowledge provides a hypothesis, but obviously does not remove the possibility of a coincidental match between hypothesis and HRF timing that does not reflect neural activity. A second approach is to examine group data. Assuming that there is no reliable relationship in HRF shape between different brain areas across subjects, consistent findings should reflect neural rather than HRF differences. Finally, the application of independent modalities to measure timing (e.g., MEG and EEG, possibly obtained simultaneously with fMRI data) may be useful in establishing the accuracy of these fMRI‐based techniques.
In keeping with the first two approaches, we identified directional interactions between areas that, based on previous work, we hypothesized to be present a priori. More anterior areas such as the SMA exerted a leading influence on more posterior areas, including the primary somatomotor cortices, and this influence was reflected by either a positive or a negative voxel value depending on whether the SMA or LM1 was chosen as the seed ROI. These relationships appeared to hold true for both single subject and group data, in keeping with neurophysiology results. It remains to be seen whether studies similar to that of Handwerker et al. [ 2004] will find consistent relationships between HRFs from different areas across subjects. [Handwerker et al.'s [ 2004] Figure 7 suggests that this possibility might exist, in that the relative time‐to‐peak between different areas (e.g., M1 and SEF) showed a significant correlation across subjects]. If so, this study and other studies in which group Granger causality or phase delay maps have been produced will need to be re‐evaluated in that light.
As for the exclusion of inputs from other areas—an ability that distinguishes both conditional Granger causality and conditional coherence—the BOLD data confirmed that such analyses can be fruitful. Conditioning the coherence analysis for a right premotor seed on the stimulus does not markedly decrease the observed interactions of this seed with the rest of the brain; if anything, the coherence appears more widespread, arguing (as suggested by the simulations of Fig. 4b) that influences from the stimuli and the SMA are both contributing to right premotor interactions with more posterior areas. Conditioning on the SMA supported the idea (as suggested by the resting connectivity) that the intrinsic right premotor connectivity with posterior regions was modulated by the stimulus but more directly linked to the SMA. The conditional GCD map was consistent with this idea; conditioning on the stimulus or the SMA removed much of the right premotor influence on posterior areas, and the magnitude of this influence appeared to be less when conditioning on the SMA. Of course, conditional analyses cannot determine whether the residual coherence or conditional Granger causality is not due to yet another spurious connection produced by input from an unexamined brain area, but the initial connectivity analysis (and knowledge of the underlying neurophysiology) can certainly serve as a guide for other potentially relevant sources.
Summary
Given the above simulation and data findings, how should a researcher best decide whether to apply Granger causality or coherency techniques to his/her data? In our hands, the methods gave converging results that reflected both their analytical underpinnings and the nature of the BOLD signal. Nonetheless, that GCD might reflect both coupling strength and latency information should be taken into account; if the goal is to find areas whose activity predicts the activity in other areas, and conditional analyses are important, it may be most useful. On the other hand, if separating coupling strength and latency differences is important, and provided that the amount of data is not limiting, coherency may be more appropriate. In the data we address here, we show that the two methods are more similar than different. Both methods point to the existence of a gradient of temporal influence within known motor areas that is consistent with the known neurophysiology.
Of course, further work to compare and validate both these and the expanding number of multivariate fMRI techniques will be helpful in allowing researchers to best choose the appropriate technique(s) for future studies; future directions for this work are many. Given other methodological issues that can potentially influence the results, including techniques for noise reduction/preprocessing, the possibility for the incorporation of nonlinear terms in the Granger causality models, and methods for generation of group maps, further studies will very likely improve on our results. As mentioned above, comparisons to related techniques such as partial directed coherence and the directed transfer function [e.g., Eichler, 2006; Winterhalder et al., 2005; Kaminski et al., 2001] have not been addressed in this article, but are certainly worthy of investigation and have recently been applied to fMRI data by Stilla and colleagues [ 2007] and Deshpande and colleagues [ 2009]. Similarly, Lauritzen and colleagues [Lauritzen et al., 2008] have made efforts to improve the reliability of the phase delay calculation. Other work could also profitably explore how the use of the exploratory techniques we used could guide the use of more directed, hypothesis‐driven methods in data analysis. Regardless, taking advantage of the temporal information in fMRI data, whatever the form of the analysis techniques, can only add to the utility of fMRI in systems and cognitve neuroscience research.
Supporting information
Additional Supporting Information may be found in the online version of this article.
Supplementary Figure 1. Shown here is a direct comparison of representative slices from both a single subject and from the group of subjects for both spatially smoothed and unsmoothed time series data derived from an SMA seed region, as derived by T‐test across subjects and thresholded at p < 0.001, uncorrected. For the individual subject data, spatial smoothing changes the character of the map more markedly for phase delay than for GCD, in both eliminating some clusters and demonstrating others more robustly. For the group data, both measures are significantly affected by smoothing, with the pixilated appearance of the unsmoothed data replaced by a map that highlights motor and sensory regions.
Supplementary Figure 2. Shown here are all significant values, without thresholding, for both the group coherence and GCS maps shown in (A) figure 7 and (B) figure 10.
REFERENCES
- Abler B,Roebroeck A,Goebel R,Höse A,Schönfeldt‐Lecuona C,Hole G,Walter H ( 2006): Investigating directed influences between activated brain areas in a motor‐response task using fMRI. Magn Reson Imaging 24: 181–185. [DOI] [PubMed] [Google Scholar]
- Bagarinao E,Sato S ( 2002): Algorithm for vector autoregressive model parameter estimation using an orthogonalization procedure. Ann Biomed Eng 30: 260–271. [DOI] [PubMed] [Google Scholar]
- Bernasconi C,Koenig P ( 1999): On the directionality of cortical interactions studied by structural analysis of electrophysiological recordings. Biol Cybern 81: 199–210. [DOI] [PubMed] [Google Scholar]
- Biswal B,Yetkin FZ,Haughton VM,Hyde JS ( 1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34: 537–541. [DOI] [PubMed] [Google Scholar]
- Bressler SL,Tang W,Sylvester CM,Shulman GL,Corbetta M ( 2008): Top‐down control of human visual cortex by frontal and parietal cortex in anticipatory visual spatial attention. J Neurosci 28: 10056–10061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brovelli A,Ding M,Ledberg A,Chen Y,Nakamura R,Bressler SL ( 2004): Beta oscillations in a large‐scale sensorimotor cortical network: Directional influences revealed by Granger causality. Proc Natl Acad Sci USA 101: 9849–9854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y,Bressler SL,Ding M ( 2006a) Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J Neurosci Meth 150: 228–237. [DOI] [PubMed] [Google Scholar]
- Chen Y,Bressler SL,Knuth KH,Truccolo WA,Ding M ( 2006b): Stochastic modeling of neurobiological time series: Power, coherence, Granger causality, and separation of evoked responses from ongoing activity. Chaos 16: 026113. [DOI] [PubMed] [Google Scholar]
- Curtis CE,Sun FT,Miller LM,D'Esposito M ( 2005): Coherence between fMRI time‐series distinguishes two spatial working memory networks. Neuroimage 26: 177–183. [DOI] [PubMed] [Google Scholar]
- Deshpande G,LaConte S,James GA,Peltier S,Hu X ( 2009): Multivariate Granger causality analysis of fMRI data. Hum Brain Mapp 30: 1361–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler M ( 2006): On the evaluation of information flow in multivariate systems by the directed transfer function. Biol Cybern 94: 469–482. [DOI] [PubMed] [Google Scholar]
- Formisano E,Goebel R ( 2003): Tracking cognitive processes with functional MRI mental chronometry. Curr Opin Neurobiol 13: 174–181. [DOI] [PubMed] [Google Scholar]
- Fuhrmann‐Alpert G,Sun FT,Handwerker D,D'Esposito M,Knight RT ( 2007): Spatio‐temporal information analysis of event‐related BOLD responses. Neuroimage 34: 1545–1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genovese CR,Lazar NA,Nichols T ( 2002): Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage 15: 870–878. [DOI] [PubMed] [Google Scholar]
- Geweke JF ( 1982): Measurement of linear dependence and feedback between multiple time series. J Am Stat Assoc 77: 304–324. [Google Scholar]
- Geweke JF ( 1984): Measures of conditional linear dependence and feedback between time series. J Am Stat Assoc 79: 907–915. [Google Scholar]
- Goebel R,Roebroeck A,Kim DS,Formisano E ( 2003): Investigating directed cortical interactions in time‐resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magn Reson Imaging 21: 1251–1261. [DOI] [PubMed] [Google Scholar]
- Granger CWJ ( 1969): Investigating causal relations by econometric models and cross‐spectral methods. Econometrica 37: 424–438. [Google Scholar]
- Handwerker DA,Ollinger JM,D'Esposito M ( 2004): Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage 21: 1639–1651. [DOI] [PubMed] [Google Scholar]
- Harrison L,Penny WD,Friston K ( 2003): Multivariate autoregressive modeling of fMRI time series. Neuroimage 19: 1477–1491. [DOI] [PubMed] [Google Scholar]
- Hesse W,Moeller E,Arnold M,Schack B ( 2003): The use of time‐variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. J Neurosci Methods 124: 27–44. [DOI] [PubMed] [Google Scholar]
- Ikeda A,Luders HO,Burgess RC,Shibasaki H ( 1992): Movement‐related potentials recorded from supplementary motor area and primary motor area: Role of supplementary motor area in voluntary movements. Brain 115: 1017–1043. [DOI] [PubMed] [Google Scholar]
- Josephs O,Turner R,Friston K ( 1997): Event‐related fMRI. Hum Brain Mapp 5: 243–248. [DOI] [PubMed] [Google Scholar]
- Kaminski M,Ding M,Truccolo WA,Bressler SL ( 2001): Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 85: 145–157. [DOI] [PubMed] [Google Scholar]
- Lauritzen TZ,D'Esposito M,Heeger DJ,Silver MA ( 2008): Human attention networks revealed by fMRI coherency analysis. Computational and Systems Neuroscience (CoSyNe) Meeting (Abstract). [Google Scholar]
- Lee D,Quessy S ( 2003): Activity in the supplementary motor area related to learning and performance during a sequential visuomotor task. J Neurophysiol 89: 1039–1056. [DOI] [PubMed] [Google Scholar]
- Menon RS,Thomas CG,Gati JS ( 1997): Investigation of BOLD contrast in fMRI using multi‐shot EPI. NMR Biomed 10: 179–182. [DOI] [PubMed] [Google Scholar]
- Menon RS,Luknowsky DC,Gati JS ( 1998): Mental chronometry using latency‐resolved functional MRI. Proc Natl Acad Sci USA 95: 10902–10907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller LM,Sun FT,Curtis CE,D'Esposito M ( 2005): Functional interactions between oculomotor regions during prosaccades and antisaccades. Hum Brain Mapp 26: 119–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T,Hayasaka S ( 2003): Controlling the family‐wise error rate in functional neuroimaging: A comparative review. Stat Methods Med Res 12: 419–446. [DOI] [PubMed] [Google Scholar]
- Nichols T,Holmes A ( 2001): Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum Brain Mapp 15: 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkel DH,Gerstein GL,Moore GP ( 1967): Neuronal spike trains and stochastic point processes. II. Simultaneous spike trains. Biophys J 7: 419–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roebroeck A,Formisano E,Goebel R ( 2005): Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage 25: 230–242. [DOI] [PubMed] [Google Scholar]
- Rosenberg JR,Amjad AM,Breeze P,Brillinger DR,Halliday DM ( 1989): The Fourier approach to the identification of functional coupling between neuronal spike trains. Prog Biophys Mol Biol 53: 1–31. [DOI] [PubMed] [Google Scholar]
- Rypma B,Berger JS,Prabhakaran V,Bly BM,Kimberg DY,Biswal BB,D'Esposito M ( 2006): Neural correlates of cognitive efficiency. Neuroimage 33: 969–979. [DOI] [PubMed] [Google Scholar]
- Sack AT,Jacobs C,De Martino F,Staeren N,Goebel R,Formisano E ( 2008): Dynamic premotor‐to‐parietal interactions during spatial imagery. J Neurosci 28: 8417–8429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato JR,Junior EA,Takahashi DY,de Maria Felix M,Brammer MJ,Morettin PA ( 2006): A method to produce evolving functional connectivity maps duuring the course of an fMRI experiement using wavelet‐based time‐varying Granger causality. Neuroimage 31: 187–196. [DOI] [PubMed] [Google Scholar]
- Stilla R,Deshpande G,LaConte S,Hu X,Sathian K ( 2007): Posteromedial parietal cortical activity and inputs predict tactile spatial acuity. J Neurosci 27: 11091–11102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun FT,Miller LM,D'Esposito M ( 2004): Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage 21: 647–658. [DOI] [PubMed] [Google Scholar]
- Sun FT,Miller LM,D'Esposito M ( 2005): Measuring temporal dynamics of functional networks using phase spectrum of fMRI data. Neuroimage 28: 227–237. [DOI] [PubMed] [Google Scholar]
- Sun FT,Miller LM,Rao AA,D'Esposito M ( 2007): Functional connectivity of cortical networks involved in bimanual motor sequence learning. Cereb Cortex 17: 1227–1234. [DOI] [PubMed] [Google Scholar]
- Weilke F,Spiegel S,Boecker H,von Einsiedel HG,Conrad B,Schwaiger M,Erhard P ( 2001): Time‐resolved fMRI of activation patterns in M1 and SMA during complex voluntary movement. J Neurophysiol 85: 1858–1863. [DOI] [PubMed] [Google Scholar]
- Winterhalder M,Schelter B,Hesse W,Schwab K,Leistritz L,Klan D,Bauer R,Timmer J,Witte H ( 2005): Comparison of linear signal processing techniques to infer directed interactions in multivariate neural systems. Signal Processing 85: 2137–2160. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found in the online version of this article.
Supplementary Figure 1. Shown here is a direct comparison of representative slices from both a single subject and from the group of subjects for both spatially smoothed and unsmoothed time series data derived from an SMA seed region, as derived by T‐test across subjects and thresholded at p < 0.001, uncorrected. For the individual subject data, spatial smoothing changes the character of the map more markedly for phase delay than for GCD, in both eliminating some clusters and demonstrating others more robustly. For the group data, both measures are significantly affected by smoothing, with the pixilated appearance of the unsmoothed data replaced by a map that highlights motor and sensory regions.
Supplementary Figure 2. Shown here are all significant values, without thresholding, for both the group coherence and GCS maps shown in (A) figure 7 and (B) figure 10.