A Comparative Analysis of the Equilibrium Dynamics of a Designed Protein Inferred from NMR, X-ray and Computations

Abstract

A detailed analysis of high-resolution structural data and computationally predicted dynamics was carried out for a designed sugar binding protein. The mean-square-deviations in the positions of residues derived from Nuclear Magnetic Resonance (NMR) models, and those inferred from X-ray crystallographic B-factors for two different crystal forms were compared with the predictions based on the Gaussian Network Model (GNM), and the results from molecular dynamics (MD) simulations. GNM systematically yielded a higher correlation than MD, with experimental data, suggesting that the lack of atomistic details in the coarse-grained GNM is more than compensated for by the mathematically exact evaluation of fluctuations using the native contacts topology. Evidence is provided that particular loop motions are curtailed by intermolecular contacts in the crystal environment causing a discrepancy between theory and experiments. Interestingly, the information conveyed by X-ray crystallography becomes more consistent with NMR models and computational predictions when ensembles of X-ray models are considered. Less precise (broadly distributed) ensembles indeed appear to describe the accessible conformational space under native state conditions better than B-factors. Our results highlight the importance of utilizing multiple conformations obtained by alternative experimental methods, and analyzing results from both coarse-grained models and atomic simulations, for accurate assessment of motions accessible to proteins under native state conditions.

Introduction

Understanding structure and dynamics is essential for elucidating protein function that is governed by the complement of accessible energetically favored motions as seen for ligand/substrate binding in catalysis and protein-protein interactions in signaling and regulation.

It has long been appreciated that native proteins are not confined to a single, static conformation, but sample numerous substates under equilibrium conditions.^1-3 Similarly, the denatured state also consists of an ensemble of conformations. The main difference between the two states is simply that the native ensemble is narrow, confined to fluctuating conformations that maintain the native fold, whereas the denatured ensemble consists of a wide range of conformations. Both experiments and computations indicate that ensemble-based approaches provide superior information on the properties of a given molecule and the advantages of ensemble-based approaches have been demonstrated for Nuclear Magnetic Resonance (NMR)⁴ and X-ray structure refinement.⁵ Novel methods that simultaneously and synergistically determine structure and dynamics, called dynamic ensemble refinement,^{6, 7} hold great promise for providing insight into equilibrium dynamics.

Focused efforts in developing and interpreting relaxation measurements, primarily by NMR spectroscopy, provide increased understanding of the temporal and spatial scales that are associated with the broad range of protein motions. Small-scale (≤ 1.5 Å) motions, such as the small fluctuations in the positions of backbone and side chain atoms occur on femto- to picosecond time scales. These are accessible via NMR Lipari-Szabo order parameters (S²)⁸ or short (< 1 ns) molecular dynamics (MD) simulations.⁹ This fast motional regime is also reflected in the X-ray crystallographic temperature factors^{10, 11} or can be studied using infrared or fluorescence correlation spectroscopy.¹² Mid-scale motions that take place over hundreds of pico- to nanoseconds or low microseconds may comprise loop or terminal-end fluctuations as well as peptide plane motions (change in dihedral angles) and other local dynamics information. This regime can be also be extracted via NMR Lipari-Szabo order parameters (S²) as long as these motions are faster than the overall correlation time (τ_c). Computationally, this regime may be probed by performing long (10-100 ns) MD simulations.¹³ This mid-scale range has also been evoked to contribute to the spread of conformers in NMR ensembles¹⁴ or may be accessible from collections of X-ray structures of the same protein in different crystal isomorphs.¹⁵ Slow motions are most frequently associated with large displacement (> 15 Å) of entire secondary structure elements, domains or subunits. If these occur on the micro- to millisecond timescale, they can be detected in the T₂ or T_1ρ Carr–Purcell–Meiboom–Gill (CPMG) type NMR relaxation experiments.¹⁶ Such motions may also be been studied in the crystal by Laue diffraction.¹⁷ On the computational side, this regime is beyond the range accessible by MD.

To overcome the limitations of MD simulations and predict the mechanisms of low frequency, or ‘global’, modes of motion, coarse-grained models and methods based on inter-residue contact topology have been proposed, such as the elastic network models (ENMs) introduced a decade ago.^18-21 ENMs have been broadly used in normal mode analysis (NMA) of known structures,²² and shown to yield results that correlate with those from principal component analysis of ensembles of structures.²³ Such large scale movements were evoked in a recent study of ubiquitin where an ensemble of conformations based on residual dipolar couplings was determined.⁶ The ensemble covered a conformational space similar to that seen for the X-ray structures of ubiquitin complexed with different substrates, and were consistent with structural changes along a well-defined principal direction of motion.⁶

ENMs have gained widespread use given their simplicity and ability to yield a unique, analytical solution for low frequency motions (e.g., cooperative domain movements), without requiring knowledge of detailed force fields or implementation of expensive energy minimization algorithms.^{24, 25} Notably, global modes are insensitive to details of force field parameters or specific interactions at the atomic scale.^{26, 27} They are uniquely defined by the native contact topology for a particular structure, and provide insights into the potentially functional motions intrinsically favored by the proteins' native structure.²⁸

We previously investigated the correlation between (i) the mean-square (ms) deviations (MSDs) in atomic coordinates for NMR ensembles, (ii) the B-factors observed in X-ray crystallographic structures, and (iii) the equilibrium fluctuations in residue positions predicted by a simple ENM, the Gaussian Network Model (GNM),^{19, 20} for a large set of proteins structurally characterized by both techniques.²⁹ GNM results exhibited then a better correlation with the NMR data than with X-ray data.²⁹ We suggested that the superior correlation with NMR data may arise from the larger spectrum of modes accessible in solution, which may be represented by the NMR ensemble, as opposed to the crystalline environment where the largest amplitude modes of motion may be suppressed by crystal contacts. Another study by Phillips and coworkers³⁰ demonstrated that the GNM results for B-factors outperform those predicted by models that attribute the observed mobilities exclusively to rigid-body motions.³¹ More recent applications suggest that the ENM methodology provides a reasonable estimate of the anisotropic displacement parameters^{32, 33} and can assist in the structural refinement of supramolecular complexes.³⁴

Despite these practical successes there still remain a number of uncertainties about the origin of the agreement between the GNM results and experimental ensembles. In principle, the GNM exclusively depends on inter-residue contact topology. Thus, the results for a given protein are uniquely determined, irrespective of the experimental conditions. On the other hand, different crystal packing arrangements may result in disparaging B-factors for the same protein crystallized under varying conditions. Song and Jernigan pointed out that selected modes may be favored or suppressed, depending on different crystal packing geometries.³⁵ Phillips and coworkers noted that crystal packing selects conformers from the ensemble of structures accessible in solution.³⁶ Song and Jernigan further showed that calculations based exclusively on rigid body motions yield a correlation of about 0.52 with experimental B-factors (compared to a correlation of 0.59 obtained with the GNM),³⁵ which suggested that the experimental B-factors could not be fully attributed to internal or external motions. A systematic study of the optimal parameters that reproduce experimental B-factors indeed revealed that rigid body motions account for nearly 60% of total fluctuations,³⁵ in accord with the observations made by Diamond.³⁷ A similar conclusion was reached by Hinsen, who recently showed that crystal packing considerably modifies the distributions of atomic fluctuations, and that thermal fluctuations are not necessarily the dominant contribution to the crystallographic Debye-Waller factors, compared with other contributions such as static disorder and lattice defects.³⁸ Therefore, the observed discrepancies between the GNM predictions and X-ray B-factors could arise from packing of the protein in the crystal lattice, from rigid body motions of the molecules in the crystal environment, or approximations (such as the lack of amino acid specificity) inherent to the GNM method.

Comparing GNM, X-ray and NMR models the question arises why one observes better agreement between GNM and NMR RMSDs, compared to X-ray B-factors. The width of the distribution among the NMR models usually results from a combination of sparse data and motion of the polypeptide chain in solution. Furthermore, most methods for calculating NMR ensembles use Nuclear Overhauser effect (NOE) distances as the predominant constraints, which represent a similar contact topology inherent to the GNM analysis. Thus, the good agreement between NMR data and GNM predictions could be caused by the commonality in methodology and similar inherent assumptions in the two approaches.

To address these open questions, we undertook a comprehensive analysis for a designed sugar-binding protein, LKAMG, which we have structurally characterized by both NMR and X-ray crystallography (Koharudin et al., accompanying paper). We simultaneously analyzed the ensemble of NMR models and the X-ray models obtained from two crystal forms, as well as computational data from both the GNM analysis and full atomic MD simulations, for a rigorous assessment of the origins of similarities and differences between the experimental and computational data. Our results show that ensembles, NMR or X-ray, agree well with GNM predictions. The noted consistency of MD and GNM results point to the dominance of inter-residue contact topology (basic ingredient of the GNM) in equilibrium dynamics, even if a detailed force field with non-linear and specific interactions is used, as in MD simulations. Interestingly, our data suggest that less precise ensembles appear to describe the accessible conformational space under native state conditions better than tight ensembles.

Materials and Methods

Materials

We used two sets of independently determined structures of LKAMG, a cyanovirin-N homolog (CVNH) chimera, as our defined model system, determined by NMR spectroscopy and X-ray crystallography. LKAMG is a small protein of 107 residues. It is monomeric both in solution and in the crystalline state. LKAMG crystals were obtained in two different space groups, p21 and p212121, designated as X1 and X2 throughout this manuscript. The NMR structure was solved using commonly used methodology³⁹ and a final ensemble comprising 100 conformers with the lowest energy was selected from the calculated 4000 structural models. The backbone RMSD of the NMR ensemble with respect to the mean was 0.23 ± 0.04 Å and the lowest energy model is designated as N1. Details about the design, expression, and structural characterization of the protein by both methods are given in an accompanying manuscript (Koharudin et al., accompanying paper). We have additionally constructed a homology model of LKAMG, called H1, using a cyanovirin-N structure [Protein Data Bank (PDB) ID:2EZM]⁴⁰ as template in MODELLER 8v2.⁴¹ The sequence identity between LKAMG and its template was 29%. H1 has been adopted as the starting structure in MD simulations.

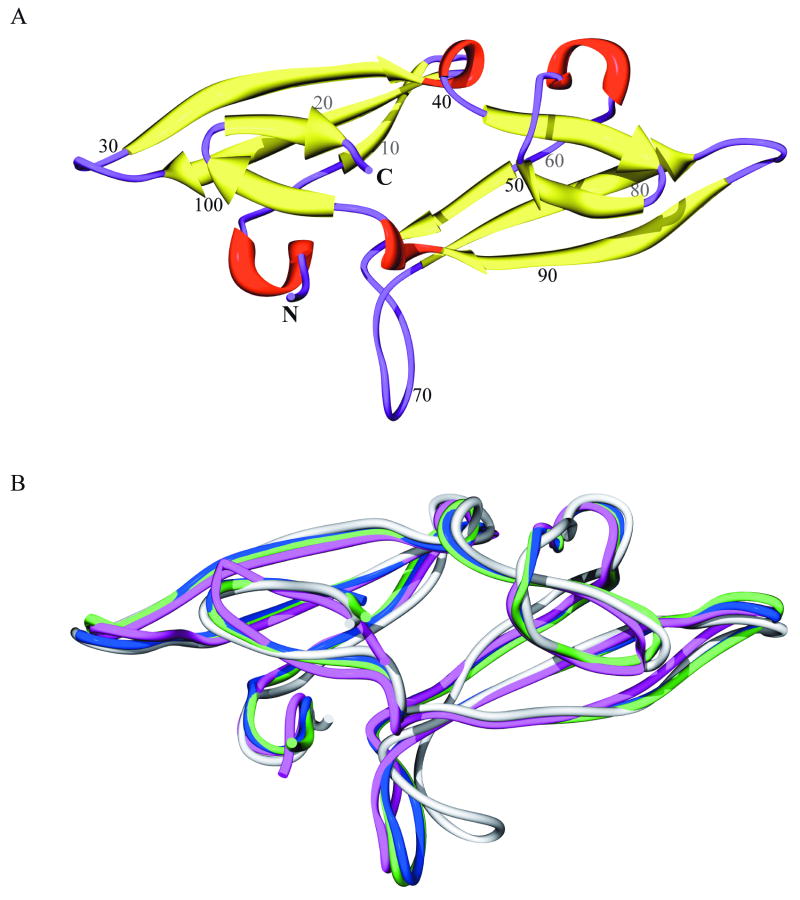
The structure of LKAMG is displayed in Figure 1A. The protein has a pseudo-symmetric architecture comprised of two domains, and closely resembles other members of the CVNH family. Each domain is composed of a three-stranded β-sheet on top of which resides a β-hairpin (β-strands are colored yellow). The two domains are connected by short helical turns (red). In addition, three loops (residues 25-29, 68-73, 81-87; colored purple) protrude out from the core structure. A superposition of the X-ray models X1 and X2 (blue and green), the NMR conformer N1 (magenta) and the homology model H1 (gray) is displayed in Figure 1B. Table I lists the root-mean-square differences (RMSDs) in the backbone atom coordinates of these models. The RMSDs vary from 0.36 Å (between X1 and X2) to 2.01 Å (between N1 and H1).

Figure 1. Structure of the designed protein, LKAMG.

(A) Ribbon representation, color-coded according to secondary structure; β-strands are shown in yellow, helical turns in red, and loops and chain termini in purple. Amino acid sequence positions are labeled at every 10^th residue. (B) Best-fit superposition of four different structural models for LKAMG in modified ribbon representation; the X-ray models X1 and X2 are shown in blue and green, respectively, the lowest energy conformer of the NMR ensemble N1 in magenta, and the homology model H1 in gray.

Table I. Backbone RMSD (Å) between different LKAMG structural models. ^(a).

	X1	X2	N1	H1
X1	-	0.36	0.99	1.69
X2	-	-	0.96	1.78
N1	-	-	-	2.01
H1	-	-	-	-

^(a)X1 and X2 are the p21 and p212121 crystal structures, respectively; N1 is the lowest energy conformer in the NMR solution structure ensemble; H1 is the homology model.

RMSD Calculation for the Ensemble of NMR Models

The RMSD in the position of residue i is calculated as

$$<{(\Delta {\mathit{R}}_i)}^2{>}^{\frac{1}{2}}=\sqrt{\frac{{\sum }_{k=1}^m{\left|{\mathit{r}}_{i,k}-\overline{{\mathit{r}}_i}\right|}^2}{m}}$$ (1)

where r̄_i designates the position of that particular residue averaged over all optimally superimposed models (m of them). The MSDs in residue positions, <(ΔR_i)²> as a function of residue index i are referred to as the fluctuations profile in residue positions.

Generation of NMR-like ensembles from the X-ray models

NMR-like ensembles were created using inter-proton distance constraints with commonly employed methodology.³⁹ In order to extract inter-proton distances from X-ray models, hydrogen atoms were added using REDUCE.⁴² In this manner, standardized geometry and optimized orientations for OH, SH, NH₃⁺, Met methyls, Asn and Gln sidechain amino groups, and His rings were created. Since we use high resolution X-ray models (1.56 Å and 1.36 Å for the p21 and p212121 data, respectively), one-cycle of refinement in the presence of the added hydrogen atoms was carried out using PHENIX.⁴³ The resulting models exhibit R and R_free values of 0.1607 and 0.2018 for the p21 and 0.1669 and 0.1972 for the p212121 structures, respectively. Inter-protons distances shorter than or equal to 5 Å were then extracted using MOLMOL⁴⁴ and a total of 3972 and 3982 inter-protons distances were generated for the p21 and p212121 structures, respectively. Note that a total of 2756 inter-proton distances were used for calculating the NMR ensemble. Therefore, an equal number of constraints is used in the pseudo-X-ray ensemble with ∼ 70% of the complete constraints set. In order to mimic the structure calculation methodology by NMR, we classified these distances according to three NOE classes (strong, medium, and weak) and added distance corrections to the upper bounds to allow for some distance variability. The upper bound was set to 3.0, 4.0, and 6.0 Å for any extracted distances that were less or equal to 2.5 Å (strong NOE), less or equal to 3.5 Å but more than 2.5 Å (medium NOE), and less or equal to 5.0 Å but more than 3.5 Å (weak NOE), respectively. This correction reflects distance allowances of 0.5, 0.5, and 1.0 Å for the short, medium, and long distances. From the total set of distance constraints, we randomly removed 20% or 50% of the data, yielding the 80% or 50% distance sets. Inter-proton distances were measured including exchangeable hydrogens, some of which may not be observable in the experimental setting due to fast exchange with solvent. No intra-residue proton distances, however, were included. Note, removal of the exchangeable hydrogens from the lists did not affect the generated NMR-like ensembles in any significant manner (data not shown).

Fluctuations and collective modes predicted by the Gaussian Network Model

In the GNM, the structure is modeled as a 3-dimensional elastic network of n nodes. The position of each node is determined by the α-carbons. The network topology is described by a N × N Kirchhoff matrix Γ

$${\mathbf{\Gamma }}_{ij}=\{\begin{array}{ccc}-1& \mathit{\text{if}}\hfill & i\ne j\mathit{\text{and}}{r}_{ij}\le r_c\hfill \\ 0& \mathit{\text{if}}& i\ne j\mathit{\text{and}}{r}_{ij}>r_c\hfill \\ -{\sum }_{i,i\ne j}{\mathbf{\Gamma }}_{ij}\hfill & \mathit{\text{if}}\hfill & i=j\hfill \end{array}$$ (2)

where r_c is the cutoff distance that defines pairs of residues to be connected in the network. r_ij is the equilibrium distance between residue i and residue j, calculated using the Protein Data Bank (PDB)⁴⁵ coordinates. The cross-correlations between the fluctuations ΔR_i and ΔR_j of the nodes i and j are given by¹⁹

$$\langle \Delta {\mathit{R}}_i\cdot \Delta {\mathit{R}}_j\rangle =(3k_{B}T/\gamma ){[{\mathbf{\Gamma }}^{-1}]}_{ij}$$ (3)

where k_B is the Boltzmann constant, T is the absolute temperature and γ is a uniform spring constant. The inverse of Γ is expressed in terms of the nonzero eigenvalues λ_k (1 ≤ k ≤ N-1) and corresponding eigenvectors u_k of Γ as²⁰

$${\mathbf{\Gamma }}^{-\text{1}}={\sum }_{k=1}^{N-1}{\lambda }_k^{-1}{\mathit{u}}_k{\mathit{u}}_k^T$$ (4)

which permits us to express the ms fluctuations of a given residue as a sum over the contributions of all modes

$$<{(\Delta {\mathit{R}}_i)}^2>={\sum }_{k=1}^{N-1}\frac{3k_{B}T}{\gamma }{({\lambda }_k^{-1}{\mathit{u}}_k{\mathit{u}}_k^T)}_{ii}$$ (5)

Here the subscript ii designates the i^th diagonal element of the matrix enclosed in parenthesis. The X-ray crystallographic B-factors are compared with the theoretical predictions using

$$B_i\equiv \frac{8{\pi }^2}{3}<{(\Delta {\mathit{R}}_i)}^2>={\sum }_{k=1}^{N-1}\frac{8{\pi }^2{k}_{B}T}{\gamma }{({\lambda }_k^{-1}{\mathit{u}}_k{\mathit{u}}_k^T)}_{ii}$$ (6)

The GNM predictions for (i) NMR model N1, (ii) the mean structure of NMR ensemble, or (iii) those averaged over all models in the NMR ensemble were found to be almost identical (correlation coefficients above 0.95); hence we use NMR model N1 as a representative model for the NMR ensemble.

Comparison of MD essential modes with GNM global modes

The MD simulations were performed using NAMD⁴⁶ with the Charmm22 force field.⁴⁷ Three runs were performed with explicit water for a total duration of 10 ns, each, at constant temperature (298 K) and pressure (1 atm). Instantaneous conformations were saved every 1ps excluding the first 1.5 ns portion of the trajectories (Supplementary Figure S1 panel A). The resulting M snapshots where organized in the fluctuation trajectory matrix

$$\Delta \mathit{R}={\left[\begin{array}{cccc}\Delta {\mathit{R}}_1(t_1)& \Delta {\mathit{R}}_1(t_2)& \cdots & \Delta {\mathit{R}}_1(t_M)\\ \Delta {\mathit{R}}_2(t_1)& \Delta {\mathit{R}}_2(t_2)& \cdots & \Delta {\mathit{R}}_2(t_M)\\ \Delta {\mathit{R}}_3(t_1)& \Delta {\mathit{R}}_3(t_2)& \cdots & \Delta {\mathit{R}}_3(t_M)\\ \cdots \hfill & \cdots \hfill & \cdots & \cdots \hfill \\ \Delta {\mathit{R}}_N(t_1)& \Delta {\mathit{R}}_N(t_2)& \cdots & \Delta {\mathit{R}}_N(t_M)\end{array}\right]}_{3N\times M}$$ (7)

ΔR_i(t_j) is the 3-dimensional vector representing the departure of the i^th α-carbon from its mean position, at the j^th snapshot. Multiplication of ΔR by its transpose yields the 3N × 3N covariance matrix A. A can be viewed as an N × N supermatrix, the ij^th ‘element’ of which is the 3 × 3 matrix

$${\mathit{A}}_{ij}=N{\left[\begin{array}{ccc}<\Delta X_i\Delta X_j>& <\Delta X_i\Delta Y_j>& <\Delta X_i\Delta Z_j>\\ <\Delta Y_i\Delta X_j>& <\Delta Y_i\Delta Y_j>& <\Delta Y_i\Delta Z_j>\\ <\Delta Z_i\Delta X_j>& <\Delta Z_i\Delta Y_j>& <\Delta Z_i\Delta Z_j>\end{array}\right]}_{3\times 3}$$ (8)

The cross-correlation between the fluctuations of residues i and j is found from the trace of A_ij as

$$<\Delta {\mathit{R}}_i\cdot \Delta {\mathit{R}}_j>=(1/N)tr\left[{\mathit{A}}_{ij}\right]$$ (9)

These cross-correlations may be conveniently organized in an N × N covariance matrix C, the diagonal elements of which are simply the ms fluctuations of residues. C may be expressed in terms of its eigenvalues (s_l) and eigenvectors (q_l) as

$$\mathit{C}={\sum }_l{s}_l{\mathit{q}}_l{\mathit{q}}_l^T$$ (10)

The eigenvalues serve as weights for square displacements induced by different modes. Trajectories along the essential modes 1, 2, 4 and 16 of an MD run are illustrated in the Supplementary Figure S1 panel B. C is the counterpart of Γ⁻¹ Likewise, s_l is the counterpart of $(3k_{B}T/\gamma ){\lambda }_k^{-1}$, and q_l is the counterpart of u_k. Therefore the eigenvalues extracted from MD can be directly compared to the reciprocal eigenvalues from the GNM. Likewise, the top-ranking eigenvectors (corresponding to the lowest frequency, or global, modes) may be directly compared. The cumulative square correlation {σ²(k)}_ltot between a given GNM mode (e.g., u_k) and an ensemble of l_tot MD modes is evaluated from

$$\{{\sigma }^2(\text{k})\}{}_{\mathit{\text{ltot}}}={\sum }_l{\text{cos}}^2({\mathit{u}}_k,{\mathit{q}}_l)$$ (11)

where the summation is performed for 1 ≤ l ≤ l_tot.

Results and Discussion

Comparison of the two computational approaches

The main impetus for our current study was to uncover any reasons that cause the better agreement between predicted equilibrium dynamics by GNM and the NMR RMSDs compared to X-ray B-factors. In order to exclude any potential errors that may arise from neglecting nonlinear effects in the GNM, we first compared the results predicted by the GNM with those obtained by MD simulations.

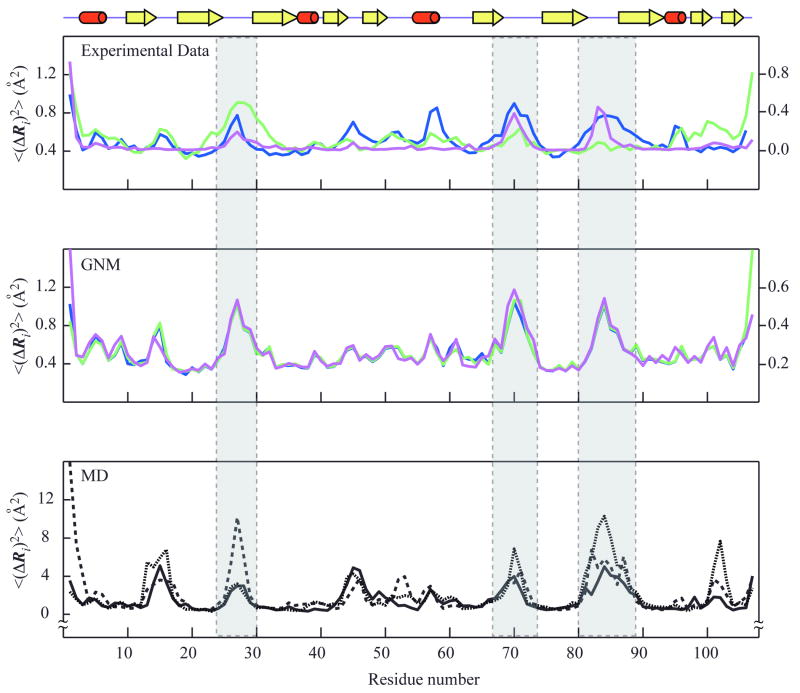
Figure 2 compares the MSDs, <(ΔR_i)²>, 1 ≤ i ≤ N, extracted from experimental data (NMR ensemble and X-ray crystallographic B-factors) with the square fluctuations computed by MD and GNM. The MSDs refer to the positions of the α-carbons with respect to their mean positions. The MSD profiles based on NMR, X1 and X2 data, designated as <(ΔR_i)²>_NMR, <(ΔR_i)²>_X1, and <(ΔR_i)²>_X2, are colored magenta, blue, and green, respectively (top panel). <(ΔR_i)²>_GNM-N1, <(ΔR_i)²>_GNM-X1 and <(ΔR_i)²>_GNM-X2 are their counterparts predicted by the GNM, using the NMR model N1 and the two crystal structures X1 and X2, respectively, as input (middle panel). <(ΔR_i)²>_MD1, <(ΔR_i)²>_MD2 and <(ΔR_i)²>_MD3 are the square fluctuations profiles observed in three independent MD runs (bottom panel). The correlation coefficients between these profiles are summarized in Table II.

Figure 2. Mean-square fluctuations profiles of LKAMG from experimental data and computations.

The fluctuations in the positions of the residues, <(ΔR_i)²>, are plotted as a function of residue position along the polypeptide chain, 1 ≤ i ≤ N. The upper panel displays the MSDs from experimental data, <(ΔR_i)²>_NMR, <(ΔR_i)²>_X1 and <(ΔR_i)²>_X2 colored magenta, blue and green, respectively. Crystallographic fluctuations are extracted from the B-factors, using B_i = (8 π²/3) <(ΔR_i)²>, The left and right ordinates correspond to NMR and X-ray data, respectively. The middle panel displays the square fluctuations predicted by the GNM for the different structural models, <(ΔR_i)²>_GNM-N1 (magenta,), <(ΔR_i)²>_GNM-X1 (blue), and <(ΔR_i)²>_GNM-X2 (green). The lower panel shows the results from three MD runs, <(ΔR_i)²>_MD1 (solid black), <(ΔR_i)²>_MD2 (dotted black), and <(ΔR_i)²>_MD3 (dashed black). A schematic representation of the LKAMG secondary structure is displayed on top. The three loop regions are indicated by the gray columns.

Table II. Correlation coefficients for mean-square fluctuations deviations in residue positions observed in experiments and computations.^(a).

< (ΔRi)2>	NMR	GNM (N1)	X1	GNM(X1)	X2	GNM(X2)	MD1	MD2	MD3
NMR	-	0.80	0.64	0.77	0.31	0.78	0.54	0.60	0.65
GNM (N1)	-	-	0.76	0.95	0.50	0.95	0.62	0.61	0.58
X1	-	-	-	0.76/0.72(b)	0.25	0.76	0.69	0.62	0.60
GNM(X1)	-	-	-	-	0.52	0.99	0.69	0.65	0.61
X2	-	-	-	-	-	0.51/0.69(b)	0.18	0.49	0.13
GNM(X2)	-	-	-	-	-	-	0.68	0.66	0.63
MD1	-	-	-	-	-	-	-	0.64	0.79
MD2	-	-	-	-	-	-	-	-	0.65
MD3	-	-	-	-	-	-	-	-	-

^(a)Computational results were obtained by GNM predictions for the NMR model N1, and the X-ray models X1 and X2, as well as by MD simulations MD1-3. Boldface entries refer to correlations between experimental data and the corresponding computational predictions.

^(b)0.76 and 0.51 are the correlation coefficients based on the GNM predictions for the isolated protein, and 0.72 and 0.69 are for the protein in the lattice (see Figure 5).

As can be appreciated from the results presented in Table II, GNM predictions for different models (N1, X1 or X2) are highly correlated, also reflected by the very similar profiles in Figure 2 (middle panel). The pairwise correlations between <(ΔR_i)²>_GNM-N1, <(ΔR_i)²>_GNM-X1 and <(ΔR_i)²>_GNM-X2 are all equal to or higher than 0.95. Such close agreement is not surprising since GNM results are primarily defined by the coarse-grained distribution of inter-residue contacts (C^α-C^α pairs within an interaction cutoff distance of r_c = 7 Å). The three models N1, X1 and X2, which differ in their backbone coordinates by less than 1 Å (Table I), are expected to exhibit very similar contact topologies.

The correlations between GNM and MD profiles, on the other hand, vary from 0.58 (between <(ΔR_i)²>_GNM-N1 and <(ΔR_i)²>_MD3) to 0.69 (between <(ΔR_i)²>_GNM-X1 and <(ΔR_i)²>_MD1) and are mainly influenced by the particular trajectories (MD1, MD2, and MD3). This level of agreement is reasonable, given the fundamentally different assumptions and methodologies inherent to the two types of computations: GNM is a low resolution approach, based exclusively on inter-residue contact topology; MD includes full atomic details with elaborate force fields. Notably, GNM yields consistent solutions for the fluctuations behavior of LKAMG and results are obtained within seconds. MD runs, on the other hand, take weeks, and the results suffer from sampling inaccuracies, as evidenced by the correlations of 0.64, 0.65 and 0.79 between pairs of MD runs. What is even more striking is that GNM results consistently agree better with experimental data, either NMR or X-ray, than MD results, as will be discussed below.

Two further comparative analyses of the two sets of computational results were carried out focusing on (i) their level of agreement with experimental data, and (ii) the spectra of modes predicted in each case.

Comparison of computational and experimental data

As shown in Table II, the fluctuations profiles predicted by the GNM for the models N1 (<(ΔR_i)²>_GNM-N1), X1 (<(ΔR_i)²>_GNM-X1) and X2 (<(ΔR_i)²>_GNM-X2) yielded respective correlation coefficients of 0.80, 0.76 and 0.51 with their experimental counterparts, <(ΔR_i)²>_NMR, <(ΔR_i)²>_X1 and <(ΔR_i)²>_X2, respectively. For the MD trajectories, on the other hand, respective correlation coefficients of {0.54, 0.69 and 0.18} were found between <(ΔR_i)²>_MD1 (from MD1) and {<(ΔR_i)²>_NMR, <(ΔR_i)²>_X1 and <(ΔR_i)²>_X2} and their counterparts for MD2 and MD3 were {0.60, 0.62 and 0.49} and {0.65, 0.60, and 0.13}, respectively. These entries are listed in boldface in the Table II.

These results clearly show that the fluctuations profiles predicted by the GNM exhibit higher correlation with experimental data compared to those obtained by MD. It is also interesting to note that the correlation between the results from the three different MD runs is 0.69 ± 0.08, indicating that the results from MD simulations are not as robust as those from GNM, despite the fact that all MD runs were performed with the same starting structure (H1), while GNM calculations yielded almost identical profiles, although performed using different structural models.

Additionally, it can also be easily noticed that, in both cases, the computational results obtained for X2 exhibit poorer agreement with the experimental data, compared to those obtained for N1 and X1. It is worth noting, however, that, even for the X2 data, GNM systematically yielded a higher correlation than MD, suggesting that the lack of atomistic details in the GNM is more than compensated for by the mathematically exact evaluation of fluctuations using the complete, collective coupling of all residues. A detailed analysis pertaining to the comparison of the X2 data with computational predictions is discussed below.

Comparison of essential modes from MD and GNM

To provide a more in-depth analysis of the GNM and MD results, we decomposed the predictions into the contributions of the underlying modes and compared both methods' individual (top-ranking) modes. In doing so, we verified that the motions in different time regimes predicted by GNM are comparable to those sampled by MD simulations. There is, however, no one-to-one correspondence between pairs of modes.

GNM equilibrium fluctuations result from the superposition of N-1 normal modes for a protein of N residues. On the other hand, the essential dynamics analysis of a MD trajectory yields 3N-6 modes (unless the number of snapshots M is smaller than 3N-6). As described in the Methods, the 3N × 3N covariance matrix derived from a given MD trajectory may be conveniently organized into an N × N covariance matrix C of residue fluctuations, the eigenvalues and eigenvectors of which can be directly compared to those predicted by the GNM. We focused on the top-ranking modes at the low frequency end of the spectrum. These modes, also referred to as the global or essential modes,⁴⁸ define those motions that contribute the most to the observed dynamics, and are usually relevant to functional changes in conformation.^{25, 28}

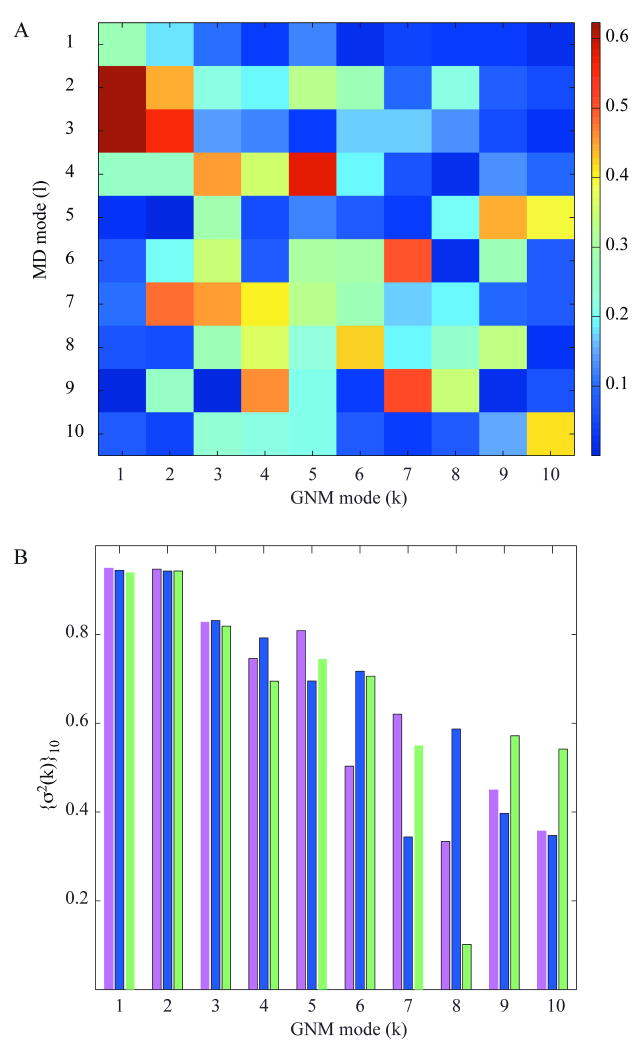
The correlation coefficients between the top-ranking modes extracted from MD and those predicted by the GNM are displayed in Figure 3A. Two pertinent observations emerge: (i) a given MD mode can be correlated with more than one GNM mode. For example, the MD mode 3 exhibits a correlation of 0.5 or higher with both modes 1 and 2 predicted by the GNM (see the corresponding brown and red boxes in Figure 3A), and (ii) the order of the modes in the two methods differ (for example, the 4^th MD mode is highly correlated with the 5^th GNM mode; i.e., the red boxes are not necessarily clustered along the diagonal). This analysis shows that it is hard, if not impossible, to identify a unique counterpart of each GNM mode in MD, or vice versa, probably due to different types and scales of movements represented by these modes. Yet, similarities between preferred modes of motions could be detected by consolidating the results using subsets of modes. We examined the combined contributions of the first 10 MD modes in relation to the individual GNM modes k in the range k ≤ 10. The cumulative correlation cosine (squared) {σ²(k)}₁₀ between the set of 10 MD modes and the k^th GNM mode (Eq. 11 in Methods) is shown in Figure 3B. The result for the first GNM mode is 0.95, shown by the magenta bar at k = 1, i.e., the combined first 10 MD modes [{σ²(k)}₁₀]^½ overlap to 97% with the 1^st GNM mode. The overlap with the 2^nd GNM mode is equally high and only gradually decreases with mode number, remaining above 0.75 for 5 out of 10 GNM modes. Note that the 10 MD modes represent only a small fraction (less than ten percent) of the entire set of modes retrieved by decomposing the MD covariance matrix C. However, their weighted contribution amounts to 98% while that of first 10 GNM modes represents 47% of the predicted motions.

Figure 3. Correlation map for essential modes predicted by the GNM and derived from MD.

(A) Correlations, [q_l · u_k], between the essential modes q_l (1 ≤ l ≤ 10) retrieved from MD1 and those (u_k, 1≤ k ≤ 10) predicted by the GNM. (B) Cumulative correlations (sum over cosines squared; see Eq. 12) for the first ten essential MD modes and individual GNM modes predicted for the models N1 (magenta), X1 (blue) and X2 (green). See Supplementary Figure S2 for a more extensive comparison of the mode spectra obtained by MD and GNM.

The above numbers refer to GNM calculations performed with N1 as the model. Similar results were obtained using the X-ray models X1 and X2, shown by blue and green bars in Figure 3B. The correlation falls below 0.1 beyond the 20^th GNM mode. The dependence of {σ²(k)}l_tot on k, for l_tot = 10, 20 and 30 MD modes is provided in Supplementary Figure S2 panel A for all GNM modes 1 ≤ k ≤ N-1; and panel B in the same figure displays the joint contribution {σ²(l)}k_tot of k_tot = 10, 20 and 30 GNM modes to the l^th MD mode. Interestingly, there is a hierarchical influence of relatively higher frequency MD modes on the higher GNM modes, confirming consistency between the two spectra of modes. MD simulations and GNM predictions are thus comparable with regard to the dominant, usually biologically relevant, low frequency modes. The differences between the MD and GNM fluctuation profiles mainly originate from higher frequency modes that are known to be noisy.

The close relationship between NMR and GNM - is the agreement simply based on the similarity in methodology?

The above analysis indicates that MSDs predicted by the GNM consistently exhibit a better correlation with experimental data than MD results, and that the level of correlation between the fluctuations predicted by GNM and the MSD extracted from the NMR ensemble is higher than that between GNM and X-ray B-factors. NMR calculations use inter-residue distances data from NOEs as the predominant constraints, and GNM analysis is also based on knowledge of inter-residue contact topology. In order to critically evaluate whether the good correlation between the distribution of the conformers in an NMR ensemble and GNM-predicted fluctuations arises mainly from the similarity in the methodologies for NMR structure determination/refinement and for GNM calculations, we analyzed six differently calculated ensembles of structures that were derived from the X-ray models X1 and X2. For each crystal structure, three ensembles of 30 conformers each were generated, using the standard constraints-based NMR structure determination procedure. As constraints, 100%, 80%, and 50% of all possible inter-proton distance constraints were used. These ensembles are designated as X1- and X2-ensembles. The final 30 conformer ensembles exhibit backbone RMSD values of 0.32 ± 0.07 Ǻ, 0.33 ± 0.06 Ǻ, and 0.43 ± 0.06 Å when 100%, 80%, and 50% of constraints were used, respectively. The corresponding values for the X2-ensembles are 0.29 ± 0.06 Å, 0.37 ± 0.06 Å, and 0.40 ± 0.07 Å, respectively. As expected, there is a correlation between the ensemble precision and the number of constraints used to generate these ensembles, i.e. the ensemble RMSDs increase with decreasing number of constraints.³⁹

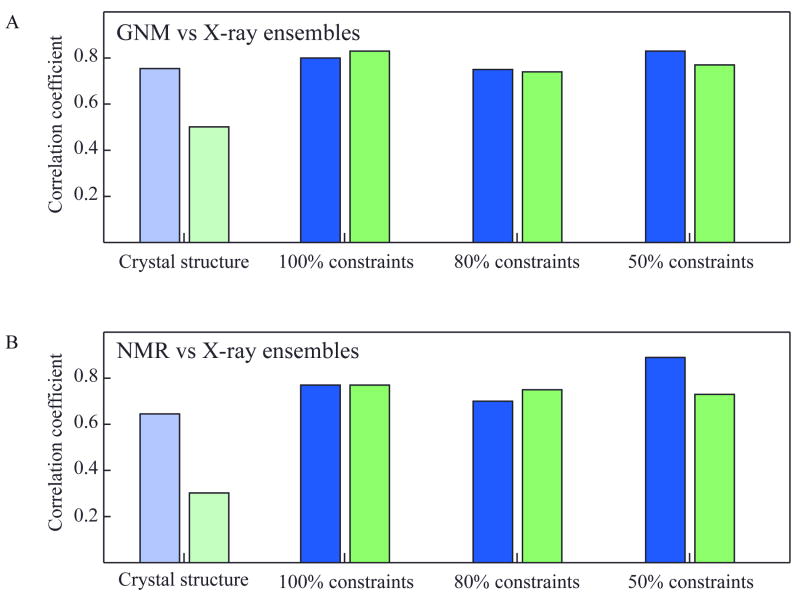
Using these so-called pseudo X-ray ensembles, we compared their MSDs with the fluctuations predicted by GNM and with the MSDs extracted from NMR data (N1) (Figure 4). Figure 4A displays the correlation coefficients between the MSDs in α-carbon coordinates <(ΔR_i)²>_ensemble for each X-ray ensemble and the fluctuations predicted by the GNM for the single crystal structures X1 (blue) and X2 (green); and Figure 4B displays the correlation coefficients between the MSDs <(ΔR_i)²>_ensemble for each X-ray ensemble and the MSDs extracted from the original NMR data (N1). For comparative purposes, the correlations between the experimental B-factors and their GNM counterparts (Table II and Figure 4A) and between the experimental B-factors and the experimental MSD from the NMR ensemble (Table II and Figure 4B) are displayed by the light-colored bars on the panels.

Figure 4. Correlations between residue fluctuations from theoretical predictions and inferred from pseudo X-ray ensembles (panel A) and NMR experiments (panel B).

Results for pseudo X-ray ensembles X1 and X2 are shown in blue and green bars. Theoretical data in panel A refers to GNM results obtained for the original crystal structures (X1 or X2). Experimental data in panel B refers to the RMSDs in C^α-positions between the models in the solution NMR ensemble. Results are displayed for three pseudo-X-ray ensembles, generated using 100%, 80% and 50% of the total constraints set. The light-colored bars on the left refer to the comparison of the original structures' B-factors with GNM theory (A) and NMR experiments (B).

If only methodological similarities between NMR structure determination and GNM would play a role in their better correlation, we would expect that decreasing the number of constraints used for generating the pseudo ensembles would increase the correlation between these pseudo ensemble MSDs and the predicted GNM fluctuation for both X1 and X2 pseudo ensembles. Since the ensemble precision would be loosened with decreasing number of constraints, it might be mimicking the GNM methodology of using C^α-C^α distances of 7 Å. As can be appreciated from Figure 4A, we did not observe this effect. For X1 pseudo ensembles, the correlations of the ensemble MSDs with the GNM predicted fluctuations were 0.80, 0.75, and 0.83 for the 100%, 80%, and 50% constraints employed, respectively. Therefore, the degree of correlation is very similar, irrespective of how many constraints were employed. For the X2 ensembles, the correlations are 0.83, 0.74, and 0.77 for the 100%, 80%, and 50% constraints set, respectively, similar to what is observed for the X1 ensembles. Therefore, our data show that the methodological similarity between NMR structure determination and GNM analysis is not a major factor causing good agreement between GNM predictions and NMR ensemble data.

Most importantly, we also noticed that the X-ray ensembles' MSDs are in better agreement with the equilibrium fluctuations inferred from GNM than the sole use of X-ray crystallographic B-factors. This is especially true for the X2 pseudo ensembles. As can be appreciated from Figure 4A and 4B, the correlations among the MSD profiles of both X1 and X2 ensembles agree equally well with their GNM predictions (panel A) and with the experimental NMR data (panel B), across the three different constraint sets. While there seems to be no noticeable change comparing the pseudo X1 ensembles and their GNM predictions versus the X1 B-factors and the GNM prediction, a large improvement in the correlations was seen in the X2 case.

Similar behavior was noted in the comparison of the pseudo X1 and X2 ensemble MSDs with the experimental NMR MSD. For X1, no significant differences in correlation were observed for all three ensemble MSDs and the corresponding experimental NMR MSD (0.77, 0.70, and 0.89 for 100%, 80%, and 50%, respectively) versus the correlation between the X1 B-factors and the NMR MSD (0.64). In contrast, a large improvement in the correlation between the pseudo X2 ensembles and the experimental NMR MSDs (0.77, 0.75, and 0.73 for 100%, 80%, and 50%, respectively) was noted, compared to the poor correlation of 0.31 between the B-factors and the NMR MSDs. Based on these findings, we conclude that it is preferable to consider the MSDs obtained from an ensemble of conformers, rather than solely considering the B-factors from a single crystal structure, for assessing the equilibrium fluctuation behavior of residues.

Interactions between neighboring molecules affect the dynamics in the crystal lattice

One may ask why improvements in the correlation were only found for X2 and not for X1? In order to answer this question, we analyzed the distinctive behavior of the X1- and X2-models and how it may relate to influencing B-factors. As pointed out previously, crystal packing can influence residue motions since the interactions between one molecule and its neighbors can dampen equilibrium motions.^{30, 35, 37} The fluctuations accessible in the crystal environment may therefore deviate from those observed in solution (or under physiological conditions), depending on the extent of intermolecular contacts in a given crystal lattice.^{30, 35, 37} Motions in the crystal will also deviate from those calculated by the GNM, since the GNM, by definition, predicts the ‘intrinsic’ dynamics in the absence of intermolecular interactions. It therefore is critical in any comparative assessment of the equilibrium dynamics to consider the isolated molecule and that in the crystal environment and elucidate any biases induced by crystal contacts.

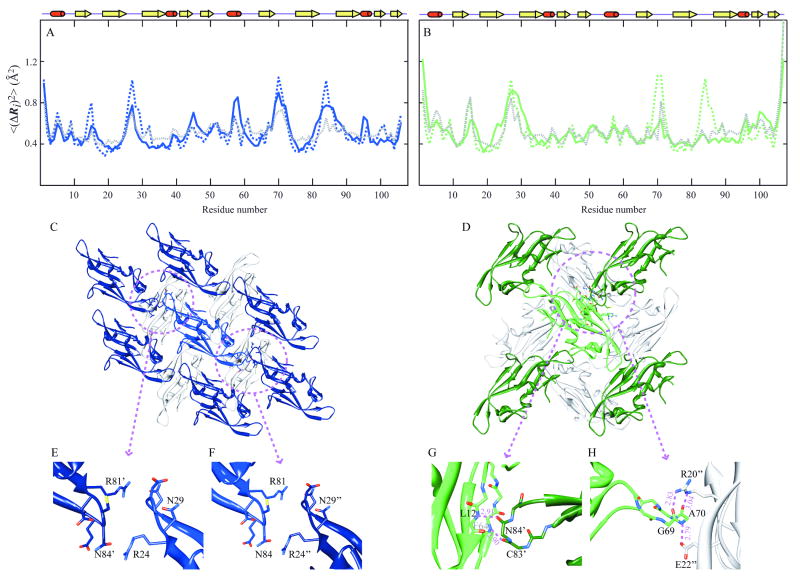
We therefore carried out additional GNM calculations that took into account inter-molecular contacts between adjacent proteins in the crystal lattices, including all immediate neighbors in the crystal lattice (Figure 5, panels C and D). The resulting MSD profiles for the crystal forms X1 and X2 are shown by the dashed gray curves in Figure 5 along with the experimental data (<(ΔR_i)²>_X1, blue, and <(ΔR_i)²>_X2, green, by solid curves). For comparative purposes, we also display the GNM predictions for the isolated protein (dotted blue and green curves). No significant differences are observed for the two sets of GNM results for X1 (correlation coefficients of 0.76 and 0.72 for the isolated and lattice embedded chain, respectively), while for X2 an increase from 0.51 to 0.69 is noted.

Figure 5. Comparison of theoretical and experimental residue fluctuations based on crystal packing of LKAMG in two different lattices.

Panels A and B refer to the crystal structures X1 and X2, respectively. Mean-square fluctuations of residues predicted by the GNM for the isolated protein (dashed blue in panel A, dashed green in panel B) and those in the crystal lattice (dashed gray in both panels) are compared with those inferred from X-ray crystallographic B-factors (solid blue and green in the respective panels). (C) and (D) ribbon diagram of LKAMG surrounded by its first neighbors in the respective p21 (X1) and p212121 (X2) crystal forms. The total number of surrounding molecules is 14 and 12 in the respective crystals. Four symmetrically related molecules on the upper plane are not displayed in each diagram for clarity. Encircled regions are enlarged in panels E, F, G, and H. Panels (E) and (F) highlights the inter-molecular contacts in X1, (G) and (F) those in X2.

Closer examination of the fluctuations profiles reveals that the three loops comprising residues 25-29, 68-73 and 81-87 are predicted by the GNM to be the most mobile regions. In the case of X1, these regions, indeed, exhibit relatively high B-factors. For X2, on the other hand, motions in loops 68-73 and 81-87 are dampened as evidenced by the experimentally observed smaller B-factors. The GNM calculations performed in the presence of neighboring molecules in the crystal lattice unambiguously reveal that the observed deviations are related to crystal packing. Note, a total of 15 (X1) or 13 (X2) molecules, including the central molecule of interest, were considered in the GNM predictions, and the fluctuations profiles for the central molecules are shown in the figure.

The different behavior of the GNM predictions for the two X-ray models in the context of their crystal neighbors is related to the different arrangement of individual proteins in the two different crystal space groups, p21 and p212121. In the X1 structure, one molecule is surrounded by 14 neighbors (Figure 5C) and the loop comprising residues 25-29 of the central molecule is in close contact with the 81-87 loop in the translationally related neighboring molecule (Figure 5E). In the contact region, the side chains of Arg24 and Asn29 of one molecule engage in electrostatic interactions with Asn84 and Arg81 of the neighboring molecule. Another intermolecular interaction involves the 68-73 and 94-96 loops (not shown). Clearly, such crystal contacts will influence the observed fluctuations, causing slight suppressions in GNM-predicted motions, compared to those obtained for the isolated protein.

In X2, each individual molecule is surrounded by 12 neighbors (Figure 5D) and the 81-87 loop makes intimate backbone contacts with residues in β-strands 1 (7-13) and 6 (59-68) of the neighboring molecule. In particular, the backbone oxygen atom of Cys83 forms a hydrogen bond with the amide of Phe64, and that of Asn84 with the Leu12 amide (Figure 5G). In addition, a number of side chain-backbone interactions are observed, including those involving Ala70-N and Glu22-Oε, Ala70-O and Arg20-Nε, and Gly69-O and Arg20-Nη. Clearly, such intimate interactions exert a significant effect on the fluctuations profile, and the experimentally observed suppression of residue motions in the crystal structure is reproduced by the GNM calculations performed for the X2 lattice.

Conclusion

The current work extends our previous analysis of NMR and X-ray structure parameters and GNM predictions.²⁹ In order to uncover the origin of the correlation between NMR data and computations, we undertook a detailed analysis for a specific protein. We chose LKAMG, given its small size, high thermodynamic stability and its multiple structures solved in our laboratory to high resolution. Multiple experimental and computational methods were applied to examine its structure and dynamics, allowing us to assess the limitations inherent to the different methodologies, and reconciling the apparent disparate data derived using different methodologies.

We previously suggested that the lower correlation between X-ray crystallographic B-factors and GNM results may be caused by the inaccessibility of large-scale motions in the crystal lattice, while solution NMR ensembles may inherently contain such motional characteristics.²⁹ Although compelling, the validity of this conjecture, and/or the contribution of other effects, had to be established. The present study provides data to that effect. Furthermore, in view of potential errors due to lack of specificity and nonlinear effects in the GNM predictions, we also compared the GNM results with MD simulations that use realistic force fields.

Our results show that the fluctuations profiles predicted by the GNM and observed in MD simulations exhibit a correlation of 0.64 ± 0.04 (comparable to the correlation between the individual MD runs), despite their fundamental differences in terms of the underlying model (e.g., all atoms vs. only α-carbons, specific nonlinear potentials vs. nonspecific, linear potentials) and method (simulations vs. unique analytical solution). Strikingly, GNM exhibits even higher correlation than MD with the experimental data, suggesting that the improved accuracy of the mathematically ‘exact’ GNM method that takes into account the entire network of structural interactions more than counterbalances the lack of precision/specificity in the model. An important feature of elastic network models is their ability to capture the cohesiveness and cooperativity in the overall structures. This cohesiveness accounted for by the network connectivity appears to play a dominant role in defining the accessible motions. Since GNM results can be generated extremely rapidly, our data suggest that they can be securely and effectively used to assess the equilibrium dynamics of proteins. The relatively good correlation between the GNM results obtained for different conformers (N1, X1, X2) also support the notion that GNM is relatively insensitive to atomic details.

An interesting finding pertains to the crystallographic data. The GNM predictions did not exhibit comparable correlations with the B-factors of the two crystal structures, although both X-ray structures are of the same protein and were solved to similar resolution: the correlation with X2 B-factors was distinctively lower than that with X1 B-factors (Table II). Likewise, all MD runs yielded poorer correlation with X2 data, pointing to an inherent feature of the X2 data. We therefore generated NMR-like ensembles of conformers, called X2-ensembles, using different sets of distance constraints extracted from the X-ray model. Three sets with 50-100% of the complete distance constraints were considered. The resulting MSD profiles exhibited distinctively better agreement with both GNM predictions and NMR data. This suggests that the inferior behavior observed for the X2 predictions originates from incomplete coverage of the accessible conformational space. Examination of the crystal contacts in the X2 structure substantiates this conclusion and GNM calculations in the presence of crystallographic neighbors confirmed that the origin of discrepancy between theory/computations and experiments lies in crystal contacts.

Our results also lend credence to the view that ensembles of conformers, rather than unique structures, allow computational methods to assess equilibrium dynamics more accurately.^{5, 6, 49, 50} Not surprisingly, higher accuracy comes at the expense of lower precision, paralleling the lack of precision in coarse-grained analytical approaches such as GNM compared to MD simulations. However, useful information on structural dynamics, otherwise inaccessible, can be extracted in this fashion.