The Energetics of Allosteric Regulation of ADP Release From Myosin Heads

Abstract

Myosin molecules are involved in a wide range of transport and contractile activities in cells. A single myosin head functions through its ATPase reaction as a force generator and as mechanosensor, and when two or more myosin heads work together in moving along an actin filament, the interplay between these mechanisms contributes to collective myosin behaviors. For example, the interplay between force generating and force sensing mechanisms coordinates the two heads of a myosin V molecule in its hand-over-hand processive stepping along an actin filament. In muscle, it contributes to the Fenn effect and smooth muscle latch. In both examples, a key force sensing mechanism is the regulation of ADP release via interhead forces that are generated upon actin myosin binding. Here we present a model describing the mechanism of allosteric regulation of ADP release from myosin heads as a change, ΔΔG-_D, in the standard free energy for ADP release that results from the work, Δμ_mech, performed by that myosin head upon ADP release, or ΔΔG-_D = Δμ_mech. We show that this model is consistent with previous measurements for strain-dependent kinetics of ADP release in both myosin V and muscle myosin II. The model makes explicit the energetic cost of accelerating ADP release, showing that acceleration of ADP release during myosin V processivity requires ∼ kT of energy whereas the energetic cost for accelerating ADP release in a myosin II-based actin motility assay is only ∼0.4 kT. The model also predicts that the acceleration of ADP release involves a dissipation of interhead forces. To test this prediction, we use an in vitro motility assay to show that the acceleration of ADP release from both smooth and skeletal muscle myosin II correlates with a decrease in interhead force. Our analyses provide clear energetic constraints for models of the allosteric regulation of ADP release and provide novel, testable insights into muscle and myosin V function.

INTRODUCTION

Despite their functional differences both muscle myosin II and myosin V share many mechanochemical features. First, they both function as enzymes that catalyze the hydrolysis of ATP and bind an actin filament cofactor to further activate the hydrolysis of ATP (1, 2). Second, they are molecular motors that generate force upon strong binding to actin (3-5). Finally, they are mechanosensors with biochemical transitions that are altered by applied forces (6, 7). In both myosin V and muscle myosin II, the interplay between force-generating and force-sensing mechanisms is critical for their cellular function. When two or more myosin heads function together in moving along an actin filament, the force generating biochemistry of one myosin head influences the force sensing biochemistry of other myosin heads. In myosin V molecules, this mechanochemical feedback coordinates the two heads of a processive myosin V molecule, allowing it to follow a hand-over-hand mechanism in transporting vesicles long distances along actin filaments without diffusing away from the actin filament (8-14). In muscle, the interplay between force-generating and force-sensing mechanisms leads to behaviors such as the Fenn effect (the force-dependence of heat output observed in all muscle types) (7, 15) and latch (the efficient maintenance of force observed in smooth muscle) (16, 17). In this paper, we propose a novel thermodynamic model to describe these effects. To test this model, we develop and implement an in vitro assay for measuring changes in both intermolecular forces and actin-myosin biochemistry during myosin-based actin motility.

Strong binding of myosin to an actin filament induces a discrete lever arm rotation, which is widely thought to be the primary mechanism by which myosin generates force and moves actin filaments (18, 19). Myosin undergoes an additional, smaller lever arm rotation associated with the release of ADP (20, 21). However, rather than acting as a force generating mechanism, this second rotation is thought to function as a force sensing mechanism; the distinction being that the former is associated with a negative (work performing) free energy change whereas the latter has a positive (work absorbing) free energy change (17, 22). The basic mechanism for myosin force sensing is that a force applied in a direction that assists the lever arm rotation accelerates ADP release, whereas a force applied in a direction that resists the rotation slows ADP release. The question addressed in this paper is how does the force-generating transition of one myosin head affect the force-sensing transitions of other myosin heads?

According to early muscle models (23) actin-binding of a given myosin head produces a positive intrahead mechanical strain, which is subsequently relaxed upon sliding of the actin filament. Unloaded actin filament sliding decreases the strain in all myosin heads bound to that filament, eventually pulling myosin heads into regions of negative force and strain, where they resist actin movement (24). The effect of this variable strain on the kinetics of ADP release is historically described through arbitrarily defined strain-dependent kinetics, presumably as an estimate of the effects of strain on myosin's active site. With these models an energetic link between myosin force-generating and force-sensing transitions is muddled.

Recently, theoretical and experimental studies of smooth muscle myosin and non-muscle myosins I, V, and VI indicate that strain-dependent kinetics of ADP release and ADP binding can be described as a change in mechanical potential (or work), Δμ_mech, associated with these transitions (11, 22, 25, 26). In these models, Δμ_mech has been described in terms of either a generalized potential or as a mean-force potential, F·d, where upon ADP release myosin rotates a distance d against (or with) a mean interhead force, F. The problem with many of these models is that they do not explicitly describe the acceleration of ADP release as a dissipative mechanical process through which interhead forces are diminished, and thus they lack a proper description of the energetic origins, limits, and costs of the allosteric regulation of ADP release.

In this paper, extending a previous model for the interhead strain generated upon actin-myosin binding (27), we describe Δμ_mech as a change in interhead strain that occurs when the lever arm rotates upon ADP release. We apply this model to both myosin V processivity (a simple two-head complex) and muscle shortening (a many-head complex) and show that it is consistent with estimates of the effects of interhead strain on ADP affinity. To further test this model, we use a novel in vitro assay and show that the acceleration of ADP release observed during myosin II-based actin motility correlates with a dissipation of interhead forces. This model and supporting data provide significant new insights into the fundamental mechanism for the interplay between myosin force generating and force sensing transitions and offer potential new mechanisms for allosteric regulation of proteins in general.

METHODS

Protein purification

Skeletal muscle myosin was purified from chicken pectoralis muscle as previously described (28) and stored in glycerol at −20° C. Smooth muscle myosin was purified from gizzard as previously described (29) and stored at 4° C on ice. Actin was isolated from chicken pectoralis (30) and stored on ice at 4° C. For in vitro motility assays, actin was incubated with tetramethylrhodamine isothiocyanate (TRITC) phalloidin overnight.

Buffers

Myosin buffer (300mM KCl, 25mM Imidazole, 1mM EGTA, 4mM MgCl₂, 10mM DTT), actin buffer (50mM KCl, 50mM Imidazole, 2mM EGTA, 8mM MgCl₂, 10mM DTT) and motility buffer (50mM KCl, 50mM Imidazole, 2mM EGTA, 8mM MgCl₂, 10mM DTT, 0.007 to 1mM ATP, 0.5% Methyl Cellulose) were prepared and stored at 4° C.

Activity assays

The velocity of fluorescently-labeled actin filaments sliding over a bed of myosin molecules was measured using an in vitro motility assay at 25° C. Flow cells were prepared by attaching a nitrocellulose-coated cover slip to a microscope slide with 0.125 mm shim spacers. Flow cells for the motility assay were prepared as follows; 2 × 40 μl washes of myosin with a one minute incubation period, 2 × 40 μl washes with 0.5 mg/ml BSA, 2 × 40 μl washes of actin with a one minute incubation period, 2 × 40 μl washes with actin buffer, and 2 × 40 μl washes with motility buffer. Experiments were performed with myosin preparations that were less than two months old. With these preparations we found little if any effect of purification of “dead head” myosin through actin spin down or actin blocking protocols, indicating actin motility was unaffected by dead heads, thus in these experiments we did not further purify dead heads prior to our experiments. Motility assays were performed using a Nikon TE2000 epifluorescence microscope with fluorescent images digitally acquired with a Roper Cascade 512B (Princeton Instruments, Trenton, NJ) camera. For each flow cell, we recorded three 30-second image sequences from three different fields, each containing approximately 10 to 15 actin filaments. Data obtained from these three fields constitutes one (n = 1) experiment. For each image sequence, we analyzed actin movement using Simple PCI tracking software (Compix, Sewickley, PA) to obtain actin sliding velocities, V. Objects were defined by applying an exclusionary area threshold to minimize background noise. Intersect filters were applied to exclude intersecting filaments. The velocities of the moving actin filaments were plotted as a histogram and fitted to a Gaussian distribution. The average velocity, V, for the field was taken from the mean of the Gaussian fit. Velocities obtained from the Gaussian distributions of the three image fields per flow cell were used to calculate an average velocity for the flow cell. These experiments were repeated at least three times for each condition. To measure the extent to which actin filaments break over time, we used ImageJ (31) to measure the average actin filament length within a single image obtained both at the beginning of a motility experiment and after five minutes of myosin-based actin motility.

RESULTS and DISCUSSION

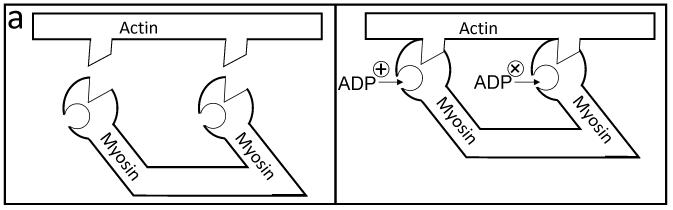
From a purely biochemical perspective, the allosteric regulation of myosin's ADP affinity by actin binding can be depicted by the cartoon in Figure 1a. Briefly, an actin filament acts as an allosteric effector, which upon binding both heads of a myosin dimer decreases ADP affinity for one head and increases ADP affinity for the other head. In myosin, our understanding of this cooperative mechanism is enhanced by our ability to measure myosin mechanical transitions.

Figure 1.

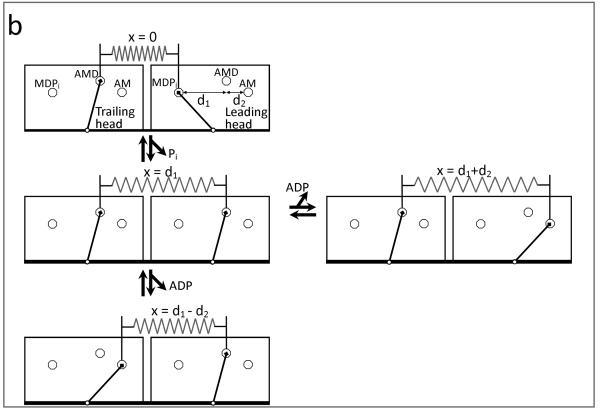
Kinetic and physical models for allosteric regulation of ADP release from myosin. (a) Actin binding to two myosin heads (left to right) increases the ADP affinity for one head and decreases the ADP affinity for the second head. (b) A four state mechanochemical model accounts for the allosteric regulation illustrated in (a) in terms of an interhead strain (spring) that changes with changes in the biochemistry of either head (A = actin, M = myosin, D = ADP, and P_i = inorganic phosphate). With one myosin head bound to actin in the A.M.D state (top), interhead strain is generated when a second head strongly binds to actin (top to middle left), stretching a compliant element (spring) a discrete distance d₁. Here the spring represents the effective stiffness of all compliant elements that exist between the two heads (e.g., actin, flexible lever arm, myosin coiled coil, etc.). When both myosin heads are bound to actin in the A.M.D state, ADP release can occur either from the trailing head (middle left to bottom), relaxing the compliant element a distance d₂, or from the leading head (middle left to right), stretching the compliant element a distance d₂. If ADP is released from the trailing head, as seen in the bottom pathway, strain is dissipated in assisting ADP release. The pathway to the right depicts the release of ADP from the leading head, which requires work to generate strain thereby slowing the ADP release rate.

Figure 1b makes explicit a model – implied by numerous studies (11, 22, 25, 26) – for the regulation of ADP release. Specifically, with one myosin head (the trailing head) bound to an actin filament (Fig. 1b, top), the binding of a second (leading) myosin head to that same filament (Fig. 1b, top to middle left) induces a discrete structural change, generating mechanical strain, μ_mech = ½κ·d₁², between the two heads, where κ is the stiffness of the linking mechanical element and d₁ is the distance the element is stretched upon strong actin binding. This strain can be generated between the two heads of a myosin dimer or between two or more myosin heads in muscle or an in vitro motility assay. Upon ADP release from the leading head (Fig. 1b, middle left to right), the interhead strain increases to μ_mech = ½ κ·(d₁+d₂)² , where d₂ is the distance the spring is stretched with the second lever arm rotation associated with ADP release. The work, Δμ_mech, performed by the leading (positively strained) myosin head with this transition is

$$\Delta {\mu }_{\mathrm{mech}}=-[1∕2\kappa \cdot {{\mathrm{d}}_1}^2-1∕2\kappa \cdot {({\mathrm{d}}_1+{\mathrm{d}}_2)}^2]$$ (1)

If ADP is released from the trailing head (Fig. 1b, middle left to bottom) rather than the leading head the interhead strain decreases to μ_mech = ½ κ·(d₁ − d₂)², and the work performed with this transition is

$$\Delta {\mu }_{\mathrm{mech}}=-[1∕2\kappa \cdot {{\mathrm{d}}_1}^2-1∕2\kappa \cdot {({\mathrm{d}}_1-{\mathrm{d}}_2)}^2]$$ (2)

Similar to the mechanochemical formalism put forth by Huxley and Hill (23, 32) – only here Δμ_mech is a change in interhead strain rather than intrahead strain – the mechanical work (Δμ_mech) performed with a biochemical transition contributes to the standard free energy (i.e., the work that can be extracted from the system) for that biochemical transition. Thus the free energy change for ADP release, ΔG_−D°, is made more negative (more favorable) by Δμ_mech when ADP is released from the trailing head, or

$$\Delta {\mathrm{G}}_{-\mathrm{D}}=\Delta {\mathrm{G}}_{-{\mathrm{D}}^{°}}-(1∕2\kappa \cdot {{\mathrm{d}}_1}^2-1∕2\kappa \cdot {({\mathrm{d}}_1-{\mathrm{d}}_2)}^2),$$

whereas when ADP is released from the leading head, the standard free energy change for ADP release,

$$\Delta {\mathrm{G}}_{-\mathrm{D}}=\Delta {\mathrm{G}}_{-{\mathrm{D}}^{°}}-(1∕2\kappa \cdot {{\mathrm{d}}_1}^2-1∕2\kappa \cdot {({\mathrm{d}}_1+{\mathrm{d}}_2)}^2),$$

is made energetically less favorable by Δμ_mech. In contrast to many models of allosteric regulation, here the allosteric effects of actin binding on ADP release do not result from altering the active site of myosin. Rather the standard free energy for ADP release is altered by the work performed on myosin (Δμ_mech) upon ADP release, or ΔΔG_−D = Δμ_mech. The source for this energy (Δμ_mech) is well defined as the free energy for actin-myosin binding. The fraction, a, of Δμ_mech performed before the activation energy barrier for the lever arm rotation dictates the extent to which Δμ_mech affects the rate for ADP release,

$${\mathrm{k}}_{-\mathrm{D}}={\mathrm{k}}_{-{\mathrm{D}}^{°}}\cdot \exp (-\mathrm{a}\cdot \Delta {\mu }_{\mathrm{mech}})$$ (3)

and ADP binding

$${\mathrm{k}}_{+\mathrm{D}}={\mathrm{k}}_{+{\mathrm{D}}^{°}}\cdot \exp ((1-\mathrm{a})\cdot \Delta {\mu }_{\mathrm{mech}}).$$ (4)

This model makes explicit the energetic costs and constraints for allosteric regulation. Although the work performed by a single actin-myosin binding event is not in theory limited; the average work performed by an ensemble of binding events (either many sequential single molecule events or binding events of many myosin heads) is limited by the actin-myosin binding energy (13, 33). As previously described, this binding energy can be partitioned between interhead work (Δμ_mech) and the external work performed in moving an external load along an actin filament (27). Thus the work (Δμ_mech) performed in accelerating ADP release diminishes the capacity of myosin to perform external work. Although not the focus of this paper, this point is best illustrated by considering the different ways in which an external load can affect Δμ_mech. An external load would have no effect on Δμ_mech if it pulls on the leading-head side of the interhead compliance (Fig. 1b). In this case the acceleration of ADP release from the trailing head would be unaltered by an external load at the expense of the energy available to perform work in moving against that load. In contrast, if applied to the trailing-head side of the interhead compliance, an external load would diminish Δμ_mech, disrupting ADP regulation while restoring the energy available to perform external work.

We begin by applying this model to myosin V. Figure 2 shows a multi-pathway kinetic scheme for myosin V processivity, previously proposed based on measurements of the ADP dependence of myosin V processivity. According to this model, during the processive stepping of myosin V along an actin filament, ADP release can occur from the trailing head with the leading head either dissociated from (Fig. 2, top left to right) or bound to actin (Fig. 2, bottom left to right). Consistent with single-headed myosin V kinetic studies (1), the ADP binding constant for the top (unstrained) transition was estimated to be 1 μM whereas the ADP binding constant for the bottom (strained) transition was shown to be 60 μM (11). This reflects a difference in the standard free energy change for ADP release of ΔΔG_−D = −kT·ln(60/1) ≈ −4kT. The above model predicts that ΔΔG_−D equals the work (Eq. 2) performed by the trailing myosin head upon ADP release (Fig. 2, bottom left to right). Single molecule studies indicate that upon actin binding a myosin head displaces an actin filament a distance d₁ = 25 nm and then further moves a distance d₂ = 5 nm upon ADP release (6). Using these values to solve for ΔΔG_−D = Δμ_mech = −4kT, we obtain an interhead stiffness, κ, of 0.14 pN/nm, consistent with experimental studies (26). As discussed above, the work performed upon actin binding of the leading head (½κ·d₂²) is limited by the actin-myosin binding energy. Here 44 pN·nm ≈ 11 kT of the actin-myosin binding energy is used to generate interhead strain, and roughly 36% of this energy is used to accelerate ADP release. The remaining energy is available for use with the powerstroke that occurs upon ATP-induced detachment of the trailing head (27).

Figure 2.

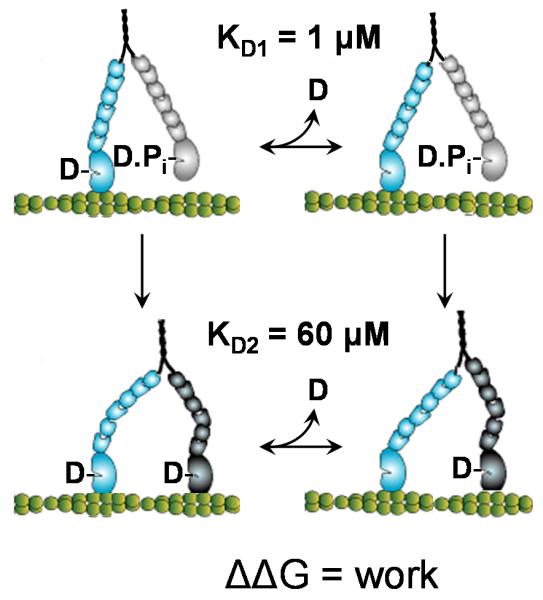
Multiple kinetic pathways of myosin V. During its hand-over-hand processive walking along an actin filament, the trailing head of myosin V can release ADP either with or without the leading head bound to actin. When ADP dissociation from the trailing head occurs before the leading head strongly binds to actin (top), no strain is imposed on the trailing head. The binding constant for this transition is 1 μM (11). When ADP dissociation from the trailing head occurs with the leading head strongly bound to actin (bottom) intrahead strain makes this transition more favorable. The binding constant for this transition is 60 μM (11).

Strain dependent kinetics are not unique to myosin V. It has long been argued that because there is no net force on an actin filament during unloaded sliding, the positive forces (and strain) generated by actin-myosin binding must be offset by negative forces (and strain) that resist actin movement (23, 24). According to most muscle models, this change in strain alters the rate of ADP release. However whether the strain that affects the rate of ADP release is intrahead as described in Huxley-like models (23) or interhead like in Fig. 1b and as described in collective force generating models of muscle contraction (34) remains unclear. In the former intrahead model, forces equilibrate within a myosin head and the force generated by one myosin head does not affect the mechanics of neighboring myosin heads. In the latter interhead model, forces equilibrate among myosin heads and the force generated by one myosin head influences the mechanics of neighboring myosin heads.

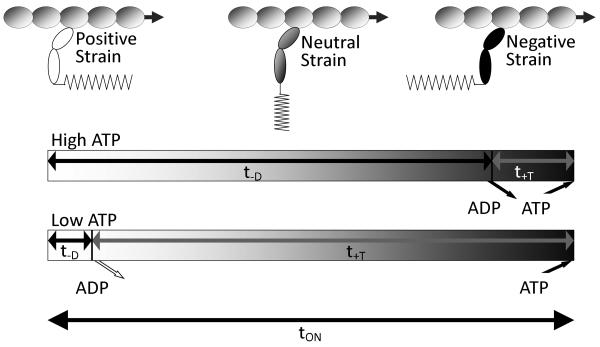
To study the effect of myosin head strain on the rate of ADP release from muscle myosin II heads and to better characterize the mechanism by which the variable strain generated during unloaded actin sliding alters ADP release from these heads, we use an in vitro motility assay. Figure 3 illustrates how myosin head strain changes over the time, τ_on, it remains bound to an actin filament during muscle shortening or in an in vitro motility assay. When a myosin head binds to an actin filament (Fig. 3, left) it generates a positive strain in a direction that assists actin movement. As the actin filament moves with time (Fig 3, left to right), the strain associated with the bound head decreases and eventually becomes negatively strained. Finally, ATP binding to myosin induces dissociation from actin (Fig. 3, right). The actin-myosin attachment time is the sum of the time myosin spends waiting for ADP release, T_−D = 1/k_−D, and the time myosin spends waiting for ATP to bind, T_+T = 1/k_+T[ATP], where k_−D is the ADP release rate and k_+T is the second order ATP-induced actin-myosin dissociation rate. The model in Fig. 3 predicts that by altering the ATP concentration, we can vary the average strain at which ADP release occurs. At high ATP concentrations ([ATP] >> k_−D/k_+T), most of the actin-myosin attachment time, τ_on, is spent waiting for ADP to be released, or τ_on ∼ T_−D. In this case ADP release occurs on average from negatively strained heads. In contrast, at low ATP concentrations ([ATP] << k_−D/k_+T), most of the actin-myosin attachment time, τ_on, is spent waiting for ATP to bind, or τ_on ∼ T_+T. In this case, ADP release occurs on average from positively strained heads. Thus we would expect actin sliding velocities obtained at low [ATP] to exhibit an ADP release rate that is slowed by positive strain, and actin sliding velocities obtained at high [ATP] to exhibit an ADP release rate that is accelerated by negative strain. A transition between these two extreme strain-dependent ADP release rates is predicted to occur at [ATP] = k_−D/k_+T.

Figure 3.

Depiction of how the average myosin head strain changes over the course of its actin-attachment time, τ_on, in an unloaded in vitro motility assay. Upon strong binding to actin (left), a myosin head generates a positive strain (in the direction of actin movement). Over time (left to right), actin movement decreases this strain eventually pulling the myosin head so that it becomes negatively strained before detaching from actin (right) (24). This balance of forces is required in an unloaded motility assay at any ATP concentration. At high [ATP] (top time line), most of a myosin head's actin attachment time is spent waiting for ADP to be released and ATP binding quickly follow. Under these conditions ADP release occurs, on average, from negatively strained heads. At low [ATP] (bottom time line), most of a myosin head's actin attachment time is spent waiting for ATP to bind. Under these conditions ADP release occurs, on average, from positively strained heads. The scale of the low [ATP] time line is roughly 10-fold smaller than that of the high [ATP] time line.

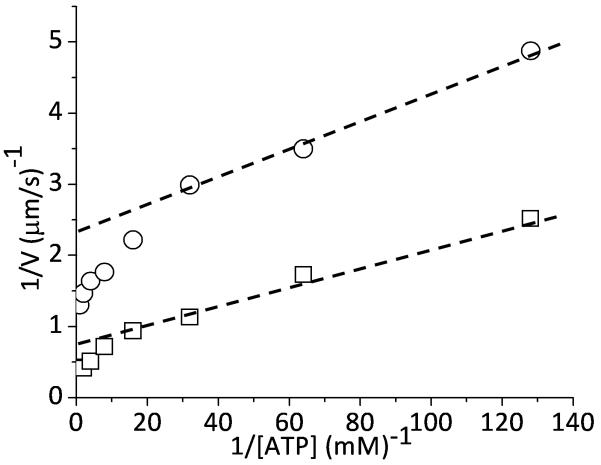
In fact, an [ATP]-dependent shift in the kinetics underlying actin sliding velocities has been reported (35), but until now has not been analyzed in terms of strain-dependent kinetics. Using an in vitro motility assay, we obtain actin sliding velocities at different ATP concentrations for both skeletal and smooth muscle myosin. In Fig. 4 we graph, in a double reciprocal plot, the ATP-dependence of actin sliding velocities, V, for both muscle myosin types. It is widely assumed that V varies inversely with the actin-myosin attachment time, τ_on, or d/V = τ_on = (1/k_−D + 1/k_+T[ATP]), where d is a proportionality constant often equated with myosin's step size (∼8 nm) (24). Fitting low [ATP] velocity data to this equation (dashed lines, Fig. 4), we obtain values for k_{−D(+strain)} of 55 s⁻¹ for smooth and 174 s⁻¹ for skeletal muscle myosin. At saturating [ATP], 1/V_max = 1/k_−D, and from V_max we estimate values for k_{−D(−strain)} of 96 s⁻¹ for smooth muscle myosin and 291 s⁻¹ for skeletal myosin. For both smooth and skeletal muscle myosin, there is roughly a two-fold difference between k_{−D(−strain)} and k_{−D(+strain).}

Figure 4.

The effect of [ATP] on actin sliding velocities, V, measured in a motility assay using smooth (○) and skeletal (□) muscle myosin and graphed in a double reciprocal plot. The dashed lines are a linear fit of velocities obtained at low [ATP].

According to a simple physical model (Eqs. 1 thru 3), this two-fold change in k_−D results from a two-fold difference between exp[(½a·κ·d₁² − ½a·κ·(d₁ − d₂)²)/kT] and [(½a·κ·d₁² − ½ a·κ·(d₁ + d₂)²)/kT]. If we assume that d₁ = 8 nm and d₂ = 2 nm for a muscle myosin head (7, 36), we obtain a value for a·κ of approximately 0.1 pN/nm. This is similar to the interhead stiffness estimated above for myosin V, but it is significantly less than the intrahead stiffness estimates of 1 – 2 pN/nm for a single skeletal muscle myosin head (37). One possible explanation for this discrepancy is that the strain that influences ADP release is interhead rather than intrahead. In other words, Eq. 2 describes the net change in strain in all compliant elements (head-head linkages, myosin-surface linkages, S2 hinge, etc.) that are affected when ADP is released from a given head. In this case, κ in Eq. 2 represents an effective interhead stiffness.

According to the above analysis, in a motility assay at high [ATP] the average work performed in accelerating ADP release from a single smooth or skeletal myosin head is ½κ·d₁² − ½κ·(d₁ − d₂)² ≈ 0.35 kT, assuming a = 1. Interestingly, the energetic cost for accelerating ADP release from muscle myosin (0.35 kT) is considerably less than that estimated above for myosin V (4 kT), consistent with the coordination of heads being more critical for the function of myosin V. The strain used to accelerate ADP release is ultimately generated by the weak-to-strong binding transition. For muscle myosin the energetic cost for the strain generated with the weak-to-strong transition is ½κ·d₁² = 3.2 pN·nm ≈ 0.8 kT, of which ∼45% is used to accelerate ADP release.

As discussed above, a strain-dependent model for allosteric regulation of ADP release from myosin predicts that the acceleration of ADP release involves a relaxation of interhead strain and a dissipation of interhead forces (Fig. 1b). Specifically, our model (Fig. 3) predicts that in a motility assay performed at high [ATP], the acceleration of ADP release would involve a dissipation of interhead forces; whereas at low [ATP], the slowing of ADP release would involve an increase in interhead forces. Consistent with this prediction, we have shown previously that at high [ATP], the acceleration of ADP release coincides with P_i-independent actin sliding velocities, consistent with low interhead forces. Whereas at low [ATP], the transition to slower ADP release rates accompanies a shift to P_i-dependent sliding velocities, consistent with a shift to high interhead forces (35).

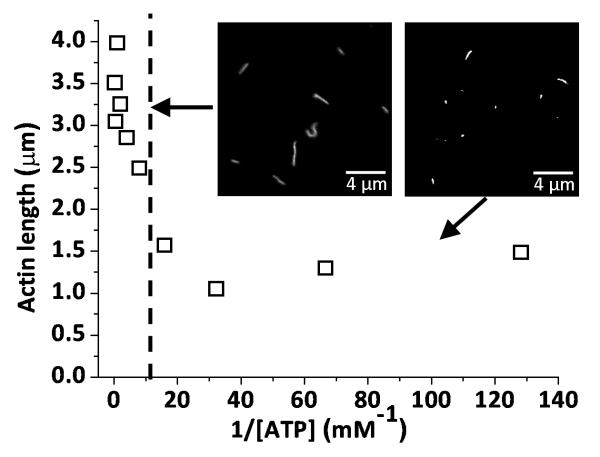
To further test the model prediction that acceleration of ADP release at high [ATP] coincides with a dissipation of interhead forces, we studied the rate at which actin filaments break in a motility assay as an indicator of the interhead forces exerted on the actin filament. Figure 5 shows the ATP-dependence of average actin filament lengths measured in a skeletal muscle myosin-based motility assay five minutes after flow cells were incubated with actin filaments and motility buffer. These data show a sudden transition from long filaments at ATP concentrations above approximately 100 μM to short filaments at ATP concentrations below 100 μM, indicating a transition from high interhead forces to low interhead forces when ATP concentrations are increased above 100 μM. In this assay, we observed little or no breaking of actin filaments over a five minute period in the absence of myosin, indicating that actin filament breaking is myosin dependent. We observed no effect of ATP on actin filament lengths in the absence of myosin, indicating that the ATP-dependence of actin filament breaking is also myosin-dependent. We observed little or no actin filament re-annealing during these experiments, indicating that re-annealing does not contribute to the observed change in actin filament lengths over time. Finally, when 10 nM TRITC-actin, 100 μg/ml myosin, and 10 μM ATP are mixed in motility buffer and imaged in a flow cell, we observe that actin filament breaking occurs primarily during myosin-based motility and not through actin-myosin interactions in solution. These results suggest that actin filament breaking observed in a motility assay at low [ATP] results from ATP- and myosin-dependent mechanics.

Figure 5.

The [ATP]-dependence of average actin filament length (□) measured in a skeletal muscle myosin II-based motility assay. Measurements were made five minutes after incubation in a motility assay. The vertical dashed line marks the approximate [ATP] above which we observe an accelerated ADP release rate (35), a loss of Pi-dependence of V (35), and minimal filament breaking, all consistent with the acceleration of ADP release being involving dissipation of interhead forces. The mean filament length at high [ATP] (left of the dashed line) is 3.18 μm. The mean filament length at low [ATP] (right of the dashed line) is 1.35 μm. The insets are characteristic images of fluorescently labeled actin filaments obtained at 1 mM ATP (left) and 10 μM ATP (right).

The ATP concentration (∼100 μM) above which we observe diminished actin filament breaking (Fig. 5) is remarkably similar to the critical [ATP] at which we observe a transition from a slow ADP release rate to an accelerated ADP release rates in Fig. 4. Likewise, it is the ATP concentration above which actin sliding velocities, V, become independent of P_i (35). Together these results provide strong support for the hypothesis in Fig. 1b that ADP release is accelerated by the work performed on myosin through the relaxation of interhead strain.

CONCLUSIONS

We propose a model that describes the allosteric regulation of ADP release as a change in the free energy for ADP release, ΔΔG_−D, caused by the mechanical work performed, Δμ_mech, with this transition in stretching interhead compliant elements, or ΔΔG_−D = Δμ_mech. This model is consistent with estimates for ΔΔG_−D in myosin V and accurately describes the acceleration of ADP release measured herein using an in vitro motility assay. Most notably, the prediction that the acceleration of ADP release is a mechanically dissipative process is consistent with our observations of a correlation between the acceleration of ADP release and the dissipation of interhead forces. This model presents an intriguing alternative to allosteric models that involve an altered active site. Although we cannot rule out the possibility that interhead strain can alter the active site of myosin, our analysis suggests that inter-molecular mechanical work is the predominant mechanism for allosteric regulation of ADP release from myosin. The model of interhead strain dependent kinetics makes several interesting predictions. For example, the model predicts that a change in interhead compliance will alter ADP release kinetics in a well-defined way (Eq. 2). The model presented herein describes a one-dimensional strain; however, models of three-dimensional strain, which would be most applicable to the lattice spacing in muscle, might reveal additional insights into the strain-dependence of ADP release in muscle.