A Hierarchical Algorithm for MR Brain Image Parcellation

Abstract

We introduce an algorithm for segmenting brain magnetic resonance (MR) images into anatomical compartments such as the major tissue classes and neuro-anatomical structures of the gray matter. The algorithm is guided by prior information represented within a tree structure. The tree mirrors the hierarchy of anatomical structures and the sub-trees correspond to limited segmentation problems. The solution to each problem is estimated via a conventional classifier. Our algorithm can be adapted to a wide range of segmentation problems by modifying the tree structure or replacing the classifier. We evaluate the performance of our new segmentation approach by revisiting a previously published statistical group comparison between first-episode schizophrenia patients, first-episode affective psychosis patients, and comparison subjects. The original study is based on 50 MR volumes in which an expert identified the brain tissue classes as well as the superior temporal gyrus, amygdala, and hippocampus. We generate analogous segmentations using our new method and repeat the statistical group comparison. The results of our analysis are similar to the original findings, except for one structure (the left superior temporal gyrus) in which a trend-level statistical significance (p=0.07) was observed instead of statistical significance.

I. Introduction

NEUROSCIENCE studies frequently use geometric models of brain structures for the detection of morphological differences between patient groups [1], [2]. For example, in a recent review of the literature, the most robust MR findings in schizophrenia are: enlarged lateral ventricles (77% of studies); medial temporal lobe (amygdala-hippocampal complex and/or parahippocampal gyrus) volume reduction (77% of studies); and gray matter volume reduction of the superior temporal gyrus (100% of studies) [3], [4]. These models are often based on manual segmentations made by experts who outline the structures of interest in MR images [5]. Generally, this process is not only time consuming, but inter- and intra-operator variability negatively impacts the reliability of such studies [6]. We address this issue by proposing a fully automatic, hierarchical segmentation algorithm that robustly parcellates images generated through standard clinical MRI acquisition into neuroanatomical structures.

Commonly used automatic segmenters for brain MR images identify gray matter, white matter, and cerebrospinal fluid with acceptable performance [7]-[17]. Nevertheless, neuroscientists are in great need of reliable segmentations of substructures of major tissue compartments for analyzing group differences in anatomy. Unfortunately, identifying these structures poses a serious challenge as their boundaries do not always coincide with tissue boundaries and may, therefore, not be visible in MR images (Figure 1). Automatic segmenters typically rely on prior information [18] in order to delineate these “invisible” boundaries. However, the use of prior information is not without risk as it can bias the automatic segmentation results [19]. Some successful attempts have been made to solve this problem, although current techniques are tailored and tuned to specific segmentation problems [20]-[23]. Moreover, the tuning results in assumptions making the implementations often difficult to adjust to other segmentation problems that deviate from the specific scenario. For example, the segmentation of compartments with large spatial variations within a population, such as lesions in elderly patients, are difficult to segment with methods based on label propagation via image registration of a template [24]-[29]. Furthermore, many of these methods are restricted to MR images from a certain acquisition protocol (e.g., high band width multiecho FLASH [21]).

Fig. 1.

The example shows different types of MR images of the same cortical region with corresponding segmentation. The boundary between dura and cerebrospinal fluid (blue-green boundary) is shown in the T₂-weighted image while the boundary of the cortex (gray regions) is better shown in the T₁-weighted image. Neither T₁ -nor T₂ weighted images, however, display the boundaries between the corresponding subcortical structures (each gray region corresponds to a different subcortical structure.)

This paper makes the following original contributions: We describe a segmentation algorithm guided by prior information represented within a tree structure. The tree captures the hierarchical relationship between anatomical structures and each sub-tree corresponds to a limited segmentation problem with a solution estimated through an EM implementation. We evaluate the accuracy of our algorithm by revisiting the clinical study by [30] segmenting 50 cases into the major brain compartments and the superior temporal gyrus, amygdala, and hippocampus. Based on our automatic segmentations, we detect similar group differences as in [30] between first-episode schizophrenia patients, first-episode affective psychosis patients, and comparison subjects with the exception of the left superior temporal gyrus in which only a trend was observed (p=0.07) but no significant difference.

We relate the segmentation of medical images to a tree representing the hierarchical relationship between anatomical structures. Unlike [31]-[33], where the tree structure contains the image at different resolutions, the nodes of our tree represent anatomical structures and the edges of the tree capture the hierarchy between different regions of interest. For example, the structure “brain” is a parent node of “gray matter”, “white matter”, and “cerebrospinal fluid”. The key idea is that prior information and segmentation parameters can be stored at each node and standard classification algorithms can be used to perform the segmentation. The process starts at the root of the tree, segmenting the image into the children of the root. A recursive process follows where each child becomes a root and the Region of Interest (ROI) associated with the new root is segmented into its children.

One advantage of this technique is its flexibility. For example, designing a new segmentation framework only requires the modification of the tree structure and its associated priors and parameters.

We show how an Expectation-Maximization (EM) segmentation algorithm can make full use of the tree structure. Unlike [7], [9], [13], [17], the observed data of our EM model is composed of image data and the tree structure. This results in an algorithm that can, for example, parcellate gray matter into its sub-structures.

We provide a validation of our algorithm using clinical data. We automatically segment 50 MR volumes into gray matter, white matter, and cerebrospinal fluid and further parcellate the gray matter into the superior temporal gyrus, the amygdala, and the hippocampus. The data set was previously manually segmented by a human expert and analyzed to study morphometric differences between first-episode schizophrenia patients, first-episode affective psychosis patients, and comparison subjects [30]. We repeat the statistical group comparison with our automated parcellations and find similar group differences for all structures except the left superior temporal gyrus, where we do not reach significance (p=0.07). To our knowledge, this is the first time that a fully automatic parcellator has been evaluated by revisiting a previously published statistical group comparison study based on manual segmentations.

The remainder of this paper is organized as follows. In Section II, we introduce the parcellation framework that is guided by the tree structure. The tree describes each anatomical structure of the segmentation problem in terms of its relation to other structures and structure-specific prior information. We modify a class of EM segmenters [7], [9], [13], [17] to be guided by the tree structure. We provide an example of an EM implementation in which the influence of prior and image information is varied throughout the tree. These modifications allow these segmenters to partition the major brain compartments into their sub-structures as defined by the segmentation tasks. In Section III, we revisit the previously published statistical group comparison between first-episode schizophrenia patients, first-episode affective psychosis patients, and comparison subjects [30] to evaluate the performance of our new segmentation approach.

II. Methods

Automatic segmentation algorithms for MR images usually treat every anatomical structure as an independent object or at best model local dependencies. For example, algorithms modeling the segmentation problem via Markov Random fields [11], [13], [34], [35] enforce spatial consistency within an anatomical region but do not explicitly define large-range dependencies across anatomical structures. We propose to model the anatomy with a hierarchical data structure (tree) that defines the substructure relations and organizes structure-specific atlas information. The approach provides a systematic and flexible framework that can be easily adapted to many different segmentation problems. It also subdivides the segmentation process into subproblems that are easier to solve than trying to parcellate all structures at once. In this article we use this principle to design a robust and flexible segmentation algorithm, where a solution to each subproblem is determined via an instance of the EM algorithm. However, this type of hierarchical method is not restricted to EM implementations.

A. Tree Representation for Anatomical Regions

As described above, for the purpose of segmentation, we represent anatomical information with a tree data structure. The root of the tree describes the region to segment, the leaves represent the final structures of interests, and the inner nodes are intermediate coarser anatomical ROIs. A node X is a child of another node Y if the structure associated with X is a substructure of the structure associated with Y. Figure 2 shows an example of a tree where an image is to be segmented into background (BG), cerebrospinal fluid (CSF), white matter (WM), and gray matter (GM). The root represents the whole image (IMAGE) and the four structures (BG, GM, WM, CSF) are described by the leaves of the tree. The intra-cranial cavity (ICC) is an intermediate node with the children GM, WM, and CSF. Note that the depth of the leaves does not need to be constant.

Fig. 2.

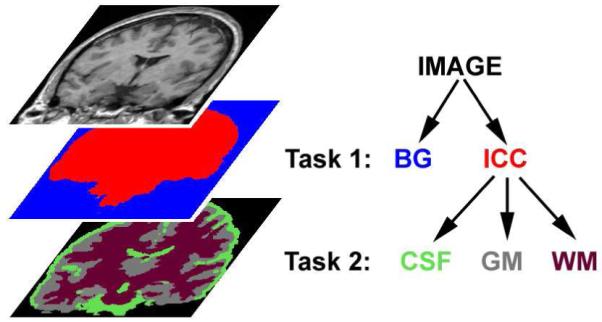
The relationships of anatomical structures are represented as a tree. Here, background (BG) and intra-cranial cavity (ICC) define the first task while cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM) comprise the second task.

Typically, a segmentation process has two types of inputs: one is the region to segment and the other is the set of information associated with each structure of interest. Common structure-specific information for MR segmentation includes class-conditional intensity models and space-conditioned label probabilities. In our framework, the set of structure-specific information is stored at the leaves of the tree. The information is then propagated from the leaves to the root in order to provide structure-specific information at each node of the tree. Section II-B will show how to combine the structure-specific information of children nodes to define meaningful structure-specific information of the parent.

The segmentation process, on the other hand, is achieved from top to bottom. The root is segmented into its children using the propagated structure-specific information, then each subtree is further segmented using the output of the higher-level segmentation as its input. The segmentation of each subtree is constrained to a unique ROI that does not overlap with the ROIs associated with the subtrees of the other children. The process is repeated until all leaves have been reached.

This technique has some convenient properties. First, when segmenting a subtree, only a subregion of the image is considered and a few structures are segmented at a time, which simplifies the segmentation problem. Second, the structure-specific information is only stored at the leaves, as the structure-specific information of an inner node is the combination of its children’s structure-specific information. The design of our segmentation framework is also flexible and reduces storage cost.

One drawback of the approach, however, is that it cannot recover from errors made in higher-level segmentations. One might address this issue by using the tree to specify a graphical model for statistical inference, but this is outside of the scope of this article.

Figure 3 shows a schematic representation of how information is propagated in the brain tissue classification example of Figure 2. Our algorithm first defines the task of segmenting the entire MR image into BG and ICC. The method produces the ROIs for ICC (shown in red), and BG (shown in blue). The second segmentation task is defined by the subtree rooted at ICC, thus the ROI of ICC is further segmented into CSF, GM, and WM. Once all leaves have been reached by this recursive process, the segmentation results associated with the leaves separate the entire image into BG, CSF, GM and WM.

Fig. 3.

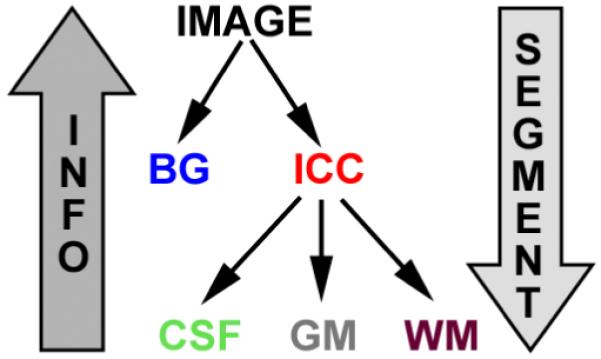
Propagating data within the tree structure. Structure-specific information (INFO) is propagated upward from the leaves to the root, while the segmentation process (SEGMENT) is propagated downward from the root to the leaves. Algorithm 1 provides a schematic description of the corresponding algorithm.

Algorithm 1 presents a synoptic view of our tree-based segmentation process. The algorithm takes as its inputs the image I, the root of a tree $\mathcal{R}$, the region of interest $\mathcal{R}OI$, and the current label map $\mathcal{L}$. By default, the $\mathcal{R}OI$ of the initial invocation is the entire image. The algorithm assesses the children of the root, $\text{CHILD}\left(\mathcal{R}\right)$, and the leaves of the tree, $\text{LEAF}\left(\mathcal{R}\right)$. Note, that if $\mathcal{R}$ is a leaf then $\text{LEAF}\left(\mathcal{R}\right)=\left\{\mathcal{R}\right\}$. The algorithm segments image I into the set of children $\text{CHILD}\left(\mathcal{R}\right)$ over an $\mathcal{R}OI$ via SEGMENT(·). SEGMENT(·) is a placeholder for a class of conventional segmenters. These classifiers segment an image into the anatomical structures $\text{CHILD}\left(\mathcal{R}\right)$ based on the structure-specific information $\mathcal{H}$, which in our case depends on the leaves $\text{LEAF}\left(\mathcal{R}\right)$.

In order to map the tree structure into SEGMENT(·), we now define the function $\mathcal{A}(\cdot )$ that maps a node of the tree ${\mathcal{R}}^{\prime }\in \mathcal{R}$ to an index $\mathcal{A}\left({\mathcal{R}}^{\prime }\right)\in \mathbb{N}$ that conforms to the framework of SEGMENT(·). For example in Figure 2, the node BG might be mapped to index 1 and the node ICC to index 2. If $\mathcal{A}(\cdot )$ is applied to a set of nodes it will return the set of corresponding indices. In the next section, we provide an example for such an algorithm.

After SEGMENT(·) determines a label map for the $\mathcal{R}OI$, a recursive call is made, where each child ${\mathcal{R}}^{\prime }\in \text{CHILD}\left(\mathcal{R}\right)$ becomes a root of a sub-tree with a new region of interest $\left(\mathcal{R}O{I}^{\prime }\right)$ defined by the results of the segmentation of the parent. The process stops once all leaves have been visited.

In summary, our algorithm segments the image into the structures of interests by propagating the structure-specific information upwards and the segmentation results downwards.

Algorithm 1.

TreeSegment(I,$\mathcal{R}$,$\mathcal{R}OI$,$\mathcal{L}$)

define $\text{CHILD}\left(\mathcal{R}\right)$←set of children of root $\mathcal{R}$

define $\text{LEAF}\left(\mathcal{R}\right)$←set of leaves of tree with root $\mathcal{R}$

define $\mathcal{H}$ ←set of structure-specific information defined    by $\text{LEAF}\left(\mathcal{R}\right)$ for nodes in $\text{CHILD}\left(\mathcal{R}\right)$

update $\mathcal{L}$ in $\mathcal{R}OI$ with results of   Segment(I,$\mathcal{R}OI$,$\mathcal{A}\left(\text{CHILD}\left(\mathcal{R}\right)\right)$,$\mathcal{H}$ )

for each node ${\mathcal{R}}^{\prime }$ in $\text{CHILD}\left(\mathcal{R}\right)$ that is not a leaf  define $\mathcal{R}O{I}^{\prime }$ ← all voxels x with ${\mathcal{L}}_x=\mathcal{A}\left({\mathcal{R}}^{\prime }\right)$  TreeSegment(I ,${\mathcal{R}}^{\prime }$,$\mathcal{R}O{I}^{\prime }$,$\mathcal{L}$)

B. An Anatomically-Guided EM Approach

EM segmentation algorithms have become a popular tool to perform MR image segmentation [7], [9], [13], [17]. They not only segment the image into a label map, which is the unknown data in the EM formulation, but also incorporate an estimation of parameters related to either the image acquisition (e.g., intensity inhomogeneities [7]), or the segmentation process (e.g., atlas registration parameters [36]). To achieve this, the EM algorithm basically alternates between computing the unknown data (its expectation) given the parameters and observed data and refining the estimation of the parameters based on the observed data and the newly computed expected value of the unknown data [37]. We modify the underlying structure of these techniques by incorporating the tree structure as part of the structure-specific information associated with the segmentation problem.

In most voxel-based EM segmenters, the class assignments of the voxels, $\mathcal{T}$, are considered to be hidden data, while the image I is observed data, and the parameters θ encompass the image acquisition parameters, usually the effect of the intensity inhomogeneity. At each iteration i, the method improves the estimate θ^i- of the Maximum A Posteriori (MAP) probability solution by solving the following estimation problem

$$\begin{array}{cc}\hfill {\theta }^i\leftarrow & \underset{\theta }{\overset{\arg \max }{}}{E}_{\mathcal{T}\mid I,{\theta }^{i-1}}\left(\log P(\theta ,\mathcal{T}\mid I)\right)\hfill \\ \hfill =& \underset{\theta }{\overset{\arg \max }{}}\sum _{\mathcal{T}}P(\mathcal{T}\mid I,{\theta }^{i-1})\cdot \log P(\theta ,\mathcal{T}\mid I).\hfill \end{array}$$ (1)

We modify this MAP estimation problem with the data tree structure resulting in an algorithm that can be used for SEGMENT(·), the segmenter in the earlier defined Algorithm 1. Based on Algorithm 1, the input to the algorithm SEGMENT(·) is the image I, the region of interest $\mathcal{R}OI$, the set of indices $\text{CHILD}\triangleq \mathcal{A}\left(\text{CHILD}\left(\mathcal{R}\right)\right)$ into which the $\mathcal{R}OI$ should be segmented, and a set of structure-specific information $\mathcal{H}$ that is defined by the tree structure. We incorporate $\mathcal{H}$ in the probabilistic model of Eq. (1) by expanding the underlying incomplete data model. The observed data is now composed of the image I and the structure-specific data $\mathcal{H}$ so that Eq. (1) becomes:

$${\theta }^i\leftarrow \underset{\theta }{\overset{\arg \max }{}}{E}_{\mathcal{T}\mid I,\mathcal{H},{\theta }^{i-1}}\left(\log P(\theta ,\mathcal{T}\mid I,\mathcal{H})\right).$$ (2)

The voxel class assignments, $\mathcal{T}$, are represented by a space-indexed collection of indicator random vectors, ${\mathcal{T}}_x\in \{e_1,\dots ,e_N\}$, where x represents one of the voxels in the $\mathcal{R}OI$ and N stands for the number of structures to be segmented. The vector e_j is equal to one at position j, and zero everywhere else. If we assume voxel-wise independence of $\mathcal{T}$ then the MAP estimation problem changes to

$${\theta }^i\leftarrow \underset{\theta }{\overset{\arg \max }{}}\sum _x{E}_{{\mathcal{T}}_x\mid I,\mathcal{H},{\theta }^{i-1}}\left(\log P(\theta \mid {\mathcal{T}}_x,I,\mathcal{H})\right),$$ (3)

where we abbreviate with Σ_x the sum over all voxels x in the domain $\mathcal{R}OI$.

The expected value in Eq. (3) depends on structure-specific information $\mathcal{H}$ associated with each child (e.g., a Gaussian intensity model or a spatial probability atlas). As we described in Section II-A, only the leaves contain this information. Thus, the expected value $E_{{\mathcal{T}}_x\mid I,\mathcal{H},{\theta }^{i-1}}\left(\log P(\theta \mid {\mathcal{T}}_x,I,\mathcal{H})\right)$ needs to be expressed as the sum over all the indices associated with the leaves of the tree, which we name $\text{LEAF}\triangleq \mathcal{A}\left(\text{LEAF}\left(\mathcal{R}\right)\right)$. The MAP estimation problem then expands to

$$\begin{array}{cc}\hfill {\theta }^i\leftarrow \underset{\theta }{\overset{\arg \max }{}}\sum _x\sum _{j\in \text{LEAF}}& P({\mathcal{T}}_x=e_j\mid I,\mathcal{H},{\theta }^{i-1})\hfill \\ \hfill \cdot & \log P(\theta \mid {\mathcal{T}}_x=e_j,I,\mathcal{H}).\hfill \end{array}$$ (4)

The EM algorithm determines a solution to Eq. (4) in two steps. The Expectation-Step (E-Step) computes the “weight”, which is the posterior probability $P({\mathcal{T}}_x=e_j\mid I,\mathcal{H},{\theta }^{i-1})$ of an anatomical structure associated with index j being present at a specific voxel x, given the estimate of the parameters θ^i-1 and the image I. Using Bayes’ rule, the weights are defined as

$$\begin{array}{cc}\hfill {\mathcal{W}}_{x,j}& \triangleq P({\mathcal{T}}_x=e_j\mid I,\mathcal{H},{\theta }^{i-1})\hfill \\ \hfill & =\frac{P(I\mid {\mathcal{T}}_x=e_j,{\theta }^{i-1},\mathcal{H})\cdot P({\mathcal{T}}_x=e_j\mid {\theta }^{i-1},\mathcal{H})}{P(I\mid {\theta }^{i-1},\mathcal{H})}.\hfill \end{array}$$ (5)

In the class-conditional model on image intensities, $P(I\mid {\mathcal{T}}_x=e_j,{\theta }^{i-1},\mathcal{H})$ represents the intensity model (often defined to be a Gaussian distribution ) and $P({\mathcal{T}}_x=e_j\mid {\theta }^{i-1},\mathcal{H})$ represents space-conditioned probabilities (i.e. a probabilistic atlas) associated with each structure [9]. We provide examples for the two conditional probabilities in the next section.

The second step of the EM algorithm is the Maximization-Step (M-Step), which improves the estimate θ^i-1 based on the weights $\mathcal{W}$:

$${\theta }^i\leftarrow \underset{\theta }{\overset{\arg \max }{}}\sum _x\sum _{j\in \text{LEAF}}{\mathcal{W}}_{xj}\cdot \log P(\theta \mid {\mathcal{T}}_x=e_j,I,\mathcal{H}).$$ (6)

Once the EM process has converged, we need to extract the labeling $\mathcal{L}$ of the $\mathcal{R}OI$ defined at $\mathcal{R}$ into its substructure. This is achieved by first computing the weight of each child, j ∈ CHILD based on the weights of its leaves:

$${\tilde{\mathcal{W}}}_{x,j}\triangleq \sum _{k\in {\text{LEAF}}_j}{\mathcal{W}}_{x,k}.$$ (7)

We call $\tilde{\mathcal{W}}$ hierarchical Weights. We then assign each voxel in the $\mathcal{R}OI$ to the index of the child with maximum hierarchical weight:

$${\mathcal{L}}_x\triangleq \arg \underset{j\in \text{CHILD}}{\overset{\max }{}}{\tilde{\mathcal{W}}}_{x,j}.$$ (8)

The label map $\mathcal{L}$ is returned to the hierarchical algorithm as described in Section II-A.

If we now define the structure-specific parameters as $\mathcal{H}\triangleq \{\text{LEAF},{\text{LEAF}}_1,\dots ,{\text{LEAF}}_c\}$ - the set of all leaves and the leaves of all c children of the root - then we can replace the function call SEGMENT(·) in Algorithm 1 with the previously developed EM implementation, whose schematic description is given below:

Algorithm 2.

Segment(I,$\mathcal{R}OI$,CHILD,$\mathcal{H}$)

repeat

E-Step: Calculate $\mathcal{W}$ according to Eq. (5)

M-Step: Update θi according to Eq. (6)

until θi converges in$\mathcal{R}OI$

define $\tilde{\mathcal{W}}$ according to Eq. (7)

define label map $\mathcal{L}$ according to Eq. (8)

return $\left(\mathcal{L}\right)$

C. Segmenting Different Types of Boundaries

A robust and automatic parcellator for MR images has to accurately model different types of boundaries. For example, the definition of boundaries often depends on the MR acquisition pulse sequence. In Figure 1, the boundary between dura (blue in the label map) and CSF (green) is shown in the T₂-weighted image, and the T₁-weighted image visualizes the boundary between white matter (red) and the cortical substructures (gray). A segmentation problem is simplified in the existing segmentation framework by restricting each partial segmentation task towards one type of boundary.

However, the current framework does not capture the relationship between the boundaries and their appearances in the observed image data. For example, in the images of Figure 1, the segmentation algorithm guided by the tree structure of Figure 2 first detects the boundary between air and CSF, and subsequently identifies the remaining structures. For both segmentation tasks, the algorithm considers the T₁- and T₂-weighted images as equally important, which is clearly not the case. This deficiency can negatively bias the results due to image artifacts, such as partial voluming and noise. We address this issue by expanding the hierarchical structure-specific information with “influence parameters” that control the impact of different components of the observed data on the segmentation result.

The choice of influence parameters is closely linked to the specific EM implementation. We confine our discussion to a model similar to Wells et al. [7]. This model is easily adapted to our problem of brain tissue parcellation. We note, however, that the concept of influence parameters can also be integrated into the voxel-based segmenter such as [9], [13].

In [7], the parameter θ captures the image inhomogeneity. Based on this model, the conditional probability $P({\mathcal{T}}_x=e_j\mid \theta ,\mathcal{H})$ is defined to be independent of the parameters and the likelihood $P(I\mid {\mathcal{T}}_x=e_j,{\theta }^{\prime },\mathcal{H})$ only depends on the intensity I_x of image I at voxel x so that Eq. (5) simplifies to

$${\mathcal{W}}_{x,j}=\frac{1}{Z_x}P(I\mid {\mathcal{T}}_x=e_j,{\theta }^{\prime },\mathcal{H})\cdot P({\mathcal{T}}_x=e_j\mid \mathcal{H}).$$ (9)

If we now ignore the hierarchical parameter $\mathcal{H}$ then we can define Eq. (9) according to already existing EM models. Using the intensity model by [7], the likelihood $P(I_x\mid {\mathcal{B}}_x,{\mathcal{T}}_x=e_j)=\mathcal{N}(I_x;{\mathcal{B}}_x+{\mu }_j,{{\rm Y}}_j)$ is defined as a Gaussian distribution of the intensity I_x with the mean intensity μ_j and variance Υ_j of label j, and ${\mathcal{B}}_x$ being the image inhomogeneity $\mathcal{B}$ at voxel x. Unlike in [7], the prior $P({\mathcal{T}}_x=e_j)$ is spatially varying over the image domain as originally suggested in [9]. This distribution over space is captured by the probabilistic atlas $\mathcal{F}(j,x)$ of index j enabling the algorithm to distinguish anatomical structures with similar intensity patterns.

In the remainder of this section we extend the previous discussed distributions to our hierarchical concept within the EM framework, which is summarized by the maximization problem of Eq. (6). We do so by including “influence parameters” controlling the impact of structure-specific information on the segmentation results into $P({\mathcal{T}}_x=e_j\mid \mathcal{H})$ and $P(I_x\mid {\mathcal{B}}_x,{\mathcal{T}}_x=e_j,\mathcal{H})$.

1) Intensity-based Confidence Parameters

In general, each input channel in an MR acquisition sequence provides contrast for a different set of boundaries (see Section I). We incorporate this observation into our hierarchical model by controlling the impact of the input channels at each segmentation task. We add to the structure-specific information $\mathcal{H}$ the vector of intensity based influence-parameters ${\zeta }_{\mathcal{H}}$, with ${\zeta }_{\mathcal{H},k}$ defining the influence of input channel k in the segmentation task. We can then extend the original structure-specific Gaussian intensity distribution $\mathcal{N}({\mathcal{B}}_x+{\mu }_j,{{\rm Y}}_j)$ with ${\zeta }_{\mathcal{H}}$ by creating the following distribution in a lower dimensional space

$$P(I_x\mid {\mathcal{B}}_x,{\mathcal{T}}_x=e_j,\mathcal{H})=\mathcal{N}(I_x;{\zeta }_{\mathcal{H}}^T({\mathcal{B}}_x+{\mu }_j),{\zeta }_{\mathcal{H}}^T{{\rm Y}}_j{\zeta }_{\mathcal{H}}).$$ (10)

This model makes the assumption that ${\zeta }_{\mathcal{H}}$ is of the form ${\zeta }_{\mathcal{H}}=e_k$, which is equivalent to ignoring all input channels except the k^th one. We note that it is straightforward to extend this model to multiple input channels.

We now return to our previous example to show how ${\zeta }_{\mathcal{H}}$ is adjusted to the two different segmentation tasks described by Figure 2. We define the T₁-weighted as the first and the T₂-weighted as the second input channel. For the first segmentation task the boundary between background and ICC is clearly defined by the T₂-weighted, but not the T₁-weighted input channel, which results in ζ_IMAGE = e₂. For the second segmentation task, the boundary between WM, GM, and CSF is clearly outlined by the T₁-weighted images, so that the influence parameter is altered to ζ_ICC=e₁.

We have now extended the hierarchical framework by the influence parameters ${\zeta }_{\mathcal{H}}$ that define the influence of the input channels in a given segmentation task.

2) Regulating the Influence of Spatial Priors

Some boundaries are not visible in any of the input channels (see Section I). Our method identifies these boundaries via spatial priors. Spatial priors are also important for distinguishing ROIs with similar intensity patterns. However, they increase the risk of introducing biases in the segmentation results. We address this issue by carefully tailoring the use of spatial prior information to each segmentation task.

We control the impact of spatial priors by altering the definition of $P({\mathcal{T}}_x=e_{\mathcal{R}}\mid \mathcal{H})$ in a similar fashion to the conditional intensity probability of the previous section. We add the parameter ${\lambda }_{\mathcal{H}}\in [0,1]$ to the hierarchical parameter definition $\mathcal{H}$, where ${\lambda }_{\mathcal{H}}$ defines the influence of the spatial prior in $\mathcal{H}$. The conditional probability for each structure j ∈ Leaf is defined as the convex combination of a stationary prior and the probabilistic atlas

$$P({\mathcal{T}}_x=e_j\mid \mathcal{H})\triangleq (1-{\lambda }_{\mathcal{H}})\cdot \frac{1}{d}+{\lambda }_{\mathcal{H}}\cdot \mathcal{F}(j,x),$$ (11)

where d are the number of indices in Leaf.

In the example of Figure 2, the atlas information is of great importance for the first task because BG and ICC have similar intensity patterns. We therefore set λ_IMAGE to 1. For the second task, λ_ICC is set close to 0 as the boundaries are clearly defined by the input channels. In addition, the atlas fails to fully capture the relatively large and complex spatial inter-subject variations of each of the three tissue major compartments and therefore would bias the results.

After defining the conditional intensity distribution and the spatial prior, we revisit the definition of the weights. The E-Step, which calculates the weights $\mathcal{W}$ for each structure j ∈ Leaf defined by Eq. (9), is modified with respect to Eq. (10) and Eq. (11) to

$$\begin{array}{cc}\hfill {\mathcal{W}}_{x,j}\triangleq \frac{1}{Z_x}& \cdot \frac{e^{-\frac{1}{2}}{\left({\zeta }_{\mathcal{H}}^T(I_x-{\mathcal{B}}_x-{\mu }_j)\right)}^T{{\rm Y}}_j^{\prime -1}\left({\zeta }_{\mathcal{H}}^T(I_x-{\mathcal{B}}_x-{\mu }_j)\right)}{\sqrt{{(2\cdot \pi )}^n\mid {{\rm Y}}_j^{\prime }\mid }}\hfill \\ \hfill & \cdot ((1-{\lambda }_{\mathcal{H}})\cdot \frac{1}{d}+{\lambda }_{\mathcal{H}}\mathcal{F}(j,x)).\hfill \end{array}$$

Here, ${{\rm Y}}_j^{\prime }\triangleq {\zeta }_{\mathcal{H}}^T\cdot {{\rm Y}}_j\cdot {\zeta }_{\mathcal{H}}$, |·| is the determinant, and Z_x is the normalization term, which is the sum over all structures of the products of the conditional intensity probabilities and the conditional spatial probabilities. The impact of these modified distributions on the estimation of the parameters in the M-Step is straightforward.

We complete the discussion of the influence parameters by specifying the structure-specific information $\mathcal{H}$ of Algorithm 1 to reflect the developments of this section.

$$\begin{array}{cc}\hfill \mathcal{H}\triangleq & \{\text{LEAF},{\text{LEAF}}_1,\dots ,{\text{LEAF}}_c,({\mu }_1,{{\rm Y}}_1),\dots ({\mu }_d,{{\rm Y}}_d),\hfill \\ \hfill & \mathcal{F}(1,\cdot ),\dots ,\mathcal{F}(d,\cdot ),{\zeta }_{\mathcal{H}},{\lambda }_{\mathcal{H}}\}\hfill \end{array}$$

is now defined by the sets of leaves {LEAF,LEAF₁, . . . ,LEAF_c}, the structure-specific intensity parameters {(μ₁,Υ₁), . . . (μ_d,Υ_d)}, the spatial priors $\{\mathcal{F}(1,\cdot ),\dots ,\mathcal{F}(d,\cdot )\}$ for all d leaves, and the influence parameters ${\zeta }_{\mathcal{H}}$ and ${\lambda }_{\mathcal{H}}$.

In summary, we have defined a hierarchical segmentation framework that is guided by structure-specific information arranged as a tree. The tree is organized according to the relationships between anatomical regions. We then integrated a class of EM segmenters into the proposed framework. We further adopted one implementation [7] to increase the robustness of the method by extending the underlying EM model with influence parameters. Our implementation with corresponding source code of the algorithm is publicly available through the 3D Slicer [38], a software tool targeted towards medical imaging. In the remainder of this article we will show that this framework can accurately segment the major compartments as well as certain cortical structures from brain MR images.

III. Results: Revisiting a Schizophrenia Study

Hirayasu et al. [30] performed a brain morphometry study to compare gray matter volumes of ROIs between first-episode schizophrenia patients, first-episode affective psychosis patients, and healthy comparison subjects. First, a semiautomatic process classified the brain MR images into GM, WM, and CSF [39]. These three compartments defined the volume of the ICC that provided an approximate correction factor for global head size. An expert then manually delineated the posterior and anterior region of the superior temporal gyrus, amygdala, hippocampus, and parahippocampal gyrus inside the GM. The volumes of each anatomical structure were computed from the segmentations and used to detect possible morphometric differences between the three groups. The major finding of the analysis was a statistically significant difference in the volume of the left posterior superior temporal gyrus in the schizophrenic group compared to the other two groups.

In order to attempt to evaluate the performance of our hierarchical EM segmentation algorithm, we repeated the entire study using parcellations automatically generated by our new framework. We automatically segment the brain into CSF, WM, GM, superior temporal gyrus, amygdala, and hippocampus on all but one case, whose original data could not be retrieved. We then performed a statistical analysis similar to the one in [30] to detect possible volume differences between groups. The original study divided each anatomical structure into posterior and anterior region. However, this information was not available for the STG.

The study by [30] also included the parahippocampal gyrus, which we did not consider. This decision was made after detecting a low degree of spatial overlap in the data set used for inter-rater reliability in [30]. We measured the overlap through the Dice score [40] of the segmentations of two experts. The parahippocampal gyrus received a mean score of 68%, which was 8% lower than the average score of any other structure.

A. Study Data

The data set consists of 50 subjects: 16 schizophrenia (SZ) patients (13 male, 3 female), 17 affective (AFF) patients (14 male, 3 female; 12 bipolar, manic, 2 bipolar, mixed, 2 major depressive disorder), and 17 comparison (NC) subjects (15 male, 2 female). The acquisition protocol included two MR pulse sequences acquired on a 1.5 Tesla General Electric Scanner (GE Medical Systems, Milwaukee, WI). First, a SPoiled Gradient-Recalled (SPGR) sequence yielded a coronal MR volume of size 256 × 256 × 124 with voxel dimensions 0.9375 × 0.9375 × 1.5 mm³. Second, a double-echo spinecho sequence gave two axial MR volumes (proton density and T₂-weighted) of size 256 × 256 × 54 with voxel dimensions 0.9375 × 0.9375 × 3 mm³. For each subject, both axial volumes were co-registered and resampled to the SPGR volume coordinate space using a mutual information rigid registration algorithm [7].

B. Configuring the Hierarchical EM algorithm

1) Designing the Hierarchical Tree

As we have seen in section II-B, the key component to our segmentation technique is the organization of the structure-specific information and segmentation parameters into a tree structure. For our current problem, we describe the segmentation problem using the following hierarchy (Figure 4). First, the root (IMAGE) is separated into BG and ICC. Second, the ICC is partitioned into CSF, GM and WM. Third, GM is subdivided into the right and left superior temporal gyrus (rSTG/lSTG), the right and left amygdala-hippocampus region (rAM-HI/lAM-HI), and “all GM except STG and AM-HI” (GM-other). Finally, rAM-HI is further parcellated into right hippocampus (rHIP) and amygdala (rAMY), and lAM-HI into left hippocampus (lHIP) and amygdala (lAMY).

Fig. 4.

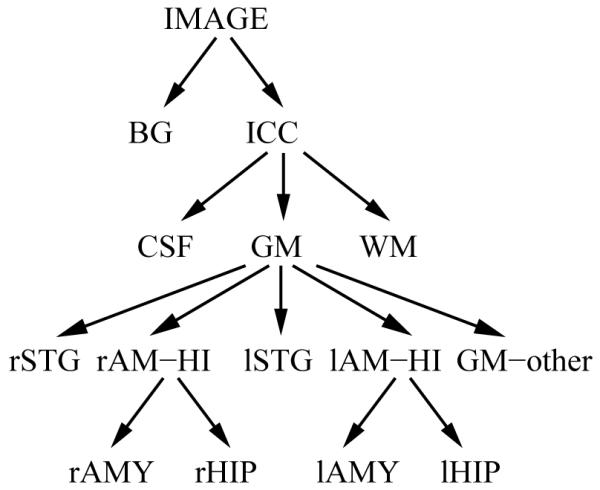
The tree describes the organization of the atlas information.

Next, we populate the tree with the structure-specific information (intensity model and spatial prior, see section II-B) and parameters (confidence in input type and spatial priors, see section II-C) necessary for the segmentation. Following [9] the intensity model is a Gaussian distribution whose mean and variance is learned from the data. The confidence parameters are organized as follows: The segmentation of IMAGE into CSF and ICC relies on the T₂-weighted image to better detect the boundary between CSF and dura mater. It makes use of the spatial prior (λ_IMAGE = 1 in Eq. (11)) so that structures outside the brain with similar intensities of brain tissues do not get included in the ICC. After this step all subsequent segmentations only make use of the SPGR image, as SPGR acquired according to the protocol of Section III-A offers better contrast between GM, WM and CSF. The spatial priors are largely ignored (λ_ICC ≈ 0) in the segmentation of ICC into GM, WM and CSF, because the SPGR images show enough contrast between these structures. The spatial priors, if not perfectly aligned, might also decrease the performance of the segmenter. However, our hierarchical approach relies on the spatial priors $({\lambda }_{\mathcal{H}}=1)$ for all the deeper levels of the tree as there is very little, if any, contrast between GM substructures in a SPGR and T₂-weighted images.

We now have a full description of the algorithm through our tree representation. Unfortunately, the spatial priors needed for our problem are not readily available. We thus build structure-specific information for the specific segmentation problem at hand.

2) Building the Spatial Priors

A spatial prior represents the probability of a structure to be present at a certain location in an image, independent of the input images, intensity model or segmentation parameters. A popular approach to create a prior is to (i) build a probabilistic atlas based on many individual segmentations and (ii) warp this atlas into subject space. The warped atlas is then used as the spatial priors for segmenting the subject’s MR images [19], [41].

The null-hypothesis of the study, which we would like to reject, is that the volumes of the anatomical structures do not significantly differ between the three groups. In this spirit, we generate the atlas only from the manual segmentations associated with the NC group. The atlas is built by first choosing a subject at random within the set of data. This subject is called the template. Second, all subjects from the NC group are individually registered to the template using an affine registration algorithm [42]. The resulting affine transformations are applied to the corresponding manual segmentations. The label specific atlas is then defined by the ratio at each voxel location of the presence of the label within the set of aligned segmentations.

The spatial priors specific to each subject are created by warping the atlas to the subject. The warp is obtained using a B-splines algorithm [27] (based on the original work by Rueckert et al. [25]), which aligns the SPGR image of the template to the SPGR of the subject. Furthermore, we explicitly define the posterior and anterior boundaries across structures via the label maps of [30] as this boundary is defined by anatomical landmarks that were not provided in the training data set. An expert can quickly perform this task by identifying the first slice and the last slice showing the fornix along the border of the lateral ventricle.

As we are trying to reproduce the original study [30], using its manual segmentations to create an atlas for the automatic segmentation clearly introduces a bias with respect to the NC and may lead to overly optimistic evaluation results. Our solution was for subjects belonging to the NC group to remove the associated manual data from the atlas when segmenting the subject. This “leave-one-out” process is commonly used in machine learning to evaluate classification algorithms. Another approach would be to randomly pick a subset of subjects from the group and create an atlas only using these subjects. Unfortunately, our sample size does not permit us to perform this more conservative approach.

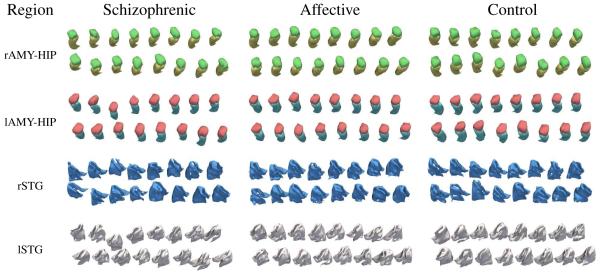
We have completed the description of the implementation, whose results for the STG and AM-HI are shown in Figure 5, and we turn to the analysis of its performance.

Fig. 5.

3D models based on automatic segmentations of the amygdala-hippocampus region (red = lAMY, blue = lHIP, green = rAMY, yellow = rHIP) and the superior temporal gyrus (white = lSTG, blue = rSTG). The result of the group comparison based on these 3D volumes is summarized in Table III.

C. Manual vs. Automatic Segmentations

In order to compare our automatic segmentations to the manual tracings of [30], we performed three types of analysis on the segmentations of all 50 subjects. First, we computed Pearson’s correlation between the manual and automatic methods based on the absolute volume of each structure. Second, we compared manual (MAN) and automatic (AUT) segmentations by computing the volume difference (VD)

$$VD\triangleq \frac{\mid \text{MAN}\mid -\mid \text{AUT}\mid }{(\mid \text{MAN}\mid +\mid \text{AUT}\mid )}$$

where |A| represents the volume of A. VD is scaled between -1 and 1. A negative score corresponds to the automatic segmentation being larger. Third, we measured the spatial overlap between the manual and automatic segmentations using the Dice score [40]. The results of these three metrics applied to our study are shown in Table I.

TABLE I.

Comparing automatic to manual segmentations over all 50 cases via mean Dice score and standard deviation, mean Volume Difference (VD) and Pearson’s correlation. In all structures used for this study the matrices indicate high correlation

Region	Voxel Overlap	Volume Overlap
	Mean Dice±SD	Mean VD	Pearson (N = 50)
lSTG	0.702 ± 0.035	-0.022 ± 0.061	r=0.664, p <0.001
rSTG	0.693 ± 0.033	0.040 ± 0.061	r=0.620, p <0.001
lAMY	0.867 ± 0.028	0.010 ± 0.065	r=0.881, p <0.001
rAMY	0.852 ± 0.030	-0.021 ± 0.070	r=0.811, p <0.001
lHIP	0.808 ± 0.029	-0.016 ± 0.069	r=0.724, p <0.001
rHIP	0.813 ± 0.043	0.037 ± 0.073	r=0.618, p<0.001
ICC	-	-0.056 ± 0.005	r=0.993, p<0.001

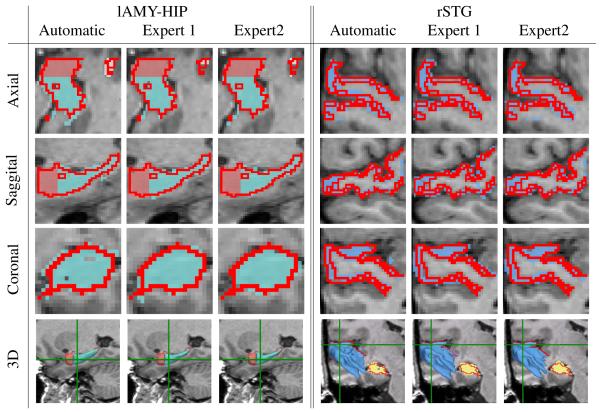
To help interpret the mean Dice score, we also analyzed the four cases used for inter-rater reliability in [30]. These cases were segmented by the rater of this study as well as two additional experts (see Figure 6). As in the case of the automatic segmentations, we computed the mean Dice score for the two additional experts by comparing their segmentations to the label maps of the rater of this study. The combined score of the two experts as well as the mean score of our automatic method in those four cases are shown in Table II. For each structure, the results of our implementation received slightly lower scores than the manual ones. If we now interpret the Dice score of the experts as an indication for the ambiguity of the boundary location of a structure then the discrepancy between the two types of segmentations is directly linked to this ambiguity. The discrepancy is highest for the left and right STG (6.6% and 4.8%), where the manual raters received the lowest Dice scores (76.7 % and 76.2 %). The discrepancy is lowest for the left amygdala (2.4%), where the experts receive the highest score (87.7%).

Fig. 6.

Comparison of automatic and manual segmentations for one scan. The red line outlines the segmentation generated by the rater of the study in Hirayasu et al. [30]. The label maps and 3D models correspond to the segmentations of our method (Automatic) and the two experts of the comparison study. The green lines in the last row represent the coronal and axial slice. The example illustrates the difficulties in segmenting structures with ambiguous boundaries as is evident from the variations among the experts segmentations.

TABLE II.

Comparing mean Dice score of automatic segmentations with the ones produced by two experts used for the comparison study in [30]

Method	lSTG	rSTG	lAMY	rAMY	lHIP	rHIP
Manual	0.767	0.762	0.877	0.873	0.862	0.857
Automatic	0.701	0.714	0.853	0.830	0.826	0.828

If we now return to Table I, we are pleased to report that the average Dice score ranges quite high from 70% (for STG) to 86% (AMY). The volumes of all structures are highly correlated between manual and automatic groups as VD is, on average, very small, and the p-values of the Pearson’s Correlation for all volumes indicate high correlation between manual and automatic segmentations.

D. Detecting Group Differences from Automatic Segmentations

We saw that the automatic segmentations are highly correlated with the ones used in [30]. We further evaluate our method by performing a statistical analysis on our data to compare diagnostic groups. In the next section, we follow the experimental statistical design of [30] to compare the volumes of our anatomical structures of interest between the schizophrenic (SZ), first-episode affective psychosis (AFF), and normal control (NC) groups.

Statistical Analysis

In order to correct for brain size, the relative volume of each segmented structure was computed by dividing its absolute volume by the ICC volume. We then studied these volumes in a hierarchical statistical framework. First, a mixed-model MANCOVA (Hotelling-Lawley trace) of the relative volumes was performed. The diagnostic (SZ, AFF, NC) was used as the between-subject factor, and side (left and right hemispheres) and region (STG, AMY, HIP) as the within-subject factors. The covariates were age of the subject at the time of the MR acquisition and parental socioeconomic status. This analysis was followed by a one-way ANOVA and post-hoc Least Square Difference (LSD) for each structure individually. Results were considered “significant” for p-values smaller than 0.05 and a “trend” for p-values smaller than 0.1. Table III and Figure 7 summarize the comparison.

TABLE III.

Mean and standard deviation of relative volumes of each anatomical structure and group (16 first-episode schizophrenia patients, 17 first-episode affective patients, and 17 controlled subjects) based on atomatic and manual segmentations. These measurements were input to the one-factor ANOVA, which determines for each structure significant or non-significant (n.s.) differences between the three groups

Region	Schizophrenic	Affective	Controlled	One-Factor ANOVA1
left superior temporal gyrus  automatic  manual	0.56 ±0.07%2 0.52 ±0.05%	0.58 ±0.07% 0.57 ±0.09%	0.60 ±0.05% 0.58 ±0.07%	F2,47 = 1.76 F2,47 = 4.183	n.s. p = 0.021
right superior temporal gyrus  automatic  manual	0.55 ±0.08% 0.58 ±0.07%	0.55 ±0.04% 0.61 ±0.06%	0.56 ±0.05% 0.62 ±0.09%	F2,47 = 0.4 F2,47 = 1.337	n.s. n.s.
left amygdala  automatic  manual	0.14 ±0.02% 0.15 ±0.03%	0.13 ±0.02% 0.13 ±0.03%	0.13 ±0.03% 0.14 ±0.04%	F2,47 = 2.033 F2,47 = 1.066	n.s. n.s.
right amygdala  automatic  manual	0.13 ±0.02%3 0.13 ±0.03%	0.14 ±0.03% 0.13 ±0.03%	0.16 ±0.03% 0.15 ±0.03%	F2,47 = 3.443 F2,47 = 3.253	p = 0.040 p = 0.048
left hippocampus  automatic4  manual	0.24 ±0.03% 0.23 ±0.03%	0.27 ±0.03% 0.25 ±0.05%	0.28 ±0.04% 0.28 ±0.03%	F2,47 = 5.567 F2,47 = 5.935	p = 0.007 p = 0.005
right hippocampus  automatic  manual	0.26 ±0.03% 0.28 ±0.03%	0.26 ±0.05% 0.28 ±0.05%	0.25 ±0.03% 0.28 ±0.03%	F2,47 = 0.024 F2,47 = 0.099	n.s. n.s.

¹covariates were the age of the subject at the time of the MR acquisition and the parental socioeconomic status.

²A trend for smaller volume in schizophrenic compared to control group (post-hoc test: p = 0.07)

³Significantly smaller volume in schizophrenics compared to controls (post-hoc test: p = 0.018)

⁴Significantly smaller volume in schizophrenics compared to controls (post-hoc test: p = 0.002) and affective (post-hoc test: p = 0.024)

Fig. 7.

Each graph shows the mean and standard deviation of the relative volumes specific to an anatomical structure according to the three groups - first-episode schizophrenia patients, first-episode affective patients, and normal control subjects.

The MANCOVA comparison revealed an almost significant group × hemisphere × region interaction (F_4,86 = 2.44, p = 0.052). The One-Factor ANOVA showed a significant group difference in the right amygdala (F_2,47 = 3.44, p = 0.04) and the LSD revealed a significantly smaller volume in first-episode schizophrenics compared to controls (p = 0.04). The One-Factor ANOVA also revealed a significant group difference in the left hippocampus (F_2,47 = 5.567, p = 0.0007) and the LSD revealed a significant smaller volume in first-episode schizophrenics compared to controls (p = 0.002) and first-episode affective psychosis group (p = 0.024). Although no significant results were found for the STG, the LSD test showed a trend of decrease in volume in first-episode schizophrenic compared to controls (p = 0.07).

E. Discussion of the Results

In our comparison study, we observed:

• a significantly smaller right AMY in SZ compared to NC,

• a significantly smaller left HIP in the SZ group compared to the other two groups,

• a trend of smaller left STG in the SZ group than in the NC group.

Our statistical analysis based on automatic segmentations agreed with the manual segmentation results except for the left superior temporal gyrus. This analysis is also consistent with reports in the literature, as the superior temporal gyrus and medial temporal regions (e.g., amygdala-hippocampal complex) are among the most consistently reported regions where schizophrenic patients exhibit volume deficits using both manual ROI methods [3] and Voxel-Based Morphometry (VBM) [43]. Of further note, hippocampal volume deficits are consistently reported in schizophrenia [3], [44]. Functionally, the amygdala is more related to emotional processing, and anatomically the amygdala has substantial neuronal connections with the subgenual anterior cingulate cortex that has been reported to be specifically altered in affective psychosis [45].

Our failure to reproduce the left STG results shows that the framework can still be improved. The STG is a highly convoluted structure, especially in schizophrenia [46], and the spatial prior atlas may contain too much uncertainty to accurately define the boundary. We also note that human raters have more difficulty segmenting this structure than the amygdala-hippocampal complex (see II). We are hopeful that with more data to define the spatial priors and a different tuning of the parameters we will be able to better segment this structure.

One interesting question about using automatic segmenters for this type of study is the impact of the atlas on the results. On the one hand, if one uses one atlas per population in order to get optimal segmentation results, this introduces a bias when performing statistical analysis. On the other hand, if one chooses the conservative approach of building a single atlas based on the segmentations of the NC group (as we did), one risks not properly capturing information specific to a population. One might address this problem by building an atlas based on the 50 subjects via leave-one-out validation. However, this still makes the assumption that a unimodal atlas properly represents the variations across the three groups. Blezek et al. [47] pointed out that populations are often better represented by multiple atlases.

We therefore re-ran the experiment using a separate atlas for each group (see Appendix). The study showed much lower p-values for five of the six structures previously reported in [30] and led to additional discoveries not discussed in [30]. These results, however, cannot be considered unbiased as having a separate atlas for each group can distort the statistics.

We further investigated this hypothesis by segmenting the NC group once with each atlas. If the three atlases did not bias the results then the study should not report any significant differences between the three types of segmentations. This, however, was not the case in this study: with the exception of the left STG, we found significant group differences for five of the six structures. In conclusion, neither using a single atlas nor multiple atlases seemed to properly represent the variations within the data set. This area may benefit from additional research.

In summary, we revisited the study of [30] in order to evaluate the accuracy of our fully automatic parcellator. We recorded similar findings between groups but could not reproduce the result of a smaller left STG in SZ.

IV. Conclusion

We introduced a parcellation algorithm for brain MR images that can be adapted to a wide variety of segmentation scenarios. The algorithm is guided by a tree-structured representation of data that organizes the structure-specific anatomical information. The tree also defines the set of segmentation tasks that are solved by a voxel-based segmenter. The tree structure can be modified and the segmenter can be replaced to adapt our algorithm to other segmentation problems.

We provided an implementation of our parcellation approach using an EM segmenter for brain tissue classification. We modified the approach by expanding its observed data model with our tree structure. In addition, we introduced influence parameters that control the impact of spatial priors and image information at each segmentation subproblem. These new features enabled the brain tissue classifier to further partition the tissue classes into their substructures

We evaluated the accuracy of the implementation by revisiting the study of [30]. The study consists of 50 subjects separated into first-episode schizophrenia, first-episode affective psychosis, and the normal controls. Our study finds similar results for all structures except the left STG, where we detected a trend for a smaller volume in SZ but no statistically significant difference (p=0.07). We discussed how choosing the correct atlas can impact the performance of the algorithm and statistical analysis. We are hopeful that with more training data some of the challenges faced in this study can be overcome. To aid in this effort, we plan on investigating robust ways of computing accurate atlases without biasing the statistical analysis.

Appendix

We repeated the study of Section III automatically segmenting each case with an atlas associated with the corresponding group. The group-specific atlases were created by applying the instructions of Section III-B.2 to the data set of each group. For example, the atlas for the first-episode schizophrenic was based on segmentations assigned to that group. The results of this study are shown in Table IV.

TABLE IV.

The result of the study described in Section III when generating the automatic segmentation by using a separate atlas for each group. For five out of the six structures, the p-value is significantly lower than the study based on the manual segmentations (see Table I). The higher significance of this study is probably a result of the bias introduced by segmenting the cases based on separate atlases for each group

Region	Schizophrenic	Affective	Controlled	One-Factor ANOVA1
left superior temporal gyrus	0.55 ±0.07%	0.61 ±0.07%	0.62 ±0.04%	F2,47 = 4.64	p = 0.015
right superior temporal gyrus	0.59 ±0.09%	0.61 ±0.05%	0.57 ±0.04%	F2,47 = 0.99	n.s.
left amygdala	0.14 ±0.02%	0.12 ±0.01%2	0.14 ±0.01%	F2,47 = 11.69	p = 0.0001
right amygdala3	0.12 ±0.01%	0.12 ±0.01%	0.15 ±0.02%	F2,47 = 17.66	p < 0.0001
left hippocampus	0.21 ±0.02%4	0.25 ±0.02%	0.27 ±0.02%	F2,47 = 35.17	p < 0.0001
right hippocampus	0.26 ±0.02%5	0.28 ±0.02%	0.27 ±0.02%	F2,47 = 4.04	p = 0.024

¹covariates were the age of the subject at the time of the MR acquisition and the parental socioeconomic status.

²Significantly smaller (post-hoc test: for schizophrenics p < 0.001, control groups p = 0.004).

³Significantly smaller in both patient groups compared to the controlled group (post-hoc test: p < 0.001).

⁴Significantly smaller (post-hoc test: affective psychosis p < 0.001, control groups p < 0.001).

⁵Significantly smaller compared to affective psychosis group (post-hoc test: p = 0.016).

The table shows much lower p-values in the One-Factor ANOVA in every structure but the right superior temporal gyrus compared to the manual segmentations reported in Table III. This is coupled with additional findings in the post-hoc analysis. These additional findings are properly due to the bias introduced by segmenting the subjects with group specific atlases.