FLOW DYNAMIC COMPARISON BETWEEN RECESSED HINGE AND OPEN PIVOT BI-LEAFLET HEART VALVE DESIGNS

Abstract

The flow dynamics through the peripheral and hinge regions of a bi-leaflet mechanical heart valve are complex and result in abnormally high shear stresses particularly during the closing phase of the valve function. It has been observed that, the late stages of closure is more significant in the dynamics of platelet activation; therefore, the later stages of closure is simulated by solving the two-dimensional Navier–Stokes equations using an Eulerian Levelset based sharp interface Cartesian grid method. Using a fixed Cartesian mesh incorporating local mesh refinement for solution accuracy and efficiency, the flow through and within a recessed hinge design and an open pivot hinge design is compared. Platelets are modelled as point particles by Lagrangian particle tracking algorithm with one way coupling. A dilute particle flow is assumed and particle-particle interactions are neglected. It was observed that the hinge region of the open pivot valve indicated a lower potential for activation of platelets compared to that in valves with a recessed hinge design.

Introduction

One of the major problems associated with implanted mechanical valve prostheses is the tendency for thrombus formation and ensuing embolic complications. In bi-leaflet heart valves thrombus formation is predominantly found in the hinge region as well as in the valve housing [1, 2]. Thrombus formation and thromboembolism in the hinge region could pose a threat by causing impedance to the motion of the leaflet. When the implant is in the mitral position, the risk of major embolism is twice compared to the aortic position [3] as the valve in the mitral position resists a flow with maximum pressure that the left ventricle generates.

Various studies have shown that the late stages of valve closure could be more damaging to blood elements resulting in platelet activation and thrombus initiation than during the other phases of the cardiac cycle [4, 5]. High shear stress is generally accepted as a dominant factor in damaging the blood cells as well as activating the platelets [6]. It has also been observed that platelets get activated under low magnitudes of shear stress if exposed for a large duration of time [7, 8]. Thus the time of exposure to shear stress becomes an important factor in the activation of platelets. The relationship between the shear stress, its exposure time and the activation of platelets has been studied experimentally [4, 7–9]. Experiments which have focused on studying platelet deposition [7] in arterial stenosis have reported flow separation and recirculation being conducive to platelet activation and aggregation. Flow through complex geometries such as the hinge region of a bi-leaflet heart valve, and in the gap between the leaflet and the housing result in high velocity magnitudes and elevated shear stresses due to the presence of instantaneous high shear stress magnitudes. Regions of flow separation and recirculation are also present downstream to these high shear flow regions. Platelets which pass through these small gaps are exposed to a range of shear stress magnitudes and get entrained in the recirculation region prevailing in the vicinity of the valve thus increasing the exposure time of the platelets to shear. Many studies have been conducted in the past to delineate the effects of flow through the hinge fields of various bi-leaflet valves. All the studies reported high shear stress in the vicinity of the hinge region followed by the development of recirculation region and stagnation zones where platelets could get trapped. Gross et al. [10] reported a velocity magnitude of 2.55 m/sec during the reverse flow phase in the hinge flow pocket with regions of re-circulation and stagnation. The flow also experienced a maximum shear stress of 700 dynes/cm². In an in-vitro study of the St-Jude Medical Regent bi-leaflet valve, Ellis et al. [11] observed the development of re-circulation zones in the vicinity of the hinge pocket during the forward flow phase. Simon et al. [1] compared the hinge flow fields of St. Jude and Carbomedics bi-leaflet mechanical heart valves under aortic and mitral conditions experimentally in a pulsatile flow loop using a three-component laser velocimetry. Velocity measurements exhibited common features such as forward flow patterns and leakage jets for the two valves even though the magnitudes of velocities and shear stress were different. The difference in the magnitudes of the velocity and turbulent stresses were attributed to the local differences in the hinge geometry between the two valves. The importance of the geometry of the hinge region and its effect on the flow dynamics was further highlighted by Gao et al. [13]. In that study they compared the flow in the hinge region of a Medtronic parallel, St-Jude medical valve and On-X valve and observed that the On-X valve did not present recirculation and stagnation region whereas the Medtronic parallel did, concluding that On-X and St Jude hinge regions were less thrombogenic than the hinge regions of the Medtronic valve.

The geometry of the hinge region is thus crucial in determining the flow dynamics in its vicinity and its effect on the activation of platelets which pass through the hinge region. Motion of the leaflet inside the hinge recess and the constricted design gives rise to a recirculation region and a leakage jet as observed in the previous experimental and computational studies. It was also observed that the platelet activation in the hinge region was found to be in the same order of magnitude when compared to that found in the leaflet edges although the shear stress found in the leaflet edge was three times larger than that in the hinge [4, 14]. One possible explanation could be a greater residence time for the platelets in the hinge region than at the leaflet edge. At present there are two popular hinge designs to a bi-leaflet mechanical heart valve. First one is that we see in designs such as those in Medtronic and St. Jude bi-leaflet heart valves where the leaflet ear pivots inside a recess in the housing which allows the leaflet to rotate. On the other hand, an open-pivot design has been incorporated in the ATS bi-leaflet valve without recesses in the valve housing potentially avoiding regions of flow stasis. The leaflet is held in its position by two hemispheres in the housing. The housing has a convergent-divergent geometry around the hemispheres allowing the leaflet to rotate at a specified angle. The present computational study will focus on the local flow and simulated platelet activation in the hinge region of an open pivot design in a two dimensional computational analysis and comparison of the results with those for a recessed hinge design.

Methods

The two-dimensional Navier-Stokes equation in the non-dimensional form is solved:

$$\overrightarrow{\nabla }·\overrightarrow{u}=0$$ (1)

$$\frac{\partial u}{\partial t}+\overrightarrow{u}·\overrightarrow{\nabla }·\overrightarrow{u}=-\overrightarrow{\nabla }·p+\frac{1}{Re}{\nabla }^2\overrightarrow{u}$$ (2)

In the above equation $Re=\frac{\rho VD}{\mu }$ is the Reynolds number where ρ, V, D, μ are fluid density, velocity, length scale and fluid viscosity respectively. The equations are solved by an Eulerian level-set based sharp interface Cartesian grid method that has been described in detail and validated with several test problems previously [2–5]. Incorporation of the local mesh refinement algorithm [19, 20] allows fast flow computation and solution accuracy. The mesh is automatically refined or coarsened based on the gradient and the curvature of the velocity field hence enabling efficiency and accuracy.

Platelets are modeled as point particles by the Lagrangian particle tracking algorithm [21] with one way coupling. The flow influences the particles but not otherwise and particle-particle interactions are neglected. Platelets are assumed to be spheres with a diameter of 2 μm. Particle concentration, velocities and activation parameter are computed for each particles that are seeded in the domain. A particle momentum equation in the non-dimensional form is solved to calculate particle velocity as

$$\frac{d\overrightarrow{v}}{dt}=\frac{\partial v}{\partial t}+\overrightarrow{v}·\nabla \overrightarrow{v}=\overrightarrow{f}$$ (3)

In the above equation v⃗ is the non dimensional particle velocity vector, f⃗ is the total non-dimensional force on the particle including the drag and lift forces [6].

Platelet activation parameter

As the platelets pass through the constricted gaps such as the hinge region, they are exposed to high shear stresses. This may be followed by their entrapment in the recirculation regions just distal to the hinge region where the residence time is high, thereby increasing the time of exposure of the platelets to high shear [22, 23]. The platelet activation model used in this study incorporates the effects of both the magnitude of shear stress and its time of exposure and can be expressed as:

$${\alpha }_T=\underset{0}{\overset{T}{\int }}\left|\tau \right|dt$$ (4)

The limit T on the integral represents the residence time of each particle in the flow domain. The shear stress acting on the particle is computed at the particle location from the underlying grid via bilinear interpolation. This parameter incorporates, for each particle, the history of shear stress and residence time encountered by the particle as it traverses the flow domain.

Simulation Conditions

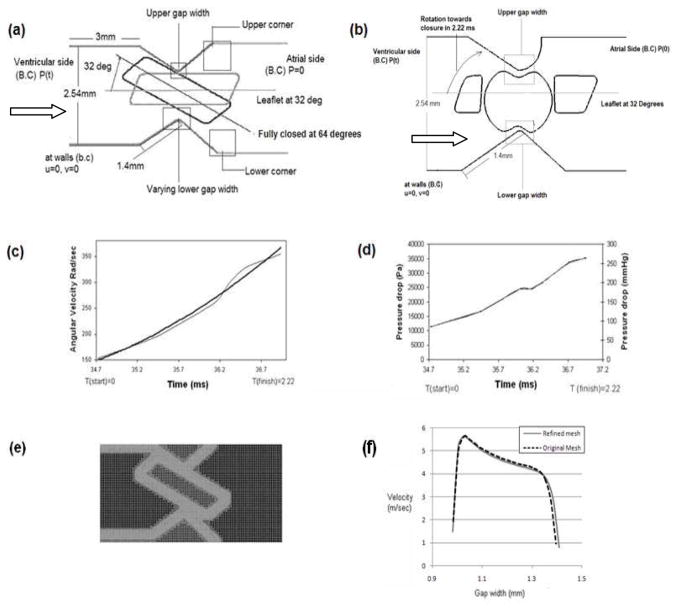
The 2D models were generated by considering one quarter of the valve by taking advantage of the symmetry of the valves as described in Govindarajan et al. (14). The two-dimensional geometry of the hinge region for the simulation was obtained by making a planar cut in the hinge region that includes the leaflet part which interacts with the housing. The nominal dimensions of both the recessed hinge and the open pivot geometry are shown in figures 1(a) and (b) respectively. It is noted that except for the rotating leaflet at either side of the pivoting hemisphere, the hinge geometry of the open pivot valve and hence the gap width at the upper and lower side of the pivoting region stays the same. Our previous study [4] showed that as the Medtronic bi-leaflet valve begins its closure owing to the ventricular pressure, it takes about 35 ms to complete its first half of closure. At this point the leaflet is 32° from the vertical. The second half leading to complete closure takes only about 2.22 ms to complete after which the leaflet positions itself at 64° from the vertical. This second phase of rotation is rapid; the angular velocity of the leaflet increases exponentially. It was observed that it is during this phase that the fluid dynamics becomes more interesting with regard to the platelet activation. The motion of the leaflet ear that is in the hinge region is imparted by the motion of the leaflet. The angular velocity calculated in the previous fluid structural interaction study that focused on the overall valve leaflet dynamics is prescribed as the motion of the leaflet part in the hinge region and the rotational speed of the leaflet was specified based on the calculations performed in [4]. The pressure drop between the ventricular and atrial sides of the leaflet in the leaflet pivot region that was computed from the earlier study was also employed as the time-dependent pressure boundary condition for the analysis. The previous analysis was performed with the nominal valve dimensions for a Medtronic bi-leaflet heart valve. We specified the same leaflet motion and pressure boundary conditions for the open pivot valve design as well in order to compare the local fluid dynamics due to the geometrical differences in the recessed hinge and the open pivot designs. The data on the leaflet angular velocity as well as the pressure drop across the hinge region employed in this study during the last 2.22 ms of valve closure are shown in Figures 1(c) and (d) respectively. No-slip condition was assumed at the walls. The fluid was assumed to be incompressible with a density of 1050 kg/m³ and a viscosity coefficient of 0.0035 Kgm⁻¹s⁻¹, representative of the human blood at 37° C. The flow was solved using a fixed Cartesian grid solver employing a local mesh refinement algorithm for efficiency and accuracy. Grid refinement study was conducted and the selected levels of refinement proved to be adequate to capture the flow. The computational mesh with finer grids near the leaflet boundary is depicted in Figure 1(e). Grid refinement study was conducted by reducing the base mesh size to half its original value and it was observed that the computed velocity magnitudes of both the studies had a percentage difference of less than 0.5%. Figure 1(f) shows the comparison of velocity plotted at the lower gap width, at time 1.34 ms. Based on these results, we employed the base mesh for the analysis described in this work.

Figure 1.

(a) nominal dimensions of the recessed hinge geometry; (b) nominal dimensions of the open pivot hinge geometry; (c) angular velocity of the leaflet starting at 32 degrees moving towards closure, curve fitting is used for interpolation; (d) time varying pressure drop at the vicinity of the hinge region specified as pressure boundary condition; (e) plot of the Cartesian grid with local mesh refinement on the hinge geometry. The mesh is adapted according to the gradients of flow for efficiency and accuracy; and (f) comparison of velocity profiles at an instant in the lower gap width with the base mesh and the finer mesh density.

Results

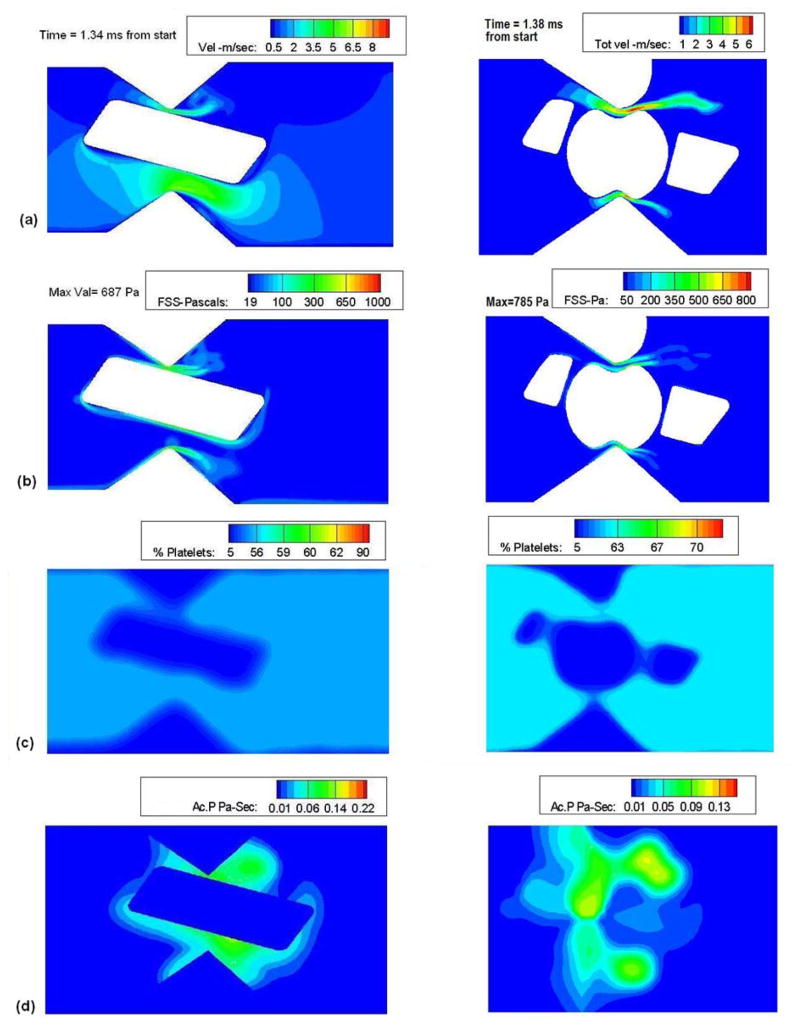
Figure 2 shows a comparison of the velocity, shear stress, platelet concentration and platelet activation of recessed hinge and the open pivot at 1.3ms. In the case of the recessed hinge, the jet velocity was found to be higher in the upper gap width as there was no obstruction to flow. But as the valve starts to close, the bulk of the flow is directed toward the lower gap width owing to the rotation of the leaflet ear. In figure 2(a), we can see that the velocity magnitudes are similar in both the upper and lower gap widths of the recessed hinge. But the dynamics in the open pivot design is significantly different from the recessed hinge. Because of the contour presented by the fixed hemisphere and the rotating leaflet, the velocity magnitude in the upper gap width is higher than the lower gap width. It is also noteworthy comparing the two velocity contours that a very small re-circulating pattern develops at the upper gap width of the recessed hinge. Platelets which pass through the narrow gap width may be trapped in this region of recirculation where the residence time is high. With an open pivot design, re-circulation zones are not observed, which is a better environment to platelets with regards to its activation. Figure 2(b) shows the shear stress contours of the two valves. At this time the maximum value of shear stress was found to be in the upper gap width of the recessed hinge and was found to be 690 Pa while it was observed that the open pivot design experienced a higher shear stress magnitude of 785 Pa. This is because of the constricted flow in the upper gap width due to the motion of the leaflet and the hinge geometry. It was observed that the platelet concentration did not increase significantly in both the cases suggesting that the platelets do not spend a long time in the vicinity of the hinge region. The activation parameter was calculated for every particle seeded in the domain and it was found that the value was somewhat higher for the recessed hinge than the open pivot at 1.3ms as shown in figure 2(d). The reason for a lower activation parameter for the open pivot could be the better wash out provided by a much higher velocity jet at the upper gap width of the open pivot design and an absence of the any re-circulation region.

Figure 2.

(a) velocity; (b) shear stress; (c) platelet concentration and (d) platelet activation of recessed hinge and the open pivot at 1.3ms.

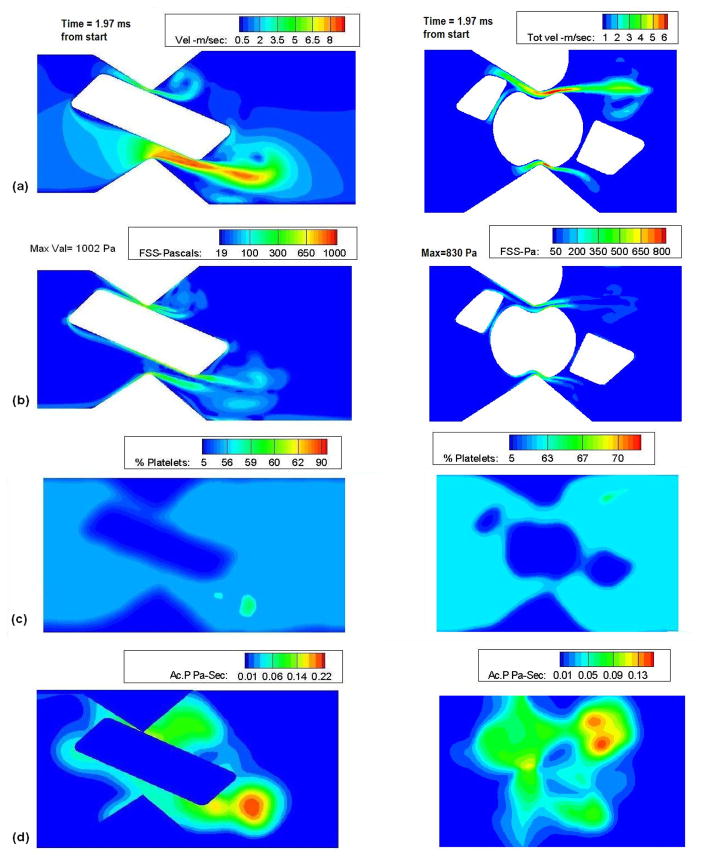
From figure 3(a), which shows the next set of contours at time 2ms, we can observe that the maximum leakage jet velocity region has shifted from the upper gap width to the lower gap width in the case of recessed hinge design and the jet has become stronger. This is obviously due to the bulk of the flow driven through the lower gap width as the leaflet ear obstructs the flow in the upper gap width. We can also observe from the velocity contour that the core of the vortex that starts to shed from the trailing edge of the leaflet ear has relatively lower velocity magnitude than the axial velocity of leakage jet itself.

Figure 3.

(a) velocity: (b) shear stress; (c) platelet concentration and (d) platelet activation of recessed hinge and the open pivot at 1.97ms.

Similar dynamics is developed in the open pivot case as well but at a lower intensity. The velocity jet did get stronger but remained in the upper gap width and we could also see the boundary layer leaving the hemispherical pivot rolling up into a small vortical structure. Figure 3(b) shows the shear stress magnitudes of both valves. We can see that the maximum value has now shifted to the trailing edge of the leaflet and has increased to approximately 1000 Pa. This is where the boundary layer that was attached to the leaflet ear leaves the trailing edge of the ear and rolls up into vortical structures. The platelets that were entrained in the boundary layer attached to the leaflet ear are carried along into the shear layer and trapped inside the vortical structures that subsequently develop. Compared to the recessed hinge, the shear stress magnitude was found to be lower in the case of the open pivot design. The platelets which pass through the narrow gap widths between surface of the hemisphere and the housing of the open pivot valve experience a high shear stress and could get trapped into the re-circulation that developed downstream. Figure 3(c) shows the concentration plots of both the cases at 2ms which confirms the dynamics explained above. The activation parameter increases as the valves move towards closure and it was observed that the activation parameter for the recessed hinge was higher than that of the open pivot valve.

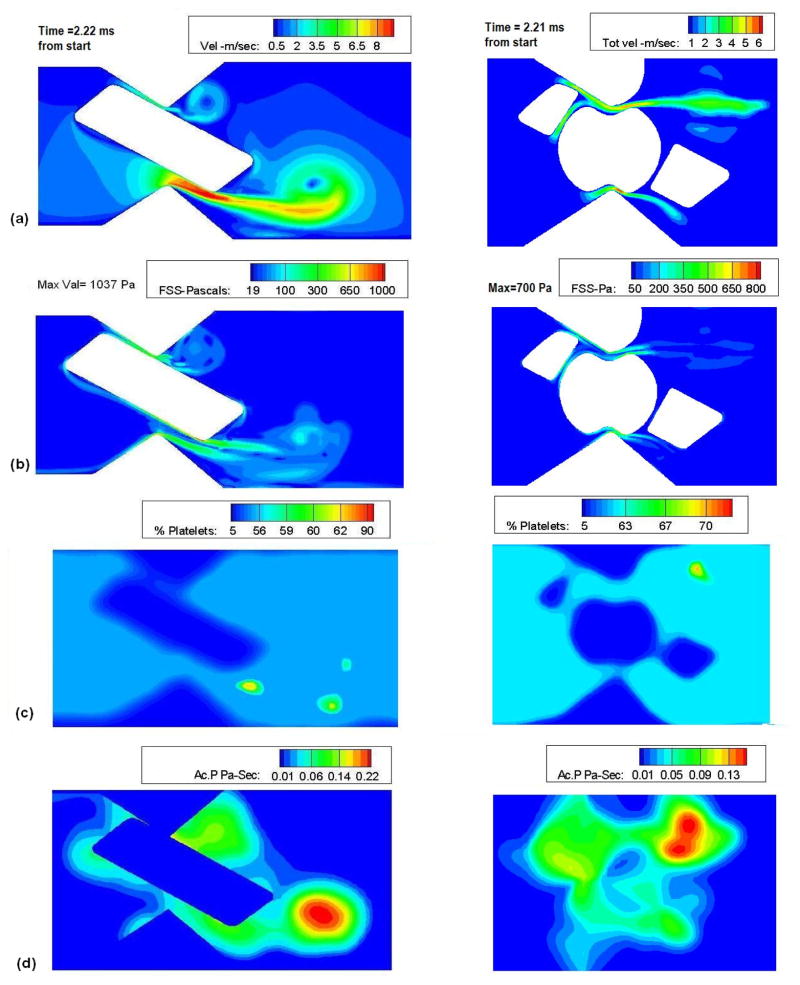
Figure 4(a) shows the contours of velocity, shear stress, and platelet concentration and activation parameter at the instant of closure. The jet becomes stronger with time and presents a maximum velocity magnitude of 9.8 m/sec at the lower gap width at the time of closure in the recessed hinge. The center of the vortex that is shed from the leaflet ear has a velocity magnitude of the order of 1 m/sec at the time of closure. The particles that are trapped in this re-circulation are carried in the axial direction at a low velocity as opposed to those being washed out by the leakage jet. This would increase the residence time of the platelets that are exposed to high shear stress in the vicinity of the hinge region.

Figure 4.

(a) velocity; (b) shear stress; (c) platelet concentration; and (d) platelet activation of recessed hinge and the open pivot at 2.2ms, at the instant of the valve closure.

At the instant of closure, the leakage velocity through the upper and lower gap widths of the open pivot hinge was found to be quite similar in magnitude. This could be due to the stationary hemisphere that pivots the leaflet. The maximum leakage velocity was found to be 7 m/sec at the time of closure. The small vortical structure that was observed previously appears to be advecting away along with the jet. It was also observed that the velocity magnitude of the vortical structure is approximately 3 m/sec which is relatively higher than what was observed in the recessed hinge. This also means that the platelets trapped in these vortical structures are carried away from the hinge pocket at a higher rate thus reducing the residence time of the platelets in the vicinity of the hinge region. The shear stress magnitude also reached its maximum and was observed to be 1047 Pa in the case of the recessed hinge and 700 Pa in the case of the open pivot design. This lower magnitude in the latter case could be due to the stationary hemispherical pivot which does not move relative to the fluid motion. Particle concentration contours in figure 4(c) shows the relative concentration being higher in the re-circulation zones for both the cases. Activation parameter for the recessed hinge at the end of simulation was calculated to be 0.23 Pa-Sec and 0.16 Pa-Sec for the open pivot design.

Summary of results

The fluid dynamics in both the cases were significantly different owing to the difference in geometry. In the recessed hinge design, the leaflet ear was pivoted inside a groove in the housing which held the leaflets in its place and allowed the valve to rotate. In the case of the open pivot design, the leaflet was held in position by a hemispherical pivot and the leaflet rotated pivoting on the hemispheres.

Recessed hinge

The maximum leakage jet velocity regions vary with time as the valve rotates. Initially the jet velocity was higher at the upper gap width as there was no obstruction to the flow. But as the valve starts to close, owing to the rotation of the leaflet the bulk of the flow is diverted through the lower gap width and there is very little flow through the upper gap width. The jet becomes stronger with time and presents a maximum velocity magnitude of 9.8 m/sec at the lower gap width at the time of closure. At the trailing edge of the leaflet, the boundary layer separated from the leaflet and rolling up to form vortical structures which had a much lower velocity of advection in the axial direction. The shear stress value increased as the valve moved toward its closure and reached a maximum value of 1047 Pa. This maximum value was found to be in the trailing edge of the leaflet ear from where the vortical structures start developing. The platelets which pass through the surface of the leaflet ear are exposed to high shear and subsequently get trapped in the vortical structures thus increasing its residence time in the vicinity of the hinge region. This was also evident from the concentration plots, particularly toward the end of the closure where we could observe higher concentration of particles in the regions of re-circulation. The maximum activation parameter at the end of the simulation was calculated to be 0.23 Pa-Sec, a value close to that calculated at the leaflet [4].

Open pivot

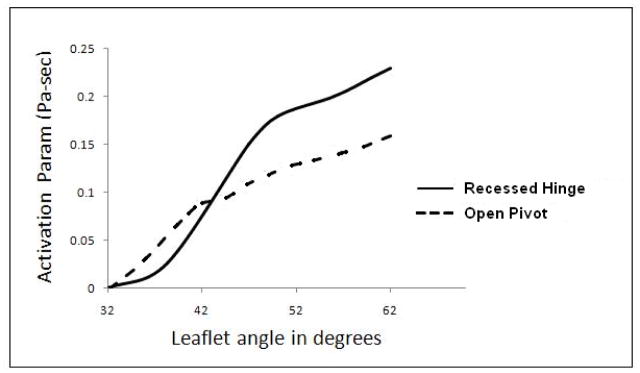
Except for the rotating leaflet at either side of the pivoting hemisphere, the hinge geometry of the open pivot valve and hence the gap width at the upper and lower side of the pivoting region stays the same. The maximum leakage velocity in this case was observed to be lower than the recessed hinge design. Vortical structures develop at the downstream of the hinge region, but they seem to be dissipating away from the hinge pocket which can be observed from the velocity contours. The axial velocity of the vortical structures was observed to be higher than that observed in the recessed hinge. This could prove advantageous in the open pivot design as platelets trapped in the vortical structures could advect away from the high shear stress region sooner than in the recessed hinge design. The shear stress magnitude was found to be lower than that observed in the case of recessed hinge. This could be due to the presence of the stationary hemisphere which pivots the leaflet and occupies a major portion of the hinge geometry. In the recessed hinge this part is occupied by the leaflet ear which moves at a direction opposite to the direction of flow at a very high angular velocity thereby influencing the shear stress magnitude. Also its is clear from the velocity contours that the boundary layer separation occurs at the stationary hemisphere and not at the trailing edge of the leaflet (Boundary layer separation occurred at the trailing edge in the case of recessed hinge valve. Figure 5 shows the comparison of calculated activation parameters at different stages of closure for both the valves. Although, initially the activation parameter was higher for the open pivot design, as the valve moved toward closure, the activation parameter value decreased compared to the recessed hinge. The platelet activation parameter at the instant of complete closure was calculated to be 30 % lower than the recessed hinge suggesting improved hemodynamics in the open pivot design.

Figure 5.

Comparison of calculated activation parameters at different stages of closure for both the hinge designs.

Discussion

This study compared the flow structures between the hinge region of an open pivot design valve and a recessed hinge design, its implication on the platelets under physiological mitral conditions focusing on the closure phase of the valve. This was done computationally using a fixed Cartesian mesh and local mesh refinement. Angular velocity and inlet pressure data were obtained from a previous study [7] which focused on flow through the leaflet edges and the gap width between the leaflet edge and the housing. Previous experimental studies on the hinge region have reported the presence of recirculation in the vicinity of the hinge region. Both the cases studied here encountered recirculation and high shear stress magnitudes, but lesser in the open pivot design on both aspects which could be accounted for the stationary hemisphere pivoting the valve. It was observed that the vortical structures advect away carrying the trapped platelets away from the hinge pocket faster in the open pivot design than the recessed hinge design. Colantuni et al. [24] observed that platelets released serotonin when they were subjected to shear stress greater than 700 Pa for exposure times of 1–5 ms. Platelet lysis was noticed by Anderson et al. [25] when platelets were exposed to shear stress of more than 16 Pa for a period of 5 min. For a period of 30 s, shear stress of more than 60 Pa was required to damage platelets. Gross et al. [10], Ellis et al. [11] and Gao et al. [13] in their hinge studies have observed recirculation and stagnation zones in the vicinity of the hinge region similar to the present study. The combination of high shear stress and locally re-circulating flows can be highly significant for platelet activation and deposition. Both the cases experienced velocities of the same order of magnitude at the gap width between the leaflet and the housing. The shear stress was observed to be lower in the open pivot design compared to that observed in the recessed hinge design which could have played a role in lowering the activation potential. Also, the wash out phenomenon seemed to be better in the case of open pivot design as the vortical structures had a higher advection velocity. But the recessed hinge design had a much lower axial velocity for the vortical structures which could increase the residence time of the platelets in the hinge pocket. Gross et al. [8] observed a similar flow pattern in their study of the hinge region where the recirculation zone did not get washed with the flow. Platelets caught in such a vortical structure are likely to remain in the vicinity of the hinge. High shear stresses experienced by the platelets and high residence time in this region make this region highly vulnerable to thrombus formation. Comparison of the activation parameter obtained for flow through the recessed hinge and that for open pivot showed that the tendency for the platelets to activate is lesser in the open pivot design from which we can conclude that the open pivot possesses improved hemodynamics compared to the recessed hinge design.

Limitations

In the present study the flow through the hinge geometry is calculated in a two-dimensional setting. Three-dimensional effects are likely to be important in hinge flows; computations of such flows, in view of the complex and highly constricted geometry of the hinge are challenging and are part of ongoing work. Within the limitations of two-dimensionality the present study examines the flow in the hinge region of the recessed hinge design and compares it with the open pivot design which shows some improvement in hemodynamics. Our platelet model is solely based on shear stress time integral experienced by the platelets that passes through the hinge region. Studies have suggested that a specific relationship exists for the activation of platelets in arterial flows [9–11]. Platelets get activated beyond a minimum shear stress as in the shear stress time integral model. Apart from shear stress, there are many other factors which could influence the process of platelet activation, such as the presence of foreign surfaces such as a mechanical valve leaflet, agonist synthesis and release by activated platelets and concentration, platelet-phospholipid dependent thrombin generation, and thrombin inhibition by heparin etc. These complex biochemical effects are not included in the present model. The current particle tracking algorithm assumes a dilute flow with low platelet loading in blood. It neglects the effect of platelet loading on blood flow as well as interaction of platelets with other platelets and red blood cells. The interaction of the larger and far more numerous bi-concave shaped red blood cells and platelets needs to be analyzed to study the precise activation mechanism of the platelets due to the fluid induced stresses. This requires multi-scale modeling that will incorporate the effects of the particulate nature of blood, including cell-cell and cell-surface interactions. Efforts are underway to develop a model that would simulate the effects of interaction of red blood cells and its effect on the flow as well as platelet- platelet and RBC- Platelet interaction through the hinge region.