GENERALIZED PARTIALLY LINEAR MIXED-EFFECTS MODELS INCORPORATING MISMEASURED COVARIATES

Abstract

In this article we consider a semiparametric generalized mixed-effects model, and propose combining local linear regression, and penalized quasilikelihood and local quasilikelihood techniques to estimate both population and individual parameters and nonparametric curves. The proposed estimators take into account the local correlation structure of the longitudinal data. We establish normality for the estimators of the parameter and asymptotic expansion for the estimators of the nonparametric part. For practical implementation, we propose an appropriate algorithm. We also consider the measurement error problem in covariates in our model, and suggest a strategy for adjusting the effects of measurement errors. We apply the proposed models and methods to study the relation between virologic and immunologic responses in AIDS clinical trials, in which virologic response is classified into binary variables. A dataset from an AIDS clinical study is analyzed.

1 Introduction

In recent years, the relation between viral load and CD4 cell counts has been well studied (Wu et al., 1999; Wu, 2002; Liang, Wu, and Carroll, 2003). These studies have investigated the concordance and discordance between virologic and immunologic variables and may help clinicians more deeply understand AIDS pathogenesis and improve therapy regimes. Analysis of these AIDS data poses statistical challenges. A common feature of the markers, such as viral load measurements and CD4+ cell counts, used to evaluate antiviral therapy is that their measurement produces longitudinal data-that is, a series of independent and dependent variables obtained by taking repeated measurements, over time, from any one subject. Consideration of the features of longitudinal data, such as within-subject and between-subject variations and the correlation structure, is of practical interest.

Antiretroviral therapy for HID-1 infected patients has greatly improved in recent years. Administration of drug cocktails consisting of three or more drugs may reduce and maintain virus load copies below the detection limit in many patients, although it is unlikely that combination therapies alone can eradicate HID in infected patients because long-lived infected cells and sites within the body exist where drugs may not be effective. Because of the success of highly active antiretroviral therapy for HID infection, viral load in AIDS patients is suppressed and reaches to magnitudes that are below the limit of quantification, and AIDS becomes a chronic disease. Clinicians and patients are therefore sometimes only interested in maintaining the viral load below the detection limit, and in how the immune system (measured by CD4 cell counts) relates to this suppression.

Our primary goal in this paper is to propose a generalized partially linear mixed-effects model (GPLMeM) to study the relation between binary viral load measurement and CD4 cell count. Our focus is not only on the population characteristic but also on individual diversities. This is particularly important in AIDS research because that there is generally a large between-subject variation, which indicates the importance of estimating each individual’s parameters for the individualization of treatment management and care of patients with AIDS. We propose a new method to explore the population and individual characteristics by combining local linear regression (Fan and Gijbels, 1996), penalized quasilikelihood (PQL, Breslow and Clayton, 1993), and local quasilikelihood (Severini and Staniswalis, 1994) techniques.

For longitudinal binary data analysis, generalized linear mixed-effects models (GLMeM) have been proposed to incorporate the between-subject and within-subject variations. See, for example, Breslow and Clayton (1993) and Schall (1991) for the PQL method, Zeger and Karim (1991) for the Gibbs sampler. Wang et al. (1998) considered generalized linear mixed models when one of the covariates is measured with error, and they proposed a simulation extrapolation (SIMEX, Stefanski and Cook, 1995) estimation method.

To weaken model assumption for possible misspecification and to avoid the curse of dimensionality of fully nonparametric regression in the presence of several predictor variables, semipara-metric models have been studied and used for longitudinal data analysis in literature (Severini and Staniswalis, 1994). Lin and Carroll (2001) studied marginal semiparametric mixed-effects models and used the generalized estimating equation to estimate the parameter of interest. Wu and Zhang (2002) and Ke and Wang (2001) proposed semiparametric nonlinear mixed-effects models. Lin and Zhang (1999), Zhang (2004), and Zhang et al. (1998) used the smoothing spline to fit semi-parametric mixed-effects models. These authors considered between-subject and within-subject variations in their estimation methods, but they mainly aimed at delineating population features, while individual characteristics are ignored.

The article is organized as follows. In Section 2 we formally introduce the model’s framework, propose an estimation algorithm, and develop asymptotic results; extend to the case that X is measured with error; and discuss practical implementation of the methods. We illustrate the methods by conducting a small simulation experiment and extensively analyzing a data set from an AIDS study in Section 3 and provide a discussion in Section 4. The proof of the theoretical results is given in the Appendix.

2 Generalized Partially Linear Mixed-effects Models

2.1 Model

Suppose that data are obtained from n independent subjects with outcome variables Y_ij, linear covariates X_ij(p × 1) and A_ij(q × 1), and nonlinear scalar Z_ij, where i = 1, …, n indicates the subjects; j = 1, …, n_i indicates the observation of the ith subject. Given the covariates X_ij, Z_ij, A_ij, and unobserved q × 1 random effects vectors b_i and unobserved random effects function c_i(·), the observations Y_ij are assumed to be independent with means μ_ij and variance ϕω_ijV(μ_ij), where ω_ij is a known weight and V(·) is a known variance function. The GPLMeM of Y given X, Z is specified by

$$g({\mu }_{ij})=X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+\theta (Z_{ij})+c_i(Z_{ij}),$$ (2.1)

where g(·) is a known monotonic differentiable link function, β is a p × 1 vector, and θ(·) and c_i(·) are unknown smoothing functions. c_i(·) indicates the random-effects, which can be regarded as a realization of a stochastic process with mean zero. The random effects b_i are independent of c_i(·) and are independently distributed N(0, Σ_b), where the covariance matrix Σ_b is determined by finite parameters. Given the covariates X_ij, A_ij and Z_ij, and b_i and c_i(·), the observations Y_ij and Y_ik are independent; i.e., E(Y_ij|X_ij, Z_ij) = E{Y_ij|X_ij, Z_ij, (X_ik, Z_ik)_k≠j}. In longitudinal data, Z_ij are often the treatment times, and X_ij, A_ij, and Y_ij are the observations of the ith subject at time Z_ij, for example, in the AIDS data set studied later.

2.2 Estimation

To estimate the parametric and nonparametric parts β, b_i, θ(·), and c_i(·), we combine local linear regression, the PQL technique, and the quasilikelihood principle. We estimate these parameters by considering local PQL, then we update the estimate of β and b_i, using all data points, by relying on the global PQL. In local PQL, we approximate θ(·) and c_i(·) by linear functions:

$$\begin{array}{l}\theta (z)\approx \theta (z_0)+{\theta }^{\prime }(z_0)(z-z_0)\equiv {\alpha }_0+{\alpha }_1(z-z_0)\\ c_i(z)\approx c_i(z_0)+c_i^{\prime }(z_0)(z-z_0)\equiv {{\nu }_i}_0+{{\nu }_i}_1(z-z_0).\end{array}$$

Denote α = (α₀, α₁)^T, ν_i = (ν_i0, ν_i1)^T, ${\mathrm{\Lambda }}_{ij}=\left(\begin{array}{c}1\\ Z_{ij}-z_0\end{array}\right)$. In a neighborhood of z₀, model (2.1) can be approximated by a GLMeM and described as

$$g({\mu }_{ij})=X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+{\mathit{\alpha }}^{\text{T}}{\mathrm{\Lambda }}_{ij}+{\mathit{\nu }}_i^{\text{T}}{\mathrm{\Lambda }}_{ij},$$

where ν_i ~ N(0, Σ_ν) are random effects. In a conventional GLMeM setting, we can estimate α, β, b_i, and ν_i by using the PQL principle; i.e., maximize

$$-\sum _{i=1}^n\left\{\sum _{j=1}^{n_i}Q({\stackrel{\sim }{\mu }}_{ij},y_{ij})+{\mathit{\nu }}_i^{\text{T}}{\mathrm{\sum }}_{\nu }^{-1}{\mathit{\nu }}_i+{\mathbf{b}}_i^{\text{T}}{\mathrm{\sum }}_b^{-1}{\mathbf{b}}_i\right\}$$

with respect to α, β, b_i, and ν_i, where ${\stackrel{\sim }{\mu }}_{ij}=g^{-1}(X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+{\mathrm{\Lambda }}_{ij}^{\text{T}}\mathit{\alpha }+{\mathrm{\Lambda }}_{ij}^{\text{T}}{\mathit{\nu }}_i)$ and $Q(s,y)=-2{\int }_y^s{V}^{-1}(t)(y-t)dt$.

To consider the localization, we propose a locally PQL approach. The motivation of doing so is essentially the same as localization in conventional nonparametric regression.

Denote ρ_k(t) = {dg⁻¹)(t)/dt}^k/[σ²V{g⁻¹(t)}] and q_k(t,y) = ∂^kQ{g⁻¹(t), y}/∂t^k for k = 1, 2, 3. Let k_j = ∫ u^jK(u)du, μ_j = ∫ u^jK²(u)du for j = 1, 2, $N={\sum }_{i=1}^n{n}_i$, and $M={\sum }_{i=1}^n{n}_i^2$.

Step 1

For each fixed z₀, we consider the maximization

$$-\sum _{i=1}^n\left\{\sum _{j=1}^{n_i}{K}_h(Z_{ij}-z_0)Q({\stackrel{\sim }{\mu }}_{ij},y_{ij})+{\mathit{\nu }}_i^{\text{T}}{\mathrm{\sum }}_{\nu }^{-1}{\nu }_i+{\mathbf{b}}_i^{\text{T}}{\mathrm{\sum }}_b^{-1}{\mathbf{b}}_i\right\}$$ (2.2)

with respect to α, β, b_i, and ν_i. K_h(·) = K(·/h)/h, K(·) is a kernel function, and h is a bandwidth.

Take the differential of (2.2) on α, β, b_i, and ν_i. Step 1 is equivalent to solving the equations

$$\sum _{i=1}^n\sum _{j=1}^{n_i}{K}_h(Z_{ij}-z_0)(Y_{ij}-{\stackrel{\sim }{\mu }}_{ij}){\rho }_1({\stackrel{\sim }{\mu }}_{ij})\left(\begin{array}{c}1\\ Z_{ij}-z_0\\ X_{ij}\end{array}\right)=0$$ (2.3)

and, for each i,

$$\sum _{j=1}^{n_i}{K}_h(Z_{ij}-z_0)(Y_{ij}-{\stackrel{\sim }{\mu }}_{ij}){\rho }_1({\stackrel{\sim }{\mu }}_{ij})\left(\begin{array}{c}{A}_{ij}\\ 1\\ Z_{ij}-z_0\end{array}\right)=\left(\begin{array}{cc}{\mathrm{\sum }}_b^{-1}& 0\\ 0& {\mathrm{\sum }}_{\nu }^{-1}\end{array}\right)\left(\begin{array}{c}{\mathbf{b}}_i\\ {\mathit{\nu }}_i\end{array}\right).$$ (2.4)

Denote $Y_{ij}^{\ast }=g({\stackrel{\sim }{\mu }}_{ij})+(Y_{ij}-{\stackrel{\sim }{\mu }}_{ij})g^{\prime }({\stackrel{\sim }{\mu }}_{ij}),{\stackrel{\sim }{\mathbf{Y}}}_i={(Y_{i1}^{\ast },\dots ,Y_{i{n}_i}^{\ast })}^{\text{T}}$, Z_i = (Z_i1,…Z_ini)^T, and A_i similarly. Let K_ih = diag{K_h(Z_i1 − z₀), …, K_h(Z_ini − z₀)}, R_i = diag(R_i1, …, R_ini) with R_ij = {g′(μ̃_ij)}²V(μ̃_ij).

Equations (2.3) and (2.4) are approximately equivalent to iteratively fitting the following linear mixed-effects (Laird and Ware, 1982) model:

$${\mathbf{K}}_{ih}^{1/2}{\stackrel{\sim }{\mathbf{Y}}}_i={\mathbf{K}}_{ih}^{1/2}\{{\mathbf{J}}_i(\mathit{\alpha }+{\mathit{\nu }}_i)+{\mathbf{X}}_i\mathit{\beta }+{\mathit{A}}_i{\mathbf{b}}_i\}+{\mathit{\epsilon }}_i$$ (2.5)

where ε_i ~ (0, R_i) and J_i = (Λ_i1, ···, (Λ_ini)^T.

Consequently, the estimates defined by step 1 are approximately given in closed-form expressions (Davidian and Giltinan, 1995):

$$\begin{array}{l}\left(\begin{array}{c}\widehat{\mathit{\alpha }}\\ \widehat{\mathit{\beta }}\end{array}\right)={\left\{\sum _{i=1}^n{({\mathbf{J}}_i,{\mathbf{X}}_i)}^{\text{T}}{\mathbf{\Omega }}_i({\mathbf{J}}_i,{\mathbf{X}}_i)\right\}}^{-1}\left\{\sum _{i=1}^n{({\mathbf{J}}_i,{\mathbf{X}}_i)}^{\text{T}}{\mathbf{\Omega }}_i{\stackrel{\sim }{\mathbf{Y}}}_i\right\}\\ \left(\begin{array}{c}{\widehat{\mathbf{b}}}_i\\ {\widehat{\mathit{\nu }}}_i\end{array}\right)=\left(\begin{array}{cc}{\mathrm{\sum }}_b& 0\\ 0& {\mathrm{\sum }}_{\nu }\end{array}\right){({\mathbf{J}}_i,{\mathbf{A}}_i)}^{\text{T}}{\mathbf{\Omega }}_i\left\{{\stackrel{\sim }{\mathbf{Y}}}_i-({\mathbf{J}}_i,{\mathbf{A}}_i)\left(\begin{array}{c}\widehat{\mathit{\alpha }}\\ \widehat{\mathit{\beta }}\end{array}\right)\right\},\end{array}$$

where ${\mathbf{\Omega }}_i={\mathbf{K}}_{ih}^{1/2}{\mathrm{\sum }}_i^{-1}{\mathbf{K}}_{ih}^{1/2}$ with ${\mathrm{\sum }}_i={\mathbf{R}}_i+{\mathbf{K}}_{ih}^{1/2}({\mathbf{J}}_i{\mathrm{\sum }}_{\nu }{\mathbf{J}}_i^{\text{T}}+{\mathbf{A}}_i{\mathrm{\sum }}_b{\mathbf{A}}_i^{\text{T}}){\mathbf{K}}_{ih}^{1/2}$. &thetas;(z₀) and c_i(z₀) are estimated by θ̂(z₀) = α̂₀ and ĉ_i(z₀) = ν_i0.

Note that β and b_i are global parameters and their estimates given in step 1 are based only on local information. We update their estimate, using all data, by considering a global penalized quasilikelihood procedure:

Step 2

Update estimates of β and b_i by maximizing the object function

$$-\sum _{i=1}^n\left\{\sum _{j=1}^{n_i}Q({\stackrel{\sim }{\mu }}_{ij}^{\ast },y_{ij})+{\mathbf{b}}_i^{\text{T}}{\mathrm{\sum }}_b^{-1}{\mathbf{b}}_i\right\}$$ (2.6)

with respect to β and b_i, where ${\stackrel{\sim }{\mu }}_{ij}^{\ast }=g^{-1}\{X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+{\widehat{\alpha }}_0(Z_{ij})+{\widehat{\nu }}_{i0}(Z_{ij})\}$.

The expressions containing matrices Σ_b, Σ_ν, and R_i, which are generally unknown and need to be estimated. To estimate these matrices, one may use the maximum and the restricted maximum likelihood methods to estimate the unknown components of Σ_b, Σ_ν, and R_i under the normality assumption. To implement these non-trivial methods, the EM-algorithm and New-Raphson methods have been proposed(Laird and Ware, 1982; Davidian and Giltinan, 1995). The standard statistical software packages such as SAS and Splus/R provide user-friendly functions to implement these methods( lme Splus/R function and the SAS procedure SAS MIXED). After obtaining the point estimates of the unknown components, we have Σ̂_b, Σ̂_ν, and R̂_i, and then Σ̂_i and Ω̂_i. The estimators of α, β, b_i, and μ_i thus can be obtained by substitution of Σ̂_i and Ω̂_i in steps 1 and 2.

2.3 Asymptotic Results

We claim the following condition, which is standard in the literature describing the generalized partially linear models.

Condition

1. The function q₂(t, y) < 0 for t ∈ R and y in the range of the response variable.

2. The random-effects functions c_i(z) are iid and have zero mean gaussian marginal distribution, and have the same distribution as a random-effects curve c(z), a two times continuously differentiable function.

3. The density function f(z) of Z is positive and continuous at the point z₀.

4. The functions θ(·) and θ⁽²⁾(·) are continuous at the point z₀.

5. With R = X^Tβ+A^Tb+θ(Z)+c(Z), $E\{q_1^2(R,Y)\mid z\},E\{q_1^2(R,Y)X\mid z\}$, and $E\{q_1^2(R,Y)X{X}^{\text{T}}\mid z\}$ are twice differentiable in z.

6. $E\{q_2^2(R,Y)\}<\infty$ and $E\{q_1^{2+\delta }(R,Y)\}<\infty$, for some δ > 2.

   Mh/N → λ, a finite nonnegative constant.

   Let γ_y(z₁, z₂) be the covariance of [Y − g⁻¹{X^Tβ + A^Tb + θ(Z) + c(Z)}]ρ₁{X^Tβ + A^Tb+ θ (Z) + c(Z)} for Z = z₁ and z₂. γ_y(z₁, z₂) is continuous on z₁ and z₂.

   The functions V″(·) and g‴(·) are continuous.

Theorem 1

Consider the estimator θ̂(z₀) given in step 1. Then, as n → ∞, h → 0 and Nh → ∞, and under the specified condition, we have the asymptotic expansion

$$\begin{array}{c}\widehat{\theta }(z_0)-\theta (z_0)=b_{\theta }(z_0)+\frac{1}{Nf(z_0)E\{{\rho }_2(R)\mid Z=z_0\}}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1({\eta }_{ij},y_{ij})K_h(Z_{ij}-z_0)\\ +o_P\left\{{(Nh)}^{-1/2}+h^2\right\},\end{array}$$ (2.7)

and hence

$${(Nh)}^{1/2}\left\{\widehat{\theta }(z_0)-\theta (z_0)-b_{\theta }(z_0)\right\}\stackrel{D}{\to }N\{0,{\sigma }_{\theta }^2(z_0)\},$$ (2.8)

where

$$b_{\theta }(z_0)=\frac{h^2}{2}{\kappa }_2\left[{\theta }^{″}(z_0)+\frac{E\{c^{″}(Z){\rho }_2(R)\mid Z=z_0\}}{E\{{\rho }_2(R)\mid Z=z_0\}}\right]$$

and

$${\sigma }_{\theta }^2(z_0)=\frac{{\mu }_{0}E\{{\rho }_2(R)\mid Z=z_0\}+\lambda f(z_0){\gamma }_y(z_0,z_0)}{f(z_0){[E\{{\rho }_2(R)\mid Z=z_0\}]}^2}.$$

Theorem 2

Let β̂ be the estimate given in step 2. Under the condition, as n → ∞, Nh⁴ → 0 and Nh²/log(1/h) → ∞,

$$N^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(\mathbf{0},{\mathbf{B}}^{-1}{\mathrm{\sum }}_1{\mathbf{B}}^{-1}),$$ (2.9)

where B = E[ρ₂(R)XX^T] and ${\mathrm{\sum }}_1=cov\left(q_1(R,Y)\left[X-\frac{E\{{\rho }_2(R)X\mid Z\}}{E\{{\rho }_2(R)\mid Z\}}\right]\right)$.

As in generalized partially linear models for cross-sectional data, theorem 2 indicates that in order to estimate β at the root–n rate, one must undersmooth the nonparametric part θ(·). This undersmoothing request is standard in the kernel literature, although ordinary bandwidth rates are permissible in partially linear models.

2.4 Implementation

To obtain the estimates by fitting (2.5), we give an initial value for μ̃_ij, say ${\stackrel{\sim }{\mu }}_{ij}^{(0)}$, and then have the working response variable

$${\stackrel{\sim }{Y}}_{ij}^{(0)}=g({\stackrel{\sim }{\mu }}_{ij}^{(0)})+(Y_{ij}-{\stackrel{\sim }{\mu }}_{ij}^{(0)})g^{\prime }({\stackrel{\sim }{\mu }}_{ij}^{(0)}).$$

For a given bandwidth h, we fit model (2.5) and obtain estimates α̂, β̂, b̂_i, and ν̂_i. Update $g({\widehat{\mu }}_{ij})={\widehat{\alpha }}_0+{\widehat{\nu }}_{i0}+X_{ij}^{\text{T}}\widehat{\mathit{\beta }}+A_{ij}^{\text{T}}{\widehat{\mathbf{b}}}_i$ and g′(μ̂_ij). Correspondingly, Ỹ_ij can be updated as g(μ̂_ij) + (y_ij − μ̂_ij)g′(μ̂_ij), and fit (2.5) again. Repeat these procedures until convergence, and collect the final estimates θ̂ (z₀) = α̂₀, ĉ_i(z₀) = ν̂_i0.

During the process of the implementation, one should keep in mind that the bandwidth needs to be selected in the estimation procedure involved in step 1. Theorem 2 indicates that undersmoothing the nonparametric part is necessary to guarantee to estimate β at the root-n rate. Because only the rates of convergence for the bandwidth h are necessary for the same limiting distribution for the estimators of β, we select h by using the empirical bias bandwidth selection method (Ruppert, 1997) in our data analysis. In our numerical analysis below, we select initial values by fitting the data by a generalized linear mixed-effects model. Because iteration is needed, we set the maximum number of iteration to be 30. Computation results for our numerical analysis are obtained within 18 iterations. This adoption leads to potentially burdensome computation, which may be attenuated with a powerful computation platform.

2.5 Measurement errors in covariates

In practice, the covariates may not be exactly observable, and like CD4 cell counts in our AIDS dataset analyzed later, are measured with substantial errors. The estimators and inference may be biased if one ignores these measurement errors. We need to adjust the resulting bias. In this special case, we denote X_ij by X_i(Z_ij), the true covariates of subject i, and W_ij by W_i(Z_ij), the observed values of X_ij at time Z_ij. Suppose we have the measurement error model,

$$W_i(z)=X_i(z)+u_i(z),$$ (2.10)

where W_i(z) is the observed value and X_i(z) is the underlying true value for the ith patient at treatment time z. The error u_i(z) represents measurement error in the CD4+ cell counts. We assume that u_i(z) is a mean zero process, and {X_i(z), u_i(z)} are mutually independent. Fuller (1987) and Carroll, Ruppert, and Stefanski (1995) provided a good survey of measurement error models. Buonaccorsi, Demidenko, and Tosteson (2000) studied measurement errors in linear mixed-effects models. Higgins, Davidian, and Giltinan (1997) proposed a two-step approach to deal with measurement errors in nonlinear mixed-effects models. Wang et al. (1998) studied generalized linear mixed measurement error models. Liang and Ren (2005) investigated generalized partially linear models with errors-in-variables and proposed a measurement error calibration based on a SIMEX algorithm. The computation burden in a similar platform is tremendously expensive, although its implementation is straightforward. In this paper we adjust measurement error by using a mixed-effects regression spline model, as done by Higgins et al. (1997); a similar idea was used by Liang, Wu, and Carroll (2003).

The data points repeatedly measured along time z are similar to replications if we can assume that the measured variable is a smooth function of z. Shi, Weiss, and Taylor (1996) and Rice and Wu (2001) have modeled the natural history of the CD4+ cell process in untreated HID-infected patients by using a mixed-effects regression spline model. Model the CD4+ cell counts as follows:

$$X_i(Z_{ij})=\sum _{k=0}^p{\xi }_k{\psi }_k(Z_{ij})+\sum _{k=0}^q{\eta }_{ik}{\phi }_k(Z_{ij})={\mathbf{\Psi }}_i(Z_{ij})\mathit{\xi }+{\mathbf{\Phi }}_i(Z_{ij}){\mathit{\eta }}_i,$$ (2.11)

where Ψ_i(z) = {ψ₀(z), ψ₁(z), ···, ψ_p(z)} and Φ_i(z) = {φ₀(z), φ₁(z), ···, φ_q(z)} are basis functions such as cubic B-spline basis, ξ = (ξ₀, ξ₁, ···, ξ_p)^T is a fixed-effect parameter vector, and η_i = (η_i0, η_i1, ···, η_iq)^T is a random effect vector with mean zero and covariance matrix Σ_η (Σ_η may be unstructured or can be specified with a special structure). The selection of the number (p and q) and locations of knots for regression splines can be achieved by using cross-validation (Eubank, 1999). Rice and Wu (2001) suggest setting p = q and ψ_k(z) = φ_k(z). Model (2.11) is a standard linear mixed-effects model, which can be fitted by using the LME function of Splus (Pinheiro and Bates, 2000).

Higgins et al. (1997) have proposed a two-step approach to deal with measurement errors in time-dependent covariates in nonlinear mixed-effects models. The first step is to estimate the covariate function by fitting an appropriate model for covariate processes, and then fit the nonlinear mixed-effects model by plugging in the estimates of the covariates in the second step. This is essentially similar to the regression calibration idea (Carroll et al. 1995). By applying a similar idea to our model for measurement error in CD4+ cell counts, we fit a LME model,

$$W_i(Z_{ij})={\mathbf{\Psi }}_i(Z_{ij})\mathit{\xi }+{\mathbf{\Phi }}_i(Z_{ij}){\mathit{\eta }}_i+{\mathbf{u}}_i,$$ (2.12)

and obtain an estimate Ŵ_ij of W_ij, which is regarded as X_ij.

3 Numerical Illustration

In this section, we first conduct a small simulation study for an illustration. We then use the proposed methods to analyze a data set from an AIDS study. In our numerical analysis, we calculate the naive estimates, i.e., those obtained by ignoring measurement errors, the proposed estimates. We use the quartic kernel k(u) = 15/16(1 − u²)²I_(|u|≤1) for nonparametric regression.

3.1 A Small Simulation Experiment

We performed a small simulation experiment and the data were generated from a logistic model, whose log(odd) can be expressed as

$$\text{logit}\{Y_{ij}=1\mid X_{ij},Z_{ij}\}=X_{ij}(\beta +b_i)+{\theta }_i(Z_{ij}),W_{ij}=X_{ij}+U_{ij}i=1,\dots ,n,j=1,\dots ,m,$$

where X_ij is independent uniform (0, 1) components, Z_ij is uniformly distributed U(0, 1), and U_i is normally distributed $N(0,{\sigma }_u^2)$. The parameter β is equal to 1.85, and the nonparametric function is θ_i(z) = (1 + c_1i) cos(2πz) + (2 + c_2i) sin(2πz) with (c_1i, c_2i) being 2-dimensional normal distribution $N(0,{\sigma }_b^2{\mathbf{I}}_2)$.

We consider a combination of (n, m) = (20, 30), (40, 50), (60, 70), σ_u = 0.1, 0.25, and σ_b = 0.1. In each of configurations, we run 500 replications. We calculate the proposed estimates and the naive estimates (i.e., we ignore the measurement errors). The estimated values of β are summarized in Table 1.

Table 1.

The estimates with standard errors (s.e.) of the parameter β for the simulated data. “Mean”: the means of the estimated values; “s.e.”: sample standard errors based on 500 replications.

n	m	σu	Proposed		Naive
			mean	s.e.	mean	s.e.
20	30	0.1	1.876	0.355	1.784	0.352
40			1.873	0.256	1.759	0.243
60			1.887	0.305	1.742	0.299
20	50		1.831	0.338	1.65	0.337
40			1.822	0.227	1.67	0.266
60			1.848	0.18	1.706	0.201
20	70		1.824	0.238	1.672	0.238
40			1.796	0.214	1.627	0.208
60			1.813	0.18	1.628	0.185
20	30	0.25	1.89	0.343	1.298	0.354
40			1.885	0.317	1.257	0.326
60			1.891	0.264	1.253	0.264
20	50		1.822	0.258	1.128	0.254
40			1.799	0.237	1.1	0.248
60			1.832	0.207	1.179	0.206
20	70		1.821	0.239	1.127	0.219
40			1.79	0.197	1.128	0.194
60			1.809	0.192	1.089	0.195

The results are in accord with the theory for measurement error models. The simulation results based on the proposed method indicate that the naive estimator of β is markedly biased, while the estimated values based on the proposed method is much closer to the true value than the naïve estimate of β.

3.2 Data Analysis

Let Y be binary viral load, X be CD4 cell counts and Z be the treatment time. An ordinary logistic mixed-effects model says that the logit of Y = 1 satisfies

$$\text{logit}\{E(Y_{ij}\mid X_{ij},Z_{ij},b_{1i},b_{2i})\}={\alpha }_0+{\alpha }_1{X}_{ij}+{\alpha }_2{Z}_{ij}+b_{1i}{X}_{ij}+b_{2i}{Z}_{ij},$$ (3.1)

where b_1i and b_2i reflect the individual variations. The merit of this model includes its computational convenience and easy interpretation of the model parameter. However, this model may not be able to capture some curvature, as we shall see later because drug resistance, and noncompliance probably contribute nonlinearly along the treatment time. An alternative is a partially logistic mixed-effects model, described as

$$\text{logit}\{E(Y_{ij}\mid X_{ij},Z_{ij},b_{1i},c_i)\}=X_{ij}\beta +X_{ij}{b}_{1i}+\theta (Z_{ij})+c_i(Z_{ij}),$$ (3.2)

where θ(z) and c_i(z) are unknown smoothing functions, which describe the population characteristic and individual diversities.

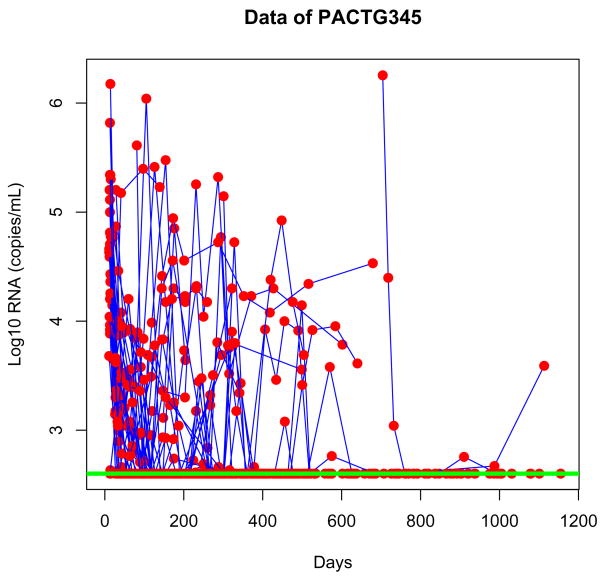
In this section, we present the results of analysis of an AIDS clinical study conducted by the Pediatric AIDS Clinical Trials Group (PACTG 345, Scott et al., 2001). In this study, 33 patients were enrolled as cohort II. Specimens were obtained on days 0, 1, 3, 7, 14, 28, 56, …, 1115, and 559 observations were obtained with 256 HID-1 RNA measurements below the detection limit of 400 copies/mL: 45% viral load observations were therefore suppressed below the detection limit. Figure 1 presents the individual observations of plasma HID RNA concentration (viral load) after initial antiretroviral treatments. A main objective of the treatment is to suppress the viral load below the limit of detection.

Figure 1.

Individual viral load measurements of plasma HID RNA concentration in the PACTG 345 study. The detection limit of 400 copies of HID RNA per mL of plasma is indicated by the horizontal line.

The purpose of this analysis focuses on whether the viral load is suppressed and how the of CD4 cell counts change during the treatment. We apply the model and estimation method described in section 2 to explore this data set and address the concerns mentioned in Section 1 by modeling the dynamic relation between the binary response (with or without viral suppression) and CD4 cell counts during the treatment period of about 3 years.

Let Y_ij = 1 if the viral load of the ith subject at time Z_ij is below the detection limit, and 0 otherwise. In this analysis, we consider 4 scenarios: (i) model (3.1) and ignoring consideration of measurement error in CD4+ cell counts; (ii) model (3.1) with consideration of measurement error in CD4+ cell counts; (iii) model (3.2), ignoring measurement error in CD4+ cell counts; and (iv) model (3.2) with consideration of measurement error in CD4+ cell counts. When considering measurement errors in CD4+ cell counts and using the method proposed in subsection 2.5 to produce the “true” CD4+ cell counts, the smoothing parameters (the number of knots) are selected by the model selection criterion BIC and the location of knots is selected at the quantiles of the data (Eubank, 1999). We obtain p = q = 3. To stabilize the variance and computational algorithms, we centered the covariate CD4+ cell counts and took a log-transformation for time in the model fitting. We fitted the model by using the LME function of Splus.

The population estimated values of the parameter β for these 4 scenarios are presented in Table 2. Comparing the estimates of β under (i) scenarios to (iii) and (ii) to (iv), we saw that models (3.1) and (3.2) derive remarkably different results. We also compared the estimates obtained with or without considering measurement error in the CD4+ cell counts. The estimates attenuated toward zero regardless of the models (3.1) or (3.2) used when the measurement error in the covariate is not considered. This finding is similar to that in standard linear or nonlinear regression models with measurement error (Carroll et al. 1995).

Table 2.

Estimates of the parameters in scenarios (i)–(iv), based on PACTG 345 data

	(i)	(ii)	(iii)	(iv)
β̂	−0.272	−0.358	−0.692	−1.046
SE	0.10	0.143	0.134	0.223
Pvalue	0.007	0.0014	< 10−4	< 10−4

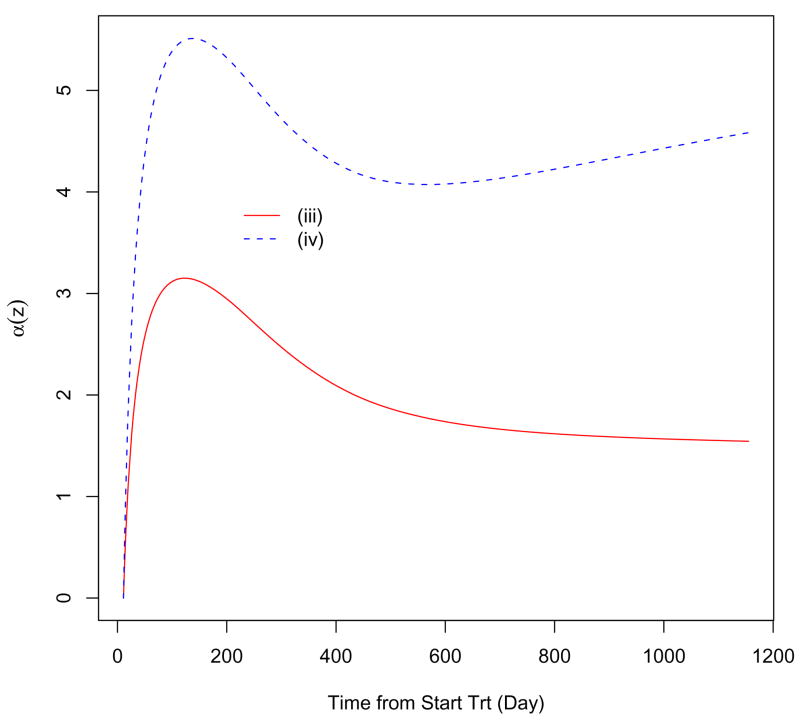
The population estimates of θ(z) for scenarios (iii) and (iv) are shown in Figure 2. Two population curves have similar patterns; that is, the curves rise rapidly at first and then maintain a steady decline from day 56 to the end of treatment. However, a consideration of measurement error reflects a sharper increase at the beginning.

Figure 2.

Population curve estimates of θ(z) considering measurement errors (solid line) and ignoring measurement errors (dashed line).

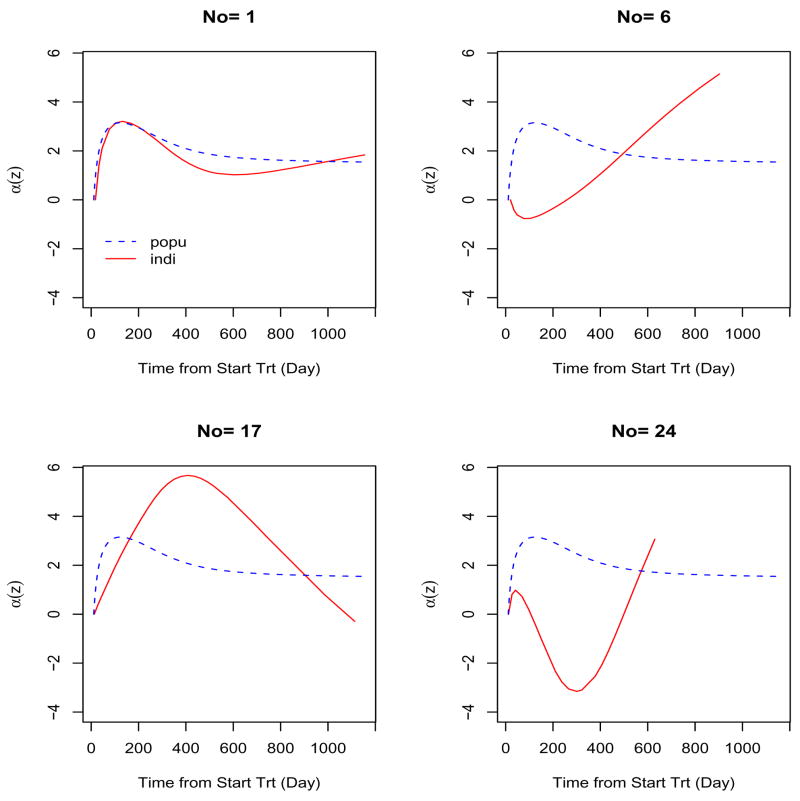
Recalling the viral load of each subject shown in Figure 1, we note that the between-subject variation can not be ignored and the individual curves, α_i(z) = θ(z) + c_i(z), may not follow the pattern of the population curve. We present the results for 4 individual subjects, and these results illustrate the principal advantage of the proposed model and developed methods in that the estimates can be obtained for both population and individuals. Because the patterns for the same individual under scenarios (iii) and (iv) are similar, we report in detail only the results for the case in which measurement errors in CD4+ cell counts are ignored. Figure 3 shows the individual estimates from 4 patients. For comparison, the corresponding population estimate is also plotted. The population and individual estimates are different not only in magnitude but also in patterns of change. The individual curve for subject 1 almost follows the population curve. The individual curves of the other 3 subjects are totally different from the population curve. Curves of subjects 6 and 24 decline sharply at first and then rebound later, to the end of treatment, but have different rebounding times. In contrast, the curve of subject 17 follows a convex shape. Given this large between-subject variation, the estimated trajectories of the individual curves become very important for individualizing treatment management and care for AIDS patients.

Figure 3.

Selected individual curve estimates (solid line), with the population curve estimate (dashed line) provided for comparison.

4 Discussion

In order to study the relation between binary virologic variables and immunologic variables, repeatedly measured indices of success of suppression of viral load (the virologic variable) and CD4+ cell counts (the immunologic variable) in AIDS clinical trials, we proposed a semiparamet-ric mixed-effects model, which can parsimoniously reflect both population and individual relationships between the two longitudinal variables. Similar models have been reported in the literature. However, most published studies focused only on the estimation of the population characteristic, although between-subject and within-subject variations have been incorporated. The method proposed in this article extends existing methods and allows us to estimate the population profile and individual diversities.

In step 1 we minimized the objective function with respect to α, β, b_i and ν_i. Alternatively, we may specify initial values β⁽⁰⁾ and ${\mathbf{b}}_i^{(0)}$, and maximize the objective function (a similar form to (2.2) but replacing β and b_i with β⁽⁰⁾ and ${\mathbf{b}}_i^{(0)}$) with respect to α and ν_i. This alternative may increase efficiency (see Carroll et al., 1997 for a related discussion), but it increases computation efforts.

When considering measurement errors in CD4 cell counts, we used a mixed-effects based approach to calibrate the effect of measurement error. This calibration may also be achieved by using a SIMEX-based procedure such as Liang and Ren (2005). However, additional information is required to estimate the covariance matrix cov(X) in implementing the SIMEX procedure. This investigation also increases computation efforts.

In this article, we develop a method using local linear regression. There are a lot of alternative ways for local linear approximation in step 1, including higher degree local polynomial kernel methods and smoothing and regression splines. The details for these methods require a further investigation in our setting. We chose the local linear smoother because theoretical results can be derived and the estimators of nonparametric components do not suffer from boundary effects (Fan and Gijbels, 1996).

Model (2.1) may be extended to a generalized additive partially linear mixed-effect model, of the form

$$g({\mu }_{ij})=X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+\sum _{k=1}^K{\theta }_k(Z_{ij}^{(k)})+\sum _{k=1}^K{c}_{ik}(Z_{ij}^{(k)}).$$

The study of this model is interesting and requires tedious efforts, but is beyond the scope of this paper.

Appendix

A.1 Proof of Theorem 1

Let c_n = (Nh)^−1/2,

$${\mathbf{\Xi }}_{ij}^{\ast }=\left(\begin{array}{c}1\\ (Z_{ij}-z_0)/h\\ X_{ij}\end{array}\right),{\mathit{\beta }}^{\ast }=\left(\begin{array}{c}{c}_n^{-1}\{{\alpha }_0-\theta (z_0)\}\\ c_n^{-1}h\{{\alpha }_1-{\theta }^{\prime }(z_0)\}\\ c_n^{-1}(\stackrel{\sim }{\mathit{\beta }}-\mathit{\beta })\end{array}\right),{\widehat{\mathit{\beta }}}^{\ast }=\left(\begin{array}{c}{c}_n^{-1}\{{\widehat{\alpha }}_0-\theta (z_0)\}\\ c_n^{-1}h\{{\widehat{\alpha }}_1-{\theta }^{\prime }(z_0)\}\\ c_n^{-1}(\widehat{\mathit{\beta }}-\mathit{\beta })\end{array}\right),$$

and let f(z) denote the density function of Z_ij. Denote further ${\overline{\eta }}_{ij}={\overline{\eta }}_{ij}(z_0)=X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\widehat{\mathbf{b}}}_i+\theta (z_0)+{\theta }^{\prime }(z_0)(Z_{ij}-z_0)+{\widehat{c}}_i^{\prime }(z_0)+{\widehat{c}}_i^{\prime }(z_0)(Z_{ij}-z_0)$. (2.3) implies that β̂^* maximizes

$${\ell }_n({\mathit{\beta }}^{\ast })=h\sum _{i=1}^n\sum _{j=1}^{n_i}[Q\{g^{-1}(c_n{\mathit{\beta }}^{\ast \text{T}}{\mathbf{\Xi }}_{ij}^{\ast }+{\overline{\eta }}_{ij}),Y_{ij}\}-Q\{g^{-1}({\overline{\eta }}_{ij}),Y_{ij}\}]K_h(Z_{ij}-z_0),$$

with respect to β^*. By the concavity of the function ℓ_n(β^*) and Taylor expansion of the function Q{g⁻¹(·), Y_ij} with respect to β^*, we obtain that

$${\ell }_n({\mathit{\beta }}^{\ast })={\mathbf{W}}_n^{\text{T}}{\mathit{\beta }}^{\ast }+\frac{1}{2}{\mathit{\beta }}^{\ast \text{T}}{\mathbf{A}}_n{\mathit{\beta }}^{\ast }\{1+o_P(1)\},$$ (A.1)

where ${\mathbf{W}}_n=h{c}_n{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{n_i}}{q}_1({\overline{\eta }}_{ij},Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{K}_h(Z_{ij}-z_0)$ and ${\mathbf{A}}_n=h{c}_n^2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{n_i}}{q}_2({\overline{\eta }}_{ij},Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{\mathbf{\Xi }}_{ij}^{\ast \text{T}}{K}_h(Z_{ij}-z_0)$. Furthermore, let ${\eta }_{ij}^0=X_{ij}^{\text{T}}\mathit{\beta }+A_{ij}^{\text{T}}{\mathbf{b}}_i+\theta (z_0)+{\theta }^{\prime }(z_0)(Z_{ij}-z_0)+c_i(z_0)+{\widehat{c}}_i^{\prime }(z_0)(Z_{ij}-z_0)$. Without loss of generality, assume that the means of random-effects terms b̂_i − b_i, ĉ(z₀) − c_i(z₀), and ${\widehat{c}}_i^{\prime }(z_0)-c_i^{\prime }(z_0)$ are zeros. Then

$$\begin{array}{l}{\mathbf{A}}_n=h{c}_n^2\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_2({\eta }_{ij}^0,Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{\mathbf{\Xi }}_{ij}^{\ast \text{T}}{K}_h(Z_{ij}-z_0)\\ +h{c}_n^2\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_3({\zeta }_{ij},Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{\mathbf{\Xi }}_{ij}^{\ast \text{T}}({\overline{\eta }}_{ij}-{\eta }_{ij}^0)K_h(Z_{ij}-z_0),\end{array}$$ (A.2)

where ζ_ij is between ${\eta }_{ij}^0$ and η̄_ij. Note that $({\overline{\eta }}_{ij}-{\eta }_{ij}^0)=A_{ij}^{\text{T}}({\widehat{\mathbf{b}}}_i-{\mathbf{b}}_i)+\{{\widehat{c}}_i(z_0)-c_i(z_0)\}+\{{\widehat{c}}_i^{\prime }(z_0)-c_i^{\prime }(z_0)\}(Z_{ij}-z_0)$. Using an argument similar to the proof of (A.9) of Carroll et al. (1997) and condition (i) yield that the second term in the (A.2) is of order o(h). We therefore have

$${\mathbf{A}}_n=h{c}_n^2\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_2({\eta }_{ij}^0,Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{\mathbf{\Xi }}_{ij}^{\ast \text{T}}{K}_h(Z_{ij}-z_0)+o(h)\triangleq {\mathbf{A}}_n^0+o(1).$$

In a similar way, we obtain that

$${\mathbf{W}}_n=h{c}_n\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1({\eta }_{ij}^0,Y_{ij}){\mathbf{\Xi }}_{ij}^{\ast }{K}_h(Z_{ij}-z_0)+o(c_n^{-1}{h}^2)\triangleq {\mathbf{W}}_n^0+o(c_n^{-1}{h}^2).$$

Let

$$\mathbf{A}(X)=\left(\begin{array}{ccc}1& 0& X^{\text{T}}\\ 0& {\kappa }_2& 0\\ X& 0& X{X}^{\text{T}}\end{array}\right);\mathbf{B}(X)=\left(\begin{array}{ccc}{\mu }_0& 0& {\mu }_0{X}^{\text{T}}\\ 0& {\mu }_2& 0\\ {\mu }_{0}X& 0& {\mu }_{0}X{X}^{\text{T}}\end{array}\right).$$

We write ${({\mathbf{A}}_n^0)}_{ij}={(E{\mathbf{A}}_n^0)}_{ij}+O_P\left({\{var{({\mathbf{A}}_n^0)}_{ij}\}}^{1/2}\right)$ and deal with the first two moments of ${\mathbf{A}}_n^0$. Note that $q_2(x,y)=\{y-g^{-1}(x)\}{\rho }_1^{\prime }(x)-{\rho }_2(x)$. We find for the first moment, with η̄ = X^Tβ + A^Tb + θ(z₀) + θ(z₀)(Z − z₀) + c(z₀) + c′(z₀)(Z − z₀),

$$\begin{array}{l}E{\mathbf{A}}_n^0=E\left[E\left\{q_2(\overline{\eta },Y){\mathbf{\Xi }}^{\ast }{\mathbf{\Xi }}^{\ast \text{T}}{K}_h(Z-z_0)\mid \mathbf{X},\mathbf{b}\right\}\right]\\ =E\left[\{g^{-1}(R)-g^{-1}(\overline{\eta })\}{\rho }_1^{\prime }(\overline{\eta }){\mathbf{\Xi }}^{\ast }{\mathbf{\Xi }}^{\ast \text{T}}{K}_h(Z-z_0)\right]\\ -E\left\{{\rho }_2(\overline{\eta }){\mathbf{\Xi }}^{\ast }{\mathbf{\Xi }}^{\ast \text{T}}{K}_h(Z-z_0)\right\}.\end{array}$$ (A.3)

The first term in (A.3) is of order O(h²). It follows that

$$\begin{array}{l}E{\mathbf{A}}_n^0=-E\{{\rho }_2(\overline{\eta }){\mathbf{\Xi }}^{\ast }{\mathbf{\Xi }}^{\ast \text{T}}{K}_h(Z-z_0)\}+O(h^2)\\ =-E\left(E\left[{\rho }_2\{R+O(h)\}{\mathbf{\Xi }}^{\ast }{\mathbf{\Xi }}^{\ast \text{T}}\mid Z=z_0\right]K_h(Z-z_0)\right)+O(h^2)\\ =-f(u)E\{{\rho }_2(R)\mathbf{A}(X)\mid Z=z_0\}+o(1)\equiv \mathbf{A}+o(1).\end{array}$$ (A.4)

In an analogous way we can show that

$$var{({\mathbf{A}}_n^0)}_{ij}=O(c_n^2).$$ (A.5)

Combining (A.4) and (A.5), we obtain

$${\mathbf{A}}_n^0=-\mathbf{A}+o_P(1).$$ (A.6)

Therefore, by (A.1),

$${\ell }_n({\mathit{\beta }}^{\ast })={\mathbf{W}}_n^{0\text{T}}{\mathit{\beta }}^{\ast }-\frac{1}{2}{\mathit{\beta }}^{\ast \text{T}}\mathbf{A}{\mathit{\beta }}^{\ast }+o_P(1).$$ (A.7)

By applying the convexity lemma (Pollard, 1991), we obtain that ${\widehat{\mathit{\beta }}}^{\ast }={\mathbf{A}}^{-1}{\mathbf{W}}_n^0+o_P(1)$. Hence the asymptotic normality of β̂^* will follow from that of ${\mathbf{W}}_n^0$, which we will establish below. By the definition of ${\mathbf{W}}_n^0$ and using Taylor’s expansion we get for the first moment,

$$\begin{array}{l}E{\mathbf{W}}_n^0=c_n^{-1}E[E\{q_1(\overline{\eta },Y){\mathbf{\Xi }}^{\ast }{K}_h(Z-z_0)\mid \mathbf{X},\mathbf{b}\}]\\ =c_n^{-1}E\left[\{g^{-1}(R)-g^{-1}(\overline{\eta })\}{\rho }_1(\overline{\eta }){\mathbf{\Xi }}^{\ast }{K}_h(Z-z)\right]\\ =\frac{1}{2}{c}_n^{-1}E\left[(g^{-1}{)}^{\prime }(R)\{c^{″}(z_0)+{\theta }^{″}(z_0)\}{(Z-z_0)}^2{\rho }_1(\overline{\eta }){\mathbf{\Xi }}^{\ast }{K}_h(Z-z_0)\right]+o(c_n^{-1}{h}^2)\\ =c_n^{-1}\frac{1}{2}{\theta }^{″}(z_0)h^{2}f(z_0)E\left\{{\rho }_2(R){({\kappa }_2,0,{\kappa }_2{X}^{\text{T}})}^{\text{T}}\mid Z=z_0\right\}\\ +c_n^{-1}\frac{1}{2}{h}^{2}f(z_0)E\left\{c^{″}(Z){\rho }_2(R){({\kappa }_2,0,{\kappa }_2{X}^{\text{T}})}^{\text{T}}\mid Z=z_0\right\}+o(c_n^{-1}{h}^2).\end{array}$$ (A.8)

It follows from these statements and (A.6) that

$$c_n^{-1}\{\widehat{\theta }(z_0)-\theta (z_0)-b_{\theta }(z_0)+o_p(h^2)\}={[f(z_0)E\{{\rho }_2(R)\mid Z=z_0\}]}^{-1}{S}_n\{1+o_p(1)\},$$

where $S_n=c_n{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{s}_{ij}$ with s_ij = q₁(η_ij, y_ij)K_h(Z_ij − z₀). We have

$$var(S_n)=c_n^2\sum _{i=1}^{n}var\left(\sum _{j=1}^{n_i}{s}_{ij}\right)=J_{n1}+J_{n2}$$

where

$$J_{n1}=c_n^2\sum _{i=1}^n\sum _{j=1}^{n_i}var(s_{ij})\text{and}{J}_{n2}=c_n^2\sum _{i=1}^n\sum _{j_1\ne j_2}cov(s_{i{j}_1},s_{i{j}_2}).$$

It is easy to see that

$$var(s_{ij})=h{\mu }_{0}f(z_0)E\{{\rho }_2(R)\mid Z=z_0\}+o(1)$$

and

$$J_{n1}={\mu }_{0}f(z_0)E\{{\rho }_2(R)\mid Z=z_0\}+o(1).$$

Furthermore, for j₁ ≠ j₂, by condition (h)

$$cov(s_{i{j}_1},s_{i{j}_2})=E\{{\gamma }_y(Z_{i{j}_1},Z_{i{j}_2})K_h(Z_{i{j}_1}-z_0)K_h(Z_{i{j}_2}-z_0)\}=h^2{f}^2(z_0){\gamma }_y(z_0,z_0)\{1+o_p(1)\},$$

which, combined with condition (g), yields that

$$J_{n2}=h^2{f}^2(z_0){\gamma }_y(z_0,z_0)c_n^2\sum _{i=1}^n{n}_i(n_i-1)\{1+o(1)\}=\lambda f^2(z_0){\gamma }_y(z_0,z_0)\{1+o(1)\}.$$

It follows that

$$var(S_n)={\mu }_{0}f(z_0)E\{{\rho }_2(R)\mid Z=z_0\}+\lambda f^2(z_0){\gamma }_y(z_0,z_0)+o(1).$$

Finally, using condition (f), it can be shown that Liapounov’s condition is satisfied and hence Theorem 1 holds, as claimed.

A.2 Proof of Theorem 2

First of all, we note that under the specified condition, in a proof similar to that for theorem 2 of Carroll et al. (1997), we can establish

$$\begin{array}{r}\underset{z\in D}{sup}\left|\widehat{\theta }(z_0)-\theta (z_0)-\frac{1}{Nf(z)E\{{\rho }_2(R)\mid Z=z_0\}}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1({\eta }_{ij},y_{ij})K_h(Z_{ij}-z_0)\right|\\ =O_P\{h^2{c}_n+c_n^2{log}^{1/2}(1/h)\}.\end{array}$$ (A.9)

Let ζ̂ = N^1/2(β̂ − β₀), ${\widehat{m}}_{ij}=\widehat{\theta }(Z_{ij})+X_{ij}^{\text{T}}\mathit{\beta }+{\widehat{c}}_i(Z_{ij})+A_{ij}^{\text{T}}{\mathbf{b}}_i$, and $m_{ij}=\theta (Z_{ij})+X_{ij}^{\text{T}}{\mathit{\beta }}_0+c_i(Z_{ij})+A_{ij}^{\text{T}}{\mathbf{b}}_i$. Then, ζ̂ maximizes

$${\ell }_n(\zeta )=\sum _{i=1}^n\sum _{j=1}^{n_i}\left[Q\left\{g^{-1}({\widehat{m}}_{ij}+N^{-1/2}{X}_{ij}^{\text{T}}\zeta ),Y_{ij}\right\}-Q\left\{g^{-1}({\widehat{m}}_{ij}),Y_{ij}\right\}\right]$$ (A.10)

with respect to ζ. By Taylor’s expansion, we have

$${\ell }_n(\zeta )=N^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1({\widehat{m}}_{ij},Y_{ij})X_{ij}^{\text{T}}\zeta +\frac{1}{2}{\zeta }^{\text{T}}{\mathbf{B}}_n\zeta ,$$ (A.11)

where

$${\mathbf{B}}_n=\frac{1}{N}\sum _{i=1}^n\sum _{j=1}^{n_i}\left[Y_{ij}{\rho }_1^{\prime }\left\{g^{-1}({\widehat{m}}_{ij}+{\zeta }_{\mathit{nij}})\right\}-{\rho }_3\left\{g^{-1}({\widehat{m}}_{ij}+{\zeta }_{\mathit{nij}}^{\prime })\right\}\right]X_{ij}{X}_{ij}^{\text{T}},$$

with ζ_nij and ${\zeta }_{\mathit{nij}}^{\prime }$ between 0 and $N^{-1/2}{X}_{ij}^{\text{T}}\zeta$, independent of Y_ij, and with ${\rho }_3(x)=-g^{-1}(x){\rho }_1^{\prime }(x)-{\rho }_2(x)$. It can be shown that

$${\mathbf{B}}_n=-E\{{\rho }_2(R)X{X}^{\text{T}}\}+o_P(1)=-\mathbf{B}+o_P(1).$$ (A.12)

Using similar arguments as for obtaining (A.12), we get

$$\begin{array}{r}{N}^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1({\widehat{m}}_{ij},Y_{ij})X_{ij}=N^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_1(m_{ij},Y_{ij})X_{ij}+N^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_2(m_{ij},Y_{ij})\\ \left\{\widehat{\theta }(Z_{ij})-\theta (Z_{ij})\right\}{X}_{ij}+O_P\left\{N^{1/2}{c}_n^2{log}^{1/2}(1/h)\right\}.\end{array}$$

By (A.9), the second term in the above expression can be expressed as

$$\begin{array}{r}{N}^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}{q}_2(m_{ij},Y_{ij})\frac{1}{\mathit{Nhf}(Z_{ij})E\{{\rho }_2(R)\mid Z_{ij}\}}\left\{\sum _{l=1}^n\sum _{s=1}^{n_i}{q}_1({\eta }_{ls},y_{ls})K_h(Z_{ls}-Z_{ij})\right\}{X}_{ij}\\ +O_P\left\{n^{1/2}{c}_n^2{log}^{1/2}(1/h)\right\}\\ \equiv T_{n1}+O_P\left\{N^{1/2}{c}_n^2{log}^{1/2}(1/h)\right\}.\end{array}$$

T_n1 can further be simplified as

$$T_{n1}=N^{-1/2}\sum _{l=1}^n\sum _{s=1}^{n_i}{q}_1({\eta }_{ls},y_{ls})\frac{E\{{\rho }_2(R)X\mid Z_{ls}\}}{E\{{\rho }_2(R)\mid Z_{ls}\}}+O_P(N^{1/2}{h}^2)$$ (A.13)

Combining (A.10)–(A.13) we obtain that

$${\ell }_n(\zeta )=N^{-1/2}\sum _{i=1}^n\sum _{j=1}^{n_i}\omega (Z_{ij},Y_{ij},X_{ij})-\frac{1}{2}{\zeta }^{\text{T}}\mathbf{B}\zeta +o_P(1),$$

where

$$\mathrm{\Omega }(Z_{ij},Y_{ij},X_{ij})=q_1(m_{ij},Y_{ij})\left[X_{ij}-\frac{E\{{\rho }_2(R)X\mid Z_{ij}\}}{E\{{\rho }_2(R)\mid Z_{ij}\}}\right].$$

By the convexity lemma (Pollard, 1991) we find that $\widehat{\zeta }={\mathbf{B}}^{-1}{N}^{-1/2}{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}\mathrm{\Omega }(Z_{ij},Y_{ij},X_{ij})+o_P(1)$, from which it follows that

$$N^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })\stackrel{D}{\to }N(0,{\mathbf{B}}^{-1}{\mathrm{\sum }}_1{\mathbf{B}}^{-1}),$$

as claimed.