Binding kinetics of histone chaperone Chz1 and variant histone H2A.Z-H2B by relaxation dispersion NMR spectroscopy

Abstract

The genome of eukaryotic cells is packed into a compact structure called chromatin that consists of DNA as well as both histone and non-histone proteins. Histone-chaperones associate with histone proteins and play important roles in the assembly of chromatin structure and transport of histones in the cell. The recently discovered histone-chaperone Chz1 associates with the variant histone H2A.Z of budding yeast and plays a critical role in the exchange of the canonical histone pair H2A-H2B for the variant H2A.Z-H2B. Here, we present an NMR approach that provides accurate estimates for the rates of association and dissociation of Chz1 and H2A.Z-H2B. The methodology exploits the fact that in a 1:1 mixture of Chz1 and H2A.Z-H2B the small amounts of unbound proteins that are invisible in spectra produce line-broadening of signals from the complex that can be quantified in terms of the thermodynamics and kinetics of the exchange process. The dissociation rate constant measured, 22±2 s⁻¹, provides an upper bound for the rate of transfer of H2A.Z-H2B to the chromatin remodeling complex and the faster than diffusion association rate, 10⁸±10⁷ M⁻¹s⁻¹, establishes the importance of attractive electrostatic interactions that form the chaperone:histone complex.

Introduction

Chromosomal DNA molecules of eukaryotic cells are many times longer than the diameter of the nucleus and consequently the DNA is packed into a compact nucleoprotein complex called chromatin that comprises DNA, histones and non-histone proteins^{1, 2}. The first level of compaction consists of coiling 147 base pairs of DNA around a protein complex to form the nucleosome, the structural unit of chromatin. The nucleosome is a disc shaped structure with a diameter of ~100 Å, where the DNA is coiled in a superhelix around a hetero-octamer of histone proteins consisting of two molecules each of H2A, H2B, H3 and H4^{3, 4}. The packing of DNA and the formation of nucleosomes restricts access to the cellular machinery, although conformational fluctuations at a rate of several times/sec do occur that transiently lift stretches of DNA from histone surfaces so that DNA can be accessed by regulatory proteins⁵. In addition, cellular signals are given that loosen DNA-histone contacts, facilitating further interactions with proteins. One mechanism by which cells regulate gene expression involves exploiting changes in histone-DNA and histone-histone interactions within and between nucleosomes, for example by posttranslational modifications of the histones or by replacing canonical histones with histone variants. Emerging evidence now indicates that histone variants are essential for the epigenetic control of gene expression⁶. Their incorporation into nucleosomes marks chromatin regions and histone variants are likely to play major roles in controlling chromosomal architecture with their deregulation linked to cancers and mental disorders^{6, 7}.

The histone variant H2A.Z has ≈60% sequence identity to the canonical form H2A, is highly conserved during evolution and is found in many species including humans. H2A.Z has a large variety of biological functions^{6, 8} and is essential for viability. For example, deletion of H2A.Z in Xenopus leavis (African clawed frog) leads to embryos with malformed trunks⁹, in Mus musculus (mouse) deletion of H2A.Z is lethal¹⁰, while in yeast H2A.Z (Htz1) is important for cell growth ¹¹. Recently the chromatin remodeling complex SWR1 was discovered, which specifically exchanges H2A for H2A.Z in yeast^{12, 13, 14}. The Swc2 subunit of SWR1 recognizes the unique C-terminal region of H2A.Z ¹⁵ and catalyses the in vitro exchange of H2A–H2B for H2A.Z-H2B in an ATP-dependent manner in the presence of histone chaperones such as Chz1¹⁶ that contains a highly conserved sequence motif, CHZ (residue 94–115), for recognition of H2A.Z-H2B.

Despite the importance of histone-chaperone interactions, very little is known about them. Recently the structure of yeast H2A.Z-H2B bound to Chz1 was solved by solution NMR spectroscopy¹⁷, revealing a unique fold for the Chz1 chaperone comprising a long irregular chain capped by two short helices. However the stability of the Chz1:H2A.Z-H2B complex is not known, nor is the rate of binding of Chz1 to H2A.Z-H2B (k_on), and importantly the rate of complex dissociation (k_off) that represents an upper limit for the rate of substitution of H2A.Z-H2B for H2A.H2B has also not been determined. Here we report a method based on relaxation dispersion NMR that enables measurement of accurate kinetic and thermodnamic parameters of the Chz1/H2A.Z-H2B binding reaction. A dissociation constant, K_D~0.2 μM obtained, that agrees well with values derived from ITC measurements, along with values of k_on=10⁸ ±10⁷ M⁻¹ s⁻¹ and k_off=22±2s⁻¹ that describe the association and dissociation of the complex, respectively.

Association/dissociation of Chz1:H2A.Z-H2B

In what follows we consider the binding of Chz1 to H2A.Z-H2B, which as we will show below, can be described by the following equilibrium

$$\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1\underset{k_{\text{on}}}{\overset{k_{\text{off}}}{\rightleftharpoons }}\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}+\text{Chz}1$$ [1]

where k_on is the second order rate constant of binding, k_off is the first order rate constant of dissociation and the dissociation constant, K_D, is given by:

$$K_{\text{D}}=\frac{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}][\text{Chz}1]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]}=\frac{k_{\text{off}}}{k_{\text{on}}}$$ [2]

This binding equilibrium can be studied by Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion NMR spectroscopy^{18, 19}. Here relaxation compensated^{20, 21} transverse relaxation rates of nuclear spins, R₂, that are proportional to the line-widths of peaks in spectra are measured during a fixed delay in the presence of a variable effective radio frequency field that is applied in the form of a train of refocusing pulses²². Variations in R₂ as a function of the number of refocusing pulses indicate the presence of millisecond time-scale chemical exchange. An analysis of relaxation dispersion profiles, R₂ vs. ν_CPMG, where the radio frequency field ν_CPMG is proportional to the number of refocusing pulses applied, yields exchange rates and the populations of the chemically exchanging sites along with structural information in the form of chemical shift differences between the exchanging sites, Δϖ.

Our strategy for this relaxation dispersion study has been to use a single sample with very close to 1:1 composition of Chz1:H2A.Z-H2B. The relatively high affinity of the complex (sub-μM dissociation constant, see below) ensures that both proteins are largely in the bound form with a small fraction (≈1%) in the free state. Exchange between the dominant bound conformation that is NMR observable and the low populated NMR invisible free states leads to line-broadening of the peaks in spectra of the complex that can be quantified by the relaxation dispersion methodology described above. Importantly, by isotopic labeling of both molecular components (i.e., chaperones and histones) with ¹⁵N it becomes possible to study the binding reaction by quantifying the exchange process using probes from both Chz1 and H2A.Z-H2B, so that accurate kinetic parameters can be determined. It is worth noting that samples prepared with excess of one of the binding partners are non-optimal since signals from the molecule in excess become severely broadened in both free and bound states as the fractional populations in each state become similar^{23, 24}.

For the general dissociation reaction, $\text{P}:\text{L}\underset{k_{\text{on}}}{\overset{k_{\text{off}}}{\leftrightarrow }}\text{P}+\text{L}$, fits of relaxation dispersion profiles that derive from sites in P provide measures of k_ex = k_on[L] + k_off and the fractional population of each of the apo and ligand bound states, p_P = [P]/([P]+[P:L]), p_P:L = 1−p_P, respectively. Thus, by monitoring the binding event from sites on H2A.Z-H2B where the pseudo first-order association constant is k′_on = k_on[Chz1] and from probes on Chz1 that are sensitive to k″_on = k_on[H2A.Z-H2B], additional information is obtained relative to when only a single molecular species (Chz1 or H2A.Z-H2B) is studied. This is critical for the accurate measurement of K_D and hence k_on = k_off/K_D from relaxation dispersion data (see below) in cases where binding affinities are high (μM). It is worth noting, however, that when affinities are significantly lower (mM range) dispersion measurements that focus on only one of the two binding partners often provide accurate K_D values (see below).Figures 1A and 1B show two typical ¹⁵N relaxation dispersion profiles from sites in the Chz1:H2A.Z-H2B complex (experimental data in circles), where the exchange dynamics is monitored by Ala 124 of Chz1 (A) and Glu 75 of H2A.Z (B), respectively. The observation of relaxation dispersion profiles that are not flat (i.e., decreasing R₂ as a function of increasing ν_CPMG) is unequivocal evidence for millisecond chemical exchange, in the simplest model exchange is between a highly populated ground state, in this case the Chz1:H2A.Z-H2B complex and a low populated and thermally excited state whose origin is established below. The dispersion profiles for all residues from either Chz1 or H2A.Z-H2B are fit together to a model of two-site chemical exchange (solid lines), as described in the legend to the figure. χ²_red values of 0.90 (Chz1) and 0.68 (H2A.Z-H2B) were obtained for the two data sets, where χ²_red=χ²/DF and DF is the number of degrees of freedom (see legend to Figure 1), indicating that the 2-state model of Eq. [1] is appropriate. Additional evidence that the exchange reaction probed by relaxation dispersion is 2-state is provided by results from combined fits of amide ¹H and ¹⁵N dispersion profiles that are derived from separate regions of Chz1. For 2-state exchange, equivalent exchange parameters are expected when data from different residues are analyzed using a 2-state model since all probes in the protein report on the same process. This is what is observed here; values of (p_P,k_ex) = (1.5±0.03%,1510±50s⁻¹) and (1.6±0.02%,1470±40s⁻¹) are obtained from fits that include dispersion profiles from residues 25–43 and 48–61, respectively. In cases where exchange is more complex than 2-state large deviations in rates can be observed when sets of data are fitted to the simple 2-state model, as has been noted in relaxation dispersion studies of folding of a number of smaller modular domains^{25, 26}.

Figure 1.

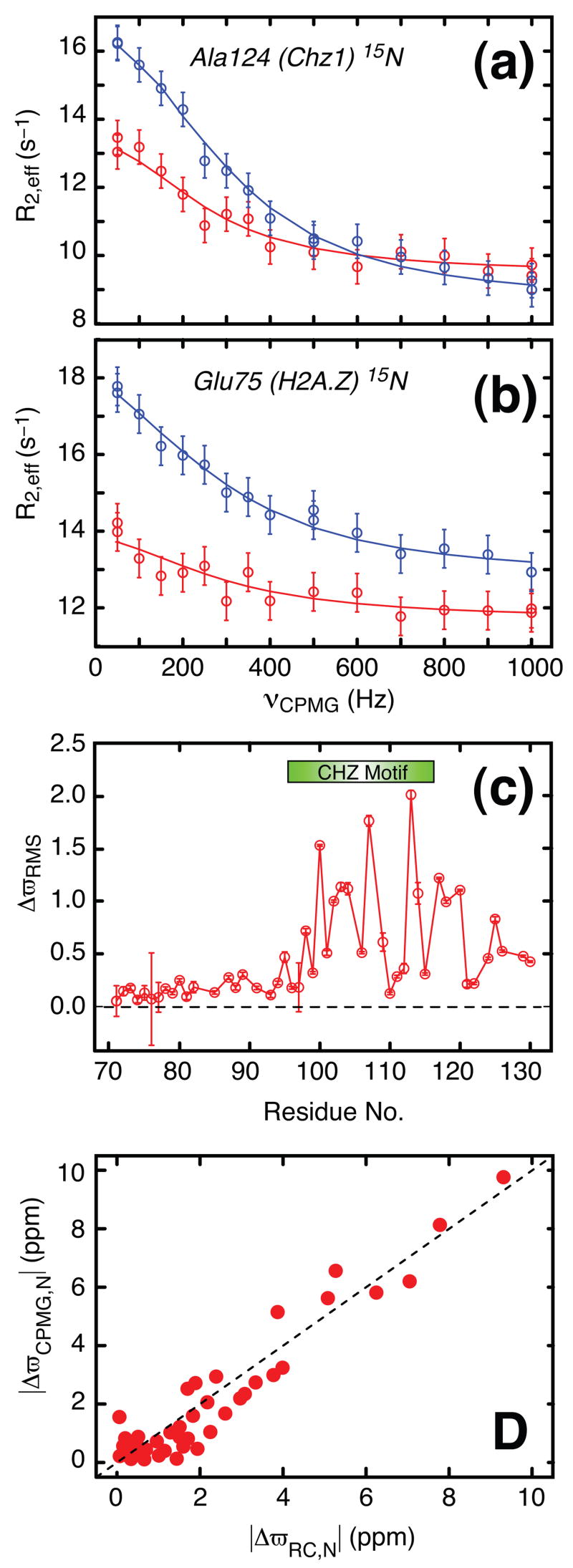
Amide ¹H and ¹⁵N relaxation dispersion profiles have been recorded on a complex comprising the single stranded H2A.Z-H2B protein and the chaperone Chz.core (residues 71–132 of Chz1), prepared as described previously¹⁷. Both protein constituents were U-¹⁵N, ²H labeled. The NMR sample was prepared with [H2A.Z-H2B]_Total≈1 mM, [Chz1]_Total ≈1 mM and 25 mM MES, 0.2 M NaCl, 1 mM EDTA, 10% D₂O, pH = 6.0. Representative ¹⁵N relaxation dispersion profiles from Ala124 of Chz1 (a) and Glu 75 of H2A.Z (b) recorded at static magnetic field strengths of 18.8 T (blue) and 11.7 T (red), 35°C are shown. The vertical lines associated with each measurement (circle) are error estimates; error values of 1% of R₂, 0.3 s⁻¹ or the standard deviation (SD) of duplicate measurements (whichever is the largest) were assigned to the ¹⁵N rates, while errors in ¹HN transverse relaxation rates were based on maximum(3% of R₂, 0.75 s⁻¹, SD of duplicate measurements). The solid lines are fits of a two-site exchange model to the data: |Δϖ|=2.3±0.1 ppm for Ala124(Chz), |Δϖ|=1.8±0.1ppm for Glu75(H2A.Z). Exchange rates and populations are given in the text. (c) Residue specific Δϖ_RMS values calculated as described in the legend to Figure 2. The CHZ motif (residue 95–115) is highlighted with a green bar. (d) Correlation plot of ¹⁵N chemical shift differences for Chz1 measured in a CPMG relaxation dispersion experiment, Δϖ_CPMG,N, versus the difference between the assigned chemical shifts of the bound state of Chz1 and random roil values²⁷, Δϖ_RC,N. Relaxation dispersion profiles were recorded using Varian Inova NMR spectrometers operating at static magnetic field strengths of 11.7 T and 18.8 T (500 and 800 MHz ¹H frequency), respectively. Constant-time²² relaxation compensated²⁰ TROSY-based pulse schemes were used for recording ¹H ³⁴ and ¹⁵N ²¹ relaxation dispersion profiles. A constant-time relaxation delay of 25 ms (40 ms) was used for the proton (nitrogen) dispersion profiles. Effective ¹⁵N transverse relaxation rates (R_2,eff) were measured for 14 different ν_CPMG frequencies between 50 and 1000 Hz, while the proton dispersion profiles were sampled at 15 different ν_CPMG frequencies between 80 and 1840 Hz. Data sets were processed with the NMRPipe program³⁵ and signal intensities quantified using the program FuDA (flemming@pound.med.utoronto.ca; http://pound.med.utoronto.ca/software). Relaxation dispersion profiles, R_2,eff(ν_CPMG), were generated from peak intensities, I(ν_CPMG), in a series of 2D ¹HN-¹⁵N correlation maps measured as a function of CPMG frequency (ν_CPMG=1/2τ, where τ is the time between two successive refocusing pulses). Peak intensities were converted into effective relaxation rates via R_2,eff= ln[I₀/I(ν_CPMG)]/T_relax, where I₀ is the peak intensity in a reference spectrum recorded without the constant-time relaxation delay T_relax. Details of the procedure by which dispersions profiles are fit are provided in the legend to Figure 3.

Millisecond chemical exchange is from the Chz1, H2A.Z-H2B binding event

As described above an important parameter that is obtained from fits of dispersion data is the chemical shift differences between probes in ground and excited states that can be used to provide information about the nature of the exchange process. Such differences are shown in Figure 1C for the Chz1 chaperone that includes weighted contributions from both ¹HN and ¹⁵N chemical shifts, Δϖ_RMS (see legend to Figure 2). Figure 1D illustrates the changes in ¹⁵N chemical shifts of amide nitrogen probes in ¹⁵N-labeled Chz1 that are measured from CPMG data, |Δϖ_CPMG,N|, vs. differences between the assigned ¹⁵N chemical shifts of Chz1 in the complex and the corresponding values that are expected in a random coil conformation²⁷, |Δϖ_RC,N|. The excellent correlation clearly implies that the low populated state of Chz1 that is probed by relaxation dispersion has¹⁵N chemical shifts that correspond to random coil values. This is expected for the free form of Chz1 that is known to be largely unstructured on the basis of a previous NMR study¹⁷. Thus, the Chz1 dispersion data derives from a binding reaction of the sort considered in Eq. [1].

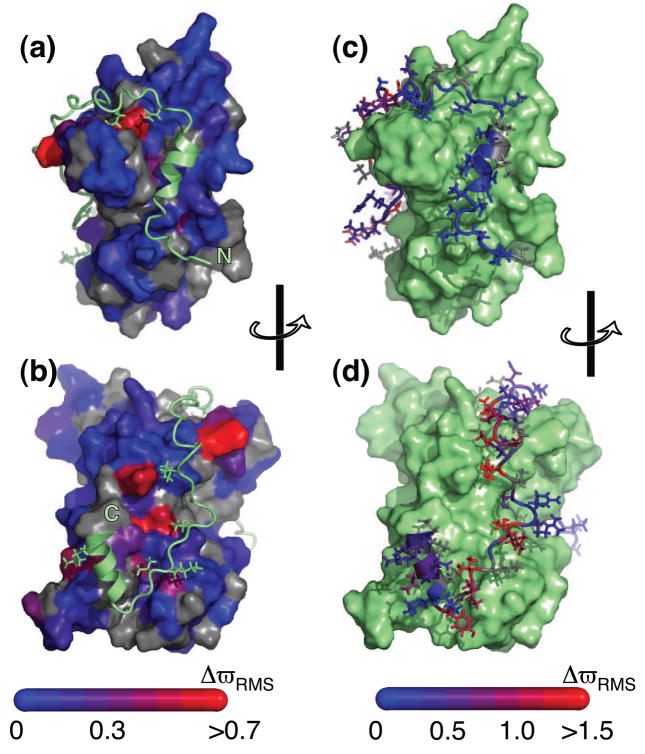
Figure 2.

Structure of Chz1:H2A.Z-H2B¹⁷ color-coded according to values of normalized changes of chemical shift, Δϖ_RMS (see below). (a) and (b) plot Δϖ_RMS for H2A.Z-H2B with the corresponding values for Chz1 in (c) and (d). Selected side-chains are included to illustrate contacts between the two binding partners. Differences in chemical shifts |Δϖ| have been obtained for all residues for which relaxation dispersions are available: Δϖ= ϖ(Chz1) − ϖ(H2A.Z-H2B:Chz1) and Δϖ(H2A.Z-H2B) − ϖ(H2A.Z-H2B:Chz1) for amide probes attached to Chz1 and H2AZ.H2B, respectively. The obtained Δϖ values were normalized for each residue according to the distributions observed in the BMRB database (http://www.bmrb.wisc.edu) $\mathrm{\Delta }{\omega }_{\text{RMS}}=\sqrt{\frac{1}{2}(\mathrm{\Delta }{\omega }_{\text{N}}^2/\mathrm{\Delta }{\omega }_{\text{STD},\text{N}}^2+\mathrm{\Delta }{\omega }_{\text{H}}^2/\mathrm{\Delta }{\omega }_{\text{STD},\text{H}}^2)}$ where Δϖ_STD,N = 3.8 ppm, Δϖ_STD,H = 0.6 ppm. For some residues only Δϖ_N or Δϖ_H was available and the normalized chemical shift change was calculated according to Δϖ_RMS= |Δϖ_N|/Δϖ_STD,N or Δϖ_RMS = |Δϖ_H|/Δϖ_STD,H, respectively.

Relaxation dispersion profiles are also observed for nuclei of H2A.Z-H2B but in contrast to Chz1 the chemical shift differences that are obtained from fits of the H2A.Z-H2B data do not correlate with a “bound to random coil” transition. Figure 2 shows the normalized chemical shift changes, Δϖ_RMS (see legend to figure) obtained from a combined analysis of both ¹HN and ¹⁵N relaxation dispersion data. The milli-second chemical exchange observed for both amide proton and nitrogen probes of H2A.Z-H2B report directly on Chz1 binding, since the Δϖ_RMS changes localize to residues that are proximal to the binding surface of Chz1 in the structure of the complex¹⁷ as shown in Figures 2A and 2B. Thus, kinetic parameters obtained from independent analyses of relaxation dispersion profiles of H2A.Z-H2B (k_ex,H2A.Z-H2B; p_H2A.Z-H2B) or Chz1 (k_ex,Chz1;p_Chz1) report mutually on the association/dissociation event and can therefore be combined to extract accurate values of k_off, k_on and K_D.

Not surprisingly only small chemical shift changes in amide ¹HN and ¹⁵N nuclei of H2A.Z-H2B are observed, (Δϖ_RMS<0.8 and only four residues with Δϖ_RMS>0.5), suggesting that only small changes to the H2A.Z-H2B structure occur upon binding of Chz1. Indeed, the shift changes likely reflect changes in hydrophobic interactions and perturbations to the electrostatic environment that accompany binding (see below). In contrast, the binding event is accompanied by much larger structural changes to Chz1, established by the large chemical shift differences (Δϖ_RMS > 1.0) that are observed for many residues of Chz1 (Figure 2D). Interestingly, only small Δϖ_RMS values are observed for the N-terminal end of Chz1 (residues 71–91, Figures 1C, 2C) that are consistent with smaller changes in structure upon binding.

Extraction of dissociation and association rate constants

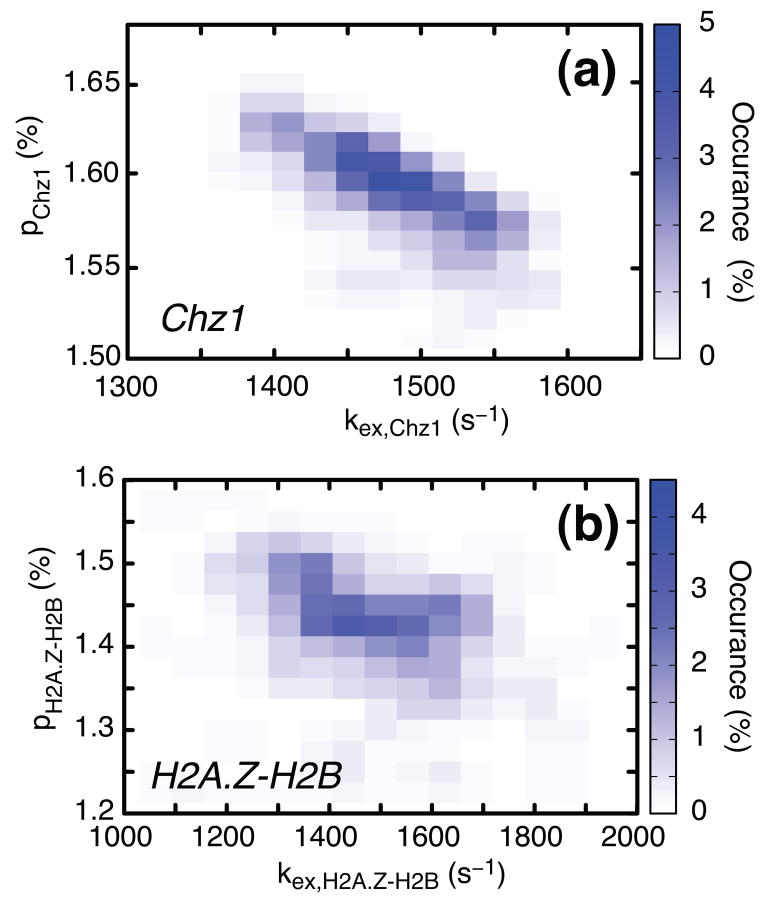
Separate fits of relaxation dispersion profiles derived from backbone amide probes in H2A.Z-H2B and Chz1 (35°C) to a model of two-site chemical exchange according to Eq. [1] produced values of exchange parameters (k_ex,H2AZ.H2B; p_H2AZ.H2B)=(1520±165 s⁻¹; 1.40±0.09%) (based on 52 nitrogen dispersions, 46 amide proton dispersions) and (k_ex,Chz1; p_Chz1)=(1490±100 s⁻¹; 1.59±0.03%) (31 nitrogen dispersion profiles and 22 amide proton profiles). Distributions of rate constants and populations that are consistent with the experimental data, Figure 3, have been estimated from bootstrap calculations (see legend to Figure 3).

Figure 3.

Relaxation dispersion profiles derived from amide probes of Chz1 (dataset 1) and H2A.Z-H2B (dataset 2) were analyzed separately to give two sets of global exchange parameters, (k_ex,Chz1; p_Chz1) and (k_ex,H2A.Z-H2B; p_H2A.Z-H2B), shown in (a) and (b) respectively, where k_ex,Chz1=k_off+[H2A.Z-H2B]k_on, k_ex,H2A.Z-H2B=k_off+[Chz1]k_on and p_H2A.Z-H2B, p_Chz1 are defined in Eq. [3]. Values of exchange rates, populations and chemical shift differences between states were extracted from separate fits of dispersions in each of datasets 1 and 2 using in-house written software³⁶ (flemming@pound.med.utoronto.ca; http://pound.med.utoronto.ca/software) by minimization of ${\chi }^2(\zeta )=\sum \frac{{(R_{2,\text{eff}}^{\text{calc}}(\zeta )-R_{2,\text{eff}}^{exp})}^2}{{(\sigma R_{2,\text{eff}}^{\text{exp}})}^2}$ where $R_{2,\text{eff}}^{exp}$ and $R_{2,\text{eff}}^{exp}$ are experimental effective relaxation rates and their uncertainties, respectively, $R_{2,\text{eff}}^{\text{calc}}$ are model relaxation rates obtained by numerical integration of the Bloch-McConnell equations³⁷ for a two-site chemical exchange model, ζ denotes the set of adjustable model parameters and the summation in the expression for χ² above is over the number of experimental data points. In all fits of experimental dispersion profiles we have assumed that the intrinsic relaxation rates were the same for both exchanging states. Amide ¹⁵N and ¹HN dispersion profiles recorded at both 500 and 800 MHz were analyzed together to extract exchange parameters and shift differences. After fitting all dispersion profiles, residues were excluded if the two-site model did not generate statistically significant improvements in fits over a model of no exchange at the 98% confidence level (p-level < 2%) or (ii) if the reduced χ² value for an individual profile was greater than 3.0. Using these criteria, 22 (46) ¹HN and 31 (52) ¹⁵N profiles were retained for Chz1 (H2A.Z-H2B) from the preliminary analysis and used to extract the final set of exchange rates, populations and chemical shift differences. For each of the two exchanging molecules, H2A.Z-H2B and Chz1, distributions of the kinetic exchange parameters that are consistent with the experimental data have been obtained from a bootstrap method³⁸. In the bootstrap procedure each of the experimental observations (dispersion profiles) in the original data set is selected randomly an arbitrary number of times so that the size of the sample does not change. Here each of the n (n=52+46=98 for H2A.Z-H2B and n=31+22=53 for Chz1) relaxation dispersion profiles (¹⁵N and ¹HN) are numbered from 1 to n, a set of random numbers between 1 and n generated, and the pair of experimental dispersion profiles (500 and 800 MHz) corresponding to number j selected each time j appears in the set of n random numbers. The n pairs of experimental dispersion profiles chosen in this manner are fit globally to produce values of (p_b,k_ex) and the procedure repeated 200 times.

The populations of free Chz1 and free H2A.Z-H2B, p_Chz1 and p_H2A.Z-H2B, respectively, are given by

$$\begin{array}{l}{p}_{\text{Chz}1}=\frac{[\text{Chz}1]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]+[\text{Chz}1]}\approx \frac{[\text{Chz}1]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]}\\ p_{\text{H2AZ.H2B}}=\frac{[\text{H2A.Z}-\text{H2B}]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]+[\text{H2A.Z}-\text{H2B}]}\approx \frac{[\text{H2A.Z}-\text{H2B}]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]},\end{array}$$ [3]

from which the dissociation constant K_D is determined directly from the relations

$$\begin{array}{r}\frac{[\text{Chz}1]}{[\text{H2A.Z}-\text{H2B}:\text{Chz1}]}=\frac{p_{\text{Chz}1}}{1-p_{\text{Chz}1}}\text{and}\frac{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}]}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz1}]}=\frac{p_{\text{H}2\text{AZ}.\text{H}2\text{B}}}{1-p_{\text{H}2\text{AZ}.\text{H}2\text{B}}}\\ K_{\text{D}}=\frac{p_{\text{Chz}1}{p}_{\text{H}2\text{AZ}.\text{H}2\text{B}}[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz1}]}{(1-p_{[\text{H}2\text{AZ.H}2\text{B}})(1-p_{\text{Chz}1})}\approx p_{\text{Chz}1}{p}_{\text{H}2\text{AZ}.\text{H}2\text{B}}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}]}_{\text{Total}}\end{array}$$ [4]

where [H2A.Z-H2B]_Total is the total concentration of histone (≈1 mM) and we have made use of the fact that p_Chz1, p_H2A.Z-H2B ≪1. Substituting values for p_Chz1, p_H2A.Z-H2B and [H2A.Z-H2B]_Total into Eq. [4] gives a dissociation constant, K_D= 0.0159×0.0140×1mM= 0.22± 0.02 μm. Errors in K_D were estimated from the distribution of values (± 1 standard deviation) obtained using a bootstrap procedure, described in the legend to Figure 3, neglecting any error in the estimation of the total histone concentration. The distribution of K_D values so obtained is shown in Figure 4A.

Figure 4.

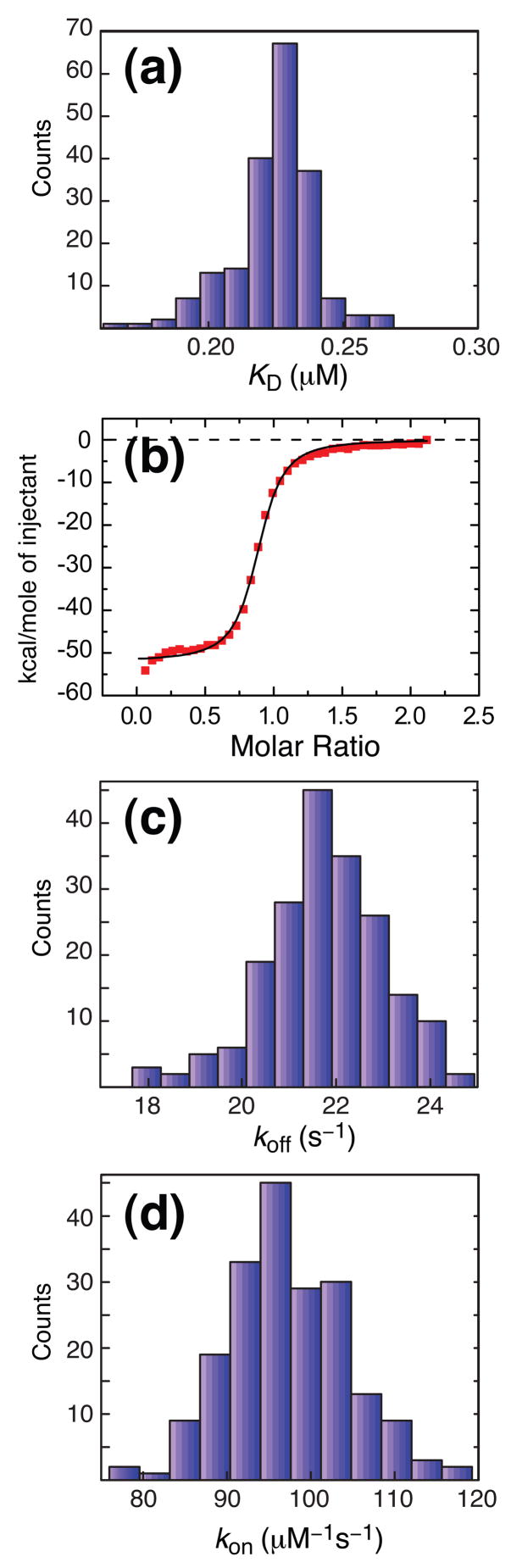
Values of K_D, k_off and k_on for the Chz1, H2A.Z-H2B interaction (35°C) derived from NMR relaxation dispersion data along with ITC titration data for the H2A.Z-H2B/Chz1 binding reaction. The 200 values of {p_Chz1(i);k_ex,Chz1(i)}_i≤200 and {p_{H2A.Z- H2B}(j);k_ex,H2AZ.H2B(j)}_j≤200 generated from the bootstrap analysis described in the legend to Figure 3 were used to calculate the distributions according to (a) K_D(i)= p_Chz1(i)p_H2A.Z-H2B(i)[H2A.Z-H2B]_Total, (c) k_off calculated using Eq [5] and {p_Chz1(i);k_ex,Chz1(i)}_i≤200, {p_H2A.Z-H2B(j);k_ex,H2A.Z-H2B(j)}_j≤200, while (d) k_on was calculated as k_on(i)= k_off(i)/K_D(i). (b) Integrated enthalpy vs. [Chz1]/[H2A.Z-H2B] ratio that is obtained from ITC data recorded at 35 °C. These experiments were preformed using a sample with a single stranded H2A.Z-H2B concentration of 15 μM in a chamber of 1.4 ml. 39 injections (each of 7 μl) of a 200 μM Chz1 solution were made and the heat released analyzed using standard Origin software (http://www.originlab.com) to obtain a K_D of 0.10 μM.

The relaxation dispersion derived dissociation constant has been cross-validated using isothermal titration calorimetry (ITC) that estimates K_D values on the basis of enthalpy changes upon binding. For example, in an exothermic reaction the release of heat upon addition of ligand is monitored and quantified in terms of ΔH_bind, K_D, and the stoichiometry of the binding. The dissociation constant for the Chz1:H2A.Z-H2B complex determined from ITC, K_D,ITC, is 0.10±0.01 μm (Figure 4B), in good agreement with the value derived from CPMG relaxation dispersion; the free energy changes, ΔG_bind, upon binding calculated from K_D values determined by the two methods differ from each other by 5%. The close agreement provides further evidence that the simple two-state model of association, Eq. [1], is an adequate description of the binding event and that the millisecond chemical exchange process reported by the relaxation dispersion experiments are due to the association of Chz1with H2AZ.H2B.

The sum of the kinetic rates that are derived from the CPMG experiments focusing on H2AZ.H2B or Chz1 in the reaction of Eq. [1] are given by:

$$k_{\text{ex},\text{H}2\text{AZ}.\text{H}2\text{B}}+k_{\text{ex},\text{Chz}1}=\frac{k_{\text{off}}}{p_{\text{H}2\text{AZ}.\text{H}2\text{B}}}+\frac{k_{\text{off}}}{p_{\text{Chz}1}}=k_{\text{off}}\frac{p_{\text{H}2\text{AZ}.\text{H}2\text{B}}+p_{\text{Chz}1}}{p_{\text{H}2\text{AZ}.\text{H}2\text{B}}{p}_{\text{Chz}1}}$$ [5a]

Thus, is straightforward to show that k_off for the reaction is given by

$$k_{\text{off}}=(k_{\text{ex},\text{H}2\text{AZ}.\text{H}2\text{B}}+k_{\text{ex},\text{Chz}1})=\frac{p_{\text{H}2\text{AZ.H}2\text{B}}{p}_{\text{Chz}1}}{p_{\text{H}2\text{AZ.H}2\text{B}}+p_{\text{Chz}1}}=22\pm 2{\text{s}}^{-1},$$ [5b]

where the error estimation is again based on a bootstrap procedure. Figure 4C plots the distribution of k_off values that are obtained. The second order association rate constant, k_on, can be calculated from the values of K_D and k_off, k_on = k_off/K_D = 10⁸±10⁷ M⁻¹s⁻¹. Distributions of k_on that are consistent with the experimental data are shown in Figure 4D. Finally, it should be noted that the Chz1 construct used here includes only the core region (residues 71–132) of the full length chaperone and also that the unstructured tails of the histones are missing. These very flexible regions do not participate in the structure of the complex¹⁷ and it is therefore unlikely that their presence would significantly change any of the kinetic or thermodynamic parameters that have been measured in this study. Further, as indicated in the legend to Figure 1 we have used a single chain construct of H2A.Z-H2B rather than the natural two-chain histone complex. Information on the kinetics and thermodynamics of association of the individual histones are not available, precluding an analysis of how the connection between the histone pairs might influence the measured rates and K_D reported here.

Figure 4 shows that accurate values of K_D, k_off and k_on have been obtained by combining exchange parameters extracted from fits of dispersion profiles recorded on both Chz1 and H2A.Z-H2B. The value of k_on = 10⁸±10⁷ M⁻¹s⁻¹ is two orders of magnitude faster than the diffusion limit (≈10⁵–10⁶ M⁻¹s⁻¹)^{28, 29}. Attractive electrostatic forces between H2A.Z-H2B and Chz1 therefore must contribute strongly to the association. The NMR derived structure of the Chz1:H2A.Z-H2B complex shows that the chaperone has a biopolar charge distribution comprised of 5 negatively charged residues in its N-terminal helix and 3 positively charged moieties in the C-terminal region of the molecule that interact with oppositely charged residues from the histones¹⁷. Moreover, the large value for k_on argues that conformational changes of Chz1 and H2A.Z-H2B that accompany binding are not limiting for association and that Chz1 likely samples its histone bound conformation in the free state.

Although accurate values of k_off can be extracted from independent fits of data sets derived from either Chz1 or H2A.Z-H2B, in cases of high affinity binding it is not possible to extract values of K_D or k_on from a single set of dispersion data recorded on only one of the molecular players. Consider for example the case where dispersion profiles are obtained only for probes on Chz1. Noting that [Chz1]_Total = [Chz1] + [Chz1:H2A.Z-H2B] and [H2A.Z-H2B]_Total= [H2A.Z-H2B] + [Chz1:H2A.Z-H2B] it follows from Eq. [1] that

$$\begin{array}{l}{K}_D={[\text{Chz}1]}_{\text{Total}}{p}_{\text{Chz}1}\left(\frac{{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}]}_{\text{Total}}}{[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}:\text{Chz}1]}-1\right)\\ =\frac{p_{\text{Chz}1}}{1-p_{\text{Chz}1}}({[\text{H}2\text{A}.\text{Z}-\text{H}2\text{B}]}_{\text{Total}}-(1-p_{\text{Chz}1}){[\text{Chz}1]}_{\text{Total}})\end{array}$$ [6]

Eq. [6] establishes that accurate values of K_D can be obtained for this high affinity complex only if the concentrations of Chz1 and H2AZ.H2B are known to very high precision. For example in the case where [Chz1]_Total = 1 mM, [H2A.Z-H2B]_Total = 0.95 mM, K_D = 0.22 μM a K_D value that is 14 fold too large is obtained if [Chz1]_Total = [H2A.Z-H2B]_Total = 1 mM is assumed (in Eq [6]), where [Chz1]_Total is in error by only 5%. Errors in protein concentration on the order of 10% are the norm in most biophysical studies. The methodology presented using dispersion data from both molecular players of a binding reaction circumvents this problem. In principle accurate values of K_D and k_on could also be obtained by performing dispersion experiments as a function of ligand³⁰ but this requires significantly more measuring time relative to the approach described here. The dispersion method is also advantageous relative to other techniques that measure binding by affixing one of the partners to a solid support^{31, 32, 33} since in the case of very rapid association processes the support itself may well slow down the rate of binding. It is worth emphasizing that the use of relaxation dispersion NMR techniques for the study of ligand binding processes is not at all restricted to complexes with K_D values on the order of 1 μM or less (as is the case in the application considered presently). Indeed, the example presented here is particularly challenging because of the high affinity of the complex. In cases were affinities are in the mM range, for example, it is often possible to extract reasonably accurate K_D values from dispersion measurements that focus on only one of the ligands. For example, suppose that the affinity of the Chz1/histone complex were 2 mM and that experiments were recorded with [Chz1]_Total = 1 mM, [H2A.Z-H2B]_Total = 0.1 mM. In this case errors of 10% in estimates of [Chz1]_Total and [H2A.Z-H2B]_Total translate into uncertainties in K_D of less than 25%, much less than for high affinity interactions.

Chaperones such as Chz1 deliver variant histones to chromatin remodeling complexes that subsequently catalyze a histone exchange reaction. The dissociation rate, k_off = 22±2 s⁻¹ calculated here provides, therefore, an upper bound for the rate by which the histones H2A.Z-H2B are delivered by Chz1 to the chromatin remodeling complex SWR1 that then subsequently catalyzes the replacement of the canonical histones H2A-H2B with H2A.Z-H2B. Interestingly, this rate of transfer is on the order of the rate of nucleosome unwrapping, 20–90 s⁻¹, that has been determined by FRET experiments⁵, suggesting that the exchange event may be assisted by thermal fluctuations occurring spontaneously in chromatin. The application presented here involving a histone/chaperone binding reaction illustrates the utility of NMR spectroscopy in obtaining accurate exchange parameters that are critical to understanding the underlying physical chemistry behind this important biological process.