Abstract
An RNA kissing complex formed by the dimerization initiation site (DIS) plays a critical role in the survival and infectivity of HIV virus. Two DIS kissing sequences, Mal and Lai, have been found in most HIV-1 variants. Formation and stability of these RNA kissing complexes depend crucially on cationic conditions, particularly Mg2+. Using optical tweezers, we investigated the mechanical unfolding of single RNA molecules with either Mal-type (GUGCAC) or Lai-type (GCGCGC) kissing complexes under various ionic conditions. The force required to disrupt the kissing interaction of the two structures, the rip force, is sensitive to concentrations of KCl and MgCl2; addition of 3 mM MgCl2 to 100 mM KCl changes the rip force of Mal from 21±4 pN to 46±3 pN. From the rip force distribution, the kinetics of breaking the kissing interaction is calculated as a function of force and cation concentration. The two kissing complexes have distinct unfolding transition states, as shown by different values of ΔX‡, the distance from the folded structure to the unfolding transition state. ΔX‡ of Mal is ~0.6 nm smaller than that of Lai suggesting that fewer kissing base pairs are broken at the transition state of the former, consistent with observations that the Lai-type kissing complex is more stable and requires significantly more force to unfold than the Mal-type. Importantly, neither K+ nor Mg2+ significantly changes the position of the transition state along the reaction coordinate. However, increasing concentrations of cations increase the kinetic barrier. We derived a cation specific parameter, m, to describe how the height of the kinetic barrier depends on the concentration of cations. Our results suggest that Mg2+ greatly slows down the unfolding of the kissing complex, but has moderate effects on the formation kinetics of the structure.
Keywords: Kissing RNA, metal ion binding, single-molecule, mechanical unfolding, optical tweezers
Introduction
The majority of retroviral particles contain two copies of their viral genomic RNAs.1; 2 In human immunodeficiency virus 1 (HIV-1), dimerization of viral RNA greatly enhances recombination during reverse transcription, contributing to the hypermutation in the viral genome.3; 4 The crucial site to initiate such dimerization lies in the 5′-untranslated region (UTR) of the viral RNA, known as the dimerization initiation site (DIS).3 The DIS of HIV-1 is made up of a single hairpin with a loop containing a palindromic sequence.5; 6 DIS hairpins from two viral RNAs can form a kissing complex by base pairing the loop nucleotides.7; 8 Once packaged into a single viral particle, this initial viral RNA dimer can evolve into a mature dimer with multiple interactions between the two strands.1–3; 9 Formation of the initial dimer is critical for viral survival, as evidenced by the fact that mutations in the loop sequence of the DIS hairpin results in significant reduction in viral replication, RNA packaging, reverse transcription and infectivity.1
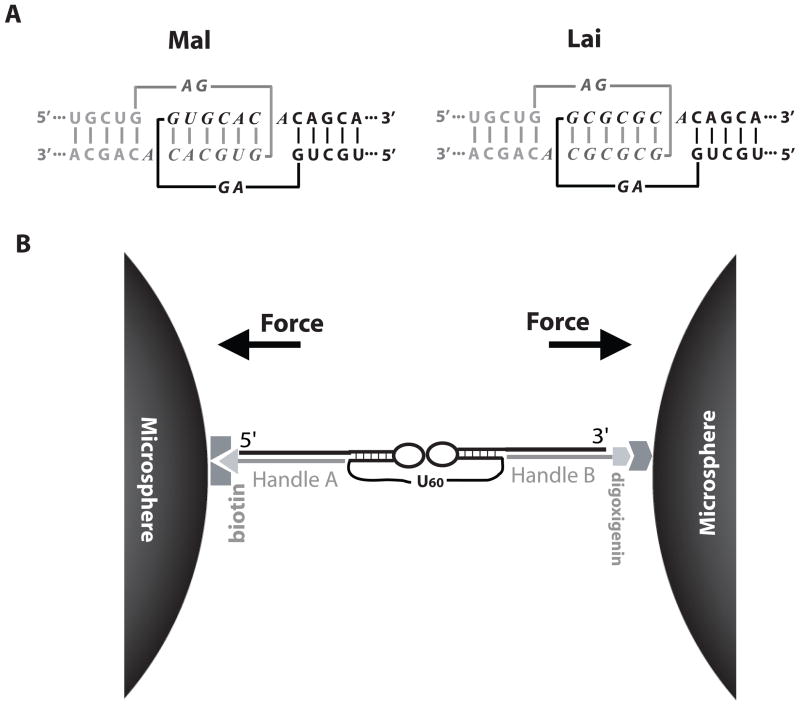
The 9-nucleotide apical loop of the HIV-1 DIS hairpin contains a 6-nucleotide palindromic sequence capable of forming tertiary kissing base pairs with its counterpart (Figure 1a). This palindromic sequence is highly conserved.4 Out of a total of 64 possible combinations of palindromic hexanucleotides, there are only two sequences commonly found in HIV-1 strains: GUGCAC and GCGCGC. The former was first discovered in the Mal isolate and the latter in the Lai isolate. The Mal DIS kissing sequence is conserved in clades A, C, F, G and H of the M (major) group HIV-1 as well as in the O (outlying) group virus.10 The Lai DIS kissing sequence is conserved in clades B and D of the M group virus. Conservation of the DIS kissing sequence is surprising at first glance since classification of clades in the M group is solely based on the sequence of the envelope (env) gene, which is distally located downstream of the DIS hairpin. This observation reemphasizes the crucial role of the DIS kissing complex in the dimerization of viral RNA. Since a single copy of the viral RNA is much less likely to be packaged and to be infective, only dimerized RNAs can pass mutations to the next generation. Consistent with this hypothesis, matching of the DIS kissing sequences, i.e. pairing Mal with Mal or Lai with Lai, appears to be a major restriction for intersubtype recombination of viral genomes.11
Figure 1.
Experimental design. (a) Mal and Lai types of DIS kissing complexes from HIV-1. The two hairpins are shown in black and grey. Loop sequences are shown in italic letters. (b) A pair of kissing hairpins linked by 60 Us are tethered between two micron-size beads via two dsDNA/RNA handles (a total of ~2.5 kb). An optical trap device was used to manipulate the beads to apply forces in the direction shown by arrows. See Figure S1 and S2 for more detail. The drawing is not to scale.
The two DIS kissing complexes are structurally similar. In all crystal structures 12–15 and recent NMR solution structures,16; 17 the two hairpins in the kissing complexes are positioned so that the A-form helices of the hairpin stems are in nearly perfect co-axial stacking. The palindromic hexanucleotides from the two hairpin loops form a segment of a right-handed A-form helix. Between the kissing base pairs and the hairpin stem, the six unpaired nucleotides can adopt several conformations depending on the sequence and crystallographic/solution condition. However, an early NMR structure showed that the Lai type kissing complex was bent and the kissing base pairs were distorted from A-form geometry seen in the crystal structure.18 The structural polymorphism could reflect the dynamics of DIS kissing complexes in solution.
Energetics of kissing base pairs and especially their salt dependence are significantly different from those of secondary structures.19; 20 The Lai DIS kissing complex is formed by six G•C base pairs whereas that of Mal contains four G•C and two A•U base pairs. Based on GC percentage of the kissing base pairs, one would predict that the Lai type kissing complex is more stable than the Mal. However, stabilities of the two structures depend differently on Mg2+ ion.19–22 In the absence of divalent cations (with ~300 mM KCl), the Lai kissing complex is significantly more stable than Mal. However, in the presence of 5 mM Mg2+, both kissing complexes show similar Kd in the nM range.21 Consistently, the crystal structure of the Mal kissing complex reveals a bound Mg2+ ion unseen in the structure of the Lai kissing complex; this was hypothesized to contribute to the difference in cation dependence.12
Mg2+ effects on non-catalytic RNA structures are commonly examined by thermal melting or calorimetry.23 However, Mg2+ ions catalyze hydrolysis of RNA at elevated temperatures, and the two HIV DIS kissing complexes are very stable structures that require nearly boiling temperature to be disrupted in high concentrations of Mg2+.20 Moreover, these techniques are best at studying thermodynamic effects of Mg2+ on RNA stability; it is usually difficult and costly to study kinetics of folding. Optical tweezers provides a practical way to apply force to a single RNA molecule and monitor its structural change in real time. Here, we used this new technique to probe the dissociation of the DIS kissing complexes.
Results
Experimental design
Previously we investigated the mechanical unfolding of a minimal kissing complex containing only two kissing base pairs derived from Maloney Murine Leukemia Virus (MMLV).24 Here we followed the same experimental design to study the HIV DIS kissing complexes, in which an intramolecular DIS kissing complex is flanked by two double-stranded DNA/RNA (dsDNA/RNA) handles (Figure 1b). The two handles are chemically modified at their ends allowing the RNA and handles to be tethered between a pair of micron-size beads through affinity interactions.25 The long DNA/RNA handles (1.2 and 1.3 kb, respectively) separate the two beads by almost 1 μm to minimize the surface effect of the beads on the kissing structure.24–32 The entire system is assembled in a flow chamber, in which one bead is held by a force-measuring laser trap and the other bead is on the tip of a nano-manipulator driven micropipette (Figure S1).33
Each DIS kissing complex consists of two hairpins linked with 60 uracil nucleotides (Figure 1b). The single-stranded linker is designed so that the kissing complex can be pulled and relaxed multiple times. Each hairpin has an 18 base pair stem and a 9-nucleotide loop, either Mal or Lai type. The stems have the native sequences, except that a few G•U mismatches were engineered into different positions of each stem (Figure S2) to prevent alternative folding. The two hairpins are predicted to have similar stabilities by Mfold.34
Pulling/relaxation patterns of kissing complexes in low ionic strength
In a pulling experiment, a single RNA molecule is repeatedly stretched and relaxed as the force and extension of the molecule are recorded as a function of time.24–32 dsDNA/RNA handles display worm-like-chain non-linear elasticity similar to dsDNA.35; 36 As the handles are extended, force increases monotonically with extension (Figure 2). Single-step unfolding of secondary and tertiary structures is indicated by “rips” in the force-extension curves, displaying a negative slope distinct from the stretching of the handles. When force is relaxed, extension of the handles decreases smoothly, however refolding of the RNA single strand is shown by “zips”, characterized also by a negative slope, in the force-extension curve that abruptly shorten the extension. The negative slope of rips and zips reflects movement of the trapped bead in the laser trap as extension of the molecule changes during unfolding/refolding; the magnitude of this slope corresponds to the spring constant of the trap.37 We defined the unfolding/rip force as the force where rupture of the structure starts, and the zip force as the force where refolding begins. In unfolding, ΔX, the change in the end-to-end distance of the molecule at the rip force, reflects the number of single-stranded nucleotides released from folded structures. In refolding, ΔX is defined as the decrease in the extension of the molecule at the zip force.
Figure 2.
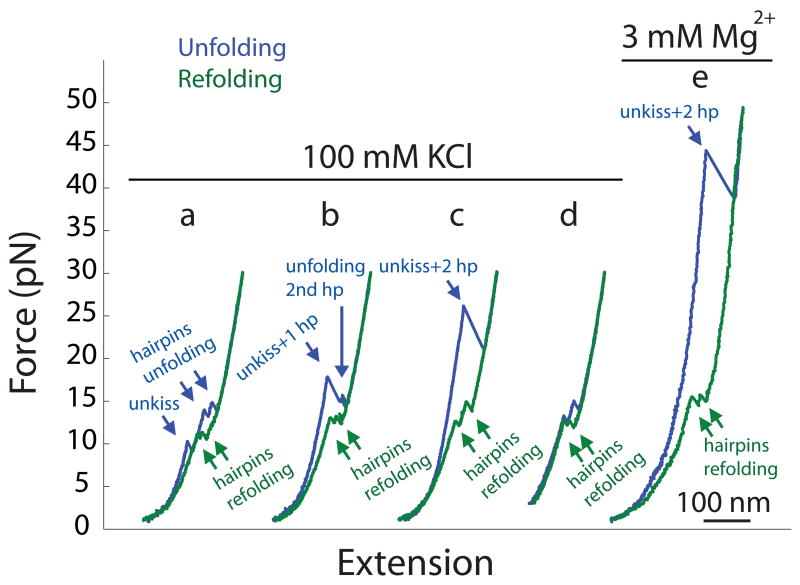
Force-extension curves of unfolding the Mal type kissing complex. Single RNA molecules were pulled and relaxed at a rate of ~5 pN/s in 100 mM KCl (a–d) or with an additional 3 mM MgCl2 (e). (d) shows an experiment in which force was lowered only to 3 pN to prevent the formation of kissing interaction by the two folded hairpins.
We repeatedly pulled and relaxed single molecules of the Mal-type kissing complex between 0.5 pN and 30 pN at a fixed rate of ~5 pN/s in 100 mM KCl pH 8.0 at 22 °C. Unfolding force-extension curves show either three, two or one rips (Figure 2 a–c). 12% of unfolding trajectories show three-step unfolding, each with ΔX of ~15 nm; 15% have 2 rips, the first rip bigger than the second one; the remainder of unfolding events show a single, big rip. Noticeably, the rip force of the first transition is about 10 pN in the three-step unfolding, between 15 and 20 pN in the two-step unfolding, and mostly over 20 pN in the single-step unfolding (Figure 3). All refolding trajectories display two zips that mainly occur between 10 and 18 pN.
Figure 3.
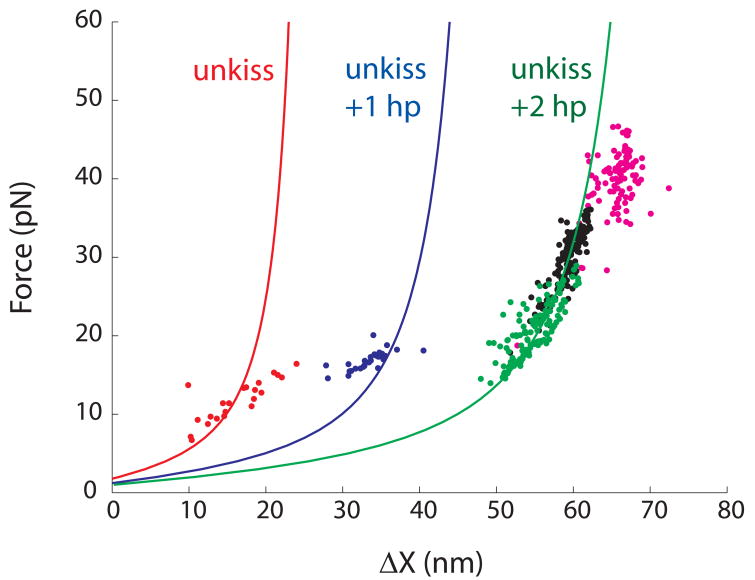
Force-ΔX relationships of the first transitions in mechanical unfolding of Mal are computed using a worm-like-chain model for RNA (solid curves, see Figure S4 for detail). Experimental values of first rips in three-step (red), two-step (blue) and one-step unfolding (green) collected in 100 mM KCl are plotted as dots. The entire RNA always unfolds in a single step in either 1 M KCl (black or 100 mM KCl with 3 mM MgCl2 (magenta).
Similar mechanical unfolding/refolding patterns were observed in the MMLV kissing complex, albeit transitions occur at different forces.24 Using a series of mutant molecules and nanomanipulation methods, we proved that in the MMLV kissing complex, the first unfolding step is always disruption of the kissing interaction (“unkiss”); and that when the unkiss occur at forces higher than the transition forces of the hairpins, breaking of the kiss becomes rate-limiting (Figure S3). On refolding of the MMLV kissing complex, the two hairpins fold first, followed by formation of the kiss at lower force. Hierarchical mechanical unfolding and refolding was also observed in an adenine riboswitch which contains a kissing complex.38
We did a series of experiments to test whether the Mal-type kissing complex follows the same unfolding/folding pathways and to rule out the possibility that the first transition is unfolding of one hairpin. First, we pulled individual hairpins. Transition forces and ΔX of individual hairpins are consistent with those of the second and third transitions in the three-step unfolding as well as the second transition in the two-step unfolding (data not shown). Second, values of ΔX of all observed transitions are consistent with our hypothesis and the structural model. As transitions occur at various forces, we modeled the force-ΔX relationship for unfolding and refolding using a worm-like-chain model (Figure S4).35 Figure 3 shows the force-extension relationship of the unfolding transitions: disruption of the kissing interaction or “unkiss” only (red curve); double-transition or breaking of kissing and one of the hairpins together (blue curve); and unfolding of the entire RNA into a single strand in a single step (green curve). Values of experimentally observed first transitions (dots, colored according to type of the transition) fit reasonably well with our model. Third, Figure 3 also shows a wide distribution of the first unfolding forces (7–30 pN) indicating that the rate constant of breaking the kissing interaction is relatively force insensitive. In contrast, both hairpins unfold and refold within a 5 pN force range. Most importantly, in all observed traces, hairpins were always unfolded before the force reached 20 pN confirming that the high rip forces represent the breaking of the kiss. Fourth, we did a “force-jump” experiment 28 in which force is rapidly raised from 1 pN to above 25 pN and kept constant (Figure S5). Hairpins are unstable at such forces and their lifetimes are estimated to be much less than 1 millisecond. Yet the entire structure was intact for seconds followed by a single-step unfolding that increased the extension by ~60 nm. Once unfolded, the RNA remained as a single strand for up to 5 minutes. Only when force is subsequently lowered below 18 pN, does refolding and unfolding of hairpins start to appear (Figure S6). Therefore, as in the MMLV kissing complex, at forces higher than the transition forces of the hairpins, the kissing interaction protects the hairpins from unfolding and the unkiss becomes the rate-limiting first step in unfolding. We thus conclude that the Mal-type kissing complex unfolds by a single pathway, despite different force-extension patterns.
We interpret the two zips in the refolding trajectories as the refolding of the hairpins (Figure 2 a–c). Kissing is likely to occur at low force at which ΔX is too small to be visible in the force-extension curve. To probe the kissing interaction, we lowered the force to different values and pulled again. As shown in Figure 2d, when the lowest force was kept above 2 pN, the unfolding trajectories show only two rips corresponding to the unfolding of the hairpins, indicating that no kissing complex was formed. This experiment further confirms that disruption of kissing is the first step of unfolding and that kissing only forms after the folding of the hairpins. When force was decreased to between 0.5 pN and 2 pN, we observed two sets of the unfolding curves: disruption of the kissing interaction and of the hairpins (Figure 2 a–c), and unfolding of only the hairpins (Figure 2d). As expected, the fraction of the former set of trajectories increases when the lowest force approaches zero. Clearly, the kissing occurs between 0.5 pN and 2 pN at an unloading rate of ~5 pN/s.
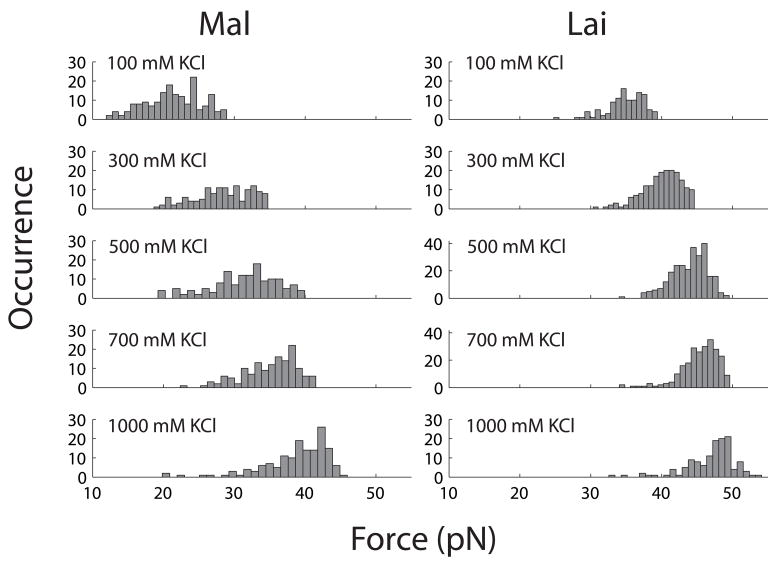
We also studied mechanical unfolding of the Lai-type kissing complex under the same condition. Since Lai and Mal types of kissing complexes are almost identical except for two nucleotides in each of the hairpin loops, their unfolding and refolding pathways are similar. All force-extension curves of Lai shows a single big rip with ΔX of >55 nm on unfolding and two zips on refolding. Its rip forces distributed mainly between 30 pN and 40 pN (Figure 4). At such high forces, we would also expect the Mal kissing complex be unfolded into single strand in a single step (Figure 3). The rip forces of Lai are significantly higher than those of Mal under the same condition, which is consistent with results from thermal melting experiments under similar ionic conditions.19; 20; 39 Notably, the rip force distribution of Mal is about twice as wide as that of Lai (Figure 4) showing that unfolding kinetics of the Mal kissing is less force dependent. We also tested the kissing forces of Lai by lowering force to different values. The kissing forces of Lai range from 1 pN to 3 pN.
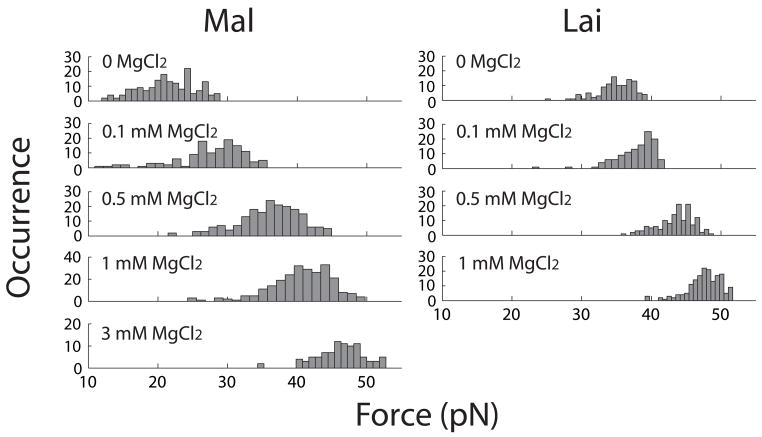
Figure 4.
Effect of KCl on distribution of first rip (unkiss) forces in unfolding Mal and Lai types of kissing complexes. Each distribution was split into 20 bins.
Ionic effects on the rip forces of kissing complexes
Thermal stability of kissing complexes are critically dependent on the ionic strength and type of ions.19; 20; 39 We further examined the mechanical stability of the Mal and Lai kissing interactions in various concentrations of KCl and MgCl2. As discussed above, we treated the first unfolding transitions as the disruption of the kiss.
When KCl concentration is increased from 100 mM to 1 M, rip forces of both types of kissing complexes increase (Figure 4). The mean rip force of Mal is ~20 pN in 100 mM KCl and ~40 pN in 1 M KCl. As comparison, the mean rip force of Lai raises from ~35 pN in 100 mM KCl to ~48 pN in 1 M KCl. Increase of the rip forces also changes the patterns of the unfolding force-extension curves. At and above 300 mM KCl, nearly all curves of Mal display a single big rip similar to the one shown in Fig. 2c. In bulk experiments, Mg2+ is more effective than monovalent cations in raising the thermal stability of kissing complexes. Here, we saw a similar effect on the mechanical stability. Adding merely 3 mM MgCl2 to a solution containing 100 mM KCl raises the mean rip force of the Mal kissing complex by ~25 pN (Figure 2e); and 1 mM MgCl2 changes the average rip force of Lai by over 10 pN (Figure 5). Previous bulk experiments,19–21 which covered a wider concentration range of Mg2+, show that 3 mM is slightly below the Kd of Mg2+ for both kissing complexes. These studies also show that differences in the thermal stability between Mal and Lai decreases as [Mg2+] increases. Although working in low Mg2+ concentrations, we observed a similar trend as differences in the rip force of the two kissing structures became narrower at high salt concentrations (Figure 5).
Figure 5.
Effect of MgCl2 on distribution of first rip (unkiss) forces in unfolding Mal and Lai types of kissing complexes. All unfoldings were studied in 100 mM KCl and various concentrations of MgCl2. Each distribution was split into 20 bins.
Ionic effects on the disruption of kissing interactions are more pronounced than on the unfolding/refolding of the hairpins. Addition of 3 mM MgCl2 increases the unfolding and refolding forces of the hairpins by ~3 pN, but raises the unkiss force by ~25 pN (compare Figure 2 a-d with 2e). We recently found that adding either 10 mM MgCl2 or 1 M NaCl to RNA hairpins, such as TAR, changes the transition forces by less than 5 pN.40 Also, the ionic effect on the formation of the kissing complex from the two hairpins is also comparatively small. The two hairpins appear to kiss at forces between 2 and 3 pN in a solution containing 100 mM KCl and 3 mM MgCl2. As a result of different ionic effects on unfolding and refolding kinetics, hysteresis between unfolding and refolding force-extension curves increases with ionic strength (Figure 2).
The force-dependent rip size in high salt concentrations roughly fits the worm-like-chain prediction (Figure 3 black dots), although force-ΔX relations in 3 mM Mg2+ (magenta dots) appear to be slightly different from predicted values. Ionic strength and type of ions affect mechanical properties of nucleic acids, such as persistence length and contour length.41–46 The worm-like-chain model we use does not incorporate such effects since these parameters, especially at high forces, are not available for RNA. We also assumed that the kissing complex is a rigid body that does not change in extension when pulled. However, the kissing complexes may deform under tension. The ends of the dsDNA/RNA handles may also fray at high forces, increasing the apparent rip size. Prediction of ΔX-F relationship will be improved by incorporating these factors.
Force-dependent kinetics of breaking the kissing interactions
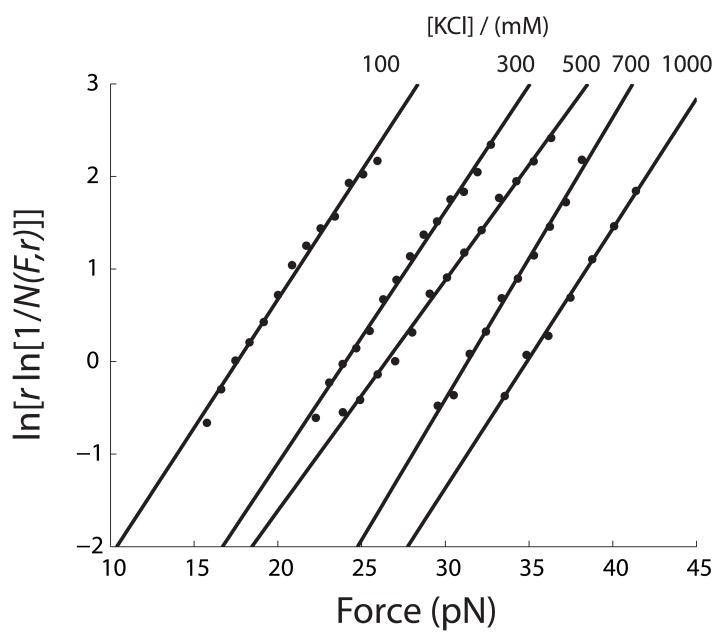
The distribution of rip forces reflects the force-dependent unfolding kinetics of a structure. Previously, Evans and Ritchie derived a formula to extrapolate unfolding kinetics from distributions of rip forces:47
| (1) |
in which N(F,r) is the fraction of folded molecule at force F and loading rate r; k0 is a factor reflecting both the rate constant at zero force and instrumental factors; ΔX‡ is the distance from the folded state to the transition state; kB the Boltzmann constant; and T the temperature in kelvin. The linear region of ln[r ln[1/N(F,r)]] vs. F is usually 10% to 90% of ln[r ln[1/N(F,r)]].25; 37; 48; 49 Assuming that disruption of the kissing complex is a single-step process, we fitted the force distribution of breaking the kissing complexes shown in Figure 4 and 5 at each ionic condition to Eq. 1 (Figure 6 and S7). Values of ΔX‡ and lnk0 (Table 1 and 2) were then used to obtain kF,unkiss, the unfolding rate constant at a given force F, using the following equation:
| (2) |
Figure 6.
Kinetic parameters for unfolding the Mal kissing complex were obtained by fitting the distribution of rip forces (Figure 4) to Eq. 1. See Table 1 for values.
Table 1.
Kinetic parameters of unfolding kissing complexes in various concentrations of KCl.
| Mal | Lai | |||||
|---|---|---|---|---|---|---|
| [KCl] (mM) | ΔX‡ (nm) | k0 | n$ | ΔX‡ (nm) | k0 | n$ |
| 100 | 1.14±0.04 | (2.0±0.8)×10−3 | 174 | 1.91±0.08 | (1.2±0.8)×10−7 | 110 |
| 300 | 1.12±0.03 | (4±2)×10−4 | 136 | 1.80±0.02 | (3.4±0.7)×10−8 | 186 |
| 500 | 1.02±0.02 | (3±1)×10−4 | 141 | 1.90±0.06 | (3±1)×10−9 | 269 |
| 700 | 1.25±0.04 | (2.0±0.8)×10−5 | 145 | 1.98±0.06 | (6±1)×10−10 | 239 |
| 1000 | 1.15±0.04 | (1.5±0.6)×10−5 | 151 | 1.72±0.08 | (4±2)×10−9 | 128 |
Table 2.
Kinetic parameters of unfolding kissing complexes in various concentrations of MgCl2.
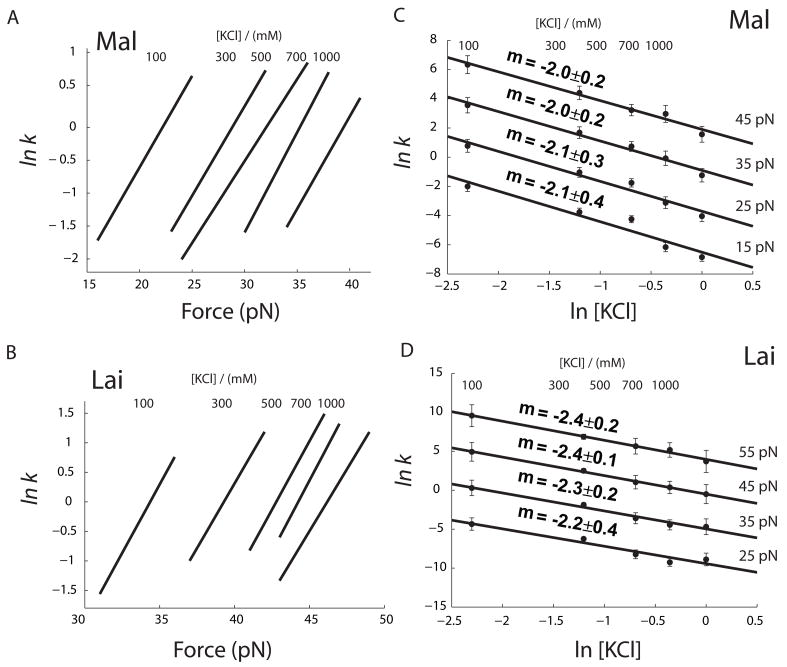
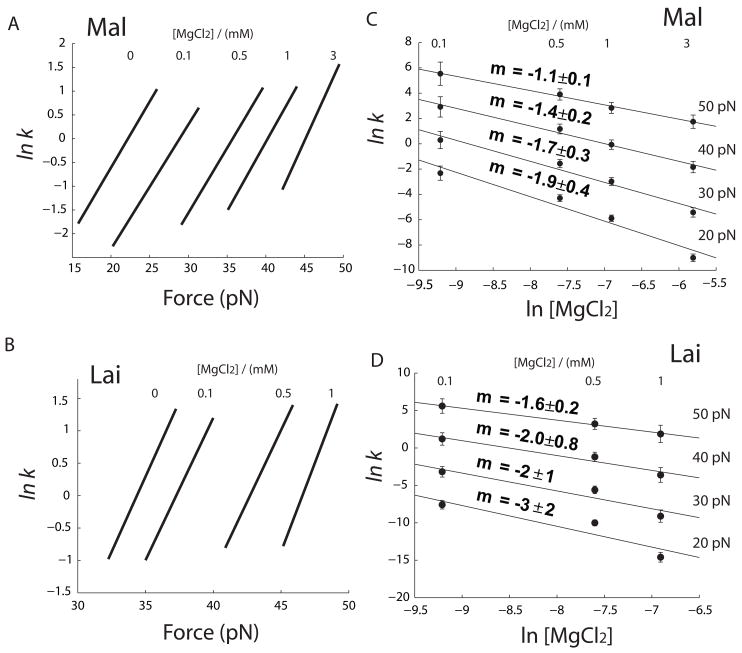
Using this method, we calculated force-dependent unfolding rates of the two kissing complexes under various ionic conditions (a and b in both Figure 7 and 8). It is obvious from these plots that increase of both KCl and MgCl2 change ΔX‡ only slightly, but significantly decrease the value of lnk0. Moreover, ΔX‡ of each structure has similar value in either KCl or MgCl2 (Table 1 and 2). Hence, the distance from the folded state to the transition state is not much affected by the type or concentration of cations. However, decrease in the y-axis intercept lnk0 shows that the unfolding kinetics is slowed by increasing concentration of cations.
Figure 7.
Effect of KCl on unfolding kinetics of kissing complexes. (a and b) Force-unfolding rate constants at each [KCl] are calculated using Eq. 2 and parameters in Table 1. Force range of each curve represents ~80% of the rip force distribution. In c and d, unfolding rate vs. [KCl] at four different forces were calculated using parameters in Table 1 and Eq. 3. Error bars represents 95% level of confidence. Solid lines are fit using Eq. 3. Parameters are summarized in Table 2.
Figure 8.
Effect of MgCl2 on unfolding kinetics of kissing complexes. (a and b) Force dependence of unfolding rate constant at various [MgCl2]. (c and d) Effect of MgCl2 at four different forces. Solid lines are fit using Eq. 4. Parameters are summarized in Table 2.
The ln k vs F plots show clearly, but indirectly, the effect of salt. Based on these analyses, we further explored how the unfolding rate depends on the concentration of cations. We estimated rate constants of unfolding kissing complexes as a function of [KCl] or [MgCl2] at different forces (c and d in both Figure 7 and 8). It is well known that the logarithm of Keq of RNA folding is usually a linear function of logarithm of cation concentration,50; 51 however, salt effects on kinetics are scarce in the literature. We used the following empirical equations to describe the salt dependence of unkiss rate:
| (3) |
| (4) |
As shown in panels c and d in Figure 7 and 8, Eq. 3 and 4 fit reasonably well the measured data.
The unkiss rate constant can be further characterized as a function of both force and salt concentrations. It is relatively straightforward in the case of KCl because ΔX‡ and mKCl are constant in the experimental concentration range of KCl. KCl affects only k0 in Eq. 2 but not ΔX‡. Therefore, we can rewrite Eq. 2 as:
| (5) |
in which lnk′0 is y-axis intercept when kF is rate constant extrapolated to zero force and zero salt. If we choose ΔX‡ of 1.1 nm and mKCl of −2.0 for Mal, lnk0 is −2.2. lnk0 for Lai is −2.1 with ΔX‡ of 1.85 nm and mKCl of −2.3. We can add another term to the right side of Eq. 5 to account for the effect of MgCl2.
| (6) |
When titration of Mg2+ is done in the presence of a fixed concentration of KCl, Eq. 6 can be simplified as
| (7) |
Eq. 7 describes Mg2+ dependent unkiss kinietcs reasonably well (Figure 8 c and d) with a caveat that mMgCl2 may be force dependent. ΔX‡ for each kissing structure is nearly constant (Figure 8 a and b). Values of mMgCl2, measured in a solution of 100 mM KCl, may not be applied to other ionic conditions because competition between monovalent and divalent metal ions in binding to nucleic acids is thermodynamically complicated.50; 52
Discussion
Errors of ΔX‡
Mechanical pulling experiments are non-linear processes and their error propagation has not been well documented. In a typical experiment, all observations under one condition are pooled together to generate a force distribution (Figures 4 and 5), from which kinetic parameters are extracted (Figure 6). The error bars shown in the Figure 6 and standard deviations in the Tables 1 and 2 reflect the goodness of fitting force distributions to Eq. 1. The real experimental errors are likely to be larger.
In previous works, we arbitrarily set the threshold for the number of observations as 100, expecting a 10% standard deviation of ΔX‡.24; 25; 28 Such estimation is consistent with our simulations, which include 0.1 pN force fluctuation (data not shown). Following this logic, we expect that errors of ΔX‡ in this study are also about 10%. Hence, we conclude that values of ΔX‡ for breaking each of the two kissing complexes are within the error range (Tables 1 and 2) and therefore, ΔX‡ of each kissing structure appears not to be affected by cation concentrations.
Experimental limitations
At the highest measured concentrations of MgCl2 (3 mM for Mal and 1 mM for Lai), ΔX‡ appears to become slightly larger than at lower concentrations. Under such ionic conditions, both kissing complexes were largely unfolded at >40 pN with some observations even over 50 pN (Figure 5). The RNA molecules showed significantly higher tendency to break their tethering from the beads at >50 pN than at <50 pN. This is likely because the interactions between digoxigenin and anti-digoxigenin antibody, by which the molecule is attached to the trapped bead, start to dissociate at about 50 pN. Hence, rip forces over 50 pN were under-observed and the apparent force distributions under these two ionic conditions were smaller than the true ones. The smaller force distributions in turn resulted in larger value of ΔX‡. We also pulled both complexes at higher concentrations of MgCl2 (up to 10 mM). The molecules broke from beads too often to obtain reliable force distributions. However, it is evident that the kissing complexes become even more stable at these conditions. Many pulling curves showed no rupture at all up to 60 pN; and when a single-step unfolding transition was visible, the rips occurred mostly over 50 pN.
The tendency that tethers broke often at high forces may also affect values of mMgCl2. mMgCl2 shows a decreasing trend as force increases. Because unkiss forces increase rapidly with divalent cations, we have less data in MgCl2 than in KCl, and therefore the uncertainty of mMgCl2 is larger than that of mKCl. On the other hand, the kissing tends to break at higher forces in higher concentration of MgCl2; under-sampling of high rip forces may also skew the values of mMgCl2.
Mechanical strength of kissing complexes
We previously studied a minimal kissing complex with only two G•C base pairs.24 Here, we investigated two DIS kissing complexes, both with six kissing base pairs but different sequences. All three kissing complexes show different unfolding forces. Distributions of the unfolding forces, and consequently, values of ΔX‡, are also distinct for each structure (0.65 nm for two base pairs; 1.2 nm for 4 G•C, 2 A•U; and 1.8 nm for 6 G•C). As ΔX‡ describes force-dependent kinetics,37; 47 kinetics of mechanical unfolding of kissing structures clearly depends both on the number and sequence of tertiary base pairs.
All three kissing complexes have smaller unkiss ΔX‡ than hairpins (~5 nm). Their unkiss force distributions are significantly broader than those of hairpins. Their unkiss rate constants are less force dependent than those of hairpins. Such difference in mechanical unfolding of kissing complexes and hairpins likely results from how force is applied to the structure. The three kissing complexes are pulled from opposite ends (Figure 1b). The direction of applied force approximately overlaps the axis of the kissing helix such that all kissing base pairs are under tension and that more than one base pairs are broken at the transition state. In contrast, when a hairpin is “unzipped”, the ripping fork progresses from the bottom of the helix, breaking one base pair at a time (Figure S8). The difference in how force is applied affects the value of ΔX‡, rupture force distribution and force-dependent unfolding kinetics. A somewhat similar case is mechanical unwinding of double-stranded DNA. A long DNA, such as 48 kbp lambda DNA, “melts” at ~65 pN when force is applied to the 5′- and 3′-ends that are on different ends of the DNA.36 When force is applied to 5′- and 3′-ends of the same end of the DNA, the two strands are separated at ~15 pN.53 The direction effect is characteristic of mechanical unfolding, distinct from thermal and chemical denaturation.
Physical meaning of ΔX‡
The distance to the transition state, ΔX‡, characterizes the position of the transition state along the reaction coordinate;23 it reveals whether the transition state is similar to reactant or to product. In simple reactions, like single-step unfolding of a hairpin, ΔX‡ can be used to interpret the number of base pairs unfolded at the transition state.37 ΔX‡ of 0.65 nm for breaking the minimal kissing with two base pairs suggests that at the transition state, the end-to-end distance of the molecule has been extended more than two base pairs.24 Therefore, both kissing base pairs must be disrupted at the transition state. This interpretation is also reasonable to account for the wide rip force distribution and the rip forces as high as 30 pN, which a single base pair is unlikely to withstand. Both Mal and Lai kissing complexes have 6 tertiary base pairs, and their ΔX‡unkiss are about 1.2 nm and 1.8 nm, respectively. The unfolding transition state of Mal is closer to the folded state than that of Lai (Figure 9a) and fewer base pairs (certainly less than 6) are broken at the transition state of Mal. Details of the kissing structures at the unfolding transition state are still unclear, given so many possible configurations. If breaking two base pairs yields ΔX‡ of 0.65 nm, Mal and Lai kissing complexes may have 3–4 and 5–6 base pairs broken at their mechanical unfolding transition states, respectively. It is safe to conclude that ΔX‡unkiss and thereby the position of the unfolding transition state along the reaction coordinate depend on both the number and sequence of kissing base pairs.
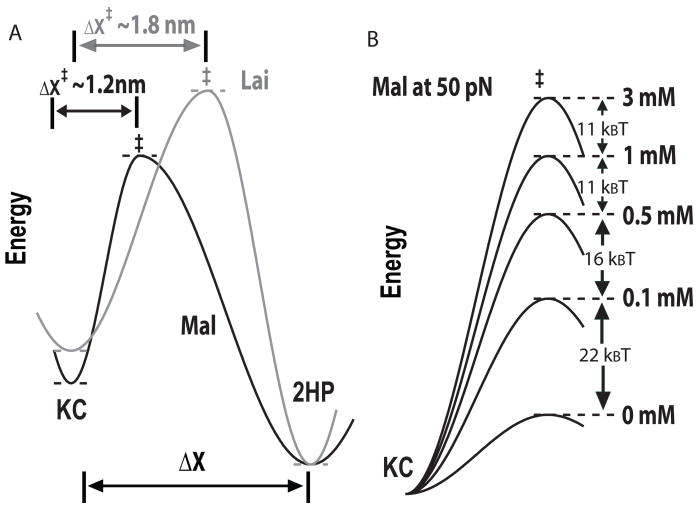
Figure 9.
Unfolding transition state of the two kissing complexes. (a) An illustration of different unfolding transition states of Mal and Lai types kissing complexes. (b) Effect of Mg2+ on the height of kinetic barrier of Mal at 50 pN was calculated using parameters in Table 2. For better comparison, folding energies of the kissing complex under all ionic conditions were arbitrarily set as the same.
Large ΔX‡ also means that more kissing base pairs are broken at the transition state of Lai than of Mal, suggesting a higher kinetic barrier to unfold Lai. Rip forces and unfolding mechanical work are higher for Lai than for Mal. Consistently, values of k0 for breaking Lai are smaller than those for Mal (Tables 1 and 2) suggesting that at the same force, the kinetic barrier of unfolding Lai kissing complex is higher (Figure 9a).
Interestingly, when proteins are mechanically unfolded by atomic force microscopy, the unfolding ΔX‡ is significantly smaller than those for breaking the kissing interactions.54 It remains a question whether this difference results from different perturbation methods with very different loading rates (atomic force methods typically use loading rates one or two orders of magnitude higher than optical tweezers), or it truly reflects the different mechanical properties of proteins and RNA.
Physical meaning of m
To our surprise, K+ and Mg2+ do not affect ΔX‡unkiss much but significantly decrease the lnk0 in Eq. 2. Therefore, the metal ions do not change the position of the unfolding transition state along the reaction coordinate but effectively raise the kinetic barrier relative to the folded state (Figure 9b). From a different viewpoint, the folded state is greatly stabilized by cations such that the kinetic barrier from the folded state to the transition state is raised. As evident in Eq. 5, m is particularly useful to describe how much the kinetic barrier is increased with ionic concentration.
It is tempting to think that m equals the number of bound ions changed at the transition state. However, such oversimplified explanation may not hold ground. In the KCl titration, concentrations of K+ and Cl− are both varied; rigorous treatment of such case is complex and sometimes controversial.51 In the MgCl2 titration, as total concentration of Cl− is dominated by that of KCl, mMgCl2 is closely related to the Mg2+ released at the unfolding transition state of kissing. Significantly, mKCl and mMgCl2 for unfolding both kissing complexes are negative, consistent with observations that DNA/RNA helix→coil transitions are associated with metal ion release 41; 55 and that cations stabilize the kissing structures thermodynamically.19–22 It is also clear that Mg2+ is more effective than K+ in stabilizing the two kissing complexes.
Both Mal and Lai kissing complexes release about 2 K+ ions at their unfolding transition states (Figure 7 c and d). Since less base pairs are broken at the transition state of Mal, mKCl/ΔX‡unkiss for Mal is higher than that for Lai suggesting that more K+ ions are associated with the Mal type kissing base pairs broken at its transition state. Values of mMgCl2 of the two kissing complexes are within the error range (Figure 8 c and d). The physical meaning of m/ΔX‡unkiss remains unclear.
Differences in the mean rip forces of the two kissing complexes become smaller at high concentration of Mg2+ (Figure 5). Similarly, as concentration of Mg2+ increases, differences in the thermal stability of the two kissing complexes becomes narrow.19–21 Our results suggest that the Mg2+ effect on the unfolding kinetics, reflected by mMgCl2, plays at least a partial role in the convergence of the thermal stabilities of the two kissing complexes at high Mg2+ concentrations.
Fast dissociation of cations
If a ligand binds tightly to a receptor, we expect to distinguish the ligand-bound and ligand-free species by two distinct populations of rip forces. In contrast, as the ionic strength increases, the rip force distribution gradually moves towards high force (Figure 4 and 5). Such moving distribution, analogous to moving peaks in chromatography and ultracentrifugation,56 indicates that the structure exchanges multiple metal ions rapidly with the solution. Loosely bound Mg2+ also play a critical role in stabilizing the RNA tertiary structures, as demonstrated by a recent study on an RNA pseudoknot.57
Unkiss kinetics at zero force
It is tempting to estimate zero-force unfolding kinetics from mechanical unfolding measurements. In bulk studies, equilibrium dissociation constants for the DIS kissing complexes are a few nM or higher 19; 20 and association rate constants for kissing complexes are often about 106 M−1s−1.58; 59 Hence, the dissociation rate constants should be in the range of 10−3 s−1. Mechanical unfolding rates extrapolated to zero force appear to overshoot (Figure S9). The difference in zero force unfolding rates measured by different methods reflects different mechanisms underlying thermal, chemical and mechanical denaturation. Also, the bulk experiments measured dimer dissociation, but in our experiment, an intramolecular kissing complex is unfolded.
Thermal stability and mechanical unfolding
Several thermodynamic studies show that stability of both DIS kissing complexes depends on [Mg2+].19–21 The equilibrium constant of an unfolding reaction can be expressed as the ratio of the unfolding rate to the folding rate. We were not able to quantify the folding free energy because in our experiments, formation of the kissing interaction was not directly observed. However, by changing the lowest force in pulling experiments, we can find forces that perturb the kissing (Figure 2d). 3 mM Mg2+ only changes the kissing force of Mal by 1–2 pN, as compared to >20 pN difference in rip force. The difference is likely because formation of the kissing interaction involves intramolecular diffusion, whose rate is not as sensitive to electrostatic forces as the unfolding rate. Hence, Mg2+ has larger effect on unkiss than kissing under mechanical tension.
Conclusion
Previous studies established that the Mal and Lai kissing complexes have different thermal stabilities and Mg2+ differentially affects such stabilities.19–21 Here we demonstrated that rupture forces of the Lai kissing complex are much higher than those of Mal. This observation indicates that the rate of unfolding the Lai kissing is much slower than that of Mal at the same force. Moreover, we have found that cations, particularly Mg2+, decrease the unfolding rate of the two kissing complexes. The cation effect is specific both to the type of cation and to the sequence of kissing base pairs. Furthermore, we have shown that neither K+ nor Mg2+ significantly changes the position of the transition state along the reaction coordinate. Instead, cations increase the kinetic barrier. A cation specific parameter, m, is used to describe empirically how the height of the kinetic barrier depends on the concentration of cations. Also, our results suggest that Mg2+ greatly slows down the unfolding of the kissing complex, but has moderate effects on the formation kinetics of the structure.
During translation and viral RNA replication, RNA structures are mechanically disrupted and their counterions are displaced as molecular machines like helicases and ribosomes translocate along the RNA.60; 61 Mg2+ ions play two opposite roles: they stabilize RNA structures but also enhance NTPase activity of the molecular machines. Metal ions can affect pause, rate, and direction of translocation by the motors 62. Salt-dependent unfolding kinetics is crucial to functions of RNA-based molecular motors and our study is a step towards such understanding.
Materials and Methods
Preparation of RNA
Mal and Lai sequences were cloned between Sma I site in pUC57 vector by Genscript (Piscatway, NJ). Sequences flanking the insert (1.3 kb upstream and 1.2 kb downstream) were used as handles. Preparation of the molecule shown in Figure 1 was described in detail previously.24; 25; 28 Briefly, a transcription template, including a T7 promoter, handles and the kissing structure, is generated by PCR from the plasmids. Then an RNA about 2.6 kb were transcribed in vitro by T7 RNA polymerase. Two dsDNA handles were also made by PCR. The DNA handle upstream of the kissing structure was biotinylated at the 3′-end and the downstream DNA handle contained a digoxigenin group at the 5′-terminus. The annealed molecule can be attached to a pair of beads coated with streptavidin and anti-digoxigenin antibody, respectively (Figure 1).
Optical tweezers
Dual-beam optical tweezers were used to study the folding of the kissing complexes.33 The antidigoxigenin-coated bead was held by a force-measuring optical trap in a flow chamber. The streptavidin-coated bead was mounted on the tip of a micropipette by suction. The extension of the molecule was changed by moving a piezoelectric flexure stage, on which the micropipette was mounted (Figure S1). Force is measured by the spring constant of the trap and distance of the trapped bead from the center of the trap. Change in the extension of the molecule was measured by relative movements of the trapped bead and the piezoelectric flexure stage. Force and extension of the molecule were recorded at a rate of 100 Hz.
Folding experiments
All unfolding/refolding experiments were done at 22±1 °C. Various concentrations of MgCl2 were added to a solution containing 10 mM HEPES pH 8.0 and 100 mM KCl. In titration of KCl, all solutions had 10 mM HEPES pH 8.0.
Supplementary Material
Eight additional figures show the following: Figure S1 Setup of an optical tweezers’ experiment; Figure S2 Detailed structure of the Mal type kissing complex; Figure S3 Unfolding and refolding pathways of the kissing complex; Figure S4 Estimation of ΔX as a function of force; Figure S5 Long lifetime of the kissing structures at high force; Figure S6 Hopping of the two hairpins at near equilibrium force; Figure S7 Evans and Ritchie analyses of unkiss force distributions; Figure S8 Direction of applied force in unfolding tertiary and secondary structures; and Figure S9 Unkiss rate constants extrapolated to zero force.
Acknowledgments
We thank Dr. Wei Cheng, Dr. Gang Chen and Dr. Jin-Der Wen for suggestions and comments on the manuscript. This work was supported by National Institute of Health Grant GM-10840 (I.T.) and a grant from University at Albany (P.T.X.L.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Pan T.X. Li, Email: panli@albany.edu.
Ignacio Tinoco, Jr., Email: intinoco@lbl.gov.
References
- 1.Paillart JC, Shehu-Xhilaga M, Marquet R, Mak J. Dimerization of retroviral RNA genomes: an inseparable pair. Nat Rev Microbiol. 2004;2:461–72. doi: 10.1038/nrmicro903. [DOI] [PubMed] [Google Scholar]
- 2.D’Souza V, Summers MF. How retroviruses select their genomes. Nat Rev Microbiol. 2005;3:643–55. doi: 10.1038/nrmicro1210. [DOI] [PubMed] [Google Scholar]
- 3.Greatorex J. The retroviral RNA dimer linkage: different structures may reflect different roles. Retrovirology. 2004;1:22. doi: 10.1186/1742-4690-1-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brunel C, Marquet R, Romby P, Ehresmann C. RNA loop-loop interactions as dynamic functional motifs. Biochimie. 2002;84:925–44. doi: 10.1016/s0300-9084(02)01401-3. [DOI] [PubMed] [Google Scholar]
- 5.Paillart JC, Marquet R, Skripkin E, Ehresmann B, Ehresmann C. Mutational analysis of the bipartite dimer linkage structure of human immunodeficiency virus type 1 genomic RNA. J Biol Chem. 1994;269:27486–93. [PubMed] [Google Scholar]
- 6.Skripkin E, Paillart JC, Marquet R, Ehresmann B, Ehresmann C. Identification of the primary site of the human immunodeficiency virus type 1 RNA dimerization in vitro. Proc Natl Acad Sci U S A. 1994;91:4945–9. doi: 10.1073/pnas.91.11.4945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paillart JC, Skripkin E, Ehresmann B, Ehresmann C, Marquet R. A loop-loop “kissing” complex is the essential part of the dimer linkage of genomic HIV-1 RNA. Proc Natl Acad Sci U S A. 1996;93:5572–7. doi: 10.1073/pnas.93.11.5572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Clever JL, Wong ML, Parslow TG. Requirements for kissing-loop-mediated dimerization of human immunodeficiency virus RNA. J Virol. 1996;70:5902–8. doi: 10.1128/jvi.70.9.5902-5908.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Russell RS, Liang C, Wainbeerg MA. Is HIV-1 RNA dimerization a prerequisite for packaging? Yes, no, probably? Retrovirology. 2004;1:23. doi: 10.1186/1742-4690-1-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Renjifo B, Essex M. HIV-1 subtypes and recombinants. In: Essex M, Mboup S, Kanki PJ, Marlink PJ, Tlou SD, editors. AIDS in Africa. Vol. 2. Springer; New York: 2002. pp. 138–57. [Google Scholar]
- 11.Chin MP, Rhodes TD, Chen J, Fu W, Hu WS. Identification of a major restriction in HIV-1 intersubtype recombination. Proc Natl Acad Sci U S A. 2005;102:9002–7. doi: 10.1073/pnas.0502522102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ennifar E, Yusupov M, Walter P, Marquet R, Ehresmann B, Ehresmann C, Dumas P. The crystal structure of the dimerization initiation site of genomic HIV-1 RNA reveals an extended duplex with two adenine bulges. Structure. 1999;7:1439–49. doi: 10.1016/s0969-2126(00)80033-7. [DOI] [PubMed] [Google Scholar]
- 13.Ennifar E, Dumas P. Polymorphism of bulged-out residues in HIV-1 RNA DIS kissing complex and structure comparison with solution studies. J Mol Biol. 2006;356:771–82. doi: 10.1016/j.jmb.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 14.Ennifar E, Paillart JC, Bodlenner A, Walter P, Weibel JM, Aubertin AM, Pale P, Dumas P, Marquet R. Targeting the dimerization initiation site of HIV-1 RNA with aminoglycosides: from crystal to cell. Nucleic Acids Res. 2006;34:2328–39. doi: 10.1093/nar/gkl317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ennifar E, Walter P, Ehresmann B, Ehresmann C, Dumas P. Crystal structures of coaxially stacked kissing complexes of the HIV-1 RNA dimerization initiation site. Nat Sturct Biol. 2001;8:1064–8. doi: 10.1038/nsb727. [DOI] [PubMed] [Google Scholar]
- 16.Kieken F, Paquet F, Brule F, Paoletti J, Lancelot G. A new NMR solution structure of the SL1 HIV-1Lai loop-loop dimer. Nucleic Acids Res. 2006;34:343–52. doi: 10.1093/nar/gkj427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baba S, Takahashi K, Noguchi S, Takaku H, Koyangi Y, Yamamoto N, Kawai G. Solution RNA structures of the HIV-1 dimerization initiation site in the kissing-loop and extended-duplex dimers. J Biochem. 2005;138:583–92. doi: 10.1093/jb/mvi158. [DOI] [PubMed] [Google Scholar]
- 18.Mujeeb A, Clever JL, Billeci TM, James TL, Parslow TG. Structure of the dimer initiation complex of HIV-1 genomic RNA. Nat Sturct Biol. 1998;5:432–6. doi: 10.1038/nsb0698-432. [DOI] [PubMed] [Google Scholar]
- 19.Lorenz C, Piqaneau N, Schroeder R. Stabilities of HIV-1 DIS type RNA loop-loop interactions in vitro and in vivo. Nucleic Acids Res. 2006;34:334–42. doi: 10.1093/nar/gkj435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Weixlbaumer A, Werner A, Flamm C, Westhof E, Schroeder R. Determination of thermodynamic parameters for HIV DIS type loop-loop kissing complexes. Nucleic Acids Res. 2004;32:5126–33. doi: 10.1093/nar/gkh841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Paillart JC, Westhof E, Ehresmann B, Ehresmann C, Marquet R. Non-canonical interactions in a kissing loop complex: the dimerization initiation site of HIV-1 genomic RNA. J Mol Biol. 1997;270:36–49. doi: 10.1006/jmbi.1997.1096. [DOI] [PubMed] [Google Scholar]
- 22.Jossinet F, Paillart JC, Westhof E, Hermann T, Skripkin E, Lodmell JS, Ehresmann B, Ehresmann C, Marquet R. Dimerization of HIV-1 genomic RNA of subtypes A and B: RNA loop structure and magnesium binding. RNA. 1999;5:1222–34. doi: 10.1017/s1355838299990982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li PTX, Vieregg J, Tinoco I., Jr How RNA unfolds and refolds. Annu Rev Biochem. 2008;77:27.1–24. doi: 10.1146/annurev.biochem.77.061206.174353. [DOI] [PubMed] [Google Scholar]
- 24.Li PTX, Bustamante C, Tinoco I., Jr Unusual Mechanical Stability of A Minimal RNA Kissing Complex. Proc Natl Acad Sci U S A. 2006;103:15847–52. doi: 10.1073/pnas.0607202103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liphardt J, Onoa B, Smith SB, Tinoco I, Jr, Bustamante C. Reversible unfolding of single RNA molecules by mechanical force. Science. 2001;292:733–7. doi: 10.1126/science.1058498. [DOI] [PubMed] [Google Scholar]
- 26.Collin D, Ritort F, Jarzynski C, Smith SB, Tinoco I, Jr, Bustamante C. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature. 2005;437:231–4. doi: 10.1038/nature04061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dumont S, Cheng W, Serebrov V, Beran RK, Tinoco I, Jr, Pyle AM, Bustamante C. RNA translocation and unwinding mechanism of HCV NS3 helicase and its coordination by ATP. Nature. 2006;439:105–8. doi: 10.1038/nature04331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li PTX, Collin D, Smith SB, Bustamante C, Tinoco I., Jr Probing the Mechanical Folding Kinetics of TAR RNA by Hopping, Force-Jump and Force-Ramp Methods. Biophys J. 2006;90:250–60. doi: 10.1529/biophysj.105.068049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Liphardt J, Onoa B, Smith SB, Tinoco I, Jr, Bustamante C. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski’s equality. Proc Natl Acad Sci U S A. 2002;296:1832–5. doi: 10.1126/science.1071152. [DOI] [PubMed] [Google Scholar]
- 30.Onoa B, Dumont S, Liphardt J, Smith SB, Tinoco I, Jr, Bustamante C. Identifying kinetic barriers to mechanical unfolding of the T. thermophila ribozyme. Science. 2003;299:1892–5. doi: 10.1126/science.1081338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen G, Wen JD, Tinoco I., Jr Single-molecule mechanical unfolding and folding of a pseudoknot in human telomerase RNA. RNA. 2007;13:2175–88. doi: 10.1261/rna.676707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Green L, Kim CH, Bustamante C, Tinoco I., Jr Characterization of the mechanical unfolding of RNA pseudoknots. J Mol Biol. 2008;375:511–28. doi: 10.1016/j.jmb.2007.05.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Smith SB, Cui Y, Bustamante C. Optical-trap force transducer that operates by direct measurement of light momentum. Methods Enzymol. 2003;361:134–62. doi: 10.1016/s0076-6879(03)61009-8. [DOI] [PubMed] [Google Scholar]
- 34.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–15. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bustamante C, Marko JF, Siggia ED, Smith SB. Entropic elasticity of lambda-phage DNA. Science. 1994;265:1599–600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 36.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–9. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 37.Tinoco I, Jr, Li PTX, Bustamante C. Determination of ther modynamics and kinetics of RNA reactions by force. Q Rev Biophys. 2006;39:325–60. doi: 10.1017/S0033583506004446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Greenleaf WJ, Frieda KL, Foster DAN, Woodside MT, Block SM. Direct observation of hierarchical folding in single riboswitch aptamers. Science. 2008;319:630–3. doi: 10.1126/science.1151298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lodmell JS, Ehresmann B, Ehresmann C, Marquet R. Convergence of natural and artificial evolution on an RNA loop-loop interaction: the HIV-1 dimerization initiation site. RNA. 2000;6:1267–76. doi: 10.1017/s1355838200000698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vieregg J, Bustamante C, Tinoco I., Jr Measurement of the Effect of Monovalent Cations on RNA Hairpin Stability. J Am Chem Soc. 2007;129:14966–73. doi: 10.1021/ja074809o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bloomfield VA, Crothers DM, Tinoco I., Jr . Interaction of nucleic acids and water and ions. In: Bloomfield VA, Crothers DM, Tinoco I Jr, editors. Nucleic acids: structures, perperties, and functions. University Science Books; Sausalito, California: 2000. [Google Scholar]
- 42.Baumann CG, Smith SB, Bloomfield VA, Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proc Natl Acad Sci U S A. 1997;94:6185–90. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dessinges MN, Maier B, Zhang Y, Peliti M, Bensimon D, Croquette V. Stretching single stranded DNA, a model polyelectrolyte. Phys Rev Lett. 2002;89:248102. doi: 10.1103/PhysRevLett.89.248102. [DOI] [PubMed] [Google Scholar]
- 44.Maier B, Bensimon D, Croquette V. Replication by a single DNA polymerase of a stretched single-stranded DNA. Proc Natl Acad Sci U S A. 2000;97:12002–7. doi: 10.1073/pnas.97.22.12002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Seol Y, Skinner GM, Visscher K. Elastic properties of a single-stranded charged homopolymeric ribonucleotide. Phys Rev Lett. 2004;93:118102. doi: 10.1103/PhysRevLett.93.118102. [DOI] [PubMed] [Google Scholar]
- 46.Seol Y, Skinner GM, Visscher K, Buhot A, Halperin A. Stretching of homopolymeric RNA reveals single-stranded helices and base-stacking. Phys Rev Lett. 2007;98:158103. doi: 10.1103/PhysRevLett.98.158103. [DOI] [PubMed] [Google Scholar]
- 47.Evans E, Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wen JD, Manosas M, Li PTX, Smith SB, Bustamante C, Ritort F, Tinoco I., Jr Force unfolding kinetics of RNA using optical tweezers. I. Effects of experimental variables on measured results. Biophys J. 2007;92:2996–3009. doi: 10.1529/biophysj.106.094052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Manosas M, Wen JD, Li PTX, Smith SB, Bustamante C, Tinoco I, Jr, Ritort F. Force Unfolding Kinetics of RNA using Optical Tweezers. II. Modeling Experiments. Biophys J. 2007;92:3010–21. doi: 10.1529/biophysj.106.094243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Draper DE, Grilley D, Soto AM. Ions and RNA folding. Annu Rev Biophys Biomol Struct. 2005;34:221–43. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 51.Record MT, Jr, Zhang W, Anderson CF. Analysis of effects of salts and uncharged solutes on protein and nucleic acid equilibria and processes: a practical guide to recognizing and interpreting polyelectrolyte effects, Hofmeister effects, and osmotic effects of salts. Adv Protein Chem. 1998;51:281–353. doi: 10.1016/s0065-3233(08)60655-5. [DOI] [PubMed] [Google Scholar]
- 52.Woodson SA. Metal ions and RNA folding: a highly charged topic with a dynamic future. Curr Opin Chem Biol. 2005;9:104–9. doi: 10.1016/j.cbpa.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 53.Bockelmann U, Thomen P, Essevaz-Roulet B, Viasnoff V, Heslot F. Unzipping DNA with Optical Tweezers: High Sequence Sensitivity and Force Flips. Biophys J. 2002;82:1537–53. doi: 10.1016/S0006-3495(02)75506-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Garcia-Manyes S, Brujic J, Badilla CL, Fernández JM. Force-clamp spectroscopy of single-protein monomers reveals the individual unfolding and folding pathways of i27 and ubiquitin. Biophys J. 2007;93:2436–46. doi: 10.1529/biophysj.107.104422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cantor CR, Schimmel PR. Biophysical Chemistry. III. W. H. Freeman; New York: 1980. Nucleic acid structural transitions. [Google Scholar]
- 56.Gilbert GA, Jenkins RC. Boundary problems in the sedimentation and electrophoresis of complex systems in rapid reversible equilibrium. Nature. 1956;177:853–4. doi: 10.1038/177853a0. [DOI] [PubMed] [Google Scholar]
- 57.Soto AM, Misra V, Draper DE. Tertiary structure of an RNA pseudoknot is stabilized by “diffuse” Mg2+ ions. Biochemistry. 2007;46:2973–83. doi: 10.1021/bi0616753. [DOI] [PubMed] [Google Scholar]
- 58.Nordgren S, Slagter-Jäger JG, Wagner GH. Real time kinetic studies of the interaction between folded antisense and target RNAs using surface plasmon resonance. J Mol Biol. 2001;310:1125–34. doi: 10.1006/jmbi.2001.4802. [DOI] [PubMed] [Google Scholar]
- 59.Nair TM, Myszka DG, Davis DR. Surface plasmon resonance kinetic studies of the HIV TAR RNA kissing hairpin complex and its stabilization by 2-thiouridine modification. Nucleic Acids Res. 2000;28:1935–40. doi: 10.1093/nar/28.9.1935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cheng W, Dumont S, Tinoco I, Jr, Bustamante C. NS3 helicase actively separates RNA strands and senses sequence barriers ahead of the opening fork. Proc Natl Acad Sci USA. 2007;104:13954–9. doi: 10.1073/pnas.0702315104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wen JD, Lancaster L, Hodges C, Zeri AC, Yoshimura SH, Noller HF, Bustamante C, Tinoco I., Jr Following translation by single ribosomes one codon at a time. Nature. 2008;452:598–603. doi: 10.1038/nature06716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lohman TM, Tomko EJ, Wu CG. Non-hexameric DNA helicases and translocases: mechanisms and regulation. Nat Rev Mol Cell Biol. 2008;9:391–401. doi: 10.1038/nrm2394. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Eight additional figures show the following: Figure S1 Setup of an optical tweezers’ experiment; Figure S2 Detailed structure of the Mal type kissing complex; Figure S3 Unfolding and refolding pathways of the kissing complex; Figure S4 Estimation of ΔX as a function of force; Figure S5 Long lifetime of the kissing structures at high force; Figure S6 Hopping of the two hairpins at near equilibrium force; Figure S7 Evans and Ritchie analyses of unkiss force distributions; Figure S8 Direction of applied force in unfolding tertiary and secondary structures; and Figure S9 Unkiss rate constants extrapolated to zero force.