An Essay on Understanding the Mind

Abstract

Several conjectures by A. S. Iberall on life and mind are used as a backdrop to sketch a theory of mental activity that respects both the contents of thought and the dynamics of thinking. The dynamics, in this case, refers fundamentally to animated, meaningfully coupled self-organizing processes (coordination dynamics) and exhibit multistability, switching, and, because of symmetry breaking, metastability. The interplay of 2 simultaneously acting forces underlies the metastable mind: the tendency for the coordinating elements to couple together (integration) and the tendency for the elements to express their individual autonomy (segregation). Metrics for metastability are introduced that enable these cooperative and competitive tendencies to be quantified. Whereas bistability is the basis for polarized, either/or thinking, the metastable régime—which contains neither stable nor unstable states, no states at all, in fact—gives rise to a far more fluid, complementary mode of operation in which it is possible for apparent contraries to coexist in the mind at the same time.

BEGINNING

By way of reminiscence, and apropos the topic of this contribution, the photograph in Figure 1 was taken at a symposium on Nonlinearities in Brain Function, organized by Eugene Yates and Arnold Mandell, held at the Kroc Ranch in Santa Ynez, California, from March 1 through March 5, 1982. As remarked upon previously (Kelso, 1995, p. 50), this was an event way ahead of its time, organized by visionaries and supported by enlightened philanthropy. A quarter of a century ago there were no Centers or Institutes for Complex Systems and the like yet, and no one was talking about “brain dynamics,” a field of research that very much stirs the air of contemporary neuroscience. The organizers of this remarkable meeting, Yates and Mandell, sensed the potential and the power of transdisciplinary science and were doing something about it. The man we honor in these lectures was living testament to that. Arthur Iberall (“Ibby”) was the centerpiece of the Kroc symposium, holding court every evening, laying out his homeokinetics manifesto in a unique and irrepressible way. Only once can I remember him being told to shut up. Ibby was both generalist and specialist, theorist and experimenter, scientist and engineer, physicist and biologist, swimmer and poet-and much, much more. Was it Georges Braque who said, “Le conformisme commence à la definition”? Iberall was no conformist so there is no point in trying to classify him. The usual categories fail and words are not the thing. Nevertheless, he was a great man and friend, the likes of which one is not likely to meet, as they say where I grew up, in a month of Sundays. For students with an interest in the history of science and especially “the sciences of complexity” who also want to get a sense of the man and the range of his intellect in one swift glimpse, consider Iberall's (1994) short article in Physics Today, where he chastises a Nobel laureate for, shall we say, pontificating with blinders on. For those in the know, the reply is revealing enough.

FIGURE 1.

Participants at the Kroc Foundation Symposium Nonlinearities in Brain Function, March 1–5, 1982. Front row (left to right): Eugene Yates, Albert Goldbeter, Anna Wirz-Justice, Arthur Winfree, Kirstie Bellman, Alice Kroc, Arnold Mandell. Middle row: William Smith, Scott Kelso, Victor Denenberg, Alan Garfinkel, Peter Whybrow, Donald Walter. Back row: Walter Carey, Erol Basar, Pierre Flor Henry, Ross Adey, Arthur Iberall, Michael Turvey, Doyne Farmer, Ralph Abraham.

ON NATURE, LIFE, AND MIND

What did Iberall have to say about nature, life, and mind? Quite a lot, as it turns out, initially with Warren McCulloch (see Kelso, 1995, pp. 114–115). On the occasion of his 80th birthday, he and his colleague of 60 years, Harry Soodak, provided a primer that contains his principles of homeokinetics along with a number of conjectures about their application to matters of nature, life, mind, brain and humankind (Iberall & Soodak, 1998). Among those pertinent to the present concerns (words italicized to convey effect) are: (1) the notion of a homeokinetic oscillator, a unit of some generality that underlies nature's self-organization of forms and functions, even complex ones; (2) said unit consists of an energy storing nonlinear element and is conceived of as bistable; (3) the energy to snap the element in a direction from one ‘stable’ position to another is very small (the quotation marks around ‘stable’ are theirs); (4) the human is conceived as a nonlinear marginally stable storage device who can ‘self-urge’ (Ibby's words) onboard sources in any number of directions (Ibby loved telling the story of a young boy's bar mitzvah; when asked by his father what he was today, he replied, “Today I am a fountain pen” ). The idea is that people snap into a direction by . . . “always taking a binary decision mind set, e.g., to trade or to rob, to persuade or to rape, to buy or to sell, to be or not to be, to kill or not to kill, to eat or not to eat, to scratch or not to scratch a body itch” (p. 29); (5) complexity develops from interacting or synergetic engine processes; (6) by virtue of very weak interactions “whose complex character we do not quite understand yet,” a kind of mutual entrainment is possible, which may leave a memory after the interaction is over (for a recent example of social memory following entrainment, see Oullier, DeGuzman, Jantzen, Lagarde, & Kelso, 2008); (7) a direction of common agreement often emerges, a higher order chemistry or command-control system typical of any complex system; (8) the laws and rules for command-control (a term that Ibby liked despite its linguistic similarity to discredited ‘commands to muscles’ schemes for motor control; see, e.g., Turvey, Fitch & Tuller, 1982) lie in a homeokinetic spectrum in the person's body, brain, and mind; this ushered in and grounded the field of biospectroscopy (see Yates, this issue, and for an application Goodman & Kelso, 1983); (9) the human mind operates, as does nature, by a “peculiar fumbling mode” identified as “reverie,” suggesting that thought has its own typical space and time scale; and (10) consonant with 3 and 4, command-control is catalytic, chemically based linguistic signals causing low energy switching among action modes.

It is a tribute to Iberall's powers of divination that empirical traces of many of his proposals continue to permeate the literature and will be touched upon as we proceed. The foregoing list is presented here principally as a backdrop for where this article is headed, which is to sketch a theory of thoughts and thinking that attempts to: (1) accommodate both the content of thoughts and the dynamics of thinking and (2) narrow the gap between the language and science of molecules and cellular machinery (genetics, neuroscience) and the language and science of mind and behavior (cognitive science, neurology, psychiatry). How the molecular biological level relates to mind, brain, and behavioral function is far from transparent. As Kandel (2006) has recently concluded, a conceptual shift is needed from studying elementary processes such as single proteins, genes, and cells to studying complex systems of nerve cells, the functioning of whole organisms, and the interactions of organisms. “Biology,” says Kandel (2006), “will have to focus more on human beings as the model system of choice” (p. 423). He kids not.

Ultimately (and there is no point in beating about the bush) we need a language and science of experience, of everything we human beings take for granted—as Virginia Wolf would say, “an ordinary mind on an ordinary day”—that connects to a language and science of body∼brain activity.

The central thesis of this article can be stated bluntly: Minds, brains, and bodies, yours and mine, immersed as they are in their own worlds, both outside and inside, share a common underlying dynamics. They are cut fundamentally, as Maxine Sheets-Johnstone (2004) says, from the same dynamic cloth. The dynamics here refers to equations of motion for key coordination variables or order parameters that characterize patterns of behavior on multiple levels of description: patterns of brain activity, patterns of cognition and emotion, patterns of human interaction, patterns of the mind. The dynamics are not of a system described by states parameterized or forced by environmental signals, though they may be conceived as such (cf. Rosen, 1991). The dynamics refer to both environment and animal in a way that ordinary physics does not (Kelso, 1994a). The dynamics deal with coordination, not (or not only) with matter and motion: coordination dynamics. Coordination dynamics deals specifically with informationally coupled, self-organizing systems, where information is meaningful and specific to coordination tasks and functions: functional information (for the origins of the notion of information as form, see references and discussion in Kugler, Kelso, & Turvey, 1980, 1982). Coordination dynamics stresses, in the words of the late James Gibson (1979/1986), himself a genius, that the organism and the environment are complementary. Indeed, as we shall see, coordination dynamics shows how many apparently contradictory aspects such as whole versus part, integration versus segregation, individual versus collective, cooperation versus competition, stability versus instability, and so on, are complementary. In doing so, coordination dynamics opens up a path to reconciling contradictions, dualisms, binary oppositions, and the like in all walks of life, illuminating thereby the complementary nature (Kelso & Engstrøm, 2006; see also Kelso, 2005).¹

TOWARD A COMPLEMENTARY SCIENCE OF BODY, BRAIN, MIND, AND BEHAVIOR

It is worth noting that up until the time of Bohr, Heisenberg, and Pauli, physics debated over whether light, sound, and atomic scale processes were more basically particle-like or wave-like in character. Philosophy spoke of thesis and antithesis, of dialectic tension, of self and not self, of the qualitative and the quantitative, the objective and the subjective, as if they were either/or divisions. This tendency to dichotomize, to divide the world into opposing categories (the binary decision mind-set, see 3 earlier) appears to be a ‘built in’ property of human beings, perhaps arising very early in development and independent of cultural background (Spelke, 2006).

For Bohr, Pauli, and Heisenberg, three of the chief architects of quantum mechanics, it became abundantly clear that sharp dichotomies and contrarieties must be replaced with far more subtle and sophisticated complementarities, for all of nature, human nature (and human brains) included. Probably Pauli (1994) expressed it best:

To us the only acceptable point of view appears to be one that recognizes both sides of reality—the quantitative and the qualitative, the physical and the psychical—as compatible with each other. It would be most satisfactory of all if physics and psyche could be seen as complementary aspects of the same reality. (p. 260)

The remarkable developments of quantum mechanics demonstrating the essential complementarity of both light and matter should have ushered in not just a novel epistemology but a generalized complementary science. However, they did not. Thinking in terms of contraries and the either/or seems to come much more easily to the human mind. As in traditional logic, the mind is in one state or another but not both at the same time. Much harder to grasp is the notion that contraries are complementary: Contraria sunt complementa, as Bohr's famous coat of arms says. That mind-set might change, however, if complementary aspects and their dynamics were found not just at the remote level of the subatomic processes dealt with by quantum mechanics but also at the level of human beings, human brains, and human behavior. In particular, over the last 25 years or so, due to the efforts of people working in and across many fields, a multilevel, interdisciplinary science of coordination has emerged called coordination dynamics. A broad range of coordinative phenomena have been studied and explained using the concepts, methods, and tools of coordination dynamics (Fuchs & Jirsa, 2008; Jirsa & Kelso, 2004; Kelso, 1995; Tschacher & Dauwalder, 2003, for reviews). Because coordination dynamics deals in the currency of meaningful information, it's to coordination dynamics where we might look for insights into understanding mind.

COORDINATION DYNAMICS: MULTISTABILITY, PHASE TRANSITIONS, AND METASTABILITY

New empirical and theoretical developments in the science of coordination suggest that the reason the mind fragments the world into dichotomies (and more important, how opposing tendencies may be reconciled) is deeply connected to the way the human brain works, in particular its multi- and metastable dynamics (Bressler & Kelso, 2001; Fingelkurts & Fingelkurts, 2004; Friston, 1997; Jirsa & Kelso, 2004; Kelso, 1995; Oullier & Kelso, 2006; Tschacher & Dauwalder, 2003; Velazquez, 2005, for reviews). Etymologically, “metastability” comes from the Latin meta (beyond) and stabilis (able to stand). In coordination dynamics, metastability corresponds to a regime near a saddle-node or tangent bifurcation in which stable coordination states no longer exist (e.g., inphase synchronization where the relative phase between oscillating components lingers at zero), but attraction remains to where those fixed points used to be (“remnants of attractor repellors”; see Figure 2). This gives rise to a dynamical flow consisting of both phase trapping and phase scattering. Metastability is thus the simultaneous realization of two competing tendencies: the tendency of the components to couple together and the tendency for the components to express their intrinsic independent behavior. According to a recent review (Fingelkurts & Fingelkurts, 2004),

Metastability is an entirely new conception of brain functioning where the individual parts of the brain exhibit tendencies to function autonomously at the same time as they exhibit tendencies for coordinated activity. (Kelso, 1991, 1992, 1995; Bressler & Kelso, 2001; see also Bressler, 2003)

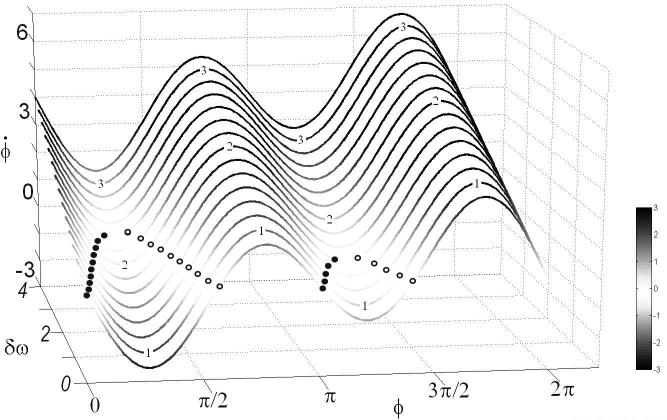
FIGURE 2.

Elementary coordination law (Eq. 1). Surface formed by a family of flows of the coordination variable ϕ (in radians) for increasing values of δω between 0 and 4. For this example, the coupling is fixed: a = 1 and b = 1. When $\stackrel{.}{\varphi }$ reaches zero (flow line becoming white), the system ceases to change and fixed point behavior is observed. Note that the fixed points here refer to emergent collective states produced by nonlinearly coupled elements. Stable and unstable fixed points at the intersection of the flow lines with the isoplane $\stackrel{.}{\varphi }$ = 0 are represented as filled and open circles, respectively. To illustrate the different regimes of the system, three representative lines labeled 1 to 3 fix δω at increasing values. Following the flow line 1 from left to right, two stable fixed points (filled circles) and two unstable fixed points (open circles) exist. This flow belongs to the multistable (here bistable) regime. Following line 2 from left to right, one pair of stable and unstable fixed points is met on the left, but notice the complete disappearance of fixed point behavior on the right side of the figure. That is, a qualitative change (bifurcation; phase transition) has occurred due to the loss of stability of the coordination state near antiphase, π rad. The flow now belongs to the monostable regime. Following line 3 from left to right, no stable or unstable fixed points exist yet coordination has not completely disappeared. This flow corresponds to the metastable regime, a subtle blend of coupling and intrinsic differences between the rhythmic elements in which behavior is neither completely ordered (synchronized) nor completely disordered (desynchronized).

A number of neuroscientists have embraced metastability as playing a role in various cognitive functions, including consciousness (e.g., Edelman, 2004; Edelman & Tononi, 2000; Freeman & Holmes, 2005; Friston, 1997; Koch, 2005; Sporns, 2004; Varela, Lachaux, Rodriguez, & Martinerie, 2001; see Kelso & Tognoli, 2007, for review). Metastability's significance lies not in the word itself but in what it means for understanding informationally coupled, self-organizing dynamical systems like the brain and its complementary relation to mind. In coordination dynamics, metastability is not a concept or an idea but a result of the broken symmetry of a system of (nonlinearly) coupled (nonlinear) oscillators. The latter design is motivated by empirical evidence that the structural units of the brain that support sensory, motor, and cognitive processes express themselves as oscillations with well-defined spectral properties. At least 12 different rhythms from the infraslow (less than 1 Hz) to the ultrafast (more than 100 Hz) have been identified, all connected to various behavioral and cognitive functions (e.g., Chen, Ding, & Kelso, 2003a). Indeed, brain oscillations are considered one of the most important phenotypes for studying the genetics of complex (non-Mendelian) disorders (Begleiter & Porjesz, 2006). The mechanisms that give rise to rhythms and synchrony exist on different levels of organization: single neurons oscillate due to voltage-gated ion channels depolarizing and hyperpolarizing the membrane; network oscillations, for example, in hippocampus and neocortex, strongly depend on the activity of inhibitory GABAergic interneurons in the central nervous system (so-called inhibition-based rhythms; see, e.g., Whittington, Traub, Kopell, Ermentrout, & Buhl, 2000); neuronal groups or assemblies form as transient coalitions of discharging neurons with mutual interaction. Neuronal communication occurs by means of synapses and glia. Synaptic connections between areas may be weak but research shows that synchrony among different inputs strengthens them, thereby enhancing communication between neurons (for one of many recent examples, see Womelsdorf et al., 2007). Phase coupling, for example, allows groups of neurons in distant and disparate regions of the brain to synchronize together (e.g., Canolty et al., 2006). According to coordination dynamics, nonlinear coupling among oscillatory processes that possess different intrinsic frequencies is necessary to generate the broad range of behaviors observed, including pattern formation, multistability, phase transitions, switching (sans “switches”), hysteresis, and so forth. Although the mechanisms of coupling multiple oscillations within and between levels of organization are manifold, the principle is clear enough: patterns of behavior arise as an emergent consequence of self-organized interactions among neurons and neuronal populations and this self-organization is a fundamental source of cognitive, affective, behavioral and social function (Başar, 2004; Buzsáki, 2006; Kelso, 1995; Oullier et al., 2008; Schmidt & Richardson, 2008; Van Orden, Holden, & Turvey, 2005).

Metastability was originally discovered when experimental observations of sensorimotor coordination (Kelso, DelColle, & Schöner, 1990) made it necessary to extend the elementary HKB coordination law (Haken, Kelso, & Bunz, 1985; Schöner, Haken, & Kelso, 1986) to handle the interaction of oscillatory components with different intrinsic properties² (Kelso et al., 1990; Kelso, 1995, chap. 4). This breaks the symmetry of the original HKB equation, which describes changes of the order parameter relative phase over time ($\stackrel{.}{\varphi }$):

$$\stackrel{.}{\varphi }=\delta \omega -a\text{sin}\varphi -2b\text{sin}2\varphi +\sqrt{Q}{\xi }_t,$$ (1)

where ϕ is the relative phase between two interacting components, a and b are parameters p setting the strength of attracting regions in the system's dynamical landscape, $\sqrt{Q}{\xi }_t$ is a (delta-correlated) noise term of strength Q, and δω is a symmetry breaking term expressing the fact that each coordinating element possesses its own intrinsic behavior (Kelso et al., 1990; see Park & Turvey, 2008, for further discussion).

The introduction of the symmetry breaking term δω in Eq. 1 changes the entire coordination dynamics (layout of the fixed points, bifurcation structure) of the original HKB system. This is important to realize because it is the subtle interplay between the coupling (k = b/a) and the symmetry breaking term δω in Equation 1 that gives rise to metastability³ (see Kelso, 2002, for further discussion).

$$K_{12}=({\stackrel{.}{X}}_1-{\stackrel{.}{X}}_2)\{\alpha +\beta {(X_1-X_2)}^2\}.$$ (3)

where X₁ and X₂ are the individual components, the dots are their time derivatives and α and β are coupling parameters (Haken, Kelso & Bunz, 1985). A nontrivial aspect of HKB is that it derives patterns of coordination from the individual components and their nonlinear interaction (see Kelso, 2007b for steps and rationale).

Equation 1 is weird. Even though it is an order parameter equation of motion that is designed to describe collective behavior (in words, phi dot is a function of phi), it includes also a parameter that arises as a result of differences among the individual components. Eq. 1 is thus a strange mixture of the whole and the parts, the global and the local, the cooperative and the competitive, the collective and the individual. Were the components identical, δω would be zero and we would not see component differences affecting the behavior of the whole. Eq. 1 would simply reflect the behavior of the collective untarnished by component properties, a purely emergent interaction—the HKB equation. It is the fact that both the components and their (nonlinear) interaction appear at the same level of description that gives rise to the array of coexisting tendencies characteristic of metastability. Eq. 1 is a basic representation of a synergy: a low dimensional dynamic of a metastable organization in which the tendency of the parts to act together coexists with a tendency of the parts to do their own thing (Kelso, 1995, chap. 4; for more on synergies, see Kelso, 2007a, 2000b, in press). It is metastability that endows the synergy with robustness and flexibility, enabling the same parts to participate in multiple functions. If the synergy is a unit of life, then it is metastability that brings it alive.

The flow of the coordination dynamics across a range of δω values is shown in Figure 2 for a fixed value of the coupling parameter, k = b/a = 1, where a = 1 and b = 1). Stable fixed points (attractors) are presented as filled circles and unstable fixed points (repellors) as open circles. Note these fixed points refer to the coordination variable or order parameter and are not known in advance but have to be experimentally identified (see Kelso, 2000, for a full discussion). Here, fortuitously for the brain, fixed points of the coordination variable φ represent the phase and frequency relationship between oscillatory processes. The surface shown in Figure 2 defines three regions under the influence of the symmetry breaking term δω. In the first region, present in the lower part of the surface, the system is multistable: two stable attracting fixed points (filled circles) represent possible alternative states. Which one the system settles in depends on initial conditions and the size of the basin of attraction. In an intermediate region, following the line labeled 2 from left to right, the weakest attractor near antiphase (right side) disappears after it collides with its associated repellor somewhere near δω = 1.3, but the strongest attractor (left side) is still present as well as its repellor partner. Finally, in the third region, in the upper part of the surface, the dynamics become metastable. Following the line labeled 3 from left to right, no fixed points exist anymore: this part of the surface no longer intersects the isoplane $\stackrel{.}{\varphi }$ = 0 where the fixed points are located. Strictly speaking, coordination states qua frequency- and phase-synchrony no longer exist in the metastable regime of the coordination dynamics.

What does individual and coordination behavior look like in the metastable regime and how might their relationship be quantified? A unique flow now exists in which the dynamics may be characterized by places where the trajectory of the coordination variable relative phase converges and pauses around the horizontal and places where the trajectory drifts or diverges from the horizontal. Let us define the former as a dwell time and the latter as an escape time. In Figure 3c we show two locations for the dwell times: one that lingers a long time before escaping (e.g., Figure 3c, annotation 1), slightly above the more stable inphase pattern near 0 rad (modulo 2π), and the other that lingers only briefly (e.g., Figure 3c, annotation 2), slightly above π (modulo 2π). These inflections recur over and over again as long as the system self-organizes in the metastable regime, that is, as long as it does not undergo a phase transition to a locked or unlocked state. Despite the complete absence of phase-locked attractors, the coordinating elements in the metastable regime do not behave totally independently. Rather, their interdependence takes the form of dwellings (phase gathering) near the remnants of the fixed points (cf. Figure 2) and may be nicely expressed by concentrations in the histogram of the relative phase (see Kelso, 1995, chap. 4).

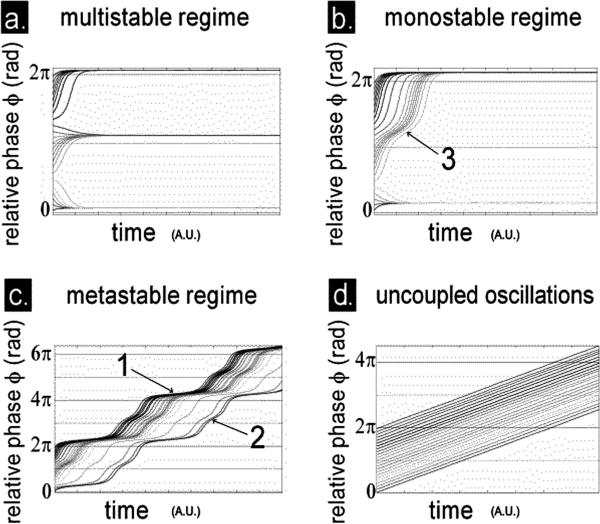
FIGURE 3.

How the key coordination variable or order parameter of the coordination law (Eq. 1) behaves over time. Shown is a family of trajectories of the relative phase φ over time (in arbitrary units, A.U.) arising from a range of initial conditions sampled between 0 and 2π radians, in the multistable (a), monostable (b), and metastable regimes (c) of Eq. 1. For the uncoupled case (d), the trajectories never converge, indicating that the oscillations are completely independent of each other. Trajectories in the multistable regime (a) converge either to an attractor located slightly above 0 rad. modulo 2π or to another attractor located slightly above π rad. modulo 2π. In the monostable regime (b), trajectories converge to an attractor located slightly above 0 rad. modulo 2π. In the trajectories of relative phase for the metastable regime (c, unwrapped to convey continuity), there is no longer any persisting convergence to the attractors but rather a succession of periods of rapid drift (escapes) interspersed with periods inflecting toward, but not remaining on, the horizontal (dwells). Note dwells near 0 rad. modulo 2π in the metastable regime (e.g., dwell at about 4π rad. annotated 1 in c) and nearby π rad. modulo 2π (dwell at about 3π rad. annotated 2 in c.) are reminiscent of the transient obtained for certain initial conditions in the monostable regime (b, annotation 3). The key point is that in the metastable regime the system's behavior is neither completely ordered (synchronized, cf. a, b) nor completely disordered (desynchronized, cf. d) but a subtle blend of both.

METRICS FOR METASTABILITY: A START

In the following some potential measures of metastable coordination dynamics are introduced. Notice that all the usual measures used previously in coordination dynamics to measure and quantify stability and loss of stability such as local and global relaxation times, switching times, fluctuations, and so on, no longer apply in the metastable regime (see Kelso, Schöner, Scholz, & Haken, 1987; Schöner & Kelso, 1988, for reviews of theory and experiments establishing the utility of these quantities). The reason of course is that in the metastable regime, all fixed point states have vanished leaving only traces of coordination, “ghosts” or “remnants” of where the fixed points once were. Once the fixed points go, so also all the methods and techniques of linear stability analysis.⁴ This means we have to be creative about finding new ways to capture metastable coordination.

Pure cases

A dwell time may be defined by how long a collective or coordinative tendency persists in a system or data set; an escape time is how long the coordinating elements express their individual autonomy in a system or data set.⁵ Consider first the pure cases. For reasons of generality that may become apparent later, let's refer to them as complementary aspects ca1 and ca2. An example of a pure case is illustrated in Figure 3d: there is no coupling and the oscillators are completely independent (ca1). Examples of another pure case are illustrated in Figures 3a and 3b. Whether in the mono- or bistable regimes, the oscillators are locked together, coupled in phase- and frequency-locked states (ca2), which constitute asymptotically stable states of the coordination dynamics. The metastable regime is in-between the two pure cases and is a blend of two tendencies: one for the elements to bind together and the other for the elements to behave independently. Such coexisting tendencies may be denoted as a complementary pair, ca1∼ca2. Notice that the transition from a metastable regime to a mono- or multistable regime constitutes the creation of functional information (Kelso, 1994a, 2002; Kelso & Engstrøm, 2006). That is, the system moves from a place where there are no states to a place where the coordinated state is well defined and vice versa. Notice also that in the metastable regime near the saddle-node bifurcation, information in the classical Shannonian sense (and presumably “information processing”) is at a maximum. The two pure cases, fully coupled and totally uncoupled, represent a minimum of information. They are what they are forever.

The k number

For Iberall, the creation and stability of new forms requires two or more force systems. The physical intuition is of a generalized Reynolds number. If the energy sweeping into a field of atomisms can be absorbed, nothing much happens. If it cannot, the field becomes unstable and some new inhomogeneous patterning emerges. The generalized Reynolds number is dimensionless and expresses a competition between a global, convective process and a local diffusive transport or propagative process. The resulting form or pattern is a collective, cooperative effect. Note again how the complementary pairs competition∼cooperation and local∼global come into play. Formally, the generalized Reynolds number (Re) can be written as follows:

$$Re=V\left(convection\right)∕V\left(diffusion\right),$$

with unity (Re_critical = 1) reflecting the critical value at which the transition to new forms occurs. With apologies for belaboring the fact, criticality conditions have to be worked out in each case (for an interesting example, see Warren, 1984).

Along the same lines of reasoning, a k number may be defined as follows:

$$k=dwelltime∕escapetime$$

The dimensionless k number appears to provide a measure of the quality of metastability. The mathematical expression is trivial:

Limit

$$e\to 0;k=d∕e\to \infty$$

In words, as the escape time (e) approaches zero, the dwell time (d) relative to (e) gets larger and larger. This means that there is a stronger and stronger tendency for the individual elements to bind together than to stay apart. Likewise,

Limit

$$e\to \infty ;k=d∕e\to 0$$

In words, as the escape time (e) gets larger and larger, the dwell time (d) relative to (e) gets smaller and smaller. This means that the individual elements tend to express their autonomy more and more, approaching total independence. In analogy to the generalized Reynolds number, a critical k number expresses when the tendency to coordinate overcomes the tendency to stay apart, and vice-versa. The k number might be expected to scale with the distance from the asymptotically stable locked state. But how? This will again depend on the details of the system. Were this process analogous to so-called Type-1 intermittency, the distribution of dwell times should scale as the distance^−1/2 from the critical surface where the parameterized function (Eq. 1) lifts off the origin. Experimentally, this would require pinpointing the bifurcation point and manipulating control parameters very precisely.⁶ More generally, comparing k numbers, the ratio of dwell and escape times, across a range of levels of observation of the same and different systems may even reveal scale-free properties (for examples, see Billock, DeGuzman, & Kelso, 2001; Chen, Ding, & Kelso, 1997, 2003b; Eguiluz, Chialvo, Cecchi, Baliki, & Apkarian, 2005; Van Orden et al., 2005).

METASTABLE COORDINATION DYNAMICS OF THE BRAIN

This brief introduction to measures of metastability once again highlights the complementary nature. Only together, as a complementary pair, do apparently contrasting phenomena, such as individual ∼ collective, integration ∼ segregation, local ∼ global, cooperation∼competition, attraction∼repulsion, convergence∼divergence, dwell∼escape, and so on, exhaust the knowledge necessary for understanding. We are reminded once again of Von Holst's (1939/1973) classic analysis of coordination: Both the “magnet effect” and the “maintenance tendency” are needed for a complete description of coordination in all its forms (see also Turvey & Schmidt, 1994). The metastable regime of the coordination law (Eq. 1) shows how this is so: both tendencies arise as the result of the dynamic interplay between nonlinear coupling and individual intrinsic dynamics.

How might the brain make use of metastability? For a fuller discussion of this question, including “The Freeman-Kelso Dialogue,” the reader is referred to Kelso & Tognoli (2007). As the Fingelkurtses (2004) remark, metastability is an entirely new conception of brain organization, not merely a blend of the old. Individualist tendencies for the diverse regions of the brain to express their independence coexist with coordinative tendencies to couple and cooperate as a whole. As we have seen, in the metastable brain local segregative and global integrative processes coexist as a complementary pair, not as conflicting theories. Metastability, by reducing the strong hierarchical coupling between the parts of a complex system while allowing them to retain their individuality, leads to a looser, more secure, more flexible form of functioning that promotes the creation of information. Too much autonomy of the component parts means no chance of their coordinating and communicating together. On the other hand, too much interdependence and the system gets stuck; global flexibility is lost.

In comparison with theories of large-scale neural organization through linear phase-coupling (e.g., Eckhorn et al., 1988; Gray, König, Engel, & Singer, 1989; Varela et al., 2001) the ability of metastable dynamics to coordinate or compute without attractors opens a large set of possibilities.⁷ The classical view of phase-locked coordination prescribes that each recruited element loses its intrinsic behavior and obeys the dictates of the assembly. When such situations arise, from the functional point of view, individual areas cease to exert an influence for the duration of the synchronized state, and the pertinent spatial level of description becomes the synchronous assembly itself. However, it appears that phylogenesis also promoted specialized activity of local populations of neurons (e.g., Chklovskii, Schikorski, & Stevens, 2002; Ebbesson, 1984). In theories of large-scale integration through phase synchronization, the expression of local activity can exist only when the area is not enslaved into an assembly, whereas in the metastable regime, the tendency for individual activity is continually preserved (see also Friston, 1997).

As exemplified explicitly in the elementary coordination law (Eq. 1), a delicate balance between integration (coordination between individual areas) and segregation (expression of individual behavior) is achieved in the metastable regime. Studies of interareal connectivity both at the anatomical and functional level (Friston, 1997; Tononi, Sporns, & Edelman, 1998) support the notion that the region between complete integration and complete segregation is the most favorable for cognition: measures of complexity reach a maximum when there is a balance between segregative and integrative forces. Note, however, that such measures are based upon stationarity assumptions whereas metastability in coordination dynamics is a “stationary transient.” Although the holding and releasing of the relative phase over time appears to be of a transient nature, it is actually quite stationary.

METASTABLE MIND

What are the implications of metastable coordination dynamics for understanding the mind? Like nature and nurture, the contents of the mind and the dynamics of the mind are inextricably connected. Thoughts are not static: like the flow of a river, they emerge and disappear as patterns in a constantly shifting dynamic system (Kelso, 1995). Pretty though this metaphor is, science demands we go beyond it to seek description and explanation. As in other, more mature fields it is crucial to have a theory or at least a conceptual framework of what one is trying to understand. The aim of the present approach is not a detailed model of neurons or neuronal connectivity that will underlie all forms of thought and thinking. Nor is this the forum to present a comprehensive account of the supporting neurophysiological and behavioral evidence. Rather, in the spirit of the person we honor here, the purpose is to stimulate insight into how mind, brain, and behavior might be connected in a unified way.

Figure 4 is intended to convey the gist of the story. On the left side of the middle panel, two areas of the brain (for the sake of simplicity) are shown to be active. This acknowledges a simple fact—or at least a dominant assumption in contemporary neuroscience: The contents of thoughts depend on the neural structures activated. Reciprocally, the neural structures activated influence—directly or indirectly—the contents of thoughts. If one is imagining producing a pattern of sensorimotor coordination, such as syncopating to a rhythmic stimulus, fMRI studies show that the same neural structures are active as would normally be engaged in the act of syncopation itself (Oullier, Jantzen, Steinberg, & Kelso, 2005). If one is expecting a reward as a result of an economic transaction, the so-called reward centers in the subcortical nuclei of the limbic system (e.g., nucleus accumbens, ventral tegmental area) and associated pathways are activated (e.g., Knutson, Adams, Fong, & Hommer, 2001). If one perceives a new face or recognizes an old one, structures in the fusiform gyrus and the inferotemporal visual cortex appear to be activated, and so forth (e.g., Haxby et al., 1996). Thoughts crop up from within, contemporaneous with the activation of neural structures associated with memory and emotion such as the hippocampus and amygdala, and they can be triggered from without by a familiar sound, touch, sight, or smell. Occasionally insightful thoughts arise too. Though much remains to be learned about what exactly constitutes the contents of thought—which are inherently context-dependent—thoughts appear to have neural correlates.⁸ However, identifying thought-specific structures and circuitry using brain mapping, important though it may be, is hardly sufficient to tell us how thinking works. Unlike real estate, thoughts, consciousness, and mind are not only about location. The overuse and abuse of the terminology of “states”—mental states, psychological states, physiological states, emotional states, and so on—muffles any sense of dynamics.

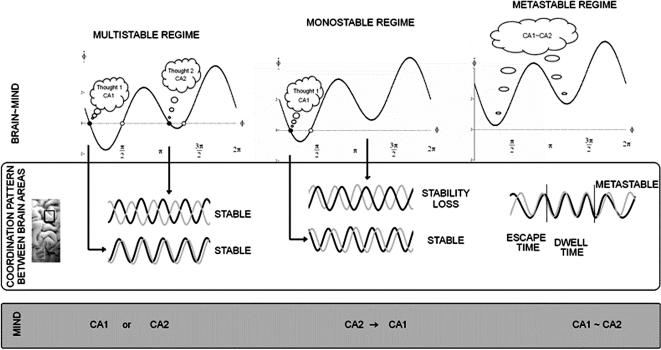
FIGURE 4.

Sketch of a dynamical law of thought and thinking (with homage to Boole, 1854/2005). Middle panel represents synaptically coupled brain oscillations from two brain areas (for the sake of simplicity) whose activation is meaningful and specific to the content of “thoughts.” Here “thought” is used in a generic sense; the states could refer to patterns of perceiving, emoting, remembering, deciding, acting, and so on. Top left panel shows the layout of the fixed points of the relative phase dynamics (Eq. 1) in the multi- (here bi-)stable regime. Solid circles are stable and attracting; open circles are unstable and repelling (see also Figure 2). Two states are stable, corresponding to particular phase relations between oscillatory groups of neurons, representing two stable “thought” patterns (ca1 and ca2) for exactly the same parameter values. Which one is realized depends on initial and boundary conditions. Many factors—developmental, social, cultural, learning, memory, and so on—may contribute to the process of stabilizing brain coordination states. Top middle panel shows that the formerly stable pattern near antiphase switches to near inphase as a result of changing circumstances. Any ambiguity due to bistability has been removed, a “decision” or “selection” has been made, and as a result, the system is monostable, stuck in one thought pattern. The switching mechanism is dynamic instability induced by changing control parameters (e.g., the coupling between the neural populations, which may be altered by neuromodulators). Fluctuations (not explicitly represented here) also play a key role in spontaneous switching. Top right panel shows that all states, both stable and unstable, have disappeared. This is the metastable régime. Now “thoughts” no longer correspond to fixed point, fully synchronized states of the coordination dynamics but rather to coexisting tendencies or dispositions that have characteristic dwell times. The lowest panel, called “Mind,” illustrates the classical dual nature of either/or, binary oppositions (ca1 or ca2), mind (and mind-set), switching (ca2 to ca1 and vice versa), and the mind and mind-set of the complementary nature, where both “thoughts” are held in the mind at the same time (ca1∼ca2). Even polarization∼reconciliation may be considered a complementary pair.

Active, dynamic processes like “perceiving,” “attending,” “remembering,” and “deciding” that are associated with the word thinking are not restricted to particular brain locations but rather emerge as patterns of interaction among widely distributed neural ensembles and in general between human beings and their worlds. One of the great riddles of contemporary neuroscience is how the multiple, diverse, and specialized areas of the brain are coordinated to give rise to thinking and coherent goal-directed behavior. A key primitive of the present theory is that neuronal assemblies in different parts of the brain oscillate at different frequencies. Such oscillatory activity is a prime example of self-organization in the brain. But oscillation, though necessary, is not sufficient. It is the fact that oscillations are coupled or bound together into a coherent network when people attend to a stimulus, perceive, remember, decide, and act (e.g., Başar, 2004; Bressler & Kelso, 2001; Buzsáki, 2006; Kelso, 1995; Singer, 2005; Varela et al., 2001, for reviews). This is a dynamic, self-assembling process, parts of the brain engaging and disengaging in time, as in a proverbial country square dance in rural Connecticut. In the simplest case shown in the left column of Figure 4, oscillations in different brain regions can lock “inphase,” brain activities rising and falling together, or “antiphase,” one oscillatory brain activity reaching its peak as another hits its trough and vice versa. Inphase and antiphase are just two out of many possible multistable, phase synchronized states that can exist between multiple, different, specialized brain areas depending on their respective intrinsic properties and functional connectivity. More broadly, as Iberall intuited, the organism and its environment are embedded in a nested frame of rhythms ranging from rest activity and sleep cycles to circadian and seasonal rhythms that both modify and are modified by behavior, development, and aging.

Coming back to the brain, different aspects of a moving scene, separate remembered parts of a significant experience, even different ideas that arise in a conversation may be bound together into coherent forms by synaptic coupling of (oscillatory) neural populations. The key proposal, conveyed in the top panel of Figure 4, is that thoughts (figuratively shown as balloons) are “coded” as relative phases between oscillating brain areas. Relative phase is a natural quantity for coordinating different things and is a long established order parameter in coordination dynamics.⁹ Phase is also the means by which excitatory and inhibitory neurons communicate with each other in so-called central pattern generators (e.g., Grillner, 1985). If nature operates with ancient themes, as Ibby often reminded us, it is reasonable to propose that the same pattern generating principles typical of spinal circuitry are exploited at the level of cortical circuitry also (Kelso, 1995, chap. 8; Ikegaya et al., 2004). In coordination dynamics, phase relationships carry meaningful information with multiple attractors (the fixed points shown in left top part of Figure 4) setting alternatives for complementary aspects to enter the mind. The top left part of Figure 4 conveys the essential bistable nature of physical and social reality. Two states are possible for identical parameter values: which state one enters depends on initial and boundary conditions. Baldly put, bistability is the basis of polarization and the either/or. Note that this does not necessarily imply any judgment of good or bad. Polarization, for example, may be seen as the driving tension behind scientific progress in the sense of Thomas Kuhn (1962), and bistability may be exploited for solving ill-defined problems where the consideration of multiple interpretations of data is an advantage. Bistable, and in general multistable coordination dynamics confers many advantages on living things, in particular multifunctionality (see, e.g., Kelso, 1991).

Why is it that some thoughts seem to persist longer than others? Coordination dynamics suggests that the persistence of a thought depends on the stability of the brain's relative phase dynamics. Some thoughts persist longer than others because the phase relations underlying them are more stable. In Figure 4 (top left), the negative slope through the ordinate near inphase (“thought 1”) is greater, hence more stable, than its antiphase counterpart (“thought 2”). This proposition is supported by experiments and specific neurally based modeling, which shows that different patterns of spatiotemporal brain activity are differentially stable (Jantzen & Kelso, 2007; Jirsa, Fuchs, & Kelso, 1998; Kelso et al., 1992; Meyer-Lindenberg, Ziemann, Hajak, Cohen, & Berman, 2002). For example, applying transient perturbations to Supplementary Motor Area (SMA) and lateral premotor cortex using Transcranial Magnetic stimulation induces transitions from antiphase to inphase coordination but not vice versa (Meyer-Lindenberg, et al., 2002). Even more tellingly, recent fMRI work shows that increases in BOLD amplitude in a network of brain areas that includes pre-SMA, premotor cortex, cerebellum, and insula increases linearly as pattern stability decreases (Jantzen & Kelso, 2007; Jantzen, Steinberg, & Kelso, under review).¹⁰ Such evidence suggests that disruption of a distributed network of brain areas—in contrast to a discrete switch in a particular locus—results in the destabilization and eventual dismantling of a less stable coordination pattern in favor of a more stable one.

So what makes thoughts switch? When it comes to the nervous system, it is always tempting to ask, as does Abbott (2006), “Where are the switches in this thing?” (see also Martin, 2006). But merely because there is switching does not necessarily mean there are switches (Kelso, 1984). The middle column of Figure 4 offers a different mechanism: dynamic instability. Multistability and spontaneous switching in perception as in the alternating vase or faces in ambiguous Rubin figures, Necker cubes, the continuous wagon wheel illusion, and so forth, continue to be a subject of much fascination in cognitive psychology and neuroscience (e.g., Billock & Tsou, 2007; Van Rullen et al., 2004; for review, see Kelso, 1995, chap. 7 and articles in Kruse & Stadler, 1995). The picture shown in Figure 4 (middle column) is based on considerable experimental evidence demonstrating that switching in both brain and behavior is a self-organized process that takes the form of a nonequilibrium phase transition (e.g., Daffertshofer, Peper, & Beek, 2000; Freeman & Holmes, 2005; Fuchs, Deecke, & Kelso, 2000; Fuchs, Kelso, & Haken, 1992; Fuchs, Mayville, et al., 2000; Kelso, 1984; Kelso et al., 1990; Kelso, Scholz, & Schöner, 1986; Kelso et al., 1992; Mayville, Bressler, Fuchs, & Kelso, 1999; Wallenstein, Kelso, & Bressler, 1995). Fluctuations play a key role, testing the stability of states and enabling the system to discover new states. In coordination dynamics, once the system settles into an attractor, a certain amount of noise or a perturbation is required to switch it to another attractor. Or, if internal or external conditions change when the system is near instability, a bifurcation or phase transition may occur, causing the system to switch from being multistable to monostable or vice versa (see Ditzinger & Haken, 1989, 1990, for excellent examples of such modeling). Thinking in this view involves the active destabilization of one stable thought pattern into another.

A different view emerges from the flow of the relative phase dynamics in the metastable regime (Figure 4, right). Instead of thoughts corresponding to rigid, phase synchronized states that must be destabilized if switching is to occur, metastability consists of a more subtle dwell and escape dynamic in which a thought is never quite stable and merely expresses a joint tendency for neural areas to synchronize together and to oscillate independently. Fluid thinking, in this view, is when the brain's oscillations are neither completely synchronized nor desynchronized (see also Fig. 3c). In the metastable regime, successive visits to the remnants of the fixed points are intrinsic to the time course of the system and do not require any external source of input. Switching occurs, of course, but continuously and without the need for additive noise or changes in parameters. From the perspective of coordination dynamics, the time the system dwells in each remnant depends on a subtle blend of the asymmetry of the rhythmic elements (longer dwelling for smaller asymmetry) and the strength of the coupling (longer dwelling for larger values of a and b in Eq. 1).

The metastable regime offers scientific grounds for Iberall's intuition of “reverie”: thoughts come and go fluidly as the oscillatory units of the brain express both an interactive integrative dynamic and an individualistic segregative dynamic. Metastable coordination dynamics also rationalizes William James's (1890) beautiful metaphor of the stream of consciousness as the flight of a bird whose life journey consists of “perchings” (viewed here as phase gathering, integrative tendencies) and “flights” (phase scattering, segregative tendencies). Both tendencies appear to be crucial: the former to summon and create thoughts, the latter to release individual brain areas to participate in other acts of cognition, emotion, and action.

In some traditions, it is not the contents of thoughts that matter but their “stickiness.” In the metastable regime of the coordination dynamics, the “stickiness” of thoughts depends on how close the neural system is to the fixed points of the relative phase dynamics. Sticky thoughts have long dwell times and a high probability density of near perfect phase synchrony between the brain's oscillations. Passing thoughts, as the name suggests, have short dwell times and low probability density. Stickiness means that the coupling interaction between neural populations is stronger than the tendency of these populations to express their individual autonomy and/or to disengage from one neural coalition to participate in others. Very sticky thoughts correspond to phase trapping between the brain's oscillations and may be pathological. Well-known manifestations of too much synchronization in the brain are diseases like Parkinson's disease and epilepsy. On the other hand, it appears that certain diseases such as schizophrenia appear to be characterized by a reduction in oscillatory brain activity and a relative absence of long range phase synchrony (Uhlhaas & Singer, 2006). Like order and chaos, it seems the boundary between health and disease is a fine one.

A few further remarks may be in order. One, hinted at earlier, is that environmental, intentional, attentional, emotional, learning, and memory processes are all capable of both stabilizing and destabilizing the coordination dynamics. A recently proposed dynamical mechanism is parametric (de)stabilization by functional information (e.g., Fink et al., 2000; Jirsa et al., 2000; Kelso et al., 2001; see also Kay & Warren, 2001). The neural mechanisms of parametric stabilization by intention are beginning to be uncovered (Jantzen, Bertollo, deLuca, Comani, & Kelso, 2007; Kelso, Scholz, & Schöner, 1988; Scholz & Kelso, 1990). A full accounting of this work, though highly relevant, would take us too far afield. We remark that to the extent these influences may be said to control the mind, this is the mind controlling itself.

Second, certain views on meditation view the mind (pardon the pun)—with its beliefs, biases, and prejudices based on past experience and memory—as an obstacle to being truly aware, to seeing what is. Awareness is where the mind stops wandering and thinking is the pause between two thoughts, where the brain is not trapped in a coherent state. Here we may say that for thought not to interfere, there should be no “binding” among brain areas; all the parts of the brain should be in a default state poised, as it were, to respond to any input. Metastabilty resolves, nay embraces, any paradox between “content full” thought and “content less” awareness: the flow of the dynamics allows both.

Third, notice in Figure 4 and throughout this discussion that the linkage between events at different levels, from neural to psychological and experiential, is by virtue of shared pattern or coordination dynamics, not because any single level is any more or less fundamental than any other. Thus, psychological terms like “stickiness” or “unhooking” or “trapping” or even “task difficulty” have explicit meaning in terms of meta- and multistable coordination dynamics. This amounts to transcendence if not translation.

ENDING

Thought is matter and thinking is matter in motion—coordinated motion. Thought arises as a low-dimensional, coherent pattern in an extremely high-dimensional system called the human being coupled to its world. The slightest fluctuation can trigger a thought. Context matters. The coordination dynamics of thinking is essentially nonlinear and contains multistability and switching—which may be debilitating when it leads to polarization. Coordination dynamics differs from other theories of self-organization, including Iberall's homeokinetics, because it deals primarily in the currency of functional information: the two “forces” that drive coordination dynamics deal fundamentally with meaningful information exchange in living things. One force is the strength of coupling between the elements; this allows information to be distributed to all participating elements and is a key to integrative, collective action. The other is the ability of individual elements to express their autonomy and thereby minimize the influence of others. Self-organization in the metastable regime is the interplay of both. This is the architecture of mind—metastable mind.