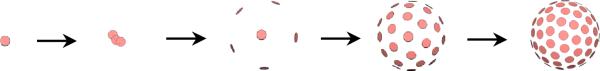Shape Modeling and Analysis with Entropy-Based Particle Systems

Abstract

This paper presents a new method for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on any specific surface parameterization. The method requires very little preprocessing or parameter tuning, and is applicable to a wider range of problems than existing methods, including nonmanifold surfaces and objects of arbitrary topology. The proposed method is to construct a point-based sampling of the shape ensemble that simultaneously maximizes both the geometric accuracy and the statistical simplicity of the model. Surface point samples, which also define the shape-to-shape correspondences, are modeled as sets of dynamic particles that are constrained to lie on a set of implicit surfaces. Sample positions are optimized by gradient descent on an energy function that balances the negative entropy of the distribution on each shape with the positive entropy of the ensemble of shapes. We also extend the method with a curvature-adaptive sampling strategy in order to better approximate the geometry of the objects. This paper presents the formulation; several synthetic examples in two and three dimensions; and an application to the statistical shape analysis of the caudate and hippocampus brain structures from two clinical studies.

1 Introduction

Statistical analysis of sets of similar shapes requires quantification of shape differences, which is a fundamentally difficult problem. One widely used strategy for computing shape differences is to compare the positions of corresponding points among sets of shapes, often with the goal of producing a statistical model of the set that describes a mean and modes of variation. Medical or biological shapes, however, are typically derived from the interfaces between organs or tissue types, and usually defined implicitly in the form of segmented volumes, rather than explicit parameterizations or surface point samples. Thus, no a priori relationship is defined between points across surfaces, and correspondences must be inferred from the shapes themselves, which is a difficult and ill-posed problem.

Until recently, correspondences for shape statistics were established manually by choosing small sets of anatomically significant landmarks on organs or regions of interest, which would then serve as the basis for shape analysis. The demand for more detailed analyses on ever larger populations of subjects has rendered this approach unsatisfactory. Brechbühler, et al. pioneered the use of spherical parameterizations for shape analysis that can be used to implicitly establish relatively dense sets of correspondences over an ensemble of shape surfaces [1]. Their methods, however, are purely geometric and seek only consistently regular parameterizations, not optimal correspondences. Davies et al. [2] present methods for optimizing correspondences among point sets that are based on the information content of the set, but these methods still rely on mappings between fixed spherical surface parameterizations. Most shapes in medicine or biology are not derived parametrically, so the reliance on a parameterization presents some significant drawbacks. Automatic selection of correspondences for nonparametric, point-based shape models has been explored in the context of surface registration [3], but because such methods are typically limited to pairwise correspondences and assume a fixed set of surface point samples, they are not sufficient for the analysis of sets of segmented volumes.

This paper presents a new method for extracting dense sets of correspondences that also optimally describes ensembles of similar shapes. The proposed method is nonparametric, and borrows technology from the computer graphics literature by representing surfaces as discrete point sets. The method iteratively distributes sets of dynamic particles across an ensemble of surfaces so that their positions optimize the information content of the system. This strategy is motivated by a recognition of the inherent tradeoff between geometric accuracy (a good sampling) and statistical simplicity (a compact model). Our assertion is that units of information associated with the model implied by the correspondence positions should be balanced against units of information associated with the individual surface samplings. This approach provides a natural equivalence of information content and reduces the dependency on ad-hoc regularization strategies and free parameters. Since the points are not tied to a specific parameterization, the method operates directly on volumetric data, extends easily to higher dimensions or arbitrary shapes, and provides a more homogeneous geometric sampling as well as more compact statistical representations. The method draws a clear distinction between the objective function and the minimization process, and thus can more readily incorporate additional information such as high-order geometric information for adaptive sampling.

2 Related Work

The strategy of finding of parameterizations that minimize information content across an ensemble was first proposed by Kotcheff and Taylor [4], who represent each two-dimensional contour as a set of N samples taken at equal intervals from a parameterization. Each shape is treated as a point in a 2N-dimensional space, with associated covariance Σ and cost function, ${\sum }_k\log ({\lambda }_k+\alpha )$, where λ_k are the eigenvalues of Σ , and α is a regularization parameter that prevents the thinnest modes (smallest eigenvalues) very from dominating the process. This is the same as minimizing log |Σ + αI|, where I is the identity matrix, and |·| denotes the matrix determinant.

Davies et al. [2] propose a cost function for 2D shapes based on minimum description length (MDL). They use quantization arguments to limit the effects of thin modes and to determine the optimal number of components that should influence the process. They propose a piecewise linear reparameterization and a hierarchical minimization scheme. In [5] they describe a 3D extension to the MDL method, which relies on spherical parameterizations and subdivisions of an octahedral base shape, with smoothed updates that are represented as Cauchy kernels. The parameterization must be obtained through another process such as [1], which relaxes a spherical parameterization onto an input mesh. The overall procedure requires significant data preprocessing, including a sequence of optimizations—first to establish the parameterization and then on the correspondences—each of which entails a set of free parameters or inputs in addition to the segmented volumes. A significant concern with the basic MDL formulation is that the optimal solution is often one in which the correspondences all collapse to points where all the shapes in the ensemble happen to be near (e.g., crossings of many shapes). Several solutions have been proposed [5, 6], but they entail additional free parameters and assumptions about the quality of the initial parameterizations.

The MDL formulation is mathematically related to the min-log noted |Σ + αI| approach, as noted by Thodberg[6]. Styner et al. [7] describe an empirical study that shows ensemble-based statistics improve correspondences relative to pure geometric regularization, and that MDL performance is virtually the same as that of min-log |Σ + αI|. This last observation is consistent with the well-known result from information theory: MDL is, in general, equivalent to minimum entropy [8].

Another body of relevant work is the recent trend in computer graphics towards representing surfaces as scattered collections of points. The advantage of so-called point-set surfaces is that they do not require a specific parameterization and do not impose topological limations; surfaces can be locally reconstructed or subdivided as needed [9]. A related technology in the graphics literature is the work on particle systems, which can be used to manipulate or sample [10] implicit surfaces. A particle system manipulates large sets of particles constrained to a surface using a gradient descent on radial energies that typically fall off with distance. The proposed method uses a set of interacting particle systems, one for each shape in the ensemble, to produce optimal sets of surface correspondences.

3 Methods

3.1 Entropy-Based Surface Sampling

We treat a surface as a subset of ${\Re }^d$, where d = 2 or d = 3 depending whether we are processing curves in the plane or surfaces in a volume, respectively. The method we describe here deals with smooth, closed manifolds of codimension one, and we will refer to such manifolds as surfaces. We will discuss the extension to nonmanifold curves and surfaces in Section 5. We sample a surface $\mathcal{S}\subset {\Re }^d$ using a discrete set of N points that are considered random variables Z = (X₁, X₂, . . . , X_N) drawn from a probability density function (PDF), p(X). We denote a realization of this PDF with lower case, and thus we have z = (x₁, , x₂, . . . , x_N), where z ∈ S^N. The probability of a realization x is p(X = x), which we denote simply as p(x).

The amount of information contained in such a random sampling is, in the limit, the differential entropy of the PDF, which is H[X] = –∫_S p(x) log p(x)dx = –E{log p(X)}, where E{·} is the expectation. When we have a sufficient number of points sampled from p, we can approximate the expectation by the sample mean [8], which gives $H\left[X\right]\approx -(1∕N){\sum }_i\log p\left(x_i\right)$. We must also estimate p(x_i). Density functions on surfaces can be quite complex, and so we use a nonparametric, Parzen windowing estimation of this density using the particles themselves. Thus we have

$$p\left(x_i\right)\approx \frac{1}{N(N-1)}\sum _{j=1,j\ne i}^{N}G(x_i-x_j,{\sigma }_i)$$ (1)

where G(x_i – x_j, σ_i) is a d-dimensional, isotropic Gaussian with standard deviation σ_i. The cost function C, is therefore an approximation of (negative) entropy: $-H\left[X\right]\approx C(x_1,\dots ,x_N)={\sum }_i\log \frac{1}{N(N-1)}{\sum }_{j\ne i}G(x_i-x_j,{\sigma }_i)$,

In this paper, we use a gradient-descent optimization strategy to manipulate particle positions. The optimization problem is given by:

$$\widehat{z}=\arg \underset{z}{\min }E\left(z\right)\mathrm{s}.\mathrm{t}.x_1,\dots ,x_N\in \mathcal{S}.$$ (2)

The negated gradient of C is

$$-\frac{\partial C}{\partial x_i}=\frac{1}{{\sigma }_i^2}\frac{\sum _{j\ne i}^N(x_i-x_j)G(x_i-x_j,{\sigma }_i)}{\sum _{j\ne i}^{N}G(x_i-x_j,{\sigma }_i)}={\sigma }_i^{-2}\sum _{j\ne i}^N(x_i-x_j)w_{ij},$$ (3)

where ${\sum }_j{w}_{ij}=1$. Thus to minimize C, the surface points (which we will call particles) must move away from each other, and we have a set of particles moving under a repulsive force and constrained to lie on the surface. The motion of each particle is away from all of the other particles, but the forces are weighted by a Gaussian function of inter-particle distance. Interactions are therefore local for sufficiently small σ. We use a Jacobi update with forward differences, and thus each particle moves with a time parameter and positional update $x_i\leftarrow x_i-\gamma \frac{\partial C}{\partial x_i}$ where γ is a time step and γ < σ² for stability.

The preceding minimization produces a uniform sampling of a surface. For some applications, a strategy that samples adaptively in response to higher order shape information is more effective. From a numerical point of view, the minimization strategy relies on a degree of regularity in the tangent planes between adjacent particles, which argues for sampling more densely in high curvature regions. High-curvature features are also considered more interesting than flat regions as important landmarks for biological shapes. To this end, we extend the above uniform sampling method to adaptively oversample high-curvature regions by modifying the Parzen windowing in Eqn. 1 as follows

$$\tilde{p}\left(x_i\right)\approx \frac{1}{N(N-1)}\sum _{j=1,j\ne i}^{N}G\left(\frac{1}{k_j}(x_i-x_j),{\sigma }_i\right)$$ (4)

where k_j is a scaling term proportional to the curvature magnitude computed at each neighbor particle j. The effect of this scaling is to warp space in response to local curvature. A uniform sampling based on maximum entropy in the warped space translates into an adaptive sampling in unwarped space, where points pack more densely in higher curvature regions. The extension of Eqn 3 to incorporate the curvature-adaptive Parzen windowing is straightforward to compute since k_j is not a function of x_i, and is omitted here for brevity.

There are many possible choices for the scaling term k. Meyer, et al. [11] describe an adaptive surface sampling that uses the scaling $k_i=\frac{1+\rho {\kappa }_i\left(\frac{s}{2\pi }\right)}{\frac{1}{2}s\cos (\pi ∕6)}$ where κ_i is the root sum-of-squares of the principal curvatures at surface location x_i. The user-defined variables s and ρ specify the ideal distance between particles on a planar surface, and the ideal density of particles per unit angle on a curved surface, respectively. Note that the scaling term in this formulation could easily be modified to include surface properties other than curvature.

The surface constraint in both the uniform and adaptive optimizations is specified by the zero set of a scalar function F(x). This constraint is maintained, as described in several papers [10], by projecting the gradient of the cost function onto the tangent plane of the surface (as prescribed by the method of Lagrange multipliers), followed by iterative reprojection of the particle onto the nearest root of F by the method of Newton-Raphson. Principal curvatures are computed analytically from the implicit function as described in [12]. Another aspect of this particle formulation is that it computes Euclidean distance between particles, rather than the geodesic distance on the surface. Thus, we assume sufficiently dense samples so that nearby particles lie in the tangent planes of the zero sets of F. This is an important consideration; in cases where this assumption is not valid, such as highly convoluted surfaces, the distribution of particles may be a ected by neighbors that are outside of the true manifold neighborhood. Limiting the influence of neighbors whose normals differ by some threshold value (e.g. 90 degrees) does limit these effects. The question of particle interactions with more general distance measures remains for future work.

Finally, we must choose a σ for each particle, which we do automatically, before the positional update, using the same optimality criterion described above. The contribution to C of the ith particle is simply the probability of that particle position, and optimizing that quantity with respect to σ gives a maximum likelihood estimate of σ for the current particle configuration. We use Newton-Raphson to find σ such that ∂p(x_i, σ)/∂σ = 0, which typically converges to machine precision in several iterations. For the adaptive sampling case, we find σ such that ∂p̃(x_i, σ)/∂σ = 0, so that the optimal σ is scaled locally based on the curvature.

There are a few important numerical considerations. We must truncate the Gaussian kernels, and so we use G(x, σ) = 0 for |x| > 3σ. This means that each particle has a finite radius of influence, and we can use a spatial binning structure to reduce the computational burden associated with particle interactions. If σ for a particle is too small, a particle will not interact with its neighbors at all, and we cannot compute updates of σ or position. In this case, we update the kernel size using σ ← 2 × σ, until σ is large enough for the particle to interact with its neighbors. Another numerical consideration is that the system must include bounds σ_min and σ_max to account for anomalies such as bad initial conditions, too few particles, etc. These are not critical parameters. As long as they are set to include the minimum and maximum resolutions, the system operates reliably.

The mechanism described in this section is, therefore, a self tuning system of particles that distribute themselves using repulsive forces to achieve optimal distributions, and may optionally adjust their sampling frequency locally in response to surface curvature. For this paper we initialize the system with a single particle that finds the nearest zero of F, then splits (producing a new, nearby particle) at regular intervals until a specific number of particles are produced and reach a steady state. Figure 1 shows this process on a sphere.

Fig. 1.

A system of 100 particles on a sphere, produced by particle splitting.

3.2 The Entropy of The Ensemble

An ensemble $\mathcal{E}$ is a collection of M surfaces, each with their own set of particles, i.e. $\mathcal{E}=z^1,\dots ,z^M$. The ordering of the particles on each shape implies a correspondence among shapes, and thus we have a matrix of particle positions $P=x_j^k$, with particle positions along the rows and shapes across the columns. We model $z^k\in {\Re }^{Nd}$ as an instance of a random variable Z, and propose to minimize the combined ensemble and shape cost function

$$Q=H\left(Z\right)-\sum _{k}H\left(P^k\right),$$ (5)

which favors a compact ensemble representation balanced against a uniform distribution of particles on each surface. The different entropies are commensurate so there is no need for ad-hoc weighting of the two function terms.

For this discussion we assume that the complexity of each shape is greater than the number of examples, and so we would normally choose N > M. Given the low number of examples relative to the dimensionality of the space, we must impose some conditions in order to perform the density estimation. For this work we assume a normal distribution and model p(Z) parametrically using a Gaussian with covariance Σ. The entropy is then given by

$$H\left(Z\right)\approx \frac{1}{2}\log \mid \Sigma \mid =\frac{1}{2}\sum _{j=1}^{Nd}\log {\lambda }_j,$$ (6)

where λ₁, ..., λ_Nd are the eigenvalues of Σ.

In practice, Σ will not have full rank, in which case the entropy is not finite. We must therefore regularize the problem with the addition of a diagonal matrix αI to introduce a lower bound on the eigenvalues. We estimate the covariance from the data, letting Y denote the matrix of points minus the sample mean for the ensemble, which gives Σ = (1/(M – 1))YY^T. Because N > M, we perform the computations on the dual space (dimension M), knowing that the determinant is the same up to a constant factor of α. Thus, we have the cost function G associated with the ensemble entropy:

$$\log \mid \Sigma \mid \approx G\left(P\right)=\log \mid \frac{1}{M-1}{Y}^{T}Y,\mid \text{and}-\frac{\partial G}{\partial P}=Y{(Y^{T}Y+\alpha I)}^{-1}.$$ (7)

We now see that α is a regularization on the inverse of Y^TY to account for the possibility of a diminishing determinant. The negative gradient –∂G/∂P gives a vector of updates for the entire system, which is recomputed once per system update. This term is added to the shape-based updates described in the previous section to give the update of each particle:

$$x_j^k\leftarrow \gamma \left[-\partial G∕\partial x_j^k+\partial E^k∕\partial x_j^k\right].$$ (8)

The stability of this update places an additional restriction on the time steps, requiring γ to be less than the reciprocal of the maximum eigenvalue of (Y^TY + αI)^–1, which is bounded by α. Thus, we have γ < α, and note that α has the practical effect of preventing the system from slowing too much as it tries to reduce the thinnest dimensions of the ensemble distribution. This also suggests an annealing approach for computational efficiency (which we have used in this paper) in which α starts off somewhat large (e.g., the size of the shapes) and is incrementally reduced as the system iterates.

The choice of a Gaussian model for p(Z = z) is not critical for the proposed method. The framework easily incorporates either nonparametric, or alternate parametric models. In this case, the Gaussian model allows us to make direct comparisons with the MDL method, which contains the same assumptions. Research into alternative models for Z is outside the scope of this paper and remains of interest for future work.

3.3 A Shape Modeling Pipeline

The particle method outlined in the preceding sections may be applied directly to binary segmentation volumes, which are often the output of a manual or automated segmentation process. A binary segmentation contains an implicit shape surface at the interface of the labeled pixels and the background. Any suitably accurate distance transform from that interface may be used to form the implicit surface necessary for the particle optimization. Typically, we use a fast-marching algorithm [13], followed by a slight Gaussian blurring to remove the high-frequency artifacts that can occur as a result of numerical approximations.

A collection of shape segmentations must often be aligned in a common coordinate frame for modeling and analysis. We first align the segmentations with respect to their centers of mass and the orientation of their first principal eigenvectors. Then, during the optimization, we further align shapes with respect to rotation and translation using a Procrustes algorithm [14], applied at regular intervals after particle updates. Because the proposed method is completely generalizable to higher dimensions, we are able to process shapes in 2D and 3D using the same C++ software implementation, which is templated by dimension. For all the experiments described in this paper, the numerical parameter σ_min is set to machine precision and σ_max is set to the size of the domain. For the annealing parameter α, we use a starting value roughly equal to the diameter of an average shape and reduce it to machine precision over several hundred iterations. Particles are initialized on each shape using the splitting procedure described in Section 3.1, but are distributed under the full correspondence optimization to keep corresponding points in alignment. We have found these default settings to produce reliably good results that are very robust to the initialization. Processing time on a 2GHz desktop machine scales linearly with the number of particles in the system and ranges from 20 minutes for a 2D system of a few thousand particles to several hours for a 3D system of tens of thousands of particles.

4 Results

This section details several experiments designed to validate the proposed method. First, we compare models generated using the particle method with models generated using MDL for two synthetic 2D datasets. Next, a simple experiment on tori illustrates the applicability of the method to nonspherical topologies. Finally, we apply the method to a full statistical shape analysis of several 3D neuroanatomical structures from published clinical datasets.

We begin with two experiments on closed curves in a 2D plane and a comparison with the 2D open-source Matlab MDL implementation given by Thodberg [6]. In the first experiment, we used the proposed, particle method to optimize 100 particles per shape under uniform sampling on 24 box-bump shapes, similar to those described in [6]. Each shape was constructed as a fast-marching distance transform from a set of boundary points using cubic b-splines with the same rectangle of control, but with a bump added at a random location along the top of its curve. This example is interesting because we would, in principle, expect a correspondence algorithm that is minimizing information content to discover this single mode of variability in the ensemble.

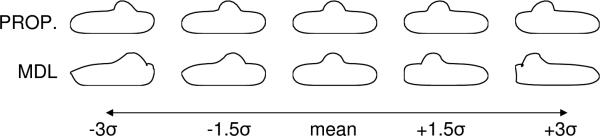
MDL correspondences were computed using 128 nodes and mode 2 of the Matlab software, with all other parameters set to their defaults (see [6] for details). Principal component analysis identified a single dominant mode of variation for each method, but with different degrees of leakage into orthogonal modes. MDL lost 0.34% of the total variation from the single mode, while the proposed method lost only 0.0015%. Figure 2 illustrates the mean and three standard deviations of the first mode of the two different models. Shapes from the particle method remain more faithful to those described by the original training set, even out to three standard deviations where the MDL description breaks down. A striking observation from this experiment is how the relatively small amount of variation left in the minor modes of the MDL case produce such a significant effect on the results of shape deformations along the major mode.

Fig. 2.

The box-bump experiment.

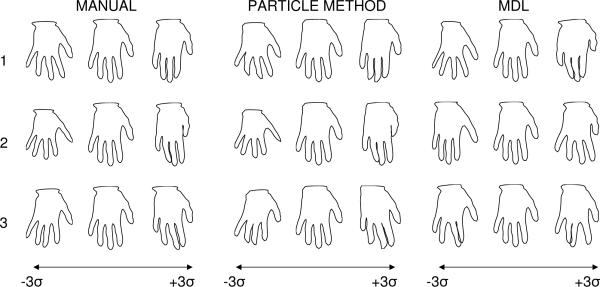
The second experiment was conducted on the set of 18 hand shape contours described in [2], again applying both the particle method and MDL using the same parameters as described above. Distance transforms from from spline-based contour models again form the inputs. In this case, we also compared results with a set of ideal, manually selected correspondences, which introduce anatomical knowledge of the digits. Figure 3 compares the three resulting models in the top three modes of variation to ±3 standard deviations. A detailed analysis of the principal components showed that the proposed particle method and the manually selected points both produce very similar models, while MDL differed significantly, particularly in first three modes.

Fig. 3.

The mean and ±3 std. deviations of the top 3 modes of the hand models.

Non-spherical Topologies

Existing 3D MDL implementations rely on spherical parameterizations, and are therefore only capable of analyzing shapes topologically equivalent to a sphere. The particle-based method does not have this limitation. As a demonstration of this, we applied the proposed method to a set of 25 randomly chosen tori, drawn from a 2D, normal distribution parameterized by the small radius r and the large radius R. Tori were chosen from a distribution with mean r = 1, R = 2 and σ_r = 0.15, σ_R = 0.30, with a rejection policy that excluded invalid tori (e.g., r > R). We optimized the correspondences using a uniform sampling and 250 particles on each shape. An analysis of the resulting model showed that the particle system method discovered the two pure modes of variation, with only 0.08% leakage into smaller modes.

Shape Analysis of Neuroanatomical Structures

As a further validation of the particle method, we performed hypothesis testing of group shape differences on data from two published clinical studies. The first study addresses the shape of the hippocampus in patients with schizophrenia. The data consists of left and right hippocampus shapes from 56 male adult patients versus 26 healthy adult male controls, segmented from MRI using a template-based semiautomated method [15]. The second study addresses the shape of the caudate in males with schizo-typal personality disorder. The data consists of left and right caudate shapes from 15 patients and 14 matched, healthy controls, and was manually segmented from MRI brain scans of the study subjects by clinical experts [16]. All data in these studies is normalized with respect to intercranial volume.

For each study, we aligned and processed the raw binary segmentations as described in Section 3.3, including Procrustes registration. Models were optimized with 1024 correspondence points per shape and the curvature-adaptive sampling strategy, which proved more effective than uniform sampling. Separate models were created for left and right structures using the combined data from patient and normal populations. Models were generated without knowledge of the shape classifications so as not to bias the correspondences to one class or the other. On inspection, all of the resulting models appear to be of good quality; each major mode of variation describes some plausible pattern of variation observed in the training data. As an example, Figure 4 shows several surface meshes of shapes generated from the pointsets of the right hippocampus model.

Fig. 4.

Surface meshes of the mean and two modes of variation at ±3 standard deviations of the right hippocampus model.

After computing the models, we applied statistical tests for group differences at every surface point location. The method used is a nonparametric permutation test of the Hotelling T² metric with false-discovery-rate (FDR) correction, and is described in [17]. We used the open-source implementation of the algorithm [17], with 20,000 permutations among groups and an FDR bound set to 5%. The null hypothesis for these tests is that the distributions of the locations of corresponding sample points are the same regardless of group.

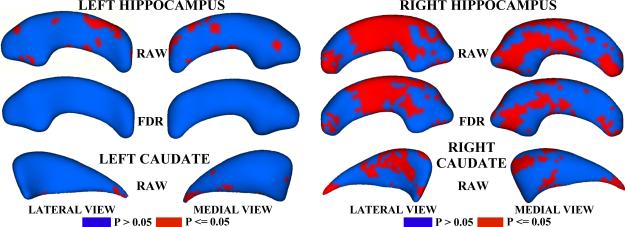
Figure 5 shows the raw and FDR-corrected p-values for the left and right hippocampi from the schizophrenia study. Areas of significant group differences (p <= 0.05) are shown in red. Areas with insignificant group differences (p > 0.05) are shown in blue. The right hippocampus shows significant differences in the mid-region and the tail, even after FDR-correction. The left hippocampus appears to exhibit few group differences, with none detected after FDR correction. Differences in the tail, especially on the right side were also observed by Styner, et al. in [7]. Our results also correlate with those reported for the spherical harmonics method (SPHARM) [15] and spherical wavelet analysis [18].

Fig. 5.

P-value maps for the hippocampus and caudate shape analyses, shown on the mean shape. Red indicates significant group differences (p <= .05)

Raw p-values for the caudate analysis are shown at the bottom of Fig 5. No significant differences on either shape were found after FDR correction. The raw p-values, however, suggest that both structures may exhibit group differences in the tail, and that the right caudate contains more group differences than the left, an observation that agrees with results given in [17], [16], [15], and [18]. The current formulation of the particle method optimizes point correspondences under the assumption of a Gaussian model with a single mean, and may introduce a conservative bias that reduces group differences. We are investigating methods, such as nonparametric density estimation, for addressing this issue.

5 Conclusions

We have presented a new method for constructing statistical representations of ensembles of similar shapes that relies on an optimal distribution of a large set of surface point correspondences, rather than the manipulation of a specific surface parameterization. The proposed method produces results that compare favorably with the state of the art, and statistical analysis of several clinical datasets shows the particle-based method yields results consistent with those seen in the literature. The method works directly on volumes, requires very little parameter tuning, and generalizes easily to accommodate alternate sampling strategies such as curvature adaptivity. The method can extend to other kinds of geometric objects by modeling those objects as intersections of various constraints. For instance, the nonmanifold boundaries that result from interfaces of three or more tissue types can be represented through combinations of distance functions to the individual tissue types. Curves can be represented as the intersection of the zero sets of two scalar fields or where three different scalar fields achieve equality (such as the curves where three materials meet). The application of these extensions to joint modeling of multiple connected objects is currently under investigation.