Using the Whole Cohort in the Analysis of Case-Cohort Data

Abstract

Case-cohort data analyses often ignore valuable information on cohort members not sampled as cases or controls. The Atherosclerosis Risk in Communities (ARIC) study investigators, for example, typically report data for just the 10%–15% of subjects sampled for substudies of their cohort of 15,972 participants. Remaining subjects contribute to stratified sampling weights only. Analysis methods implemented in the freely available R statistical system (http://cran.r-project.org/) make better use of the data through adjustment of the sampling weights via calibration or estimation. By reanalyzing data from an ARIC study of coronary heart disease and simulations based on data from the National Wilms Tumor Study, the authors demonstrate that such adjustment can dramatically improve the precision of hazard ratios estimated for baseline covariates known for all subjects. Adjustment can also improve precision for partially missing covariates, those known for substudy participants only, when their values may be imputed with reasonable accuracy for the remaining cohort members. Links are provided to software, data sets, and tutorials showing in detail the steps needed to carry out the adjusted analyses. Epidemiologists are encouraged to consider use of these methods to enhance the accuracy of results reported from case-cohort analyses.

BACKGROUND AND MOTIVATION

One of the principal justifications for large cohort studies is the ability to conduct substudies on selected participants so that expensive covariates need not be ascertained for everyone. The nested case-control study (1), in which individually matched controls are sampled from case risk sets, is the oldest and most widely used design for collection of additional covariates to estimate hazard rates and ratios in the context of Cox regression (2). The case-cohort design (3–5), in which controls are sampled without regard to failure times as part of a “subcohort” (cohort random sample), has become more popular as its advantages have become better known. For example, the single subcohort may be used to estimate population frequencies of covariates (e.g., genotypes), to select controls for multiple failure time outcomes (e.g., diagnoses of diabetes and heart disease), and to conduct analyses by using multiple time scales (e.g., time-on-study and attained age). Sometimes, the nested case-control design is infeasible because the vital status of cohort members needed for risk set construction is unknown prior to their selection into a potential subcohort (6).

Published analyses of case-cohort studies routinely fail to utilize all available data. The original analysis method (5) does not accommodate case sampling or stratified sampling of controls and makes inefficient use of cases not in the subcohort. Hence, most analyses today utilize the “robust” approach of Barlow et al. (7, 8). This approach involves Cox regression, with case and control observations weighted by their inverse sampling probabilities (9). A major drawback to both approaches is that they ignore information on cohort members not sampled as cases or controls. Survey statisticians (10) and biostatisticians (11) have each proposed methods for recovery of this information by adjusting the sampling weights. These methods are now implemented in the freely available R statistical system (http://cran.r-project.org/) in the NestedCohort package of Mark and Katki (12) and the survey package of Lumley (13). Both packages accommodate stratified random sampling of cases and controls on the basis, for example, of rare covariate patterns (14).

In this paper, our goal is to demonstrate important strengths as well as limitations of these newly available tools. We compare results obtained by using adjusted weights with those obtained with standard weights in a reanalysis of data from a published case-cohort study and in analyses of simulated case-cohort samples.

The Atherosclerosis Risk in Communities (ARIC) study (15) often uses case-cohort methodology. The cohort consists of 15,972 participants under active follow-up since 1987–1989 for atherosclerosis and its clinical sequelae. Using samples of stored biologic tissue, ARIC investigators studied candidate genotypes (16–18) and biomarkers of inflammation (19, 20) as possible risk factors for coronary heart disease and related endpoints. Ballantyne et al. (20) identified 12,819 ARIC participants who were free from coronary heart disease and had plasma samples taken at their second follow-up visit (1990–1992). Stored plasma for participants who developed incident coronary heart disease prior to 1999, or who were selected in a cohort random sample, was assayed for levels of lipoprotein-associated phospholipase A₂ (Lp-PLA₂) and C-reactive protein. Cohort sampling was stratified into 8 strata based on age, sex, and ethnicity. After exclusions because of missing data, 608 cases and 740 noncases remained for estimation of hazard ratios for coronary heart disease in tertiles of Lp-PLA₂ and C-reactive protein using a weighted Cox regression analysis appropriate for stratified case-cohort studies (7, 14).

As do many epidemiologists, ARIC investigators (16–20) ignored most of their data. Apart from known sampling fractions, their analyses involved only those cases or controls sampled as part of the substudy. Since cases were deliberately overrepresented, the substudy included many of the most informative subjects. Nonetheless, important variables in the regression models were ignored for nearly 90% of the cohort. The Ballantyne et al. study (20) ignored data on smoking history, low density lipoprotein and high density lipoprotein cholesterol, and diabetes, all of which were used for secondary adjustment of the hazard ratios for Lp-PLA₂ and C-reactive protein. Other data items were ignored that, although not used in the regression, were correlated with biomarkers measured for sampled participants and hence provided potentially valuable information about them. Through reanalysis of the Ballantyne et al. data, we demonstrate in the sequel how main cohort data may be incorporated into the analysis to improve precision of regression coefficients.

Survey statisticians recognize the case-cohort study as a 2-phase, stratified sampling design. The first-phase sample is the cohort itself, considered a sample from some target population. The second-phase sample, stratified by using information from phase 1, consists of cases and controls in the subcohort. We first describe 2-phase designs and summarize some statistical properties of weighted estimates. Next, we report reanalyses of the Ballantyne et al. (20) case-cohort data. Finally, we report results of analyses of simulated case-cohort data from the National Wilms Tumor Study (NWTS) (21, 22). The NWTS data, R code for the survey package, and related tutorials are available online (http://faculty.washington.edu/norm/IEA08.html).

TWO-PHASE STUDIES AND WEIGHTED ANALYSES

Two-phase stratified sampling

Suppose the N subjects in the cohort (phase 1 sample) are classified into K strata on the basis of information known for everyone and that the numbers N_k of subjects in each stratum are determined (N = N₁ + N₂ + ··· + N_K). For the substudy (phase 2 sample), n_k ≤ N_k subjects are sampled at random without replacement (no subject is sampled more than once) from the kth stratum, with the sampling from each stratum conducted independently. The total number of subjects sampled at phase 2, for whom biologic material is analyzed or additional information otherwise obtained, is $n=n_1+n_2+···+n_K$. Associated with each subject is a sampling weight N_k/n_k depending on only the subject's stratum. In a weighted analysis, the contribution from a sampled subject is up-weighted so the total contribution from each stratum is representative of the total contribution assuming all cohort members from that stratum had been analyzed.

Table 1 illustrates the design using the ARIC data. The slight differences in totals from those reported previously (20) arise because some participants, including 9 in the original substudy, had not given proper consent. A few more, including 3 in the original substudy, lacked information on body mass index. This factor was the most important predictor of C-reactive protein and hence a key auxiliary variable. After exclusions for missing values of baseline variables for main cohort subjects, and for missing biomarker variables at phase 2, N = 12,345 remained in the main cohort and n = 1,336 remained at phase 2, including 604 coronary heart disease cases. Sampling of the original subcohort had been stratified on sex, race, and age. The cases were treated as an additional, ninth stratum (K = 9) in our analyses. Table 1 shows the distribution of cohort and sampled subjects over the strata, with the standard sampling weights in the last row. Since they are based on observed sampling fractions, the weights are slightly different and more accurate than those used previously (20). The weight of 1.2 for cases illustrates the importance of being able to handle sampling of both cases and controls in case-cohort analyses (23).

Table 1.

Stratified Sampling Design for the Atherosclerosis Risk in Communities Study

	Non-CHD Cases (Controls)								CHD Cases	Totals, no.
	Black				White
	Female		Male		Female		Male
	Age <55 Years	Age ≥55 Years	Age <55 Years	Age ≥55 Years	Age <55 Years	Age ≥55 Years	Age <55 Years	Age ≥55 Years
Stratum (k)	1	2	3	4	5	6	7	8	9
Cohort Nk	1,133	719	598	393	2,782	2,213	1,959	1,818	730	12,345
Sample nk	59	54	42	71	88	154	117	147	604	1,336
Weights Nk/nk	19.2	13.3	14.2	5.5	31.6	14.4	16.7	12.4	1.2

Abbreviation: CHD, coronary heart disease.

Weighted estimates and their sampling properties

Let β denote the regression coefficients (log hazard ratios) in the Cox model. If complete data on covariates and event times were available for all N cohort subjects, we would fit the model to the cohort data to obtain an estimate ${\tilde{\mathrm{\beta }}}_N$. Ordinarily, ${\tilde{\mathrm{\beta }}}_N$ cannot be observed. A weighted analysis of the n subjects sampled at phase 2, however, yields an observable estimate 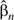whose sampling variance is the sum of 2 components: 1) the variance of the unobserved ${\tilde{\mathrm{\beta }}}_N$, which represents the usual uncertainty in generalizing results for the N cohort subjects to the target population; and 2) the variance of 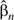− 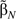, which represents the additional uncertainty from not having complete data for the entire cohort. We refer to these as the phase 1 and phase 2 components of variance, respectively.

Improving precision

Survey statisticians adjust the weights to reduce the phase 2 variance when auxiliary variables V, correlated with variables in the regression model, are available for all subjects. The simplest method, poststratification, replaces the K sampling strata with a finer stratification incorporating the auxiliary information. In an ARIC case-cohort study of glutathione-S-transferase genotypes as a susceptibility factor in smoking-related coronary heart disease, smoking data were ignored for all but 10% of subjects even though smoking was a risk factor of primary interest (16). Poststratification on smoking history would have improved the analysis. Poststratified analyses of simulated case-control data have been reported for the NWTS cohort (24).

Calibration (25, 26) adjusts the weights to be as close as possible to the sampling weights subject to the constraint that the cohort total of V is equal to its weighted sum among sampled subjects. Estimation (11) uses as weights the reciprocals of inclusion probabilities estimated from a logistic regression model that predicts which cohort subjects are sampled at phase 2. Here, the requirement is that the observed total of V in the sample equals the predicted total: the sum over the cohort of V multiplied by the estimated sampling probability. It is important to include the sampling strata as a factor (“dummy” variables) in the logistic model to account for the bias in the phase 2 sample. If dummy variables corresponding to the original or finer (poststratified) strata are the only auxiliary variables, calibrated and estimated weights are identical, being equal to inverse sampling fractions for each stratum. Adjusted weights increase precision through their dependence on the auxiliary information available for all cohort subjects.

As described in a companion paper for statisticians (27), Cox regression coefficients obtained by using calibrated and estimated weights have very similar theoretical properties. Both are consistent and asymptotically normal. Depending on the choice of auxiliary variables, both can attain minimum variance in the class of “augmented” inverse probability weighted estimates (11, 12). To approximate the optimum choice of auxiliary variables, we adopted the “plug-in” approach of Kulich and Lin (28). It requires separate models for prediction of the values of each partially missing variable (ascertained for phase 2 subjects only) and is likely of greatest use when there are only 1 or 2 such variables. The method has 4 steps:

1. Develop weighted regression models from the phase 2 data for prediction of the partially missing variables from information available for all subjects. (For the Ballantyne et al. study (20), this means prediction of Lp-PLA₂ and C-reactive protein.)

2. Use the prediction equations to impute values of the partially missing variables for all cohort subjects.

3. Using imputed values for the partially missing variables and known values for other variables, fit the Cox model to the whole cohort and determine the imputed delta-beta (estimated influence function contribution obtained as a residual in the R coxph program) for each cohort subject.

4. Use the imputed delta-betas as auxiliary variables in calibration or estimation of the weights, and estimate β by weighted Cox regression analysis of the phase 2 data.

As demonstrated below, adjustment by calibration or estimation has the potential to reduce the phase 2 variances for some regression coefficients to negligible levels. The variances for others are left virtually unchanged.

RESULTS

Reanalysis of ARIC data

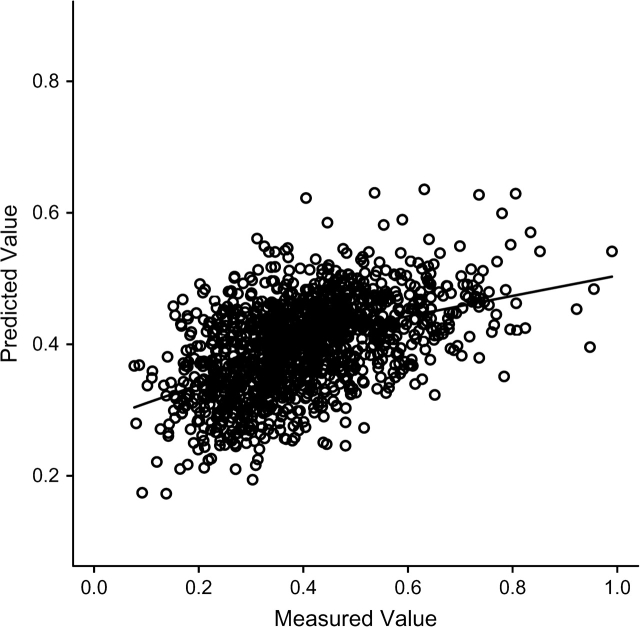
Similar procedures were followed and similar results obtained for the separate analyses of C-reactive protein and Lp-PLA₂. Following the 4 steps just described, we first predicted Lp-PLA₂ by using linear regression on white race, male sex, low density lipoprotein cholesterol, high density lipoprotein cholesterol, systolic and diastolic blood pressures, and the sex × race interaction (coefficients not shown). The prediction was not very successful, with $R^2=0.28$ (Figure 1). Nonetheless, it was used to impute Lp-PLA₂ (step 2) and thus to calculate auxiliary variables (step 3) used for adjustment of weights.

Figure 1.

Scatter plot and nonparametric regression curve showing predicted values of lipoprotein-phospholipase A₂ (μg/L) plotted against measured values. Predicted values are based on weighted linear regression from phase 2 data (the Atherosclerosis Risk in Communities case-cohort study).

Results are shown in Table 2. Variances for each regression coefficient are obtained by summing the squares of the phase 1 and phase 2 standard errors. Hazard ratios and 95% confidence intervals for the middle and upper tertiles of Lp-PLA₂ relative to the lowest were 1.05 (95% confidence interval: 0.76, 1.46) and 1.18 (95% confidence interval: 0.85, 1.64), respectively, when estimated by using standard weights. The corresponding estimates reported by ARIC—in model 2, Table 4 of Ballantyne et al. (20)—were 1.02 (95% confidence interval: 0.73, 1.43) and 1.16 (95% confidence interval: 0.85, 1.65). In spite of differences in data sets and the fact that ARIC used slightly different sampling weights and a slightly different method of variance estimation (7), the results of the reanalysis were close to the original, particularly with regard to precision as measured by widths of the confidence intervals.

Table 2.

Results of Reanalysis of Data From a Case-Cohort Study of Lp-PLA₂: the Atherosclerosis Risk in Communities Study^a

Model Term	Standard Weights			Calibrated Weights			Estimated Weights
	Coef	SE1	SE2	Coef	SE1	SE2	Coef	SE1	SE2
Age in years/10	0.420	0.073	0.075	0.393	0.073	0.012	0.432	0.073	0.015
Male sex	0.762	0.088	0.091	0.791	0.088	0.019	0.742	0.088	0.022
White race	0.037	0.098	0.090	0.159	0.099	0.016	0.101	0.100	0.029
Former smoker	−0.421	0.093	0.126	−0.464	0.092	0.017	−0.459	0.092	0.020
Never smoked	−0.552	0.099	0.129	−0.557	0.099	0.016	−0.622	0.099	0.020
SBP/100	1.554	0.207	0.267	1.539	0.208	0.046	1.580	0.207	0.048
LDL-C/100	0.777	0.106	0.151	0.786	0.106	0.045	0.748	0.108	0.047
HDL-C/100	−2.539	0.329	0.392	−2.361	0.329	0.052	−2.736	0.334	0.060
Diabetes	0.572	0.092	0.127	0.738	0.090	0.019	0.531	0.093	0.026
Lp-PLA2 0.310–	0.052	0.110	0.126	0.054	0.111	0.127	0.050	0.111	0.127
Lp-PLA2 0.422–	0.163	0.108	0.129	0.182	0.108	0.130	0.154	0.108	0.130

Abbreviations: Coef, regression coefficient; HDL-C, high density lipoprotein cholesterol (mg/L); LDL-C, low density lipoprotein cholesterol (mg/L); Lp-PLA₂ 0.310– and 0.422–, approximate middle and upper tertiles, respectively, of lipoprotein-associated phospholipase A₂ (μg/L); SBP, systolic blood pressure (mm Hg); SE₁, phase 1 standard error; SE₂, phase 2 standard error.

^aN = 12,345; n = 1,336 including 604 coronary heart disease cases.

Table 4.

Stratified Sampling Design for the National Wilms Tumor Study

	Totals, no.	Favorable Histology				Unfavorable Histology
		Stage I–II		Stage III–IV		Stage I–II		Stage III–IV
		Age <1 Yeara	Age ≥1 Years	Age <1 Year	Age ≥1 Years	Age <1 Year	Age ≥1 Years	Age <1 Year	Age ≥1 Years
	Main Study Cohort or Phase 1 Sample (N  = 3,915)
Cases	669	57	232	10	208	15	41	29	77
Controls	3,246	452	1,620	40	914	12	107	2	99
% Relapsed	17.1	11.2	12.5	20.0	18.5	55.5	27.7	93.5	43.8
	Phase 2 Sample (n  = 1,329)
Cases	669	57	232	10	208	15	41	29	77
Controls	660	120	160	40	120	12	107	2	99

^aAge in years at diagnosis of Wilms tumor.

When standard weights were used, the contribution of phase 2 sampling to the overall variance exceeded the phase 1 contribution for all but 1 coefficient. For the adjustment covariates known for all, both calibration and estimation reduced the estimated phase 2 standard error dramatically, calibration consistently more so. The overall standard errors were very similar to the estimates (phase 1 standard error) if complete data had been available for all subjects. For the tertiles of Lp-PLA₂, however, there was virtually no change; in fact, both adjustment methods resulted in very slight increases in the phase 2 standard error. The phase 1 standard errors were nearly identical for the 3 weighting schemes, reflecting the fact that they all represent variability in the unobserved ${\tilde{\mathrm{\beta }}}_N$.

Results for C-reactive protein (not shown) were similar, with R² = 0.21. The increase in precision by adjustment of the weights was again confined to coefficients of baseline covariates.

To investigate possible improvement in precision when studying the interaction between a partially missing covariate and 1 available for everyone, we searched for baseline covariates that exhibited an interaction with Lp-PLA₂. Table 3 reports findings for a model having a grouped linear × linear interaction with systolic blood pressure. When standard weights were used, the hazard ratios estimated separately for the middle and upper tertiles of Lp-PLA₂ relative to the lowest, for subjects with average systolic blood pressure, were exp(0.137) = 1.15 (95% confidence interval: 0.81, 1.62) and exp(0.303) = 1.35 (95% confidence interval: 0.95, 1.92), respectively. This finding was consistent with a grouped linear model having a hazard ratio of approximately 1.156 per tertile. The interaction coefficient suggested that the per-tertile hazard ratio decreased by a factor of exp(−0.0672) = 0.935 for each 10-mm Hg increase in systolic blood pressure. Although of clinically important magnitude, this decrease was not statistically significant (Z = −1.89, P = 0.062).

Table 3.

Results of Reanalysis of Data From a Case-Cohort Study of Lp-PLA₂: Interaction With SBP

Model Terma	Standard Weights			Calibrated Weights			Estimated Weights
	Coef	SE1	SE2	Coef	SE1	SE2	Coef	SE1	SE2
Lp-PLA2 0.310–	0.137	0.118	0.130	0.139	0.119	0.131	0.138	0.118	0.131
Lp-PLA2 0.422–	0.303	0.121	0.132	0.306	0.122	0.131	0.299	0.121	0.131
Lp-PLA2 × SBP	−0.672	0.204	0.302	−0.681	0.205	0.274	−0.692	0.205	0.274

Abbreviations: Coef, regression coefficient; Lp-PLA₂ 0.310– and 0.422–, approximate middle and upper tertiles, respectively, of lipoprotein-associated phospholipase A₂ (μg/L); SBP, systolic blood pressure (mm Hg); SE₁, phase 1 standard error; SE₂, phase 2 standard error.

^aThe covariates age in years/10, male sex, white race, former smoker, never smoked, SBP/100, low density lipoprotein cholesterol/100, high density lipoprotein cholesterol/100, and diabetes were also included in the model, but results for only Lp-PLA₂ and its interaction with SBP are shown. The interaction term used “grouped linear” values of 1, 2, 3 for the 3 tertiles of Lp-PLA₂ and centered SBP (in units of 100 mm Hg) at its mean value.

Calibration and estimation of the weights reduced the phase 2 standard errors of the adjustment covariates (not shown) and left effectively unchanged those for the main effects of Lp-PLA₂ (Table 3), just as observed for the no-interaction model. There was, however, a reduction of about 10% in the phase 2 standard error of the interaction coefficient. This reduction led to changes in the associated test statistics, Z = −2.10, P = 0.036 for calibration and Z = −2.02, P = 0.043 for estimation, both now significant. Because systolic blood pressure was selected from among several covariates examined for interaction effects, it would be imprudent to draw substantive conclusions from this reanalysis. It serves primarily to illustrate the potential for improvement in precision of interaction coefficients, even when there is none for the corresponding main effects.

Simulated case-cohort data

The NWTS cohort consisted of 3,915 patients with Wilms tumor diagnosed during 1980–1994 and followed until the earliest of disease progression or death for “event-free survival.” Baseline covariates available for all patients from the registering institutions included “favorable” vs. “unfavorable” histology, stage of disease (I–IV), age at diagnosis, and tumor diameter. Histology evaluated by the central reference laboratory was also available for everyone, which allowed repeated drawing of stratified phase 2 samples in which central histology was treated as known for sampled subjects only. Since the normally unobservable ${\tilde{\mathrm{\beta }}}_N$ was available, the phase 2 variance could be determined empirically. Institutional histology was strongly related to central histology: of 439 unfavorable history tumors (central laboratory), 324 were classified unfavorable history by the patient's institution, for a sensitivity of 74%; 3,418 of 3,476 favorable histology tumors were correctly classified, for a specificity of 98%.

Sixteen strata were formed on the basis of event-free survival, stage, institutional histology, and age (2 groups each). All subjects were sampled from the 13 smallest strata: all cases, all institutional unfavorable history, and all patients less than 1 year of age with stage III–IV disease (Table 4). Since the 13 strata all had a sampling weight of 1, they could be collapsed into a single analysis stratum with no effect on the results. Random samples of sizes 120, 160, and 120 were selected from the 3 largest strata to yield a phase 2 sample consisting of all 669 cases and 660 sampled controls. Kulich and Lin (28) used nearly the same sampling scheme with the NWTS data to evaluate their “combined, doubly weighted” estimate for the same problem. Their sample sizes varied, with expectations of 120, 160, and 120 for the 3 sampled strata, which would be expected to decrease precision very slightly in comparison with fixed sample sizes.

Ten thousand stratified phase 2 samples were drawn in this fashion. For each, we estimated Cox regression coefficients by using standard weights, calibrated weights, and estimated weights following the 4-step procedure. The Cox and imputation models, which used different variable codings to achieve the best fit for their distinct purposes, were again those of Kulich and Lin (28). The Cox model included central histology, age as a piecewise linear variable with change point at 1 year, stage (III–IV vs. I–II), diameter, and the interactions histology × age and stage × diameter. Central histology (unfavorable history) was imputed by using institutional histology, stage (IV vs. I–III), age (>10 years vs. ≤10 years), tumor diameter (linear), and the interaction histology × stage in the logistic regression equation. The R² value between true and predicted unfavorable history was 0.59. Imputed delta-betas, augmented by addition of 1 for numerical reasons, served as auxiliary variables for calibration. For estimation, delta-betas multiplied by sampling weights served as auxiliaries.

Results are shown in Table 5. The first 2 columns display the coefficients ${\tilde{\mathrm{\beta }}}_N$ estimated by using all 3,915 patients and the corresponding robust standard errors (29). Averages of 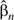over the 10,000 simulations (not shown) were close to ${\tilde{\mathrm{\beta }}}_N$, regardless of adjustment method. The standard errors calculated by the R survey package incorporate separate estimates of the robust phase 1 and “design-based” phase 2 variance components (30). The mean squared error of estimation of ${\ti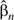lde{\mathrm{\beta }}}_N$ by is the observed phase 2 variance component.

Table 5.

Results From 10,000 Simulated Phase 2 Samples From the National Wilms Tumor Study

Model Term	Phase 1 Estimates		Summary Statistics for Phase 2 Estimates
			Standard Weights		Calibrated Weights		Estimated Weights
	${\tilde{\beta }}_N$	SE1	ASE	SMSE	ASE	SMSE	ASE	SMSE
Unfavorable history	4.042	0.503	0.537	0.192	0.519	0.136	0.518	0.139
Age0	−0.661	0.321	0.360	0.162	0.325	0.037	0.324	0.061
Age1	0.104	0.015	0.026	0.021	0.017	0.006	0.017	0.012
Stage	1.346	0.259	0.346	0.237	0.270	0.072	0.271	0.103
Diameter	0.069	0.015	0.021	0.015	0.015	0.005	0.015	0.007
Stage × diameter	−0.076	0.020	0.029	0.021	0.021	0.006	0.021	0.009
Unfavorable histology × age0	−2.635	0.552	0.612	0.285	0.592	0.243	0.590	0.249
Unfavorable histology × age1	−0.058	0.033	0.051	0.047	0.049	0.047	0.048	0.049

Abbreviations: Age₀ and Age₁, piecewise linear terms for age at diagnosis (years) before and after 1 year, respectively; ASE, average (total) standard error; diameter, diameter (cm) of the excised tumor; SE₁, robust phase 1 standard error; SMSE, square root of mean squared phase 2 error; stage: binary indicator of stage III–IV disease.

Results agreed well with the sampling properties outlined above. Consider, for example, the standard errors for unfavorable history shown in the first row of Table 5. The total variance estimated by using standard weights, 0.537² = 0.288, was approximately equal to the sum of the phase 1 and phase 2 components, 0.503² + 0.192² = 0.290. Since this relation holds only in expectation and in large samples, of course, not all table entries exhibit it so closely.

Calibration and estimation both improved precision. Gains were greatest for covariates known for all: age, stage, and tumor diameter. Ratios of standard to adjusted square root of the mean squared error for the 5 model terms involving these covariates alone ranged from 3.0 to 4.4 (median = 3.5) for calibration and from 1.7 to 2.7 (median = 2.3) for estimation. In several instances, the phase 2 variance was negligible in comparison with phase 1. Substantial gains were also achieved for the unfavorable history main effect, whose phase 2 standard error was reduced by 29%, and more modest gains for the interaction effect of unfavorable history with the initial slope of age. The phase 2 standard error for the interaction of unfavorable history with age beyond 1 year was effectively unchanged, but the lack of change matters little in view of the small, statistically insignificant coefficient. Overall performance using calibrated and estimated weights was quite comparable to that of the “combined, doubly weighted” estimate shown in Table 3 of Kulich and Lin (28).

DISCUSSION AND CONCLUSIONS

Substantial gains were observed from calibration and estimation of the sampling weights in the simulated NWTS case-cohort studies. While most pronounced for baseline covariates known for all, important gains were also observed for the main effect and an interaction involving unfavorable history. These gains were possible because there was a strong surrogate, institutional histology, for the partially missing variable. By reducing the number of slides sent to the central reference laboratory from 3,915 to 1,329, and thereby lowering costs, the investigators could in principle have estimated the hazard ratios of interest with little loss of precision. (Central histology was essential, of course, for many other purposes.)

Comparable gains were observed for only baseline covariates upon reanalysis of the ARIC case-cohort data, most likely because of lack of good predictors for Lp-PLA₂ and C-reactive protein. Our limited experience in other contexts indicates that R² for prediction of the partially missing variable should be at least 0.5 to substantially improve precision of the corresponding regression coefficient. Modest, but important gains were evident, however, for the linear interaction of Lp-PLA₂ with systolic blood pressure. This finding suggests that the methodology might usefully be applied to the ARIC case-cohort study of glutathione-S-transferase and smoking (16) and to other studies of genotype-environment interaction in which the environmental factor is known for everyone. Even if there is no obvious improvement in precision of estimation of principal risk factors, the knowledge that they have made more complete use of the available information should give epidemiologists greater confidence in their results.

Our simulations demonstrated that efficiency gains from weighted Cox regression with calibrated or estimated weights were similar to those found with the more complicated estimate of Kulich and Lin (28). It too was designed to achieve near optimality in the class of augmented inverse probability weighted estimates. Theoretically, the best choice for auxiliary variables would be conditional expectations, given the phase 1 data, of influence function contributions for the Cox model (11). We approximated these unknown quantities by using imputation, as described in the 4-step procedure. Further numerical work involving alternative choices for auxiliary variables, and further practical comparisons of calibration and estimation, are warranted.

The goal of our case-cohort analyses was to approximate as closely as possible results that we would have obtained had we been able to fit the standard (unweighted) Cox model to complete data for the entire cohort. Such results are usually expressed as point and interval estimates of model parameters under the assumption that the cohort is a simple random sample from a target population described by the model. In fact, the ARIC cohort was constructed by survey sampling of approximately 4,000 adults 45–64 years of age from each of 4 US communities. The target population is best viewed as a hypothetical population comprising a large mix of subjects “like those” in the 4 communities (31). If results differed systematically between communities, the appeal of generalizing to this target would be lessened.

We considered Cox regression modeling of stratified case-cohort data. The principle of increasing precision through adjustment of sampling weights applies much more generally. The R survey package accommodates a variety of analyses of data from 2-phase stratified samples including estimation and log-linear modeling of population frequencies in contingency tables and estimation of regression coefficients in generalized linear models. Adjustment of sampling weights using auxiliary variables enhances precision in these analyses. The NestedCohort package is restricted to Cox regression and adjustment by estimation. However, it provides estimates of the baseline (cumulative) hazard function and thus of failure probabilities, which are important in many applications (12).

Stratified case-cohort studies involve data missing by design. Sometimes, as for biomarkers in the ARIC study, phase 2 data are also missing by chance (12). The methods proposed here assume that, within each stratum, the phase 2 subjects with complete data still constitute a random sample from the cohort. This assumption may be relaxed by adding variables to the logistic model used to predict which subjects are sampled for phase 2 and have complete data. Of course, one can never be certain that the probability of having complete data does not further depend on the missing values themselves, so the possibility of bias remains when data are missing by chance.

Stratified case-cohort studies based on large cohorts are increasingly common designs in epidemiology. Analyses to date have largely ignored relevant information available for the parent cohort. Improvements in statistical methodology described here, and their implementation in the freely available R software system, can help prevent this waste of valuable information. We have demonstrated that adjustment of sampling weights via calibration or estimation, using information available for the entire cohort, can sometimes dramatically improve the precision of estimated hazard ratios. We have also provided links to related R code, data sets, and tutorials and we encourage readers to utilize these tools.

Glossary

Abbreviations

ARIC

Atherosclerosis Risk in Communities

Lp-PLA₂

lipoprotein-associated phospholipase A₂

NWTS

National Wilms Tumor Study